EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 592 (August 2016) A&A, 592 (2016) A31 Full HTML
Free Access
Issue
A&A
Volume 592, August 2016
Article Number A31
Number of page(s) 22
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201527974
Published online 12 July 2016

© ESO, 2016

1. Introduction

As first realised by Batrla et al. (1987), methanol masers come in two varieties, termed Class I and II by Menten (1991a,b). Class II methanol masers are closely associated with high-mass young stellar objects (YSOs) and arise from the hot molecular layers heated by the embedded YSOs before and after the formation of an ultracompact Hii region. When they occur after the formation of an ultracompact Hii region, they frequently coexist with hydroxyl (OH) masers (Menten et al. 1992) and are, like the OH masers (Cesaroni & Walmsley 1991), most likely pumped by far-infrared radiation in dense (n ~ 107 cm-3) warm (T ~ 150 K) gas (Sobolev & Deguchi 1994a,b; Sobolev et al. 1997). In contrast, Class I masers are collisionally pumped and their occurrence can be explained from the basic properties of the CH3OH molecule (Lees 1973).

The presence of a Class II methanol maser associated with a star forming core provides unambiguous and sufficient proof of the presence of a high-mass protostellar or young stellar object (Urquhart et al. 2015), and more than a thousand of these sources have been found in Galaxy-wide surveys (Green et al. 2009). In contrast, until recently relatively little attention was paid to Class I methanol masers. However, recent observational results have changed this situation. Cyganowski et al. (2009) show that these masers are associated with shocked material in protostellar outflows and thus trace very early stages of massive star formation. It is also worth noting that Class I masers have also been detected from a few outflows associated with low-mass protostars (Kalenskii et al. 2010a). Moreover, Sjouwerman et al. (2010b) and Pihlström et al. (2014) report the detection of Class I methanol masers towards supernova remnants (see Frail 2011, for an overview).

Additionally, Sarma & Momjian (2009, 2011) report the discovery of circular polarisation in the 36 and 44 GHz Class I maser lines, which they interpret as a result of the Zeeman effect. These results suggest that Class I masers could be exploited to measure magnetic fields in interstellar shocks and could deliver inputs for magneto-hydrodynamic modelling of shock models. From the point of view of modelling, recent progress in the calculation of collisional rate coefficients has resulted in numbers that now allow meaningful modelling of methanol excitation over a wide range of interstellar conditions (Rabli & Flower 2010).

The aim of our study is to investigate the properties of bright Class I methanol masers focussing mainly on masers with brightness temperatures higher than the critical value corresponding to the saturated intensity Js beyond which maser amplification becomes linear rather than exponential (see Elitzur 1992; Hollenbach et al. 2013). These masers are usually associated with regions of massive star formation, while lower luminosity Class I masers are reported in supernovae remnants (e.g., Pihlström et al. 2014). We assume the masers to be pumped by collisions with the para form of H2 and compute the pump and decay rates, as well as the pump efficiency for the most commonly observed Class I methanol maser transitions. An implicit assumption is that the escape probabilities of the relevant transitions populating the upper and lower maser levels are highly anisotropic allowing coherence along the line of sight, while a large velocity gradient in the plane of the sky allows relatively high escape probabilities in other directions. This type of velocity field is expected to be produced by a shock propagating perpendicular to the line of sight; moreover, a shock of this kind is expected to produce a maser volume of high aspect ratio oriented along the line of sight. The shock is also expected to cause a rise in the methanol abundance as is suggested by some of the observational data discussed in Sect. 2 of this article.

Table 1

Known interstellar Class I methanol maser transitions.

In this context, we have concentrated on geometry independent maser characteristics and their dependence on physical properties such as density and temperature. We have thus computed the maser output per cubic centimetre and have estimated the densities and methanol abundances at which maser action is quenched. We do not, on the other hand, attempt to compute maser beaming angles and brightness temperatures, although we do focus on size scales (roughly 10–300 AU) corresponding to the observed maser diameters. Our hope is that our results in combination with future interferometric work will allow an increased understanding of the structure of interstellar shocks and the dissipation of mechanical energy in regions of star formation. In a follow-up study, we plan to implement geometry effects in our model to compute brightness temperatures and beaming angles and properly model observations of Class I masers in massive star forming regions.

In Sect. 2 we give a review of the observational properties of Class I methanol masers, followed in Sect. 3 by a description of previous studies on the pumping mechanism for Class I masers. In Sect. 4 we present our model for the pumping of Class I methanol masers, and compute the photon production rates of high-gain masers as a function of the physical parameters of the gas. In Sect. 5, we compare our model results with the observed properties of Class I masers. In Sect. 6 we conclude with possible observational and theoretical perspectives to improve our knowledge of Class I masers.

2. Phenomenology of Class I methanol masers

After the first example of a Class I methanol maser was discovered, the 25 GHz Jk = 2−Jk = 1E transitions in Orion-KL (Barrett et al. 1971), it took 15 years before these lines were found in other regions (Menten et al. 1986), and before the 44 GHz 70 → 61-A+ and the 36 GHz 4-1 → 30-E methanol masers (Morimoto et al. 1985) were discovered. This paucity of detections of the 25 GHz lines was partially a result of the masers’ relatively modest luminosities and because they are frequently found offset from traditional tracers of star formation such as strong infrared sources and ultracompact Hii regions (Menten et al. 1986). As discussed above, an association between Class I methanol masers and protostellar outflows was established later on.

Table 1 reports all known Class I methanol maser transitions to date. For reference, examples of spectra of Class I masers are given in Fig. 1 towards DR21-W and NGC 2264 where the 4-1 → 30E line also shows broader thermal emission. The 44 GHz 70 → 61-A+ and 95 GHz 80 → 71-A+ lines are generally the most widespread and the strongest Class I transitions observed (e.g., Haschick et al. 1990; Val’tts et al. 2000), and therefore they have traditionally been the target of searches for Class I methanol masers in astronomical sources (e.g., Bachiller et al. 1990; Slysh et al. 1994; Kurtz et al. 2004; Ellingsen 2005; Cyganowski et al. 2009; Chen et al. 2011). The next most widespread Class I masers are the 36 GHz 4-1→30-E and 84 GHz 5-1 → 40-E transitions (e.g., Haschick & Baan 1989; Kalenskii et al. 2001; Voronkov et al. 2014). Recent observations at high angular resolution (Voronkov et al. 2007; Britton & Voronkov 2012) show that even the 25 GHz masers are more common than previously thought. The new capabilities of the upgraded VLA and ATCA interferometers allow the simultaneous observations of several transitions in the J2 → J1E series thus allowing better investigation of these masers. The masers at 9.9 GHz, 23.4 GHz, and 104 GHz are rare and they have been detected in only a handful of objects (see Voronkov et al. 2012). Interestingly, many of the remaining Class I masers fall within ALMA bands.

2.1. Occurrence of Class I methanol masers

In contrast to Class II masers, which typically coincide with hot molecular cores, ultracompact Hii regions, OH masers, and near-IR sources (e.g., Menten et al. 1988a,b), Class I methanol masers are frequently found in the general vicinity of intermediate- and high-mass star formation, but often significantly offset (up to a parsec) from prominent centres of activity, such as infrared sources or compact radio sources (Menten et al. 1986). Based on large samples of sources, Kurtz et al. (2004) and Voronkov et al. (2014) concluded that the vast majority of Class I masers at 44 and 36 GHz are within 1 pc of a Class II methanol maser at 6.7 GHz, taken as indicative of the position of the YSO. We note, incidentally, that the only two cases reported by Kurtz et al. (2004) where Class I masers coincide with Class II features are observed with coarse angular resolution (~0.1−0.2 pc).

Plambeck & Menten (1990) suggested that Class I methanol masers trace the swept-up interaction region of outflows with ambient material. This scenario is supported by an increasing number of observations that reveal a coincidence between Class I masers and other molecular shock tracers (e.g., Johnston et al. 1992; Kurtz et al. 2004; Voronkov et al. 2006, 2010a). Cyganowski et al. (2009) surveyed a sample of massive young stellar objects with extended 4.5 μm emission attributed to shocked H2 in outflows and found a detection rate of 44 GHz Class I methanol masers of ~89%. In addition, Class I masers also seem to be associated with molecular outflows from low-mass young stellar objects (Kalenskii et al. 2010a,b). It is important to note that Class I masers may be a unique tool for investigating outflow activity where other standard shock tracers are too weak to be detected. Figure 2, for example, shows a zoom in DR21(OH) where several Class I maser lines clearly trace bow shocks in a bipolar outflow (Araya et al. 2009) not detected in Spitzer H2 observations likely owing to extinction (Davis et al. 2007).

A location in the swept-up interaction region of outflows with ambient material may be a natural explanation for some of the observed properties of Class I masers. In C-shocks we expect that the high relative velocities of charged grains and neutral gas cause methanol ice to be sputtered from the grain surface and released into the gas leading to the high methanol abundance and column density required for observable maser emission. Usually, no high-velocity Class I maser emission is observed and the observed features are clustered within a few km s-1 around the ambient velocity. These features can be explained by the fact that paths moving perpendicular to the line of sight have the longest velocity-coherent gain length and have, naturally, velocities close to νLSR. However, it should be noted that Voronkov et al. (2014) recently reported a small number of high-velocity Class I maser components, which are largely blue-shifted and detected more easily at 36 GHz.

thumbnail Fig. 1

For both NGC 2264 (left) and DR21-W (right), lowest spectrum: absorption in the CH3OH 20 → 3-1-E line; other spectra: various maser transitions taken with differing velocity resolutions and a number of telescopes. Adopted from Menten (1991a). All spectra where taken between 1988 and 1990. The spectra of the 4-1 → 30-E and 70 → 1-A+ lines are from Haschick et al. (1990) and those of the 20 → 3-1-E lines were taken with the Green Bank 140-foot telescope. The remaining spectra were taken with the IRAM 30 m telescope.

Class I masers, however, do not exclusively trace molecular outflows. They have also been detected in other astrophysical environments in the presence of shocked gas, for example at the interaction of supernova remnants with the molecular cloud (e.g., Szczepanski et al. 1989; Haschick et al. 1990; Pihlström et al. 2011), in cloud-cloud collisions (e.g., Sobolev 1992), and in layers where expanding Hii regions interact with the ambient molecular environment (Voronkov et al. 2010b). Widespread Class I methanol masers have been observed towards the Galactic Centre (Yusef-Zadeh et al. 2013). In this case, the authors have proposed that induced photodesorption by cosmic rays is responsible for the emission instead of large-scale shocks. Recently, Ellingsen et al. (2014) has reported the first tentative detection of Class I maser emission at 36 GHz in the nearby galaxy NGC 253. This detection would be intriguing since so far only the two Class II methanol maser lines that are by far the most prominent in our Galaxy (the 6.7 GHz and 12.2 GHz lines, e.g., Menten 1991b) have been detected in a few nearby galaxies (Green et al. 2008; Sjouwerman et al. 2010a; Ellingsen et al. 2010).

2.2. Class I methanol maser spot sizes

Estimates of spot sizes for Class I masers have in general been based upon VLA measurements and VLBI non-detections (e.g., Barrett et al. 1976; Lonsdale et al. 1998). For example, Johnston et al. (1997) used VLA observations of the 62−61-E line at 25.018 GHz to conclude that spot sizes in Orion-KL were in the range 22−56 AU. Slysh & Kalenskii (2009) have also reported that the 44 GHz maser has average spot sizes of 50 AU in OMC-2 and in NGC 2264, and have concluded that Class I maser spots are much larger than Class II maser spots, which have typical sizes of a few AU (Moscadelli et al. 1999; Sanna et al. 2010), implying brightness temperatures of the order of 1012K.

thumbnail Fig. 2

Spitzer IRAC image of the DR21(OH) region (3.6 μm blue, 4.5 μm green, 8.0 μm red). The images were retrieved from the Spitzer archive. The red crosses mark the positions of 36 GHz masers from Fish et al. (2011). Cyan contours represent the integrated intensity of the thermal 42 → 31-E methanol line (Zapata et al. 2012) which traces the E-W outflow seen in the Class I masers.

Recently, Matsumoto et al. (2014) detected the 44 GHz maser in the massive star forming region IRAS 18151-1208 for the first time with a VLBI experiment. They found that most of the maser emission is not due to a compact point source, but originates from a spatially extended structure which accounts for about 73% of the total flux of the maser. The strongest maser feature has a linear size of ~15 AU × 9 AU and a brightness temperature of ~1010 K, but this should be regarded as a lower limit to the real spot size given the severe filtering of extended emission that affects the data. We note that several masers may have a compact high brightness temperature core surrounded by a larger envelope (hundreds of AU) of lower brightness.

The sizes and brightness temperatures measured for the other features are listed in Table 2 together with typical isotropic luminosities for different Class I masers from the literature. The scatter in the most commonly observed lines at 36 GHz and 44 GHz can be larger than reported as large samples were observed in these transitions. For the 25 GHz series, values reported for the brightness temperature and the spot size are for the 62−61 line only and are measured in Orion-KL. For all lines the reported brightness temperatures and spot sizes are based on interferometric observations and are in most of the cases based on only one source. In the following discussion, we will assume spot sizes of 50 AU and 100 AU.

Table 2

Summary of typical Class I maser luminosities, Liso, brightness temperatures, Tb, and spot sizes.

2.3. Are Class I masers saturated?

Observed brightness temperatures are upwards of 106 K when observed with high linear resolution and linear sizes in the range 10−100 AU (see Table 2), whereas the expected limiting brightness temperature Ts for an unsaturated maser (see Sect. 5.2) is typically 105(4π/ Ωb) K, where Ωb is the maser beam solid angle. Moreover, saturated masers are expected to show little or no evidence of variation. Indeed, saturated masers undergo linear amplification, whereas unsaturated masers should amplify exponentially. This suggests qualitatively that unsaturated masers should vary on much shorter time scales than their saturated counterparts. A reasonable guess for the variation time scale of a saturated maser would be lspot/ νsh, where lspot is the maser spot size and νsh is the shock velocity. Taking lspot = 100 AU and a shock velocity of 30 km s-1, we find a time scale of ~15 yrs. This is consistent with most observations (Menten et al. 1988c; Kurtz et al. 2004) which show that Class I masers have little time variation. Dedicated observations of Class I masers to detect variability over time scales of several years are lacking, however, and variability of Class I masers is basically still an uncharted territory.

We also note that theory suggests that with increasing amplification, unsaturated masers are expected first to narrow and then to re-broaden until the line width approaches the intrinsic value determined by local turbulent and thermal broadening. However, observationally, the line profiles of different Class I masers are found to be very similar (e.g., Batrla & Menten 1988; Plambeck & Menten 1990; Voronkov et al. 2014). In particular for the DR21(OH) region, interferometric observations show that all 84 GHz components have counterparts in the 95 GHz line at identical velocities (e.g., Plambeck & Menten 1990) and that several transitions are spatially coincident (from the 36 GHz line to the 229 GHz maser, Fish et al. 2011, their Fig. 1 and references therein). It is worth noting, however, that real observed maser emission is likely a mixture of both saturated and unsaturated contributions. Taken all together, the observational properties seem to suggest that bright Class I masers are at least partially saturated.

3. Previous excitation studies on Class I masers

thumbnail Fig. 3

Partial rotational level diagram of E-type (left) and A-type methanol (right). Known Class I maser transitions are connected by red lines with frequencies indicated; blue dotted lines connect anti-inverted transitions. We note that all of the maser lines originating in the J2 → J1E series near 25 GHz are indicated by dotted red lines.

Previous statistical equilibrium studies on CH3OH Class I masers made use of collisional rates based on experimental results by Lees & Oka (1969) and Lees & Haque (1974). These rates show a propensity for Δk = 0 collisions and a dependence upon ΔJ as 1/ΔJ. The propensity for Δk = 0 over Δk = 1 collisions causes molecules to preferentially de-excite down a k stack (see Fig. 3), leading to a situation where the lower levels in the k = −1 stack are overpopulated relative to those in the k = 0 stack (for CH3OH-E), resulting in maser action in the J-1 → (J−1)0-E series and enhanced absorption in the 20 → 3-1E line, the second most prominent Class II maser line. Similar mechanisms lead to inversion in the 9-1 → 8-2 and 11-1 → 10-2-E lines. Analogously, the K = 0 ladder of CH3OH-A is overpopulated, leading to the J0 → (J−1)1-A+ masers and to the anti-inversion of the 51 → 60A+ Class II transition, the strongest Class II maser line. Indeed, observations showed that the 20 → 3-1E and 51 → 60A+ Class II lines are detected in absorption toward a number of Class I sources (e.g., Batrla et al. 1987; Menten 1991b) and also in dark clouds (Walmsley et al. 1988).

However, while the previously used collisional rates can reproduce the anti-inversion at 12.18 GHz and 6.7 GHz and several Class I masers (4-1 → 30E at 36 GHz, 5-1 → 40E at 84 GHz, 70 → 61A+ at 44 GHz, 80 → 71A+ at 95 GHz, and 90 → 81A+ 146 GHz; see Fig. 3), they do not account for the Class I maser series J2 → J1E at 25 GHz. For this reason, Johnston et al. (1992) suggested an ad hoc additional preference for the Δk = 3 collisions and the assumption that Δk = 2 collisions are not allowed to be able to collisionally pump the J2 → J1E Class I masers. Alternatively, Cragg et al. (1992) modelled the pumping of interstellar methanol masers using the hard sphere model of Goldreich & Kwan (1974), which represents the extreme case of completely unselective collisions. In this case, all Class I masers, including the J2 → J1E series, appear for densities in the range 102−105 cm-3.

The general conclusion of previous models of Class I masers is that these lines are collisionally excited and that they mase in different density ranges. These general results have recently been confirmed by McEwen et al. (2014) and Nesterenok (2016).

4. Statistical equilibrium results

We performed large velocity gradient (LVG) calculations using a modified version of the code presented by Leurini et al. (2004) with a plane-parallel slab geometry appropriate for shocks. Following a standard formalism (Elitzur 1992), the maser levels are described by pump (Pm) and loss (Γm) rates that regulate the interactions of the different maser systems with all other levels (which we refer to as the maser reservoir)

where m = 1,2 are the two levels of the maser system, ni the CH3OH density in level i, n the molecular hydrogen density, Aim the Einstein coefficients for spontaneous emission (with Aim = 0 for i<m), Cim the temperature dependent collisional rates, βim the escape probability (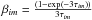), for a slab geometry, and τim the optical depth (perpendicular to the line of sight) given by Eq. (2) of Leurini et al. (2004). The pump and loss rates are obtained by solving the level populations for the full system (maser and reservoir) in the absence of maser radiation. We also note that we neglect in these calculations the continuum dust opacity when computing βim and thus assume that the opacity at wavelengths of transitions feeding maser levels is small.

We updated the code with the more recent collisional rates for the torsional ground states of A- and E-type methanol from Rabli & Flower (2010). The rates were computed for temperatures in the range from 10 to 200 K including rotational states up to J = 15 for collisions with para-H2. We assume in this study that collisions with ortho-H2 can be neglected or, equivalently, that the abundance ratio of ortho- to para-H2 is low. This needs to be investigated in future work, but we note that if the ratio of ortho- to para-H2 is low in the pre-shock gas, this may also hold in the post-shock layer because the time taken to traverse the shock may be too short to thermalise the ratio. Indeed, Wilgenbus et al. (2000) found that significant conversion from para- to ortho-H2 starts at 700 K in C-type shocks (and at T> 1000 K in J-type).

We ran models for densities between 104 and 109 cm-3 and temperatures, T, of 20–400 K. Since collisional de-excitation rates from Rabli & Flower (2010) are computed for temperatures up to 200 K, we use the rates computed at 200 K for higher temperatures. We used specific column densities (N/ Δν) of CH3OH-A and -E between 1014 and 1018 cm-2 km-1 s. In the absence of any external radiation field except the cosmic background, all known Class I maser transitions should be reproduced and the Class II 20 → 3-1E and 51 → 60A+ masers should be anti-inverted. All Class I transitions reported in Table 2 show inversion in the analysed range of physical conditions. In addition, the 20 → 3-1E transition and the 51 → 60A+ line present anti-inversion as expected. In particular, the range of densities for which the lines are anti-inverted depends on the temperature and column density. For the same value of T, the 20 → 3-1E line is anti-inverted at densities lower than the 51 → 60A+ transition. The absorption temperature increases with methanol column density and kinetic temperature.

In the following discussion, we present the pumping mechanisms that lead to maser action in the Class I lines and the dependency of the masers on the physics of the gas. We should note that although the general behaviour is similar to the results recently published by McEwen et al. (2014), our calculations produce inversion in the 36 GHz line at lower densities (104−105 cm-3) than found by McEwen et al. (2014) (106 cm-3). The main difference between our models and those by McEwen et al. (2014) is that the latter use a 30 K dust radiation field, while our models include only the cosmic radiation field. This assumption is justified by the fact that Class I masers are usually found far from continuum sources (e.g., Voronkov et al. 2014). To test our results, we benchmarked our code with the RADEX LVG code (van der Tak et al. 2007) with a uniform slab geometry. The results of the two codes are consistent up to a specific column density of 1017 cm-2 km-1 s.

4.1. Pump and loss rates

In this paper, we confine ourselves to calculating the maser efficiency and other characteristics of saturated masers following the formalism used by Hollenbach et al. (2013) for water masers. We define the methanol maser emission measure, ξ, which is a measure of the rate at which pump photons are produced. It is defined as the ratio of the product of the molecular hydrogen and methanol number densities over the velocity gradient in the plane of the sky: 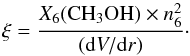(3)Here, X6(CH3OH) is the methanol abundance (n(CH3OH) /n(H2)) in units of 10-6 (we assume equal abundances for A- and E-type methanol), n6 the H2 number density in units of 106 cm-3, and dV/ dr the velocity gradient in units of km s-1 pc-1 (for rough estimates, we assume a shock velocity of 30 km s-1 and a shock width of 1016 cm; see Schilke et al. 1997; Gusdorf et al. 2008). We note that ξ can also be expressed in terms of the ratio of methanol column density (in the plane of the sky) to line width, N(CH3OH)/dν:

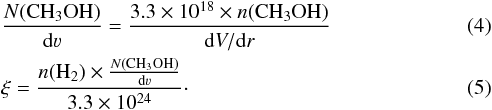To investigate the pumping mechanism of Class I methanol masers, we define effective pump and loss rates of a given maser system as P = Pu−Pl and L = Γu−Γl, and study their behaviour as functions of ξ for different temperatures and densities. As an example, P and L for the 36 GHz lines are represented in Fig. 4, which shows that both the relative population rates of the upper and lower maser levels, as well as their relative decay rates, play a role in causing population inversion. This process does not depend significantly on the temperature, while it does depend on the volume density of the gas, which emphasises the importance of collisions for Class I masers. The other Class I masers behave similarly.

thumbnail Fig. 4

Effective pump and loss rate for the 36 GHz maser at different densities and for a temperature of 200 K (upper panels) and at different temperatures for n = 106 cm-3 (lower panels). It is possible to convert ξ to methanol abundance using Eq. (3).

4.2. Conditions for population inversion

Figure 5 shows the excitation temperature of the 44 GHz and of the 62−61-E 25.018 GHz (representative of the 25 GHz series) masers to illustrate the range of n and ξ where the lines are inverted and where the pump and loss rates are meaningful quantities for a temperature of 200 K. For completeness, similar plots for the 36 GHz, 84 GHz, and 95 GHz lines are shown in Appendix A (Fig. A.1). Table 3 summarises the value of ξ, ξq, at which population inversion is quenched for temperatures of 80 K and of 200 K for different Class I maser lines at different densities. From Eq. (5), the specific methanol column density at which each maser line quenches can be derived. At a temperature of 200 K, the 36 GHz line thermalises around a few 1017 cm-2 km-1 s independently of density for n> 106 cm-3; a similar behaviour is shown by the 84 GHz lines, which also quenches at ~1017 cm-2 km-1 s for all densities. The same is found for the other lines reported in Table 3: they all quench at a constant specific column density of approximately 1017 cm-2 km-1 s independently of volume density in the range 105−107 cm-3, which suggests that there is a critical methanol column density at which quenching occurs. At a lower temperature of 80 K, the specific column density at which the quenching occurs increases to approximately 1018 cm-2 km-1 s at a volume density of 108 cm-3 except for the 62−61-E 25.018 GHz line. To give a complete view of the range of parameters where the Class I maser lines are inverted, we also plot their excitation temperatures as functions of densities for a temperature of 200 K and a specific column density of 1017 cm-2 km-1 s (Fig. 6). Figure 6 clearly illustrates the effect that varying the volume density has on individual lines: the 25 GHz series quenches at the highest volume density and it is inverted for n> 106 cm-3; the 36 GHz, 44 GHz, and 95 GHz lines are those inverted over the broadest range of volume densities. Figure 6 also shows that the 84 GHz may be not inverted at low densities (a few 104 cm-3). However, this behaviour is found only at high specific column densities (>1016 cm-2 km-1 s) and in a narrow range of densities.

thumbnail Fig. 5

Excitation temperature, Tex, of the 44 GHz (upper panel) and of the 62−61-E 25.018 GHz line (lower panel) at different densities and for a temperature of 200 K. Curves are plotted until Tex becomes positive. It is possible to convert ξ to methanol abundance using Eq. (3). We note that with increasing ξ, the excitation temperature typically transits from −infinity to +infinity before thermalising. The discrete nature of our grid in ξ occasionally obscures this fact.

4.3. Maser emission

We follow the formalism developed by Elitzur et al. (1989) and Hollenbach et al. (2013) for H2O masers and describe the maser emission through the pump rate coefficient (q), the maser loss rate (Γ), and the inversion efficiency of the pumping scheme (η) as

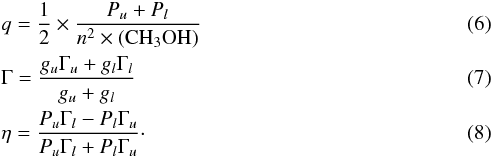Here gu and gl are the statistical weights for the upper and lower level of a given maser system. We note that our definition of η is different from that of Hollenbach et al. (2013) because we do not assume that the upper and lower levels of a given maser system have the same decay rates.

Figures 7−9 show our results for the 44 GHz, the 36 GHz, and the 25.018 GHz masers for η, q, and Γ /n6 (the loss rate divided by density in units of 106 cm-3) as functions of ξ for a range of densities and temperatures relevant for Class I masers. The parameters Γ and q are the sum of a collisional part and a radiative part: at low ξ, collisions are negligible and Γ and q are dominated by their radiative part, which decreases with increasing values of ξ. Their collisional part is proportional to the H2 density and has a weak dependence on temperature. Hence, Γ /n6 is fairly flat as a function of ξ when collisions dominate, while q decreases slowly with ξ in this regime. Results for the other Class I maser lines are shown in Appendix A, Figs. A.2 and A.3. For the 44 GHz and the 95 GHz lines, Γ, q, and η have a very weak dependence on density and on temperature (above 80 K) as function of ξ (Figs. 7 and A.3). On the other hand, the 36 GHz, 84 GHz, and the 25 GHz lines show a stronger dependency on density; the 25 GHz line is the most sensitive to changes in the volume density of the gas (Figs. 8, 9, and A.2). All Class I masers analysed in this study do not show a strong dependence on temperature.

Table 3

ξq for various Class I lines at different densities for T = 80 K and 200 K.

thumbnail Fig. 6

Excitation temperature of the 44 GHz, 95 GHz, and 36 GHz lines (lower panels), and the 84 GHz and 62−61-E masers (upper panels) for a temperature of 200 K and a specific column density of 1016 cm-2 km-1 s (left) and of 1017 cm-2 km-1 s (right) as functions of volume density. The dashed horizontal line separates maser from non-maser behaviour. Vertical lines mark the transitions from maser to non-maser behaviour.

thumbnail Fig. 7

Modelling results for the 44 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).

thumbnail Fig. 8

Modelling results for the 36 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).

thumbnail Fig. 9

Modelling results for the 62−61-E 25.018 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).

4.4. Effects of the physical parameters on Class I masers

The parameters η and q discussed in the previous sections can be used to characterise the maser emission (e.g., Hollenbach et al. 2013). The photon production rate Φm at line centre of a saturated maser is directly linked to the observed flux (Fm) of a given maser through the geometry of the maser and can be defined as 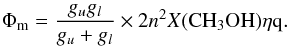(9)Figures 10 and 11 show the dependence of Φm for several Class I methanol lines (36 GHz, 44 GHz, 95 GHz, and the 25 GHz series) as functions of ξ for different densities and temperatures for a range of parameters for which the lines are inverted. For the J2−J1-E series we show our model results for the photon production rate for lines between J = 2 and 10. The photon production rate of the 84 GHz line is presented in Appendix A (Fig. A.4). For all lines, the photon production rates follow almost a single curve as functions of ξ independently of volume density. All lines are basically unaffected by T. For the 25 GHz series, we find that the photon production rate increases with J with a peak between J = 8 and 10 (see discussion in Sect. 5.3).

In Fig. 12, we compare the photon production rates for the 62 → 61 line with those of the 36 GHz and 44 GHz masers for densities of 106 cm-3, 107 cm-3, and 108 cm-3. Clearly, the 62 → 61 line (and in general the whole J2 → J1 series at 25 GHz, see Fig. 11) behaves in a different fashion from the other maser transitions discussed in this article and is the Class I maser most sensitive to density. This is not surprising. The 36 GHz, 44 GHz, 84 GHz, and 95 GHz masers are all directly connected to backbone ladders (k = −1 for E-type and K = 0 for A-type) and are inverted mainly because of the predominance of Δk = 0 collisions. This is not the case for the J2 → J1 series whose inversion mechanism is more complex and which depends on Δk ≠ 0 collisions to build up population in the k = 1 and 2 E-type ladders. As seen in Fig. 6, the 62−61-E transition is only inverted at high densities above 106 cm-3 in contrast to the other Class I masers treated here. Moreover, the density dependence of the photon production rate in 62−61-E is steeper than in backbone-linked lines and the dependence on ξ (emission measure) is flatter. This is clearly shown in Fig. 12 at a density of 107 cm-3 where the 36 and 44 GHz masers have photon production rates that are very similar and behave roughly as ξ0.7. The photon production rate for the 62−61-E line on the other hand is close to the backbone-linked lines at low ξ, but has a much flatter ξ dependence (roughly ξ0.4) and consequently has a much lower photon output at ξ values approaching unity. It is clear from our models that at densities of the order of 106 cm-3 the photon output in the 25 GHz lines is much lower than at 36 GHz or 44 GHz. Indeed, observations suggest a much lower photon output at 25 GHz than in backbone lines (e.g., Menten et al. 1986; Haschick et al. 1990; Voronkov et al. 2006), but higher quality interferometric observations are needed to draw conclusions.

It is interesting to note that despite the decrease in η and q with ξ (see Fig. 7), the production rate increases with ξ until thermalisation is reached, thus suggesting that the high ξ before quenching (corresponding to specific column densities of 1016−1017 cm-2 km-1 s; see Table 3 and Sect. 4.2) are responsible for the observed bright masers. This implies that high ξ values are needed for high photon production rate and that therefore masers with high brightness temperatures trace high methanol emission measures. These values are reached at high densities, high temperatures, and high methanol column densities (Eq. (3)). In particular, the 36 GHz line can reach higher photon production rates than the 84 GHz, the 44 GHz, and the 95 GHz masers because it generally quenches at higher values of ξ for T< 200 K. A similar result has been obtained by McEwen et al. (2014) who find (at a temperature of 80 K and a methanol abundance of 10-7) that optimal masing conditions at 36 GHz are at densities roughly an order of magnitude higher than at 44 GHz.

thumbnail Fig. 10

Modelling results for the 44 GHz, 36 GHz, and 95 GHz maser photon production rates, and for their ratios at 200 K for various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). The horizontal dashed line in the panels showing the 44 GHz to 36 GHz ratio marks the peak value of the flux-density ratio distribution reported by Voronkov et al. (2014). It is possible to convert ξ to methanol abundance using Eq. (3).

thumbnail Fig. 11

Modelling results for the photon production rate of the J2−J1-E (J = 2−10) series at 25 GHz maser at 200 K for various densities (bottom panel) and at n = 107 cm-3 and several temperatures (upper panel). It is possible to convert ξ to methanol abundance using Eq. (3).

thumbnail Fig. 12

Bottom panel: comparison of the maser photon production rates for the 44 GHz, 36 GHz, and 25 GHz (J = 6) for various densities at 200 K. For example, the solid red and blue curves in the middle panel show a power law of ξ0.4 and ξ0.7, respectively. Top panel: modelling results for the ratios of the 62−61-E maser photon production rate to that of the 44 GHz and 36 GHz lines for various densities at 200 K. It is possible to convert ξ to methanol abundance using Eq. (3).

Modelling intensities of saturated maser lines is not straightforward because the outcome depends on the geometry of the maser. In particular, the observed flux of a given maser transition depends on the geometry and on whether the maser is beamed towards us or not. However, under the assumption that different maser lines of frequencies ν1 and ν2 are emitted by the same volume of gas and that they are both saturated, the observed ratios of their fluxes, F1 and F2, is geometry independent and it can be written as a function of the ratio between their photon production rates: 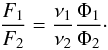(10)Figure 10 shows the Φ1/ Φ2 ratio of the modelled maser photon production rates of the 36  GHz, 44  GHz, and 95  GHz maser lines for different densities and temperature as functions of ξ. Figure 12 shows the photon production rate ratios of 62−61-E transition relative to the 44  GHz and 36  GHz lines. For completeness, the ratio between the 84  GHz maser and the 36  GHz line are shown in Fig. A.4. The ratio Φ44 GHz/ Φ95 GHz is relatively flat and does not vary with density for a fixed temperature of 200 K. On the other hand, it decreases with temperature for a fixed density of 106 cm-3. The ratio Φ44 GHz/ Φ36 GHz has a different behaviour as a function of temperature and density. At a fixed density of 106 cm-3, the ratio increases with T, while at T = 200 K it decreases with volume density. Finally, Φ36 GHz/ Φ84 GHz decreases with density and temperature (Fig. A.4).

5. Discussion

5.1. Maser luminosities

The luminosity of a given maser transition is defined as

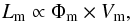(11)where Vm is the maser volume. As discussed in Sect. 2.2, spot sizes for Class I masers are not well constrained. For a cylindrical geometry, a spot size of 100 AU and an aspect ratio α = llos/R = 10, where llos is the length oriented along the line of sight and R the radius, we derive maser luminosities for the 44 GHz, 95 GHz, 36 GHz, and 84 GHz lines, and the 62−61-E maser (representative of the 25 GHz series) of 1041 photons s-1 for 80 K and 200 K for emission measures ξ of 0.1 or 0.2. The corresponding luminosities for a spot size of 50 AU are approximately 1039 photons s-1. The maser luminosity is linked to the observed isotropic luminosity, Liso, through the formula 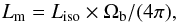(12)where Ωb is the beaming angle. For a cylindrical maser spot with llos = αR oriented along the line of sight, Ωb = π × (R/llos)2 = π/α2 making the assumption that the beam solid angle is purely determined by geometry (not necessarily the case; see Hollenbach et al. 2013 for a discussion). For an aspect ratio α of 10 (corresponding to ~10-3 steradian), observations of Class I masers (Liso = 1041−1045  photons s-1; see Table 2) imply maser luminosities between between 1038 and 1042 photons s-1 in agreement with our models.

For a collisionally excited maser, it is thus reasonable to expect that high density and a high methanol abundance is required. This general expectation is confirmed by the results of our computations which show that the maser photon output per unit volume increases with the methanol emission measure ξ defined by Eq. (3). From Eqs. (11) and (12), it can be seen that a small maser volume can be compensated for either by a larger Φm or by a small beaming angle. The former requires higher emission measures (or higher density and methanol abundance), while the latter becomes geometrically unlikely at a certain point (aspect ratios for the masing volume higher than 10 seem improbable). We can get some insights into the implications of this based on our computations of the photon production rates. From Fig. 10, we note that in the most common lines, a photon emissivity per unit volume of 10-6 photons s-1 cm-3 at ξ = 0.1 is achieved, while (see Fig. 12) the 25 GHz emissivity is almost an order of magnitude smaller.

From the methanol emission measure assuming velocity gradients of the order of 5 × 104 km s-1 pc-1 and a standard methanol abundance of 10-6 (e.g., Menten et al. 1988d; Kama et al. 2010), we find n(H2) = 7 × 107 cm-3 consistent with a high density explanation of the masers.

Such high densities are consistent with the magnetic field measurement of Sarma & Momjian (2011; see also Momjian & Sarma 2012). They have detected a Zeeman pattern in the 44 GHz maser towards OMC2 and estimate a line of sight field of 18 mG (with high uncertainty owing to the poorly known Landé factor). If one uses the correlation between density and magnetic field of Crutcher (1999), this corresponds to a H2 density of 107 cm-3, although with a very large uncertainty. We note here that Sarma and Momjian found a value ten times lower based on a different argument and we cannot exclude this. However, we conclude that the Zeeman result certainly favours high densities (upwards of 106 cm-3) in the masing gas.

5.2. Maser saturation

thumbnail Fig. 13

Js and Ts as function of ξ for different densities and temperatures for the 44 GHz (solid line) and 95 GHz (dashed lines) transitions a), and for the 36 GHz (solid line) and 84 GHz (dashed lines) masers b). It is possible to convert ξ to methanol abundance using Eq. (3).

The intensity of a maser reaches saturation at a value Js given by 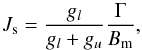(13)where Bm is the Einstein coefficient for stimulated emission of the maser transition and Γ the loss rate (Eq. (7)). The corresponding brightness temperature Ts of the line is 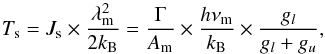(14)where λm and νm are the wavelength and frequency of the maser line, kB the Boltzmann constant, h the Planck constant, and Am the Einstein coefficient for spontaneous emission of the maser transition. In this way, we do not correct for any given geometry to keep results general. Using A44 GHz = 2.0 × 10-7 s-1, A95 GHz = 2.1 × 10-6 s-1, A36 GHz = 1.5 × 10-7 s-1, A84 GHz = 2.0 × 10-6 s-1, and A25.018 GHz = 8.6 × 10-8 s-1 (from the Cologne database for molecular spectroscopy; Müller et al. 2001, 2005), we find brightness temperatures at saturation up to approximately 105 K for the 44  GHz, 95  GHz, 36  GHz, and 84  GHz lines for a temperature of 200 K and a density of 108 cm-3. The 62−61-E has lower values of Ts (~5000 K). We show in Figs. 13 and 14 our computed values for Js and Ts as a function of ξ for a range of temperatures and densities. For the 44 GHz, 95 GHz, 36 GHz, and 84 GHz masers, we find similar behaviour; Ts increases with the volume density of the gas. The 25 GHz lines behave differently and show very little dependence on density. All lines are basically unaffected by changes in temperature. Moreover, the Ts of the masers scale with the density of the gas approximately as 4 × 103n6 for the 44 GHz, and as 3 × 103n6 for the 36 GHz transition, and the Ts of the 95 GHz and 84 GHz lines can be obtained from the same relations corrected by a factor (44 GHz/95 GHz)2 and (36 GHz/84 GHz)2, respectively. From these relations, it is possible to derive constraints on the beaming angle Ωb of a given maser: if brightness temperatures of 109 K are observed, as in IRAS 18151–1208 for the 44 GHz line (Matsumoto et al. 2014), then assuming that the density of the gas is ~108 cm-3, Ωb is larger than 5 × 10-3 for a saturated maser. Similar values of Ωb are estimated for the 25.018 GHz line (Ωb = 0.03−0.003 for Tb = 106−107 K; see Table 2).

5.3. Comparison with observations

In Sect. 2.3 we speculated that the Class I masers with the lowest excitation requirements are saturated, as suggested by their slow variability (in general) and by the similar velocity profiles of different transitions found in several sources. Under this assumption, and assuming that different lines are emitted by the same volume of gas, we can compare observed line ratios to our model results to verify whether our calculations reproduce the observations. Recently, Voronkov et al. (2014) have reported observations of a sample of 71 Class I maser methanol sources in the 36 GHz and 44 GHz lines with the ATCA array. These authors find that the 44 GHz to 36 GHz flux-density ratio has a wide distribution with a peak at 2.5 (corresponding to Φ44 GHz/ Φ95 GHz ~ 3); only 14% of the 292 maser groups discussed by Voronkov et al. (2014) were found to be stronger at 36 GHz than at 44 GHz (see their Fig. 6). The authors also comment that owing to the complexity of spectral profiles, this is likely an upper limit to the number of groups where the 36 GHz flux is stronger than at 44 GHz. These results seem to reflect our model predictions, which show that the 44 GHz line is always stronger than the 36 GHz maser except at low temperatures and high densities (see Figs. 10 and 12). These conditions are probably met in regions with little or no star formation activity. Indeed Pratap et al. (2008) reported enhanced maser emission at 36 GHz relative to the 44 GHz maser line toward such regions. Moreover, observations of supernovae remnants find 36 GHz maser emission in the absence of a detectable 44 GHz line (e.g., Pihlström et al. 2014). Regarding other flux ratios, no large sample of sources observed at high angular resolution is available. Fontani et al. (2010) detected the 44 GHz and the 95 GHz masers in a sample of high-mass star forming regions with the Nobeyama telescope. Seven sources in the sample are detected in both lines in a similar range of velocities and with similar line widths. Their observed Φ44 GHz/ Φ95 GHz ratio has an average value of ~5 and ranges between 1 and 11, while the modelled ratio is never higher than 1. Clearly, our modelled Φ44 GHz/ Φ95 GHz fails to reproduce the observations. However, a note of caution is needed in the case of single-dish observations because the maser locations can be significantly offset from the pointing positions and because of the different beam sizes of the different lines (38′′ and 18′′ for the observations reported by Fontani et al. 2010).

Concerning the relative intensities of the J2 → J1 lines at 25 GHz, it is noteworthy that our calculations predict that the ratio between the photon production rates of the 62 → 61 line to the 32 → 31 transition is close to 3 and slightly increases with density (Fig. 11), in reasonable agreement with observations (Menten et al. 1986). These observations also show that the J2 → J1 lines usually peak at J = 6, while our results show a peak around J = 9. This may be the effect of the relatively high kinetic temperature we adopted for our calculations, 200 K.

Another implication of our results is that in sources where the 25 GHz lines are seen in absorption (e.g., W3OH, NGC 7538 Menten et al. 1986) the density must be lower than 106 cm-3, and the 36 GHz and 44 GHz masers should be detected. This is indeed the case for both W3OH and NGC 7538 (e.g., Haschick & Baan 1989; Haschick et al. 1990; Kurtz et al. 2004), although the large beam of the single-dish observations does not allow verification of the spatial association of the lines.

Our results show that interferometric surveys in the 25 GHz lines and in the millimetre masers (at 84 GHz and 95 GHz) would be very useful. Figure 12 shows a comparison of our computed photon production rates at 200 K for densities between 106 and 108  cm-3. One interpretation of the small minority of objects with high 44 GHz to 36 GHz flux-density ratio might be that they are high emission measure (methanol abundance) objects with ξ larger than 0.1 and density above 107 cm-3. Certainly, a good interferometric survey is needed at 25 GHz and in the mm lines to make further progress.

6. Outlook

Refining estimates of the beaming angle and related quantities will require a proper resolution of the radiative transport problem for a plausible geometry as well as a more consistent set of interferometric data. This will allow a more reliable estimate of the expected brightness temperature and line profile. To what extent does finite inclination of the shock propagation direction to the line of sight affect observed profiles? Is shock structure important and does this affect the observed maser structure? What angular size differences are expected between different Class I masers? Answers to these questions will become important for the new generation of interferometric results from the VLA and ALMA, for example.

As noted above, we conclude that bright Class I methanol masers are mainly high-temperature high-density structures with methanol maser emission measures ξ close to the limits set by collisional quenching (roughly a hydrogen density of 108 cm-3). The basic physics is very similar to that discussed by Hollenbach et al. (2013) for water masers and we find, for example, that in the case of methanol (as for water), the maser efficiency at high density is determined by the collisional selection rules rather than the relative radiative decay rates from the upper and lower maser levels. The fall-off of maser efficiency η with ξ is similar to that found by Hollenbach et al. (2013) for water masers, as is the increase of the saturated maser photon production rate Φ with ξ. Thus, relatively high post shock densities and temperatures (though not sufficiently high to cause dissociation of H2) are needed to account for most bright Class I masers. The results of Momjian & Sarma (2012) discussed above suggest that magnetic fields may be important in the dynamics of the structures that give rise to methanol masers, and we conclude that C-shocks (rather than J-shocks) give rise to Class I masers. The linear sizes observed (10−100 AU, see Table 2) are consistent with this. Kaufman & Neufeld (1996) have studied the structure of C-shocks in the parameter range of interest to us and find shock widths of roughly 10 AU (dependent on pre-shock density, ionisation degree, etc.) with compression factors (post shock/pre-shock density ratio) of the order of the Alfven Mach number νsh/ νa (where νsh is the shock velocity and νa the Alfven velocity). The post-shock temperatures are of the order of a few hundred K and the Alfven Mach number is typically a factor of 10. Thus for post-shock densities of the order of 107 cm-3, we expect pre-shock densities of the order of 106 cm-3. Hence, we can conclude that saturated Class I masers are likely to occur in regions of high ambient density and pressure. High-mass star forming regions are thus a more likely locale for Class I methanol masers than lower pressure clouds close to the Sun.

In this context, calculations based on a C-shock geometry (analogous to those of Hollenbach et al. 2013, and Kaufman & Neufeld 1996) are clearly needed to produce brightness temperature and line profiles for Class I masers that can be compared with observations. The computations of maser efficiency and photo production rate in this article are a first step. A comprehensive set of interferometric data which allow study of the spatial relationship between maser spots and their development in time is also clearly needed. In view of the importance of magnetic fields, calculations taking account of all Stokes parameters as well as more Zeeman measurements are needed as well. The essential first step here is to obtain reliable determinations of the Landé factors for the different maser transitions.

Another important question to be investigated is the possible influence of o-H2 collisions on the properties of Class I masers. It is unclear what the ortho-to-para abundance ratio will be in the shocks we postulate, but it is clear that o-H2 collisions have different selection rules than p-H2 collisions (Rabli & Flower 2010) and that, if the o/p ratio is approximately equal to or greater than 1, this will change our results appreciably. It could conceivably switch off the maser. Thus, calculations assuming different o/p ratios are needed.

One important consequence of such studies is obtaining direct observational information about C-shock structure. Masers allow this to be studied both in time and space. It seems likely that it will be possible to measure proper motions in Class I masers and also effects due to inhomogeneities in the pre–shock medium. There are presumably gradients in temperature and density along the direction of shock propagation and differences in the spatial distribution of Class I masers may provide a guide to this. Understanding C-shock structure on the other hand is a valuable input to studies of the interaction of protostellar outflows with their surroundings. We conclude that further work along these lines is needed.

thumbnail Fig. 14

Js and Ts as function of ξ for different densities and temperatures for the 62−61-E maser. It is possible to convert ξ to methanol abundance using Eq. (3).

7. Summary and conclusions

Using new collisional rates for collisions of CH3OH with para-H2, we computed the pump and decay rates as well as the pump efficiency for the most commonly observed Class I methanol maser transitions with the aim of investigating the physical conditions leading to bright Class I masers in regions of massive star formation. This is, to our knowledge, the first time that calculations of this type have been carried out for methanol masers. We hope that our results can be applied to an appropriate model of the geometry of saturated Class I methanol masers in order to compute a realistic brightness temperature distribution and beaming solid angle. Ultimately, one hopes that this may allow insight into the structure and velocity field of the shocks responsible for Class I maser emission. Our analysis of the photon production rates has allowed a few tentative conclusions on the properties of the high-gain masers such as those observed towards IRAS 18151-1208 by Matsumoto et al. (2014). They can be summarised as follows:

  • 1.

    We predict inversion in all transitions where maser emission isobserved.

  • 2.

    The production rates of all Class I masers increase with ξ until thermalisation is reached. This implies that masers with high brightness temperature trace high methanol emission measure reached at high densities (n(H2) ~ 107−108 cm-3), high temperatures (>100 K), and high methanol column densities with methanol maser emission measures close to the limits set by collisional quenching.

  • 3.

    Class I masers can reasonably be separated into the three families: the (J + 1)-1−J0-E type series, the (J + 1)0−J1-A type, and the J2−J1-E series at 25 GHz.

  • 4.

    The 25 GHz lines behave in a different way from the other maser transitions likely because they are inverted through Δk ≠ 0 collisions. In particular, they are only inverted at high densities above 106 cm-3 in contrast to other Class I masers, which mase already at densities of approximately 104 cm-3.

  • 5.

    Under the assumption that Class I masers are saturated, our calculations reproduce reasonably well most of the observed properties of Class I methanol masers in star forming regions. In particular, they predict that the 44 GHz line is almost always stronger than the 36 GHz maser, except at low temperatures and high densities and that the luminosity of the 25 GHz series is lower than that of the other Class I masers. The observed constant ratio between different lines in the 25 GHz series is also reproduced.

  • 6.

    Maser emission in the 25 GHz lines is not expected at low densities. Therefore, detection of all three families in the same maser feature is a clear indication of high densities (>106 cm-3). On the other hand, detection of maser emission at 36 GHz and 44 GHz with no corresponding 25 GHz masers indicates densities lower than 106 cm-3 and probably larger size scales than the spot sizes of the order of 50 AU observed in some sources.

  • 7.

    The maser luminosities derived from our model predictions for the photon production rates are in agreement with observed isotropic luminosities for maser beam angles of the order of 10-3 steradian.

Acknowledgments

We thank the anonymous referee for helpful comments that have improved the content and overall clarity of this manuscript. C.M.W. would like to acknowledge travel support from the Science Foundation Ireland (Grant 13/ERC/I12907). C.M.W. acknowledges the hospitality of the MPIfR during the course of this work.

References

  1. Araya, E. D., Kurtz, S., Hofner, P., & Linz, H. 2009, ApJ, 698, 1321 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bachiller, R., Gomez-Gonzalez, J., Barcia, A., & Menten, K. M. 1990, A&A, 240, 116 [NASA ADS] [Google Scholar]
  3. Barrett, A. H., Schwartz, P. R., & Waters, J. W. 1971, ApJ, 168, L101 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barrett, A. H., Ho, P., & Martin, R. N. 1975, ApJ, 198, L119 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barrett, A. H., Hot, P. T. P., Martin, R. N., et al. 1976, Astrophys. Lett., 18, 13 [NASA ADS] [Google Scholar]
  6. Batrla, W., & Menten, K. M. 1988, ApJ, 329, L117 [NASA ADS] [CrossRef] [Google Scholar]
  7. Batrla, W., Matthews, H. E., Menten, K. M., & Walmsley, C. M. 1987, Nature, 326, 49 [NASA ADS] [CrossRef] [Google Scholar]
  8. Breckenridge, S. M., & Kukolich, S. G. 1995, ApJ, 438, 504 [NASA ADS] [CrossRef] [Google Scholar]
  9. Britton, T. R., & Voronkov, M. A. 2012, in IAU Symp. 287, eds. R. S. Booth, W. H. T. Vlemmings, & E. M. L. Humphreys, 282 [Google Scholar]
  10. Buxton, R. B., Barrett, A. H., Ho, P. T. P., & Schneps, M. H. 1977, AJ, 82, 985 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cesaroni, R., & Walmsley, C. M. 1991, A&A, 241, 537 [NASA ADS] [Google Scholar]
  12. Chen, X., Ellingsen, S. P., Shen, Z.-Q., Titmarsh, A., & Gan, C.-G. 2011, ApJS, 196, 9 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chui, M. F., Cheung, A. C., Matsakis, D., Townes, C. H., & Cardiasmenos, A. G. 1974, ApJ, 187, L19 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cragg, D. M., Johns, K. P., Godfrey, P. D., & Brown, R. D. 1992, MNRAS, 259, 203 [NASA ADS] [CrossRef] [Google Scholar]
  15. Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cyganowski, C. J., Brogan, C. L., Hunter, T. R., & Churchwell, E. 2009, ApJ, 702, 1615 [NASA ADS] [CrossRef] [Google Scholar]
  17. Davis, C. J., Kumar, M. S. N., Sandell, G., et al. 2007, MNRAS, 374, 29 [NASA ADS] [CrossRef] [Google Scholar]
  18. Elitzur, M. 1992, Astronomical masers (Kluwer Academic Publishers) [Google Scholar]
  19. Elitzur, M., Hollenbach, D. J., & McKee, C. F. 1989, ApJ, 346, 983 [NASA ADS] [CrossRef] [Google Scholar]
  20. Ellingsen, S. P. 2005, MNRAS, 359, 1498 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ellingsen, S. P., Breen, S. L., Caswell, J. L., Quinn, L. J., & Fuller, G. A. 2010, MNRAS, 404, 779 [NASA ADS] [CrossRef] [Google Scholar]
  22. Ellingsen, S. P., Chen, X., Qiao, H.-H., et al. 2014, ApJ, 790, L28 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fish, V. L., Muehlbrad, T. C., Pratap, P., et al. 2011, ApJ, 729, 14 [NASA ADS] [CrossRef] [Google Scholar]
  24. Fontani, F., Cesaroni, R., & Furuya, R. S. 2010, A&A, 517, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Frail, D. A. 2011, Mem. Soc. Astron. It., 82, 703 [NASA ADS] [Google Scholar]
  26. Gaines, L., Casleton, K. H., & Kukolich, S. G. 1974, ApJ, 191, L99 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gan, C.-G., Chen, X., Shen, Z.-Q., Xu, Y., & Ju, B.-G. 2013, ApJ, 763, 2 [NASA ADS] [CrossRef] [Google Scholar]
  28. Goldreich, P., & Kwan, J. 1974, ApJ, 189, 441 [NASA ADS] [CrossRef] [Google Scholar]
  29. Green, J. A., Caswell, J. L., Fuller, G. A., et al. 2008, MNRAS, 385, 948 [NASA ADS] [CrossRef] [Google Scholar]
  30. Green, J. A., Caswell, J. L., Fuller, G. A., et al. 2009, MNRAS, 392, 783 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gusdorf, A., Cabrit, S., Flower, D. R., & Pineau Des Forêts, G. 2008, A&A, 482, 809 [Google Scholar]
  32. Haschick, A. D., & Baan, W. A. 1989, ApJ, 339, 949 [NASA ADS] [CrossRef] [Google Scholar]
  33. Haschick, A. D., Menten, K. M., & Baan, W. A. 1990, ApJ, 354, 556 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hills, R., Pankonin, V., & Landecker, T. L. 1975, A&A, 39, 149 [NASA ADS] [Google Scholar]
  35. Hollenbach, D., Elitzur, M., & McKee, C. F. 2013, ApJ, 773, 70 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hunter, T. R., Brogan, C. L., Cyganowski, C. J., & Young, K. H. 2014, ApJ, 788, 187 [NASA ADS] [CrossRef] [Google Scholar]
  37. Johnston, K. J., Gaume, R., Stolovy, S., et al. 1992, ApJ, 385, 232 [NASA ADS] [CrossRef] [Google Scholar]
  38. Johnston, K. J., Gaume, R. A., Wilson, T. L., Nguyen, H. A., & Nedoluha, G. E. 1997, ApJ, 490, 758 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kalenskii, S. V., Bachiller, R., Berulis, I. I., et al. 1992, AZh, 69, 1002 [NASA ADS] [Google Scholar]
  40. Kalenskii, S. V., Liljestroem, T., Val’tts, I. E., et al. 1994, A&AS, 103, 129 [NASA ADS] [Google Scholar]
  41. Kalenskii, S. V., Slysh, V. I., Val’Tts, I. E., Winnberg, A., & Johansson, L. E. 2001, Astron. Rep., 45 [Google Scholar]
  42. Kalenskii, S. V., Johansson, L. E. B., Bergman, P., et al. 2010a, MNRAS, 405, 613 [NASA ADS] [Google Scholar]
  43. Kalenskii, S. V., Kurtz, S., Slysh, V. I., et al. 2010b, Astron. Rep., 54, 932 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kama, M., Dominik, C., Maret, S., et al. 2010, A&A, 521, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Kaufman, M. J., & Neufeld, D. A. 1996, ApJ, 456, 250 [NASA ADS] [CrossRef] [Google Scholar]
  46. Kogan, L., & Slysh, V. 1998, ApJ, 497, 800 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kurtz, S., Hofner, P., & Álvarez, C. V. 2004, ApJS, 155, 149 [NASA ADS] [CrossRef] [Google Scholar]
  48. Lees, R. M. 1973, ApJ, 184, 763 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lees, R. M., & Haque, S. 1974, Can. J. Phys., 52, 2250 [Google Scholar]
  50. Lees, R. M., & Oka, T. 1969, J. Chem. Phys., 51, 3027 [NASA ADS] [CrossRef] [Google Scholar]
  51. Leurini, S., Schilke, P., Menten, K. M., et al. 2004, A&A, 422, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Liechti, S., & Wilson, T. L. 1996, A&A, 314, 615 [NASA ADS] [Google Scholar]
  53. Lonsdale, C. J., Doeleman, S. S., Liechti, S., et al. 1998, BAAS, 30, 1355 [NASA ADS] [Google Scholar]
  54. Matsakis, D. N., Wright, M. C. H., Townes, C. H., et al. 1980, ApJ, 236, 481 [NASA ADS] [CrossRef] [Google Scholar]
  55. Matsumoto, N., Hirota, T., Sugiyama, K., et al. 2014, ApJ, 789, L1 [NASA ADS] [CrossRef] [Google Scholar]
  56. McEwen, B. C., Pihlström, Y. M., & Sjouwerman, L. O. 2014, ApJ, 793, 133 [NASA ADS] [CrossRef] [Google Scholar]
  57. Mehringer, D. M., & Menten, K. M. 1997, ApJ, 474, 346 [NASA ADS] [CrossRef] [Google Scholar]
  58. Mehrotra, S. C., Dreizler, H., & Mäder, H. 1985, Naturforschung, 40, 683 [Google Scholar]
  59. Menten, K. 1991a, in Atoms, Ions and Molecules: New Results in Spectral Line Astrophysics, ASP Conf. Ser., 16, 119 [NASA ADS] [Google Scholar]
  60. Menten, K. M. 1991b, ApJ, 380, L75 [NASA ADS] [CrossRef] [Google Scholar]
  61. Menten, K. M., & Batrla, W. 1989, ApJ, 341, 839 [NASA ADS] [CrossRef] [Google Scholar]
  62. Menten, K. M., Walmsley, C. M., Henkel, C., & Wilson, T. L. 1986, A&A, 157, 318 [NASA ADS] [Google Scholar]
  63. Menten, K. M., Johnston, K. J., Wadiak, E. J., Walmsley, C. M., & Wilson, T. L. 1988a, ApJ, 331, L41 [NASA ADS] [CrossRef] [Google Scholar]
  64. Menten, K. M., Reid, M. J., Moran, J. M., et al. 1988b, ApJ, 333, L83 [NASA ADS] [CrossRef] [Google Scholar]
  65. Menten, K. M., Walmsley, C. M., Henkel, C., & Wilson, T. L. 1988c, A&A, 198, 267 [NASA ADS] [Google Scholar]
  66. Menten, K. M., Walmsley, C. M., Henkel, C., & Wilson, T. L. 1988d, A&A, 198, 253 [NASA ADS] [Google Scholar]
  67. Menten, K. M., Reid, M. J., Pratap, P., Moran, J. M., & Wilson, T. L. 1992, ApJ, 401, L39 [NASA ADS] [CrossRef] [Google Scholar]
  68. Momjian, E., & Sarma, A. P. 2012, AJ, 144, 189 [NASA ADS] [CrossRef] [Google Scholar]
  69. Morimoto, M., Kanzawa, T., & Ohishi, M. 1985, ApJ, 288, L11 [NASA ADS] [CrossRef] [Google Scholar]
  70. Moscadelli, L., Menten, K. M., Walmsley, C. M., & Reid, M. J. 1999, ApJ, 519, 244 [Google Scholar]
  71. Moscadelli, L., Goddi, C., Cesaroni, R., Beltrán, M. T., & Furuya, R. S. 2007, A&A, 472, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Müller, H. S. P., Menten, K. M., & Mäder, H. 2004, A&A, 428, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
  75. Nakano, M., & Yoshida, S. 1986, PASJ, 38, 531 [NASA ADS] [Google Scholar]
  76. Nesterenok, A. V. 2016, MNRAS, 455, 3978 [NASA ADS] [CrossRef] [Google Scholar]
  77. Pelling, M. 1975, MNRAS, 172, 41 [NASA ADS] [CrossRef] [Google Scholar]
  78. Pihlström, Y. M., Sjouwerman, L. O., & Fish, V. L. 2011, ApJ, 739, L21 [NASA ADS] [CrossRef] [Google Scholar]
  79. Pihlström, Y. M., Sjouwerman, L. O., Frail, D. A., et al. 2014, AJ, 147, 73 [NASA ADS] [CrossRef] [Google Scholar]
  80. Plambeck, R. L., & Menten, K. M. 1990, ApJ, 364, 555 [NASA ADS] [CrossRef] [Google Scholar]
  81. Plambeck, R. L., & Wright, M. C. H. 1988, ApJ, 330, L61 [NASA ADS] [CrossRef] [Google Scholar]
  82. Pratap, P., Shute, P. A., Keane, T. C., Battersby, C., & Sterling, S. 2008, AJ, 135, 1718 [NASA ADS] [CrossRef] [Google Scholar]
  83. Rabli, D., & Flower, D. R. 2010, MNRAS, 406, 95 [NASA ADS] [CrossRef] [Google Scholar]
  84. Sarma, A. P., & Momjian, E. 2009, ApJ, 705, L176 [NASA ADS] [CrossRef] [Google Scholar]
  85. Sarma, A. P., & Momjian, E. 2011, ApJ, 730, L5 [NASA ADS] [CrossRef] [Google Scholar]
  86. Sanna, A., Moscadelli, L., Cesaroni, R., et al. 2010, A&A, 517, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Sastry, K. V. L. N., Lees, R. M., & de Lucia, F. C. 1984, J. Mol. Spectr., 103, 486 [Google Scholar]
  88. Schilke, P., Walmsley, C. M., Pineau des Forets, G., & Flower, D. R. 1997, A&A, 321, 293 [NASA ADS] [Google Scholar]
  89. Sjouwerman, L. O., Murray, C. E., Pihlström, Y. M., Fish, V. L., & Araya, E. D. 2010a, ApJ, 724, L158 [NASA ADS] [CrossRef] [Google Scholar]
  90. Sjouwerman, L. O., Pihlström, Y. M., & Fish, V. L. 2010b, ApJ, 710, L111 [NASA ADS] [CrossRef] [Google Scholar]
  91. Slysh, V. I., & Kalenskii, S. V. 2009, Astron. Rep., 53, 519 [NASA ADS] [CrossRef] [Google Scholar]
  92. Slysh, V. I., Kalenskij, S. V., & Val’tts, I. E. 1993, ApJ, 413, L133 [NASA ADS] [CrossRef] [Google Scholar]
  93. Slysh, V. I., Kalenskii, S. V., Valtts, I. E., & Otrupcek, R. 1994, MNRAS, 268, 464 [NASA ADS] [CrossRef] [Google Scholar]
  94. Slysh, V. I., Kalenskii, S. V., Val’tts, I. E., & Golubev, V. V. 1997, ApJ, 478, L37 [NASA ADS] [CrossRef] [Google Scholar]
  95. Slysh, V. I., Kalenskii, S. V., Val’tts, I. E., Golubev, V. V., & Mead, K. 1999, ApJS, 123, 515 [NASA ADS] [CrossRef] [Google Scholar]
  96. Slysh, V. I., Kalenskiĭ, S. V., & Val’Tts, I. E. 2002, Astron. Rep., 46, 49 [Google Scholar]
  97. Sobolev, A. M. 1992, Sov. Astron., 36, 590 [NASA ADS] [Google Scholar]
  98. Sobolev, A. M., & Deguchi, S. 1994a, ApJ, 433, 719 [NASA ADS] [CrossRef] [Google Scholar]
  99. Sobolev, A. M., & Deguchi, S. 1994b, A&A, 291, 569 [NASA ADS] [Google Scholar]
  100. Sobolev, A. M., & Strelnitskii, V. S. 1983, Sov. Astron. Lett., 9, 12 [NASA ADS] [Google Scholar]
  101. Sobolev, A. M., Cragg, D. M., & Godfrey, P. D. 1997, A&A, 324, 211 [NASA ADS] [Google Scholar]
  102. Sobolev, A. M., Wallin, B. K., & Watson, W. D. 1998, ApJ, 498, 763 [NASA ADS] [CrossRef] [Google Scholar]
  103. Szczepanski, J. C., Ho, P. T. P., Haschick, A. D., & Baan, W. A. 1989, in The Center of the Galaxy, ed. M. Morris, IAU Symp., 136, 383 [NASA ADS] [Google Scholar]
  104. Tsunekawa, S., Ukai, T., Toyama, A., & Takagi, K. 1995, Department of Physics, Toyama University, Japan, http://www.sci.u-toyama.ac.jp/phys/4ken/atlas/ [Google Scholar]
  105. Urquhart, J. S., Moore, T. J. T., Menten, K. M., et al. 2015, MNRAS, 446, 3461 [NASA ADS] [CrossRef] [Google Scholar]
  106. Val’tts, I. E., Dzyura, A. M., Kalenskii, S. V., et al. 1995, Astron. Rep., 39, 18 [NASA ADS] [Google Scholar]
  107. Val’tts, I. E., Ellingsen, S. P., Slysh, V. I., et al. 2000, MNRAS, 317, 315 [NASA ADS] [CrossRef] [Google Scholar]
  108. van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Voronkov, M., Sobolev, A., Ellingsen, S., Ostrovskii, A., & Alakoz, A. 2005, Ap&SS, 295, 217 [NASA ADS] [CrossRef] [Google Scholar]
  110. Voronkov, M. A., Brooks, K. J., Sobolev, A. M., et al. 2006, MNRAS, 373, 411 [NASA ADS] [CrossRef] [Google Scholar]
  111. Voronkov, M. A., Brooks, K. J., Sobolev, A. M., et al. 2007, in IAU Symp. 242, eds. J. M. Chapman & W. A. Baan, 182 [Google Scholar]
  112. Voronkov, M. A., Caswell, J. L., Britton, T. R., et al. 2010a, MNRAS, 408, 133 [NASA ADS] [CrossRef] [Google Scholar]
  113. Voronkov, M. A., Caswell, J. L., Ellingsen, S. P., & Sobolev, A. M. 2010b, MNRAS, 405, 2471 [NASA ADS] [Google Scholar]
  114. Voronkov, M. A., Walsh, A. J., Caswell, J. L., et al. 2011, MNRAS, 413, 2339 [NASA ADS] [CrossRef] [Google Scholar]
  115. Voronkov, M. A., Caswell, J. L., Ellingsen, S. P., et al. 2012, in IAU Symp. 287, eds. R. S. Booth, W. H. T. Vlemmings, & E. M. L. Humphreys, 433 [Google Scholar]
  116. Voronkov, M. A., Caswell, J. L., Ellingsen, S. P., Green, J. A., & Breen, S. L. 2014, MNRAS, 439, 2584 [NASA ADS] [CrossRef] [Google Scholar]
  117. Walmsley, C. M., Menten, K. M., Batrla, W., & Matthews, H. E. 1988, A&A, 197, 271 [NASA ADS] [Google Scholar]
  118. Wilgenbus, D., Cabrit, S., Pineau des Forêts, G., & Flower, D. R. 2000, A&A, 356, 1010 [NASA ADS] [Google Scholar]
  119. Wilson, T. L., Zeng, Q., Huettemeister, S., & Dahmen, G. 1996, A&A, 307, 209 [NASA ADS] [Google Scholar]
  120. Yanagida, T., Sakai, T., Hirota, T., et al. 2014, ApJ, 794, L10 [NASA ADS] [CrossRef] [Google Scholar]
  121. Yusef-Zadeh, F., Cotton, W., Viti, S., Wardle, M., & Royster, M. 2013, ApJ, 764, L19 [NASA ADS] [CrossRef] [Google Scholar]
  122. Zapata, L. A., Loinard, L., Su, Y.-N., et al. 2012, ApJ, 744, 86 [NASA ADS] [CrossRef] [Google Scholar]
  123. Zeng, Q., Lou, G. F., & Li, S. Z. 1987, Ap&SS, 132, 263 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Additional figures

Here we present the additional figures discussed in Sect. 4. We first present the excitation temperatures of the 36 GHz, 84 GHz, and 95 GHz masers as functions of ξ for 200 K and for different densities to complement the plots for the other lines presented in the main text (Fig. A.1). Figures A.2–A.3 illustrate the maser loss rate Γ, the pump rate coefficient q, and the inversion efficiency η as functions of ξ for the 84 GHz and 95 GHz masers at various densities and temperatures. Finally, in Fig. A.4 we present the photon production rates of the 36 GHz and 84 GHz lines as functions of the methanol maser emission measures for different physical parameters.

thumbnail Fig. A.1

Excitation temperature of the 36 GHz (upper panel), 84 GHz (middle panel), and 95 GHz lines (lower panel) at different densities and for a temperature of 200 K. Curves are plotted until Tex becomes positive. It is possible to convert ξ to methanol abundance using Eq. (3).

thumbnail Fig. A.2

Modelling results for the 84 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).

thumbnail Fig. A.3

Modelling results for the 95 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).

thumbnail Fig. A.4

Modelling results for the 36 GHz (bottom) and 84 GHz (middle) maser photon production rates, and for their ratios (top) at 200 K for various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). It is possible to convert ξ to methanol abundance using Eq. (3).

All Tables

Table 1

Known interstellar Class I methanol maser transitions.

In the text
Table 2

Summary of typical Class I maser luminosities, Liso, brightness temperatures, Tb, and spot sizes.

In the text
Table 3

ξq for various Class I lines at different densities for T = 80 K and 200 K.

In the text

All Figures

thumbnail Fig. 1

For both NGC 2264 (left) and DR21-W (right), lowest spectrum: absorption in the CH3OH 20 → 3-1-E line; other spectra: various maser transitions taken with differing velocity resolutions and a number of telescopes. Adopted from Menten (1991a). All spectra where taken between 1988 and 1990. The spectra of the 4-1 → 30-E and 70 → 1-A+ lines are from Haschick et al. (1990) and those of the 20 → 3-1-E lines were taken with the Green Bank 140-foot telescope. The remaining spectra were taken with the IRAM 30 m telescope.
In the text
thumbnail Fig. 2

Spitzer IRAC image of the DR21(OH) region (3.6 μm blue, 4.5 μm green, 8.0 μm red). The images were retrieved from the Spitzer archive. The red crosses mark the positions of 36 GHz masers from Fish et al. (2011). Cyan contours represent the integrated intensity of the thermal 42 → 31-E methanol line (Zapata et al. 2012) which traces the E-W outflow seen in the Class I masers.
In the text
thumbnail Fig. 3

Partial rotational level diagram of E-type (left) and A-type methanol (right). Known Class I maser transitions are connected by red lines with frequencies indicated; blue dotted lines connect anti-inverted transitions. We note that all of the maser lines originating in the J2 → J1E series near 25 GHz are indicated by dotted red lines.
In the text
thumbnail Fig. 4

Effective pump and loss rate for the 36 GHz maser at different densities and for a temperature of 200 K (upper panels) and at different temperatures for n = 106 cm-3 (lower panels). It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. 5

Excitation temperature, Tex, of the 44 GHz (upper panel) and of the 62−61-E 25.018 GHz line (lower panel) at different densities and for a temperature of 200 K. Curves are plotted until Tex becomes positive. It is possible to convert ξ to methanol abundance using Eq. (3). We note that with increasing ξ, the excitation temperature typically transits from −infinity to +infinity before thermalising. The discrete nature of our grid in ξ occasionally obscures this fact.
In the text
thumbnail Fig. 6

Excitation temperature of the 44 GHz, 95 GHz, and 36 GHz lines (lower panels), and the 84 GHz and 62−61-E masers (upper panels) for a temperature of 200 K and a specific column density of 1016 cm-2 km-1 s (left) and of 1017 cm-2 km-1 s (right) as functions of volume density. The dashed horizontal line separates maser from non-maser behaviour. Vertical lines mark the transitions from maser to non-maser behaviour.
In the text
thumbnail Fig. 7

Modelling results for the 44 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. 8

Modelling results for the 36 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. 9

Modelling results for the 62−61-E 25.018 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. 10

Modelling results for the 44 GHz, 36 GHz, and 95 GHz maser photon production rates, and for their ratios at 200 K for various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). The horizontal dashed line in the panels showing the 44 GHz to 36 GHz ratio marks the peak value of the flux-density ratio distribution reported by Voronkov et al. (2014). It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. 11

Modelling results for the photon production rate of the J2−J1-E (J = 2−10) series at 25 GHz maser at 200 K for various densities (bottom panel) and at n = 107 cm-3 and several temperatures (upper panel). It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. 12

Bottom panel: comparison of the maser photon production rates for the 44 GHz, 36 GHz, and 25 GHz (J = 6) for various densities at 200 K. For example, the solid red and blue curves in the middle panel show a power law of ξ0.4 and ξ0.7, respectively. Top panel: modelling results for the ratios of the 62−61-E maser photon production rate to that of the 44 GHz and 36 GHz lines for various densities at 200 K. It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. 13

Js and Ts as function of ξ for different densities and temperatures for the 44 GHz (solid line) and 95 GHz (dashed lines) transitions a), and for the 36 GHz (solid line) and 84 GHz (dashed lines) masers b). It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. 14

Js and Ts as function of ξ for different densities and temperatures for the 62−61-E maser. It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. A.1

Excitation temperature of the 36 GHz (upper panel), 84 GHz (middle panel), and 95 GHz lines (lower panel) at different densities and for a temperature of 200 K. Curves are plotted until Tex becomes positive. It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. A.2

Modelling results for the 84 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. A.3

Modelling results for the 95 GHz maser pumping at T = 200 K and various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). Plotted are the maser loss rate Γ divided by n6, the pump rate coefficient q, and the inversion efficiency η as functions of ξ. It is possible to convert ξ to methanol abundance using Eq. (3).
In the text
thumbnail Fig. A.4

Modelling results for the 36 GHz (bottom) and 84 GHz (middle) maser photon production rates, and for their ratios (top) at 200 K for various densities (left panel) and at n = 106 cm-3 and several temperatures (right panel). It is possible to convert ξ to methanol abundance using Eq. (3).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.