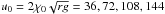| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201628713 | |
| Published online | 28 June 2016 | |
Damping of prominence longitudinal oscillations due to mass accretion
1 School of Mathematics and Statistics (SoMaS), The University of Sheffield, Hicks Building, Hounsfield Road, Sheffield S3 7RH, UK
e-mail: m.s.ruderman@sheffield.ac.uk
2 Space Research Institute (IKI) Russian Academy of Sciences, 117810 Moscow, Russia
3 Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
4 Universidad de La Laguna, Dept. Astrofísica, 38206 La Laguna, Tenerife, Spain
Received: 14 April 2016
Accepted: 9 May 2016
We study the damping of longitudinal oscillations of a prominence thread caused by the mass accretion. We suggested a simple model describing this phenomenon. In this model we considered a thin curved magnetic tube filled with the plasma. The prominence thread is in the central part of the tube and it consists of dense cold plasma. The parts of the tube at the two sides of the thread are filled with hot rarefied plasma. We assume that there are flows of rarefied plasma toward the thread caused by the plasma evaporation at the magnetic tube footpoints. Our main assumption is that the hot plasma is instantaneously accommodated by the thread when it arrives at the thread, and its temperature and density become equal to those of the thread. Then we derive the system of ordinary differential equations describing the thread dynamics. We solve this system of ordinary differential equations in two particular cases. In the first case we assume that the magnetic tube is composed of an arc of a circle with two straight lines attached to its ends such that the whole curve is smooth. A very important property of this model is that the equations describing the thread oscillations are linear for any oscillation amplitude. We obtain the analytical solution of the governing equations. Then we obtain the analytical expressions for the oscillation damping time and periods. We find that the damping time is inversely proportional to the accretion rate. The oscillation periods increase with time. We conclude that the oscillations can damp in a few periods if the inclination angle is sufficiently small, not larger that 10°, and the flow speed is sufficiently large, not less that 30 km s-1. In the second model we consider the tube with the shape of an arc of a circle. The thread oscillates with the pendulum frequency dependent exclusively on the radius of curvature of the arc. The damping depends on the mass accretion rate and the initial mass of the threads, that is the mass of the thread at the moment when it is perturbed. First we consider small amplitude oscillations and use the linear description. Then we consider nonlinear oscillations and assume that the damping is slow, meaning that the damping time is much larger that the characteristic oscillation time. The thread oscillations are described by the solution of the nonlinear pendulum problem with slowly varying amplitude. The nonlinearity reduces the damping time, however this reduction is small. Again the damping time is inversely proportional to the accretion rate. We also obtain that the oscillation periods decrease with time. However even for the largest initial oscillation amplitude considered in our article the period reduction does not exceed 20%. We conclude that the mass accretion can damp the motion of the threads rapidly. Thus, this mechanism can explain the observed strong damping of large-amplitude longitudinal oscillations. In addition, the damping time can be used to determine the mass accretion rate and indirectly the coronal heating.
Key words: hydrodynamics / waves / Sun: chromosphere / Sun: corona / Sun: filaments, prominences / Sun: oscillations
© ESO, 2016
1. Introduction
The first observation of a large-amplitude longitudinal oscillation (LALO) was reported by Jing et al. (2003). In this oscillation a large portion of the cool prominence-mass moved parallel to the filament axis with a total displacement of 140 Mm and the velocity amplitude of 92 km s-1, which is clearly in the range of large-amplitude motions according to the classification by Oliver & Ballester (2002). It seems that in this motion the thread moved parallel to itself and to the local magnetic field. The oscillation period was about 80 min with the damping time about 210 min, that is 2.6 times the period. These numbers indicate that the oscillation damping was very strong. More events have since been reported by Jing et al. (2006), Vršnak et al. (2007), Zhang et al. (2012), Li & Zhang (2012), Luna et al. (2014), Bi et al. (2014), and Shen et al. (2014). The range of the velocity amplitude was between 20 and 100 km s-1, the period between 40 and 160 min, and the damping time between 1 and 3.8 periods. Again these observations indicate a very strong damping. We expect the damping mechanism to be very efficient as it damps very energetic LALOs so rapidly.
The origin of the prominence mass is an open question, but it has been long known that the mass must come from the chromosphere (Pikelner 1971). It is unclear how the chromospheric mass is deposited into the corona. At present, the evaporation-condensation model (Antiochos & Klimchuk 1991) is the most advanced in its ability to explain thermal properties, speed, and mass of prominences (e.g., Antiochos et al. 2000; Karpen et al. 2001, 2005; Karpen & Antiochos 2008; Xia et al. 2011, 2014; Luna et al. 2012b; Keppens & Xia 2014). In this model the coronal heating localized at the footpoints of the prominence magnetic structure produces the chromospheric plasma evaporation. This evaporated hot plasma flows along the field lines and condenses because of the optically thin radiation of the corona in dipped parts of the magnetic field lines, forming a cool prominence. Once the prominence is formed the same mechanism produces a constant accretion of mass into the prominence thread.
The damping mechanism of LALOs is poorly understood. Several damping mechanisms have been suggested but not rigorously tested, for example, energy leakage by the sound wave emission (Kleczek & Kuperus 1969) or some form of dissipation (Tripathi et al. 2009; Oliver 2009). A model of the LALOs based on numerical simulation was constructed (Luna et al. 2012b, 2016; Luna & Karpen 2012), demonstrating that the restoring force is the projected gravity on magnetic tubes where the threads oscillate. In this model the motion is strongly damped by the steady accretion of mass onto the threads by the evaporation-condensation process. It was found that the temporal dependence of the thread velocity is described by a Bessel function rather than by a sinusoid. This indicates that the accretion of mass by the threads not only damps the motion but also produces observable changes in the temporal profile of the oscillation.
In the model suggested by Luna & Karpen (2012) the prominence threads were considered as point-like particles (0 dimension) with the increasing mass moving along a rigid field line. In this article we improve the model of Luna & Karpen (2012) by considering a 1D thread model moving in a rigid magnetic tube in the presence of an accretion flow. The paper is organized as follows. In the next section the model is presented and the equations governing the thread motion are derived. In Sect. 3 we consider the prominence thread oscillations in a magnetic tube consisting of a arc of a circle with two straight parts attached at its ends. In Sect. 4 we study the thread oscillations in a magnetic tube shaped like an arc of a circle. Section 5 contains a summary of the results and our conclusions.
2. Derivation of governing equations
In the equilibrium there is a magnetic tube of constant cross-section. In Cartesian coordinates x,y,z with the z-axis vertical, the tube’s axis is in the xz-plane. Its shape is determined by the equations  (1)where s is the arclength measured along the axis. Ruderman (2015) showed that a magnetic tube with a constant cross-section radius and an arbitrary axis shape can be embedded in a potential magnetic field. Hence the functions x(s) and z(s) can be chosen arbitrarily. The gravity acceleration is g = (0,0,−g). The magnetic tube length is ℓ, meaning that 0 ≤ s ≤ ℓ. There is a dense plasma with the density ρp per unit length between s = p and s = q. The plasma density per unit length in s<p and s>q is ρe<ρp. Below we assume that ρp and ρe are constant. The unit tangent vector to the tube axis is l = (x′(s),0,z′(s)), where the prime indicates the derivative. The projection of the gravity acceleration on the tube axis is l·g = −gz′(s). The projection on the tube axis of the gravity force acting on the element of the dense prominence thread from s to s + Δs is −gρpz′(s) Δs. Then the total projection of the gravity force acting on the thread is
(1)where s is the arclength measured along the axis. Ruderman (2015) showed that a magnetic tube with a constant cross-section radius and an arbitrary axis shape can be embedded in a potential magnetic field. Hence the functions x(s) and z(s) can be chosen arbitrarily. The gravity acceleration is g = (0,0,−g). The magnetic tube length is ℓ, meaning that 0 ≤ s ≤ ℓ. There is a dense plasma with the density ρp per unit length between s = p and s = q. The plasma density per unit length in s<p and s>q is ρe<ρp. Below we assume that ρp and ρe are constant. The unit tangent vector to the tube axis is l = (x′(s),0,z′(s)), where the prime indicates the derivative. The projection of the gravity acceleration on the tube axis is l·g = −gz′(s). The projection on the tube axis of the gravity force acting on the element of the dense prominence thread from s to s + Δs is −gρpz′(s) Δs. Then the total projection of the gravity force acting on the thread is ![\begin{eqnarray} f_g = -\int_p^q g\rho_p z'(s)\,{\rm d}s = g\rho_p[z(p) - z(q)]. \label{eq:2} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq28.png) (2)We assume that there is continuous plasma evaporation at the tube footpoints that creates the plasma flows at the two sides of the thread. The flow speed is v = const and the flows are directed toward the thread at both sides. The plasma flux at both sides is the same and equal to ρev. The thread velocity is u, and we assume that the plasma flow speed is larger than the thread speed, v> | u |.
(2)We assume that there is continuous plasma evaporation at the tube footpoints that creates the plasma flows at the two sides of the thread. The flow speed is v = const and the flows are directed toward the thread at both sides. The plasma flux at both sides is the same and equal to ρev. The thread velocity is u, and we assume that the plasma flow speed is larger than the thread speed, v> | u |.
Our main assumption is that the accreting material is instantaneously absorbed by the thread, and its density, temperature and velocity become the same as those of the thread material. Due to accretion the velocity of the left end of the thread is smaller than u, while the velocity of the right end of the thread is larger than u. The relative velocity of the rarefied plasma flow and the thread is v−ṗ at the left thread end, and 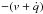 at the right thread end, where the dot indicates the time derivative. Hence, the rate of thread length increase at the left end is ρe(v−ṗ) /ρp, while at the right end it is
at the right thread end, where the dot indicates the time derivative. Hence, the rate of thread length increase at the left end is ρe(v−ṗ) /ρp, while at the right end it is 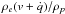 . It then follows that
. It then follows that 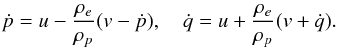 (3)As a result, we obtain
(3)As a result, we obtain 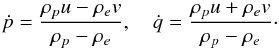 (4)The mass of the thread is M(t) = ρp(q−p). Differentiating this relation and using Eq. (4) we obtain
(4)The mass of the thread is M(t) = ρp(q−p). Differentiating this relation and using Eq. (4) we obtain 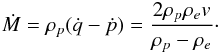 (5)Integrating this equation yields
(5)Integrating this equation yields 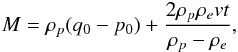 (6)where p = p0 and q = q0 at t = 0.
(6)where p = p0 and q = q0 at t = 0.
Consider a system consisting of the thread and two volumes of rarefied plasma attached to the thread at the left and the right. The length of the left volume is (v−ṗ)Δt, while the length of the right volume is 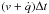 . The linear momentum of this system is
. The linear momentum of this system is
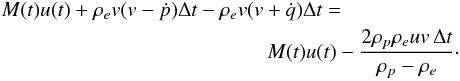 (7)After time Δt the plasma in both volumes is absorbed by the thread. The thread mass and velocity become M(t + Δt) and u(t + Δt). The change in the linear momentum is equal to the impulse of force fg Δt,
(7)After time Δt the plasma in both volumes is absorbed by the thread. The thread mass and velocity become M(t + Δt) and u(t + Δt). The change in the linear momentum is equal to the impulse of force fg Δt,
![\begin{eqnarray} && M(t+\Delta t) u(t+\Delta t) - M(t)u(t) +\, \frac{2\rho_p\rho_e uv\,\Delta t} {\rho_p - \rho_e} =\nonumber\\ &&\hspace*{5.5cm} g\rho_p[z(p) - z(q)]\Delta t . \label{eq:6b} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq52.png) (8)Dividing this relation by Δt and taking Δt → 0 we obtain
(8)Dividing this relation by Δt and taking Δt → 0 we obtain ![\begin{eqnarray} \frac{{\rm d}(Mu)}{{\rm d}t} = g\rho_p[z(p) - z(q)] - \frac{2\rho_p\rho_e u \, v}{\rho_p - \rho_e} \cdot \label{eq:7} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq54.png) (9)Using Eq. (6) we transform this equation to
(9)Using Eq. (6) we transform this equation to ![\begin{eqnarray} \left(q_0 - p_0 + \frac{2\rho_e vt}{\rho_p - \rho_e}\right)\dot{u} = g[z(p) - z(q)] - \frac{4\rho_e uv}{\rho_p - \rho_e} \cdot \label{eq:8} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq55.png) (10)Equations (4) and (10) constitute the system of equations for u, p and q.
(10)Equations (4) and (10) constitute the system of equations for u, p and q.
We consider the model presented in this section to be one of the first steps in understanding the damping mechanisms of LALOs, and we are well aware of its limitations. In this model we neglect many physical effects that, probably, exist in reality. We consider the plasma motion in LALOs as one-dimensional while in reality it is three-dimensional. The account of variation of the plasma parameters across the magnetic tube can result, for example, in the distortion of the boundary between the hot and cold plasmas which can complicate the process of hot plasma accretion. Probably, the most vulnerable assumption of our model is that the hot accreting plasma is instantaneously accommodated by the cold dense thread. Obviously the real process of hot plasma accretion is much more complex. The collision of flows of the hot and cold plasmas can cause formation of a very complex interaction region involving shocks. The relaxation of this region would, probably, involve heat conduction, ionisation and recombination. How much all these complicated processes will affect the damping of LALOs remains an open question. It should be addressed in the future by considering more sophisticated models.
3. Prominence oscillations in a magnetic tube with two straight parts
To obtain the solution to the system of Eqs. (4) and (10) we need to specify the magnetic tube shape. To make the problem as simple as possible we assume that the tube axis is composed of an arc of a circle with two straight lines attached to its ends such that the whole curve is smooth (see Fig. 1).
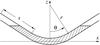 |
Fig. 1 Sketch of the equilibrium. The magnetic tube axis consists of an arc of a circle of radius r with the two straight lines attached. The dense prominence thread occupies the shaded area. Recall that we consider a one-dimensional problem and neglect the variation of all quantities across the magnetic tube. |
Hence, we take 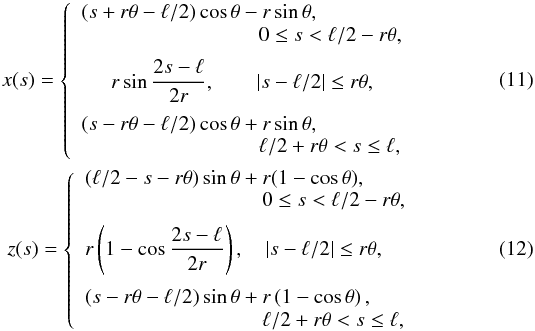 where θ is the angle that forms half of the arc with respect to the centre of curvature as plotted in Fig. 1. We introduce the dimensionless variables
where θ is the angle that forms half of the arc with respect to the centre of curvature as plotted in Fig. 1. We introduce the dimensionless variables 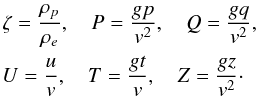 (13)Then we rewrite the system of Eqs. (4) and (10) in the dimensionless form as
(13)Then we rewrite the system of Eqs. (4) and (10) in the dimensionless form as ![\begin{eqnarray} &&\left(Q_0 - P_0 + \frac{2T}{\zeta - 1}\right)\frac{{\rm d}U}{{\rm d}T} = Z(P) - Z(Q) - \frac{4U}{\zeta - 1} , \label{eq:10}\\[3mm] &&\frac{{\rm d}P}{{\rm d}T} = \frac{\zeta U - 1}{\zeta - 1}, \quad \frac{{\rm d}Q}{{\rm d}T} = \frac{\zeta U + 1}{\zeta - 1}\cdot \label{eq:11} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq62.png) Now we assume that p<ℓ/ 2−rθ and q>ℓ/ 2 + rθ at any time, that is the ends of the dense thread are always on the straight parts of the magnetic tube. As a result, we obtain
Now we assume that p<ℓ/ 2−rθ and q>ℓ/ 2 + rθ at any time, that is the ends of the dense thread are always on the straight parts of the magnetic tube. As a result, we obtain 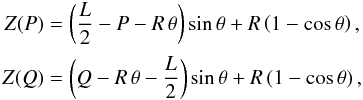 (16)where L = gℓ/v2 and R = gr/v2. It follows from this equation that
(16)where L = gℓ/v2 and R = gr/v2. It follows from this equation that 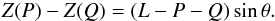 (17)Substituting this result in Eq. (14), differentiating the obtained equation, and using Eq. (15), we obtain the equation for U,
(17)Substituting this result in Eq. (14), differentiating the obtained equation, and using Eq. (15), we obtain the equation for U, ![\begin{eqnarray} \frac {\rm d}{{\rm d}T}\left([(Q_0 - P_0)(\zeta - 1) + 2T]\frac{{\rm d}U}{{\rm d}T} + 4U\right) = -2\zeta U\sin\theta . \label{eq:17} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq70.png) (18)Introducing the new variable σ = (Q0−P0)(ζ−1) + 2T we rewrite this equation as
(18)Introducing the new variable σ = (Q0−P0)(ζ−1) + 2T we rewrite this equation as 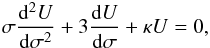 (19)where
(19)where 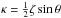 . Below we assume that Z(P0) = Z(Q0), which implies that P0 + Q0 = L. It then follows from Eqs. (14) and (17) that
. Below we assume that Z(P0) = Z(Q0), which implies that P0 + Q0 = L. It then follows from Eqs. (14) and (17) that 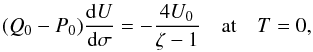 (20)where U0 = U(0). As a result, we have the following initial conditions for U:
(20)where U0 = U(0). As a result, we have the following initial conditions for U: 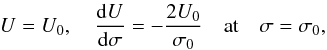 (21)where σ0 = (ζ−1)(Q0−P0). The variable substitution
(21)where σ0 = (ζ−1)(Q0−P0). The variable substitution  (22)reduces Eq. (21) to the Bessel equation
(22)reduces Eq. (21) to the Bessel equation 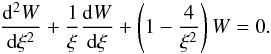 (23)The general solution to this equation is
(23)The general solution to this equation is 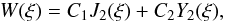 (24)where J2 and Y2 are the Bessel functions of the first and second kind, and C1 and C2 are arbitrary constants. Returning to the original variables we obtain
(24)where J2 and Y2 are the Bessel functions of the first and second kind, and C1 and C2 are arbitrary constants. Returning to the original variables we obtain ![\begin{eqnarray} U(\sigma) = \frac1\sigma\big[C_1 J_2\big(2\sqrt{\kappa\sigma}\big) + C_2 Y_2\big(2\sqrt{\kappa\sigma}\big)\big], \label{eq:24} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq87.png) (25)Substituting Eq. (25) in Eq. (21) yields
(25)Substituting Eq. (25) in Eq. (21) yields 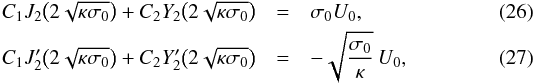 where the prime indicates the derivative of the Bessel function with respect to its argument. Using the identity (Abramowitz & Stegun 1972)
where the prime indicates the derivative of the Bessel function with respect to its argument. Using the identity (Abramowitz & Stegun 1972) 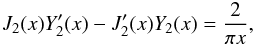 (28)we obtain from Eq. (27)
(28)we obtain from Eq. (27) ![\begin{eqnarray} \begin{array}{l} \displaystyle C_1 = \pi\sigma_0 U_0\big[\!\sqrt{\kappa\sigma_0}\, Y'_2\big(2\sqrt{\kappa\sigma_0}\big) + Y_2\big(2\sqrt{\kappa\sigma_0}\big)\big], \vspace*{2mm} \\ \displaystyle C_2 = -\pi\sigma_0 U_0\big[\!\sqrt{\kappa\sigma_0}\, J'_2\big(2\sqrt{\kappa\sigma_0}\big) + J_2\big(2\sqrt{\kappa\sigma_0}\big)\big]. \end{array} \label{eq:27} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq90.png) (29)Typically ζ ~ 100, while the initial length of the dense thread is a few Mm, lp = q0−p0 ≳ 2 Mm. If we take v ≲ 50 km s-1 and g = 274 m/s2, then Q0−P0 ≳ 0.2 and σ0 ≳ 20. In addition, the radius of curvature could be estimated as of the order of r = 60 Mm (see, Luna et al. 2014). We consider threads that are larger than the arched part of the tube, so lp ≥ 2rθ. For lp ≳ 2 Mm this inequality can be satisfied if we take θ = 1°. Hence, we assume below that θ ≳ 1°. With these considerations κ ≳ 0.8. Taking into account that σ ≥ σ0 we arrive at the estimate
(29)Typically ζ ~ 100, while the initial length of the dense thread is a few Mm, lp = q0−p0 ≳ 2 Mm. If we take v ≲ 50 km s-1 and g = 274 m/s2, then Q0−P0 ≳ 0.2 and σ0 ≳ 20. In addition, the radius of curvature could be estimated as of the order of r = 60 Mm (see, Luna et al. 2014). We consider threads that are larger than the arched part of the tube, so lp ≥ 2rθ. For lp ≳ 2 Mm this inequality can be satisfied if we take θ = 1°. Hence, we assume below that θ ≳ 1°. With these considerations κ ≳ 0.8. Taking into account that σ ≥ σ0 we arrive at the estimate 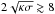 . For such values of the argument we can use the asymptotic expressions for the Bessel functions (Abramowitz & Stegun 1972) namely
. For such values of the argument we can use the asymptotic expressions for the Bessel functions (Abramowitz & Stegun 1972) namely 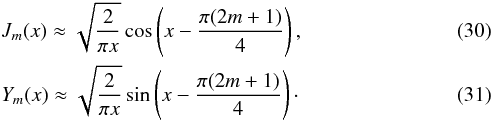 Then it follows from Eq. (29) that
Then it follows from Eq. (29) that ![\begin{eqnarray} &&C_1 \approx \frac{\sigma_0 U_0}\kappa\sqrt[4]{\pi^2\kappa\sigma_0} \cos\left(2\sqrt{\kappa\sigma_0} - \frac{5\pi}4\right), \quad \label{eq:29}\\ &&C_2 \approx \frac{\sigma_0 U_0}\kappa\sqrt[4]{\pi^2\kappa\sigma_0} \sin\left(2\sqrt{\kappa\sigma_0} - \frac{5\pi}4\right)\cdot \label{eq:29a} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq107.png) Substituting Eqs. (32) and (33) into Eq. (25) and using Eqs. (30) and (31) we transform it to the approximate form
Substituting Eqs. (32) and (33) into Eq. (25) and using Eqs. (30) and (31) we transform it to the approximate form 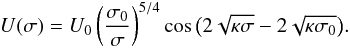 (34)This equation can be rewritten as
(34)This equation can be rewritten as 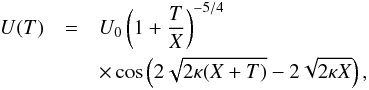 (35)where
(35)where 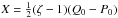 . In Fig. 2 we have plotted four examples of the temporal evolution of the oscillating threads given by the previous equation.
. In Fig. 2 we have plotted four examples of the temporal evolution of the oscillating threads given by the previous equation.
 |
Fig. 2 Temporal evolution of the velocity of the thread given by Eq. (35) normalized to the initial velocity U0 as function of time, t. We have assumed a typical situation of ζ = 100, r = 60 Mm, with g = 274 m s-2. For clarity, we have split the different cases studied into two panels. In a) a thread with lp = 2.1 Mm and θ = 1° is considered with v = 10 km s-1 (black curve) and v = 30 km s-1 (orange curve). In b) a thread with lp = 5 Mm and θ = 3° is considered with v = 10 km s-1 (red curve) and v = 30 km s-1 (blue curve). |
The maximum displacement of the thread occurs when the argument of cosine is approximately equal to 2πm, m = 0,1,... at times 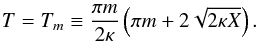 (36)Then the nth oscillation period is given by
(36)Then the nth oscillation period is given by ![\begin{eqnarray} \Pi_n = T_n - T_{n-1} = \frac\pi{2\kappa}\left[\pi(2n-1) + 2 \sqrt{2\kappa X}\right], \label{eq:33} \end{eqnarray}](/articles/aa/full_html/2016/07/aa28713-16/aa28713-16-eq126.png) (37)where n = 1,2,... This indicates that the period of the oscillation depends of the cycle of the oscillation. In general this period, Πn increases with time. In Fig. 2 the increase of the period for each oscillation is clear. The dimensional period Pn is
(37)where n = 1,2,... This indicates that the period of the oscillation depends of the cycle of the oscillation. In general this period, Πn increases with time. In Fig. 2 the increase of the period for each oscillation is clear. The dimensional period Pn is 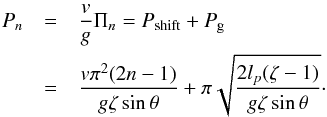 (38)The second term in the expression for Pn is associated with the gravity as a restoring force,
(38)The second term in the expression for Pn is associated with the gravity as a restoring force, 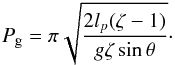 (39)This term gives the oscillation period when v = 0. We can recover the oscillation period found by Luna & Karpen (2012) and Luna et al. (2012a) if we assume that θ is small. Then sinθ ≈ θ and
(39)This term gives the oscillation period when v = 0. We can recover the oscillation period found by Luna & Karpen (2012) and Luna et al. (2012a) if we assume that θ is small. Then sinθ ≈ θ and 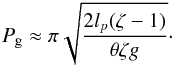 (40)In addition, Luna & Karpen (2012) and Luna et al. (2012a) assumed that the thread filled the dipped part of the flux tube meaning that rθ = lp/ 2. Then taking into account that, for typical prominences, the density contrast is very large meaning that 1−1 /ζ ~ 1, we finally arrive at
(40)In addition, Luna & Karpen (2012) and Luna et al. (2012a) assumed that the thread filled the dipped part of the flux tube meaning that rθ = lp/ 2. Then taking into account that, for typical prominences, the density contrast is very large meaning that 1−1 /ζ ~ 1, we finally arrive at 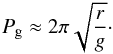 (41)Note that Eq. (38) gives a more general expression. The first term in Eq. (38), Pshift, introduces the period shift. During each cycle of the oscillation the period increases by
(41)Note that Eq. (38) gives a more general expression. The first term in Eq. (38), Pshift, introduces the period shift. During each cycle of the oscillation the period increases by 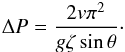 (42)The period shift is related to the accretion rate onto the thread associated with the rarefied plasma. When the accretion rate increases so does the period shift. Pshift = 0 when there is no accretion.
(42)The period shift is related to the accretion rate onto the thread associated with the rarefied plasma. When the accretion rate increases so does the period shift. Pshift = 0 when there is no accretion.
We define the damping time Td by the condition that the oscillation amplitude decreases e times at T = Td with respect to the value at T = 0 . Then, using Eq. (35), we obtain 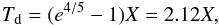 (43)and, in the dimensional variables,
(43)and, in the dimensional variables, 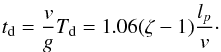 (44)This relation indicates that the oscillation damping time is inversely proportional to the accretion speed. The larger v is, the smaller the value of td is, and consequently, the stronger the damping is. Similarly, the larger the thread length lp is, the weaker the damping is. The reason for this is that the term (ζ−1)lp is essentially the mass of the thread at t = 0. The damping occurs because of the increase of the thread mass and the decrease of its momentum. Hence, the larger the initial thread mass the more time is needed to damp its movement.
(44)This relation indicates that the oscillation damping time is inversely proportional to the accretion speed. The larger v is, the smaller the value of td is, and consequently, the stronger the damping is. Similarly, the larger the thread length lp is, the weaker the damping is. The reason for this is that the term (ζ−1)lp is essentially the mass of the thread at t = 0. The damping occurs because of the increase of the thread mass and the decrease of its momentum. Hence, the larger the initial thread mass the more time is needed to damp its movement.
In this section we have assumed that the cold thread is larger than the arched part of the tube, lp ≥ 2rθ. Typical prominence threads are equal or smaller than 10 Mm but larger than a blob of 1 Mm. In our previous studies we found that r should be of the order of tens of Mm. In particular, in Luna et al. (2014) we determined the radius of curvature of the dipped field lines of an observed filament as approximately equal to 60 Mm. Using these numbers we obtain that the angle θ ≤ 5°. The speed of the accretion flow, v, depends on the coronal heating at the flux-tube footpoints (see, e.g. Karpen et al. 2003). Based on the simulations by Luna et al. (2012b) and the results by Karpen et al. (2005) we can estimate that the speed of the hot flows is of the order of 30 km s-1. We also take a typical value of ζ = 100 (see Labrosse et al. 2010). To plot Fig. 2 we have considered four sets of parameters. Figure 2a corresponds to a thread of initial length lp = 2.1 Mm and θ = 1°. The black line corresponds to the accretion velocity v = 10 km s-1 and the orange line corresponds to v = 30 km s-1. The difference in the accretion flow produces important changes in the damping time, td (Eq. (44)), and in the period shift, ΔP (Eq. (42)), but not in the gravity period, Pg (Eq. (39)). The damping and the period shift is stronger for the high accretion velocity (orange curve). For the case with v = 10 km s-1 (black line) Pg is 48.8 min, the shift is 3.4 min and the damping time is 367 min, and for the case with v = 30 km s-1 (orange line) Pg is also 48.8 min, the shift is 10.3 min and the damping time is 122 min. Due to the shift the period defined as the time interval between two consecutive maxima changes for each oscillation. With Eq. (38) we can compute the period of the nth cycle, as Pn = 3.4(2n−1) + 48.8 min = 52.2, 55.7, 59.1, ... min for the first set of parameters (black line). For the second set of parameters corresponding to the orange line the nth period is Pn = 10.3(2n−1) + 48.8 min = 59.1, 69.5, 79.8, ...min. From this panel we clearly see the dependence of the damping time and the period shift on the accretion velocity. Larger values of the accretion velocity produce stronger damping, that is shorter damping times, and larger period shifts. A similar result can be seen in Fig. 2b for a larger thread of initial length lp = 5 Mm. In this case the damping and the period shift is weaker than in the case with shorter threads (Fig. 2a). In fact, stronger damping, that is smaller damping time, involves larger period shifts. It is possible to combine Eqs. (39), (42), and (44) to obtain 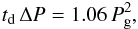 (45)where we have assumed that the density contrast is large enough and taken ζ−1 ≈ ζ. This relation reflects the fact that, for a given gravity period Pg, a strong damping (small td) corresponds to a large period shift (large ΔP) and vice versa. This behaviour is clear in both panels in Fig. 2. In Fig. 2a both cases have the same gravity period Pg. The oscillation plotted in the orange curve has stronger damping and also larger period shift than in the case showed by the black curve. A similar effect can be seen in Fig. 2b.
(45)where we have assumed that the density contrast is large enough and taken ζ−1 ≈ ζ. This relation reflects the fact that, for a given gravity period Pg, a strong damping (small td) corresponds to a large period shift (large ΔP) and vice versa. This behaviour is clear in both panels in Fig. 2. In Fig. 2a both cases have the same gravity period Pg. The oscillation plotted in the orange curve has stronger damping and also larger period shift than in the case showed by the black curve. A similar effect can be seen in Fig. 2b.
As we have already pointed out, it follows from Eq. (44) that the damping time is proportional to the initial length of the thread and inversely proportional to the speed of the accretion flow. This means that the damping is stronger for smaller initial threads and for stronger accretion flows. Using Eq. (6) it is possible to relate the damping time with the mass of the thread at the initial time and the rate of mass accretion as 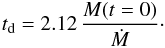 (46)This indicates that the damping is stronger in longitudinal oscillations produced in prominences with small thread mass.
(46)This indicates that the damping is stronger in longitudinal oscillations produced in prominences with small thread mass.
4. Prominence oscillations in a circular arched dip
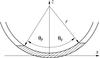 |
Fig. 3 Sketch of the equilibrium. The magnetic tube axis is an arc of a circle of radius r. The prominence occupies the shaded area. We again recall that we consider a one-dimensional problem and neglect the variation of all quantities across the magnetic tube. |
In this section we consider prominence oscillations in a magnetic tube that has the shape of an arc of a circle of radius r. The equilibrium state is shown in Fig. 3. We introduce the angles θp and θq between the lines connecting the centre of the circular arc and the ends of the dense prominence thread. These angles are given by 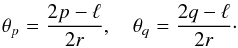 (47)For this geometry we have
(47)For this geometry we have  (48)Introducing the dimensionless variables
(48)Introducing the dimensionless variables 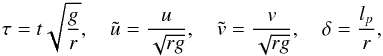 (49)we can rewrite the system of Eqs. (4) and (10) as
(49)we can rewrite the system of Eqs. (4) and (10) as 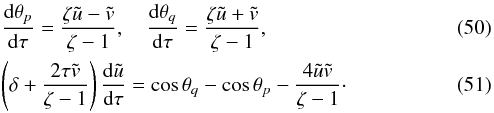 Prominence threads have typical lengths of a few Mm and the radius of curvature of several tens of Mm. Then we can assume that the length of the thread is much smaller than the radius of the dip curvature, l/r ≪ 1. This condition is equivalent to θq−θp ≪ 1 meaning that we can use the approximate relation
Prominence threads have typical lengths of a few Mm and the radius of curvature of several tens of Mm. Then we can assume that the length of the thread is much smaller than the radius of the dip curvature, l/r ≪ 1. This condition is equivalent to θq−θp ≪ 1 meaning that we can use the approximate relation 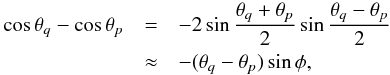 (52)where φ = (θq + θp)/2. Since the typical value of ζ is 100, below we neglect 1 in comparison to ζ. Then, using Eq. (52), we obtain from Eq. (50)
(52)where φ = (θq + θp)/2. Since the typical value of ζ is 100, below we neglect 1 in comparison to ζ. Then, using Eq. (52), we obtain from Eq. (50) 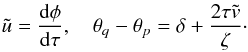 (53)With the aid of these results we reduce the Eq. (51) to
(53)With the aid of these results we reduce the Eq. (51) to 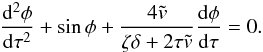 (54)Below we assume that initially the dense thread is in equilibrium and then it is pushed and starts to oscillate. In accordance with this we impose the initial conditions
(54)Below we assume that initially the dense thread is in equilibrium and then it is pushed and starts to oscillate. In accordance with this we impose the initial conditions 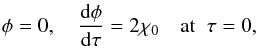 (55)where χ0 is a constant related to the initial impulse given to the thread by some external trigger.
(55)where χ0 is a constant related to the initial impulse given to the thread by some external trigger.
4.1. Linear theory with strong damping
We first consider small-amplitude oscillations and assume that φ ≪ 1. Thus, we can use the approximate relation sinφ ≈ φ and reduce Eq. (54) to 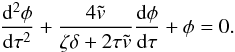 (56)The variable substitution
(56)The variable substitution 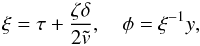 (57)reduces Eq. (56) to
(57)reduces Eq. (56) to 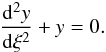 (58)The general solution to this equation is a linear combination of sinξ and cosξ. Then, returning to the original variables and using the initial conditions Eq. (55), we write the solution to Eq. (56) as
(58)The general solution to this equation is a linear combination of sinξ and cosξ. Then, returning to the original variables and using the initial conditions Eq. (55), we write the solution to Eq. (56) as 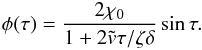 (59)This solution describes oscillations with constant period Π = 2π in the dimensionless variables. Thus, in this model, the period is constant and in the dimensional variables it is given by
(59)This solution describes oscillations with constant period Π = 2π in the dimensionless variables. Thus, in this model, the period is constant and in the dimensional variables it is given by 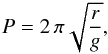 (60)which recovers the result by Luna & Karpen (2012). Luna et al. (2012a, 2016) numerically simulated the motion of perturbed localized cold plasma supported by a two-dimensional dipped magnetic field. They found that the back-reaction of the field on the plasma oscillation is very weak, validating the simpler assumption of rigid flux tubes in the present study. In particular, they found that the oscillation period was practically the same as that found by Luna & Karpen (2012).
(60)which recovers the result by Luna & Karpen (2012). Luna et al. (2012a, 2016) numerically simulated the motion of perturbed localized cold plasma supported by a two-dimensional dipped magnetic field. They found that the back-reaction of the field on the plasma oscillation is very weak, validating the simpler assumption of rigid flux tubes in the present study. In particular, they found that the oscillation period was practically the same as that found by Luna & Karpen (2012).
The amplitude of the oscillations is given by the initial dimensionless velocity 2χ0 = u0/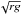 , and the damping time depends of the factor
, and the damping time depends of the factor 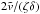 . This solution implies that the damping rate changes with time similarly to what was found in the previous section. The damping is stronger at the initial stage of the oscillation close to τ = 0, then later it decreases for larger τ. It is now convenient to introduce another dimensionless time
. This solution implies that the damping rate changes with time similarly to what was found in the previous section. The damping is stronger at the initial stage of the oscillation close to τ = 0, then later it decreases for larger τ. It is now convenient to introduce another dimensionless time 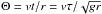 . As in the previous section we define the dimensionless damping time Θd by the condition that the oscillation amplitude decreases e times at Θ = Θd. Thus,
. As in the previous section we define the dimensionless damping time Θd by the condition that the oscillation amplitude decreases e times at Θ = Θd. Thus, 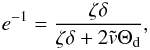 (61)and we obtain
(61)and we obtain 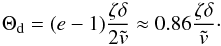 (62)In terms of dimensional variables we have
(62)In terms of dimensional variables we have 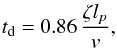 (63)which implies that the damping is sufficiently strong for small threads and for the large accretion speed. Using Eq. (6) it is possible to rewrite Eq. (63) as
(63)which implies that the damping is sufficiently strong for small threads and for the large accretion speed. Using Eq. (6) it is possible to rewrite Eq. (63) as 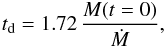 (64)which implies that the damping time not only depends on the mass accretion rate, but also on the initial mass of the thread. Equation (64) is almost identical to Eq. (46). They differ only in the constant at the front of the ratio of the initial mass and the mass accretion rate, and then only by a small amount. Equation (63) shows that strong damping is associated with large accretion rates and small initial thread masses. In Fig. 4 we plot the temporal evolution of φ for several values of parameters lp and v. In all the cases the period is P = 49 min. We clearly see from this figure that the larger lp the weaker the damping is, that is the larger the damping time is. Similarly, the larger the accretion velocity the stronger the damping is, that is the smaller the damping time is.
(64)which implies that the damping time not only depends on the mass accretion rate, but also on the initial mass of the thread. Equation (64) is almost identical to Eq. (46). They differ only in the constant at the front of the ratio of the initial mass and the mass accretion rate, and then only by a small amount. Equation (63) shows that strong damping is associated with large accretion rates and small initial thread masses. In Fig. 4 we plot the temporal evolution of φ for several values of parameters lp and v. In all the cases the period is P = 49 min. We clearly see from this figure that the larger lp the weaker the damping is, that is the larger the damping time is. Similarly, the larger the accretion velocity the stronger the damping is, that is the smaller the damping time is.
Luna & Karpen (2012) found that the temporal evolution of the oscillation velocity was given by a Bessel function of order one and the damping is produced by the phase in the argument of this function. However, here we have found that the temporal evolution of the velocity is given by the sine divided by a linear function of its argument. The phase of the argument is half that found in the case studied by Luna & Karpen (2012). The difference between the two models is in how the hot evaporated mass is deposited in the cool thread. Luna & Karpen (2012) assumed that the hot flows adapt to the motion of the thread and accretion at both sides of the thread is symmetric. Then, the momentum transferred to the thread by the hot evaporated flows is cancelled and the net momentum transfer is zero. In this case the damping is exclusively produced by the change of mass of the thread. In contrast, in the current work we assume that the hot evaporated flows are not affected by the motion of the thread. In this case there is a net transfer of the hot plasma flow momentum to the thread. This is given by the last term on the right hand side of Eq. (7). If we drop this term and solve the differential Eq. (10), then we recover the temporal evolution found by Luna & Karpen (2012). In a more realistic scenario that also includes the thermodynamic processes, the process of the momentum deposition is, probably, something in between these two extreme scenarios.
 |
Fig. 4 Angular position φ(τ) normalized to its amplitude 2χ0 as a function of t for various values of the parameters v and lp. We have taken g = 274 m s-2 and typical values of ζ = 100 and r = 60 Mm. In all cases the period is 49 min. The black curve corresponds to v = 30 km s-1 and lp = 2 Mm, the green curve to v = 10 km s-1 and lp = 2 Mm, the red curve to v = 40 km s-1 and lp = 5 Mm, and the blue curve to v = 10 km s-1 and lp = 5 Mm. The damping times for these combinations of parameters are td = 55.6, 166.7, 138.9, and 416.7 min, respectively. |
4.2. Nonlinear weakly damped oscillations
When there is no accretion (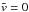 ) Eq. (54) reduces to the equation of nonlinear pendulum. Its small-amplitude oscillation is described by φ(τ) = φ0sinτ, where φ0 is the constant oscillation amplitude. In that case the characteristic time of the variation of function φ(τ) is 1. The characteristic time remains the same for nonlinear oscillations when the oscillation amplitude is smaller than or of the order of π/ 2. Damping of oscillations due to accretion can be considered as slow if the dimensionless damping time is much larger than one. Since one is approximately equal to one sixth of the oscillation period, which is 2π, this implies that the damping can be considered as slow if it is larger than or of the order of the oscillation period. This observation inspires us to search for a solution to the Eq. (54) describing slowly damped nonlinear oscillations. To do this we introduce the “slow” time τ1 = ϵτ, where ϵ ≪ 1 is of the order of the ratio of the characteristic oscillation time to the damping time. Then we consider φ as a function of two variables, τ and τ1. The damping is slow when the last term on the right-hand side of Eq. (54) is small. In accordance with this we put
) Eq. (54) reduces to the equation of nonlinear pendulum. Its small-amplitude oscillation is described by φ(τ) = φ0sinτ, where φ0 is the constant oscillation amplitude. In that case the characteristic time of the variation of function φ(τ) is 1. The characteristic time remains the same for nonlinear oscillations when the oscillation amplitude is smaller than or of the order of π/ 2. Damping of oscillations due to accretion can be considered as slow if the dimensionless damping time is much larger than one. Since one is approximately equal to one sixth of the oscillation period, which is 2π, this implies that the damping can be considered as slow if it is larger than or of the order of the oscillation period. This observation inspires us to search for a solution to the Eq. (54) describing slowly damped nonlinear oscillations. To do this we introduce the “slow” time τ1 = ϵτ, where ϵ ≪ 1 is of the order of the ratio of the characteristic oscillation time to the damping time. Then we consider φ as a function of two variables, τ and τ1. The damping is slow when the last term on the right-hand side of Eq. (54) is small. In accordance with this we put 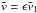 . After that Eq. (54) is transformed to
. After that Eq. (54) is transformed to 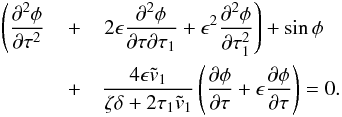 (65)Below we assume that φ is a periodic function of τ with the period Π that will be determined later. Note that, in general, Π can depend on τ1. We search for a solution to Eq. (65) in the form of expansion
(65)Below we assume that φ is a periodic function of τ with the period Π that will be determined later. Note that, in general, Π can depend on τ1. We search for a solution to Eq. (65) in the form of expansion 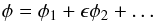 (66)Substituting this expansion in Eq. (65) and collecting terms of the order of unity we obtain the equation of nonlinear pendulum
(66)Substituting this expansion in Eq. (65) and collecting terms of the order of unity we obtain the equation of nonlinear pendulum 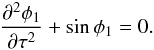 (67)Using Eq. (55) we obtain the initial conditions for φ1,
(67)Using Eq. (55) we obtain the initial conditions for φ1, 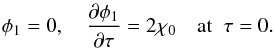 (68)It is straightforward to obtain the first integral of Eq. (67) satisfying the initial conditions Eq. (68),
(68)It is straightforward to obtain the first integral of Eq. (67) satisfying the initial conditions Eq. (68), 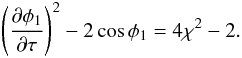 (69)The quantity χ2 is proportional to the energy of the oscillation. When there is no damping the energy is conserved and χ = χ0. However the energy decreases because of the damping, meaning that χ is a function of τ1. This function satisfies the initial condition χ = χ0 at τ1 = 0.
(69)The quantity χ2 is proportional to the energy of the oscillation. When there is no damping the energy is conserved and χ = χ0. However the energy decreases because of the damping, meaning that χ is a function of τ1. This function satisfies the initial condition χ = χ0 at τ1 = 0.
The angle φ1 takes its maximum when ∂φ1/∂τ = 0. Then it follows from Eq. (69) that the oscillation amplitude is 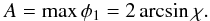 (70)Below we assume that the oscillation amplitude does not exceed π/ 2. This condition implies that
(70)Below we assume that the oscillation amplitude does not exceed π/ 2. This condition implies that 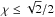 . We introduce the new dependent variable ψ related to φ1 by
. We introduce the new dependent variable ψ related to φ1 by 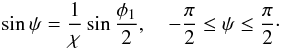 (71)It follows from Eq. (69) that the absolute value of the right-hand side of this equation does not exceed one, so it always can be solved with respect to ψ. Now Eq. (69) reduces to
(71)It follows from Eq. (69) that the absolute value of the right-hand side of this equation does not exceed one, so it always can be solved with respect to ψ. Now Eq. (69) reduces to 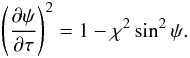 (72)It follows from this equation that
(72)It follows from this equation that 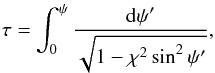 (73)where we have imposed the condition that ψ is an increasing function of τ, which corresponds to the first quarter of the first oscillation period. Then using the relation (Korn & Korn 1961) sn(τ;χ) = sinψ, where sn(τ;χ) is the elliptic sine, and Eq. (71), we eventually obtain
(73)where we have imposed the condition that ψ is an increasing function of τ, which corresponds to the first quarter of the first oscillation period. Then using the relation (Korn & Korn 1961) sn(τ;χ) = sinψ, where sn(τ;χ) is the elliptic sine, and Eq. (71), we eventually obtain 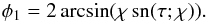 (74)This equation is valid for any τ ≥ 0. The oscillation period is four times the time needed for φ1 to vary from 0 to A. Since ψ = 0 when φ1 = 0 and ψ = π/ 2 when φ1 = A, it follows that the oscillation period is Π = 4K(χ), where K(χ) is the complete elliptic integral of the first kind given by (Korn & Korn 1961)
(74)This equation is valid for any τ ≥ 0. The oscillation period is four times the time needed for φ1 to vary from 0 to A. Since ψ = 0 when φ1 = 0 and ψ = π/ 2 when φ1 = A, it follows that the oscillation period is Π = 4K(χ), where K(χ) is the complete elliptic integral of the first kind given by (Korn & Korn 1961) 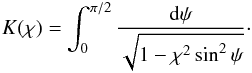 (75)To account for the effect of accretion we go to the next order approximation. We remind the reader that now χ is a function of τ1. Collecting the terms of the order of ϵ in Eq. (65) yields
(75)To account for the effect of accretion we go to the next order approximation. We remind the reader that now χ is a function of τ1. Collecting the terms of the order of ϵ in Eq. (65) yields 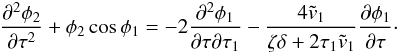 (76)Since φ is a periodic function of τ with the period Π, the same is true for φ2. We multiply Eq. (76) by ∂φ1/∂τ and integrate with respect to τ from 0 to Π. Then, using Eq. (67) and the integration by parts, we obtain on the left-hand side
(76)Since φ is a periodic function of τ with the period Π, the same is true for φ2. We multiply Eq. (76) by ∂φ1/∂τ and integrate with respect to τ from 0 to Π. Then, using Eq. (67) and the integration by parts, we obtain on the left-hand side
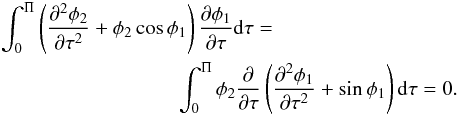 (77)This implies that the right-hand side is also zero, which gives the equation
(77)This implies that the right-hand side is also zero, which gives the equation 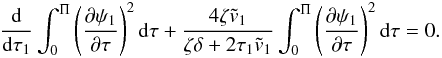 (78)In this equation we use the ordinary derivative because the integral in this equation only depends on τ1. Using Eq. (69) yields
(78)In this equation we use the ordinary derivative because the integral in this equation only depends on τ1. Using Eq. (69) yields 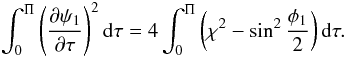 (79)Then, with the aid of Eqs. (71) and (73) we obtain
(79)Then, with the aid of Eqs. (71) and (73) we obtain 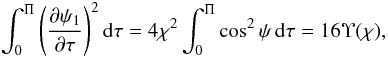 (80)where
(80)where 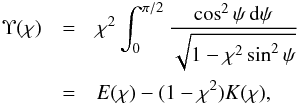 (81)and the complete elliptic integral of the second kind E(χ) is given by (Korn & Korn 1961)
(81)and the complete elliptic integral of the second kind E(χ) is given by (Korn & Korn 1961) 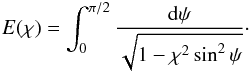 (82)Using Eq. (80) we transform Eq. (78) to
(82)Using Eq. (80) we transform Eq. (78) to 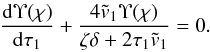 (83)It follows from this equation that
(83)It follows from this equation that 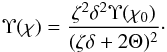 (84)Recall that
(84)Recall that 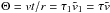 , and χ0 is the value of χ at the initial time (τ1 = 0). It follows from Eq. (81) that Υ(χ) is a monotonically increasing function. Then it follows from Eq. (84) that χ decreases with time. Using the expression for the oscillation amplitude A in terms of χ we conclude that A also decreases with time, which is an expected result. Again we define the dimensionless damping time Θd as the time when the oscillation amplitude becomes e times smaller than the initial amplitude A0. Using Eqs. (70) and (84) we obtain
, and χ0 is the value of χ at the initial time (τ1 = 0). It follows from Eq. (81) that Υ(χ) is a monotonically increasing function. Then it follows from Eq. (84) that χ decreases with time. Using the expression for the oscillation amplitude A in terms of χ we conclude that A also decreases with time, which is an expected result. Again we define the dimensionless damping time Θd as the time when the oscillation amplitude becomes e times smaller than the initial amplitude A0. Using Eqs. (70) and (84) we obtain  (85)Rewriting this expression in the dimensional variables gives the expression for the dimensional damping time td,
(85)Rewriting this expression in the dimensional variables gives the expression for the dimensional damping time td, 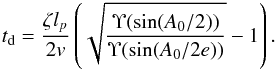 (86)The theory becomes especially simple in the linear approximation that we obtain assuming that χ ≪ 1. Then A = 2χ, sn(τ;χ) = sinτ, and K(χ) = E(χ) = π/ 2. Using these relations and Eq. (81) we obtain that Π = 2π and Υ = πχ2/ 2. Now we obtain from Eqs. (84) and (86) that
(86)The theory becomes especially simple in the linear approximation that we obtain assuming that χ ≪ 1. Then A = 2χ, sn(τ;χ) = sinτ, and K(χ) = E(χ) = π/ 2. Using these relations and Eq. (81) we obtain that Π = 2π and Υ = πχ2/ 2. Now we obtain from Eqs. (84) and (86) that 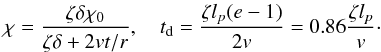 (87)Finally, it follows from Eq. (84)
(87)Finally, it follows from Eq. (84) 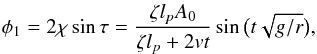 (88)where A0 = 2χ0. We see that the expression for td coincides with that given by Eq. (62). It is also straightforward to verify that Eq. (88) coincides with Eq. (59). Hence, we recovered the results obtained in Sect. 4.2.
(88)where A0 = 2χ0. We see that the expression for td coincides with that given by Eq. (62). It is also straightforward to verify that Eq. (88) coincides with Eq. (59). Hence, we recovered the results obtained in Sect. 4.2.
In Fig. 5 the dependence of A on Θ for ζ = 100, δ = 1/12, and two values of the initial amplitude A0 = 2arcsinχ0, A0 = π/ 8 and A0 = π/ 2, are shown. We did not show the curve obtained using the linear theory because it almost completely coincides with that corresponding to A0 = π/ 8. We see that the nonlinearity only slightly reduces the damping time. For ζ = 100 and δ = 1/12 the linear theory gives Θd = 7.16, while the nonlinear theory gives Θd = 7.11 when A0 = π/ 8 and Θd = 6.52 when A0 = π/ 2. Hence, even when A0 = π/ 2 the nonlinearity reduces the damping time by less than 10%.
 |
Fig. 5 Dependence of the oscillation amplitude A on the dimensionless time Θ = vt/r. The solid and dashed curves correspond to the initial amplitude A0 = π/ 2 and A0 = π/ 8, respectively. The vertical lines indicate the damping time Θd. |
When there is no damping the oscillation period is equal to 4K(χ0). However, due to damping χ decreases with time.
Consider the sequence { τn }, n = 0,1,..., where φ = 0 at τ = τ2n, φ takes its local maximum when τ = τ2n + 1, and it takes its local minimum when τ = τ2n + 3. The nth oscillation cycle corresponds to the variation of τ from τ2n−2 to τ2n + 2. The angle φ increases from 0 to its local maximum when τ varies from τ2n to τ2n + 1, then it decreases back to 0 when τ varies from τ2n + 1 to τ2n + 2, continues to decrease to reach its local minimum when τ varies from τ2n + 2 to τ2n + 3, and finally returns to 0 when τ varies from τ2n + 3 to τ2n + 4. Hence, we split each oscillation period into four quarters. Since χ is a slowly varying function of τ we can neglect its variation in any quarter of the period. Each quarter of period corresponds to the variation of ψ by π/ 2. Then, using Eqs. (73) and (75), we obtain the recurrence relation 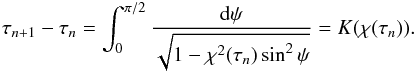 (89)The nth oscillation period is given by
(89)The nth oscillation period is given by 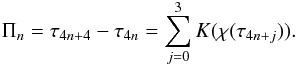 (90)The function χ(τ) is defined by Eq. (84).
(90)The function χ(τ) is defined by Eq. (84).
Since χ is a monotonically decreasing function of τ and K(χ) is a monotonically decreasing function of χ, it follows that { Πn } is a monotonically decreasing sequence. When τ → ∞, χ → 0, K(χ) → π/ 2, and Πn → 2π. The stronger the damping the faster χ(τ) decreases and, consequently, the faster the sequence { Πn } decreases. The larger the initial amplitude A0 the larger χ0 is and, consequently, the larger the difference between the initial period, Π1, and the limiting period value 2π is. However this difference is not very big even for quite large initial oscillation amplitudes. When A0 = π/ 2 we obtain Π1< 4K(χ0) ≈ 7.42, meaning that, even for this large value of the oscillation amplitude, the difference between Π1 and 2π is less than 20%.
As an example, using Eqs. (84), (89), and (90) we calculated oscillation periods 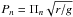 for A0 = π/ 2, ζ = 100, g = 274 m s-2, r = 60 Mm, lp = 2 Mm, and v = 30 km s-1. We obtained P1 = 53.9 min, P2 = 50.4 min, P3 = 49.7 min, and P4 = 49.4 min,
for A0 = π/ 2, ζ = 100, g = 274 m s-2, r = 60 Mm, lp = 2 Mm, and v = 30 km s-1. We obtained P1 = 53.9 min, P2 = 50.4 min, P3 = 49.7 min, and P4 = 49.4 min, 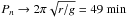 as n → ∞. Hence, in this particular example the period only decreases by 10%.
as n → ∞. Hence, in this particular example the period only decreases by 10%.
In Fig. 6 we have plotted the full numerical solutions for typical values of parameters. We clearly see the nonlinear effects but also we see that these effects are not significant. The orange curve corresponds to A0 = π/ 2 that, in dimensional variables, corresponds to the initial velocity equal to 180 km s-1. We see that it is only slightly different from the black curve corresponding to the initial velocity equal to 36 km s-1.
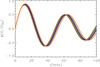 |
Fig. 6 Temporal evolution of the angle φ described by Eq. (54) normalized to the initial dimensionless velocity 2χ0 as function of time, t. We have taken g = 274 m s-2 and typical values of ζ = 100, r = 60 Mm, and lp = 2 Mm. Black, green, red, blue, and orange lines correspond to the initial velocities of |
5. Summary and conclusion
In this article we have studied the damping of longitudinal oscillations of a prominence thread caused by the mass accretion of the evaporated chromospheric plasma. We considered a thin curved magnetic tube of an arbitrary shape. The prominence thread is in the central part of the tube and it consists of a dense cold plasma. The parts of the tube at the two sides of the thread are filled with a hot rarefied plasma. The restoring force in the prominence oscillation is the gravity projected onto the flux tube. We assumed that there are flows of coronal rarefied plasma towards the thread. These flows are caused by the plasma evaporation at the magnetic tube footpoints. The coronal heating is localized at the chromosphere and at the bottom of the corona produces the evaporation. The hot evaporated plasma condenses in the already-formed prominence thread by the thermal non-equilibrium instability. Our main assumption is that the hot evaporated plasma is instantaneously accommodated by the thread when it arrives at the thread, and its temperature and density become equal to those of the thread. Then we derived the system of three ordinary differential equations describing the thread dynamics.
The equations describing the thread oscillation are valid for an arbitrary shape of the magnetic tube axis. The only restriction is that it is a planar curve in a vertical plane. Of course the oscillation properties depend on a particular shape of the magnetic tube. We considered two particular models. In the first one the magnetic tube axis is composed of an arc of a circle with two straight lines attached to its ends in such a way that the whole curve is smooth. A very important property of this model is that the equations describing the thread oscillations are linear for any oscillation amplitude under the restriction that the thread ends remain on the straight parts of the tube. We obtained the solution to the governing equations in terms of Bessel functions. We showed that, for typical parameters of solar prominences, the Bessel functions can be approximated by trigonometric functions. Then we obtained the analytical expressions for the oscillation damping time and periods. We found that the damping time is inversely proportional to the accretion rate and proportional to the initial mass of the thread. The oscillation period depends strongly on the angle between the straight parts of the tube axis and the horizontal direction. The larger this angle, the smaller the period is. We also found that the period increases with time and, in each cycle, the time of the maximum thread displacement is shifted. We found that the larger the damping the larger the period shift for a given oscillation period.
In the second model we studied, the shape of the tube axis is an arc of a circle. We considered the linear as well as the nonlinear regime. In the linear regime we assumed that the displacement of the thread is small in comparison with the radius of curvature of the dipped flux tube. We found that the period is equal to the period of the pendulum oscillation and it does not change with time. The damping time is inversely proportional to the mass accretion rate and proportional to the initial mass of the thread. In the nonlinear regime, we assumed that the damping is slow meaning than the damping time is much larger than the characteristic oscillation time. It is important to note that the characteristic oscillation time is the oscillation period divided by 2π. This implies that the damping can be considered as slow even when the damping time is of the order of the oscillation period. To study the thread oscillations we used the two-scale approach where the oscillations are described by the solution of the nonlinear pendulum problem with slowly varying amplitude. We showed that the nonlinearity only slightly reduces the damping time. Again the damping time is inversely proportional to the accretion speed and proportional to the initial mass. In this model the oscillation periods decrease with time. This behaviour is in contrast with that found in the first model. The larger the initial oscillation amplitude the larger the reduction in the oscillation periods is. However, even for the largest initial oscillation amplitude considered in our article this reduction does not exceed 20%.
We conclude that the mass accretion can damp the motion of the threads rapidly. Thus, this mechanism can explain the observed strong damping of large-amplitude longitudinal oscillations. In addition, the damping time can be used to determine the mass accretion rate and indirectly the coronal heating. More work is needed to increase the complexity of the model by including stratification of the plasma, the physical processes in condensation of the thermal instability, and consider 2D and 3D models of the magnetic geometry in order to understand the interaction of the plasma with the magnetic field. In addition, the damping by radiative losses should be considered in a full model. Zhang et al. (2013) found that effect of the radiative losses can be significant in these oscillations. Recently, Ballester (2016) found that a temporal variation of the background temperature in combination with radiative losses can produce period shifts and damping of the slow modes in a prominence. These improvements to the model will be a topic for future research.
Acknowledgments
This paper was inspired by two ISSI workshops, in Bern, Switzerland, in March and November 2015. The authors acknowledgesupport from the International Space Science Institute (ISSI) to the Team 314 on “large-amplitude oscillations in prominences” led by M. Luna. M.R. acknowledges the financial support from the Science and Technology Facilities Council (STFC). M. Luna acknowledges the support of the Spanish Ministry of Economy and Competitiveness through projects AYA2011-24808, AYA2010-18029 and AYA2014-55078-P. This work contributes to the deliverables identified in FP7 European Research Council grant agreement 277829, “magnetic connectivity through the solar partially ionized atmosphere” (PI: E. Khomenko).
References
- Abramowitz, M., & Stegun, I. 1972, Handbook of Mathematical Functions (National Bureau of Standards) [Google Scholar]
- Antiochos, S. K., & Klimchuk, J. A. 1991, ApJ, 378, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Antiochos, S. K., MacNeice, P. J., & Spicer, D. S. 2000, ApJ, 536, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Ballester, J. L., Carbonell, M., Soler, R., & Terradas, J. 2016, A&A, 591, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bi, Y., Jiang, Y., Yang, J., et al. 2014, ApJ, 790, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, J., Lee, J., Spirock, T. J., & Wang, H. 2006, Sol. Phys., 236, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, J., Lee, J., Spirock, T. J., et al. 2003, ApJ, 584, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., & Antiochos, S. K. 2008, ApJ, 676, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Antiochos, S. K., Hohensee, M., Klimchuk, J. A., & MacNeice, P. J. 2001, ApJ, 553, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Antiochos, S. K., Klimchuk, J. A., & MacNeice, P. J. 2003, ApJ, 593, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Tanner, S. E. M., Antiochos, S. K., & DeVore, C. R. 2005, ApJ, 635, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., & Xia, C. 2014, ApJ, 789, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Kleczek, J., & Kuperus, M. 1969, Sol. Phys., 6, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Korn, G., & Korn, T. 1961, Mathematical Handbook for Scientists and Engineers (New York: McGraw-Hill) [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J. C., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Li, T., & Zhang, J. 2012, ApJ, 760, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., & Karpen, J. 2012, ApJ, 750, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Díaz, A. J., & Karpen, J. 2012a, ApJ, 757, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Karpen, J. T., & DeVore, C. R. 2012b, ApJ, 746, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Knizhnik, K., Muglach, K., et al. 2014, ApJ, 785, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Terradas, J., Khomenko, E., Collados, M., & Vicente, A. D. 2016, ApJ, 817, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R. 2009, Space Sci. Rev., 149, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., & Ballester, J. L. 2002, Sol. Phys., 206, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Pikelner, S. B. 1971, Sol. Phys., 17, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S. 2015, Sol. Phys., 290, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Liu, Y. D., Chen, P. F., & Ichimoto, K. 2014, ApJ, 795, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Tripathi, D., Isobe, H., & Jain, R. 2009, Space Sci. Rev., 149, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Vršnak, B., Veronig, A. M., Thalmann, J. K., & Žic, T. 2007,A&A, 471, 295 [Google Scholar]
- Xia, C., Chen, P. F., Keppens, R., & van Marle, A. J. 2011, ApJ, 737, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, C., Keppens, R., Antolin, P., & Porth, O. 2014, ApJ, 792, L38 [Google Scholar]
- Zhang, Q. M., Chen, P. F., Xia, C., & Keppens, R. 2012, A&A, 542, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Q. M., Chen, P. F., Xia, C., Keppens, R., & Ji, H. S. 2013, A&A, 554, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Sketch of the equilibrium. The magnetic tube axis consists of an arc of a circle of radius r with the two straight lines attached. The dense prominence thread occupies the shaded area. Recall that we consider a one-dimensional problem and neglect the variation of all quantities across the magnetic tube. |
| In the text | |
 |
Fig. 2 Temporal evolution of the velocity of the thread given by Eq. (35) normalized to the initial velocity U0 as function of time, t. We have assumed a typical situation of ζ = 100, r = 60 Mm, with g = 274 m s-2. For clarity, we have split the different cases studied into two panels. In a) a thread with lp = 2.1 Mm and θ = 1° is considered with v = 10 km s-1 (black curve) and v = 30 km s-1 (orange curve). In b) a thread with lp = 5 Mm and θ = 3° is considered with v = 10 km s-1 (red curve) and v = 30 km s-1 (blue curve). |
| In the text | |
 |
Fig. 3 Sketch of the equilibrium. The magnetic tube axis is an arc of a circle of radius r. The prominence occupies the shaded area. We again recall that we consider a one-dimensional problem and neglect the variation of all quantities across the magnetic tube. |
| In the text | |
 |
Fig. 4 Angular position φ(τ) normalized to its amplitude 2χ0 as a function of t for various values of the parameters v and lp. We have taken g = 274 m s-2 and typical values of ζ = 100 and r = 60 Mm. In all cases the period is 49 min. The black curve corresponds to v = 30 km s-1 and lp = 2 Mm, the green curve to v = 10 km s-1 and lp = 2 Mm, the red curve to v = 40 km s-1 and lp = 5 Mm, and the blue curve to v = 10 km s-1 and lp = 5 Mm. The damping times for these combinations of parameters are td = 55.6, 166.7, 138.9, and 416.7 min, respectively. |
| In the text | |
 |
Fig. 5 Dependence of the oscillation amplitude A on the dimensionless time Θ = vt/r. The solid and dashed curves correspond to the initial amplitude A0 = π/ 2 and A0 = π/ 8, respectively. The vertical lines indicate the damping time Θd. |
| In the text | |
 |
Fig. 6 Temporal evolution of the angle φ described by Eq. (54) normalized to the initial dimensionless velocity 2χ0 as function of time, t. We have taken g = 274 m s-2 and typical values of ζ = 100, r = 60 Mm, and lp = 2 Mm. Black, green, red, blue, and orange lines correspond to the initial velocities of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.