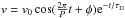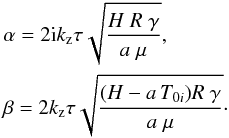| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201527953 | |
| Published online | 22 June 2016 | |
Prominence oscillations: Effect of a time-dependent background temperature
1
Departament de FísicaUniversitat de les Illes Balears,
07122
Palma de Mallorca,
Spain
e-mail:
joseluis.ballester@uib.es
2
Departament de Ciències Matemàtiques i Informàtica, Universitat de
les Illes Balears, 07122
Palma de Mallorca,
Spain
3 Institute of Applied Computing & Community Code
(IAC 3), Universitat de les Illes Balears, Spain
Received: 14 December 2015
Accepted: 18 February 2016
Context. Small amplitude oscillations in prominences have been known about for a long time, and from a theoretical point of view, these oscillations have been interpreted in terms of standing or propagating linear magnetohydrodynamic (MHD) waves. In general, these oscillations were studied by producing small perturbations in a background equilibrium with stationary physical properties.
Aims. Taking into account that prominences are dynamic plasma structures, the assumption of a stationary equilibrium is not realistic. Therefore, our main aim is to study the effects produced by a non-stationary background on slow MHD waves, which could be responsible for prominence oscillations.
Methods. Assuming that the radiation term is proportional to temperature and constant external heating, we have derived an expression for the temporal variation of the background temperature, which depends on the imbalance between heating and cooling processes. Furthermore, radiative losses, together with parallel thermal conduction, have also been included as damping mechanisms for the waves.
Results. As temperature increases with time, the period of slow waves decreases and the amplitude of the velocity perturbations is damped. The inclusion of radiative losses enhances the damping. As temperature decreases with time, the period of slow waves increases and the amplitude of velocity perturbations grows while, as expected, the inclusion of radiative losses contributes to the damping of oscillations.
Conclusions. There is observational evidence that, in different locations of the same prominence, oscillations are damped or amplified with time. This temporal damping or amplification can be obtained by a proper combination of a variable background temperature, together with radiative damping. Furthermore, decayless oscillations can also be obtained with an appropriate choice of the characteristic radiation time.
Key words: magnetohydrodynamics (MHD) / waves / Sun: filaments, prominences
© ESO, 2016
1. Introduction
Prominences are one of the most intriguing structures of the solar atmosphere, displaying a very dynamic behaviour. Quiescent solar prominences are clouds of cool and dense plasma that are suspended against gravity by forces thought to be of magnetic origin. They form over a wide range of latitudes on the Sun (Mackay 2015) but always along inversion polarity lines. On the other hand, high-resolution Hα observations obtained with the Swedish Solar Telescope (SST) in La Palma (Lin et al. 2005) and the Dutch Open Telescope (DOT) in Tenerife (Heinzel & Anzer 2006) allowed us to observe filament threads in great detail (see Lin 2010, for a review). The measured average width of resolved thin threads is about 0.3 arcsec (~210 km), while their length is between 5 and 40 arcsec (~3500−28 000 km). The fine threads of solar filaments seem to be partially filled with cold plasma (Lin et al. 2005), typically two orders of magnitude denser and cooler than the surrounding corona, and it is generally assumed that they outline the magnetic flux tubes in which they reside (Engvold 1998, 2008; Lin 2004; Lin et al. 2005, 2008; Okamoto et al. 2007). This idea is strongly supported by observations that suggest that threads are skewed with respect to the filament long axis in a similar way to what has been found for the magnetic field in prominences (Leroy 1980; Bommier et al. 1994; Bommier & Leroy 1998), although other interpretations (Heinzel & Anzer 2006) have also been proposed.
Prominences and filaments are subject to different types of oscillatory motions. Small amplitude oscillations have been known about for a long time and are a commonly observed phenomenon (Oliver & Ballester 2002; Arregui et al. 2012). Observational studies have revealed a wide range of characteristic periods, which can be classified in four groups (Lin 2011): very short (≤1 min), short (1 min−20 min), intermediate (20−40 min), and long (40−100 min). These oscillations appear to be of local nature, the detected Doppler velocities usually range from the noise level (about 0.1 km s-1) to 2 − 3 km s-1, and observational evidence reveals that, in many cases, once excited, are damped in short spatial and temporal scales. Commonly, these oscillations have been interpreted in terms of linear magnetohydrodynamic (MHD) waves and, to explain the temporal and spatial damping, different mechanisms (thermal processes, resonant damping in non-uniform media, partial ionization, etc) have been invoked. The relevance of each mechanism can be assessed by comparing the spatial and temporal scales that are produced by each of them with those obtained from observations.
Regarding thread oscillations, the analysis of high-resolution ground (Lin 2004; Lin et al. 2009) and space-based observations (Okamoto et al. 2007) enabled us to determine wave properties such as periods, wavelengths, and phase speeds. Thread oscillations also display fast attenuation. For example, Lin (2004) detected pronounced Doppler velocity oscillations with a 26 min period, which could only be observed for 2−3 periods, after which they became strongly damped. Ning et al. (2009) analyzed the oscillatory behaviour of several threads in the spine of a quiescent prominence that had been observed with Hinode/SOT. They found that many prominence threads exhibited vertical and horizontal oscillatory motions, that the corresponding periods did not substantially differ for a given thread, and that the oscillations were strongly damped. Most of these observations have been interpreted in terms of fast kink waves (Arregui et al. 2008; Van Doorsselaere et al. 2008; Lin et al. 2009) while the damping mechanism that is able to produce a damping ratio (τD/P), with τD the damping time and P the period, and that is compatible with observations, seems to be resonant absorption (Arregui et al. 2008; Soler et al. 2009a) in an inhomogeneous magnetic flux tube. The efficiency of various damping mechanisms of kink waves in prominence threads has been compared and discussed in Soler et al. (2014).
 |
Fig. 1 Doppler velocities (km s-1) as a function of time for six different spatial locations in a prominence. Dots denote observational data, while solid lines correspond to an analytical fit such as: |
 |
Fig. 2 Left panel: temporal variation of the prominence plasma temperature for H = 8.5 × 10-6 W m-3 and different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). Right panel: temporal variation of the prominence plasma temperature for H = 3.5 × 10-7 W m-3 and different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). In these plots T0i = 10 000 K. |
 |
Fig. 3 Left panel: temporal variation of the prominence plasma temperature for τ = 3000 s and different values of the heating function H = 8.5 × 10-6 W m-3 (continuous line), 1 × 10-5 W m-3 (dashed line), 1.5 × 10-5 W m-3 (dotted line). Right panel: temporal variation of the prominence plasma temperature for τ = 3000 s and different values of the heating function H = 1 × 10-6 W m-3 (continuous line), 5.5 × 10-7 W m-3 (dashed line), 1.5 × 10-7 W m-3 (dotted line). T0i = 10 000 K. |
In the case of quiescent prominences, Molowny-Horas et al. (1999) analyzed longitudinal velocity maps constructed from time series of Hβ filtergrams of a polar crown prominence and they found different spatial locations that display oscillations with periods between 28 and 95 min, suggesting the presence of slow magnetoacoustic waves, damping times between 140 and 377 min, with damping ratios in the range 2−6. They also found a location where oscillations, with a period of 28 min, were amplified with an amplification time of about 140 min (see Fig. 1). Later on, Terradas et al. (2002) did a more detailed study of the same prominence and, after a spatial analysis of Doppler signals, they found regions that display periodic motions in a very clear way. In one of these regions, close to the top edge of the prominence, propagating features were tracked and waves that propagate in two opposite directions with periods around 75 min, wavelengths of 70 000 km and propagation speeds of 15 km s-1, were identified. These propagation speeds suggest, again, that the oscillations were produced by slow magnetoacoustic waves. Berger et al. (2008) obtained high resolution movies of quiescent prominences that were observed with SOT onboard the Hinode satellite. These movies showed the very dynamic behaviour of quiescent prominences and enabled the identification of several waves that were propagating upwards with speeds compatible with the sound speed at a temperature of 10 000 K, implying that these waves are of magnetoacoustic origin. The damping of slow waves was analyzed using either non-adiabatic energy equations, involving heating, optically thin radiation and thermal conduction (Carbonell et al. 2004; Terradas et al. 2001, 2005; Soler et al. 2008), or ion-neutral collisions (Forteza et al. 2007, 2008; Soler et al. 2009b), or viscosity. However, the efficiency of these mechanisms in the damping of slow waves is limited.
In many studies of coronal loops oscillations, either for transverse or longitudinal oscillations, the temperature and density of the oscillating loop were considered constant during the observed time interval. However, observational evidence suggests that the oscillating loops observed in EUV go through a cooling phase. As a result, several authors (Aschwanden & Terradas 2008; Morton & Erdélyi 2009, 2010; Morton et al. 2010; Ruderman 2011b; Erdélyi et al. 2011; Al-Ghafri & Erdélyi 2013; Al-Ghafri et al. 2014; Williamson & Erdélyi 2014a,b) have recently considered the effect of a time-dependent temperature or density background on slow and fast kink waves that are responsible for longitudinal and transverse coronal loop oscillations, respectively, as well as in the resonant damping of fast kink waves (Ruderman 2011a; Williamson & Erdélyi 2014c). In general, these studies assume that the cooling time or the timescale of density variation is longer than the period of oscillation, which allows us to use the WKB method to solve the problem. Furthermore, transverse decayless oscillations in coronal loops have also been observed and theoretical interpretations have been provided (Aschwanden & Schrijver 2011; Nisticò et al. 2013; Anfinogentov et al. 2013; Hindman & Jain 2014). Finally, Wang et al. (2012) observed transverse oscillations with growing amplitude in a multistranded coronal loop.
Prominences/filaments are dynamic structures (Berger et al. 2008), embedded in the solar corona, heated by coronal and chromospheric radiation while, at the same time, they cool by radiation. Furthermore, energetic events, like jets, subflares, small eruptions, etc, produce impulsive releases of energy that heat and disturb prominences located in the neighbourhood. For instance, the excitation of large amplitude longitudinal oscillations in filaments has been attributed to the injection of energy that comes from an energetic event, which happened close to the filament, producing a flow of hot plasma, which pushes the cold plasma located at the dips of the magnetic configuration (Luna & Karpen 2012; Luna et al. 2012, 2014; Zhang et al. 2013). In general, it would be reasonable to expect that, after an impulsive heating, which increases the prominence temperature, the prominence cools down again by radiation.
On the other hand, the imbalance between prominence heating and cooling processes should produce a temporal variation of prominence temperature. However, this fact has not been considered in the studies of prominence oscillations. As such, when prominence oscillations are excited in a plasma whose temperature changes with time, the effect of this variable temperature background on the oscillations should be considered. In this paper, our main goal is to make a first attempt to study the behaviour of slow MHD waves in an unbounded medium, with physical properties akin to those of solar prominences, in which the temperature changes with time owing to the imbalance between heating and cooling processes. Apart from considering a background whose temperature changes with time, perturbed radiation and thermal conduction as damping mechanisms for waves are also considered, and we have sought full analytical or numerical solutions to the MHD equations that govern the behaviour of slow MHD waves when all these physical processes are taken into account.
The structure of the paper is as follows: in Sect. 2, the model and time-dependent linearised equations for MHD waves are presented, while in Sects. 3 and 4, the results obtained for slow waves are discussed and, finally, in Sect. 5, we draw our conclusions.
2. Basic equilibrium and governing equations
As the background configuration, we consider a homogeneous plasma with physical properties akin to those of solar quiescent prominences, in which the temperature changes as a function of time. The plasma is infinite in all directions and threaded by a uniform and horizontal magnetic field. The general MHD equations that describe the fully ionised background plasma are
![\begin{eqnarray} &&\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec v)=0, \\ &&\rho\frac{\partial \vec v}{\partial t} + \rho (\vec v \cdot \nabla) \vec v = -\nabla p + \frac{1}{\mu_0}(\nabla \times \vec B) \times \vec B, \\ &&\frac{R}{\tilde \mu}\rho^{\gamma}\left[\frac{\partial}{\partial t} \frac{T}{\rho^{\gamma - 1}} + (\vec v \cdot \nabla)\frac{T}{\rho^{\gamma -1}} \right] = -(\gamma - 1)\cal L, \\ &&p = \frac{R}{\tilde \mu} \rho T, \\ &&\nabla \cdot \vec B = 0, \\ &&\frac{\partial \vec B}{\partial t} = \nabla \times (\vec v \times \vec B), \end{eqnarray}](/articles/aa/full_html/2016/07/aa27953-15/aa27953-15-eq38.png) with v being the velocity, B the magnetic field, μ0 the magnetic permeability of free space, γ the ratio of specific heats, R the gas constant,
with v being the velocity, B the magnetic field, μ0 the magnetic permeability of free space, γ the ratio of specific heats, R the gas constant, 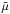 the mean molecular weight, T the temperature, ρ the plasma density, p the plasma pressure, while ℒ is given by
the mean molecular weight, T the temperature, ρ the plasma density, p the plasma pressure, while ℒ is given by 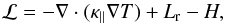 (7)encompassing thermal conduction, radiation, and external heating, respectively. Here κ∥ is the component along the magnetic field of the thermal conductivity tensor κ, which for applications in the solar atmosphere, is approximated by its parallel component to the magnetic field, namely
(7)encompassing thermal conduction, radiation, and external heating, respectively. Here κ∥ is the component along the magnetic field of the thermal conductivity tensor κ, which for applications in the solar atmosphere, is approximated by its parallel component to the magnetic field, namely 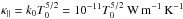 . The magnetic field is considered uniform and horizontal, B = B0ẑ, and the background state can be described as follows:
. The magnetic field is considered uniform and horizontal, B = B0ẑ, and the background state can be described as follows:
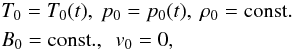 (8)where T0, p0, ρ0, B0, and v0 = 0 are the background quantities that correspond to temperature, pressure, density, magnetic field, and velocity, respectively, and we assumed a constant density and no background flow. As such, the MHD equations describing the background state are
(8)where T0, p0, ρ0, B0, and v0 = 0 are the background quantities that correspond to temperature, pressure, density, magnetic field, and velocity, respectively, and we assumed a constant density and no background flow. As such, the MHD equations describing the background state are
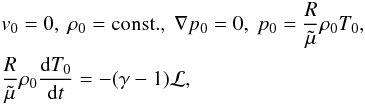 (9)where ℒ = Lr − H is now the heat-loss function and thermal conduction is absent because we only have a time-dependent temperature. The balance between radiation, Lr, and heating, H, determines how the background temperature evolves with time; when Lr > H, the background temperature will decrease with time, and when Lr < H, the opposite happens.
(9)where ℒ = Lr − H is now the heat-loss function and thermal conduction is absent because we only have a time-dependent temperature. The balance between radiation, Lr, and heating, H, determines how the background temperature evolves with time; when Lr > H, the background temperature will decrease with time, and when Lr < H, the opposite happens.
In our study, and for the sake of simplicity, we assume that the radiation term is proportional to plasma temperature, Lr = aT0(t) with a constant, while the external heating term, H, is assumed to be constant. Hence, from Eq. (9), and imposing T0i as the initial temperature, we obtain ![\begin{equation} T_0(t) = \frac{H}{a} +\left(T_{0i}-\frac{H}{a}\right)\exp\left[-\frac{t} {\tau}\right] \label{eqT1} , \end{equation}](/articles/aa/full_html/2016/07/aa27953-15/aa27953-15-eq67.png) (10)where
(10)where 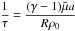 , and τ is a characteristic time that governs the rate at which plasma temperature increases or decreases. When H = aT0i, the heat-loss function is equal to zero and the plasma temperature remains constant and equal to T0i. However, when initially Lr<H, the plasma temperature increases with time, which means that radiation also increases with time, and when the radiative term becomes equal to the heating term the temperature attains a constant value. When initially Lr>H, the opposite happens, radiation decreases with time and, finally, becomes equal to H and the temperature also becomes constant. Furthermore, Fig. 2 displays, for two different values of the external heating, H, and different characteristic times, the temporal increase or decrease of the plasma temperature. Finally, Fig. 3 shows the temporal behaviour of the temperature for a fixed value of the characteristic time and different values of the heating term.
, and τ is a characteristic time that governs the rate at which plasma temperature increases or decreases. When H = aT0i, the heat-loss function is equal to zero and the plasma temperature remains constant and equal to T0i. However, when initially Lr<H, the plasma temperature increases with time, which means that radiation also increases with time, and when the radiative term becomes equal to the heating term the temperature attains a constant value. When initially Lr>H, the opposite happens, radiation decreases with time and, finally, becomes equal to H and the temperature also becomes constant. Furthermore, Fig. 2 displays, for two different values of the external heating, H, and different characteristic times, the temporal increase or decrease of the plasma temperature. Finally, Fig. 3 shows the temporal behaviour of the temperature for a fixed value of the characteristic time and different values of the heating term.
Next, we imposed small perturbations on the background state, taking only motions and propagation in the XZ plane into consideration. Consequently, Alfvén waves, which are insensitive to plasma temperature, are not taken into account, and the linearised MHD equations are
![\begin{eqnarray} &&\frac{\partial \rho_1}{\partial t} + \rho_0\left(\frac{\partial v_{1x}}{\partial x}+\frac{\partial v_{1z}}{\partial z}\right) =0, \label{conti} \\ &&\rho_0\frac{\partial \vec v_1}{\partial t} =-\nabla p_1 +\frac{1}{\mu_0}\left(\nabla \times \vec B_1\right) \times \vec B_0, \\ &&\frac{R}{\tilde \mu}\left[\rho_1\frac{\partial T_0}{\partial t}+\rho_0 \frac{\partial T_1}{\partial t} + \left(\gamma - 1\right) \rho_0 T_0 \left(\frac{\partial v_{1x}}{\partial x}+\frac{\partial v_{1z}}{\partial z}\right) \right] = \nonumber \\ && \,\qquad \qquad -\left(\gamma - 1\right) \left(aT_1-\kappa_0 T_0^{5/2}\nabla^2 T_1\right), \\ &&p_1 = \frac{R}{\tilde \mu} \left(\rho_0 T_1+T_0 \rho_1\right), \\ &&\frac{\partial B_{1x}}{\partial x} + \frac{\partial B_{1z}}{\partial z} = 0, \\ &&\frac{\partial B_{1x}}{\partial t} = \frac{\partial \left(v_{1x} B_0\right)}{\partial z}, \\ &&\frac{\partial B_{1z}}{\partial t} = -\frac{\partial \left(v_{1x} B_0\right)}{\partial x}, \label{induz} \end{eqnarray}](/articles/aa/full_html/2016/07/aa27953-15/aa27953-15-eq74.png) where ρ1, T1, p1, B1, v1x, v1z represent density, temperature, pressure, magnetic field, and velocity perturbations, respectively. Since we are interested in studying the behaviour of slow waves, we now take only motions along the magnetic field into account, i.e. we consider only the perturbed velocity component v1z, the parallel wavenumber kz (kx = 0), and T0(t). Hence we describe the temporal and spatial behaviour of the perturbations as follows:
where ρ1, T1, p1, B1, v1x, v1z represent density, temperature, pressure, magnetic field, and velocity perturbations, respectively. Since we are interested in studying the behaviour of slow waves, we now take only motions along the magnetic field into account, i.e. we consider only the perturbed velocity component v1z, the parallel wavenumber kz (kx = 0), and T0(t). Hence we describe the temporal and spatial behaviour of the perturbations as follows: 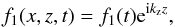 (18)where f1(t) is the time dependent amplitude of the perturbations. As such, the linearised Eqs. (11)−(17) become
(18)where f1(t) is the time dependent amplitude of the perturbations. As such, the linearised Eqs. (11)−(17) become 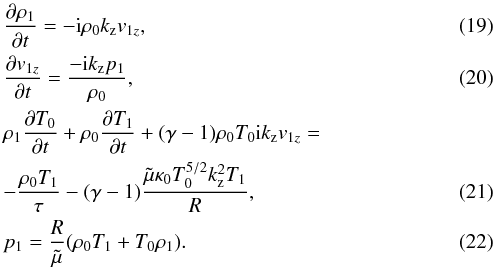 Equations (19)−(22) describe slow waves that propagate along the magnetic field (parallel propagation) in a background plasma whose temperature changes with time, and where the damping of perturbations is produced by radiation and thermal conduction. After straightforward manipulations, the following differential equation, involving velocity and temperature perturbations, can be obtained:
Equations (19)−(22) describe slow waves that propagate along the magnetic field (parallel propagation) in a background plasma whose temperature changes with time, and where the damping of perturbations is produced by radiation and thermal conduction. After straightforward manipulations, the following differential equation, involving velocity and temperature perturbations, can be obtained: 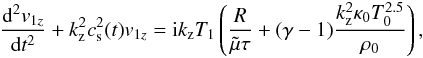 (23)with
(23)with 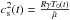 being the time-dependent sound speed squared. We note that the right hand side of Eq. (23) contains the effect of the wave-damping mechanisms, namely, radiative cooling of perturbations and thermal conduction.
being the time-dependent sound speed squared. We note that the right hand side of Eq. (23) contains the effect of the wave-damping mechanisms, namely, radiative cooling of perturbations and thermal conduction.
Since we are interested in prominence plasmas, we consider the following set of parameters which are typical of quiescent prominences: 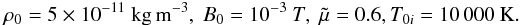 Using these numerical values, the sound speed, cs, at t = 0 is 15.18 km s-1. Finally, the wavelengths that are typically observed in prominence oscillations correspond to wavenumbers which are in the range 10-8 − 10-6 m-1.
Using these numerical values, the sound speed, cs, at t = 0 is 15.18 km s-1. Finally, the wavelengths that are typically observed in prominence oscillations correspond to wavenumbers which are in the range 10-8 − 10-6 m-1.
3. Results
To proceed with our study, we take the following approach: First, we study the effect on slow waves produced by a background equilibrium whose temperature changes with time (increasing or decreasing); next, the additional effects, which are due to the inclusion of damping mechanisms for the waves such as radiation and parallel thermal conduction, are considered.
3.1. Exponential increase of the background temperature
First of all, we assume that, initially, Lr<H and, therefore, the prominence plasma temperature increases with time following Eq. (10). To know the effect produced on slow waves, we neglect the damping mechanisms terms in the right-hand side of Eq. (23), obtaining for v1z the following ordinary differential equation: 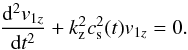 (24)Solving Eq. (24), together with initial conditions v1z(0) = 1 and
(24)Solving Eq. (24), together with initial conditions v1z(0) = 1 and 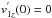 , an analytical solution can be obtained which is
, an analytical solution can be obtained which is 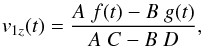 (25)where
(25)where
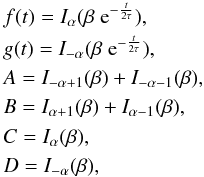 with Iν(z) the modified Bessel function of the first kind and
with Iν(z) the modified Bessel function of the first kind and
This analytical solution clearly indicates that we do not have pure harmonic oscillations.
 |
Fig. 4 Temporal behaviour of the perturbed velocity for a prominence plasma with a background temperature that increases with time (continuous line) and for a prominence plasma with a constant background (T0i = 10 000 K) temperature (dashed line). H = 3.5 × 10-5 W m-3, τ = 3000 s. The velocity amplitude has been normalized. |
 |
Fig. 5 Temporal variation of the ratio between the instantaneous, P(t), and the initial, P(0), oscillatory period in a prominence plasma whose background temperature increases with time for different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). H = 8.5 × 10-6 W m-3. |
Figure 4 shows a comparison between the amplitudes of the perturbed velocity for a constant and variable background temperature. While, for a constant background temperature, the perturbed velocity amplitude and the period remain constant, in the case of an exponential growth of the background temperature, the velocity amplitude, as well as the period, decrease with time. However, in the case of a variable background temperature, we can observe that, initially, the amplitude suffers an important decrease, which is due to the fact that initially the increase of the temperature is very steep but, later on, the amplitude decrease is smoother because of a smoother temporal variation of the temperature (see Fig. 2, left panel). On the other hand, the temporal behaviour of the period is due to the temporal variation of the sound speed. From Eq. (24), the frequency of the oscillations can be approximated by 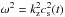 and, from it, the period for a fixed wavenumber, kz, is given by
and, from it, the period for a fixed wavenumber, kz, is given by 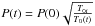 , where P(0) is the period at t = 0, whose value, in our case, is 1379 s. Figure 5 displays the temporal behaviour of the ratio between the time-dependent period and the initial one for different characteristic radiation times, showing that, for short values of τ, the temporal change of the period with respect to the initial one is smaller than for long values of τ. Figure 6 shows the time behaviour of the amplitude of the perturbed velocity for different characteristic radiation times. Two features can clearly be seen in this plot: the first is that the time change of the period becomes more important for long characteristic times, in agreement with Fig. 5, and the second one refers to the temporal change of the amplitude which, within the same time window, is greater for longer characteristic times. This latter effect should be related to the decrease in the period since, for long characteristic times, more oscillations are present within the same time window.
, where P(0) is the period at t = 0, whose value, in our case, is 1379 s. Figure 5 displays the temporal behaviour of the ratio between the time-dependent period and the initial one for different characteristic radiation times, showing that, for short values of τ, the temporal change of the period with respect to the initial one is smaller than for long values of τ. Figure 6 shows the time behaviour of the amplitude of the perturbed velocity for different characteristic radiation times. Two features can clearly be seen in this plot: the first is that the time change of the period becomes more important for long characteristic times, in agreement with Fig. 5, and the second one refers to the temporal change of the amplitude which, within the same time window, is greater for longer characteristic times. This latter effect should be related to the decrease in the period since, for long characteristic times, more oscillations are present within the same time window.
Finally, analytical expressions for the time dependent amplitude of density, pressure, and temperature perturbations can also be obtained:
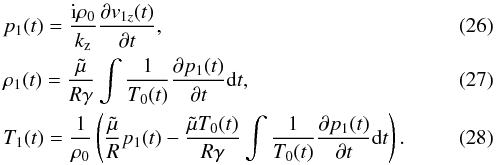 Hence, once the analytical solution for Eq. (24) is known, using Eqs. (26)−(28), the time behaviour of these perturbations can be determined.
Hence, once the analytical solution for Eq. (24) is known, using Eqs. (26)−(28), the time behaviour of these perturbations can be determined.
 |
Fig. 6 Temporal behaviour of the perturbed velocity for a prominence plasma with a background temperature that increases with time for different characteristic times. τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). T0i = 10 000 K, H = 3.5 × 10-5 W m-3, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
3.2. Exponential increase of the background temperature and radiative damping of perturbations
Next, in the right-hand side of Eq. (23), when we consider only the perturbed term that corresponds to the radiative damping of perturbations, our differential equation is 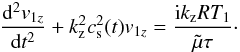 (29)Since, from Eq. (29), we cannot obtain an analytical expression for v1z, combining Eqs. (19)−(22) we end up with a system of three coupled equations for the velocity, density and temperature perturbations such as,
(29)Since, from Eq. (29), we cannot obtain an analytical expression for v1z, combining Eqs. (19)−(22) we end up with a system of three coupled equations for the velocity, density and temperature perturbations such as,
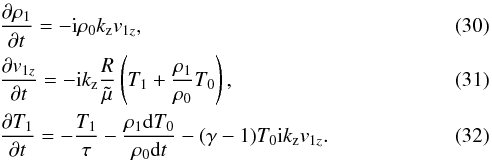 with thermal conduction neglected, which have been solved together with initial conditions v1z(0) = 1, T1(0) = 0 and ρ1(0) = 0. Figure 7 shows the temporal behaviour of the amplitude of the perturbed velocity for a prominence plasma whose background temperature increases with time, and for a prominence plasma whose background temperature also increases with time but radiative damping of perturbations is taken into account. This figure shows that the modification of the period with respect to the previous case is negligible and that an additional damping appears due to the radiative damping of perturbations.
with thermal conduction neglected, which have been solved together with initial conditions v1z(0) = 1, T1(0) = 0 and ρ1(0) = 0. Figure 7 shows the temporal behaviour of the amplitude of the perturbed velocity for a prominence plasma whose background temperature increases with time, and for a prominence plasma whose background temperature also increases with time but radiative damping of perturbations is taken into account. This figure shows that the modification of the period with respect to the previous case is negligible and that an additional damping appears due to the radiative damping of perturbations.
 |
Fig. 7 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature increases with time (continuous line) and for a prominence plasma whose temperature increases with time and radiative damping of perturbations is included (dashed line). T0i = 10 000 K, H = 3.5 × 10-5 W m-3, τ = 3000 s, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
 |
Fig. 8 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature increases with time and radiative damping of perturbations is included (continuous line) and for exp [ − t/τD ] cos [ ωt ] (dashed line). T0i = 10 000 K, H = 3.5 × 10-5 W m-3, τ = τD = 3000 s, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
On the other hand, in observations of time-damped prominence oscillations, which are attributed to slow waves, it is common to assume a constant background temperature and to fit the time behaviour of the observed doppler velocity with an expression similar to exp [ − t/τD ] cos [ ωt ], where τD represents the damping time, ω = kcs(0) is the angular frequency, and k the wavenumber. Therefore, in Fig. 8, we compare the temporal behaviour of the amplitude of the perturbed velocity for a variable background temperature with radiative damping of perturbations with that of the exponential decrease of the amplitude that is given by the expression stated before. This figure points out that there is a strong difference between both behaviours. In the first instance, when the exponentially decaying harmonic function is considered, the amplitude decreases rapidly while the period remains constant. However, in the case of a variable background, together with radiative damping of perturbations, the amplitude decreases in a continuous way, but not as quickly as in the previous case, and the period also decreases. In summary, a big difference between both behaviours is observed, which can be of interest for the interpretation of observations.
Figure 9 displays a comparison betweeen the amplitudes of perturbed velocity, in the case of a variable background temperature and radiative losses, for different characteristic times, and it shows that the damping is enhanced for short τ, specially when τ is of the order of P. On the other hand, when different numerical values for the heating term are considered, allowing reasonables increases of the prominence plasma temperature, the effect on the amplitudes is almost negligible. Finally, once all the perturbations have been determined from Eqs. (30)−(32), we can obtain the pressure perturbation from Eq. (22).
 |
Fig. 9 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature increases with time, radiative damping of perturbations included, and different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). T0i = 10 000 K, H = 3.5 × 10-5 W m-3, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
3.3. Exponential increase of the background temperature, radiative damping of perturbations, and thermal conduction
Taking into account the radiative damping of perturbations and thermal conduction in the right hand side of Eq. (23), we expect a negligible contribution to the damping to come from thermal conduction owing to the small values of the wavenumbers that are typically observed in prominence oscillations, and considered here. Combining Eqs. (19)−(22), we end up with a system of three coupled equations for the velocity, density, and temperature perturbations, such as
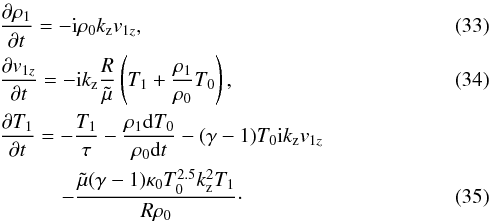 Equations (33)−(35) have been solved numerically, together with initial conditions v1z(0) = 1, T1(0) = 0 and ρ1(0) = 0, and Fig. 10 shows a comparison between the amplitudes of the perturbed velocity for a prominence plasma with a variable background temperature and radiative damping of perturbations included and, for the case of a variable background temperature, radiative damping of perturbations and thermal conduction together. This figure shows that the period is almost unchanged and that the additional contribution to the damping, which comes from thermal conduction, is absolutely negligible.
Equations (33)−(35) have been solved numerically, together with initial conditions v1z(0) = 1, T1(0) = 0 and ρ1(0) = 0, and Fig. 10 shows a comparison between the amplitudes of the perturbed velocity for a prominence plasma with a variable background temperature and radiative damping of perturbations included and, for the case of a variable background temperature, radiative damping of perturbations and thermal conduction together. This figure shows that the period is almost unchanged and that the additional contribution to the damping, which comes from thermal conduction, is absolutely negligible.
 |
Fig. 10 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature increases with time with radiative damping of perturbations included (continuous line), and for a prominence plasma whose temperature increases with time, with radiative damping of perturbations and thermal conduction included (dashed line). H = 3.5 × 10-5 W m-3, τ = 3000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
 |
Fig. 11 Temporal behaviour of the perturbed velocity for a prominence plasma with constant temperature (T0i = 10,000 K) background (dashed line) and with a background temperature that decreases with time (continuous line). H = 1 × 10-6 W m-3, τ = 3000 s, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
3.4. Exponential decrease of the background temperature
If we now assume that initially Lr>H, therefore the prominence plasma temperature decreases with time following Eq. (10). Furthermore, we neglect the damping mechanisms terms in the right-hand side of Eq. (23), in which case the analytical solution that corresponds to Eq. (24), with initial conditions v1z(0) = 1 and v′1z(0) = 0, is also given by Eq. (25). Again, this analytical solution indicates that we do not have pure harmonic oscillations. Figure 11 shows a comparison between the temporal behaviour of the amplitudes of perturbed velocity for a prominence plasma with a constant temperature and with a background temperature which decreases in time. As before, for a constant background temperature, the perturbed velocity amplitude and period remain constant. But when the background temperature decreases exponentially in time, the amplitude of the perturbed velocity amplitude, as well as the period, increase with time. As in the previous case, the temporal behaviour of the period is due to the temporal change of the sound speed and, for a fixed wavenumber kz, is given, as before, by 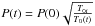 , where P(0) is the period at t = 0 whose value, in our case, is 1379 s. Figure 12 shows the temporal behaviour of the period for different characteristic times, and shows that for small τ the temporal change of the period, with respect to the initial one, is stronger than for large τ. Furthermore, Fig. 13 shows that the amplification of the oscillation is bigger for short characteristic times. As before, the rest of the perturbations can be obtained from Eqs. (26)−(28), once the time derivative of the perturbed velocity is known.
, where P(0) is the period at t = 0 whose value, in our case, is 1379 s. Figure 12 shows the temporal behaviour of the period for different characteristic times, and shows that for small τ the temporal change of the period, with respect to the initial one, is stronger than for large τ. Furthermore, Fig. 13 shows that the amplification of the oscillation is bigger for short characteristic times. As before, the rest of the perturbations can be obtained from Eqs. (26)−(28), once the time derivative of the perturbed velocity is known.
 |
Fig. 12 Temporal variation of the ratio between the instantaneous, P(t), and the initial, P(0), oscillatory period in a prominence plasma whose background equilibrium temperature decreases exponentially with time for different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line), H = 1 × 10-6 W m-3, T0i = 10 000 K. |
 |
Fig. 13 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time for different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). T0i = 10 000 K, H = 1 × 10-6 W m-3, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
 |
Fig. 14 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time (continuous line) and for a prominence plasma whose temperature decreases with time and radiative damping of perturbations included (dashed line). T0i = 10 000 K, H = 1 × 10-6 W m-3, τ = 3000 s, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
 |
Fig. 15 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time and radiative damping of perturbations included, for different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). T0i = 10 000 K, H = 1 × 10-6 W m-3, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
3.5. Exponential decrease of the background temperature and radiative damping of perturbations
When radiative damping of perturbations is taken into account, Eq. (29), with the sound speed decreasing exponentially with time, provides the relationship between velocity and temperature perturbations, and Eqs. (30)−(32), together with the same initial conditions as in Sect. 3.2, are solved numerically. Figure 14 displays, for a fixed characteristic time, the temporal behaviour of the velocity perturbations for a prominence plasma whose temperature decreases with time, as well as a prominence plasma whose temperature decreases with time, together with radiative damping of perturbations. We can observe that the period is almost unmodified by the presence of radiative damping of perturbations which affects the amplitude of the velocity perturbation. Afterwards, we explored the temporal behaviour of the velocity perturbations when different characteristic times were considered. Figure 15 shows that, for small values of the characteristic time, the damping of oscillations is stronger. However, this figure might suggest that, for a sufficiently small characteristic time, the oscillations could be amplified or become of constant amplitude, which gives way to what is known as decayless oscillations, e.g. those which have been found in transverse oscillations of coronal loops (Aschwanden & Schrijver 2011; Nisticò et al. 2013; Anfinogentov et al. 2013; Hindman & Jain 2014). This behaviour is seen in Fig. 16 where we can observe that, during most of the shown time interval, the amplitude of the oscillation is more or less constant while the period changes with time. In fact, looking in detail at the temporal behaviour of the oscillation, it seems that the oscillation goes through a short phase of amplification, remains constant for some time, and finally starts to initiate a very smooth decay at a time that is close to the characteristic time. Then, as the background temperature decreases with time, it seems that we have several possibilities, since the decreasing temperature tries to amplify the oscillation while radiative losses try to damp it. When the characteristic time is short, radiative damping dominates and the oscillation is quickly attenuated, while for long characteristic times, amplification plays a role that is not negligible. Finally, when, for a fixed value of the characteristic time, we consider different values of the heating term, the effect on the oscillations is negligible.
 |
Fig. 16 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time and radiative damping of perturbations included. H = 1.5 × 10-7 W m-3, τ = 7000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
3.6. Exponential decrease of the background temperature, radiative damping of perturbations, and thermal conduction
When radiative damping of perturbations and thermal conduction are taken into account, Eq. (23), with the sound speed decreasing exponentially with time, show the relationship between velocity and temperature perturbations. Equations (33)−(35), together with the same boundary conditions as in Sect. 3.3, have been solved numerically. Again, as is suggested by Eq. (23), the period is almost unmodified by the inclusion of radiative losses and thermal conduction, which only have an influence on the damping. On the other hand, the additional effect on the damping, which is produced by the inclusion of thermal conduction, is negligible, as was seen in Sect. 3.3, owing to the small wavenumbers considered.
4. Energy considerations
The total energy density of the slow wave is given by, 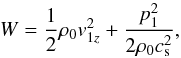 (36)and we have computed this quantity in three different cases: (a) prominence plasma with a constant temperature; (b) prominence plasma with a temperature that decreases/increases with time, and (c) prominence plasma with a temperature that decreases/increases with time, together with radiative losses. Figure 17 shows that, in the case of a constant background temperature, the total energy density remains constant with time, as expected. However, when temperature increases with time, the total energy density decreases with time, while, when radiative losses are included, this decrease is enhanced. Conversely, Fig. 18 shows that, when temperature decreases with time, the total energy density increases with time. However, when radiative losses are included, the total energy density also decreases with time.
(36)and we have computed this quantity in three different cases: (a) prominence plasma with a constant temperature; (b) prominence plasma with a temperature that decreases/increases with time, and (c) prominence plasma with a temperature that decreases/increases with time, together with radiative losses. Figure 17 shows that, in the case of a constant background temperature, the total energy density remains constant with time, as expected. However, when temperature increases with time, the total energy density decreases with time, while, when radiative losses are included, this decrease is enhanced. Conversely, Fig. 18 shows that, when temperature decreases with time, the total energy density increases with time. However, when radiative losses are included, the total energy density also decreases with time.
 |
Fig. 17 Temporal behaviour of the slow wave total energy density for a prominence plasma (a) with a constant temperature (continuous line); (b) with a temperature that increases with time (dashed line); (c) with a temperature that increases with time and radiative damping of the perturbations included (dotted line). H = 1 × 10-5 W m-3, τ = 3000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1. The total energy density has been normalized with respect to its initial value. |
 |
Fig. 18 Temporal behaviour of the slow wave total energy density for a prominence plasma (a) with a constant temperature (continuous line); (b) with a temperature which decreases with time (dashed line); (c) with a temperature that decreases with time and radiative damping of the perturbations included (dotted line). H = 1 × 10-6 W m-3, τ = 3000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1. The total energy density has been normalized with respect to its initial value. |
To understand the temporal behaviour of the total energy density shown in Figs. 17 and 18, we could start from the linearized continuity, momentum, and energy equations to obtain, after some straightforward manipulations, the following expression: 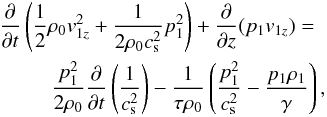 (37)in which the terms on the left-hand side provide the temporal variation of the total energy density of the wave and the divergence of the wave energy density flux, respectively, while on the right-hand side, the first term comes from the temporal change of the sound speed and the second accounts for radiative losses. Thermal conduction was not taken into account owing to its negligible effect on the oscillations. Equation (37) is a continuity equation in which the right-hand side terms represent a source/sink, which accounts for the generation or removal of the wave energy density per unit time. Therefore, when the right-hand side is positive, the wave energy density increases with time while, when it is negative, the opposite happens. When the background temperature is constant and radiative losses are neglected, the right-hand side term is zero and the wave energy density remains constant in time. However, when a variable background temperature is considered and radiative losses are neglected, the temporal changes, amplification, or damping of wave energy density are due to the sink/source term involving the time-dependent sound speed. Finally, when a variable background temperature and radiative losses are considered together, the right-hand term is always negative, which produces a temporal decrease in the wave-energy density, either for increasing or decreasing background temperature. In summary, with the help of Eq. (37) the temporal behaviour of the slow wave-energy density, as shown in Figs. 17 and 18, can be understood.
(37)in which the terms on the left-hand side provide the temporal variation of the total energy density of the wave and the divergence of the wave energy density flux, respectively, while on the right-hand side, the first term comes from the temporal change of the sound speed and the second accounts for radiative losses. Thermal conduction was not taken into account owing to its negligible effect on the oscillations. Equation (37) is a continuity equation in which the right-hand side terms represent a source/sink, which accounts for the generation or removal of the wave energy density per unit time. Therefore, when the right-hand side is positive, the wave energy density increases with time while, when it is negative, the opposite happens. When the background temperature is constant and radiative losses are neglected, the right-hand side term is zero and the wave energy density remains constant in time. However, when a variable background temperature is considered and radiative losses are neglected, the temporal changes, amplification, or damping of wave energy density are due to the sink/source term involving the time-dependent sound speed. Finally, when a variable background temperature and radiative losses are considered together, the right-hand term is always negative, which produces a temporal decrease in the wave-energy density, either for increasing or decreasing background temperature. In summary, with the help of Eq. (37) the temporal behaviour of the slow wave-energy density, as shown in Figs. 17 and 18, can be understood.
On the other hand, by considering only the case in which the background temperature changes with time, the damping or amplification of the oscillations could be understood in the following qualitative way: when the background temperature increases, the pressure of the background plasma increases, since density is kept constant. This means that, as time goes by, the motion of the perturbations through the background plasma is more difficult, which leads to the damping of the velocity amplitude. The opposite happens when the background temperature decreases. Furthermore, when the background temperature decreases with time and radiative losses are also taken into account, the two effects act as competing mechanisms, so that the velocity amplitude can be eventually damped.
5. Conclusions
Usually, prominence oscillations have been studied by perturbing a background equilibrium whose physical properties do not change with time (an extensive review of different studies can be found in Arregui et al. 2012). However, observations of prominences suggest that they are very dynamic plasma structures whose physical properties, such as temperature, density, pressure, etc, can change with time. Therefore, in this paper we have made a first attempt to study the effects produced by a non-stationary plasma on slow MHD waves, which could be responsible for some prominence oscillations. To carry out this study, we have assumed that the radiation term is proportional to the plasma temperature and that the external heating term is constant. Hence, from the initial equilibrium, we have derived the expression for the temporal change of temperature when radiation or heating initially dominate. Taking this approach, we have found that the background temperature increases or decreases with time at a rate that is governed by a characteristic time. Taking all of this into account, we have considered the case of slow waves that propagate along the magnetic field and we have studied the temporal behaviour of its velocity perturbations.
When the background temperature increases with time, the period of slow waves decreases with time owing to the time dependent sound speed, and this decrease is faster for long characteristic times. On the other hand, the velocity perturbations are damped in time, but once the radiation term becomes equal to the external heating, the amplitude becomes constant. Furthermore, the initial damping of the velocity perturbations is slightly enhanced for long characteristic times, which is due to the period decrease. This allows for more oscillations within a fixed time window. When radiative losses are taken into account, the oscillations become damped in time as expected, and this damping is enhanced for short characteristic times. However, when different numerical values of the heating term are considered, the damping rate is almost unaffected. Finally, when thermal conduction is included, the temporal behaviour of velocity perturbations is not affected because the contribution to the damping that comes from parallel thermal conduction is negligible due to the small wavenumbers that are typically involved in prominence oscillations. In summary, the joint effect of an increasing background temperature, radiative losses, and thermal conduction modify the temporal behaviour of the slow waves’ velocity perturbations that propagate along the magnetic field, with respect to the case of a constant temperature background plus radiative losses and thermal conduction. The main differences are: the period decreases with time, instead of remaining constant, and the damping of the oscillations is not strictly exponential, as happens when a constant temperature background equilibrium and radiative damping of perturbations together are considered, because the behaviour of the amplitude comes from an interplay between the variable background temperature, which decreases the amplitude, and the damping associated with the perturbed radiation term.
When the background temperature decreases with time, the period of slow waves increases with time owing to the time-dependent sound speed, and this increase is faster for short characteristic times. Also, velocity perturbations are amplified over time, and this amplification is stronger for short characteristic times. When radiative losses are also taken into account, we are left with several possibilities: for short characteristic times, the overall effect could be a time-damping of the oscillations, however, when the numerical value of the characteristic time is increased, the oscillations initially amplify, then become constant and, later on, become damped; finally, increasing the characteristic time even more, the oscillations are always amplified within the time window under consideration. As before, the further inclusion of thermal conduction does not produce any remarkable effect on the damping owing to the low wavenumber considered. In summary, the joint effect of a background equilibrium whose temperature decreases in time, together with radiative losses can modify the behaviour of the oscillations. In this case, the oscillatory period increases with time, while temporal amplification or damping of the oscillations, as well as decayless oscillations can happen. Similar behaviours have been found in theoretical studies of cooling and oscillating coronal loops (Al-Ghafri & Erdélyi 2013; Al-Ghafri et al. 2014).
Furthermore, we could take all the above situations together by assuming, for instance, that during a certain time interval a temporal decrease of the temperature happens, followed by a temporal increase of the temperature during another time interval. The temporal behaviour of the velocity perturbation is shown in Fig. 19, where the initial increase of the amplitude and period, is followed by a decrease of both quantities. This behaviour indicates how the character of the oscillations changes in time owing to temporal changes of a physical property, like the temperature, of prominence plasma.
 |
Fig. 19 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time between t = 0 s and t = 10 000 s, and increases with time between t = 10 000 s and t = 20 000 s. (τ = 3000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1, H = 1 × 10-6 W m-3 and H = 1 × 10-5 W m-3, respectively.) |
From the observational point of view, these features are of great interest for the analysis of prominence oscillations since they could explain time changes of the oscillatory period, as well as the amplification or damping of the oscillations, etc. Also, and taking into account the intrinsic inhomogeneity of the prominence medium, we could expect that, in different prominence locations, appropiate combinations of a variable background temperature, together with radiative losses, could give place to time amplified or damped oscillations as was observed in Molowny-Horas et al. (1999). Furthermore, we note the different temporal behaviours of the perturbed variables. For instance, when the background temperature increases with time the velocity and density perturbations decrease with time while, conversely, pressure and temperature perturbations increase with time. Therefore, while Doppler velocity information would suggest an attenuation of the oscillations, spectral line parameters such as intensity, line width, etc, which could be related to pressure or temperature perturbations (Heinzel et al. 2014), suggest the opposite is true. However, forward modelling of the spectral line indicators would be necessary to establish the relation between the variation of plasma perturbations and the temporal evolution of spectral line parameters. At the same time, these considerations indicate the inherent difficulty in interpretating the prominence oscillations owing to the many different effects that can be involved.
We have not explored the behaviour of velocity perturbations associated with fast waves. The reason is that fast waves are only slightly affected by thermal mechanisms and, in addition, since the phase speed of these waves is a combination of sound and Alfvén speeds, we also do no expect the period of fast waves to be affected since our constant Alfvén speed is dominant over the sound speed for any time interval of interest.
In this study, we have only considered a temporal change of the background temperature while the background density was kept constant. Of course, other assumptions about the radiation term could have been assumed. However, we expect that the overall behaviour of slow waves would be similar and that the only difference would be how fast the waves are affected by the changing background temperature. Furthermore, other assumptions about time changes of the background density, effect of gravity, etc, could have been performed too. On the other hand, a structureless medium has been assumed as a first step when ascertaining the effects on slow MHD waves that are responsible for some prominence oscillations and that are produced by the presence of a variable background. Future research in this topic should be related to considering a structured medium. In particular, the influence of a variable background on the oscillatory properties of filament threads is an example of great interest and deserves to be studied. Finally, we should also remember that prominences are partially ionized plasmas (Parenti 2014) and that changes in the background temperature could also affect plasma parameters such as the ionization degree, mean molecular weight, resistivities, collision frequencies, etc. Therefore, a more realistic approach should take into account the effect of the temporal changes of all these parameters on MHD waves. However, in the case of parallel propagation, the linearized equations for slow waves, taking into account partial ionization effects, are the same as in Sect. 2, which leads to the same results. In the case of oblique propagation, the linearized equations for fast and slow waves are coupled and, then, slow waves are weakly damped because of Cowling’s resistivity (Forteza et al. 2007; Soler et al. 2009b). The study of the behaviour of MHD waves in a partially ionized prominence plasma with a time-dependent background temperature is left for future study.
Acknowledgments
The authors acknowledge the support received from MINECO under grant AYA2014-54485-P and FEDER funds. Financial support from ISSI and discussions within ISSI team on Large amplitude oscillations in prominences are also gratefully acknowledged. R. Soler acknowledges support from MINECO and UIB through a “Ramón y Cajal” grant (RYC-2014-14970). J. Terradas acknowledges support from MINECO and UIB through a “Ramón y Cajal” grant (RYC-2010-06991).
References
- Al-Ghafri, K. S., & Erdélyi, R. 2013, Sol. Phys., 283, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Al-Ghafri, K. S., Ruderman, M. S., Williamson, A., & Erdélyi, R. 2014, ApJ, 786, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Anfinogentov, S., Nisticò, G., & Nakariakov, V. M. 2013, A&A, 560, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., Terradas, J., Oliver, R., & Ballester, J. L. 2008, ApJ, 682, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I., Oliver, R., & Ballester, J. L. 2012, Liv. Rev. Sol. Phys., 9, 2 [Google Scholar]
- Aschwanden, M. J., & Schrijver, C. J. 2011, ApJ, 736, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., & Terradas, J. 2008, ApJ, 686, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. E., Shine, R. A., Slater, G. L., et al. 2008, ApJ, 676, L89 [Google Scholar]
- Bommier, V., & Leroy, J. L. 1998, in IAU Colloq. 167: New Perspectives on Solar Prominences, eds. D. F. Webb, B. Schmieder, & D. M. Rust, ASP Conf. Ser., 150, 434 [Google Scholar]
- Bommier, V., Landi Degl’Innocenti, E., Leroy, J.-L., & Sahal-Brechot, S. 1994, Sol. Phys., 154, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Carbonell, M., Oliver, R., & Ballester, J. L. 2004, A&A, 415, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engvold, O. 1998, in IAU Colloq. 167: New Perspectives on Solar Prominences, eds. D. F. Webb, B. Schmieder, & D. M. Rust, ASP Conf. Ser., 150, 23 [Google Scholar]
- Engvold, O. 2008, in IAU Symp. 247, eds. R. Erdélyi, & C. A. Mendoza-Briceno, 152 [Google Scholar]
- Erdélyi, R., Al-Ghafri, K. S., & Morton, R. J. 2011, Sol. Phys., 272, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Forteza, P., Oliver, R., Ballester, J. L., & Khodachenko, M. L. 2007, A&A, 461, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forteza, P., Oliver, R., & Ballester, J. L. 2008, A&A, 492, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., & Anzer, U. 2006, ApJ, 643, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., Zapiór, M., Oliver, R., & Ballester, J. L. 2014, A&A, 562, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hindman, B. W., & Jain, R. 2014, ApJ, 784, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, J. L. 1980, in Japan-France Seminar on Solar Physics, eds. F. Moriyama, & J. C. Henoux, 155 [Google Scholar]
- Lin, Y. 2004, Ph.D. Thesis, University of Oslo, Norway [Google Scholar]
- Lin, Y. 2010, Space Sci. Rev., 112 [Google Scholar]
- Lin, Y. 2011, Space Sci. Rev., 158, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L., Wiik, J. E., & Berger, T. E. 2005, Sol. Phys., 226, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Martin, S. F., Engvold, O., Rouppe van der Voort, L. H. M., & van Noort, M. 2008, Adv. Space Res., 42, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Soler, R., Engvold, O., et al. 2009, ApJ, 704, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., & Karpen, J. 2012, ApJ, 750, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Díaz, A. J., & Karpen, J. 2012, ApJ, 757, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Knizhnik, K., Muglach, K., et al. 2014, ApJ, 785, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H. 2015, in Solar Prominences, eds. J.-C. Vial, & O. Engvold (Springer), Astrophys. Space Sci. Lib., 415, 355 [Google Scholar]
- Molowny-Horas, R., Wiehr, E., Balthasar, H., Oliver, R., & Ballester, J. L. 1999, in JOSO Annu. Rep., 126 [Google Scholar]
- Morton, R. J., & Erdélyi, R. 2009, ApJ, 707, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, R. J., & Erdélyi, R. 2010, A&A, 519, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, R. J., Hood, A. W., & Erdélyi, R. 2010, A&A, 512, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ning, Z., Cao, W., Okamoto, T. J., Ichimoto, K., & Qu, Z. Q. 2009, A&A, 499, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okamoto, T. J., Tsuneta, S., Berger, T. E., et al. 2007, Science, 318, 1577 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Oliver, R., & Ballester, J. L. 2002, Sol. Phys., 206, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Parenti, S. 2014, Liv. Rev. Sol. Phys., 11 [Google Scholar]
- Ruderman, M. S. 2011a, A&A, 534, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. S. 2011b, Sol. Phys., 271, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2008, ApJ, 684, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2009a, ApJ, 699, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Oliver, R., Ballester, J. L., & Goossens, M. 2009b, ApJ, 695, L166 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2014, in IAU Symp. 300, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, 48 [Google Scholar]
- Terradas, J., Oliver, R., & Ballester, J. L. 2001, A&A, 378, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terradas, J., Molowny-Horas, R., Wiehr, E., et al. 2002, A&A, 393, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terradas, J., Carbonell, M., Oliver, R., & Ballester, J. L. 2005, A&A, 434, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2008, ApJ, 676, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Ofman, L., Davila, J. M., & Su, Y. 2012, ApJ, 751, L27 [Google Scholar]
- Williamson, A., & Erdélyi, R. 2014a, Sol. Phys., 289, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Williamson, A., & Erdélyi, R. 2014b, Sol. Phys., 289, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Williamson, A., & Erdélyi, R. 2014c, Sol. Phys., 289, 4105 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q. M., Chen, P. F., Xia, C., Keppens, R., & Ji, H. S. 2013, A&A, 554, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Doppler velocities (km s-1) as a function of time for six different spatial locations in a prominence. Dots denote observational data, while solid lines correspond to an analytical fit such as: |
| In the text | |
 |
Fig. 2 Left panel: temporal variation of the prominence plasma temperature for H = 8.5 × 10-6 W m-3 and different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). Right panel: temporal variation of the prominence plasma temperature for H = 3.5 × 10-7 W m-3 and different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). In these plots T0i = 10 000 K. |
| In the text | |
 |
Fig. 3 Left panel: temporal variation of the prominence plasma temperature for τ = 3000 s and different values of the heating function H = 8.5 × 10-6 W m-3 (continuous line), 1 × 10-5 W m-3 (dashed line), 1.5 × 10-5 W m-3 (dotted line). Right panel: temporal variation of the prominence plasma temperature for τ = 3000 s and different values of the heating function H = 1 × 10-6 W m-3 (continuous line), 5.5 × 10-7 W m-3 (dashed line), 1.5 × 10-7 W m-3 (dotted line). T0i = 10 000 K. |
| In the text | |
 |
Fig. 4 Temporal behaviour of the perturbed velocity for a prominence plasma with a background temperature that increases with time (continuous line) and for a prominence plasma with a constant background (T0i = 10 000 K) temperature (dashed line). H = 3.5 × 10-5 W m-3, τ = 3000 s. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 5 Temporal variation of the ratio between the instantaneous, P(t), and the initial, P(0), oscillatory period in a prominence plasma whose background temperature increases with time for different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). H = 8.5 × 10-6 W m-3. |
| In the text | |
 |
Fig. 6 Temporal behaviour of the perturbed velocity for a prominence plasma with a background temperature that increases with time for different characteristic times. τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). T0i = 10 000 K, H = 3.5 × 10-5 W m-3, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 7 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature increases with time (continuous line) and for a prominence plasma whose temperature increases with time and radiative damping of perturbations is included (dashed line). T0i = 10 000 K, H = 3.5 × 10-5 W m-3, τ = 3000 s, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 8 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature increases with time and radiative damping of perturbations is included (continuous line) and for exp [ − t/τD ] cos [ ωt ] (dashed line). T0i = 10 000 K, H = 3.5 × 10-5 W m-3, τ = τD = 3000 s, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 9 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature increases with time, radiative damping of perturbations included, and different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). T0i = 10 000 K, H = 3.5 × 10-5 W m-3, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 10 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature increases with time with radiative damping of perturbations included (continuous line), and for a prominence plasma whose temperature increases with time, with radiative damping of perturbations and thermal conduction included (dashed line). H = 3.5 × 10-5 W m-3, τ = 3000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 11 Temporal behaviour of the perturbed velocity for a prominence plasma with constant temperature (T0i = 10,000 K) background (dashed line) and with a background temperature that decreases with time (continuous line). H = 1 × 10-6 W m-3, τ = 3000 s, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 12 Temporal variation of the ratio between the instantaneous, P(t), and the initial, P(0), oscillatory period in a prominence plasma whose background equilibrium temperature decreases exponentially with time for different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line), H = 1 × 10-6 W m-3, T0i = 10 000 K. |
| In the text | |
 |
Fig. 13 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time for different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). T0i = 10 000 K, H = 1 × 10-6 W m-3, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 14 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time (continuous line) and for a prominence plasma whose temperature decreases with time and radiative damping of perturbations included (dashed line). T0i = 10 000 K, H = 1 × 10-6 W m-3, τ = 3000 s, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 15 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time and radiative damping of perturbations included, for different characteristic times, τ = 1500 s (continuous line), 3000 s (dashed line), 6000 s (dotted line). T0i = 10 000 K, H = 1 × 10-6 W m-3, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 16 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time and radiative damping of perturbations included. H = 1.5 × 10-7 W m-3, τ = 7000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1. The velocity amplitude has been normalized. |
| In the text | |
 |
Fig. 17 Temporal behaviour of the slow wave total energy density for a prominence plasma (a) with a constant temperature (continuous line); (b) with a temperature that increases with time (dashed line); (c) with a temperature that increases with time and radiative damping of the perturbations included (dotted line). H = 1 × 10-5 W m-3, τ = 3000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1. The total energy density has been normalized with respect to its initial value. |
| In the text | |
 |
Fig. 18 Temporal behaviour of the slow wave total energy density for a prominence plasma (a) with a constant temperature (continuous line); (b) with a temperature which decreases with time (dashed line); (c) with a temperature that decreases with time and radiative damping of the perturbations included (dotted line). H = 1 × 10-6 W m-3, τ = 3000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1. The total energy density has been normalized with respect to its initial value. |
| In the text | |
 |
Fig. 19 Temporal behaviour of the perturbed velocity for a prominence plasma whose temperature decreases with time between t = 0 s and t = 10 000 s, and increases with time between t = 10 000 s and t = 20 000 s. (τ = 3000 s, T0i = 10 000 K, kz = 3 × 10-7 m-1, H = 1 × 10-6 W m-3 and H = 1 × 10-5 W m-3, respectively.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.