| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201527822 | |
| Published online | 10 June 2016 | |
Cosmic microwave background reconstruction from WMAP and Planck PR2 data⋆
Laboratoire AIM, UMR CEA-CNRS-Paris 7, Irfu, SAp/SEDI, Service
d’Astrophysique, CEA Saclay,
91191
Gif-sur-Yvette Cedex,
France
e-mail:
jbobin@cea.fr
Received: 24 November 2015
Accepted: 12 March 2016
We describe a new estimate of the cosmic microwave background (CMB) intensity map reconstructed by a joint analysis of the full Planck 2015 data (PR2) and nine years of WMAP data. The proposed map provides more than a mere update of the CMB map introduced in a previous paper since it benefits from an improvement of the component separation method L-GMCA (Local-Generalized Morphological Component Analysis), which facilitates efficient separation of correlated components. Based on the most recent CMB data, we further confirm previous results showing that the proposed CMB map estimate exhibits appealing characteristics for astrophysical and cosmological applications: i) it is a full-sky map as it did not require any inpainting or interpolation postprocessing; ii) foreground contamination is very low even on the galactic center; and iii) the map does not exhibit any detectable trace of thermal Sunyaev-Zel’dovich contamination. We show that its power spectrum is in good agreement with the Planck PR2 official theoretical best-fit power spectrum. Finally, following the principle of reproducible research, we provide the codes to reproduce the L-GMCA, which makes it the only reproducible CMB map.
Key words: cosmic background radiation / methods: data analysis
The reconstructed CMB map and the code are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/591/A50
© ESO, 2016
1. Introduction
The cosmic microwave background (CMB) provides a snapshot of our Universe at the time of recombination. It is therefore a unique probe for cosmologists since it carries crucial information about the dawn of the Universe and the evolution to its current state. We show that the ability to estimate a clean full-sky CMB map is critical to accurately study its statistical properties at large scales (Rassat et al. 2014); these properties depend on the primordial fluctuations from which they arise.
Maps of the CMB have been reconstructed from the frequency channels of the WMAP mission (Bennett 2013) and the Planck mission in 2013 (Planck Collaboration XII 2014). In 2015, the Planck consortium released the full Planck data (Planck Release 2 or PR2) from which CMB maps were derived (Planck Collaboration IX 2016). Thanks to longer integration time, the instrumental noise was significantly reduced with respect to the Planck PR1 data released in 2013. Data calibration was dramatically improved, which further reduces the impact of instrumental systematics (Planck Collaboration I 2016). Understanding the beam transfer function (Planck Collaboration VI 2016; Planck Collaboration VIII 2016) largely reduces the uncertainty of the data, especially at small scales.
The reconstruction of a clean CMB map from multiple frequency channels is well known to be a challenging task, since it requires removing spurious astrophysical foreground contaminations. These emissions mainly include:
-
In the low frequency regime, below 100 GHz: the predominant source of contamination comes from galactic synchrotron and free-free emissions (Gold et al. 2011; Planck Collaboration X 2016), especially at a large angular scale. Spinning dust (Planck Collaboration XX 2011; Planck Collaboration XXV 2016) highly correlates with thermal dust emission.
-
In the high frequency regime, above 100 GHz: at higher frequencies, the dominant source of contamination is thermal dust emission (Planck Collaboration XIX 2011), especially at the vicinity of the galactic center. The cosmic infrared background (Planck Collaboration XXX 2014) provides significant emission at all galactic latitudes at the highest frequencies (i.e., 545 and 857 GHz).
Estimating a clean CMB map from frequency channels was shown to be best carried out by component separation methods (Leach 2008; Planck Collaboration XII 2014; Planck Collaboration IX 2016). To that respect, the CMB maps released by the Planck consortium in 2015 were computed with four different component separation techniques: Commander (Eriksen et al. 2008), Needlet ILC (NILC; Delabrouille et al. 2009), SEVEM (Fernández-Cobos et al. 2012), and SMICA (Delabrouille et al. 2003). These methods were extensively described in Planck Collaboration IX (2016).
In Bobin et al. (2014b), we introduced a new CMB map using a recent sparsity-based component separation technique, coined Local-Generalized Morphological Component Analysis (L-GMCA; see Bobin et al. 2013). The proposed CMB map was further based on a joint processing of the Planck 2013 (PR1) and WMAP nine-year data. We showed that in contrast to the available CMB maps, the proposed L-GMCA-based estimate is a clean full-sky estimate that did not require any masking or inpainting technique for large-scale statistical studies (Rassat et al. 2014). Furthermore, we demonstrated that the L-GMCA CMB map was the only map to explicitly project the thermal Sunyaev-Zel’dovich (SZ) effect (Bobin et al. 2014b). For these reasons, the L-GMCA CMB map was used for different cosmological studies (Ben-David & Kovetz 2014; Aiola et al. 2015; Lanusse et al. 2014; Luzzi et al. 2015; Notari & Quartin 2015).
Contributions
This paper presents a novel estimation of the CMB map reconstructed from the Planck 2015 data (PR2) and the WMAP nine-year data (Bennett 2013), which updates the CMB map we published in Bobin et al. (2014b). This new map is based on the sparse component separation method L-GMCA (Bobin et al. 2013). Additionally, the map benefits from the latest advances in this field (Bobin et al. 2015), which allows us to accurately discriminate between correlated components. In this update to our previous work, we show that this new map presents significant improvements with respect to the available CMB map estimates.
-
It is a full-sky map, based on the latest CMB data, which did not require any interpolation or inpainting technique.
-
It provides a very clean estimation of the galactic region with very low levels of foreground residuals.
-
It has no detectable thermal SZ contamination, which makes the L-GMCA a good candidate for kinetic SZ studies (Hill et al. 2016).
The rest of the paper is organized as follows: Sect. 2 briefly describes the improved L-GMCA method and its application to the Planck PR2 and WMAP nine-year data. Evaluations and comparisons of the L-GMCA CMB map with the official Planck 2015 CMB maps are detailed in Sect. 3.
2. Sparse component separation for CMB reconstruction
The L-GMCA algorithm.From the viewpoint of applied mathematics, reconstructing the CMB from multifrequency data is known as a blind source separation problem (see Comon & Jutten 2010 for a general review). In this framework, the observations are assumed to be a linear combination of n components so that the m frequency channels verify at each pixel k, ![\begin{equation} \forall i=1,\cdots,m; \, x_i[k] = \sum_{j=1}^n a_{ij} s_j[k] + z_i[k] , \end{equation}](/articles/aa/full_html/2016/07/aa27822-15/aa27822-15-eq8.png) (1)where sj stands for the jth component, aij is a scalar that models the contribution of the jth component to channel i, and zi models the instrumental noise or model imperfections. This problem is customarily recast into the matrix formulation
(1)where sj stands for the jth component, aij is a scalar that models the contribution of the jth component to channel i, and zi models the instrumental noise or model imperfections. This problem is customarily recast into the matrix formulation 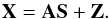 (2)The ability to accurately discriminate between the components to be reconstructed highly depends on the precise modeling of their statistical properties. With the exception of Commander, which is a parameterized Bayesian method, the CMB maps that were derived for processing the Planck PR2 data all build upon second-order statistics.
(2)The ability to accurately discriminate between the components to be reconstructed highly depends on the precise modeling of their statistical properties. With the exception of Commander, which is a parameterized Bayesian method, the CMB maps that were derived for processing the Planck PR2 data all build upon second-order statistics.
In contrast, the L-GMCA (Local-Generalized Morphological Component Analysis) method (Bobin et al. 2013) is based on a different separation principle: the sparse modeling of the components. Such a modeling is motivated by the fact that foreground components have a sparse distribution in the wavelet domain; few wavelet coefficients contain most of the energy of the components. It is very important to recall that modeling the data in the wavelet domain only changes its statistical distribution without altering its information content. Sparse signal modeling in the wavelet domain is very well adapted to efficiently describe the statistics of non-Gaussian and nonstationary processes. This has been shown to significant improve the extraction of foreground components such as galactic foregrounds and point sources (Bobin et al. 2013; Sureau et al. 2014).
In this follow up to previous work, we define A as the mixing matrix and Φ as a wavelet transform; we assume that each source sj can be sparsely represented in Φ and sj = αjΦ, where α is a Ns × T matrix whose rows are αj. The multichannel noiseless data Y can be written as 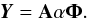 (3)The L-GMCA algorithm estimates mixing parameters (i.e., the mixing matrix A and the components S), which yields the sparsest components S. This is formalized by the following optimization problem:
(3)The L-GMCA algorithm estimates mixing parameters (i.e., the mixing matrix A and the components S), which yields the sparsest components S. This is formalized by the following optimization problem: 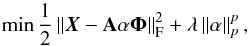 (4)where typically p = 0 and
(4)where typically p = 0 and 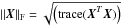 is the Frobenius norm.
is the Frobenius norm.
Similar to the version used to analyse the Planck PR1 data, the properties of the L-GMCA algorithm we used to process the WMAP nine-year and Planck 2015 data are described as follows: i) it accurately accounts for the individual point-spread function (PSF) of each individual frequency channel; ii) it implements a mechanism to deal with the spatial variations of the components’ spectra; and iii) a sparsity-based post-processing technique is used to provide a clean estimation of the galactic center. Full details are given in Bobin et al. (2014b).
List of products made available in this paper in the spirit of reproducible research, available here: http://www.cosmostat.org/research/cmb/planck_wpr2/
Improvement of the L-GMCA algorithm.Additionally, the new version of the L-GMCA algorithm includes very recent advances in blind source separation. Indeed, most component separation methods are customarily based on some separation principle to discriminate between the components to be estimated. This includes their statistical independence or their decorrelation. However, most foreground components in full-sky microwave observations do not verify these basic statistical assumptions: i) at small and medium scales (i.e., typically for ℓ> 100), distinct components such as synchrotron and thermal dust emissions have high emissivity in similar regions of the sky, especially at the vicinity of the galactic center. In addition, components such as spinning dust and thermal dust emissions are well known to be spatially correlated. These types of similarities lead to the presence of partial correlations between components with different physical nature. At large scales (i.e., typically for ℓ< 100), only few spherical harmonics are observed. Subsequently, even theoretically decorrelated components exhibit some correlation, customarily named chance correlations, which can be regarded as partial correlation between the components. However, it has been well established that partial correlations dramatically hamper the efficiency of component separation methods (Bobin et al. 2014a, 2015).
To limit the impact of these partial correlations, the current implementation of the L-GMCA algorithm includes very recent advances in blind source separation (Bobin et al. 2015). This refinement relies on the fact that partial correlations between components very likely impact a small subset of the sparse wavelet coefficients of the components. This algorithm then builds upon a weighting scheme that penalizes correlated entries, which are the most detrimental for separation. For that purpose, the problem described in Eq. (4) is substituted with the following minimization problem: 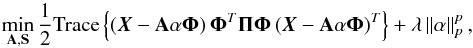 (5)where the matrix Π is a diagonal weight matrix. According to Bobin et al. (2015), partial correlations between the components are very likely to be traced by nonsparse columns of the source matrix S in the wavelet domain, which is given by SΦT. Therefore, the weighting strategy we proposed in Bobin et al. (2015) consists in penalizing samples of the sources with respect to their sparsity level in the wavelet domain using the aforementioned weighting scheme. More precisely, given an estimate of the components
(5)where the matrix Π is a diagonal weight matrix. According to Bobin et al. (2015), partial correlations between the components are very likely to be traced by nonsparse columns of the source matrix S in the wavelet domain, which is given by SΦT. Therefore, the weighting strategy we proposed in Bobin et al. (2015) consists in penalizing samples of the sources with respect to their sparsity level in the wavelet domain using the aforementioned weighting scheme. More precisely, given an estimate of the components 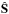 , the weighting matrix is computed as follows:
, the weighting matrix is computed as follows: ![\begin{equation} \forall i=1,\cdots,T; \quad \left[{\bf \Pi}\right]_{i,i} = \frac{1}{\|[\hat{\bf S}{\bf \Phi}^T]^{(i)}\|_q + \epsilon} , \end{equation}](/articles/aa/full_html/2016/07/aa27822-15/aa27822-15-eq37.png) (6)where [Π]i,i is the ith diagonal element of Π,
(6)where [Π]i,i is the ith diagonal element of Π, ![\hbox{$[\hat{\bf S}{\bf \Phi}^T]^{(i)}$}](/articles/aa/full_html/2016/07/aa27822-15/aa27822-15-eq39.png) is the ith column of
is the ith column of 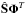 , ϵ is a small scalar to avoid numerical issues, and q ≤ 1 so as to measure the sparsity level of the components. Based on this relationship, the weight matrix Π is updated iteratively during the minimization process with respect to the estimated sources. For an exhaustive description of this extension, see Bobin et al. (2015).
, ϵ is a small scalar to avoid numerical issues, and q ≤ 1 so as to measure the sparsity level of the components. Based on this relationship, the weight matrix Π is updated iteratively during the minimization process with respect to the estimated sources. For an exhaustive description of this extension, see Bobin et al. (2015).
Application of the L-GMCA to the WMAP nine-year and Planck PR2 dataThe L-GMCA algorithm is precisely defined by a set of parameters, which are similar to the ones we used to analyze the Planck PR1 data in (Bobin et al. 2014b). The wavelet transform is defined by filters in the spherical harmonic domain, which are identical to the bands described in Bobin et al. (2014b). Following Bobin et al. (2014b), we added the IRIS map (Miville-Deschênes & Lagache 2005) as an extra observation. Its use is limited to a region that is located on the galactic center. For more details about the application of the L-GMCA, see Bobin et al. (2013, 2014b).
In the following, the CMB map derived from the joint analysis of the Planck PR2 and WMAP9 data is denoted by WPR2 L-GMCA.
Reproducible research
In the spirit of participating in reproducible research, we have made all codes and resulting products that constitute the main results of this paper public. In Table 1 we list all the products that will be freely available as a result of this paper. The L-GMCA code, the L-GMCA CMB maps, and the CMB power spectrum will be made available1.
3. Conclusion
We provide a new CMB map based on a combination of the WMAP nine-year and Planck PR2 data using sparse component analysis. It builds upon the L-GMCA algorithm, sparsity-based component separation method with the addition of the most recent advances on sparse component separation. We show that the proposed estimation procedure yields a clean full-sky CMB map with no significant foreground residuals on the galactic center. In contrast to the currently available CMB maps derived from the Planck 2015 data, the proposed L-GMCA WPR2 map contains no detectable tSZ contamination. The properties of the L-GMCA WPR2 map can be summarized as follows:
-
It is the only full-sky clean CMB map based on the Planck PR2 data that does not require any inpainting techniques.
-
It is free of tSZ contamination, which makes it the unique reasonable candidate for kSZ studies (Hill et al. 2016).
-
Its power spectrum using a 75% mask is in good agreement with the Planck best-fit theoretical power spectrum.
Acknowledgments
This work was funded by the PHySIS project (contract No. 640174) and the DEDALE project (contract No. 665044), within the H2020 Framework Program of the European Commission. We used Healpix software (Gorski et al. 2005), iSAP2 software, WMAP data3, and Planck data4. We would like to thank J. Borrill from providing simulations of the point sources components and CIB components.
References
- Abrial, P., Moudden, Y., Starck, J., et al. 2007, J. Fourier Anal. Appl., 13, 729 [Google Scholar]
- Aiola, S., Kosowsky, A., & Wang, B. 2015, Phys. Rev. D, 91, 043510 [NASA ADS] [CrossRef] [Google Scholar]
- Ben-David, A., & Kovetz, E. 2014, MNRAS, 445, 2116 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20 [Google Scholar]
- Bobin, J., Starck, J.-L., Sureau, F., & Basak, S. 2013, A&A, 550, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bobin, J., Rapin, J., Starck, J.-L., & Larue, A. 2014a, in Proc. IEEE Int. Conf. Image Processing, 6021 [Google Scholar]
- Bobin, J., Sureau, F., Starck, J.-L., Rassat, A., & Paykari, P. 2014b, A&A, 563 [Google Scholar]
- Bobin, J., Rapin, J., Starck, J.-L., & Larue, A. 2015, IEEE Trans. Signal Proc., 63, 1199 [CrossRef] [Google Scholar]
- Comon, P., & Jutten, C. 2010, Handbook of blind source separation (Elsevier) [Google Scholar]
- Delabrouille, J., Cardoso, J.-F., & Patanchon, G. 2003, MNRAS, 346, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Delabrouille, J., Cardoso, J.-F., Jeune, M. L., et al. 2009, A&A, 493, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eriksen, H. K., Jewell, J. B., Dickinson, C., et al. 2008, APJ, 676, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Cobos, R., Vielva, P., Barreiro, R. B., & Martínez-González, E. 2012, MNRAS, 420, 2162 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- Gorski, K., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, C., Ferraro, S., Battaglia, N., Liu, J., & Spergel, D. 2016, ArXiv e-prints [arXiv:1603.01608] [Google Scholar]
- Hivon, E., Górski, K. M., Netterfield, C. B., et al. 2002, ApJ, 567, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Lanusse, F., Paykari, P., Starck, J., et al. 2014, A&A, 571 [Google Scholar]
- Leach, S. 2008, A&A, 491 [Google Scholar]
- Luzzi, G., Génova-Santos, R. T., Martins, C. J. A. P., De Petris, M., & Lamagna, L. 2015, J. Cosmol. Astropart. Phys., 9, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M.-A., & Lagache, G. 2005, ApJS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Notari, A., & Quartin, M. 2015, J. Cosmol. Astropart. Phys., 6, 47 [Google Scholar]
- Planck Collaboration XIX. 2011, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2011, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XII. 2014, A&A, 571, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XV. 2014, A&A, 571, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXX. 2014, A&A, 571, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2015, A&A, submitted [arXiv:1507.02704] [Google Scholar]
- Planck Collaboration I. 2016, A&A, in press, DOI: 10.1051/0004-6361/201527101 [Google Scholar]
- Planck Collaboration VI. 2016, A&A, in press, DOI: 10.1051/0004-6361/201525813 [Google Scholar]
- Planck Collaboration VIII. 2016, A&A, in press, DOI: 10.1051/0004-6361/201525820 [Google Scholar]
- Planck Collaboration IX. 2016, A&A, in press, DOI: 10.1051/0004-6361/201525936 [Google Scholar]
- Planck Collaboration X. 2016, A&A, in press, DOI: 10.1051/0004-6361/201525967 [Google Scholar]
- Planck Collaboration XXV. 2016, A&A, in press, DOI: 10.1051/0004-6361/201526803 [Google Scholar]
- Rassat, A., Starck, J.-L., Paykari, P., Sureau, F., & Bobin, J. 2014, J. Cosmol. Astropart., 08, 006 [CrossRef] [Google Scholar]
- Starck, J.-L., Fadili, M. J., & Rassat, A. 2013, A&A, 550, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sureau, F., Starck, J., Bobin, J., Paykari, P., & Rassat, A. 2014, A&A, 566, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Map and power spectrum estimation
 |
Fig. A.1 Top: estimated power spectrum of the WPR1 L-GMCA map (red). The solid black line is the Planck-only, best-fit Cℓ provided by the Planck consortium. Bottom: power spectrum in logarithmic scale. Error bars are set to 1σ. |
Following (Bobin et al. 2014b), the L-GMCA algorithm is applied to the five WMAP nine-year maps (offset-corrected maps) and the nine averages of the Planck PR2 half-ring maps. The CMB is then derived by applying the inverse of the mixing matrices estimated with the L-GMCA algorithm. Estimates of the noise maps are derived from random noise realizations for the WMAP channels. These realizations were computed using the noise covariance matrices provided by the WMAP consortium. To estimate noise maps from the Planck PR2 data, half differences of half mission maps were used as a proxy for a single data noise realization.
Next, the CMB power spectrum is estimated by computing the cross-correlation between the two half-ring maps. In contrast to the CMB signal, noise decorrelates between half rings; the noise bias then vanishes when cross-correlating half-ring maps. Subsequently, the cross-correlation provides an estimate of the CMB power spectrum that is free of any noise-related bias. In the case of WMAP, such virtual half-ring maps can be obtained by calculating the difference and sum of the WMAP data and a single data noise realization.
The power spectrum is evaluated from a sky coverage of 75%; the corresponding common mask is composed of a point source and galactic mask chosen from the Planck consortium masks, which is identical to the analysis mask used in (Bobin et al. 2014b).
The estimation procedure is described by the following processing steps:
-
1.
Inpainting the masked maps: following (Bobin et al. 2014b), the masked maps are first inpainted prior to deconvolution to avoid potential processing artifacts especially at the vicinity of remaining point sources. This procedure keeps the estimation of the power spectrum unaltered since it is eventually evaluated from the 75% of the sky that is kept unchanged through the inpainting step.
-
2.
Deconvolution of the maps: the masked and inpainted maps are deconvolved to infinite resolution up to ℓ = 3200.
-
3.
Mask correction: correcting for the effect of the mask is made by applying the MASTER mask deconvolution technique (Hivon et al. 2002).
-
4.
Correcting for unresolved point sources and the remainder of CMB: as noticed in (Bobin et al. 2014b), the CMB power spectrum is still biased by the contamination of the unresolved point sources, especially at high ℓ> 1500. In (Planck Collaboration XV 2014; Bobin et al. 2014b), a simple first-order correction was performed for the contribution of the unresolved point sources; the power spectrum is either modeled by a constant or scale-independent spectrum. However this correction did not correctly account for the exact effect of the separation process on the unresolved point sources and the CIB. In the current paper, we apply the exact same estimation procedure to simulated points sources and CIB (i.e., applying the inverse of the mixing matrices derived from LGMCA). Their contribution is then removed from the estimated power spectrum.

Fig. A.2 Top: difference between the power spectrum estimated from the WPR1 L-GMCA map and the Planck-only, best-fit Cℓ provided by the Planck consortium. Bottom: difference between the estimated and theoretical power spectra in logarithmic scale. Error bars are set to 1σ.
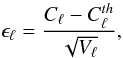 where Vℓ stands for the variance of the estimated power spectrum. This can be tested by computing the error χ2 and the p-value of the resulting value. Different tests have been carried out for various ranges of multipoles [ 2,ℓmax ] with ℓmax = 500,1000,2000. The results are shown in Table A.1. The second row of this table shows the p-value of the χ2 computed in different ranges of multipoles. The third row shows the number of samples of the normalized error ϵℓ with amplitudes higher than 3σ. The likeliness of the observed number of extreme values is provided assuming that the error follows a standard Gaussian distribution. These tests do not show any statistically significant discrepancy between the LGMCA power spectrum and the Planck best-fit power spectrum.
where Vℓ stands for the variance of the estimated power spectrum. This can be tested by computing the error χ2 and the p-value of the resulting value. Different tests have been carried out for various ranges of multipoles [ 2,ℓmax ] with ℓmax = 500,1000,2000. The results are shown in Table A.1. The second row of this table shows the p-value of the χ2 computed in different ranges of multipoles. The third row shows the number of samples of the normalized error ϵℓ with amplitudes higher than 3σ. The likeliness of the observed number of extreme values is provided assuming that the error follows a standard Gaussian distribution. These tests do not show any statistically significant discrepancy between the LGMCA power spectrum and the Planck best-fit power spectrum.
Compatibility check of the estimated power spectrum with the best-fit Planck PR2 power spectrum.
Appendix B: Evaluation of the L-GMCA CMB map
 |
Fig. B.1 CMB map estimated using the L-GMCA algorithm from the WMAP nine-year and Planck PR2 data. |
Following Bobin et al. (2014b), we assessed various measures of contamination signatures to evaluate potential deviations from the expected characteristics of the CMB map and we perform comparisons with the four official CMB maps provided by the Planck consortium in 2015.
Appendix B.1: The quality map: a measure of the CMB map power excess
In Bobin et al. (2014b), we emphasized that estimating the quality of a reconstructed CMB map from real data without any strong assumption about the expected map is a challenging task. To that purpose, we defined the so-called quality map, which only relies on the assumption that the Λ-CDM best-fit power spectrum Cℓ provides a good approximation of the expected power of the CMB in the spherical harmonic domain. Therefore, this allows us to compare the local deviation around each pixel k in the estimated CMB map to its expected power that the best-fit Cℓ indicates and assess its compatibility with the expected noise level. We refer to Bobin et al. (2014b) for a precise definition of the quality map.
We recall that the SMICA and Commander maps were inpainted; they therefore have partial sky coverage. As a consequence, we set to zero the pixels in Q, which turn out to be inpainted. The quality maps are shown in Fig. B.2. In this figure significant excesses are indicated with yellow and red. Dark blue pixels are likely related to statistical fluctuations. Similar to (Bobin et al. 2014b), the SEVEM and NILC maps exhibit more contamination in the galactic plane than SMICA and L-GMCA. Outside the galactic plane, none of these maps present significant contamination.
Appendix B.2: Galactic center estimation
Figure B.1 reveals that foreground residuals are mainly visible at the vicinity of the galactic plane. To better highlight these differences, we show in the Fig. B.3 an illustrative region that is located in the galactic center. In this region, the Commander and SMICA maps were post-processed using an inpainting technique. In the case of the Commander map, a significant portion of the sky (up to 18% for ℓ> 1000) was filled in with a constrained Gaussian realization. With the exception of the Commander map, the maps released by the Planck consortium all exhibit significant foreground residuals. Conversely, the L-GMCA map does not show any visible foreground emission residual. Similar to the WPR1 L-GMCA we published in (Bobin et al. 2014b), the joint processing of the WMAP and Planck data enables a better separation of the foreground components, which further leads to a cleaner estimate of the CMB map in the galactic center.
Appendix B.3: Detecting traces of SZ contamination
In Bobin et al. (2014b), we noticed that another major difference between the CMB maps released by the Planck consortium and the L-GMCA CMB map was that the latter did not exhibit any detectable trace of thermal Sunyaev Zel’dovich (tSZ) effect. For that purpose, we made use of an interesting property of the tSZ effect: its contribution can be neglected at 217 GHz. Subsequently, the difference between the HFI-217GHz channel map and any estimate of the CMB map should cancel out the CMB without revealing tSZ residuals.
Figure B.4 shows the difference maps of the estimated CMB maps with the PR2 HFI frequency map at 217GHz. The Coma cluster appears clearly in the four maps provided by the Planck consortium. Conversely, the L-GMCA map does not exhibit any detectable trace of tSZ contamination, since L-GMCA method is the only method to explicitly project out the thermal SZ emission during the component separation. This therefore makes the proposed L-GMCA CMB map the perfect candidate to study the kinetic SZ effect.
Appendix B.4: Higher-order statistics of the reconstructed CMB maps
An effective evaluation of the level of foreground contamination can be performed by evaluating the Gaussianity or non-Gaussianity of the estimated CMB map. To that purpose and as advocated in Bobin et al. (2014b), higher order statistics (HoS) provide a model-independent measure of non-Gaussianity (NG).
One major difficulty is that all the maps have not been post-processed in the same way: some of them have been inpainted. To perform fair comparisons, we chose to first inpaint all the maps with a combination of our point source mask and the SMICA mask of inpainted pixels (retaining 95% of the sky) using the sparse inpainting technique described in Abrial et al. (2007).
Figure B.5 shows the skewness (third-order cumulant) and the kurtosis (fourth-order cumulant) of the estimated CMB maps for the seven first wavelet scales. These values are computed using the same sky coverage defined by the combined SMICA mask of inpainted pixels. The error bars are derived from 100 Monte-Carlo simulations. Each Monte-Carlo simulation is composed of an independent CMB Gaussian realization, which we generated according to the Planck PR2 best-fit power spectrum. Independent noise realization are computed based on the WPR2 L-GMCA map. With the exception of the CMB map reconstructed with SEVEM, we observe no strong departures from Gaussianity on the first seven scales. None of these maps exhibit non-Gaussianity for medium and large scales (i.e., for wavelet scales corresponding to ℓ< 1600). A refined characterization of the NG consists in computing the same statistics in different bands of latitude per wavelet scale. Figure B.6 shows the normalized skewness on scales 0 to 5 and Fig. B.7 (bottom) shows the kurtosis on scales 0 to 5. Normalization was performed with respect to the error derived from 100 Monte-Carlo
simulations of a combination of pure CMB and noise maps derived from L-GMCA.
 |
Fig. B.2 Top: PR2 NILC and SEVEM CMB quality maps. Middle, PR2 SMICA, and PR2 Commander quality maps. Bottom: WPR2 L-GMCA quality map. |
 |
Fig. B.3 Galactic center region, centered at (l,b) = (80.0,0). Top: PR2 NILC and SEVEM CMB maps, and bottom: PR2 SMICA, Commander maps, and WPR2 L-GMCA CMB maps. |
 |
Fig. B.4 Coma cluster area. Top: HFI-217 GHz map and difference map between HFI-217GHz and WPR2 L-GMCA CMB map. Middle-left: difference map between HFI-217GHz CMB maps and the PR2 NILC CMB map. Middle-right: difference map between HFI-217GHz CMB maps and SEVEM. Bottom-left: difference map between HFI-217GHz CMB maps and SMICA CMB map. Bottom-right: difference map between HFI-217GHz CMB maps and the Commander CMB map. |
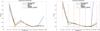 |
Fig. B.5 High order statistics computed at various wavelet scales for the high resolution masks inside the 95% analysis mask: skewness (left) and kurtosis (top right). Error bars are set to 1sigma, based on the noise level of the L-GMCA map. |
 |
Fig. B.6 Normalized skewness computed at various wavelet scales for the high resolution masks inside the 95% analysis mask. The normalization is made with respect to the noise level of the L-GMCA map. |
 |
Fig. B.7 Normalized kurtosis computed at various wavelet scales for the high resolution masks inside the 95% analysis mask. The normalization is made with respect to the noise level of the L-GMCA map. |
From this evaluation, we can conclude that, with the exception of the first wavelet scale, all maps are compatible with the Gaussianity assumption at all galactic latitudes for scales corresponding to ℓ< 1600. In the finest scale, for ℓ> 1600, the SEVEM and SMICA CMB maps show statistically significant non-Gaussian residuals, which are located on the galactic center. These features are detected both with their skewness and kurtosis statistics in the top-left panel of Figs. B.6 and B.7. In addition, the NILC map exhibits a slight level of non-Gaussianity at a galactic latitude of about + 45°. Apart from these features, all the maps are compatible with Gaussianity at all scales for galactic latitudes larger than 20°. The Commander CMB map exhibits no non-Gaussian features; however, a significant part (i.e., about 18% at small scales) has been masked and filled in with a constrained Gaussian realization. The L-GMCA WPR2 map is therefore the only map that does not show any non-Gaussian statistics, even on the galactic plane, which did not require any inpainting or interpolation procedure.
All Tables
List of products made available in this paper in the spirit of reproducible research, available here: http://www.cosmostat.org/research/cmb/planck_wpr2/
Compatibility check of the estimated power spectrum with the best-fit Planck PR2 power spectrum.
All Figures
 |
Fig. A.1 Top: estimated power spectrum of the WPR1 L-GMCA map (red). The solid black line is the Planck-only, best-fit Cℓ provided by the Planck consortium. Bottom: power spectrum in logarithmic scale. Error bars are set to 1σ. |
| In the text | |
 |
Fig. A.2 Top: difference between the power spectrum estimated from the WPR1 L-GMCA map and the Planck-only, best-fit Cℓ provided by the Planck consortium. Bottom: difference between the estimated and theoretical power spectra in logarithmic scale. Error bars are set to 1σ. |
| In the text | |
 |
Fig. B.1 CMB map estimated using the L-GMCA algorithm from the WMAP nine-year and Planck PR2 data. |
| In the text | |
 |
Fig. B.2 Top: PR2 NILC and SEVEM CMB quality maps. Middle, PR2 SMICA, and PR2 Commander quality maps. Bottom: WPR2 L-GMCA quality map. |
| In the text | |
 |
Fig. B.3 Galactic center region, centered at (l,b) = (80.0,0). Top: PR2 NILC and SEVEM CMB maps, and bottom: PR2 SMICA, Commander maps, and WPR2 L-GMCA CMB maps. |
| In the text | |
 |
Fig. B.4 Coma cluster area. Top: HFI-217 GHz map and difference map between HFI-217GHz and WPR2 L-GMCA CMB map. Middle-left: difference map between HFI-217GHz CMB maps and the PR2 NILC CMB map. Middle-right: difference map between HFI-217GHz CMB maps and SEVEM. Bottom-left: difference map between HFI-217GHz CMB maps and SMICA CMB map. Bottom-right: difference map between HFI-217GHz CMB maps and the Commander CMB map. |
| In the text | |
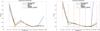 |
Fig. B.5 High order statistics computed at various wavelet scales for the high resolution masks inside the 95% analysis mask: skewness (left) and kurtosis (top right). Error bars are set to 1sigma, based on the noise level of the L-GMCA map. |
| In the text | |
 |
Fig. B.6 Normalized skewness computed at various wavelet scales for the high resolution masks inside the 95% analysis mask. The normalization is made with respect to the noise level of the L-GMCA map. |
| In the text | |
 |
Fig. B.7 Normalized kurtosis computed at various wavelet scales for the high resolution masks inside the 95% analysis mask. The normalization is made with respect to the noise level of the L-GMCA map. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


