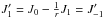| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201526547 | |
| Published online | 13 June 2016 | |
Vortex waves in sunspots
1 IRAP–CNRS UMR 5277, 14 Av. E. Belin, 31400 Toulouse, France
e-mail: Arturo.LopezAriste@irap.omp.eu
2 Université de Toulouse, UPS-OMP, Institut de Recherche en Astrophysique et Planétologie, 31400 Toulouse, France
3 High Altitude Observatory (NCAR). 3080 Center Green Dr. Boulder, CO 80301, USA
4 Instituto de Astrofísica de Canarias. C/ Vía Láctea s/n, 38200 La Laguna, Spain
5 Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
Received: 18 May 2015
Accepted: 1 April 2016
Context. Waves in the magnetized solar atmosphere are one of the favourite means of transferring and depositing energy into the solar corona. The study of waves brings information not just on the dynamics of the magnetized plasma, but also on the possible ways in which the corona is heated.
Aims. The identification and analysis of the phase singularities or dislocations provide us with a complementary approach to the magnetoacoustic and Aflvén waves propagating in the solar atmosphere. They allow us to identify individual wave modes, shedding light on the probability of excitation or the nature of the triggering mechanism.
Methods. We use a time series of Doppler shifts measured in two spectral lines, filtered around the three-minute period region. The data show a propagating magnetoacoustic slow mode with several dislocations and, in particular, a vortex line. We study under what conditions the different wave modes propagating in the umbra can generate the observed dislocations.
Results. The observed dislocations can be fully interpreted as a sequence of sausage and kink modes excited sequentially on average during 15 min. Kink and sausage modes appear to be excited independently and sequentially. The transition from one to the other lasts less than three minutes. During the transition we observe and model the appearance of superoscillations inducing large phase gradients and phase mixing.
Conclusions. The analysis of the observed wave dislocations leads us to the identification of the propagating wave modes in umbrae. The identification in the data of superoscillatory regions during the transition from one mode to the other may be an important indicator of the location of wave dissipation.
Key words: Sun: chromosphere / sunspots
© ESO, 2016
1. Introduction
Waves are ubiquitous and easily seen in sunspot umbra. Waves propagate in all directions but, in particular, upwards towards the chromosphere and corona, and they are probably triggered by undetermined acoustic events below the photosphere or by solar oscillations themselves as they interact with the magnetic field of the sunspot. In this upwards propagation waves interact and are often guided by the organised and mostly vertical field of the sunspot. The particular thermodynamic and magnetic conditions of the sunspot lead to a description of the propagation of waves along a magnetized cylinder (Edwin & Roberts 1983). Such a scenario allows the determination of dispersion relations that couple the periods, wavelengths and phase velocities of those modes that are allowed to propagate freely along the magnetic field. Other than Alfvén waves, which are difficult to detect in the photosphere, we find slow and fast modes propagating at velocities between the sound and the Alfvén velocities, with different degrees of interaction with the background magnetic field. That same scenario also allows the determination of propagating modes as per the amplitude distribution over the wavefront of the transverse and longitudinal components of the wave. Sausage and kink modes are thus found to be solutions of the wave equation in cylindrical coordinates. While those names arise in the limit of an infinitely thin magnetic cylinder, it is common, as is done in this paper, to extend those names to wave modes with a phase that does not depend on the azimuth coordinate θ of the cylinder (sausage) or that has a bijective dependence eiθ on this coordinate (kink). Higher modes, with phases varying with eimθ and m ≥ 2, are generically referred to as flute modes.
Even though these waves have been observed for a long time and with greater and greater temporal and spatial resolutions, there are many open questions concerning the nature, origin and role of these waves in the solar dynamics (Khomenko & Collados 2015). In this work, we are concerned with the nature and modal distribution of the observed waves. We address this question not by exploring the possible solutions of the dispersion relation in terms of frequencies and phase velocities, but in terms of particular topological features stable under perturbations called dislocations. As a first result of this work, the easy identification of dislocations in observed waves over the lower solar atmosphere permits an unambiguous identification of kink waves. Traditionally, identifying a kink or sausage mode implied the measurement of the frequency and wavelength of the waves, which were then introduced in a dispersion relation. Real waves are not single frequency and dispersion relations are strongly model dependent. Hence clear identification of sausages or kinks is difficult to make. Another method to distinguish those wave modes is to make use of the incompressibility of the kink mode; measures of weak intensity variations, but strong magnetic field or velocity amplitudes are therefore signatures of a kink mode. However, this once more depends on difficult measurements of velocity amplitudes. Magnetic field variations have only been measured on a few occasions (see Sect. 4 in Khomenko & Collados 2015) and their interpretation is difficult in view of the opacity fluctuations of the spectral lines used in the measure. Even with such measurements in hand, one still has to appeal to a model to interpret observations and to define the meaning of weak and strong in those comparisons, As we see in this paper, dislocations are unambiguous signatures of a kink spotted directly on the time series of the observed wave. Beyond that initial identification, the kink wave itself is a combination of two sub-modes characterised by a sign change of the phase. No dispersion relation or model can tell those two mode polarisations apart, however, through dislocations we can. We observe that the two kink modes do not appear in combination, rather they appear isolated. Either we observe m = + 1 or m = −1.
Dislocations are singularities of the phase of a wave (Nye & Berry 1974). If we are limited to a real wave, it is not obvious how to define dislocations or to tell them apart from other features as nodes. However, by expressing the wave in its full complex nature, the definition is obvious. Let a given scalar wave to be expressed as
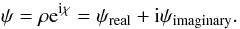 All the time and space dependencies are implicit in the amplitude ρ and phase χ. A given point in space and time is a dislocation of the wave if ρ = 0 and χ is singular or undetermined. Or, equivalently, if ψreal = ψimaginary = 0. Evidently this can only happen at particular and isolated points of the wave. For comparison, a node is defined as ψreal = 0 or as ψimaginary = 0 and, in either case, it is due to the phase of the node cancelling the wave. This is not a dislocation: the amplitude ρ is not zero and the phase is perfectly well defined at the node. Writing the complex form of the wave is hence critical to correctly identify dislocations. López Ariste et al. (2015) described how to write this complex form starting from the observation of a wave in terms of real numbers. In the same work, the concept of non-trivial monodromy was applied to a data set of coronal waves as a method to identify dislocations in the data.
All the time and space dependencies are implicit in the amplitude ρ and phase χ. A given point in space and time is a dislocation of the wave if ρ = 0 and χ is singular or undetermined. Or, equivalently, if ψreal = ψimaginary = 0. Evidently this can only happen at particular and isolated points of the wave. For comparison, a node is defined as ψreal = 0 or as ψimaginary = 0 and, in either case, it is due to the phase of the node cancelling the wave. This is not a dislocation: the amplitude ρ is not zero and the phase is perfectly well defined at the node. Writing the complex form of the wave is hence critical to correctly identify dislocations. López Ariste et al. (2015) described how to write this complex form starting from the observation of a wave in terms of real numbers. In the same work, the concept of non-trivial monodromy was applied to a data set of coronal waves as a method to identify dislocations in the data.
Dislocations have been found in all kinds of ondulatory phenomena. Originally found and described for sound waves (Nye & Berry 1974), they have also been described for such unrelated phenomena as sea tides (Berry 1981). Dislocations became part of mainstream physics when they were found in light associated with laser beams carrying intrinsic angular momentum (Harris et al. 1994; Allen et al. 1992; Bazhenov et al. 1992). López Ariste et al. (2013) showed that waves carrying dislocations were solutions of the basic MHD wave equation and that, in particular, the kink mode carries a vortex dislocation in its geometrical axis (Fig. 2 depicts the two basic types of dislocations: vortex and edge). Also, López Ariste et al. (2015) found dislocations in observations of coronal waves and described them as a consequence of the interference of sausage and either kink or Alfvén modes propagating at different phase speeds along coronal loops.
Other than the description of a wave feature that can be easily spotted in almost any observation of solar waves, dislocations have a series of interesting characteristics. First, they are topological features of the wave that cannot disappear with a change of scale or amplitude of the propagating waves. They are stable under perturbations and cannot disappear unless the wave is dissipated or interacts with another wave carrying a dislocation of opposite sign, as if it were a charged particle. A given wave that carries a dislocation can therefore be identified and labelled by it. In our present case, sausage modes carry no dislocation, but kink modes carry a vortex dislocation at their centre. As we noted above, the observation of one of those dislocations in the data unambiguously points to a propagating kink mode, and this is done independently of measured periods and velocities. The topological nature of the dislocations also makes them stable under strong changes in the propagation of the wave. For example they survive the transition of a photospheric wave into a shock wave high in the chromosphere.
In this paper, we study the dislocations found in a particular data set of umbral oscillations. The data, described in Sect. 2, have the particularity that, by chance, a vortex dislocation lies exactly under the spectrograph slit used in the observation. This enables a detailed description of the waves propagating in that sunspot and the transitions from one mode to the other (Sect. 3). We identify a succession of sausage and kink modes lasting for a few periods (less than ten in all of the cases, or about 1 h) before being overridden by another wave mode. The mechanism that triggers these waves below the photosphere must therefore have timescales of tens of minutes and be able to excite individual modes (sausage and kink modes) in succession. The second important result of the present work is that the Sun excites either one or the other mode but not both at the same time. This is in contrast to usual excitations in numerical simulations or theoretical analysis, where both modes are excited simultaneously. Furthermore, through dislocations we can also identify the kink mode with m = + 1 from the kink mode with m = −1. These two sub-modes or polarisations of the kink mode are degenerated in energy. In the literature it is argued that they should appear simultaneously. Thanks to the dislocations we now observe that this is not the case: we observe either one or the other. The excitation mechanism of these waves is able to discriminate between energy-degenerate waves and excite one polarisation but not the other. Finally, higher flute modes that can be easily spotted as a higher order dislocation do not appear either in this or in any other data set we have studied. We conclude that these flute modes are never or seldom excited in the solar atmosphere. Through dislocations we are able to constraint how these waves are excited.
The exceptional data set we study allows us one further analysis in Sect. 4: as one wave mode disappears substituted by a new mode, the dislocation moves in a perfectly predictable manner. Umbral points separated by a few hundred kilometres may then pass from oscillating in phase to oscillating in opposition as the dislocation moves between them. This change in phase is caused by a curious phenomenon called superoscillation that makes the wave temporally oscillate faster than its nominal Fourier frequency. This phenomenon has been identified in other waves (Berry 1994) and we see it here for the first time in solar magnetoacoustic waves. Whether this phase behaviour of neighbouring umbral points may help dissipate the energy of the wave through viscous collisions is left as an open question attached to these superoscillations.
2. Observations
Figure 1 shows the Doppler velocities in the umbra of a sunspot from active region NOAA9176 observed on October 1, 2000. The spectral region around 10 830 Å was observed with the TIP instrument (Martínez Pillet et al. 1999) at the VTT. This region contains two major spectral lines. The bluest spectral line, at 10 827 Å, is from Si I and forms in the photosphere. At longer wavelengths there is the resonant line of the triplet system of HeI that forms in the chromosphere, between 1000 and 2000 km above the formation region of the Si I line. The spectrograph slit was placed across the umbra of the leading sunspot of NOAA9176 and a time series 59 min long was taken with a cadence of 7.8 s. The photospheric spectra were inverted with LILIA (Socas-Navarro 2001), an LTE inversion code. The chromospheric He I lines were inverted with a Milne-Eddington code. We retain only the Doppler velocity along the line of sight. At latitude 10°S and heliocentric longitude 19°W, the line of sight makes an angle of 21 deg with the local vertical and hence it is not a bad approximation to say that the measured velocities were roughly vertical and that the wave propagates along the magnetic field lines which also are considered vertical. The signal was filtered in Fourier space leaving only the frequencies in the range 5.5−6.5 mHz to isolate the waves with periods of around 3 min (Centeno et al. 2006, 2009). Waves in that range of frequencies originating in the photosphere can climb unscathed into the chromosphere, unlike the dominant photospheric waves at 5 min which are reflected at the chromospheric cutoff. The observed waves that are filtered at 3 min can be considered to be the same in the photosphere and in the chromosphere with a phase lag due to the time travel between both layers. Estimated at about 7.2 min, this phase lag translates in a group speed of about 4 km s-1, which is compatible with the sound speed that varies between 4 and 9 km s-1. Centeno et al. (2006) conclude from this that the observed waves are slow body waves (Edwin & Roberts 1983), a conclusion that is supported by the considerations on the direction of propagation at the end of the next section.
 |
Fig. 1 Observation of waves in the Si I line formed in the photosphere (top) and the He I line formed in a chromosphere (bottom). The images show a time series of Doppler velocities along the line of sight measured in the two spectral lines along a spectrograph slit placed across the umbra of a sunspot (NOAA9176) observed by the VTT on October 1, 2000 at latitude 10°S and heliocentric longitude 19°W. The measured velocities have been Fourier-filtered to show only the waves in the range of 3-min period. |
In Fig. 1 several dislocations are visible. Our first interest goes to the line of dislocations found between minutes 26 and 40.3 at position 20 arcsec along the slit in the photosphere, and about 2 arcsec less in the chromosphere. The phase lag between the chromosphere and the photosphere cited above can be seen here in the different starting times of the dislocation in those layers. Compared to the examples of basic dislocations shown in (López Ariste et al. 2013, 2015) we recognise a vortex dislocation. We notice that this vortex is a horizontal line (constant in time) except for the starting and ending times, when it bends upwards. After it is finished around time 41 min we find, in the photosphere, an edge dislocation followed by wavefronts that are bent for the rest of the duration of the time series, while in the chromosphere the wavefronts are just tilted. Other edge dislocations are visible in the photosphere around times 13 min and 14.3 min while in the chromosphere we find a last one at 3.2 min near the bottom of the slit.
All these dislocations have clear positions along the slit, which crosses the umbra at a particular place and time: either at fixed times for the case of the edge dislocations or at definite spans of time for the vortex. If we draw a cartoon of the umbra with coordinates (x,y) defining directions along and across the slit, respectively, and with coordinate z representing the vertical, we can describe our waves as propagating along z and having dislocations fixed in x by their position along the slit, in y by the position of the slit over the umbra and in z by the formation height of the observed lines. If we accept that we can express the propagating waves as
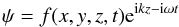 where k and ω are the wavenumber and characteristic frequency of the carrier wave, and f(x,y,z,t) is a complex amplitude varying locally, then the dislocations appear when
where k and ω are the wavenumber and characteristic frequency of the carrier wave, and f(x,y,z,t) is a complex amplitude varying locally, then the dislocations appear when
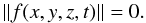 We are trying to solve this equation to explain the observed dislocations.
We are trying to solve this equation to explain the observed dislocations.
 |
Fig. 2 Wavefronts of a sausage mode (left) and a kink mode (right). In both figures the propagation direction z is vertical and assumed to be along the magnetic field. The sausage mode presents a suite of isolated plane wavefronts, while the kink mode shows a connected helical wavefront with the dislocation line in its axis. |
3. Interpretation of the observed dislocations
Following the framework of a magnetized tube with constant magnetic field along the z direction, as developed by Edwin & Roberts (1983), the available data shows that, in our case, this magnetic tube can be roughly associated with the sunspot umbra. Since, to a good approximation, the observed velocity is vertical, along the magnetic field, and the phase speed was estimated to be compatible with the speed of sound in the photosphere and the low chromosphere, we can exclude Alfvén waves from our scenario and restrict ourselves to magnetoacoustic waves. Following the identification of the observed waves as magnetoacoustic waves, we write a solution for the velocity vector of such wave in cylindrical coordinates as follows: 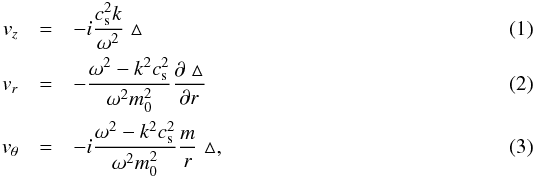 where cs is the speed of sound, k is the wavenumber along z, ω is the characteristic frequency of the carrier wave, and m is the azimuthal index (also called the charge of the dislocation). The parameter ▵ is the divergence of v given by
where cs is the speed of sound, k is the wavenumber along z, ω is the characteristic frequency of the carrier wave, and m is the azimuthal index (also called the charge of the dislocation). The parameter ▵ is the divergence of v given by 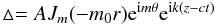 (4)where A is a constant scalar amplitude, Jm are the Bessel functions of first order and integer index m, and m0 is a spatial scale of the wave distribution in the plane transverse to the propagation, which can be associated with the wavenumber of an eventual transverse propagation of the wave, whose explicit form is given by Edwin & Roberts (1983). The typical values of m0 are so small in the solar atmosphere that the first zeroes of the Bessel functions J0 and J1 are well beyond the boundary of the sunspot. Hence we can exclude from our possible explanations the possibility of interpreting the dislocations as some kind of node associated with those nodes in a standing transverse wave.
(4)where A is a constant scalar amplitude, Jm are the Bessel functions of first order and integer index m, and m0 is a spatial scale of the wave distribution in the plane transverse to the propagation, which can be associated with the wavenumber of an eventual transverse propagation of the wave, whose explicit form is given by Edwin & Roberts (1983). The typical values of m0 are so small in the solar atmosphere that the first zeroes of the Bessel functions J0 and J1 are well beyond the boundary of the sunspot. Hence we can exclude from our possible explanations the possibility of interpreting the dislocations as some kind of node associated with those nodes in a standing transverse wave.
We have assumed that our observations measure vz, while we have no information of the transverse velocities vr and vθ. The dispersion relation (see e.g. Edwin & Roberts 1983) provides us with several pairs of k and ω for which the propagation is possible. For all of these pairs the phase speed is bound between two characteristic speeds, cT and cS, setting the range of speeds for our work. cs is the speed of sound in the medium, while cT is given by
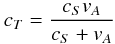 in terms of that same speed of sound and the Alfvén velocity. In the observed data, wavefronts far away from dislocations are almost straight lines with almost constant amplitude along the slit, and hence along the umbra. This means that the Bessel function Jm(−m0r) is almost constant along the slit, and hence, m0 is a small number bound by the condition
in terms of that same speed of sound and the Alfvén velocity. In the observed data, wavefronts far away from dislocations are almost straight lines with almost constant amplitude along the slit, and hence along the umbra. This means that the Bessel function Jm(−m0r) is almost constant along the slit, and hence, m0 is a small number bound by the condition 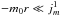 , where
, where 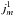 is the first zero (other than the trivial r = 0 for m ≥ 1) of the Bessel function. This condition is satisfied if the wavelength of the wave is at least equal to half the radius of the cylinder, i.e. half the radius of the umbra.
is the first zero (other than the trivial r = 0 for m ≥ 1) of the Bessel function. This condition is satisfied if the wavelength of the wave is at least equal to half the radius of the cylinder, i.e. half the radius of the umbra.
Having set the probable range of variation of the wave parameters (velocity, frequency, and wavenumber), the solutions for the slow magnetoacoustic wave can be classified by its azimuthal number m. As mentioned in the introduction, we call the m = 0 solutions sausage modes, while m = 1 waves are referred to as kink modes. Flute modes with m ≥ 2 are not seen in our data and we do not refer to them any more1.
We find it instructive to plot the wavefront of vz for the sausage and kink modes in three dimensions. In Fig. 2 the propagation direction is the vertical axis, and we plot only those surfaces where the phase of the real part of the wave is 0. Sausage modes (left plot) are mere plane waves and appear as a succession of disconnected planes. Kink modes (right plot) have the characteristic helical shape of a vortex wave. Unlike plane waves, there is no succession of wavefronts, but a single three-dimensional wavefront coiling in time (or in z) around the axis of the vortex. In this axis, at r = 0, the phase of the wave is not defined, it is singular: this is by definition a vortex dislocation. Kink modes carry therefore a vortex dislocation at their core. Our observations of Fig. 1 can be reproduced by placing a hypothetical slit on the wave representations of Fig. 2. In the case of a sausage mode, through this slit one observes, as a function of time, something like the plot in the left panel of Fig. 3, i.e. a succession of parallel plane waves. For a kink mode, if the slit is placed far from the axis of the vortex, the image along the slit is something similar, but if the slit happens to cross the axis of the vortex, a jump of π in the phase is observed, as shown in the right panel of Fig. 3. This vortex line is analogous to what we see in Fig. 1 of between minutes 26 and 40.3, while elsewhere we observe plane waves that are compatible with a sausage wave mode.
 |
Fig. 3 Time series of velocities along a spectral slit for a sausage mode (left) and a kink mode (right). In the case of a kink (right panel), the slit crosses the singularity at the axis and a vortex line of dislocations is visible at a fixed position at all times. |
Hence, the full interpretation of the waves seen in Fig. 1 is a sequence of sausage and kink modes excited down in the photosphere and propagating upwards. Each one of the modes lasts for several minutes, as long as the photospheric trigger succeeds in exciting just one particular mode at the observed period of 3 min. After that time, it is overridden by another wave mode. Figure 4 shows a simulated time series of a sausage mode that at minute 21 disappears and is substituted by a vortex, which in turn disappears at minute 48 when a new sausage mode appears.
Beyond the evident reproduction of the observed vortex by our simple scenario, a few new features appear. First, in the simulation we also see the line of vortex bending upwards at the transitions between one mode to the other. This interesting feature is discussed in the next section. Second, it is tempting to claim that it would not be too difficult to arrange the time and smoothness of the transitions between the modes to see an edge dislocation appear at the transitions. Keeping this possibility in mind, the vortex is visible because the slit happens to cross the symmetry axis of the vortex. This coincidence allows us to see the vortex line in its full splendour, but it is clear that on many other occasions the axis of the vortex is off the slit and not directly measured. Figure 5 shows such a case, with a vortex whose axis sits outside the slit by a mere 10% of the sunspot radius, or about 2 arcsecs, with all other parameters equal to Fig. 4.
 |
Fig. 4 Sausage wave is substituted by a kink wave at minute 21. From then on the vortex line of dislocations is seen until at minute 48 the kink wave gives way to another sausage wave. The sequence reproduces the main dislocation line of Fig. 1, including the upwards shift of the line near its extremes. |
 |
Fig. 5 In the same conditions as Fig. 4 we place the slit 2 arcsecs away so that the axis of the kink wave is left outside the slit. The time series of the Doppler velocities shows an isolated edge dislocation at the transition from sausage to kink modes, followed by a series of bent wavefronts similar to those seen in Fig. 1. |
The vortex line has disappeared and has been substituted by a line of bent wavefronts. At the transition between the sausage and kink modes we find an isolated edge dislocation, whose actual shape depends on the relative phases between the two modes. Our scenario also appears to explain the isolated edge dislocations seen in Fig. 1 and the line of bent wavefronts found in the photospheric time series starting at minute 44.8; in both cases we are looking at a vortex wave, a kink mode, propagating upwards but whose axis lies outside our observing slit. If the amplitudes and phases are right, an isolated edge dislocation appears at the transition between the sausage and kink modes. The further away the slit is from the axis of the vortex wave, the less bent the wavefronts are. The missed vortex at minute 44.8 may be reproduced if the slit is about 2 arcsec off the axis of that particular wave vortex. We find that all the other edge dislocations are followed by deformed wavefronts, although in a less clear manner. Our interpretation bases its strength on the two clear cases of the captured vortex line and the missed vortex at minute 44.8, and from that example we generalise our scenario.
López Ariste et al. (2015) gave a completely different explanation for the dislocations observed in coronal loops. Their scenario also included sausage and kink waves propagating along the loop, but instead of a transition from one mode to the other they claimed a superposition of both waves at the moment of appearance of the edge dislocation. In that case, because of the geometry of the observation, the natural dislocations carried by the kink mode were not observable. The observed dislocation could only be explained as an interference between waves. In the present case, the vortex line present at the centre of the kink wave is plainly visible, prompting a simpler scenario. One could nevertheless try, as López Ariste et al. (2015), and call for wave interference. Indeed, rigorously speaking, the observed edge dislocations could be explained as the sausage and a kink waves interfering at the right height and time. The result of the interference would only be an observable edge dislocation if the ratio of amplitudes between both waves was the appropriate ratio. Unlike the case of the coronal loop, such a scenario would require what we believe are highly improbable constraints to explain the edge dislocations alone, but would not explain the vortex dislocation, or the observation of the dislocation at the photosphere, and then 7.2 min later, at the chromosphere. We therefore disregard that scenario for magnetoacoustic waves in sunspot umbrae in favour of the simpler explanation gave above.
3.1. Direction of propagation of the wave
The observation of the vortex line in both the photosphere and chromosphere gives us some information on the direction of propagation. In our interpretation of these waves, the singularities lie along a one-dimensional line in the propagation direction. From the observation of the vortex, we conclude that the slit of the spectrograph crosses this line at two heights: in the photosphere as revealed by the Si i line and in the chromosphere as revealed by the He i line. The distance between these two layers is, following Centeno et al. (2006), about 1600 km in the umbra of sunspots. Given that the observed sunspot was at 21° away from the disk centre, if the waves were propagating vertically, the vortex line would have been observed at two different positions along the slit separated by just 0.8 arcsec. The vortex line is indeed seen at a different position along the slit in the photosphere and chromosphere (see Fig. 1) but the distance is much larger than 0.8 arcsec. We measured it to be of 1.4 arcsec. The two observations are taken simultaneously in two spectral lines that are less than 3 Å apart, and the two vortex lines are simultaneously seen at both heights for a long time. There are therefore no instrumental or observational issues that could explain this difference of position and we conclude that the wave is not propagating vertically.
If, as concluded by Centeno et al. (2006), the wave is a slow body wave, it would propagate along the magnetic field lines, which are perhaps not strictly vertical. The inversion of the spectropolarimetric data of the Si i line infers an inclination of the magnetic field with respect to the line of sight of 30° on average along the slit. Unfortunately we do not have a reliable estimate of the azimuth of the field. The knowledge of the inclination is however enough to see that, if the wave were following a field line tilted 30°, the average distance between the two formation heights would grow to 1850 km and, depending on the azimuth of the field with respect to the orientation of the slit, this height difference would be projected onto a difference along the slit of 1.3 arcsec. This is not yet the observed value, but it is close enough, given the uncertainties involved, to conclude that most probably the propagation is along the magnetic field which itself is slightly tilted with respect to the local vertical. This propagation along field lines, deduced from the observation of the vortex, confirms the identification of the wave as a slow body mode.
3.2. Degeneracy of the m = ±1 kink waves
In our description of the observations we used the charge m = + 1 for the vortex wave. From the point of view of energetics, this solution is degenerate with m = −1, or with any combination of both. Because they have the same energy, all those submodes of the kink wave have the same probability of excitation in the solar atmosphere unless the initial conditions are somehow able to distinguish them. Two questions arise: how can we tell that the m = + 1 solution solely responsible for the observed waves? and, if this is the case, what mechanism can excite one but not the other, when both are degenerate in energy?
To answer the first question, we first clarify how the observations (real numbers) are related with our complex analytical functions in Eq. (3). We disregard recipes like taking the real part or calling for counter-propagating waves resulting in stationary, non-propagating, oscillations. At a particular position x, the observations can be described as φ(x,t) = A(x,t)cos(ωt + α(x,t)), where amplitude A and local phase α can vary from point to point. Therefore 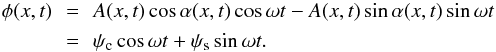 The complex wave
The complex wave
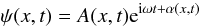 with
with 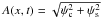 and
and 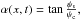 has the same frequency, amplitude and phase at every point (x,t). Given any complex wave as those in Eq. (3) we can plot the real φ(x,t) following this recipe. With this clarification we can now compare the combination of the sausage and kink modes using m = + 1 of Fig. 4 with an analogous wave constructed using m = −1, or even a third wave made up of a linear combination of m = + 1 and m = −1 with equal weights. We call this the linear polarisation mode. This last case is the one that gives the kink wave its name: m = + 1 and m = −1 have the same expressions for vr and vθ2. However, vz is comprised of two modes with opposite signs that cancel out: a kink wave made of a perfect mixture of m = −1 and m = + 1 has no vz component. Figure 6 illustrates that as the sausage wave disappears and is replaced by the linearly polarized kink wave, the measured vz would show no oscillation. This is not what is observed and we can discard this case. The observations discussed in this paper require that one of the modes (m = + 1 or m = −1) dominates over the other. Figure 6 (left and middle panels) show the two other cases (m = + 1 and m = −1, respectively). The concavity (convexity) of the null (vortex) line allows us to tell them apart in the observations. This can be understood by realising, in the chosen reference system, a cut at a given height of the m = + 1 mode has a phase retardance of one side of the singularity line and the m = −1 mode has the opposite. The bending of the singularity line is due to the phase matching of the incoming kink mode with the sausage mode. The phase matching conditions happen sooner (at a given height in the atmosphere) where the wave has a phase advance.
has the same frequency, amplitude and phase at every point (x,t). Given any complex wave as those in Eq. (3) we can plot the real φ(x,t) following this recipe. With this clarification we can now compare the combination of the sausage and kink modes using m = + 1 of Fig. 4 with an analogous wave constructed using m = −1, or even a third wave made up of a linear combination of m = + 1 and m = −1 with equal weights. We call this the linear polarisation mode. This last case is the one that gives the kink wave its name: m = + 1 and m = −1 have the same expressions for vr and vθ2. However, vz is comprised of two modes with opposite signs that cancel out: a kink wave made of a perfect mixture of m = −1 and m = + 1 has no vz component. Figure 6 illustrates that as the sausage wave disappears and is replaced by the linearly polarized kink wave, the measured vz would show no oscillation. This is not what is observed and we can discard this case. The observations discussed in this paper require that one of the modes (m = + 1 or m = −1) dominates over the other. Figure 6 (left and middle panels) show the two other cases (m = + 1 and m = −1, respectively). The concavity (convexity) of the null (vortex) line allows us to tell them apart in the observations. This can be understood by realising, in the chosen reference system, a cut at a given height of the m = + 1 mode has a phase retardance of one side of the singularity line and the m = −1 mode has the opposite. The bending of the singularity line is due to the phase matching of the incoming kink mode with the sausage mode. The phase matching conditions happen sooner (at a given height in the atmosphere) where the wave has a phase advance.
 |
Fig. 6 Comparison of solutions using the m = + 1 mode of the kink wave (left panel, same as Fig. 4), the m = −1 mode (centre) and an equally weighted mixture of both (right, called linear polarisation) which corresponds to a pure kink in the transverse plane. |
The observations show that one mode clearly dominates over the other and, from the bend of the singularity line, that m = + 1 dominates. How can we excite one polarisation over the other, or over any combination of them, since they are degenerate in energy? The answer must be in the excitation mechanism that shows a preference, in spite of the energy degeneracy. At present, all we can confidently say is that we observe a particular vortex that is dominated by the m = + 1 mode. Perhaps at a different time, or at a different location in the umbra, an m = −1 mode will be excited. Our observations do show, however, that either the excitation mechanism or the non-ideal propagation conditions, are able to favour one over the other.
4. Dynamics of the vortex singularity: superoscillations
An unexpected feature visible in Fig. 1 and reproduced in Fig. 4 is the upwards shift of the line of dislocations at both ends, when the transition between the sausage plane wave and the kink vortex wave takes place. While it was too subtle to pay attention to in the first examination of the observations, it appears now to be an integral part of the scenario since it is naturally reproduced in the computations. The basic explanation to this feature was given by Berry (1994) in another context, and we reproduce their argument particularised to our present case.
 |
Fig. 7 Time series of the velocities of two points in the umbra as a singularity moves between them. Originally in phase, at the approach of the singulariy both change period before settling in perfect quadrature when the singularity stops moving. Left: simulated case; right: points at 16 and 23 arcsec along the slit from observations in Fig. 1. |
We have modelled the observed velocity of any single wave mode as
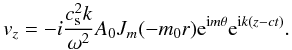 For m = 0, the sausage mode, the previous expression has no phase singularity, no dislocation. It does have an infinite number of nodes with zero amplitude but in those nodes the phases are well defined. In particular, vz of a sausage mode has a well-defined amplitude at r = 0. The kink mode, on the other hand, has a phase singularity, a dislocation, at r = 0. It also has, as the sausage mode, many nodes of zero amplitude, but a well-defined phase, at the other infinite zeros of J1(−m0r). In kink and sausage modes, however, the small value of m0 places all those nodes outside the sunspot and beyond the borders of our observation. Our concern is limited to that singularity at r = 0 of the kink mode that we have modelled and see to correspond to the observations in the previous section. The vortex line of dislocations is found at the point r = 0 of the coordinate system with respect to which we described the propagation of the kink wave. Since it is a coordinate value, it is fixed in time and the line of dislocations is horizontal, fixed at r = 0, in both the observations and simulations as long as we have a kink mode propagating. In the transition from one wave mode to the other, from sausage to kink, the dislocation line bends upwards. Since we prefer not to move our reference system, the shift of the dislocation line can only mean that the singularity is changing place and it is no longer at r = 0. Leaving aside all unimportant factors during the transition from sausage mode to kink mode, we can write the observed velocity amplitude as
For m = 0, the sausage mode, the previous expression has no phase singularity, no dislocation. It does have an infinite number of nodes with zero amplitude but in those nodes the phases are well defined. In particular, vz of a sausage mode has a well-defined amplitude at r = 0. The kink mode, on the other hand, has a phase singularity, a dislocation, at r = 0. It also has, as the sausage mode, many nodes of zero amplitude, but a well-defined phase, at the other infinite zeros of J1(−m0r). In kink and sausage modes, however, the small value of m0 places all those nodes outside the sunspot and beyond the borders of our observation. Our concern is limited to that singularity at r = 0 of the kink mode that we have modelled and see to correspond to the observations in the previous section. The vortex line of dislocations is found at the point r = 0 of the coordinate system with respect to which we described the propagation of the kink wave. Since it is a coordinate value, it is fixed in time and the line of dislocations is horizontal, fixed at r = 0, in both the observations and simulations as long as we have a kink mode propagating. In the transition from one wave mode to the other, from sausage to kink, the dislocation line bends upwards. Since we prefer not to move our reference system, the shift of the dislocation line can only mean that the singularity is changing place and it is no longer at r = 0. Leaving aside all unimportant factors during the transition from sausage mode to kink mode, we can write the observed velocity amplitude as 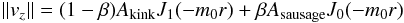 (5)where Akink and Asausage encode all those unimportant factors. The transition from sausage to kink takes place as β → 0. Written as this, it is clear that as long as β is not zero, there is no zero amplitude at r = 0 and no dislocation at that point. The singularity is somewhere else. Examining the case in which β = ϵ ≪ 1, and, for the sake of simplicity, assuming Akink = Asausage = 1, we find
(5)where Akink and Asausage encode all those unimportant factors. The transition from sausage to kink takes place as β → 0. Written as this, it is clear that as long as β is not zero, there is no zero amplitude at r = 0 and no dislocation at that point. The singularity is somewhere else. Examining the case in which β = ϵ ≪ 1, and, for the sake of simplicity, assuming Akink = Asausage = 1, we find 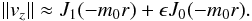 (6)At the singularity we require ∥ vz ∥ = 0. Since ϵ ≪ 1, though not zero, we can expect to find the singularity near r = 0. In the neighbourhood of r = 0 we can use the usual power series expansion of the Bessel functions to write
(6)At the singularity we require ∥ vz ∥ = 0. Since ϵ ≪ 1, though not zero, we can expect to find the singularity near r = 0. In the neighbourhood of r = 0 we can use the usual power series expansion of the Bessel functions to write 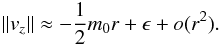 (7)Setting that simplified approximation to zero to find the singularity, we find the new dislocation at
(7)Setting that simplified approximation to zero to find the singularity, we find the new dislocation at
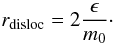 Since the overlooked amplitudes Akink and Asausage are in reality complex numbers, we should make sure that they allow the dislocation found above. Keeping their modulus at one, but allowing for a phase difference, we find after straightforward computations that the new dislocation is at
Since the overlooked amplitudes Akink and Asausage are in reality complex numbers, we should make sure that they allow the dislocation found above. Keeping their modulus at one, but allowing for a phase difference, we find after straightforward computations that the new dislocation is at  with α the eventual phase difference between the kink and sausage modes. Provided that this phase is constant during the transition, we see the dislocation moving in a given direction as the value of ϵ changes. As ϵ approaches zero and the sausage mode leaves room for the kink mode, the dislocation sits at its original place at r0. As it grows, making the sausage contribution more and more important, the dislocation changes place. At some point, the above approximation will not be valid. One could extend it to second order to find the correction, but soon the sausage mode has a large enough amplitude to make the singularity of the kink mode invisible nevertheless.
with α the eventual phase difference between the kink and sausage modes. Provided that this phase is constant during the transition, we see the dislocation moving in a given direction as the value of ϵ changes. As ϵ approaches zero and the sausage mode leaves room for the kink mode, the dislocation sits at its original place at r0. As it grows, making the sausage contribution more and more important, the dislocation changes place. At some point, the above approximation will not be valid. One could extend it to second order to find the correction, but soon the sausage mode has a large enough amplitude to make the singularity of the kink mode invisible nevertheless.
The bending of the vortex line corresponds to the progressive shift in position of the singularity as the sausage mode overtakes the kink mode. This shift in position of the singularity now has some interesting consequences. We imagine an ion sitting at a predefined position (x,y) in the umbra of a sunspot. Its velocity along the line of sight as it feels the wave passing by is given by vz. If such an ion is far away from the singularity of the kink wave its velocity perturbation due to the wave is a plane sinusoidal with a typical 3-min period. A sausage mode would make no difference to the velocity of this ion: it would also show a sinusoidal velocity perturbation. Near the singularity, and as long as the singularity does not change its position with respect to the ion, the velocity is still a plain sinusoidal with the same period. The scenario changes when the singularity moves. The rapid change of the phase of the wave around the singularity forces the ion to change its velocity quicker than in the other cases, since there is an extra phase term due to the shift of the singularity. This can be seen in Fig. 7 for both the analytical (left plot) and observed cases (right plot). The separation between the two points in the analytical case was chosen to be 0.5% of the value of 1 /m0, while in the observed case is of 7 arcsec. In both the analytical and the observed plots we see two time series waves that start in phase and then temporarily change frequencies to shift into quadrature. The first part of the plot corresponds to the sausage mode, when all points in the umbra oscillate mostly in phase, while the second part corresponds to the propagation of the kink mode with the vortex line right between the two points.
This change of relative phase is achieved by a temporal modification of the frequency of the two waves: in one of them this local frequency increases well beyond its Fourier frequency ω, while the other slows down. This modification lasts as long as the transition between the two waves and only in the region around the singularity. Because of the temporal change in frequency this phenomenon has been dubbed superoscillation in other fields of physics (Berry 1994) and we observe it here in solar magnetoacoustic waves for the first time. Around the singularity there is a strong phase gradient. While the singularity is fixed in place, this is of no consequence since the amplitudes of the wave decay exponentially as we approach the singularity; hence this strong phase mixing concerns regions of the wave with almost null amplitude and energy. The scenario is different during the transition between the sausage mode and kink mode, when the superoscillation appears. As the singularity appears and changes position it introduces strong phase gradients both spatial and temporal among the ions sitting next to its position. Neighbouring ions that were oscillating in phase accelerate or slow down until they oscillate in opposition of phase. We speculate that during this process there is a chance for viscous wave dissipation.
5. Conclusions
We identify and study a series of wavefront dislocations in a time series of magnetoacoustic waves observed in the umbra of a sunspot through Doppler velocimetry in the photospheric Si I line and in the chromospheric He I line, which are both in the 1083 nm spectral region. The data are particularly interesting in that they capture a full line of dislocations lasting over 14 min or about five wave periods. After examining the magnetoacoustic wave solutions we conclude that during that period a kink wave was propagating upwards and that (by chance) the slit crossed the axis of symmetry of that wave mode. The full time series can be interpreted as a series of sausage and kink modes with transitions that last less than one wave period.
The lucky coincidence of having the slit right on top of the axis of symmetry allowed us to unambiguously interpret the observed line of dislocations. After this identification we are also able to simulate what would have happened if the slit were slightly off the axis of symmetry. The simulations show that often in such situation an edge dislocation appears followed by a series of bent, but not dislocated, wavefronts. This description matches nicely the edge dislocations also observed in the data, thus confirming the scenario of sausage and kink waves excited sequentially at or below the photosphere. The triggering mechanism typically lasts about five periods or roughly 15 min, after which a new mode is excited. When a kink mode is excited, there is an axis of symmetry that can be found thanks to the position of the dislocations, precisely for the vortex line and vaguely for the edge dislocations. Without a model of the nature of the triggering mechanism of these waves, it is difficult to identify the reason for this axis to be in any one location in the umbra. In the data, however, we can see that over the course of an hour four kink modes with different axes are excited. It is clear that their positions are dependent on the particular conditions of each excitation and not on the general geometry of the sunspot umbra or its magnetic field.
In general, through the concept of wavefront dislocation and its easy identification in the data, we have been able to distinguish the propagation of kink and sausage modes. We did this without using any model-dependent dispersion relation or depending on difficult measurements and comparisons of velocity or magnetic field variations. This easy identification has led us to realise that kink and sausage modes are not excited simultaneously, but sequentially and independently. This, along with the measured probability of excitation of each of these modes, set strong constraints on the excitation mechanisms at work. Dislocations also allow us to discriminate among the different polarisations of the kink mode. We observe that, in spite of being degenerated in energy, the m = + 1 and m = −1 modes are not excited simultaneously. This means that the excitation mechanism of these waves is not just a simple unstructured energy input into the atmosphere.
Finally, during the transition from a sausage to a kink mode (lasting less than 3 min) the dislocation changes place in a predictable manner. This position change is seen both in the simulations and in the data as an apparent upwards bend in the edges of the dislocation line. As the singularity moves during this transition, we witness the appearance of the interesting phenomenon of superoscillations. Before the kink mode is excited, two ions sitting next to one another over the umbra oscillate in phase; as the kink mode reaches them, a singularity appears that moves among them. At the end of the process, the two ions sit on either side of the vortex line and are oscillating in quadrature. This transition from in phase to in quadrature is made by a temporal change of the period of the oscillations of the two ions: one of them slows down, while the other speeds up its oscillatory frequency, eventually beyond its maximum Fourier frequency, hence the name of superoscillation.
During the time of the superoscillation, neighbouring ions rapidly change the relative phase of their oscillations. This phase mixing may induce wave dissipation around the vortex line
(Heyvaerts & Priest 1983), at least at the time of the transition, associated with the presence of the superoscillation. Whether this is of any dynamical consequence for the solar atmosphere is left for future work.
References
- Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C., & Woerdman, J. P. 1992, Phys. Rev. A, 45, 8185 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bazhenov, V. Y., Soskin, M. S., & Vasnetsov, M. V. 1992, J. Mod. Opt., 39, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Berry, M. V. 1981, in Les Houches Lecture Series Session XXXV, eds. R. Balian, M. Kléman, & J.-P. Poirier (North-Holland: Amsterdam), 453 [Google Scholar]
- Berry, M. V. 1994, in Quantum Coherence and Reality; in celebration of the 60th Birthday of Yakir Aharonov, eds. J. S. Anandan, & J. L. Safko (World Scientific), 55 [Google Scholar]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Centeno, R., Collados, M., & Trujillo Bueno, J. 2009, ApJ, 692, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, M., Hill, C. A., Tapster, P. R., & Vaughan, J. M. 1994, Phys. Rev. A, 49, 3119 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Khomenko, E., & Collados, M. 2015, Liv. Rev. Sol. Phys., 12, 6 [CrossRef] [Google Scholar]
- López Ariste, A., Collados, M., & Khomenko, E. 2013, Phys. Rev. Lett., 111, 081103 [NASA ADS] [CrossRef] [Google Scholar]
- López Ariste, A., Luna, M., Arregui, I., Khomenko, E., & Collados, M. 2015, A&A, 579, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez Pillet, V., Collados, M., Sánchez Almeida, J., et al. 1999, in High Resolution Solar Physics: Theory, Observations, and Techniques, 183, 264 [Google Scholar]
- Nye, J. F., & Berry, M. V. 1974, Roy. Soc. London Proc. Ser. A, 336, 165 [Google Scholar]
- Socas-Navarro, H. 2001, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation, 236, 487 [Google Scholar]
All Figures
 |
Fig. 1 Observation of waves in the Si I line formed in the photosphere (top) and the He I line formed in a chromosphere (bottom). The images show a time series of Doppler velocities along the line of sight measured in the two spectral lines along a spectrograph slit placed across the umbra of a sunspot (NOAA9176) observed by the VTT on October 1, 2000 at latitude 10°S and heliocentric longitude 19°W. The measured velocities have been Fourier-filtered to show only the waves in the range of 3-min period. |
| In the text | |
 |
Fig. 2 Wavefronts of a sausage mode (left) and a kink mode (right). In both figures the propagation direction z is vertical and assumed to be along the magnetic field. The sausage mode presents a suite of isolated plane wavefronts, while the kink mode shows a connected helical wavefront with the dislocation line in its axis. |
| In the text | |
 |
Fig. 3 Time series of velocities along a spectral slit for a sausage mode (left) and a kink mode (right). In the case of a kink (right panel), the slit crosses the singularity at the axis and a vortex line of dislocations is visible at a fixed position at all times. |
| In the text | |
 |
Fig. 4 Sausage wave is substituted by a kink wave at minute 21. From then on the vortex line of dislocations is seen until at minute 48 the kink wave gives way to another sausage wave. The sequence reproduces the main dislocation line of Fig. 1, including the upwards shift of the line near its extremes. |
| In the text | |
 |
Fig. 5 In the same conditions as Fig. 4 we place the slit 2 arcsecs away so that the axis of the kink wave is left outside the slit. The time series of the Doppler velocities shows an isolated edge dislocation at the transition from sausage to kink modes, followed by a series of bent wavefronts similar to those seen in Fig. 1. |
| In the text | |
 |
Fig. 6 Comparison of solutions using the m = + 1 mode of the kink wave (left panel, same as Fig. 4), the m = −1 mode (centre) and an equally weighted mixture of both (right, called linear polarisation) which corresponds to a pure kink in the transverse plane. |
| In the text | |
 |
Fig. 7 Time series of the velocities of two points in the umbra as a singularity moves between them. Originally in phase, at the approach of the singulariy both change period before settling in perfect quadrature when the singularity stops moving. Left: simulated case; right: points at 16 and 23 arcsec along the slit from observations in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.