| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425411 | |
| Published online | 04 May 2016 | |
Multiply imaged quasi-stellar objects in the Gaia survey
1 Extragalactic Astrophysics and Space Observations (AEOS), Institut d’Astrophysique et de Géophysique, Liège University, Allée du 6 Août, 17 (Sart Tilman, Bât. B5c), 4000 Liège, Belgium
2 National Astronomical Observatory of Japan (NAOJ), 650 N. A’ohoku Place, Hilo, 96720 HI, USA
e-mail: finet@naoj.org
Received: 26 November 2014
Accepted: 9 October 2015
Aims. We report a study on the statistical properties of the multiply imaged quasi-stellar objects (QSOs) to be detected within the Gaia survey.
Methods. We considered two types of potential deflectors, the singular isothermal sphere (SIS) and the singular isothermal ellipsoid (SIE), to estimate the number of multiply imaged quasars as well as the normalized distributions of the redshifts of the lensed sources and of their associated deflectors. We also investigated the distribution of the lensing events as a function of their angular size and apparent magnitude. We compared the Gaia survey for multiply imaged quasars to typical ground-based surveys and to an ideal survey that would be carried out with a perfect instrument from space.
Results. Of the 6.64 × 105 QSOs brighter than G = 20 to be detected by Gaia, we expect the discovery of about 2886 multiply imaged sources, 450 of which are expected to be produced by a late-type galaxy. We expect only ~1600 of these multiply imaged quasars to have an angular separation between their images that is large enough to be resolved from seeing-limited observations, and ~80 of them to have more than two lensed images.
Key words: gravitational lensing: strong / quasars: general / cosmological parameters
© ESO, 2016
1. Introduction
The Gaia mission1 is currently conducting an all-sky coverage for a total duration of five years. The satellite is equipped with three different instruments: an astrometric instrument, a radial velocity spectrometer, and a photometric instrument. The latter produces two low-resolution spectra in the blue and the red, from which the GBS, GRS, and the global G-band magnitudes are derived (see Jordi et al. 2006, 2010 for the description of the photometric system). The survey is expected to be complete down to the G-band magnitude G = 20.
The main goal of the mission is to make a three-dimensional map of our Galaxy based on measurements of the photometry, astrometry, and proper motion of ~109 stars. Radial velocity measurements will be obtained for a subsample of brighter objects. The satellite is also expected to detect a very large number of extragalactic objects, some of which will be quasi-stellar objects (QSOs). The detection of QSOs will be difficult at low Galactic latitudes (|b| < 25−30°). Judging from the QSO detection in the remaining 60% of the sky, this will probably lead to the detection of 5.5−7 × 105 QSOs (Mignard 2012; Robin et al. 2012; Slezak 2007). This very large sample, in combination with the astrometry precision of the survey of down to ~25 μ-as, will lead to the direct construction of a new celestial reference frame in the optical that is at least a hundred times denser than the international celestial reference frame (ICRF), which will enable testing general relativity (Mignard 2005). We expect that multiply imaged QSOs are detected among these sources through gravitational lensing by foreground-deflecting galaxies, which could be detected down to an angular separation of ~0.2′′ (Mignard 2012).
Imaging with Gaia is made by reconstructing 2D-images from multiple 1D-drift scan images acquired in different directions (Harrison 2011). As a result of the peculiar drift-scan imaging mode of Gaia, it is necessary to properly estimate the properties of the lensed population of QSOs to define a detection strategy for the lensing events. The statistical properties of the QSOs to be detected have been studied by Slezak (2007). In this paper we concentrate on studying the expected statistical properties of the population of lensed QSOs. This information will be used to define the best strategy for detecting these lensing events throughout the different scans generated by the satellite.
Because of the very large number of sources detected by Gaia, we expect the gravitational lenses to constitute an unprecedentedly large sample. In addition to the scientific interest of each individual lensed source, these multiply imaged sources will constitute a statistical sample that may be used to constrain the cosmological mass density parameter Ωm through the statistics of gravitational lensing in the sample, and the lensed sources will also be used to study the evolution in the population of deflecting galaxies.
A previous rough estimation of the number of expected gravitational lenses in the Gaia mission has already been performed (Finet et al. 2012), and Mignard (2008) has studied the effect of gravitational lensing on the reference frame constituted by the sources. We here report an in-depth study of their expected statistical properties.
We introduce the mathematical formalism in the next section. We first derive an expression for the probability of a source to be lensed, alternatively modeling the deflectors by spherical (Sect. 2.1.1) and elliptical (Sect. 2.1.2) singular isothermal mass distributions. We then introduce in Sect. 2.2 the joint probability distribution of the Gaia QSOs in the redshift-absolute magnitude plane that we use in the next subsections to calculate various expected distributions of astrophysical parameters linked to the lensed population. Specifically, the average lensing optical depth in the sample and the redshift distributions of the lensed sources and of the deflectors are derived. Finally, we derive an expression for the distributions of the lensed sources as a function of their apparent magnitude and the angular separation between the lensed images.
In Sect. 3 we present the observational data on which we base our simulations, we derive the best-fit parameter for the QSO luminosity function (LF) evolution models, based on the LF of Richards et al. (2006) and Palanque-Delabrouille et al. (2013), from which we infer the joint probability density of the sources for simulation purposes. Finally, in Sect. 4 we present the results of the simulations and study the effect of the cosmological mass density parameter Ωm and that of the smallest angular separation resolvable in the survey. The latter is done by comparing the results for a perfect instrument, the Gaia observatory, and typical ground-based surveys.
2. Mathematical formalism for gravitational-lensing statistics
2.1. Lensing optical depth
Multiple images of a background source arise when a foreground galaxy is located close enough to the source line of sight. In the present work, the sources considered are point-like QSOs. To calculate the probability for a source to be lensed as a result of a foreground deflector near its line of sight, it is therefore crucial to accurately model the volume density of the potential deflecting galaxies. The comoving volume density of deflectors with a line-of-sight velocity dispersion in the range σ to σ + dσ is given by the velocity dispersion function (VDF)  , which is modeled by the modified Schechter function (Sheth et al. 2003; Mitchell et al. 2005; Choi et al. 2007; Chae 2010)
, which is modeled by the modified Schechter function (Sheth et al. 2003; Mitchell et al. 2005; Choi et al. 2007; Chae 2010) ![\begin{equation} \Phi_{\sigma}\left (\sigma\right ) {\rm d}\sigma= \Phi_{\ast} \dfrac{\beta}{\Gamma\left (\alpha/\beta\right )} \left (\frac{\sigma}{\sigma_{\ast}}\right )^{\alpha} \exp\left [-\left (\frac{\sigma}{\sigma_{\ast}}\right )^{\beta}\right ] \dfrac{{\rm d}\sigma}{\sigma}, \label{eq_def_VDF} \end{equation}](/articles/aa/full_html/2016/06/aa25411-14/aa25411-14-eq17.png) (1)where Φ∗ and σ∗ are the characteristic volume density and line-of-sight velocity dispersion, α and β are the VDF slope at low and high σ, and
(1)where Φ∗ and σ∗ are the characteristic volume density and line-of-sight velocity dispersion, α and β are the VDF slope at low and high σ, and  is the complete gamma function.
is the complete gamma function.
Thanks to their larger mass, early-type galaxies are more efficient deflectors than late-type galaxies, which tend to form lensed images with a smaller angular separation. The latter, although more numerous, were shown to constitute typically less than 10% of the lensing events in a flux limited sample from ground-based observations (Keeton et al. 1998; Kochanek et al. 2000). Nevertheless, the fraction of lensing events that is due to late-type galaxies increases with a better angular resolution of the survey (e.g., the CLASS survey where ~25% of the lenses are due to spiral galaxies, cf. Browne et al. 2003). Therefore, thanks to the very good angular resolution of the Gaia survey, we expect late-type galaxies to contribute to a significant fraction of the lensed sources. In our simulations, we consider the population of deflectors to be formed by both early- and late-type galaxies.
Most of the lensing statistics studies of the evolution with redshift of the deflector population are consistent with a no-evolution scenario or very small effect of the evolution (Chae 2010; Oguri et al. 2012). For our estimation we thus neglected the evolution effect in the deflector galaxy VDF and used the value of the VDF parameters measured in the local Universe by Choi et al. (2007), that is, for early-type galaxies Φ∗ ,E = 8 × 10-3h3 Mpc-3, σ∗ ,E = 161km s-1 and (αE,βE) = (2.32,2.67), and for late-type galaxies Φ∗ ,L = 66 × 10-3h3 Mpc-3, σ∗ ,L = 91.5km s-1 and (αL,βL) = (0.69,2.10).
2.1.1. Singular isothermal sphere deflector
As a first approximation, the total mass distribution of early- and late-type galaxies is well modeled by means of the singular isothermal sphere (SIS) profile, that is, by a spherically symmetric mass distribution with a volume density scaling as ∝r-2, where r is the distance to the deflector center (see, e.g., Koopmans et al. 2006, 2009 for an observational confirmation of the almost isothermal behavior of the galaxy mass distribution). Such a deflector may lead to the formation of at most two lensed images of a background source, with an angular separation equal to twice the Einstein ring angular radius θE, which is given by  (2)where Dds (respectively Dos) is the angular diameter distance between the deflector (respectively the observer) and the source, and c is the speed of light.
(2)where Dds (respectively Dos) is the angular diameter distance between the deflector (respectively the observer) and the source, and c is the speed of light.
A deflector located in the deflector plane (perpendicular to the source line of sight) at a redshift zd will lead to the formation of multiple images of a source at redshift zs with apparent magnitude m if it is located inside an area ΣSIS called the lensing cross section, which is centered on the projected source position and is defined by (Turner et al. 1984)  (3)where Dod is the angular diameter distance between the observer o and the deflector d. We have introduced the coordinates y = (y1,y2), the projection on the deflector plane of the source position, normalized to the scale factor DodθE, that is, the Einstein radius.
(3)where Dod is the angular diameter distance between the observer o and the deflector d. We have introduced the coordinates y = (y1,y2), the projection on the deflector plane of the source position, normalized to the scale factor DodθE, that is, the Einstein radius.
The amplification bias B(m,y) is introduced to take into account the favorable bias in the calculation of the source lensing optical depth, which arises because of the flux amplification in the lensing event, which for instance leads to the inclusion in flux-limited samples of sources that are intrinsically fainter. In our simulations, we estimated the amplification bias by means of the source differential number counts function (DNCF) 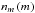 as a function of their apparent magnitude m, through the relation
as a function of their apparent magnitude m, through the relation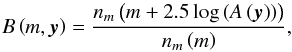 (4)where A(y) is the total amplification of the lensing event, that is, the sum of the multiple image amplification moduli.
(4)where A(y) is the total amplification of the lensing event, that is, the sum of the multiple image amplification moduli.
The integration area Sy in Eq. (3) represents the area (normalized to the scale factor) in which the presence of a deflector leads to the formation of a lensing event, defined as the detection of two lensed images by the survey strategy. Depending on the survey angular resolution, the associated 2D integration interval Sy varies, and so does the lensing cross section.
The probability  for a source with a redshift zs and an apparent magnitude m to be multiply imaged, or the lensing optical depth, is obtained by integrating the density of deflectors (over all possible values of σ) located within the envelope of the lensing cross sections at each intermediate redshift z, defined as the lensing volume (Nemiroff 1989). This leads to the expression
for a source with a redshift zs and an apparent magnitude m to be multiply imaged, or the lensing optical depth, is obtained by integrating the density of deflectors (over all possible values of σ) located within the envelope of the lensing cross sections at each intermediate redshift z, defined as the lensing volume (Nemiroff 1989). This leads to the expression 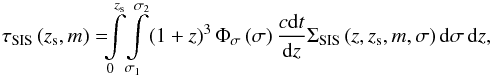 (5)where σ is in the range σ1 to σ2 associated with the deflector population, and cdt/dz is the infinitesimal light-distance element, which in a flat FLRW universe is expressed as (Peebles 1993)
(5)where σ is in the range σ1 to σ2 associated with the deflector population, and cdt/dz is the infinitesimal light-distance element, which in a flat FLRW universe is expressed as (Peebles 1993) ![\begin{equation} \frac{c{\rm d}t}{{\rm d}z_{\rm d}} = \frac{c}{H_{0}\left (1+z_{\rm d}\right )}\, \left [\left (1+z_{\rm d}\right )^{3} \Omega_{\rm m} + \left ( 1-\Omega_{\rm m}\right )\right ]^{-1/2}, \label{eq_def_cdtdz} \end{equation}](/articles/aa/full_html/2016/06/aa25411-14/aa25411-14-eq60.png) (6)where Ωm is the present-day value of the cosmological mass density parameter. The integration over σ in Eq. (5) may be performed analytically under the assumption of a non-evolving deflector population. Using Eqs. (2) and (3), ΣSIS may be expressed as
(6)where Ωm is the present-day value of the cosmological mass density parameter. The integration over σ in Eq. (5) may be performed analytically under the assumption of a non-evolving deflector population. Using Eqs. (2) and (3), ΣSIS may be expressed as  (7)where
(7)where  . Inserting the latter expression into Eq. (5) and integrating over the σ range [σ1,σ2[ → [0, + ∞[, we obtain
. Inserting the latter expression into Eq. (5) and integrating over the σ range [σ1,σ2[ → [0, + ∞[, we obtain 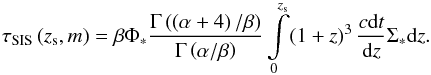 (8)
(8)
2.1.2. Singular isothermal ellipsoid deflector
To reproduce lensing configurations with more than two lensed images, as observed among the known gravitational lens systems, a new model was introduced by Kormann et al. (1994): the singular isothermal ellipsoid (SIE). This model introduces an internal ellipticity into the mass distribution, which is characterized by the axis ratio q between the axes of the projected mass distribution on the deflector plane. The SIE mass profile may produce two, three (cusp configuration), or four lensed images depending on the position of the source relative to the caustics (defined as the lines of infinite amplification in the source plane). Non-singular mass profiles may produce an additional highly deamplified central lensed image, which is difficult to detect because it is very faint and dimmed by dust extinction in the deflector. Because this central lensed image is not likely to be detected in the Gaia images, we here only consider the lensed images produced by the SIE model that are effectively detected on the CCD frames.
When considering an SIE deflector, the lensing cross section in Eq. (3) now depends on the deflector axis ratio. We may define a lensing event as the detection of multiple images or as the detection of a given number i of lensed images (two, three, or four), regardless of whether we account for the ability of the instrument to resolve lensed images with a too small angular separation. Consequently, depending on the definition of the lensing event, the area Sy in Eq. (3) varies, and we therefore define different cross sections: ΣSIE corresponds to the detection of multiple images irrespective of their number, and ΣSIE,i to the detection of i lensed images.
The volume density of the deflectors is now also a function of the axis ratio q. Because of the lack of observational constraints on the q−σ correlation for the deflectors, we assume that the distribution of the axis ratio is independent of the deflector line-of-sight velocity dispersion. The number density of deflectors with a line-of-sight velocity dispersion and axis ratio in the range σ to σ + dσ and q to q + dq, respectively, is thus 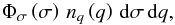 (9)where nq(q) is the normalized distribution as a function of the axis ratio q for early- or late-type galaxies, and where the deflector VDF
(9)where nq(q) is the normalized distribution as a function of the axis ratio q for early- or late-type galaxies, and where the deflector VDF  is given by Eq. (1).
is given by Eq. (1).
Koopmans et al. (2006) and Sluse et al. (2012) have independently confirmed through studying various gravitational lens samples that elliptical galaxy isophotes and the isodensity curves of their projected mass distribution have well-correlated ellipticities and major-axis directions. The normalized distribution nq(q) can thus be estimated from the distribution of the isophotes of early-type galaxies as measured by Choi et al. (2007) in the local Universe.
To calculate the lensing optical depth  for a source with deflectors modeled by SIE mass profiles, we need to integrate over both variables σ and q (Huterer et al. 2005), which leads to
for a source with deflectors modeled by SIE mass profiles, we need to integrate over both variables σ and q (Huterer et al. 2005), which leads to  (10)The integration over σ can be performed using Eq. (7) while adopting the same assumptions as for the SIS case. This leads to
(10)The integration over σ can be performed using Eq. (7) while adopting the same assumptions as for the SIS case. This leads to  (11)We have developed software toolboxes using Matlab, allowing us to calculate the lensing cross sections and optical depths by modeling the deflectors by means of both the SIS and the SIE mass distribution (Eqs. (3), (5), and (11)).
(11)We have developed software toolboxes using Matlab, allowing us to calculate the lensing cross sections and optical depths by modeling the deflectors by means of both the SIS and the SIE mass distribution (Eqs. (3), (5), and (11)).
2.2. QSO joint probability density d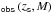
The sources detected in a survey are characterized by their absolute magnitude M and their redshift zs. Each source has a probability  to be detected with a redshift and an absolute magnitude in the ranges zs to zs + dzs and M to M + dM, respectively. Furthermore, we may define the joint probability density
to be detected with a redshift and an absolute magnitude in the ranges zs to zs + dzs and M to M + dM, respectively. Furthermore, we may define the joint probability density  associated with
associated with  by means of the relation
by means of the relation  (12)For an already existing survey,
(12)For an already existing survey,  may be estimated from the normalized smoothed histogram in the
may be estimated from the normalized smoothed histogram in the  plane of the detected sources. However, for prospective simulation purposes,
plane of the detected sources. However, for prospective simulation purposes,  can be estimated by means of the QSO luminosity function
can be estimated by means of the QSO luminosity function 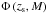 (Oguri & Marshall 2010) by means of the relation
(Oguri & Marshall 2010) by means of the relation  (13)where
(13)where
-
 accounts for selection biases in the
accounts for selection biases in the
 plane, which occur during the detection procedure of the sources. For a perfect flux-limited
sample, this function equals one in the region ofthe
plane, which occur during the detection procedure of the sources. For a perfect flux-limited
sample, this function equals one in the region ofthe
 plane which leads to an apparent magnitude brighterthan
the survey limiting magnitude.
plane which leads to an apparent magnitude brighterthan
the survey limiting magnitude.
-
N QSO is the total number of QSOs detected within the survey;
-
d V c /d z is the differential contribution at redshift z to the total comoving volume accessible by the survey, which in a flat expanding FLRW universe may be expressed as
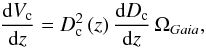 (14)
where
D
c
is the line-of-sight comoving distance at redshift
z
,
(14)
where
D
c
is the line-of-sight comoving distance at redshift
z
,
 its differential contribution, and ΩGaia
is the solid angle covered by the survey in which QSO detection is possible.
its differential contribution, and ΩGaia
is the solid angle covered by the survey in which QSO detection is possible.
The joint probability density dobs(zz,M) is closely related to observable distributions of the source population. Indeed, the marginal distribution  obtained by integrating
obtained by integrating  over M is the normalized redshift distribution of the sources. Similarly, the differential number counts function (DNCF) as a function of the apparent magnitude may be estimated by
over M is the normalized redshift distribution of the sources. Similarly, the differential number counts function (DNCF) as a function of the apparent magnitude may be estimated by  (15)where
(15)where  and
and  are the distance modulus and K-correction at redshift zs, respectively.
are the distance modulus and K-correction at redshift zs, respectively.
2.3. Source statistical properties
The joint probability density of the source population is directly linked to the distribution of the sources in the  plane and to their observable distributions nz and nm. It may be used as a weighting factor to estimate the mathematical expectation of any function of zs and M.
plane and to their observable distributions nz and nm. It may be used as a weighting factor to estimate the mathematical expectation of any function of zs and M.
We assume that we have an expression for the lensing optical depth  as a function of zs and M for a given source. This expression is trivially obtained from
as a function of zs and M for a given source. This expression is trivially obtained from  ,
,  and
and  (Eqs. (5) and (11)) considering
(Eqs. (5) and (11)) considering  . Its mathematical expectation ⟨τ⟩ is simply given by
. Its mathematical expectation ⟨τ⟩ is simply given by  (16)where ⟨τ⟩ represents the fraction of sources in the detected population to have undergone a gravitational lensing event.
(16)where ⟨τ⟩ represents the fraction of sources in the detected population to have undergone a gravitational lensing event.
Similarly, the expected normalized redshift distribution of the deflectors 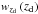 is given by (Oguri et al. 2012)
is given by (Oguri et al. 2012)  (17)and the expected normalized redshift distribution of the lensed sources by (Oguri & Marshall 2010)
(17)and the expected normalized redshift distribution of the lensed sources by (Oguri & Marshall 2010)  (18)By integrating over the source redshift, we may also derive the normalized distribution
(18)By integrating over the source redshift, we may also derive the normalized distribution  as a function of the apparent magnitude m of the lensed sources
as a function of the apparent magnitude m of the lensed sources 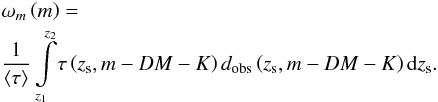 (19)Finally, we define the normalized probability density ωθE of observing a gravitational lens system with an angular configuration θE in the lensed population. From the definition of θE in Eq. (2), we may trivially derive the following relations
(19)Finally, we define the normalized probability density ωθE of observing a gravitational lens system with an angular configuration θE in the lensed population. From the definition of θE in Eq. (2), we may trivially derive the following relations  (20)where
(20)where  . Furthermore, from the definition of the lensing cross section in Eq. (3), we have
. Furthermore, from the definition of the lensing cross section in Eq. (3), we have  (21)where
(21)where  is the lensing cross section evaluated for the typical value of θE = θ∗. Inserting Eqs. (20) and (21) in the definition of τSIS in Eq. (5) and making use of Eq. (1), we may derive the expression of τSIS for which the integration is done over θE rather than σ. Deriving this expression with respect to θE, we find
is the lensing cross section evaluated for the typical value of θE = θ∗. Inserting Eqs. (20) and (21) in the definition of τSIS in Eq. (5) and making use of Eq. (1), we may derive the expression of τSIS for which the integration is done over θE rather than σ. Deriving this expression with respect to θE, we find  (22)The normalized probability density ωθE is then simply obtained by averaging the previous expression over the detected population of sources
(22)The normalized probability density ωθE is then simply obtained by averaging the previous expression over the detected population of sources  (23)Using the joint probability density
(23)Using the joint probability density  as a weighting factor to average quantities over the entire population of sources detected in the survey, we have derived expressions for the mean optical depth ⟨τ⟩ (Eq. (16)), and of the normalized redshift distributions expected for the deflectors ωzd (Eq. (17)) and for the lensed sources ωzs (Eq. (18)). We also derived the normalized distributions ω as a function of the apparent magnitude m and Einstein angle θE of the lensed sources (Eqs. (19) and (23), respectively).
as a weighting factor to average quantities over the entire population of sources detected in the survey, we have derived expressions for the mean optical depth ⟨τ⟩ (Eq. (16)), and of the normalized redshift distributions expected for the deflectors ωzd (Eq. (17)) and for the lensed sources ωzs (Eq. (18)). We also derived the normalized distributions ω as a function of the apparent magnitude m and Einstein angle θE of the lensed sources (Eqs. (19) and (23), respectively).
The fundamental quantity needed is the joint probability density  corresponding to the expected Gaia survey sources, which we estimate in the next section.
corresponding to the expected Gaia survey sources, which we estimate in the next section.
3. Observational constraints
In this section, we describe the observational constraints used to estimate the joint probability density 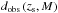 for the Gaia survey.
for the Gaia survey.
3.1. QSO luminosity function
 |
Fig. 1 Luminosity function as a function of the absolute magnitude Mi in the SDSS i-band for different redshift bins. We have included the LF determined by Richards et al. (2005) and Palanque-Delabrouille et al. (2013) (converted to Mi magnitude). The different fitted models correspond to no contraints on the redshift behavior of M∗ and Φ∗ (dashed light gray line), to an evolution model for Φ∗ and M∗ is fitted freely (light gray line), and to M∗ and Φ∗ both constrained by an evolution model (continuous black line). The latter is the final evolution model chosen for the simulations, see main text for the full description. |
Thanks to Eq. (13), 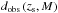 may be estimated through the LF of the observed sources. We need an estimate of the QSO LF and its behavior with redshift, spanning over the entire redshift and absolute magnitude ranges probed by the Gaia Survey. Various evolution models of the QSO optical LF have been proposed (e.g., Richards et al. 2005, 2006; Palanque-Delabrouille et al. 2013; Ross et al. 2013 for some recent works). Unfortunately, none of them fully spans the entire redshift and absolute magnitude ranges accessed by the Gaia Survey.
may be estimated through the LF of the observed sources. We need an estimate of the QSO LF and its behavior with redshift, spanning over the entire redshift and absolute magnitude ranges probed by the Gaia Survey. Various evolution models of the QSO optical LF have been proposed (e.g., Richards et al. 2005, 2006; Palanque-Delabrouille et al. 2013; Ross et al. 2013 for some recent works). Unfortunately, none of them fully spans the entire redshift and absolute magnitude ranges accessed by the Gaia Survey.
In the remainder of this section, we consider the binned luminosity function derived by Richards et al. (2006) as a function of the Mi magnitude (based on the SDSS-DR3) and that derived by Palanque-Delabrouille et al. (2013) in the SDSS g-band based on the SDSS-III and the MMT data, and we fit an evolution model on the combined data. Palanque-Delabrouille et al. (2013) have derived the binned LF versus the Mg continuum absolute magnitude associated with the SDSS g-band, with the zero point of the continuum K-correction at z = 2. For the conversion from Mg to Mi, we follow Ross et al. (2013) and convert through (24)This transformation is derived assuming the continuum to be a single power-law with a spectral index αν = −0.5, which they used to define the continuum.
(24)This transformation is derived assuming the continuum to be a single power-law with a spectral index αν = −0.5, which they used to define the continuum.
The derived binned luminosity functions from Richards et al. (2006) and Palanque-Delabrouille et al. (2013) are depicted in Fig. 1, both expressed as a function of the Mi magnitudes for the different redshift bins. Shen & Kelly (2012) have also derived the QSO LF from the SDSS-DR7 in the same redshift and apparent ranges as Richards et al. (2006) and their results agree very well. We used the result from Richards et al. (2006) because the redshift bins are similar to those of Palanque-Delabrouille et al. (2013).
We followed Richards et al. (2006) and used absolute magnitudes M of the continuum, with a zero point of the continuum K-correction at redshift z = 2. We determined the K-correction for the Gaia G-band using the G-band spectral transmission function (Jordi et al. 2010) with the QSO synthetic spectrum derived by Vanden Berk et al. (2001) from SDSS QSO spectra. We define the continuum absolute magnitude and derive the Gaia G-band K-correction in Appendix A.
To facilitate the comparison with previous results, we determined the LF evolution considering absolute magnitudes Mi in the SDSS i-band. We converted the absolute magnitudes Mi to the Gaia G-band absolute magnitude M using the transformation law derived in Appendix A, based on the QSO spectrum from Vanden Berk et al. (2001), the G-band K-correction previously described, and SDSS i-band K-correction given in Richards et al. (2006).
To model the LF, we used the conventional double power-law form for the QSO LF in terms of absolute magnitudes ![\begin{equation} \Phi\left (z_{\rm s},M\right ) = \Phi_{\ast} \left [10^{0.4 \left (1 + \alpha\right ) \left (M - M_{\ast}\right )}+10^{0.4 \left (1 + \beta\right ) \left (M - M_{\ast}\right )} \right ]^{-1}, \end{equation}](/articles/aa/full_html/2016/06/aa25411-14/aa25411-14-eq132.png) (25)where M∗ and Φ∗ are the characteristic absolute magnitude and number density, respectively, and α and β are the bright and faint end slopes of the LF, respectively.
(25)where M∗ and Φ∗ are the characteristic absolute magnitude and number density, respectively, and α and β are the bright and faint end slopes of the LF, respectively.
For the slope parameters, we considered β = −1.45 and α = −3.31 (values taken from Richards et al. 2005 from the analysis of the combined SDSS and 2dF samples) over the entire redshift range.
We first fit the combined data in each redshift bin assuming constant slope parameters α and β, fitting Φ∗ and M∗ without any evolution model constraints on their behavior as a function of the redshift. The resulting LF is shown as a dashed light gray curve in Fig. 1, and the values of the best-fit parameters are shown in Fig. 2 as light gray circles for the different redshift bins. The rather large error bars arise because Φ∗ and M∗ are highly correlated.
 |
Fig. 2 Behavior of the LF Φ∗ and M∗ parameters as a function of the QSO redshift. The dark continuous line shows the fit model used in our simulations. The light gray markers show the best fit parameters for Φ∗ and M∗ when fitting the LF separately in each redshift bin, without any evolution model constraints. When constraining the evolution of the characteristic density, the best parameters are found to be log Φ∗ ,lowz = −5.85, αΦ∗ = −0.77 ± 0.31, and zref = 2.09 ± 0.28. |
Following the results of Ross et al. (2013), we assumed that log Φ∗ is constant for z< 2.05 (z< 2.2 in Ross et al. 2013) and that it can be fitted as linearly evolving for higher z. We thus assumed an evolution model for Φ∗ given by  (26)In each redshift bin we then fit the value of M∗ for each Φ∗ given by the model. The best-fit parameters are log Φ∗ ,lowz = −5.85, αΦ∗ = −0.77 ± 0.31, and zref = 2.09 ± 0.28.
(26)In each redshift bin we then fit the value of M∗ for each Φ∗ given by the model. The best-fit parameters are log Φ∗ ,lowz = −5.85, αΦ∗ = −0.77 ± 0.31, and zref = 2.09 ± 0.28.
The behavior of Φ∗ as a function of the redshift is shown in the lower panel of Fig. 2, and the corresponding fitted values of M∗ are shown as dark gray markers on the upper panel.
Finally, motivated by the smooth redshift evolution of M∗, we fit the evolution of M∗ by a third-order polynomial. The fit is shown in the upper panel of Fig. 2. The best-fit parameters are [c3,c2,c1,c0] = [−0.0427,0.5484,−2.7563,−22.8766].
The final evolution model used for M∗ and log Φ∗ are shown as a function of the redshift, as a continuous dark gray line in Fig. 2. The corresponding LF is represented for the different redshift bins in Fig. 1 as a continuous dark gray line. We represent for each redshift bin the faintest sources detectable by Gaia assuming G = 20 is the faintest magnitude achievable. The limit is shown as a vertical light gray dash-dotted line. The conversion from G to Mi is made using the color  evolution as a function of the redshift, described in Appendix A, while adopting the SDSS i-band K-correction.
evolution as a function of the redshift, described in Appendix A, while adopting the SDSS i-band K-correction.
In the range accessible to the Gaia mission, our LF evolution model fits the data over the entire redshift range very well.
3.2. Joint probability density
To estimate the joint probability density  for the Gaia survey, we used the QSO-LF function derived in Sect. 3.1 to compute
for the Gaia survey, we used the QSO-LF function derived in Sect. 3.1 to compute  through Eq. (13).
through Eq. (13).
 |
Fig. 3 Left: joint probability density |
 |
Fig. 4 Left: average lensing optical depth as a function of the survey angular resolution θmin for early- and late-type galaxy deflectors. We modeled the deflectors as SIS (⟨τSIS⟩-continuous black line) and SIE mass distributions (⟨τSIE⟩-continuous gray line). In the latter case, we also show the average optical depth with detection of two lensed images (⟨τSIE,2⟩ – dashed gray line). Right: fraction of lensed sources detected with three (light gray) or four (dark gray) lensed images as a function of θmin. The results for the case of early- and late-type galaxy deflectors are shown with continuous and dash-dotted lines, respectively. In both panels we indicate the typical value of θmin for the Gaia survey and typical seeing-limited ground-based observations. |
We limited the redshift range to 0 <z ≲ 4.5. Although the spectro-photometric imaging of Gaia will enable detecting QSOs with a higher redshift, the limiting magnitude of G = 20 corresponds to very bright QSOs at redshift higher than z ~ 4.5, which are very rare.
The resulting  is shown in the
is shown in the  plane in the left panel of Fig. 3. The gray scale is proportional to the probability of detection, a darker gray indicating a higher probability of detection. For clarity, we indicate the magnitude cutoff of the survey G = 20 as well as the brighter cutoff G = 16 that was imposed because of the scarcity of such bright QSOs. For sources fainter than G = 20, dobs is null because the detection probability of these sources is assumed to be null.
plane in the left panel of Fig. 3. The gray scale is proportional to the probability of detection, a darker gray indicating a higher probability of detection. For clarity, we indicate the magnitude cutoff of the survey G = 20 as well as the brighter cutoff G = 16 that was imposed because of the scarcity of such bright QSOs. For sources fainter than G = 20, dobs is null because the detection probability of these sources is assumed to be null.
To assess the ability of the derived  to reproduce the observed properties of the real sources, we compared the DNCF
to reproduce the observed properties of the real sources, we compared the DNCF 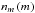 as a function of the apparent magnitude derived with Eq. (15) to observational sets that were used to determine the LF by applying the magnitude and redshift cuts of the observational samples to the joint probability density.
as a function of the apparent magnitude derived with Eq. (15) to observational sets that were used to determine the LF by applying the magnitude and redshift cuts of the observational samples to the joint probability density.
Richards et al. (2006) have estimated the QSO DNCF in the SDSS i-band on the basis of the SDSS-DR3 QSO catalog for sources restricted to the redshift ranges 0.3 <z< 2.2 and 3 <z< 5. In the lower redshift range, the survey is complete down to i ≃ 19. For the fainter magnitudes, we used the DNCF from the 2SQ/6QZ survey (also given in Richards et al. 2006). The different data sets are displayed in the right panel of Fig. 3.
We derived the DNCF from  through Eq. (13) by restricting the redshift range to 0.3 <z< 2.2 and 3 <z< 5. The results are shown in the right panel of Fig. 3 as continuous and dashed light gray curves. The simulated DNCF agree very well with the observational data. Following Richards et al. (2006), we used as definition of a QSO a source with an absolute magnitude in the continuum of the SDSS i-band (with zero point at z = 0) brighter than −22.5, considering a flat expanding universe with H0 = 70 km s-1 Mpc-1 and Ωm = 0.3. In the same figure, we represent with a dark gray line the expected DNCF
through Eq. (13) by restricting the redshift range to 0.3 <z< 2.2 and 3 <z< 5. The results are shown in the right panel of Fig. 3 as continuous and dashed light gray curves. The simulated DNCF agree very well with the observational data. Following Richards et al. (2006), we used as definition of a QSO a source with an absolute magnitude in the continuum of the SDSS i-band (with zero point at z = 0) brighter than −22.5, considering a flat expanding universe with H0 = 70 km s-1 Mpc-1 and Ωm = 0.3. In the same figure, we represent with a dark gray line the expected DNCF 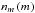 of the entire Gaia population that we used in Eq. (4) to calculate the amplification bias.
of the entire Gaia population that we used in Eq. (4) to calculate the amplification bias.
Comparison of the mean lensing optical depth and the expected number of detected multiply imaged quasars for different values of the survey angular resolution corresponding to a perfect survey (θmin = 0′′), Gaia (θmin = 0.2′′), and typical ground-based observations (θmin = 0.6′′).
Combining Eqs. (13) and (14), the normalization factor of the joint probability density is ΩGaia/NQSO, that is, the number of QSOs detected per steradian, from which we may trivially derive the total number of QSOs expected to be detected in the survey. Considering that QSOs will be detectable over 60% of the sky (thus excluding the low galactic latitude fields), this leads to the expected detection of 6.64 × 105 sources brighter than G = 20. Mignard (2012) has estimated the surface density of QSOs brighter than G = 20 and concluded that the Gaia survey should expect the discovery of 5.5 to 7 × 105 QSOs; this result agrees well with our own estimate. Slezak (2007) also previously estimated the number of QSOs to be detected: 7.2 × 105.
4. Results
We have computed the mean lensing optical depth ⟨τ⟩ for the whole population of QSOs by means of Eq. (16) for different values of the survey angular resolution θmin (i.e., the minimum image separation for which point-like sources with similar amplification may be distinguished). In Eq. (16), we alternatively considered the lensing optical depth τ for deflectors modeled as SIS (τSIS in Eq. (5)) and as SIE deflectors (Eq. (11)), considering the population of both early- and late-type galaxies. When considering SIE deflectors, we calculated both τSIE and τSIE,i. In Fig. 4 we represent as a function of the angular resolution θmin of the survey the dependence of the different average optical depths ⟨τSIS⟩, ⟨τSIE⟩ and ⟨τSIE,i⟩ and the evolution of the fraction of events with formation of three or four lensed images, that is, ⟨τSIE,3⟩/⟨τSIE⟩ and ⟨τSIE,4⟩/⟨τSIE⟩, for both types of galaxy populations.
The average total optical depths ⟨τSIS⟩ and ⟨τSIE⟩ show a very similar behavior: they both decrease as θmin increases because lensing events with images too close to each other are not resolved by the survey and are detected as single sources. In Table 1 we list the numerical values of the lensing optical depth for different values of the θmin parameter, representative of a perfect survey (θmin = 0′′), the Gaia survey (θmin = 0.2′′), and seeing-limited ground-based observations (θmin = 0.6′′). θmin represents the smallest angular separation between two point-like sources with similar brightness for which the survey source detection procedure is capable to separate the two lensed images. We considered θmin to be independent of the relative brightness between the lensed images. This assumption is motivated by the fact that the regions contributing the most to the lensing cross sections are the most amplified (where the source is located inside and near the tangential caustics). For these configurations, the brighter and closer lensed images are located near the tangential critical curve and show similar amplification (see, e.g., Schneider et al. 1992, Chap. 6). For typical ground-based observations, we considered seeing-limited observations (typically ~1−1.2′′). With PSF-fitting techniques, we may at best resolve point-like images with the same brightness separated by half the PSF full width at half maximum, that is, by half of the seeing value.
 |
Fig. 5 Left: expected normalized distributions ω as a function of the redshift of the lensed sources (zs) and of the deflectors (zd). For comparison, we also include the normalized redshift distribution of the sources (ωQSO). The simulations were made assuming θmin = 0.2′′. We indicate the median value of each distribution ( |
For the early-type galaxy population, the average lensing optical depth for a perfect survey is 3.994 × 10-3 (3.747 × 10-3 for the SIE lens model), and this is only a few percent lower for the Gaia survey, that is, 3.917 × 10-3 (3.663 × 10-3). For seeing-limited ground-based surveys, however, about one-third of the lensed sources are unresolved, with the mean lensing optical depth dropping to 2.718 × 10-3(2.431 × 10-3). Considering the estimated number of 6.64 × 105 sources to be detected by the Gaia survey, there are thus 2653 (2490) expected lensed sources, out of which 2602 (2433) should be detected by the Gaia survey. On the other hand, the seeing-limited ground-based follow-up of the lensing events will only be possible for 1806 (1615) of these sources, unless adaptive optics observations are made possible using large telescopes.
Although the late-type galaxy populations are more numerous, they are less efficient deflectors because of their lower mass. For the Gaia survey, the average lensing optical depth due to the late-type galaxy population is 0.84 × 10-3 (0.68 × 10-3 for the SIE lens model), but because they tend to form lensing events with lensed images closer to one another, they represent a negligeable fraction for typical seeing-limited ground-based observations. This deflector population is expected to lead to the formation of 558 (453 for the SIE lens model) multiply imaged quasars.
In conclusion, combining the expectation for the early- and late-type galaxy populations, the Gaia survey is expected to lead to the detection of 3160 (2886 for the SIE lens model) multiply imaged quasars.
These results are consistent with a former simplified estimate of the number of gravitational lens systems to be detected by Gaia by Finet et al. (2012), who found ⟨τ⟩ = 5.9 × 10-3 for the SIS deflectors without taking into account the finite instrument resolution and considering only the population of early-type galaxies. The authors used a flat FLRW universe with Ωm = 0.27 and H0 = 72 km s-1 Mpc-1. Considering the same universe model and a perfect instrument, we find ⟨τSIS⟩ = 4.3 × 10-3. The slight differences probably arise because they considered sources as bright as G = 15 to be affected by a larger amplification bias and a redshift range up to z = 5, which slightly overestimates the very high redshift sources that have a higher optical depth.
⟨τSIS⟩and ⟨τSIE⟩ lead to a very similar estimate of the number of lensed sources to be detected and show a similar behavior as a function of the angular resolution parameter θmin, as seen in Fig. 4. Nevertheless, the SIS model leads to a lensing optical depth estimate about 10% higher than that of the SIE model. This is because the SIE mass distribution, initially introduced to conserve the projected mass inside iso-density curves with respect to the SIS case (Kormann et al. 1994), does not preserve the size of the geometrical cross section, that is, the area inside the caustics. For very elliptical deflectors, the geometrical cross section of the SIE deflector is smaller than that of the SIS because the radial caustic curve flattens when the ellipticity increases. Furthermore, the probability for a lensed source to have a given total amplification is different for the two mass distributions, thus leading to a different amplification bias effect (Huterer et al. 2005).
Figure 4 shows that of the gravitationally lensed sources, the configurations with two detected images are the most likely. Furthermore, the fraction of events with two lensed images increases as θmin increases, from 91.7% for a perfect survey to 94.8% for θmin = 0.6′′ (cfr Table 1) for the early-type galaxy deflectors, because some configurations with three or four formed images have only two resolved images. We see a similar behavior for the results considering the late-type deflectors. We represent in Fig. 4 the evolution of the fraction of events with three or four detected lensed images as a function of θmin. From Table 1, considering the early-type galaxy deflectors, we see that 204 lensed sources are expected to be composed of four lensed images (three with three lensed images), but because of the limited angular resolution of the satellite, only 134 (62) are expected to be detected with four (three) observable lensed images. Of these, 75 (9) lensing events with three (four) lensed images will be observable by means of seeing-limited ground-based observations, which will complement the times series and spectra acquired by the satellite. The late-type population is expected to lead to the formation of 57 events with more than two lensed images among the lensed sources in the Gaia survey, none of which could be detected in a seeing-limited ground-based survey.
The lensed sources to be detected by the Gaia mission will thus constitute an unprecedented statistical sample, at least an order of magnitude larger than the existing ones, such as the ground-based SDSS Quasar Lens Search sample (62 lensed sources, 26 in the statistical sample, see Inada et al. 2012) or the 13 lenses from the CLASS statistical sample (Browne et al. 2003).
In the left panel of Fig. 5, we show the expected normalized redshift distributions of the lensed sources  and of the deflectors
and of the deflectors 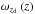 . We computed these distributions using Eqs. (17) and (18), assuming the typical angular resolution of Gaia θmin = 0.2′′. For the normalized deflector redshift distribution, we represent the expected distributions for the early- and the late-type deflector populations. For comparison, we represent the normalized redshift distribution of the sources (ωQSO) obtained by integrating
. We computed these distributions using Eqs. (17) and (18), assuming the typical angular resolution of Gaia θmin = 0.2′′. For the normalized deflector redshift distribution, we represent the expected distributions for the early- and the late-type deflector populations. For comparison, we represent the normalized redshift distribution of the sources (ωQSO) obtained by integrating  over M. As the latter is a normalized joint distribution, its marginal distribution ωQSO is normalized as well.
over M. As the latter is a normalized joint distribution, its marginal distribution ωQSO is normalized as well.
 |
Fig. 6 Left: normalized redshift distribution of the deflectors |
We also indicate the median value of each distribution ( ,
, 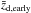 ,
,  and
and  ). We clearly observe a shift for the lensed population toward higher redshifts compared to the entire population of QSOs, with a distribution shifting from
). We clearly observe a shift for the lensed population toward higher redshifts compared to the entire population of QSOs, with a distribution shifting from  to
to  . This is mainly explained by the increase in geometrical lensing volume with the source redshift, which introduces a favorable bias toward sources located farther away. The shape of ωzs is also influenced by the amplification bias, which in our case favors low-redshift sources. Because these sources have on average a brighter apparent magnitude (than those with a higher redshift), their amplification bias calculated through Eq. (4) is larger because of the steeper slope of the DNCF for these magnitudes.
. This is mainly explained by the increase in geometrical lensing volume with the source redshift, which introduces a favorable bias toward sources located farther away. The shape of ωzs is also influenced by the amplification bias, which in our case favors low-redshift sources. Because these sources have on average a brighter apparent magnitude (than those with a higher redshift), their amplification bias calculated through Eq. (4) is larger because of the steeper slope of the DNCF for these magnitudes.
The normalized redshift distributions of the deflectors are different for the early- and the late-type galaxy deflectors. For a perfect instrument (i.e., θmin = 0′′), these distributions would be identical, as demonstrated in Appendix B. But in this simulation we considered θmin = 0.2′′. This excludes lensing events with lensed images whose image separation is too small. Therefore, the fraction of rejected lensing events is higher for the late-type galaxy population. Furthermore, for a given source redshift, the first lensing events to be rejected are those with a higher deflector redshift (because the Einstein angular radius scales as  ). This leads to a normalized deflector redshift distribution that peaks at lower redshift for the late-type galaxy population.
). This leads to a normalized deflector redshift distribution that peaks at lower redshift for the late-type galaxy population.
The normalized distributions as a function of redshift of the lensed sources  and of the deflectors
and of the deflectors 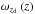 show no dependence on the chosen deflector model: both the SIS and SIE models lead to exactly the same distributions. Furthermore, the normalized redshift distribution of the lensed sources
show no dependence on the chosen deflector model: both the SIS and SIE models lead to exactly the same distributions. Furthermore, the normalized redshift distribution of the lensed sources  is identical when considering early- or late-type galaxy populations.
is identical when considering early- or late-type galaxy populations.
In the right panel of Fig. 5 we illustrate the normalized distribution  of the lensed sources as a function of their apparent magnitude computed from Eq. (19) for the SIS lens model. For comparison, we show the DNCF as a function of magnitude of all the detected sources, normalized by NQSO/ ΩGaia, the number of sources detected per solid angle in the magnitude range 16 <m< 20. The distribution of the lensed sources presents an excess of brighter sources, benefiting from the amplification bias. In our simulations, we found no effect of the angular resolution θmin on
of the lensed sources as a function of their apparent magnitude computed from Eq. (19) for the SIS lens model. For comparison, we show the DNCF as a function of magnitude of all the detected sources, normalized by NQSO/ ΩGaia, the number of sources detected per solid angle in the magnitude range 16 <m< 20. The distribution of the lensed sources presents an excess of brighter sources, benefiting from the amplification bias. In our simulations, we found no effect of the angular resolution θmin on  . Neither did we find differences between the ωm distributions when considering the early- and late-type deflector populations.
. Neither did we find differences between the ωm distributions when considering the early- and late-type deflector populations.
We now analyze the effect of the finite instrumental resolution on these different distributions. We showed that modeling the deflectors by means of the SIE and SIS mass distributions leads to exactly the same normalized distributions  and
and 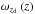 , therefore we only considered the SIS deflectors in the remaining part to minimize the computation time. In the left panel of Fig. 6 we display the normalized distribution of the deflectors
, therefore we only considered the SIS deflectors in the remaining part to minimize the computation time. In the left panel of Fig. 6 we display the normalized distribution of the deflectors 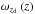 and its cumulative function as a function of the deflector redshift for three different values of the angular resolution θmin corresponding to the perfect instrument case, the Gaia mission, and typical ground-based observations.
and its cumulative function as a function of the deflector redshift for three different values of the angular resolution θmin corresponding to the perfect instrument case, the Gaia mission, and typical ground-based observations.
The normalized and cumulative distributions corresponding to θmin = 0′′ and θmin = 0.2′′ look similar. When compared to the ground-based observations (θmin = 0.6′′), we conclude that the effect of the loss in resolution power is to miss the lensing events with a deflector at higher redshift. This may be easily understood for the SIS case. An SIS deflector produces two lensed images separated by an angle equal to twice the Einstein angle θE. From the definition of the Einstein angle in Eq. (2), θE scales as  (27)For a source at a redshift zs,
(27)For a source at a redshift zs,  is a decreasing function of the deflector redshift, consequently, θE decreases as the deflector redshift zd increases, which will produce lensing events with images closer to each other, the first to be discarded as θmin increases.
is a decreasing function of the deflector redshift, consequently, θE decreases as the deflector redshift zd increases, which will produce lensing events with images closer to each other, the first to be discarded as θmin increases.
 |
Fig. 7 Left: average optical depth ⟨τ⟩ (considering all deflector types) as a function of cosmological matter density parameter Ωm, modeling the deflectors with the SIS and SIE models. Right: normalized redshift distributions ωzs and ωzd of the lensed sources and of the deflectors (for the early-type galaxy population) for different values of Ωm = 0,0.3 and 1. All simulations were produced for θmin = 0.2′′. |
We now consider the cumulative distribution as a function of the deflector redshifts. For simplicity, we only considered here the early-type galaxy population. For the ground-based observations, 90% of the observed lensed sources have a deflector with a redshift lower than z = 0.88. Most of the studies of the evolution effect in the deflector population based on lensing statistics are compatible with a no-evolution scenario or very little evolution of the deflectors (Oguri & Marshall 2010; Chae 2010; and Oguri et al. 2012). But it is very inefficient to use ground-based observations (from which most of the statistical samples of lenses are issued) to study the evolution of the deflector population because they cut out all lens systems with a deflector at high redshift and are thus only suitable for studying the low-redshift population (typically, z< 0.88).
For the Gaia mission, ~30% of the detected lenses that are due to the early-type galaxy population will have a deflector at a redshift higher than z> 0.88, that is, ~800 lenses assuming the 2433 lenses to be detected, and ~240 lensed sources will have a deflector in the redshift range 1.27 <zd< 2. The statistical sample of lenses to be unveiled by the Gaia mission will thus provide a sample that is very well suited for the evolution study of the population of early- and late-type galaxies at high redshift because of both the very large number of sources and the high angular resolution power with which the lensed sources are detected.
We also computed the normalized distribution  of the lensed sources as a function of redshift for different values of θmin. The angular resolution parameter θmin has no effect at all on
of the lensed sources as a function of redshift for different values of θmin. The angular resolution parameter θmin has no effect at all on  . This implies that the relative decrease in the lensing optical depth due to an increase in θmin is independent of the source redshift and absolute magnitude. To understand this, we computed the cumulative distribution of dτ/dzd normalized to the source optical depth for a perfect survey, that is,
. This implies that the relative decrease in the lensing optical depth due to an increase in θmin is independent of the source redshift and absolute magnitude. To understand this, we computed the cumulative distribution of dτ/dzd normalized to the source optical depth for a perfect survey, that is,  (28)The behavior of the cumulative distribution in Eq. (28) as a function of redshift is shown in Fig. 6. We show two different sources at redshift zs = 2 and 4, considering three different angular resolutions θmin = 0,0.6 and 1′′, and modeling the deflector with both the SIS and SIE deflectors. For clarity, we do not show the case for θmin = 0.2′′.
(28)The behavior of the cumulative distribution in Eq. (28) as a function of redshift is shown in Fig. 6. We show two different sources at redshift zs = 2 and 4, considering three different angular resolutions θmin = 0,0.6 and 1′′, and modeling the deflector with both the SIS and SIE deflectors. For clarity, we do not show the case for θmin = 0.2′′.
We first consider θmin = 0′′ (shown as a black dashed line). For this case, the normalized cumulative distributions are identical for the SIS and SIE cases. Because the distributions corresponding to the different zs differ, the differential contribution to the lensing optical depth is different for the two sources. Nevertheless, for the θmin = 0.6′′ instrumental resolution we observe that the fraction of the optical depth lost due to an increase in θmin is the same for zs = 2 and 4 for both the SIS and SIE cases. The fraction of the optical depth lost due to an increase in θmin is thus independent of redshift, or in other words, the ratio  (29)is independent of the source redshift. We computed the same distribution for sources with different apparent magnitudes and found no effect of the source magnitude on the distribution in Eq. (28).
(29)is independent of the source redshift. We computed the same distribution for sources with different apparent magnitudes and found no effect of the source magnitude on the distribution in Eq. (28).
As a consequence, the behavior as a function of θmin of the average optical depth ⟨τ⟩ can be computed by considering a perfect instrument and calculating the ratio in Eq. (29) for a source with a randomly chosen redshift and magnitude.
4.1. Effect of Ωm
In the left panel of Fig. 7 we show the evolution of the average lensing optical depth ⟨τ⟩ as a function of the cosmological matter density parameter Ωm, assuming a flat FLRW universe and considering the finite angular resolution θmin = 0.2′′ corresponding to the Gaia survey. We observe a very high dependence of the average optical depth as a function of Ωm with an order of magnitude difference between an empty universe and a universe full of matter (Ωm = 0 and 1, respectively). For this reason, using the fraction of lensed sources in a sample of sources has been proposed by Turner et al. (1984) to constrain the value of Ωm.
The observed behavior agrees very well when modeling the deflectors by means of the SIS and SIE deflectors, although the SIS model always slightly overestimates the lensing optical depth.
In our simulations for the SIE deflector, we observed no dependence as a function of Ωm of the relative fraction of lensing events on a given number of lensed images.
In the right panel of Fig. 7 we show the expected normalized redshift distribution of the lensed sources  and of the deflectors
and of the deflectors  for the three different values of Ωm = 0,0.3 and 1. For the sake of clarity, we only show the deflector redshift distribution corresponding to the early-type galaxy population, but the one associated with the late-type population presents a similar behavior. As previously mentioned, the obtained normalized redshift distributions ωzs and ωzd are identical for the SIS and SIE models. To minimize the computing time, we present the distributions obtained for the SIS model case.
for the three different values of Ωm = 0,0.3 and 1. For the sake of clarity, we only show the deflector redshift distribution corresponding to the early-type galaxy population, but the one associated with the late-type population presents a similar behavior. As previously mentioned, the obtained normalized redshift distributions ωzs and ωzd are identical for the SIS and SIE models. To minimize the computing time, we present the distributions obtained for the SIS model case.
Finally, in Fig. 8 we represent the normalized distribution ωθE as a function of Einstein angle θE of the lensed sources for different values of Ωm. These distributions were obtained with the help of Eq. (23). We considered the deflectors to be modeled with SIS deflectors and an angular resolution θmin = 0.2′′ corresponding to the Gaia survey. We find a very small dependence of  on the cosmological model parameter value.
on the cosmological model parameter value.
We also computed the normalized distribution  as a function of apparent magnitude m and found no effect of Ωm.
as a function of apparent magnitude m and found no effect of Ωm.
 |
Fig. 8 Effect of the cosmological matter density parameter Ωm on the normalized Einstein angular radius distribution |
5. Conclusions
Of the 6.64 × 105 QSOs that are brighter than G = 20 to be detected in the Gaia survey, we expect about 2886 to be multiply imaged sources and that 450 of these are produced by a late-type galaxy. We have modeled the deflector population by means of the SIE and SIS mass distributions and found both model predictions to agree very well, although the SIS model overestimates the mean lensing optical depth by ~10%. Most of the multiply imaged sources will be composed of two images, but we expect more than 250 lensed sources with more than two lensed images detected.
We expect only ~1600 of the multiply imaged quasars to have an angular separation between their images that is large enough to be resolved from seeing-limited observations (i.e., considering a ground-based survey without an adaptive optics system), allowing the acquisition of ground-based data to complement the spectra and time series provided by the satellite, ~80 of them having more than two lensed images detected.
We showed that lenses with a deflector at high redshift tend to be missed as the angular resolution of a survey becomes worse because these events are characterized by a smaller Einstein angular radius. Thanks to its angular resolution of θmin = 0.2′′, the lensed sources discovered in the Gaia survey will thus provide a unique statistical sample of lensed sources from which to study the evolution effects of the deflecting galaxy population, with the detection of ~800 lenses at a redshift between 0.8 and 2.
We did not consider the influence of the deflector environment, which may produce an additional shear and convergence to the gravitational potential. Oguri et al. (2005) have shown that the additional convergence produced by the galaxy environment may increase the lensing probability (especially at large angular separation) by boosting the image separation and amplification bias, mainly driven by convergence. Huterer et al. (2005) showed that the external shear increases the fraction of quads in a sample of lensed sources. Our estimate of the number of lenses to be discovered by Gaia may thus slightly underestimate the lenses and quads to be discovered. We also neglected multiple deflectors at different redhshifts because the probability for such an event would be on the order of ⟨τ⟩2 ~ 10-5, which is negligible compared to the lensing probability by a single deflector.
We computed the normalized redshift distributions of the lensed sources ωzs and of the deflectors ωzd and found that these normalized distributions are the same whether the deflectors are modeled by means of the SIS or the SIE mass distributions. The normalized deflector redshift distribution expected for the late-type galaxy population peaks at a higher redshift than that for the early-type one.
Furthermore, ωzs is independent of the angular resolution of the survey. As a consequence, we conclude that the fraction of the optical depth lost by a source when increasing θmin is independent of source redshift.
Finally, we analyzed the effect of the cosmological matter density parameter Ωm on the average lensing optical depth and on the distributions as a function of the redshift of the lensed sources and deflectors. We conclude that all three are sensitive to the cosmological model parameter value and may be used to constrain the cosmological model. We found no effect of Ωm on the fraction of lensed sources as a function of the number of lensed images or on the apparent magnitude distribution of the lensed sources.
References
- Browne, I. W. A., Wilkinson, P. N., Jackson, N. J. F., et al. 2003, MNRAS, 341, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, K.-H. 2010, MNRAS, 402, 2031 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, Y.-Y., Park, C., & Vogeley, M. S. 2007, ApJ, 658, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Finet, F., Elyiv, A., & Surdej, J. 2012, Mem. Soc. Astron. It., 83, 944 [NASA ADS] [Google Scholar]
- Harrison, D. L. 2011, Exp. Astron., 31, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Huterer, D., Keeton, C. R., & Ma, C.-P. 2005, ApJ, 624, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Inada, N., Oguri, M., Shin, M.-S., et al. 2012, AJ, 143, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Jordi, C., Høg, E., Brown, A. G. A., et al. 2006, MNRAS, 367, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keeton, C. R., Kochanek, C. S., & Falco, E. E. 1998, ApJ, 509, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S., Falco, E. E., Impey, C. D., et al. 2000, ApJ, 543, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmans, L. V. E., Treu, T., Bolton, A. S., Burles, S., & Moustakas, L. A. 2006, ApJ, 649, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmans, L. V. E., Bolton, A., Treu, T., et al. 2009, ApJ, 703, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Kormann, R., Schneider, P., & Bartelmann, M. 1994, A&A, 284, 285 [NASA ADS] [Google Scholar]
- Mignard, F. 2005, eds. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 5 [Google Scholar]
- Mignard, F. 2008, eds. C. Charbonnel, F. Combes, & R. Samadi, in SF2A-2008: Proc. Annual Meeting of the French Society of Astronomy and Astrophysics, 23 [Google Scholar]
- Mignard, F. 2012, Mem. Soc. Astron. It., 83, 918 [NASA ADS] [Google Scholar]
- Mitchell, J. L., Keeton, C. R., Frieman, J. A., & Sheth, R. K. 2005, ApJ, 622, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Nemiroff, R. J. 1989, ApJ, 341, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., & Marshall, P. J. 2010, MNRAS, 405, 2579 [NASA ADS] [Google Scholar]
- Oguri, M., Keeton, C. R., & Dalal, N. 2005, MNRAS, 364, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Inada, N., Strauss, M. A., et al. 2012, AJ, 143, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Palanque-Delabrouille, N., Magneville, C., Yèche, C., et al. 2013, A&A, 551, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peebles, P. 1993, Principles of Physical Cosmology (Princeton University Press) [Google Scholar]
- Richards, G. T., Croom, S. M., Anderson, S. F., et al. 2005, MNRAS, 360, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Strauss, M. A., Fan, X., et al. 2006, AJ, 131, 2766 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Luri, X., Reylé, C., et al. 2012, A&A, 543, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ross, N. P., McGreer, I. D., White, M., et al. 2013, ApJ, 773, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (Springer-Verlag) [Google Scholar]
- Shen, Y., & Kelly, B. C. 2012, ApJ, 746, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., Bernardi, M., Schechter, P. L., et al. 2003, ApJ, 594, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Slezak, E., & Mignard, F. 2007, Tech. Rep., Observatoire de la Côte d’Azur, GAIA-C2-TN-OCA-ES- 001-1 [Google Scholar]
- Sluse, D., Chantry, V., Magain, P., Courbin, F., & Meylan, G. 2012, A&A, 538, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, E. L., Ostriker, J. P., & Gott, J. R. 1984, ApJ, 284, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Gaia G-band K-correction and magnitude conversion
We here describe the different relations used to convert absolute magnitudes between the Gaia and the SDSS photometric systems.
We followed Richards et al. (2006) and express the absolute magnitudes M in the Gaia G-band as magnitudes of the continuum, with a zero point of the continuum K-correction at redshift z = 2. M is thus defined by  (A.1)where Kem is the contribution from the emission lines and Kcont,z = 2 the continuum K-correction with zero point at redshift z = 2.
(A.1)where Kem is the contribution from the emission lines and Kcont,z = 2 the continuum K-correction with zero point at redshift z = 2.
 |
Fig. A.1 K-correction in the Gaia photometric G-band as a function of redshift. We represent the total K-correction (K) with zero point of the continuum contribution at z = 2, the continuum contributions with zero points at z = 0 and z = 2 (Kcont and Kcont,z = 2), and the emission line contribution (Kem). |
To estimate the K-correction of the Gaia photometric G-band, we computed the correlation between the G-band spectral transmission function (in terms of wavelengths) with the QSO synthetic spectrum derived from SDSS QSO spectra by Vanden Berk et al. (2001). The synthetic spectrum ranging from 3800 to 9200 Å could not cover the entire wavelength range of the G filter (3210−11020 Å in the observer comoving reference frame). Because the synthetic spectrum was well fitted by a continuum spectrum with spectral index αν = −0.46 between the Ly-α and Hβ lines, and αν = −1.58 for wavelengths longer than the Hβ line (Vanden Berk et al. 2001), we extrapolated the synthetic spectrum toward longer wavelengths assuming a continuum spectrum with spectral index αν = −1.58.
We computed the contribution of the continuum to the K-correction assuming a break in the spectral index, considering the zero points of the K-Correction at z = 0 and z = 2, Kcont and Kcont,z = 2, respectively. The behavior of Kcont,z = 2 as a function of redshift is displayed in Fig. A.1.
Finally, the contribution to the apparent magnitude of the emission lines Kem is given by Kem = K−Kcont,z = 2. The computed K-correction is shown as a function of redshift in Fig. A.1.
To convert the absolute magnitudes Mi from the SDSS i-band to the Gaia G-band absolute magnitude M, we used the K-correction for the SDSS i-band given in Richards et al. (2006), the G-band K-correction previously described, and calculated an average apparent magnitude transformation between the Gaia G-magnitude and SDSS-i magnitude as follows: ![\appendix \setcounter{section}{1} \begin{eqnarray} \left <G-i\right >\left (z\right ) &=& -2.5 \log \left [\dfrac{\int\! S\left (\lambda \left (1 + z\right )\right ) T_{G}\left (\lambda\right ){\rm d}\lambda}{\int\! S\left (\lambda \left (1 + z\right )\right ) T_{i}\left (\lambda\right ) {\rm d}\lambda} \right ]\nonumber\\ &&+2.5 \log \left [\dfrac{\int\! \lambda^{-2} T_{G}\left (\lambda\right ){\rm d}\lambda}{\int\! \lambda^{-2} T_{i}\left (\lambda\right ){\rm d}\lambda} \right ], \end{eqnarray}](/articles/aa/full_html/2016/06/aa25411-14/aa25411-14-eq281.png) (A.2)where
(A.2)where  is the synthetic QSO spectrum from Vanden Berk et al. (2001),
is the synthetic QSO spectrum from Vanden Berk et al. (2001),  and
and  are the spectral transmission of the G and i bands, considering both magnitudes in the AB-magnitude system. The behavior of
are the spectral transmission of the G and i bands, considering both magnitudes in the AB-magnitude system. The behavior of  as a function of redshift is shown in Fig. A.2.
as a function of redshift is shown in Fig. A.2.
 |
Fig. A.2 Average color transformation |
The absolute magnitude average transformation is given by  (A.3)where
(A.3)where  and
and  are the K-corrections in the G- and SDSS i-band, respectively.
are the K-corrections in the G- and SDSS i-band, respectively.
Appendix B: ωzd dependence on the deflector type
In this appendix, we demonstrate that ωzd is independent of the deflector type under the assumption of constant deflector comoving density and a perfect instrument. For simplicity, we consider the case of deflectors modeled by an SIS mass distribution.
The expression of τSIS in Eq. (8) can be further developed by inserting the expression of  which, using the definition of θE in Eq. (2) and that of ΣSIS in Eq. (3), may be written as
which, using the definition of θE in Eq. (2) and that of ΣSIS in Eq. (3), may be written as  (B.1)Inserting the latter expression into Eq. (8) leads to
(B.1)Inserting the latter expression into Eq. (8) leads to  (B.2)where we defined
(B.2)where we defined  . The coefficient in brackets includes all the dependence on the parameters describing the VDFs (Φ∗,σ∗,α,β), which may refer to either early- or late-type galaxies. In our development, the deflector comoving density is assumed constant, therefore the VDF parameters do not depend on the redshift.
. The coefficient in brackets includes all the dependence on the parameters describing the VDFs (Φ∗,σ∗,α,β), which may refer to either early- or late-type galaxies. In our development, the deflector comoving density is assumed constant, therefore the VDF parameters do not depend on the redshift.
We may obtain an expression for  by differentiating the former expression of τSIS with respect to the deflector redshift z. The result is
by differentiating the former expression of τSIS with respect to the deflector redshift z. The result is ![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{{\rm d} \tau}{{\rm d}z}\left (z_{\rm s},z_{\rm d},M\right )& = & \left (\left (\dfrac{4 \pi \sigma_{\ast}^{2}}{c^{2}}\right )^{2} \beta\Phi_{\ast} \dfrac{\Gamma\left (\left (\alpha + 4\right )/\beta\right )}{\Gamma\left (\alpha/\beta\right )}\right )\nonumber\\[2.5mm] &&\times \zeta\left (z, z_{\rm s}\right ) \iint\limits_{S_{y}} B\left (m,\vec{y}\right ) {\rm d}\vec{y}. \label{eq_def_dtdzd} \end{eqnarray}](/articles/aa/full_html/2016/06/aa25411-14/aa25411-14-eq295.png) (B.3)For a perfect instrument, τSIS and
(B.3)For a perfect instrument, τSIS and  depend in an identical way on the VDF parameters, shown in the first factor of Eqs. (B.2) and (B.3). Therefore, when calculating the normalized redshift
depend in an identical way on the VDF parameters, shown in the first factor of Eqs. (B.2) and (B.3). Therefore, when calculating the normalized redshift
distribution of the deflectors by inserting Eqs. (B.2) and (B.3) into the definition of ωzd (Eq. (18)) and using the definition of ⟨τ⟩ (Eq. (16)), the factors containing the VDF parameters cancel each other out as long as we assume no redshift or absolute magnitude dependence of the VDF parameters. For a perfect instrument, ωzd is thus identical for early- and late-type galaxy deflectors because it does no longer depend on the parameters defining the deflector VDF (Φ∗,σ∗,α, and β).
However, when the finite angular resolution of the survey is taken into account, the integration area for the lensing cross section Sy is now a function of the ratio θmin/θ∗, with  . This dependence on σ∗ leads to different results for the two deflector types because this parameter differs for the early- and late-type galaxy VDF.
. This dependence on σ∗ leads to different results for the two deflector types because this parameter differs for the early- and late-type galaxy VDF.
All Tables
Comparison of the mean lensing optical depth and the expected number of detected multiply imaged quasars for different values of the survey angular resolution corresponding to a perfect survey (θmin = 0′′), Gaia (θmin = 0.2′′), and typical ground-based observations (θmin = 0.6′′).
All Figures
 |
Fig. 1 Luminosity function as a function of the absolute magnitude Mi in the SDSS i-band for different redshift bins. We have included the LF determined by Richards et al. (2005) and Palanque-Delabrouille et al. (2013) (converted to Mi magnitude). The different fitted models correspond to no contraints on the redshift behavior of M∗ and Φ∗ (dashed light gray line), to an evolution model for Φ∗ and M∗ is fitted freely (light gray line), and to M∗ and Φ∗ both constrained by an evolution model (continuous black line). The latter is the final evolution model chosen for the simulations, see main text for the full description. |
| In the text | |
 |
Fig. 2 Behavior of the LF Φ∗ and M∗ parameters as a function of the QSO redshift. The dark continuous line shows the fit model used in our simulations. The light gray markers show the best fit parameters for Φ∗ and M∗ when fitting the LF separately in each redshift bin, without any evolution model constraints. When constraining the evolution of the characteristic density, the best parameters are found to be log Φ∗ ,lowz = −5.85, αΦ∗ = −0.77 ± 0.31, and zref = 2.09 ± 0.28. |
| In the text | |
 |
Fig. 3 Left: joint probability density |
| In the text | |
 |
Fig. 4 Left: average lensing optical depth as a function of the survey angular resolution θmin for early- and late-type galaxy deflectors. We modeled the deflectors as SIS (⟨τSIS⟩-continuous black line) and SIE mass distributions (⟨τSIE⟩-continuous gray line). In the latter case, we also show the average optical depth with detection of two lensed images (⟨τSIE,2⟩ – dashed gray line). Right: fraction of lensed sources detected with three (light gray) or four (dark gray) lensed images as a function of θmin. The results for the case of early- and late-type galaxy deflectors are shown with continuous and dash-dotted lines, respectively. In both panels we indicate the typical value of θmin for the Gaia survey and typical seeing-limited ground-based observations. |
| In the text | |
 |
Fig. 5 Left: expected normalized distributions ω as a function of the redshift of the lensed sources (zs) and of the deflectors (zd). For comparison, we also include the normalized redshift distribution of the sources (ωQSO). The simulations were made assuming θmin = 0.2′′. We indicate the median value of each distribution ( |
| In the text | |
 |
Fig. 6 Left: normalized redshift distribution of the deflectors |
| In the text | |
 |
Fig. 7 Left: average optical depth ⟨τ⟩ (considering all deflector types) as a function of cosmological matter density parameter Ωm, modeling the deflectors with the SIS and SIE models. Right: normalized redshift distributions ωzs and ωzd of the lensed sources and of the deflectors (for the early-type galaxy population) for different values of Ωm = 0,0.3 and 1. All simulations were produced for θmin = 0.2′′. |
| In the text | |
 |
Fig. 8 Effect of the cosmological matter density parameter Ωm on the normalized Einstein angular radius distribution |
| In the text | |
 |
Fig. A.1 K-correction in the Gaia photometric G-band as a function of redshift. We represent the total K-correction (K) with zero point of the continuum contribution at z = 2, the continuum contributions with zero points at z = 0 and z = 2 (Kcont and Kcont,z = 2), and the emission line contribution (Kem). |
| In the text | |
 |
Fig. A.2 Average color transformation |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




