| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201526636 | |
| Published online | 18 April 2016 | |
Giant quiescent solar filament observed with high-resolution spectroscopy
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
e-mail:
ckuckein@aip.de
Received: 29 May 2015
Accepted: 6 March 2016
Aims. An extremely large filament was studied in various layers of the solar atmosphere. The inferred physical parameters and the morphological aspects are compared with smaller quiescent filaments.
Methods. A giant quiet-Sun filament was observed with the high-resolution Echelle spectrograph at the Vacuum Tower Telescope at Observatorio del Teide, Tenerife, Spain, on 2011 November 15. A mosaic of spectra (ten maps of 100″ × 182″) was recorded simultaneously in the chromospheric absorption lines Hα and Na i D2. Physical parameters of the filament plasma were derived using cloud model (CM) inversions and line core fits. The spectra were complemented with full-disk filtergrams (He i λ10830 Å, Hα, and Ca ii K) of the Chromospheric Telescope (ChroTel) and full-disk magnetograms of the Helioseismic and Magnetic Imager (HMI).
Results. The filament had extremely large linear dimensions (~817 arcsec), which corresponds to about 658 Mm along a great circle on the solar surface. A total amount of 175119 Hα contrast profiles were inverted using the CM approach. The inferred mean line-of-sight (LOS) velocity, Doppler width, and source function were similar to previous works of smaller quiescent filaments. However, the derived optical thickness was higher. LOS velocity trends inferred from the Hα line core fits were in accord but weaker than those obtained with CM inversions. Signatures of counter-streaming flows were detected in the filament. The largest brightening conglomerates in the line core of Na i D2 coincided well with small-scale magnetic fields as seen by HMI. Mixed magnetic polarities were detected close to the ends of barbs. The computation of photospheric horizontal flows based on HMI magnetograms revealed flow kernels with a size of 5–8 Mm and velocities of 0.30–0.45 km s-1 at the ends of the filament.
Conclusions. The physical properties of extremely large filaments are similar to their smaller counterparts, except for the optical thickness, which in our sample was found to be higher. We found that a part of the filament, which erupted the day before, is in the process of reestablishing its initial configuration.
Key words: Sun: filaments, prominences / Sun: chromosphere / Sun: activity / Sun: magnetic fields / methods: data analysis / techniques: spectroscopic
© ESO, 2016
1. Introduction
Filaments are still a puzzling topic in solar physics. Although many studies have been carried out in the past decades, new high-resolution observations open the door to a better understanding of this common solar phenomenon. Filaments are located in the corona, with their lower parts in the chromosphere. They appear as elongated dark features on the disk, whereas above the limb, they shine bright against the dark background of space and are called prominences. These two terms are often used interchangeably in literature. We can distinguish between three types of filaments: quiescent, intermediate, and active region (AR) filaments (e.g., Engvold 2015). The main difference among them depends on the magnetic flux density found around the filament. Active region filaments are found in areas of high magnetic flux density. In comparison, quiescent filaments are found outside of ARs, have much larger dimensions, and lie higher in the atmosphere (e.g., Aulanier & Démoulin 2003; Lites 2005) than AR filaments. The term intermediate filaments is used when no clear classification into quiescent or AR is possible.
In this study, we concentrate on quiescent filaments, which have been extensively studied in previous works by other authors. For a complete review of filaments we refer to Tandberg-Hanssen (1995), Mackay et al. (2010), Parenti (2014), and Vial & Engvold (2015). In almost all filaments an elongated main axis is identified, which is better known as the spine. In addition, small structures, which are called barbs, protrude from the spine toward both sides. Barbs appear to be rooted in the photosphere – among parasitic polarities (e.g., Martin 1998; Chae et al. 2005; López Ariste et al. 2006).
The typical length of filaments is between 60 and 600 Mm (Tandberg-Hanssen 1995). Nevertheless, larger filaments exist (>600 Mm) but are scarcely discussed in literature. In one of the few instances, Anderson & Martin (2005) showed that extraordinary long filament channels, which evolve into filaments, are formed by merging of smaller channels. The authors observed a channel that reached a maximum length of 160 heliographic degrees along the northern hemisphere. Whether the resulting filament, after merging, presents the same physical properties as the former smaller individual filaments is still unknown. Yazev & Khmyrov (1988) reported on a giant filament with an extension of up to 800 Mm. This particular aspect of extreme linear dimensions is the main driver for the present work.
Filaments are supported against gravity by magnetic field lines. Previous works favored a twisted magnetic field configuration (e.g., van Ballegooijen & Martens 1989; DeVore & Antiochos 2000; Guo et al. 2010; Kuckein et al. 2012; Yelles Chaouche et al. 2012), although non-twisted field scenarios also exist (e.g., Kippenhahn & Schlüter 1957). Following this argument, a giant helical structure can support an extremely large filament in the solar atmosphere. This structure is anchored tens of megameters below in the photosphere. The question that naturally arises is how stable such a filament is. Quiescent filaments are much more stable than their smaller AR counterparts and can survive for several weeks. Nevertheless, emerging and submerging flows as well as shearing motions close to the polarity inversion line are responsible for the destabilization of the filament, which often leads to flares or coronal mass ejections. As a consequence, a partial or complete eruption of the filament can occur.
The spectral line that is by far most frequently used to study the morphology of filaments is the chromospheric Hαλ6562.8 Å line. It reveals the smallest fine structure detected in filaments (e.g., Lin et al. 2005; Heinzel & Anzer 2006) and provides information about the chirality and mass flows (e.g., Martin 1998). Doppler shifts of the Hα line have been the key for retrieving line-of-sight (LOS) velocities in filaments. Martres et al. (1981) found that blueshifts (<4 km s-1) were long-lasting and localized in dark structures. Furthermore, high velocities (7 km s-1) were detected in transient events. Based on the observation that the highest Hα velocities were correlated to high-brightness horizontal gradients, Martres and collaborators concluded that the filament and surrounding bright regions are part of one dynamical and geometrical structure. Dynamical Hα fine structures of a quiescent filament were the topic studied by Mein et al. (1994). The filament is formed by an accumulation of tiny thin threads. The authors modeled these Hα threads, and the best fit between observed and simulated quantities was obtained for an optical thickness of τ0 = 0.2, a source function of S0 = 0.06, and a mean upward velocity of v0 = 1.7 km s-1. Observations of the Hα line in the red and blue wing revealed counter-streaming flows, that is, simultaneous flows in opposite directions, in the spine and barbs of filaments (Zirker et al. 1998). Velocities of individual knots of mass were in the range of 5–20 km s-1. Nevertheless, much higher velocities were detected when tracking individual knots observed in He ii 304 Å along a quiescent prominence. The typical inferred values were ~30 km s-1 with peaks of up to 75 km s-1 (Wang 1999).
A well-known method for inferring physical parameters from the Hα line is the cloud model (CM) inversion technique developed by Beckers (1964). This relatively simple model assumes a cloud of material suspended above the photosphere (the basic assumptions are discussed in Sect. 3.3). Various properties such as the optical thickness, LOS velocity, Doppler width, and source function can be obtained from inverting the contrast profiles derived from the Hα line. For instance, Maltby (1976) applied CM inversions to filament features. The author found up- and downflows on the order of few km s-1 in the filament. Using the first-order differential cloud model (DCM), Schmieder et al. (1991) detected high velocities of up to ± 15 km s-1 at the footpoints of the filament. Beckers’s CM technique was used by Chae et al. (2006) to infer the physical parameters of a quiescent filament observed at Big Bear Solar Observatory. Two-dimensional maps of the parameters were computed. If the contrast was high enough, the Hα contrast profiles were correctly fitted. The authors concluded that the LOS velocities retrieved by CM inversions are much more reasonable than those obtained by the line core fits.
It has not been studied whether the optical thickness and the length of the filament are correlated. Chae et al. (2006) and Schmieder et al. (2003) used CM inversions to retrieve the optical thickness in filaments that are relatively small compared to the one we study here. The authors reported optical thickness values of 0.83 ± 0.47 and 0.66, respectively.
Improved CM versions have been used to examine other chromospheric features, including fibrils (e.g., Bray 1974), arch filaments (e.g., Alissandrakis et al. 1990), mottles (e.g., Bray 1973), and surges (e.g., Gu et al. 1994). Tziotziou (2007) reviewed the different CM inversion techniques and their application to various chromospheric features.
Another chromospheric line, the Na i D2 line at λ5890 Å, has been used for plasma diagnostics in prominences. For instance, Landman (1983) computed line ratios of this line and other lines to derive physical parameters such as the prominence electron density. The sodium line is optically thin in prominences and is commonly studied together with the neighboring Na i D1 line at λ5896 Å (Landman 1981). Observations revealed that most prominences with significant emission in Na i D2 and Mg b had pronounced centrally reversed Hα profiles (Stellmacher & Wiehr 2005).
 |
Fig. 1 Limb-darkening-corrected Hα full-disk image obtained with ChroTel on 2011 November 15 (top). Full-disk SDO/HMI magnetogram scaled between ±100 G (bottom). The rectangular contours outline the regions scanned with the Echelle spectrograph of the VTT. |
 |
Fig. 2 Hα profile acquired with the Echelle spectrograph at the VTT. The profile belongs to the spine of the filament and is located at label b in Fig. 3. The shaded area represents the spectral range used to compute the contrast profiles. |
In summary, there have been numerous studies looking at the plasma properties of quiescent filaments either by observations or modeling. The motivation of this work is to examine these properties in an uncommonly large quiescent filament that covered half of the solar disk based on simultaneous observations in the Hα and Na i D2 spectral lines (see Fig. 1). Preliminary results were presented by Kuckein et al. (2014). In Sect. 4 we focus on the results of CM inversions and additionally compute the Doppler shifts to compare the two methods for the Hα line. Furthermore, using magnetograms, we identify magnetic features below the barbs of the filament and additionally compute photospheric horizontal motions in search of converging flows.
2. Observations
The giant filament was already present on the backside of the Sun before rotating to the front side. The leading extremity of the filament became visible between 2011 November 8–9 at the eastern solar limb. The filament was continuously present during its disk passage until November 22, when it lifted off as part of a coronal mass ejection (CME) at the western solar limb. The dynamical aspects of this filament were discussed in Diercke (2014), and a peer-reviewed publication is forthcoming.
The high-resolution ground-based observations of the giant quiescent filament were acquired on 2011 November 15 with the Echelle spectrograph of the German Vacuum Tower Telescope (VTT, von der Lühe 1998) at the Observatorio del Teide, Tenerife, Spain. The very good seeing conditions facilitated scanning the whole filament from east to west across the northern hemisphere of the Sun. The observing strategy was to divide the filament into ten pieces with a scanned area of 100″ × 182″ each. Consecutive scans with a duration of ~10 min overlapped, ensuring the continuity of the filament in the reconstructed mosaic. The scanning device is an integral part of the Kiepenheuer-Institute Adaptive Optics System (KAOS, Berkefeld et al. 2010) at the VTT. The lock-point of KAOS was in the center of the scanned area, and the whole filament was scanned piecewise with a spatial step of 0.32′′ between 11:38 and 13:20 UT. The extreme points of the filament were located at heliographic coordinates (35° East, 37° North) and (18° West, 11° North). The filament length was roughly 817′′.
Two PCO.4000 CCD cameras were mounted at the Echelle spectrograph to record simultaneously spectra in two different spectral regions: (1) the chromospheric Hα line at λ6562.8 Å within a spectral range of 8 Å (see Fig. 2), and (2) the Na i D2 line at λ5889.9 Å within a spectral range of 7 Å. The spectral sampling was 4.2 and 3.6 mÅ pixel-1, respectively. The pixel size along the slit was 0.16′′, which was half the spatial step when scanning the solar surface. Exposure times were 600 ms. The rms noise in the spectra was about 1.2% in terms of the continuum intensity. The mosaics in Fig. 3 were each assembled from ten slit-reconstructed images displaying the intensity at different wavelengths: Hα + 0.5 Å, Hα line core, Hα−0.5 Å, and Na i D2 line core.
In addition to the spectroscopic observations, full-disk images of the Chromospheric Telescope (ChroTel, Bethge et al. 2011), mounted on the flat roof of the VTT building, were used in this study. ChroTel acquires images at several chromospheric wavelengths (Hαλ6563 Å, He i λ10830 Å, and Ca ii K λ3933 Å) with a cadence of 3 min. Furthermore, full-disk magnetograms of the Helioseismic and Magnetic Imager (HMI, Schou et al. 2012) onboard the Solar Dynamics Observatory (SDO, Pesnell et al. 2012) were used to interpret the spectra in the context of the photospheric magnetic field.
 |
Fig. 3 Large filament represented as a mosaic of ten individual slit-reconstructed images centered on Hα + 0.5 Å, Hα line core, Hα−0.5 Å, and Na i D2 line core (top to bottom). We number the maps from left to right (1–10). The labels a–d indicate the locations of the contrast profiles shown in Fig. 5. |
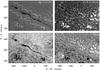 |
Fig. 4 Region-of-interest cropped from ChroTel and HMI full-disk images around 12:30 UT showing Hα, Ca ii K, and He i line core intensity images, and a time-averaged (11:30–13:20 UT) HMI magnetogram (top left to bottom right). The magnetogram is clipped between ±30 G. The step-function-like contours in the Hα and HMI panels outline the mosaic of the Echelle spectrograph observations (see Fig. 3). Intensity thresholding of the Hα filament and subsequent morphological dilation was used to create the generous contours of the filament in the Ca ii K and HMI panels. |
Standard image reduction procedures were carried out for Echelle spectra and ChroTel images including dark and flat-field corrections. The Echelle spectrum was normalized to the continuum using the Fourier Transform Spectrometer (FTS) spectrum from the Kitt Peak National Observatory (Neckel & Labs 1984). In addition, ChroTel images were corrected for limb darkening. The ChroTel Hα full-disk image is presented in Fig. 1 along with an HMI magnetogram. The extremely long filament clearly followed the magnetic polarity inversion line (PIL), which is faintly seen in the magnetogram. A more detailed magnetogram underlying the filament is shown in Fig. 4.
3. Data analysis
High-resolution spectroscopic observations of giant filaments are rare considering the time needed to scan a structure with a size comparable to the solar radius and the excellent seeing conditions required for a good performance of the adaptic optics system. In the following, we describe the morphology of this filament and derive the Doppler velocities from Hα and Na i D2 line shifts. Furthermore, we focus on the Hα line and use CM inversions to infer some of the filament plasma properties.
3.1. Morphological description
This filament is made special by its huge linear dimension. The Hα filtergram in Fig. 3 shows that the filament has a linear extension of ~817′′, which corresponds to about 658 Mm along a great circle on the solar surface. In the following, positions are given in heliocentric coordinates as provided on the axes of Fig. 3. Close to its eastern end, the filament has a gap between 300′′ E and 250′′ E. The gap is even larger in the He i image depicted in Fig. 4, and it is located where the filament is broadest. Multi-wavelength time-lapse movies from the Atmospheric Imaging Assembly (AIA, Lemen et al. 2012) show a filament eruption on 2011 November 14 at this location, which was associated with a non-geoeffective CME. Thin threads, visible in both Hα and He i, fan out from both edges of the gap and indicate that the filament returns to its original condition, when it was still a single structure.
This filament exhibits two structural components: the spine and barbs. The slit-reconstructed Hα line core image in Fig. 3 clearly shows the spine of the filament between 150′′ E and 125′′ W as well as several barbs, which are threads that protrude from the main axis (see, e.g., labels c and d). The same structure is also visible in the He i line core image in Fig. 4. By contrast, the filament is barely seen in the Ca ii K line core image in Fig. 4, although some absorption is detected along the spine. Surprisingly, there is Ca ii K absorption in the gap between both filament portions, supporting the notion that plasma is again filling up the filament channel.
HMI magnetograms were used to obtain information about the photospheric magnetic field below the filament. Quiescent filaments are found outside of active regions. Hence, the magnetic signal below and in the close surroundings of the filament is very weak. For this reason, a deep magnetogram was composed, which is presented in Fig. 4. All 45-second-cadence magnetograms between 11:30 and 13:20 UT were corrected for differential rotation and then averaged. Assuming that field lines in the quiet Sun are perpendicular to the surface, the magnetic field was corrected for LOS projection effects by dividing the magnetogram by μ = cosθ, where θ is the heliocentric angle. Clipping the magnetogram between ± 30 G reveals that the filament tightly follows the PIL. The polarities begin to mix at the PIL at the left end of the more extended portion of the filament (~250′′ E). A small bipolar emerging flux region (EFR) is present at around 225′′ N and 150′′ W, which is close to the right end of the filament. The EFR appears bright in the Hα mosaic. This does not imply that the Hα line was in emission, however, it only means that the line core is substantially shallower and also that the line wing is enhanced compared to line profiles belonging to the quiet Sun. In comparison, the He i line core image in Fig. 4 reveals strong absorption at the same location.
The spine of the filament is visible in the off-band slit-reconstructed images at Hα ± 0.5 Å depicted in Fig. 3. Interestingly, the spine is seen in both off-band images. Thus, the Hα line profile is very broad in this area of the filament. This distinct characteristic is also easily recognizable in contrast profiles belonging to the spine, for example, the one labeled b in Fig. 5. This contrast profile stands out because of its broad and deep shape. The Hα line-wing mosaics also reveal information about the Doppler line shifts. The barb labeled d appears prominently in the Hα + 0.5 Å image, whereas it is very faint in the Hα−0.5 Å image. Consequently, the spectra belonging to this barb are mainly redshifted. Nevertheless, inside the barb, adjacent dark features, which are either seen in the Hα + 0.5 Å or in the Hα−0.5 Å images, are consistent with counter-streaming flows, as has been reported by Diercke (2014) using SDO/AIA data of the same filament. Many but not all barbs show a similar behavior. For example, the barb at 175′′ E is darker in the Hα−0.5 Å image than in the Hα + 0.5 Å image. Thus, this area of the filament is blueshifted. These findings are compared with the inferred velocities from the CM in Sect. 4.2.
Brightenings accompany the filament on both sides in the Na i D2 mosaic. A comparison with the HMI magnetograms reveals that at least the largest conglomerates of brightenings coincide with small-scale magnetic fields. Hence, these brightenings can be used as a tracer of the magnetic field. In the Na i D2 line core images, no signs of the spine or of the barbs are apparent.
3.2. Line-of-sight Hα and Na I D2 velocities
Doppler shifts of the Hα and Na i D2 line cores were derived by using a least-squares parabola fit. On average, the selected width of the broad Hα line core for the parabola fit spanned ~750 mÅ. A smoothing over 8 pixels in the spectral dimension was performed twice. Because the Hα line originates in the chromosphere, it is not affected by the convective blueshift. Thus, the assumption that up- and downflows are balanced in the quiet-Sun chromosphere is justified to establish a reference for the inferred Doppler velocities.
The Na i D2 line contains a noticeable line-blend between the core and the blue wing. Therefore, we used a narrower region around the line core (~145 mÅ) to derive the Doppler velocities. Previous to the parabola fit, we slightly smoothed the spectra. For this purpose, we used a finer method than was applied to the Hα line that consisted of a convolution with a normalized Gaussian with a FWHM of 17 mÅ. The Na i D2 reference line-center position is also the average position of all quiet-Sun profiles within one map. Since the filament covers such a large area on the Sun, global velocity gradients were removed by subtracting a linear fit from each of the ten velocity maps. This effect was negligible for the Hα line, which in general showed larger Doppler shifts. Hence, the subtraction was only made for the velocities inferred from the Na i D2 line.
 |
Fig. 5 Four selected Hα contrast profiles. The dots represent the observed contrast profiles, while the solid line shows the best fit from the CM inversion. Panels a) and b) belong to very opaque regions of the filament seen in Hα, whereas panels c) and d) belong to the barbs of the filament. The exact locations are indicated in Fig. 3. |
3.3. Cloud model inversions
In his seminal work, Beckers (1964) introduced the cloud model to analyze spicules observed in Hα. This approach can also be applied to Hα spectra of filaments or any type of feature exhibiting clouds of absorbing plasma in the chromosphere (see also Tziotziou 2007, for a review on CM inversion techniques). As in spicules, there is a significant difference between the contrast of Hα intensity profiles inside and in the surroundings of filaments. This property can be used to solve the radiative transfer equation in a simplified manner. The three CM assumptions are that (1) the physical parameters are constant in height; (2) the source function S does not depend on the wavelength; and (3) the line absorption coefficient has a Gaussian behavior. Under these circumstances, the radiative transfer equation can be written as ![\begin{equation} \label{eq:rt} C(\lambda) \equiv \frac{I(\lambda) - I_0(\lambda)}{I_0(\lambda)} = \left(\frac{S}{I_0(\lambda)} - 1 \right) \Big[1 - \exp\Big(-\tau(\lambda)\Big)\Big], \end{equation}](/articles/aa/full_html/2016/05/aa26636-15/aa26636-15-eq38.png) (1)where C(λ) is the contrast profile, I(λ) is an observed spectral profile, I0(λ) is the mean quiet-Sun spectral profile, S the average source function of the cloud, and τ(λ) is defined as
(1)where C(λ) is the contrast profile, I(λ) is an observed spectral profile, I0(λ) is the mean quiet-Sun spectral profile, S the average source function of the cloud, and τ(λ) is defined as 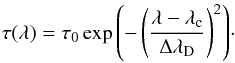 (2)The optical thickness of the cloud is constant and denoted by τ0. The parameters inside the brackets in Eq. (2) are the central wavelength λc and the Doppler width ΔλD of the line. The LOS velocity of the absorbing cloud material can be derived as
(2)The optical thickness of the cloud is constant and denoted by τ0. The parameters inside the brackets in Eq. (2) are the central wavelength λc and the Doppler width ΔλD of the line. The LOS velocity of the absorbing cloud material can be derived as 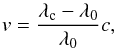 (3)where λ0 is the central wavelength of the Hα line and c the speed of light.
(3)where λ0 is the central wavelength of the Hα line and c the speed of light.
The contrast profiles C(λ) can be calculated for each pixel using the mean quiet-Sun profile I0(λ) and the observed intensity profile I(λ). For this purpose, a smaller spectral range was selected, which widely covered the Hα line. The spectral range is indicated by the shaded area in Fig. 2. The observed profiles I(λ) were convolved with a normalized Gaussian (FWHM = 9.8 mÅ) to slightly smooth the profiles. For the quiet-Sun profile, only pixels with low-contrast Hα structures were selected. These spectra were aligned with respect to an arbitrary spectrum to avoid line broadening, and then the mean quiet-Sun profile was computed. Four examples of contrast profiles are presented in Fig. 5. Their exact location is indicated by labels a–d in Fig. 3. The number of spectral points was reduced to 79 by employing a ten-pixel binning (dots in Fig. 5). The trimmed-down number of spectral points is still sufficient for reliable CM fits.
The aim of CM inversions is to fit each contrast profile C(λ) by modifying the four parameters of Eq. (1): τ0, v, ΔλD, and S. To increase the efficiency and improve the convergence of the fitting algorithm, it is necessary to provide a reasonable initial estimate of the input parameters. A data base of 50 000 contrast profiles was created subject to the following limits for the randomly chosen input parameters: τ0 ∈ [ 0,3 ], v ∈ [ −38,38 ] km s-1, ΔλD ∈ [ 0.08,0.70 ] Å, and S ∈ [ 0,0.4 ]. These limits were based on former cloud-model studies regarding filaments (e.g., Alissandrakis et al. 1990; Chae et al. 2006). Each observed contrast profile is cross-checked against the templates in the data base, and the parameters yielding the lowest χ2-value are selected for Levenberg-Marquardt least-squares minimization (Moré 1977). The solid lines in Fig. 5 represent the best fits to the respective Hα contrast profiles. The fit parameters are given in Table 1.
 |
Fig. 6 Mosaic of Hα (top) and Na i D2 (bottom) Doppler velocities corresponding to the slit-reconstructed images in Fig. 3. The velocities were inferred from the line core fits. The mosaics were rotated to place the filament in a horizontal position. The superimposed black contours mark the outer boundaries of the filament as seen in Hα line core images. Doppler velocities were clipped between ±2 km s-1. |
Hα and Na i D2 average LOS velocities (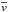 ), standard deviation (σ), and number of points (#) used for the statistics.
), standard deviation (σ), and number of points (#) used for the statistics.
4. Results
Velocity patterns and morphological changes characterize the evolution of (large-scale) filaments. Therefore, we first present the LOS velocities based on spectral line profiles to retrieve the plasma properties for chromospheric features. In addition to this, we show the physical parameters inferred from the CM inversions and compare them with previous works of smaller filaments. The coupling between the barbs of the filament and the underlying magnetic field is analyzed using HMI magnetograms. Finally, photospheric horizontal proper motions provide information of the flows below the filament.
4.1. Line-of-sight velocities
A map of the LOS velocities inferred from the line core fits is shown in Fig. 6. The smooth black contour generously outlines the border of the filament. In the upper (lower) panel, the velocities retrieved from the Hα (Na i D2) Doppler shifts are shown clipped between ± 2 km s-1. For Hα, the spine of the filament exhibits blueshifts as a general trend, that is, upward flows. This is also confirmed when calculating the average Doppler shifts along all the spine (maps 5–7), as presented in Table 2. On average, the spine moves upward at −0.288 km s-1. The average LOS velocity of the whole filament is also blueshifted (−0.225 km s-1), which can be seen in the upper left panel of the histogram in Fig. 7. The average quiet-Sun velocity frequency distribution was computed using maps 1–3 (excluding pixels belonging to dark structures of the filament and bright points seen in the Na i D2 line core image for both lines) and has an approximately Gaussian shape (lower-left panel in Fig. 7). Its average value is slightly blueshifted, yielding −0.07 km s-1. Interestingly, the right-hand gap of the filament does not show significant changes in velocity. If the Hα contours were to be removed, it would not be possible to distinguish the gap. In contrast, this is not the case for the left-hand gap, which is much larger because the velocities show a different pattern than at the spine.
 |
Fig. 7 Frequency distributions of the Doppler velocities inferred from the line core fits of the Hα (left) and Na i D2 (right) lines in the filament (top) and in the quiet Sun (bottom). The bin size is 0.2 km s-1. |
The average LOS velocities inferred from the Na i D2 Doppler shifts inside the filament are one order of magnitude lower (−0.023 km s-1) than those of Hα . The Na i D2 line seems not to be greatly affected by the filament. Another piece of evidence for this is that no alteration of the velocity pattern caused by the filament can be seen in Fig. 6 (bottom panel). The velocity histograms on the right-hand side of Fig. 7 reveal that the range of velocities is approximately a factor of 2 smaller than for Hα.
4.2. Cloud model results
A total of 175 322 Hα contrast profiles that covered the giant filament region were subjected to CM inversions as described in the previous section. After rejecting failed inversions, 175119 were left for the statistical analysis. The present study is statistically more complete than previous works because of the large amount of inverted contrast profiles. The most common type of contrast profiles typically have an !-like shape (see Fig. 5). When computing a correlation among all contrast profiles and considering that their correlation has to reach at least 95%, up to 42.7% show an !-like shape. The second most common type (37.1%) is similar to the !-like shape, but without the central hump. The !-like-shaped contrast profiles dominate but are not exclusively present in the filament spine, that is, in the second half of map 5 and along maps 6 and 7 (see Fig. 3). Interestingly, barbs c and d are also dominated by the most common type of contrast profiles. However, the barb-like structures seen in map 5 are more widely populated by the second most common type of contrast profiles. The other parts of the filament do not have a clear tendency toward a specific type of contrast-profile shapes. Variations of the Hα profiles caused by unresolved counter-streaming flows might slightly modify some shapes of contrast profiles. In the sample, the depth of the contrast profiles can reach up to C(λ) = −0.65.
Figure 5 illustrates that contrast profiles belonging to the darkest Hα filament structures (profiles a and b) are deeper than those belonging to the threads of the filament (profiles c and d). The inferred physical parameters for these profiles a and b are shown in Table 1. The darker profiles a and b show consistently higher values of the optical thickness than the threads, 2.97 and 2.77, respectively.
 |
Fig. 8 From top to bottom, maps of Doppler width ΔλD, optical thickness τ0, LOS velocity v, and source function S of the filament inferred from the Hα CM inversions. |
The parameters retrieved from the CM inversions are presented in Fig. 8. The maps reveal that the parameters are not uniformly distributed along the filament. There is a good correlation between the LOS velocities and the Hα ± 0.5 Å intensity maps displayed in Fig. 3. For instance, barb d appears dark in the Hα + 0.5 Å image. As a consequence, this thread appears mainly redshifted in the inferred velocity map. Indeed, the inferred CM value yields 4.41 km s-1 (see Table 1). Hence, material is flowing downward, although some minority upward trend is also seen. Yet not all barbs show the same behavior. The group of barbs left to barb c (map 5 in Fig. 3) is more dominated by blueshifts. Therefore, we cannot conclude from this giant filament whether barbs systematically contribute to mass supply or loss of filaments. Counter-streaming flows inside barbs are good candidates to explain this behavior.
The Hα ± 0.5 Å intensities reveal information about the line shifts. Patches with antiparallel directions of the LOS velocities occur in close proximity. A possible explanation are waves that move along the filament, similar to the vertical oscillatory motions found by Okamoto et al. (2007). However, in the absence of time-series data, this hypothesis cannot be confirmed.
Histograms of optical thickness, LOS velocity, Doppler width, and source function are shown in Fig. 9. The histograms were computed independently for each scan and then added to present statistics over the whole filament. There was always an overlap between one map and the following while scanning the filament, which introduces data points that were counted twice. However, although the overlapped areas were co-spatial, they were not scanned at the same time. Therefore, the information encoded in the contrast profiles is new.
Statistics of the Hα CM parameters.
 |
Fig. 9 Frequency distributions of the four CM parameters: optical thickness τ0, LOS velocity v, Doppler width ΔλD, and source function S (top left to bottom right). |
The histograms together with their statistics in Table 3 reveal some interesting facts that we compare to previous works from Schmieder et al. (2003) and Chae et al. (2006). These two studies included CM inversions of Hα contrast profiles in a smaller quiescent filament. At a first glance, the histograms of optical thickness and source function resemble a triangular shape, whereas the velocity and Doppler width have a Gaussian shape. The optical thickness has a mean value of 1.59, which is high compared to 0.66 and 0.83 ± 0.47 retrieved from the cloud model inversions with a constant source function by Schmieder et al. (2003) and Chae et al. (2006), respectively. The LOS velocity histogram is clearly centered at rest (~0.07 km s-1), with a quite large dispersion of σ = 2.46 km s-1. The dominant Doppler width values are in the range 0.36 and 0.42 Å, on average 0.39 Å, with a positive skewness. This range closely agrees with the two filaments studied by Schmieder et al. (2003) and Chae et al. (2006). The source function peaks at around 0.07, with negative skewness, which lies in between the values found by Schmieder et al. (2003) and Chae et al. (2006), 0.05 and 0.10, respectively.
Our results do not necessarily have to match the outcome of other works. On the one hand, the filament under study is peculiar because it has extraordinary linear dimensions and might also be in a different stage of its lifetime than the other two filaments. On the other hand, stray-light or different instrument profiles can affect the CM inversions, since they are sensitive to the line depth and shape. To test for these effects, we performed two additional CM inversions of map 6. In the first inversion we added 5% stray-light to the observed profiles, and in the second we convolved the observed profiles with a Gaussian (with a FWHM of 50 mÅ) simulating a different instrument, for instance, a Fabry-Pérot interferometer. We conclude that adding stray-light only affects the source function by increasing its value by the same amount as the added stray-light. All other CM parameters remain almost the same. When convolving with a Gaussian, we found an increase of ~3% of the mean optical thickness compared to the original inversions. The velocity trends were conserved. In conclusion, the inferred optical thickness can indeed be affected by different instrument profiles. However, we expect that within the above limitations, the retrieved mean value of the optical thickness can be compared among different instruments. In addition, the selection of a proper quiet-Sun profile is crucial (Bostanci & Al Erdoğan 2010) because it also affects the outcome of the CM inversions and can be of the same order of magnitude as additive stray-light or different instrument profiles.
4.3. Reconstituting the filament within the filament channel
On the left-hand side of the filament, a large gap is seen in the Hα and He i λ10830 Å images. The gap appeared after part of the filament erupted the day before. Remarkably, fine Hα threads that appeared at the edges of the gap were detected. These threads seemed to indicate that the filament was again filling up the gap with plasma. Hα filtergrams of the Kanzelhöhe Observatory from November 15 also showed dynamic plasma features appearing in the gap, mainly close to the edges. ChroTel filtergrams of the Ca ii K line confirmed this hypothesis as absorption of this line was detected inside the gap. We therefore suggest that the filament was in the process of reestablishing its initial configuration.
4.4. Coupling between barbs and the photospheric magnetic field
Is there evidence for a connection between the barbs of the filament and the underlying magnetograms from HMI? In the past, it has been reported that barbs are rooted in patches of minority polarity among the dominant polarity on each side of the filament (Martin 1998). In a later study, Chae et al. (2005) found evidence that barbs end at minor polarity inversion lines. Similarly, López Ariste et al. (2006) showed that the endpoints of barbs are next to parasitic polarity features.
To address this question, a thorough alignment among the slit-reconstructed Hα line core images and an averaged deep magnetogram was performed. The magnetic field below the filament was weak. To increase the signal, several magnetograms were corrected and averaged as described in Sect. 3. The magnetograms were chosen to match, in time and space, the 10 min scan of the VTT (a total amount of 14 images). To scrutinize very small magnetic fields close to the ends of barbs, we added 13 min before and after the VTT scan, increasing the number of magnetograms to 48 (~36 min). We note that the magnetic structures did not wash out or cancel each other when the number of images was increased from 14 to 48.
Bright features of the slit-reconstructed line core Na i D2 images and magnetic structures in the magnetograms are well correlated. Therefore, the Na i D2 images were used as an intermediate step for the alignment. The Hα and Na i D2 images are well aligned and only differ on a subpixel scale. Figure 10 shows the barbs as seen in the Hα line core corresponding to maps 6 and 7. Superimposed is the corresponding averaged HMI magnetogram with a blue (negative polarity) to red (positive polarity) color scale clipped at 25 G. The faintest magnetic structures have 2 G, while stronger fields (>25 G) appear saturated with white color. The filament is tightly confined by the stronger polarities, which lie on either side of the spine. Mixed polarities can be seen along the whole filament and even farther away. Interestingly, as reported by the aforementioned authors and more recently by Joshi et al. (2013), these mixed polarities also appear at some ends of barbs, for example, inside the white circle of the right-hand panel of Fig. 10. However, this does not occur everywhere and can therefore not be generalized to all barbs. We can at least confirm that this property is also present in extremely large filaments. In this particular case, the magnetogram shows fields of up to ~14 G inside the white circle.
 |
Fig. 10 Overview of the barbs from the filament seen in maps 6 and 7 of the slit-reconstructed Hα line core data from Fig. 3. Overlying is the HMI magnetogram clipped at 25 G. The color scale extends from blue (negative polarity) to red (positive polarity), and white represents saturated values. |
 |
Fig. 11 Frequency distributions for speed (left), divergence (middle), and vorticity (right) of horizontal proper motions computed by applying DAVE to HMI magnetograms. The number of points that went into the computation of the frequency distributions for the quiet Sun (solid line) and the filament (dash dotted) are nqs = 2 772 670 and nfil = 149 007, respectively. |
4.5. Horizontal proper motions
We computed the horizontal proper motions using LOS magnetograms from HMI. We took one-hour time-series of magnetograms centered on 12:22 UT. We applied the differential affine velocity estimator (DAVE; Schuck 2005, 2006) to geometrical foreshortening-corrected magnetograms to retrieve flow fields. After this correction the FOV of the magnetograms was 649 × 466 Mm. The code DAVE assumes an affine velocity profile, and the underling physics is based on the magnetic induction equation. The horizontal flows are estimated using temporal and spatial derivatives of the magnetic field. We used the Scharr (2007) kernel for the spatial derivatives, a five-point stencil for the temporal derivative, and a sampling window of 11 pixels (3.5 Mm; Balthasar et al. 2014) in computing the velocity by DAVE. The temporal derivatives were computed using a sliding average of 16 magnetograms that corresponded to 12 min. In the end, the velocities were averaged for an hour.
In the DAVE velocity map we observed regular, diverging supergranulation cells, as were previously seen by Magara & Kitai (1999), Rondi et al. (2007), and Schmieder et al. (2014) in velocity maps computed using photospheric continuum images. The mean quiet-Sun velocity of 0.096 ± 0.069 km s-1 is within the range given by Diercke (2014). In general, the divergence and vorticity based on flux-transport velocities are an order of magnitude larger than those derived from LCT measurements (Verma et al. 2012). The global properties of the quiet Sun and the photosphere below the observed filament are virtually the same. The respective frequency distributions for flow speed, divergence, and vorticity in Fig. 11 are almost identical. The velocity distribution can be approximated with a log-normal probability density function (PDF), and the divergence and vorticity distribution both obey Gaussian PDFs (centered on zero and with FWHM of 0.012 and 0.009 s-1, respectively). Any differences between quiet-Sun and filament distributions are most likely selection effects. For example, randomly picking an area of similar size as the filament region leads to comparable deviations of the frequency distributions. Only the EFR exhibits horizontal proper motions on larger scales, which are significantly different from the quiet-Sun flow field, meaning that they possess higher flow speeds and contain extended regions of positive divergence.
The likeness of photospheric horizontal flow fields for quiet Sun and filaments hampers detecting any peculiar flows in and around the giant filament by visual inspection (cf., Rondi et al. 2007). Only by close examination, we identified several flow kernels with a size of 5–8 Mm located at the ends of the filament with speeds of up to 0.30–0.45 km s-1. These kernels consist of closely spaced sinks and sources, whereby sinks are predominantly confined to the photospheric region below the filament and sources to the exterior. This configuration contributes to the enhancement of the magnetic field at the ends of the filament. In particular, this might be an indication that the filament is in the process of filling the gap between the eastern and western part, which was previously expelled during a CME. This finding agrees with what Schmieder et al. (2014) reported, who also found converging motions at the edges of the filament channel especially near footpoints of the filament.
5. Discussion and conclusions
The excellent seeing conditions on 2011 November 15 lasted the entire morning until well after local noon, which was a fortuitous occasion allowing us to capture this data set. The adaptive optics reliably locked on granulation and ten consecutive scans with high-resolution Echelle spectroscopy covered the giant filament, which had linear dimensions of ~817′′ (658 Mm along a great circle).
We performed CM inversions using the Hα line and retrieved valuable information about the physical parameters inside the filament. A total amount of 175 119 Hα contrast profiles, covering the whole filament, were inverted with very reasonable fits. Chae et al. (2006) showed a contrast profile located inside the spine of the filament with almost the same shape as ours. The depth of our contrast profiles reached up to C(λ) = −0.65. Deeper contrast profiles were related to darker Hα structures of the filament and hence showed higher values of the optical thickness. While the average values inferred from the CM inversions for the LOS velocity, Doppler width, and source function were similar or lay in between the values found by Schmieder et al. (2003) and Chae et al. (2006), the mean optical thickness was higher in our data set (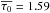 ). Caution should be taken when comparing the physical parameters inferred from CM inversions between different instruments. We have shown that stray-light heavily affects the results of the source function. In addition, simulating our profiles as observed by a different instrument with lower spectral resolution yielded variations of the mean optical thickness. Nevertheless, these variations were small on average (<3%). The analyzed filament is of particular interest because of its large horizontal extension. From a speculative point of view, huge filaments might also have an increased optical thickness. We have seen that the filament under study has an average optical thickness that is higher than the average value provided by Schmieder et al. (2003) and Chae et al. (2006) of smaller filaments. Optically thick areas were mainly, but not exclusively, found along the spine and even in barbs (e.g., see barb d in Fig. 8).
). Caution should be taken when comparing the physical parameters inferred from CM inversions between different instruments. We have shown that stray-light heavily affects the results of the source function. In addition, simulating our profiles as observed by a different instrument with lower spectral resolution yielded variations of the mean optical thickness. Nevertheless, these variations were small on average (<3%). The analyzed filament is of particular interest because of its large horizontal extension. From a speculative point of view, huge filaments might also have an increased optical thickness. We have seen that the filament under study has an average optical thickness that is higher than the average value provided by Schmieder et al. (2003) and Chae et al. (2006) of smaller filaments. Optically thick areas were mainly, but not exclusively, found along the spine and even in barbs (e.g., see barb d in Fig. 8).
 |
Fig. 12 Dots show the contrast profile (left) and observed Hα profile (right). The profile belongs to the spine of the filament and is located at label b in Fig. 3. The red line shows the CM fit (left) and the Hα parabola line core fit (right). The inferred velocities for the CM and line core fits are −3.11 and −2.50 km s-1, respectively. |
As a comparison, we performed Hα line core fits to infer the LOS velocities. The average velocities indicated that the filament, as a whole structure, had an upward motion toward higher layers of the atmosphere. This ascent was rather slow, on average −0.225 km s-1, and was slightly more marked in the spine (−0.288 km s-1), which is also perceptible in Fig. 6. This small generic upward trend was not confirmed from the CM-inferred mean velocity, however, where the velocities were higher, but on average canceled out. This yielded a value close to zero. Still, we found that the velocity trend inferred from the two methods, that is, from CM inversions versus line core fits, correlates well. As reported by Chae et al. (2006), we also confirmed that velocities inferred from CM inversions had higher values than those retrieved from line core fits (see Figs. 7 and 9). This was also reflected in the standard deviation, which was a factor of ~2 higher for the CM inferred velocities. Figure 12 shows an example of the different velocities inferred for the same pixel using the two different techniques. While the CM fit on the left-hand side of Fig. 12 yielded a velocity of −3.11 km s-1, the Hα line core fit on the right-hand side provided a lower velocity of −2.50 km s-1. Chae et al. (2006) ascribed this difference to the information provided by the line core fits of the averaged line shifts between the underlying photosphere and the filament. The slow rise of the spine of the filament could be a precursor of a following eruption. A continuous rise of plasma might lead to a destabilization of the filament. Five days later, on 2011 November 20 at around 16:00 UT, half of the filament lifted off as part of a CME that was observed with SDO/AIA. The fact that this huge filament underwent several eruptive events, before and after our data sets were recorded on 2011 November 15, reveals the unstable nature of extremely large filaments. It is still surprising that the filament survived during the whole disk passage, disappearing on the western solar limb by the end of November 15.
A thorough inspection of the CM-inferred velocities along the filament (Fig. 8) revealed that the velocity pattern is inhomogeneous, with different concentrations of up and downflows. This pattern was found throughout the filament, that is, during the ~100 min, which were necessary to scan the whole filament with the slit scanner. A close examination of barb d in both Hα ± 0.5 Å images revealed dark features that were only seen in the blue or red Hα line wing image. The spatial separation between them was less than 1′′. Thus, this indicated oppositely directed or counter-streaming flows that could also be seen in the associated Doppler and CM velocity maps. In addition, Diercke (2014) found these counter-streaming flows in the spine of this filament by analyzing SDO/AIA time series. We are aware that if this phenomenon occurs within the resolution element, the CM inversions will only provide an average of the physical parameters in this area. Hence, the lower-than-expected velocities for counter-streaming flows in barb d might be ascribed to not fully resolved threads with oppositely directed flows.
The Na i D2 inferred Doppler velocities were unaffected by the filament. Large conglomerates of brightenings matched magnetic field concentrations seen in the HMI magnetograms. Since the Hα and Na i D2 data were simultaneously recorded at the VTT, we could easily align the Hα slit-reconstructed images with HMI. We detected mixed polarities at the end of barbs extending from the giant filament, as has been reported for other smaller filaments in previous works (e.g., Martin 1998; Chae et al. 2005; López Ariste et al. 2006; Joshi et al. 2013). This is not the case for all barbs of this giant filament, however (see Fig. 10).
The global properties of horizontal proper motions for the quiet Sun and the photosphere below the filament were virtually the same. Only minute inspection of flow speed and divergence revealed flow kernels with a flow speed of 0.30–0.45 km s-1 and a size of 5–8 Mm, in which magnetic flux was transported toward the filament, in particular at the ends of the filament. This finding might also indicate that the big gap seen at the left-hand side of the filament is being refilled by plasma, which means that the filament is reestablishing its initial configuration.
Our study has revealed that extremely large quiescent filaments have similar properties as their smaller counterparts. Therefore, although this filament was a single structure when it appeared at the front side of the Sun, it could have been made out of junctions of smaller filaments as proposed by Anderson & Martin (2005). The origin and stability of such huge structures in the solar chromosphere remains a mystery and a challenge for the next generation of solar telescopes. The spatial resolution provided by SDO/HMI is insufficient to reveal any small details about the flux transport toward the filament. Spectropolarimetric observations with high temporal and spatial resolution both in the photosphere and chromosphere are needed to elucidate how a filament forms along the filament channel. New multi-wavelength observations with, for instance, the GREGOR Fabry-Pérot Interferometer (GFPI, Denker et al. 2010; Puschmann et al. 2012) and the Grating Infrared Spectrograph (GRIS, Collados et al. 2012) at the GREGOR solar telescope (Schmidt et al. 2012), for example, are a necessity to accomplish this challenging task.
Acknowledgments
The authors thank S. F. Martin, A. Warmuth, and A. Diercke for carefully reading the manuscript and for helpful comments. The authors also thank the anonymous referee for the thorough review and highly appreciate the constructive comments on the paper. Discussions with P. Schwartz within the framework of the Deutscher Akademischer Austauschdienst (DAAD) project PPP Slowakei 5706565721 “Das magnetische Vektorfeld solarer Filamente” are gratefully acknowledged. C.K. thanks ISSI for enabling interesting discussions. The Vacuum Tower Telescope and the Chromospheric Telescope are operated by the Kiepenheuer Institute for Solar Physics in Freiburg, Germany, at the Spanish Observatorio del Teide, Tenerife, Canary Islands. The ChroTel filtergraph has been developed by the Kiepenheuer Institute in cooperation with the High Altitude Observatory in Boulder, Colorado, USA. NSO/Kitt Peak FTS data were produced by NSF/NOAO. H-alpha data were provided by the Kanzelhöhe Observatory, University of Graz, Austria. M.V. acknowledges support by SOLARNET, a project of the European Commission’s FP7 Capacities Programme for the period April 2013–March 2017 under Grant Agreement No. 312495. C.D. was supported by grant DE 787/3-1 of the German Science Foundation (DFG).
References
- Alissandrakis, C. E., Tsiropoula, G., & Mein, P. 1990, A&A, 230, 200 [NASA ADS] [Google Scholar]
- Anderson, M., & Martin, S. F. 2005, in Large-scale Structures and their Role in Solar Activity, eds. K. Sankarasubramanian, M. Penn, & A. Pevtsov, ASP Conf. Ser., 346, 201 [Google Scholar]
- Aulanier, G., & Démoulin, P. 2003, A&A, 402, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balthasar, H., Beck, C., Louis, R. E., Verma, M., & Denker, C. 2014, A&A, 562, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beckers, J. M. 1964, Ph.D. Thesis, Sacramento Peak Observatory, USA [Google Scholar]
- Berkefeld, T., Soltau, D., Schmidt, D., & von der Lühe, O. 2010, Appl. Opt., 49, G155 [CrossRef] [Google Scholar]
- Bethge, C., Peter, H., Kentischer, T. J., et al. 2011, A&A, 534, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bostanci, Z. F., & Al Erdoğan, N. 2010, MSAI, 81, 769 [Google Scholar]
- Bray, R. J. 1973, Sol. Phys., 29, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Bray, R. J. 1974, Sol. Phys., 38, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Moon, Y.-J., & Park, Y.-D. 2005, ApJ, 626, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Park, Y.-D., & Park, H.-M. 2006, Sol. Phys., 234, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Collados, M., López, R., Páez, E., et al. 2012, Astron. Nachr., 333, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Denker, C., Balthasar, H., Hofmann, A., Bello González, N., & Volkmer, R. 2010, in Proc. SPIE, 7735, 6 [Google Scholar]
- DeVore, C. R., & Antiochos, S. K. 2000, ApJ, 539, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Diercke, A. 2014, Bachelor Thesis, Universität Potsdam, Germany [Google Scholar]
- Engvold, O. 2015, in Astrophys. Space Sci. Libr. 415, eds. J.-C. Vial, & O. Engvold, 31 [Google Scholar]
- Gu, X. M., Lin, J., Li, K. J., et al. 1994, A&A, 282, 240 [NASA ADS] [Google Scholar]
- Guo, Y., Schmieder, B., Démoulin, P., et al. 2010, ApJ, 714, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., & Anzer, U. 2006, ApJ, 643, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, A. D., Srivastava, N., Mathew, S. K., & Martin, S. F. 2013, Sol. Phys., 288, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Schlüter, A. 1957, Z. Astrophys., 43, 36 [Google Scholar]
- Kuckein, C., Martínez Pillet, V., & Centeno, R. 2012, A&A, 539, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuckein, C., Denker, C., & Verma, M. 2014, in IAU Symp. 300, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, 437 [Google Scholar]
- Landman, D. A. 1981, ApJ, 251, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Landman, D. A. 1983, ApJ, 269, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L., Wiik, J. E., & Berger, T. E. 2005, Sol. Phys., 226, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W. 2005, ApJ, 622, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- López Ariste, A., Aulanier, G., Schmieder, B., & Sainz Dalda, A. 2006, A&A, 456, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Magara, T., & Kitai, R. 1999, ApJ, 524, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, P. 1976, Sol. Phys., 46, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, S. F. 1998, Sol. Phys., 182, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Martres, M.-J., Mein, P., Schmieder, B., & Soru-Escaut, I. 1981, Sol. Phys., 69, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Mein, N., Mein, P., & Wiik, J. E. 1994, Sol. Phys., 151, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Moré, J. J. 1977, in Lect. Notes Math. 630, Numerical Analysis, ed. G. A. Watson (Berlin: Springer-Verlag), 105 [Google Scholar]
- Neckel, H., & Labs, D. 1984, Sol. Phys., 90, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, T. J., Tsuneta, S., Berger, T. E., et al. 2007, Science, 318, 1577 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Parenti, S. 2014, Liv. Rev. Sol. Phys., 11, 1 [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Puschmann, K. G., Denker, C., Kneer, F., et al. 2012, Astron. Nachr., 333, 880 [NASA ADS] [Google Scholar]
- Rondi, S., Roudier, T., Molodij, G., et al. 2007, A&A, 467, 1289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharr, H. 2007, in Complex Motion, eds. B. Jähne, R. Mester, B. Barth, & H. Scharr (Berlin: Springer), Lect. Notes Comput. Sci., 3417, 14 [Google Scholar]
- Schmidt, W., von der Lühe, O., Volkmer, R., et al. 2012, Astron. Nachr., 333, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Raadu, M. A., & Wiik, J. E. 1991, A&A, 252, 353 [NASA ADS] [Google Scholar]
- Schmieder, B., Tziotziou, K., & Heinzel, P. 2003, A&A, 401, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmieder, B., Roudier, T., Mein, N., et al. 2014, A&A, 564, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Schuck, P. W. 2005, ApJ, 632, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Schuck, P. W. 2006, ApJ, 646, 1358 [NASA ADS] [CrossRef] [Google Scholar]
- Stellmacher, G., & Wiehr, E. 2005, A&A, 431, 1069 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tandberg-Hanssen, E. 1995, The Nature of Solar Prominences (Dordrecht, The Netherlands: Kluwer Academic Publishers), Astrophys. Space Sci. Libr., 199 [Google Scholar]
- Tziotziou, K. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 217 [Google Scholar]
- van Ballegooijen, A. A., & Martens, P. C. H. 1989, ApJ, 343, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Verma, M., Balthasar, H., Deng, N., et al. 2012, A&A, 538, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vial, J.-C., & Engvold, O. 2015, Solar Prominences, Astrophys. Space Sci. Libr., 415 [Google Scholar]
- von der Lühe, O. 1998, New Astron. Rev., 42, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M. 1999, ApJ, 520, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Yazev, S. A., & Khmyrov, G. M. 1988, Adv. Space Res., 8, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Yelles Chaouche, L., Kuckein, C., Martínez Pillet, V., & Moreno-Insertis, F. 2012, ApJ, 748, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Zirker, J. B., Engvold, O., & Martin, S. F. 1998, Nature, 396, 440 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Hα and Na i D2 average LOS velocities (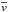 ), standard deviation (σ), and number of points (#) used for the statistics.
), standard deviation (σ), and number of points (#) used for the statistics.
All Figures
 |
Fig. 1 Limb-darkening-corrected Hα full-disk image obtained with ChroTel on 2011 November 15 (top). Full-disk SDO/HMI magnetogram scaled between ±100 G (bottom). The rectangular contours outline the regions scanned with the Echelle spectrograph of the VTT. |
| In the text | |
 |
Fig. 2 Hα profile acquired with the Echelle spectrograph at the VTT. The profile belongs to the spine of the filament and is located at label b in Fig. 3. The shaded area represents the spectral range used to compute the contrast profiles. |
| In the text | |
 |
Fig. 3 Large filament represented as a mosaic of ten individual slit-reconstructed images centered on Hα + 0.5 Å, Hα line core, Hα−0.5 Å, and Na i D2 line core (top to bottom). We number the maps from left to right (1–10). The labels a–d indicate the locations of the contrast profiles shown in Fig. 5. |
| In the text | |
 |
Fig. 4 Region-of-interest cropped from ChroTel and HMI full-disk images around 12:30 UT showing Hα, Ca ii K, and He i line core intensity images, and a time-averaged (11:30–13:20 UT) HMI magnetogram (top left to bottom right). The magnetogram is clipped between ±30 G. The step-function-like contours in the Hα and HMI panels outline the mosaic of the Echelle spectrograph observations (see Fig. 3). Intensity thresholding of the Hα filament and subsequent morphological dilation was used to create the generous contours of the filament in the Ca ii K and HMI panels. |
| In the text | |
 |
Fig. 5 Four selected Hα contrast profiles. The dots represent the observed contrast profiles, while the solid line shows the best fit from the CM inversion. Panels a) and b) belong to very opaque regions of the filament seen in Hα, whereas panels c) and d) belong to the barbs of the filament. The exact locations are indicated in Fig. 3. |
| In the text | |
 |
Fig. 6 Mosaic of Hα (top) and Na i D2 (bottom) Doppler velocities corresponding to the slit-reconstructed images in Fig. 3. The velocities were inferred from the line core fits. The mosaics were rotated to place the filament in a horizontal position. The superimposed black contours mark the outer boundaries of the filament as seen in Hα line core images. Doppler velocities were clipped between ±2 km s-1. |
| In the text | |
 |
Fig. 7 Frequency distributions of the Doppler velocities inferred from the line core fits of the Hα (left) and Na i D2 (right) lines in the filament (top) and in the quiet Sun (bottom). The bin size is 0.2 km s-1. |
| In the text | |
 |
Fig. 8 From top to bottom, maps of Doppler width ΔλD, optical thickness τ0, LOS velocity v, and source function S of the filament inferred from the Hα CM inversions. |
| In the text | |
 |
Fig. 9 Frequency distributions of the four CM parameters: optical thickness τ0, LOS velocity v, Doppler width ΔλD, and source function S (top left to bottom right). |
| In the text | |
 |
Fig. 10 Overview of the barbs from the filament seen in maps 6 and 7 of the slit-reconstructed Hα line core data from Fig. 3. Overlying is the HMI magnetogram clipped at 25 G. The color scale extends from blue (negative polarity) to red (positive polarity), and white represents saturated values. |
| In the text | |
 |
Fig. 11 Frequency distributions for speed (left), divergence (middle), and vorticity (right) of horizontal proper motions computed by applying DAVE to HMI magnetograms. The number of points that went into the computation of the frequency distributions for the quiet Sun (solid line) and the filament (dash dotted) are nqs = 2 772 670 and nfil = 149 007, respectively. |
| In the text | |
 |
Fig. 12 Dots show the contrast profile (left) and observed Hα profile (right). The profile belongs to the spine of the filament and is located at label b in Fig. 3. The red line shows the CM fit (left) and the Hα parabola line core fit (right). The inferred velocities for the CM and line core fits are −3.11 and −2.50 km s-1, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


