| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201527941 | |
| Published online | 22 February 2016 | |
Substellar companions in low-mass eclipsing binaries
NSVS 01286630, NSVS 02502726, and NSVS 07453183
1 Astronomical Institute, Faculty of Mathematics and Physics, Charles University in Prague, 180 00 Praha 8, V Holešovičkách 2, Czech Republic
e-mail: wolf@cesnet.cz
2 Astronomical Institute, Academy of Sciences, 251 65 Ondřejov, 298 Fričova, Czech Republic
3 Observatory Valašské Meziříčí, Vsetínská 78, 757 01 Valašské Meziříčí, Czech Republic
4 Trhové Sviny Observatory, Trocnovská 1188, 374 01 Trhové Sviny, Czech Republic
5 Department of Theoretical Physics and Astrophysics, Masaryk University, 611 37 Brno, Kotlářská 2, Czech Republic
Received: 10 December 2015
Accepted: 13 January 2016
Aims. As part of our long-term observational project we aim to measure very precise mid-eclipse times for low-mass eclipsing binaries, which are needed to accurately determine their period changes. Over two hundred new precise times of minimum light recorded with CCD were obtained for three eclipsing binaries with short orbital periods: NSVS 01286630 (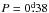 ), NSVS 02502726 (
), NSVS 02502726 (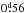 ), and NSVS 07453183 (
), and NSVS 07453183 (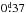 ).
).
Methods. O−C diagrams of studied stars were analysed using all reliable timings, and new parameters of the light-time effect were obtained.
Results. We derived for the first time or improved the very short orbital periods of third bodies of between one and seven years for all measured low-mass systems. We calculated that the lowest masses of the third components are between those of red and brown dwarfs. The multiplicity of these systems also plays an important role in the precise determination of their physical parameters. This research is part of an ongoing collaboration between professional astronomers and the Czech Astronomical Society, Variable Star and Exoplanet Section.
Key words: stars: fundamental parameters / stars: individual: NSVS 01286630 / stars: individual: NSVS 02502726 / stars: individual: NSVS 07453183 / binaries: eclipsing
© ESO, 2016
1. Introduction
The study of low-mass eclipsing binaries (LMB) provides an important observational test of theoretical models of stellar structure and evolution. In past years, a number of studies have shown that the observed radii for these most populous stellar objects in our Galaxy are about 10−20% larger and the temperatures 5% cooler then predicted by stellar models for masses between 0.3 M⊙ and 0.8 M⊙ (Baraffe et al. 1998; López-Morales 2007; Morales et al. 2008). This discrepancy in stellar models for this mass interval is due to differences in metallicity, magnetic activity, or to the interpretation of the light curve when stellar spots are very frequent (Morales et al. 2008). Morales et al. (2010) suggested that a considerable spot coverage (~35%) induces systematic deviation in the radii and effective temperatures derived from the light curves and that a concentration of spots near the poles could explain the radius discrepancy between models and observations. On the other hand, only about 30 LMB with determined masses, radii, and temperatures are currently detected because of their low brightness. LMB in Kepler database were recently studied by Coughlin et al. (2011). They found statistical evidence that the radii of these binary systems decrease with orbital period.
LITE parameters for selected LMB.
A significant number of close binaries form as inner binaries in triple systems, and the tertiary components play an important role in the formation of tight pairs (Eggleton & Kisseleva-Eggleton 2006; Fabrycky & Tremaine 2007). The presence of the tertiary component causes a cyclical variation of the eclipse times of a binary star. This means that we can simply discover multiple systems by searching for periodic features in the observed O−C diagram. The detection of such a system is of great interest because the mass and orbit of the companion can be directly determined from the O−C diagram. If timing data have a precision of a few seconds, the eclipsing binaries showing this effect offer the opportunity of detecting substellar companions, such as giant planets and brown dwarfs (Lee et al. 2009; Hinse et al. 2012; Pribulla et al. 2012).
We here report on long-term mid-eclipse time monitoring of three LMB. These selected systems are all faint low-mass objects in the northern hemisphere that were all discovered relatively recently by McIntyre & Shaw (2005) or Coughlin & Shaw (2007). Their orbital periods are between 9 and 13 h. With the exception of NSVS 02502726, no spectroscopic observations have been published for these binary systems.
The magnetic activity of LMBs was recently studied by Zhang et al. (2014); their study includes two of our three systems. For NSVS 02502726 they found a weak continuous secular decrease of the orbital period dP/ dt = −2.1(0.8) × 10-7 d/yr. For NSVS 07453183 they detected the first flare-like event at phase 0.39 and found a period change at cycle 6500.
Until now, there has been no period variation analysis of these LMB, only one study of NSVS 02502726, where an orbital period analysis revealed that the period decreases continuously by −5.9 × 10-7 d/yr with a weak sinusoidal variation (Lee et al. 2013).
2. Observations of mid-eclipses
One of the best methods to detect a tertiary component in an orbiting eclipsing binary is to search for strictly periodic variations in the mid-eclipse times that are caused by the light travel delay associated with orbital motion, the so-called light time effect (LITE, Irwin 1959; Mayer 1990; Wolf 2014). If the orbital period of the third star is short (up to one year), then additional dynamical perturbations of the inner orbit can occur that also create changes in the mid-eclipse times (Borkovits et al. 2011, 2016).
High-precision CCD photometry and precise mid-eclipse time estimation enable us to find small apparent period changes and derive the physical parameters of the next orbiting bodies that are of a substellar size and mass. Monitoring LMBs is a long-term observational project, which requires only moderate or small telescopes equipped with a CCD camera. Moreover, a long observing time is needed, which is currently unavailable at large telescopes, but is more practical for small amateur telescopes equipped with modern detectors.
During the past eight years, we have accumulated over 104 photometric observations at selected phases during primary and secondary eclipses and derived over 200 precise times of minimum light for selected systems. New CCD photometry was obtained mostly at the Ondřejov Observatory, Czech Republic, using the 0.65 m (f/ 3.6) reflecting telescope with the CCD cameras Apogee AP7p or Moravian Instruments G2-3200 and VRI photometric filters. The next precise CCD photometry was carried out at the Valašské Meziříčí Observatory, Czech Republic, using the 0.3 m Celestron Ultima telescope with the CCD camera SBIG ST-7 or G2-1600 and VRI filters and Trhové Sviny Observatory, Czech Republic, using the 0.2 m Newtonian telescope with the CCD camera Atik 314L+ without filters. Some additional measurements were obtained at Masaryk University Observatory (MUO), Brno, Czech Republic, where the 0.6 m telescope with the CCD camera SBIG ST-8XME was used.
All CCD measurements were dark-subtracted and then flat-fielded using sky exposures taken at either dusk or dawn. Aphot, a synthetic aperture photometry and astrometry software, was routinely used for data obtained at Ondřejov observatory. The C-Munipack1 was used to reduce some of our CCD images obtained at MUO, Valašské Meziříčí and Trhové Sviny. Relative photometry was performed using suitable comparison stars. No correction for differential extinction was applied because of the proximity of the comparison stars to the variable and the resulting negligible differences in air mass.
The new times of primary and secondary minima and their errors were generally determined by fitting the light curve by Gaussians or polynomials of the third or fourth order; we used the least-squares method. All new times are given in Tables A.1−A.3, where epochs are calculated from the ephemeris given in Table 1. The other columns are self-explaining.
Physical properties of selected LMB and parameters of their third bodies.
3. Period variations
A detailed analysis of the period variations of LMB can be performed using eclipse times observed during long observation periods. Because these systems undergo several hundreds of orbital cycles in a year and because their eclipses are very short and usually deep and quite symmetric, it is relatively easy to obtain individual timings of mid-eclipses to an accuracy of only a few seconds and thus to search for small changes in binary period.
We propose the light-time effect (LITE) in all systems studied by means of an O−C diagram analysis. For an accurate calculation, the method originally described by Irwin (1952) and later by Mayer (1990) was routinely used. There are seven independent variables (T0,Ps,P3,e3,A,ω3,T3) determined in this procedure, where Ps is the sidereal period, P3 is the orbital period of the third body, A is a semiamplitude, and e3 represents the eccentricity. The zero epoch is given by T0, and the corresponding position of the periastron is represented by ω3.
In addition to the new mid-eclipse times, we have collected all reliable times of minimum light available in the literature. All new and very precise CCD mid-eclipse times were used with a weight of 10, some of our less precise measurements were weighted by a factor of 5, while the earlier times were given a weight of 1 because of the large scatter in these data. This simple weighting scheme gives us more reliable results then the formal error of the mid-eclipse time determination.
3.1. NSVS 01286630
 |
Fig. 1 Current O−C diagram for the eclipse times of NSVS 01286630. The sinusoidal blue curve represents the LITE with the short period of 3.6 yr. The individual primary and secondary minima are denoted by circles and triangles, resp. Larger symbols correspond to the CCD measurements, which were given higher weights in the calculations. The eclipse timing residuals are plotted in the bottom panel. |
The detached eclipsing binary NSVS 01286630 (in SIMBAD as NSVS 1135262, in NSVS database also as NSVS 1171590, 2MASS J18470859+7842292, Vmax = 13m.087) is a rather neglected binary system with a short orbital period of 9.2 h. It was listed in the table of new LMB collected by Shaw & López-Morales (2007), where the precise orbital period 0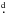 38390916 d is given. We adopted the following linear ephemeris throughout:
38390916 d is given. We adopted the following linear ephemeris throughout:  To our knowledge, no modern photometric, spectroscopic or period study of this system exists so far. All eclipse times are given in Table A.1. A total of 112 reliable times of minimum light were included in our analysis, with 54 secondary eclipses among them. The computed LITE parameters and their internal errors of the least-squares fit are given in Table 1. It lists the ratio of periods
To our knowledge, no modern photometric, spectroscopic or period study of this system exists so far. All eclipse times are given in Table A.1. A total of 112 reliable times of minimum light were included in our analysis, with 54 secondary eclipses among them. The computed LITE parameters and their internal errors of the least-squares fit are given in Table 1. It lists the ratio of periods 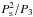 and indicates possible dynamical interactions between the orbits that could be observed. The reduced chi-square value,
and indicates possible dynamical interactions between the orbits that could be observed. The reduced chi-square value, 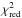 , is also calculated. The O−C residuals for all times of minimum with respect to the linear ephemeris are shown in Fig. 1. The non-linear predictions, corresponding to the fitted parameters, are plotted as a continuous blue curve.
, is also calculated. The O−C residuals for all times of minimum with respect to the linear ephemeris are shown in Fig. 1. The non-linear predictions, corresponding to the fitted parameters, are plotted as a continuous blue curve.
3.2. NSVS 02502726
The detached and double-lined eclipsing binary NSVS 02502726 (also 2MASS J08441103+5423473, GSC 03798-01207; Vmax = 13m.41; B−V = 1m.26) is a newly discovered but relatively well-studied low-mass eclipsing binary system with a short orbital period (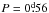 ). It was discovered as a variable object in the NSVS database by Coughlin & Shaw (2007). Cakirli et al. (2009) presented optical spectroscopy and differential photometry and obtained the first precise absolute parameters of the components: M1 = 0.714(19) M⊙, M2 = 0.347(12) M⊙, R1 = 0.674(6) R⊙, and R2 = 0.763(7) R⊙.
). It was discovered as a variable object in the NSVS database by Coughlin & Shaw (2007). Cakirli et al. (2009) presented optical spectroscopy and differential photometry and obtained the first precise absolute parameters of the components: M1 = 0.714(19) M⊙, M2 = 0.347(12) M⊙, R1 = 0.674(6) R⊙, and R2 = 0.763(7) R⊙.
Recently, the physical properties and absolute dimensions of NSVS 02502726 were studied by Lee et al. (2013). They improved the results of Cakirli et al. (2009) and revealed that the period probably decreases continuously by −5.9 × 10-7 d/yr or a weak sinusoidal variation with a period of 2.51 yr. Their physical parameters are listed in Table 2. They also concluded that the primary agrees well with the empirical mass-radius relation from LMB, but the secondary is oversized by about 85%. See also the short history presented in this paper, where the following precise linear light elements were derived:  A lower period decrease dP/ dt = −2.1(0.8) × 10-7 d/yr for this LMB was recently found by Zhang et al. (2014). Using SuperSWASP photometry (Pollaco et al. 2006), we were able to derive the next additional times of minimum light with less precision using the light-curve profile fitting method. A total of 68 reliable times of minimum light were used in our analysis, including 32 secondary eclipses. These eclipse times are listed in Table A.2. The computed LITE parameters are listed in Table 1, the complete O−C diagram is shown in Fig. 2.
A lower period decrease dP/ dt = −2.1(0.8) × 10-7 d/yr for this LMB was recently found by Zhang et al. (2014). Using SuperSWASP photometry (Pollaco et al. 2006), we were able to derive the next additional times of minimum light with less precision using the light-curve profile fitting method. A total of 68 reliable times of minimum light were used in our analysis, including 32 secondary eclipses. These eclipse times are listed in Table A.2. The computed LITE parameters are listed in Table 1, the complete O−C diagram is shown in Fig. 2.
 |
Fig. 2 O−C graph for NSVS 02502726. See legend to Fig. 1. The blue curve represents the LITE of the orbiting third body with a period of 6.9 years in a moderately eccentric orbit (e ≃ 0.47). |
3.3. NSVS 07453183
 |
Fig. 3 O−C graph for the times of minimum of NSVS 07453183. The very short period of the third body on a circular orbit of 418 days is plotted. See also legend to Fig. 1. |
 |
Fig. 4 For clarity, the O−C diagram for eclipse times of NSVS 07453183 phased using the newly derived third body period of 418 days. |
The low-mass eclipsing binary NSVS 07453183 (Vmax = 12m.5) is a faint northern object with a short orbital period of about 8.8 h . Its variability was discovered by McIntyre & Shaw (2005) using the publicly available Northern Sky Variability Survey (Wozniak et al. 2004). Recently, the BVR photometry and period analysis of NSVS 07453183 were derived by Zhang et al. (2014), who also detected a flare-like event. We propose the following linear ephemeris for the current use: 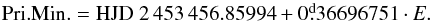 Since the above-mentioned papers were published, numerous new mid-eclipse times have been obtained, which allowed us to reduce the observational uncertainties. They are listed in Table A.3. A total of 58 precise times of minimum light were used in our analysis, including 28 secondary eclipses. Some of older mid-eclipse times of McIntyre & Shaw (2005) were omitted due to the large scatter of these data. The computed LITE parameters are given in Table 1, the current O−C diagrams are shown in Figs. 3 and 4.
Since the above-mentioned papers were published, numerous new mid-eclipse times have been obtained, which allowed us to reduce the observational uncertainties. They are listed in Table A.3. A total of 58 precise times of minimum light were used in our analysis, including 28 secondary eclipses. Some of older mid-eclipse times of McIntyre & Shaw (2005) were omitted due to the large scatter of these data. The computed LITE parameters are given in Table 1, the current O−C diagrams are shown in Figs. 3 and 4.
4. Discussion
The detection of LITE in LMB provides the opportunity of testing the stellar multiplicity among low-mass stars and also prove current models of stellar evolution. The derived parameters of the third-body orbit allow us to determine the mass function f(M) of the triple system ![\begin{eqnarray*} f(M) = \frac{M_3^3 \sin^3 i_3}{(M_1+M_2+M_3)^2} = \frac{1}{P^2_3} \, \left[\frac {173.15 \, A} {\sqrt{1 - e_3^2 \cos^2 \omega_3}} \right] ^3, \end{eqnarray*}](/articles/aa/full_html/2016/03/aa27941-15/aa27941-15-eq46.png) where P3 is the period of the third body (in years) and Mi are the masses of components. The systemic radial velocity of the eclipsing pair have an amplitude
where P3 is the period of the third body (in years) and Mi are the masses of components. The systemic radial velocity of the eclipsing pair have an amplitude 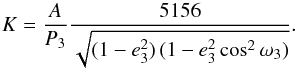 Assuming a coplanar orbit (i3 = 90°), we can obtain a lower limit for the mass of the third component M3,min. These values for the third body of individual systems are collected in Table 2. The amplitude of the dynamical contribution of the third body Adyn is given approximately by (Borkovits et al. 2015)
Assuming a coplanar orbit (i3 = 90°), we can obtain a lower limit for the mass of the third component M3,min. These values for the third body of individual systems are collected in Table 2. The amplitude of the dynamical contribution of the third body Adyn is given approximately by (Borkovits et al. 2015) 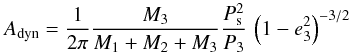 and is negligible for our triple systems.
and is negligible for our triple systems.
Another possible mechanism for cyclical period variation is a magnetic activity cycle for systems with a late-type secondary star (Applegate 1992). However, the newly derived LITE periods (1−7 years) of selected LMB are too short for the magnetic cycle when compared with a mean value around 40−50 years in Algols and RS CVn binaries (Lanza & Rodono 1999). This mechanism cannot contribute significantly to the observed period changes. The pure LITE solution given above is sufficient. Moreover, the reduced chi-square value, which is close to unity in all systems, supports this result.
For NSVS 02502726 we could clearly expect the brown dwarf that is well below the mass limit of 0.08 M⊙ (de Pater & Lissauer 2010) as the unseen third body orbiting the eclipsing pair.
For NSVS 07453138 the third component could be an M1 red dwarf with a bolometric magnitude of about +8.3 mag (Harmanec 1988). Assuming a K3 + K4 eclipsing pair, the third star produces only 7% of the total light. Finally, for NSVS 01286630 the lowest mass of the third body is close to 0.1 M⊙; we cannot clearly distinguish whether this is a red or brown dwarf star.
5. Conclusions
The LITE in eclipsing binaries has been used for decades to test the multiplicity of stellar systems. Our study provided accurate information on the period changes of three main-sequence low-mass binary systems that were selected randomly from the list of Shaw & López-Morales (2007). With the exception of NSVS 02502726, the LITE period has been presented here for the first time. Even without optical spectroscopy, they support the idea that these objects are multiple stellar systems. The sinusoidal term in the orbital period strongly suggested a third body in all systems, most probably a red or brown dwarf. Additional timing variations with small amplitudes might be produced by the asymmetries of the eclipse light curves through stellar activity such as star spots and pulsations.
The observed percentages of triple and higher-order systems of Sun-like stars in the solar neighborhood, including stellar and brown dwarf components, are only 8% ± 1% and 3% ± 1%, respectively (Raghavan et al. 2010). Thus our results significantly contribute to this class of rare systems in our Galaxy.
The sample of well-known LMB needs to be increased; observations of additional systems would be very useful. It would also be highly desirable to obtain new, high-dispersion spectroscopic observations with high signal-to-noise ratios.
Acknowledgments
This research was supported by the Research Program MSM0021620860 Physical Study of objects and processes in the Solar System and in Astrophysics of the Ministry of Education of the Czech Republic and partially by the Czech Science Foundation, grants Nos. 205/06/0217 and P209/10/0715, and in its final stage by the grant GA15-02112S. K.H. was supported by the project RVO:67985815. The authors would also like to thank Lenka Kotková and Kateřina Hoňková, Ondřejov observatory, and M. Zejda and J. Liška, Masaryk University Brno, for their important contribution to photometric observations. The following internet-based resources were used in research for this paper: the SIMBAD database and the VizieR service operated at CDS, Strasbourg, France; the NASA’s Astrophysics Data System Bibliographic Services; the O−C Gateway of the Variable Star and Exoplanet Section, Czech Astronomical Society2. We gratefully acknowledge useful suggestions by the referee.
References
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschild, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Borkovits, T., Csizmadia, Sz., Forgacs-Dajka, E., & Hegedüs, T. 2011, A&A, 528, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Hajdu, T., Sztakovics, J., et al. 2016, MNRAS, 455, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Cakirli, Ö., Ibanoglu, C., & Gungor, C. 2009, New Astron., 14, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Coughlin, J. L., & Shaw, J. S. 2007, J. Southeast. Ass. for Research in Astr., 1, 7 [NASA ADS] [Google Scholar]
- Coughlin, J. L., López-Morales, M., Harrison, T. E., et al. 2011, AJ, 141, 78 [NASA ADS] [CrossRef] [Google Scholar]
- de Pater, I., & Lissauer, J. J., in Planetary Sciences, 2nd edn. (Cambridge University Press), 2010 [Google Scholar]
- Eggleton, P. P., & Kisseleva-Eggleton, L. 2006, Ap&SS, 304, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Frabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Harmanec, P. 1988, Bull. Astr. Inst. Czech., 39, 329 [Google Scholar]
- Hinse, T. C., Lee, J. W., Gozdziewski, K., et al. 2012, MNRAS, 420, 3609 [NASA ADS] [CrossRef] [Google Scholar]
- Hoňková, K., Juryšek, J., Lehký, M., Šmelcer, L., et al. 2015, OEJV, 168 [Google Scholar]
- Irwin, J. B. 1952, ApJ, 116, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J. B. 1959, AJ, 64, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., & Rodono, M. 1999, A&A, 349, 887 [NASA ADS] [Google Scholar]
- Lee, J. W., Kim, S. L., Kim, C. H., et al. 2009, AJ, 137, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. W., Youn, J. H., Kim, S. L., & Lee, C. U. 2013, AJ, 145, 16 [NASA ADS] [CrossRef] [Google Scholar]
- López-Moráles, M. 2007, ApJ, 660, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, P. 1990, Bull. Astr. Inst. Czech., 41, 231 [Google Scholar]
- McIntyre, T., & Shaw, J. S. 2005, IAPPPComm., 101, 38 [NASA ADS] [Google Scholar]
- Morales, J. C., Ribas, I., & Jordi, C. 2008, A&A, 478, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morales, J. C., Gallardo, J., Ribas, I., et al. 2010, ApJ, 718, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D. L., Skillen, I., & Collier Cameron, A. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Pribulla, T., Vaňko, M., Ammler-von Eiff, M., et al. 2012, Astron. Nachr., 333, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJSS, 190, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, J. S., & López-Morales, M. 2007, ASP Conf. Ser., 362, 15 [Google Scholar]
- Wolf, M. 2014, Contrib. Astron. Obs. Skalnaté Pleso, 43, 93 [Google Scholar]
- Wozniak, P. R., Vestrand, W. T., Akerlof, C. W., et al. 2004, AJ, 127, 2436 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L.-Y., Pi, Q.-F., & Yang, Y.-G. 2014, MNRAS, 442, 2620 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Tables of mid-eclipse times
Minima timings of NSVS 01286630.
Minima timings of NSVS 02502726.
Minima timings of NSVS07453183.
All Tables
All Figures
 |
Fig. 1 Current O−C diagram for the eclipse times of NSVS 01286630. The sinusoidal blue curve represents the LITE with the short period of 3.6 yr. The individual primary and secondary minima are denoted by circles and triangles, resp. Larger symbols correspond to the CCD measurements, which were given higher weights in the calculations. The eclipse timing residuals are plotted in the bottom panel. |
| In the text | |
 |
Fig. 2 O−C graph for NSVS 02502726. See legend to Fig. 1. The blue curve represents the LITE of the orbiting third body with a period of 6.9 years in a moderately eccentric orbit (e ≃ 0.47). |
| In the text | |
 |
Fig. 3 O−C graph for the times of minimum of NSVS 07453183. The very short period of the third body on a circular orbit of 418 days is plotted. See also legend to Fig. 1. |
| In the text | |
 |
Fig. 4 For clarity, the O−C diagram for eclipse times of NSVS 07453183 phased using the newly derived third body period of 418 days. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


