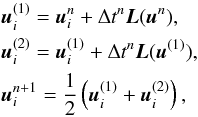| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 16 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201527815 | |
| Published online | 23 February 2016 | |
A well-balanced finite volume scheme for the Euler equations with gravitation
The exact preservation of hydrostatic equilibrium with arbitrary entropy stratification
Seminar for Applied Mathematics (SAM), Department of
Mathematics,
ETH Zürich,
8092
Zürich,
Switzerland
e-mail:
roger.kaeppeli@sam.math.ethz.ch
Received: 24 November 2015
Accepted: 27 December 2015
Context. Many problems in astrophysics feature flows which are close to hydrostatic equilibrium. However, standard numerical schemes for compressible hydrodynamics may be deficient in approximating this stationary state, where the pressure gradient is nearly balanced by gravitational forces.
Aims. We aim to develop a second-order well-balanced scheme for the Euler equations. The scheme is designed to mimic a discrete version of the hydrostatic balance. It therefore can resolve a discrete hydrostatic equilibrium exactly (up to machine precision) and propagate perturbations, on top of this equilibrium, very accurately.
Methods. A local second-order hydrostatic equilibrium preserving pressure reconstruction is developed. Combined with a standard central gravitational source term discretization and numerical fluxes that resolve stationary contact discontinuities exactly, the well-balanced property is achieved.
Results. The resulting well-balanced scheme is robust and simple enough to be very easily implemented within any existing computer code that solves time explicitly or implicitly the compressible hydrodynamics equations. We demonstrate the performance of the well-balanced scheme for several astrophysically relevant applications: wave propagation in stellar atmospheres, a toy model for core-collapse supernovae, convection in carbon shell burning, and a realistic proto-neutron star.
Key words: hydrodynamics / methods: numerical / convection / stars: interiors / stars: neutron
© ESO, 2016
1. Introduction
Many interesting astrophysical phenomena can be modeled by the Euler equations with gravitational source terms. They express the conservation of mass, momentum, and total energy, as given by ![\begin{eqnarray} \label{eq:intro0010} &&\frac{\partial \rho}{\partial t} + \nabla \cdot \left( \rho \boldsymbol{\varv} \right) = 0 \\[1mm] \label{eq:intro0020} &&\frac{\partial \rho \boldsymbol{\varv}}{\partial t} + \nabla \cdot \left( \boldsymbol{\varv} \rho \boldsymbol{\varv} \right) + \nabla p = - \rho \nabla \phi \\[1mm] \label{eq:intro0030} &&\frac{\partial E}{\partial t} + \nabla \cdot \left[ \left( E + p \right) \boldsymbol{\varv} \right] = - \rho \boldsymbol{\varv} \cdot \nabla \phi . \end{eqnarray}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq1.png) Here, ρ is the mass density, ν the velocity, and
Here, ρ is the mass density, ν the velocity, and 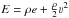 , where the total energy is the sum of internal and kinetic energy. The pressure p is related to the specific internal energy and the density through an equation of state p = p(ρ,e).
, where the total energy is the sum of internal and kinetic energy. The pressure p is related to the specific internal energy and the density through an equation of state p = p(ρ,e).
The source terms on the right-hand side of the momentum and energy equations model the effect of the gravitational forces on the fluid. They are proportional to the gradient of the gravitational potential φ, which can either be a given function or in the case of self-gravity, it can be determined by the Poisson equation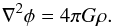 (4)In many situations one has to deal with flows close to hydrostatic equilibrium
(4)In many situations one has to deal with flows close to hydrostatic equilibrium 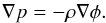 (5)Here, the interest relies in robust and accurate resolution of flows close to hydrostatic equilibrium. The numerical approximation of near steady flows is challenging for standard finite volume schemes because they do not necessarily satisfy a discrete equivalent of the balance of pressure gradient and gravitational forces, represented by Eq. (5). As a result, equilibrium states are not preserved exactly but are approximated with an error proportional to the truncation error. If one is interested in the simulation of small perturbations on top of the equilibrium, the numerical resolution has to be increased to the point that the truncation errors do not obscure the phenomena of interest. This need in resolution may become prohibitively large (especially in multiple dimensions).
(5)Here, the interest relies in robust and accurate resolution of flows close to hydrostatic equilibrium. The numerical approximation of near steady flows is challenging for standard finite volume schemes because they do not necessarily satisfy a discrete equivalent of the balance of pressure gradient and gravitational forces, represented by Eq. (5). As a result, equilibrium states are not preserved exactly but are approximated with an error proportional to the truncation error. If one is interested in the simulation of small perturbations on top of the equilibrium, the numerical resolution has to be increased to the point that the truncation errors do not obscure the phenomena of interest. This need in resolution may become prohibitively large (especially in multiple dimensions).
Many remedies have been proposed to overcome the aforementioned difficulties. The simplest solution consists of subtracting the (assumed known) stationary state at each time step. In this way the truncation errors are exactly canceled (see, e.g., Dedner et al. 2001). However, this requires that the stationary state is known a priori. Another approach in the finite volume methodology is to introduce the effect of gravity into the Riemann solver. The idea is that the Riemann solver should recognize pressure differences induced by gravity and prevent the propagation of resulting waves. Perhaps, the earliest approach of this type, was already presented in the original description of the piecewise parabolic method of Colella & Woodward (1984): the influence of the gravity source term was incorporated into the characteristic evolution step. For Rusanov or local Lax-Friedrichs type Riemann solvers, Käppeli et al. (2011) have subtracted the gradients induced by gravity in the dissipative flux terms. Yet another strategy for finite volume schemes is to introduce a subgrid model which incorporates the stationary state into the reconstruction process, see, e.g., Freytag et al. (2012), Mellema et al. (1991), Zingale et al. (2002).
Greenberg & Leroux (1996) introduced the concept of a well-balanced scheme, i.e., a scheme which satisfies exactly a discrete equivalent of an underlying stationary state. Many well-balanced schemes have been designed, especially for the shallow water equations with non-trivial bottom topography, see, e.g., Lefloch & Thanh (2003), LeVeque (1998), Audusse et al. (2004) and references therein.
Well-balanced schemes for certain classes of hydrostatic equilibrium have been presented by LeVeque (1998, 2011), Botta et al. (2004), Fuchs et al. (2010), Xing & Shu (2013), Desveaux et al. (2014), Käppeli & Mishra (2014), Chandrashekar & Klingenberg (2015), Li & Xing (2015). However, Eq. (5) only specifies a mechanical equilibrium. All the afore mentioned well-balanced schemes need to assume a certain thermal equilibrium in order to uniquely determine the stationary state. For instance, Käppeli & Mishra (2014) have designed a well-balanced scheme under the further assumption of isentropic (isothermal) conditions. Then Eq. (5) can be explicitly integrated to h + φ = const. (g + φ = const.), where h is the specific enthalpy (g the Gibbs free energy). These expressions can then be used to build a well-balanced scheme for the isentropic (isothermal) case.
In this paper, we design well-balanced first- and second-order accurate finite volume schemes for approximating the Euler equations with gravitation without any assumption of a thermal equilibrium. The main ingredient of our scheme is the use of a straightforward discretization of hydrostatic equilibrium Eq. (5) as basis for the pressure reconstruction. The schemes are well-balanced for any consistent Riemann solver capable of resolving a stationary contact discontinuity. Moreover, the scheme allows for any explicit or implicit time integration.
The rest of the paper is organized as follows: the well-balanced finite volume scheme is presented in Sect. 2. Numerical results are presented in Sect. 3 and discussion and conclusions are provided in Sect. 4.
2. Numerical method
2.1. One-dimensional Cartesian case
We first consider the Euler equations with gravitation (1)−(3)in one space dimension and write them in the compact form: 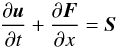 (6)with
(6)with ![\begin{equation} \label{eq:nm_1dcart0020} \begin{aligned} \boldsymbol{u} = \left[ \begin{array}{c} \rho \\ \rho \varv_x \\ E \end{array}\right] \end{aligned} \; , \quad \begin{aligned} \boldsymbol{F} = \left[ \begin{array}{c} \rho \varv_x \\ \rho \varv_x^2 + p \\ (E + p) \varv_x \end{array}\right] \end{aligned} \quad \mathrm{and} \quad \begin{aligned} \boldsymbol{S} = - \left[ \begin{array}{c} 0 \\ \rho \\ \rho \varv_x \end{array}\right] \frac{\partial \phi}{\partial x} \end{aligned} , \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq16.png) (7)where u, F and S are the vectors of conserved variables, fluxes and source terms. Moreover, we denote the primitive variables by w = [ ρ,νx,p ] T. The system is closed by an equation of state (EoS) p = p(ρ,e) which relates the pressure p to density ρ and specific internal energy e (or any other related thermodynamic quantity such as temperature or specific entropy). The form of the EoS does not matter for the methods presented. Several types of EoSs are employed in the applications described later in the paper, including ideal, hybrid (polytropic and ideal) and tabulated EoSs.
(7)where u, F and S are the vectors of conserved variables, fluxes and source terms. Moreover, we denote the primitive variables by w = [ ρ,νx,p ] T. The system is closed by an equation of state (EoS) p = p(ρ,e) which relates the pressure p to density ρ and specific internal energy e (or any other related thermodynamic quantity such as temperature or specific entropy). The form of the EoS does not matter for the methods presented. Several types of EoSs are employed in the applications described later in the paper, including ideal, hybrid (polytropic and ideal) and tabulated EoSs.
For the numerical approximation of Eq. (6), the spatial domain is discretized by cells or finite volumes Ii = [ xi−1 / 2,xi + 1 / 2 ] of regular size Δx = xi + 1 / 2 − xi−1 / 2. Varying cell sizes can easily be accommodated for (see Appendix A). By integrating Eq. (6)over a cell Ii we obtain a semi-discrete finite volume scheme for the evolution of the cell-averaged conserved variables ui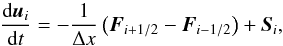 (8)where Fi + 1 / 2,j is the numerical flux at cell interface and Si is the gravity source term.
(8)where Fi + 1 / 2,j is the numerical flux at cell interface and Si is the gravity source term.
The numerical flux is obtained by solving (approximately) the Riemann problem at cell interfaces 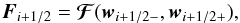 (9)where the wi + 1 / 2 − and wi + 1 / 2 + are the cell interface extrapolated primitive variables. The only requirement on the numerical flux for the hydrostatic equilibrium preserving scheme elaborated below is, that it is capable of resolving stationary contact discontinuities, i.e.,
(9)where the wi + 1 / 2 − and wi + 1 / 2 + are the cell interface extrapolated primitive variables. The only requirement on the numerical flux for the hydrostatic equilibrium preserving scheme elaborated below is, that it is capable of resolving stationary contact discontinuities, i.e., ![\begin{equation} \label{eq:nm_1dcart0060} \boldsymbol{\mathcal{F}} \left( [\rho_L,0,p]^T ,[\rho_R,0,p]^T \right) = [0,p,0]^T , \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq33.png) (10)where ρL (ρR) is the density on the left (right) side of the contact discontinuity and p the constant pressure. For example the HLLC (Toro et al. 1994) and Roe (Roe 1981) approximate Riemann solvers have this property. In the following, we use the HLLC Riemann solver with wave speed estimates according to Batten et al. (1997).
(10)where ρL (ρR) is the density on the left (right) side of the contact discontinuity and p the constant pressure. For example the HLLC (Toro et al. 1994) and Roe (Roe 1981) approximate Riemann solvers have this property. In the following, we use the HLLC Riemann solver with wave speed estimates according to Batten et al. (1997).
The gravitational source term is evaluated by standard spatially second-order accurate centered differences ![\begin{equation} \label{eq:nm_1dcart0070} \boldsymbol{S}_{i} = - \left[ \begin{array}{c} 0 \\ \rho_i \\ (\rho \varv_x)_i \end{array} \right] \frac{\phi_{i+1} - \phi_{i-1}}{2 \Delta x} , \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq36.png) (11)where the φi are the cell-centered values of the gravitational potential. This is a common choice in astrophysical simulations. Moreover, note that the above expression is exact for a linear gravitational potential, i.e., a constant gravitational acceleration.
(11)where the φi are the cell-centered values of the gravitational potential. This is a common choice in astrophysical simulations. Moreover, note that the above expression is exact for a linear gravitational potential, i.e., a constant gravitational acceleration.
The cell interface extrapolated values of the primitive variables wi−1 / 2 + and wi + 1 / 2 − are obtained by a reconstruction procedure from the cell-averaged conserved variables. The simplest reconstruction assumes a piecewise constant distribution of the conserved variables within the cell. This results in Godunov’s (Godunov 1959) method, which is first-order accurate in space. Spatial accuracy is increased by higher-order non-oscillatory polynomial reconstructions (Laney 1998; LeVeque 2002; Toro 1997). Prominent choices are piecewise linear (e.g., MUSCL van Leer 1979) and piecewise parabolic (PPM, Colella & Woodward 1984) reconstructions.
However, standard reconstructions will not preserve a discrete hydrostatic equilibrium. In the next section, we present a novel reconstruction which can preserve a discrete hydrostatic equilibrium up to machine precision, i.e., a well-balanced reconstruction.
A fully discrete scheme is obtained by choosing an integrator for the system of ordinary differential Eq. (8). This is discussed in Sect. 2.2.
2.1.1. Well-balanced local hydrostatic pressure reconstruction
A standard finite volume scheme (8)may not preserve a discrete equivalent of a hydrostatic equilibrium 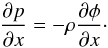 (12)This deficiency is most obvious for a first-order scheme. The piecewise constant reconstruction is indeed incompatible with the pressure stratification induced by gravity. The pressure difference at cell interfaces is interpreted as a propagating wave by the Riemann solver. Hence, the equilibrium is destroyed.
(12)This deficiency is most obvious for a first-order scheme. The piecewise constant reconstruction is indeed incompatible with the pressure stratification induced by gravity. The pressure difference at cell interfaces is interpreted as a propagating wave by the Riemann solver. Hence, the equilibrium is destroyed.
Higher-order reconstructions, such as piecewise linear (e.g., MUSCL), parabolic (e.g., PPM) or polynomials of even higher degree, will reduce the pressure difference at the cell interface and therefore improve the situation. However, the pressure profile resulting from gravitational stratification is in general not a simple polynomial function. Hence, the pressure jump at cell interfaces will be proportional to the reconstruction’s truncation error. Piece-wise polynomial reconstructions are thus inappropriate to represent a hydrostatic equilibrium.
In the following we construct a finite volume scheme that exactly (or up to machine precision) preserves a discrete version of hydrostatic equilibrium Eq. (12). We reconstruct the equilibrium pressure within the ith cell according the hydrostatic equilibrium as follows 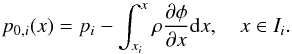 (13)To evaluate explicitly the above integral, we need to find a reconstruction of the density and the gradient of the gravitational potential. We assume a constant density distribution within the cell, i.e.,
(13)To evaluate explicitly the above integral, we need to find a reconstruction of the density and the gradient of the gravitational potential. We assume a constant density distribution within the cell, i.e., 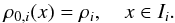 (14)Similarly, we assume the gravitational potential to be piecewise linear, i.e, linear over each staggered cell Ii + 1 / 2 = [ xi,xi + 1 ]
(14)Similarly, we assume the gravitational potential to be piecewise linear, i.e, linear over each staggered cell Ii + 1 / 2 = [ xi,xi + 1 ]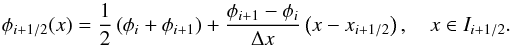 (15)This results in a piecewise constant distribution of (∂φ/∂x)i + 1 / 2 over Ii + 1 / 2.
(15)This results in a piecewise constant distribution of (∂φ/∂x)i + 1 / 2 over Ii + 1 / 2.
Now the hydrostatic pressure reconstruction (13)can be explicitly evaluated and at cell interfaces we obtain 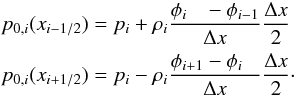 (16)
(16)
Note that this reconstruction is consistent with the central discretization of the momentum source term (11), i.e., 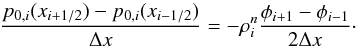 (17)Consider now the reconstructed pressure at the left side of the interface p0,i(xi + 1 / 2), i.e., extrapolated from cell i, and at the right side of the interface p0,i + 1(xi + 1 / 2), i.e., extrapolated from cell i + 1. If we have pressure equilibrium at the interface, i.e., p0,i(xi + 1 / 2) = p0,i + 1(xi + 1 / 2), we find that
(17)Consider now the reconstructed pressure at the left side of the interface p0,i(xi + 1 / 2), i.e., extrapolated from cell i, and at the right side of the interface p0,i + 1(xi + 1 / 2), i.e., extrapolated from cell i + 1. If we have pressure equilibrium at the interface, i.e., p0,i(xi + 1 / 2) = p0,i + 1(xi + 1 / 2), we find that 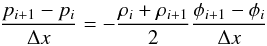 (18)holds. This is the discrete hydrostatic equilibrium, which is preserved by our hydrostatic pressure reconstruction. As can be shown easily (by Taylor expansions), Eq. (18)is a spatially second-order accurate approximation of Eq. (12).
(18)holds. This is the discrete hydrostatic equilibrium, which is preserved by our hydrostatic pressure reconstruction. As can be shown easily (by Taylor expansions), Eq. (18)is a spatially second-order accurate approximation of Eq. (12).
It should be noted that Eq. (12)represents only a mechanical equilibrium. No thermal equilibrium is implied and the hydrostatic equilibrium may be physically unstable to convection, for instance. Similarly, the discrete hydrostatic equilibrium (18), which is preserved by our reconstruction, represents only a mechanical equilibrium. No assumption is made on a thermal equilibrium; that is, no explicit temperature or entropy profile has to be assumed for the hydrostatic reconstruction. Therefore, our reconstruction preserves discrete hydrostatic equilibria with arbitrary temperature or entropy stratification. This represents a substantial generalization of the reconstruction advocated by Käppeli & Mishra (2014).
2.1.2. First-order scheme
It is now straightforward to assemble a spatially first-order accurate well-balanced scheme. The density and velocity are reconstructed in a piecewise constant manner (the corresponding cell averages are used). The pressure is reconstructed with the hydrostatic reconstruction. In summary, the cell interface extrapolated variables read ![\begin{equation} \label{eq:nm_1dcart_wb_1st0010} \boldsymbol{w}_{i\mp1/2\pm} = \left[ \begin{array}{c} \rho_{i} \\ \varv_{x,i} \\ p_{0,i}(x_{i\mp1/2}) \end{array} \right] , \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq54.png) (19)where the p0,i(xi ± 1 / 2) are given by Eq. (16).
(19)where the p0,i(xi ± 1 / 2) are given by Eq. (16).
Suppose we are given initial data fulfilling the discrete equilibrium (18)and νx = 0. It is then easy to check, that the semi-discrete finite volume scheme (8)with the above reconstruction of the primitive variables, a numerical flux with property (10)and the source term discretization (11)leads to , 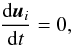 (20)i.e., the discrete hydrostatic initial data is preserved exactly (or up to machine precision). Thus, the scheme is well-balanced.
(20)i.e., the discrete hydrostatic initial data is preserved exactly (or up to machine precision). Thus, the scheme is well-balanced.
2.1.3. Second-order scheme
Although the scheme derived in the previous section is capable to resolve a spatially second-order accurate discrete hydrostatic equilibrium (Eq. (18)), any perturbation on top of the equilibrium is only resolved with spatial first-order accuracy. Therefore a higher-order extension is desirable for practical applications. In the following, we design a spatially second-order accurate extension of our well-balanced scheme.
Spatial second-order accuracy is achieved with a piecewise linear reconstruction of the primitive variables. A standard non-oscillatory piecewise linear reconstruction for some state variable q is given by 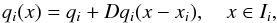 (21)where Dqi denotes a (limited) slope. A simple choice for the slope is the so-called generalized minmod limiter (see, e.g., Kurganov & Tadmor 2000)
(21)where Dqi denotes a (limited) slope. A simple choice for the slope is the so-called generalized minmod limiter (see, e.g., Kurganov & Tadmor 2000) 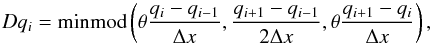 (22)where the minmod function is defined by
(22)where the minmod function is defined by 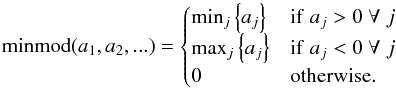 (23)For θ = 1 (θ = 2), this yields the traditional minmod (monotonized centered) limiter. In all numerical experiments presented below we set θ = 2. Applying the standard reconstruction (21)and (22)to density, velocity and pressure results in spatially second-order accurate interface values.
(23)For θ = 1 (θ = 2), this yields the traditional minmod (monotonized centered) limiter. In all numerical experiments presented below we set θ = 2. Applying the standard reconstruction (21)and (22)to density, velocity and pressure results in spatially second-order accurate interface values.
However, a standard piecewise linear reconstruction of the pressure will not preserve the discrete hydrostatic equilibrium (18). To design an equilibrium preserving pressure reconstruction within the ith cell pi(x), we decompose it into an equilibrium p0,i(x) and a perturbation p1,i(x) part (Botta et al. 2004; Käppeli & Mishra 2014): 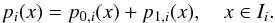 (24)We stress that the perturbation part is not assumed to be small. The equilibrium pressure reconstruction p0,i(x) is simply given by Eq. (13). Note that no special equilibrium preserving reconstruction needs to be applied to the density, on account of the assumed piecewise constant equilibrium distribution (14).
(24)We stress that the perturbation part is not assumed to be small. The equilibrium pressure reconstruction p0,i(x) is simply given by Eq. (13). Note that no special equilibrium preserving reconstruction needs to be applied to the density, on account of the assumed piecewise constant equilibrium distribution (14).
The data for the reconstruction of the pressure perturbation p1,i(x) is obtained by extrapolating the equilibrium pressure reconstruction p0,i(x) of the ith cell to the neighboring cells i − 1 and i + 1: 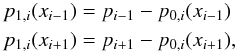 (25)where the equilibrium pressure reconstruction p0,i(x) is given by Eq. (13):
(25)where the equilibrium pressure reconstruction p0,i(x) is given by Eq. (13): 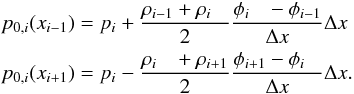 (26)Note that p1,i(xi) = pi − p0,i(xi) = 0 holds, i.e., the equilibrium reconstruction equals the cell average pi at the cell center. Now, a piecewise linear reconstruction (21)and (22)can be applied to the pressure perturbation in a straightforward manner. The reconstruction is sketched in Fig. 1.
(26)Note that p1,i(xi) = pi − p0,i(xi) = 0 holds, i.e., the equilibrium reconstruction equals the cell average pi at the cell center. Now, a piecewise linear reconstruction (21)and (22)can be applied to the pressure perturbation in a straightforward manner. The reconstruction is sketched in Fig. 1.
In summary, the cell interface extrapolated variables read ![\begin{equation} \label{eq:nm_1dcart_wb_2nd0060} \boldsymbol{w}_{i\mp1/2\pm} = \left[ \begin{array}{c} \rho_{i}(x_{i\mp1/2}) \\ \varv_{x,i}(x_{i\mp1/2}) \\ p_{0,i}(x_{i\mp1/2}) + p_{1,i}(x_{i\mp1/2}) \end{array} \right] , \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq75.png) (27)where p0,i(xi ± 1 / 2) is given by Eq. (16).
(27)where p0,i(xi ± 1 / 2) is given by Eq. (16).
Note that if we are given data fulfilling the discrete hydrostatic equilibrium (18), then the reconstruction preserves the equilibrium exactly (or up to machine precision) since in this case the pressure perturbation vanishes by design, i.e., p1,i(x) = 0. Hence, the scheme is still well-balanced. But now, thanks to the piecewise linear reconstruction of the equilibrium perturbation, the scheme is also spatially second-order accurate for perturbations of the equilibrium.
 |
Fig. 1 Piecewise linear well-balanced reconstruction of the pressure. The pressure profile (black line) within the ith cell is decomposed into an equilibrium (blue line) and a perturbation part p(x) = p0,i(x) + p1,i(x). The equilibrium pressure p0,i(x) is simply given by Eq. (13). The point values of the perturbation are then computed at neighboring cell centers xi ± 1 by extrapolation of the equilibrium pressure reconstruction p0,i(xi ± 1). A piecewise linear monotonicity preserving reconstruction can then be applied to the pressure perturbation data, i.e., p1,i(xi ± 1) = pi ± 1 − p0,i(xi ± 1) and p1,i(xi) = 0. |
2.2. Time integration
The temporal domain is discretized into time steps Δtn = tn + 1 − tn where the superscript n labels the different time levels. The system of ordinary differential equations (ODE) (8)can then be integrated in time with a suitable explicit or implicit integrator (see, e.g., Gottlieb et al. 2001).
For instance, a fully discrete first-order scheme results with the simple explicit Euler time integration 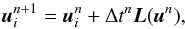 (28)where L stands for the right hand side of Eq. (8)with the gravitational source term Eq. (11)and the spatially first-order hydrostatic reconstruction Eq. (19).
(28)where L stands for the right hand side of Eq. (8)with the gravitational source term Eq. (11)and the spatially first-order hydrostatic reconstruction Eq. (19).
For full second-order accuracy, we use the second-order strong stability preserving (SSP) Runge-Kutta time stepping (Gottlieb et al. 2001)
where now the spatially second-order hydrostatic equilibrium reconstruction Eq. (27)is used.
We emphasize, that implicit time integrators could also be used. Though, for our convenience, we only present results computed with the above explicit time integrators.
2.3. Multi-dimensional extension
We now describe the extension of the above schemes for hydrostatic equilibrium to the multi-dimensional case. Unfortunately, the resulting scheme is only exact, i.e., well-balanced, if the direction of the gravitational force is exactly aligned with one coordinate axis or the fluid has constant density. However, as we demonstrate in Sect. 3.4, the scheme also considerably improves the preservation of hydrostatic equilibrium in this suboptimal case.
For the sake of simplicity of presentation, we treat the two-dimensional Cartesian case explicitly and the extension to other geometries and three dimensions is analogous. The two-dimensional Euler equations with gravity in Cartesian coordinates are given by 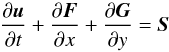 (30)with
(30)with ![\begin{equation} \label{eq:nm_multiD_0020} \begin{aligned} \boldsymbol{u} = \left[ \begin{array}{c} \rho \\ \rho \varv_x \\ \rho \varv_y \\ E \end{array} \right] \end{aligned} \; , \; \begin{aligned} \boldsymbol{F} = \left[ \begin{array}{c} \rho \varv_x \\ \rho \varv_x^2 + p \\ \rho \varv_y \varv_x \\ (E + p) \varv_x \end{array} \right] \end{aligned} \; , \; \begin{aligned} \boldsymbol{G} = \left[ \begin{array}{c} \rho \varv_y \\ \rho \varv_x \varv_y \\ \rho \varv_y^2 + p \\ (E + p) \varv_y \end{array} \right] \end{aligned} \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq89.png) (31)and
(31)and ![\begin{equation} \label{eq:nm_multiD_0030} \begin{aligned} \boldsymbol{S} = \boldsymbol{S}_x + \boldsymbol{S}_y = - \left[ \begin{array}{c} 0 \\ \rho \\ 0 \\ \rho \varv_x \end{array} \right] \frac{\partial \phi}{\partial x} - \left[ \begin{array}{c} 0 \\ 0 \\ \rho \\ \rho \varv_y \end{array} \right] \frac{\partial \phi}{\partial y} \end{aligned} . \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq90.png) (32)The primitive variables are given by w = [ ρ,νx,νy,p ] T.
(32)The primitive variables are given by w = [ ρ,νx,νy,p ] T.
Space is discretized into cells or finite volumes Ii,j = [ xi−1 / 2,xi + 1 / 2 ] × [ yj−1 / 2,yj + 1 / 2 ] of uniform (for simplicity) size Δx = xi + 1 / 2−xi−1 / 2 and Δy = yj + 1 / 2 − yj−1 / 2. By integrating (30)over a cell Ii,j we obtain a semi-discrete scheme for the evolution of the cell-averaged conserved quantities ui,j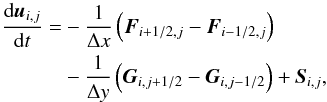 (33)where Fi + 1 / 2,j = ℱ(wi + 1 / 2 − ,j,wi + 1 / 2 + ,j) and
(33)where Fi + 1 / 2,j = ℱ(wi + 1 / 2 − ,j,wi + 1 / 2 + ,j) and 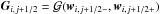 are the numerical fluxes in the respective direction and Si,j is the gravity source term. The wi + 1 / 2 ± ,j and wi,j + 1 / 2 ± are the cell interface extrapolated primitive variables.
are the numerical fluxes in the respective direction and Si,j is the gravity source term. The wi + 1 / 2 ± ,j and wi,j + 1 / 2 ± are the cell interface extrapolated primitive variables.
The discrete gravitational source term is evaluated by standard spatially second-oder accurate centered differences: ![\begin{equation} \label{eq:nm_multiD_0050} \boldsymbol{S}_{i,j} = - \left[ \begin{array}{c} 0 \\ \rho_{i,j} \\ 0 \\ (\rho \varv_x)_{i,j} \end{array} \right] \frac{\phi_{i+1,j} - \phi_{i-1,j}}{2 \Delta x} - \left[ \begin{array}{c} 0 \\ 0 \\ \rho_{i,j} \\ (\rho \varv_y)_{i,j} \end{array} \right] \frac{\phi_{i,j+1} - \phi_{i,j-1}}{2 \Delta y} \cdot \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq103.png) (34)The hydrostatic reconstruction of Sects. 2.1.1–2.1.3 can then by applied in x- and y-direction independently:
(34)The hydrostatic reconstruction of Sects. 2.1.1–2.1.3 can then by applied in x- and y-direction independently: ![\begin{equation} \label{eq:nm_multiD_0060} \boldsymbol{w}_{i\mp1/2\pm,j} = \left[ \begin{array}{c} \rho_{i,j}(x_{i\mp1/2},y_j) \\ \varv_{x,i,j}(x_{i\mp1/2},y_j) \\ \varv_{y,i,j}(x_{i\mp1/2},y_j) \\ p_{0,i,j}(x_{i\mp1/2},y_j) + p_{1,i,j}(x_{i\mp1/2},y_j) \end{array} \right] \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq106.png) (35)and
(35)and ![\begin{equation} \label{eq:nm_multiD_0070} \boldsymbol{w}_{i,j\mp1/2\pm} = \left[ \begin{array}{c} \rho_{i,j}(x_i,y_{j\mp1/2}) \\ \varv_{x,i,j}(x_i,y_{j\mp1/2}) \\ \varv_{y,i,j}(x_i,y_{j\mp1/2}) \\ p_{0,i,j}(x_i,y_{j\mp1/2}) + p_{1,i,j}(x_i,y_{j\mp1/2}) \end{array} \right] , \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq107.png) (36)where the density and the velocity are reconstructed piecewise linearly in a standard way.
(36)where the density and the velocity are reconstructed piecewise linearly in a standard way.
As in the one-dimensional case, the pressure reconstruction proceeds in two steps. First the equilibrium pressure is reconstructed to cell interfaces p0,i,j(xi ∓ 1 / 2,yj) and p0,i,j(xi,yj ∓ 1 / 2) by applying Eq. (16)in a straightforward dimension-by-dimension manner 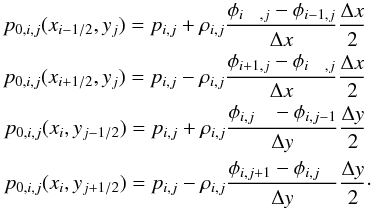 (37)The equilibrium perturbations at cell interface p1,i,j(xi ∓ 1 / 2,yj) and p1,i,j(xi,yj ∓ 1 / 2) are also obtained by applying the procedure outlined in Sect. 2.1.3 in a dimension-by-dimension manner.
(37)The equilibrium perturbations at cell interface p1,i,j(xi ∓ 1 / 2,yj) and p1,i,j(xi,yj ∓ 1 / 2) are also obtained by applying the procedure outlined in Sect. 2.1.3 in a dimension-by-dimension manner.
It follows from a simple calculation (analogue to the derivation of Eq. (18)), that the two-dimensional equilibrium preserved by the hydrostatic reconstruction would be 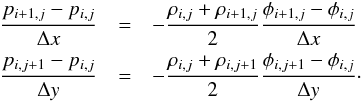 At first sight, the latter two expressions seem to be suitable discretizations of hydrostatic equilibrium (5)in two dimensions. However, it turns out that this is only true if a discrete curl operator applied to the right-hand-side of the above equations vanishes, i.e., the integrability condition for (5)is fulfilled in a discrete sense. This is in general not the case and therefore our scheme is in general not mathematically well-balanced in the multidimensional case. However, we repeat that the scheme is well-balanced if the direction of the gravitational force is exactly aligned with a coordinate axis.
At first sight, the latter two expressions seem to be suitable discretizations of hydrostatic equilibrium (5)in two dimensions. However, it turns out that this is only true if a discrete curl operator applied to the right-hand-side of the above equations vanishes, i.e., the integrability condition for (5)is fulfilled in a discrete sense. This is in general not the case and therefore our scheme is in general not mathematically well-balanced in the multidimensional case. However, we repeat that the scheme is well-balanced if the direction of the gravitational force is exactly aligned with a coordinate axis.
3. Numerical tests
In this section we present a series of numerical experiments to demonstrate the applicability and performance of the proposed well-balanced scheme. For comparison, we also present results obtained with a standard (unbalanced) base scheme, i.e., without hydrostatic reconstruction. Moreover, given the limited resolution and utility of first-order schemes, only results obtained with the second-order schemes are shown.
To specify a timescale on which a model reacts to perturbations of its hydrostatic equilibrium, we set the sound crossing time as 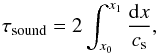 (38)where cs is the speed of sound and the integral has to be taken over the extent of the stationary state of interest.
(38)where cs is the speed of sound and the integral has to be taken over the extent of the stationary state of interest.
In some test cases, we also quantify the accuracy of the numerically obtained solutions by computing the errors as 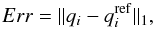 (39)with ∥ . ∥ 1 denotes the L1-norm. Here q is a selected quantity of interest (e.g., density, pressure, ...) and qref is a reference solution, i.e., the stationary state to be maintained discretely or an interpolated numerically obtained reference solution on a very fine mesh.
(39)with ∥ . ∥ 1 denotes the L1-norm. Here q is a selected quantity of interest (e.g., density, pressure, ...) and qref is a reference solution, i.e., the stationary state to be maintained discretely or an interpolated numerically obtained reference solution on a very fine mesh.
In all simulations presented below, we have employed a CFL number of CCFL = 0.9.
3.1. Hydrostatic atmospheres
As a first numerical experiment, we consider the very simple setting of a one-dimensional hydrostatic atmosphere in a constant gravitational field 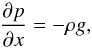 (40)where g is the constant gravitational acceleration. Then, the gravitational potential is a simple linear function φ(x) = gx. This type of setup is relevant for the simulation of wave propagation in stellar atmospheres (e.g., Bogdan et al. 2003; Fuchs et al. 2010).
(40)where g is the constant gravitational acceleration. Then, the gravitational potential is a simple linear function φ(x) = gx. This type of setup is relevant for the simulation of wave propagation in stellar atmospheres (e.g., Bogdan et al. 2003; Fuchs et al. 2010).
To explicitly integrate (40)an assumption on a thermodynamic variable (e.g., entropy or temperature) profile has to be made. We consider two idealized cases: isentropic and isothermal profiles. Note that we use the scheme proposed in this paper. This has to be contrasted with the scheme of Käppeli & Mishra (2014), which could handle either the isentropic or the isothermal case at a time. Arbitrary entropy/temperature stratifications are considered in the astrophysical applications below.
For this example, we assume a monoatomic ideal gas EoS 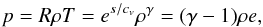 (41)where we set R = 1, cv = 3R/ 2 and γ = 5 / 3.
(41)where we set R = 1, cv = 3R/ 2 and γ = 5 / 3.
The computational domain is set to [ 0,L ], where L = 2, and is uniformly discretized by N cells, i.e., we set the cell size Δx = L/N, the cell interfaces xi + 1 / 2 = Δxi, i = 0,...,N, and the cell centers xi = (xi−1 / 2 + xi + 1 / 2) / 2, i = 1,...,N. We choose N = 32,64,128,256,512,1024,2048 for the resolution, respectively.
The density and pressure are then initialized by solving the discrete hydrostatic equilibrium 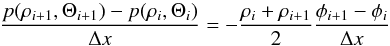 (42)numerically with a Newton-Raphson method. Here Θ is assumed to be given and stands for either specific entropy s or temperature T.
(42)numerically with a Newton-Raphson method. Here Θ is assumed to be given and stands for either specific entropy s or temperature T.
The boundaries are treated as follows. As demanded by a second-order scheme, we specify two ghost cells at each end of the physical domain. For the density ρ, velocity νx and the thermodynamic variable Θ we apply very simple transmissive boundary conditions with zero-order extrapolation: 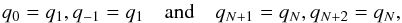 (43)where q = ρ,νx,Θ. The pressure is extrapolated according the discrete hydrostatic equilibrium, i.e., by numerically solving Eq. (42)for the ghost cells starting from the pressure of the last cell of the physical domain.
(43)where q = ρ,νx,Θ. The pressure is extrapolated according the discrete hydrostatic equilibrium, i.e., by numerically solving Eq. (42)for the ghost cells starting from the pressure of the last cell of the physical domain.
For the isentropic atmosphere, we set the density and pressure to ρ0 = 1 and p0 = 1 at the base, i.e., at x = 0. This results in an entropy 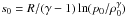 , which is put over the whole domain. The hydrostatic atmosphere is then initialized by solving numerically Eq. (42)with the EoS (41)and s0. The resulting isentropic atmosphere has a sound crossing time of τsound ≈ 4.4.
, which is put over the whole domain. The hydrostatic atmosphere is then initialized by solving numerically Eq. (42)with the EoS (41)and s0. The resulting isentropic atmosphere has a sound crossing time of τsound ≈ 4.4.
Similarly for the isothermal atmosphere, we set the density and pressure to ρ0 = 1 and p0 = 1 at the base. This yields a temperature of T0 = p/Rρ = 1 over the whole domain. The hydrostatic atmosphere is then initialized numerically. The resulting isothermal atmosphere has a sound crossing time of τsound ≈ 3.2.
3.1.1. Well-balanced property
We begin by numerically verifying the well-balancing properties of the scheme. To this end we evolve the isentropic and isothermal atmospheres with the well-balanced and a standard second-order scheme for two sound crossing times, i.e., tf = 2τsound. At the end of the simulation, we compute the L1-norm of the difference (39)between the initial and the final state. This reflects how well a discrete hydrostatic state can be preserved by the corresponding scheme.
The results for the isentropic and isothermal atmospheres are shown in Fig. 2 for the pressure. The results for the density are similar and are not displayed. From the figure it is clear that the well-balanced scheme is able to maintain the discrete equilibrium up to machine precision. The standard scheme is not able to preserve the discrete hydrostatic equilibrium exactly. The committed error is proportional to the scheme’s truncation error, which scales as a certain power l of the mesh width Δxl.
From the figure, it appears that the standard scheme converges to the discrete hydrostatic atmosphere, i.e., the initial state, with roughly the third power of the mesh width. At first sight, this superconvergence may seem surprising since the schemes are only of second-order accuracy. However, such a superconvergence has been observed before and has been attributed to the fact that the base scheme may be asymptotically high order, i.e, it has a higher order of accuracy at a steady state, compared to its designed order of accuracy, see Fjordholm et al. (2011).
 |
Fig. 2 L1-norm of the difference between the initial and final pressure for the isentropic (solid and dashed blue lines) and isothermal (solid and dashed red lines) atmospheres. The solid and dashed lines represent the simulation performed with the standard and the well-balanced (WB) schemes, respectively. The apparent third-order superconvergence of the standard scheme is explained in the text. |
3.1.2. Wave propagation
Next we test the ability of the well-balanced and the standard schemes to propagate waves on top of the hydrostatic atmospheres. For brevity, only the results for the isentropic atmosphere are shown. The results for the isothermal atmosphere are analog. We impose a periodic velocity perturbation at the bottom of the atmosphere 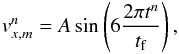 where m = −1,0 is the boundary cell index. The amplitude A is varied in order to compare the ability of the schemes for the propagation of small (A = 10-8), intermediate (A = 10-6) and large (A = 10-1) waves. The simulation is stopped at tf = 1.8, shortly before the waves reach the upper boundary.
where m = −1,0 is the boundary cell index. The amplitude A is varied in order to compare the ability of the schemes for the propagation of small (A = 10-8), intermediate (A = 10-6) and large (A = 10-1) waves. The simulation is stopped at tf = 1.8, shortly before the waves reach the upper boundary.
The errors in velocity for the standard and well-balanced schemes are shown in Fig. 3. The errors were computed on the basis of a reference solution obtained with the well-balanced scheme at high resolution (N = 8192).
For the small amplitude A = 10-8 case, we observe the superiority of the well-balanced (dashed blue) versus the standard (solid blue) scheme, i.e., the error is orders of magnitude smaller. The well-balanced scheme shows a rough second-order convergence. Although way off, the standard schemes seems to show third-order convergence. However, this is related to the superconvergence already mentioned in Sect. 3.1.1. Figure 4 shows the velocity profile for the standard (solid red) and the well-balanced (dashed red) schemes for N = 512, together with the reference solution (solid blue). The well-balanced scheme is able to resolve the wave pattern very accurately. On the other hand, the standard scheme shows spurious deviations because of its inability to properly resolve the hydrostatic background.
 |
Fig. 3 L1-norm error between the numerical and reference (N = 8192) velocity for the isentropic atmosphere. The blue, red and green line correspond to the wave amplitudes A = 10-8,10-6,10-1, respectively. The solid and dashed lines represent the simulation performed with the standard and the well-balanced (WB) schemes, respectively. |
For the large amplitude (A = 10-1) case, the standard and the well-balanced schemes do equally well. Both show a rate of convergence close to one. This has to be expected, because the large amplitude waves quickly steepen into saw-tooth waves, propagating up the atmosphere. The velocity profile for both schemes and the reference solution are shown in Fig. 4. This case shows, that the well-balanced reconstruction does not destroy the shock-capturing properties of the base scheme.
The intermediate amplitude (A = 10-6) case is interesting. At low resolutions (≤128), the well-balanced scheme is clearly superior. In this regime, the standard scheme shows superconvergence with roughly order three. This is the regime, where the committed error is dominated by the hydrostatic atmosphere, while the wave pattern is totally unresolved. At higher resolutions (>128), the committed error is dominated by the wave pattern and the expected second-order accuracy is recovered. The well-balanced scheme shows a rate of convergence of roughly two over the full resolution range.
 |
Fig. 4 Velocity profile for the small (left) and large (right) amplitude waves running down the isentropic atmosphere. The solid/dashed red lines are the solutions obtained with the standard/well-balanced scheme with N = 512, respectively. In solid blue is also shown a reference solution obtained with the well-balanced scheme and N = 8192. |
Characteristic data for the toy core-collapse model.
3.2. Toy model of core-collapse
We consider a toy model of core-collapse supernova from Janka et al. (1993). This test simulates in spherical symmetry the collapse, bounce, evolution of the induced shock waves and formation of a proto-neutron star (PNS) for a simplified model of a stellar core and EoS. The forming PNS is nearly in hydrostatic equilibrium as it evolves very slowly on a timescale, very much longer compared to the hydrostatic timescale (Gρ)− 1 / 2. Since the PNS is the result of a very dynamic process, it is interesting to investigate how accurately the well-balanced scheme captures the resulting near equilibrium state. Moreover, the problem also tests the robustness of the scheme with non-ideal EoS and strong shocks. Note that the gravitational potential is dictated by self-gravity in this test.
The initial configuration is an equilibrium polytrope with polytropic index n = 3 (corresponding to a polytropic γ = 4 / 3), polytropic constant K = 4.897 × 1014 (in cgs units) and a central density ρc = 1010g / cm3. This corresponds to a total mass of M ≈ 1.44 M⊙ and a radius R ≈ 1.54 × 103 km.
The EoS is simple, analytic and consists of a purely polytropic part and a thermal part. The total pressure and internal energy density are given by  where the subscripts refer to the respective part.
where the subscripts refer to the respective part.
The polytropic part is given by 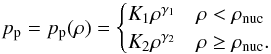 (46)The nuclear density parameter ρnuc marks the separation from the low density (i.e., subnuclear) regime with polytropic constant K1 and exponent γ1 and the high density (i.e., supranuclear) regime with polytropic constant K2 and exponent γ2. The polytropic internal energy density is given by
(46)The nuclear density parameter ρnuc marks the separation from the low density (i.e., subnuclear) regime with polytropic constant K1 and exponent γ1 and the high density (i.e., supranuclear) regime with polytropic constant K2 and exponent γ2. The polytropic internal energy density is given by 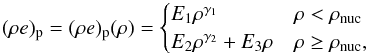 (47)where E1, E2 and E3 are constants. The constants follow from requiring continuity of pressure and internal energy at ρnuc once the parameters ρnuc, K1, γ1 and γ2 have been fixed:
(47)where E1, E2 and E3 are constants. The constants follow from requiring continuity of pressure and internal energy at ρnuc once the parameters ρnuc, K1, γ1 and γ2 have been fixed: 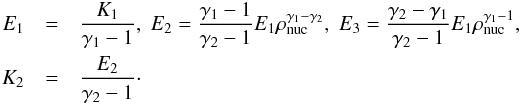 For the polytropic constant we have used K1 = 4.897 × 1014cgs, i.e., the same value as for computing the equilibrium polytrope. For the subnuclear density regime we set the polytropic exponent to γ1 = 1.325. This is slightly smaller than the equilibrium configuration and leads to the collapse of the polytrope. For supranuclear densities we set the polytropic exponent to γ2 = 2.5. This mimics the stiffening of the EoS due to repulsive nuclear forces and nucleon degeneracy.
For the polytropic constant we have used K1 = 4.897 × 1014cgs, i.e., the same value as for computing the equilibrium polytrope. For the subnuclear density regime we set the polytropic exponent to γ1 = 1.325. This is slightly smaller than the equilibrium configuration and leads to the collapse of the polytrope. For supranuclear densities we set the polytropic exponent to γ2 = 2.5. This mimics the stiffening of the EoS due to repulsive nuclear forces and nucleon degeneracy.
The thermal pressure pth is related to the thermal internal energy density (ρe)th through an ideal gas relation with ratio of specific heats γth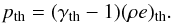 (48)The thermal internal energy density is computed by subtracting the polytropic internal energy density from the total one
(48)The thermal internal energy density is computed by subtracting the polytropic internal energy density from the total one 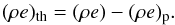 (49)We use the value γth = 1.5 corresponding to a mixture of relativistic and non-relativistic gases. For further details we refer to Janka et al. (1993).
(49)We use the value γth = 1.5 corresponding to a mixture of relativistic and non-relativistic gases. For further details we refer to Janka et al. (1993).
The polytrope is then set up on the radial domain [ 0,1.5 × 103 ]km and discretized by N = 128,256,512,1024,8192 cells with an exponentially growing cell spacing Δri = ai − 1Δr1, i = 2,...,N. Here a ≥ 1 is the grid scaling parameter and Δr1 the size of the first cell. See Table 1 for their resolution dependent values. For the inner boundary we use reflective conditions. On the outer boundary we use zeroth-order extrapolation. This avoids the use of an artificial atmosphere (the polytrope has a finite radius), but allows for matter in or outflow. However, we stop the simulation before any significant matter outflow due to the explosion takes place.
We then evolved numerically the polytrope with the standard and the new well-balanced second-order schemes for all the resolutions from t = 0 up to t = 110ms. The polytrope starts to collapse due to the pressure deficit stemming from the lowering of the EoS’s polytropic exponent from 4 / 3 to 1.325. This collapse goes on until the central density exceeds ρnuc, where the EoS stiffens. This allows the so-called inner core, i.e., the inner part that collapses subsonically, to progressively halt the collapse and, eventually, to find a new equilibrium configuration, i.e., the PNS. Starting at the center of the inner core, where the density is largest, successive mass shells are gradually stopped. Pressure waves move out in radius and accumulate near the sonic point, i.e., the point where the collapse velocity equals the sound velocity, where they steepen into a shock wave. Due to its inertia, the inner core overshoots its equilibrium and rebounds behind the shock wave. This is the so-called core bounce. In the following we define the time of bounce as the time when the average density within the innermost 2km reaches its maximum.
 |
Fig. 5 Central density as a function of time for the standard (left panel) and the well-balanced (right panel) scheme. In both panels the (blue) dashed, (red) dash-dotted, (green) dotted and the (black) solid line represent the simulation with N = 128,256,512,8192, respectively. |
 |
Fig. 6 Density as a function of radius for the standard and well-balanced schemes with N = 256 (left panel) and N = 512 (right panel). In both panels the (black) solid, (blue) dashed and the (red) dash-dotted line represent the reference solution (the well-balanced with N = 8192 in both panels), the solutions computed with standard and the well-balanced scheme, respectively. For both resolution, the well-balanced solutions are indistinguishable from the reference. |
The bounce of the inner core generates outward directed velocities at and somewhat below the shock. An explosion shock is born. Schematically, the explosion shock is launched and energized by the rebounding inner core “piston” thereby gravitationally unbinding a substantial amount of mass. With the chosen parameters, the toy model of core-collapse always results in a formidable explosion.
In Table 1 we have compiled the time and the density at bounce for the standard and well-balanced schemes. The simulations with N = 8192, giving a central resolution of 25m, serve as references. Regarding the time of bounce, we observe that all the simulations give results that differs from each other only by a few tenths of ms. Similarly, the bounce density is also somewhat scattered around 3.6 × 1014g / cm3. But nevertheless, we observe a slight trend that the well-balanced scheme seems to bounce slightly later.
The PNS is slowly evolving towards an equilibrium. Its hydrostatic timescale, i.e., the typical time in which an equilibrium reacts to perturbations, is very short 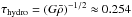 ms. Here we define
ms. Here we define 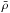 as the average density over the region where ρ ≥ ρnuc. A measure of how well a numerical scheme can resolve this near-equilibrium is given by the evolution of the central density. In Fig. 5 we show the central density as a function of time. The reference solutions (solid black lines) show that after the bounce and a few following oscillations, the central density remains nearly constant. From the figure we observe that the standard scheme has difficulties to maintain the central density at low resolutions N< 512. Even for N = 512 a slight drift is visible. On the other hand, the well-balanced scheme resolves the equilibrium pretty well at all resolutions. The final central density is presented in Table 1. We note that the well-balanced scheme with N = 128 slightly overestimates the final central density. For N> 128 the well-balanced scheme is very close to the one of the reference solution. However, the standard scheme seems to need a resolution of at least N = 1024 in order to be close to the reference final central density.
as the average density over the region where ρ ≥ ρnuc. A measure of how well a numerical scheme can resolve this near-equilibrium is given by the evolution of the central density. In Fig. 5 we show the central density as a function of time. The reference solutions (solid black lines) show that after the bounce and a few following oscillations, the central density remains nearly constant. From the figure we observe that the standard scheme has difficulties to maintain the central density at low resolutions N< 512. Even for N = 512 a slight drift is visible. On the other hand, the well-balanced scheme resolves the equilibrium pretty well at all resolutions. The final central density is presented in Table 1. We note that the well-balanced scheme with N = 128 slightly overestimates the final central density. For N> 128 the well-balanced scheme is very close to the one of the reference solution. However, the standard scheme seems to need a resolution of at least N = 1024 in order to be close to the reference final central density.
 |
Fig. 7 Energies and total energy conservation as a function of time from the standard (left) and well-balanced (right) scheme with N = 512. In both panels, the solid (blue) line is the internal energy Eint, the dashed (green) line is the kinetic energy Ekin, the dash-dotted (red) line is minus the gravitational energy −Egrav and the dotted (black) line is the total energy conservation ΔE. |
Integrated quantities for the toy core-collapse model at final time.
In Fig. 6 we show the density profile at final time t = 110. At this time the main shock wave, initiated during core bounce, is very close to the outer boundary. The flow below 100km is nearly hydrostatic with Mach numbers MS< 0.01 at r = 100km and MS< 0.001 below r = 50km. In between r = 100km and the main shock wave there are some secondary shock waves, initiated through post-bounce oscillations of the PNS, running up the polytrope. In the left (right) panel are shown the solutions obtained with the standard and well-balanced scheme with N = 256 (N = 512). In both panels the solution obtained with the well-balanced scheme and N = 8192 serves as a reference. We note that in both panels the solutions from the well-balanced scheme are indistinguishable from the reference solution. On the other hand, the solutions from the standard scheme gives a very inaccurate density profile for N = 256. Even for N = 512 there are still some visible deviations in the region 10 ≤ r ≤ 100km. Note that in this region the density varies by roughly four orders of magnitude. The well-balanced scheme has no problems with these steep density variations.
In Table 2 we have compiled some integrated quantities at final time. There, Eint, Ekin and Egrav are the internal, kinetic and gravitational energy integrated of the whole domain, respectively. The error in total energy conservation is given by ΔE(t) = Etot(t) − Etot(0), where the total energy is Etot = Eint + Ekin + Egrav. We observe that the well-balanced scheme for N ≥ 256 results in internal and gravitational energies that lie within a few 0.1% from the reference values. Even for N = 128 the error is of the order of only ≈1−2%. On the other hand, for N = 128,256,512 the standard scheme deviates by more than 49%,16% and 4%, respectively. We note that it takes a resolution of N ≥ 1024 for the standard scheme to be as accurate as the well-balanced scheme with N = 256. The internal and gravitational energies are captured so well by the well-balanced scheme, because the energies are dominated by matter nearly in hydrostatic equilibrium, i.e., the PNS.
For the kinetic energy the differences between the standard and the well-balanced scheme are less pronounced for resolutions N ≥ 512. Both schemes show errors of roughly ≈1%. But for N = 128,256 the well-balanced scheme shows significantly less deviation from the reference value.
The superior performance of the well-balanced scheme is also reflected in the error of total energy conservation. Again we attribute this to the fact that a large part of matter is in near hydrostatic equilibrium, which is very well captured by the well-balanced scheme.
In Fig. 7 we display the internal, kinetic and gravitational energy and total energy conservation error as a function of time for both schemes at N = 512. We note especially that the energy conservation error grows steadily after bounce (t>tb) for the standard scheme. The well-balanced scheme shows a roughly constant total energy error.
We have also computed the total explosion energy and ejected mass for both schemes and all resolutions. We define the total explosion energy as the weighted energy integral over the computational domain 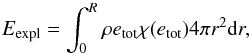 (50)where etot = e + v2/ 2 + φ is the total specific energy and the weighting function is
(50)where etot = e + v2/ 2 + φ is the total specific energy and the weighting function is 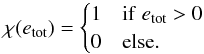 (51)Similarly we define the total ejected mass as
(51)Similarly we define the total ejected mass as 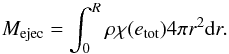 (52)These numbers for all the simulations at final time are given in Table 2. There we see that the two schemes do roughly equally well.
(52)These numbers for all the simulations at final time are given in Table 2. There we see that the two schemes do roughly equally well.
 |
Fig. 8 Spherically averaged profiles at initial time of the stellar convection simulation. Left panel: density (solid line) and pressure (dashed line). Right panel: temperature (solid line) and specific entropy (dashed line). The dotted lines represent the original profiles from the one-dimensional stellar evolution code. The red region is where the energy source term is non-zero. |
3.3. Three-dimensional stellar convection
Next we consider a simplified model for convective carbon shell burning in a massive star. In recent years, the multi-dimensional simulation of certain phases of stellar evolution has attracted considerable attention, see, e.g., Arnett & Meakin (2011), Brun & Palacios (2009), Meakin & Arnett (2007, 2006), Viallet et al. (2011), Woodward et al. (2013) and references therein. As the convective motions are realized on top of a hydrostatic state, we believe that well-balanced schemes are ideally suited for simulating such configurations. However, given the numerical focus of this paper we apply considerable simplifications to the physical modeling for the sake of presentation.
We consider a 20 M⊙ star with Z = 0.02 metallicity stemming from a stellar evolution NuGrid data set (Pignatari et al. 2013; Pignatari 2014, priv. comm.). Carbon shell burning ignites when the star is ~8.9 × 106 yr from the zero-age main sequence and lasts for ~15 yr. Around that time, the star shows the typical onion skin structure. The carbon shell overlies an oxygen-neon core and underlies helium and hydrogen burning shells.
As the computational domain we choose a spherical wedge embedded in the equatorial plane. The radial extent is set to r ∈ [ 5′000,40′000 ] km, which encompasses the convective carbon burning region and parts of the stably stratified oxygen-neon core below and carbon shell above. In azimuthal and polar direction we set ϕ ∈ [ 0,π/ 3 ] rad and θ ∈ [ π/ 3,2π/ 3 ] rad, respectively. The boundaries in radial direction are reflecting, i.e., solid wall boundary conditions, and the azimuthal and polar directions are periodic.
We use the stellar EoS thoroughly described in Timmes & Swesty (2000), which includes contributions of (photon) radiation, nuclei, electrons and positrons. The radiation is treated as a blackbody in local thermodynamic equilibrium and the nuclei are modeled by an ideal gas. The electrons and positrons are treated in a tabular manner together with a thermodynamically consistent interpolation procedure. We use the publicly available version of this EoS, Timmes (2013).
 |
Fig. 9 Spherically averaged profiles at the end of the simulation for the resolution Nr = 128. In each panel, the black lines are the initial profiles, the blue lines were computed with the standard scheme and the red lines with the well-balanced scheme. Left panel: density (solid lines) and pressure (dashed lines) profiles. Right panel: temperature (solid lines) and specific entropy (dashed lines) profiles. Note that the initial profiles are nearly indistinguishable from the well-balanced profiles at final time. |
 |
Fig. 10 Spherically averaged kinetic energy as a function of time. The left panel was computed with the standard scheme and the right one with the well-balanced scheme, both with radial resolution Nr = 128. |
Instead of solving a suitable nuclear reaction network for carbon burning, we impose a constant energy release in a region at the base of the carbon shell ![\begin{eqnarray*} % \epsilon = \begin{cases} q & \mathrm{if} \; r \in [1.19,1.35] \times 10^4 \; \mathrm{km} \\ 0 & \mathrm{elsewhere}, \end{cases} \end{eqnarray*}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq276.png) where q = 2 × 1011 erg/g/s. We note that this heating rate is much stronger (~100 times) than with a nuclear reaction network. We nevertheless evolve as passively advected scalars the abundances of H1, He4, C12, O16, Ne20 and Si28 to get the pressure contributions from nuclei correctly, i.e., in addition to Eqs. (1)−(3), we evolve the following equations
where q = 2 × 1011 erg/g/s. We note that this heating rate is much stronger (~100 times) than with a nuclear reaction network. We nevertheless evolve as passively advected scalars the abundances of H1, He4, C12, O16, Ne20 and Si28 to get the pressure contributions from nuclei correctly, i.e., in addition to Eqs. (1)−(3), we evolve the following equations 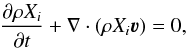 where i = H,He,C,O,Ne,Si. The mass fractions fulfill the constraint that their sum is equal to one. When evolving the above equations discretely this constraint is usually violated. Well-balancing does not help to fulfill the constraint and special methods such as the Consistent Multi-fluid Advection (CMA) by Plewa & Müller (1999) would have to be used. But since we are not performing a detailed chemical evolution, we have ignored the constraint on the mass fractions. However, our well-balanced scheme could be combined with the CMA method in a straightforward manner. We further ignore the effects of radiative diffusion, which may be justified by the high opacity and our short simulation time (~1 h of physical time).
where i = H,He,C,O,Ne,Si. The mass fractions fulfill the constraint that their sum is equal to one. When evolving the above equations discretely this constraint is usually violated. Well-balancing does not help to fulfill the constraint and special methods such as the Consistent Multi-fluid Advection (CMA) by Plewa & Müller (1999) would have to be used. But since we are not performing a detailed chemical evolution, we have ignored the constraint on the mass fractions. However, our well-balanced scheme could be combined with the CMA method in a straightforward manner. We further ignore the effects of radiative diffusion, which may be justified by the high opacity and our short simulation time (~1 h of physical time).
We numerically evolve the three-dimensional equations of hydrodynamics in spherical coordinates with a source term ρϵ added to the right hand-side of the energy Eq. (3). For the radial direction we have chosen two resolutions Nr = 64 128 corresponding to uniform cell sizes of Δr ≈ 547, 273 km, respectively. The azimuthal and polar directions are discretized by Nϕ = Nθ = 64 cells, which corresponds to an angular cell extent of Δϕ = Δθ = π/ 192 ≈ 1.636 × 10-2 rad.
The initial conditions are built by putting into discrete hydrostatic equilibrium the profiles from the one-dimensional stellar evolution simulation. To this end, we solve for the pressure in Eq. (18)using the Timmes EoS and assuming the density, entropy, composition and gravitational potential from the stellar evolution profile. The result of this discrete hydrostatic integration is shown in Fig. 8 for the Nr = 128 radial resolution. In the left panel are displayed the density (solid line) and the pressure (dashed line). The right panel of the same figure displays the temperature (solid line) together with specific entropy (dashed line). In both panels, the dotted lines represent the respective quantity from the one-dimensional stellar evolution profile. The region where the entropy is flat is the convective carbon burning region. The stably stratified regions below and above are the oxygen-neon core and the inactive parts of the carbon shell, respectively. We observe that our initial conditions and the original stellar evolution simulation profiles are not exactly identical. However, given the change in EoS and the simplified physical modeling, we think that our initial conditions still reflect the conditions from the stellar evolution simulation, quite well. Moreover, the region where the heating source term is non-zero (mimicking nuclear burning) is shown in red. We also add a random velocity perturbation in the region r ∈ [ 1.2,2.2 ] × 104 km of size 10-3 with respect to the local sound speed. Note that we do not incorporate self-gravity and the spherically symmetric gravitational potential is left unchanged during the simulations. Since the gravity force is then exactly aligned with the radial axis, the well-balanced pressure reconstruction is mathematically well-balanced even in this three-dimensional setting.
We then evolved the setup with the standard and the well-balanced schemes at the two radial resolutions for 3600 s of physical time. This is indeed just a tiny fraction of the duration of the carbon shell burning phase, but nevertheless long enough to show the improvements due to the well-balanced reconstruction. In Fig. 9 we show the spherically averaged density/pressure (left panel) and the temperature/specific entropy (right panel) at final time for the high radial resolution Nr = 128 (the Nr = 64 simulation shows the same trends and is not shown for brevity). In both panels, the blue lines stem from the standard scheme and the red ones from the well-balanced scheme. As reference, the black lines show the initial profiles. From the left panel we observe that the well-balanced scheme is able to maintain the hydrostatic structure very well. It is only at the composition interface between the core and the carbon shell and at the top of the carbon shell that the density/pressure slightly differs from the initial profile. The same applies to the temperature/specific entropy profiles in the right panel. The standard scheme on the other hand shows very strong deviations, especially near the boundaries. Especially the temperature and the specific entropy show some spurious features. We want to stress that the same boundary conditions have been applied to the simulations with the standard and well-balanced schemes1.
In Fig. 10 we show the spherically averaged kinetic energy as a function of radius and time for the Nr = 128 radial resolution. On the left (right) is shown the simulation with the standard (well-balanced) scheme. Focusing on the well-balanced results (right panel), we see a violent onset of convection which is triggered by the initial velocity perturbations and the initially slightly negative gradient in specific entropy. These violent initial motions flatten the entropy gradient and then settle down, reaching a steady state after roughly 1000 s. After 1500 s most of the kinetic energy is contained in the convective carbon shell, i.e., the region where the specific entropy is flat. Below the carbon shell no sizable motions are present as is expected due to the absence of convection there. Above the convective region, some wave motions are present. These waves are triggered by convective plumes overshooting into the stably stratified layers. The same applies for the well-balanced simulation with Nr = 64 radial resolution (not shown).
 |
Fig. 11 Density, temperature, electron abundance and radial velocity profiles. The black lines represent polar-averaged profiles of the innermost 250 km of a sophisticated axisymmetric simulation at time t = 250 ms post bounce. These profiles are then put into hydrostatic equilibrium and used to initialize the three-dimensional simulation of the PNS. The red dots show a scatter plot of all the cells in the three-dimensional domain for the resolution N = 50. Note that the red dots degenerate almost everywhere to a red line. |
The situation is very different in the left panel of Fig. 10 showing the results from the standard scheme. There, most of the kinetic energy is near the lower boundary. We attribute this again to the lack of the standard scheme to resolve (a discrete) hydrostatic equilibrium. This problem may be ameliorated by using much higher numerical resolution, which, however, is extremely costly in computational resources (especially in the three-dimensional case considered here).
We observe that well-balancing greatly improves the simulation of convective phenomena inside the evolved star considered here. Although our physical model was highly simplified, we believe that well-balancing confers many advantages in more physically refined models.
3.4. Three-dimensional proto-neutron star
As a final test, we simulate the hydrostatic evolution of a PNS in three-dimensional Cartesian coordinates. As mentioned in Sect. 2.3, the proposed scheme is only well-balanced if gravity forces are aligned with one coordinate axis. This is indeed not the case here. Hence, this test assesses the performance of the scheme under suboptimal conditions.
We obtain the PNS profile from a sophisticated axisymmetric Newtonian simulation of the collapsing core of a 15 M⊙ progenitor. The simulation used the Lattimer-Swesty EoS with nuclear compressibility K = 220 MeV (LS220) and an advanced spectral leakage scheme for the approximate neutrino transport treatment. For details we refer to Perego et al. (2015). Figure 11 shows the innermost 250 km of the averaged (in polar direction) density, temperature, electron abundance and radial velocity profiles at t = 250 ms after bounce. At this time the supernova shock wave is between 110 and 170 km, which is visible in the radial velocity panel. This disparity is due to shock oscillations caused by the standing accretion shock instability. Below ≈100 km, matter is subsonically accreting onto the PNS and underneath ≈50 km, matter is nearly in hydrostatic equilibrium.
 |
Fig. 12 Maximum density as a function of time for resolutions Δx = Δy = Δz = 2,1,0.5 km represented by the solid, dashed and dotted lines, respectively. The blue lines have been obtained with the well-balanced scheme, while the red ones with the standard scheme. The right panel shows a close-up to distinguish the well-balanced computations. |
The initial conditions are produced by putting into hydrostatic equilibrium the averaged (in polar direction) profiles from the axisymmetric simulation. To this end, we integrate the hydrostatic equilibrium Eq. (12)using the LS220 EoS and assuming the temperature, electron abundance and gravitational potential averaged (in polar direction) profiles from the axisymmetric simulation. The velocity is simply set to zero. These hydrostatic profiles are then mapped to our three-dimensional Cartesian domain D = [ −50,50 ] 3 km3. The red dots in Fig. 11 represent a scatter plot of the hydrostatic profiles in D. As apparent from the figure, the hydrostatic integration has barely any influence on the density structure, i.e., the configuration is indeed very close to hydrostatic equilibrium.
The three-dimensional hydrostatic PNS is then evolved with the well-balanced and the standard schemes for ≈40 ms, corresponding to twenty sound crossing times, and three different resolutions N = Nx = Ny = Nz = 50,100,200. The resolutions correspond to cell sizes of Δx = Δy = Δz = 2,1,0.5 km, respectively. The boundary conditions are treated in the same manner as in the hydrostatic atmospheres case, i.e., Eq. (43), but applied in a direction-by-direction manner.
As a first measure on how well the numerical schemes are able to resolve the hydrostatic equilibrium, we look at the temporal evolution of the maximum density. In Fig. 12 we show the evolution of the maximum density for the different schemes and resolutions (solid, dashed and dotted blue/red lines for the resolution N = 50,100,200 and well-balanced/ standard scheme, respectively). From the left panel of the figure it is apparent, that the standard scheme (red lines) has enormous problems to keep the density close to the initial value. Even the highest resolution with 500 m mesh size (dotted red line) shows a steady decrease by more than 1% in the maximum density. On the other hand, the well-balanced schemes are able to hold the maximum density very well. In the right panel of Fig. 12 a close-up on the well-balanced simulation is shown. We observe that the well-balanced scheme is able to keep the maximum density within ≈0.2% at all resolutions.
 |
Fig. 13 Density, temperature, electron abundance and specific entropy profiles. The solid black lines are the initial profiles and the blue/red dots are the profiles at final time for the well-balanced/standard scheme with resolution N = 100, i.e., Δx = Δy = Δz = 1 km. Note that the well-balanced results are nearly indistinguishable from the initial profiles. |
In Fig. 13 we show the density, temperature, electron abundance and specific entropy profiles at final time for the well-balanced/standard (blue/red dots) with resolution N = 100, i.e., Δx = Δy = Δz = 1 km. As a reference the initial profiles (solid black lines) are also shown. We observe that the well-balanced scheme is nearly indistinguishable from the reference black lines, which implies that the hydrostatic equilibrium is resolved very well. The standard scheme shows large spurious deviations. As a matter of fact, the well-balanced scheme maintains the hydrostatic equilibrium.
Hence, we conclude that the well-balanced scheme considerably improves the resolution of general multidimensional equilibria, even thought, it is not mathematically well-balanced in the three-dimensional test case presented here.
4. Conclusion
We have presented a second-order well-balanced scheme for hydrostatic equilibrium without any assumption of a thermal equilibrium. The scheme relies on a pressure reconstruction which is consistent with a spatially second-order accurate discrete version of the underlying hydrostatic equilibrium. Given this discrete reconstruction no assumption has to be made concerning the thermal profile, such as isothermal or isentropic, of the equilibrium. The well-balanced reconstruction is extremely simple and computationally efficient, since it is only (very) marginally more expensive than any (limited) piecewise linear reconstruction in primitive variables. The gravitational source terms are discretized with standard central differences. Therefore the scheme can be integrated in existing codes with minimal effort. Moreover, it can be implemented within both explicit and implicit time stepping schemes.
We have presented several test cases of astrophysical interest. The one-dimensional tests confirm that the scheme is indeed well-balanced and that the numerical resolution of systems close to hydrostatic equilibrium is greatly improved, particularly at coarse grid resolutions. Results for wave propagation in a hydrostatic atmosphere has shown a significant gain in accuracy with the well-balanced scheme, i.e., several orders of magnitude for small amplitude waves. At larger wave amplitudes, the well-balanced scheme does as well as the standard scheme. Moreover, the well-balanced reconstruction does not deteriorate the robustness of the Godunov-type base scheme. As seen in the toy core-collapse model, the well-balanced scheme works even when regions close to hydrostatic equilibrium and highly dynamic regions with strong shocks coexist in the simulation domain.
The two multi-dimensional test cases show the same gain in accuracy and even more so, in the computational efficiency, on account of using the well-balanced reconstruction. The simulation of convective carbon shell burning has demonstrated the drastic improvement with which the well-balanced scheme can evolve convection within a stellar environment. Even in the suboptimal case, when gravitational forces are not perfectly aligned with one grid axis, making the reconstruction not exactly well-balanced, the well-balanced scheme greatly increases the accuracy. This was shown in the hydrostatic proto-neutron star test. The tremendous gain in computational efficiency of the well-balanced scheme, comes from the fact that numerical resolution has only to be invested for approximating the physical phenomena of interest, rather than resolving the hydrostatic equilibrium.
Acknowledgments
The authors were supported in part by ERC STG. N 306279, SPARCCLE. The authors thank M. Pignatari and R. Hirschi for discussions concerning the simulation of stellar convection inside massive stars. Moreover we thank M. Pignatari for providing us with a profile from a NuGrid data set. R.K. also thanks the Swiss High Performance and High Productivity (HP2C) initiative under project “Supernova”. The authors acknowledge the computational resources provided by the Swiss Super Computing Center (CSCS), under the allocation grant s414, and the BRUTUS and EULER clusters of ETHZ.
References
- Arnett, W. D., & Meakin, C. 2011, ApJ, 733, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Audusse, E., Bouchut, F., Bristeau, M.-O., Klein, R., & Perthame, B. 2004, SIAM J. Sci. Comput., 25, 2050 [CrossRef] [MathSciNet] [Google Scholar]
- Batten, P., Clarke, N., Lambert, C., & Causon, D. M. 1997, SIAM J. Sci. Comput., 18, 1553 [CrossRef] [Google Scholar]
- Bogdan, T. J., Carlsson, M., Hansteen, V. H., et al. 2003, ApJ, 599, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Botta, N., Klein, R., Langenberg, S., & Lützenkirchen, S. 2004, J. Comput. Phys., 196, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., & Palacios, A. 2009, ApJ, 702, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrashekar, P., & Klingenberg, C. 2015, SIAM J. Sci. Comput., 37, 82 [CrossRef] [Google Scholar]
- Colella, P., & Woodward, P. R. 1984, J. Comput. Phys., 54, 174 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dedner, A., Kröner, D., Sofronov, I., & Wesenberg, M. 2001, J. Comput. Phys., 171, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Desveaux, V., Zenk, M., Berthon, C., & Klingenberg, C. 2014, Springer Proceedings in Mathematics & Statistics, 77, 217 [CrossRef] [Google Scholar]
- Fjordholm, U. S., Mishra, S., & Tadmor, E. 2011, J. Comput. Phys., 230, 5587 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Fuchs, F., McMurry, A., Mishra, S., Risebro, N., & Waagan, K. 2010, J. Comput. Phys., 229, 4033 [Google Scholar]
- Godunov, S. K. 1959, Mat. Sb. (N.S.), 47 (89), 271 [Google Scholar]
- Gottlieb, S., Shu, C.-W., & Tadmor, E. 2001, SIAM Rev., 43, 89 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Greenberg, J., & Leroux, A. 1996, SIAM J. Num. Anal., 33, 1 [Google Scholar]
- Janka, H.-T., Zwerger, T., & Moenchmeyer, R. 1993, A&A, 268, 360 [NASA ADS] [Google Scholar]
- Käppeli, R., & Mishra, S. 2014, J. Comput. Phys., 259, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Käppeli, R., Whitehouse, S. C., Scheidegger, S., Pen, U.-L., & Liebendörfer, M. 2011, ApJS, 195, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Kurganov, A., & Tadmor, E. 2000, J. Comput. Phys., 160, 241 [Google Scholar]
- Laney, C. B. 1998, Computational Gasdynamics (Cambridge University Press) [Google Scholar]
- Lefloch, P. G., & Thanh, M. D. 2003, Commun. Math. Sci., 1, 763 [CrossRef] [MathSciNet] [Google Scholar]
- LeVeque, R. J. 1998, J. Comput. Phys., 146, 346 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- LeVeque, R. J. 2002, Finite Volume Methods for Hyperbolic Problems, Cambridge Texts in Applied Mathematics, 1st edn. (Cambridge University Press) [Google Scholar]
- LeVeque, R. 2011, J. Sci. Comput., 48, 209 [CrossRef] [Google Scholar]
- Li, G., & Xing, Y. 2015, J. Sci. Comput., DOI: 10.1007/s10915-015-0093-5 [Google Scholar]
- Meakin, C. A., & Arnett, D. 2006, ApJ, 637, L53 [CrossRef] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Mellema, G., Eulderink, F., & Icke, V. 1991, A&A, 252, 718 [NASA ADS] [Google Scholar]
- Perego, A., Cabezón, R., & Käppeli, R. 2015, ArXiv e-prints [arXiv:1511.08519] [Google Scholar]
- Pignatari, M., Herwig, F., Hirschi, R., et al. 2013, ApJS, submitted [arXiv:1307.6961] [Google Scholar]
- Plewa, T., & Müller, E. 1999, A&A, 342, 179 [NASA ADS] [Google Scholar]
- Roe, P. L. 1981, J. Comput. Phys., 43, 357 [Google Scholar]
- Timmes, F. X. 2013, http://cococubed.asu.edu/code_pages/eos.shtml [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Toro, E. F. 1997, Riemann Solvers and Numerical Methods for Fluid Dynamics. A Practical Introduction (Springer-Verlag GmbH) [Google Scholar]
- Toro, E. F., Spruce, M., & Speares, W. 1994, Shock Waves, 4, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leer, B. 1979, J. Comput. Phys., 32, 101 [Google Scholar]
- Viallet, M., Baraffe, I., & Walder, R. 2011, A&A, 531, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woodward, P. R., Herwig, F., & Lin, P.-H. 2013, ApJ, submitted [arXiv:1307.3821] [Google Scholar]
- Xing, Y., & Shu, C.-W. 2013, J. Sci. Comput., 54, 645 [CrossRef] [Google Scholar]
- Zingale, M., Dursi, L. J., ZuHone, J., et al. 2002, ApJS, 143, 539 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Non-uniform mesh
Here we list a few expressions for the case of a non-uniform mesh. Only one-dimensional expressions are given and the multi-dimensional ones follow easily. The gravity source (11)then reads ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:appendix01_0010} \boldsymbol{S}_{i}^{n} = \left[ \begin{array}{c} 0 \\ - \rho_i^n \\ - (\rho \varv_x)_i^n \end{array} \right] \left( \frac{\partial \phi}{\partial x} \right)_i , \end{equation}](/articles/aa/full_html/2016/03/aa27815-15/aa27815-15-eq312.png) (A.1)where the gradient of the gravitational potential is computed as
(A.1)where the gradient of the gravitational potential is computed as 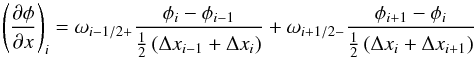 (A.2)with the weights given by
(A.2)with the weights given by 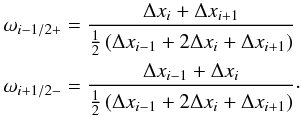 (A.3)\newpageThe discrete hydrostatic pressure reconstruction to cell interfaces reads
(A.3)\newpageThe discrete hydrostatic pressure reconstruction to cell interfaces reads 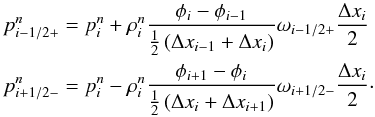 (A.4)The hydrostatic equilibrium, which is preserved by this reconstruction, follows then immediately as in Sect. 2.1.1.
(A.4)The hydrostatic equilibrium, which is preserved by this reconstruction, follows then immediately as in Sect. 2.1.1.
All Tables
All Figures
 |
Fig. 1 Piecewise linear well-balanced reconstruction of the pressure. The pressure profile (black line) within the ith cell is decomposed into an equilibrium (blue line) and a perturbation part p(x) = p0,i(x) + p1,i(x). The equilibrium pressure p0,i(x) is simply given by Eq. (13). The point values of the perturbation are then computed at neighboring cell centers xi ± 1 by extrapolation of the equilibrium pressure reconstruction p0,i(xi ± 1). A piecewise linear monotonicity preserving reconstruction can then be applied to the pressure perturbation data, i.e., p1,i(xi ± 1) = pi ± 1 − p0,i(xi ± 1) and p1,i(xi) = 0. |
| In the text | |
 |
Fig. 2 L1-norm of the difference between the initial and final pressure for the isentropic (solid and dashed blue lines) and isothermal (solid and dashed red lines) atmospheres. The solid and dashed lines represent the simulation performed with the standard and the well-balanced (WB) schemes, respectively. The apparent third-order superconvergence of the standard scheme is explained in the text. |
| In the text | |
 |
Fig. 3 L1-norm error between the numerical and reference (N = 8192) velocity for the isentropic atmosphere. The blue, red and green line correspond to the wave amplitudes A = 10-8,10-6,10-1, respectively. The solid and dashed lines represent the simulation performed with the standard and the well-balanced (WB) schemes, respectively. |
| In the text | |
 |
Fig. 4 Velocity profile for the small (left) and large (right) amplitude waves running down the isentropic atmosphere. The solid/dashed red lines are the solutions obtained with the standard/well-balanced scheme with N = 512, respectively. In solid blue is also shown a reference solution obtained with the well-balanced scheme and N = 8192. |
| In the text | |
 |
Fig. 5 Central density as a function of time for the standard (left panel) and the well-balanced (right panel) scheme. In both panels the (blue) dashed, (red) dash-dotted, (green) dotted and the (black) solid line represent the simulation with N = 128,256,512,8192, respectively. |
| In the text | |
 |
Fig. 6 Density as a function of radius for the standard and well-balanced schemes with N = 256 (left panel) and N = 512 (right panel). In both panels the (black) solid, (blue) dashed and the (red) dash-dotted line represent the reference solution (the well-balanced with N = 8192 in both panels), the solutions computed with standard and the well-balanced scheme, respectively. For both resolution, the well-balanced solutions are indistinguishable from the reference. |
| In the text | |
 |
Fig. 7 Energies and total energy conservation as a function of time from the standard (left) and well-balanced (right) scheme with N = 512. In both panels, the solid (blue) line is the internal energy Eint, the dashed (green) line is the kinetic energy Ekin, the dash-dotted (red) line is minus the gravitational energy −Egrav and the dotted (black) line is the total energy conservation ΔE. |
| In the text | |
 |
Fig. 8 Spherically averaged profiles at initial time of the stellar convection simulation. Left panel: density (solid line) and pressure (dashed line). Right panel: temperature (solid line) and specific entropy (dashed line). The dotted lines represent the original profiles from the one-dimensional stellar evolution code. The red region is where the energy source term is non-zero. |
| In the text | |
 |
Fig. 9 Spherically averaged profiles at the end of the simulation for the resolution Nr = 128. In each panel, the black lines are the initial profiles, the blue lines were computed with the standard scheme and the red lines with the well-balanced scheme. Left panel: density (solid lines) and pressure (dashed lines) profiles. Right panel: temperature (solid lines) and specific entropy (dashed lines) profiles. Note that the initial profiles are nearly indistinguishable from the well-balanced profiles at final time. |
| In the text | |
 |
Fig. 10 Spherically averaged kinetic energy as a function of time. The left panel was computed with the standard scheme and the right one with the well-balanced scheme, both with radial resolution Nr = 128. |
| In the text | |
 |
Fig. 11 Density, temperature, electron abundance and radial velocity profiles. The black lines represent polar-averaged profiles of the innermost 250 km of a sophisticated axisymmetric simulation at time t = 250 ms post bounce. These profiles are then put into hydrostatic equilibrium and used to initialize the three-dimensional simulation of the PNS. The red dots show a scatter plot of all the cells in the three-dimensional domain for the resolution N = 50. Note that the red dots degenerate almost everywhere to a red line. |
| In the text | |
 |
Fig. 12 Maximum density as a function of time for resolutions Δx = Δy = Δz = 2,1,0.5 km represented by the solid, dashed and dotted lines, respectively. The blue lines have been obtained with the well-balanced scheme, while the red ones with the standard scheme. The right panel shows a close-up to distinguish the well-balanced computations. |
| In the text | |
 |
Fig. 13 Density, temperature, electron abundance and specific entropy profiles. The solid black lines are the initial profiles and the blue/red dots are the profiles at final time for the well-balanced/standard scheme with resolution N = 100, i.e., Δx = Δy = Δz = 1 km. Note that the well-balanced results are nearly indistinguishable from the initial profiles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.