| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 43 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527329 | |
| Published online | 17 February 2016 | |
SOPHIE velocimetry of Kepler transit candidates
XVII. The physical properties of giant exoplanets within 400 days of period⋆,⋆⋆
1 Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
e-mail: alexandre.santerne@astro.up.pt
2 Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
3 CNRS, Canada-France-Hawaii Telescope Corporation, 65-1238 Mamalahoa Hwy., Kamuela, 96743, USA
4 Observatoire Astronomique de l’Université de Genève, 51 chemin des Maillettes, 1290 Versoix, Switzerland
5 Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre & Marie Curie, 98bis boulevard Arago, 75014 Paris, France
6 Observatoire de Haute-Provence, Université d’Aix-Marseille & CNRS, 04870 Saint-Michel l’Observatoire, France
7 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
8 CNRS, IPAG, 38000 Grenoble, France
9 LUPM, Université Montpellier II, CNRS, UMR 5299, Place E. Bataillon, 34095 Montpellier, France
10 INAF–Osservatorio Astrofisico di Torino, via Osservatorio 20, 10025 Pino Torinese, Italy
11 Laboratoire Lagrange, UMR 7239, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300 Nice, France
12 Department of Astronomy, Columbia University, Pupin Physics Laboratory, 550 West, 120th Street, New York, NY 10027, USA
13 Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
Received: 8 September 2015
Accepted: 27 October 2015
While giant extrasolar planets have been studied for more than two decades now, there are still some open questions as to their dominant formation and migration processes, as well as to their atmospheric evolution in different stellar environments. In this paper, we study a sample of giant transiting exoplanets detected by the Kepler telescope with orbital periods up to 400 days. We first defined a sample of 129 giant-planet candidates that we followed up with the SOPHIE spectrograph (OHP, France) in a 6-year radial velocity campaign. This allowed us to unveil the nature of these candidates and to measure a false-positive rate of 54.6 ± 6.5% for giant-planet candidates orbiting within 400 days of period. Based on a sample of confirmed or likely planets, we then derived the occurrence rates of giant planets in different ranges of orbital periods. The overall occurrence rate of giant planets within 400 days is 4.6 ± 0.6%. We recovered, for the first time in the Kepler data, the different populations of giant planets reported by radial velocity surveys. Comparing these rates with other yields, we find that the occurrence rate of giant planets is lower only for hot Jupiters but not for the longer-period planets. We also derive a first measurement of the occurrence rate of brown dwarfs in the brown-dwarf desert with a value of 0.29 ± 0.17%. Finally, we discuss the physical properties of the giant planets in our sample. We confirm that giant planets receiving moderate irradiation are not inflated, but we find that they are on average smaller than predicted by formation and evolution models. In this regime of low-irradiated giant planets, we find a possible correlation between their bulk density and the iron abundance of the host star, which needs more detections to be confirmed.
Key words: planetary systems / binaries: spectroscopic / techniques: radial velocities / techniques: spectroscopic / techniques: photometric
Based on observations made with SOPHIE on the 1.93 m telescope at Observatoire de Haute-Provence (CNRS), France.
RV data (Appendices C and D) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/587/A64
© ESO, 2016
1. Introduction
Twenty years after the discovery of the first extrasolar giant planet around a main sequence star (Mayor & Queloz 1995), not all questions about extrasolar giant planets (EGPs) have been answered. Their formation, migration, and evolution are far from having been fully understood. As an example, both the well-adopted core – accretion model (e.g. Mordasini et al. 2009b) and the latest results from the disk – instability model (e.g. Nayakshin 2015a,b) are able to reproduce the observed correlation of giant-planet formation rates with the metallicity of host stars (Santos et al. 2001), thereby reopening the question about their dominant formation process. Another example is the inflation of some giant, highly irradiated planets that could not be modelled with reasonable physical ingredients (e.g. Almenara et al. 2015).
Different physical processes are currently proposed to explain their strong inflation (see e.g. Baraffe et al. 2014, for a review), but this question has still not been completely solved. Even the definition of what a giant planet may be is still an open question at both extremes: the lower mass planets (Hatzes & Rauer 2016) and the brown dwarf regime (Schneider et al. 2011; Chabrier et al. 2014). When the orbital obliquity is put into the picture, it raises even more questions about the complexity in the planet formation and evolution (Winn et al. 2010; Hébrard et al. 2010; Triaud 2011; Dawson 2014).
At a time when small planets in the habitable zone are being found (e.g. Jenkins et al. 2015), characterising EGPs is still of high importance for answering these questions. Moreover, since their formation process is tightly connected, it is important to understand the formation processes of the large planets before exploring those of the smallest ones. A lot of constraints on EGPs have already been added by radial velocity (RV) surveys (e.g. Santos et al. 2001; Udry et al. 2003; Howard et al. 2010; Mayor et al. 2016; Adibekyan et al. 2013; Dawson & Murray-Clay 2013). However, these planets do not have a radius measurement (except for a few of them, e.g. Moutou et al. 2009), which does not allow one to understand their density diversity or their atmospheric physical properties.
The population of transiting EGPs receiving a moderate or low irradiation is still poorly explored, with only five objects characterised well (mass and radius significantly measured) with orbital periods longer than a month (Santerne et al. 2014). These planets, which are rarely seen in transit1, pave the way between the hot Jupiters and the solar system giants, so they can offer unprecedented information for understanding the physics of the atmosphere, the formation, and the migration of such planets. In this context, the Kepler space telescope (Borucki et al. 2009) has detected giant-planet candidates with orbital periods as long as several hundred days (Coughlin et al. 2015), so that it is probing this population of low-irradiation planets.
Giant transiting exoplanets are easily mimicked by other stellar objects, thereby leading to false positives (e.g. Brown 2003; Torres et al. 2005; Cameron 2012), making it difficult to interpret the candidates without establishing their nature. Spectroscopic follow-up can easily reveal blended multiple stellar systems (Santerne et al. 2012b; Kolbl et al. 2015), and high-resolution imaging (e.g. Lillo-Box et al. 2014) can unveil close-by companions. However, to firmly establish their planetary nature, one has to detect their Doppler signature or use statistical methods (also known as planet-validation, see Santerne et al. 2014, for an illustration of both methods). To correctly interpret the transit detections, follow-up observations are therefore needed, especially for the population of giant exoplanets.
In this paper, we present the results and interpretation of a six-year RV campaign with the SOPHIE spectrograph (Observatoire de Haute-Provence, France) of a complete sample of giant transiting candidates detected by Kepler within 400 days of orbital periods. This paper completes and extends the work presented in Santerne et al. (2012b). In Sect. 2, we define the giant-planet candidate sample detected by Kepler and selected for our RV follow-up programme. In Sect. 3, we present the performed spectroscopic observations, their analysis, and the nature of the candidates that are discussed case by case in Appendix A. In Sect. 4, we computed the false-positive rate of Kepler exoplanet giant-planet (EGP) candidates within 400 days and compare it with previous estimations. In Sect. 5, we measure the occurrence rates of EGPs and brown dwarfs (BD) in different ranges of orbital periods that we compare with the values determined in other stellar populations (e.g. the solar neighbourhood). In Sect. 6, we discuss some physical properties of these EGPs and the ones of their host stars. Finally, we make a summary of the main results of this paper and draw our conclusions in Sect. 7. The spectroscopic data are listed in the Appendices C and D.
2. The giant-planet candidate sample
To select the EGP candidates, we used the list of Kepler objects of interest (KOI), which has been successively published in Borucki et al. (2011a,b), Batalha et al. (2013), Burke et al. (2014), Rowe et al. (2015), Mullally et al. (2015), and Coughlin et al. (2015). The latest release corresponds to the candidates detected based on the full dataset of the Kepler prime mission (from quarters Q1 to Q17). These candidates are listed in the NASA exoplanet archive2, together with their orbital and transit parameters. We used the cumulative KOI table as of 2015 June 5. In this table, there are 8826 KOIs. We first removed all the KOIs that were already identified as false positives using the Kepler data. These false positives are mostly background eclipsing binaries (EBs) and background transiting planets that produce an in-transit astrometric signal, called the centroid effect (Batalha et al. 2010; Bryson et al. 2013). Among all the KOIs, 4661 are not obvious false positives and are labelled as planet candidates in the catalogue. These candidates have a host star magnitude in the Kepler bandpass (Kp) ranging from 8.2 to 19.5, with a median of 14.6.
From this list of 4661 candidates, we kept only the 2481 ones that transit a host star with a magnitude Kp< 14.7. This was chosen to match the maximum magnitude for which the SOPHIE spectrograph (see Sect. 3) could reach a RV photon noise better than 20 m s-1 for slow-rotating stars in a maximum of 3600 s of exposure time (Santerne et al. 2013b). Such precision is the minimum needed to significantly detect the RV signal of a Jupiter-mass planet with orbital periods of up to a few tens of days (e.g. Santerne et al. 2011b, 2014).
To select the candidates that are compatible with an EGP, we kept the KOIs that have a reported transit depth (δ) between 0.4% and 3%. Very few EGPs have been found so far with a transit depth below 0.4%, and most of them are transiting evolved stars: e.g. KOI-428 (Santerne et al. 2011a), WASP-72 (Gillon et al. 2013), WASP-73 (Delrez et al. 2014). At the other extreme, only one EGP has been found with a transit depth greater than 3%, KOI-254 (Johnson et al. 2012), whose M-dwarf host represents a small fraction of the KOIs (Dressing & Charbonneau 2013). We are therefore confident that those criteria select the majority of the EGPs transiting FGK dwarfs. We did not select the giant-planet candidates based on their estimated radius because this value depends strongly on the 40% uncertain estimated radius of the host (Huber et al. 2014). The complete selection of candidates based on their estimated radius is therefore uncertain. Moreover, the transit depth is a directly measured observable, and as such are more reliable than the estimated planetary radius. By selecting candidates based on their transit depth, however, one might have some contamination from low-mass EBs or small planets transiting small stars.
Among the giant-planet candidates we finally selected all those with an orbital period (P) of less than 400 days. This insures that at least three transits were observed during the entire duration of the Kepler prime mission. By applying the three selection criteria (Kp< 14.7, 0.4% <δ< 3%, and P< 400 d), we find 129 KOIs on 125 target stars. They are displayed in Fig. 1 and listed in Table B.1, together with their various ID, their main orbital and transit parameters (period, depth, and scaled distance to star), as well as their host properties as determined by Huber et al. (2014).
Santerne et al. (2012b) used the same criteria in terms of magnitude limits and transit depths, but the candidate periods were limited to 25 days. The new sample extends the sample for periods up to 400 days and contains three times more candidates than the previous study.
 |
Fig. 1 Planet candidates detected by the Kepler telescope in the Q1–Q17 dataset. Their transit depth is displayed here as a function of their orbital period. The size of the circle is relative to the magnitude of the host. The grey region in the upper panel represents the selection criteria used to define the giant-planet candidate sample (see text). The lower panel is a zoom to this selected population of candidates. |
3. Unveiling the nature of the candidates
3.1. SOPHIE observations and reduction
We observed the candidate sample with the SOPHIE spectrograph (Bouchy et al. 2009c) mounted on the 1.93 m telescope at the Observatoire de Haute-Provence (France). SOPHIE is a fibre-fed high-resolution stable spectrograph dedicated to high-precision RV measurements (Perruchot et al. 2008; Bouchy et al. 2009c, 2013). The observations were done as part of a large programme dedicated to Kepler targets and funded by the French Programme of Planetology3 from 2010 July14 to 2015 July15.
During these six observing campaigns, this programme collected more than 1000 spectra on 154 different targets, spread over more than 370 nights, cumulating more than 640 h of open-shutter time. Each target was observed between two and 51 different epochs with a typical precision of about 20 m s-1.
Most observations were performed using the high-efficiency (HE) mode of SOPHIE with an instrumental resolution of ~39 000. For a few targets brighter than Kp = 12, we observed them using the high-resolution mode (HR), which has an instrumental resolution of ~75 000 and a better light scrambling (Perruchot et al. 2011), providing better precision. All spectra were reduced using the online pipeline. We computed the weighted cross-correlation function (CCF) using a G2 mask (Baranne et al. 1996; Pepe et al. 2002). This mask has been optimised for solar-type stars, which is the main population observed by Kepler.
When necessary, we corrected the CCFs affected by the Moon’s background light following the procedure described in Baranne et al. (1996). We then measured the RV, bisector span, and full width half maximum (FWHM). All the measurements are reported in Tables C.1–C.3 and analysed in Appendix A. The errors on the RV are estimated using the method explained in Bouchy et al. (2001) and in Appendix A of Boisse et al. (2010). For the bisector and FWHM, we used the photon noise factors listed in Santerne et al. (2015). These spectroscopic diagnostics are used to reveal the presence of contaminating stars, therefore likely false positives that might be the source of the transit event (Santos et al. 2002; Torres et al. 2005). Several stars that present a ~100 m s-1 scatter in FWHM, including the RV constant star HD 185144 (Santerne et al. 2014), we concluded this scatter was from the insufficient thermal control of the instrument that introduces slight changes in focus (Courcol et al. 2015). For this reason, we used the FWHM as a vetting tool only if the variation is much larger than 100 m s-1.
We corrected the RV from the CCD charge transfer inefficiency (Bouchy et al. 2009a) using the calibration described in Santerne et al. (2012b). Following Santerne et al. (2014), we also corrected instrumental drifts in the RV using the ones measured on the constant star HD 185144 on the same nights. The RV we used for this correction are listed in Table D.1. This allowed us to reach an rms down to 13 m s-1 over more than two years on stars as faint as Kp = 14.5, which is equivalent to the photon noise.
 |
Fig. 2 Comparison of the Teff, log g, and [Fe/H] we derived by spectroscopy with the ones derived photometrically by Huber et al. (2014) for the 37 targets listed in Table B.2. Open and filled circles are for stars hotter and cooler than the Sun (respectively). The log g of the giant host KOI-5976 is not displayed here for the sake of clarity in the plot. |
3.2. Stellar atmospheric analyses
3.2.1. Stellar atmospheric parameters
To support the determination of the nature of the candidates showing no significant RV variation (within 3σ, see Sect. 3.3.3), we performed a detailed spectral analysis of the targets4. This allowed us to improve the upper limits on the candidate mass and to identify evolved stars that are hosts of false positives. Some spectra have a signal-to-noise ratio (S/N) that is too low for a detailed spectral analysis. Among the 125 candidates hosts, we selected 12 stars with no significant RV variation and a S/N high enough to analyse their SOPHIE spectra. We derived the atmospheric parameters of those 12 stars after correcting for their RV shifts and the cosmic-ray impacts. We subtracted the sky contamination (using the spectra of Fibre B) from the target spectra (in Fibre A), after correcting for the relative efficiency of the two fibres. To derive the atmospheric parameters, namely the effective temperature (Teff), surface gravity (log g), metallicity ([Fe/H]), and microturbulence (ξt), we followed the methodology described in Sousa et al. (2008) and Tsantaki et al. (2013). This method relies on measurement of the equivalent widths (EWs) of Fe i and Fe ii lines and on imposing excitation and ionization equilibrium.
The analysis was performed by assuming local thermodynamic equilibrium using a grid of model atmospheres (Kurucz 1993) and the radiative transfer code MOOG (Sneden 1973). The iron line lists for this analysis were taken from Sousa et al. (2008) for the hotter stars (>5200 K) and from Tsantaki et al. (2013) for the cooler ones. The EWs were measured automatically with the ARES 2.0 code (Sousa et al. 2015). To ensure accurate measurements of the EWs, we excluded any lines with errors over 20% of their absolute values. We corrected the observed log g using the asteroseismic calibration of Mortier et al. (2014). The derived parameters are reported in Table B.2 and discussed case by case in Appendix A. We finally updated the stellar fundamental parameters using the Dartmouth stellar evolution tracks of Dotter et al. (2008).
In Table B.2, we also list the spectroscopic parameters of 25 planet hosts derived by our team and published in previous papers (e.g. Almenara et al. 2015; Bonomo et al. 2015). These stellar parameters were derived using either the MOOG (as described above) or the VWA software. Comparison between the two on some targets have shown no significant differences (e.g. Santerne et al. 2014). These stellar parameters are also available in SWEET-Cat5 (Santos et al. 2013). For the other candidates or planet hosts, we used the spectroscopic parameters found in the literature (e.g. Huber et al. 2014). For some targets we used an ESPaDOnS6 (Bonomo et al. 2015) or HARPS-N7 co-added spectrum (Hébrard et al. 2014). In total, we thus have 37 stars from our sample for which we could derive precise parameters from a spectroscopic analysis.
We determined the υsini⋆ of the single-line spectra using the average width of the SOPHIE CCF and the relations in the Appendix B of Boisse et al. (2010). We estimated the (B − V) of the host stars based on their atmospheric parameters reported by Huber et al. (2014) and the calibration from Pecaut & Mamajek (2013). We did not use the observed (B − V) because it is affected by unknown interstellar extinction, which would introduce systematic noise. The method of Boisse et al. (2010) finds an uncertainty of 1 km s-1 that we conservatively increased by 20% to account for the errors in the Teff and in the (B − V) calibration. For fast-rotating stars (υsini⋆≳ 10 km s-1), we fitted the CCF with a rotation profile as described in Santerne et al. (2012a) to determine their υsini⋆ . We list their measured values and uncertainties in Table B.3.
3.2.2. Comparison with Huber et al. (2014)
We compared the results from the spectral analyses we performed in the context of this spectroscopic follow-up of Kepler giant-planet candidates with the ones of Huber et al. (2014), derived based on colour photometry. In Fig. 2, we compare the Teff, log g, and [Fe/H] of the 37 stars, derived by spectroscopy with the ones independently reported by Huber et al. (2014).
We find agreement between the spectroscopic and photometric Teff with a systematic offset of ΔTeff = TeffSpectro−TeffHuber + 14 = − 51± 298 K. The log g values are very noisy, and no systematic offset is found with Δlog g = log gSpectro− log gHuber+14 = −0.01 ± 0.04 cm s-2. However, for the [Fe/H], some stars seem to have a lower photometric metallicity compared with the spectroscopic one. The systematic offset is Δ[Fe/H] = [Fe/H]Spectro− [Fe/H]Huber+14 = 0.17 ± 0.04 dex. This systematic offset agrees perfectly with the value found by the massive low-resolution spectroscopic survey of the Kepler fields performed with LAMOST (Dong et al. 2014). We find that this offset in the stellar metallicity seems to depend on the stellar effective temperature. If we divided our list of targets into two subsamples (see Fig. 2), one for stars that are cooler or one for those hotter than the Sun, this systematic offset is Δ[Fe/H]cool = 0.09 ± 0.06 dex and Δ[Fe/H]hot = 0.22 ± 0.05 dex. Stellar rotation, which is higher for the hot stars, might be one of the reasons for this discrepancy. This Teff – [Fe/H] trend might also be an artefact of the spectroscopic method, used either for our analyses or for calibrating the photometric values in Huber et al. (2014). Torres et al. (2012) have already pointed out some systematic effects in the determination of the spectroscopic parameters, especially for stars hotter than 6000 K. We expect these systematics to be particularly strong at relatively low S/N (typically <50), which is the regime of S/N for the spectra of most of the Kepler targets.
Wang & Fischer (2015) propose a correction of the metallicities from the Kepler input catalogue (Brown et al. 2011) using the spectroscopic data from Buchhave et al. (2014). Since Huber et al. (2014) used the same spectroscopic data to calibrate their metallicities, this correction is no longer valid.
3.3. Nature of the candidates
The nature of the candidates is unveiled case by case in the Appendix A, reported in Table B.1, and displayed in Fig. 3. We present below a summary of the different populations of candidates.
 |
Fig. 3 Same as lower panel of Fig. 1, but the labels indicate the nature of the candidates: BD stands for brown dwarfs, EB for eclipsing binaries, CEB for contaminating binaries, and No Var for the unsolved cases that show no significant variation in radial velocity. |
3.3.1. Bona fide planets and brown dwarfs
In the sample of 129 giant-planet candidates, 30 of them are bona fide planets already established and characterised by other spectroscopic facilities (e.g. Latham et al. 2010; Endl et al. 2011; Gandolfi et al. 2013) by transit timing variation analyses (e.g. Ofir et al. 2014) and by the “multiplicity-boost” validation (Rowe et al. 2014). Except for a few cases, we did not observe them with SOPHIE, relying on the candidate nature that has been secured in the respective papers. In this sample, our team established and characterised 18 EGPs and brown dwarfs that have already been published in previous papers of this series.
The distinction between EGPs and brown dwarfs has been widely discussed (e.g. Chabrier et al. 2014) and remains uncertain unless we know the formation history of these objects. With a mass of ~18 M♃, Kepler-39 b (Bouchy et al. 2011) is somewhat arbitrarily considered as a brown dwarf. Considering it as a planet would not change the results of this paper significantly, except for Sect. 5.3. The other two massive substellar companions in our sample (KOI-205 b (~40 M♃) and KOI-415 b (~62 M♃): Díaz et al. 2013; Moutou et al. 2013a) are very likely to be brown dwarfs. Finally, the case of the 78 M♃-companion to KOI-189 has been classified as a very-low-mass star by Díaz et al. (2014b). This leads to a total number of bona fide EGPs in our candidate sample of 45 and 3 brown dwarfs. All the references are provided in Table B.1.
3.3.2. Eclipsing binaries and contaminating eclipsing binaries
Among the 129 candidates, we detected 63 EBs that show up to three different sets of lines in the spectra. The spectroscopic observations, analyses, and conclusions are described in Appendix A or in Santerne et al. (2012b). When two or three sets of lines are detected in the spectra, we fitted the cross-correlation function with two or three Gaussian profiles (respectively). For these cases, we estimated the RV photon noise using the following equation: ![\begin{equation} \sigma_{\rm RV}\, [\kms] = A_{i} \times \frac{\sqrt{FWHM\, [\kms]}}{CTRS [\%] \times S/N}, \end{equation}](/articles/aa/full_html/2016/03/aa27329-15/aa27329-15-eq34.png) (1)with AHE = 3.4 and AHR = 1.7 for both instrumental modes of SOPHIE. The S/N is the S/N per pixel computed by averaging the flux in the 200 pixels at the centre of the spectral order #26 (i.e. at about 550 nm), and CTRS is the contrast of the averaged line profile. This photon-noise estimate has been calibrated on a set of standard stars, following the same procedure as described in Bouchy et al. (2005).
(1)with AHE = 3.4 and AHR = 1.7 for both instrumental modes of SOPHIE. The S/N is the S/N per pixel computed by averaging the flux in the 200 pixels at the centre of the spectral order #26 (i.e. at about 550 nm), and CTRS is the contrast of the averaged line profile. This photon-noise estimate has been calibrated on a set of standard stars, following the same procedure as described in Bouchy et al. (2005).
Among those 63 EBs, 48 are spectroscopic binaries showing one or two set(s) of lines (hence an SB1 or SB2). In most cases, we observed them only two or three times, which is not enough to fully characterise the mass and eccentricity of these binaries. To estimate the companion mass of an SB1, we assumed a circular orbit at the transit ephemeris and no significant RV drift. Several caveats in our analyses might significantly change the reported companion masses. First, the circular orbit assumption is not reasonable for binaries with an orbital period longer than about ten days (Halbwachs et al. 2003; Raghavan et al. 2010). Second, the primary mass estimate from Huber et al. (2014) that we used might be affected by the presence of a stellar companion. Finally, if the orbital periods of these binary are twice the ones detected by Kepler, the reported masses are also wrong.
For SB2 binaries, we used the slope of their RV correlation to measure the binary mass ratio (Wilson 1941). As for the SB1, we observed most of them only very few times, which limits the possibility of determining their mass and eccentricity.
These spectroscopic binaries are stars eclipsing the target. Their eclipse depth is likely not to be diluted by a substantial third light; otherwise, we would have detected it in our spectroscopic data. They are able to mimic a giant-planet candidate because they have a grazing eclipse with a depth compatible with the one of an EGP. A few binaries are stars with an EGP-like radius, whose identification is impossible from the light curve alone, unless they present a deep secondary eclipse (as in Zhou & Huang 2013) or a large beaming, ellipsoidal, or reflection effect.
In this sample of EBs, we detected 16 eccentric systems (2 already characterised in Santerne et al. 2012b, and 14 new ones described in the Appendix A) that present only a secondary eclipse, the primary eclipse invisible from Earth (Santerne et al. 2013a). Two other candidates are secondary-only EBs in more complex multiple stellar systems. These numbers are fully compatible with the predictions of Santerne et al. (2013a).
We also found 15 stellar systems that either present three stellar components in the spectra, or SB2 with RV that are not anti-correlated, revealing the presence of a third, unseen star in the system. Those candidates, most likely triple systems, have an eclipse depth that is severely diluted by the target star. In these cases, even a relatively deep eclipse might mimic the transit depth of a planet. Moreover, if the EB is eccentric, only the primary or secondary eclipse could be visible. Triple systems might be difficult to identify by spectroscopy because the brightest star in the system is not the eclipsed star. Moreover, if the eclipsing system is physically bound with the target star, they are most likely blended in both photometry and spectroscopy. Using the variation in the line profile (the bisector and the FWHM, see Santerne et al. 2015), we identified some triple systems with relatively faint companions compared with the target star. However, if the eclipse host contributes to less than about 5% of the total flux of the system (magnitude difference more than 3, or mass ratio lower than ~0.5), we would not be able to detect the second set of lines in the cross-correlation functions or its impact on the target line-profile shape. If such systems are present in our sample, we would not be able to identify them as false positives. Therefore, the actual number of diluted EBs might exceed what we found.
In the Table B.1 and in the rest of the paper, we refer to the 48 systems with an undiluted eclipse depth as eclipsing binaries (or EB). We also refer to the 15 ones with a diluted eclipse depth, which are either triple systems or background EBs, as contaminating eclipsing binaries (or CEB).
Among the 63 EBs we detected, 54 are already included in the Kepler EB catalogue (v3)9 of Kirk et al. (in prep.). The other nine are unveiled by our observations and were not previously identified as such based on the Kepler light curve. In this catalogue, we found two candidates listed as EB, but our observations do not support this statement. In previous versions of the catalogue, some bona fide exoplanets were also listed (as discussed already in Santerne et al. 2012b).
3.3.3. No variation cases
For 18 giant-planet candidates, we found no significant RV, bisector, or FWHM variation. The nature of these candidates remains uncertain: they might be planets that have too low a mass for our RV precision or they might be diluted EBs with a large flux ratio between the eclipse host and the target star, which make them undetectable in our spectroscopic data.
Assuming these candidates are planets, we derived their upper limits in mass. For that, we analysed the data with the MCMC algorithm of the PASTIS software (Díaz et al. 2014a). We used a uniform prior for the RV amplitudes (between 0 and 100 km s-1) for the systemic RV (between −100 km s-1 and +100 km s-1) and for the argument of periastron (between 0° and 360°). For the eccentricity, we used a Beta distribution as a prior, as recommended by Kipping (2013). We fixed the periods and epochs of transit to the ones found by Kepler. When only two or three different observed epochs were available, we fixed the eccentricity to zero. When enough RV were available, we fitted a Keplerian orbit. If sub-giant planet candidates were detected in the light curve of the same system, we also included them in the model, even if their RV contribution is expected to be negligible. The choice of the model (circular vs. eccentric), as well as the number of planets, is described in Appendix A, together with the derived upper limits. We report these upper limits on the mass of the candidates, assuming they are planets, in Table B.4.
Among the 18 unsolved cases, one has a mass constraint that is still compatible with a brown dwarf (KOI-2679.01), and another one has a mass constraint compatible with a low-mass star (KOI-3783.01). Those two cases are giant-planet candidates transiting fast-rotating stars for which precise RV measurements are difficult to obtain.
3.3.4. Particular cases
Some candidates we observed have masses that have already been constrained by spectroscopy or TTV analysis. Our mass constraints are fully compatible except in two cases. The first case is KOI-1353.01. Assuming a circular orbit, we find a planet mass of 1.55 ± 0.34M♃, while Schmitt et al. (2014b) report a mass of 0.42 ± 0.05M♃ for the same planet based on a TTV analysis. Our mass constraint is therefore significantly higher (at the 3.3σ) than the one found by TTVs. At least three reasons could explain this discrepancy: first, we find a host that is also more massive at the 3.7σ level; second, the star is active, which might have significantly affected our RV or the transit times (Barros et al. 2013; Oshagh et al. 2013), and finally this planet might be significantly eccentric even if a low eccentricity has been reported by Schmitt et al. (2014b). For this case, more data and better precision are needed to make a firm conclusion.
The second case is KOI-372.01 for which the mass has recently been reported in Mancini et al. (2015) based on RV observations with the CAFE spectrograph. They found a RV amplitude of 132 ± 6 m s-1, while our SOPHIE HR RV shows no significant variation with an rms of 24 m s-1. The analysis of the SOPHIE spectra and their comparison with the CAFE observations will be presented in a forthcoming paper (Demangeon et al., in prep.). We considered this case as unsolved.
Finally, KOI-3663 b/Kepler-86 b, previously validated statistically by Wang et al. (2013), reveals some line-profile variations correlated with the RV data (see Appendix A.41). More observations are needed to conclude something about this case, and KOI-3663 b might not be a planet but a triple system. Without further evidence, we consider it as a planet in the rest of this article.
4. The false-positive rate
Based on the results of our spectroscopic survey, we can measure the false-positive rate of the Kepler giant-planet candidates, an extension of the previous rate 34.8 ± 6.5% measured by Santerne et al. (2012b) for EGPs within a 25-day orbital period.
4.1. The giant-planet false-positive rate
Among the 129 selected KOIs, we identified 34.9 ± 5.2% planets, 2.3 ± 1.3% brown dwarfs, 37.1 ± 5.4% EBs, 11.6 ± 3.0% CEBs, and 14.0 ± 3.2% unsolved cases, assuming a Poisson noise (see Fig. 4).
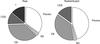 |
Fig. 4 Pie charts showing the distribution by nature of the giant-planet candidates: (left) the observed distribution of the candidates; (right) the underlying distribution of the candidates under the assumption that the unsolved cases are composed of 75% of planets and 25% of contaminating eclipsing binaries (see text). BD refers to brown dwarfs, EB to eclipsing binaries, CEB to contaminating eclipsing binaries, and the question mark to the unsolved cases. |
The unsolved cases are neither EBs nor brown dwarfs, otherwise a large RV variation would have been detected. They could be either planets with a mass lower than what can be detected with SOPHIE or a stellar or planetary companion eclipsing a different star than the target one. In this case, if the flux ratio between the target and the eclipse host is low enough, it is not possible to detect its contribution on the spectra, either by detecting its impact on the target line-profile shape (Santerne et al. 2015) or by detecting directly its line in the spectrum. This CEB could be either bound or chance-aligned with the target star. Following Santerne et al. (2012b), we assumed that the unsolved cases are composed of planets and CEBs with the same ratio as the observed one. This means that 75 ± 11% of these unsolved cases are assumed to be planets, and 25 ± 6% are likely to be faint CEBs.
We then find that the giant-planet candidates sample is composed of 45.3 ± 5.9% planets, 2.3 ± 1.3% brown dwarfs, 37.2 ± 5.4% EBs, and 15.1 ± 3.4% CEBs. This distribution of the nature of the giant-planet candidates is displayed in Fig. 4. This gives a giant-planet false-positive rate of 54.6 ± 6.5%. Depending on the nature of the unsolved cases, the false-positive rate has a lower limit of 51.2 ± 6.3% (if all unsolved cases are planets) and an upper limit of 65.1 ± 7.1% (if they are false positives). This value does not account for the false positives (about 50% of the total number of EGP transit detection) already identified by the Kepler team.
If we repeat this analysis by dividing the sample in two, one for candidates with periods of less than 25 days (i.e. an updated value for the sample of Santerne et al. 2012b) and one for the candidates with periods longer than 25 days, we find that the false-positive rate is 53.4 ± 8.5% and 56.4 ± 10.1%, respectively. The value for the short-period sample is higher than the one reported in Santerne et al. (2012b) for two reasons: (1) new candidates have been found on stars that were not observed by Kepler in 2012; and (2) in this study we include the candidates that were flagged with a poor vetting flag in Borucki et al. (2011b) and rejected from the Santerne et al. (2012b) sample.
The false-positive rate is, however, not uniform over orbital periods. If we split the sample in three for candidates with periods of less than 10 days, between 10 and 85 days, and between 85 and 400 days (see Sect. 5 for the reasons of this sub-sample selection), we find false-positive rates of 46.7 ± 9.3%, 68.6 ± 12.9%, and 50.2 ± 12.1% (respectively). The false-positive rate is therefore the lowest for short-period candidates and the highest for intermediate-period ones.
4.2. Comparison with other false-positive rate estimates
The false-positive rate of the Kepler mission is a key element that describes the reliability of the Kepler candidate catalogue for statistical analyses. Together with the pipeline completeness (Christiansen et al. 2013, 2015), this information is needed to accurately assess the underlying occurrence of planets, down to Earth-size planets in the habitable zone. The latter is the main objective of the Kepler prime mission (Borucki et al. 2009; Batalha 2014).
By modelling the expected distribution of planets and binaries in the Kepler field of view, Morton & Johnson (2011) found that the median false-positive probability among the Borucki et al. (2011b) candidates was as low as 5%. This value was not supported by spectroscopic observations of a sample of 44 giant candidates, which revealed a false-positive rate as high as 34.8 ± 6.5% (Santerne et al. 2012b), or by the narrow-band GTC photometry of four small candidates in which two were found to be false positives (Colón et al. 2012).
Later on, Fressin et al. (2013) performed a new modelling of the expected population of planets and EBs in the Kepler field of view, based on the Batalha et al. (2013) candidate list. They found a median value of 9.4% with a higher rate (29.3 ± 3.1% within 25 days) for the giant-planet candidates, which is compatible with the measurement of 34.8 ± 6.5% (Santerne et al. 2012b). This median value was then revised by Santerne et al. (2013a) from 9.4% to 11.3% by accounting for secondary-only false positives.
Recently, Désert et al. (2015) have found a false-positive rate as low as 1.3% (upper limit of 8.8% at 3σ) based on the Spitzer near-infrared photometry of 51 candidates. However, this small set of candidates were selected to be representative of the KOI list from Borucki et al. (2011b) and not a well-defined sample. As pointed out by the authors, the extrapolation of the false-positive rate from this small sample, which represents 1.1% only of the planet candidates known today, to the entire sample of candidates, should be done with caution. Among these 51 Spitzer targets, 33 of them are orbiting in multiple systems that are known to have a very low a priori probability of being false positives (Lissauer et al. 2012, 2014). The 18 remaining ones are relatively small planets, and only two are EGPs10.
Using high-resolution spectroscopy and RV, we find that more than half of the giant-planet candidates are actually not planets. This value is significantly higher than all the other values reported so far. This value is, however, difficult to compare with the previous ones for two main reasons: (1) the list of candidates is different – we used the Q1–Q17 candidate list from Coughlin et al. (2015), while most of the aforementioned studies used the Q1–Q6 candidate list from Batalha et al. (2013), with half as many candidates11 – and (2) the selection criteria are also different. As an example, Fressin et al. (2013) selected as giant-planet candidates all transit detections with an expected radius between 6 and 22 R⊕, while our selection criteria are based on the observed transit depth (see Sect. 2). Therefore, we do not compare the numbers directly, but qualitatively discuss the differences and similarities found. Since the work of Fressin et al. (2013) is the most up-to-date simulation of the entire catalogue of candidates, we focus on the comparison between our observations and their results.
Fressin et al. (2013) predict a false-positive rate of 17.7 ± 2.9% for all the giant planet candidates within 418 days12. This value is significantly lower than our observational value. However, Fressin et al. (2013) did not consider the possibility that EBs mimics the transit of an EGP. The underlying reason is that such false positives have a V-shaped transit (i.e. an impact parameter b≳ 1) and can be easily rejected. Some grazing planets, such as CoRoT-10 b (Bonomo et al. 2010) or KOI-614 b (Almenara et al. 2015), also present the same V-shaped transit. Since those V-shaped candidates actually are in the catalogues, this scenario of false positive should be considered, as in Morton (2012).
By not considering EBs as an important source of false positives, Fressin et al. (2013) overestimated the occurrence rate of EGPs in the Kepler field of view. Since they used this occurrence rate of EGPs to estimate the number of planets transiting a physical companion to the target star, they also overestimated the abundance of this false-positive scenario. Since this scenario is the main source of false positives in the Kepler list of candidates (according to Fressin et al. 2013), it has an impact on all the population of planets.
Not all the EBs we identified are members of the Kepler EB catalogue (14% are missing – Kirk et al., in prep.) and two (KOI-1271.01 and KOI-6132.01) members of this catalogue were not confirmed by our data to be EBs. The completeness of this catalogue, which is used to estimate the number of false positives involving stellar systems, is thus lower than expected, and the number of false positives composed of stellar systems is underestimated in the Fressin et al. (2013) analysis.
As an illustration, Fressin et al. (2013) predict that among all target stars observed by Kepler, there are 4.7 triple systems, 8.0 background EB, and about 24.5 planets transiting physical companion to the target star that mimic EGPs. By observing only 125 stars among the bright half of the candidates, we found 15 candidates that we considered as CEBs. They are very likely bound with the target stars (hence triple systems) because they have a systemic RV similar to the target one13. This number of triple systems is three times more than the one predicted by Fressin et al. (2013) for all the candidates. We therefore observe roughly six times more triple systems than predicted14. On the other hand, we found no clear evidence of planets transiting a physical companion to the target star. They might, however, be among the unsolved cases. Therefore we observe a higher rate of triple systems than false positives made of planets, which is the opposite of what Fressin et al. (2013) predicted. The aforementioned reasons might explain this discrepancy. We note that only 66% of the EGP candidates were released in Batalha et al. (2013), which might also explain this difference with Fressin et al. (2013).
Using the method described in Morton (2012), Morton et al. (in prep.) find a false-positive rate of 42% in the same sample of EGPs. Among the 129 KOIs, only six are false positives with a low false-positive probability (<10%) according to their method. Out of the six, five are actually low-mass stars and are therefore undistinguishable from an EGP using photometry only.
4.3. Extrapolation towards smaller planet candidates
Even if our spectroscopic observations bring no constraints to the large sample of small-planet candidates detected by Kepler, we can use the EGPs as a reference to qualitatively extrapolate the false-positive rate of small planets.
4.3.1. Undiluted-depth eclipsing binaries
The populations of small-planet candidates should be much less contaminated by EBs. Grazing eclipses (by stars or the rare brown dwarfs) can produce any transit depth, but their occurrence rate is expected to decrease for transit depths below 1% (Santerne et al. 2013a). Therefore, this source of false positives should completely disappear towards shallower candidates.
4.3.2. Diluted-depth eclipsing binaries and transiting planet
Shallower transits produce lower S/N events at a given stellar magnitude, and the false-positive diagnoses are expected to be less efficient for shallow transits; for instance, the duration of the transit ingress and egress or the presence of a secondary eclipse is poorly constrained if the primary transit S/N is low. Therefore, false positives that mimic small planets are more difficult to screen out compared to the large ones.
In addition, the dilution ratio also affects the analysis. A planet candidate transiting a star of magnitude mt with an observed depth of δt can be mimicked by an eclipse of depth δc on a contaminating star of magnitude mc, such as 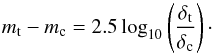 (2)Decreasing δt is achieved by decreasing δc and/or increasing mc: i.e. fainter false-positive hosts and/or smaller companions. Those fainter hosts could be either smaller or farther away stars that are, in both cases, more common, as previously discussed by Brown (2003).
(2)Decreasing δt is achieved by decreasing δc and/or increasing mc: i.e. fainter false-positive hosts and/or smaller companions. Those fainter hosts could be either smaller or farther away stars that are, in both cases, more common, as previously discussed by Brown (2003).
4.3.3. The false-positive rate of small planets
By combining both of the effects discussed in Sect. 4.3.2, we thus expected that the total number of false positives invoking diluted-depth transits or eclipses increases towards smaller candidates and that we would be less efficient to rule them out. However, the false-positive rate is defined as the relative fraction of false positives against bona fide planets amongst the candidates. Thus, decreasing the transit depth of the candidates corresponds to exploring smaller planet populations that are more common according to planet-formation synthesis (e.g. Mordasini et al. 2009b; Nayakshin 2015a) and the results from radial velocity surveys (e.g. Howard et al. 2010; Mayor et al. 2016). Therefore, even if the absolute number of false positive increases by decreasing the transit depths, the relative value (i.e the false-positive rate) might not necessarily increase.
We discussed previously that the absolute number of false positives is expected to increase towards smaller planet candidates. As pointed out by Latham et al. (2011) and Lissauer et al. (2011), however, about one third of the candidates smaller than Jupiter are found in multiple systems, in agreement with the first results of RV surveys (e.g. Bouchy et al. 2009b; Mayor et al. 2016). Furthermore, those multiple candidates have a very low a priori probability of being false positives (Lissauer et al. 2012, 2014). Therefore, our predicted increase in false positives towards small planet candidates should be mostly concentrated on the candidates that are not in multiple systems. Any physical interpretation of the nature of these small-and-single, unconfirmed candidates might thus lead to wrong conclusions.
4.4. Comparison between giant-planet and false-positive host properties
Several studies have tried to infer some planet–star property correlation, such as with the effective temperature of the host star (e.g. Howard et al. 2012) or its metallicity (e.g. Buchhave et al. 2014; Wang & Fischer 2015), since they provide direct tests of planet-formation theories. However, if the false positives are not accounted for and have a different host parameter distribution, they might alter the underlying correlation. To test this, we display in Fig. 5 the cumulative distributions of the effective temperature and iron abundance of the planets and false positive hosts, as well as all the Kepler targets observed during Q1–Q16. As planets we only considered here the 45 that have been well established in our sample. The stellar parameters are from Huber et al. (2014).
 |
Fig. 5 Cumulative distribution functions (CDF) of the effective temperature (top panel) and the iron abundance (bottom panel) for all the Kepler targets (solid and thick line), the secured EGPs in our sample (solid line), and the false positives identified by our spectroscopic surveys (dashed line). The stellar parameters are from Huber et al. (2014). |
We find that most stars hotter than 6500 K host false positives and very few host EGPs. This might be an observational bias since planets around hot, fast-rotating, and active stars are more difficult to find and characterise than those around Sun-like stars. We also find relatively few EGPs orbiting stars cooler than the Sun and that the giant planets tend to orbit metal-rich stars, which confirms the RV results (e.g. Sousa et al. 2011, see also Sect. 6.3).
We computed the Anderson-Darling (AD) test15 between the distributions of the giant-planet and the false-positive hosts with the Kepler targets and candidates host (p-values listed in Table B.5). We find that the distributions of stellar effective temperature and iron abundance between the target stars and candidate hosts (all KOIs) are different16. This is also the case between the giant-planet hosts and both the target stars and the candidate hosts. However, the distributions of [Fe/H] and Teff are not significantly different between the false-positive hosts and the target stars. Those results are expected since the fraction of binaries is relatively constant in the regime of stars that we are the most sensitive to (Teff between 5000 K and 6500 K and [Fe/H] between −0.4 dex and 0.4 dex; Raghavan et al. 2010).
By comparing the distributions of stellar properties for different samples of stars hosting either EGPs, false positives, candidates, or just field stars, we show that the presence of false positives has two main implications. First, the determination of the occurrence rate of EGPs as a function of the stellar properties based on the candidates list cannot be correct with ~55% false positives. Then, one may overestimate the occurrence of small planets orbiting metal-rich stars, if a significant percentage of the false positives are made of EGPs transiting stellar companions to the target star (as claimed by Fressin et al. 2013). On the other hand, if small planets are mostly mimicked by EBs, their metallicity distribution might not be significantly different than the field stars. Therefore, determining the planet occurrence rate as a function of the stellar host properties, without screening out the false positives, should be done with caution, because it might lead to incorrect results.
5. Giant-planet occurrence rates
In this section, we analyse the secured and likely EGPs in our sample. The first information we can derive from this cleaned sample is the occurrence rate of EGPs.
5.1. The occurrence rate of giant planets within 400 days
To measure the occurrence rate of planets, we need to determine: (1) a reference stellar sample; (2) the number of transiting planets in this reference stellar sample; and (3) the various corrections that should be applied, such as the number of non-transiting planets and the planets missed by incompleteness of the pipeline. We discuss these points below.
5.1.1. The stellar reference sample
The Kepler prime mission focused on solar-like stars (Huber et al. 2014), so we defined our stellar reference sample to match the properties of such stars. Our transit-candidate selection is biased towards dwarf hosts and is quite insensitive to sub-giant and giant hosts around which Jovian planets have transit depth shallower than 0.4%. Thus, we need to determine how many FGK dwarfs Kepler observed.
In previous works that attempt to measure the occurrence rates of planets (e.g. Howard et al. 2012; Petigura et al. 2013), the observed atmospheric parameters (Teff, log g) were used to select solar-like dwarfs, to fit the historical Morgan-Keenan classification of stars (Morgan & Keenan 1973). Using these selection criteria, it is however difficult to make the distinction between main-sequence and sub-giant stars in the regime of early G- and F-type stars. For example, a star with Teff = 5000 K and log g = 4.1 cm s-2 (at solar metallicity) is a sub-giant, while another star with the same surface gravity but with a Teff of 6500 K is still in the main sequence. Because of their large radius, planets transiting sub-giants and giant stars are more difficult to detect. Thus, a stellar reference sample composed by a substantial number of evolved stars might lead to underestimating the planet occurrence rates (unless this effect is taken into account). This problem does not occur for late G-, K-, and M-type stars because their lifetime in the mainn sequence is longer than the age of the universe. Since both the Teff and log g vary during the evolution of stars in the main sequence and beyond, they are not the best parameters for selecting a stellar reference sample.
To determine our stellar reference sample, we chose the stellar mass and radius as selection parameters. The mass of stars does not change significantly during their evolution, except at very late stages. The mass is also the fundamental parameter used in planet-formation synthesis (e.g. Mordasini et al. 2009a), since it is expected to scale with the mass of the disk for the mass range considered here (Andrews et al. 2013). During the main sequence and sub-giant phases, the stellar radius increases in a strictly monotonic way. These reasons make the stellar mass and radius better parameters for selecting a stellar sample only composed of main-sequence stars. This requires defining the radius of stars at the end of their main-sequence life.
We used the latest version of the STAREVOL stellar evolution code (Charbonnel & Palacios 2004; Lagarde et al. 2012, Amard et al., in prep.), with the solar composition following Asplund et al. (2009). The metallicity is fixed to a solar value (Z = 0.0134) and the mixing length parameter calibrated to a solar model taken as αMLT = 1.702. We determined the end of the main sequence as when the hydrogen abundance in the core is X(H i) < 10-7. The main parameters of solar-type stars at the end of the main sequence are listed in Table B.6. We adopted the stellar radius listed in this table as the maximum value for selecting dwarf stars. Figure 6 displays all the Kepler targets, candidate host, and the bright giant-planet hosts in the M⋆ − R⋆ space. The adopted maximum radius for the dwarf stars is also represented.
 |
Fig. 6 Stellar mass-radius diagramme of the targets observed by Kepler during the quarters Q1–Q16 (black dots), the candidate hosts (white circles), and the bright giant-planet hosts (red circles). The data are from Huber et al. (2014) except for the giant-planet hosts, which are taken from Table B.7. The size of the mark for the two latter samples corresponds to the Kepler magnitude. The grey region displays the selected dwarfs. One secured EGP transits a star bigger than 2.5 R⊙ (KOI-680) and is not represented here. |
During the Kepler prime mission, a relatively small fraction of dwarf stars were observed with M⋆< 0.7 M⊙ (10.0%) and M⋆> 1.4 M⊙ (3.9%). By selecting only the dwarfs that have a magnitude Kp< 14.7, only 6.2% of them are smaller than 0.7 M⊙, and 9.1% are more massive than 1.4 M⊙. By selecting the bright dwarfs in the range 0.7–1.4 M⊙, which corresponds to a spectral type F5–K5 (Cox 2000), we selected 84.8% of the observed bright dwarfs. Because a relatively small number of bright low-mass or massive dwarfs have been observed by Kepler, measuring the occurrence rate of EGPs around those stars will be strongly limited by the small size of the sample.
To determine our stellar reference sample, we selected the Kepler targets that have a magnitude Kp< 14.7, a mass in the range M⋆ ∈ [0.7;1.4] M⊙, and a radius smaller than the ones listed in Table B.6. We used the stellar parameters of Huber et al. (2014) and found a total number of bright, solar-type dwarfs observed by Kepler of 58831. In spite of the large uncertainties on the stellar masses (~20%) and radii (~40%) in the Huber et al. catalogue, the total number of dwarfs is expected to be statistically accurate.
If we select the stellar reference sample based on Teff∈ [4410;6650] K and log g∈ [4.0;4.9] cm s-2, we find a number of 59 873 bright dwarfs observed by Kepler17. Thus, selecting the stellar reference sample based on Teff and log g or stellar mass and radius does not change our results significantly.
5.1.2. Sample of transiting planets
Once the reference sample has been well defined, we need to determine how many EGPs in total are transiting those stars. In our giant-planet candidate sample, there are 45 secured transiting planets and 18 candidates that could be either planets or false positives. Since we expected the majority of the latter to be planets, we consider them as “likely planets”. We report in Table B.7 the transit, planet, and stellar parameters of these 63 objects from the literature values. When planets have been analysed in different papers, we kept the most updated or complete analysis of the systems as adopted values. Similarly, we adopted the stellar parameters fromTorres et al. (2012) or Santos et al. (2013), for example, when available, because those studies used higher-S/N data than in the discovery papers, leading to more reliable results. By default, when no detailed analysis of the photometric or spectroscopic data had been reported, we used the transit and planet parameters provided in NASA exoplanet archive18 and the stellar parameters from Huber et al. (2014). The parameters in Table B.7 are thus heterogeneous.
5.1.3. Survey corrections
We identified six corrections that have to be accounted for to derive the occurrence rates of EGPs within 400 days based on our data. We call them 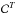 ,
, 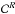 ,
, 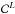 ,
, 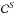 ,
, 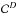 , and
, and 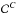 . We describe and discuss them below.
. We describe and discuss them below.
-
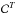 : correction for the geometric transit probability (the upper script T refers to transit probability). Following Howard et al. (2012), for each planet transiting a star of radius R⋆ with a semi-major axis a, there are a/R⋆ times more planets (both transiting and non-transiting). Therefore, we defined the correction for the transit probability as
: correction for the geometric transit probability (the upper script T refers to transit probability). Following Howard et al. (2012), for each planet transiting a star of radius R⋆ with a semi-major axis a, there are a/R⋆ times more planets (both transiting and non-transiting). Therefore, we defined the correction for the transit probability as 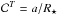 . This parameter is directly measured on the light curve and does not rely on the stellar parameters.
. This parameter is directly measured on the light curve and does not rely on the stellar parameters. -
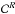 : correction for the probability that the planet host belongs to the stellar reference sample or not (the upper script R refers to the reference sample). To estimate this correction, we bootstrapped the planet-host mass and radius 1000 times within their uncertainty, assuming they follow a Gaussian distribution. Then, we applied our reference sample criteria, defined in Sect. 5.1.1, and determined
: correction for the probability that the planet host belongs to the stellar reference sample or not (the upper script R refers to the reference sample). To estimate this correction, we bootstrapped the planet-host mass and radius 1000 times within their uncertainty, assuming they follow a Gaussian distribution. Then, we applied our reference sample criteria, defined in Sect. 5.1.1, and determined 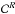 as the number of hosts that satisfy the reference sample cirteria. The values of
as the number of hosts that satisfy the reference sample cirteria. The values of 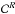 range from 0% for evolved stars like KOI-680 (Almenara et al. 2015) to 100% for well-characterised solar-like dwarfs like KOI-1 (aka TrES-2; Huber et al. 2014).
range from 0% for evolved stars like KOI-680 (Almenara et al. 2015) to 100% for well-characterised solar-like dwarfs like KOI-1 (aka TrES-2; Huber et al. 2014). -
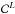 : correction for the likelihood of the object to be a planet or not. (The upper script L refers to planet likelihood.) The majority of the EGPs considered here have been established well using various techniques (
: correction for the likelihood of the object to be a planet or not. (The upper script L refers to planet likelihood.) The majority of the EGPs considered here have been established well using various techniques (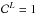 ). For the candidates for which we detected no significant RV variation, we failed in ruling out all false-positive scenarios, as already discussed in Sects. 3.3.3 and 4. However, we estimated in Sect. 4 that about 75% of them should be planets, so
). For the candidates for which we detected no significant RV variation, we failed in ruling out all false-positive scenarios, as already discussed in Sects. 3.3.3 and 4. However, we estimated in Sect. 4 that about 75% of them should be planets, so 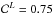 .
. -
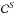 : correction to the selection criteria used to define the transiting EGP sample (the upper script S refers to the selection criteria). Depending on the stellar and planetary radii, the transit depth of EGPs might be lower than 0.4% or higher than 3%. These selection criteria were defined to include the majority of planets, but a few might have been missed, mostly grazing planets. To estimate this correction, we simulated 105 mock planetary systems. The stellar mass and radius were chosen uniformly within our definition of solar-type dwarfs (see Sect. 5.1.1)19. The orbital inclination was drawn from a sine distribution, which corresponds to a uniform distribution of both the inclination and longitude of ascending node. The period was fixed to ten days, which is close to the median of the giant-planet periods, and we considered circular orbits. Then, we assumed a radius distribution of EGPs that corresponds to the observed one (based on EGP radius listed in the NASA exoplanet archive). This radius distribution is an asymmetric Gaussian such as
: correction to the selection criteria used to define the transiting EGP sample (the upper script S refers to the selection criteria). Depending on the stellar and planetary radii, the transit depth of EGPs might be lower than 0.4% or higher than 3%. These selection criteria were defined to include the majority of planets, but a few might have been missed, mostly grazing planets. To estimate this correction, we simulated 105 mock planetary systems. The stellar mass and radius were chosen uniformly within our definition of solar-type dwarfs (see Sect. 5.1.1)19. The orbital inclination was drawn from a sine distribution, which corresponds to a uniform distribution of both the inclination and longitude of ascending node. The period was fixed to ten days, which is close to the median of the giant-planet periods, and we considered circular orbits. Then, we assumed a radius distribution of EGPs that corresponds to the observed one (based on EGP radius listed in the NASA exoplanet archive). This radius distribution is an asymmetric Gaussian such as 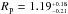 R♃. We used the JKTEBOP code (Southworth 2008), assuming the limb darkening coefficients from Claret & Bloemen (2011) to simulate the transit light curve and determine the transit depth. Finally,
R♃. We used the JKTEBOP code (Southworth 2008), assuming the limb darkening coefficients from Claret & Bloemen (2011) to simulate the transit light curve and determine the transit depth. Finally, 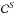 is defined as the percentage of planets with transit depth in the range [0.4%;3%] over the total number of transiting planets. We determined this correction per bin on stellar mass that we displayed in Fig. 7. The mean value of
is defined as the percentage of planets with transit depth in the range [0.4%;3%] over the total number of transiting planets. We determined this correction per bin on stellar mass that we displayed in Fig. 7. The mean value of 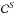 over all stellar masses is 77%, with values ranging from 37% for the lowest mass stars in our reference sample to 91% for Sun-like stars.
over all stellar masses is 77%, with values ranging from 37% for the lowest mass stars in our reference sample to 91% for Sun-like stars. -
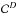 : correction to the non-uniform distribution dwarf stars (the upper script D refers to dwarf distribution). We have more chances a priori of finding a transiting planet among the most abundant population of stars (i.e. stars with mass in the range 1–1.1 M⊙). However, the distribution of giant-planet hosts might be (and actually is) different. To completely account for this effect, we would need to explore all the stellar parameters (at least the mass and [Fe/H]) simultaneously, but we do not have a stellar reference sample large enough for that. For a first-order correction, we only considered the distribution of stellar masses. We defined
: correction to the non-uniform distribution dwarf stars (the upper script D refers to dwarf distribution). We have more chances a priori of finding a transiting planet among the most abundant population of stars (i.e. stars with mass in the range 1–1.1 M⊙). However, the distribution of giant-planet hosts might be (and actually is) different. To completely account for this effect, we would need to explore all the stellar parameters (at least the mass and [Fe/H]) simultaneously, but we do not have a stellar reference sample large enough for that. For a first-order correction, we only considered the distribution of stellar masses. We defined 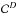 as the normalised distribution of dwarf masses in the stellar reference sample. This distribution is displayed in Fig. 7, where the values of
as the normalised distribution of dwarf masses in the stellar reference sample. This distribution is displayed in Fig. 7, where the values of 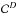 range from 0.25 to 2.14.
range from 0.25 to 2.14. -
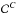 : correction to account for the detection pipeline completeness, i.e. the number of transiting planets missed by the detection pipeline. (The upper script C refers to the completeness.) This has been thoroughly studied in Christiansen et al. (2013, 2015). In particular, they find that the detection efficiency of EGPs transiting bright, solar-type dwarfs is better than 95% over orbital periods up to 400 days (Christiansen et al., priv. comm.) based on the Q1–Q17 data. Therefore, we assigned a value of
: correction to account for the detection pipeline completeness, i.e. the number of transiting planets missed by the detection pipeline. (The upper script C refers to the completeness.) This has been thoroughly studied in Christiansen et al. (2013, 2015). In particular, they find that the detection efficiency of EGPs transiting bright, solar-type dwarfs is better than 95% over orbital periods up to 400 days (Christiansen et al., priv. comm.) based on the Q1–Q17 data. Therefore, we assigned a value of  for all EGPs in our sample.
for all EGPs in our sample.
The values of the all correction factors, except for  which is constant, are provided in Table B.8.
which is constant, are provided in Table B.8.
 |
Fig. 7 Correction factors to compensate for the candidates selection ( |
5.1.4. The occurrence rates and their uncertainties
The occurrence rate is defined as the ratio between the number of transiting planets, nt, corrected by the six aforementioned effects over the total number of dwarfs in the reference sample, N⋆: 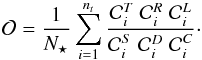 (3)The main uncertainty is based on the fact that we are dealing with relatively small number statistics. This occurrence rate is only based on 63 transiting planets (secured and likely). Thus, we consider that our uncertainty is dominated by a Poisson noise that scales with the number of detected transiting planets (nt), and we define the occurrence rate uncertainty,
(3)The main uncertainty is based on the fact that we are dealing with relatively small number statistics. This occurrence rate is only based on 63 transiting planets (secured and likely). Thus, we consider that our uncertainty is dominated by a Poisson noise that scales with the number of detected transiting planets (nt), and we define the occurrence rate uncertainty, 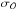 , as
, as 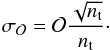 (4)Applying the last two equations in the entire sample, we find that the occurrence rate of EGPs within 400 days is 4.6 ± 0.6%.
(4)Applying the last two equations in the entire sample, we find that the occurrence rate of EGPs within 400 days is 4.6 ± 0.6%.
 |
Fig. 8 Occurrence rates of giant planets as a function of the orbital period. The horizontal bars indicate the range of periods used in a given bin. |
We computed the occurrence rates in different bins of orbital periods, as in Fressin et al. (2013). Tables B.6–B.8 provide all the values needed to derive the occurrence rates of EGPs in different ranges of orbital periods. Our derived values are displayed in Fig. 8 and listed in Table B.9. This shows that the overall occurrence rate of EGPs increases towards longer orbital periods. However, this increase is not monotonic. We can clearly see the pile-up of hot Jupiters at about five days followed by a sharp decrease in the occurrence rate for planets with orbital periods in the range of 10–17 days. The occurrence rate in this period range is one order of magnitude lower than the one at 5 days. Then, the occurrence rate increases up to about 85 days before reaching a plateau up to 400 days.
These variations in the occurrence rate highlight the underlying populations of hot Jupiters, period-valley giants, and temperate giants that were already pointed out by RV surveys more than a decade ago by Udry et al. (2003), among others. These populations of giant planets, especially the pile-up of hot Jupiters, were however not confirmed by previous analyses of the Kepler detections (Howard et al. 2012; Fressin et al. 2013). The reason for that is the presence of false positives that have a different period distribution and dilute the underlying distribution of planets.
5.2. Comparison with other yields
We now compare our results with the two major estimates of the giant-planet occurrence rates: the one of Fressin et al. (2013) that is also based on Kepler photometry (using only the Q1–Q6 results), and the one of Mayor et al. (2016) that is based on HARPS and CORALIE RV. All analyses were performed on similar stellar populations (FGK dwarfs) located in different regions: a few hundred parsec above the galactic plane for the Kepler field of view (FOV) and in the solar neighbourhood for HARPS and CORALIE. However, the selection of the EGPs is slightly different between the analyses: while we selected EGPs based on their deep transit, Fressin et al. (2013) selected all planets with an expected radius in the range 6–22 R♃, and Mayor et al. (2016) considered the limit for the runaway accretion of 50 M⊕ to select EGPs. These differences in the definition of what is an EGP is clearly a limitation for this comparison, so it should be interpreted with caution.
To compare our results with the ones of Mayor et al. (2016), we re-computed the occurrence rates of EGPs in their period ranges and masses above 50 M⊕. We used their detection limits to correct for the missing planets and derive the occurrence rates. We assumed an uncertainty that follows a Poisson noise on the number of detected planets, as in Eq. (4). Our determination of the Mayor et al. (2016) occurrence rates for the different ranges of periods is reported in Table B.9. We also report the values from Fressin et al. (2013) there. In this table, we report both the values in each bin of periods and the cumulative values.
We find no significant difference (within less than 1σ) between our estimation of the EGP occurrence rates and the one using the Mayor et al. data in all the bins. The values of the occurrence rate integrated within 400 days are also compatible between the three analyses.
 |
Fig. 9 Comparison of the occurrence rates of the three populations of giant planets. The black marks represent values based on RV surveys and the white ones are from photometric surveys. |
To compare the results between the three studies further, we computed the occurrence rates for each population of EGPs: the hot Jupiters with orbital periods of less than ten days, the period-valley giants with orbital periods between 10 and 85 days, and finally the temperate giants with orbital periods between 85 and 400 days. We also compared the values found in the literature for the occurrence rate of hot Jupiters. All these values are listed in Table B.9 and plotted in Fig. 9.
The four occurrence rates of hot Jupiters based on the Kepler data (i.e. Howard et al. 2012; Santerne et al. 2012b; Fressin et al. 2013, and this work) are fully compatible, in spite of differences in the candidate or planet selections, and in the stellar reference sample. The reported values are in the range 0.4–0.5% for FGK dwarfs. However, this value seems to be systematically different from the values measured independently by RV in the California Planet Survey (Wright et al. 2012) and the Swiss-led planet survey (Mayor et al. 2016). The latter values are also fully compatible with the estimates from the CoRoT space mission, in both galactic directions (towards the centre and anti-centre of the galaxy, Santerne 2012; Moutou et al. 2013b). In spite of their large uncertainties, these four estimates reported an occurrence rate of ~1%, hence about twice more hot Jupiters than in the Kepler field (see Fig. 9). Bayliss & Sackett (2011) report a hot-Jupiter occurrence rate as low as 0.10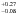 % from the ground-based SuperLupus survey. This is, however, based on very small statistics, since only one hot Jupiter has been established in this survey with two other candidates. Therefore, this result is difficult to interpret and to compare with other transit surveys, which detected several tens of planets.
% from the ground-based SuperLupus survey. This is, however, based on very small statistics, since only one hot Jupiter has been established in this survey with two other candidates. Therefore, this result is difficult to interpret and to compare with other transit surveys, which detected several tens of planets.
This difference, if real, might be explained by various effects. First, it might be an overestimation of the Kepler pipeline completeness. This is quite unlikely since hot Jupiters present high-S/N transits so are easily detected. Even though they would have been missed by the Kepler detection pipeline, they would have been found by the Planet Hunters community (Fischer et al. 2012). Then, it might be an overestimation of the numbers of dwarfs in the reference sample. If the log g of the Kepler targets are systematically overestimated, there would be a large number of giant and subgiant stars in our reference sample. As discussed in Sect. 3.2.2, we have no evidence for this systematic bias in the log g. Finally, the discrepancy with RV results could come from an overestimation of the hot Jupiter population in RV surveys, due to the minimum mass parameter rather than the true mass. Some low-mass stars with low inclination (as in Díaz et al. 2012; Wright et al. 2013) could contaminate the sample. This is, however, quite unlikely since they would produce line-profile variations (Santerne et al. 2015) that were monitored by Mayor et al. (2016). If this difference between the occurrence rates of hot Jupiters found by Kepler and other instruments is real, it should have a physical origin. The metallicity of the host star is well known for driving the formation rate of EGPs (e.g. Santos et al. 2001). Therefore, if the different stellar populations probed by these surveys have significantly different metallicities, it should have an impact on the number of EGPs found. The median metallicity of dwarfs in the solar neighbourhood has been found to be of about −0.08 dex (Sousa et al. 2008) and ~0 dex for both CoRoT pointing directions (Gazzano et al. 2010; Cortés et al. 2015). The median metallicity of the Kepler dwarfs in our reference sample is −0.18 dex using the values from Huber et al. (2014) or −0.03 dex from LAMOST (Dong et al. 2014). The difference in metallicity is about 0.15–0.2 dex between the Kepler dwarfs (using the metallicities from Huber et al. 2014), and the ones from the solar neighbourhood and the CoRoT fields could well explain a factor of two in the occurrence rates of EGPs, as predicted by Fischer & Valenti (2005), among others.
Recently, Wang et al. (2015) have suggested that the difference of hot Jupiters between the solar neighbourhood and the Kepler FOV might be explained by the difference in stellar multiplicity rate, hence affecting their formation rate. To test that, we can use the percentage of detached EBs as a proxy of the stellar multiplicity rate. Using the results of Raghavan et al. (2010), Santerne et al. (2013a) estimated a fraction of EBs with transit depth deeper than 3% in the solar neighbourhood to be 0.53 ± 0.14%. In the Kepler FOV, it has been estimated to be 0.79 ± 0.02% using the second version of the Kepler EB catalogue (Slawson et al. 2011). In the CoRoT fields, the value is 0.94 ± 0.02% (Deleuil et al., in prep.). Therefore, if the stellar multiplicity rate was the reason for the difference in the occurrence rate of hot Jupiters, there should be even fewer of those planets in the CoRoT fields, which seems excluded. If the multiplicity affects the formation rate of EGPs, it is probably a second-order effect compared with the stellar metallicity.
 |
Fig. 10 Hatzes & Rauer (2016) diagram of exoplanets, showing the bulk density as function of their mass. The open circles are the giant planets defined in our sample and the dots are other planets. We kept as planets only those with a density characterised at a level better than 1σ. The arrows represent the candidates in our sample for which it was only possible to derive an upper limit on their mass (see Table B.4). The vertical bars attached to the arrow are the uncertainties on the densities imposed by the uncertainties on the radii. The dashed line represents the empirical lower envelope density for giant and low-mass planets (see Eq. (5)). |
The occurrence rates of period-valley giants also show about a factor of two between our value and the ones of Mayor et al. (2016) and Fressin et al. (2013). With only one independent estimation of the occurrence rate outside the Kepler FOV, this difference might be only the results of small number statistics and thus is not significant.
In the population of the temperate EGPs, the three values are fully compatible. The occurrence rate in the Kepler FOV is not lower by a factor of two compared with the solar neighbourhood. However, this population of transiting planets is the most difficult one to establish by RV, since the expected amplitudes are lower than for shorter period planets. As a result, only half of the Kepler objects used to compute the occurrence rate in this period range are well established20.
5.3. Occurrence rate of brown dwarfs in the brown-dwarf desert
We identified three transiting candidates that have a mass in the brown dwarf regime. These objects have orbital periods of less than 400 days and thus are rare members of the so-called brown-dwarf desert (Armitage & Bonnell 2002). The orbital periods probed by Kepler and our observations correspond to the “driest region” of this desert (Ma & Ge 2014; Ranc et al. 2015). In spite of their very low number, we can derive a first measurement of their occurrence rate. We followed the same procedure as for EGPs, with the same stellar reference sample (see Sect. 5.1.1). We list the adopted parameters of these brown dwarfs in Table B.10 and in Table B.11 their occurrence correction factors, similar to the ones described in Sect. 5.1.3. We derived an overall occurrence rate of brown dwarfs within 400 days of orbital period to be as low as 0.29 ± 0.17%21. Therefore brown dwarfs are about 15 times less common than EGPs in the considered range of periods.
This value is fully compatible with the one derived by Csizmadia et al. (2015) based on the CoRoT data. The brown dwarfs detected by CoRoT, however, have orbital periods shorter than ten days, while in our sample, they have periods between 10 and 170 days. This difference is most likely due to small number statistics.
6. The physical properties of giant planets and their hosts
In this section we analyse the physical properties of the 63 EGPs (secured and likely) in more detail in our sample and discuss them in the context of the other planets characterised so far, using the physical properties listed in Table B.7.
6.1. Mass and density of giant planets
Our spectroscopic survey of Kepler giant-planet candidates provides mass constraints for 40 giant exoplanets (15 well characterised and 25 upper limits). The 23 remaining planets were characterised by other means (e.g. other spectroscopic facilities or TTVs analysis) published in the literature. Combined with the radius measured by Kepler, this allows us to derive the bulk density of these exoplanets. We display their bulk density as a function of their mass in Fig. 10, as in Hatzes & Rauer (2016).
As expected, the large majority of the EGPs in our sample follow the same trend as pointed out in Hatzes & Rauer (2016): the bulk density of EGPs strongly correlate with their mass. This is a direct consequence of the fact that the radius of EGPs and brown dwarfs is nearly constant (within ~30%) over two decades in mass, provided they are mostly made of hydrogen and helium (Guillot 2005).
However, three objects that we considered as EGPs in our sample are clearly outliers in this diagram. We annotate their name in Fig. 10. First, there is the case of KOI-410.01 which has a radius (according to Rowe & Thompson 2015) of 4.9 R♃ for a mass upper limit of 3.4 M♃ (Bouchy et al. 2011). This gives this candidate an extremely low density of less than 0.02 g cm-3. Therefore, KOI-410.01 is either a unique case of extreme inflation for a hot Jupiter, or most likely it is not a planet but a CEB. Kepler-63 b (Sanchis-Ojeda et al. 2013) and KOI-221.01 (this work) are well above the giant-planet branch. These two objects are most likely low-mass planets contaminating our giant-planet sample. These three outliers with no mass determination are probably not EGPs and will not be considered in the rest of the discussion.
Using all the planets that have so far been characterised well, we find an empirical lower envelope from the density-mass diagram of planets (see Fig. 10). This lower envelope has the functional form of ![\begin{equation} \label{lowerenv} \rho_{\rm lower}\, [\rho_{\jupiter}] = \sqrt{\left(\frac{M_{\rm p}^{1.5}}{2.2^{3}}\right)^{2} + \left(\frac{0.04}{M_{\rm p}^{0.5}}\right)^{2}} , \end{equation}](/articles/aa/full_html/2016/03/aa27329-15/aa27329-15-eq105.png) (5)with Mp the planet mass expressed in M♃ . This form was defined using all exoplanets with a mass constrained at better than 1σ. Considering only those constrained at better than 3σ does not change the form of this lower envelope.
(5)with Mp the planet mass expressed in M♃ . This form was defined using all exoplanets with a mass constrained at better than 1σ. Considering only those constrained at better than 3σ does not change the form of this lower envelope.
Assuming this lower density envelope for exoplanets, we find that Kepler-63 b and KOI-221.01 have lower limits in mass of 0.035 M♃ (11 M⊕) and 0.019 M♃ (6.2 M⊕), respectively. For a given mass, we expect to find objects close to this limit that have the largest amount of hydrogen and helium (i.e. lowest fraction of heavy elements), highest irradiation level, and youngest age of the sample (see Guillot 2005). Evaporation also plays a role and could explain the functional form of Eq. (10), at least in the low-mass domain (see Lopez et al. 2012; Owen & Wu 2013).
Applying the same lower density envelope to all the EGPs in our sample for which we only have a upper-limit constraint, we can estimate their minimum mass and thus their minimum RV amplitude. This can be used then to determine the precision needed by future follow-up observations to characterise these objects. We list in Table B.12 the minimum mass we find for these candidates and planets along with their minimum RV amplitude assuming a circular orbit.
Finally, from the population of giant and low-mass planets in this M – ρ diagram, five objects do not seem to follow the global trend: Kepler-51 b, c, d (Masuda 2014), Kepler-79 d (Jontof-Hutter et al. 2014), and Kepler-87 c (Ofir et al. 2014). These planets are very low-mass low-density planets. No modelling of their internal structure has been reported in the literature so far. We believe that determining the internal structure of such low-density planets might be challenging for current models, but this would allow us to better understand the nature of these particular objects. We note, however, that these five planets have been characterised thanks to TTV analyses, which might be biased in the presence of an unseen (i.e. non-transiting) companion or in the presence of stellar activity (Oshagh et al. 2013; Barros et al. 2013). Some cases of TTV-mass determination were revealed to be systematically lower than RV mass determination as pointed out by Weiss & Marcy (2014). To date, very few objects have been characterised independently by both techniques (Weiss et al. 2013; Barros et al. 2014; Bruno et al. 2015). A RV follow-up of these very low-mass low-density planets might reveal a completely different nature for these objects.
6.2. Radius vs. irradiation
The radii of EGPs largely depends on the irradiation level that they receive, which regulates the rate at which they cool down and contract (Guillot et al. 1996). This is controlled both by their atmosphere and interior radiative zone, with a higher irradiation implying a warmer atmosphere and a slower contraction. However, some EGPs, like KOI-680 (Almenara et al. 2015), exhibit a radius that cannot be explained by conventional models, up to about 2 R♃. The reason for this inflation of EGPs is not yet completely understood. Different physical processes have been proposed, such as mechanisms driven by stellar flux heating, tidal heating, or Ohmic dissipation (see Baraffe et al. 2014, for a review). To identify the inflation mechanism, but also to further understand how the atmosphere controls the contraction, we need to characterise EGPs over a wide range of physical properties. By exploring a sample of giant transiting exoplanets up to orbital periods of 400 days, we probed planets receiving a wide range of stellar insolation flux. This insolation flux is defined as 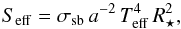 (6)with σsb = 5.6704 × 10-5 the Stefan–Boltzmann constant, a the semi-major axis of the planet, and Teff and R⋆, the effective temperature and radius of the host star.
(6)with σsb = 5.6704 × 10-5 the Stefan–Boltzmann constant, a the semi-major axis of the planet, and Teff and R⋆, the effective temperature and radius of the host star.
We display in Fig. 11 the measured radius of EGPs from our sample as a function of the stellar insolation flux they received. In this figure, we make the distinction between the secured and likely exoplanets and show the other EGPs22 detected and characterised by ground-based observatories such as Super-WASP (Pollacco et al. 2006) and HAT (Bakos et al. 2004), and from the CoRoT space telescope (Baglin et al. 2006).
 |
Fig. 11 Top panel: radius of giant planets as a function of their stellar insolation flux Seff. The open circles indicate the secured planets, the Epen squares the likely ones, and the dots the non-Kepler objects. The solid line represent the best model of Eq. (7) and the grey regions represent the 1, 2, 3σ (from dark to light grey) confidence interval for this best model, as described by the covariance matrix provided in Eq. (8). Bottom panel: normalised cumulative distribution (CDF) of the radius of giant planets listed in Table B.7 for objects receiving more (dashed thick line) or less (solid thick line) insolation flux than 108 erg cm-2 s-1. The prediction from Mordasini et al. (2012b) is shown for comparison (age of 5 Gyr – solid thin line). This prediction is for planet with orbit >0.1 au, which correspond to 1.4 × 108 erg cm-2 s-1 for a Sun-like star. |
First, we can see that thanks to ~4.5 years of observation, Kepler was able to explore EGPs that receive about 100 times less flux from their stars than the ones found by ground-based observatories, hence paving the way between hot Jupiters and the solar system giants. The least irradiated object in our sample is KOI-1411.01 (likely a planet) with an insolation of Seff ≈ 6.8 × 105 erg cm-2 s-1. This is only 13 times more than received by Jupiter. Among the non-Kepler detections, only CoRoT-9 b (Deeg et al. 2010) is an EGP with an insolation below 107 erg cm-2 s-1.
Then, as already pointed out by Demory & Seager (2011), there is a clear lack of inflated EGPs receiving a moderate irradiation (see Fig. 11). Only KOI-3681.01 shows a radius of about 2 R♃ for an insolation of ~107 erg cm-2 s-1, but it does have a large uncertainty. However, our preliminary results show that the stellar host is not a F-IV star as reported by Huber et al. (2014) but a dwarf with a radius of about half the value reported in Table B.7. Thus this planet is much smaller and less irradiated than it appears here. All planets with an insolation of Seff< 108 erg cm-2 s-1 have a radius smaller than ~1.2 R♃ (see Fig. 11). A few objects show a radius of ~0.5 R♃ for an insolation of Seff ≈ 108 erg cm-2 s-1, but they likely have a different composition than H–He gas giants.
In Fig. 11 (lower panel), we display the cumulative histograms of the EGP radius (both likely and secured planets) for the ones receiving more or less insolation than 108 erg cm-2 s-1. The Anderson-Darling test gives a p value at the level of 2 × 10-4, which shows they have the same distribution. This clearly shows that the atmosphere of EGPs receiving a high insolation are dominated by different physical processes than the low-insolation ones.
Fitting all the planets displayed in Fig. 11, we find that the distribution of EGP radius might be modelled as a function of the insolation flux with the following relation: 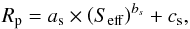 (7)with as = 1.895 × 10-4, bs = 0.371, cs = 0.772, and the following covariance matrix, derived by bootstrapping the planets 105 times23:
(7)with as = 1.895 × 10-4, bs = 0.371, cs = 0.772, and the following covariance matrix, derived by bootstrapping the planets 105 times23: 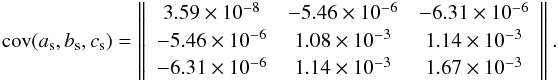 (8)This shows that EGPs in the Kepler field with moderate and low irradiation (Seff< 108 erg cm-2 s-1) tend to have a radius of cs = 0.77 ± 0.04R♃. This value is lower than the one predicted by Mordasini et al. (2012b) of ~1 R♃. By computing the Anderson-Darling test between the two distributions24, we find a p-value that they are similar at the level of 5 × 10-3. This means the two distributions are significantly different. The main difference resides in the fact that Mordasini et al. (2012b) predicted a pile-up of EGPs at about 1 R♃, while the observed distribution is nearly uniform between 0.6 R♃ and 1.2 R♃. However, he radius uncertainty is relatively high and might explain this discrepancy.
(8)This shows that EGPs in the Kepler field with moderate and low irradiation (Seff< 108 erg cm-2 s-1) tend to have a radius of cs = 0.77 ± 0.04R♃. This value is lower than the one predicted by Mordasini et al. (2012b) of ~1 R♃. By computing the Anderson-Darling test between the two distributions24, we find a p-value that they are similar at the level of 5 × 10-3. This means the two distributions are significantly different. The main difference resides in the fact that Mordasini et al. (2012b) predicted a pile-up of EGPs at about 1 R♃, while the observed distribution is nearly uniform between 0.6 R♃ and 1.2 R♃. However, he radius uncertainty is relatively high and might explain this discrepancy.
One might argue that our selection criteria might have biased this value, but given the absence of inflated planets in the regime of moderate irradiation, we might only have missed EGPs with transit depths shallower than 0.4%. If they exist, they would be even smaller than our selected ones, hence increasing the discrepancy. The choice of the functional form might also bias this value. Computing the median radius for planets with Seff< 108 erg cm-2 s-1, we find a value of 0.865 ± 0.05R♃ (see Fig. 11), which is still compatible with cs. This would indicate that the mean radius of EGPs receiving a moderate or low irradiation is smaller than the one predicted in Mordasini et al. (2012b). The precise characterisation and modelling of these objects (as done in e.g. Havel et al. 2011) receiving a low irradiation should allow us to better understand the physics of the atmosphere of EGPs and provide new insight into planet formation.
6.3. Planet-host properties
One of the main ingredients of EGP formation is the metallicity of the disk (e.g. Mordasini et al. 2012a; Nayakshin 2015b). The correlation between the fraction of giant-planet hosts and their metallicity was revealed early in the solar neighbourhood (Santos et al. 2001) and revised as the number of detections increased (Fischer & Valenti 2005; Johnson et al. 2010; Sousa et al. 2011; Mortier et al. 2013). Using our sample of secured giant transiting exoplanets, we might test this correlation in the Kepler FOV.
For homogeneity, we used only the metallicity reported for all the Kepler targets by Huber et al. (2014) for both exoplanet hosts and field stars, selecting only the dwarf stars that respect the criteria defined in Sect. 5.1.1. We then computed the number of transiting giant-planet hosts as a function of iron abundance (Fig. 12). The planet-metallicity correlation is clearly visible in the Kepler giant-planet sample. We fitted this correlation with a power law of the form ![\begin{equation} \log_{10}\left(f({\rm [Fe/H]})\right) = a_{\rm F}\times{\rm [Fe/H]} + b_{\rm F} , \end{equation}](/articles/aa/full_html/2016/03/aa27329-15/aa27329-15-eq128.png) (9)with aF = 1.82, bF = − 2.77, and the following covariance matrix, obtained by bootstrapping 1000 times the values within their uncertainties:
(9)with aF = 1.82, bF = − 2.77, and the following covariance matrix, obtained by bootstrapping 1000 times the values within their uncertainties: 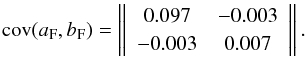 (10)Our value of aF is fully compatible with all the values reported for the solar neighbourhood in the aforementioned papers. Since we are using transit hosts here, the value of bF cannot be compared directly with RV results. Indeed, our value of bF integrates the transit probability over the entire sample.
(10)Our value of aF is fully compatible with all the values reported for the solar neighbourhood in the aforementioned papers. Since we are using transit hosts here, the value of bF cannot be compared directly with RV results. Indeed, our value of bF integrates the transit probability over the entire sample.
 |
Fig. 12 Fraction of dwarf stars transited by a giant planet as a function of the stellar iron abundance. The solid line is the best model found and the grey regions represent the 1, 2, and 3σ confidence intervals (from dark to light grey). |
We also explored the correlation between the occurrence of planets and the mass of the host. This correlation is well established in RV detections, but we failed to confirm it. Assuming a correlation with a functional form of  (as in, e.g. Johnson et al. 2010; Mortier et al. 2013), we find that bM = 1.9 ± 1.3. We are limited here by a lack of precision and too small a sample.
(as in, e.g. Johnson et al. 2010; Mortier et al. 2013), we find that bM = 1.9 ± 1.3. We are limited here by a lack of precision and too small a sample.
Finally, we searched for a possible correlation between the density of EGPs and their host star metal content, and did so directly from the observational data and independently of any model. A correlation between the core mass and the stellar metalicity has been proposed earlier on the basis of a comparison between theoretical interior models and observations of transiting planets (Guillot et al. 2006; Burrows et al. 2007; Miller & Fortney 2011; Moutou et al. 2013b). Except for highly irradiated planets, the bulk density of the planet might be used as a proxy for their core mass (for the same age, a planet with a massive core will have a higher density than a planet with no core). We thus selected the objects in our giant-planet sample with a stellar insolation of Seff< 109 erg cm-2 s-1 (Fig. 13)25.
 |
Fig. 13 Correlation between the bulk density of giant planets receiving a moderate irradiation as a function of the iron abundance of their host star. The solid line is the best model found, and the grey regions represent the 1, 2, and 3σ confidence intervals (from dark to light grey). |
We fitted this correlation with a model of the form ![\begin{equation} \log_{10}\rho_{\rm p} = a_{\rho}\times{\rm [Fe/H]} + b_{\rho} , \end{equation}](/articles/aa/full_html/2016/03/aa27329-15/aa27329-15-eq137.png) (11)with ρp the density of the planet expressed in Jupiter unit, aρ = 1.07, bρ = − 0.47, and the following covariance matrix, obtained by bootstrapping 1000 times the values within their uncertainties:
(11)with ρp the density of the planet expressed in Jupiter unit, aρ = 1.07, bρ = − 0.47, and the following covariance matrix, obtained by bootstrapping 1000 times the values within their uncertainties: 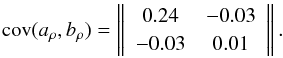 (12)This corresponds only to a hint of correlation at the 2.2σ level. If we removed the two low-mass EGPs in the Kepler-51 system (see Sect. 6.1), this significance drops to 1.3σ. To confirm this possible correlation, it is important to characterise more EGPs in this regime of low irradiation.
(12)This corresponds only to a hint of correlation at the 2.2σ level. If we removed the two low-mass EGPs in the Kepler-51 system (see Sect. 6.1), this significance drops to 1.3σ. To confirm this possible correlation, it is important to characterise more EGPs in this regime of low irradiation.
7. Summary and conclusion
In this paper, we studied the physical properties of giant exoplanets orbiting within 400 days of period. For that, we used the latest catalogue of Kepler transit candidates (Coughlin et al. 2015) in which we defined sample of EGP candidates (see Sect. 2) as the 129 candidates having a transit depth between 0.4% and 3%, a period up to 400 days, and a host star brighter than Kp = 14.7. These 129 objects orbit 125 different stars. We performed an extensive RV follow-up of these candidates using the SOPHIE spectrograph on the 1.93-m telescope of the Observatoire de Haute-Provence during six observing seasons. This allowed us to unveil the nature of the candidates, and we found that 45 bona fide planets (30 already known and 15 new ones characterised by our team), 3 sub-stellar companions that are likely brown dwarfs, 63 multiple stellar systems (SB1, SB2, and SB3), out of which 48 are eclipsing binaries, and 15 are more complex stellar systems. Finally, for 18 objects, we rejected that they are grazing EBs or brown dwarfs, but we could not establish their planetary nature. For these, we were able to put an upper limit on their mass.
We then derived a false-positive rate of 54.6 ± 6.5% for the EGPs, with a value ranging from 51.2 ± 6.3% to 65.1 ± 7.1% depending on the true nature of the unsolved cases (see Sect. 4). This value is significantly higher than all the previously derived values (Morton & Johnson 2011; Santerne et al. 2012b; Fressin et al. 2013). We argued that this higher rate of false positives could have a significant and non-uniform impact on the various planet populations derived by Fressin et al. (2013). We also showed that the absolute number of false positives is expected to increase towards candidates with a smaller radius.
In Sect. 4.4, we compared the properties of the false-positive, giant-planet candidate hosts with the ones of the target stars. We found no statistical difference between the metallicity distribution of false-positive, candidate hosts and the target stars, while there is a difference between giant-planet host properties and other categories. This implies that either the number of candidate host (in which a majority of candidates are smaller than Neptune) does not depend on metallicity or – more speculatively – there is a substantial fraction of false positives among the catalogue of planet candidates. Therefore, the nature of the candidates should be carefully scrutinised before inferring exoplanet properties, which can then be used to constrain planet formation models.
Thanks to our spectroscopic survey of the giant-planet candidates detected by Kepler, we cleaned this sample of false positives. This allowed us to derive an occurrence rate of EGPs orbiting F5–K5 dwarfs within 400-day periods of 4.6 ± 0.6%. By computing this occurrence rate as a function of orbital periods, we recovered the three populations of giant planets already identified by RV surveys in the solar neighbourhood (e.g. Udry et al. 2003): the hot Jupiters orbiting with periods of up to ten days, the period-valley giants with periods between 10 and ~85 days, and the population of temperate giants with periods longer than ~100 days. We note that these populations of giant planets, in particular the pile-up of hot Jupiters, were not recovered in previous studies of the Kepler candidates (Howard et al. 2012; Fressin et al. 2013). This was only possible because we rejected more than half of the candidates from our sample as false positives, which have a different period distribution.
The occurrence rate of hot Jupiters in the Kepler field seems systematically lower by a factor of ~2 compared with other surveys. Even if this difference is not statistically significant, it could result from the EGP-host metallicity correlation (e.g. Santos et al. 2001; Fischer & Valenti 2005). This lower occurrence rate of hot Jupiters compared with the HARPS and CORALIE RV surveys (Mayor et al. 2016), for example, has no counterparts for EGPs with orbital periods longer than ~85 days. The reasons for these differences, if real, might be caused by the mechanisms that only form hot Jupiters.
In Sect. 5.3, we provided an estimate of the formation rate of brown dwarfs in the brown-dwarf desert, at the level of 0.29 ± 0.17% for orbital periods of less than 400 days. Finally, in Sect. 6, we studied the physical properties of the EGPs in our sample and the ones of their host stars. We find that EGPs receiving an insolation lower than Seff< 108 erg cm-2 s-1 are not inflated and exhibit a median radius of ~0.8 R♃. This confirms the results of Demory & Seager (2011), with more objects receiving a moderate irradiation, and they were all filtered out by spectroscopic means. Interestingly, we find that the radius distribution of EGPs with a moderate irradiation is significantly different from the one predicted by Mordasini et al. (2012b). These planets are found to be, on average, smaller than predicted. The detailed characterisation of the internal structure of these moderate-irradiation planets should provide new constraints on planet formation and evolution theories. In particular, we find a hint of a correlation between the bulk density of these planets and the metallicity of the host stars. This correlation needs, however, to be confirmed with more planets in this regime. We also confirm that the EGP-host metallicity correlation previously found by RV surveys (e.g. Sousa et al. 2011; Johnson et al. 2012; Mortier et al. 2013) holds for the transit exoplanet population in the Kepler field. This suggests that similar formation processes are at work in both fields, at least for EGPs.
To probe any relation between the occurrence of EGPs and the properties of the stellar field, it is mandatory to explore more stellar populations. Measuring the abundance of the α elements of the hosts could also provide information about the galactic populations these planet hosts belong to Adibekyan et al. (2012). Different stellar populations are currently observed by the K2 mission (Howell et al. 2014) and will be explored by the upcoming space missions TESS and PLATO. This will give us a unique opportunity to probe the difference in the properties of planet population further in different stellar environments. This would, however, require a deep characterisation of the stellar fields, which will be possible thanks to the GAIA mission. Similar studies using the ground-based photometric surveys like SuperWASP (Pollacco et al. 2006) and HAT-Net (Bakos et al. 2004) could also provide us with unprecedented constraints on EGP formation and migration, but calibrating the detection limits might be challenging because of the lack of uniformity in the data. Note that TESS (Ricker et al. 2015) and PLATO (Rauer et al. 2014) will be observing much brighter stars than the Kepler targets. We will therefore have access to better RV precision with the SOPHIE spectrograph, allowing us to do similar work on the populations of smaller planets, down to hot super-Earths and warm Neptunes (Courcol et al. 2015).
The SWEET-Cat is available at: http://www.astro.up.pt/resources/sweet-cat/
The values and errors reported in this paragraph correspond to the mean and its uncertainty computed as 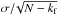 , with σ the standard deviation, N the number of points, and kf the number of free parameters (Gott et al. 2001). Here, kf = 1.
, with σ the standard deviation, N the number of points, and kf the number of free parameters (Gott et al. 2001). Here, kf = 1.
The Kepler EB catalogue is available at: http://keplerebs.villanova.edu
As discussed in Bognár et al. (2015), this seems not to be the case of KOI-3783.01.
The Anderson-Darling test is recommended by Hou et al. (2009) to estimate the probability that two random variables are drawn from the same underlying distribution. It is more sensitive to the differences in the wings of the distribution, whereas the Kolmogorov–Smirnov (KS) test is mostly sensitive to its median. Both tests are non-parametric and distribution free. The AD test is more computationally expensive than the KS test.
This corresponds to F5–K5 dwarfs according to Cox (2000).
While the maximum stellar radius is defined based on the evolution tracks (see Table B.6), we determined the minimum stellar radius as the lower envelope of the Kepler targets.
This was done by drawing a statistically large number (in this case 105) of planets from the interpolated distribution of Mordasini et al. (2012b) at 5 Gyr.
If we limit to Seff< 108 erg cm-2 s-1, we do not have enough well-characterised planets to search for a correlation. None of the planets in our sample with Seff< 109 erg cm-2 s-1 exhibits a radius larger than ~1.2 R♃. Thus we can consider that this sub-sample of planets is not significantly inflated.
Acknowledgments
We thank the referee for his/her time reviewing this quite long paper and for the fruitful comments and suggestion that improved the quality of this manuscript. A.S. thanks Jon Jenkins, Natalie Batalha, and Jessie Christiansen for their help concerning the Kepler data, catalogue of KOIs, and pipeline completeness. A.S. also thanks Gibor Basri for his suggestion to derive the occurrence rate of brown dwarfs, Maxime Marmier for the updated detection list of the HARPS and CORALIE survey, as well as Pedro Figueira and Olivier Mousis for fruitful discussions and his valuable comments on the manuscript. We are all grateful to the staff at the Observatoire de Haute-Provence for maintaining the SOPHIE spectrograph and the 1.93-m telescope. In particular, we acknowledge the difficult but essential work of the telescope operators: Jean-Pierre Troncin, Stéphane Favard, Didier Gravallon (a.k.a “Le Didou de l’OHP”), and Florent Zapillon. The Porto group acknowledges the support by the European Research Council/European Community under the FP7 through Starting Grant agreement number 239953 and support from Fundação para a Ciência e a Tecnologia (FCT, Portugal) in the form of grants reference SFRH/BPD/70574/2010 and PTDC/FIS-AST/1526/2014. NCS also acknowledges the support from FCT in the form of grant reference PTDC/CTE-AST/098528/2008 and through Investigador FCT contract of reference IF/00169/2012 as well as POPH/FSE (EC) by FEDER funding through the programme “Programa Operacional de Factores de Competitividade – COMPETE”. A.S. is supported by the European Union under a Marie Curie Intra-European Fellowship for Career Development with reference FP7-PEOPLE-2013-IEF, number 627202. A.S.B. acknowledges funding from the European Union Seventh Framework Programme (FP7/2007–2013) under Grant agreement number 313014 (ETAEARTH). S.C.C.B. acknowledges support by grants 98761 by CNES and the FCT through the Investigador FCT Contract No. IF/01312/2014. Part of this work was supported by FCT through the research grant UID/FIS/04434/2013. J.M.A. acknowledges funding from the European Research Council under the ERC Grant Agreement n. 337591-ExTrA. This research has made use of the VizieR catalogue access tool, the CDS, Strasbourg, France. The original description of the VizieR service was published in A&AS 143, 23. This research has made use intensively of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
References
- Adibekyan, V. Z., Delgado Mena, E., Sousa, S. G., et al. 2012, A&A, 547, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 560, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Almenara, J. M., Damiani, C., Bouchy, F., et al. 2015, A&A, 575, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J., & Bonnell, I. A. 2002, MNRAS, 330, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, 36th COSPAR Scientific Assembly, 36, 3749 [Google Scholar]
- Bakos, G., Noyes, R. W., Kovács, G., et al. 2004, PASP, 116, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Torres, G., Pál, A., et al. 2010, ApJ, 710, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Fortney, J., & Sotin, C. 2014, Protostars and Planets VI, 763 [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barros, S. C. C., Boué, G., Gibson, N. P., et al. 2013, MNRAS, 430, 3032 [NASA ADS] [CrossRef] [Google Scholar]
- Barros, S. C. C., Díaz, R. F., Santerne, A., et al. 2014, A&A, 561, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batalha, N. M. 2014, Proc. Nat. Acad. Sci., 111, 12647 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Gilliland, R. L., et al. 2010, ApJ, 713, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bayliss, D. D. R., & Sackett, P. D. 2011, ApJ, 743, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G. 2013, Ph.D. Thesis, Institute of Astronomy [Google Scholar]
- Boisse, I., Eggenberger, A., Santos, N. C., et al. 2010, A&A, 523, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bognár, Z., Lampens, P., Frémat, Y., et al. 2015, A&A, 581, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonomo, A. S., Santerne, A., Alonso, R., et al. 2010, A&A, 520, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonomo, A. S., Hébrard, G., Santerne, A., et al. 2012, A&A, 538, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonomo, A. S., Sozzetti, A., Santerne, A., et al. 2015, A&A, 575, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Jenkins, J., et al. 2009, Science, 325, 709 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011a, ApJ, 728, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011b, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchy, F., Pepe, F., & Queloz, D. 2001, A&A, 374, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Pont, F., Melo, C., et al. 2005, A&A, 431, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Isambert, J., Lovis, C., et al. 2009a, EAS Pub. Ser., 37, 247 [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Mayor, M., Lovis, C., et al. 2009b, A&A, 496, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Hébrard, G., Udry, S., et al. 2009c, A&A, 505, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Bonomo, A. S., Santerne, A., et al. 2011, A&A, 533, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Díaz, R. F., Hébrard, G., et al. 2013, A&A, 549, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., Lecavelier des Etangs, A., Hébrard, G., et al. 2015, A&A, 579, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradley, P. A., Guzik, J. A., Miles, L. F., et al. 2015, AJ, 149, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M. 2003, ApJ, 593, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Latham, D. W., Everett, M. E., & Esquerdo, G. A. 2011, AJ, 142, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Bruno, G., Almenara, J.-M., Barros, S. C. C., et al. 2015, A&A, 573, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bryson, S. T., Jenkins, J. M., Gilliland, R. L., et al. 2013, PASP, 125, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Bizzarro, M., Latham, D. W., et al. 2014, Nature, 509, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, C. J., Bryson, S. T., Mullally, F., et al. 2014, ApJS, 210, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Hubeny, I., Budaj, J., & Hubbard, W. B. 2007, ApJ, 661, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera, J., Csizmadia, S., Lehmann, H., et al. 2014, ApJ, 781, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. C. 2012, Nature, 492, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Johansen, A., Janson, M., & Rafikov, R. 2014, Protostars and Planets VI, 619 [Google Scholar]
- Charbonnel, C., & Palacios, A. 2004, Stellar Rotation, 215, 440 [Google Scholar]
- Christiansen, J. L., Clarke, B. D., Burke, C. J., et al. 2013, ApJS, 207, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Christiansen, J. L., Clarke, B. D., Burke, C. J., et al. 2015, ApJ, 810, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colón, K. D., Ford, E. B., & Morehead, R. C. 2012, MNRAS, 426, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Colón, K. D., Morehead, R. C., & Ford, E. B. 2015, MNRAS, 452, 3001 [NASA ADS] [CrossRef] [Google Scholar]
- Cortés, C., Maciel, S. C., Vieira, S., et al. 2015, A&A, 581, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coughlin, J. L., Mullally, F., Thompson, S. E., et al. 2015, arXiv e-prints [arXiv:1512.06149] [Google Scholar]
- Courcol, B., Bouchy, F., Pepe, F., et al. 2015, A&A, 581, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, A. N. 2000, Allen’s Astrophysical Quantities (New York: AIP Press) [Google Scholar]
- Csizmadia, S., Hatzes, A., Gandolfi, D., et al. 2015, A&A, 584, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, R. I. 2014, ApJ, 790, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, R. I., Johnson, J. A., Fabrycky, D. C., et al. 2014, ApJ, 791, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Deeg, H. J., Moutou, C., Erikson, A., et al. 2010, Nature, 464, 384 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deleuil, M., Almenara, J.-M., Santerne, A., et al. 2014, A&A, 564, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delrez, L., Van Grootel, V., Anderson, D. R., et al. 2014, A&A, 563, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demory, B.-O., & Seager, S. 2011, ApJS, 197, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J.-M., Charbonneau, D., Demory, B.-O., et al. 2011, ApJS, 197, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J.-M., Charbonneau, D., Torres, G., et al. 2015, ApJ, 804, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Devor, J., Charbonneau, D., O’Donovan, F. T., Mandushev, G., & Torres, G. 2008, AJ, 135, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, R. F., Santerne, A., Sahlmann, J., et al. 2012, A&A, 538, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Damiani, C., Deleuil, M., et al. 2013, A&A, 551, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Almenara, J. M., Santerne, A., et al. 2014a, MNRAS, 441, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, R. F., Montagnier, G., Leconte, J., et al. 2014b, A&A, 572, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dong, S., Zheng, Z., Zhu, Z., et al. 2014, ApJ, 789, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Dressing, C. D., & Charbonneau, D. 2013, ApJ, 767, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, E. W., Borucki, W. J., Koch, D. G., et al. 2010, ApJ, 713, L136 [NASA ADS] [CrossRef] [Google Scholar]
- Endl, M., MacQueen, P. J., Cochran, W. D., et al. 2011, ApJS, 197, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Endl, M., Caldwell, D. A., Barclay, T., et al. 2014, ApJ, 795, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Esteves, L. J., De Mooij, E. J. W., & Jayawardhana, R. 2015, ApJ, 804, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Faigler, S., Tal-Or, L., Mazeh, T., Latham, D. W., & Buchhave, L. A. 2013, ApJ, 771, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., Schwamb, M. E., Schawinski, K., et al. 2012, MNRAS, 419, 2900 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B., Ragozzine, D., Rowe, J. F., et al. 2012, ApJ, 756, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Demory, B.-O., Désert, J.-M., et al. 2011, ApJS, 197, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Fressin, F., Torres, G., Charbonneau, D., et al. 2013, ApJ, 766, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E. 2013, ApJ, 770, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Gandolfi, D., Parviainen, H., Fridlund, M., et al. 2013, A&A, 557, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Parviainen, H., Deeg, H. J., et al. 2015, A&A, 576, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gazzano, J.-C., de Laverny, P., Deleuil, M., et al. 2010, A&A, 523, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Anderson, D. R., Collier-Cameron, A., et al. 2013, A&A, 552, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gott, J. R., III, Vogeley, M. S., Podariu, S., & Ratra, B. 2001, ApJ, 549, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2005, Annual Review of Earth and Planetary Sciences, 33, 493 [Google Scholar]
- Guillot, T., Burrows, A., Hubbard, W. B., Lunine, J. I., & Saumon, D. 1996, ApJ, 459, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hadden, S., & Lithwick, Y. 2014, ApJ, 787, 80 [Google Scholar]
- Halbwachs, J. L., Mayor, M., Udry, S., & Arenou, F. 2003, A&A, 397, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatzes, A. P., Rauer, H. 2016, ApJL, submitted [arXiv:1506.05097] [Google Scholar]
- Havel, M., Guillot, T., Valencia, D., & Crida, A. 2011, A&A, 531, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hébrard, G., Désert, J.-M., Díaz, R. F., et al. 2010, A&A, 516, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hébrard, G., Almenara, J.-M., Santerne, A., et al. 2013, A&A, 554, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hébrard, G., Santerne, A., Montagnier, G., et al. 2014, A&A, 572, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Ragozzine, D., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hou, A., Parker, L. C., Harris, W. E., & Wilman, D. J. 2009, ApJ, 702, 1199 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A. W., Marcy, G. W., Johnson, J. A., et al. 2010, Science, 330, 653 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Silva Aguirre, V., Matthews, J. M., et al. 2014, ApJS, 211, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Borucki, W. J., Koch, D. G., et al. 2010, ApJ, 724, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Twicken, J. D., Batalha, N. M., et al. 2015, AJ, 150, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Jontof-Hutter, D., Lissauer, J. J., Rowe, J. F., & Fabrycky, D. C. 2014, ApJ, 785, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Gazak, J. Z., Apps, K., et al. 2012, AJ, 143, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2014, MNRAS, 440, 2164 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, D. G., Borucki, W. J., Rowe, J. F., et al. 2010, ApJ, 713, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Kolbl, R., Marcy, G. W., Isaacson, H., & Howard, A. W. 2015, AJ, 149, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012, A&A, 543, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Latham, D. W., Borucki, W. J., Koch, D. G., et al. 2010, ApJ, 713, L140 [NASA ADS] [CrossRef] [Google Scholar]
- Latham, D. W., Rowe, J. F., Quinn, S. N., et al. 2011, ApJ, 732, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., Fortney, J. J., & Miller, N. 2012, ApJ, 761, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Lillo-Box, J., Barrado, D., & Bouy, H. 2014, A&A, 566, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lissauer, J. J., Ragozzine, D., Fabrycky, D. C., et al. 2011, ApJS, 197, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Marcy, G. W., Rowe, J. F., et al. 2012, ApJ, 750, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Marcy, G. W., Bryson, S. T., et al. 2014, ApJ, 784, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, M. N., Lundkvist, M., Silva Aguirre, V., et al. 2014, A&A, 570, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ma, B., & Ge, J. 2014, MNRAS, 439, 2781 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Lillo-Box, J., Southworth, J., et al. 2015, ArXiv e-prints [arXiv:1504.04625] [Google Scholar]
- Masuda, K. 2014, ApJ, 783, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2016, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Miller, N., & Fortney, J. J. 2011, ApJ, 736, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009a, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009b, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., Klahr, H., & Henning, T. 2012a, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Georgy, C., et al. 2012b, A&A, 547, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morgan, W. W., & Keenan, P. C. 1973, ARA&A, 11, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Mortier, A., Santos, N. C., Sousa, S., et al. 2013, A&A, 551, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Sousa, S. G., Adibekyan, V. Z., Brandão, I. M., & Santos, N. C. 2014, A&A, 572, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, T. D. 2012, ApJ, 761, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, T. D., & Johnson, J. A. 2011, ApJ, 738, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Moutou, C., Hébrard, G., Bouchy, F., et al. 2009, A&A, 498, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Bonomo, A. S., Bruno, G., et al. 2013a, A&A, 558, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Deleuil, M., Guillot, T., et al. 2013b, Icarus, 226, 1625 [NASA ADS] [CrossRef] [Google Scholar]
- Mullally, F., Coughlin, J. L., Thompson, S. E., et al. 2015, ApJS, 217, 31 [Google Scholar]
- Müller, H. M., Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nayakshin, S. 2015a, MNRAS, 454, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S. 2015b, MNRAS, submitted [arXiv:1502.07585] [Google Scholar]
- O’Donovan, F. T., Charbonneau, D., Mandushev, G., et al. 2006, ApJ, 651, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Ofir, A., Dreizler, S., Zechmeister, M., & Husser, T.-O. 2014, A&A, 561, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oshagh, M., Santos, N. C., Boisse, I., et al. 2013, A&A, 556, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., & Wu, Y. 2013, ApJ, 775, 105 [Google Scholar]
- Pál, A., Bakos, G. Á., Torres, G., et al. 2008, ApJ, 680, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perruchot, S., Kohler, D., Bouchy, F., et al. 2008, Proc. SPIE, 7014 [Google Scholar]
- Perruchot, S., Bouchy, F., Chazelas, B., et al. 2011, Proc. SPIE, 8151, [Google Scholar]
- Petigura, E. A., Howard, A. W., & Marcy, G. W. 2013, Proc. Nat. Acad. Sci., 110, 19273 [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ranc, C., Cassan, A., Albrow, M. D., et al. 2015, A&A, 580, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exper. Astron., 38, 249 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astronomical Telescopes, Instruments, and Systems, 1, 014003 [Google Scholar]
- Rowe, J. F., & Thompson, S. E. 2015, ArXiv e-prints [arXiv:1504.00707] [Google Scholar]
- Rowe, J. F., Bryson, S. T., Marcy, G. W., et al. 2014, ApJ, 784, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Rowe, J. F., Coughlin, J. L., Antoci, V., et al. 2015, ApJS, 217, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Winn, J. N., Marcy, G. W., et al. 2013, ApJ, 775, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Santerne, A. 2012, Ph.D. Thesis, Aix-Marseille University [Google Scholar]
- Santerne, A., Díaz, R. F., Bouchy, F., et al. 2011a, A&A, 528, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Bonomo, A. S., Hébrard, G., et al. 2011b, A&A, 536, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Moutou, C., Barros, S. C. C., et al. 2012a, A&A, 544, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Díaz, R. F., Moutou, C., et al. 2012b, A&A, 545, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Fressin, F., Díaz, R. F., et al. 2013a, A&A, 557, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Díaz, R. F., Almenara, J.-M., et al. 2013b, SF2A-2013: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, 555 [Google Scholar]
- Santerne, A., Hébrard, G., Deleuil, M., et al. 2014, A&A, 571, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Díaz, R. F., Almenara, J.-M., et al. 2015, MNRAS, 451, 2337 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2001, A&A, 373, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2002, A&A, 392, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmitt, J. R., Wang, J., Fischer, D. A., et al. 2014a, AJ, 148, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. R., Agol, E., Deck, K. M., et al. 2014b, ApJ, 795, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slawson, R. W., Prša, A., Welsh, W. F., et al. 2011, AJ, 142, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. A. 1973, Ph.D. Thesis [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A&A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, J. H., Fabrycky, D. C., Agol, E., et al. 2013, MNRAS, 428, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Shporer, A., Jenkins, J. M., Rowe, J. F., et al. 2011, AJ, 142, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Shporer, A., O’Rourke, J. G., Knutson, H. A., et al. 2014, ApJ, 788, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Konacki, M., Sasselov, D. D., & Jha, S. 2005, ApJ, 619, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Fischer, D. A., Sozzetti, A., et al. 2012, ApJ, 757, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Triaud, A. H. M. J. 2011, A&A, 534, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsantaki, M., Sousa, S. G., Adibekyan, V. Z., et al. 2013, A&A, 555, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tingley, B., Parviainen, H., Gandolfi, D., et al. 2014, A&A, 567, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., Mayor, M., & Santos, N. C. 2003, A&A, 407, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J., & Fischer, D. A. 2015, AJ, 149, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Fischer, D. A., Barclay, T., et al. 2013, ApJ, 776, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Fischer, D. A., Horch, E. P., & Huang, X. 2015, ApJ, 799, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, L. M., & Marcy, G. W. 2014, ApJ, 783, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, L. M., Marcy, G. W., Rowe, J. F., et al. 2013, ApJ, 768, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, O. C. 1941, ApJ, 93, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Marcy, G. W., Howard, A. W., et al. 2012, ApJ, 753, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Roy, A., Mahadevan, S., et al. 2013, ApJ, 770, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, G., & Huang, C. X. 2013, ApJ, 776, L35 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Results from the spectroscopic observations
Appendix A.1: General informations
We present in this appendix the observation and their analysis we performed on each candidate. The radial velocities and their diagnoses are listed in Tables C.1–C.3. For some candidates, we refer to the data validation (DV) summary produced by the Kepler team. They are available at the NASA exoplanet archive26.
Some candidates turn out to be false positives and are actually member of the Kepler EB catalogue (Kirk et al., in prep.). This is the case for the following candidates: KOI-129.01, KOI-138.01, KOI-198.01, KOI-368.01, KOI-449.01, KOI-969.01, KOI-976.01, KOI-1020.01, KOI-1227.01, KOI-1232.01, KOI-1326.01, KOI-1452.01, KOI-1483.01, KOI-1645.01, KOI-1784. 01, KOI-3411.01, KOI-3720.01, KOI-3721.01, KOI-3782.01, KOI-3783.01, KOI-3787.01, KOI-3811.01, KOI-5034.01, KOI-5086.01, KOI-5132.01, KOI-5436.01, KOI-5529.01, KOI-5708. 01, KOI-5745.01, KOI-5976.01, KOI-6066.01, KOI-6175.01, KOI-6235.01, KOI-6460.01, KOI-6602.01, KOI-6800.01, KOI-6877.01, KOI-6933.01, KOI-7044.01, KOI-7054.01, KOI-7065. 01, and KOI-7527.01.
Our observations also confirm the results of Kolbl et al. (2015) for the candidates: KOI-969.01, KOI-1020.01, KOI-1137.01, KOI-1227.01, KOI-1326.01, KOI-1452.01, KOI-1645. 01, KOI-1784.01, KOI-3721.01, and KOI-3782.01.
Appendix A.2: KOI-129.01
KOI-129.01 is a 24-day planet candidate reported for the first time in Burke et al. (2014) and flagged as a false positive. However, in the later candidate releases, this object was no longer flagged as a false positive. We obtained two SOPHIE HE RV which exhibit a variation at the level of about 10 km s-1 in phase with the Kepler ephemeris. Assuming there is no significant drift in the data and a circular orbit at the transit ephemeris, we find that the RV semi-amplitude is K = 6.16 ± 0.04 km s-1. Assuming a host mass of 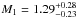 M⊙ from Huber et al. (2014), it gives a companion mass of M2 = 0.11 ± 0.01 M⊙. The planet candidate KOI-129.01 is therefore a false positive and likely a very low mass star.
M⊙ from Huber et al. (2014), it gives a companion mass of M2 = 0.11 ± 0.01 M⊙. The planet candidate KOI-129.01 is therefore a false positive and likely a very low mass star.
Appendix A.3: KOI-138.01
KOI-138.01 is a 49-day planet candidate reported for the first time in Borucki et al. (2011b). We obtained five different epochs with SOPHIE HE. They present a large RV variation in anti-phase with the Kepler ephemeris. Assuming no significant drift in the data and fixing the orbital period to the one observed by Kepler, we find that the orbit has a RV amplitude of K = 22.31 ± 0.08 km s-1, an eccentricity of e = 0.33 ± 0.01, an argument of periastron of ω = 240.0 ± 0.4°, and an epoch of periastron of Tp = 2 454 922.61 ± 0.04. Assuming a host mass of 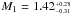 M⊙ from Huber et al. (2014), the companion has a mass of M2 = 0.63 ± 0.07 M⊙. The RV orbit also gives an epoch of secondary eclipse to be Tocc = 2 454 973.542 ± 0.046, which coincides with the epoch of transit that Kepler detected of T0 = 2 454 973.766221 ± 3.24 × 10-4. Therefore, the candidate KOI-138.01 is not a transiting planet but a secondary-only EB.
M⊙ from Huber et al. (2014), the companion has a mass of M2 = 0.63 ± 0.07 M⊙. The RV orbit also gives an epoch of secondary eclipse to be Tocc = 2 454 973.542 ± 0.046, which coincides with the epoch of transit that Kepler detected of T0 = 2 454 973.766221 ± 3.24 × 10-4. Therefore, the candidate KOI-138.01 is not a transiting planet but a secondary-only EB.
Appendix A.4: KOI-198.01
KOI-198.01 is a 87-day planet candidate reported for the first time in Burke et al. (2014), and flagged as a false positive. It is no longer flagged as a false positive in the latter candidates releases. We obtained only two different epochs with SOPHIE HE. They show a RV span of about 10 km s-1 in anti-phase with the Kepler ephemeris. The large RV variation observed by SOPHIE is not compatible with a planet. We therefore conclude this candidate is a false positive. Given that the RV are in anti-phase with the Kepler ephemeris, we expected this candidate to be a secondary-only EB.
Appendix A.5: KOI-201.01
The giant-planet candidate KOI-201.01 was announced in Borucki et al. (2011b) with an orbital period of 4.2 days. The SOPHIE spectroscopic observations reported by Santerne et al. (2012b) did not allow them to detected the Doppler signature of the planet. Recent observations with the HARPS-N spectrograph27 allowed us to detect this signature and characterise the mass of the candidate, confirming also its planetary nature. The analysis of this system will be presented in a forthcoming paper (Hébrard et al., in prep.).
Appendix A.6: KOI-221.01
A giant-planet candidate was reported in Borucki et al. (2011a) with an orbital period of about 3 days. It was however found with a transit depth of about 0.37%, which was below the minimum depth selected by Santerne et al. (2012b). With more Kepler data, the transit depth was revised to be slightly above 0.4% (Mullally et al. 2015) and this candidate is thus within our selection criteria. With more data, it was also possible to find a Earth-size candidate at 6 days (Burke et al. 2014). We observed it twice with SOPHIE HE and find no significant RV, bisector nor FWHM variation. We fitted the RV with two circular orbits at the Kepler ephemeris and find that K221.01< 99 m s-1 and K221.02< 156 m s-1, at the 99% level. Assuming a host mass of 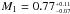 M⊙Huber et al. (2014), we find that the candidates have masses of M221.01< 0.65M♃ and M221.02< 1.16M♃, within a probability of 99%. We can therefore exclude that these candidates are stars or brown dwarfs eclipsing the target star, but we can not rule out other false-positive scenarios.
M⊙Huber et al. (2014), we find that the candidates have masses of M221.01< 0.65M♃ and M221.02< 1.16M♃, within a probability of 99%. We can therefore exclude that these candidates are stars or brown dwarfs eclipsing the target star, but we can not rule out other false-positive scenarios.
Appendix A.7: KOI-351.01 and KOI-351.02
The target star KOI-351 was found to host seven transiting planet candidates (Cabrera et al. 2014) with orbital periods of 332d (KOI-351.01), 211d (KOI-351.02), 60d (KOI-351.03), 92d (KOI-351.04), 9d (KOI-351.05), 6d (KOI-351.06), and 125d (KOI-351.07). Only the two outermost planets are giant-planet candidates within our selection criteria. We obtained five RV with SOPHIE HE. They have a rms of 16 m s-1 which is compatible with the uncertainties. The bisector and FWHM do not show significant variation with rms of 27 m s-1 and 80 m s-1 (respectively). We modelled the RV with a 7-orbit model with fixed eccentricities to zero and ephemeris fixed at the Kepler ones. We find upper limits at the 99% level for the amplitude of the planets of K351.01< 35.5 m s-1, K351.02< 29.0 m s-1, K351.03< 63.6 m s-1, K351.04< 81.0 m s-1, K351.05< 29.4 m s-1, K351.06< 102.6 m s-1, and K351.07< 29.1 m s-1.
Assuming a stellar host mass of M1 = 0.99 ± 0.10 M⊙ (Schmitt et al. 2014a), we derived upper limits on the mass of these exoplanets, at the 99% confidence interval, of M351.01< 1.16M♃, M351.02< 0.82M♃, M351.03< 1.17M♃, M351.04< 1.76M♃, M351.05< 0.29M♃, M351.06< 1.04M♃, and M351.07< 0.78M♃. All these planets but the last one (KOI-351.07) were validated by the planet-likelihood multiplicity-boost (Lissauer et al. 2014; Rowe et al. 2014). Within the assumptions aforementioned, we can confirm that, if the objects are transiting the target star, they have a mass within the planetary range.
Appendix A.8: KOI-368.01
The target star KOI-368 was found to host a giant-planet candidate with a period of 110d (Borucki et al. 2011b). However, Zhou & Huang (2013) detected a clear secondary eclipse and conclude that the companion is a M dwarf. We observed this candidate host twice with SOPHIE HE and find a wide line profile (υsini⋆ = 86.5 ± 0.6 km s-1) which does not show significant RV variation. Because of its large rotation profile, we were not able to measure the bisector. We fitted these two measurements assuming a circular orbit and find that K< 5.06 km s-1, at the 99% level. Assuming a host mass of M1 = 2.3 ± 0.1 M⊙ (Zhou & Huang 2013), we derived an upper limit on the mass of the companion of M2< 0.21 M⊙, at the 99% level and assuming a circular orbit. Our mass constraint is compatible with the late M-dwarf type claimed by Zhou & Huang (2013).
Appendix A.9: KOI-372.01
KOI-372.01 is a 125-day planet candidate reported for the first time in Borucki et al. (2011b). The Kepler light curve of this candidate reveals large photometric variability at the level of ~1.5% due to stellar activity. We observed it with SOPHIE HR and HE. We find a RV rms of 24 m s-1 which is not compatible with the recent solution published by Mancini et al. (2015) of K = 132 ± 6 m s-1. The RV and their in-depth analysis will be presented in Demangeon et al. (in prep.). We consider that the nature of this candidate is still unknown for the statistical analysis of this papier.
We derived the stellar atmospheric parameters that are reported in Table B.2. They correspond to a mass of M = 1.02 ± 0.04 M⊙, a radius of 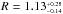 R⊙, and an age of 6.7
R⊙, and an age of 6.7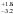 Gyr.
Gyr.
Appendix A.10: KOI-449.01
The planet candidate KOI-449.01 has an orbital period of ~252 days and was announced in Burke et al. (2014) as a false positive. In later candidates lists, it was no longer flagged as a false positive. We observed this candidate three times with SOPHIE HE but detected no significant RV (rms of 23 m s-1), nor bisector or FWHM variation (rms of 119 m s-1 and 52 m s-1, respectively). By fitting a circular orbit at the Kepler ephemeris, we find that K< 1.1 km s-1 within a probability of 99%. Assuming a host mass of 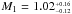 M⊙ (Huber et al. 2014), this corresponds to an upper limit on the mass of this candidate of M449.01< 37.0M♃. Therefore, within the circular approximation, we can exclude an EB as the source of the transit event. However, we can not exclude a transiting brown dwarf, nor a background source of false positive.
M⊙ (Huber et al. 2014), this corresponds to an upper limit on the mass of this candidate of M449.01< 37.0M♃. Therefore, within the circular approximation, we can exclude an EB as the source of the transit event. However, we can not exclude a transiting brown dwarf, nor a background source of false positive.
This candidate is listed as an EB in Kepler EB catalogue (Kirk et al, in prep.) with a double period, showing some odd-even transits depth difference which suggest that this candidate is an EB in a circular orbit at twice the reported period. Since we detected no variation in the target star, we conclude this candidate is a CEB and not a transiting planet.
Appendix A.11: KOI-464.01
The candidate KOI-464.01 has an orbital period of ~58 days, reported for the first time by Borucki et al. (2011b). Another candidate transiting the same star at ~5 days was also found with a transit depth of 800 ppm. We observed it five times with SOPHIE HE and detected any clear variation neither in the RV (rms of 27 m s-1), nor in the bisector (rms of 18 m s-1), and FWHM (rms of 47 m s-1). We fitted these RV assuming two circular orbits at the Kepler ephemeris. We find upper limits on the amplitude of both candidates, at the 99% confidence level of K464.01< 21.1 m s-1 and K464.02< 21.9 m s-1. Assuming a host mass of 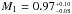 M⊙ (Huber et al. 2014), we find upper limits on the mass of these candidate of M464.01< 0.68M♃ and M464.02< 0.29M♃, at the 99% level.
M⊙ (Huber et al. 2014), we find upper limits on the mass of these candidate of M464.01< 0.68M♃ and M464.02< 0.29M♃, at the 99% level.
Appendix A.12: KOI-531.01
The transit candidate KOI-531.01 has an orbital period of ~3.7 days. It was reported for the first time by Borucki et al. (2011b) with a wrong transit depth of 0.25% due to a bad transit fit. Therefore, it was not included in the sample of Santerne et al. (2012b). The corrected transit depth being of 0.53% (Dressing & Charbonneau 2013), the candidate is now included in this sample. We secured five different epochs on this candidate with SOPHIE HE. The RV, bisector and FWHM present a large dispersion with a rms of 280 m s-1, 306 m s-1, and 351 m s-1 for median uncertainties of 64 m s-1, 115 m s-1, and 160 m s-1, respectively. The bisector is clearly correlated with the RV (see Fig. A.1), with a Spearman correlation coefficient of ρ = 0.70 ± 0.25. This candidate is clearly not a transiting planet, which would not have produced such large variation of the line-profile shape. Only a blended system, like a triple system, might explain the observed correlation between the RV and bisector (Santerne et al. 2015). This actually confirms the recent multi-color observations with the GTC obtained by Colón et al. (2015).
 |
Fig. A.1 Bisector Vspan as a function of the RV for the target star KOI-531. |
Appendix A.13: KOI-617.01
The giant candidate KOI-617.01 was revealed by Borucki et al. (2011a). It has an orbital period of ~38 days. We secured four observations of this star with SOPHIE HE that revealed a clear SB2. By fitting the cross-correlation function with two Gaussians, we derived the RV of both components. We call the star A the component with the deepest line profile and star B the one with the faintest line profile in the CCF. We then fitted those RV with a combined Keplerian orbit, fixing only the orbital period to the transit one. We find an epoch of periastron of Tp ≈ 2 456 130.23, an eccentricity of e ≈ 0.23, an argument of periastron of ω ≈ 277°, and RV amplitudes of KA ≈ 39.56 km s-1 and KB ≈ − 42.71 km s-1 for stars A and B (respectively). This gives a mass ratio between the two stars of q ≈ 0.93. Assuming a primary mass of M1 ≈ 1.056 M⊙, (Huber et al. 2014), the secondary mass is of about M2 ≈ 0.98 M⊙. Note that the orbital ephemeris determined with the RV gives an epoch of primary and secondary eclipse of about 24 550 012.02 and 2 455 031.67, respectively. The transit epoch detected by Kepler (2 455 031.60) is compatible with the secondary eclipse of this binary system. KOI-617 is thus a case of secondary-only EB, and not a transiting planet.
Appendix A.14: KOI-620.01 and KOI-620.02
Two EGP candidates (KOI-620.01 and KOI-620.02) were detected on the target star KOI-620 by Borucki et al. (2011a) and Batalha et al. (2013) with orbital periods of ~45 and ~130 days (respectively). Note that another set of transit was detected with a period of ~85 days and a depth of 0.2% (Batalha et al. 2013), which is outside our selection criteria. Their transits exhibit transit timing variation which allowed Steffen et al. (2013) to confirm their planetary nature. The same authors constrained the mass of the inner planet to be less than 3.23 M♃. More recently, Masuda (2014) constrained the mass of the three planets in this system using their transit timing and found masses of a few Earth masses, leading to unexpected low density for these giant objects, with ρp ≤ 0.05 g cm-3.
We obtained seven different epochs with SOPHIE HE of KOI-620. We detect no significant RV variation (rms = 14 m s-1). The line bisector does not show variations above the noise level (rms = 24 m s-1). The FWHM shows some variation at the level of rms = 157 m s-1, which is likely instrumental.
We fitted three circular orbits to these data fixing the ephemeris to the ones derived thanks to Kepler. We find that K620.01< 45 m s-1, K620.02< 91 m s-1, and K620.03< 43 m s-1 at the 99% level. Assuming a stellar mass of 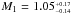 M⊙ (Huber et al. 2014), those limits correspond to upper limit on the planetary masses to M620.01< 0.85M♃, M620.02< 2.43M♃, and M620.03< 1.01M♃ with a 99% confidence interval. Given the large uncertainties of our photon-noise limited spectroscopic observations, the derived upper limit in mass are fully compatible with the mass constraints from Steffen et al. (2013) and Masuda (2014).
M⊙ (Huber et al. 2014), those limits correspond to upper limit on the planetary masses to M620.01< 0.85M♃, M620.02< 2.43M♃, and M620.03< 1.01M♃ with a 99% confidence interval. Given the large uncertainties of our photon-noise limited spectroscopic observations, the derived upper limit in mass are fully compatible with the mass constraints from Steffen et al. (2013) and Masuda (2014).
Appendix A.15: KOI-969.01
A giant-planet candidate with a period of 18 days was revealed in Burke et al. (2014) with a depth of 0.36%. This candidate was not known at the time of the observation of Santerne et al. (2012b). Its transit depth was then revised to be of 0.45% (Rowe et al. 2015), which includes it in our sample. We observed it twice with SOPHIE HE that revealed a clear SB2 of two stars of similar flux. We fitted the cross-correlation function with a two-Gaussian profile to derive the RV of both stars. We call star A the one with the smallest RV variation and star B the one with the largest variation. The RV variation of both stars is anti-correlated, which gives a mass ratio of 99.6%. The RV of the star A are in phase with the Kepler ephemeris, indicating that the primary eclipse was detected in the light-curve. This candidate is not a transiting planet but an equal-mass EB.
Appendix A.16: KOI-976.01
A transiting candidate has been reported on KOI-976 by Borucki et al. (2011b) with an orbital period of ~52 days. We observed this star twice with SOPHIE HE. The cross-correlation function displayed in Fig. A.2 revealed a multiple stellar system, with at least three components. Given the large dilution produced by those stars, the true depth of this transiting candidate should be much larger than the observed one (2.67%). Therefore, we conclude that this candidate is most likely a triple system or a background EB, and not a transiting planet. The derived RV of the three stellar components, by fitting three Gaussian profiles.
 |
Fig. A.2 Cross-correlated a function of the target star KOI-976 revealing at least three stellar components: a wide and shallow component and two narrower and deeper components. The legend indicates the orbital phase of the transiting candidate. An arbitrary offset in flux has been set between the two observations. The red lines are the three-Gaussian fits to the CCFs. |
Appendix A.17: KOI-1020.01
The candidate KOI-1020.01 was revealed by Borucki et al. (2011b). It has an orbital period of about 37 days. We observed this candidate six times with SOPHIE HE which revealed a clear SB2 with two lines of similar contrast and FWHM. We fitted the cross-correlation function with a two-Gaussian function and derived the RV of both stars. Since is it not possible to distinguish from the spectra which component is the brightest one, we arbitrarily called star A the most blue-shifted star, and star B the most red-shifted component at the first observation. We fitted the derived RV of both stars with a combined Keplerian orbit, fixing the period to the transit one. We find that the data are best fitted with an epoch of periastron of Tp = 2 456 136.35, an eccentricity of e = 0.43, an argument of periastron of ω = 51.2°, and amplitudes of KA = 45.9 km s-1 and KB = − 46.1 km s-1. Star A is therefore slightly more massive than star B, with a mass ratio of q ≈ 99.5%. Those derived orbital parameters predict an epoch of primary eclipse of 2 454 996.9, which corresponds to the event detected by Kepler, with an epoch of 2 454 997.1. The candidate KOI-1020 is thus a nearly equal-mass binary, and not a transiting planet. Given the large eccentricity of this system and its inclination, the secondary eclipse is not observable from the Earth.
Appendix A.18: KOI-1089.01
The EGP candidate KOI-1089.01 has an orbital period of ~87 days. It was revealed by Borucki et al. (2011b) together with a smaller planet candidate at 12.2 days. Using multi-color GTC observations, Tingley et al. (2014) found that KOI-1089.01 is an EGP blended with another, unseen star. We secured eight epochs on this star with SOPHIE HE. We detect any significant RV variation in these data (rms = 21 m s-1). We find no significant variation in the bisector (rms = 53 m s-1) nor FWHM (rms = 137 m s-1). We analysed the SOPHIE RV together with the FIES data reported by Tingley et al. (2014). We modelled two Keplerian orbits fixing the ephemeris to the ones found by Kepler. We find that, at the 99% confidence interval, the amplitude of both transiting planet candidates is K1089.01< 67 m s-1 and K1089.02< 37 m s-1.
We derived the stellar atmospheric parameter that are reported in Table B.2.Those parameters give a stellar mass of 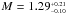 M⊙, a radius of
M⊙, a radius of 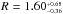 R⊙, and an age of 3.1 ± 1.3 Gyr. Combining both results, the candidates have upper-mass limits of M1089.01< 1.12M♃ and M1089.02< 0.46M♃, at the 99% level. We can therefore exclude any massive object transiting KOI-1089 at ~12 days, but we can not firmly rule out a background source of transit based on these data. We also improved the upper limit on the mass of KOI-1089.01 reported by Tingley et al. (2014).
R⊙, and an age of 3.1 ± 1.3 Gyr. Combining both results, the candidates have upper-mass limits of M1089.01< 1.12M♃ and M1089.02< 0.46M♃, at the 99% level. We can therefore exclude any massive object transiting KOI-1089 at ~12 days, but we can not firmly rule out a background source of transit based on these data. We also improved the upper limit on the mass of KOI-1089.01 reported by Tingley et al. (2014).
Appendix A.19: KOI-1137.01
The candidate KOI-1137.01 was listed among the potential transiting planet in Burke et al. (2014), with a transit depth of 1.5%. In the latest candidate release (Mullally et al. 2015), its transit depth has been revised to 4.2%. Since this is outside our selection criteria, we did not include it in the analysis. However, we observed it after the Burke et al. (2014) candidate release, and we report here its nature. We secured four observations of this candidates with SOPHIE HE. They exhibit a clear RV variation in phase with the Kepler ephemeris (rms = 270 m s-1). They also show a clear variation of the line-profile bisector (rms = 2.7 km s-1) as well as in the FWHM (rms = 640 m s-1). Moreover, we clearly detect a second set of stellar lines in the cross-correlation function of two spectra. We conclude that this candidate is a triple system or a background EB, but not a transiting planet.
Appendix A.20: KOI-1227.01
The candidate KOI-1227.01 was released by Borucki et al. (2011b). It has an orbital period of 2.1 days, but was not included in the candidate sample from Santerne et al. (2012b) due to its poor vetting statuts in Borucki et al. (2011b). We observed it twice with SOPHIE HE which revealed a clear SB2 with both component of similar flux. We fitted the cross-correlation function with a two-Gaussian function. We call the star A (B) the one which show RV variation in phase (anti-phase, respectively) with the Kepler ephemeris. Then, we fitted the RV of both stars with a combined circular orbit fixing the ephemeris to the transit ones. We find that the RV amplitude is KA ≈ 72.67 km s-1 and KB ≈ − 71.99 km s-1.
It is quite surprising that KA> | KB | (hence MA<MB), since A varies in phase with the transit ephemeris and thus should be the most massive star in the system. The solution might be that this nearly equal-mass binary is orbiting at twice the period detected by Kepler. In such situation, the primary and secondary eclipse would have the same depth and duration. So, assuming that the true period is 4.2 days (the epoch of primary eclipse is kept to T0 ≈ 2 454 966.576), the amplitudes are KA ≈ 81.65 km s-1 and KB ≈ − 82.43 km s-1. This gives a mass ratio of q ≈ 99.0%, with MA>MB. In any case, this candidate is not a transiting planet, but a nearly equal-mass binary.
Appendix A.21: KOI-1230.01
KOI-1230.01 is a 166-day period candidate revealed in Borucki et al. (2011b). The host was found to be a giant star, with a log g of about 3 cm s-2. We collected ten SOPHIE HE RVs. They present a large variation in phase with Kepler ephemeris. Fitting these data with a Keplerian orbit with the ephemeris fixed at the transit ones, we find an amplitude K1230.01 = 17.87 ± 0.03 km s-1, an eccentricity e = 0.6944 ± 0.0009, an argument of periastron of ω = 131.37 ± 0.06°. Assuming a stellar host of M1 = 1.78 ± 0.19 M⊙ (Huber et al. 2014), the companion has a mass of M2 = 0.59 ± 0.04 M⊙ . This candidate is therefore an EB and not a transiting planet. This system will be further analysed in Bruno et al. (in prep.).
Appendix A.22: KOI-1232.01
The giant-planet candidate KOI-1232.01 was revealed in Burke et al. (2014) and flagged as a false positive. It was not flagged as a false positive in the later candidate releases. It has an orbital period of 119.4 days. We secured three different epochs with SOPHIE HE. They revealed a large RV variation. Three measurements are not enough to fully constrain the orbit of such long period candidate. By assuming a circular orbit, no significant drift, and the transit ephemeris, we find that the RV amplitude is K = 13.74 ± 0.06 km s-1. For this candidate, Huber et al. (2014) reported a host mass of 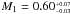 M⊙. This would give a companion mass of M2 = 0.29 ± 0.02 M⊙. This candidate is therefore an EB and not a transiting planet.
M⊙. This would give a companion mass of M2 = 0.29 ± 0.02 M⊙. This candidate is therefore an EB and not a transiting planet.
Appendix A.23: KOI-1271.01
A giant-planet candidate has been detected on the target star KOI-1271 by Batalha et al. (2013) with a period of 162 days. It was found by Ford et al. (2012) to have large transit timing variation at the level of a few hours, but no other transiting candidate was found in the Kepler light-curve. We secured 14 SOPHIE HE observations of this star. They have a RV rms of 47 m s-1, a bisector rms of 79 m s-1, and a FWHM rms of 116 m s-1. They are compatible with the typical uncertainty on this star.We analysed the RVs using one Keplerian orbit at the transit ephemeris. We find a hint of RV variation of K1271.01 = 28 ± 17 m s-1, (K1271.01< 77.5 m s-1 within the 99% confidence interval) an eccentricity of 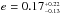 , and an argument of periastron of
, and an argument of periastron of 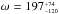 °.
°.
We derived the stellar atmospheric parameters that are reported in Table B.2. We find a host mass of 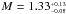 M⊙, a radius of
M⊙, a radius of 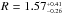 R⊙, and an age of 2.14
R⊙, and an age of 2.14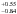 Gyr. Combining the results from the RV and stellar atmospheric results, we find that this candidate has a mass of M1271.01 = 0.84 ± 0.49M♃ (i.e. an upper limit at 99% of 2.35 M♃ ). We can therefore rule out that this candidate is an eclipsing brown dwarf or binary. Given the transit timing variation and the hint of RV signal, we conclude that this candidate is likely a planet, without a firm establishment of its nature. Note that this candidate is in the Kepler EB catalogue (Kirk et al., in prep.) but we find no reason for that (the DV summary shows no odd – even transits depth differences, nor significant centroids). Some confirmed exoplanets have already been misclassified as EB in this catalogue (Santerne et al. 2012b).
Gyr. Combining the results from the RV and stellar atmospheric results, we find that this candidate has a mass of M1271.01 = 0.84 ± 0.49M♃ (i.e. an upper limit at 99% of 2.35 M♃ ). We can therefore rule out that this candidate is an eclipsing brown dwarf or binary. Given the transit timing variation and the hint of RV signal, we conclude that this candidate is likely a planet, without a firm establishment of its nature. Note that this candidate is in the Kepler EB catalogue (Kirk et al., in prep.) but we find no reason for that (the DV summary shows no odd – even transits depth differences, nor significant centroids). Some confirmed exoplanets have already been misclassified as EB in this catalogue (Santerne et al. 2012b).
Appendix A.24: KOI-1326.01
The giant-planet candidate was announced in Burke et al. (2014) with an orbital period of ~53 days and a false positive flag. In later candidate releases, this candidate is no longer flagged as a false positive. We observed it twice with SOPHIE HE and find two line profiles in the cross-correlated function, revealing a clear SB2. We fitted a two-Gaussian function to the cross-correlation function. We call star A the one with the deepest line profile and star B, the one with the shallowest line profile. The two stars show anti-correlated RV variations with a slope of q = 85.8%, corresponding to the mass ratio between the two stars. This confirms that star A is more massive than star B. However, the variation of star A is observed in anti-phase with Kepler ephemeris, revealing that the transit epoch match with the secondary eclipse of this binary system. This candidate is clearly not a transiting planet, but a nearly equal-mass secondary-only EB.
Appendix A.25: KOI-1353.01
A giant-planet candidate has been announced by Borucki et al. (2011b) with a period of ~125 days. Another transiting candidate was found by Batalha et al. (2013) with a period of 34.5 days and a depth of about 400 ppm. Finally, a third set of transit was discovered by the planet hunters community with a period of 66 days and reported in Schmitt et al. (2014b). These authors also performed a transit timing variation analysis of the candidates and found that the mass of the EGP was of M1353.01 = 0.42 ± 0.05M♃. Their derived masses for the inner and middle planets are 7.3 ± 6.8M⊕ and 4.0 ± 0.9M⊕. They also reported that the orbits are nearly circular.
We observed this system with SOPHIE HE seven times. The RV, bisector and FWHM present rms of 45 m s-1, 42 m s-1, and 117 m s-1 (respectively). We fitted these RV with a model of three circular orbits at the ephemeris provided by Kepler (see Fig. A.3). We find upper limit at the 99% on the RV amplitudes of Kinner< 25 m s-1 and Kmiddle< 56 m s-1 for the inner (P = 34 d) and middle (P = 66 d) planets, respectively. For the outer, EGP, we detect an amplitude of Kouter = 51 ± 11 m s-1. At the 99% level, this amplitude is Kouter ∈ [23,78] m s-1.
 |
Fig. A.3 Phase-folded RV curve of KOI-1353.03 together with the best circular model found. |
We derived the stellar atmospheric parameters that are reported in Table B.2. We find a host mass of 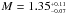 M⊙, a radius of
M⊙, a radius of 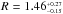 R⊙, and an age of 1.71 ± 0.95 Gyr. Combining the RV results and our spectroscopic parameters, we find an upper limit at the 99% limit on the mass of inner and middle planets to be Minner< 0.52M♃ and Mmiddle< 1.41M♃, respectively. For the outer, EGP, we have a mass constraint of Mouter = 1.55 ± 0.34M♃ (Mouter ∈ [0.68,2.43]M♃at the 99% level). Thus, the EGP is found significantly (at 3.3σ) more massive by RV than by transit timing variation, as already found by Weiss & Marcy (2014) for other planetary systems. Note that the star shows a photometric variability of more than 1.5%, which could have impacted both our RV and the transit times measurements (Oshagh et al. 2013; Barros et al. 2013). For the other planets, the masses derived by spectroscopy are fully compatible with the ones derived by Schmitt et al. (2014b).
R⊙, and an age of 1.71 ± 0.95 Gyr. Combining the RV results and our spectroscopic parameters, we find an upper limit at the 99% limit on the mass of inner and middle planets to be Minner< 0.52M♃ and Mmiddle< 1.41M♃, respectively. For the outer, EGP, we have a mass constraint of Mouter = 1.55 ± 0.34M♃ (Mouter ∈ [0.68,2.43]M♃at the 99% level). Thus, the EGP is found significantly (at 3.3σ) more massive by RV than by transit timing variation, as already found by Weiss & Marcy (2014) for other planetary systems. Note that the star shows a photometric variability of more than 1.5%, which could have impacted both our RV and the transit times measurements (Oshagh et al. 2013; Barros et al. 2013). For the other planets, the masses derived by spectroscopy are fully compatible with the ones derived by Schmitt et al. (2014b).
Appendix A.26: KOI-1391.01
A giant-planet candidate was found on the target star KOI-1391 by Borucki et al. (2011b) with an orbital period of almost 8 days. It was not observed by Santerne et al. (2012b) because of its bad vetting status. We secured two observations with SOPHIE HE and find a large RV variation. Assuming a circular orbit, no significant drift and the Kepler ephemeris, we find an amplitude of K = 32.93 ± 0.04 km s-1. Assuming a stellar host of 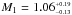 M⊙ (Huber et al. 2014), the companion has a mass of M2 = 0.39 ± 0.04 M⊙. This candidate is therefore an EB and not a transiting planet.
M⊙ (Huber et al. 2014), the companion has a mass of M2 = 0.39 ± 0.04 M⊙. This candidate is therefore an EB and not a transiting planet.
Appendix A.27: KOI-1411.01
A giant-planet candidate with a period of ~305 days was found by Burke et al. (2014) on the target star KOI-1411. We observed this star five times with SOPHIE HE. They present no significant RV variation in phase with the Kepler ephemeris. The rms are 15 m s-1, 39 m s-1, and 74 m s-1 for the RV, bisector and FWHM (respectively), which are compatible with the typical uncertainty on this star. We fitted the RV with a Keplerian orbit at the transit ephemeris. We find an upper limit at 99% on the amplitude K1411.01< 67 m s-1.
We derived the stellar atmospheric parameters that are reported in Table B.2. We find a host mass of  M⊙, a radius of
M⊙, a radius of 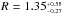 R⊙, and an age of 5.0±2.6 Gyr. Combining the RV results and the spectroscopic parameters, we have an upper limit at the 99% level on the mass of this candidate to be M1411.01< 2.13M♃. We can therefore reject that this candidate is an eclipsing brown dwarf or binary but we can not firmly conclude on its nature.
R⊙, and an age of 5.0±2.6 Gyr. Combining the RV results and the spectroscopic parameters, we have an upper limit at the 99% level on the mass of this candidate to be M1411.01< 2.13M♃. We can therefore reject that this candidate is an eclipsing brown dwarf or binary but we can not firmly conclude on its nature.
Appendix A.28: KOI-1426.02 and KOI-1426.03
Three different sets of transits were detected in the Kepler data of the target star KOI-1426 by Borucki et al. (2011b). They have orbital periods of 39d (KOI-1426.01), 75d (KOI-1426.02), and 150d (KOI-1426.03). Only the two last ones are compatible with an EGP according to our selection criteria. Based on the planet-likelihood multiplicity boost described in Lissauer et al. (2014), Rowe et al. (2014) validated the planetary nature of the two innermost planets. However, the outer planet presenting a grazing transit (impact parameter of b ≈ 1.0), they did not validated it.
We observed this system six times with SOPHIE HE and find no significant variation. The rms are 13 m s-1, 33 m s-1, and 100 m s-1 for the RV, bisector and FWHM (respectively), which is compatible with the typical photon noise for this target. We fitted the derived RV with a three-circular orbit model at the transit ephemeris. We don’t have enough data to constrain the eccentricity of all the planets. We find upper limits at the 99% level on the amplitude of all the planets to Kinner< 37 m s-1, Kmiddle< 21 m s-1, and Kouter< 39 m s-1. Assuming a host mass of 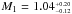 M⊙ (Huber et al. 2014), we have an upper limit on the mass of the candidates to Minner< 0.69M♃, Mmiddle< 0.45M♃, and Mouter< 1.03M♃, with a confidence interval of 99%. We can therefore rule out that any of these planet candidates is an EB nor transiting brown dwarf or even a massive EGP.
M⊙ (Huber et al. 2014), we have an upper limit on the mass of the candidates to Minner< 0.69M♃, Mmiddle< 0.45M♃, and Mouter< 1.03M♃, with a confidence interval of 99%. We can therefore rule out that any of these planet candidates is an EB nor transiting brown dwarf or even a massive EGP.
Appendix A.29: KOI-1431.01
A giant-planet candidate was detected on the target star KOI-1431 by Batalha et al. (2013). It has an orbital period of about 345 days, which locates it in the habitable zone of its host star according to Gaidos (2013). We observed it seven times with SOPHIE HE. They do not show significant variation. The rms are 13m s-1, 18 m s-1, and 74 m s-1 for the RV, bisector and FWHM (respectively), which are compatible with the uncertainties. We fitted these data using a Keplerian orbit at the transit ephemeris. We find an upper limit at the 99% limit on the amplitude of K1431.01< 24 m s-1.
We derived the stellar atmospheric parameters that are reported in Table B.2. We find a host mass of 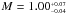 M⊙, a radius of
M⊙, a radius of 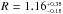 R⊙, and an age of 8.9
R⊙, and an age of 8.9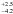 Gyr. By combining both analyses, we find an upper limit at the 99% level on the mass of KOI-1431.01 of M1431.01< 0.73M♃. We can therefore exclude scenarios of false positive invoking a brown dwarf or a star eclipsing KOI-1431. We can even rule out a massive EGP. However, we can not firmly establish its nature.
Gyr. By combining both analyses, we find an upper limit at the 99% level on the mass of KOI-1431.01 of M1431.01< 0.73M♃. We can therefore exclude scenarios of false positive invoking a brown dwarf or a star eclipsing KOI-1431. We can even rule out a massive EGP. However, we can not firmly establish its nature.
Appendix A.30: KOI-1452.01
A transiting giant-planet candidate was found on the target star KOI-1452 with an orbital period of 1.15 days by Borucki et al. (2011b). However, it was reported with a poor vetting flag and thus, not observed by Santerne et al. (2012b). We observed it twice with SOPHIE HE which revealed a SB2 with fast-rotating primary (υsini⋆ = 36.2 ± 0.2 km s-1) and a very faint secondary. We call star A the brightest component and star B the faintest one. We were able to derive the RV of both stars. We fitted the RV of both stars with circular orbits at the Kepler ephemeris. We find that KA ≈ 48.0 km s-1 and KB ≈ − 91.2 km s-1, which gives a mass ratio of q ≈ 52.6%. If the host has a mass of M1 ~ 1.46 M⊙ (Huber et al. 2014), thus the secondary has a mass of M2 ~ 0.77 M⊙. Note that we detected a secondary eclipse in the Kepler data with a depth of about 500 ppm. Therefore, this candidate is not a transiting planet but an EB.
Appendix A.31: KOI-1465.01
Borucki et al. (2011b) reported a giant-planet candidate around the star KOI-1465 with an orbital period of almost 10 days. It was not observed by Santerne et al. (2012b) because of its bad vetting status. We secured five observations with SOPHIE HE and find a large RV variation in phase with the Kepler ephemeris. Assuming a circular orbit, no significant drift and the Kepler ephemeris, we find an amplitude of K = 19.32 ± 0.03 km s-1. Assuming a stellar host of 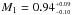 M⊙ (Huber et al. 2014), the companion has a mass of M2 = 0.22 ± 0.02 M⊙. This candidate is therefore an EB and not a transiting planet.
M⊙ (Huber et al. 2014), the companion has a mass of M2 = 0.22 ± 0.02 M⊙. This candidate is therefore an EB and not a transiting planet.
Appendix A.32: KOI-1483.01
We secured two SOPHIE HE observations on KOI-1483 which hosts a giant-planet candidate at ~186 days (Burke et al. 2014). The RV exhibit a large variation in phase with the Kepler ephemeris. Assuming a circular orbit, no significant drift and the Kepler ephemeris, we find that the amplitude is K = 4.40 ± 0.02 km s-1. Assuming a primary star mass of M1 = 0.93 ± 0.10 M⊙ (Huber et al. 2014), it gives a companion mass of M2 = 0.12 ± 0.01 M⊙. This candidate is therefore an eclipsing low-mass star and not a transiting planet.
Appendix A.33: KOI-1546.01
The target star KOI-1546 has been found to host a transiting giant-planet candidate with a period of 0.9d by Borucki et al. (2011b). It was not observed by Santerne et al. (2012b) because of its bad vetting status. We secured two observations with SOPHIE HE that revealed a hint of variation with K ≈ 77 m s-1 if the orbit is circular. However, the analysis of the line profile of the star also reveal a bisector variation (~250 m s-1), anti-correlated with the RV as well as a large FWHM variation (~900 m s-1) correlated with the RV. This is an evidence that the stellar host is blended with an unseen blended star which has a narrower line-profile width (Santerne et al. 2015). We concluded that this system is either a triple system or a background EB, but not a transiting planet. Note that a stellar companion located at 0.6′′ and about 1 mag fainter in the i-band has been detected by Lillo-Box et al. (2014) in lucky imaging. If this companion is the host of the transit event, the companion might still be compatible with an inflated hot jupiter. Further observations are needed to confirm this.
Appendix A.34: KOI-1574.01
Four different sets of transits were found in the Kepler light curve of the target star KOI-1574: one giant-planet candidate at 114 days (Borucki et al. 2011b, KOI-1574.01), one Saturn-size candidate at 574 days (Burke et al. 2014, KOI-1574.02), and two Earth-size candidates at 5.8d and 9d (KOI-1574.03 and KOI-1574.04, respectively; Rowe et al. 2015). Only the EGP at 114 days is within our selection criteria. The two large and long-orbital periods objects have already been confirmed thanks to the transiting timing variation analysis performed by Ofir et al. (2014). However, they reported a different period for the outermost planet of 192 d, i.e. one third of the period found by Burke et al. (2014). They reported planetary masses for the two giant objects of M1574.01 = 1.02 ± 0.03M♃ and M1574.02 = 6.5 ± 0.8M⊕.
We secured five observations of KOI-1574 with SOPHIE HE. The data have a rms of 12 m s-1 which is compatible with the uncertainties. The bisector and FWHM have rms of 44 m s-1 and 38 m s-1, respectively. We fitted four circular orbits to the data fixing the orbital ephemeris to the transit ones. For KOI-1574.02, we choose the period of 572 days. We detect a hint of variation for the EGP at 114 days, with an amplitude of K1574.01 = 41 ± 20 m s-1, and an upper limit of K1574.01< 90 m s-1 within the 99% confidence interval. For the other planets, we find upper limits at the 99% level on their amplitudes of K1574.02< 39 m s-1, K1574.03< 66 m s-1, and K1574.04< 67 m s-1.
Assuming a stellar host mass of M1 = 1.08 ± 0.06 M⊙ (Ofir et al. 2014), it gives a mass constraint for the EGP in our sample of M1574.01 = 1.05 ± 0.47M♃ (M1574.01< 2.25M♃ at the 99% level). This value is fully compatible with the one derived by the transit timing analysis of Ofir et al. (2014). For the other planet candidates, we find upper limits on the mass at the 99% level of M1574.02< 1.66M♃, M1574.03< 0.61M♃, and M1574.04< 0.68M♃. Assuming that KOI-1574.02 orbits with a period of 192 d, as stated by Ofir et al. (2014), does not change significantly our constraints on the mass of KOI-1574.01. For the other planets, the upper limits at 99% change to M1574.02< 1.91M♃, M1574.03< 0.58M♃, and M1574.04< 1.10M♃.
We conclude that none of these transiting candidates is an eclipsing brown dwarf or low-mass star eclipsing the target star. We confirm they have a mass within the planetary range.
Appendix A.35: KOI-1645.01
The giant-planet candidate KOI-1645.01 was found by Burke et al. (2014) with an orbital period of 41 days. We observed it twice with SOPHIE HE and find a clear SB2. We fitted the cross-correlation function with a two-Gaussian profile to derive the RV of both stars. We call star A the one with the deepest line profile and star B the one with the shallowest line profile. The variation of both stars is anti-correlated, which gives a mass ratio of 87.6%. The star A exhibits a RV variation in anti-phase with the Kepler ephemeris, revealing that the secondary eclipse was detected in the light-curve. This candidate is not a transiting planet but a secondary-only EB.
Appendix A.36: KOI-1783.01
A giant-planet candidate was found to transit the host star KOI-1783 with a period of 134d by Batalha et al. (2013). We observed it twice with SOPHIE HE and find no significant RV variation. The bisector and FWHM variation are also compatible with their photon noise. By fitting a circular orbit with no drift at the transit ephemeris, we find an upper limit at the 99% level on the RV amplitude of K< 81.3 m s-1.
We derived the stellar atmospheric parameters that are reported in Table B.2. We find a host mass of 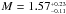 M⊙, a radius of
M⊙, a radius of 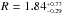 R⊙, and an age of 1.2 ± 0.5 Gyr. Combining the two analyses, we derive an upper limit on the mass of this candidate of M1783.01< 2.83M♃, within the 99% confidence interval. We can therefore exclude a star or brown dwarf eclipsing the target star, but we can not firmly establish the planetary nature of this candidate.
R⊙, and an age of 1.2 ± 0.5 Gyr. Combining the two analyses, we derive an upper limit on the mass of this candidate of M1783.01< 2.83M♃, within the 99% confidence interval. We can therefore exclude a star or brown dwarf eclipsing the target star, but we can not firmly establish the planetary nature of this candidate.
Appendix A.37: KOI-1784.01
A giant-planet candidate was revealed by Batalha et al. (2013) with a period of 5 days and a depth of less than 0.4%. It was not included in the sample of Santerne et al. (2012b). However, it was revised in Rowe et al. (2015) with a depth of more than 0.4%, which included it in our giant sample. We observed it twice with SOPHIE HE and find a clear SB2. We fitted the cross-correlation functions with a two-Gaussian function to derive the RV of both stars. We call star A the one with the deepest line profile and star B the one with the shallowest line profile. The RV of both stars are not correlated, which indicate that this system is not just an EB, but a more complex system, likely a triple. Assuming a circular orbit, the star B shows RV variation in phase with the Kepler ephemeris with an amplitude of KB = 14.13 ± 0.46 km s-1. Assuming a solar-mass for this star B, the companion would have a mass of about 0.12 M⊙. However, if the mass of star B is much lower, the companion could be in the brown dwarf regime. Therefore, this candidate is not a transiting planet but likely a triple system.
Appendix A.38: KOI-1788.01
A giant-planet candidate transiting the target star KOI-1788 every 71 days (KOI-1788.01) has been reported by Batalha et al. (2013). The planet hunters community found another planet-candidate transiting this star, with an orbital period of nearly one year (KOI-1788.02; Wang et al. 2013). We observed this target six times with SOPHIE HE. The derived RV have a rms of 13 m s-1. The bisector and FWHM present some variation, with rms of 108 m s-1 and 76 m s-1 (respectively). These line-profile variation might be caused by the large activity of the star, which also imprint a photometric variability on the Kepler light curve at the level of ~4%. We fitted these data with two circular orbits at the Kepler ephemeris. We find upper limits on the amplitude of both planet candidates, at the 99% level, of K1788.01< 22.6 m s-1 and K1788.02< 77.2 m s-1.
We derived the stellar atmospheric parameters that are reported in Table B.2. We find a host mass of 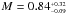 M⊙, a radius of
M⊙, a radius of 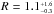 R⊙, and an age of 12.5 ± 8.4 Gyr. Combining the two analyses, we find upper limits on the mass of both candidates of M1788.01< 0.48M♃ and M1788.02< 3.0M♃, within 99% interval confidence. We can therefore exclude brown dwarfs or stars eclipsing the target star, but we can not firmly establish the nature of these candidates.
R⊙, and an age of 12.5 ± 8.4 Gyr. Combining the two analyses, we find upper limits on the mass of both candidates of M1788.01< 0.48M♃ and M1788.02< 3.0M♃, within 99% interval confidence. We can therefore exclude brown dwarfs or stars eclipsing the target star, but we can not firmly establish the nature of these candidates.
Appendix A.39: KOI-2679.01
The giant-planet candidate KOI-2679.01 was revealed in Burke et al. (2014) with an orbital period of 111 days. We secured two observations with SOPHIE HE that revealed a unique and wide line profile, with υsini⋆ = 29.8 ± 0.2 km s-1. The RV do not show significant variation, nor the bisector and FWHM. We fitted a circular orbit at the Kepler ephemeris and find that K2679.01< 1.41 km s-1, at the 99% level. Assuming a host mass of 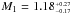 M⊙, the candidate mass has an upper limit of M2679.01< 40.3M♃, at the 99% level. We can therefore exclude that KOI-2679.01 is an EB, but we can not firmly establish its nature.
M⊙, the candidate mass has an upper limit of M2679.01< 40.3M♃, at the 99% level. We can therefore exclude that KOI-2679.01 is an EB, but we can not firmly establish its nature.
Appendix A.40: KOI-3411.01
A giant-planet candidate was found to transit the target star KOI-3411 with an orbital period of 27 days (Rowe et al. 2015). We secured two observations with SOPHIE HE which revealed a clear SB2. We fitted the cross-correlation function with a two-Gaussian function. We call star A the line with the deepest profile and star B the one with the shallowest profile. The velocities of both stars are anti-correlated with a slope of 76.8%, which corresponds to the mass ratio q = MB/MA. The variation of the star A, the most massive one in the system, is in phase with the Kepler ephemeris. This means that the transit epoch observed by Kepler corresponds to the primary eclipse of this binary. This candidate is not a transiting planet but a primary-only EB.
Appendix A.41: KOI-3663.01
A giant-planet candidate was revealed by the planet hunters community in Wang et al. (2013) with an orbital period of 283 days. This candidate is located in the habitable zone. Based on statistical considerations, the same authors validated this candidate as a planet. Using Keck RV, they also excluded a 80 M♃ companion at the 95.7% probability. We secured four spectra of this host star with SOPHIE HE. The RV, bisector and FHWM have an rms of 20 m s-1, 37 m s-1, and 141 m s-1 (respectively). We find a hint of correlation between the observed RV and the line-profile bisector. The Spearman correlation coefficient is 0.80 ± 0.28. More observations are needed to confirm this correlation and the planetary nature of this candidate.
 |
Fig. A.4 Bisector Vspan as a function of the RV for the target star KOI-3663. |
In their blend exclusion, Wang et al. (2013) ruled out the possibility that this candidate is a triple system based on the fact that a deep secondary eclipse would have been detected in the Kepler light-curve. However, with an orbital period of 283 days, even a small eccentricity and a non-perfect orbital alignment with the line-of-sight might show either the primary or secondary eclipse of a binary. So, the absence of secondary eclipse does not firmly ruled out the scenario of a triple system. Our observed bisector correlation would indicate, if confirmed, that this candidate is blended with a binary star, thus likely in a triple system. Without the confirmation it is a triple system, we consider this candidate as a planet, as reported in Wang et al. (2013).
We derived the stellar atmospheric parameters that are reported in Table B.2. We find a host mass of 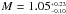 M⊙, a radius of
M⊙, a radius of 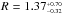 R⊙, and an age of 6.8 ± 4.5 Gyr.
R⊙, and an age of 6.8 ± 4.5 Gyr.
Appendix A.42: KOI-3678.01
The giant-planet candidate transiting the target star KOI-3678 with a period of 161 days was announced by Rowe et al. (2015). We observed it four times with SOPHIE HE. The observed rms of the RV, bisector and FWHM are 23 m s-1, 16 m s-1, and 36 m s-1, respectively. There is a hint of RV variation. Assuming a circular orbit, we find K = − 31 ± 11 m s-1, hence the RV are in anti-phase with the Kepler ephemeris. The target star exhibits a photometric variability at the level of about 1% peak-to-valley. Considering a υsini⋆ of 4.5 ± 1.2 km s-1, we expect an activity-induced RV signal at the level of 45 m s-1, which is compatible with our observed variation. No clear bisector nor FWHM correlation is found with the RV. For this reason, we did not attempt to model the RV. Assuming that any circular orbit with an amplitude of three times the rms would have been clearly significantly detected, we can put some constraints to K3678.01< 70 m s-1. Assuming a host mass of 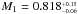 M⊙, we can constrain the mass of the transiting candidates to M3678.01< 1.43M♃, within 99% of probability. We can therefore exclude that a massive planet, brown dwarf or star is transiting/eclipsing the target star, but we can not firmly conclude on the nature of this candidate.
M⊙, we can constrain the mass of the transiting candidates to M3678.01< 1.43M♃, within 99% of probability. We can therefore exclude that a massive planet, brown dwarf or star is transiting/eclipsing the target star, but we can not firmly conclude on the nature of this candidate.
Appendix A.43: KOI-3680.01
The giant-planet candidate KOI-3680.01 was revealed in Rowe et al. (2015) with an orbital period of 141 days. We observed it with SOPHIE HE. The RV show a significant variation that correspond to a M ~ 2.2M♃ planetary companion in an eccentric orbit. This planet will be further characterised in a forthcoming paper (Hébrard et al., in prep.).
Appendix A.44: KOI-3681.01
The giant-planet candidate KOI-3681.01 was revealed in Rowe et al. (2015) with an orbital period of 2018 days. We observed it with both SOPHIE HE and HR. The RV in both instrumental configuration show a significant variation that correspond to a M ~ 4.4M♃ planetary companion in an eccentric orbit. This planet will be further characterised in a forthcoming paper.
Appendix A.45: KOI-3683.01
A giant-planet candidate was found to transit the target star KOI-3683 with an orbital period of 214 days (Rowe et al. 2015). We observed it twice with SOPHIE HE and find no significant variation at the level of the photon noise for the RV, bisector and FWHM. Assuming a circular orbit at the Kepler ephemeris, we fitted these two RV and find that K3683.01< 53 m s-1 at the 99% level.
We derived the stellar atmospheric parameters that are reported in Table B.2. We derived a host mass of 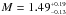 M⊙, a radius of
M⊙, a radius of 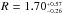 R⊙, and an age of 1.4 ± 0.7 Gyr. Combining the two analyses, we find that the candidate has a mass of M3683.01< 2.08M♃, at the 99% level. We can therefore exclude a star or brown dwarf eclipsing the target star, but we can not firmly establish its planetary nature based on these data.
R⊙, and an age of 1.4 ± 0.7 Gyr. Combining the two analyses, we find that the candidate has a mass of M3683.01< 2.08M♃, at the 99% level. We can therefore exclude a star or brown dwarf eclipsing the target star, but we can not firmly establish its planetary nature based on these data.
Appendix A.46: KOI-3685.01
Rowe et al. (2015) reported two transiting candidates around the target star KOI-3685: one giant-planet candidate with an orbital period of 209 days (KOI-3685.01) and a 1.6-R⊕ super-Earth at 7 days (KOI-3685.02). This system was not validated by Rowe et al. (2014) because the giant-planet candidate has an impact parameter compatible with 1.0 with 1σ (i.e. a grazing transit). We secured two observations of this target star with SOPHIE HE. The cross-correlation functions reveal a clear SB2 that we fitted with a two-Gaussian function (see Fig. A.5). We call star A the star with the deepest line profile and star B the one with the shallowest line profile. Thus, star A is supposed to be the brightest component of the system. Note that for the first observation the two stars are blended. The RV uncertainties we estimated are probably under-estimated.
 |
Fig. A.5 Cross-correlated function of the target star KOI-3685 revealing two stellar components. The legend indicates the orbital phase of the transiting candidate. An arbitrary offset in flux has been set between the two observations. The red lines are the two-Gaussian fits to the CCFs. |
If the RV variation of star B is real, both stars shows RV variation in anti-phase. From the slope of the RV correlation between the two stars, it is possible to determine their mass ratio. So, if the observed variation are caused by the orbit of star B around star A, we find a mass ratio of q ≈ 13.7. This means that star B would be about 14 times more massive than star A. Assuming a mass – luminosity relation such as ΔL = q3.5, star B should be about 104 times more luminous than star A. This is hardly compatible with the fact that star A has a deeper line profile than star B. In such case, we would not be able to detect the spectral lines from star A. Thus, the RV variation of star A should be explained by another object in the system. Given their relatively close RV, it is likely that star A and B are bound, but are orbiting in a long period.
We fitted a circular orbit to the RV of star A at the ephemeris of KOI-3685.01 and KOI-3685.02. In both cases, the variation is seen in phase with the ephemeris, but the derived amplitudes are K3685.01 ~ 7.7 km s-1 and K3685.02 ~ 152 km s-1 for KOI-3685.01 and KOI-3685.02 (respectively). A RV of 152 km s-1 at 7 days would required a stellar host of more than 10 M⊙ in order to keep the mass ratio q ≤ 1. Thus, we concluded that the variation seen on star A is caused by the orbit of KOI-3685.01. Since the stars are blended, it is difficult to determine the mass of the host, KOI-3685 A. Assuming this star is a solar-like star, KOI-3685.01 would have a mass of about M3685.01 = 0.25 M⊙ and is clearly in the stellar domain. Therefore, the system KOI-3685 is composed by at least three stars: A, B and .01 that we call now star C. In this system, it is likely that the star B orbits the binary AC. This system is already listed in the Kepler EB catalogue.
In this complex system, the super-Earth candidate KOI-3685.02 could either transit the star A, B, or even C. In any case, its transit depth is severely diluted. The dilution is much greater if it transits star C. Using the asterodensity profiling (Kipping 2014) and assuming that this candidate has a circular orbit, we find that the density of the transit host is ρ = 0.18 ± 0.05 ρ⊙. However, according to Kipping (2014), the blend-effect which is expected to be strong in this case, makes that this value of ρ is under-estimated. Therefore, using the asterodensity profiling of this candidate, we can only poorly constrain the density of the host to be ρ> 0.18 ρ⊙. This does not allow us to determine on which star this candidate transits. However, given the large dilution, this candidate is expected to be substantially larger than 1.6 R⊕.
Appendix A.47: KOI-3689.01
A giant-planet candidate was announced by Rowe et al. (2015) to transit the target star KOI-3689 every 5.24 days. This candidate was not included in the sample of Santerne et al. (2012b) because this target was not observed at that time. KOI-3689 was only observed by Kepler during the quarter 1028. We observed it twice with SOPHIE HE and find no variation in the RV, bisector and FWHM above the photon-noise floor. We fitted the RV with a circular orbit and find that K3689.01< 56 m s-1 within a probability of 99%.
We derived the stellar atmospheric parameters that are reported in Table B.2. We derived a host mass of M = 1.27 ± 0.20 M⊙, a radius of 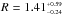 R⊙, and an age of 2.5
R⊙, and an age of 2.5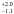 Gyr. Combining the two results, we find that the candidate has an upper limit on its mass of M3689.01< 0.61M♃, at the 99% level. We can therefore exclude a massive planet, brown dwarf or a star transiting/eclipsing the target star. However, we can not rule a diluted transit on a background or companion star.
Gyr. Combining the two results, we find that the candidate has an upper limit on its mass of M3689.01< 0.61M♃, at the 99% level. We can therefore exclude a massive planet, brown dwarf or a star transiting/eclipsing the target star. However, we can not rule a diluted transit on a background or companion star.
Appendix A.48: KOI-3720.01
We observed twice with SOPHIE HE the target star KOI-3720. This star host a giant-planet candidate with an orbital period of 213 days (Rowe et al. 2015). The cross-correlation function revealed a wide line profile with υsini⋆ = 24.7 ± 0.1 km s-1. The derived RV show a large variation that we fitted with a circular orbit. We find K3720.01 = 4.80 ± 0.06 km s-1. Assuming a host mass of 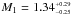 M⊙ (Huber et al. 2014), we find that the companion has a mass of M2 = 0.18 ± 0.02 M⊙. This candidate is therefore not a transiting planet but clearly an EB.
M⊙ (Huber et al. 2014), we find that the companion has a mass of M2 = 0.18 ± 0.02 M⊙. This candidate is therefore not a transiting planet but clearly an EB.
Appendix A.49: KOI-3721.01
A giant-planet candidate was found to transit the target star KOI-3721 with an orbital period of 6.41 days (Rowe et al. 2014). This candidate was not observed in the sample of Santerne et al. (2012b) because it was only observed by Kepler during the quarter 10, which was not available at that time. We observed it twice with SOPHIE HE. The observed cross-correlated functions revealed a clear SB2. We derived the RV of both stars by fitting a two-Gaussian function. We call star A the one with the deepest line profile and star B the one with the shallowest line profile. The star A do not show RV variation at the level of the photon noise. However, the star B shows a large RV variation. Fitting this variation with a circular orbit at the Kepler ephemeris, we find that K3721B = − 44.99 ± 0.87 km s-1 and a systemic RV of γ3721B = − 0.22 ± 0.82 km s-1. The RV amplitude being negative, the variation of the star B is in anti-phase with the Kepler ephemeris. Then, the RV of both stars are not correlated. So, if both the star A and B are bound, they are probably orbiting with a long orbital period and not at 6.41 days.
Another object should thus be invoked to explained the observed transit and the RV of the star B. Two reasons might explain the variations in anti-phase of the star B: (1) the ephemeris are wrong and the true period is twice the observed one; (2) this system is a secondary-only EB. We tried fixing the orbital period at two times 6.41 days keeping the epoch of primary transit to the one reported in (Rowe et al. 2014) or shifted by half a double-period (hence, shifted by 6.41 days). In both cases, the RV observations are covering a very small fraction of the expected circular-orbit variation (orbital phases of 0.13 and 0.37 or phases of 0.63 and 0.87). So, fitting the RV of the star B at these new ephemeris gives huge values of K3721B to about ±18 000 km s-1, which is unphysical for stars. We assumed that this scenario of a binary with twice the observed period is not reasonable.
The only other scenario to explain the anti-correlated variation of the star B is to have a secondary-only EB, likely bound with another, brighter star. Even if having a secondary-only EB in a triple system is quite unlikely to occur, Santerne et al. (2013a) predicted that about ten Kepler candidates could be of that type. It would required the binary KOI-3721 B to be eccentric with a period of 6.4 days, which is quite surprising with such orbital period. This is not impossible if the system is under a Lidov–Kozai resonance (Lidov 1962; Kozai 1962). Note that Devor et al. (2008) already reported eccentric EBs among the transatlantic exoplanet survey data with orbital period as small as 2 days.
It is clear that this candidate is not a transiting planet, but it is most likely a triple system. In this system, Kolbl et al. (2015) detected three stellar components which confirm the triple system scenario.
Appendix A.50: KOI-3780.01
The target star KOI-3780 was found to host a giant-planet candidate with a period of 28 days (Rowe et al. 2015). We observed this target twice with SOPHIE HE and find a large RV variation, in phase with the Kepler ephemeris. We fitted this variation with a circular orbit at the transit ephemeris and find an amplitude of K = 33.29 ± 0.23 km s-1. Assuming a host mass of 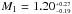 M⊙, we find that the companion has a mass of M2 = 0.75 ± 0.08 M⊙. Therefore, this candidate is not a transiting planet but clearly an EB.
M⊙, we find that the companion has a mass of M2 = 0.75 ± 0.08 M⊙. Therefore, this candidate is not a transiting planet but clearly an EB.
Appendix A.51: KOI-3782.01
A giant-planet candidate with a period of 187 days was reported by Rowe et al. (2015). We observed it three times with SOPHIE HE which reveal a clear SB2. We fitted the cross-correlation functions with a two-Gaussian profile to derive the RV of both stars. We call star A the one with the deepest line profile and star B the one with the shallowest line profile. The RV of both stars are anti-correlated which gives a mass ratio of 81.4%. The variation of star A is anti-correlated with the transit ephemeris, indicating that Kepler detected the secondary eclipse of this binary system. This candidate is not a transiting planet but a secondary-only EB.
Appendix A.52: KOI-3783.01
A giant-planet candidate was found to transit the target star KOI-3782 with an orbital period of 197 days (Rowe et al. 2015). We observed it four times with SOPHIE HE. The cross-correlation functions revealed a wide line profile with a υsini⋆ = 71.7 ± 0.1 km s-1. We fitted them with a rotation profile as described in Santerne et al. (2012a). For that fast-rotating star, we failed in fitting the Vspan asymmetry diagnosis, because the profile of the star is clearly not Gaussian. We report instead the BIS diagnosis (see Santerne et al. 2015, for a review on line-profile asymmetry diagnoses). Our RV have a rms of 115 m s-1 with a typical photon noise of about 600 m s-1. We fitted these RV with a Keplerian orbit at the transit ephemeris. We find that the RV amplitude is K3783.01< 4.49 km s-1 with a probability of 99%. Assuming a host mass of 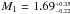 M⊙ (Huber et al. 2014), we find a companion mass upper limit of M3783.01< 0.13 M⊙ at the 99% level. The bisector does not show variation above the photon noise floor, relatively high for this target. Because of the fast rotation of the host star, our spectroscopic measurements are not able to rule out a low-mass star eclipsing the target star. We can not resolved the nature of this giant-transiting candidate.
M⊙ (Huber et al. 2014), we find a companion mass upper limit of M3783.01< 0.13 M⊙ at the 99% level. The bisector does not show variation above the photon noise floor, relatively high for this target. Because of the fast rotation of the host star, our spectroscopic measurements are not able to rule out a low-mass star eclipsing the target star. We can not resolved the nature of this giant-transiting candidate.
Recently, Bognár et al. (2015) characterised the host star KOI-3787 as a γ-Doradus or δ-Scuti star. They also found that the transit event duration was too short for being host by this hot star and concluded it could be a false positive. According to their results, the host of the transit event is a star about eight times fainter than the target star. We don’t have a S/N high enough to detect this contaminating star, which is most likely blended within the broad line profile of the target star. For these reasons, we consider this candidate as a chance-aligned EB and not as a transiting planet.
Appendix A.53: KOI-3784.01
A giant-planet candidate was found to transit the target star KOI-3784 every 23.87 days (Rowe et al. 2015). This candidate was not included in the sample of Santerne et al. (2012b) because it was observed by Kepler only during the quarter 10, which was not available at that time. We observed it twice with SOPHIE HE which revealed a clear SB2. We fitted the cross-correlated function with a two-Gaussian function and derived the RV of both stars. We call star A the one with the deepest line profile and star B the one with the shallowest line profile. The RV of both stars are anti-correlated. Using the slope of this anti-correlation, we measured a mass ratio of q = MB/MA ≈ 94.4%. This confirms that the star A is the most massive component of this binary system. The RV variation of star A is in anti-phase with the Kepler ephemeris, indicating that the transit epoch corresponds to the secondary eclipse of this binary. This candidate is clearly not a transiting planet but a nearly equal-mass secondary-only EB.
Appendix A.54: KOI-3787.01
We observed twice with SOPHIE HE the giant-planet candidate host KOI-3787, revealed by Rowe et al. (2015) with an orbital period of 142 days. The derived RV show a large variation in phase with the Kepler ephemeris. We fitted these data with a circular orbit at the transit period and epoch and find an amplitude of K = 5.00 ± 0.01 km s-1. Assuming a host mass of 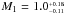 M⊙, we find that the companion has a mass of M2 = 0.14 ± 0.01 M⊙. Therefore, this candidate is not a transiting planet but a low-mass EB.
M⊙, we find that the companion has a mass of M2 = 0.14 ± 0.01 M⊙. Therefore, this candidate is not a transiting planet but a low-mass EB.
Appendix A.55: KOI-3811.01
The target star KOI-3811 was found to host a giant-planet candidate that transits every 290 days (Rowe et al. 2015). We observed it twice with SOPHIE HE. The cross-correlation function revealed a clear SB2 that we fitted with a two-Gaussian function. The star A (B) is the one with the deepest (shallowest) line profile. The two stars show anti-correlated RV variations, with a slope of q = 77.0%. This corresponds to their mass ratio. The variation of the star A is in anti-phase with Kepler ephemeris, which means that the transit detected by Kepler is the secondary eclipse of this eccentric system. We conclude that this candidate is not a transiting planet but a secondary-only EB.
Appendix A.56: KOI-5034.01
A giant-planet candidate was found on the target star KOI-5034 with an orbital period of 283 days (Mullally et al. 2015). We observed it twice with SOPHIE HE. The cross-correlation function revealed a clear SB2 that we fitted with a two-Gaussian function. The RV of both stars are clearly anti-correlated with a slope close to 1.0, revealing a nearly-equal mass binary. However, given the different orbital phase observations (0.34 and 0.26), the two velocities show a relatively small variation for an equal-mass binary. This requires that the system is eccentric. Without more spectroscopic observations, we can not constrain the stellar masses and eccentricity of this system. This candidate is clearly not a transiting planet but an EB.
Appendix A.57: KOI-5086.01
The candidate KOI-5086.01 was announced by Mullally et al. (2015) with an orbital period of 22 days. We secured three observations with SOPHIE HE that revealed a clear RV variation in anti-phase with the Kepler ephemeris. We concluded this system is a secondary-only EB. The light curve exhibits clear eclipse depth variation revealing that this EB is likely in a higher-order multiple stellar system. Since the RV variation is observed on the brightest star, we consider it as an EB.
Appendix A.58: KOI-5132.01
A giant-planet candidate was announced by Mullally et al. (2015) on the target star KOI-5132 with an orbital period of 44 days. We observed it four times with SOPHIE HE. The RV clearly show a large variation in anti-phase with the Kepler ephemeris indicating a secondary-only EB. We fitted these data with a Keplerian orbit fixing the epoch of the secondary eclipse as the epoch of transit detected by Kepler and fixing the orbital period to the transit one. We find a best-fit model with an eccentricity of e = 0.18 and an amplitude of K = 25.12 km s-1. Assuming a host mass of M1 = 1.98 M⊙ (Huber et al. 2014), the companion has a mass of M2 = 0.81 M⊙, clearly in the stellar domain. Therefore, this candidate is not a transiting planet but a secondary-only EB.
Appendix A.59: KOI-5384.01
The giant-planet candidate KOI-5384.01 was announced with an orbital period of almost 8 days (Mullally et al. 2015). We observed it twice with SOPHIE HE and find a wide line profile in the cross-correlation function. We fitted it with a rotation profile as described in Santerne et al. (2012a). We found that υsini⋆ = 43.6 ± 0.3 km s-1. The BIS shows a significant variation of about 9 km s-1. This is a hint for a blended stellar component, but we don’t have enough data to confirm this. We fitted the derived RV with a circular orbit at the Kepler ephemeris. We find an amplitude of K5384.01< 2.43 km s-1 within a probability of 99%. Assuming a host mass of 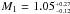 M⊙ (Huber et al. 2014), the candidate has a mass constraint of M5384.01< 27.0M♃, at the 99% level. We can therefore exclude a massive brown dwarf or a star eclipsing the target star, but we can not firmly establish the planetary nature of this candidate. Note that this candidate is listed in the Kepler EB catalogue (Kirk et al, in prep.) with a double period. It is also listed as a detached EB in Bradley et al. (2015), but with the nominal period found by (Mullally et al. 2015). We conclude that this system is likely a CEB.
M⊙ (Huber et al. 2014), the candidate has a mass constraint of M5384.01< 27.0M♃, at the 99% level. We can therefore exclude a massive brown dwarf or a star eclipsing the target star, but we can not firmly establish the planetary nature of this candidate. Note that this candidate is listed in the Kepler EB catalogue (Kirk et al, in prep.) with a double period. It is also listed as a detached EB in Bradley et al. (2015), but with the nominal period found by (Mullally et al. 2015). We conclude that this system is likely a CEB.
Appendix A.60: KOI-5436.01
A giant-planet candidate with a period of 28 days was reported in Mullally et al. (2015). We observed it twice with SOPHIE HE which reveal a clear SB2. We fitted the cross-correlation functions with a two-Gaussian profile to derive the RV of both stars. We call star A the one with the deepest line profile and star B the one with the shallowest line profile. The RV of both stars are anti-correlated, which indicates a mass ratio of 67.5%. The variation of star A is in anti-phase with the transit ephemeris, revealing that Kepler observed the secondary eclipse of this binary system. This candidate is not a transiting planet but a secondary-only EB.
Appendix A.61: KOI-5529.01
The Kepler space telescope detected a giant-planet candidate transiting the star KOI-5529 every 70 days (Mullally et al. 2015). We observed it twice with SOPHIE HE. The cross-correlation function revealed three different sets of stellar lines that we fitted with a three-Gaussian profile (see Fig. A.6). We identify the stars A, B, and C as the deepest to the shallowest line profile. The stars A and B show large and anti-correlated RV variation, while star C shows a small and marginally significant variation. We interpreted these data as the signature of a triple system, with A and B orbiting with a period of 70 days, and C orbiting with a much longer orbital period.
 |
Fig. A.6 Cross-correlated function of the target star KOI-5529 revealing three stellar components. The legend indicates the orbital phase of the transiting candidate. An arbitrary offset in flux has been set between the two observations. The red lines are the three-Gaussian fits to the CCFs. |
The slope of the correlation between the variations of A and B is of 96.9%, with A the most massive star among the two. The variation of the star A is in anti-phase with the Kepler ephemeris, which reveals that Kepler observed the secondary eclipse of this system. It is clear that this candidate is not a transiting planet but likely a triple system with a secondary-only EB.
Appendix A.62: KOI-5708.01
A giant-planet candidate was found on the target star KOI-5708 by Mullally et al. (2015) with an orbital period of almost 8 days. This candidate was not known at the time of the observations of Santerne et al. (2012b), and thus, was not included in their sample. We observed it twice with SOPHIE HE. We find a large RV variation in phase with the Kepler ephemeris. Assuming this variation is caused by the transiting object, we fitted a circular orbit and find an amplitude of K = 17.58 ± 0.02 km s-1. Assuming a host mass of 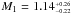 M⊙ (Huber et al. 2014), it gives a companion mass of M2 = 0.20 ± 0.03 M⊙. This candidate is clearly not a transiting planet but a EB.
M⊙ (Huber et al. 2014), it gives a companion mass of M2 = 0.20 ± 0.03 M⊙. This candidate is clearly not a transiting planet but a EB.
Appendix A.63: KOI-5745.01
The target star KOI-5745 hosts a giant-planet candidate with an orbital period of 11 days (Mullally et al. 2015). It was not included in the giant-candidate sample from Santerne et al. (2012b) because it was discovered after their observations. We observed it twice with SOPHIE HE which revealed a clear SB2. We fitted the cross-correlation functions with a two-Gaussian profile. Note that the two line profiles are blended at the second epoch, so our photon noise uncertainties are likely underestimated. We call star A and B the brightest and faintest components of the system, identified based on their line-profile depth (the deepest is the brightest). The RV variations of both stars are anti-correlated, which allow us to measure their mass ratio q = MB/MA = 91.1%. The RV of the star A are in anti-phase with the transit ephemeris which means that Kepler detected the secondary eclipse of this system. It is not possible to fit this system using circular orbits, but we don’t have enough point to measure the eccentricity and masses of the stars in this system. Therefore, this system is not a transiting planet but a secondary-only EB.
Appendix A.64: KOI-5976.01
A giant-planet candidate was detected on the target star KOI-5976 with an orbital period of 2.7 days (Mullally et al. 2015). It was not included in the sample from Santerne et al. (2012b) because it was not reported as a candidate in Batalha et al. (2013). We observed it eight times with SOPHIE HE. The RV, bisector and FHWM present rms of 40 m s-1, 48 m s-1, and 99 m s-1 (respectively). We detected a hint of RV variation with 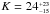 m s-1 assuming a circular orbit, with a large jitter of
m s-1 assuming a circular orbit, with a large jitter of 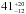 m s-1. We did not detect significant correlation between the RV and the bisector nor FWHM.
m s-1. We did not detect significant correlation between the RV and the bisector nor FWHM.
We derived the stellar atmospheric parameters that are reported in Table B.2. We find that these parameters correspond to a mass of 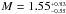 M⊙, a radius of
M⊙, a radius of 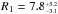 R⊙, and an age of 2.7
R⊙, and an age of 2.7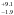 Gyr. The host is therefore clearly a giant star. Assuming that the transit occurs on the target star, with a depth of 1.3%, the companion would have a radius of
Gyr. The host is therefore clearly a giant star. Assuming that the transit occurs on the target star, with a depth of 1.3%, the companion would have a radius of 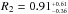 R⊙. This is clearly not compatible with the expected radius of an EGP. Moreover, this large stellar radius corresponds to a circular orbit at
R⊙. This is clearly not compatible with the expected radius of an EGP. Moreover, this large stellar radius corresponds to a circular orbit at 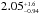 days. If the a companion is transiting this host star every 2.7 days, it is likely orbiting very close to the stellar surface, or even inside the star.
days. If the a companion is transiting this host star every 2.7 days, it is likely orbiting very close to the stellar surface, or even inside the star.
Since we did not detect a large RV variation on the target star, we conclude that this candidate is most likely a triple system with a giant primary star and not a transiting planet.
Appendix A.65: KOI-6066.01
A giant-planet candidate was announced by Mullally et al. (2015) to transit the target star KOI-6066 every 14 days. It was not reported by Batalha et al. (2013) and thus not included in the sample of Santerne et al. (2012b). We observed it twice with SOPHIE HE and find a large RV variation in phase with the Kepler ephemeris. We fitted them with a circular orbit at the transit ephemeris and find an amplitude of K = 23.00 ± 0.03 km s-1. Assuming a host mass of 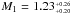 M⊙ (Huber et al. 2014), we find that the companion has a mass of M2 = 0.56 ± 0.04 M⊙. Therefore, this candidate is not a transiting planet but an EB.
M⊙ (Huber et al. 2014), we find that the companion has a mass of M2 = 0.56 ± 0.04 M⊙. Therefore, this candidate is not a transiting planet but an EB.
Appendix A.66: KOI-6114.01
A giant-planet candidate transiting the target star KOI-6114 was first announced by Mullally et al. (2015) with an orbital period of 25 days. It was then flagged as a false-positive. Before this change of disposition in the archive, we secured two spectra with SOPHIE HE. The cross-correlation function revealed a shallow and narrow line with a large variation in phase with the Kepler ephemeris and with K = 6.66 ± 0.14 km s-1, assuming a circular orbit. We interpreted these data as a triple system with a very hot or fast rotating star which does not contribute to the cross-correlation function besides its continuum flux. This scenario is compatible with the effective temperature of the host found by Huber et al. (2014) of Teff = 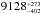 K. Therefore, we confirm this candidate is not a transiting planet but a triple system. Since it is now considered as a false-positive in the latest candidate release, we did not include it in our sample.
K. Therefore, we confirm this candidate is not a transiting planet but a triple system. Since it is now considered as a false-positive in the latest candidate release, we did not include it in our sample.
Appendix A.67: KOI-6124.01
A giant-planet candidate was found on the target star KOI-6124 (Mullally et al. 2015) with a period of 7 days. It was later on flagged as a false positive. In the mean time, we secured two spectra with SOPHIE HE that revealed a wide line profile with large RV variation. We estimated the υsini⋆ of the host star to be υsini⋆ = 51.3 ± 0.8 km s-1. The RV show variation in anti-phase with the transit ephemeris, indicating that Kepler detected the secondary eclipse of this binary. We confirm this candidate is not a transiting planet but a secondary-only EB.
Appendix A.68: KOI-6132.01
Mullally et al. (2015) reported two candidates transiting the target star KOI-6132: a giant-planet candidate at 33 days (KOI-6132.01) and a Neptune-size planet at 8 days (KOI-6132.02). Another set of transit was also detected with a period of 12 days (KOI-6132.03) but was rejected as false-positive by the same authors. We observed it six times with SOPHIE HE. We find no significant RV variation. The rms are 69 m s-1, 64 m s-1, and 51 m s-1 for the RV, bisector and FWHM. We fitted two circular orbits at the ephemeris of the two candidates and found that K6132.01< 109 m s-1 and K6132.02< 120 m s-1 at the 99% level. Assuming a host mass of 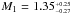 M⊙ (Huber et al. 2014), it corresponds to companion mass of M6132.01< 2.25M♃ and M6132.02< 1.50M♃, at the 99% level. We can thus reject that these candidates are EB or brown dwarfs but we can not firmly establish their planetary natures.
M⊙ (Huber et al. 2014), it corresponds to companion mass of M6132.01< 2.25M♃ and M6132.02< 1.50M♃, at the 99% level. We can thus reject that these candidates are EB or brown dwarfs but we can not firmly establish their planetary natures.
Appendix A.69: KOI-6175.01
A giant-planet candidate was found on the target star KOI-6175 with a period of 10 days (Mullally et al. 2015). We observed it twice with SOPHIE HE which revealed a large RV variation. By fitting this variation with a circular orbit at the Kepler ephemeris, we find K = 20.13 ± 0.03 km s-1. Assuming a host mass of M1 = 1.38 ± 28 M⊙ (Huber et al. 2014), the companion has a mass of M2 = 0.29 ± 0.04 M⊙. Therefore, we conclude that this candidate is not a transiting planet but an EB.
 |
Fig. A.7 Odd (left) and even (right) transits of the candidate KOI-6235.01. |
Appendix A.70: KOI-6235.01
A giant-planet candidate was found on the target star KOI-6235 with an orbital period of 2.05 days (Mullally et al. 2015). We observed it six times with SOPHIE HE. The rms of the RV, bisector and FWHM are 67 m s-1, 94 m s-1, and 198 m s-1 (respectively). Those rms are larger than the typical photon noise uncertainty on these measurements. We find a hint of RV variation with K = 89 ± 12 m s-1 assuming a circular orbit at the transit ephemeris. There is also a hint of correlation between the bisector and the RV. The FWHM also shows some variations.
Huber et al. (2014) reported that the host is a giant star, with a radius of 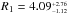 R⊙. Therefore, with a transit depth of 0.5%, the transiting companion would have a radius of R2 = 0.38 ± 0.16R⊙. If the transit occurs on the target star, it would be too deep to be compatible with a planet. Moreover, by analysing the transits of this candidate, we found a significant odd – even depth difference (see Fig. A.7), revealing that this candidate is clearly not a transiting planet but most likely a triple system with a giant primary and a nearly-equal mass EB with a period of 4.1 days.
R⊙. Therefore, with a transit depth of 0.5%, the transiting companion would have a radius of R2 = 0.38 ± 0.16R⊙. If the transit occurs on the target star, it would be too deep to be compatible with a planet. Moreover, by analysing the transits of this candidate, we found a significant odd – even depth difference (see Fig. A.7), revealing that this candidate is clearly not a transiting planet but most likely a triple system with a giant primary and a nearly-equal mass EB with a period of 4.1 days.
Appendix A.71: KOI-6251.01
The giant-planet candidate KOI-6251.01 was found by Mullally et al. (2015) with an orbital period of 15 days. The first estimate of its transit depth was of 0.5% (Mullally et al. 2015), but was later on revised to slightly above 3%. This candidate was initially in our candidate list and observed twice with SOPHIE HE. Finally, since its transit depth is now outside our selection criteria, this candidate is no longer in our sample. We find a wide line profile in the cross-correlation function that we fitted with a rotation profile as in Santerne et al. (2012a) which gives a υsini⋆ = 19.1 ± 0.3 km s-1. The derived RV present a large variation in phase with the Kepler ephemeris. By fitting a circular orbit at the transit ephemeris, we find an amplitude of K = 11.68 ± 0.70 km s-1. Assuming a host mass of 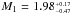 M⊙ (Huber et al. 2014), the companion has a mass of M2 = 0.21 ± 0.03 M⊙. Therefore, this candidate is not a transiting planet but an EB.
M⊙ (Huber et al. 2014), the companion has a mass of M2 = 0.21 ± 0.03 M⊙. Therefore, this candidate is not a transiting planet but an EB.
Appendix A.72: KOI-6460.01
A giant-planet candidate was found by Coughlin et al. (2015) to transit the target star KOI-6460 every 1.2 days. This candidate was not reported in previous KOIs released and thus, was not included in the sample of Santerne et al. (2012b). The DV summary shows that this candidate is actually a slightly eccentric EB at twice the reported orbital period. The true primary eclipse depth is of about 20%. We conclude this candidate is clearly not a transiting planet but an EB. For this reason, we did not observed it with SOPHIE.
Appendix A.73: KOI-6602.01
A giant-planet candidate was found by Coughlin et al. (2015) to transit the target star KOI-6602 every 0.65 days. This candidate was not reported in previous KOIs released and thus, was not included in the sample of Santerne et al. (2012b). The DV summary shows that this candidate is actually an EB with a primary eclipse depth is of about 10%. We conclude this candidate is clearly not a transiting planet but an EB. For this reason, we did not observed it with SOPHIE.
Appendix A.74: KOI-6800.01
A giant-planet candidate was found by Coughlin et al. (2015) to transit the target star KOI-6800 every 2.54 days. This candidate was not reported in previous KOIs released and thus, was not included in the sample of Santerne et al. (2012b). The DV summary shows that this candidate is actually a slightly eccentric EB at twice the reported orbital period. We conclude this candidate is clearly not a transiting planet but an EB. For this reason, we did not observed it with SOPHIE.
Appendix A.75: KOI-6877.01
A giant-planet candidate was found by Coughlin et al. (2015) to transit the target star KOI-6877 every 281 days. The host star is actually a red-giant star with a radius of almost R = 9.4 ± 0.1R⊙ (Beck 2013). With a transit depth of about 0.8%, the companion would have a radius compatible with a K dwarf and not with the one of an EGP. Moreover, the transit has a box shaped and could actually be the secondary eclipse of this EB. For this reason, we did not observed it with SOPHIE.
Appendix A.76: KOI-6933.01
A giant-planet candidate was found by Coughlin et al. (2015) to transit the target star KOI-6933 every 7.2 days. A visual inspection of the DV summary reveal that this target is a clear EB with an eclipse depth of more than 40%. We conclude this candidate is clearly not a transiting planet but an EB. For this reason, we did not observed it with SOPHIE.
Appendix A.77: KOI-7044.01
A giant-planet candidate was found by Coughlin et al. (2015) to transit the target star KOI-7044 every 1.3 day. The host star is actually a red-giant star with a radius of about R = 13R⊙ (Huber et al. 2014). With a transit depth of about 0.7%, the companion would have a radius compatible with a G dwarf and not with the one of an EGP. Moreover, the DV summary shows a odds – even transit depth difference indicating that this system is a CEB with twice the reported period. For this reason, we did not observed it with SOPHIE.
Appendix A.78: KOI-7054.01
A giant-planet candidate was found by Coughlin et al. (2015) to transit the target star KOI-7054 every 0.53 day. This candidate was not reported in previous KOIs released and thus, was not
included in the sample of Santerne et al. (2012b). A visual inspection of the light-curve showed that this candidate is actually an EB at twice the reported orbital period with a primary eclipse depth of about 50%. We conclude this candidate is clearly not a transiting planet but an EB. For this reason, we did not observed it with SOPHIE.
Appendix A.79: KOI-7065.01
A giant-planet candidate was found by Coughlin et al. (2015) to transit the target star KOI-7065 every 0.74 day. A visual inspection of the DV summary reveal that this target is a clear EB with a deep secondary eclipse. We conclude this candidate is clearly not a transiting planet but an EB. For this reason, we did not observed it with SOPHIE.
Appendix A.80: KOI-7527.01
A giant-planet candidate was found by Coughlin et al. (2015) to transit the target star KOI-7527 every 1.3 days. This candidate was not reported in previous KOIs released and thus, was not included in the sample of Santerne et al. (2012b). A visual inspection of the light-curve revealed the presence of a clear secondary eclipse with a depth of about 0.8%. We conclude this candidate is clearly not a transiting planet but an EB. For this reason, we did not observed it with SOPHIE.
Appendix B: Additionnal tables
Compilation of the results from the spectroscopic analyses performed in the context of the spectroscopic follow-up of Kepler giant-planet candidates.
Measured υsini⋆ based on the SOPHIE CCFs.
Derived upper limits on the mass of the candidates for which we detected no significant RV variation.
Estimated p-values from the Anderson–Darling (AD) tests for the distributions of Teff and [Fe/H] between all the Kepler targets, all the KOIs, the giant-planet hosts, and false-positive hosts.
Stellar parameters at the end of the main sequence from the STAREVOL evolution tracks.
Adopted parameters for the giant planets and their host.
Values of the correction factors used to derive the occurrence rates of giant planets in the Kepler FOV.
Occurrence rates of giant planets for different ranges of orbital periods from different studies. All values are in percent.
Adopted parameters for the brown dwarfs and their host.
Values of the correction factors used to derive the occurrence rates of brown dwarfs in the Kepler FOV.
Assumed lower limit in mass and RV amplitude (assuming a circular orbit) for the objects for which only an upper limit in mass was determined.
All Tables
Compilation of the results from the spectroscopic analyses performed in the context of the spectroscopic follow-up of Kepler giant-planet candidates.
Derived upper limits on the mass of the candidates for which we detected no significant RV variation.
Estimated p-values from the Anderson–Darling (AD) tests for the distributions of Teff and [Fe/H] between all the Kepler targets, all the KOIs, the giant-planet hosts, and false-positive hosts.
Stellar parameters at the end of the main sequence from the STAREVOL evolution tracks.
Values of the correction factors used to derive the occurrence rates of giant planets in the Kepler FOV.
Occurrence rates of giant planets for different ranges of orbital periods from different studies. All values are in percent.
Values of the correction factors used to derive the occurrence rates of brown dwarfs in the Kepler FOV.
Assumed lower limit in mass and RV amplitude (assuming a circular orbit) for the objects for which only an upper limit in mass was determined.
All Figures
 |
Fig. 1 Planet candidates detected by the Kepler telescope in the Q1–Q17 dataset. Their transit depth is displayed here as a function of their orbital period. The size of the circle is relative to the magnitude of the host. The grey region in the upper panel represents the selection criteria used to define the giant-planet candidate sample (see text). The lower panel is a zoom to this selected population of candidates. |
| In the text | |
 |
Fig. 2 Comparison of the Teff, log g, and [Fe/H] we derived by spectroscopy with the ones derived photometrically by Huber et al. (2014) for the 37 targets listed in Table B.2. Open and filled circles are for stars hotter and cooler than the Sun (respectively). The log g of the giant host KOI-5976 is not displayed here for the sake of clarity in the plot. |
| In the text | |
 |
Fig. 3 Same as lower panel of Fig. 1, but the labels indicate the nature of the candidates: BD stands for brown dwarfs, EB for eclipsing binaries, CEB for contaminating binaries, and No Var for the unsolved cases that show no significant variation in radial velocity. |
| In the text | |
 |
Fig. 4 Pie charts showing the distribution by nature of the giant-planet candidates: (left) the observed distribution of the candidates; (right) the underlying distribution of the candidates under the assumption that the unsolved cases are composed of 75% of planets and 25% of contaminating eclipsing binaries (see text). BD refers to brown dwarfs, EB to eclipsing binaries, CEB to contaminating eclipsing binaries, and the question mark to the unsolved cases. |
| In the text | |
 |
Fig. 5 Cumulative distribution functions (CDF) of the effective temperature (top panel) and the iron abundance (bottom panel) for all the Kepler targets (solid and thick line), the secured EGPs in our sample (solid line), and the false positives identified by our spectroscopic surveys (dashed line). The stellar parameters are from Huber et al. (2014). |
| In the text | |
 |
Fig. 6 Stellar mass-radius diagramme of the targets observed by Kepler during the quarters Q1–Q16 (black dots), the candidate hosts (white circles), and the bright giant-planet hosts (red circles). The data are from Huber et al. (2014) except for the giant-planet hosts, which are taken from Table B.7. The size of the mark for the two latter samples corresponds to the Kepler magnitude. The grey region displays the selected dwarfs. One secured EGP transits a star bigger than 2.5 R⊙ (KOI-680) and is not represented here. |
| In the text | |
 |
Fig. 7 Correction factors to compensate for the candidates selection ( |
| In the text | |
 |
Fig. 8 Occurrence rates of giant planets as a function of the orbital period. The horizontal bars indicate the range of periods used in a given bin. |
| In the text | |
 |
Fig. 9 Comparison of the occurrence rates of the three populations of giant planets. The black marks represent values based on RV surveys and the white ones are from photometric surveys. |
| In the text | |
 |
Fig. 10 Hatzes & Rauer (2016) diagram of exoplanets, showing the bulk density as function of their mass. The open circles are the giant planets defined in our sample and the dots are other planets. We kept as planets only those with a density characterised at a level better than 1σ. The arrows represent the candidates in our sample for which it was only possible to derive an upper limit on their mass (see Table B.4). The vertical bars attached to the arrow are the uncertainties on the densities imposed by the uncertainties on the radii. The dashed line represents the empirical lower envelope density for giant and low-mass planets (see Eq. (5)). |
| In the text | |
 |
Fig. 11 Top panel: radius of giant planets as a function of their stellar insolation flux Seff. The open circles indicate the secured planets, the Epen squares the likely ones, and the dots the non-Kepler objects. The solid line represent the best model of Eq. (7) and the grey regions represent the 1, 2, 3σ (from dark to light grey) confidence interval for this best model, as described by the covariance matrix provided in Eq. (8). Bottom panel: normalised cumulative distribution (CDF) of the radius of giant planets listed in Table B.7 for objects receiving more (dashed thick line) or less (solid thick line) insolation flux than 108 erg cm-2 s-1. The prediction from Mordasini et al. (2012b) is shown for comparison (age of 5 Gyr – solid thin line). This prediction is for planet with orbit >0.1 au, which correspond to 1.4 × 108 erg cm-2 s-1 for a Sun-like star. |
| In the text | |
 |
Fig. 12 Fraction of dwarf stars transited by a giant planet as a function of the stellar iron abundance. The solid line is the best model found and the grey regions represent the 1, 2, and 3σ confidence intervals (from dark to light grey). |
| In the text | |
 |
Fig. 13 Correlation between the bulk density of giant planets receiving a moderate irradiation as a function of the iron abundance of their host star. The solid line is the best model found, and the grey regions represent the 1, 2, and 3σ confidence intervals (from dark to light grey). |
| In the text | |
 |
Fig. A.1 Bisector Vspan as a function of the RV for the target star KOI-531. |
| In the text | |
 |
Fig. A.2 Cross-correlated a function of the target star KOI-976 revealing at least three stellar components: a wide and shallow component and two narrower and deeper components. The legend indicates the orbital phase of the transiting candidate. An arbitrary offset in flux has been set between the two observations. The red lines are the three-Gaussian fits to the CCFs. |
| In the text | |
 |
Fig. A.3 Phase-folded RV curve of KOI-1353.03 together with the best circular model found. |
| In the text | |
 |
Fig. A.4 Bisector Vspan as a function of the RV for the target star KOI-3663. |
| In the text | |
 |
Fig. A.5 Cross-correlated function of the target star KOI-3685 revealing two stellar components. The legend indicates the orbital phase of the transiting candidate. An arbitrary offset in flux has been set between the two observations. The red lines are the two-Gaussian fits to the CCFs. |
| In the text | |
 |
Fig. A.6 Cross-correlated function of the target star KOI-5529 revealing three stellar components. The legend indicates the orbital phase of the transiting candidate. An arbitrary offset in flux has been set between the two observations. The red lines are the three-Gaussian fits to the CCFs. |
| In the text | |
 |
Fig. A.7 Odd (left) and even (right) transits of the candidate KOI-6235.01. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


