| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527269 | |
| Published online | 25 January 2016 | |
Fossil groups in the Millennium simulation
From the brightest to the faintest galaxies during the past 8 Gyr
1 Instituto de Astronomía Teórica y Experimental, IATE, CONICET, Córdoba, Argentina
e-mail: mjkanagusuku@gmail.com
2 Observatorio Astronómico, Universidad Nacional de Córdoba, Laprida 854, X5000BGR, Córdoba, Argentina
Received: 28 August 2015
Accepted: 11 November 2015
Aims. We investigate the evolution of bright and faint galaxies in fossil and non-fossil groups.
Methods. We used mock galaxies constructed based on the Millennium run simulation II. We identified fossil groups at redshift zero according to two different selection criteria, and then built reliable control samples of non-fossil groups that reproduce the fossil virial mass and assembly time distributions. The faint galaxies were defined as having r-band absolute magnitudes in the range [−16, −11]. We analysed the properties of the bright and faint galaxies in fossil and non-fossil groups during the past 8 Gyr.
Results. We observed that the brightest galaxy in fossil groups is typically brighter and more massive than their counterparts in control groups. Fossil groups developed their large magnitude gap between the brightest galaxies around 3.5 Gyr ago. The brightest galaxy stellar masses of all groups show a notorious increment at that time. By analysing the behaviour of the magnitude gap between the first and the second, third, and fourth ranked galaxies, we found that at earlier times, fossil groups comprised two large brightest galaxies with similar magnitudes surrounded by much fainter galaxies, while in control groups these magnitude gaps were never as large as in fossils. At early times, fossil groups in the faint population were denser than non-fossil groups, then this trend reversed, and finally they became similar at the present day. The mean number of faint galaxies in non-fossil systems increases in an almost constant rate towards later times, while this number in fossil groups reaches a plateau at z ~ 0.6 that lasts ~2 Gyr, and then starts growing again more rapidly.
Conclusions. The formation of fossil groups is defined at the very beginning of the groups according to their galaxy luminosity sampling, which could be determined by their merging rate at early times.
Key words: methods: numerical / methods: statistical / galaxies: groups: general
© ESO, 2016
1. Introduction
The true nature of fossil groups in the Universe still puzzles the astronomical community. These peculiar systems are one of the most intriguing places in the Universe where giant elliptical galaxies are hosted.
Since their definition at the beginning of the past decade (Jones et al. 2003), the existence of these systems with a very luminous X-ray source (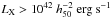 ) and a very optically dominant central galaxy (magnitude gap between the two brightest galaxies, ΔM12, greater than 2), many studies were performed to unveil their formation scenario. Several of these attempts have intended to quantify their incidence rate, dynamical masses, physical properties, etc. (see for instance, Mendes de Oliveira et al. 2006; Cypriano et al. 2006; Khosroshahi et al. 2006b,a). A special mention should be given to a recent effort to collect observational evidence to study fossil systems, which it is known as the “Fossil Group Origins” project. This is a collaboration to study galaxy systems previously identified as fossil groups by Santos et al. (2007), which has attempted to address several questions such as studying high-redshift massive systems and their fossil-like behaviour (Aguerri et al. 2011), the intrinsic difference between the brightest central galaxies in fossils and normal galaxy systems (Méndez-Abreu et al. 2012), the correlation between their optical and X-ray luminosity (Girardi et al. 2014), confirming the fossil nature of part of the original group sample (Zarattini et al. 2014), and analysing the dependence of the luminosity function on the magnitude gap (Zarattini et al. 2015).
) and a very optically dominant central galaxy (magnitude gap between the two brightest galaxies, ΔM12, greater than 2), many studies were performed to unveil their formation scenario. Several of these attempts have intended to quantify their incidence rate, dynamical masses, physical properties, etc. (see for instance, Mendes de Oliveira et al. 2006; Cypriano et al. 2006; Khosroshahi et al. 2006b,a). A special mention should be given to a recent effort to collect observational evidence to study fossil systems, which it is known as the “Fossil Group Origins” project. This is a collaboration to study galaxy systems previously identified as fossil groups by Santos et al. (2007), which has attempted to address several questions such as studying high-redshift massive systems and their fossil-like behaviour (Aguerri et al. 2011), the intrinsic difference between the brightest central galaxies in fossils and normal galaxy systems (Méndez-Abreu et al. 2012), the correlation between their optical and X-ray luminosity (Girardi et al. 2014), confirming the fossil nature of part of the original group sample (Zarattini et al. 2014), and analysing the dependence of the luminosity function on the magnitude gap (Zarattini et al. 2015).
There is another approach to understand the real nature of these peculiar galaxy systems, and that is through numerical experiments. From some of these studies carried out using numerical simulations, we were able to deepen our understanding of the different formation scenarios (see for instance D’Onghia et al. 2005; von Benda-Beckmann et al. 2008). When these experiments are performed using a combination of a large cosmological simulation and a semi-analytical model of galaxy formation, very interesting analyses can be done. In the past years, several studies have used synthetic galaxies to analyse the evolution of fossil groups. Particularly, very reliable results were obtained for those semi-analytical surveys constructed based on one of the largest numerical simulations currently available, the Millennium simulation (Springel et al. 2005, hereafter MS). Using this tool, Dariush et al. (2007) were the first to confirm that fossil systems identified in the MS assembled a larger portion of their masses at higher redshifts than non-fossil groups, suggesting that the most likely scenario for fossil groups is that they are not a distinct class of objects, but simply examples of systems that collapsed earlier. In a later work, Dariush et al. (2010) suggested refinements to the fossil definition to enhance its efficiency in detecting old systems. On the other hand, in the first work of this series, Díaz-Giménez et al. (2008) studied the evolution of the first-ranked galaxies in the MS, finding that despite the earlier assembly time of fossil systems, first-ranked galaxies in fossil groups assembled half of their final mass and experienced their last major merger later than their non-fossil counterparts, implying that they followed a different evolutionary pathway. In a second work, Díaz-Giménez et al. (2011) intended to characterise the outskirts of fossil groups in contrast with those observed in normal groups. They observed that the environment was different for fossil and non-fossil systems with similar masses and formation times along their evolution, encouraging the idea that their surroundings could be responsible for the formation of their large magnitude gap. Hence, consensus has clearly yet to be reached regarding the nature of fossil systems.
Some of the formation scenario proposed for fossil systems led us to feed a particular working hypothesis: that the population of faint galaxies inhabiting these galaxy systems might have undergone a different evolutionary history than is expected in normal systems. Several works have intended to understand the role of the faint galaxy population in fossil groups. For instance, the early work of D’Onghia & Lake (2004), who suggested that it is expected that fossil groups may lack faint galaxies, in what they called the missing satellite problem in cold dark matter cosmologies. Further analysis performed using the luminosity function of fossil group galaxy members by Mendes de Oliveira et al. (2009) has shown that there is no significant evidence that this problem with faint galaxies actually occurs. In addition, Sales et al. (2007) used the MS-I to show that the galaxy luminosity function in fossil groups is consistent with the predictions of a lambda cold dark matter universe. Analysing the faint-end slope of the galaxy luminosity function in observational fossil groups, Proctor et al. (2011) have observed that the faint luminosity tail is well represented by an almost flat slope, suggesting that the faint galaxy population is not affected by living in fossil systems. Nevertheless, most of these works agree that the faint galaxy population is represented by galaxies mainly down to −17 absolute magnitudes, hence, a wide range of faint galaxies are out of their analysis. More recently, an observational work of Lieder et al. (2013) has attempted to gather information about a fainter population of galaxies. These authors analysed the faint galaxy population of a fossil system down to an absolute magnitude of −10.5 in the R-band. They observed that the photometric properties of faint galaxies are consistent with those of normal groups or clusters, including a normal abundance of faint satellites. However, more substantial evidence is needed to confirm these observational findings.
Gozaliasl et al. (2014) explored the influence of the faint galaxy population in the formation history of fossil systems and used the MS-I to study the evolution of the luminosity function parameters in fossil and non-fossil systems. They confirmed that roughly 80% of the fossil systems identified at early epochs (z ~ 1) have lost their magnitude gaps before reaching the present time. Analysing the faint-end slope of the luminosity function, they observed that there is almost no evolution of the faint population in fossils, while there is a considerable increment of this population in non-fossil systems. However, as a result of the nature of the simulation, they considered as faint galaxies only those down to ~−16 in the r-band.
Therefore, to obtain a complete understanding of the evolution of the faint galaxy population in fossil groups, a more suitable set of synthetic galaxies is needed. Such galaxies can be extracted from the high-resolution N-body numerical simulation, the Millennium run simulation II (Boylan-Kolchin et al. 2009), which is perfect for resolving dwarf galaxies using semi-analytic recipes. A particular set of recipes was applied to this simulation by Guo et al. (2011), producing a highly suitable sample of mock galaxies. The semi-analytic model has been tuned to reproduce the z = 0 stellar mass function and luminosity function, making it a suitable tool to understand the evolution of faint galaxies. Therefore, we here use this publicly available tool to study the evolution of the brightest galaxies in fossil groups from a semi-analytical point of view and determine whether the population of faint galaxies in fossil is affected by the formation history of these systems compared to the same population in groups considered non-fossils.
The layout of this paper is as follows: in Sect. 2 we briefly described the set of semi-analytic galaxies used in this work. We identify groups and classify them into fossil and non-fossil groups in Sect. 3. In Sect. 4 we analyse the evolution of the brightest members of fossil and non-fossil groups, while the selection of the faint population and the analysis of its distribution are included in Sect. 5. Finally, we summarise our work and discuss the results in Sect. 6.
2. Mock galaxies
We used a simulated set of galaxies extracted from the semi-analytic model of galaxy formation developed by Guo et al. (2011), which has been applied based on the Millennium run simulation II (Boylan-Kolchin et al. 2009).
2.1. N-body simulation
The Millennium run simulation II is a cosmological tree-particle-mesh (Xu 1995) N-body simulation that evolves 10 billion (21603) dark matter particles in a 100 h-1 Mpc periodic box, using a comoving softening length of 1 h-1 kpc (Boylan-Kolchin et al. 2009). The cosmological parameters of this simulation are consistent with WMAP1 data (Spergel et al. 2003), that is, a flat cosmological model with a non-vanishing cosmological constant (ΛCDM): Ωm = 0.25, Ωb = 0.045, ΩΛ = 0.75, σ8 = 0.9, n = 1 and h = 0.73. The simulation was started at z = 127, with the particles initially positioned in a glass-like distribution according to the ΛCDM primordial density fluctuation power spectrum. The mass resolution is 125 times better than obtained in the Millennium run simulation I (Springel et al. 2005), which means that the mass of each particle is 6.9 × 106h-1 ℳ⊙. With this resolution, halos of typical dwarf spheroids are resolved, and halos similar to the mass of our Milky Way have hundreds of thousands of particles (Boylan-Kolchin et al. 2009).
2.2. Semi-analytic model
We adopted the simulated set of galaxies built by Guo et al. (2011). This particular semi-analytic model fixed several open questions present in some of its predecessors, such as the efficiency of supernova feedback and the fit of the stellar mass function of galaxies at low redshifts. Guo et al. (2011) also introduced a more realistic treatment of satellite galaxy evolution and of mergers, allowing satellites to continue forming stars for a longer period of time and reducing the excessively rapid reddening of the satellite. The model also treats the tidal disruption of satellite galaxies. Compared to previous versions of the semi-analytical models, the model of Guo et al. has fewer galaxies than its predecessors, at any redshifts and in any environment. This is the result of a stronger stellar feedback that reduces the number of low-mass galaxies, and a model of stellar stripping, which contributes to reduce the number of intermediate- to low-mass galaxies (Vulcani et al. 2014).
This model produces a complete sample when considering galaxies with stellar masses higher than ~106.4h-1 ℳ⊙. This implies that the galaxy sample is almost complete down to an absolute magnitude in the rSDSS-band of −11.
Since different cosmological parameters have been found from WMAP7 (Komatsu et al. 2011), it might be argued that the studies carried out in the present simulation produce results that do not agree with the current cosmological model. However, Guo et al. (2013) have demonstrated that the abundance and clustering of dark halos and galaxy properties, including clustering, in WMAP7 are very similar to those found in WMAP1 for z ≤ 3, which is far inside the redshift range of interest in this work.
3. Group samples
3.1. Identification of friends-of-friends groups
Groups of galaxies were identified by using a friends-of-friends (FoF) algorithm in real space (Davis et al. 1985) applied to the mock galaxies in the simulation box.
To study different evolutionary stages of the simulated groups, we performed nine identifications in different outputs, from redshift z = 0 to z = 1.08 (~8 Gyr), each output spaced by ~ 0.1. Following Zandivarez et al. (2014), we considered that the linking length b used by the algorithm to cluster galaxies depends on the redshift as follows: 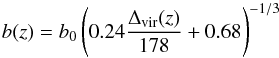 where the enclosed overdensity of haloes, Δvir, depends on the cosmology and the value of redshift according to
where the enclosed overdensity of haloes, Δvir, depends on the cosmology and the value of redshift according to ![\begin{eqnarray*} \Delta_{\rm vir}(z)=18\pi^{2}\left[1+0.399\left(\frac{1}{\Omega_{\rm m}(z)}-1\right)^{0.941}\right] \end{eqnarray*}](/articles/aa/full_html/2016/02/aa27269-15/aa27269-15-eq35.png) where
where 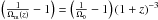 and Ω0 is the dimensionless matter density parameter at the present. We identified groups in a galaxy catalogue instead of in one of dark matter particles. Therefore, and following previous studies (Eke et al. 2004; Berlind et al. 2006; Zandivarez et al. 2014), we used a fiducial linking length of b0 = 0.14 (instead of the conventional b0 = 0.2 for DM halos), which corresponds to a contour overdensity contrast of ~433. Using this prescription, we obtained a galaxy group catalogue at z = 0 comprising 5116 systems with ten or more galaxy members.
and Ω0 is the dimensionless matter density parameter at the present. We identified groups in a galaxy catalogue instead of in one of dark matter particles. Therefore, and following previous studies (Eke et al. 2004; Berlind et al. 2006; Zandivarez et al. 2014), we used a fiducial linking length of b0 = 0.14 (instead of the conventional b0 = 0.2 for DM halos), which corresponds to a contour overdensity contrast of ~433. Using this prescription, we obtained a galaxy group catalogue at z = 0 comprising 5116 systems with ten or more galaxy members.
In Fig. 1 we show the distributions of the physical properties of the simulated galaxy groups identified at z = 0 (empty histograms). In the left column, from top to bottom, we show the 3D virial radius, the 3D velocity dispersion, and the group virial mass. The 3D virial radius was computed according to 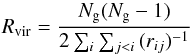 where Ng is the total number of galaxy members and rij are the 3D intergalaxy separations. The 3D group velocity dispersion, σ, was estimated as the root mean square velocity dispersion from the group galaxy members. And finally, the virial mass was computed as follows:
where Ng is the total number of galaxy members and rij are the 3D intergalaxy separations. The 3D group velocity dispersion, σ, was estimated as the root mean square velocity dispersion from the group galaxy members. And finally, the virial mass was computed as follows: 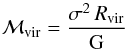 where G is the gravitational constant. The sample of groups has median virial radius of 0.14 h-1 Mpc, median velocity dispersion of 200 km s-1, and median virial mass of 1.3 × 1012h-1 ℳ⊙.
where G is the gravitational constant. The sample of groups has median virial radius of 0.14 h-1 Mpc, median velocity dispersion of 200 km s-1, and median virial mass of 1.3 × 1012h-1 ℳ⊙.
In the right column of Fig.1 we show the distributions of properties that are used in the following sections to select fossil and non-fossil systems (empty histograms).
 |
Fig. 1 Distribution of properties of the semi-analytic galaxy groups: 3D virial radius (top left panel), 3D velocity dispersion (middle left panel), virial mass (bottom left panel), ratio between stellar mass in bulge and total stellar mass of the first-ranked galaxy (top right panel), difference between the r-band absolute magnitude of the first- and second-ranked galaxies within half a virial radius (middle right panel), and difference between the r-band absolute magnitude of the first- and fourth-ranked galaxies within half a virial radius (middle right panel). Empty histograms correspond to FoF groups with 10 or more galaxy members, while grey histograms correspond to the 102 FoF groups that have virial masses higher than 1013.5h-1ℳ⊙ and whose brightest galaxy is an elliptical galaxy (ℳ∗1,bulge/ ℳ∗1,total> 0.7). |
 |
Fig. 2 Luminosity function of galaxies in groups. The solid line is the luminosity function for semi-analytical galaxies in groups with virial masses higher than 1013.5h-1ℳ⊙ and whose brightest galaxy is an elliptical galaxy. Grey region show the results for galaxies in groups in the SDSS DR7 obtained by Zandivarez & Martínez (2011). Upper and lower arrows represent the faint end slope of the luminosity function obtained by Popesso et al. (2005) and Zarattini et al. (2015), while middle arrow correspond to the value obtained in this work. |
3.2. Fossil groups
Jones et al. (2003) identified fossil groups as spatially extended X-ray sources with an X-ray luminosity 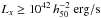 , whose optical counterpart is a bound system of galaxies with ΔM12 ≥ 2, where ΔM12 is the difference in absolute magnitude in the R-band between the brightest and the second brightest galaxies located within half the project virial radius of the systems. Using this definition, it is assumed that galaxies within half the virial radius have had time to merge within a Hubble time, and also that normal elliptical galaxies that are not located at the centre of the groups will not be chosen as potential fossil groups (Lieder et al. 2013). In addition to the conventional criteria, there exists an alternative criterion developed by Dariush et al. (2010). These authors found that imposing the magnitude gap in the R-band between the brightest and the fourth brightest galaxies within half the projected virial radius to be larger than 2.5 mag, ΔM14 ≥ 2.5, identifies 50% more early-formed systems, and such systems, on average, retain their fossil phase longer. However, the conventional criteria perform marginally better at finding early-formed groups at the high-mass end of the virial mass distribution of groups. In this work, we used the two criteria defined above to identify fossil groups with the purpose of performing comparative studies.
, whose optical counterpart is a bound system of galaxies with ΔM12 ≥ 2, where ΔM12 is the difference in absolute magnitude in the R-band between the brightest and the second brightest galaxies located within half the project virial radius of the systems. Using this definition, it is assumed that galaxies within half the virial radius have had time to merge within a Hubble time, and also that normal elliptical galaxies that are not located at the centre of the groups will not be chosen as potential fossil groups (Lieder et al. 2013). In addition to the conventional criteria, there exists an alternative criterion developed by Dariush et al. (2010). These authors found that imposing the magnitude gap in the R-band between the brightest and the fourth brightest galaxies within half the projected virial radius to be larger than 2.5 mag, ΔM14 ≥ 2.5, identifies 50% more early-formed systems, and such systems, on average, retain their fossil phase longer. However, the conventional criteria perform marginally better at finding early-formed groups at the high-mass end of the virial mass distribution of groups. In this work, we used the two criteria defined above to identify fossil groups with the purpose of performing comparative studies.
Given that we do not have X-ray luminosity in the simulation boxes, we adopted a lower cut-off in group virial masses, ℳvir ≥ 1013.5h-1 ℳ⊙ to maximise the probability that the selected systems are strong X-ray emitters (Dariush et al. 2007). Moreover, we included a criterion to ensure that the brightest galaxy of the selected groups is elliptical, as is found in all the observational fossil groups known to date. Following Bertone et al. (2007), we classified as ellipticals those galaxies whose ratio between the stellar mass of the bulge and the total stellar mass is higher than a given threshold: ℳ∗bulge/ ℳ∗tot> 0.7. The distributions of properties of the 102 FoF groups that satisfy these two criteria are shown as grey histograms in Fig. 1. We also compare the distribution of r-band absolute magnitudes of galaxies in these simulated groups with results from observations in Fig. 2. The grey region was built from the best-fitting Schechter parameters of the luminosity function of galaxies in groups identified in the SDSS DR7 by Zandivarez & Martínez (2011)1. These fits were obtained only for galaxies brighter than Mr−5log (h) = −17. The lower envelope corresponds to groups with masses ~1013.5, while the upper envelope corresponds to groups with masses higher than 1014.1. The bright end of the luminosity function of the semi-analytical galaxies in groups agrees with the observations. The behaviour of the faint-end slope of the luminosity function was compared with the observational results obtained by Popesso et al. (2005) and Zarattini et al. (2015; arrows in Fig. 2). The slopes obtained by these authors encompass the value obtained in this work of α ≃ −1.43.
 |
Fig. 3 Evolution of the median properties of fossil and control groups. The left plots correspond to the sample of fossils and controls defined using the ΔM12 magnitude gap, while the right plots correspond to the definition based on the ΔM14 magnitude gap. Panels in the first row show the evolution of the r-band absolute magnitude of the brightest galaxy of the groups; the second row shows the absolute magnitude of the second and fourth brightest galaxies; the third, fourth, and fifth rows show the evolution of the r-band absolute magnitude gap between the brightest and the second, third, and fourth brightest galaxies, respectively, the dashed horizontal lines correspond to the thresholds used to define fossil groups; the sixth row shows the stellar mass of the brightest galaxy, and the last row shows the evolution of the stellar mass of the brightest galaxy normalised to its final stellar mass. Error bands are the semi-interquartile ranges. |
Summarising, the criteria applied to the simulated groups to select fossil groups according to the two definitions are
-
fossil F12: ℳvir ≥ 1013.5h-1 ℳ⊙; ℳ∗1,bulge/ ℳ∗1,tot> 0.7; and ΔM12 ≥ 2 (Jones et al. 2003), and
-
fossil F14: ℳvir ≥ 1013.5h-1 ℳ⊙; ℳ∗1,bulge/ ℳ∗1,tot> 0.7; and ΔM14 ≥ 2.5 (Dariush et al. 2010).
We selected 14 groups as F12 and 22 groups as F14. Finally, we examined the evolution of these fossil groups at different times. We identified normal groups in each previous snapshot (see Sect. 3.1). Then, we selected those groups that hosted the progenitor of the brightest galaxy of the fossil group at z = 0. Since fossil groups are considered undisturbed and old systems, we only considered those systems that have already assembled more than the 50 per cent of their final mass at z ≳ 0.8. The samples comprise 9 fossil groups in the F12 category and 15 in the F14 category. We note that 78% of the F12 are also included in the F14 sample, in agreement with the results of Dariush et al. (2010; 75%). Conversely, 47% of the F14 satisfy the ΔM12 criterion; this percentage is higher than found by Dariush et al. (35%). This difference may be a consequence of the several restrictions imposed on our sample selection that have not been considered by these authors. Finally, we discarded 3 F14 groups to build a control sample that matches the distribution of their virial masses (see Sect. 3.3 for details). The final F14 sample comprises 12 groups.
3.3. Control groups
To perform a comparative study, we selected samples of non-fossil groups. These samples satisfy
-
non-fossil nF12: ℳvir ≥ 1013.5h-1 ℳ⊙; ℳ∗1,bulge/ ℳ∗1,tot > 0.7; and ΔM12 < 2, and
-
non-fossil nF14: ℳvir ≥ 1013.5h-1 ℳ⊙; ℳ∗1,bulge/ ℳ∗1,tot > 0.7; and ΔM14 < 2.5.
We selected 88 groups as nF12 and 80 groups as nF14. We also examined the evolution of the mass assembly of these groups and saved only those groups that assembled half of their final virial mass at redshifts higher than z ≃ 0.8. This criterion restricted the samples to 38 nF12 and 34 nF14.
Since cluster formation histories depend strongly on the mass of the systems, differences in the virial mass distributions of the fossil and non-fossil samples could introduce biases into the results. Therefore, we need subsamples of non-fossil groups that reproduce the virial mass distribution of their corresponding fossil groups for each category (“12” or “14”). After performing a two-sample comparison between the distributions of virial masses of fossil samples and 50 random selections of non-fossil samples, we selected the non-fossil group samples with the highest probability values from the two-sample Kolmogorov-Smirnov (KS) test. Moreover, given that the definition of fossil groups can be thought of as a tail of the distribution of differences in magnitudes between the brightest galaxies, we also included a similar restriction in the magnitude gap of non-fossil groups to select the opposite tail of the distribution of gaps. The upper threshold imposed to limit the magnitude gaps of control groups was chosen to obtain samples with a similar number of groups as their counterpart fossil samples. Then, the final control group samples have to fulfil the following criteria:
-
Control C12: ℳvir ≥ 1013.5h-1 ℳ⊙; ℳ∗1,bulge/ ℳ∗1,tot > 0.7; KS probability > 0.95 and ΔM12 < 0.9.
-
Control C14: ℳvir ≥ 1013.5h-1 ℳ⊙; ℳ∗1,bulge/ ℳ∗1,tot > 0.7; KS probability > 0.95 and ΔM14 < 2.
We obtained the final samples of control groups that comprise 9 C12 and 12 C14. In this way, we have constructed samples of similar numbers of fossil and control groups that have the same mass distribution, similar assembly times (old systems), but some (fossils) have been able to develop a large magnitude gap between their brightest galaxies, while the others (controls) do not.
4. Brightest galaxies
Figure 3 shows the evolution of the median of different properties of the final samples of fossil (left columns) and control (right columns) groups as a function of time (redshift) for samples defined using the ΔM12 criterion (left plots) and the ΔM14 criterion (right plots).
The first-ranked galaxies in fossil systems are typically brighter than their counterparts in control groups of the same virial mass and shows little or no evolution with time. On the other hand, the magnitude of the second- or fourth-ranked galaxies of fossil groups shows evolution with time (probably being replaced) and produces a change in the magnitude gap that is used to split between fossils and non-fossils (this is better seen in the F12 sample). The magnitude gap used to define a group as fossil is above the fixed threshold of around z ≃ 0.2 for F12 (left plot, third row), and around z ≃ 0.3 for F14 (right plot, fifth row), although many F14 have fulfilled the fossil criterion for a longer period of time (since z ~ 0.8). This means that on average, fossil systems have reached their status during the past 3.5 Gyr. Moreover, we found that the control groups C12 have not experienced a fossil phase during their whole history, while some of the C14 have had a fossil phase in the earlier stages of group formation.
We also analysed the evolution of the magnitude gap between the brightest and the second, third, and fourth brightest galaxies in each group sample. In the F12 sample, for z ≳ 0.3 the magnitude gap between the brightest and the second brightest galaxies is ΔM12 ≲ 1, while ΔM13 and ΔM14 are ~2. Hence, fossil groups at earlier times had two dominant galaxies with similar absolute magnitudes surrounded by much fainter neighbours. For z ≲ 0.2, all the magnitude gaps shown in this figure increase, and the change in ΔM12 is more noticeable. We infer that there has been a mayor event between the first- and second-ranked galaxies, and as a consequence, there has been a rearrangement in the luminosity ranking leading to the observed changes in the magnitude gaps. In the C12 groups there were no two dominant galaxies during the past 8 Gyr. The difference in absolute magnitude between one galaxy and the next in the luminosity ranking is always ~0.5 mag. A similar analysis can be performed in the F14 and C14 samples.
Analysing the stellar mass of the first ranked galaxies, it can be seen that it is higher in fossil groups than in control groups in the whole redshift range. At redshift zero, the brightest galaxy in fossils is ~50% more massive than in control groups. Moreover, the brightest galaxies in the F12 have reached ~50% of their final mass at z ≃ 0.6, while the brightest galaxies of control C12 have assembled ~50% of their final mass before z ≃ 1. This difference does not exist when analysing the F14 sample, since the brightest galaxies in these systems have assembled their mass on average at redshifts as high as in the control samples. From these panels, we observe that the stellar mass of the brightest galaxy of fossil and control groups shows a noticeable increment (≳20%) around z ≃ 0.3, regardless of how the samples are defined. This result indicates a major event in all the group samples. As a result of the different galaxy luminosity sampling of the groups, this event was also inferred when analysing the magnitude gaps for fossil groups, but it was not observable from the magnitude gaps for control groups.
Fossil groups − regardless of the criterion adopted to define them − are therefore characterised not only by their early formation times, which can also be achieved by control groups, but it is also necessary that at high redshifts two similar massive galaxies exist at their cores, while the next-ranked galaxies are much fainter. Whether a group becomes fossil is therefore defined at the very beginning of the group history by its luminosity content.
5. Faintest galaxies
To study the faint galaxy population in fossil and control groups, we selected from each system those member galaxies that lie within one virial radius of the centre of the group, whose r-band absolute magnitudes are in the range −16 ≤ Mr−5log (h) ≤ −11. Then we analysed the distribution of these galaxies around the group centres. This selection was also performed in the different evolutionary stages analysed in this work (see Sect. 3.1).
To increase the statistical significance of the results, we combined in each snapshot all groups of each category (F12, C12, F14, C14) to produce composite clusters formed with faint galaxies, properly scaled to take into account the different sizes of groups within each category. The number of faint galaxies that build the composite clusters in the different snapshots are quoted in Table 1.
Number of faint galaxies in the composite clusters at each different evolutionary stage.
 |
Fig. 4 Number density profiles of faint galaxies in fossil and control groups. The upper panel shows the number density of faint galaxies in fossils F12 and control C12 groups as a function of the 3D normalised distance to the centre of the groups. The lower panel shows the same situation as in the top panel for fossils F14 and control C14 groups. Error bars are computed using the bootstrap resampling technique. Inset panels show the ratio between the number density profiles in fossils and controls. Error bars are computed via error propagation. |
 |
Fig. 5 Ratios of number density profiles of faint galaxies in fossil and control groups at different evolutionary stages. The left plot shows the evolution of the ratio between the number density of faint galaxies in fossil F12 and control C12 groups as a function of the 3D normalised distance to the centre of the group. The right plot shows the same, but using fossils F14 and control C14. |
The centre of each individual group was defined as the position of the brightest galaxy of the group, and the distances of each faint galaxy to the centre were normalised to the 3D virial radius of its host group. Then, the number density profile of the composite cluster was computed as a function of the normalised groupcentric distances (η(r/Rvir)).
In Fig. 4 we show the number density profiles of faint galaxies in fossil and control groups at z = 0. We observe from these panels that on average, the number density profiles of faint galaxies around fossils and controls span the same range of densities and, apart from local fluctuations, a similar distribution of faint galaxies is observed, regardless of the magnitude criterion adopted to define the samples.
 |
Fig. 6 Left plot: mean number of faint galaxies in fossils (solid lines) and controls (dashed lines) as a function of redshift. The upper panel shows the evolution observed in groups defined using the ΔM12 criterion, while lower panel corresponds to groups identified according to the ΔM14 criterion. Error bars are computed using the bootstrap resampling technique. The inset panels show the ratio between the mean number of faint galaxies in fossil and control groups. Right plot: mean number of faint galaxies classified as new members (upper panels) or lost members (lower panels). Error bars are computed using the error propagation formula. |
It is interesting to compare the behaviour of the faint galaxy population in fossils and controls throughout the history of the galaxy systems. We computed the number density profiles of faint galaxies at different evolutionary stages. Figure 5 shows the evolution of the ratios between the number density profiles of faint galaxies in fossil and control groups of each category. The population of faint galaxies within fossil and control groups behave differently during their evolution compared with the behaviours observed for z = 0. The left plot of Fig. 5 (using ΔM12, Jones et al. 2003) shows that for z ≥ 0.755 the number density of faint galaxies in fossil groups was higher than observed in control groups in most of the range of normalised distances. Later, in the range 0.3 ≲ z ≲ 0.5, the opposite behaviour is observed: control groups are denser in faint galaxies than fossil groups in the whole range of distances. For the latest times (z ≲ 0.2), the distribution of faint galaxies in fossils and non-fossils tends to behave more similarly. In the right plot of Fig. 5 (using ΔM14, Dariush et al. 2010) we observe a very similar general behaviour as the previously described for the left panel, but with a tendency to show a higher density in the central regions of fossil groups than in their controls.
To better understand the evolution of the faint galaxy population, we show in the left plot of Fig. 6 the mean number of faint galaxies in fossils and controls as a function of redshifts. This number has been computed from the number density profiles as 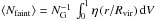 , where dV is a volume differential, and NG is the number of groups in each sample. The upper panel corresponds to groups defined with the ΔM12 criterion, while groups identified with the ΔM14 criterion are shown in the lower panel. Starting at redshift z ≃ 1, there are slightly more faint galaxies in fossil groups. In the range 0.3 ≲ z ≲ 0.6, control groups present more faint galaxies. Finally, the number of faint galaxies become similar in both group samples towards redshift zero. These results are also observed in the inset panels, where the ratios between the mean number of faint galaxies in fossil and control groups for each category are shown. This behaviour is observed for both categories of fossil groups.
, where dV is a volume differential, and NG is the number of groups in each sample. The upper panel corresponds to groups defined with the ΔM12 criterion, while groups identified with the ΔM14 criterion are shown in the lower panel. Starting at redshift z ≃ 1, there are slightly more faint galaxies in fossil groups. In the range 0.3 ≲ z ≲ 0.6, control groups present more faint galaxies. Finally, the number of faint galaxies become similar in both group samples towards redshift zero. These results are also observed in the inset panels, where the ratios between the mean number of faint galaxies in fossil and control groups for each category are shown. This behaviour is observed for both categories of fossil groups.
This clearly shows that the frequency evolution of faint galaxies for fossil and control groups is quite different. On one hand, the number of faint galaxies in control groups smoothly increases from z ≃ 1 to z = 0. On the other hand, there is an abrupt change in the evolution of the number of faint galaxies in fossils in the range 0.3 <z< 0.6: the number of faint galaxies in fossil groups ceases to increase, showing an almost constant slope. For z ≲ 0.3 the number of faint galaxies in fossils rapidly grows until it finally matches the number of faint galaxies in control groups at present.
This different behaviour between fossils and controls could be caused by different accretion rates of faint galaxies or by different missing galaxy rates inside the groups. To distinguish in this question, we split in each snapshot the faint galaxies in each group into two categories: old members and new members. We define as “old” those galaxies that have already been identified as members of the same FoF group in the previous snapshot (higher z), while the “new” members are those that were identified as members only in the corresponding snapshot. We also detected galaxies that existed in a previous snapshot and were missing in the following (“lost” members). In the right plot of Fig. 6 we show the mean number of new and lost faint galaxy members in fossils and controls as a function of redshift. In the range from z ≃ 0.7 to z ≃ 0.3 fewer new faint members are incorporated in each snapshot in both fossils and controls. However, this decrease is stronger in fossils. For z ≲ 0.3 there are fewer lost galaxies in fossils than missing galaxies in controls. These results remain valid for both fossil samples.
The almost constant number of faint galaxies observed in fossils in the range 0.3 <z< 0.6 (left plot) could be a consequence of a stronger decrease of the accretion rate of faint galaxies in fossils at these redshifts. On the other hand, the rapid growth of the number of faint galaxies in fossils, which ultimately causes the number of faint galaxies in fossils and controls to be the same at redshift zero, could be a consequence of a smaller number of missing galaxies in fossils since z ≃ 0.3.
6. Summary and conclusions
We have deepened our analysis on fossil groups from the semi-analytical point of view with a higher resolution than in previous works, by studying the evolution of the main properties of fossil systems and the distribution of the faint galaxy population that inhabits these peculiar systems.
The work was based on semi-analytical galaxies constructed by Guo et al. (2011) based on the high-resolution N-body numerical simulation, the Millennium run simulation II (Boylan-Kolchin et al. 2009). These mock galaxies are a highly suitable tool to investigate the role of dwarf galaxies embedded in larger density structures. Although our study is based on only one particular set of semi-analytical galaxies, that is, on the adopted set of recipes defined by Guo et al. (2011), this sample is one of the largest samples of faint galaxies up to date, and their recipes have been tuned specifically to improve the evolution of satellite galaxies compared to previous versions of the semi-analytical models of galaxy formation. They also carefully reproduce observational results such as the galaxy luminosity function and the stellar mass distribution in a very wide range of absolute magnitudes and stellar masses.
We identified fossil groups in our mock catalogue and then followed their evolution back in time for the past ~8 Gyr (z ~ 1). We adopted two different definitions of fossil systems that can be found in the literature: the well-known definition of Jones et al. (2003), which is based on the absolute magnitude gap between the first and second brightest galaxies in the group within half a virial radius; and the definition of Dariush et al. (2010), which is based on the absolute magnitude gap between the first and fourth brightest galaxies (see Sect. 3.2 for details). Our intention in using these two criteria was to investigate whether using different definitions affects the evolution of the brightest and faintest galaxies in fossil systems. Fossil groups also met the requirement that their virial masses are higher than 1013.5h-1 ℳ⊙ and that they assembled half of their virial masses at least 7 Gyr ago. The latter constraint led to samples of fossil groups that represents 64−68% of optical fossil groups (selected only according to group mass and magnitude gap). We have also defined reliable samples of control groups for each criterion to perform a fair comparison. These control groups have the same distributions of virial masses as fossil groups and similar early assembly times, but present a much smaller gap between the magnitudes of their brightest galaxies.
First, we analysed the evolution of the main properties of the brightest galaxies in fossil and control groups. We observed that the brightest galaxy in fossil groups is typically brighter and more massive than their counterparts in control groups. From our studies, it is clear that fossil groups start fulfilling their criterion to be considered as such around z ≃ 0.2−0.3 (Δ12> 2 or Δ14 > 2.5). We note that fossil groups defined using the Dariush et al. (2010) criterion start being fossils earlier than with the usual criterion, and therefore they maintain their fossil phase longer than with the definition of Jones et al. (2003), as stated in the work by Dariush et al. (2010). We found that the brightest galaxy in fossils defined with the classical criterion assembled half of their current stellar mass at later times than the brightest galaxies in fossils defined with the alternative criterion or in control groups. Finally, we observed that the stellar masses of the brightest galaxies of all types of groups show a notorious increment around z ≃ 0.3. In a previous work (Díaz-Giménez et al. 2008), it has been shown that the brightest galaxy in fossil groups has assembled half of its final mass later than non-fossil brightest galaxies and that it has experienced the latest major merger relatively recently (z ~ 0.3) compared to the brightest galaxies with similar stellar mass hosted in normal groups. Here, we found that the brightest galaxy in fossils and controls had a major event at the same redshift. However, it has to be noted that the brightest galaxies in fossils in this work are more massive than their counterpart in controls, which leads to the difference with the previous findings. It is interesting to note that also around the time when the major event has happened in both group types, the magnitude gap in fossil groups increases significantly, while the magnitude gap in controls is not affected. This change in the magnitude gap arises from a drastic change in the magnitude of the second-ranked galaxy in fossils. By analysing the behaviour of the magnitude gap between the first- and second-, third-, and fourth-ranked galaxies, we could infer that at earlier times, fossil groups comprised two large brightest galaxies with similar magnitudes surrounded by much fainter galaxies, and that at a redshift of around 0.2−0.3 these two galaxies merged to form the brightest galaxy that we observe today. This event probably was a dry merger given the non-significant change in the absolute magnitude of the brightest galaxy. This assumption agrees with the hypothesis of Méndez-Abreu et al. (2012), who stated that the brightest galaxies of fossil groups had suffered wet mergers only at early times, while the bulk of their mass is assembled through subsequent dry mergers. On the other hand, the brightest galaxies in control groups were not as massive as those in fossils, and the differences in magnitude with the second-, third-, and fourth-ranking galaxies were not as large as in fossils; therefore, after the merger event that they have also experienced at around z ~ 0.3, the magnitude gap is not as affected as in fossils.
The different luminosity sampling of fossil and control groups at early times could be a consequence of different merging histories before the period of time analysed in this work (≳8 Gyr). Burke & Collins (2013) analysed the brightest galaxies of clusters at z ~ 1 and demonstrated that similar mass clusters have very different merging histories. They also stated that both major and minor mergers were more common in the past. Therefore, we suggest that these merging scenarios must have been more efficient in fossils than in controls, where the two brightest central galaxies have accreted their bright companions, leading to more suitable initial conditions to the formation of the large magnitude gap at later times. Moreover, according to these arguments, it is not probable that control groups will eventually develop a large magnitude gap from merging since the rate of mergers at later times is much lower. This scenario reinforces the idea that fossil groups are a different type of systems.
Second, we studied the faint galaxy population (−16 ≤ Mr−5log (h) ≤ −11) in fossil and control groups by analysing their number density profiles around the group centres. We observed that at z = 0, fossil systems show a very similar galaxy density profile of faint galaxies when compared with their corresponding control samples. Nevertheless, when analysing their evolution with time, some differences between faint galaxies in fossil and control groups stood out: at earlier times (z ≳ 0.7), the population of faint galaxies in fossil systems is denser than observed in control groups in a wide range of distances to the centre. At later times (0.3 ≲ z ≲ 0.5), the previous trends are reversed, and control groups appears to be denser than fossil systems. In the same period of time, the mean number of faint galaxies in fossil groups remains roughly constant, while in control groups it continues growing. This almost constant number of faint galaxies observed in fossils could be a consequence of a strong decrease of the accretion rate of faint galaxies at these redshifts. For z ≲ 0.2, the mean number of faint galaxies in fossil systems grows to finally reach the values observed in control groups at z = 0. This later result agrees with the observational work of Lieder et al. (2013), who found a normal abundance of faint satellites in the NGC 6482 fossil group. This rapid growth in the number of faint galaxies could be a consequence of a smaller number of missing galaxies in fossils.
Gozaliasl et al. (2014) analysed the number of galaxies in the range of magnitudes between −18 to −16 that inhabit fossil and normal groups in the MS-I simulation and found no evolution in this population in fossil groups, while they observed an increase of ~40% in normal groups towards low redshifts. In this work, we extended their analysis to fainter galaxies and found that the number of faint galaxies grows in both fossils and controls since z ~ 1 to the present day, although this growth occurred in different ways, as we explained above.
We conclude that using either of the two different criteria to define fossil systems does not have a very strong effect on the evolution of the brightest or faintest populations. We confirm that the definition of Dariush et al. (2010) allows detecting systems that became fossils earlier, and the assembly time of its brightest galaxy occurred before the brightest galaxy that inhabits fossil groups selected with the classical definition of Jones et al. (2003).
The predictions presented in this work need to be confirmed when more observational data including fainter galaxies are available, and/or when larger high-resolution semi-analytical galaxy samples for different models of galaxy formation are released.
We introduced a shift in the M∗ parameter to account for the shift to z = 0.1 that these authors used. According to Blanton et al. (2005), r = r0.1−0.22.
Acknowledgments
The Millennium Simulation databases used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory (GAVO). We thank Qi Guo for allowing public access for the outputs of her very impressive semi-analytical model of galaxy formation. This work has been partially supported by Consejo Nacional de Investigaciones Científicas y Técnicas de la República Argentina (CONICET) and the Secretaría de Ciencia y Tecnología de la Universidad de Córdoba (SeCyT).
References
- Aguerri, J. A. L., Girardi, M., Boschin, W., et al. 2011, A&A, 527, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berlind, A. A., Frieman, J., Weinberg, D. H., et al. 2006, ApJS, 167, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bertone, S., De Lucia, G., & Thomas, P. A. 2007, MNRAS, 379, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Lupton, R. H., Schlegel, D. J., et al. 2005, ApJ, 631, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Springel, V., White, S. D. M., Jenkins, A., & Lemson, G. 2009, MNRAS, 398, 1150 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, C., & Collins, C. A. 2013, MNRAS, 434, 2856 [NASA ADS] [CrossRef] [Google Scholar]
- Cypriano, E. S., Mendes de Oliveira, C. L., & Sodré, Jr., L. 2006, AJ, 132, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Dariush, A., Khosroshahi, H. G., Ponman, T. J., et al. 2007, MNRAS, 382, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Dariush, A. A., Raychaudhury, S., Ponman, T. J., et al. 2010, MNRAS, 405, 1873 [NASA ADS] [Google Scholar]
- Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Giménez, E., Muriel, H., & Mendes de Oliveira, C. 2008, A&A, 490, 965 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-Giménez, E., Zandivarez, A., Proctor, R., Mendes de Oliveira, C., & Abramo, L. R. 2011, A&A, 527, A129 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Onghia, E., & Lake, G. 2004, ApJ, 612, 628 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., Sommer-Larsen, J., Romeo, A. D., et al. 2005, ApJ, 630, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Baugh, C. M., Cole, S., et al. 2004, MNRAS, 348, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Aguerri, J. A. L., De Grandi, S., et al. 2014, A&A, 565, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gozaliasl, G., Khosroshahi, H. G., Dariush, A. A., et al. 2014, A&A, 571, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Angulo, R. E., et al. 2013, MNRAS, 428, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, L. R., Ponman, T. J., Horton, A., et al. 2003, MNRAS, 343, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., Maughan, B. J., Ponman, T. J., & Jones, L. R. 2006a, MNRAS, 369, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., Ponman, T. J., & Jones, L. R. 2006b, MNRAS, 372, L68 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Lieder, S., Mieske, S., Sánchez-Janssen, R., et al. 2013, A&A, 559, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendes de Oliveira, C. L., Cypriano, E. S., & Sodré, Jr., L. 2006, AJ, 131, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Mendes de Oliveira, C. L., Cypriano, E. S., Dupke, R. A., & Sodré, Jr., L. 2009, AJ, 138, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez-Abreu, J., Aguerri, J. A. L., Barrena, R., et al. 2012, A&A, 537, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Böhringer, H., Romaniello, M., & Voges, W. 2005, A&A, 433, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Proctor, R. N., de Oliveira, C. M., Dupke, R., et al. 2011, MNRAS, 418, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Sales, L. V., Navarro, J. F., Lambas, D. G., White, S. D. M., & Croton, D. J. 2007, MNRAS, 382, 1901 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, W. A., Mendes de Oliveira, C. L., & Sodré, Jr., L. 2007, AJ, 134, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- von Benda-Beckmann, A. M., D’Onghia, E., Gottlöber, S., et al. 2008, MNRAS, 386, 2345 [NASA ADS] [CrossRef] [Google Scholar]
- Vulcani, B., De Lucia, G., Poggianti, B. M., et al. 2014, ApJ, 788, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, G. 1995, ApJS, 98, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Zandivarez, A., & Martínez, H. J. 2011, MNRAS, 415, 2553 [NASA ADS] [CrossRef] [Google Scholar]
- Zandivarez, A., Díaz-Giménez, E., Mendes de Oliveira, C., et al. 2014, A&A, 561, A71 [Google Scholar]
- Zarattini, S., Barrena, R., Girardi, M., et al. 2014, A&A, 565, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zarattini, S., Aguerri, J. A. L., Sánchez-Janssen, R., et al. 2015, A&A, 581, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Number of faint galaxies in the composite clusters at each different evolutionary stage.
All Figures
 |
Fig. 1 Distribution of properties of the semi-analytic galaxy groups: 3D virial radius (top left panel), 3D velocity dispersion (middle left panel), virial mass (bottom left panel), ratio between stellar mass in bulge and total stellar mass of the first-ranked galaxy (top right panel), difference between the r-band absolute magnitude of the first- and second-ranked galaxies within half a virial radius (middle right panel), and difference between the r-band absolute magnitude of the first- and fourth-ranked galaxies within half a virial radius (middle right panel). Empty histograms correspond to FoF groups with 10 or more galaxy members, while grey histograms correspond to the 102 FoF groups that have virial masses higher than 1013.5h-1ℳ⊙ and whose brightest galaxy is an elliptical galaxy (ℳ∗1,bulge/ ℳ∗1,total> 0.7). |
| In the text | |
 |
Fig. 2 Luminosity function of galaxies in groups. The solid line is the luminosity function for semi-analytical galaxies in groups with virial masses higher than 1013.5h-1ℳ⊙ and whose brightest galaxy is an elliptical galaxy. Grey region show the results for galaxies in groups in the SDSS DR7 obtained by Zandivarez & Martínez (2011). Upper and lower arrows represent the faint end slope of the luminosity function obtained by Popesso et al. (2005) and Zarattini et al. (2015), while middle arrow correspond to the value obtained in this work. |
| In the text | |
 |
Fig. 3 Evolution of the median properties of fossil and control groups. The left plots correspond to the sample of fossils and controls defined using the ΔM12 magnitude gap, while the right plots correspond to the definition based on the ΔM14 magnitude gap. Panels in the first row show the evolution of the r-band absolute magnitude of the brightest galaxy of the groups; the second row shows the absolute magnitude of the second and fourth brightest galaxies; the third, fourth, and fifth rows show the evolution of the r-band absolute magnitude gap between the brightest and the second, third, and fourth brightest galaxies, respectively, the dashed horizontal lines correspond to the thresholds used to define fossil groups; the sixth row shows the stellar mass of the brightest galaxy, and the last row shows the evolution of the stellar mass of the brightest galaxy normalised to its final stellar mass. Error bands are the semi-interquartile ranges. |
| In the text | |
 |
Fig. 4 Number density profiles of faint galaxies in fossil and control groups. The upper panel shows the number density of faint galaxies in fossils F12 and control C12 groups as a function of the 3D normalised distance to the centre of the groups. The lower panel shows the same situation as in the top panel for fossils F14 and control C14 groups. Error bars are computed using the bootstrap resampling technique. Inset panels show the ratio between the number density profiles in fossils and controls. Error bars are computed via error propagation. |
| In the text | |
 |
Fig. 5 Ratios of number density profiles of faint galaxies in fossil and control groups at different evolutionary stages. The left plot shows the evolution of the ratio between the number density of faint galaxies in fossil F12 and control C12 groups as a function of the 3D normalised distance to the centre of the group. The right plot shows the same, but using fossils F14 and control C14. |
| In the text | |
 |
Fig. 6 Left plot: mean number of faint galaxies in fossils (solid lines) and controls (dashed lines) as a function of redshift. The upper panel shows the evolution observed in groups defined using the ΔM12 criterion, while lower panel corresponds to groups identified according to the ΔM14 criterion. Error bars are computed using the bootstrap resampling technique. The inset panels show the ratio between the mean number of faint galaxies in fossil and control groups. Right plot: mean number of faint galaxies classified as new members (upper panels) or lost members (lower panels). Error bars are computed using the error propagation formula. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


