| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527255 | |
| Published online | 03 February 2016 | |
Monte Carlo simulations of intensity profiles for energetic particle propagation
1 Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstraße 36, 10623 Berlin, Germany
e-mail: robert.c.tautz@gmail.com
2 Department of Physics and Astronomy, University of Manitoba, Winnipeg, Manitoba R3T 2N2, Canada
e-mail: andreasm4@yahoo.com
Received: 26 August 2015
Accepted: 24 November 2015
Aims. Numerical test-particle simulations are a reliable and frequently used tool for testing analytical transport theories and predicting mean-free paths. The comparison between solutions of the diffusion equation and the particle flux is used to critically judge the applicability of diffusion to the stochastic transport of energetic particles in magnetized turbulence.
Methods. A Monte Carlo simulation code is extended to allow for the generation of intensity profiles and anisotropy-time profiles. Because of the relatively low number density of computational particles, a kernel function has to be used to describe the spatial extent of each particle.
Results. The obtained intensity profiles are interpreted as solutions of the diffusion equation by inserting the diffusion coefficients that have been directly determined from the mean-square displacements. The comparison shows that the time dependence of the diffusion coefficients needs to be considered, in particular the initial ballistic phase and the often subdiffusive perpendicular coefficient.
Conclusions. It is argued that the perpendicular component of the distribution function is essential if agreement between the diffusion solution and the simulated flux is to be obtained. In addition, time-dependent diffusion can provide a better description than the classic diffusion equation only after the initial ballistic phase.
Key words: plasmas / diffusion / methods: numerical / turbulence
© ESO, 2016
1. Introduction
The interplanetary medium has been, and continues to be, one of the most interesting plasmas to be studied both experimentally and theoretically. The main reasons are that the heliosphere is accessible to in situ measurements by spacecrafts, and that Earth-bound observations can be done at relatively low cost. A prominent example of such investigations are solar energetic particles (e.g., Lario et al. 2013), which are not only interesting for basic research, but which also affect us economically via the so-called space weather (see Scherer et al. 2005, for an introduction).
In the past 50 years, considerable effort has been put into the determination and prediction of energetic particle propagation in the turbulent solar wind. Accordingly, intensity profiles have been fitted to many models on a variety of refinement levels. These include transport equations – such as Parker’s (1965) transport equation or the Roelof (1969) equation – that are based on diffusion and convection (e.g., Gombosi & Owens 1981; Palmer 1982; Dröge & Kartavykh 2009; Artmann et al. 2011). In essence, a diffusive behavior of the energetic particles has been assumed so that the diffusion coefficients are free fit parameters.
Since the 1990s, numerical test-particle simulations have been used as an alternative method to determine diffusion coefficients (e.g., Michałek & Ostrowski 1996; Giacalone & Jokipii 1999; Laitinen et al. 2013; Tautz & Dosch 2013, and references therein). Because kinetic plasma theory has shown that the resulting diffusion coefficients depend sensitively on electromagnetic turbulence (see Schlickeiser 2002; Shalchi 2009, for an introduction), the diffusion coefficients can then be used to extract information about the nature of the turbulent interplanetary medium.
However, a careful inspection especially of early analytical transport theories such as quasi-linear theory (Jokipii 1966) reveals that, depending on the level of approximation, invalid results are found (e.g., Tautz et al. 2006). Exceptions are the second-order quasi-linear theory (Shalchi 2005; Tautz et al. 2008b) and the unified nonlinear theory (Shalchi 2010, 2015), which show remarkable agreement with simulations. Every additional turbulence effect that is included in an analytical description has the potential to significantly alter the results.
Accordingly, the importance of a detailed understanding of the solar wind turbulence cannot be overstated, and many models have tried to incorporate (i) the anisotropy between the directions parallel to and perpendicular to the mean magnetic field (e.g., Bieber et al. 1996; Matthaeus et al. 1990); (ii) dynamical effects (Saur & Bieber 1999; Belcher & Davis 1971); (iii) the effects of intermittency (Osman et al. 2012; Wang et al. 2014); and (iv) the dissipation of magnetic structures (Coleman Jr. 1968; Hahn & Savin 2013; Sahraoui et al. 2009).
In recent decades, however, it was realized that the transport of energetic charged particles in a turbulent magnetized medium is not always diffusive. This so-called anomalous diffusion refers to a time-dependent diffusion coefficient in the form κ ∝ tγ and is characterized as subdiffusive (γ< 1) and superdiffusive (γ> 1). Subdiffusive and sometimes superdiffusive behavior has been found on many occasions (e.g., Qin et al. 2002; Zimbardo et al. 2006; Shalchi & Kourakis 2007; Tautz 2010b; Tautz & Shalchi 2010). New theoretical models are able to take these effects into account (e.g., Zimbardo 2005; Pommois et al. 2007; Shalchi et al. 2011), but that leads to considerably more complicated expressions for the diffusion coefficients. Matters only become worse if other than the most basic turbulence models are considered. Explanations of this so-called anomalous transport in terms of the physical origin range from particles back-tracing their magnetic field lines in the case of magnetostatic turbulence – which is indeed the foundation of the compound diffusion model (e.g., Kóta & Jokipii 2000; Webb et al. 2006; Tautz et al. 2008a) – to Lévy flights in the case of intermittent turbulent structures (e.g., Zimbardo 2005).
In this article, the two approaches of determining diffusion coefficients – via the mean-square displacement of test particles and via the fit of intensity profiles – will be combined for the first time. Using the Monte Carlo simulation code Padian that was developed by Tautz (2010a), diffusion coefficients can be determined from the mean-square displacement of test particles moving in magnetic turbulence. At the same time, intensity profiles or, equivalently, the particle flux can be recorded at a given distance from the particle source. The directional-averaged intensity profiles obtained in this way are then compared to diffusion models with the diffusion coefficients either as fit parameters or as obtained directly from the simulations. In essence, the approach allows for the simulation of time profiles in a situation where the exact diffusion coefficients are already known.
In addition, the pitch-angle dependence of the incoming particles can also be resolved. This can be used for two reasons: (i) to trace the isotropization, which allows a comparison with theoretical expectations and analytical calculations (e.g., Dröge & Kartavykh 2009), and (ii) to compare simulation results directly to sector data, e.g., on the EPAC instrument (Keppler et al. 1995) on board the Ulysses spacecraft (Keppler et al. 1992) and the Low-Energy Charged Particle instrument on board Voyager 1 (see, e.g., Decker et al. 2012, for a recent application).
The paper is organized as follows. In Sect. 2, the numerical Monte Carlo code is described that will be used to evaluate the trajectories of test particles under the influence of a turbulent magnetic field. The numerical techniques required to record the flux at a given distance from the particle source are described in Sect. 3. In Sect. 4, results will be shown and the possible agreement with the solution of a generalized diffusion equation will be discussed. In Sect. 5, a summary of the results and a discussion of further applications conclude this paper.
2. PADIAN test-particle code
For the numerical simulations, the Padian Monte Carlo code (Tautz 2010a) is used to compute the parallel and perpendicular diffusion coefficient and the time profiles of energetic particles. For the turbulent electromagnetic fields the Fourier superposition model is used (Batchelor 1982; Giacalone & Jokipii 1999; Tautz & Dosch 2013), which allows the use of a power spectrum that is based on observations and/or turbulence theory. The geometry of the turbulent fields, which are superimposed on a homogeneous mean magnetic field B0, is assumed to be isotropic so that no preferred direction exists for the wave vectors of the Fourier components. The corresponding generation of turbulent magnetic fields proceeds as (Tautz & Dosch 2013) ![\begin{equation} \label{eq:dB} \delta\f B(\f r,t)=\sum_{n=1}^N\f e'_\perp A(k_n)\cos\left[k_nz'+\beta_n-\omega(k_n)t\right], \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq4.png) (1)where β is a random phase angle and where the primed coordinates are obtained from a rotation with random angles. This also allows more realistic turbulence geometries based on the observed anisotropies in the solar wind to be included (e.g., Bieber et al. 1996; Matthaeus et al. 1990; Rausch & Tautz 2013).
(1)where β is a random phase angle and where the primed coordinates are obtained from a rotation with random angles. This also allows more realistic turbulence geometries based on the observed anisotropies in the solar wind to be included (e.g., Bieber et al. 1996; Matthaeus et al. 1990; Rausch & Tautz 2013).
The wavenumbers kn are distributed logarithmically in the interval 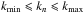 . For the minimum and maximum wavenumbers included in the turbulence generator, the following considerations apply: (i) the resonance condition states that there has to be a parallel wavenumber k∥ so that RLμk∥ = 1 with μ = cos∠(v,B0) and where RL denotes the particle’s Larmor radius. Thus, scattering predominantly occurs when a particle can interact with a wave mode over a full gyration cycle; (ii) the scaling condition requires that RLΩrelt<Lmax, where Ωrel = qB/ (γmc) is the relativistic gyrofrequency and where Lmax ∝ 1 /kmin is the maximum extension of the system, which is given by the lowest wavenumber (for which one has kmin = 2π/λmax, thereby proving the argument). In practice, the second condition determines the minimum wavenumber, while the first determines the maximum wavenumber. Here, values are chosen as kminℓ0 = 10-5 and kmaxℓ0 = 103, where ℓ0 is the turbulence bend-over scale. The sum in Eq. (1)extends over N = 512 wave modes, which is sufficient (Tautz & Dosch 2013) and yet saves computation time. Furthermore, the maximum simulation time is determined as vtmax/ℓ0 = 102, which – by using the simulation time normalized in this way – has the advantage that the behavior of the scattering parameters becomes mostly independent of the particle energy.
. For the minimum and maximum wavenumbers included in the turbulence generator, the following considerations apply: (i) the resonance condition states that there has to be a parallel wavenumber k∥ so that RLμk∥ = 1 with μ = cos∠(v,B0) and where RL denotes the particle’s Larmor radius. Thus, scattering predominantly occurs when a particle can interact with a wave mode over a full gyration cycle; (ii) the scaling condition requires that RLΩrelt<Lmax, where Ωrel = qB/ (γmc) is the relativistic gyrofrequency and where Lmax ∝ 1 /kmin is the maximum extension of the system, which is given by the lowest wavenumber (for which one has kmin = 2π/λmax, thereby proving the argument). In practice, the second condition determines the minimum wavenumber, while the first determines the maximum wavenumber. Here, values are chosen as kminℓ0 = 10-5 and kmaxℓ0 = 103, where ℓ0 is the turbulence bend-over scale. The sum in Eq. (1)extends over N = 512 wave modes, which is sufficient (Tautz & Dosch 2013) and yet saves computation time. Furthermore, the maximum simulation time is determined as vtmax/ℓ0 = 102, which – by using the simulation time normalized in this way – has the advantage that the behavior of the scattering parameters becomes mostly independent of the particle energy.
The polarization vector obeys the condition 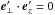 , where the primed coordinates are determined via a rotation matrix with random angles so that k has a random direction for each wave mode. Alternatively, the inclusion of plasma waves is in principle possible through a dispersion relation ω(k); here, however, magnetostatic turbulence is used with ω ≡ 0.
, where the primed coordinates are determined via a rotation matrix with random angles so that k has a random direction for each wave mode. Alternatively, the inclusion of plasma waves is in principle possible through a dispersion relation ω(k); here, however, magnetostatic turbulence is used with ω ≡ 0.
The amplitude function, 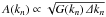 , is proportional to the square root of the turbulence power spectrum, G(k), for which a kappa-type function is used (Shalchi & Weinhorst 2009) as
, is proportional to the square root of the turbulence power spectrum, G(k), for which a kappa-type function is used (Shalchi & Weinhorst 2009) as ![\begin{equation} \label{eq:spect} G(k)\propto\frac{\abs{\ell_0k}^q}{\left[1+(\ell_0k)^2\right]^{(s+q)/2}}, \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq27.png) (2)with q = 0 for simplicity and to ensure the comparability with earlier results1. The turbulence bend-over scale, ℓ0 ≈ 0.03 au, reflects the transition from the energy range G(k) ∝ kq to the Kolmogorov-type inertial range, where G(k) ∝ k− s with s = 5/3 (Kolmogorov 1941; Bruno & Carbone 2005). A normalization factor relates the integral over the spectrum to the mean turbulence strength, but is omitted here because Eq. (1)has been designed so that the turbulent field has the correct strength. We note that there are no actual boundary conditions; however, care should be taken that particles travel no further than the maximum distance
(2)with q = 0 for simplicity and to ensure the comparability with earlier results1. The turbulence bend-over scale, ℓ0 ≈ 0.03 au, reflects the transition from the energy range G(k) ∝ kq to the Kolmogorov-type inertial range, where G(k) ∝ k− s with s = 5/3 (Kolmogorov 1941; Bruno & Carbone 2005). A normalization factor relates the integral over the spectrum to the mean turbulence strength, but is omitted here because Eq. (1)has been designed so that the turbulent field has the correct strength. We note that there are no actual boundary conditions; however, care should be taken that particles travel no further than the maximum distance 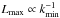 , beyond which the turbulent magnetic field pattern would repeat itself.
, beyond which the turbulent magnetic field pattern would repeat itself.
From the integration of the Newton-Lorentz equation and by averaging over an ensemble of particles, the diffusion coefficients can be calculated by determining the mean square displacement as 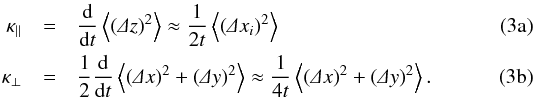 The scattering mean-free path in the direction parallel to the background magnetic field can then be obtained as λ∥ = 3κ∥/v ≈ ⟨ (Δz)2 ⟩ /(2vt) for large t.
The scattering mean-free path in the direction parallel to the background magnetic field can then be obtained as λ∥ = 3κ∥/v ≈ ⟨ (Δz)2 ⟩ /(2vt) for large t.
 |
Fig. 1 Sample trajectories starting from the rectangular blue region with an initial pitch-angle cosine of μ0 = 1, hence moving in the positive z direction. The target region is shown as the small red dot at [x,y,z] = [0,0,10]. |
 |
Fig. 2 Intensity profile for particles with rigidities R = 10-1 and a distance between the particle source and the detector of L = 100ℓ0 in linear (upper panel) and logarithmic (lower panel) units. In the SPH kernel according to Eq. (4), the base smoothing length is varied between h = 0.5ℓ0 and 3ℓ0 (see legend). An additional influence on the smoothness of the curve can be obtained through the detector size. As illustrated, the smoothing length modifies the fluctuation of the intensity profile but otherwise leaves the underlying structure unchanged. |
3. Intensity and anisotropy-time profiles
In Fig. 1, a representative sample of particle trajectories is illustrated for typical particle energies ranging from 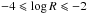 with R = γv/ (Ωℓ0) a normalized rigidity variable that is per default used in the Padian code (Tautz 2010a). All test particles – typically from 105 up to 107 – are injected instantaneously at time t = 0 with random initial positions inside a cubic region with an edge length of 0.1ℓ0. Accordingly, all length scales are normalized to the turbulence bend-over scale, ℓ0, and two dimensionless times are introduced as Ωt and vt/ℓ0. The relative strength of the isotropic turbulent magnetic fields are chosen as (δB/B0)2 = 0.1 with B0 the background magnetic field strength. In the solar wind we note that values of up to δB/B0 = 1 have been observed. Therefore, a relative turbulence strength of 0.1 is an acceptable compromise between the particles still moving predominantly along the mean magnetic field (which is helpful in order to obtain good statistics) and a sufficiently strong stochastic motion. In the range
with R = γv/ (Ωℓ0) a normalized rigidity variable that is per default used in the Padian code (Tautz 2010a). All test particles – typically from 105 up to 107 – are injected instantaneously at time t = 0 with random initial positions inside a cubic region with an edge length of 0.1ℓ0. Accordingly, all length scales are normalized to the turbulence bend-over scale, ℓ0, and two dimensionless times are introduced as Ωt and vt/ℓ0. The relative strength of the isotropic turbulent magnetic fields are chosen as (δB/B0)2 = 0.1 with B0 the background magnetic field strength. In the solar wind we note that values of up to δB/B0 = 1 have been observed. Therefore, a relative turbulence strength of 0.1 is an acceptable compromise between the particles still moving predominantly along the mean magnetic field (which is helpful in order to obtain good statistics) and a sufficiently strong stochastic motion. In the range 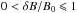 , it is to be expected that the results do not vary apart from some rescaling.
, it is to be expected that the results do not vary apart from some rescaling.
The anisotropy-time profile is then measured at a virtual spherical detector (red dot in Fig. 1), the position of which can be varied. In what follows the numerical technique will be described that allows the evaluation of time profiles, which will then be compared to solutions of the generalized diffusion equation in Sect. 4.
3.1. SPH smoothing
Within the test-particle simulations, a time profile can, in principle, be obtained by counting the rate of particles crossing the surface of a particular region of space (called the “detector”). However, due to limitations of computational power, the particle flux at any reasonable distance between the common particle origin and the detector would be too low even for 107 particles because perpendicular scattering, albeit weak, significantly reduces the number of particles arriving at the detector. A naive solution would be to increase the detector size drastically, in which case however much of the fine structure would be either lost or smeared out. In addition, the onset time would be significantly reduced if the detector size is too large.
Alternatively, the following will be inspired by the smoothed particle hydrodynamics (SPH) approach (e.g., Vaughan et al. 2008; Springel 2010). The basic idea is that all computational particles are no longer treated as pointlike physical particles. Instead, each computational particle represents an ensemble of real particles that is distributed smoothly over a defined region. A typical density distribution (the so-called SPH kernel) is given by 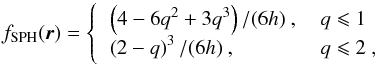 (4)and zero otherwise, where q = | r−rtarget | /h with h the smoothing length. Such a distribution is similar in shape to a Gaussian distribution, but at the same time avoids the problem of a finite density even at very large distances.
(4)and zero otherwise, where q = | r−rtarget | /h with h the smoothing length. Such a distribution is similar in shape to a Gaussian distribution, but at the same time avoids the problem of a finite density even at very large distances.
To avoid the problem of continuously decreasing fluxes for increasing distances, the detector (or target region) generally scales with the distance between target and particle origin. As shown in Fig. 2, a larger smoothing length is able to filter the high-frequency fluctuations effectively, while leaving the overall shape of the intensity profile unchanged.
In addition, it should be noted that, for a relatively small detector size such as that used in Fig. 2, almost no signal would be visible without the SPH ansatz. Therefore, it is precisely this method that allows for the generation of intensity profiles at all, even though some of the curves look rather noisy.
 |
Fig. 3 Intensity-time profiles for particles with rigidities R = 1 and a distance between the particle source and the detector of L = 10ℓ0. The effect is shown of a detector position being either along the same field line with the particle source (angle of 0°) up to a detector perpendicular to the source field line (angle of 90°). |
3.2. Sample results
For the evaluation of a sample time profile, a distance of L = 100ℓ0 (which roughly corresponds to ≈45 × 107 km) was chosen between the particle source and the detector. The target size is d = 0.1ℓ0, thus representing a compromise between the ratio of distance to target size being at least 1000 times smaller than L, but at the same time able to accumulate a sufficiently large number of particles. The SPH smoothing length is chosen so that each numerical particle represents a particle ensemble that is distributed over 10–60 times the detector size according to Eq. (4).
In Fig. 2, a typical intensity profile is shown and the effect of the SPH approach is illustrated. This technique is necessary to reduce the noise that arises from the relatively low number of simulated particles. The actual total counts (fluence) can be as low as <10 for a low rigidity and <100 for the highest rigidities considered. In general, it can be found that particles with higher energies arrive earlier, even though they experience significantly stronger scattering.
If the detector position is not along the same field line as the particle origin – which in reality should be the rule rather than the exception – the count rates are strongly reduced and the shape of the intensity profile is changed as well. In Fig. 3 this effect is illustrated for detector positions varying between 0° (i.e., being along the field line of the particle source) or 90° (i.e., being perpendicular to it). For such particles, it takes longer to begin reaching the detector (cf. Qin et al. 2011). Even though a small distance between the particle source and the detector and a relatively high particle energy are chosen for the example shown, 107 test particles were required in order to resolve the intensity profiles at large angles.
 |
Fig. 4 Pitch-angle dependent intensity profile for particles with a normalized rigidity R = 10-2 in arbitrary but linear units. Shown is the flux of particles arriving at the detector with μ ranging from + 1 (i.e., coming from the direction of the source) to − 1 (coming from the far side of the source). |
3.3. Pitch-angle dependency and anisotropy
Normally, the limited number of simulated particles does not allow the pitch-angle dependence of the incoming particles to be resolved, at least not in the form of a two-dimensional intensity profile. Therefore, a tool such as the SPH kernel is mandatory as it allows a broad density distribution to be assigned to an otherwise point-like particle.
In the literature, a commonly used measure is the time-dependent anisotropy (e.g., Schlickeiser et al. 2009), which is defined via the first moment in the pitch-angle cosine as 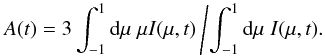 (5)Here, I(μ,t) is the pitch-angle-dependent distribution function, which is obtained for each μ value with the help of SPH smoothing. The so-defined anisotropy function provides a powerful diagnostics tool that enables heliospheric particle scattering parameters such as diffusion coefficients and mean-free paths as well as drift coefficients to be probed (e.g., Dröge 2005; Schlickeiser et al. 2009). In addition, the anisotropy can be related to a spatial gradient of the particle density (Schlickeiser 1989; Shalchi et al. 2009).
(5)Here, I(μ,t) is the pitch-angle-dependent distribution function, which is obtained for each μ value with the help of SPH smoothing. The so-defined anisotropy function provides a powerful diagnostics tool that enables heliospheric particle scattering parameters such as diffusion coefficients and mean-free paths as well as drift coefficients to be probed (e.g., Dröge 2005; Schlickeiser et al. 2009). In addition, the anisotropy can be related to a spatial gradient of the particle density (Schlickeiser 1989; Shalchi et al. 2009).
The pitch-angle dependent time profile together with the asymmetry defined in Eq. (5)are shown in Figs. 4 and 5, respectively. The result confirms the obvious expectations that, during the initial burst, particles predominantly arrive from the direction of the source. For later times the asymmetry remains positive, which emphasizes that there are always more particles moving outward.
By repeating the simulation for different particle rigidities varying between R = 10-2 and R = 1 and by noting the results shown in Fig. 5, it can be seen that
-
low-energy particles arrive predominantly from the direction of the source (i.e., A> 0) for a long time;
-
at short distances, high-energy particles have a higher probability of being backscattered behind the detector (i.e., A → 0);
-
in the limit of large times, particles tend to fill space homogeneously and move isotropically.
 |
Fig. 5 Anisotropy as obtained by taking the first and zeroth moment of the SPH profiles according to Eq. (5). For particles with different rigidities (see panel titles), the time scales are dramatically different. |
4. Time-dependent diffusion
In this section, the interpretations of the time profiles that are obtained from the virtual detector within the Padian simulation will be discussed. As is shown, the comparison of a recorded intensity profile to a solution of the diffusion equation can be impeded by two main factors: (i) the early phase cannot be correctly described by a diffusion approach and (ii) the diffusion coefficients of cosmic-ray scattering are often time-dependent also for late times. The first factor has been widely acknowledged and, accordingly, other theoretical descriptions are in use (e.g., Laitinen et al. 2013; Effenberger & Litvinenko 2014).
The second factor is illustrated in Fig. 6 and shows first the initial ballistic phase with free particle motion so that κ ∝ t. After that, either the typically diffusive or sometimes superdiffusive (for parallel transport) or mostly subdiffusive (for perpendicular transport) phases are reached. If turbulent electric fields were to be included that arise, for instance, in Alfvénic turbulence (Lee & Völk 1975; Achterberg 1981; Michałek & Ostrowski 1996), a superdiffusive behavior would be found (Tautz 2010b) that can be explained with the stochastic acceleration of particles as a result of momentum diffusion (e.g., Tautz et al. 2013, and references therein).
In what follows, the three-dimensional diffusion equation with time-dependent coefficients (see Appendix A), ![\begin{equation} \label{eq:deq} \pd[f_{\text{Diff}}]t=\left[\f\kappa(t)\cdot\nabla\right]\cdot\nabla f_{\text{Diff}}, \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq78.png) (6)is employed, which is the simplest extension of the usual diffusion equation. In the diffusion tensor, the off-diagonal drift coefficients (see, e.g., Tautz & Shalchi 2012) is neglected, as these are important only for non-turbulent and curved background magnetic fields (see the discussion in Appendix A). Therefore, the form κ = diag(κ⊥,κ⊥,κ∥) is employed, with all coefficients being functions of time.
(6)is employed, which is the simplest extension of the usual diffusion equation. In the diffusion tensor, the off-diagonal drift coefficients (see, e.g., Tautz & Shalchi 2012) is neglected, as these are important only for non-turbulent and curved background magnetic fields (see the discussion in Appendix A). Therefore, the form κ = diag(κ⊥,κ⊥,κ∥) is employed, with all coefficients being functions of time.
 |
Fig. 6 Example for the parallel (upper panel) and perpendicular (lower panel) diffusion coefficients. During the ballistic phase, the diffusion coefficients grow almost linearly in time, whereas for late times the parallel diffusion coefficient becomes almost constant. For the parallel diffusion coefficient, the transition is marked for later use by the vertical dashed line. In addition, the dot-dashed line illustrates a late superdiffusive phase with κ∥ ∝ t0.31, which has been observed for Alfvénic turbulence due to stochastic acceleration of the particles (cf. Tautz 2010b). Here, in contrast, a magnetostatic model is used, for which the solid line is found. The perpendicular diffusion coefficients, in contrast, become slightly subdiffusive in agreement with earlier results. For later use, the late-time behavior is fitted to a power law. The slope sensitively depends on the properties of the magnetic turbulence (see Tautz & Shalchi 2010) and the particle rigidity (here, R = 10-2). |
Together with the initial condition fDiff(x,y,z,t = 0) = δ3(x,y,z), the solution to Eq. (6)provides the time profile function fDiff(x,y,z,t). We note that, owing to the finite size of the source region, the point-source solution in Eq. (6)would have to be convolved with the shape of the source region. However, it turns out that the resulting corrections are negligible because of the small extension of the source region. The relevant fits that will be shown are (i) the solution of the three-dimensional diffusion equation with the time-dependent diffusion coefficients, κ(t), obtained from the simulations via the mean-square displacements and (ii) the solution of the three-dimensional diffusion equation with constant diffusion coefficients, κ(tmax), i.e., the values at the end of the simulations.
 |
Fig. 7 Time profile (intensity profile) in arbitrary linear units for particles with variable energies (see subplot titles). The distance between the particle origin and the virtual detector is L = 10ℓ0. The various curves are as follows: The black lines show the profile as obtained from the simulations using the methods described in Sect. 3. The red lines show the three-dimensional diffusion solution (with the normalization factor as an open parameter) from Eq. (7)using the diffusion coefficients as obtained from the simulations via the mean-square displacements. In addition, the result from Eq. (8)is shown for constant diffusion coefficients taken from the simulations (blue lines), i.e., κi(t = tmax). |
4.1. Detector at small distances
If for the case of instantaneous injection the distance between the particle source and the detector is small, the particles will still be in the ballistic phase, where κ ∝ t, when the intensity profile reaches its maximum. The time-dependent diffusion coefficient can therefore be written in the form of a single power law, i.e., κ = ξtγ. For this case, a solution to Eq. (6)can be obtained analytically (see Appendix A) as ![\begin{equation} \label{eq:diff3D} f_{\text{Diff}}(\f r,t)=\prod_i\frac{1}{\sqrt{4\pi\xi_it^{\gamma_i+1}}}\,\exp\!\left[-\frac{\left(1+\gamma_i\right){r_i}^2}{4\xi_it^{\gamma_i+1}}\right] \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq87.png) (7)for i ∈ {x,y,z}. The diffusion coefficients are taken directly from the simulated particle trajectories via the mean-square displacement, see Eq. (3), as κi = ⟨(Δri)2⟩/ (2t) with i ∈ { x,y,z } and are then fitted to a power law. In practice, this is done by applying a linear regression to the logarithm of κ. It should be noted, however, that this fit is not always unique because, even during the initial phase, there can be some variations and irregularities especially in the perpendicular diffusion coefficients. After that, typical values are
(7)for i ∈ {x,y,z}. The diffusion coefficients are taken directly from the simulated particle trajectories via the mean-square displacement, see Eq. (3), as κi = ⟨(Δri)2⟩/ (2t) with i ∈ { x,y,z } and are then fitted to a power law. In practice, this is done by applying a linear regression to the logarithm of κ. It should be noted, however, that this fit is not always unique because, even during the initial phase, there can be some variations and irregularities especially in the perpendicular diffusion coefficients. After that, typical values are 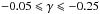 , showing that perpendicular transport is only mildly subdiffusive in isotropic turbulence (cf. Tautz & Shalchi 2010).
, showing that perpendicular transport is only mildly subdiffusive in isotropic turbulence (cf. Tautz & Shalchi 2010).
For a detector distance L = 10ℓ0, the resulting function fDiff from Eq. (7)together with the time profile recorded within the simulation are shown in Fig. 7. For both the overall shape and the peak intensity a rather poor agreement can be found, regardless of the particle rigidity. The reason is that the particle motion during the ballistic phase cannot be described in terms of a superdiffusive behavior (see Sect. 4.3).
Nevertheless, it should be noted that by neglecting the time dependence of the diffusion coefficients, there is even less agreement with the simulations. This has been checked by using the last value for the diffusion coefficient as obtained from the simulations, i.e., κi = κi(t = tmax) = const. In addition, γi = 0 is used in Eq. (7)so that fDiff corresponds to the classic diffusion solution. As shown in Fig. 7, this is clearly not an option.
 |
Fig. 8 Same as Fig. 7 but for a distance L = 100ℓ0 between the particle origin and the virtual detector. The vertical dashed lines mark the end of the initial ballistic regime as explained in Fig. 6. |
4.2. Detector at large distances
For general time-dependent diffusion coefficients, there seems to be no simple way to solve Eq. (6)analytically (Appendix A). Therefore, a numerical approach is chosen (Appendix B). To avoid the numerically challenging solution in three spatial dimensions, the perpendicular diffusion coefficients are assumed to follow a single power law, which will be that at late times. This is supported by the fact that, for the purpose of this investigation, the detector is placed on the same field line as the particle source so that the contribution from perpendicular diffusion does not appear in the exponential function.
In accordance with Eq. (7), the assumed three-dimensional solution function therefore has the form ![\begin{eqnarray} &&f_{\text{Diff}}(x,y,z,t)=f\pa(z,t)\nonumber\\ &&~~~~~~~~~~~~\times\prod_i\frac{1}{\sqrt{4\pi\xi_it^{\gamma_i+1}}}\exp\!\left[-\frac{\left(1+\gamma_i\right){r_i}^2}{4\xi_it^{\gamma_i+1}}\right], \label{eq:diff3DN} \end{eqnarray}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq95.png) (8)this time for i ∈ { x,y } alone. In Eq. (8), the parallel part, f∥(z,t) is obtained by numerically integrating the one-dimensional diffusion equation with a time-dependent diffusion coefficient, κ∥(t), as described in Appendix B.
(8)this time for i ∈ { x,y } alone. In Eq. (8), the parallel part, f∥(z,t) is obtained by numerically integrating the one-dimensional diffusion equation with a time-dependent diffusion coefficient, κ∥(t), as described in Appendix B.
In Fig. 8, a comparison is shown between the intensity profile obtained within the simulations and the semi-numerical solution of Eq. (8)for a detector distance L = 100ℓ0. Depending on the particle energy, the end of the ballistic phase is reached sooner – before the peak intensity is reached – or later. It is precisely this point that decides whether the solution from Eq. (8)is in agreement with the numerical time profile. In either case, no agreement is found with the solution that uses a constant diffusion coefficient.
In Fig. 9, the extreme case is shown with a detector distance L = 1000ℓ0 corresponding to ~ 30 au; this distance is on the order of the heliosphere itself and might therefore be applicable for anomalous cosmic rays. Here, the ballistic phase ends before a noticeable fraction of the particles reaches the detector. Accordingly, the solution in Eq. (8)is able to reproduce the simulated intensity profile with good accuracy. However, only in the case of the lowest particle energy can an agreement be found with the solution that uses a constant diffusion coefficient.
 |
Fig. 9 Same as Fig. 8 but for a distance L = 1000ℓ0 between the particle origin and the virtual detector. |
4.3. Discussion
There are three points that are crucial in order to achieve agreement between the intensity profile obtained directly from the simulated particle trajectories and the solution of the generalized diffusion equation.
First, the coefficients of perpendicular diffusion are important even though they are two to four orders of magnitude smaller than the parallel diffusion coefficient. The reason is found in the three-dimensional diffusion solution, Eq. (8), in which the perpendicular components assure a certain agreement with the simulated intensity profiles. For instance, the shape of the profile is influenced by the product of the diffusion coefficients with the peak intensity being found for tmax = L2/ (6κ∥) at a position along the mean field. In the one-dimensional case, the factor 6 is replaced by 2.
Second, the ballistic phase has to be left relatively early – compared to the maximum of the intensity profile – if the intensity profile is to be described by the generalized diffusion approach. As Laitinen et al. (2013) noted, early-time particle propagation is dominated by field-line meandering instead of diffusion. The same is also seen for thermal conduction on small scales (Hu et al. 2015). This could be decided using a quantitative measure for Gaussian diffusion like the kurtosis of the field-line displacement (Zimbardo et al. 2000). Because for early times – referring to Fig. 6 – the propagation proceeds undisturbed along the magnetic field lines, it is well known that diffusion is merely a time asymptotic model. This explains the poor agreement found in Fig. 7 even for time-dependent diffusion coefficients because the particle motion is simply not diffusive. To our knowledge there is not as yet an all-encompassing theoretical description that combines all phases of particle transport.
Third, when the ballistic phase is left, the agreement nevertheless relies on a correct incorporation of the time-dependent diffusion coefficients, as is clearly shown in Figs. 8 and 9. The assumption of constant diffusion coefficients was justified only in those cases where the first particles arrived at the detector only after the transport had completely reached the diffusive regime. It can be seen from Figs. 7 and 8 that the solutions with constant diffusion coefficients might agree better with the observed profiles if they were shifted to later times. Curiously, the delay time corresponds roughly to L/ (ℓ0R), which is the time required for a direct flight from the source region to the detector. Mathematically, however, this would not be a solution of the diffusion equation.
Comparison between the values obtained for the parallel diffusion coefficients (normalized to Ω2ℓ0) obtained directly from the test-particle trajectories via the mean-square displacements (κ∥sim) in Eq. (3)and from the fit to a three-dimensional diffusion profile with constant diffusion coefficients (κ∥fit) together with their respective estimated mean errors.
If the diffusion coefficients are taken as unknown – but time-independent – the time profiles obtained from the simulations can, in some cases, be fitted to a one-dimensional diffusion solution with a constant diffusion coefficient as a fit parameter. The results are shown in Table 1 and illustrate that the fitted diffusion coefficients show no agreement with those obtained from the simulations. This emphasizes again that (i) a one-dimensional solution is not sufficient, despite the significantly smaller perpendicular diffusion coefficients; and (ii) the assumption of a constant diffusion coefficients cannot be justified and introduces significant deviations from the true values. Accordingly, care has to be taken about the correct treatment of the time-dependent diffusion.
5. Summary and conclusion
The dilute, magnetized, and turbulent plasma of the heliosphere offers the unique opportunity to investigate fundamental problems such as the transport of energetic particles in two ways. First, it is accessible to in situ observations of both particles and magnetic fields by various spacecrafts. Second, in combination with increasingly sophisticated numerical simulation techniques, it allows the critical examination of transport theories.
Throughout the last decades, there has been increasing insight into the necessity of the kinetic approach for the description of heliospheric and astrophysical plasmas. At the same time, simple heuristic approaches remain in use so that efforts needs to be focused both on the proper understanding and application of the underlying microphysics. In this paper, a connection has been established between the diffusion coefficients obtained by using numerical test-particle simulations and those derived from the observation of intensity profiles at virtual detectors in the same simulations. This approach allows us to challenge the seemingly well-established method of fitting the solution of transport equations to obtain (constant) diffusion coefficients.
In future work we will apply the method to the propagation of solar energetic particle events, which requires the incorporation of a curved mean magnetic field in the form of the Parker spiral (Ablaßmayer et al. 2015). In the context of test-particle simulations, this has already been implemented (Tautz et al. 2011). The advantage is that this approach requires no assumptions about the radial dependence of the diffusion coefficients (e.g., Sakai 2002), because they are determined by following the particles as they continue to move outward.
The investigation of solar energetic particle transport poses further challenges. As discussed, e.g., by Dresing et al. (2012), Lario et al. (2013), solar particle events can be spread over a very wide range so that a signal can be found even on the opposite side of the field line connected to the particle origin (Qin et al. 2011). Explanations range from strong particle transport perpendicular to the mean magnetic field to an extended energetic particle distribution close to the source, but a definitive answer is still elusive. Therefore, the method presented here has the potential to complement other methods, for example by solving transport equations using finite-difference or stochastic schemes (Dröge et al. 2010).
It has not escaped our attention that the methods outlined in this paper are also applicable to other scenarios. These include the propagation of galactic and anomalous cosmic rays in the outer heliosphere and the transport of galactic and extra-galactic cosmic rays in the interstellar medium. There, however, the dynamics of the turbulent magnetic fields might not be fully captured with a Fourier superposition ansatz so that direct numerical simulations of the turbulence will be required (e.g., de Avillez & Breitschwerdt 2005). In addition, the simulation setup also allows for the inclusion of moving detectors that cross large-scale and transient structures such as shock waves.
To conclude, it has been shown that anomalous transport regimes play an important role for the interpretation of intensity and, potentially, anisotropy-time profiles, if these are used to extract the diffusion coefficients parallel to and perpendicular to the mean magnetic field. The ballistic phase, however, must be left if any agreement is to be expected. The results clearly show that an extension of the diffusion ansatz is not permitted for the early ballistic phase and yields incorrect results. Even in cases when the bulk of the particles already behave diffusively (in the sense that a time-asymptotic, constant diffusion coefficient is found), in particular the perpendicular subdiffusive transport has to be considered in order to obtain the correct results. The approach constitutes the simplest analytical continuation toward the initial ballistic phase by using the diffusion approach. As shown, this is permitted if the comparison is made well beyond the ballistic phase. Whether other analytical approaches such as the telegraph equation (e.g., Litvinenko & Schlickeiser 2013; Effenberger & Litvinenko 2014) are able to show better agreement with intensity profiles will be the subject of future work.
To ensure that magnetic field lines behave diffusively, a positive q> 1 is required (Weinhorst & Shalchi 2010).
Acknowledgments
R.C.T. acknowledges fruitful discussions with Andreas Kopp. A.S. acknowledges support by the Natural Sciences and Engineering Research Council (NSERC) of Canada.
References
- Ablaßmayer, J., Tautz, R. C., & Dresing, N. 2015, Phys. Plasmas, submitted [Google Scholar]
- Achterberg, A. 1981, A&A, 97, 259 [NASA ADS] [Google Scholar]
- Ansari, I. S., Yilmaz, F., Alouini, M.-S., & Kucur, O. 2012, in 2012 IEEE 13th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), 394 [Google Scholar]
- Artmann, S., Schlickeiser, R., Agueda, N., Krucker, S., & Lin, R. P. 2011, A&A, 535, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batchelor, G. K. 1952, Math. Proc. Camb. Phil. Soc., 48, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Batchelor, G. K. 1982, The Theory of Homogeneous Turbulence (Cambridge: University Press) [Google Scholar]
- Belcher, J. W., & Davis, L. 1971, J. Geophys. Res., 76, 3534 [NASA ADS] [CrossRef] [Google Scholar]
- Bieber, J. W., Wanner, W., & Matthaeus, W. H. 1996, J. Geophys. Res., 101, 2511 [Google Scholar]
- Brenner, S., & Scott, R. 2008, The Mathematical Theory of Finite Element Methods, Texts in Applied Mathematics (Springer) [Google Scholar]
- Bruno, R., & Carbone, V. 2005, Liv. Rev. Sol. Phys., 2, 1 [Google Scholar]
- Coleman, Jr., P. J. 1968, ApJ, 153, 371 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2005, A&A, 436, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decker, R. B., Krimigis, S. M., Roelof, E. C., & Hill, M. E. 2012, Nature, 489, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Dresing, N., Gómez-Herrero, R., Klassen, A., et al. 2012, Sol. Phys., 281, 281 [NASA ADS] [Google Scholar]
- Dröge, W. 2005, Adv. Space Res., 35, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Dröge, W., & Kartavykh, Y. Y. 2009, ApJ, 693, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Dröge, W., Kartavykh, Y. Y., Klecker, B., & Kovaltsov, G. A. 2010, ApJ, 709, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Effenberger, F., & Litvinenko, Y. E. 2014, ApJ, 783, 15 [Google Scholar]
- Fa, K. S., & Lenzi, E. K. 2005, Phys. Rev. E, 72, 011107 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, C. 1961, Trans. Am. Math. Soc., 98, 395 [Google Scholar]
- Galerkin, B. G. 1915, Vestn. Inzh. Tech., 19, 897 [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 1999, ApJ, 520, 204 [Google Scholar]
- Gombosi, T. I., & Owens, A. J. 1981, Adv. Space Res., 1, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, M., & Savin, D. W. 2013, ApJ, 776, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Hentschel, H. G. E., & Procaccia, I. 1984, Phys. Rev. A, 29, 1461 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, Y., Zeng, L., Minnich, A. J., Dresselhaus, M. S., & Chen, G. 2015, Nature Nanotechnol., 10, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Jokipii, J. R. 1966, ApJ, 146, 480 [Google Scholar]
- Keppler, E., Blake, J. B., Fränz, M., et al. 1992, Science, 257, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Keppler, E., Franz, M., Korth, A., et al. 1995, Science, 268, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. N. 1941, Proc. USSR Acad. Sci., 30, 299 [Google Scholar]
- Kóta, J., & Jokipii, J. R. 2000, ApJ, 531, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Laitinen, T., Dalla, S., & Marsh, M. S. 2013, ApJ, 773, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Lario, D., Aran, A., Gómez-Herrero, R., et al. 2013, ApJ, 764, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. A., & Völk, H. J. 1975, ApJ, 198, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzi, E. K., Mendes, R. S., Fa, K. S., da Silva, L. R., & Lucena, L. S. 2004, J. Math. Phys., 45, 3444 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E., & Schlickeiser, R. 2013, A&A, 554, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthaeus, W. H., Goldstein, M. L., & Roberts, D. A. 1990, J. Geophys. Res., 95, 20673 [Google Scholar]
- Michałek, G., & Ostrowski, M. 1996, Nonlin. Processes Geophys., 3, 66 [Google Scholar]
- Minnie, J., Bieber, J. W., & Matthaeus, W. H. 2007, ApJ, 670, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Osman, K. T., Matthaeus, W. H., Wan, M., & Rappazzo, A. F. 2012, Phys. Rev. Lett., 108, 261102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Palmer, I. D. 1982, Rev. Geophys., 20, 335 [Google Scholar]
- Parker, E. N. 1965, Planet. Space Sci., 13, 9 [Google Scholar]
- Pommois, P., Zimbardo, G., & Veltri, P. 2007, Phys. Plasmas, 14, 012311 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, G., Matthaeus, W. H., & Bieber, J. W. 2002, Geophys. Res. Lett., 29, 1048 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, G., He, H.-Q., & Zhang, B. 2011, ApJ, 738, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Rausch, M., & Tautz, R. C. 2013, MNRAS, 428, 2333 [NASA ADS] [CrossRef] [Google Scholar]
- Ritz, W. 1909, J. Reine Angew. Math., 135, 1 [Google Scholar]
- Roelof, E. C. 1969, in Lectures in high energy astrophysics, eds. H. B. Ögelmann, & J. R. Wayland Jr. (Washington, DC: NASA SP-199), 111 [Google Scholar]
- Sahraoui, F., Goldstein, M. L., Robert, P., & Khotyaintsev, Y. V. 2009, Phys. Rev. Lett., 102, 231102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sakai, T. 2002, Earth Planets Space, 54, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Saur, J., & Bieber, J. W. 1999, J. Geophys. Res., 104, 9975 [Google Scholar]
- Scherer, K., Fichtner, H., Heber, B., & Mall, U. 2005, Space Weather: The Physics Behind a Slogan (Berlin: Springer) [Google Scholar]
- Schlickeiser, R. 1989, ApJ, 336, 246 [NASA ADS] [Google Scholar]
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Berlin: Springer) [Google Scholar]
- Schlickeiser, R., Artmann, S., & Dröge, W. 2009, Open Plasma Phys. J., 2, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A. 2005, Phys. Plasmas, 12, 052905 [Google Scholar]
- Shalchi, A. 2009, Nonlinear Cosmic Ray Diffusion Theories (Berlin: Springer) [Google Scholar]
- Shalchi, A. 2010, ApJ, 720, L127 [Google Scholar]
- Shalchi, A. 2015, Phys. Plasmas, 22, 010704 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A., & Kourakis, I. 2007, A&A, 470, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shalchi, A., & Weinhorst, B. 2009, Adv. Space Res., 43, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A., Škoda, T., Tautz, R. C., & Schlickeiser, R. 2009, Phys. Rev. D, 80, 023012 [Google Scholar]
- Shalchi, A., Tautz, R. C., & Rempel, T. J. 2011, Plasma Phys. Contr. Fusion, 53, 105016 [NASA ADS] [CrossRef] [Google Scholar]
- Sokolov, I. M., Klafter, J., & Blumen, A. 2002, Phys. Today, 55, 48 [CrossRef] [Google Scholar]
- Springel, V. 2010, ARA&A, 48, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Stanislavsky, A. A. 2003, Phys. Scr., 67, 265 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tautz, R. C. 2010a, Comput. Phys. Commun., 81, 71 [Google Scholar]
- Tautz, R. C. 2010b, Plasma Phys. Contr. Fusion, 52, 045016 [Google Scholar]
- Tautz, R. C., & Dosch, A. 2013, Phys. Plasmas, 20, 022302 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., & Shalchi, A. 2010, J. Geophys. Res., 115, A03104 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., & Shalchi, A. 2012, ApJ, 744, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., Shalchi, A., & Schlickeiser, R. 2006, J. Phys. G: Nuclear Part. Phys., 32, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., Shalchi, A., & Schlickeiser, R. 2008a, ApJ, 672, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., Shalchi, A., & Schlickeiser, R. 2008b, ApJ, 685, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., Dosch, A., & Shalchi, A. 2011, J. Geophys. Res., 116, A02102 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., Lerche, I., & Kruse, F. 2013, A&A, 555, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaughan, G. L., Healy, T. R., Bryan, K. R., Sneyd, A. D., & Gorman, R. M. 2008, Int. J. Num. Meth. Fluids, 56, 37 [CrossRef] [Google Scholar]
- Wang, X., Tu, C., He, J., Marsch, E., & Wang, L. 2014, ApJ, 783, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, G. M., Zank, G. P., Kaghashvili, E. K., & le Roux, J. A. 2006, ApJ, 651, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Weinhorst, B., & Shalchi, A. 2010, MNRAS, 406, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Zimbardo, G. 2005, Plasma Phys. Contr. Fusion, 47, B755 [Google Scholar]
- Zimbardo, G., Pommois, P., & Veltri, P. 2000, Physica A, 280, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Zimbardo, G., Pommois, P., & Veltri, P. 2006, ApJ, 639, L91 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Time-dependent diffusion coefficient: analytical approach
Analytically, the problem of anomalous diffusion (e.g., Zimbardo 2005; Pommois et al. 2007; Tautz & Shalchi 2010) has been investigated with a variety of novel approaches. In the most general case, the derivation is based on a fractional Fokker-Planck (or diffusion) equation (Sokolov et al. 2002; Stanislavsky 2003), which has the general form ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:frac} \pd[^\alpha f(x,t)]{t^\alpha}=\int_0^t\df t'\:\pd{\abs x}\left[\kappa(x,t-t')\,\pd[^{\mu-1}\bigl(f(x,t')\bigr)^\nu]{\abs{x}^{\mu-1}}\right] , \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq149.png) (A.1)where ν,μ,α ∈R and where κ(x,t) = κ(t)|x|− ϑ is the generalized diffusion coefficient. General solutions (e.g., Lenzi et al. 2004; Fa & Lenzi 2005) have been derived for example in terms of the Fox H function (Fox 1961); however, these solutions are difficult to implement numerically (e.g., Ansari et al. 2012).
(A.1)where ν,μ,α ∈R and where κ(x,t) = κ(t)|x|− ϑ is the generalized diffusion coefficient. General solutions (e.g., Lenzi et al. 2004; Fa & Lenzi 2005) have been derived for example in terms of the Fox H function (Fox 1961); however, these solutions are difficult to implement numerically (e.g., Ansari et al. 2012).
For the problem at hand, however, a classic solution equation is sufficient if it is equipped with time-dependent diffusion coefficients. In Eq. (A.1), this corresponds to the linear case, which is obtained for ν = 1 and μ = 2. The additional assumptions of homogeneity, ϑ = 0 so that κ(x,t) = κ(t), and α = 1 yield the usual random walk.
If the only modification is the time-dependence in the diffusion coefficient in the form of a power-law, κ = ξtγ, a simple solution can be obtained as (see Fa & Lenzi 2005) ![\appendix \setcounter{section}{1} \begin{equation} f_{\text{1D}}(x,t)=\frac{1}{\sqrt{4\pi\xi t^{\gamma +1}}}\exp\!\left[-\frac{\left(1+\gamma\right)r^2}{4\xi\,t^{\gamma+1}}\right], \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq157.png) (A.2)which has been derived before by Batchelor (1952) (see also Hentschel & Procaccia 1984).
(A.2)which has been derived before by Batchelor (1952) (see also Hentschel & Procaccia 1984).
The generalization to three independent spatial dimensions can be easily achieved if the diffusion tensor is assumed to have a diagonal form, i.e., κ = diag(κx,κy,κ∥), which assumes that the off-diagonal elements vanish. These drift coefficients (see, e.g., Tautz & Shalchi 2012) will be neglected because drift motions are generally suppressed in turbulent magnetic fields (Minnie et al. 2007). Their importance is, therefore, limited to cases where the mean magnetic field is curved, which results in drift velocities. Generally, the values for the drift coefficients are smaller than the parallel diffusion coefficient by orders of magnitude.
Under these conditions, the solution to the three-dimensional diffusion equation, ![\appendix \setcounter{section}{1} \begin{equation} \pd[f_{\text{Diff}}]t=\left[\f\kappa(t)\cdot\nabla\right]\cdot\nabla f_{\text{Diff}} , \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq159.png) (A.3)decouples and is simply the product of the three one-dimensional solutions so that it reads
(A.3)decouples and is simply the product of the three one-dimensional solutions so that it reads ![\appendix \setcounter{section}{1} \begin{equation} f_{\text{Diff}}(\f r,t)=\prod_i\frac{1}{\sqrt{4\pi\xi_it^{\gamma_i+1}}}\exp\!\left[-\frac{\left(1+\gamma_i\right){r_i}^2}{4\xi_it^{\gamma_i+1}}\right] \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq160.png) (A.4)for i ∈ { x,y,z }. The diffusion coefficients can be inserted individually as κi(t) = ξitγi. It is this function that is used in the text to fit the time profiles that are obtained in the Padian simulation code.
(A.4)for i ∈ { x,y,z }. The diffusion coefficients can be inserted individually as κi(t) = ξitγi. It is this function that is used in the text to fit the time profiles that are obtained in the Padian simulation code.
Appendix B: Time-dependent diffusion coefficient: numerical approach
From a numerical point of view, the diffusion equation has the special property that its spatial coordinate is unlimited and that the solution function has no boundary conditions except f(x) → 0 for x → ± ∞. Therefore, a hyperbolic transformation in the spatial coordinate is done as ζ = tanh(εx) with ζ ∈ [−1,1]. This results in a distribution of the spatial grid points with a maximum density around x = 0 that is exponentially decreasing toward x → ± ∞.
The diffusion equation can then be written as ![\appendix \setcounter{section}{2} \begin{equation} \pd[f]t=\eps^2\kappa(t)\left(1-\zeta^2\right)\pd\zeta\left[\left(1-\zeta^2\right)\pd[f]\zeta\right]\cdot \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq167.png) (B.1)For the norm of the solution function, one has
(B.1)For the norm of the solution function, one has 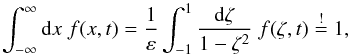 (B.2)which remains constant and therefore represents an additional constraint to the solution function. The remaining free parameter, ε, was chosen so that (i) the largest x values are 10 times larger than the detector position and (ii) the detector position falls within the domain where the tanh transformation results in a fine resolution.
(B.2)which remains constant and therefore represents an additional constraint to the solution function. The remaining free parameter, ε, was chosen so that (i) the largest x values are 10 times larger than the detector position and (ii) the detector position falls within the domain where the tanh transformation results in a fine resolution.
To compute the numerical solution, the equation is discretized in time with an implicit Euler scheme with time step dt. Consequently, in time tn with fn = f(ζ,tn) there holds ![\appendix \setcounter{section}{2} \begin{equation} \label{eq:app:B:1} f_n-\df t\left(\varepsilon^2 \kappa(t_n)\left(1-\zeta^2\right)\pd\zeta\left[\left(1-\zeta^2\right)\pd[f_n]\zeta\right]\right)=f_{n-1}. \end{equation}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq173.png) (B.3)The spatial discretization of this equation is carried out with the Ritz-Galerkin or finite element method (Ritz 1909; Galerkin 1915). The finite element method (FEM) does not solve Eq. (B.3), rather the associated variational problem, which corresponds to the principle of virtual work, and reads for all test functions v after integration by parts
(B.3)The spatial discretization of this equation is carried out with the Ritz-Galerkin or finite element method (Ritz 1909; Galerkin 1915). The finite element method (FEM) does not solve Eq. (B.3), rather the associated variational problem, which corresponds to the principle of virtual work, and reads for all test functions v after integration by parts ![\appendix \setcounter{section}{2} \begin{eqnarray} \int_{-1}^1\df\zeta\;f_n v&+&\df t\int_{-1}^1\df\zeta\;\varepsilon^2 \kappa(t_n)\left(1-\zeta^2\right)^2\pd[f_n]\zeta\,\pd[v]\zeta=\nonumber\\ &&\int_{-1}^1\df\zeta\;f_{n-1} v. \label{eq:app:B:2} \end{eqnarray}](/articles/aa/full_html/2016/02/aa27255-15/aa27255-15-eq175.png) (B.4)For the so-called P1-FEM (Brenner & Scott 2008), fn and v are linear spline functions on [− 1,1]. Therefore, the derivatives and integrals in (B.4)can be easily computed leading in every time step tn to the linear system of equations
(B.4)For the so-called P1-FEM (Brenner & Scott 2008), fn and v are linear spline functions on [− 1,1]. Therefore, the derivatives and integrals in (B.4)can be easily computed leading in every time step tn to the linear system of equations 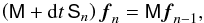 (B.5)where M is the so-called mass matrix, S the modified stiffness matrix due to the factor ε2κ(tn)(1−ζ2)2, and fn the coefficient vector for the linear spline function fn.
(B.5)where M is the so-called mass matrix, S the modified stiffness matrix due to the factor ε2κ(tn)(1−ζ2)2, and fn the coefficient vector for the linear spline function fn.
Adding to this equation the constraint that the norm of the solution should be constant, the system is overdetermined, which can be solved with the method of ordinary least squares. There, the solution to an equation of the form Ax = b is obtained by minimizing ∥ Ax−b ∥ 2 so that the solution is 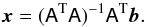 (B.6)Because the time derivative was obtained as a backward-Euler step, the solution is very robust with respect to the size of the time step, whereas it is crucial to apply the spatial transformation as described above.
(B.6)Because the time derivative was obtained as a backward-Euler step, the solution is very robust with respect to the size of the time step, whereas it is crucial to apply the spatial transformation as described above.
All Tables
Comparison between the values obtained for the parallel diffusion coefficients (normalized to Ω2ℓ0) obtained directly from the test-particle trajectories via the mean-square displacements (κ∥sim) in Eq. (3)and from the fit to a three-dimensional diffusion profile with constant diffusion coefficients (κ∥fit) together with their respective estimated mean errors.
All Figures
 |
Fig. 1 Sample trajectories starting from the rectangular blue region with an initial pitch-angle cosine of μ0 = 1, hence moving in the positive z direction. The target region is shown as the small red dot at [x,y,z] = [0,0,10]. |
| In the text | |
 |
Fig. 2 Intensity profile for particles with rigidities R = 10-1 and a distance between the particle source and the detector of L = 100ℓ0 in linear (upper panel) and logarithmic (lower panel) units. In the SPH kernel according to Eq. (4), the base smoothing length is varied between h = 0.5ℓ0 and 3ℓ0 (see legend). An additional influence on the smoothness of the curve can be obtained through the detector size. As illustrated, the smoothing length modifies the fluctuation of the intensity profile but otherwise leaves the underlying structure unchanged. |
| In the text | |
 |
Fig. 3 Intensity-time profiles for particles with rigidities R = 1 and a distance between the particle source and the detector of L = 10ℓ0. The effect is shown of a detector position being either along the same field line with the particle source (angle of 0°) up to a detector perpendicular to the source field line (angle of 90°). |
| In the text | |
 |
Fig. 4 Pitch-angle dependent intensity profile for particles with a normalized rigidity R = 10-2 in arbitrary but linear units. Shown is the flux of particles arriving at the detector with μ ranging from + 1 (i.e., coming from the direction of the source) to − 1 (coming from the far side of the source). |
| In the text | |
 |
Fig. 5 Anisotropy as obtained by taking the first and zeroth moment of the SPH profiles according to Eq. (5). For particles with different rigidities (see panel titles), the time scales are dramatically different. |
| In the text | |
 |
Fig. 6 Example for the parallel (upper panel) and perpendicular (lower panel) diffusion coefficients. During the ballistic phase, the diffusion coefficients grow almost linearly in time, whereas for late times the parallel diffusion coefficient becomes almost constant. For the parallel diffusion coefficient, the transition is marked for later use by the vertical dashed line. In addition, the dot-dashed line illustrates a late superdiffusive phase with κ∥ ∝ t0.31, which has been observed for Alfvénic turbulence due to stochastic acceleration of the particles (cf. Tautz 2010b). Here, in contrast, a magnetostatic model is used, for which the solid line is found. The perpendicular diffusion coefficients, in contrast, become slightly subdiffusive in agreement with earlier results. For later use, the late-time behavior is fitted to a power law. The slope sensitively depends on the properties of the magnetic turbulence (see Tautz & Shalchi 2010) and the particle rigidity (here, R = 10-2). |
| In the text | |
 |
Fig. 7 Time profile (intensity profile) in arbitrary linear units for particles with variable energies (see subplot titles). The distance between the particle origin and the virtual detector is L = 10ℓ0. The various curves are as follows: The black lines show the profile as obtained from the simulations using the methods described in Sect. 3. The red lines show the three-dimensional diffusion solution (with the normalization factor as an open parameter) from Eq. (7)using the diffusion coefficients as obtained from the simulations via the mean-square displacements. In addition, the result from Eq. (8)is shown for constant diffusion coefficients taken from the simulations (blue lines), i.e., κi(t = tmax). |
| In the text | |
 |
Fig. 8 Same as Fig. 7 but for a distance L = 100ℓ0 between the particle origin and the virtual detector. The vertical dashed lines mark the end of the initial ballistic regime as explained in Fig. 6. |
| In the text | |
 |
Fig. 9 Same as Fig. 8 but for a distance L = 1000ℓ0 between the particle origin and the virtual detector. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


