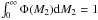| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A158 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526992 | |
| Published online | 11 February 2016 | |
Binary properties of CH and carbon-enhanced metal-poor stars⋆
1
Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles,
Campus Plaine, C.P.
226, Boulevard du
Triomphe, 1050
Bruxelles, Belgium
e-mail: ajorisse@astro.ulb.ac.be
2
Instituut voor Sterrenkunde, Katholieke Universiteit
Leuven, Celestijnenlaan
200D, 3001
Leuven,
Belgium
3
ESO, Alonso de Córdova 3107, Casilla 19001,
Santiago,
Chile
4
Dark Cosmology Centre, The Niels Bohr Institute, University of
Copenhagen, Juliane Maries Vej
30, 2100
Copenhagen,
Denmark
5
Stellar Astrophysics Centre, Department of Physics and Astronomy,
Aarhus University, 8000
Aarhus C,
Denmark
6
Observatoire de Genève, Université de Genève,
1290
Versoix,
Suisse
7
Institute of Astronomy, Cambridge University,
Cambridge CB3
OHA,
UK
Received: 18 July 2015
Accepted: 16 October 2015
The HERMES spectrograph installed on the 1.2-m Mercator telescope has been used to monitor the radial velocity of 13 low-metallicity carbon stars, among which seven carbon-enhanced metal-poor (CEMP) stars and six CH stars (including HIP 53522, a new member of the family, as revealed by a detailed abundance study). All stars but one show clear evidence for binarity. New orbits are obtained for eight systems. The sample covers an extended range in orbital periods, extending from 3.4 d (for the dwarf carbon star HE 0024-2523) to about 54 yr (for the CH star HD 26, the longest known among barium, CH, and extrinsic S stars). Three systems exhibit low-amplitude velocity variations with periods close to 1 yr superimposed on a long-term trend. In the absence of an accurate photometric monitoring of these systems, it is not clear yet whether these variations are the signature of a very low-mass companion or of regular envelope pulsations. The period – eccentricity (P − e) diagram for the 40 low-metallicity carbon stars with orbits now available shows no difference between CH and CEMP-s stars (the latter corresponding to those CEMP stars enriched in s-process elements, as are CH stars). We suggest that they must be considered as one and the same family and that their different names only stem from historical reasons. Indeed, these two families have as well very similar mass-function distributions, corresponding to companions with masses in the range 0.5–0.7 M⊙, indicative of white-dwarf companions, adopting 0.8–0.9 M⊙ for the primary component. This result confirms that CH and CEMP-s stars obey the same mass-transfer scenario as their higher-metallicity analogues, barium stars. The P − e diagrams of barium, CH, and CEMP-s stars are indeed very similar. They reveal two different groups of systems: one with short orbital periods (P< 1000 d) and mostly circular or almost circular orbits, and another with longer period and eccentric (e> 0.1) orbits. These two groups either trace different evolutionary channels during the mass-transfer episode responsible for the chemical peculiarities of the Ba/CH/CEMP-s stars, or result from the operation of tidal circularisation in a more recent past, when the current giant star was ascending the first giant branch.
Key words: binaries: general / stars: carbon
Individual radial velocities are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/586/A158
© ESO, 2016
1. Introduction
One of the most surprising results of the large wide-field spectroscopic surveys for metal-poor stars in our Galaxy (e.g. the HK, HES, and SDSS/SEGUE surveys; Beers et al. 1992; Christlieb et al. 2001; Yanny et al. 2009,respectively) is the high frequency of carbon-enhanced stars ([C/Fe] > 1.0, hereafter CEMP stars) among metal-poor stars. The results of the above surveys indicate that they represent 20% of stars with [Fe/H] < − 2 (Christlieb 2003; Lucatello et al. 2005, 2006; Aoki et al. 2013; Yong et al. 2013; Lee et al. 2013), but that frequency is increasing rapidly as metallicity decreases (Placco et al. 2014). This finding has prompted a number of high-resolution, high signal-to-noise studies aiming at understanding the origin of the abundance anomalies in these objects. The carbon-enhancement phenomenon appears in stars that exhibit four different heavy-element abundance patterns (Beers & Christlieb 2005; Masseron et al. 2010):
-
CEMP-s: [C/Fe] > + 1.0, [Ba/Fe] > + 1.0, and [Ba/Eu] > + 0.5. This most numerous class is characterised by enrichments of neutron-capture elements, with an abundance pattern compatible with the operation of the s process in asymptotic giant branch (AGB) stars. After initial studies of their binary frequency by Preston & Sneden (2001), Sneden et al. (2003b), and Lucatello et al. (2005), Starkenburg et al. (2014) finally used a large sample of stars to demonstrate that these stars are all members of binary systems. Thus, it is now established that these CEMP-s stars, along with the closely-related classical CH stars (Keenan 1942), are members of wide binary systems, where the former primary star transferred material during its AGB phase onto the presently observable companion (McClure 1984; McClure & Woodsworth 1990).
-
CEMP-rs: [C/Fe] > + 1.0 and + 0.5 > [Ba/Eu] > 0.0. This other class of CEMP stars, exhibiting large overabundances of elements produced by the s process and elements traditionally related to the r-process, was discovered by Barbuy et al. (1997) and Hill et al. (2000). A number of these stars exhibit radial-velocity variations (Sivarani et al. 2004; Barbuy et al. 2005). Here again the companion could be responsible for the peculiar abundance pattern (e.g. Masseron et al. 2010; Bisterzo et al. 2011).
-
CEMP-no: [C/Fe] > + 1.0 and [Ba/Fe] ∼ 0. Starkenburg et al. (2014) found these CEMP stars with no enhancements in their neutron-capture-element abundances (hereafter CEMP-no; Aoki et al. 2002) to have normal binary frequency. Consequently, a mass-transfer scenario comparable to that occurring in CEMP-s (and possibly in CEMP-rs) stars has not operated here.
-
CEMP-r: [C/Fe] > + 1.0 and [Eu/Fe] > + 1.0. This is the signature of a highly r-process-enhanced CEMP star, so far observed in only one object (CS22892-052; Sneden et al. 2003a).
An important question concerning the nature of CEMP stars and their various counterparts is the astrophysical origin of the carbon excess that is observed in the atmosphere of these objects. One established scenario is carbon production by nucleosynthesis in an asymptotic giant branch (AGB) star. It is usually assumed that the AGB star responsible for carbon production was once the primary of a binary system. The carbon and s-process elements produced in the interior of the AGB star and dredged to its atmosphere were subsequently transferred to a companion. Observational support for this scenario is provided by the binary nature of these objects, as established by McClure (1984) and McClure & Woodsworth (1990) for a major fraction of CH stars, and by Preston & Sneden (2001) and Lucatello et al. (2005) for a few CEMP-s stars.
The mass-transfer scenario responsible for the pollution of the atmosphere of those stars with s-process material has been the topic of many studies (e.g. Boffin & Jorissen 1988; Bonačić Marinović et al. 2008; Izzard et al. 2010), which rely on the properties of the period – eccentricity (P − e) diagram as well as on the mass-function distribution (McClure & Woodsworth 1990; Jorissen et al. 1998). For this reason, it is important to collect as many orbital data as possible for CH and CEMP-s stars, so as to build their P − e diagram and see whether it bears similarities with that of barium and extrinsic S stars (Jorissen et al. 1998; Gorlova et al. 2013), as well as to compare CH and CEMP-s binaries. Since some CEMP-s stars have very low metallicities, it is of interest to see whether this low metallicity impacts the P − e diagram (through for instance the change in the stellar size resulting from the shift of the low-metallicity giant branches towards bluer colours). For CEMP-s stars, very few orbital elements are currently known, however (see Table 4 of Lucatello et al. 2005). Thanks to the new orbits presented in this study and in the paper by Hansen et al. (2016), the sample of orbital elements for CEMP binaries has doubled. The P − e diagram drawn from this extended sample should represent a benchmark for theoretical mass-transfer studies such as those of Abate et al. (2013, 2015a,b).
The paper is organised as follows. Section 2 describes the technical details of our radial-velocity monitoring. The stellar sample is described in Sect. 3. The orbital elements are presented in Sect. 4. The mass distribution and P − e diagram are discussed in Sect. 5.2.1. Section 6 discusses how to correctly investigate a possible correlation between orbital period and s-process overabundance for these mass-transfer binaries. Conclusions are drawn in Sect. 7.
2. Radial-velocity monitoring with the HERMES spectrograph
The radial-velocity (RV) monitoring was performed with the HERMES spectrograph attached to the 1.2-m Mercator telescope from the Katholieke Universiteit Leuven, installed at the Roque de los Muchachos Observatory (La Palma, Spain). The spectrograph began regular science operations in June 2009, and is fully described in Raskin et al. (2011). The fibre-fed HERMES spectrograph is designed to be optimised both in stability as well as in efficiency. It samples the whole optical range from 380 to 900 nm in one shot, with a spectral resolution of about 86 000 for the high-resolution science fibre. This fibre has a 2.5 arcsec aperture on the sky and the high resolution is reached by mimicking a narrow slit using a two-sliced image slicer.
The HERMES/Mercator combination is precious because it guarantees regular telescope time. This is needed for our monitoring programme and the operational agreement reached by all consortium partners (KULeuven, Université libre de Bruxelles, Royal Observatory of Belgium, Landessternwarnte Tautenburg) is optimised to allow efficient long-term monitoring, which is mandatory for this programme. On average, 250 nights per year are available for the monitoring (spread equally on HERMES-consortium time, and on KULeuven time), and the observation sampling is adapted to the known variation timescale. During these nights, about 300 target stars are monitored, addressing several science cases (Van Winckel et al. 2010; Gorlova et al. 2013).
A Python-based pipeline extracts a wavelength-calibrated and a cosmic-ray cleaned spectrum. A separate routine is used for measuring RVs, by means of a cross-correlation with a spectral mask constructed from a carbon-star spectrum. A restricted region, covering the range 478.11–653.56 nm (orders 55 – 74) and containing 2103 useful spectral lines, was used to derive the RV to avoid telluric lines on the red end, and crowded and poorly exposed spectra on the blue end. A spectrum with a signal-to-noise ratio of 15 in V is usually sufficient to obtain a cross-correlation function (CCF) with a well-pronounced extremum. An example of CCF is shown in Fig. 1 for a spectrum with an average signal-to-noise ratio of 17 in the relevant spectral region.
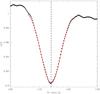 |
Fig. 1 Typical CCF for the CEMP-s star HE 1120-2122 on HJD 2 456 804.428, based on a spectrum with an exposure time of 1800 s. The Gaussian fit of the CCF is the thin solid line, restricted to the CCF core to reduce the impact of line asymmetries as much as possible. The vertical line indicates the star radial velocity, as derived from the Gaussian fit. |
A Gaussian fit is performed on the core of the CCF (to reduce the impact of line asymmetries as much as possible), with an internal precision of a few m/s on the position of the CCF centre, small enough with respect to external uncertainty factors. The most important of these is caused by pressure fluctuations occurring in the spectrograph room during the night (see Fig. 9 of Raskin et al. 2011). The exact impact of the pressure drift on the velocity measurement depends on the time elapsed between the science exposure and the arc spectrum used for wavelength calibration. The long-term accuracy (over years) of the radial velocities may be estimated from the stability of the RV standard stars monitored along with the science targets. These standard stars are taken from the list of Udry et al. (1999)1. Figure 2 shows the distribution of standard deviations for 58 radial-velocity standard stars with more than five measurements after 4.5 years of monitoring. The distribution peaks at σ(Vr) = 55 m/s, which may thus be adopted as the typical uncertainty on the radial velocities over the long term. The RV standard stars have been used as well to tie the HERMES RVs to the IAU standard system.
 |
Fig. 2 Histogram of the standard deviations of the velocity data for radial-velocity standard stars with more than five measurements spread over 4.5 years of monitoring. |
In some cases, older measurements from CORAVEL (Baranne et al. 1979) or from McClure & Woodsworth (1990) have been added to the HERMES measurements to extend the time span. In the latter case (Dominion Astrophysical Observatory velocity measurements), a zero-point correction of −0.46 km s-1 has been applied to bring them into the IAU/HERMES system (Jorissen et al. 1998). The CORAVEL measurements have been tied to the IAU system following the prescription given by Udry et al. (1999). More specifically for HD 26 (belonging to the sample that is described in the next section), which is an extreme case given its low velocity of −215 km s-1, the velocities from the northern CORAVEL have been brought into the IAU system first by adding 0.7 km s-1. This value is taken from the upper left panel of Fig. 2 of Udry et al. (1999) since the offset due to the extreme velocity overwhelms that due to the moderate B − V index of 1.16. Then, the southern CORAVEL measurements have been corrected by −1.3 km s-1; the southern measurements are so numerous that the necessary offset can be easily estimated from the shift needed to superimpose the southern and northern sequences.
3. Stellar sample
The stellar sample, containing seven CEMP-(r)s and six CH stars, is listed in Table 1. We selected the sample so as to avoid stars already monitored by Lucatello et al. (2005), and to ensure that the targets are not too far south and not too faint to be observable with HERMES/Mercator. The spectral classification is from Goswami (2005), Goswami et al. (2010), and Masseron et al. (2010), who provide detailed abundances for the CEMP stars, indicating that they indeed belong to the CEMP-s subclass (with the exception of the CEMP-rs star HE 0017+0055 studied in a companion paper; Jorissen et al. 2016). We included the star HD 145777 as well. This star was initially classified as R3 by Mayall & Cannon (1940) and R4 by Sanford (1944), but later reclassified as CH by Bidelman (1956). The same holds true for HD 187216, HIP 53522, and HIP 53832 (Vandervort 1958; Hartwick & Cowley 1985). The latter two stars are the topic of a recent paper (Sperauskas et al. 2015), which classifies them as CH-like (a class related to the CH stars, but that lacks the large spatial velocities of the CH stars; Yamashita 1975).
Moreover, an abundance analysis of HIP 53522 is presented in Appendix A. Its metallicity was found to be no lower than [Fe/H] = −0.5, a rather moderate value among CH stars, but the s-process elements are clearly enhanced by about 1.4 dex. This result is confirmed by the recent analysis by Sperauskas et al. (2015). The star HIP 53832 is very similar to HIP 53522: an abundance analysis by Zamora et al. (2009) has confirmed its CH nature, with [Fe/H] = − 0.77 and an average s-process abundance of 1.26 dex.
Properties of the stellar sample.
4. Results
4.1. Synopsis
A synopsis of the results of the radial-velocity monitoring is presented in Table 1. The stars may be divided into four different groups:
-
Star with no clear evidence for binary motion (SB?). In our sample, only HE 1429-0551 belongs to that category (Fig. B.1; for the sake of clarity, all figures with radial-velocity curves are collected in Appendix B). Although HE 1429-0551 exhibits radial-velocity variations above the 3σ level, and would thus formally qualify for being flagged as spectroscopic binary, inspection of its radial-velocity data does not reveal any clear trend that could be ascribed to an orbital motion. More observations are thus needed to issue a definite statement about the binarity of that star.
-
Stars with clear evidence for binary motion but no orbit available yet (SB). Three stars belong to that category (HD 145777, HD 187216, HE 2144-1832; Figs. B.2–B.4) plus a fourth one (HE 0017+0055; Fig. B.11), which is special in that it shows 1 yr variations on top of the long-term trend.
-
Stars with orbits available (ORB). Orbits are already available for four among the seven CEMP stars, and for four among the six CH stars (Figs. B.5–B.10). Two among these orbits show 1 yr period variations superimposed on the long-term orbit (Figs. B.12–B.13). Orbital elements are listed in Table 2.
-
Stars with short-period, low-amplitude variations superimposed on the long-term (SB+jitter) or orbital variations (ORB+jitter). This unexpected behaviour is encountered for the three systems HE 0017+0055, HE 1120-2122, and HD 76396 (Figs. B.11–B.13), and is discussed in Sect. 4.3.
Orbital elements for the eight new spectroscopic-binary systems.
Orbital elements fitting the O−C residuals of three systems.
4.2. Orbital elements
New2 orbital elements for eight systems are listed in Table 2 and the corresponding orbital solutions are found in Figs. B.5–B.10 and B.12–B.13. The orbits are not fully constrained yet for HD 26 and HD 76396 (in the former case, the period could be even longer than the currently estimated 54 yr; that period is currently the longest known among barium, CH and extrinsic S stars; see the rightmost blue cross in Fig. 6 below). The O−C residuals are consistent with the HERMES measurement errors except for HD 26, HD 76396, and HE 1120-2122, where they are much larger. As seen in Figs. B.10 and B.13, these large values for HD 26 and HD 76396 are caused by the dispersion of the old CORAVEL (Baranne et al. 1979) and McClure & Woodsworth (1990) measurements, respectively, and the standard deviation of the O−C residuals of the 22 HERMES measurements amounts to 0.126 km s-1 in the case of HD 76396. For HE 1120-2122, the large O−C residuals must be considered as a warning that the system may either be triple or be subject to velocity jitter caused by, e.g. envelope pulsations. This is discussed further in Sect. 4.3.
4.3. Systems with velocity variations of low amplitudes and periods ∼1 yr
Quite surprisingly, ∼1 yr period variations superimposed on the long-term (Keplerian) variations have been found for the three systems HE 0017+0055, HE 1120-2122, and HD 76396 (Figs. B.11–B.13). For the latter two systems, the orbital O−C residuals are larger than the HERMES spectrograph long-term accuracy of 55 m/s, indicating the presence of information in the residuals. The elements of the Keplerian orbit fitted to these residuals are listed in Table 3. For HE 0017+0055, presented in Fig. B.11, nearly eight cycles of 1 yr periodic velocity oscillation have been observed on top of the long-term trend. We found that the latter is best modelled by a quadratic polynomial of the form Vr = 3.252 × 10-7x2−0.0374x + 993.215, where x = JD−2 400 000, while the short-term oscillation is adequately represented by a Keplerian binary orbit with a period of 383 d and an eccentricity of 0.14 (Table 3). HE 0017+0055 is the topic of a dedicated paper (Jorissen et al. 2016), since it combines radial velocities from HERMES/Mercator and from the Nordic Optical Telescope.
The associated timescale for the short-term velocity variations is in all three cases close to 1 yr. This very fact could raise doubts about the validity of our result (being caused by, e.g. an inaccurate barycentric correction). However, for HE 0017+0055, it was obtained independently on the Nordic Optical Telescope (Jorissen et al. 2016), which thus gives credit to the result. Moreover, the many other systems subject to a radial-velocity monitoring with HERMES (Gorlova et al. 2013) do not reveal similarly oscillating O−C residuals, and neither do the radial-velocity standard stars nor the long-period CEMP star HE 0457-1805 in the present sample (Fig. B.6).
The remarkable feature of the Keplerian orbits fitted to the 1 yr period variations, as listed in Table 3, is the very low value of their velocity amplitude (0.1 to 0.6 km s-1), which suggests three possible interpretations: (i) an orbit with a very low inclination; (ii) a companion of very low mass; and (iii) a spurious Keplerian solution with the velocity variations originating instead in the (supposedly pulsating) atmosphere of the giant star. These possibilities are discussed in more detail in Jorissen et al. (2016). Here we only stress that Carney et al. (2003) showed that low-metallicity giants, especially in globular clusters and the Magellanic Clouds, systematically exhibit radial-velocity jitter for luminosities near or above the RGB tip (i.e. MV ≤ −1.5 or log g ≤ 1.3). These radial-velocity variations mimic Keplerian variations, with semi-amplitudes of the order of 1−1.5 km s-1 and periods of the order of 170−190 d. They are thus of shorter periods and larger amplitudes than those observed in our sample (but the metallicities are different). Moreover, the velocity jitter detected by Carney et al. (2003) appears to vary in phase with photometric variations of amplitudes about 0.15 mag. As shown by Kiss & Bedding (2003), these photometric variations are probably linked with the A−C period-luminosity sequences first identified by Wood (2000) in the Magellanic Clouds. A final conclusion about the nature of the short-term velocity variations reported here in several CH and CEMP stars must await an accurate photometric monitoring of these systems, as well as good distance estimates that will allow the determination of their position in the Hertzsprung-Russell diagram. Both diagnostics should be testable with the oncoming Gaia data.
 |
Fig. 3 The distribution of the secondary masses Φ(M2) (normalised such that
|
 |
Fig. 4 Observed distribution of the mass functions f(M1,M2) (in solar-mass units; solid black histogram) superimposed on a synthetic distribution (dashed red curve with statistical error bars) resulting from the assumptions of random orientation of the orbital planes on the sky and fixed value of Q = 0.094 M⊙. |
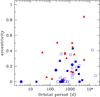 |
Fig. 5 Comparison of CEMP stars (filled symbols) and CH stars (open symbols) in the period – eccentricity (P − e) diagram. Dwarf carbon stars are represented by circles, giant carbon stars by squares (CEMP stars with unknown gravities in Table 4 are assigned giant status by default). For comparison, the sample of low-metallicity giants studied by Carney et al. (2003) is represented with red triangles. |
5. Analysis
5.1. Masses
We perform here the analysis of the mass-function distribution, following the method
outlined by Boffin et al. (1992, 1993), Cerf &
Boffin (1994), and Boffin (2010, 2012), with the mass functions collected in Table 4. The method allows us access to the distribution of
the masses of the secondary (denoted M2 in what follows), under the
assumption of a random orientation of the orbital planes, and with some a priori knowledge
of the primary masses (denoted M1). In the present situation, we may
only rely on their low metallicity to infer that they should have a low mass. The five
CH-like stars from Sperauskas et al. (2015) in
Table 4 were therefore not included in the
mass-function analysis because of their almost solar metallicity. We also restrict our
analysis to the sample of giant stars (from Table 4) so as to be able to use the argument that, since they have reached the giant
branch, their main-sequence lifetime should be shorter than the age of the Galaxy. We
therefore adopt 0.8–0.9 M⊙ as a typical mass for the primary
star, and, fortunately, the method is not too sensitive to that assumption, given the way
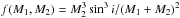 depends on M1. Figure 3 presents the distribution of the secondary masses
M2, which are peaked in the range 0.5–0.7
M⊙ (with one exception), as expected for
white-dwarf companions originating from the thermally-pulsing asymptotic giant branch
(Falcon et al. 2010). To confirm the robustness
of that conclusion, Fig. 4 shows the good agreement
between the observed distribution of the mass functions f(M1,M2)
(solid black histogram) and a synthetic distribution resulting from the assumptions of
random orientation of the orbital planes on the sky and a fixed value of 0.094
M⊙ for
depends on M1. Figure 3 presents the distribution of the secondary masses
M2, which are peaked in the range 0.5–0.7
M⊙ (with one exception), as expected for
white-dwarf companions originating from the thermally-pulsing asymptotic giant branch
(Falcon et al. 2010). To confirm the robustness
of that conclusion, Fig. 4 shows the good agreement
between the observed distribution of the mass functions f(M1,M2)
(solid black histogram) and a synthetic distribution resulting from the assumptions of
random orientation of the orbital planes on the sky and a fixed value of 0.094
M⊙ for
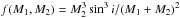 . Indeed, following McClure & Woodsworth (1990), the distribution of f(M1,M2)
for the CH systems they studied (Ref. 5 in Table 4)
is compatible with a Gaussian distribution of Q with a mean value of 0.094 M⊙ and a
standard deviation of 0.013 M⊙. At face value, this implies
M2 = 0.56
M⊙ for M1 = 0.8
M⊙, and M2 = 0.60
M⊙ for M1 = 0.9
M⊙. This is exactly what is found by our
inversion method, applied on a larger sample of CH and CEMP systems.
. Indeed, following McClure & Woodsworth (1990), the distribution of f(M1,M2)
for the CH systems they studied (Ref. 5 in Table 4)
is compatible with a Gaussian distribution of Q with a mean value of 0.094 M⊙ and a
standard deviation of 0.013 M⊙. At face value, this implies
M2 = 0.56
M⊙ for M1 = 0.8
M⊙, and M2 = 0.60
M⊙ for M1 = 0.9
M⊙. This is exactly what is found by our
inversion method, applied on a larger sample of CH and CEMP systems.
5.2. Period – eccentricity diagram
5.2.1. CEMP-s vs. CH systems
We now investigate the period – eccentricity (P − e) diagram for CH and CEMP-(r)s stars, adding to the 18 systems already available in the literature the eight new orbits from Table 2, the eight new well-constrained orbits from Hansen et al. (2016) and the five new orbits of CH-like stars from Sperauskas et al. (2015) that we merge with the CH systems. For the sake of completeness, the data used to draw the P − e diagram of Fig. 5 have been collected in Table 4, with references indicated. No differences between CEMP-s and CH systems are apparent from Fig. 5, so that in the remainder of this paper, they are treated as a single group. The orbital similarity between these two groups is a further indication that their different names stem from historical reasons, but there is no physical difference between them, apart from the fact that CH systems always involve giant primaries, whereas CEMP systems comprise dwarf primaries as well (see the d/g column in Table 4). Long-standing historical equivalents of the dwarf CEMP-s stars are the subgiant CH stars (Luck & Bond 1991) and the formerly known dwarf carbon stars, such as G77-61 (Dearborn et al. 1986; see Table 9.5 of Jorissen 2004 for a review)or the “carbon dwarf wearing a necklace”, the central star of the planetary nebula G054.2 – 03.4 (Corradi et al. 2011; Miszalski et al. 2013). The latter has not been listed explicitly in Table 4 because it is not formally known as a CH or CEMP star. It has an orbital period of 1.16 d, very similar to that of the CEMP dwarf HE 0024-2523 (3.4 d; Lucatello et al. 2003).
The orbital-period range spanned by CH/CEMP-s stars is very extended, from a few days for the CEMP dwarf HE 0024-2523 to the (estimated) 54 yr period of the CH star HD 26 (Fig. 5). Given their smaller size, dwarf carbon stars may fit into systems that are closer (and hence have shorter orbital periods) than those involving giant primaries. Orbital periods as short as that of HE 0024-2523 are not unusual among systems involving main-sequence primaries (e.g. Mathieu 1992). But HE 0024-2523 is supposed to be the post-mass-transfer stage of a system that formerly involved an AGB star. Since the AGB star could not be hosted in a system that close, the current period of 3.4 d must be the outcome of a significant orbital shrinkage. This kind of shrinkage is expected in binary-evolution channels involving a common envelope3, as must happen when an AGB star overflows its Roche lobe (e.g. Han et al. 1995; Pols et al. 2003). Abate et al. (2015a) were able to account for the short orbital period of HE 0024-2523 in this common-envelope scenario, provided that the envelope ejection was very inefficient (i.e. the fraction of the orbital energy used to unbind the common envelope is small at only a few percent). This system furthermore raises the (unsolved) question of whether or not accretion is possible during the common-envelope stage (Ricker & Taam 2008; MacLeod & Ramirez-Ruiz 2015). In the Abate et al. (2015a) scenario for HE 0024-2523, accretion did occur during a brief phase of wind accretion or wind Roche-lobe overflow prior to the common-envelope stage. A similar requirement was invoked by Miszalski et al. (2013) for the carbon star at the centre of the Necklace planetary nebula.
 |
Fig. 6 P − e diagram for CEMP-s and CH stars (crosses; squared crosses correspond to carbon dwarfs), and barium stars (from Gorlova et al. 2013,filled squares: strong barium stars – Ba4 and Ba5; open squares: mild barium stars – Ba1 to Ba3, according to the classification by Lü et al. 1983). |
 |
Fig. 7 P − e diagram for normal K giants in open clusters (black open circles; from Mermilliod et al. 2007) and for non-CEMP low-metallicity giants (red triangles; from Carney et al. 2003). |
 |
Fig. 8 Distribution dN/de of the number of systems per eccentricity bins for normal K giants in open clusters with periods in excess of 400 d (Mermilliod et al. 2007). |
At the other end of the period range (with periods in excess of 104 d) lie HD 26 and HD 76396 (Table 4), and possibly HD 145777, HD 187216, HE 1429-0551, and HE 2144-1832 as well, if these finally turn out to be very long-period binaries. The corresponding frequency of CH/CEMP-s systems with orbital periods in excess of ∼104 d must thus be of the order of 2/44 (=4.5%), and possibly up to 6/44 (=14%). These frequencies may be used to constrain the binary-evolution models of Abate et al. (2015b), which predict a lot more of these long-period systems (their Fig. 8) than is actually observed. A more detailed comparison is beyond the scope of the present paper, however.
5.2.2. CH/CEMP-s vs. metal-poor non-CEMP systems
Figure 5 also compares CH/CEMP-s systems with binary metal-poor giants that do not belong to the CH/CEMP-s family (from Carney et al. 2003). The latter systems do not bear chemical signatures of mass transfer, and may therefore be considered as pre-mass-transfer systems. It is very clear that, at a given orbital period, the post-mass-transfer CH/CEMP-s systems have on average a smaller eccentricity. A similar difference between pre- and post-mass-transfer systems has been observed among the solar-metallicity counterparts of CH/CEMP-s systems, namely the barium systems: at a given orbital period, barium systems have a smaller average eccentricity than normal K giants (Jorissen et al. 2009), as may be inferred from the comparison of Figs. 6 and 7.
Because the sample of K giants from open clusters mostly (although not exclusively; Van der Swaelmen et al., in prep.) contains pre-mass-transfer binaries, this may serve to define the initial distribution of eccentricities, which is of interest to modellers of binary-population syntheses. The distribution dN/de of the number of systems per eccentricity bins for normal K giants in open clusters is plotted in Fig. 8 for a sample restricted to P> 400 d because the eccentricity distribution at shorter periods has been altered by circularisation processes.
5.2.3. CH/CEMP-s vs. barium systems
In Fig. 6, we compare CH/CEMP-s systems, considered as a single group, with barium systems (whose orbital elements are taken from Gorlova et al. 2013). Overall, the two families cover the same region of the P − e diagram, nevertheless, with a few notable differences:
-
There are two CEMP stars with much shorter periods than barium systems, as already discussed in Sect. 5.2.1.
-
There is a lack of large eccentricity systems among CH/CEMP-s stars. This effect could result from an observational bias, since systems with high eccentricities often require a longer time coverage to derive the corresponding orbits, and CH/CEMP-s were not monitored as long as were barium systems.
-
The proportion of low-eccentricity systems is much larger among CH/CEMP-s systems. This is clearly apparent in the lower panel of Fig. 9, which compares the cumulative frequency distributions of eccentricities for barium and CH/CEMP-s stars. The shift between the cumulative distributions at low eccentricities is clearly not a consequence of the difference already reported at large eccentricities, as shown by the red dashed curve in Fig. 9, which corresponds to the sample of barium stars restricted to systems with e< 0.5. The difference persists between the CH/CEMP-s sample and this sample of barium stars restricted to low eccentricities. The tendency for the low-metallicity CH/CEMP-s systems to have lower eccentricities than their solar-metallicity barium-system counterparts must have some physical origin, yet to be clarified, related to mass transfer. The role of mass transfer in this eccentricity difference is deduced from the fact that a similar comparison for systems with no chemical anomalies (i.e. non-CEMP low-metallicity giants studied by Carney et al. 2003; and normal K giants in open clusters studied by Mermilliod et al. 2007) reveals no difference in the eccentricity distributions, despite the difference in metallicity (Fig. 7 and upper panel of Fig. 9), when the systems involved are pre-mass-transfer systems.
 |
Fig. 9 Cumulative distribution of eccentricities for CH/CEMP-s stars (blue curve in lower panel) and barium stars (black curve in lower panel). The solid black line corresponds to the full barium star sample, whereas the dashed red line corresponds to the barium star sample restricted to e< 0.5. In the upper panel, the red line corresponds to metal-deficient non-CEMP giants and the solid black curve to K giants in open clusters. |
The sample of barium systems reveals moreover the existence of a lack of systems at low e and large P (which we call the low-e large-P gap in the following). This gap is especially clearly apparent as well in samples of pre- and young main-sequence binaries (Mathieu 1992), and indicates that binaries only form as eccentric systems. In young binaries, the gap extends up to e = 0.15. At the shortest periods, the gap disappears, filled by tidally-circularised systems, and the period threshold for the gap depends on the age of the systems and the efficiency with which tides act to circularise the orbits. In evolved systems (like the post-mass-transfer barium and CEMP/CH stars; Fig. 6), the gap is still present, although to a more limited extent (up to e = 0.05). This is a signature of orbital evolution during mass transfer (see for example the binary population-synthesis models of Izzard et al. 2010, which confirm that there should be very few of these systems). For all samples with orbital eccentricities accurately known, this gap is never populated. It is thus likely that the eccentricity has not been derived with enough accuracy for the two CH/CEMP-s systems (HD 30443 and CS 29497-034) falling into the gap in Fig. 6. Low-eccentricity orbits need a good many measurements spread over the whole orbital cycle to have the eccentricity accurately determined, and this condition is sometimes difficult to achieve for long-period systems. The latter remark applies to CS 29497-034 (Barbuy et al. 2005), whereas HD 30443 has a noisy orbital solution whose eccentricity has been fixed at 0.0 (McClure & Woodsworth 1990).
To end this comparison between the orbital properties (P − e diagram and mass-function distribution) of CH/CEMP-s and barium stars, we may conclude that a mass-transfer scenario similar to that proposed to account for the chemical peculiarities of barium stars has been at work in CH/CEMP-s stars as well (McClure et al. 1980; Boffin & Jorissen 1988; Preston & Sneden 2001; Lucatello et al. 2005; Masseron et al. 2010; Izzard et al. 2010; Bisterzo et al. 2012; Abate et al. 2013; Starkenburg et al. 2014).
6. A correlation between orbital period and s-process overabundance?
The availability of orbital elements, and especially orbital periods, makes it possible to investigate a possible correlation between the orbital separation and the s-process overabundance level. This kind of correlation (or the absence thereof) provides clues about the mass-transfer process responsible for the pollution of the CEMP/CH star: Roche-lobe overflow, wind Roche-lobe overflow, or wind accretion (see Abate et al. 2013, 2015a,b). A tentative investigation of this kind of correlation was performed by Jorissen & Boffin (1992) for barium stars, but using a photometric proxy for the s-process overabundance (see also Boffin & Zacs 1994). A general trend was found albeit with a very large dispersion. On the other hand, population synthesis models of Bonačić Marinović & Pols (2004) predict a maximum overabundance level for periods around 1000 d, with the overabundance level going down at both longer and shorter periods.
With the present sample, a similar investigation may be attempted for CH/CEMP-s systems.
Several caveats have to be expressed, however. First, it is not the orbital period, but
rather the orbital separation, or even the periastron distance, which is the key dynamical
parameter controlling the mass transfer. For the sample considered, we showed in Sect. 5.1 that the masses are confined in a narrow range, both
for the primaries and the secondaries. Moreover, eccentricities remain moderate, so that
orbital periods are expected to be good proxies for the periastron distance. Second, in
low-metallicity stars, the s-process operation may produce a substantial amount of
Pb (e.g. Gallino et al. 1998; Goriely & Mowlavi 2000; Van Eck et
al. 2001, 2003, although it does not
necessarily do this in a systematic way; see the discussion by De Smedt et al. 2014). At
least for the CEMP/CH stars in Table 4, when the Pb
abundance is available, it is in fact the dominant contributor to the s-process nuclei, as is
apparent below. Therefore, the investigation of a possible correlation orbital-period –
s-process
overabundance should be restricted to those systems for which Pb abundances are available.
Finally, if, as seems likely, 13C(α,n)16O is the neutron source (Straniero et al. 1995; Neyskens et al.
2015), the number of neutrons produced does not scale with metallicity (Clayton 1988), since they result from primary seeds
[protons and 12C,
leading to 12C(p,γ)13N(β)13C(α,n)16O]. Assuming otherwise identical structures and mixing
scheme, this means that the number of neutrons made available by the above reaction chain is
always the same, irrespective of the metallicity. That number of neutrons is expressed
relative to the number of hydrogen (not Fe) atoms, and may be extracted from the observed
abundance pattern in the following way: ![\begin{eqnarray} \label{Eq:s} N_{\rm neut} &= &\! \Sigma_i (A_i - 56) \left[ N_i(\mathrm{star}) - N_i(\mathrm{scaled-solar}) \right] \nonumber\\ &= &\! \Sigma_i (A_i - 56) \; \left[ 10^{\left( [i/\mathrm{Fe}] + [\mathrm{Fe/H}] + \log N_i(\mathrm {sun})\right)} \right.\\ & & \left.- 10^{\left( [\mathrm{Fe/H}] + \log N_i(\mathrm{sun}) \right) } \right], \nonumber \end{eqnarray}](/articles/aa/full_html/2016/02/aa26992-15/aa26992-15-eq170.png) (1)where Ni(star) is the number of
nuclei of species i per 1012 hydrogen atoms observed in the star, Ai is the atomic mass
number, and the sum includes Zr (or Sr if Zr is not available), La, and Pb. Solar abundances
were adopted from Table 3 of Lodders (2008), namely
log NSr(sun) =
2.90, log NZr(sun) = 2.57, log NLa(sun) =
1.19, log NPb(sun) = 2.06. The available data
are collected in Table 4.
(1)where Ni(star) is the number of
nuclei of species i per 1012 hydrogen atoms observed in the star, Ai is the atomic mass
number, and the sum includes Zr (or Sr if Zr is not available), La, and Pb. Solar abundances
were adopted from Table 3 of Lodders (2008), namely
log NSr(sun) =
2.90, log NZr(sun) = 2.57, log NLa(sun) =
1.19, log NPb(sun) = 2.06. The available data
are collected in Table 4.
The quantity Nneut is thus a measure of the neutron contamination, sensitive to dilution. The key point here is that the number Nneut is derived from the fraction of s-process material that found its way to the CEMP/CH-star atmosphere. This material, however, is only a fraction of the total amount originally produced in the inner shell of the AGB star, which has subsequently been diluted three times: first, when brought from the AGB interior to its outer atmosphere, then when a fraction of the s-process-enriched AGB wind was captured by the companion star, and, finally, when that accreted material was diluted in the CH/CEMP-star envelope (and the latter dilution thus depends on the evolutionary status of the companion, which may have, or not, a deep convective envelope). We want to evaluate the second dilution factor, directly related to the accretion cross section, which is in turn a function of the orbital separation. This dilution factor causes the estimated number of neutrons to be less than that originally available in the AGB interior, which we suppose to be a constant and the same for all AGB stars irrespective of their mass or metallicity. Thus, any fluctuation in the estimated neutron number is attributed to the variation of the mass accretion efficiency (assuming that the other two dilutions involved are the same in all cases). We must hope that the variations of the latter two dilution factors are smaller than the effect related to the mass-accretion efficiency that we try to measure.
As far as one may judge from column Nneut in Table 4, there is no obvious trend emerging with orbital period. Therefore, our data confirm once more that the orbital period is not the only parameter governing the level of s-process overabundances in post-mass-transfer systems (see also Abate et al. 2015a, for a recent analysis). The dilution factors discussed above (and neglected in the analysis) may play an important role, or as Merle et al. (2015) have suggested, the mass of the companion WD (a proxy for the luminosity reached by its progenitor on the AGB) could be another important parameter controlling the level of s-process overabundance.
7. Conclusions
We report eight new orbits for CH and CEMP-s systems obtained by combining new radial-velocity measurements from the HERMES/Mercator spectrograph with old measurements from McClure & Woodsworth (1990). HIP 53522 is a newly discovered binary and also is a new member of the CH(-like) family, as revealed by a detailed abundance analysis. Adding these new orbits to the 33 CH/CEMP-s orbits already available in the literature, their P − e and f(M) distributions have been investigated and reveal no difference between CH and CEMP-s systems. These families should thus not be treated separately, since their different names stem from historical reasons but cover the same underlying stellar family. The analysis of the mass-function distribution of CH and CEMP-s systems points at companions having a mass peaked in the range 0.5–0.7 M⊙, thus supporting the usual scenario of s-process pollution from a former AGB star, now the white-dwarf companion. The signature of the mass-transfer scenario is also apparent from the comparison between the P − e distributions of CH/CEMP-s stars and of non-carbon-enriched, low-metallicity giants (thus being likely pre-mass-transfer systems), the former having a smaller average eccentricity at a given orbital period.
CH/CEMP-s orbits are then compared to those of barium stars, which are their higher metallicity analogues. Despite minor quantitative differences (i.e. a larger fraction of low-eccentricity orbits among CH/CEMP-s stars, and a deficit of large eccentricity systems), the global distribution of these families in the P − e diagram is similar, suggesting that they followed the same binary-evolution channel. It is not clear at this stage whether the different eccentricity distributions result from observational selection biases, or from the influence of metallicity on the outcome of the mass transfer.
At least three CH/CEMP-s stars (HE 0017+055, HE 1120-2122, and HD 76396) exhibit short-term, radial-velocity variations (with periods close to 1 yr), and it is not clear yet whether this behaviour is attributable to some intrinsic phenomenon causing velocity jitter, or whether it is due to Keplerian variations of small amplitude (see Carney et al. 2003; Jorissen et al. 2016, for a discussion of this alternative).
available at http://obswww.unige.ch/~udry/std/std.html
While the present paper was being refereed, we learned about the orbits obtained by Sperauskas et al. (2015) for HIP 53522 and HIP 53832, and by Hansen et al. (2016) for HE 0111-1346 and HE 0507-1653, in common with the present sample. The orbital elements for these systems obtained by these independent studies are very similar to ours.
The “carbon dwarf wearing a necklace” mentioned above is another example of a short-period (1.16 d), post-common-envelope system (Corradi et al. 2011; Miszalski et al. 2013).
The binaries with blue-straggler primaries, which must be post-mass-transfer binaries as are CH/CEMP-s stars, reveal a large number of nearly circular systems with periods shorter than 1000 d as well (Fig. 4 of Carney et al. 2005).
While the present paper was being refereed, we learned about the abundance analysis of that same star made independently by Sperauskas et al. (2015), with results very similar to ours.
Acknowledgments
This research has been funded by the Belgian Science Policy Office under contract BR/143/A2/STARLAB. T.M. is supported by the FNRS-F.R.S. as temporary post-doctoral researcher under grant No. T.0198.13. S.v.E. is FNRS research associate. Based on observations obtained with the HERMES spectrograph, supported by the Fund for Scientific Research of Flanders (FWO), the Research Council of K.U. Leuven, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland, and the Thüringer Landessternwarte Tautenburg, Germany.
References
- Abate, C.,Pols, O. R.,Izzard, R. G.,Mohamed, S. S., & de Mink, S. E. 2013, A&A, 552, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abate, C.,Pols, O. R.,Karakas, A. I., &Izzard, R. G. 2015a, A&A, 576, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abate, C.,Pols, O. R.,Izzard, R. G., &Karakas, A. I. 2015b, A&A, 581, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, D. M.,Ryan, S. G.,Rossi, S.,Beers, T. C., &Tsangarides, S. A. 2012, A&A, 548, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez, R., &Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Aoki, W.,Norris, J. E.,Ryan, S. G.,Beers, T. C., &Ando, H. 2002, ApJ, 567, 1166 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W.,Beers, T. C.,Christlieb, N., et al. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W.,Beers, T. C.,Lee, Y. S., et al. 2013, AJ, 145, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A.,Mayor, M., &Poncet, J. L. 1979, Vistas in Astronomy, 23, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Barbuy, B.,Cayrel, R.,Spite, M., et al. 1997, A&A, 317, L63 [NASA ADS] [Google Scholar]
- Barbuy, B.,Spite, M.,Spite, F., et al. 2005, A&A, 429, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beers, T. C., &Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C.,Preston, G. W., &Shectman, S. A. 1992, AJ, 103, 1987 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C.,Sivarani, T.,Marsteller, B., et al. 2007, AJ, 133, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeat, J.,Knapik, A., &Rutily, B. 2001, A&A, 369, 178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S.,Castelli, F., &Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
- Bidelman, W. P. 1956, Vistas in Astronomy, 2, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Bidelman, W. P., &Keenan, P. C. 1951, ApJ, 114, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S.,Gallino, R.,Straniero, O.,Cristallo, S., &Käppeler, F. 2011, MNRAS, 418, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S.,Gallino, R.,Straniero, O.,Cristallo, S., &Käppeler, F. 2012, MNRAS, 422, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Boffin, H. M. J. 2010, A&A, 524, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boffin, H. M. J. 2012, in Proc. Orbital Couples: Pas de Deux in the Solar System and the Milky Way, 41 [Google Scholar]
- Boffin, H. M. J., &Jorissen, A. 1988, A&A, 205, 155 [NASA ADS] [Google Scholar]
- Boffin, H. M. J., &Zacs, L. 1994, A&A, 291, 811 [NASA ADS] [Google Scholar]
- Boffin, H. M. J., Paulus, G., & Cerf, N. 1992, Binaries as Tracers of Star Formation (Cambridge: Cambridge University Press), 26 [Google Scholar]
- Boffin, H. M. J.,Cerf, N., &Paulus, G. 1993, A&A, 271, 125 [NASA ADS] [Google Scholar]
- BonačićMarinović, A. A., &Pols, O. R. 2004, Mem. Soc. Astron. Italiana, 75, 760 [Google Scholar]
- Bonačić Marinović, A. A.,Glebbeek, E., &Pols, O. R. 2008, A&A, 480, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bond, H. E. 1974, ApJ, 194, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carney, B. W.,Latham, D. W.,Stefanik, R. P.,Laird, J. B., &Morse, J. A. 2003, AJ, 125, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Carney, B. W.,Latham, D. W., &Laird, J. B. 2005, AJ, 129, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Cerf, N., &Boffin, H. M. J. 1994, Inverse Problems, 10, 533 [Google Scholar]
- Christlieb, N. 2003, Rev. Mod. Astron., 16, 191 [NASA ADS] [EDP Sciences] [Google Scholar]
- Christlieb, N.,Green, P. J.,Wisotzki, L., &Reimers, D. 2001, A&A, 375, 366 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clayton, D. D. 1988, MNRAS, 234, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Corradi, R. L. M.,Sabin, L.,Miszalski, B., et al. 2011, MNRAS, 410, 1349 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N. 1999, Allen’s astrophysical quantities (AIP) [Google Scholar]
- Dearborn, D. S. P.,Liebert, J.,Aaronson, M., et al. 1986, ApJ, 300, 314 [NASA ADS] [CrossRef] [Google Scholar]
- De Smedt, K., Van Winckel, H.,Kamath, D., et al. 2014, A&A, 563, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcon, R. E.,Winget, D. E.,Montgomery, M. H., &Williams, K. A. 2010, ApJ, 712, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Gallino, R.,Arlandini, C.,Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gilmore, G.,Randich, S.,Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Goriely, S., &Mowlavi, N. 2000, A&A, 362, 599 [NASA ADS] [Google Scholar]
- Gorlova, N., Van Winckel, H.,Vos, J., et al. 2013, EAS Pub. Ser., 64, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goswami, A. 2005, MNRAS, 359, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Goswami, A., &Aoki, W. 2010, MNRAS, 404, 253 [NASA ADS] [Google Scholar]
- Goswami, A.,Aoki, W.,Beers, T. C., et al. 2006, MNRAS, 372, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Goswami, A.,Karinkuzhi, D., &Shantikumar, N. S. 2010, MNRAS, 402, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N.,Asplund, M., &Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Gustafsson, B.,Edvardsson, B.,Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, Z.,Eggleton, P. P.,Podsiadlowski, P., &Tout, C. A. 1995, MNRAS, 277, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, T. T., Andersen, J., Nordström, B., et al. 2016, A&A, in press, DOI: 10.1051/0004-6361/201527409 [Google Scholar]
- Hartwick, F. D. A., &Cowley, A. P. 1985, AJ, 90, 2244 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V.,Barbuy, B.,Spite, M., et al. 2000, A&A, 353, 557 [NASA ADS] [Google Scholar]
- Izzard, R. G.,Glebbeek, E.,Stancliffe, R. J., &Pols, O. R. 2009, A&A, 508, 1359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G.,Dermine, T., &Church, R. P. 2010, A&A, 523, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jofré, P.,Heiter, U.,Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorissen, A. 2004, in Asymptotic Giant Branch Stars, eds. H. J. Habing, & H. Olofsson (New York: Springer Verlag), 461 [Google Scholar]
- Jorissen, A., & Boffin, H. M. J. 1992, in Binaries as Tracers of Star Formation, eds. A. Duquennoy & M. Mayor (Cambridge Univ. Press), 110 [Google Scholar]
- Jorissen, A., &Mayor, M. 1988, A&A, 198, 187 [NASA ADS] [Google Scholar]
- Jorissen, A., &Mayor, M. 1992, A&A, 260, 115 [NASA ADS] [Google Scholar]
- Jorissen, A., Van Eck, S.,Mayor, M., &Udry, S. 1998, A&A, 332, 877 [NASA ADS] [Google Scholar]
- Jorissen, A.,Začs, L.,Udry, S.,Lindgren, H., &Musaev, F. A. 2005, A&A, 441, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorissen, A.,Frankowski, A.,Famaey, B., & van Eck, S. 2009, A&A, 498, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorissen, A.,Hansen, T., Van Eck, S., et al. 2016, A&A, 586, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keenan, P. C. 1942, ApJ, 96, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, C. R.,Sivarani, T.,Beers, T. C., et al. 2011, AJ, 141, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kipper, T., &Jorgensen, U. G. 1994, A&A, 290, 148 [NASA ADS] [Google Scholar]
- Kiss, L. L., &Bedding, T. R. 2003, MNRAS, 343, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F. G.,Ryabchikova, T. A.,Piskunov, N. E.,Stempels, H. C., &Weiss, W. W. 2000, Balt. Astron., 9, 590 [NASA ADS] [Google Scholar]
- Lee, Y. S.,Beers, T. C.,Masseron, T., et al. 2013, AJ, 146, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2008, in Principles and Perspectives in Cosmochemistry, Astrophys. Space Sci. Proc. (Berlin, Heidelberg: Springer-Verlag), 2010, 379 [Google Scholar]
- Lu, P. K.,Dawson, D. W.,Upgren, A. R., &Weis, E. W. 1983, ApJS, 52, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S.,Gratton, R.,Cohen, J. G., et al. 2003, AJ, 125, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S.,Tsangarides, S.,Beers, T. C., et al. 2005, ApJ, 625, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S.,Beers, T. C.,Christlieb, N., et al. 2006, ApJ, 652, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., &Bond, H. E. 1991, ApJS, 77, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1974, AJ, 79, 745 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, M., &Ramirez-Ruiz, E. 2015, ApJ, 803, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Masseron, T. 2006, Ph.D. Thesis, Observatoire de Paris [Google Scholar]
- Masseron, T., van Eck, S.,Famaey, B., et al. 2006, A&A, 455, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T.,Johnson, J. A.,Plez, B., et al. 2010, A&A, 509, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathieu, R. D. 1992, in Binaries as Tracers of Star Formation, eds. A. Duquennoy, & M. Mayor (Cambridge University Press), 155 [Google Scholar]
- Mayall, M. W., &Cannon, A. J. 1940, Harvard College Observatory Bulletin, 913, 7 [NASA ADS] [Google Scholar]
- McClure, R. D. 1984, ApJ, 280, L31 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, R. D. 1997, PASP, 109, 256 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, R. D., &Woodsworth, A. W. 1990, ApJ, 352, 709 [NASA ADS] [CrossRef] [Google Scholar]
- McClure, R. D.,Fletcher, J. M., &Nemec, J. M. 1980, ApJ, 238, L35 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, I.,Zijlstra, A. A., &Boyer, M. L. 2012, MNRAS, 427, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Merle, T.,Jorissen, A.,Masseron, T., et al. 2014, A&A, 567, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merle, T., Jorissen, A., Van Eck, S., Masseron, T., & Van Winckel, H. 2015, A&A, submitted [Google Scholar]
- Mermilliod, J.-C.,Andersen, J.,Latham, D. W., &Mayor, M. 2007, A&A, 473, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miszalski, B.,Boffin, H. M. J., &Corradi, R. L. M. 2013, MNRAS, 428, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Neyskens, P., van Eck, S.,Jorissen, A., et al. 2015, Nature, 517, 174 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Placco, V. M.,Frebel, A.,Beers, T. C., &Stancliffe, R. J. 2014, ApJ, 797, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B. 2012, Astrophysics Source Code Library, 5004 [Google Scholar]
- Plez, B., &Cohen, J. G. 2005, A&A, 434, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pols, O. R., Karakas, A. I., Lattanzio, J. C., & Tout, C. A. 2003, Symbiotic Stars Probing Stellar Evolution, eds. R. L. M. Corradi, R. Mikolajewska, & T. J. Mahoney, ASP Conf. Ser., 303, 290 [Google Scholar]
- Pompéia, L., Masseron, T., Famaey, B. et al. 2011, MNRAS, 415, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Pourbaix, D.,Jancart, S., &Boffin, H. M. J. 2004, Rev. Mex. Astron. Astrofis., 21, 265 [Google Scholar]
- Preston, G. W., &Sneden, C. 2000, AJ, 120, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- Preston, G. W., &Sneden, C. 2001, AJ, 122, 1545 [NASA ADS] [CrossRef] [Google Scholar]
- Raskin, G., van Winckel, H.,Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, P. M., &Taam, R. E. 2008, ApJ, 672, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Sanford, R. F. 1944, ApJ, 99, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Sivarani, T.,Bonifacio, P.,Molaro, P., et al. 2004, A&A, 413, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, V. V., &Lambert, D. L. 1988, ApJ, 333, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C.,Cowan, J. J.,Lawler, J. E., et al. 2003a, ApJ, 591, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C.,Preston, G. W., &Cowan, J. J. 2003b, ApJ, 592, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Sperauskas, J., Začs, L., Schuster, W.J., & Deveikis, V., 2015, ApJ, submitted [Google Scholar]
- Starkenburg, E.,Shetrone, M. D.,McConnachie, A. W., &Venn, K. A. 2014, MNRAS, 441, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Straniero, O.,Gallino, R.,Busso, M., et al. 1995, ApJ, 440, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., Mayor, M., & Queloz, D. 1999, in Precise Stellar Radial Velocities, IAU Colloq., 170, ASP Conf. Ser.185, 367 [Google Scholar]
- Vandervort, G. L. 1958, AJ, 63, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eck, S.,Goriely, S.,Jorissen, A., &Plez, B. 2001, Nature, 412, 793 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Van Eck, S.,Goriely, S.,Jorissen, A., &Plez, B. 2003, A&A, 404, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Winckel, H.,Jorissen, A.,Gorlova, N., et al. 2010, Mem. Soc. Astron. Italiana, 81, 1022 [Google Scholar]
- Webbink, R. F. 1988, in Colloq. Critical Observations Versus Physical Models for Close Binary Systems, 403 [Google Scholar]
- Wood, P. R. 2000, PASA, 17, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Yamashita, Y. 1975, PASJ, 27, 325 [NASA ADS] [Google Scholar]
- Yanny, B.,Rockosi, C.,Newberg, H. J., et al. 2009, AJ, 137, 4377 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D.,Norris, J. E.,Bessell, M. S., et al. 2013, ApJ, 762, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Zamora, O.,Abia, C.,Plez, B.,Domínguez, I., &Cristallo, S. 2009, A&A, 508, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Abundance analysis of HIP 53522
This appendix describes the abundance analysis performed for HIP 53522, since this kind of analysis has not been available so far5 for that star first classified as R by Vandervort (1958) and then reclassified as CH by Hartwick & Cowley (1985) and CH-like by Sperauskas et al. (2015). The determination of its atmospheric parameters and s-process element abundances follows the same steps as in Merle et al. (2014). The HERMES/Mercator spectrum selected for the analysis was obtained on April 10, 2010 (HJD 2 455 296.567), with an exposure time of 2600 s and a signal-to-noise ratio of about 50. The synthetic spectra were convolved with a Gaussian function with full width at half maximum of 6 km s-1.
Appendix A.1: Atmospheric parameters
Previous studies of HIP 53522 (Bergeat et al. 2001; McDonald 2012) have obtained effective temperatures of 4955 and 4761 K, respectively. Surface gravity and metallicity are determined iteratively using the BACCHUS pipeline (Jofré et al. 2014) developed by one of the authors (TMa) in the context of the Gaia-ESO survey (Gilmore et al. 2012). This pipeline is based on the 1D LTE spectrum-synthesis code Turbospectrum (Alvarez & Plez 1998; Plez 2012), and facilitates an automated determination of effective temperature Teff, surface gravity log g, metallicity [Fe/H], and microturbulent velocity ξ. We use MARCS model atmospheres (Gustafsson et al. 2008) along with a selection of neutral and singly ionised Fe lines that were selected for the analysis of stellar spectra in the framework of the Gaia-ESO survey. Oscillator strengths are from the VALD database (Kupka et al. 2000). We only kept lines with reduced equivalent widths (W/λ) lower than 0.03 mÅ/Å in the analysis. We thus obtain the following atmospheric parameters: Teff= 4505 ± 160 K, log g = 1.7 ± 0.9, [Fe/H] = −0.46 ± 0.07, and ξ = 1.5 ± 0.1 km s-1. Solar abundances are from Grevesse et al. (2007), where A⊙(Fe) = 7.45.
Appendix A.2: s-process element abundances
The atomic lines used to derive abundances of s-process elements are listed in Table A.2, along with their oscillator strengths, taken from the VALD database (Kupka et al. 2000). The list includes the isotopic shifts and hyperfine structure for Ba ii lines and the hyperfine structure for La ii and Ce ii lines from Masseron (2006). Abundances are derived from the best match with a synthetic spectrum. For barium, the solar-system isotopic mix is adopted. The results of the abundance analysis are presented in Table A.1.
An average light-s-process abundance of [ls/Fe] = 1.20 ± 0.10 is obtained, based on Sr, Y, and Zr abundances, as compared to [hs/Fe] = 1.15 ± 0.10, based on Ba, La, and Ce abundances. Thus HIP 53522 is clearly enriched in s-process elements.
 |
Fig. A.1 Fe i and Fe ii abundances (represented by crosses and filled circles, respectively) derived from individual lines as a function of lower excitation potential χ (upper panel) and of reduced equivalent width W/λ (lower panel). The grey areas represent the standard deviations around the mean abundances of Fe i and Fe ii. |
Results of the chemical abundance analysis.
Lines used for deriving the s-process element abundances.
Appendix B: Radial-velocity curves
This appendix collects all figures presenting radial-velocity curves and orbits, listed in the same order as in Sect. 4: SB? (Fig. B.1), SB (Figs. B.2–B.4), ORB (i.e. orbits with no significant residuals; Figs. B.5–B.10), and finally SB+jitter or ORB+jitter (i.e. long-term trend or orbit with superimposed short-term variations; Figs. B.11–B.13). Individual radial velocities are available at the CDS.
HE 0507-1653 with its high radial velocity (350.2 km s-1; Fig. B.7) is particularly remarkable. Its proper motion has been estimated from the positions listed in the 2MASS catalogue (J05091656-1650046, epoch 1998.96, ICRS 2000: α = 77.319009,δ = −16.834616) and USNO-B catalogue (0731-0088818, epoch 1950, ICRS 2000: α = 77.318951,δ = −16.834659), namely μα = 4.3 mas yr-1, μδ = 3.1 mas yr-1. This proper motion is not especially large, and should not add a substantial contribution to the large radial velocity. An accurate space velocity cannot be computed, though, in the absence of a distance estimate for that star.
 |
Fig. B.1 Radial-velocity data for HE 1429-0551. |
 |
Fig. B.3 As Fig. B.1 for HD 187216, including data from McClure & Woodsworth (1990). |
 |
Fig. B.5 Orbital solution for HE 0111-1346. The lower panel shows the O−C deviations. |
 |
Fig. B.10 As Fig. B.5 for HD 26. The velocity point around JD 2 452 000 is from Van Eck et al. (2003), and the oldest measurements are from CORAVEL (Baranne et al. 1979). The HERMES and CORAVEL measurements are all on the IAU scale. The orbital elements are not yet fully constrained (the orbital period could be longer). |
 |
Fig. B.11 As Fig. B.1 for HE 0017+0055, showing the short- and long-term orbital fits combined (top) as well as the short-term orbit alone (red dots: HERMES velocities; blue plusses: Nordic Optical Telescope velocities; for details, see Jorissen et al. 2016, and Table 3). |
 |
Fig. B.12 As Fig. B.5 for HE 1120-2122. The lower panel shows the low-amplitude, short-period variations through the O−C residuals (see Table 3). |
 |
Fig. B.13 Top panel: as Fig. B.5 for HD 76396. Bottom panel: zoom on the HERMES data, with the O−C showing periodic variations (see Table 3). |
All Tables
All Figures
 |
Fig. 1 Typical CCF for the CEMP-s star HE 1120-2122 on HJD 2 456 804.428, based on a spectrum with an exposure time of 1800 s. The Gaussian fit of the CCF is the thin solid line, restricted to the CCF core to reduce the impact of line asymmetries as much as possible. The vertical line indicates the star radial velocity, as derived from the Gaussian fit. |
| In the text | |
 |
Fig. 2 Histogram of the standard deviations of the velocity data for radial-velocity standard stars with more than five measurements spread over 4.5 years of monitoring. |
| In the text | |
 |
Fig. 3 The distribution of the secondary masses Φ(M2) (normalised such that
|
| In the text | |
 |
Fig. 4 Observed distribution of the mass functions f(M1,M2) (in solar-mass units; solid black histogram) superimposed on a synthetic distribution (dashed red curve with statistical error bars) resulting from the assumptions of random orientation of the orbital planes on the sky and fixed value of Q = 0.094 M⊙. |
| In the text | |
 |
Fig. 5 Comparison of CEMP stars (filled symbols) and CH stars (open symbols) in the period – eccentricity (P − e) diagram. Dwarf carbon stars are represented by circles, giant carbon stars by squares (CEMP stars with unknown gravities in Table 4 are assigned giant status by default). For comparison, the sample of low-metallicity giants studied by Carney et al. (2003) is represented with red triangles. |
| In the text | |
 |
Fig. 6 P − e diagram for CEMP-s and CH stars (crosses; squared crosses correspond to carbon dwarfs), and barium stars (from Gorlova et al. 2013,filled squares: strong barium stars – Ba4 and Ba5; open squares: mild barium stars – Ba1 to Ba3, according to the classification by Lü et al. 1983). |
| In the text | |
 |
Fig. 7 P − e diagram for normal K giants in open clusters (black open circles; from Mermilliod et al. 2007) and for non-CEMP low-metallicity giants (red triangles; from Carney et al. 2003). |
| In the text | |
 |
Fig. 8 Distribution dN/de of the number of systems per eccentricity bins for normal K giants in open clusters with periods in excess of 400 d (Mermilliod et al. 2007). |
| In the text | |
 |
Fig. 9 Cumulative distribution of eccentricities for CH/CEMP-s stars (blue curve in lower panel) and barium stars (black curve in lower panel). The solid black line corresponds to the full barium star sample, whereas the dashed red line corresponds to the barium star sample restricted to e< 0.5. In the upper panel, the red line corresponds to metal-deficient non-CEMP giants and the solid black curve to K giants in open clusters. |
| In the text | |
 |
Fig. A.1 Fe i and Fe ii abundances (represented by crosses and filled circles, respectively) derived from individual lines as a function of lower excitation potential χ (upper panel) and of reduced equivalent width W/λ (lower panel). The grey areas represent the standard deviations around the mean abundances of Fe i and Fe ii. |
| In the text | |
 |
Fig. B.1 Radial-velocity data for HE 1429-0551. |
| In the text | |
 |
Fig. B.2 As Fig. B.1 for HD 145777. |
| In the text | |
 |
Fig. B.3 As Fig. B.1 for HD 187216, including data from McClure & Woodsworth (1990). |
| In the text | |
 |
Fig. B.4 As Fig. B.1 for HE 2144-1832. |
| In the text | |
 |
Fig. B.5 Orbital solution for HE 0111-1346. The lower panel shows the O−C deviations. |
| In the text | |
 |
Fig. B.6 As Fig. B.5 for HE 0457-1805. |
| In the text | |
 |
Fig. B.7 As Fig. B.5 for HE 0507-1653. |
| In the text | |
 |
Fig. B.8 As Fig. B.5 for HIP 53522. |
| In the text | |
 |
Fig. B.9 As Fig. B.5 for HIP 53832. |
| In the text | |
 |
Fig. B.10 As Fig. B.5 for HD 26. The velocity point around JD 2 452 000 is from Van Eck et al. (2003), and the oldest measurements are from CORAVEL (Baranne et al. 1979). The HERMES and CORAVEL measurements are all on the IAU scale. The orbital elements are not yet fully constrained (the orbital period could be longer). |
| In the text | |
 |
Fig. B.11 As Fig. B.1 for HE 0017+0055, showing the short- and long-term orbital fits combined (top) as well as the short-term orbit alone (red dots: HERMES velocities; blue plusses: Nordic Optical Telescope velocities; for details, see Jorissen et al. 2016, and Table 3). |
| In the text | |
 |
Fig. B.12 As Fig. B.5 for HE 1120-2122. The lower panel shows the low-amplitude, short-period variations through the O−C residuals (see Table 3). |
| In the text | |
 |
Fig. B.13 Top panel: as Fig. B.5 for HD 76396. Bottom panel: zoom on the HERMES data, with the O−C showing periodic variations (see Table 3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.