| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527041 | |
| Published online | 09 December 2015 | |
The star formation history of low-mass disk galaxies: A case study of NGC 300
1 Yunnan Observatories, Chinese Academy of Sciences, 650011 Kunming, PR China
e-mail: kxyysl@ynao.ac.cn
2 Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, 650011 Kunming, PR China
3 University of Chinese Academy of Sciences, 100049 Beijing, PR China
4 Key Laboratory for Research in Galaxies and Cosmology, Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, 200030 Shanghai, PR China
Received: 23 July 2015
Accepted: 13 October 2015
Context. Since NGC 300 is a bulgeless, isolated low-mass galaxy and it has not experienced radial migration during its evolution history, it can be treated as an ideal laboratory to test the simple galactic chemical evolution model.
Aims. Our main aim is to investigate the main properties of the star formation history (SFH) of NGC 300 and compare its SFH with that of M 33 to explore the common properties and differences between these two nearby low-mass systems.
Methods. We construct a simple chemical evolution model for NGC 300, assuming its disk forms gradually from continuous accretion of primordial gas and including the gas-outflow process. The model allows us to build a bridge between the SFH and observed data of NGC 300, in particular, the present-day radial profiles and global observed properties (e.g., cold gas mass, star formation rate, and metallicity). By means of comparing the model predictions with the corresponding observations, we adopt the classical χ2 methodology to find out the best combination of free parameters a, b, and bout.
Results. Our results show that by assuming an inside-out formation scenario and an appropriate outflow rate, our model reproduces well most of the present-day observational values. The model not only reproduces well the radial profiles, but also the global observational data for the NGC 300 disk. Our results suggest that NGC 300 may experience a rapid growth of its disk. Through comparing the best-fitting, model-predicted SFH of NGC 300 with that of M 33, we find that the mean stellar age of NGC 300 is older than that of M 33 and there is a recent lack of primordial gas infall onto the disk of NGC 300. Our results also imply that the local environment may play a key role in the secular evolution of galaxy disks.
Key words: galaxies: abundances / galaxies: evolution / galaxies: spiral / galaxies: individual: NGC 300
© ESO, 2015
1. Introduction
In order to fully understand the history of the Universe, it is essential to understand the history of the individual galaxies. However, most of disk galaxies are difficult to study in detail because of the complexities of their bulges (Byun & Freeman 1995), tidal interactions, or mergers (Barnes & Hernquist 1992). Fortunately, there are still some disk galaxies that are not involved in major mergers. These are undisturbed and bulgeless (i.e., pure-disk) systems that maintain weak spiral structures to suppress radial migration, making them excellent laboratories to study the secular evolution of galactic disks. At the same time, recent studies have found that massive galaxies have almost finished forming stars at early epochs and a large number of low-mass galaxies exist at all redshifts (e.g., Bauer et al. 2013, and references therein). Moreover, deep surveys detecting masses M∗< 1010 M⊙ have shown that galaxy stellar mass functions have steep slopes at the low-mass end (Baldry et al. 2008, 2012; Kelvin et al. 2014), indicating the necessity to understand the evolutionary history of low-mass galaxies, which are the most populous in the Universe.
The NGC 300 galaxy is the nearest isolated and nearly face-on, low-mass disk galaxy located at a distance of 2.0 Mpc (Dalcanton et al. 2009) in the Sculptor group. In addition, NGC 300 is an almost bulgeless system (Williams et al. 2013), and there is no confusion between disk and bulge populations (bulge light <20%, Vlajić et al. 2009). Both N-body simulations and the kinematics of globular clusters systems studies showed that NGC 300 has not experienced radial migrations during its evolution (Olsen et al. 2004; Gogarten et al. 2010; Nantais et al. 2010). Therefore, NGC 300 is an ideal disk galaxy to test the simple galactic chemical evolution model.
The simple chemical evolution model, which adopts parameterized descriptions for some complicated physical processes, has already been proven to be a powerful tool to explore the formation and evolution of disk galaxies (Tinsley 1980; Chang et al. 1999, 2012; Boissier & Prantzos 2000; Chiappini et al. 2001; Mollá & Díaz 2005; Yin et al. 2009; Kang et al. 2012, 2015), and it has achieved great progress in our understanding of the formation and evolution of disk galaxies in a cosmological context. However, there is still lack of this kind of research on NGC 300. In this paper, we construct a simple chemical evolution model for NGC 300 to build a bridge between its star formation history (SFH) and its observed properties, including both the radial profiles and global observational constraints.
More importantly, NGC 300 is also a near-optical twin of the Local Group galaxy M 33, and Table 1 presents a comparison of their basic properties. Several authors have found an inside-out growth scenario for NGC 300 based on its broadband colors and the color-magnitude diagram (CMD) fitting (Kim et al. 2004; Muñoz-Mateos et al. 2007; Gogarten et al. 2010). Both theoretical models (Kang et al. 2012) and observations (Williams et al. 2009) have shown that M 33 grows inside out. Although they are similar in appearance, M 33 has a disk break at ~8 kpc (Ferguson et al. 2007; Barker et al. 2007, 2011), while NGC 300 has a pure exponential disk out to ~14 kpc (Bland-Hawthorn et al. 2005). Furthermore, there is an HI bridge between M 33 and M 31 (Karachentsev et al. 2004; Putman et al. 2009), indicating the probability that they interacted with each other in the past (Braun & Thilker 2004; McConnachie et al. 2010; San Roman et al. 2010; Bernard et al. 2012). This result is confirmed by the evidence for tidal disruption of M 33’s gas disk (Rogstad et al. 1976; Deul & van der Hulst 1987; Corbelli & Schneider 1997; Karachentsev et al. 2004; Putman et al. 2009). Compared to M 33, NGC 300 is a relatively isolated system, with only dwarf galaxies nearby (Karachentsev et al. 2003; Tully et al. 2006; Williams et al. 2013). The aforementioned differences indicate that they may have significantly different evolution histories, and it should be interesting to compare the SFH of NGC 300 with that of M 33.
The outline of this paper is organized as follows. The observational constraints are presented in Sect. 2. The main ingredients of our model are described in Sect. 3. Comparisons of the model predictions with the present-day observations of NGC 300, as well as comparisons between the SFH of NGC 300 and that of M 33 are shown in Sect. 4. Section 5 presents a summary of our results.
Basic properties of NGC 300 and M 33.
2. Observational constraints
A successful chemical evolution model of NGC 300, especially one involving free parameters, should reproduce as many observational constraints as possible, including both local (concerning the radial profiles) and global constraints (concerning the whole disk). It is well known that during the evolutionary histories of galaxies, the star formation process converts cold gas into stars and stars in turn produce heavy elements by means of nucleosynthesis. These metals are then expelled into the surrounding interstellar medium (ISM) in the later stage of stellar evolution, thus enriching interstellar gas and becoming fuel for the next generation of star formation. That is, the observed present-day metallicity, atomic hydrogen gas and star formation rate (SFR) provide important constraints on the SFH of the galaxy.
2.1. Cold gas and SFR
The atomic hydrogen gas disk associated with NGC 300 is observed to extend far beyond its optical disk. The radial distribution of atomic hydrogen gas for NGC 300 disk is measured with the Australia Telescope Compact Array (ATCA) at a wavelength of λ = 21 cm (Westmeier et al. 2011), and its atomic hydrogen mass has been estimated to be MHI ~ (1.1−1.87) × 109 M⊙ (Rogstad et al. 1979; Barnes et al. 2001; Koribalski et al. 2004; Westmeier et al. 2011; Millar et al. 2011; Wiegert & English 2014). The stellar mass of the NGC 300 disk is estimated to be M∗ ~ 1.928 × 109 M⊙ (Muñoz-Mateos et al. 2007). Thus, we can easily obtain the atomic hydrogen gas fraction (defined as 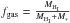 ) of NGC 300, i.e., ~0.363–0.492.
) of NGC 300, i.e., ~0.363–0.492.
Recent SFR surface density profiles of Gogarten et al. (2010) are obtained from the resolved stars, and those from Williams et al. (2013) are derived by the combination of far-ultraviolet (FUV) and 24 μm maps. In recent years, the total SFR in several regions along the NGC 300 disk has been carefully measured by both ground-based and space-based facilities (Helou et al. 2004; Gogarten et al. 2010; Binder et al. 2012; Karachentsev & Kaisina 2013; Williams et al. 2013). The current total SFR for the NGC 300 disk is estimated to be 0.08–0.30 M⊙ yr-1 using different tracers, including the X-ray luminosity (Binder et al. 2012), Hα emission (Helou et al. 2004; Karachentsev & Kaisina 2013), and luminosity in the FUV (Karachentsev & Kaisina 2013) and mid-infrared (MIR, Helou et al. 2004) bands, just a factor of several smaller than the value in the Milky Way disk, which indicates that NGC 300 is currently a rather quiescent galaxy.
2.2. Chemical abundance
Observations of the chemical abundances of a galaxy provide important constraints for the physical processes in the models of galaxy evolution, since the chemical composition is directly related to star formation process. In this case, planetary nebulae (PNe) and Hii regions are good tracers. Generally speaking, they are representative of the chemical abundance in the ISM at two different epochs during the galaxy evolution. In fact, PNe proceed from the death of low- and intermediate-mass stars (1 M⊙<M< 8 M⊙), so they have oxygen abundances approximately equal to the composition of the ISM at the epoch when their progenitors were formed. On the other hand, Hii regions are thought to represent the current chemical composition of the ISM. Moreover, oxygen is the most abundant heavy element formed in the Universe (Korotin et al. 2014; Zahid et al. 2014), and oxygen abundance is easily estimated in Hii regions because of its bright emission line. Therefore, the abundance of oxygen can be used as a proxy for the production of all heavy elements in galaxies (Zahid et al. 2014).
Global observational constraints for the disk of NGC 300.
Radial gas-phase oxygen profiles are regarded as important quantities to constrain our model. The radial gas-phase oxygen abundance for NGC 300 in the Hii regions and PNe has been studied by a number of authors (Pagel et al. 1979; Deharveng et al. 1988; Zaritsky et al. 1994; Bresolin et al. 2009; Stasińska et al. 2013; Pilyugin et al. 2014). All these studies showed that oxygen abundance decreases with radius, and the metallicity in the center is highest, although the overall abundance depends on the calibration methods adopted. The observed oxygen abundance profiles of the NGC 300 disk used to constrain the gas-phase oxygen predicted by our model are those of Bresolin et al. (2009) and Pilyugin et al. (2014), since these two papers enlarged the number of the Hii regions in whose spectra [Oiii]λ4363 can be detected.
At the same time, the characteristic oxygen abundance, which is defined as the oxygen value 12 +log (O/H) at the effective radius reff, is representative of the average value of the young component across the galaxy (Garnett 2002; Sánchez et al. 2013). The radius reff is equal to 1.685 times the exponential scale-length rd of the disk. Thus, we also use the characteristic oxygen abundance of Bresolin et al. (2009) and Pilyugin et al. (2014) to compare with the model-predicted, present-day oxygen abundance of NGC 300 to constrain our chemical evolution model.
In Table 2, we present the basic observational constraints concerning the present-day total amount of stars, atomic hydrogen gas, gas fraction, characteristic oxygen abundance, and SFR in the disk of NGC 300.
3. The model
In this section, we briefly introduce the basic assumptions and main ingredients of the model. We assume that the NGC 300 disk is composed of a set of independently evolved concentric rings with the width 500 pc, which are progressively built up by continuous infall of primordial gas (X = 0.7571,Yp = 0.2429,Z = 0) from its halo. Star formation, metal production via stellar evolution, stellar mass return, infalls of primordial gas, and outflows of metal enriched gas are taken into account in our model under the condition of both instantaneous recycling assumption (IRA) and instantaneous mixing of the ISM with stellar ejecta. Moreover, neither radial gas flows nor stellar migration is allowed in our model, since these radial flows are far from clearly understanding and introduce additional free parameters whose values might be difficult to constrain.
3.1. Gas infall rate
In order to reproduce the observed metallicity distribution of long-living stars in the solar neighborhood (G-dwarf problem, Pagel 1989; Rana 1991, and references therein), the simple closed-box model is proved to be unreasonable and the infall of gas from its halo has been introduced in the chemical evolution model (Tinsley 1980). Indeed, Mathewson et al. (1975) conclude that a long “Hi tail” extends about 2° to the southeast of the disk of NGC 300 and Westmeier et al. (2011) find that the Hi disk is more extended than its optical disk, respectively.
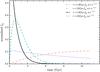 |
Fig. 1 Normalized gas infall rate with two forms. The infall rate adopted as fin(r,t) ∝ t·e− t/τ is plotted as dashed line (τ = 1.0 Gyr) and dot-dashed line (τ = 15 Gyr), while that adopted as fin(r,t) ∝ e− t/τ is shown as solid line (τ = 1.0 Gyr) and dotted line (τ = 15 Gyr), respectively. |
The infall rate, as a function of space and time, plays a key role in determining the properties of the galaxy disk, such as the gas, SFR, and metallicity. At a given radius r, the gas infall rate fin(r,t) (in units of M⊙ pc-2 Gyr-1) is assumed to be (Kang et al. 2012) 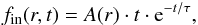 (1)where τ is the infall timescale and is a free parameter in our model. The A(r) are actually a set of separate quantities constrained by the present-day stellar mass surface density Σ∗(r,tg), tg is the cosmic age, and we set tg = 13.5 Gyr according to the standard cosmology (e.g., H0 = 70 km s-1 Mpc-1, ΩM = 0.3, and ΩΛ = 0.7). In other words, A(r) are iteratively computed by requiring the model-predicted, present-day stellar mass surface density is equivalent to its observed value (Chang et al. 2012; Kang et al. 2012). In general, the K-band luminosity strongly correlates with the accumulated star formation in the galaxy, thus it can accurately reflect the stellar disk. In this work, the present-day values of stellar mass and disk scale-length for NGC 300 are adopted to be M∗ = 1.928 × 109 M⊙ and rd = 1.29 kpc, and these two values are derived from K-band luminosity (Muñoz-Mateos et al. 2007). We assume that NGC 300 has a pure exponential disk, which is confirmed by the observations of Bland-Hawthorn et al. (2005), and Σ∗(r,tg) follows an exponential profile, thus the central stellar mass surface density can be easily obtained from
(1)where τ is the infall timescale and is a free parameter in our model. The A(r) are actually a set of separate quantities constrained by the present-day stellar mass surface density Σ∗(r,tg), tg is the cosmic age, and we set tg = 13.5 Gyr according to the standard cosmology (e.g., H0 = 70 km s-1 Mpc-1, ΩM = 0.3, and ΩΛ = 0.7). In other words, A(r) are iteratively computed by requiring the model-predicted, present-day stellar mass surface density is equivalent to its observed value (Chang et al. 2012; Kang et al. 2012). In general, the K-band luminosity strongly correlates with the accumulated star formation in the galaxy, thus it can accurately reflect the stellar disk. In this work, the present-day values of stellar mass and disk scale-length for NGC 300 are adopted to be M∗ = 1.928 × 109 M⊙ and rd = 1.29 kpc, and these two values are derived from K-band luminosity (Muñoz-Mateos et al. 2007). We assume that NGC 300 has a pure exponential disk, which is confirmed by the observations of Bland-Hawthorn et al. (2005), and Σ∗(r,tg) follows an exponential profile, thus the central stellar mass surface density can be easily obtained from 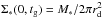 .
.
It should be emphasized that a simple exponential form of gas infall rate is widely used in the previous chemical evolution models (Matteucci & Francois 1989; Hou et al. 2000; Chiappini et al. 2001; Yin et al. 2009). To explore the difference between the exponential gas infall rate form and the form adopted in this paper, we show the two forms of the normalized gas infall rate in Fig. 1. The infall rate adopted as fin(r,t) ∝ t·e− t/τ is plotted as dashed line (τ = 1.0 Gyr) and dot-dashed line (τ = 15 Gyr), while that adopted as fin(r,t) ∝ e− t/τ is shown as a solid line (τ = 1.0 Gyr) and dotted line (τ = 15 Gyr), respectively. From Fig. 1, we can see that the gas infall rate we adopted is low in the beginning and gradually increases with time. This gas infall rate reaches the peak value when t = τ and then falls, i.e., τ → 0 corresponds to a time-declining gas infall rate, while τ → ∞ corresponds to a time-increasing gas infall rate. However, the exponential form of gas infall rate is always decreasing with time and the limiting case is corresponding to a constant. We adopt the gas infall rate as the form of fin(r,t) ∝ t·e− t/τ to include more possible scenarios in the model. In any case, the infall timescale τ determines the gas accretion history and largely describes the main properties of the SFH of the disk of NGC 300, thus we regard τ as the most important free parameter in our model.
3.2. Star formation law
 |
Fig. 2 Influence of infall timescale τ and outflow efficiency bout on the model results. Different line types correspond to various parameter groups: solid lines (τ,bout) = (0.1 Gyr,0), dotted lines (τ,bout) = (15 Gyr,0), and dashed lines (τ,bout) = (15 Gyr,1). On the left side, the radial profiles of Hi and SFR surface density are shown in the top and bottom panels; on the right side, the radial profiles of H2 and oxygen abundance are shown in the top and bottom panels, respectively. Hi data from Westmeier et al. (2011) are shown with filled squares. SFR data taken from Williams et al. (2013) are denoted with filled triangles and those taken from Gogarten et al. (2010) are shown with filled diamonds. SFR data from Gogarten et al. (2010) are recent SFRs as a function of radius. The observed oxygen abundance from Pilyugin et al. (2014) are shown as open circles, while those from Bresolin et al. (2009) are plotted with filled circles. |
The star formation law, which connects SFR surface density with interstellar gas surface density, is another significant ingredient of the model in which SFR describes the total mass of newly born stars in unit time.
Half a century ago, Schmidt (1959) surmised that SFR surface density should vary with a power n of the surface density of gas. Later, based on the observed data of a sample of 97 nearby normal and starburst galaxies, Kennicutt (1998) demonstrated the existence of a power law between galaxy-averaged SFR surface density and the galaxy-averaged total gas surface density. Recently, high-resolution investigations that separate the components of atomic hydrogen and molecular hydrogen gas have shown that SFR surface density correlates more strongly with the surface density of molecular hydrogen than with that of atomic hydrogen and total gas (Wong & Blitz 2002; Bigiel et al. 2008; Leroy et al. 2008). Indeed, multiple studies in both individual galaxies and large samples of spiral galaxies have found a linear relation between SFR surface density Ψ(r,t) and molecular gas surface density ΣH2(r,t). The linear slope is an approximately constant depletion time (tdep = ΣH2(r,t)/Ψ(r,t); e.g., Bigiel et al. 2008; Leroy et al. 2008, 2013; Rahman et al. 2011). Furthermore, based on an up-to-date set of observational data, Krumholz (2014) concludes in his recent work that “the correlation between star formation and molecular gas is the fundamental one”. These results encourage us to adopt the molecular related star formation law, i.e.,  (2)With respect to the value of molecular gas depletion time tdep, we adopt tdep = 1.9 Gyr throughout this work (Leroy et al. 2008, 2013). Kang et al. (2012) and Kubryk et al. (2015) provide more in-depth descriptions of the calculation of the ratio of molecular hydrogen to atomic hydrogen gas surface density Rmol in a galaxy disk along with present-day molecular hydrogen and atomic hydrogen gas surface density.
(2)With respect to the value of molecular gas depletion time tdep, we adopt tdep = 1.9 Gyr throughout this work (Leroy et al. 2008, 2013). Kang et al. (2012) and Kubryk et al. (2015) provide more in-depth descriptions of the calculation of the ratio of molecular hydrogen to atomic hydrogen gas surface density Rmol in a galaxy disk along with present-day molecular hydrogen and atomic hydrogen gas surface density.
3.3. Gas outflow rate
The gas-outflow process may influence the evolutionary history of NGC 300. The oxygen in the Universe is predominantly formed in massive stars (>8 M⊙) and subsequently dispersed into the ISM by supernova explosion and stellar winds, thus the oxygen in the ISM may expel from the galactic disk when the gas thermal energy exceeds the binding energy of gas. Low-mass galaxies are expected to lose a larger fraction of supernova ejecta than high-mass systems because of their shallower gravitational potentials (Kauffmann et al. 1993). Indeed, both analytical (Erb 2008) and hydrodynamic (Finlator & Davé 2008) models showed that galactic outflows are important to reproduce the stellar mass-metallicity relation of galaxies. Moreover, for galaxies with stellar mass M∗ ≤ 1010.5 M⊙, the outflow process plays a crucial role during their evolution histories (Tremonti et al. 2004; Spitoni et al. 2010; Chang et al. 2010). Finally, galaxies with rotation speed Vrot ≤ 100–150 km s-1 may expel a large part of their supernova ejecta to the circumgalactic medium (Garnett 2002). Since NGC 300 is a fairly low-mass disk galaxy (M∗ ≈ 109.29 M⊙, Muñoz-Mateos et al. 2007) with a rotation speed about Vrot ≈ 91 km s-1 (Garnett 2002), the gas-outflow process has a significant influence on the chemical enrichment during its evolution history.
We assume that the outflowing gas has the same metallicity as the ISM at the time the outflow is launched, and the outflowing gas does not fall to the disk again (Chang et al. 2010; Kang et al. 2012; Ho et al. 2015). We follow the approach of Recchi et al. (2008), i.e., the gas outflow rate fout(r,t) (in units of M⊙ pc-2 Gyr-1) is proportional to SFR surface density Ψ(r,t). Therefore, the outflow rate is given by 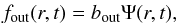 (3)where bout is the other free parameter in our model.
(3)where bout is the other free parameter in our model.
3.4. Basic equations of chemical evolution
As mentioned above, both IRA and instantaneous mixing of the ISM with ejecta are assumed, thus the chemical evolution in each ring can be expressed by the following classical set of integro-differential equations from Tinsley (1980): ![\begin{eqnarray} &&\frac{{\rm d}[\Sigma_{\rm tot}(r,t)]}{{\rm d}t}\,=\,f_{\rm{in}}(r,t)-f_{\rm{out}}(r,t),\\ \label{eq:tot}\nonumber\\ &&\frac{{\rm d}[\Sigma_{\rm gas}(r,t)]}{{\rm d}t}\,=\,-(1-R)\Psi(r,t)+f_{\rm{in}}(r,t)-f_{\rm{out}}(r,t),\\ \label{eq:gas}\nonumber\\ &&\frac{{\rm d}[Z(r,t)\Sigma_{\rm gas}(r,t)]}{{\rm d}t}\,=\,y(1-R)\Psi(r,t)-Z(r,t)(1-R)\Psi(r,t) \nonumber\\ &&\hspace*{3cm}+Z_{\rm{in}}f_{\rm{in}}(r,t)-Z_{\rm{out}}(r,t)f_{\rm{out}}(r,t), \end{eqnarray}](/articles/aa/full_html/2016/01/aa27041-15/aa27041-15-eq78.png) where Σtot(r,t) is the total (star + gas) mass surface density in the ring centered at galactocentric distance r at evolution time t, and Z(r,t) is the metallicity in the corresponding place and time. The parameter R is the return fraction and we obtain R = 0.43 after adopting stellar initial mass function (IMF) between 0.1 M⊙ and 100 M⊙ from Chabrier (2003). The parameter y is the nucleosynthesis yield and we set y = 1 Z⊙ throughout this work (Fu et al. 2009; Chang et al. 2010; Kang et al. 2012). The parameter Zin is the metallicity of the infalling gas and we assume the infalling gas is metal-free, i.e., Zin = 0. Zout(r,t) is the metallicity of the outflowing gas and we assume that the outflow gas has the same metallicity as the ISM at the time the outflows are launched, e.g., Zout(r,t) = Z(r,t) (Chang et al. 2010; Ho et al. 2015).
where Σtot(r,t) is the total (star + gas) mass surface density in the ring centered at galactocentric distance r at evolution time t, and Z(r,t) is the metallicity in the corresponding place and time. The parameter R is the return fraction and we obtain R = 0.43 after adopting stellar initial mass function (IMF) between 0.1 M⊙ and 100 M⊙ from Chabrier (2003). The parameter y is the nucleosynthesis yield and we set y = 1 Z⊙ throughout this work (Fu et al. 2009; Chang et al. 2010; Kang et al. 2012). The parameter Zin is the metallicity of the infalling gas and we assume the infalling gas is metal-free, i.e., Zin = 0. Zout(r,t) is the metallicity of the outflowing gas and we assume that the outflow gas has the same metallicity as the ISM at the time the outflows are launched, e.g., Zout(r,t) = Z(r,t) (Chang et al. 2010; Ho et al. 2015).
In summary, the infall timescale τ and the outflow coefficient bout are two free parameters in our model.
4. Model results versus observations
In this section, we present our results step by step. Firstly, we investigate the influence of free parameters on model predictions and select a best-fitting model for NGC 300. Then, we present the evolution of the total amount of atomic hydrogen gas, SFR, characteristic 12 + log (O/H), and of the gas fraction for the disk of NGC 300. Finally, we compare the SFH of NGC 300 with that of M 33.
4.1. Radial profiles
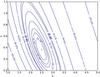 |
Fig. 3 χ2 contours plot of a,b and bout determination. χ2 contours are calculated by allowing bout to vary to minimize χ2 for each pair of values of a and b. The number of each contour shows the value of χ2. The first, second, and third ellipses are contours, which correspond to 68%, 84%, and 92% confidence level, respectively. |
 |
Fig. 4 Comparisons of the model predictions with the observations. The solid lines represent the best-fitting model results adopting (τ,bout) = (0.35r/rd + 2.47 Gyr,0.9), while the dotted and dashed lines plot the model predictions adopting (τ,bout) = (0.18r/rd + 2.24 Gyr,0.9) and (τ,bout) = (0.56r/rd + 2.71 Gyr,0.9) with 68% confidence level, respectively. The notation of the observational data is the same as that of Fig. 2. |
First of all, we explore the influence of infall timescale τ on model results and fix the gas-outflow coefficient at bout = 0. The comparison between the profiles of model predictions and the observations are shown in Fig. 2. The different line types in Fig. 2 correspond to various values of free parameters, i.e., solid lines (τ = 0.1 Gyr) and dotted lines (τ = 15.0 Gyr). Obviously, the model predictions are very sensitive to the adopted infall timescale τ. As shown in Fig. 1, the case of τ = 0.1 Gyr corresponds to a time-declining gas infall rate in which most of the cold gas has been accreted to the disk in the early stage of its history, while that of τ = 15.0 Gyr denotes a time-increasing gas infall rate in which a large fraction of cold gas is currently falling onto the disk of NGC 300. Thus, the model adopting a shorter infall timescale (solid lines) predicts lower gas surface density, lower SFR, and higher gas-phase oxygen abundance than that adopting a longer infall timescale (dotted lines). This is mainly because in our model the setting of a longer infall timescale corresponds to a slower gas accretion during the evolution history of NGC 300, thus more gas currently remain in the disk to fuel higher SFR and then results in an younger stellar population, lower metallicity, and higher cold gas content at the present time, and vice versa.
Here, we investigate the impact of the gas-outflow process on model predictions. The dashed lines in Fig. 2 represent the model results adopting (τ,bout) = (15.0 Gyr,1.0). The comparison between the dotted (τ = 15.0 Gyr,bout = 0) and dashed (τ = 15.0 Gyr,bout = 1.0) lines shows that the gas-outflow process has little influence on Hi, H2, and SFR, while it has great influence on the gas-phase metallicity. That is, the gas-outflow process carries part of the metals away from the disk and reduces the gas-phase metallicity. In other words, the observational radial gas-phase metallicity must be very important physical quantities to constrain the gas-outflow process of NGC 300.
Figure 2 also shows that the area between the solid (τ = 0.1 Gyr,bout = 0) and dashed (τ = 15.0 Gyr,bout = 1.0) lines almost covers the whole range of the observations, which suggests the possibility of constructing a model that can reproduce most of the observed features along the disk of NGC 300. Furthermore, the observed trends in Fig. 2 show that the inner stellar disk is more metal rich than that of outer region, and the observed studies also show that the stellar disk of NGC 300 grows inside out (Kim et al. 2004; Muñoz-Mateos et al. 2007; Gogarten et al. 2010). To simply describe the inside-out formation scenario of the disk, we follow the previous models of Chiosi (1980) and Matteucci & Francois (1989), and adopt a radius-dependent infall timescale τ(r) = a × r/rd + b, where a and b are the coefficients for the linear equations adopted for τ(r). Including the additional free parameter bout in the gas-outflow process, there are three free parameters (a, b, and bout) in our model.
In order to find the best combination of free parameters a, b, and bout, we adopt the classical χ2 technique to compare the model results with the corresponding observational data, including the radial profiles of Hi, SFR, and 12 + log (O/H). The boundary conditions of a,b, and bout are assumed to be 0 ≤ a ≤ 1.2, 1.0 ≤ b ≤ 5.0 and 0 <bout ≤ 0.9, respectively. In practice, we calculate the value of χ2 by comparing our model predictions with the observed data (i.e., the combination of the radial profiles of Hi, SFR, and 12 + log (O/H)), and show the χ2 contours in Fig. 3, where the number of each contour shows the value of χ2. The first, second, and third ellipses are contours, which correspond to 68%, 84%, and 92% confidence levels, respectively. It should be emphasized that, for each pair of a and b values, we change the value of bout to make sure the value of χ2 minimum. The minimum value of χ2 (12.747) denoted as a filled asterisk is shown in Fig. 3, and the corresponding value of the best combination (a,b, bout) = (0.35, 2.47 0.9) is selected as the best-fitting model.
The predictions of best-fitting model are shown as solid lines in Fig. 4. The dotted and dashed lines plot the model predictions, adopting (τ,bout) = (0.18r/rd + 2.24 Gyr,0.9) and (τ,bout) = (0.56r/rd + 2.71 Gyr,0.9) with 68% confidence level. The notation of the observed data is the same as that of Fig. 2. We see in Fig. 4 that the solid lines can nicely reproduce all the observational radial profiles, which suggests that this parameter group may reasonably describe the crucial ingredients of the main physical processes that regulate the formation and evolution of NGC 300.
4.2. Stellar disk growth
 |
Fig. 5 Relative stellar mass growth of six spatial components, including 0–0.9 kpc (dotted lines), 0.9–1.8 kpc (dot-dashed lines), 1.8–2.7 kpc (dashed lines), 2.7–3.6 kpc (long dot-dashed lines), 3.6–4.5 kpc (long dashed lines), and 4.5–5.4 kpc (solid lines).The stellar masses in the different components are normalized to their corresponding present-day values. The observations are from Fig. 6 of Gogarten et al. (2010), and the data have been offset from one another to avoid overlapping error bars. |
 |
Fig. 6 Time evolution of the stellar mass surface density profiles for the disk of NGC 300. Different line types represent the radial profile of stellar mass surface density at 3.5 Gyr (dotted lines), 8.5 Gyr (dot-dashed), 12.5 Gyr (dashed lines), and 13.5 Gyr (solid lines). The observations are from Fig. 7 of Gogarten et al. (2010), and the data have been offset from one another to avoid overlapping error bars. |
Figure 5 plots the best-fitting model predictions of the growth curves of stellar masses in different regions to quantify the inside-out assembly of NGC 300 and compares them with the measurements from Fig. 6 of Gogarten et al. (2010). These best-fitting model predictions include 0–0.9 kpc (dotted lines), 0.9–1.8 kpc (dot-dashed lines), 1.8–2.7 kpc (dashed lines), 2.7–3.6 kpc (long dot-dashed lines), 3.6–4.5 kpc (long dashed lines), and 4.5–5.4 kpc (solid lines). The stellar masses in Fig. 5 are normalized by their present-day values. Figure 6 shows the time evolution of the stellar mass surface density profile at 3.5 Gyr (dotted lines), 8.5 Gyr (dot-dashed), 12.5 Gyr (dashed lines), and 13.5 Gyr(solid lines).
 |
Fig. 7 Time evolution of the stellar-mass-size (i.e., the disk scale-length) for the disk of NGC 300 from z = 1 to z = 0. |
We see from Fig. 5 that the stellar mass in the corresponding regions has been steadily increasing to its present-day value and the outer parts of the disk formed a greater fraction of their stars at recent times than the inner parts of the disk, which is consistent with the “inside-out” formation scenario (Kim et al. 2004; Muñoz-Mateos et al. 2007; Gogarten et al. 2010). Moreover, Fig. 6 shows that the stellar mass surface density has changed more substantially in the outer regions of the disk than in the inner regions, in line with the trend of Fig. 7 in Gogarten et al. (2010). However, the best-fitting model predictions fail to reproduce the measurements of Figs. 6 and 7 from Gogarten et al. (2010). The possible reasons for this are identified as a) the stellar mass of NGC 300 in our work is ~1.928 × 109 M⊙ derived from K-band luminosity (Muñoz-Mateos et al. 2007), but in Gogarten et al. (2010) it is about ~7.0 × 109 M⊙; b) the galactocentric distances are within 5.4 kpc for the disk of NGC 300 in Gogarten et al. (2010), while ours are extend to 8.0 kpc; or a combination of these two. Thus, it is difficult to compare our results directly with the measurements from Gogarten et al. (2010, Figs. 6 and 7). Most importantly, the main trend of our best-fitting model predictions is in accordance with the information from Figs. 6 and 7 in Gogarten et al. (2010).
 |
Fig. 8 Time evolution of global atomic hydrogen gas mass, SFR, characteristic oxygen abundance, and the total gas fraction of NGC 300 disk. Vertical bars at 13.5 Gyr represent observational constraints (see Table 2). |
 |
Fig. 9 Time evolution of the radial profiles of 12 + log (O/H) for the disks of NGC 300 (left panel) and M 33 (right panel) predicted by their own best-fitting models. Different line types represent the radial profile of 12 + log (O/H) at 2 (dotted line), 5 (dashed line), 10 (dot-dashed line), and 13.5 Gyr (solid line). |
Figure 7 also shows the stellar-mass-size evolution (from z = 1 to z = 0) for the disk of NGC 300. It can be found that both the stellar mass and the scale-length of NGC 300 have been growing since z = 1, which is consistent with the results of the previous studies (Brooks et al. 2011; Brook et al. 2012).
4.3. Global evolution
The evolution of the total amount of atomic hydrogen gas, SFR, characteristic 12 + log (O/H) (defined as the oxygen value 12 + log (O/H) at the effective radius reff, which is equal to 1.685 times the radial scale-length rd of the disk) and of the gas fraction fgas predicted by the best-fitting model are shown with solid lines in Fig. 8. They are compared to the observational data shown in Table 2, which are plotted as red vertical bars at the present time, i.e., t = 13.5 Gyr.
Figure 8 shows that the best-fitting model predictions reproduce fairly well with the global observational constraints of the NGC 300 disk. It can be also found that in the first ~1 Gyr the atomic hydrogen gas assembles very quickly, but the gas fraction does not decrease and there is no star formation occurring. Although it is generally believed that almost all star formation occurs in molecular clouds, the cold gas in the earlier stage is mainly in the form of atomic gas. After the amount of atomic hydrogen exceeds a critical value, the atomic hydrogen gas begins to convert into molecular hydrogen gas and then the star formation process accelerates. Figure 8 also shows that the oxygen abundance increases during the whole evolution history, and there is greater abundance increase before the evolution age t ~ 7 Gyr compared to the later epoch. This is mainly because in the later epoch, as the infall rate of cold gas gradually decreases with time, the accumulation of molecular hydrogen gas does as well. Thus, the SFR also decreases and the oxygen abundance enrichment becomes relatively slow.
4.4. Comparison with M 33
The M 33 galaxy is nearly a twin to NGC 300 in Hubble type and mass, and we have already explored the evolution and SFH of M 33 in a previous work (Kang et al. 2012). In this section, we compare the SFH of NGC 300 predicted with the best-fitting model with that of M 33. The main ingredients and parameters of the best-fitting models for NGC 300 and M 33 are presented in Table 3, and Kang et al. (2012) provides a more in-depth description of the physical details for the model of M 33.
First of all, we plot the time evolution of the gas-phase oxygen abundance gradient of NGC 300 (left panel) and that of M 33 (right panel) in Fig. 9. Different line types represent the radial profile of 12 + log (O/H) at different times, i.e., 2 (dotted line), 5 (dashed line), 10 (dot-dashed line), and at 13.5 Gyr (solid line). The best-fitting, present-day (i.e., t = 13.5 Gyr) abundance gradients predicted with models are −0.0843 dex kpc-1 for NGC 300 disk and −0.0219 dex kpc-1 for M 33 disk from 0.2 to 6 kpc in radius, which is in good agreement with the observed gradient derived in the same radial range, i.e., −0.0842 ± 0.0065 for NGC 300 from Pilyugin et al. (2014) and −0.027 ± 0.012 for M 33 from Rosolowsky & Simon (2008). We see from Fig. 9 that NGC 300 has a steep radial metallicity gradient and a significant increase in metallicity with time. As for M 33, it has a flatter gradient and a slower increase in metallicity with time, especially in the inner parts of the disk, which indicates that M 33 may experience more gas infall at later times to dilute the metallicity. Furthermore, we find that the metallicity in NGC 300 has increased with time in all radial bins, suggesting that recently there is less infall of primordial gas. This is generally in accordance with the observed finding of Gogarten et al. (2010).
Main ingredients and parameters of the best-fitting models for NGC 300 and M 33.
 |
Fig. 10 Current radial profiles of mean stellar age for NGC 300 (solid line) and M 33 (dashed line) predicted by their own best-fitting models. |
In order to demonstrate clearly the property of the stellar ages of both NGC 300 and M 33, in Fig. 10 we plot the mean stellar ages along their disks predicted with their own best-fitting models, with a solid line for NGC 300 and a dashed line for M 33. There is a radial age gradient in both NGC 300 and M 33’s disks, that is, the cumulative age distribution shifts to younger ages as the radius increases, which is consistent with the inside-out growth of the stellar disk in NGC 300 and M 33 (Kim et al. 2004; Muñoz-Mateos et al. 2007; Williams et al. 2009; Gogarten et al. 2010). This is mainly because the short infall timescale means that a large fraction of stars formed at an early stage and, hence, these stars have large mean age. Fortunately, Gogarten et al. (2010) studied the cumulative SFH for the disk of NGC 300 out to 5.4 kpc, and they found that >90% of the stars are older than 6 Gyr in the inner regions, while only ~40% of stars are this old in the outermost parts (i.e., 4.5 <r< 5.4 kpc). Meanwhile, the model-predicted mean age of stellar populations along the NGC 300 disk is 7.70 Gyr in the central region, 3.85 Gyr at r = 5.4 kpc, and 2.97 Gyr at r = 8.0 kpc, respectively. As for M 33, Barker et al. (2011) concluded that the mean age of stellar populations at r = 9.1 kpc in M 33 is ~2–4 Gyr, and our model-predicted age at r = 9.1 kpc is 2.33 Gyr. Furthermore, our model-predicted mean stellar age in the central region of M 33 is ~6.37 Gyr. Williams et al. (2009) fitted the stellar disk growth within the inner disk of M 33, and found that most of the stars formed from 10 Gyr to 5 Gyr ago. All of these studies suggest that our model predictions are basically in agreement with the previous observational results (Williams et al. 2009; Gogarten et al. 2010; Barker et al. 2011). Furthermore, it can be also found that the stellar age of NGC 300 is older than that of M 33 throughout the studied region, especially for the inner region of the NGC 300 disk. The mean stellar age difference between the inner parts of the two galaxy disks is up to ~1.33 Gyr, while that between the outmost regions is ~0.49 Gyr. The older age of stars in NGC 300 than that in M 33 indicates a lack of infall of primordial gas and a small fraction of stars formed at later times in NGC 300 disk.
 |
Fig. 11 Evolution of gas infall rate (left panel) and sSFR (right panel) for NGC 300 (solid line) and M 33 (dashed line) predicted by their own best-fitting models. |
Specific star formation rate (sSFR) is defined as the ratio of the current SFR to the current stellar mass, sSFR = SFR/M∗. Thus, higher values of the sSFR indicate that a larger fraction of stars were formed recently, and this can be used to characterize the SFH of galaxies. The time evolution of gas infall rate and sSFR are shown in the left and right panels of Fig. 11, respectively. The left panel of Fig. 11 shows that the infall rate of NGC 300, given by our best-fitting model, is gradually increasing with time, reaches its peak at about 10 Gyr ago, and then slowly drops down, while that of M 33 achieves its peak around 6 Gyr ago and then gradually falls. Moreover, the infall rate of NGC 300 increases and falls faster than that of M 33, and the present-day infall rate of NGC 300 is much lower than that of M 33. This indicates that the buildup of the stellar disk of NGC 300 is faster than that of M 33. At the same time, the right panel of Fig. 11 reveals that the sSFR of NGC 300 is lower than that of M 33 during the whole evolution history, and the difference between them increases with time and reaches the maximum at the present time. This is also a suggestive of less gas infall and less active in star formation recently along the disk of NGC 300 than that of M 33.
 |
Fig. 12 Stellar mass growth histories of NGC 300 (solid line) and M 33 (dashed line) predicted by their own best-fitting models. Stellar masses are normalized to their present-day values, and the horizontal dotted line in the panel marks when the stellar mass achieves 50% of its final value. |
 |
Fig. 13 Growth of the disk scale-lengths for both NGC 300 (solid line) and M 33 (dashed line) predicted by their own best-fitting models. The disk scale-lengths are normalized to their sizes at z = 1. |
In Fig. 12, we show the best-fitting model predictions of the evolution of the stellar mass for both NGC 300 (solid line) and M 33 (dashed line). To make the growth history of M∗ more visible, stellar masses are normalized to their present-day values, and to compute the M∗ growth rate, the horizontal dotted line in the panel denotes when the stellar mass achieves 50% of its final value. We find that both NGC 300 and M 33 have been steadily increased to their present-day values. Furthermore, half of the total stellar mass of NGC 300 has been assembled during the last ~6 Gyr, while that of M 33 has been accumulated during the last ~4.5 Gyr. That is to say, the mean age of stellar population in NGC 300 is older than that in M 33.
Figure 13 plots the evolution of disk scale-length of NGC 300 (solid line) and M 33 (dashed line) predicted by their own best-fitting models, which are normalized to their values at z = 1. The disk sizes of both NGC 300 and M 33 show clear growth. Moreover, the scale-length of M 33 changes more significant than that of NGC 300, which indicates that there is a lower fraction of stars formed recently in the disk of NGC 300 than that of M 33.
To sum up, the aforementioned results suggest that the stellar population of NGC 300 is older than that of M 33. There is a lack of primordial gas infall onto the disk of NGC 300 and a lower fraction of stars formed recently in NGC 300 than in M 33. Our results reinforce the recent results of Gogarten et al. (2010) and Guglielmo et al. (2015) that even though the two galaxies have similar stellar mass and morphology, they have experienced different histories due to their environmental differences.
5. Summary
NGC 300 is a bulgeless and isolated low-mass disk galaxy and has not experienced migration during its evolution history. In this work, we build a bridge for the disk galaxy NGC 300 between its observed properties and its evolution history by constructing a simple chemical evolution model. Some of our conclusions are as follows.
Our results show that the model predictions are very sensitive to the adopted infall timescale. The outflow process plays an important role in shaping the gas-phase metallicity profiles along the disk of NGC 300, since it takes a large fraction of metals away from its disk during its evolution history.
Using the classical χ2 methodology, we compare the model results with the corresponding observations to find the best combination of a, b, and bout (i.e., 0.35, 2.47 and 0.9). As a result, the model adopting an inside-out formation scenario (i.e., τ = 0.35r/rd + 2.47 Gyr) and an appropriate gas outflow rate (i.e., bout = 0.9) can successfully reproduce the observed constraints of NGC 300. Our results suggest that NGC 300 likely experiences a rapid growth of its disk and its stellar population is predominately old, consistent with the previous observed results (Butler et al. 2004; Tikhonov et al. 2005; Gogarten et al. 2010).
We also compared the best-fitting, model-predicted evolution history of NGC 300 with that of M 33. We find that the mean stellar age of NGC 300 is older than that of M 33, and there is a lack of primordial gas infall onto the disk of NGC 300 and a lower fraction of stars formed recently in NGC 300 than in M 33. The comparative study of the two bulgeless systems shows that local environmental difference may play an important part in the secular evolution of the galaxy disks.
Acknowledgments
We thank the anonymous referee whose comments and suggestions have improved the quality of this paper greatly. Xiaoyu Kang and Fenghui Zhang are supported by the National Natural Science Foundation of China (NSFC) grant Nos. 11403092, 11273053, 11033008, 11373063, 11573062, and Yunnan Foundation No. 2011CI053. Ruixiang Chang is supported by the NSFC grant Nos. 11373053, 11390373, and Strategic Priority Research Program “The Emergence of Cosmological Structures” of the Chinese Academy of Sciences (CAS; grant XDB09010100).
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Glazebrook, K., & Driver, S. P. 2008, MNRAS, 388, 945 [NASA ADS] [Google Scholar]
- Baldry, I. K., Driver, S. P., Loveday, J., et al. 2012, MNRAS, 421, 621 [NASA ADS] [Google Scholar]
- Barker, M. K., Sarajedini, A., Geisler, D., Harding, P., & Schommer, R. 2007, AJ, 133, 1125 [Google Scholar]
- Barker, M. K., Ferguson, A. M. N., Cole, A. A., et al. 2011, MNRAS, 410, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E., & Hernquist, L. 1992, ARA&A, 30, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, D. G., Staveley-Smith, L., de Blok, W. J. G., et al. 2001, MNRAS, 322, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, A. E., Hopkins, A. M., Gunawardhana, M., et al. 2013, MNRAS, 434, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Barker, M. K., et al. 2012, MNRAS, 420, 2625 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Binder, B., Williams, B. F., Eracleous, M., et al. 2012, ApJ, 758, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., Vlajić, M., Freeman, K. C., & Draine, B. T. 2005, ApJ, 629, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., & Prantzos, N. 2000, MNRAS, 312, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, R., & Thilker, D. A. 2004, A&A, 417, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bresolin, F., Gieren, W., Kudritzki, R.-P., et al. 2009, ApJ, 700, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Stinson, G. S., Gibson, B. K., et al. 2012, MNRAS, 426, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, A. M., Solomon, A. R., Governato, F., et al. 2011, ApJ, 728, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, D. J., Martínez-Delgado, D., & Brandner, W. 2004, AJ, 127, 1472 [NASA ADS] [CrossRef] [Google Scholar]
- Byun, Y. I., & Freeman, K. C. 1995, ApJ, 448, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, R. X., Hou, J. L., Shu, C. G., & Fu, C. Q. 1999, A&A, 350, 38 [NASA ADS] [Google Scholar]
- Chang, R. X., Hou, J. L., Shen, S. Y., & Shu, C. G. 2010, ApJ, 722, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, R. X., Shen, S. Y., & Hou, J. L. 2012, ApJ, 753, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Chiosi, C. 1980, A&A, 83, 206 [NASA ADS] [Google Scholar]
- Corbelli, E., & Schneider, S. E. 1997, ApJ, 479, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Seth, A. C., et al. 2009, ApJS, 183, 67 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, S&T, 82, 621 [Google Scholar]
- Deharveng, L., Caplan, J., Lequeux, J., et al. 1988, A&AS, 73, 407 [NASA ADS] [Google Scholar]
- Deul, E. R., & van der Hulst, J. M. 1987, A&AS, 67, 509 [NASA ADS] [Google Scholar]
- Erb, D. K. 2008, ApJ, 674, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, A., Irwin2, M., Chapman, S., et al. 2007, in Resolving the Stellar Outskirts of M 31 and M 33, ed. R. S. De Jong, 239 [Google Scholar]
- Finlator, K., & Davé, R. 2008, MNRAS, 385, 2181 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, J., Hou, J. L., Yin, J., & Chang, R. X. 2009, ApJ, 696, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R. 2002, ApJ, 581, 1019 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gogarten, S. M., Dalcanton, J. J., Williams, B. F., et al. 2010, ApJ, 712, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Guglielmo, V., Poggianti, B. M., Moretti, A., et al. 2015, MNRAS, 450, 2749 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., Roussel, H., Appleton, P., et al. 2004, ApJS, 154, 253 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ho, I.-T., Kudritzki, R.-P., Kewley, L. J., et al. 2015, MNRAS, 448, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, J. L., Prantzos, N., & Boissier, S. 2000, A&A, 362, 921 [NASA ADS] [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, X., Chang, R., Yin, J., et al. 2012, MNRAS, 426, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, X., Chang, R., Zhang, F., Cheng, L., & Wang, L. 2015, MNRAS, 449, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., & Kaisina, E. I. 2013, AJ, 146, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Grebel, E. K., Sharina, M. E., et al. 2003, A&A, 404, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., Karachentseva, V. E., Huchtmeier, W. K., & Makarov, D. I. 2004, AJ, 127, 2031 [Google Scholar]
- Kauffmann, G., White, S. D. M., & Guiderdoni, B. 1993, MNRAS, 264, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Kelvin, L. S., Driver, S. P., Robotham, A. S. G., et al. 2014, MNRAS, 444, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kim, S. C., Sung, H., Park, H. S., & Sung, E.-C. 2004, Chinese J. Astron. Astrophys., 4, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Koribalski, B. S., Staveley-Smith, L., Kilborn, V. A., et al. 2004, AJ, 128, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Korotin, S. A., Andrievsky, S. M., Luck, R. E., et al. 2014, MNRAS, 444, 3301 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R. 2014, Phys. Rep., 539, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2015, A&A, 580, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Mathewson, D. S., Cleary, M. N., & Murray, J. D. 1975, ApJ, 195, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [NASA ADS] [CrossRef] [Google Scholar]
- McConnachie, A. W., Ferguson, A. M. N., Irwin, M. J., et al. 2010, ApJ, 723, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, W. C., White, G. L., Filipović, M. D., et al. 2011, Ap&SS, 332, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Mollá, M., & Díaz, A. I. 2005, MNRAS, 358, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2007, ApJ, 658, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Nantais, J. B., Huchra, J. P., Barmby, P., & Olsen, K. A. G. 2010, AJ, 139, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Olsen, K. A. G., Miller, B. W., Suntzeff, N. B., Schommer, R. A., & Bright, J. 2004, AJ, 127, 2674 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J. 1989, Rev. Mex. Astron. Astrofis., 18, 161 [NASA ADS] [Google Scholar]
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Kniazev, A. Y. 2014, AJ, 147, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Putman, M. E., Peek, J. E. G., Muratov, A., et al. 2009, ApJ, 703, 1486 [NASA ADS] [CrossRef] [Google Scholar]
- Rahman, N., Bolatto, A. D., Wong, T., et al. 2011, ApJ, 730, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Rana, N. C. 1991, ARA&A, 29, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Spitoni, E., Matteucci, F., & Lanfranchi, G. A. 2008, A&A, 489, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogstad, D. H., Wright, M. C. H., & Lockhart, I. A. 1976, ApJ, 204, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Rogstad, D. H., Chu, K., & Crutcher, R. M. 1979, ApJ, 229, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., & Simon, J. D. 2008, ApJ, 675, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- San Roman, I., Sarajedini, A., & Aparicio, A. 2010, ApJ, 720, 1674 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Jungwiert, B., et al. 2013, A&A, 554, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Calura, F., Matteucci, F., & Recchi, S. 2010, A&A, 514, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stasińska, G., Peña, M., Bresolin, F., & Tsamis, Y. G. 2013, A&A, 552, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tikhonov, N. A., Galazutdinova, O. A., & Drozdovsky, I. O. 2005, A&A, 431, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tinsley, B. M. 1980, Fund. Cosmic Phys., 5, 287 [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., Rizzi, L., Dolphin, A. E., et al. 2006, AJ, 132, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Vila-Costas, M. B., & Edmunds, M. G. 1992, MNRAS, 259, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Vlajić, M., Bland-Hawthorn, J., & Freeman, K. C. 2009, ApJ, 697, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Westmeier, T., Braun, R., & Koribalski, B. S. 2011, MNRAS, 410, 2217 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegert, T., & English, J. 2014, New A, 26, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. F., Dalcanton, J. J., Dolphin, A. E., Holtzman, J., & Sarajedini, A. 2009, ApJ, 695, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. F., Dalcanton, J. J., Stilp, A., et al. 2013, ApJ, 765, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, T., & Blitz, L. 2002, ApJ, 569, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Yin, J., Hou, J. L., Prantzos, N., et al. 2009, A&A, 505, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahid, H. J., Dima, G. I., Kudritzki, R.-P., et al. 2014, ApJ, 791, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Kennicutt, Jr., R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Normalized gas infall rate with two forms. The infall rate adopted as fin(r,t) ∝ t·e− t/τ is plotted as dashed line (τ = 1.0 Gyr) and dot-dashed line (τ = 15 Gyr), while that adopted as fin(r,t) ∝ e− t/τ is shown as solid line (τ = 1.0 Gyr) and dotted line (τ = 15 Gyr), respectively. |
| In the text | |
 |
Fig. 2 Influence of infall timescale τ and outflow efficiency bout on the model results. Different line types correspond to various parameter groups: solid lines (τ,bout) = (0.1 Gyr,0), dotted lines (τ,bout) = (15 Gyr,0), and dashed lines (τ,bout) = (15 Gyr,1). On the left side, the radial profiles of Hi and SFR surface density are shown in the top and bottom panels; on the right side, the radial profiles of H2 and oxygen abundance are shown in the top and bottom panels, respectively. Hi data from Westmeier et al. (2011) are shown with filled squares. SFR data taken from Williams et al. (2013) are denoted with filled triangles and those taken from Gogarten et al. (2010) are shown with filled diamonds. SFR data from Gogarten et al. (2010) are recent SFRs as a function of radius. The observed oxygen abundance from Pilyugin et al. (2014) are shown as open circles, while those from Bresolin et al. (2009) are plotted with filled circles. |
| In the text | |
 |
Fig. 3 χ2 contours plot of a,b and bout determination. χ2 contours are calculated by allowing bout to vary to minimize χ2 for each pair of values of a and b. The number of each contour shows the value of χ2. The first, second, and third ellipses are contours, which correspond to 68%, 84%, and 92% confidence level, respectively. |
| In the text | |
 |
Fig. 4 Comparisons of the model predictions with the observations. The solid lines represent the best-fitting model results adopting (τ,bout) = (0.35r/rd + 2.47 Gyr,0.9), while the dotted and dashed lines plot the model predictions adopting (τ,bout) = (0.18r/rd + 2.24 Gyr,0.9) and (τ,bout) = (0.56r/rd + 2.71 Gyr,0.9) with 68% confidence level, respectively. The notation of the observational data is the same as that of Fig. 2. |
| In the text | |
 |
Fig. 5 Relative stellar mass growth of six spatial components, including 0–0.9 kpc (dotted lines), 0.9–1.8 kpc (dot-dashed lines), 1.8–2.7 kpc (dashed lines), 2.7–3.6 kpc (long dot-dashed lines), 3.6–4.5 kpc (long dashed lines), and 4.5–5.4 kpc (solid lines).The stellar masses in the different components are normalized to their corresponding present-day values. The observations are from Fig. 6 of Gogarten et al. (2010), and the data have been offset from one another to avoid overlapping error bars. |
| In the text | |
 |
Fig. 6 Time evolution of the stellar mass surface density profiles for the disk of NGC 300. Different line types represent the radial profile of stellar mass surface density at 3.5 Gyr (dotted lines), 8.5 Gyr (dot-dashed), 12.5 Gyr (dashed lines), and 13.5 Gyr (solid lines). The observations are from Fig. 7 of Gogarten et al. (2010), and the data have been offset from one another to avoid overlapping error bars. |
| In the text | |
 |
Fig. 7 Time evolution of the stellar-mass-size (i.e., the disk scale-length) for the disk of NGC 300 from z = 1 to z = 0. |
| In the text | |
 |
Fig. 8 Time evolution of global atomic hydrogen gas mass, SFR, characteristic oxygen abundance, and the total gas fraction of NGC 300 disk. Vertical bars at 13.5 Gyr represent observational constraints (see Table 2). |
| In the text | |
 |
Fig. 9 Time evolution of the radial profiles of 12 + log (O/H) for the disks of NGC 300 (left panel) and M 33 (right panel) predicted by their own best-fitting models. Different line types represent the radial profile of 12 + log (O/H) at 2 (dotted line), 5 (dashed line), 10 (dot-dashed line), and 13.5 Gyr (solid line). |
| In the text | |
 |
Fig. 10 Current radial profiles of mean stellar age for NGC 300 (solid line) and M 33 (dashed line) predicted by their own best-fitting models. |
| In the text | |
 |
Fig. 11 Evolution of gas infall rate (left panel) and sSFR (right panel) for NGC 300 (solid line) and M 33 (dashed line) predicted by their own best-fitting models. |
| In the text | |
 |
Fig. 12 Stellar mass growth histories of NGC 300 (solid line) and M 33 (dashed line) predicted by their own best-fitting models. Stellar masses are normalized to their present-day values, and the horizontal dotted line in the panel marks when the stellar mass achieves 50% of its final value. |
| In the text | |
 |
Fig. 13 Growth of the disk scale-lengths for both NGC 300 (solid line) and M 33 (dashed line) predicted by their own best-fitting models. The disk scale-lengths are normalized to their sizes at z = 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


