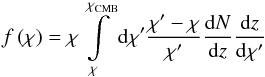| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201526940 | |
| Published online | 19 November 2015 | |
Cross-correlation of CFHTLenS galaxy catalogue and Planck CMB lensing using the halo model prescription⋆,⋆⋆
Physics department, École Normale Supérieure, 45 rue d’Ulm, 75005 Paris, France
e-mail: adrien.kuntz@ens.fr
Received: 10 July 2015
Accepted: 28 September 2015
Aims. I cross-correlate the galaxy counts from the Canada-France Hawaii Telescope Lensing Survey (CFHTLenS) galaxy catalogue and cosmic microwave background (CMB) convergence from the Planck data releases 1 (2013) and 2 (2015).
Methods. I improve on an earlier study by computing an analytic covariance from the halo model, implementing simulations to validate the theoretically estimated error bars and the reconstruction method, fitting both a galaxy bias and a cross-correlation amplitude using the joint cross and galaxy auto-correlation, and performing a series of null tests.
Results. Using a Bayesian analysis, I find a galaxy bias b = 0.92-0.02+0.02 and a cross-correlation amplitude A = 0.85-0.16+0.15 for the 2015 release, whereas for the 2013 release, I find b = 0.93-0.02+0.02 and A = 1.05-0.15+0.15.
Conclusions. I thus confirm the difference between the two releases found earlier, although both values of the amplitude now appear to be compatible with the fiducial value A = 1.
Key words: large-scale structure of Universe / cosmology: observations / cosmology: theory / gravitational lensing: weak
Based on observations obtained with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada.
A copy of the code is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/584/A53
© ESO, 2015
1. Introduction
In the framework of the standard cosmological model, galaxies form in matter overdensities that are the result of the non-linear growth of primordial inhomogeneities generated by inflation. As a photon travels from its surface of last scattering to us, its path is deflected by the large-scale structures of the Universe. Studying this weak gravitational lensing of the cosmic microwave background (CMB), which is characterized by temperature and polarization anisotropies, allows us to reconstruct a map of the integrated (over the line of sight) overdensity of matter of the Universe (Okamoto & Hu 2003).
Galaxies are expected to form inside dark matter halos, situated at the peaks of the density fluctuations. Galaxies are therefore expected to be good tracers of the large-scale structures, although their clustering characteristics may be different from the dark matter ones. The ratio between galaxy counts fluctuations and dark matter fluctuations is called the galaxy bias. Studying the cross-correlation of lensing convergence with galaxies allows this galaxy bias to be determined by a method possibly free of unaccounted-for correlated systematics effects, contrary to the auto-correlation of galaxies.
Several galaxy catalogues have been cross-correlated with the lensing convergence: Planck CMB lensing cross-correlated with NVSS quasars, MaxBCG clusters, SDSS LRGs, and the WISE Catalogue (Planck Collaboration XVII 2014), with the CFHTLenS galaxy catalogue (Omori & Holder 2015) and with high-z submillimetre galaxies detected by the Herschel-ATLAS survey (Bianchini et al. 2015); WMAP lensing cross-correlated with NVSS galaxies (Smith et al. 2007) and with LRGs and quasars from SDSS (Hirata et al. 2008); South Pole Telescope lensing cross-correlated with Blanco Cosmology Survey galaxies (Bleem et al. 2012) and with WISE quasars (Geach et al. 2013); Atacama Cosmology Telescope lensing cross-correlated with SDSS quasars (Sherwin et al. 2012).
In this paper, I cross-correlate the galaxy counts from the Canada-France Hawaii Telescope Lensing Survey (CFHTLenS) (Heymans et al. 2012; Erben et al. 2013) and the convergence all-sky map from the Planck collaboration (Planck Collaboration XVII 2014; Planck Collaboration XV 2015) for the 2013 and 2015 releases. I followed the study of Omori & Holder (2015), who found the surprising result of a significant difference between the galaxy bias inferred from the two releases. To complete their work, I computed the theoretical covariances inferred from the halo model (Cooray & Sheth 2002), fitted the joint cross and auto-correlation, implemented Gaussian simulations to check the error bars and the reconstruction method, and performed a series of null tests. The difference between the two releases, as found by Omori & Holder (2015), is recovered, although it is less significant.
This paper is organized as follows. In Sect. 2, I present the theoretical background needed for this study and correct some incomplete formulaes from the halo model. Data maps are presented in Sect. 3, and the joint cross and auto-correlation analysis is performed in Sect. 4. Section 5 presents the consistency checks I carried out: Gaussian simulations and null tests. Finally in Sect. 6 I summarize my results.
Throughout this paper, I assume a flat ΛCDM cosmology with h = 0.70, H0 = 100hkm s-1 Mpc-1, 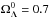 ,
, 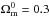 , ns = 0.97, σ8 = 0.82, and a0 = 1.
, ns = 0.97, σ8 = 0.82, and a0 = 1.
2. Theoretical background
2.1. Cross- and auto-correlation
The effect of weak gravitational lensing by large-scale structures on the CMB photons is described by a distortion matrix 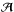 that relates the direction of observation
that relates the direction of observation 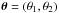 and the direction of the unlensed source θs:
and the direction of the unlensed source θs: 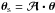 with
with 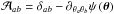 . Here, ψ is the lensing potential given by e.g. Peter & Uzan (2013), pp. 398−399:
. Here, ψ is the lensing potential given by e.g. Peter & Uzan (2013), pp. 398−399: ![\begin{equation} \psi\left(\boldsymbol{\theta}\right)=\frac{2}{c^{2}}\int_{0}^{\chi_{\rm CMB}}\frac{\chi_{\rm CMB}-\chi}{\chi\chi_{\rm CMB}}\Phi\left[\chi\boldsymbol{\theta},\chi\right]{\rm d}\chi . \end{equation}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq25.png) (1)In this equation χ is the line-of-sight comoving distance, χCMB is the comoving distance of the CMB at redshift zCMB ≃ 1090, and Φ is the gravitational potential at the point on the photon path given by χθ. The lensing convergence κ is defined as
(1)In this equation χ is the line-of-sight comoving distance, χCMB is the comoving distance of the CMB at redshift zCMB ≃ 1090, and Φ is the gravitational potential at the point on the photon path given by χθ. The lensing convergence κ is defined as 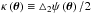 and is related to the matter overdensity δ via
and is related to the matter overdensity δ via
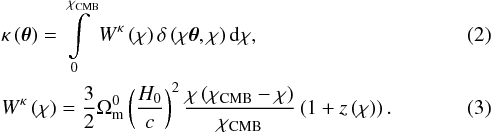 The overdensity of galaxies is defined as
The overdensity of galaxies is defined as
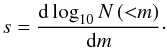 The second term in Eq. (5) is the magnification bias (Moessner et al. 1998), which occurs because the number density of galaxies is altered by gravitational lensing; it has an effect of a few percent. The dN/ dz ratio is the redshift distribution of the galaxy sample normalized such that ∫dz(dN/ dz) = 1. The over-density of galaxies is assumed to be linearly proportional to the matter over-density: δg(χθ,χ) = b(χ)δ(χθ,χ). In this article, the linear bias is assumed to be independent of χ, which is a rather good approximation given the sharply peaked redshift distribution (see Fig. 3). The fiducial value adopted for the galaxy bias is b = 1, as is suggested in the study of Omori & Holder (2015). Because the effect of the magnification bias is very weak, I take b as an overall factor of Wg for simplicity in the fitting algorithm. Figure 1 shows a plot of the two kernels Wκ and Wg.
The second term in Eq. (5) is the magnification bias (Moessner et al. 1998), which occurs because the number density of galaxies is altered by gravitational lensing; it has an effect of a few percent. The dN/ dz ratio is the redshift distribution of the galaxy sample normalized such that ∫dz(dN/ dz) = 1. The over-density of galaxies is assumed to be linearly proportional to the matter over-density: δg(χθ,χ) = b(χ)δ(χθ,χ). In this article, the linear bias is assumed to be independent of χ, which is a rather good approximation given the sharply peaked redshift distribution (see Fig. 3). The fiducial value adopted for the galaxy bias is b = 1, as is suggested in the study of Omori & Holder (2015). Because the effect of the magnification bias is very weak, I take b as an overall factor of Wg for simplicity in the fitting algorithm. Figure 1 shows a plot of the two kernels Wκ and Wg.
Decomposing 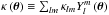 and
and 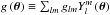 into spherical harmonics and using the Limber approximation (LoVerde & Afshordi 2008) for small angles, which consists in approximating the spherical Bessel functions by
into spherical harmonics and using the Limber approximation (LoVerde & Afshordi 2008) for small angles, which consists in approximating the spherical Bessel functions by 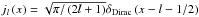 yields
yields  (7)where
(7)where 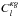 , the cross-correlation between κ and g, is defined as
, the cross-correlation between κ and g, is defined as 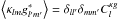 , and P(k,z) is the matter power spectrum, which I compute using the halo model (see Sect. 2.3) under the convention that
, and P(k,z) is the matter power spectrum, which I compute using the halo model (see Sect. 2.3) under the convention that 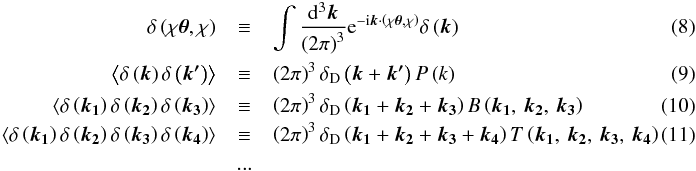 where δD stands for the Dirac delta function.
where δD stands for the Dirac delta function.
The auto-spectra are computed the same way: 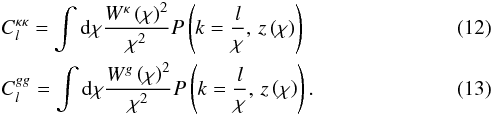
I then need an estimator for the cross- and auto-spectra and its covariance, and this is the subject of the next section.
 |
Fig. 1 Lensing kernel Wκ (dashed line) and galaxy overdensity kernel Wg (solid line) for all patches of the CFHTLenS catalogue. Both kernels are multiplied by dχ/ dz and normalized to a unit maximum. |
2.2. Estimator
The estimator used for the cross-correlation of the datasets is 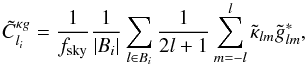 (14)replacing g with κ for the autocorrelations. Quantities with a tilde are observed data, fsky is the fraction of sky covered by the datasets, Bi is the bin in l used for the estimator, which is taken in this study as ranging from lmin = 50 to lmax = 1950 with width δl = 100, which corresponds to a number of bins Nbin = 19. The lower l cut is here because of the limited coverage of the sky imposed by the galaxy catalogue, the correlation being meaningful only below a few degrees. I numerically compute the covariance of this estimator using the halo model. Without any other approximation, the full covariance would be too heavy to compute, since it would involve six integrations. That is why I use the flat-sky approximation (Bernardeau et al. 2010), which consists in approximating the sphere by its tangential plane, and so is only valid at small angles. The spherical harmonics transform is then replaced by a simple Fourier transform:
(14)replacing g with κ for the autocorrelations. Quantities with a tilde are observed data, fsky is the fraction of sky covered by the datasets, Bi is the bin in l used for the estimator, which is taken in this study as ranging from lmin = 50 to lmax = 1950 with width δl = 100, which corresponds to a number of bins Nbin = 19. The lower l cut is here because of the limited coverage of the sky imposed by the galaxy catalogue, the correlation being meaningful only below a few degrees. I numerically compute the covariance of this estimator using the halo model. Without any other approximation, the full covariance would be too heavy to compute, since it would involve six integrations. That is why I use the flat-sky approximation (Bernardeau et al. 2010), which consists in approximating the sphere by its tangential plane, and so is only valid at small angles. The spherical harmonics transform is then replaced by a simple Fourier transform: 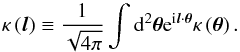 (15)The normalization is here to ensure that κ(0) = κ00. The same equation applies for g. Using Eq. (2), one finds
(15)The normalization is here to ensure that κ(0) = κ00. The same equation applies for g. Using Eq. (2), one finds 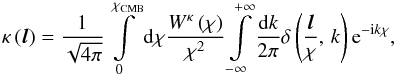 (16)and the correlator is
(16)and the correlator is 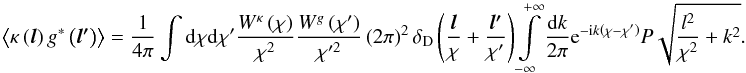 (17)In the small angle approximation, k is neglected before l/χ. (For high values of k the integral is suppressed because of the oscillatory function.) This yields
(17)In the small angle approximation, k is neglected before l/χ. (For high values of k the integral is suppressed because of the oscillatory function.) This yields 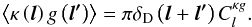 (18)The estimator of
(18)The estimator of 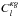 in the flat-sky approximation is
in the flat-sky approximation is 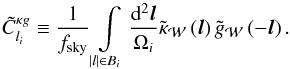 (19)The subscript
(19)The subscript 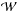 refers to the mask function: because the different surveys only probe a part of the sky, what is measured is
refers to the mask function: because the different surveys only probe a part of the sky, what is measured is 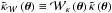 and
and 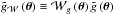 with
with  where the data are not masked and
where the data are not masked and 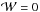 where the data are masked. Here,
where the data are masked. Here, 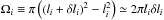 is the size of the bin i, and
is the size of the bin i, and 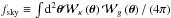 is here to ensure that
is here to ensure that 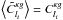 . Indeed,
. Indeed, 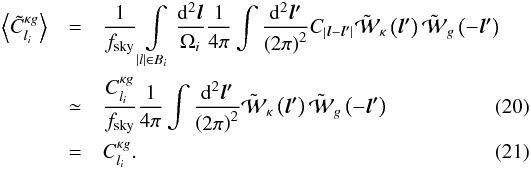
To find this expression of fsky one must assume that the size of the bin δli is larger than the typical length of variation in the Fourier transform of the mask functions, which is true in the case studied here. (δl = 100 and the typical size of a field of galaxies is ~5 degrees.)
The calculations are exactly the same for the autocorrelation, except that one must pay attention to the noise in the data, which are uncorrelated between the two maps:  The covariance of this estimator
The covariance of this estimator 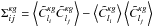 is calculated in the same way:
is calculated in the same way: ![\begin{eqnarray} \Sigma_{ij}^{\kappa g} & = & \frac{1}{4\pi f_{\rm sky}}\left[\frac{\left(2\pi\right)^{2}}{\Omega_{i}}\delta_{ij}^{K}\left(\left(C_{l_{i}}^{\kappa\kappa}+N_{l_{i}}^{\kappa\kappa}\right)\left(C_{l_{j}}^{gg}+N_{l_{i}}^{gg}\right)+\left(C_{l_{i}}^{\kappa g}\right)^{2}\right)+\bar{T}_{ij}^{\kappa g}\right]\label{eq:variance}\\ \bar{T}_{ij}^{\kappa g} & = & \intop\frac{{\rm d}^{2}\boldsymbol{l}}{\Omega_{i}}\frac{{\rm d}^{2}\boldsymbol{l'}}{\Omega_{j}}\intop {\rm d}\chi\frac{W^{\kappa}\left(\chi\right)^{2}W^{g}\left(\chi\right)^{2}}{\chi^{6}}T\left(\frac{\boldsymbol{l}}{\chi},\,-\frac{\boldsymbol{l}}{\chi},\,\frac{\boldsymbol{l'}}{\chi},\,-\frac{\boldsymbol{l'}}{\chi}\right)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\label{eq:Tbarij} \cdot \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq87.png) In this computation, I have ignored the beat-coupling effect that may arise from finite-volume survey effects (Takada & Hu 2013). The first term in Eq. (24) is the Gaussian variance, and the second term arises because of non-Gaussianity. It is important to note that while both terms are inversely proportional to the volume of the survey, only the non-Gaussian term remains constant with the binning adopted. Therefore this term can gain significant importance when the binning is large. The term
In this computation, I have ignored the beat-coupling effect that may arise from finite-volume survey effects (Takada & Hu 2013). The first term in Eq. (24) is the Gaussian variance, and the second term arises because of non-Gaussianity. It is important to note that while both terms are inversely proportional to the volume of the survey, only the non-Gaussian term remains constant with the binning adopted. Therefore this term can gain significant importance when the binning is large. The term 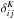 is the Kronecker delta. The covariances for the autocorrelations read as
is the Kronecker delta. The covariances for the autocorrelations read as ![\begin{eqnarray} \Sigma_{ij}^{\kappa\kappa} & = & \frac{1}{4\pi f_{\rm sky}}\left[\frac{\left(2\pi\right)^{2}}{\Omega_{i}}2\delta_{ij}^{K}\left(C_{l_{i}}^{\kappa\kappa}+N_{l_{i}}^{\kappa\kappa}\right)^{2}+\bar{T}_{ij}^{\kappa\kappa}\right]\\ \bar{T}_{ij}^{\kappa\kappa} & = & \intop\frac{{\rm d}^{2}\boldsymbol{l}}{\Omega_{i}}\frac{{\rm d}^{2}\boldsymbol{l'}}{\Omega_{j}}\intop {\rm d}\chi\frac{W^{\kappa}\left(\chi\right)^{4}}{\chi^{6}}T\left(\frac{\boldsymbol{l}}{\chi},\,-\frac{\boldsymbol{l}}{\chi},\,\frac{\boldsymbol{l'}}{\chi},\,-\frac{\boldsymbol{l'}}{\chi}\right) , \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq89.png) and similarly for the galaxies replacing κ with g. For the purpose of this study (cf Sect. 4), I also need a mixed covariance defined as
and similarly for the galaxies replacing κ with g. For the purpose of this study (cf Sect. 4), I also need a mixed covariance defined as 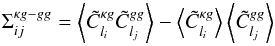 (28)and computed using the same prescription as above. The computed correlation matrix for the galaxy autocorrelation is shown in Fig. 2. It is clear that the non-Gaussian term has a non-negligible amplitude. However, in the cross-correlation covariance Σκg, the noise reconstruction of the convergence map is very high, so the Gaussian term dominates the non-Gaussian one.
(28)and computed using the same prescription as above. The computed correlation matrix for the galaxy autocorrelation is shown in Fig. 2. It is clear that the non-Gaussian term has a non-negligible amplitude. However, in the cross-correlation covariance Σκg, the noise reconstruction of the convergence map is very high, so the Gaussian term dominates the non-Gaussian one.
 |
Fig. 2 Correlation matrix Corrgg built with the covariance of Eq. (24) for the galaxy autocorrelation, using a binning of width δl = 100 from lmin = 50 to lmax = 1950. The non-Gaussian term has a strong amplitude, contrary to the one in Corrκκ and Corrκg because of the very high noise reconstruction of the convergence |
2.3. The halo model
The halo model is based on the spherical collapse model (Gunn & Gott 1972): large-scale structures formed from sufficiently overdense regions of space that collapsed under their own gravity. The remaining structures are called halos. Fitting formulaes for the number density of halos are presented in Sect. 2.3.1. Section 2.3.2 is about halo biasing with respect to dark matter; Sect. 2.3.3 presents the profiles of halos; and finally in Sect. 2.3.4, I compute the power spectrum and trispectrum in the halo model. For a thorough analysis of the halo model, see Cooray & Sheth (2002).
2.3.1. The number density of halos
A useful formula for the number density of halos at redshift z, n(m,z) is provided by Sheth & Tormen (1999), following an original formula by Press & Schechter (1974): 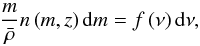 (29)where
(29)where 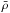 is the comoving density of the background with
is the comoving density of the background with 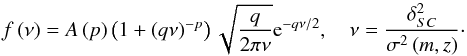 (30)In this formula, A(p) ≃ 0.322 such that
(30)In this formula, A(p) ≃ 0.322 such that 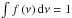 , p ≃ 0.3, q ≃ 0.75, δSC ≃ 1.68 is the critical density required for spherical collapse, and
, p ≃ 0.3, q ≃ 0.75, δSC ≃ 1.68 is the critical density required for spherical collapse, and 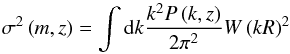 (31)is the variance of the initial density field extrapolated to the present time using the linear prediction:
(31)is the variance of the initial density field extrapolated to the present time using the linear prediction: 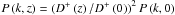 . Here, D+ is the linear growth factor,
. Here, D+ is the linear growth factor, 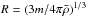 is the radius of a sphere of mean comoving density
is the radius of a sphere of mean comoving density 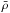 enclosing a mass m, and W is the Fourier transform of a top-hat function:
enclosing a mass m, and W is the Fourier transform of a top-hat function: 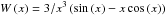 . To compute the values of the linear power spectrum, I use the CAMB routines (Lewis & Bridle 2002). The value ν = 1 defines a characteristic mass scale m∗ ≃ 4 × 1012M⊙/h at z = 0.
. To compute the values of the linear power spectrum, I use the CAMB routines (Lewis & Bridle 2002). The value ν = 1 defines a characteristic mass scale m∗ ≃ 4 × 1012M⊙/h at z = 0.
In practice, owing to the limited range of integration (v ≳ 10-2, otherwise the integration would bring unphysical values of the mass), the value of the parameter A(p) is adapted to ensure that 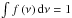 .
.
2.3.2. Halo biasing
Following Mo & White (1996) (see also Sheth & Tormen (1999) for an extension), the bias parameters of the overdensity of halos relative to the matter overdensity 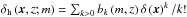 in the spherical collapse model (Gunn & Gott 1972) are given by
in the spherical collapse model (Gunn & Gott 1972) are given by 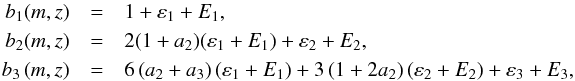 (32)with
(32)with 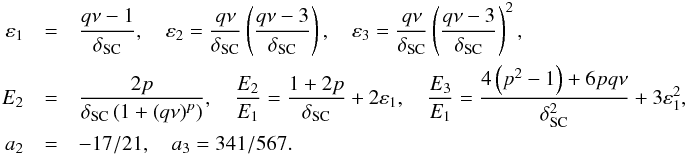 (33)These bias parameters obey the consistency relations
(33)These bias parameters obey the consistency relations 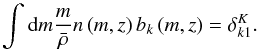 (34)Again, owing to the limited range of integration, the bias parameters are rescaled so as to ensure the consistency relations.
(34)Again, owing to the limited range of integration, the bias parameters are rescaled so as to ensure the consistency relations.
Within this framework, it is easy to compute the halo-halo correlations Phh, Bhhh, and Thhhh. The complete set of formulae for these correlations are given in Appendix A, with corrections that complete the formulae presented in Cooray & Sheth (2002).
2.3.3. Halo profiles
For the halo profile, I use a NFW profile (Navarro et al. 1997) given by 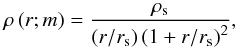 (35)where rs = Rvir/c, where c is known as the concentration parameter, and Rvir is the virialization radius defined by
(35)where rs = Rvir/c, where c is known as the concentration parameter, and Rvir is the virialization radius defined by 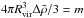 with
with 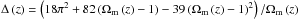 given by the spherical collapse model (Bryan & Norman 1998). The parameter ρs is obtained by requesting that
given by the spherical collapse model (Bryan & Norman 1998). The parameter ρs is obtained by requesting that 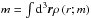 . For the concentration parameter I use (Bullock et al. 2001)
. For the concentration parameter I use (Bullock et al. 2001) 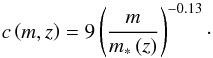 (36)In what follows I use the Fourier transform of the normalized NFW profile u(r;m) = ρ(r;m)/m, which is
(36)In what follows I use the Fourier transform of the normalized NFW profile u(r;m) = ρ(r;m)/m, which is ![\begin{eqnarray} u\left(k;m\right) & = & \frac{4\pi\rho_{\rm s}r_{\rm s}^{3}}{m}\left\{ \sin\left(kr_{\rm s}\right)\left[\mathrm{Si}\left(\left[1+c\right]kr_{\rm s}\right)-\mathrm{Si}\left(kr_{\rm s}\right)\right]-\frac{\sin\left(ckr_{\rm s}\right)}{\left(1+c\right)kr_{\rm s}}+\cos\left(kr_{\rm s}\right)\left[\mathrm{Ci}\left(\left[1+c\right]kr_{\rm s}\right)-\mathrm{Ci}\left(kr_{\rm s}\right)\right]\vphantom{\frac{\sin\left(ckr_{\rm s}\right)}{\left(1+c\right)kr_{\rm s}}}\right\} , \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq135.png) (37)where the sine and cosine integrals are
(37)where the sine and cosine integrals are 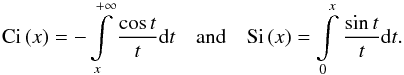 (38)
(38)
2.3.4. The power spectrum and trispectrum in the halo model
In this section I follow the formalism developed by Scherrer & Bertschinger (1991). The comoving dark matter density field is written as ![\begin{eqnarray} \rho_{\rm tot}\left(\boldsymbol{x}\right) & = & \sum_{i}\rho\left(\boldsymbol{x}-\boldsymbol{x_{i}},m_{i}\right)\nonumber \\[-1mm] & \equiv & \sum_{i}m_{i}u\left(\boldsymbol{x}-\boldsymbol{x_{i}}\right)\nonumber \\[-1mm] & = & \sum_{i}\int {\rm d}m{\rm d}^{3}\boldsymbol{x'}\delta_{\rm D}\left(m-m_{i}\right)\delta_{\rm D}^{3}\left(\boldsymbol{x'}-\boldsymbol{x_{i}}\right)m\,u\left(\boldsymbol{x}-\boldsymbol{x'},\,m\right)\!, \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq137.png) (39)where the sum is performed over the halos i and ρ is the profile of a halo of mass mi. The profile u is defined such that
(39)where the sum is performed over the halos i and ρ is the profile of a halo of mass mi. The profile u is defined such that 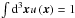 . The number density of halos is
. The number density of halos is 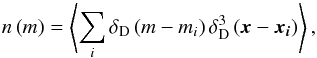 (40)such that
(40)such that 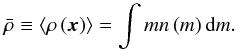 (41)It is then straightforward to compute the power spectrum in this model. It can be split into two terms: the contributions coming from the same halo and the ones coming from two different halos:
(41)It is then straightforward to compute the power spectrum in this model. It can be split into two terms: the contributions coming from the same halo and the ones coming from two different halos: ![\begin{eqnarray} &&P\left(k\right) = P^{\rm 1h}\left(k\right)+P^{\rm 2h}\left(k\right),\quad\nonumber \\&\mathrm{where}\nonumber \\ &&P^{\rm 1h}\left(k\right) = M_{02}\left(k,k\right)\nonumber \\ &&P^{\rm 2h}\left(k\right) = \left[M_{11}\left(k\right)\right]^{2}P^{\rm PT}\left(k\right) . \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq144.png) (42)The power spectrum coming from two different halos is evaluated with Eq. (A.1). In this equation, the linear power spectrum is used rather than the non-linear one. It is an approximation made so as not to overestimate the power spectrum on intermediate and small scales. On small scales, the one-halo term will dominate anyway. I have introduced the convenient notation:
(42)The power spectrum coming from two different halos is evaluated with Eq. (A.1). In this equation, the linear power spectrum is used rather than the non-linear one. It is an approximation made so as not to overestimate the power spectrum on intermediate and small scales. On small scales, the one-halo term will dominate anyway. I have introduced the convenient notation: 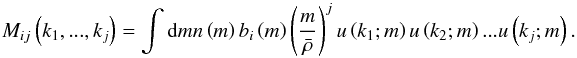 (43)These coefficients depend only on the norm of the ki. The trispectrum is evaluated in the same way. Since the entire formula is a bit long, it is given in Appendix A, with corrections to the formula given in Cooray & Hu (2001).
(43)These coefficients depend only on the norm of the ki. The trispectrum is evaluated in the same way. Since the entire formula is a bit long, it is given in Appendix A, with corrections to the formula given in Cooray & Hu (2001).
3. Data
3.1. Galaxy map
In this study, I use the galaxies from the CFHTLenS1 galaxy survey, a wide part of the Canada-France Hawaii Telescope Legacy Survey (CFHTLS), which consists in four fields centred at 2h18m00s−07d00m00s for W1, 08h54m00s−04d15m00s for W2, 14h17m54s+ 54d30m31s for W3, and 22h13m18s+ 01d19m00s for W4. Each has an area of 23−64deg2, a total survey area of 154 deg2, and a depth in the iAB band of iAB = 24.7 (Heymans et al. 2012; Erben et al. 2013). The survey area was imaged using the Megaprime wide field imager mounted at the prime focus of the Canada-France-Hawaii Telescope (CFHT) and equipped with the MegaCam camera. MegaCam comprises an array of 9 × 4 CCDs and has a field of view of 1 deg2.
I limit my analysis to galaxies in the redshift range 0.2 <z< 1.3. These galaxies have been confirmed to have a photometric redshift distribution that resembles the measured spectroscopic redshift distribution (Heymans et al. 2012). Galaxies selected with iAB< 24.5 in this redshift slice have a scatter of 0.03 <σΔz< 0.06 (where 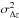 is the variance in the difference between the photometric and spectroscopic redshifts (zp−zs)/(1 + zs)) with 10% of the galaxies classified as outliers (Benjamin et al. 2013). The reduction pipeline has been set to star_flag = 0 and mask ≤1 (description of each flag can be found in Erben et al. (2013)), and the magnitude cut to 18.0 <iAB< 24.0. The resulting catalogue has a number of galaxies Ngal ≃ 6.58 × 106 and a sky coverage of fsky ≃ 3.5 × 10-3. Table 1 sums up the catalogue parameters in each patch.
is the variance in the difference between the photometric and spectroscopic redshifts (zp−zs)/(1 + zs)) with 10% of the galaxies classified as outliers (Benjamin et al. 2013). The reduction pipeline has been set to star_flag = 0 and mask ≤1 (description of each flag can be found in Erben et al. (2013)), and the magnitude cut to 18.0 <iAB< 24.0. The resulting catalogue has a number of galaxies Ngal ≃ 6.58 × 106 and a sky coverage of fsky ≃ 3.5 × 10-3. Table 1 sums up the catalogue parameters in each patch.
CFHTLenS catalogue data.
The redshift distribution dN/ dz used in Eq. (5) is obtained by averaging the individual 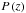 of each galaxy in each redshift bin, ranging from 0.2 <z< 1.3 with a bin size Δz of 0.05. This distribution is then fitted for analytic convenience with an incomplete gamma distribution, omitting the negligible error in redshift:
of each galaxy in each redshift bin, ranging from 0.2 <z< 1.3 with a bin size Δz of 0.05. This distribution is then fitted for analytic convenience with an incomplete gamma distribution, omitting the negligible error in redshift: 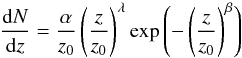 (44)as shown in Fig. 3. The best-fit values for the galaxy sample are λ = 0.78, β = 3.4, and z0 = 0.97.
(44)as shown in Fig. 3. The best-fit values for the galaxy sample are λ = 0.78, β = 3.4, and z0 = 0.97.
 |
Fig. 3 Redshift distribution of the CFHTLenS galaxies for all patches. The histogram is the recovered redshift distribution obtained by averaging the individual |
The galaxy overdensity is computed as a HEALPix2 map (Górski et al. 2005) with Nside = 2048 (corresponding to a pixel size of ~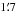 ) by
) by 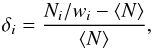 (45)where
(45)where 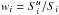 is the ratio between the unmasked surface of a HEALPix pixel and the total suface of this pixel, Ni is the number of galaxies counted in a pixel, and
is the ratio between the unmasked surface of a HEALPix pixel and the total suface of this pixel, Ni is the number of galaxies counted in a pixel, and 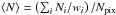 is the mean number of galaxies per pixel, corresponding to a number density of
is the mean number of galaxies per pixel, corresponding to a number density of 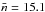 galaxies per square arcminute.
galaxies per square arcminute.
3.2. Convergence map
I use the observed and simulated convergence map from the Planck 2015 release3 (Planck Collaboration XV 2015) and compare the results with the 2013 release4 (Planck Collaboration XVII 2014). The 2015 map is produced by applying a quadratic estimator to all nine frequency bands with a galaxy and point-source mask, leaving a total of 67.3% of the sky for analysis. The 2013 map is obtained by combining only the 143 and 217 GHz channels. The 2015 map is released as a κlm map for 8 ≤ l ≤ 2048, while the 2013 map is a 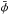 map and so is transformed into a convergence map by taking the transform
map and so is transformed into a convergence map by taking the transform 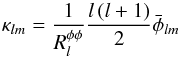 (46)where
(46)where 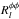 is a normalization factor explained in Planck Collaboration XVII (2014). The 2013 and 2015 masks are combined for consistency. The final mask for the cross-correlation is obtained by multiplying the convergence mask and the galaxy mask, then applied by converting the convergence multi-poles κlm in real space and multiplying with the mask.
is a normalization factor explained in Planck Collaboration XVII (2014). The 2013 and 2015 masks are combined for consistency. The final mask for the cross-correlation is obtained by multiplying the convergence mask and the galaxy mask, then applied by converting the convergence multi-poles κlm in real space and multiplying with the mask.
The noise for the auto-correlation has been estimated from the set of 100 simulated lensing maps released by the Planck team. The noise power spectrum 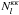 was estimated by averaging over the 100 simulations the autospectrum of the masked difference map between the reconstructed and the input lensing map.
was estimated by averaging over the 100 simulations the autospectrum of the masked difference map between the reconstructed and the input lensing map.
4. Constraints on galaxy bias and cross-correlation amplitude
Following Planck Collaboration XVII (2014) and Planck Collaboration XV (2015), I introduce a new parameter, A, named the lensing amplitude, that scales the amplitude of the cross-correlation: 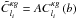 . Its expected value is obviously one. I then use the combined cross- and auto-correlation to constrain the galaxy bias b and the lensing amplitude A.
. Its expected value is obviously one. I then use the combined cross- and auto-correlation to constrain the galaxy bias b and the lensing amplitude A.
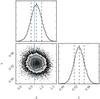 |
Fig. 4 Posterior distribution in the A−b plane, together with the marginalized distributions for each parameter, for the 2013 data. The contours show the 0.5σ, 1σ, 1.5σ, and 2σ lines from the centre to the border. The solid red line represents the fiducial value A = 1, and the dashed lines the −1σ and + 1σ error bars. |
I use the following scheme, developed by e.g. Bianchini et al. (2015) : the cross and auto-correlation are organized in a single vector following 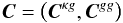 (47)where CXY is the vector containing
(47)where CXY is the vector containing 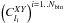 in the Nbin = 19 bins used. The total covariance matrix writes as
in the Nbin = 19 bins used. The total covariance matrix writes as 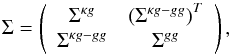 (48)where the mixed covariance
(48)where the mixed covariance 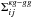 is defined in Eq. (28). The covariances are evaluated for the fiducial values A = 1 and b = 1. According to Bayes’ theorem, the posterior probability of a given set of parameters
is defined in Eq. (28). The covariances are evaluated for the fiducial values A = 1 and b = 1. According to Bayes’ theorem, the posterior probability of a given set of parameters 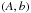 given the data C, is
given the data C, is 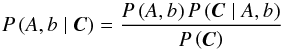 (49)where P(A,b) is the prior on the parameters, P(C|A,b) is the likelihood function for measuring C given A,b, and P(C) is a normalization factor. I assume a Gaussian likelihood function, which takes the form
(49)where P(A,b) is the prior on the parameters, P(C|A,b) is the likelihood function for measuring C given A,b, and P(C) is a normalization factor. I assume a Gaussian likelihood function, which takes the form 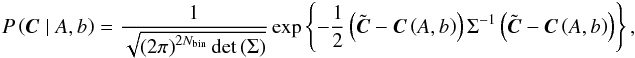 (50)and a flat prior. To sample the parameter space, I use a Monte-Carlo Markov Chain (MCMC) method employing the Python module EMCEE (Foreman-Mackey et al. 2013), which is a public implementation of the affine invariant MCMC ensemble sampler (Goodman & Weare 2010). The resulting parameters are estimated by the median of the posterior distribution after marginalizing over the other parameters with uncertainties given by the 16th and 84th percentiles. For a Gaussian distribution, the median is equal to the maximum likelihood value, and the percentiles correspond to the −1σ and + 1σ error bars; here, the recovered distributions are very close to Gaussians.
(50)and a flat prior. To sample the parameter space, I use a Monte-Carlo Markov Chain (MCMC) method employing the Python module EMCEE (Foreman-Mackey et al. 2013), which is a public implementation of the affine invariant MCMC ensemble sampler (Goodman & Weare 2010). The resulting parameters are estimated by the median of the posterior distribution after marginalizing over the other parameters with uncertainties given by the 16th and 84th percentiles. For a Gaussian distribution, the median is equal to the maximum likelihood value, and the percentiles correspond to the −1σ and + 1σ error bars; here, the recovered distributions are very close to Gaussians.
The two-dimensional posterior distribution and the marginalized ones are shown in Fig. 4 for the 2013 release, and in Fig. 5 for the 2015 release, using all the patches together. Table 2 sums up the values of parameters A and b for each patch and for the two releases with 1σ error bars, together with the χ2 calculated as 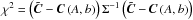 for ν = 2Nbin−2 degrees of freedom. Parameter b is mostly constrained by the galaxy auto-correlation, so it has approximately the same value for the two releases.
for ν = 2Nbin−2 degrees of freedom. Parameter b is mostly constrained by the galaxy auto-correlation, so it has approximately the same value for the two releases.
Best-fit values for A and b using both cross- and auto-correlation for the 2013 and 2015 releases.
The cross- and auto-correlations, together with the best-fit parameters theoretical prediction (with all patches together), are shown in Figs. 6 and 7.
 |
Fig. 6 CMB convergence − galaxy over-density cross-correlation |
 |
Fig. 7 As in Fig. 6, but for the galaxy auto-correlation |
5. Consistency checks
5.1. Simulations
To validate the algorithm employed to reconstruct the convergence and galaxy maps and to check the consistency of the theoretical error bars in the Gaussian limit, I created Nsim = 100 simulations of the galaxy and convergence maps. I used the Healpy synfast function to generate a set of κlm and glm and the theoretical  ,
,  , and
, and 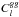 given in Eqs. (12), (7), and (13), with b = 1. The multi-pole coefficients are synthetized by
given in Eqs. (12), (7), and (13), with b = 1. The multi-pole coefficients are synthetized by 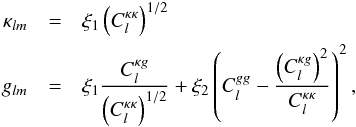 (51)where for each value of l and m> 0, ξ1 and ξ2 are two complex numbers drawn from a Gaussian distribution of mean 0 and variance 1, whereas for m = 0 they are real.
(51)where for each value of l and m> 0, ξ1 and ξ2 are two complex numbers drawn from a Gaussian distribution of mean 0 and variance 1, whereas for m = 0 they are real.
To account for the level of noise in the maps, I replaced 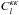 by
by 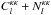 with
with 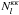 the noise given in the Planck Collaboration release. As pointed out by the Planck 2013 Wiki5, this noise is not accurate enough for the auto-correlation, but it should be sufficient for the cross-correlation, which is not biased by this noise term. The noise in the galaxy map was accounted for by drawing the number of galaxies in each pixel from a Poisson distribution with mean
the noise given in the Planck Collaboration release. As pointed out by the Planck 2013 Wiki5, this noise is not accurate enough for the auto-correlation, but it should be sufficient for the cross-correlation, which is not biased by this noise term. The noise in the galaxy map was accounted for by drawing the number of galaxies in each pixel from a Poisson distribution with mean 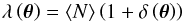 (52)where ⟨N⟩ is the mean number of galaxies per pixel of the original map, and
(52)where ⟨N⟩ is the mean number of galaxies per pixel of the original map, and 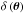 the simulated overdensity map. I then replaced the galaxy number count Ni/wi in Eq. (45) by
the simulated overdensity map. I then replaced the galaxy number count Ni/wi in Eq. (45) by 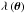 . The Poisson noise of variance
. The Poisson noise of variance 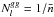 was thus included in this map with
was thus included in this map with 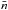 the number of galaxies per steradian.
the number of galaxies per steradian.
I then applied the spectral estimators described in the previous sections to the simulated convergence and over-density maps. The recovered 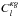 and
and 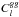 averaged over the 100 simulations are shown in Figs. 8 and 9. The mean correlation was computed as
averaged over the 100 simulations are shown in Figs. 8 and 9. The mean correlation was computed as 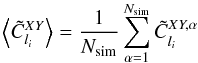 (53)where X,Y = {κ,g}, α is the number of the simulation, and i refers to the bin in l of width δl = 100. The covariance matrix of the samples was computed as
(53)where X,Y = {κ,g}, α is the number of the simulation, and i refers to the bin in l of width δl = 100. The covariance matrix of the samples was computed as 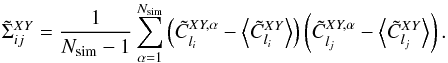 (54)For comparison, I show the theoretical error bars and the recovered simulated error bars for the mean correlation computed as
(54)For comparison, I show the theoretical error bars and the recovered simulated error bars for the mean correlation computed as 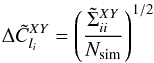 (55)with the same formula for the theoretical error bars, using only the Gaussian term in Eq. (24) because the simulations are Gaussian. They are in very good agreement.
(55)with the same formula for the theoretical error bars, using only the Gaussian term in Eq. (24) because the simulations are Gaussian. They are in very good agreement.
 |
Fig. 8 Upper panel: cross-correlation of the simulated galaxy and lensing maps using b = 1. The solid line represents the input cross-correlation, and the points represent the reconstructed cross-correlation averaged over Nsim = 100 simulations, together with the simulated error bars. Lower panel: fractional difference between the input and the recovered cross-correlations. The blue error bars are recovered from the simulations using Eq. (54) for the covariance matrix, and the red ones are analytic using Eq. (24) for the covariance, keeping only the Gaussian term. |
I also fitted a galaxy bias and a lensing amplitude following the pipeline explained in Sect. 4 and compared them to the fiducial values used in the simulations A = 1 and b = 1. To this aim I replaced the correlations 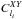 by the mean correlations
by the mean correlations 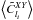 and the covariances matrices ΣXY by the mean correlation covariance
and the covariances matrices ΣXY by the mean correlation covariance 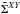 /Nsim. The fitted values of the parameters are
/Nsim. The fitted values of the parameters are 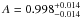 and
and 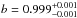 , indicating that the reconstruction is good. Figure 10 shows a corner plot of the MCMC sampler for the simulations, as in Fig. 4.
, indicating that the reconstruction is good. Figure 10 shows a corner plot of the MCMC sampler for the simulations, as in Fig. 4.
 |
Fig. 10 As in Fig. 4, but for the Gaussian simulations. The horizontal and vertical solid lines show the fiducial values A = 1 and b = 1 used in the simulations. |
5.2. Null tests
To check that there is no systematics in the pipeline descibed above, I performed a series of null tests consisting in cross-correlating a real map with the Nsim = 100 simulated maps of Sect. 5.1, both for a real convergence map with a simulated galaxy map and for a simulated convergence map with a real galaxy map, using all the patches together. The expected signal is of null amplitude, with a simulated covariance given by Eq. (54) applied to the null test simulations. As shown in Fig. 11, in both cases no significant signal was detected. The fitted values of the product A × b (which is the amplitude of the cross-correlation) are summarized in Table 3.
To validate the use of Gaussian simulations in the computation of covariances, I also cross-correlated the 100 simulated Planck maps given by the Planck collaboration with the real galaxy overdensity field. I obtain a result similar to the Gaussian simulation null test for the error bars, indicating that the use of Gaussian simulations is relevant.
 |
Fig. 11 Upper panel: mean correlation between the true lensing map of 2015 and 100 simulated galaxy maps using all patches. Middle panel: mean correlation between the true galaxy map using all patches and 100 gaussian simulated lensing maps. Lower panel: mean correlation between the true galaxy map using all patches and 100 Planck simulated lensing maps. In all cases the signal is consistent with no correlation. |
6. Summary and conclusions
I have presented the results from a joint analysis of the cross and auto-correlation of the CFHTLenS galaxy catalogue and Planck CMB lensing, checking the reliability of my result by null tests and Gaussian simulations. I found a galaxy bias of 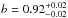 and a cross-correlation amplitude of
and a cross-correlation amplitude of 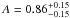 for the 2015 release, whereas for the 2013 release I found
for the 2015 release, whereas for the 2013 release I found 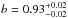 and
and 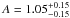 . This confirms the difference between the two releases shown by Omori & Holder (2015), but the trend is less clear, and both results are compatible with each other. These results are consistent with the amplitudes obtained from the Planck lensing autocorrelation in Planck Collaboration XV (2015): A = 0.987 ± 0.025 for the 2015 release and A = 1.005 ± 0.043 for the 2013 release. The value of the galaxy bias suggests that galaxies in this magnitude range are unbiased tracers of dark matter.
. This confirms the difference between the two releases shown by Omori & Holder (2015), but the trend is less clear, and both results are compatible with each other. These results are consistent with the amplitudes obtained from the Planck lensing autocorrelation in Planck Collaboration XV (2015): A = 0.987 ± 0.025 for the 2015 release and A = 1.005 ± 0.043 for the 2013 release. The value of the galaxy bias suggests that galaxies in this magnitude range are unbiased tracers of dark matter.
This study suggests that the joint analysis of the cross and auto-correlation can put strong constraints on the properties of tracers of dark matter. Forthcoming wide galaxy surveys probing fainter magnitudes will improve the constraining power of this kind of study, both by a larger survey area to improve statistics and a sufficient galaxy number density to avoid shot noise. They are expected to put better constraints on the cosmological model used in this paper.
Acknowledgments
I would first like to thank Simon Prunet for all the invaluable knowledge he shared with me. This work is based on observations with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This research used the facilities of the Canadian Astronomy Data Centre operated by the National Research Council of Canada with the support of the Canadian Space Agency. CFHTLenS data processing was made possible thanks to significant computing support from the NSERC Research Tools and Instruments grant programme. Some of the results in this paper have been derived using the HEALPix (Górski et al. 2005) package.
References
- Benjamin, J., Van Waerbeke, L., Heymans, C., et al. 2013, MNRAS, 431, 1547 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardeau, F., Colombi, S., Gaztanaga, E., & Scoccimarro, R. 2002, Phys. Rep., 367, 1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Bernardeau, F., Pitrou, C., & Uzan, J.-P. 2010, J. Cosmol. Astropart. Phys., 2, 015 [NASA ADS] [Google Scholar]
- Bianchini, F., Bielewicz, P., Lapi, A., et al. 2015, ApJ, 802, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Bleem, L. E., van Engelen, A., Holder, G. P., et al. 2012, ApJ, 753, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Cooray, A., & Hu, W. 2001, ApJ, 554, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Erben, T., Hildebrandt, H., Miller, L., et al. 2013, MNRAS, 433, 2545 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Geach, J. E., Hickox, R. C., Bleem, L. E., et al. 2013, ApJ, 776, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Comm. Appl. Math. Comput. Sci., 5, 65 [CrossRef] [MathSciNet] [Google Scholar]
- Goroff, M. H., Grinstein, B., Rey, S.-J., & Wise, M. B. 1986, ApJ, 311, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Gott, III, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Van Waerbeke, L., Miller, L., et al. 2012, MNRAS, 427, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Hirata, C. M., Ho, S., Padmanabhan, N., Seljak, U., & Bahcall, N. 2008, Phys. Rev. D, 78, 043520 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- LoVerde, M., & Afshordi, N. 2008, Phys. Rev. D, 78, 123506 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., & White, S. D. M. 1996, MNRAS, 282, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Moessner, R., Jain, B., & Villumsen, J. V. 1998, MNRAS, 294, 291 [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, T., & Hu, W. 2003, Phys. Rev. D, 67, 083002 [NASA ADS] [CrossRef] [Google Scholar]
- Omori, Y., & Holder, G. 2015, ArXiv e-prints [arXiv:1502.03405] [Google Scholar]
- Peter, P., & Uzan, J.-P. 2013, Primordial cosmology, 1st edn., Oxford graduate texts (Oxford: Oxford Univ. Press) [Google Scholar]
- Planck Collaboration XVII. 2014, A&A, 571, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XV. 2015, A&A, submitted [arXiv:1502.01591] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, R. J., & Bertschinger, E. 1991, ApJ, 381, 349 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sherwin, B. D., Das, S., Hajian, A., et al. 2012, Phys. Rev. D, 86, 083006 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., & Tormen, G. 1999, MNRAS, 308, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. M., Zahn, O., & Dore, O. 2007, Phys. Rev. D, 76, 043510 [NASA ADS] [CrossRef] [Google Scholar]
- Takada, M., & Hu, W. 2013, Phys. Rev. D, 87, 123504 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The halo model power spectrum, bispectrum, and trispectrum
Using the bias parameters given in Sect. 2.3.2, the halo-halo correlations are (the dependence on z is omitted for clarity, along with the k’s and m’s when not needed):
![\appendix \setcounter{section}{1} \begin{eqnarray} &&P_{\rm hh} = b_{1}\left(m_{1}\right)b_{1}\left(m_{2}\right)P^{\rm PT}\left(k\right),\nonumber \\ &&B_{\rm hhh} = b_{1}\left(m_{1}\right)b_{1}\left(m_{2}\right)b_{1}\left(m_{3}\right)B^{\rm PT}+\left[b_{2}\left(m_{1}\right)b_{1}\left(m_{2}\right)b_{1}\left(m_{3}\right)P^{\rm PT}\left(k_{2}\right)P^{\rm PT}\left(k_{3}\right)+cyc.\right],\nonumber \\ &&T_{\rm hhhh} = b_{1}\left(m_{1}\right)b_{1}\left(m_{2}\right)b_{1}\left(m_{3}\right)b_{1}\left(m_{4}\right)T^{\rm PT} + b_{3}\left(m_{1}\right)b_{1}\left(m_{2}\right)b_{1}\left(m_{3}\right)b_{1}\left(m_{4}\right)P^{\rm PT}\left(k_{2}\right)P^{\rm PT}\left(k_{3}\right)P^{\rm PT}\left(k_{4}\right)+cyc.\nonumber \\ && \qquad\qquad + b_{2}\left(m_{1}\right)b_{1}\left(m_{2}\right)b_{1}\left(m_{3}\right)b_{1}\left(m_{4}\right)\left[P^{\rm PT}\left(k_{2}\right)B^{\rm PT}\left(\boldsymbol{k_{1}}+\boldsymbol{k_{2}},\boldsymbol{k_{3}},\boldsymbol{k_{4}}\right)+\left(2\leftrightarrow3\right)+\left(2\leftrightarrow4\right)\right]+cyc.\nonumber \\ && \qquad \qquad + b_{2}\left(m_{1}\right)b_{1}\left(m_{3}\right)b_{1}\left(m_{4}\right)\left\{ b_{2}\left(m_{2}\right)P^{\rm PT}\left(k_{3}\right)P^{\rm PT}\left(k_{4}\right)\left[P^{\rm PT}\left(\left|\boldsymbol{k_{1}}+\boldsymbol{k_{3}}\right|\right)+P^{\rm PT}\left(\left|\boldsymbol{k_{1}}+\boldsymbol{k_{4}}\right|\right)\right]\right.\nonumber \\ & & \hspace*{-18mm} \hphantom{b_{2}\left(m_{1}\right)b_{1}\left(m_{3}\right)b_{1}\left(m_{4}\right)}\left.+\left(2\leftrightarrow3\right)+\left(2\leftrightarrow4\right)\vphantom{P^{\rm PT}\left(\left|\boldsymbol{k_{1}}+\boldsymbol{k_{3}}\right|\right)}\right\} +cyc\label{eq:Phh} . \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq310.png) (A.1)The formula given in Cooray & Sheth (2002) (Eq. (90)) for the trispectrum is actually incomplete. Here, PPT, BPT and TPT are the power spectrum, bispectrum, and trispectrum at lowest order in perturbation theory (see Bernardeau et al. 2002, for a review) given by
(A.1)The formula given in Cooray & Sheth (2002) (Eq. (90)) for the trispectrum is actually incomplete. Here, PPT, BPT and TPT are the power spectrum, bispectrum, and trispectrum at lowest order in perturbation theory (see Bernardeau et al. 2002, for a review) given by
![\appendix \setcounter{section}{1} \begin{eqnarray} &&B^{\rm PT}\left(\boldsymbol{k_{1}},\boldsymbol{k_{2}},\boldsymbol{k_{3}}\right) = 2F_{2}^{s}\left(\boldsymbol{k_{1}},\boldsymbol{k_{2}}\right)P^{\rm PT}\left(k_{1}\right)P^{\rm PT}\left(k_{2}\right)+\left(\boldsymbol{k_{1}}\leftrightarrow\boldsymbol{k_{3}}\right)+\left(\boldsymbol{k_{2}}\leftrightarrow\boldsymbol{k_{3}}\right)\nonumber \\ &&T^{\rm PT}\left(\boldsymbol{k_{1}},-\boldsymbol{k_{1}},\boldsymbol{k_{2}},-\boldsymbol{k_{2}}\right) = 4P^{\rm PT}\left(\boldsymbol{k_{1}}+\boldsymbol{k_{2}}\right)\left[F_{2}^{s}\left(-\boldsymbol{k_{1}},\boldsymbol{k_{1}}+\boldsymbol{k_{2}}\right)P^{\rm PT}\left(k_{1}\right)+\left(\boldsymbol{k_{1}}\leftrightarrow\boldsymbol{k_{2}}\right)\right]+\left(\boldsymbol{k_{1}}\leftrightarrow-\boldsymbol{k_{1}}\right)\nonumber \\ && \qquad\qquad \qquad \qquad \qquad + 12\left[F_{3}^{s}\left(\boldsymbol{k_{1}},-\boldsymbol{k_{1}},\boldsymbol{k_{2}}\right)P^{\rm PT}\left(k_{1}\right)^{2}P^{\rm PT}\left(k_{2}\right)+\left(\boldsymbol{k_{1}}\leftrightarrow\boldsymbol{k_{2}}\right)\right]\label{eq:PT} \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq314.png) (A.2)where the symmetrized kernels
(A.2)where the symmetrized kernels 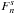 are derived in Goroff et al. (1986). There is a very small dependence of the kernels on the parameter Ωm, which is ignored in this study.
are derived in Goroff et al. (1986). There is a very small dependence of the kernels on the parameter Ωm, which is ignored in this study.
The halo model power spectrum and trispectrum are then computed as (using the notation 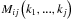 given in Eq. (43)):
given in Eq. (43)):
![\appendix \setcounter{section}{1} \begin{eqnarray} &&P\left(k\right) = P^{\rm 1h}\left(k\right)+P^{\rm 2h}\left(k\right),\quad\mathrm{where}\nonumber \\ &&P^{\rm 1h}\left(k\right) = M_{02}\left(k,k\right)\nonumber \\ &&P^{\rm 2h}\left(k\right) = \left[M_{11}\left(k\right)\right]^{2}P^{\rm PT}\left(k\right) . \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq318.png) (A.3)Since I only need terms of the form T(k1,−k1,k2,−k2) (see Eq. (25)), the trispectrum can be simplified as
(A.3)Since I only need terms of the form T(k1,−k1,k2,−k2) (see Eq. (25)), the trispectrum can be simplified as 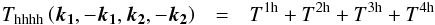 (A.4)with
(A.4)with ![\appendix \setcounter{section}{1} \begin{eqnarray} T^{\rm 1h} & = & M_{04}\left(k_{1},k_{1},k_{2},k_{2}\right)\nonumber \\ T^{\rm 2h} & = & 2M_{11}\left(k_{1}\right)M_{13}\left(k_{1},k_{2},k_{2}\right)P^{\rm PT}\left(k_{1}\right)+\left(k_{1}\leftrightarrow k_{2}\right)\nonumber \\ && + M_{12}\left(k_{1},k_{2}\right)^{2}\left[P^{\rm PT}\left(\left|\boldsymbol{k_{1}}+\boldsymbol{k_{2}}\right|\right)+\left(\boldsymbol{k_{1}}\leftrightarrow-\boldsymbol{k_{1}}\right)\right]\nonumber \\ T^{\rm 3h} & = & 2M_{11}\left(k_{1}\right)M_{11}\left(k_{2}\right)M_{12}\left(k_{1},k_{2}\right)\left[B^{\rm PT}\left(\boldsymbol{k_{1}},\boldsymbol{k_{2}},-\boldsymbol{k_{1}}-\boldsymbol{k_{2}}\right)+\left(\boldsymbol{k_{1}}\leftrightarrow-\boldsymbol{k_{1}}\right)\right]\nonumber \\ && + M_{11}\left(k_{1}\right)^{2}M_{22}\left(k_{2},k_{2}\right)P^{\rm PT}\left(k_{1}\right)^{2}+\left(k_{1}\leftrightarrow k_{2}\right)\nonumber \\ && + 4M_{11}\left(k_{1}\right)M_{11}\left(k_{2}\right)M_{22}\left(k_{1},k_{2}\right)P^{\rm PT}\left(k_{1}\right)P^{\rm PT}\left(k_{2}\right)\nonumber \\ && + 2M_{12}\left(k_{1},k_{2}\right)\left[P^{\rm PT}\left(\left|\boldsymbol{k_{1}}+\boldsymbol{k_{2}}\right|\right)+\left(\boldsymbol{k_{1}}\leftrightarrow-\boldsymbol{k_{1}}\right)\right]\left[M_{21}\left(k_{1}\right)M_{11}\left(k_{2}\right)P^{\rm PT}\left(k_{2}\right)+\left(k_{1}\leftrightarrow k_{2}\right)\right]\nonumber \\ T^{\rm 4h} & = & M_{11}\left(k_{1}\right)^{2}M_{11}\left(k_{2}\right)^{2}T^{\rm PT}\left(\boldsymbol{k_{1}},-\boldsymbol{k_{1}},\boldsymbol{k_{2}},-\boldsymbol{k_{2}}\right)\nonumber \\ && + 2M_{31}\left(k_{1}\right)M_{11}\left(k_{1}\right)M_{11}\left(k_{2}\right)^{2}P^{\rm PT}\left(k_{1}\right)P^{\rm PT}\left(k_{2}\right)^{2}+\left(k_{1}\leftrightarrow k_{2}\right)\nonumber \\ && + 2M_{21}\left(k_{1}\right)M_{11}\left(k_{1}\right)M_{11}\left(k_{2}\right)^{2}P^{\rm PT}\left(k_{2}\right)\left[B^{\rm PT}\left(\boldsymbol{k_{1}},\boldsymbol{k_{2}},-\boldsymbol{k_{1}}-\boldsymbol{k_{2}}\right)+\left(\boldsymbol{k_{1}}\leftrightarrow-\boldsymbol{k_{1}}\right)\right]+\left(k_{1}\leftrightarrow k_{2}\right)\nonumber \\ && + 2M_{21}\left(k_{1}\right)M_{11}\left(k_{2}\right)P^{\rm PT}\left(k_{2}\right)\left[M_{21}\left(k_{1}\right)M_{11}\left(k_{2}\right)P^{\rm PT}\left(k_{2}\right)+M_{11}\left(k_{1}\right)M_{21}\left(k_{2}\right)P^{\rm PT}\left(k_{1}\right)\right]\nonumber \\ & & \hspace*{-37mm}\hphantom{2M_{21}\left(k_{1}\right)M_{11}\left(k_{2}\right)P^{\rm PT}\left(k_{2}\right)}\times\left[P^{\rm PT}\left(\left|\boldsymbol{k_{1}}+\boldsymbol{k_{2}}\right|\right)+P^{\rm PT}\left(\left|\boldsymbol{k_{1}}-\boldsymbol{k_{2}}\right|\right)\right]+\left(k_{1}\leftrightarrow k_{2}\right) . \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq321.png) (A.5)This formula corrects the one of Cooray & Hu (2001), which is incomplete for both the three-halo and four-halo terms.
(A.5)This formula corrects the one of Cooray & Hu (2001), which is incomplete for both the three-halo and four-halo terms.
A code implementation in Python computing this trispectrum in the halo model is available upon request to the author.
All Tables
Best-fit values for A and b using both cross- and auto-correlation for the 2013 and 2015 releases.
All Figures
 |
Fig. 1 Lensing kernel Wκ (dashed line) and galaxy overdensity kernel Wg (solid line) for all patches of the CFHTLenS catalogue. Both kernels are multiplied by dχ/ dz and normalized to a unit maximum. |
| In the text | |
 |
Fig. 2 Correlation matrix Corrgg built with the covariance of Eq. (24) for the galaxy autocorrelation, using a binning of width δl = 100 from lmin = 50 to lmax = 1950. The non-Gaussian term has a strong amplitude, contrary to the one in Corrκκ and Corrκg because of the very high noise reconstruction of the convergence |
| In the text | |
 |
Fig. 3 Redshift distribution of the CFHTLenS galaxies for all patches. The histogram is the recovered redshift distribution obtained by averaging the individual |
| In the text | |
 |
Fig. 4 Posterior distribution in the A−b plane, together with the marginalized distributions for each parameter, for the 2013 data. The contours show the 0.5σ, 1σ, 1.5σ, and 2σ lines from the centre to the border. The solid red line represents the fiducial value A = 1, and the dashed lines the −1σ and + 1σ error bars. |
| In the text | |
 |
Fig. 5 Same as in Fig. 4, but for the 2015 data. |
| In the text | |
 |
Fig. 6 CMB convergence − galaxy over-density cross-correlation |
| In the text | |
 |
Fig. 7 As in Fig. 6, but for the galaxy auto-correlation |
| In the text | |
 |
Fig. 8 Upper panel: cross-correlation of the simulated galaxy and lensing maps using b = 1. The solid line represents the input cross-correlation, and the points represent the reconstructed cross-correlation averaged over Nsim = 100 simulations, together with the simulated error bars. Lower panel: fractional difference between the input and the recovered cross-correlations. The blue error bars are recovered from the simulations using Eq. (54) for the covariance matrix, and the red ones are analytic using Eq. (24) for the covariance, keeping only the Gaussian term. |
| In the text | |
 |
Fig. 9 Same as Fig. 8, but for |
| In the text | |
 |
Fig. 10 As in Fig. 4, but for the Gaussian simulations. The horizontal and vertical solid lines show the fiducial values A = 1 and b = 1 used in the simulations. |
| In the text | |
 |
Fig. 11 Upper panel: mean correlation between the true lensing map of 2015 and 100 simulated galaxy maps using all patches. Middle panel: mean correlation between the true galaxy map using all patches and 100 gaussian simulated lensing maps. Lower panel: mean correlation between the true galaxy map using all patches and 100 Planck simulated lensing maps. In all cases the signal is consistent with no correlation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} &&g\left(\boldsymbol{\theta}\right)=\intop_{0}^{\chi_{\rm CMB}}W^{g}\left(\chi\right)\delta\left(\chi\boldsymbol{\theta},\chi\right){\rm d}\chi,~~~~\\[-2mm] &&W^{g}\left(\chi\right)=\frac{{\rm d}N\left(z\right)}{{\rm d}z}\frac{{\rm d}z}{{\rm d}\chi}b\left(\chi\right)+\frac{3}{2}\Omega_{\rm m}^{0}\left(\frac{H_{0}}{c}\right)^{2}\left(1+z\left(\chi\right)\right)\left(5s-2\right)f\left(\chi\right)\label{eq:Wg} \end{eqnarray}](/articles/aa/full_html/2015/12/aa26940-15/aa26940-15-eq35.png)