| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 5 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201526893 | |
| Published online | 13 November 2015 | |
The stellar wind velocity field of HD 77581
1 Centrum Astronomiczne im. M. Kopernika, Bartycka 18, 00716 Warszawa, Poland
e-mail: antonism@camk.edu.pl
2 ISDC Data Center for Astrophysics, Université de Genève, Chemin d’Ecogia 16, 1290 Versoix, Switzerland
3 Observatoire de Genève, Université de Genève, Chemin des Maillettes 51, 1290 Versoix, Switzerland
Received: 3 July 2015
Accepted: 21 August 2015
Aims. The early acceleration of stellar winds in massive stars is poorly constrained. The scattering of hard X-ray photons emitted by the pulsar in the high-mass X-ray binary Vela X-1 can be used to probe the stellar wind velocity and density profile close to the surface of its supergiant companion HD 77581.
Methods. We built a high signal-to-noise and high resolution hard X-ray lightcurve of Vela X-1 measured by Swift/BAT over 300 orbital periods of the system and compared it with the predictions of a grid of hydrodynamic simulations.
Results. We obtain very good agreement between observations and simulations for a narrow set of parameters, implying that the wind velocity close to the stellar surface is twice higher than usually assumed with the standard beta law. Locally a velocity gradient of β ~ 0.5 is favoured. Even if still incomplete, hydrodynamic simulations successfully reproduce several observational properties of Vela X-1.
Key words: X-rays: binaries / hydrodynamics / stars: winds, outflows / accretion, accretion disks
© ESO, 2015
1. Introduction
The density and velocity of stellar winds in massive stars are poorly constrained close to the stellar surface. Eclipsing high-mass X-ray binaries with short orbital orbits allow the conditions of the inner stellar wind to be probed in situ. Thanks to its high X-ray flux, Vela X-1 is a perfect laboratory, with a pulsar accreting and photo-ionising the wind of its massive (B 0.5 Ib) companion. The X-ray emission produced close to the neutron star traces the instabilities of the accretion flow on large scales, which can be studied thanks to the variability of the X-ray flux and absorbing column density (Walter & Zurita Heras 2007).
The neutron star of Vela X-1 weighs MNS = 1.86 M⊙ (Quaintrell et al. 2003) and orbits its massive companion with a period of 8.96 days in an almost circular orbit (α = 1.76 R∗, e ≈ 0.09; Bildsten et al. 1997). The wind from its massive stellar companion is characterised by a mass-loss rate of ~4 × 10-6M⊙ yr-1 (Nagase et al. 1986) and a wind terminal velocity of υ∞ ≈ 1700 km s-1 (Dupree et al. 1980), which translates into a local wind velocity of 400 km s-1 at 1.2 stellar radius, assuming the commonly used β = 0.5 velocity gradient. The typical X-ray luminosity is ~4 × 1036 erg s-1, although high variability can be observed (Kreykenbohm et al. 1999).
In this paper we present the hard X-ray lightcurve of Vela X-1, which we folded along the orbit and measured with an unprecedented signal to noise thanks to almost eight years of Swift/BAT observations, and compare it with the predictions of 2D hydrodynamic simulations (Manousakis & Walter 2015). This provides some new insight into the inner stellar wind of HD 77581 and, in particular, into the β velocity law. The data and the simulations are described in Sects. 2 and 3, respectively. The comparison between data and simulation is presented in Sect. 3 and discussed in Sect. 4. Section 5 summarizes our results.
2. Swift/BAT data and analysis
The wide field of view of the Burst Alert Telescope (BAT, Krimm et al. 2013) onboard the Swift satellite allows the complete sky at hard X-rays to be monitored every few hours. For sources as bright as Vela X-1, lightcurves can be obtained in different energy bands with a resolution of 1000 s for almost a complete decade.
The Swift/BAT reduction pipeline is described in Tueller et al. (2010) and Baumgartner et al. (2013). Our pipeline is based on the BAT analysis software HEASOFT v 6.13. A first analysis was performed with the task batsurvey to create sky images in the eight standard energy bands using an input catalogue of 86 bright sources (that have the potential of being detected in single pointings) for image cleaning. Background images were then derived by removing all detected excesses with the task batclean and weight-averaged on a daily basis. The variability of the background was then smoothed pixel-by-pixel using a polynomial model with an order equal to the number of months in the data set. The BAT image analysis was then run again using these averaged background maps. The image data were stored in a database organised by sky pixel (using a fixed sky pixel grid) by properly projecting the images on the sky pixels, thereby preserving fluxes. This database can then be used to build images, spectra, or lightcurves for any sky position.
The result of our processing was compared to the standard results presented by the Swift team (lightcurves and spectra of bright sources from the Swift/BAT 70-months survey catalogue1) and very good agreement was found.
The Swift/BAT lightcurves of Vela X-1 were built in several energy bands. For each time bin and energy band, a weighted mosaic of the selected data is first produced and the source flux is extracted by assuming fixed source position and shape of the point spread function. The source signal to noise varies regularly because of intrinsic variability, its position in the BAT field of view, and distance to the Sun. The lightcurves span from ~53 370 to ~56 290 MJD, i.e. over 300 orbital periods or almost nine years.
 |
Fig. 1 Lomb-Scargle periodogram based on the Swift/BAT 14−100 keV energy band lightcurve. The red line shows the best derived orbital period, P = 8.964 ± 0.003 days. |
We used the Lomb-Scargle (Press & Rybicki 1989) technique to determine the orbital period from the 14−100 keV Swift/BAT lightcurve. The orbital period derived from the complete dataset is Porb = 8.964 ± 0.003 days. Figure 1 shows the Lomb-Scargle power (black line), together with a Gaussian fit (in red). We searched for variations in the orbital period by splitting the data into a few equally spaced time intervals. The results are listed in Table 1. The orbital period remains constant within the uncertainties, and no secular evolution can be identified. The average period, along with the mideclipse reference time MJD = 53 377.3964, was used to obtain folded lightcurves described below.
Orbital periods and uncertainties.
 |
Fig. 2 Folded lightcurve of Vela X-1 in the 14−100 keV energy band, split in 8 consecutive datasets and shifted arbitrarily. The grey curves shown at the top and bottom include all available data for comparison. |
 |
Fig. 3 Top panel: observed folded lightcurves preceding (black) and following (red) the eclipse. Bottom panel: inferred column density. The shaded vertical area indicates the eclipse. The light red horizontal area shows the artificial column density variability induced by the source’s short-term intensity variability. |
The 14–100 keV lightcurve was also split in eight successive time segments (each spanning about a year) in order to study the variability over these periods (Fig. 2). Some major flaring activity can be identified in each of the periods. Vela X-1 is known to be highly variable at hard X-rays and features major flares (Kreykenbohm et al. 2008). These flares (when averaged over a year) are not located at specific orbital phases, indicating that they are stochastic and much shorter than the orbital period.
The averaged folded lightcurve shows a clear asymmetry before and after the eclipse (Fig. 3). This asymmetry is a likely signature of the accretion wake trailing the neutron star (Blondin et al. 1990, 1991). Several sgHMXBs (Manousakis et al. 2012, and references therein) show similar behaviour. The average absorbing column density of the accretion wake can be reconstructed from the ratio of the folded lightcurves observed on both sides of the eclipse. In Fig. 3, we assume the preceding (φ = 0−0.5; black line) as the “unabsorbed” (I0) and the one following (φ = 0.5−1; red line) as the “absorbed” (I) lightcurves. We then use I = I0e− σT NH where σT ≈ 6.6 × 10-25 cm-2 is the Thompson cross-section, to infer the NH value (see bottom panel in Fig. 3). For the phases of φ ~ 0.5−0.8, the variations between the two curves are of the order of (1−2) × 1023 cm-2 and related to source flares and to inhomogeneities in the stellar wind. A very strong flare, which occurred during the first year of observation, shows up close to phase 0.5 giving some unexpectedly high NH value. Shortly before ingress (i.e., φ ~ 0.8−0.9), the flux is significantly lower, corresponding to scattering in an additional absorbing column density of the order of 8 × 1023 cm-2.
The BAT folded lightcurve during eclipse ingress and egress has an exceptional signal to noise. Besides constraining the accretion wake, the lightcurve is particularly sensitive to the velocity of the unperturbed stellar wind close to the surface of the supergiant. This is an aspect that we can probe further by comparing the observations to the results of simulations.
3. Hydrodynamic simulations
The hydrodynamic simulations are largely based on our previous work (Manousakis & Walter 2015) but are tuned to the new observational results presented here. We only provide a brief description of the simulation code. The Euler equations dictate the motion of the wind, assuming mass, momentum, and energy conservation, and account for the Roche potential and the line driven force (Blondin et al. 1990, 1991).The mesh is fixed but non-uniform, allowing high resolution around the neutron star.
The winds of hot massive stars are characterised observationally by the wind terminal velocity and the mass-loss rate. These velocities and rates are typically in the range υ∞ ~ 1000−3000 km s-1 and Ṁw ~ 10− (6−7)M⊙ yr-1, respectively (Kudritzki & Puls 2000). The wind velocity profile is described by the β-velocity law υ = υ∞(1−R∗/r)β, where β is the velocity gradient (Castor et al. 1975). The values of υ∞ and β are used to derive the CAK parameters characterising the line-driven force in our simulations using a 1D simulation. These CAK parameters are then used in the 2D code.
The ionisation of the wind by the neutron star is characterised by the ionisation parameter 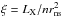 , where LX is the average X-ray luminosity and n the number density at the distance rns from the neutron star (Tarter et al. 1969). Close to the neutron star, where ξ>ξcrit ~ 102.5 erg cm s-1, the ions responsible for wind acceleration are highly ionised (Kallman & McCray 1982) and the radiative acceleration cuts off. Although the effects of the X-ray feedback on the wind acceleration force are complicated due to the large number of ions and line transitions contributing to the opacity (Abbott 1982; Stevens & Kallman 1990), a simplified approach allows the formation of a realistic shock in front of the neutron star (Fransson & Fabian 1980).
, where LX is the average X-ray luminosity and n the number density at the distance rns from the neutron star (Tarter et al. 1969). Close to the neutron star, where ξ>ξcrit ~ 102.5 erg cm s-1, the ions responsible for wind acceleration are highly ionised (Kallman & McCray 1982) and the radiative acceleration cuts off. Although the effects of the X-ray feedback on the wind acceleration force are complicated due to the large number of ions and line transitions contributing to the opacity (Abbott 1982; Stevens & Kallman 1990), a simplified approach allows the formation of a realistic shock in front of the neutron star (Fransson & Fabian 1980).
We made use of VH-12 code, which is described in depth by Blondin et al. (1990, 1991). The computational mesh employed in this study consists of 900 radial by 347 angular zones, extending from 1 to ~25 R∗ and in angle from −π to + π. The non-uniform grid is nested around the neutron star, reaching its highest resolution there, about ~109 cm. A co-rotating reference system located around the centre of mass is used. The outer boundary condition is characterized as an outflow while an absorbing boundary conditions (Hunt 1971; Blondin & Pope 2009) is used at the stellar photosphere. The initial setup (i.e., wind density, velocity, pressure as well as the CAK parameters) is described in Manousakis & Walter (2015) and leads to β ≈ 0.5−0.8 when the 2D simulation stabilises.
We performed several simulation runs with a wind terminal velocity of υ∞ ≈ 1400, 1700 km s-1, β = 0.5, 0.8, and binary separations α = 1.76, 1.77, 1.78 R∗. The mass loss rate of the donor star was always fixed to Ṁ ≈ 4 × 10-6M⊙. The time step of the simulations is ~1/10 s. The simulations ran for roughly ≳3 orbital periods. Approximately the first three days were excluded from the analysis, allowing the wind to reach a steady configuration. Assuming a mass-to-light conversion factor η = 0.1, the resulting time-averaged mass accretion rate corresponds to an X-ray luminosity in the range (2−8) × 1036 erg/s.
 |
Fig. 4 Column density as a function of orbital phase derived from a smooth wind (dashed lines) and hydrodynamic simulations (solid lines) with a wind terminal velocity, υ∞ ≈ 1400 km s-1 (derived from 1D simulation) and β = 0.5 (blue) and β = 0.8 (green). |
Simulation parameters (wind terminal velocity, beta parameter, and binary separation) and agreement (χ2) with the observed lightcurve.
 |
Fig. 5 Swift/BAT 14–100 keV energy range folded lightcurves of Vela X-1 (blue points), together with the simulated eclipse profiles (dashed lines) using a binary separation α = 1.77 R∗. Left: the lightcurves corrected for scattering (solid line) were built assuming wind terminal velocity of υ∞ = 1400 and β = 0.5. Right: same as previously for the remaining models, vXXXXbYY, where XXXX is the wind terminal velocity in km s-1 and YY is the wind β parameter. The residuals between the model and observations are shown in the bottom panel. The χ2 are listed in Table 2. |
To compare the observations with the simulations we have built synthetic lightcurves derived for each simulation run. The neutron star is emitting as a point source, and part of these X-ray photons are scattered in the stellar wind forming a diffuse source. The global intensity and geometry of the scattered emission was calculated from the illumination and Thomson optical depth of each simulation cell. This is a reasonable assumption at hard X-rays. We assumed that the accretion wake extends vertically in the range | z | = 0.5 R∗ and that a smooth stellar wind applies above these limits. The very small flux (with a relative emissivity of 10-4) observed during eclipse originates in an extended region of the wind and was accounted for. These synthetic lightcurves are shown as dashed lines in Fig. 5.
We also calculated the column density NH between the observer and the neutron star along the orbit cell by cell, excluding the highly ionised part of the wind, and corrected the synthetic lightcurve for the effect of scattering. These lightcurves are displayed as continuous lines in Fig. 5, together with the Swift/BAT data (blue points). The correspondence between the simulations and the data, measured with a reduced χ2, are listed in Table 2. An excellent match is obtained for a steep (β = 0.5) velocity law and a terminal velocity of 1400 km s-1. These parameters were the inputs to the 1D simulation used to derive the CAK parameters.
The time-averaged absorbing column density derived from the simulations are shown in Fig. 4 for β = 0.8 (green) and β = 0.5 (blue), together with the predictions from an unperturbed smooth stellar wind (dashed lines). Significant NH variability is expected from orbit to orbit. The average Swift/BAT spectrum for that phase range is not sensitive to low column densities so could not be used to further constrain the model parameters.
4. Discussion
Originally, spectroscopic observations of massive stars allow constraining the mass loss rates and the terminal velocities of stellar winds (Puls et al. 2008, and references therein). The P-Cygni line profiles used for these estimates are formed far from the massive star at a few tens of stellar radii, where the β parameter has a weak effect. Originally, the models by Castor et al. (1975) resulted in a steep β = 0.5 law, while later on a shallower β = 0.8 was introduced to match the observations (Pauldrach et al. 1986; Friend & Abbott 1986; Puls et al. 2008). Stevens (1993) discussed the difficulties of low velocity gradients and the need for gradients varying with radius. In an attempt to study the stellar winds from Wolf-Rayet stars, Springmann (1994) employed a modified β law that mimicks a steep velocity field gradient (β = 0.5) close to the stellar surface and a smoother (β = 1.0) velocity gradient further away. Such a low β parameter close to the stellar surface was also found studying the soft X-ray absorbing column density along the orbit in 4U 1700-37 with EXOSAT (Haberl et al. 1989), but these measurements were much more sensitive to ionisation than ours, based on hard X-ray data.
The line-driven instability predicts large density and velocity discontinuities that are not modelled in our simulations. According to the latest models (Sundqvist & Owocki 2013), this occurs at distances greater than one stellar radius from the stellar surface, i.e. well outside of the orbit in the case of Vela X-1, and should not play an important role in driving the X-ray variability. Gravitation and the X-ray ionisation from the neutron star, which are taken into account in our simulations, remain the main drivers of the hydrodynamics. Photoionisation influences the wind within a few tens of the orbital radius (see also Krtička et al. 2012) but leaves the wind located at ± 90° from the neutron star direction, which is responsible for the inress/egress scattering profile, largely unaffected.
The hard X-ray scattering profile measured at eclipse ingress and egress is sensitive to the density of the stellar wind at a distance of a few tenths of stellar radius from the stellar surface. At eclipse ingress, it is in also sensitive to the column density of the accretion wake formed close to the orbital radius. The density of the wind depends directly on the β parameter. A larger velocity gradient will generate a longer eclipse egress. The wind velocity at 1.2 R∗ is about twice higher with β = 0.5 than with β = 0.8 and therefore has a strong impact on the hard X-ray flux profile. The column density of the accretion wake also depends on the β parameter. A slower wind at the orbital radius will be more strongly deflected by the neutron star and form a stronger wake, i.e. a longer and more structured eclipse ingress.
 |
Fig. 6 Wind velocity field close to the surface (R∗ = 1) of the supergiant. The curve labelled as v1400b05 provides excellent agreement with the observations. The other velocity fields do not provide results consistent with the observations. The vertical dotted line indicates the orbital radius. |
Our simulation provides an excellent match for both the egress and the ingress hard X-ray lightcurves with a single set of parameters (υ∞ = 1400 km s-1 and β = 0.5, from the 1D simulation), which is remarkable. Figure 6 shows the wind velocity profiles close to the donor’s star surface derived from the 2D simulations at an angular distance of ~90° from the direction to the neutron star, to avoid the region where the neutron star is strongly perturbing the wind velocity. This 2D velocity profile (v1400b05 in Fig. 6) can be represented with the parameters β = 0.55 and υ∞ = 1700 km s-1 and stands for the unperturbed wind. These parameters agree with the measurements from Dupree et al. (1980), obtained when the neutron star was eclipsed. The simulated folded lightcurve is very sensitive to the velocity profile and constrains the velocity within about ± 100 km s-1 at 1.2 R∗. It is important to note that the X-ray data are not sensitive to the velocity of the wind beyond the orbital radius, so higher υ∞ can be accommodated if the β parameter increases towards larger distances.
The velocity law favoured by the BAT folded lightcurve is significantly steeper than the law used by Manousakis & Walter (2015). We have checked that these two velocity laws give very similar results for what concerns the variability of the accretion rate and, in particular, for the X-ray flux and off-state distributions. This is understandable because the latter are mostly driven by the conditions within about ten accretion radii. Our current best fit model (v1400b05) confirms the results of Manousakis & Walter (2015) with small deviations. The dynamical range and the durations of the off-states are very similar as presented earlier, and the histogram of the simulated variability is characterised by a similar log-normal distribution.
In the past the effects of the accretion wake have been studied in detail by Blondin et al. (1990) but not related to the variability at egress. More recently, Oskinova et al. (2012) have used a highly structured clumpy stellar wind to explain soft X-ray absorption along the orbit, resulting in strong variability and a symmetry around the eclipse, which contrasts with our data and the likely absence of clumps very close to the stellar surface.
5. Conclusion
We have analysed almost a decade of Swift/BAT data of Vela X-1. Although variable, its hard X-ray emission, folded along the orbit, features a persistent asymmetric eclipse ingress and egress, measured with high signal-to-noise. This asymmetry stems from the scattering of hard X-rays around the neutron star at small and larger scales, including in the accretion wake. The X-ray variability is related to inhomogeneities in the stellar wind largely created by the gravity and ionisation of the neutron star itself (Manousakis & Walter 2015).
The simulation matches the observed data for a narrow set of parameters, implying that the wind velocity close to the stellar surface is twice higher than usually assumed. The stellar wind in Vela X-1 shows a velocity field similar to these observed in some Wolf-Rayet stars (Springmann 1994).
The hydrodynamic simulations of the wind of Vela X-1 are still incomplete, however they already provide an excellent agreement with the observations for the smooth properties (this work) and the variability (Manousakis & Walter 2015). High-mass X-ray binaries provide information on the initial acceleration of the stellar wind. This is unique and requires testing models accurately.
Acknowledgments
This work was partially supported by the Polish NCN grants 2012/04/M/ST9/00780 and 2013/08/A/ST9/00795.
References
- Abbott, D. C. 1982, ApJ, 259, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgartner, W. H., Tueller, J., Markwardt, C. B., et al. 2013, ApJS, 207, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., & Pope, T. C. 2009, ApJ, 700, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Kallman, T. R., Fryxell, B. A., & Taam, R. E. 1990, ApJ, 356, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Stevens, I. R., & Kallman, T. R. 1991, ApJ, 371, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., Gursky, H., Black, J. H., et al. 1980, ApJ, 238, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., & Fabian, A. C. 1980, A&A, 87, 102 [NASA ADS] [Google Scholar]
- Friend, D. B., & Abbott, D. C. 1986, ApJ, 311, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Haberl, F., White, N. E., & Kallman, T. R. 1989, ApJ, 343, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, R. 1971, MNRAS, 154, 141 [NASA ADS] [Google Scholar]
- Kallman, T. R., & McCray, R. 1982, ApJS, 50, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Kreykenbohm, I., Kretschmar, P., Wilms, J., et al. 1999, A&A, 341, 141 [NASA ADS] [Google Scholar]
- Kreykenbohm, I., Wilms, J., Kretschmar, P., et al. 2008, A&A, 492, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krimm, H. A., Holland, S. T., Corbet, R. H. D., et al. 2013, ApJS, 209, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Krtička, J., Kubát, J., & Skalický, J. 2012, ApJ, 757, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R., & Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Manousakis, A., & Walter, R. 2015, A& A, 575, A58 [CrossRef] [EDP Sciences] [Google Scholar]
- Manousakis, A., Walter, R., & Blondin, J. M. 2012, A&A, 547, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagase, F., Hayakawa, S., Sato, N., Masai, K., & Inoue, H. 1986, PASJ, 38, 547 [NASA ADS] [Google Scholar]
- Oskinova, L. M., Feldmeier, A., & Kretschmar, P. 2012, MNRAS, 421, 2820 [NASA ADS] [CrossRef] [Google Scholar]
- Pauldrach, A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] [Google Scholar]
- Press, W. H., & Rybicki, G. B. 1989, ApJ, 338, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quaintrell, H., Norton, A. J., Ash, T. D. C., et al. 2003, A&A, 401, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Springmann, U. 1994, A&A, 289, 505 [NASA ADS] [Google Scholar]
- Stevens, I. R. 1993, MNRAS, 265, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., & Kallman, T. R. 1990, ApJ, 365, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., & Owocki, S. P. 2013, MNRAS, 428, 1837 [NASA ADS] [CrossRef] [Google Scholar]
- Tarter, C. B., Tucker, W. H., & Salpeter, E. E. 1969, ApJ, 156, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Tueller, J., Baumgartner, W. H., Markwardt, C. B., et al. 2010, ApJS, 186, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, R., & Zurita Heras, J. 2007, A&A, 476, 335 [Google Scholar]
All Tables
Simulation parameters (wind terminal velocity, beta parameter, and binary separation) and agreement (χ2) with the observed lightcurve.
All Figures
 |
Fig. 1 Lomb-Scargle periodogram based on the Swift/BAT 14−100 keV energy band lightcurve. The red line shows the best derived orbital period, P = 8.964 ± 0.003 days. |
| In the text | |
 |
Fig. 2 Folded lightcurve of Vela X-1 in the 14−100 keV energy band, split in 8 consecutive datasets and shifted arbitrarily. The grey curves shown at the top and bottom include all available data for comparison. |
| In the text | |
 |
Fig. 3 Top panel: observed folded lightcurves preceding (black) and following (red) the eclipse. Bottom panel: inferred column density. The shaded vertical area indicates the eclipse. The light red horizontal area shows the artificial column density variability induced by the source’s short-term intensity variability. |
| In the text | |
 |
Fig. 4 Column density as a function of orbital phase derived from a smooth wind (dashed lines) and hydrodynamic simulations (solid lines) with a wind terminal velocity, υ∞ ≈ 1400 km s-1 (derived from 1D simulation) and β = 0.5 (blue) and β = 0.8 (green). |
| In the text | |
 |
Fig. 5 Swift/BAT 14–100 keV energy range folded lightcurves of Vela X-1 (blue points), together with the simulated eclipse profiles (dashed lines) using a binary separation α = 1.77 R∗. Left: the lightcurves corrected for scattering (solid line) were built assuming wind terminal velocity of υ∞ = 1400 and β = 0.5. Right: same as previously for the remaining models, vXXXXbYY, where XXXX is the wind terminal velocity in km s-1 and YY is the wind β parameter. The residuals between the model and observations are shown in the bottom panel. The χ2 are listed in Table 2. |
| In the text | |
 |
Fig. 6 Wind velocity field close to the surface (R∗ = 1) of the supergiant. The curve labelled as v1400b05 provides excellent agreement with the observations. The other velocity fields do not provide results consistent with the observations. The vertical dotted line indicates the orbital radius. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


