EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 584 (December 2015) A&A, 584 (2015) A72 Full HTML
Highlight
Free Access
Issue
A&A
Volume 584, December 2015
Article Number A72
Number of page(s) 12
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201526822
Published online 24 November 2015

© ESO, 2015

1. Introduction

The statistical analysis and occurrence rate of the small-mass planets in the range of super-Earth to Neptune are discussed in several studies with the main motivation of better understanding the orbital and physical characteristics of this population of planets, in order to constrain their formation processes (Mordasini et al. 2012; Benz et al. 2014). The radial velocity planet search programme with the HARPS spectrograph on the ESO 3.6-m telescope (Mayor et al. 2003, 2011), a similar survey with the Keck telescope (Howard et al. 2010), and the NASA Kepler transit space mission (Borucki et al. 2011) have contributed tremendously to our knowledge of the population of small-mass/size planets around solar-type stars.

The most common planets detected by the Kepler mission peak around 2 R⊕ (Howard et al. 2012; Fressin et al. 2013; Marcy et al. 2014). Even if such planets do not exist in our solar system, they are found around more than 30% of solar-type hosts. Furthermore, many of them are found in coplanar multiple systems (Fabrycky et al. 2014; Howard et al. 2012; Figueira et al. 2012), tightly packed close to the central star, a new challenge for planet formation models to explain (Ogihara et al. 2015). Over the last 12 years the extra-solar planet zoo has also been supplied with low-mass planets detected by the HARPS GTO planet search programme and successive subsequent ESO Large programmes. Notable examples include HD 40307 (Mayor et al. 2009), HD 10180 (Lovis et al. 2011b), HD 20794, and HD 85512 (Pepe et al. 2011), or Alpha Cen B (Dumusque et al. 2012). Analysis of the results by Mayor et al. (2011) provided a list of additional super-Earth and mini-Neptunes unveiled by the survey, as well as a first statistical analysis of the properties and occurrence rates of the super-Earths and Neptune-mass planets around solar-type stars. These preliminary findings were confirmed by the excellent statistics and precision of the Kepler detections (Fressin et al. 2013).

After a decade focusing mainly on the detection and the determination of the occurrence rate of low-mass planets, a significant observational effort is now dedicated to planet characterization. Transit results provide the planets radii and in combination with radial velocities, the mean densities of the planets can be derived. Spectral features of exoplanet atmospheres may also be revealed by space and ground-based high-resolution transmission spectroscopy in the visible and near-infrared. One of the main difficulties of such characterization is the availability of bright targets favourable for follow-up observations. In particular, the determination of exquisite planetary physical parameters will be key to lifting the intrinsic degeneracy in the determination of planet composition when several components (gas, silicates, metals) and chemical species are mixed in the planet interior. This was a strong driver for transit search follow-up of super-Earths detected with radial velocities around very bright stars from space with the MOST, Hubble, or Spitzer space telescopes (Gillon et al. 2012, 2010; Demory et al. 2015a), and for the development of a new generation of space transit missions to be launched within the coming decade: CHEOPS/ESA (Fortier et al. 2014), TESS/NASA (Ricker et al. 2014), and PLATO/ESA (Rauer et al. 2014).

In order to start to fulfil the need for good estimates of planet physical parameters and considering the successful achievements with HARPS, a similar design has been implemented for the HARPS-N spectrograph. The instrument was built to become an efficient exoplanet hunter in the northern hemisphere, specifically aimed at the follow-up and characterization of the brightest transit candidates from the Kepler mission. HARPS-N is a high-precision echelle spectrograph located at the 3.6 m Telescopio Nazionale Galileo (TNG) at the Roque de los Muchachos Observatory on La Palma, Spain. It was built by an international consortium of Swiss, Italian, UK, and US partners, led by Geneva university. It began operations in August 2012. Eighty nights per year for five years were granted to the consortium for a science programme including the follow-up of Kepler candidates at high precision, and an additional survey, the Rocky Planet Search (RPS), to search for small planets around bright and quiet nearby stars in the northern hemisphere when the Kepler field is down.

While waiting for the new generation of ground- and space-based transit searches targeting bright stars, planet density estimates from the follow-up of the Kepler candidates with HARPS-N have already been presented in several papers (Pepe et al. 2013; Dumusque et al. 2014; Bonomo et al. 2014; Dressing et al. 2015). They are populating the low-radius regime of the mass-radius relation for small exoplanets with candidates for which precise mass and radius could be determined.

In this paper we present the first results from the Rocky Planet Search: a planetary system around HD 219134, composed of three inner super-Earths and an outer sub-Saturn mass planet, with the four planets spread between 0.038 and 2 AU from the central star. Thanks to the high-precision photometric observations from the Spitzer space telescope, the inner planet is observed to transit in front of the star. After a short presentation of the Rocky Planet Search programme in Sect. 2, and the stellar properties of HD 219134 in Sect. 3, the spectroscopic and photometric observations of the new system are described in Sects. 4 and 5. Section 6 provides a discussion of the stability of the system and of the composition of the inner planet. Finally, we draw our conclusions in Sect. 7.

2. The HARPS-N Rocky Planet Search programme

The guaranteed time observation (GTO) granted to the HARPS-N consortium is dedicated to two programmes: i) the confirmation of the planetary nature and the characterization of Kepler candidates and ii) a rocky planet search (RPS). The aim of the RPS programme is to perform a systematic search for low-mass planets around nearby quiet stars visible from the northern hemisphere through an intensive monitoring of the radial velocity of quiet stars at very high precision. HARPS-N is stabilized and well-controlled in pressure and temperature to minimize instrumental drifts, and so to secure sub-m/s radial velocities over long periods of time. More details on the technical aspects are presented in Cosentino et al. (2012, 2014).

Table 1

List of the RPS targets in the GTO programme on HARPS-N.

The sample: the first step in establishing the RPS programme was to select a sample of stars best suited for long-term precise radial velocity measurements. Uncertainties in such observations are mainly linked to noise from three different origins: photon noise, instrumental noise, and stellar intrinsic signals. The first important criterion for this programme was thus to concentrate on bright stars in our closest neighbourhood. This is also in the interest of potential follow-up studies for the characterization of the planet properties. The sample was thus selected from the Hipparcos catalogue within a distance limit set to 18 pc1. The second step was to focus on quiet stars. Based on the CORAVEL data and investigation in the literature, we rejected known spectroscopic binaries as well as stars with V sini ≥ 4.5 kms-1 and stars with 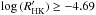log(RHK′)≥−4.69\hbox{$\log{(R^{\prime}_{\rm HK})} \ge -4.69$} from our sample. In addition, K dwarfs are favoured in our sample over G dwarfs because of their lower level of stellar “noise” (p-mode, granulation and activity jitter; Dumusque et al. 2011b). Their habitable zone is also closer in. Adding all the criteria together, we ended up with a sample of 51 quiet stars with a range of spectral types from G8 to M0. They are listed in Table 1.

Observational strategy: to minimize the effect of stellar noise with short typical time scales (p-modes and granulations), we applied the observational strategy implemented for the HARPS very high-precision observations (Pepe et al. 2011). With this strategy, we observe each target with a 15-min. exposure time to damp the p-modes effect and make a second (and possibly a third) measurement of the target well-spread in time during the night to damp the effect of granulation (for more details see Dumusque et al. 2011b). For bright stars, in order to avoid saturation the 15 min on target are split into subobservations. Typical average signal-to-noise ratio (S/N) of the spectra obtained are between 200 and 400, measured at λ = 550 nm.

With continuous monitoring during the past two years of operation of HARPS-N we have acquired hundreds of precise radial velocities of the stars in the RPS sample. The typical photon-noise precision per (sub)observation is about 0.3 ms-1. In Fig. 1, we show the radial velocity rms for all the stars in the RPS programme. This rms naturally includes photon noise, instrumental effects (telescope, spectrograph, detector), stellar intrinsic “noise”, and, of course, signatures of still undetected planets. With a mode around 1.48 ms-1, the distribution is very similar to the one obtained for the sample of solar-type stars followed at high precision with HARPS in the southern hemisphere.

thumbnail Fig. 1

Histogram of the dispersion of the radial velocity measurements of stars in the RPS programme on HARPS-N.

We present here the first result of the HARPS-N RPS programme: the discovery of a planetary system with a transiting planet around HD 219134.

3. Stellar characteristics of HD 219134

The very bright star HD 219134 has been extensively studied in the literature. Basic photometric properties of this star were taken from the Hipparcos catalogue (van Leeuwen 2007). A precise estimate of the radius of the star, R = 0.778 ± 0.005 R⊙, is available from interferometric measurements (Boyajian et al. 2012). Combined with a luminosity of 0.265 ± 0.002 L⊙, the Stefan-Boltzmann law gives Teff = 4699 ± 16 K. We adopt this value for our photometric analysis of the transiting planet in the system in Sect. 5.

Over the past few years, the star has been the object of several studies aiming at determining photospheric parameters and chemical abundance analyses (Valenti & Fischer 2005; Mishenina et al. 2008, 2012; Kovtyukh et al. 2003; Ramírez et al. 2013; Prugniel et al. 2011). Results of these studies are given in Table 2 for comparison.

We also derived the atmospheric stellar parameters directly from the HARPS-N spectra using two approaches: one based on equivalent width (EW) determination and one using the Stellar Parameter Classification tool (SPC). For the EW approach, we followed the procedure described in Sect. 3 of Dumusque et al. (2014). We used the 2014 version of the local thermodynamic equilibrium code MOOG (Sneden 1973) together with the Kurucz grid of atmosphere models (Castelli & Kurucz 2004; Kurucz 1992), while oscillator strength values in the line list from Sousa et al. (2011) were updated in accordance with the solar iron abundance log ϵ(Fe I) = 7.50 from Asplund et al. (2009). In order to construct high-quality spectra, spectra within the same visit (subobservation) were co-added, obtaining at the time of the analysis 88 spectra with S/Ns between 400 and 700. Equivalent widths were then measured for each of them and their mean and rms were used to determine the atmospheric parameters. We only retained the lines within the range 5 mÅ <EW< 100 mÅ and with a dispersion lower than either 1 mÅ or 5% of the mean EW. Despite the quality of our spectra, the preliminary analysis resulted in a poor determination of the microtubulent velocity ξt. Following the calibration from Ramírez et al. (2013) and Tsantaki et al. (2013), we decided to fix the microturbulent velocity to ξt = 0.35. The resulting atmospheric parameters are given in Table 2, with the gravity from FeII lines already increased by Δlog  g= 0.39 ± 0.15 according to the calibration in Sect. 3.1 of Mortier et al. (2014). We note that the derived parameters are dominated by systematic errors (e.g. choice of the oscillator strength, continuum placement) rather than random errors on EW measurements.

Finally, we used the SPC tool, an alternative approach to derive atmospheric parameters by cross-correlating an observed spectrum with a library of synthetic spectra (Buchhave et al. 2012, 2014). With SPC we obtain an effective temperature Teff = 4941 ± 50 K, a surface gravity of 4.63 ± 0.10, and V sini = 0.4 ± 0.5 kms-1. The metallicity derived by SPC is 0.11 ± 0.08, from a mix of metallic absorption lines in the wavelength range between 5050 and 5360 Å. The derived values are given in Table 2 as well.

Table 2

Comparative summary of the atmospheric parameters derived for HD 219134.

The mass of HD 219134, M⋆ = 0.78 ± 0.02 M⊙, was estimated through the Synthetic Clusters Isochrones & Stellar Tracks tool (SYCLIST)2. SYCLIST allows the user to determine stellar parameters through a Bayesian-based interpolation of the grid of Geneva stellar evolution models. For HD 219134, we used the Teff taken from Boyajian et al. (2012), the apparent magnitude and parallax from the Hipparcos catalogue (van Leeuwen 2007), and the metallicity derived from our spectral analysis as input parameters. For the last we used the average of the values obtained from the EW and SPC approaches.

The mean activity index log 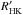RHK′\hbox{$R ^{\prime}_{\rm HK}$} is estimated from the HARPS-N spectra. We derive an average value of −5.02 with a dispersion of 0.06 dex. To estimate the rotational period of the star we used a periodogram analysis of the activity indicators, which yields a significant peak at 42.3 days (see Sect. 4.2.3).

Table 3 summarizes the stellar parameters obtained from the various catalogues and analyses mentioned above, with the final values selected for the star when several estimates are available.

Table 3

Stellar parameters considered for HD 219134.

4. Spectro-velocimetric observations

4.1. The HARPS-N data

HD 219134 has been monitored by the HARPS-N spectrograph for close to three years, from BJD = 2 456 148.7 (9 August 2012) to BJD = 2 457 195.7 (22 June 2015). To mitigate the effects of stellar oscillations, the strategy was to stay on target for 10 to 15 min. Because of the brightness of the star, the observations were split into several individual subobservations to avoid saturation. We obtained a total of 481 data points spread over 99 epochs (nightly averaged values). The nightly averaged values are shown in Fig. 2. Observations were performed using the simultaneous thorium calibration technique. The mean uncertainty on the individual RVs due to photon noise and known calibration noise is 0.4 ms-1. This corresponds to an average S/N of 268 per pixel at λ = 550 nm. The data reduction was carried out with the latest version of the HARPS-N pipeline (DRS 3.7) using the cross-correlation technique (Pepe et al. 2002; Baranne et al. 1996). In addition to precise radial velocities, the pipeline provides parameters directly estimated from the cross-correlation function (CCF) of the spectrum: CCF full width at half maximum (FWHM), CCF contrast (minimum vs. continuum), CCF bisector span inverse slope, and Ca II activity index S and log 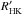RHK′\hbox{$R^{\prime}_{\rm HK}$} (Fig. 2).

The raw rms dispersion of the radial velocities is 3.57 ms-1. Once de-trended from an obvious drift, the observed radial velocities still show a dispersion of 2.77 ms-1, which is significantly above the typical dispersion of such quiet stars, calling for a search for additional coherent signals in the data.

thumbnail Fig. 2

Radial velocity (top) and activity index (bottom) time series for HD 219134.

4.2. Data analysis

4.2.1. Data modelling

The first step of the radial velocity data analysis consists in identifying significant periodic signals in the data. This was done using the generalized Lomb-Scargle periodogram algorithm (GLS, Zechmeister & Kürster 2009) applied to the nightly averaged radial velocity measurements to which a systematic error of 1 ms-1 was quadratically added. False alarm probabilities were estimated through a bootstrap approach by permuting the nightly averaged data. Once a significant peak was located at a given period, the corresponding Keplerian was adjusted and removed. The process was repeated several times until no significant peak remained. For multiple Keplerians, all parameters were re-adjusted at each step of the analysis. During the analysis, we identified one radial velocity outlier (5 σ at jdb = 56 829.7) and decided to remove it to allow for a robust frequency analysis.

thumbnail Fig. 3

Generalized Lomb-Scargle periodogram of the radial velocities of HD 219134, after removing – from top to bottom – a long-period Keplerian, and successively the 3.09-day, the 46.66-day and finally the 6.76-day signals. Dashed lines indicate 0.1%, 1%, and 10% levels of false alarm probability.

Following this procedure, a first low-frequency oscillation with a time scale of 1842 days was identified with a semi-amplitude of 5.05 ms-1 and a 0.8% false alarm probability (FAP). After removing the corresponding Keplerians, two highly significant peaks were seen in the periodogram, at 3.09 and 46.66 days, with semi-amplitudes of 2.25 and 2.10 ms-1 and FAPs smaller than 0.01% and 1%, respectively (Fig. 3). One additional peak remains at 6.76 days with a significant FAP smaller than 1% and a semi-amplitude of 1.14 ms-1. No more periodic signals remain in the data after subtraction of the corresponding four-Keplerian model. This purely frequentist approach, using the nightly average data, has the advantage of being simple and fast and is also conservative in terms of detection limits.

To double-check the purely frequentist approach, we also analysed models of different complexity ranging from one- to four-Keplerian. The best model was chosen by comparing the Bayesian information criterion (BIC, Kass & Raftery 1995) between the different models, 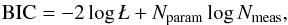BIC=−2logŁ+NparamlogNmeas,\begin{eqnarray} {\rm BIC} = -2 \log \textit{\L} + N_{\rm param} \log N_{\rm meas} , \end{eqnarray}(1)where log Ł is the maximum of the log likelihood, Nparam the number of free parameters in the model, and Nmeas is the number of measurements. In model comparisons based on the Bayes factor, when the prior information is smaller than the information provided by the data, the BIC (also known as the Schwarz criterion) indicates that the model with the highest probability is the one with the minimum BIC. A summary of the comparisons between a few models is provided in Table 4. The four-Keplerian model has the lowest BIC and differs from the three-Keplerian model by ΔBIC = 34. It is usually assumed that a ΔBIC of 20 between two models is considered strong evidence in favour of the most complex one, which leads us to adopt the four-Keplerians as our best solution.

Table 4

Comparison of tested models.

To obtain robust confidence intervals for the Keplerian parameters as well as an estimate of the additional noise present in the data (nuisance parameter, see below), we further probe the parameter space with a Markov chain Monte Carlo algorithm (MCMC) with Metropolis-Hasting. An abundant literature discusses in great detail the implementation of MCMC posterior sampling (Andrieu & Thoms 2008 for a pure statistical approach; Gregory 2005a,b, Collier Cameron et al. 2007; and Pollacco et al. 2008 for exoplanet searches). Our MCMC probes the following set of parameters: log p, 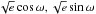ecosω,esinω\hbox{$\sqrt{e}\cos{\omega}, \sqrt{e}\sin{\omega}$}, log K, and λ0 (the mean longitude at a given epoch). For partially covered orbits, one usually prefer to probe a specific timing of the radial velocity curve instead of λ0 to reduce correlations between the orbital phase and period. The possible timing are TVmin, TVmax, or TPeriastron and the choice depends on the shape of the observed radial velocity curve.

The noise model follows a simple normal law with standard deviation derived from the observation errors and a nuisance parameter s that is also probed by the MCMC. Jeffrey’s priors are used for the period, the radial velocity semi-amplitude, and the nuisance parameter while uniform priors are used for the other parameters.

thumbnail Fig. 4

Phase-folded radial velocity measurements of HD 219134 with the corresponding Keplerian model (solid line) for each of the three inner super-Earths, after removing the contribution of all the other planets in the system. From top to bottom, we have the 3.09-, 6.76-, and 46.66-day periods.

4.2.2. Orbital solution

The orbital elements corresponding to the four-Keplerian model and transit timing constraints are listed in Table 5, while the phase folded radial velocities are shown in Figs. 4 and 5.

The shortest period signal, with a radial velocity semi-amplitude of 2.25 ms-1 at 3.09 days, is clearly identified as a super-Earth (4.32 M⊕) in a circular orbit. To derive the best orbital solution, we added a gaussian prior on its transit timing (see Sect. 5 and Table 5) mainly to improve its orientation.

One additional low-amplitude signal (K = 1.14 ms-1) is present at 6.76 days, corresponding to a planet with minimum mass of 2.78 M⊕. The existence of this signal is corroborated by both the FAP and the BIC estimators, but its strength might be affected by the inaccurate modelling of the long-period signal (see below).

The third signal with a period of 46.66 days and a semi-amplitude of 2.10 ms-1 corresponds to a super-Earth of 8.94 M⊕ with an eccentric orbit of e = 0.46. In the following section we show that this period, which is close to the rotational period of the star (42.3 days), is not of stellar origin. Its relatively high eccentricity may also originate from an imperfect modelling of the outer signal.

The long-period radial velocity trend clearly shows two extrema, which favour a Keplerian instead of a polynomial drift, with a period of 1842 days and a semi-amplitude of 5.05 ms-1. As explained below, its origin cannot be linked to any long-term stellar activity fluctuation and is undoubtedly of planetary origin. Owing to the incomplete coverage of the orbit, both the eccentricity and the period of the planet remain moderately constrained, but still lead to a good estimate of its minimum-mass, i.e. 71 M⊕.

Table 5

Orbital solution and planet inferred parameters for the four-Keplerian model (K4) of the system around HD 219134.

thumbnail Fig. 5

Radial velocity measurements as a function of time of HD 219134 with the corresponding Keplerian model (solid line) for the outer planet in the system, after removing the contribution of the three inner planets.

thumbnail Fig. 6

Star activity index as a function of the radial velocity residuals after removing the three shorter-period planet contributions for HD 219134. No clear positive correlation is observed, contrary to what is expected in the case of magnetic cycles (Lovis et al. 2011a).

4.2.3. Periodic signals: planet vs. activity-related origin

Long-period magnetic cycle: the radial velocity and activity index 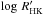log RHK′\hbox{$\log\,R^{\prime}_{\rm HK}$} measurements of the star HD 219134 are shown in Fig. 2. Although both exhibit long-term variations, the 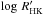log RHK′\hbox{$\log\,R^{\prime}_{\rm HK}$} time series is very stable over the first 750 days of the survey and slightly increases over the last 300 days whereas the radial velocity constantly decrease over the 1050-day observation time span. No correlation is observed between RVs and log R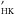′HK\hbox{$^{\prime}_{\rm HK}$} as shown in Fig. 6. The long-term trend of the 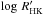log RHK′\hbox{$\log\,R^{\prime}_{\rm HK}$} is most probably related to the magnetic cycle of the star (Lovis et al. 2011a; Dumusque et al. 2011a; Meunier & Lagrange 2013) while the observed 1842-day period corresponds to a long-period companion. Moreover, at the observed level of activity, we expect a low impact of stellar activity on the observed radial velocities.

Rotation period: although different, the period of the third planet (46.7 days) is not very far from the rotational period of the star estimated from coherent variations of the activity indicators. A periodic variation of around 42.3 days is indeed observed in the log 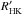RHK′\hbox{$R^{\prime}_{\rm HK}$} as well as in the CCF FWHM and in the bisector span of the radial velocities, whereas no signal appears around 46.7 days, as illustrated in Fig. 7 showing the GLS periodograms of these parameters zoomed around the periods of interest. We can therefore safely consider the 42.3 days as a valid estimation of the rotational period of the star (Prot). Conversely, no signal at 42.3 days appears in the radial velocity data, supporting the planetary solution.

thumbnail Fig. 7

From top to bottom GLS periodograms of radial velocities, log RHK′\hbox{$\log\,R^{\prime}_{\rm HK}$}, CCF bisector span, and CCF FWHM of the two-year data set, zoomed around the periods of interest. The thick red line in each panel indicates the planetary period (46.7 days) and the thick green line indicates the stellar rotation period (42.3 days). The thinner lines are the corresponding yearly aliases.

In order to avoid any misinterpretation of the stellar activity as a planetary signal, we pushed our investigations a bit further. We first examined the yearly aliases (Dawson & Fabrycky 2010) of the at 46.7- and 42.3-day signals (Fig. 7) and confirmed that one period is not an alias of the other. In a second step, we considered several subsets of the data to check the persistence of the planetary signal over time and to mitigate the possible effects of discontinuities in the data sampling. The same features are observed. This confirms that the planetary signal at 46.7 days is present in the radial velocities at any time, and that in the same data no signal appears at the estimated Prot (42.3 days).

A final argument in favour of the planetary interpretation of the signal at 46.7 days is provided in Fig. 8 by the absence of a correlation between the 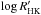logRHK′\hbox{$\log R^{\prime}_{\rm HK}$} activity index and the residuals around a three-planet solution (leaving the 46.7-day period out). Such a correlation would be expected if the radial velocity variation is induced by activity-related spots or plages on the star surface.

thumbnail Fig. 8

Radial velocities after subtracting the contributions of the planets at 3.09, 6.76, and 1842 days, shown as a function of the logRHK′\hbox{$\log R^{\prime}_{\rm HK}$} activity index detrended with a polynomial of degree 3. No correlation is observed, supporting the planetary interpretation for the 46.7-day signal.

5. Transit detection with Spitzer space telescope

5.1. Spitzer observations

Thanks to its short period of 3.09 d, HD 219134 b has an interestingly high geometric transit probability of ~9%. In February 2015, we requested 9.5 hr of Director’s Discretionary Time (DDT) on the Spitzer Space Telescope to continuously monitor the 2σ transit window of the planet as derived from our analysis of the HARPS-N RVs. As demonstrated by the co-detection and subsequent studies of the transits and occultations of 55 Cnc e (Demory et al. 2011, 2012, 2015b; Gillon et al. 2012) and the confirmation of the transiting nature of HD 97658 b (Van Grootel et al. 2014), Spitzer is indeed a very powerful facility to search for and measure with high precision the transits of low-mass RV planets thanks to its trailing orbit that allows it to monitor the same star continuously for a complete transit window, and to its ultra-high photometric precision (a few dozens of ppm per time interval of 30 min for 55 Cnc). Our programme was approved by the Spitzer Science Center (SSC) Director under the ID 11180 (PI: M. Gillon), and the SSC managed to schedule it for 14 April 2015, a few days before the end of the current visibility window of the star.

We observed HD 219134 at 4.5 μm with the Spitzer/IRAC detector (Fazio et al. 2004) in subarray mode (32 × 32 pixels windowing of the detector), the extremely fast Fowler sampling (~0.01 s) maximizing the duty cycle and S/N. No dithering pattern was applied to the telescope (continuous staring). Because HD 219434 is an extremely bright star for Spitzer, we used the shortest available integration time of 0.01s, allowing the counts to remain in the linear regime of the detector. The observations were performed on 14 April 2015 from 01h58 to 11h18 UT. We used the recently introduced PCRS peak-up mode (Grillmair et al. 2012; Ingalls et al. 2014) which was previously used by Ballard et al. (2014) to estimate the infrared transit depth of Kepler-93 b. This mode provides enhanced accuracy in the position of the target on the detector, leading to a significant decrease of the so-called pixel phase effect, which is the most important source of correlated noise in high-S/N staring mode observation with IRAC InSb arrays (e.g. Knutson et al. 2008). The run consisted of a 9hr science astronomical observational request (AOR) preceded by a short (30 min) AOR to allow the spacecraft to stabilize.

5.2. Data reduction

After downloading to Earth and basic calibration with the Spitzer pipeline S19.1.0, the images were made available to us by SSC through the Spitzer Heritage Archive (SHA) web interface3 under the form of basic calibrated data (BCD). Each subarray mode BCD is composed of a cube of 64 subarray images of 32 × 32 pixels (pixel scale = 1.2 arc second). We used the following strategy to reduce these BCDs. We first converted fluxes from the Spitzer units of specific intensity (MJy/sr) to photon counts, then aperture photometry was performed on each subarray image with the IRAF/DAOPHOT4 software (Stetson 1987). We tested different aperture radii, and selected 2.3 pixels as the radius minimizing at best the white and red noises in the residuals of a short data fitting analysis. The centre and width of the point spread functions (PSF) were measured by fitting a 2D Gaussian profile on each image. The x − y distribution of the measurements was then looked at, and measurements having a visually discrepant position relative to the bulk of the data were then discarded. For each block of 64 subarray images, we then discarded the discrepant values for the measurements of flux, background, and x- and y-positions using a 10σ median clipping for the four parameters; the resulting values were then averaged, the photometric errors being taken as the errors on the average flux measurements. Finally, a 50σ slipping median clipping was used on the resulting light curves to discard outliers (e.g. due to cosmic hits).

Our resulting light curve counted 9396 measurements. It is shown in Fig. 9, with the evolution of relevant external parameters (PSF x- and y-centre and PSF width, background). Because its time sampling ~3.4 s was much shorter than the structures of the expected transit and then the typical timescale of the Spitzer systematics, we binned the light curve to time intervals of 30s for the sake of computational speed of the data analysis. Nevertheless, we verified with a shorter version of the data analysis procedure described below that our results are insensitive to the binning of the photometry.

5.3. Data analysis

We analysed the Spitzer photometric time-series with our adaptative MCMC code (see Gillon et al. 2012 and references therein). The assumed photometric model consisted of the eclipse model of Mandel & Agol (2002) to represent the possible transit of HD 219134 b, multiplied by a baseline model aiming to represent the other astrophysical and instrumental effects at the source of photometric variations. We assumed a quadratic limb-darkening law for the star. We based the selection of the baseline model on the minimization of the BIC (Schwarz 1978).

thumbnail Fig. 9

Evolution of the following measured parameters in the Spitzer images for HD 219134: PSF centre x- and y-positions (top), PSF x- and y-widths (middle), background counts (bottom left), and stellar fluxes (bottom right). The times of the start and end of the detected transit are shown as red vertical lines.

Following Gillon et al. (2014), the instrumental models included three types of low-order polynomials. The first had as variables the x- and y-positions of the centre of the PSF to represent the pixel phase effect of the IRAC InSb arrays (e.g. Knutson et al. 2008). The second had as variables the PSF widths in the x- and/or the y-direction, its inclusion in the baseline model strongly increasing the quality of the fit for Warm Spitzer photometry (see also Lanotte et al. 2014). The third, optional, function was a polynomial of the logarithm of time + a slope to represent a sharp decrease of the detector response at the start of the AOR (“ramp” effect, Knutson et al. 2008). To improve the quality of the modelling of the pixel phase effect, especially the fitting of its highest frequency components, we supplemented the x- and y-polynomial with the Bi-Linearly-Interpolated Sub-pixel Sensitivity (BLISS) mapping method (Stevenson et al. 2012). The sampling of the positions in space was selected so that at least five measurements fall within the same subpixel. We refer the reader to Gillon et al. (2014) for more details.

thumbnail Fig. 10

Spitzer photometry divided by two different best-fit baseline models. The first (top) aims to remove position- and PSF effects, and consists of a 4th order polynomial of the PSF x-and y-centres and widths, supplemented with the BLISS mapping method (Stevenson et al. 2012) to remove high-frequency position effects. The second baseline model (bottom) adds to the first a slope and a quadratic function of the logarithm of time to model the sharp decrease in the counts at the beginning of the run (negative ramp). Both light curves are binned per 0.005d = 7.2 min intervals.

Assuming no transit of HD 219134 b, the light curve corrected for the instrumental model described above shows a transit-like structure of ~300 ppm depth that lasts ~50 min (see Fig. 10); this structure remains if higher order terms are used in the polynomial functions. Our first step was to check that this transit-like structure did not correspond to any odd behaviour of the external parameters, which was not the case (Fig. 9). Before identifying the structure with the searched transit, we nevertheless performed a large set of short MCMC analyses assuming different baseline models, and assuming or not that the structure was a transit of the planet. For each baseline model, we computed the BIC difference between the best-fit models with and without transit to estimate the Bayes factor in favour of the transit hypothesis, multiplying the likelihood term e− 0.5ΔBIC by 9/91, the prior transit/no-transit probability ratio. In these tests, we multiplied the photometric errors by a correction factor (CF, see below) of 2.72, the highest value that we ever encountered in our past experiences of high-precision photometry with Warm Spitzer. It corresponds to an AOR targeting 55 Cnc (Demory et al., in prep.) for which the PCRS peak-up mode did not work properly. In this way we assumed that the HD 219134 light curve was strongly affected by some correlated noise poorly reproduced by our instrumental model. In the end, the lowest value that we obtained for the Bayes factor under this extreme hypothesis was ~1000 in favour of the transit hypothesis. We could thus conclude with certainty the transiting nature of the planet.

We then performed a longer MCMC analysis to probe the posterior probability distribution of the transit parameters. The orbit of HD 219134 b was assumed to be circular in this MCMC analysis. The jump parameters of the MCMC, i.e. the parameters randomly perturbed at each step of the Markov Chains, were the following:

  • The stellar mass M∗, radius R∗, effective temperature Teff, and metallicity [Fe/H]. For these four parameters, normal prior probability distribution functions based on the values given in Table 3 were assumed.

  • The planet/star area ratio dF = (Rp/R∗)2.

  • The impact parameter b = acosi/R∗ of the planet, where a is the orbital semi-major axis and i is the orbital inclination. A full-transit configuration corresponds to b< 1 − Rp/R∗.

  • The time of inferior conjunction T0 for the planet, corresponding to the mid-time of the transit.

The limb-darkening of the star was modelled by a quadratic law (Claret 2000). Values for the two quadratic limb-darkening coefficients u1 and u2 were drawn at all steps of the MCMC from normal distributions with expectations and standard deviations drawn from the tables of Claret & Bloemen (2011) for the Spitzer 4.5 μm bandpass and for the stellar atmospheric parameters drawn at the same step.

Five chains of 100 000 steps were performed for each analysis, their convergence being checked using the statistical test of Gelman & Rubin (1992). They followed a preliminary chain of 100 000 steps performed to estimate the need to rescale the photometric errors, at the end of which the standard deviation of the residuals was compared to the mean photometric errors, and the resulting ratios βw were stored. The parameter βw represents the under- or overestimation of the white noise of each measurement. The red noise present in the light curve (i.e. the inability of our model to represent perfectly the data) was taken into account as described in Gillon et al. (2010), i.e. a scaling factor βr was determined from the standard deviations of the binned and unbind residuals for different binning intervals ranging from 5 to 120 min, the largest values being kept as βr. In the end, the error bars were multiplied by the correction factor CF = βr × βw. The derived values for βr and βw were 1.30 and 1.01, resulting in CF = 1.32.

thumbnail Fig. 11

Spitzer photometry divided by the best-fit baseline model and binned per 0.005d = 7.2 min, with the best-fit transit model overplotted in red. Below are shown the y-shifted residuals of the fit binned per 7.2 min and 30 min intervals. Their standard deviations are, respectively, 57 ppm and 25 ppm. Over the light curve is shown the prior probability distribution function derived for the transit timing of HD 219134 b from our analysis of the HARPS-N RVs.

Table 6 presents the resulting values plus error bars for the transit and planet physical parameters, while Fig. 11 shows the light curve corrected for the systematics, the best-fit transit model, and the residuals. We obtain a planet radius of 1.606 ± 0.086 R⊕ and an orbital inclination of 85.058 ± 0.080 degrees. Combining orbital inclination with minimum mass from spectroscopy, we finally obtain a planet mass of 4.36 ± 0.44 M⊕.

Table 6

Transit and physical parameters of HD 219134 b.

thumbnail Fig. 12

Planet mass vs. distance to the host stars for planets in the close solar neighbourhood. Transiting planets are shown as ⋆ in this diagram. These have good mass and radius (density) determinations thanks to their proximity. The planets detected by radial velocity only are also shown using the minimum-mass as a proxy for the mass (data taken from www.exoplanets.org).

thumbnail Fig. 13

Mass-radius relation for planets with radii smaller than 2.7 R⊕ and with masses determined to a precision better than 20% (updated from Dressing et al. 2015). The shaded grey region in the lower right indicates planets with iron content exceeding the maximum value predicted from models of collisional stripping (Marcus et al. 2010) . The solid lines are theoretical mass-radius curves (Zeng & Sasselov 2013) for planets with compositions of 100% H2O (blue), 25% MgSiO3 – 75% H2O (purple), 50% MgSiO3 – 50% H2O (green), 100% MgSiO3 (black), 50% MgSiO3 – 50% Fe (red), and 100% Fe (orange). In this diagram, the position of HD 219134 b is almost overlapping the point for CoRoT-7 b. It belongs to a group of planets including Kepler-36 b, Kepler-93 b, and Kepler-10 b.

6. Discussion

6.1. Dynamical stability

A very important and necessary a posteriori consistency check of a planetary system characterization is needed to verify that the dynamical evolution of the system is viable on the long term, assuring the persistence of the system from the end stage of its formation (when the protoplanetary disk disappears) until its observation today. Pure n-body integrations of the four-planet system, using both the GENGA Code (Grimm & Stadel 2014) launched through the DACE interface5, and a fourth-order Hermite scheme (Makino 1991), with initial conditions derived from the parameters in Table 5, and assuming coplanarity and an inclination of 5 degrees from the transit observation, shows that the system is stable for more than 106 orbits of the outermost planet.

A more complete analysis, taking into account general relativity and tides as well as longer-term secular effects, is beyond the scope of this paper. As expected, a preliminary check indicates, however, that general relativity and tides will act to limit the secular growth of the eccentricities of the inner planets, favouring the long-term stability of the system.

6.2. Bulk composition of the planet HD  219134 b

HD  219134 b is the nearest transiting super-Earth known today. The radius and mass of the planet have been characterized to 6% and 9% accuracy, allowing us to place tight constraints on the bulk density. It thus will become one of the best targets for internal structure and atmosphere characterization with the Spitzer and HST and the upcoming space follow-up missions, e.g. TESS, JWST, CHEOPS, and PLATO. Its position in a stellar distance vs. planetary mass diagram is provided in Fig. 12, in comparison with the other most favourable known cases for characterization within 40 pc from the Sun and up to 35 M⊕: GJ 436 b (Butler et al. 2004; Gillon et al. 2007), 55 Cnc e (Gillon et al. 2012; de Mooij et al. 2014), GJ 1214 b (Charbonneau et al. 2009), HD 97658 b (Howard et al. 2011; Dragomir et al. 2013; Van Grootel et al. 2014), GJ 3470 b (Bonfils et al. 2012; Demory et al. 2013), and HAT-P-11 b (Dittmann et al. 2009).

Combining spectroscopic and space-based photometric data, we estimate a density of 5.76 ± 1.09 g cm-3 for the planet. This density is consistent with the value of 6.90 g cm-3 that would be predicted for a 1.606 R⊕ planet obeying the Earth-like compositional model presented in Dressing et al. (2015).

The compositional tracks employed in Dressing et al. (2015; reproduced and updated in Fig. 13) are based on interior structure models by Zeng & Sasselov (2013) that represent small planets as fully differentiated iron cores surrounded by lower density magnesium silicate mantles. These models provide a useful framework for comparing relative planet compositions, but the absolute core mass fractions are underestimated slightly because the Zeng & Sasselov (2013) models do not incorporate the presence of lighter elements in the core and do not include water in the mantle. Accordingly, the Earth-like compositional track presented in Dressing et al. (2015) corresponds to a model composition of 83% MgSiO3 and 17% Fe, whereas the actual core mass fraction of the Earth is closer to 30%. Zeng et al. (2015) have recently updated their model framework to account for the presence of lighter elements in the core and the presence of water in the mantle. Employing the new models, we find that the population of highly irradiated dense planets (HD 219134b, CoRoT-7b, Kepler-10b, Kepler-36b, Kepler-78b, and Kepler-93b) are best described by a two-component iron-magnesium silicate model with a core mass fraction of approximately 22−23%.

7. Conclusion

We have presented in this paper the first result from the Rocky Planet Search (RPS) programme conducted with HARPS-N, as a planetary system of three inner super-Earths and one outer sub-Saturn planet, hosted by the bright and nearby quiet K dwarf HD 219134. The planet separations between 0.039 and 0.23 AU called for a search of potential transits of the inner planet(s) with the Spitzer space telescope. The successful detection of the transit of HD 219134 b makes the star the closest (6.5 pc) and brightest (V = 5.5) star known to date with a transiting planet (super-Earth). This system is thus becoming one of the most favourable ones for follow-up observations, in order to better constrain the system architecture or to characterize the physical properties of the planets. First, it provides an excellent constraining point in the mass-radius diagram (Fig. 13) for the composition of the planet, found to be of terrestrial-equivalent composition with a core mass fraction of the order of 22%. The quality of the measurements of the radius, mass, and then mean density actually foreshadows what can be expected from the future transit missions in preparation that will target bright stars (CHEOPS, TESS, PLATO). We also know from Kepler results that multi-transiting systems of small-size planets are numerous. It is now highly suitable to search for traces of transits of the other planets in the systems. Finally, even if a potential atmosphere around the planet is expected a priori to be tiny, the brightness of the system makes it worth trying to detect features of this atmosphere in the UV, visible, and near-infrared, from space and from the ground, especially in preparation for future measurements with larger facilities (JWST, TMT).

Note added in proof. During the refereeing process, we learned about an independent detection by Vogt et al. (Laughlin, priv. comm.) reporting additional planets in the system, based on long-term radial velocities obtained with the Keck and APF telescopes.

1

The limit was chosen iteratively in order to have a large enough sample that covers a full range of right ascension, with an overdensity during winter when the Kepler field is not visible.

4

IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.

5

DACE is a platform of the Swiss National Centre for Competence in Research “PlanetS”, which can be accessed at http:\dace.unige.ch

Acknowledgments

The HARPS-N project was funded by the Prodex programme of the Swiss Space Office (SSO), the Harvard University Origin of Life Initiative (HUOLI), the Scottish Universities Physics Alliance (SUPA), the University of Geneva, the Smithsonian Astrophysical Observatory (SAO), and the Italian National Astrophysical Institute (INAF), University of St. Andrews, Queen’s University Belfast, and University of Edinburgh. The research leading to these results has received funding from the European Union Seventh Framework programme (FP7/2007- 2013) under grant agreement No. 313014 (ETAEARTH). C.D. is supported by a National Science Foundation Graduate Research Fellowship. P.F. acknowledges support by Fundaçao para a Ciência e a Tecnologia (FCT) through Investigador FCT contracts of reference IF/01037/2013 and POPH/FSE (EC) by FEDER funding through the programme “Programa Operacional de Factores de Competitividade – COMPETE”. This work has been carried out in the frame of the National Centre for Competence in Research “PlanetS” supported by the Swiss National Science Foundation (SNSF). S.U., C.L., D.S. and F.P. acknowledge the financial support of the SNSF. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA. M. Gillon is Research Associate at the Belgian Scientific Research Fund (F.R.S-FNRS), and he is extremely grateful to NASA and SSC Director for having supported his searches for RV planets with Spitzer. P.F. further acknowledges support from Fundação para a Ciência e a Tecnologia (FCT) in the form of an exploratory project of reference IF/01037/2013CP1191/CT0001. R.D.H. was supported by STFC studentship grant ST/J500744/1 during the course of this work. CAW acknowledges support from STFC grant ST/L000709/1. This publication was made possible by a grant from the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation. This material is based upon work supported by the National Aeronautics and Space Administration under Grant No. NNX15AC90G issued through the Exoplanets Research Program.

References

  1. Andrieu, C., & Thoms, J. 2008, Statistics and Computing, 18, 343 [Google Scholar]
  2. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  3. Ballard, S., Chaplin, W. J., Charbonneau, D., et al. 2014, ApJ, 790, 12 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Benz, W., Ida, S., Alibert, Y., Lin, D., & Mordasini, C. 2014, Protostars and Planets VI, 691 [Google Scholar]
  6. Bonfils, X., Gillon, M., Udry, S., et al. 2012, A&A, 546, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bonomo, A. S., Sozzetti, A., Lovis, C., et al. 2014, A&A, 1409, A4592 [Google Scholar]
  8. Borucki, W. J., Koch, D. G., Basri, G., et al. 2011, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
  9. Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
  10. Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
  11. Buchhave, L. A., Bizzarro, M., Latham, D. W., et al. 2014, Nature, 509, 593 [NASA ADS] [CrossRef] [Google Scholar]
  12. Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
  13. Castelli, F., & Kurucz, R. L. 2004, IAU Symp., 210, poster A20 [Google Scholar]
  14. Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  15. Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
  16. Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Collier Cameron, A., Wilson, D. M., West, R. G., et al. 2007, MNRAS, 380, 1230 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in SPIE Conf. Ser., 8446, 1 [Google Scholar]
  19. Cosentino, R., Lovis, C., Pepe, F., et al. 2014, in SPIE Conf. Ser., 9147, 8 [Google Scholar]
  20. Dawson, R. I., & Fabrycky, D. C. 2010, ApJ, 722, 937 [NASA ADS] [CrossRef] [Google Scholar]
  21. de Mooij, E. J. W., López-Morales, M., Karjalainen, R., Hrudkova, M., & Jayawardhana, R. 2014, ApJ, 797, L21 [NASA ADS] [CrossRef] [Google Scholar]
  22. Demory, B.-O., Gillon, M., Deming, D., et al. 2011, A&A, 533, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Demory, B.-O., Gillon, M., Seager, S., et al. 2012, ApJ, 751, L28 [Google Scholar]
  24. Demory, B.-O., Torres, G., Neves, V., et al. 2013, ApJ, 768, 154 [NASA ADS] [CrossRef] [Google Scholar]
  25. Demory, B.-O., Ehrenreich, D., Queloz, D., et al. 2015a, MNRAS, 450, 2043 [NASA ADS] [CrossRef] [Google Scholar]
  26. Demory, B.-O., Gillon, M., Madhusudhan, N., & Queloz, D. 2015b, MNRAS, submitted [arXiv:1505.00269] [Google Scholar]
  27. Dittmann, J. A., Close, L. M., Green, E. M., Scuderi, L. J., & Males, J. R. 2009, ApJ, 699, L48 [NASA ADS] [CrossRef] [Google Scholar]
  28. Dragomir, D., Matthews, J. M., Eastman, J. D., et al. 2013, ApJ, 772, L2 [NASA ADS] [CrossRef] [Google Scholar]
  29. Dressing, C. D., Charbonneau, D., Dumusque, X., et al. 2015, ApJ, 800, 135 [NASA ADS] [CrossRef] [Google Scholar]
  30. Dumusque, X., Lovis, C., Ségransan, D., et al. 2011a, A&A, 535, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Dumusque, X., Udry, S., Lovis, C., Santos, N. C., & Monteiro, M. J. P. F. G. 2011b, A&A, 525, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  33. Dumusque, X., Bonomo, A. S., Haywood, R. D., et al. 2014, ApJ, 789, 154 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fabrycky, D. C., Lissauer, J. J., Ragozzine, D., et al. 2014, ApJ, 790, 146 [NASA ADS] [CrossRef] [Google Scholar]
  35. Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
  36. Figueira, P., Marmier, M., Boué, G., et al. 2012, A&A, 541, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Fortier, A., Beck, T., Benz, W., et al. 2014, in SPIE Conf. Ser., 9143, 2 [Google Scholar]
  38. Fressin, F., Torres, G., Charbonneau, D., et al. 2013, ApJ, 766, 81 [NASA ADS] [CrossRef] [Google Scholar]
  39. Gelman, A., & Rubin, D. B. 1992, Statist. Sci., 7, 457 [NASA ADS] [CrossRef] [Google Scholar]
  40. Gillon, M., Demory, B.-O., Barman, T., et al. 2007, A&A, 471, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Gillon, M., Deming, D., Demory, B.-O., et al. 2010, A&A, 518, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Gillon, M., Demory, B.-O., Benneke, B., et al. 2012, A&A, 539, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Gillon, M., Demory, B.-O., Madhusudhan, N., et al. 2014, A&A, 563, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Gregory, P. C. 2005a, ApJ, 631, 1198 [NASA ADS] [CrossRef] [Google Scholar]
  45. Gregory, P. C. 2005b, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with Mathematica Support (Cambridge University Press) [Google Scholar]
  46. Grillmair, C. J., Carey, S. J., Stauffer, J. R., et al. 2012, Pointing effects and their consequences for Spitzer IRAC exoplanet observations [Google Scholar]
  47. Grimm, S. L., & Stadel, J. G. 2014, ApJ, 796, 23 [NASA ADS] [CrossRef] [Google Scholar]
  48. Howard, A. W., Marcy, G. W., Johnson, J. A., et al. 2010, Science, 330, 653 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  49. Howard, A. W., Johnson, J. A., Marcy, G. W., et al. 2011, ApJ, 730, 10 [NASA ADS] [CrossRef] [Google Scholar]
  50. Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
  51. Ingalls, J. G., Carey, S. J., Lowrance, P. J., Grillmair, C. J., & Stauffer, J. R. 2014, Using drift scans to improve astrometry with Spitzer, SPIE Proc., 9143 [Google Scholar]
  52. Kass, E. R., & Raftery, E. A. 1995, J. Am. Statis. Assoc., 90, 773 [Google Scholar]
  53. Knutson, H. A., Charbonneau, D., Allen, L. E., Burrows, A., & Megeath, S. T. 2008, ApJ, 673, 526 [NASA ADS] [CrossRef] [Google Scholar]
  54. Kovtyukh, V. V., Soubiran, C., Belik, S. I., & Gorlova, N. I. 2003, A&A, 411, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Kurucz, R. L. 1992, in The Stellar Populations of Galaxies, eds. B. Barbuy, & A. Renzini, IAU Symp., 149, 225 [Google Scholar]
  56. Lanotte, A. A., Gillon, M., Demory, B.-O., et al. 2014, A&A, 572, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Lovis, C., Dumusque, X., Santos, N. C., et al. 2011a, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
  58. Lovis, C., Ségransan, D., Mayor, M., et al. 2011b, A&A, 528, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Makino, J. 1991, ApJ, 369, 200 [NASA ADS] [CrossRef] [Google Scholar]
  60. Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
  61. Marcus, R. A., Sasselov, D., Stewart, S. T., & Hernquist, L. 2010, ApJ, 719, L45 [NASA ADS] [CrossRef] [Google Scholar]
  62. Marcy, G. W., Weiss, L. M., Petigura, E. A., et al. 2014, Proc. National Academy of Science, 111, 12655 [Google Scholar]
  63. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  64. Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, ArXiv e-prints [arXiv:1109.2497] [Google Scholar]
  66. Meunier, N., & Lagrange, A.-M. 2013, A&A, 551, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Mishenina, T. V., Soubiran, C., Bienaymé, O., et al. 2008, A&A, 489, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Mishenina, T. V., Soubiran, C., Kovtyukh, V. V., Katsova, M. M., & Livshits, M. A. 2012, A&A, 547, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Mordasini, C., Alibert, Y., Georgy, C., et al. 2012, A&A, 547, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Mortier, A., Sousa, S. G., Adibekyan, V. Z., Brandão, I. M., & Santos, N. C. 2014, A&A, 572, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Ogihara, M., Morbidelli, A., & Guillot, T. 2015, A&A, 578, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Pepe, F., Cameron, A. C., Latham, D. W., et al. 2013, Nature, 503, 377 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  75. Pollacco, D., Skillen, I., Collier Cameron, A., et al. 2008, MNRAS, 385, 1576 [NASA ADS] [CrossRef] [Google Scholar]
  76. Prugniel, P., Vauglin, I., & Koleva, M. 2011, A&A, 531, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Ramírez, I., Allen de Prieto, C., & Lambert, D. L. 2013, ApJ, 764, 78 [NASA ADS] [CrossRef] [Google Scholar]
  78. Rauer, H., Catala, C., Aerts, C., et al. 2014, Exper. Astron., 38, 249 [Google Scholar]
  79. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, in SPIE Conf. Ser., 9143, 20 [Google Scholar]
  80. Schwarz, G. 1978, Ann. Statist., 6, 461 [Google Scholar]
  81. Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] [Google Scholar]
  82. Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
  84. Stevenson, K. B., Harrington, J., Fortney, J. J., et al. 2012, ApJ, 754, 136 [NASA ADS] [CrossRef] [Google Scholar]
  85. Tsantaki, M., Sousa, S. G., Adibekyan, V. Z., et al. 2013, A&A, 555, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  87. Van Grootel, V., Gillon, M., Valencia, D., et al. 2014, ApJ, 786, 2 [NASA ADS] [CrossRef] [Google Scholar]
  88. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Zeng, L., Jacobsen, S., & Sasselov, D. D. 2015, AAS Meet. Abstr., 225, 406.02 [Google Scholar]
  91. Zeng, L., & Sasselov, D. 2013, PASP, 125, 227 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

List of the RPS targets in the GTO programme on HARPS-N.

In the text
Table 2

Comparative summary of the atmospheric parameters derived for HD 219134.

In the text
Table 3

Stellar parameters considered for HD 219134.

In the text
Table 4

Comparison of tested models.

In the text
Table 5

Orbital solution and planet inferred parameters for the four-Keplerian model (K4) of the system around HD 219134.

In the text
Table 6

Transit and physical parameters of HD 219134 b.

In the text

All Figures

thumbnail Fig. 1

Histogram of the dispersion of the radial velocity measurements of stars in the RPS programme on HARPS-N.
In the text
thumbnail Fig. 2

Radial velocity (top) and activity index (bottom) time series for HD 219134.
In the text
thumbnail Fig. 3

Generalized Lomb-Scargle periodogram of the radial velocities of HD 219134, after removing – from top to bottom – a long-period Keplerian, and successively the 3.09-day, the 46.66-day and finally the 6.76-day signals. Dashed lines indicate 0.1%, 1%, and 10% levels of false alarm probability.
In the text
thumbnail Fig. 4

Phase-folded radial velocity measurements of HD 219134 with the corresponding Keplerian model (solid line) for each of the three inner super-Earths, after removing the contribution of all the other planets in the system. From top to bottom, we have the 3.09-, 6.76-, and 46.66-day periods.
In the text
thumbnail Fig. 5

Radial velocity measurements as a function of time of HD 219134 with the corresponding Keplerian model (solid line) for the outer planet in the system, after removing the contribution of the three inner planets.
In the text
thumbnail Fig. 6

Star activity index as a function of the radial velocity residuals after removing the three shorter-period planet contributions for HD 219134. No clear positive correlation is observed, contrary to what is expected in the case of magnetic cycles (Lovis et al. 2011a).
In the text
thumbnail Fig. 7

From top to bottom GLS periodograms of radial velocities, log RHK′\hbox{$\log\,R^{\prime}_{\rm HK}$}, CCF bisector span, and CCF FWHM of the two-year data set, zoomed around the periods of interest. The thick red line in each panel indicates the planetary period (46.7 days) and the thick green line indicates the stellar rotation period (42.3 days). The thinner lines are the corresponding yearly aliases.
In the text
thumbnail Fig. 8

Radial velocities after subtracting the contributions of the planets at 3.09, 6.76, and 1842 days, shown as a function of the logRHK′\hbox{$\log R^{\prime}_{\rm HK}$} activity index detrended with a polynomial of degree 3. No correlation is observed, supporting the planetary interpretation for the 46.7-day signal.

In the text
thumbnail Fig. 9

Evolution of the following measured parameters in the Spitzer images for HD 219134: PSF centre x- and y-positions (top), PSF x- and y-widths (middle), background counts (bottom left), and stellar fluxes (bottom right). The times of the start and end of the detected transit are shown as red vertical lines.
In the text
thumbnail Fig. 10

Spitzer photometry divided by two different best-fit baseline models. The first (top) aims to remove position- and PSF effects, and consists of a 4th order polynomial of the PSF x-and y-centres and widths, supplemented with the BLISS mapping method (Stevenson et al. 2012) to remove high-frequency position effects. The second baseline model (bottom) adds to the first a slope and a quadratic function of the logarithm of time to model the sharp decrease in the counts at the beginning of the run (negative ramp). Both light curves are binned per 0.005d = 7.2 min intervals.
In the text
thumbnail Fig. 11

Spitzer photometry divided by the best-fit baseline model and binned per 0.005d = 7.2 min, with the best-fit transit model overplotted in red. Below are shown the y-shifted residuals of the fit binned per 7.2 min and 30 min intervals. Their standard deviations are, respectively, 57 ppm and 25 ppm. Over the light curve is shown the prior probability distribution function derived for the transit timing of HD 219134 b from our analysis of the HARPS-N RVs.
In the text
thumbnail Fig. 12

Planet mass vs. distance to the host stars for planets in the close solar neighbourhood. Transiting planets are shown as ⋆ in this diagram. These have good mass and radius (density) determinations thanks to their proximity. The planets detected by radial velocity only are also shown using the minimum-mass as a proxy for the mass (data taken from www.exoplanets.org).

In the text
thumbnail Fig. 13

Mass-radius relation for planets with radii smaller than 2.7 R⊕ and with masses determined to a precision better than 20% (updated from Dressing et al. 2015). The shaded grey region in the lower right indicates planets with iron content exceeding the maximum value predicted from models of collisional stripping (Marcus et al. 2010) . The solid lines are theoretical mass-radius curves (Zeng & Sasselov 2013) for planets with compositions of 100% H2O (blue), 25% MgSiO3 – 75% H2O (purple), 50% MgSiO3 – 50% H2O (green), 100% MgSiO3 (black), 50% MgSiO3 – 50% Fe (red), and 100% Fe (orange). In this diagram, the position of HD 219134 b is almost overlapping the point for CoRoT-7 b. It belongs to a group of planets including Kepler-36 b, Kepler-93 b, and Kepler-10 b.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.