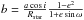| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526763 | |
| Published online | 13 November 2015 | |
Transiting exoplanets from the CoRoT space mission⋆,⋆⋆
XXVIII. CoRoT-33b, an object in the brown dwarf desert with 2:3 commensurability with its host star
1
Institute of Planetary Research, German Aerospace Center,
Rutherfordstrasse
2,
12489
Berlin,
Germany
e-mail:
szilard.csizmadia@dlr.de
2
Thüringer Landessternwarte, Sternwarte 5, Tautenburg
5, 07778
Tautenburg,
Germany
3
Dipartimento di Fisica, Universitá di Torino,
via P. Giuria 1, 10125
Torino,
Italy
4
Landessternwarte Königstuhl, Zentrum für Astronomie der
Universität Heidelberg, Königstuhl
12, 69117
Heidelberg,
Germany
5
Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
6
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
7
Leiden Observatory, University of Leiden,
PO Box 9513, 2300 RA, Leiden, The Netherlands
8
Department of Earth and Space Sciences, Chalmers University of
Technology, Onsala Space Observatory, 439 92
Onsala,
Sweden
9
Konkoly Observatory of the Hungarian Academy of
Sciences, MTA CSFK,
Budapest, Konkoly Thege Miklós
út
15-17,
Hungary
10
Sub-department of Astrophysics, Department of Physics, University
of Oxford, Oxford,
OX1 3RH,
UK
11
Department of Physics, Denys Wilkinson Building, Keble Road,
Oxford, OX1 3RH, UK
12
Instituto de Astrofísica de Canarias, 38205, La Laguna, Tenerife, Spain
13
Universidad de La Laguna, Dept. de Astrofísica, 38206,
La Laguna, Tenerife,
Spain
14
LESIA, UMR 8109 CNRS, Observatoire de Paris, UPMC, Université
Paris-Diderot, 5 place J.
Janssen, 92195
Meudon,
France
15
LAB, UMR 5804, Univ. Bordeaux & CNRS,
33270
Floirac,
France
16 INAF–Osservatorio Astrofisico di Torino Strada
Osservatorio, 20 10025 Pino Torinese ( TO), Italy
17
Observatoire astronomique de l’Université de Genève,
51 ch. des Maillettes,
1290
Versoix,
Switzerland
18 IAG-Universidade de São Paulo, 1226 Sâo Paulo, Brasil
19
Université de Nice-Sophia Antipolis, CNRS UMR 6202, Observatoire
de la Côte d’Azur, BP
4229, 06304
Nice Cedex 4,
France
20
Rheinisches Institut für Umweltforschung an der Universität zu
Köln, 50931
Aachener Strasse 209,
Germany
21
Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université
Pierre & Marie Curie, 98bis
boulevard Arago, 75014
Paris,
France
22
Institut d’Astrophysique Spatiale, Université Paris
XI, 91405
Orsay,
France
23
Center for Astronomy and Astrophysics, TU Berlin, Hardenbergstr.
36, 10623
Berlin,
Germany
24
Instituto de Astrofísica e Ciências do Espaço, Universidade do
Porto, CAUP, Rua das
Estrelas, 4150-762
Porto,
Portugal
25
LUTH, Observatoire de Paris, UMR 8102 CNRS, Université Paris
Diderot, 5 place Jules
Janssen, 92195
Meudon,
France
26
School of Physics and Astronomy, Raymond and Beverly Sackler
Faculty of Exact Sciences, 39040 Tel Aviv University, Tel Aviv, Israel
27
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse 1,
85748
Garching,
Germany
28
Department of Earth and Planetary Sciences, Weizmann Institute of
Science, 234 Herzl
St., 76100
Rehovot,
Israel
Received: 16 June 2015
Accepted: 28 July 2015
We report the detection of a rare transiting brown dwarf with a mass of 59 MJup and radius of 1.1 RJup around the metal-rich, [Fe/H] = +0.44, G9V star CoRoT-33. The orbit is eccentric (e = 0.07) with a period of 5.82 d. The companion, CoRoT-33b, is thus a new member in the so-called brown dwarf desert. The orbital period is within 3% to a 3:2 resonance with the rotational period of the star. CoRoT-33b may be an important test case for tidal evolution studies. The true frequency of brown dwarfs close to their host stars (P< 10 d) is estimated to be approximately 0.2% which is about six times smaller than the frequency of hot Jupiters in the same period range. We suspect that the frequency of brown dwarfs declines faster with decreasing period than that of giant planets.
Key words: brown dwarfs / stars: rotation / eclipses
The CoRoT space mission, launched on December 27th 2006, has been developed and is operated by CNES, with the contribution of Austria, Belgium, Brazil, ESA (RSSD and Science Programme), Germany and Spain. Based on observations made with HARPS (High Accuracy Radial velocity Planet Searcher) spectrograph on the 3.6-m European Organisation for Astronomical Research in the Southern Hemisphere telescope at La Silla Observatory, Chile (ESO program 188.C-0779).
Based on observations obtained with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias, in time allocated by the Spanish Time Allocation Committee (CAT).
© ESO, 2015
Basic data of known transiting brown dwarfs.
1. Introduction
As of June 2015, W. R. Johnston lists 2085 confirmed and 562 candidate brown dwarfs1, 427 of them are marked as located in either a binary or multiple system. Only 65 brown dwarfs are companions to FGK dwarfs at orbital distances less than 2 AU from the star (Ma & Ge 2014). Of these only nine (and one additional reported here) are transiting (Table 1) which provides the possibility of measuring the mass and radius directly. Given the meager observational data, an increase in the number of brown dwarfs with accurate parameters is necessary to obtain a better understanding of the formation, structure, and evolution of these objects. Transiting brown dwarfs offer the best possibility for characterizing them in a model-independent way.
The radii of brown dwarfs and giant planets are in the same range around 1 RJup, but the masses are quite different. Brown dwarfs straddle a border at 65 Jupiter masses. Objects with masses below this border fuse deuterium (D) while those above this mass limit fuse lithium (Li) in episodic events (e.g. Chabrier et al. 1996), and planets do not ignite their material. Spiegel et al. (2011) showed that the lower mass limit for brown dwarfs – defined by deuterium-ignition – is between 11−16 MJup depending on the actual metallicity. Planets are usually smaller in mass than brown dwarfs, but there is an overlapping region: a tiny portion of planetesimals, the so-called “super-planets” may grow up to 20−40 MJup by core-accretion (Mordasini et al. 2009), causing problems with separating these giant planets from brown dwarfs (Schneider et al. 2011). The maximum mass of brown dwarfs is about 75−80 MJup (Baraffe et al. 2002).
Chabrier et al. (2014) suggests that the borderline between giant planets and brown dwarfs should be linked to their different formation scenarios and not to the minimum mass required for deuterium ignition. Then the various formation and evolutionary mechanisms may be responsible for the nonequal frequency of brown dwarfs and planetary-mass objects around stars.
While ~50% of solar-like dwarf stars have a stellar, ~30% have a low-mass (Earth- to Neptune-sized), and ~2.5% have a higher mass (Jupiter or bigger) planetary companion, only 0.6−0.8% of solar-like stars have a brown dwarf within 5 AU (Duquennoy & Mayor 1991; Vogt et al. 2002; Patel et al. 2007; Wittenmyer et al. 2009; Sahlmann et al. 2011; Dong & Zhu 2013). The brown dwarf desert refers to this low occurrence rate of brown dwarfs as companion objects to main-sequence stars. However, the frequency of wide pairs consisting of a brown dwarf and a solar-like star (with a separation exceeding 5 AU) is significantly higher at over 2−3% (Ma & Ge 2014, and references therein). A more detailed overview of the different occurrence rates can be found in Ma & Ge (2014).
 |
Fig. 1 Upper panel: full CoRoT light curve of CoRoT-33. The gray points represent the median-normalized raw data points after a 5-point width median filtering. We only used data points with flag “0” for this curve. The red line is a convolution of the raw light curve with a Savitzky-Golay filter that enhances the light-curve variations. Middle panel: Lomb-Scargle periodogram of the light curve of CoRoT-33. The horizontal dashed line denotes the 0.01% false-alarm probability (Scargle 1982). The vertical red line marks the rotation period of the star. Lower panel: autocorrelation function (ACF) of light curve, following the subtraction of the best fitting transit model. The red dashed line marks the peak corresponding to the rotation period of CoRoT-33 (see Sect. 3.5). |
Brown dwarfs may have a different formation mechanism from giant planets, which might form via core accretion (Alibert et al. 2005). Ma & Ge (2014) proposed that brown dwarfs below 35 MJup are formed from the protoplanetary disk via gravitational instability, while those with M> 55MJup form like stellar binaries via molecular cloud fragmentation. Between masses of 35 and 55 MJup there are a significant lack of brown dwarfs orbital periods shorter than 100 days (Ma & Ge 2014) as companions to stars.
Alternative theories explaining the brown dwarf desert suggest that during the formation of a binary system consisting of a solar-type star and a brown dwarf, the migration process is so effective that brown dwarf companion spirals into the star and is engulfed. This would explain the paucity of very few brown dwarf companions found within 5 AU to solar-type stars (Armitage & Bonnell 2002). Combining this low frequency of close-in brown dwarfs with the geometric transit probability, transiting brown dwarfs should indeed be rare.
In this paper we report the discovery of a transiting brown dwarf, CoRoT-33b. With a mass of 59 Jupiter mass, CoRoT-33b lies just below to the D-Li border for brown dwarfs at 65 Jupiter masses. We also give a preliminary estimate for the frequency of close-in brown dwarfs with orbital period less than ten days.
2. Data
2.1. CoRoT observations
2.1.1. Flux measurements and transit detection
CoRoT-33 (R = 14.25 magn) was observed by the CoRoT satellite (Auvergne et al. 2009; Baglin et al. 2007) in white light for 77.4 days between 8 July 2010 and 24 September 2010. In total, 178 342 data points were collected. Various designations of the target are listed in Table 2 along with equatorial coordinates and magnitudes in different passbands.
The first transits of CoRoT-33b were discovered in the so-called Alarm Mode which triggered an oversampling rate and spectroscopic follow-up observations. After 22 July 2010 the standard 512 s sampling rate was changed to 32 s (see Surace et al. 2008; Bonomo et al. 2012). In total, 13 transits of CoRoT-33b were observed.
For the light-curve analysis we kept only those data points that were flagged with “0” by the CoRoT automatic data-pipeline which is an indication of good measurement without comment. In total, we used 1626 data points obtained with the 512 s integration time and 133 333 data points obtained with the 32 s integration time for a total of 134 959 photometric measurements.
The cleaned light curve normalized to its median value is shown in Fig. 1. Fortunately, no significant jumps, cosmic ray events, hot pixels, etc. affected this light curve. Also shown is a smoothed version of the data produced after applying a Savitzky-Golay filter. Variations due to rotational modulation can clearly be seen, which is studied in detail in Sect. 3.5.
HARPS and FIES RV measurements of the CoRoT-33 system.
2.1.2. Contamination
Figure 7 shows the Palomar Observatory Sky Survey’s image of CoRoT-33 and its environment. The solid zigzag line represents the CoRoT-photometric mask while the dashed line shows the boundaries of the CoRoT-imagette. CoRoT has a bi-prism in the optical pathway of its exoplanet channel so that a small, very low-resolution spectrum is obtained for brighter stars in the field. Therefore the point-spread function (PSF) of each object in the field of view of the exoplanet channel is roughly 46 × 23 arcsec. We found that the contribution of stars outside the mask is very small, but there are two main contaminants inside the photometric mask, denoted by Nos. 1 and 2. They are fainter than CoRoT-33 by 2.5 and 2.9 magn. Because of the large PSF of CoRoT, the contaminating sources actually produce 13 ± 4% of the total observed light in this mask. This contamination factor was calculated using the procedure described in Pasternacki et al. (2011) and is consistent with the value found independently by Gardes et al. (2011).
2.2. Radial velocity measurements
The radial velocity (RV) follow-up of CoRoT-33 was started with the HARPS spectrograph (Mayor et al. 2003) based on the 3.6-m ESO telescope (La Silla, Chile) as part of the ESO large program 188.C-0779. To monitor the Moon background light on the second fibre, HARPS was used with the observing mode obj_AB, i.e., without simultaneous thorium-argon (ThAr). The exposure time varied between 25 min and 1 h. A set of 8 spectra was recorded for CoRoT-33 with HARPS between 28 June 2013 and 15 August 2013. We reduced the HARPS data and computed RVs with the HARPS pipeline based on the cross-correlation technique (Baranne et al. 1996; Pepe et al. 2002). Radial velocities were obtained by weighted cross-correlation with a numerical K5 mask which yielded the smallest error bars. The signal-to-noise ratio (S/N) per pixel at 5500 Å is in the range 2 to 7. The first and the last measurements were affected and corrected from moonlight contamination.
Four additional RV measurements were acquired with the FIbre-fed Échelle Spectrograph (FIES; Frandsen & Lindberg 1999; Telting et al. 2014) mounted at the 2.56-m Nordic Optical Telescope (NOT) of Roque de los Muchachos Observatory (La Palma, Spain). The observations were carried out on 2, 3, 4, and 5 July 2014 under the CAT observing programme 79-NOT5/14A. We used the 1.3 ″med-res fibre, which provides a resolving power of R ≈ 47 000 in the spectral range 3600−7400 Å. The weather was clear with seeing varying between 0.6 and 1.4″ throughout the whole observing run. We followed the observing strategy as described in Buchhave et al. (2010) and Gandolfi et al. (2015) and took three consecutive exposures of 1200−1800 s per epoch observation to remove cosmic ray hits. We also acquired long-exposed (Texp = 22−24 s) ThAr spectra right before and after each epoch observation to trace the RV drift of the instrument. The data were reduced using standard IRAF and IDL routines, which included bias subtraction, flat fielding, order tracing and extraction, and wavelength calibration. The S/N of the extracted spectra is 15−20 per pixel at 5500 Å. Radial velocity measurements were derived via S/N-weighted, multiorder, cross-correlation with the RV standard star HR 5777, and observed with the same instrument set-up as the target object.
The HARPS and FIES RV measurements are listed in Table 3 along with their errors and the Julian dates of the observations in barycentric dynamical time (BJDTDB, see Eastman et al. 2010).
Physical and geometrical parameters of the CoRoT-33 system.
3. Analysis
3.1. Analysis of radial velocity data
Full width half maximum (FWHM) and bisector span (BIS) of the cross-correlation function are also listed in Table 3 and show no significant variation in phase with the radial velocity. Furthermore the radial velocity peak-to-peak amplitude (~14 km s-1) is larger than the FWHM excluding a blended or background binary scenario.
An offset between the two instruments was calculated as part of the orbit fitting process and accounted for when combining the HARPS and FIES data sets. We first tried fitting a circular orbit to the RV data. Free parameters were the offset value for each data set, the true γ-velocity and the amplitude (K) of the RV curve. The epoch and period were fixed to the values of the photometric ephemeris (these were varied within the errors). This fit yielded a considerably large reduced χ2-value: 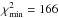 . We then also allowed the epoch and period to vary in the fitting procedure. The resulting fit yielded a slightly smaller
. We then also allowed the epoch and period to vary in the fitting procedure. The resulting fit yielded a slightly smaller 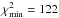 . Interestingly, the period converged to a value that is compatible within 1σ uncertainties of the period obtained from the photometric transits, but the resulting epoch obtained from the RV-analysis differed by 194 min from the photometric value. The error in the photometrically determined epoch is only 6 min, so the epoch difference is significant at the 32σ level. Assuming a circular orbit the orbital fit to the RV data produced very large χ2-values or the RV data are incompatible with the photometric ephemeris.
. Interestingly, the period converged to a value that is compatible within 1σ uncertainties of the period obtained from the photometric transits, but the resulting epoch obtained from the RV-analysis differed by 194 min from the photometric value. The error in the photometrically determined epoch is only 6 min, so the epoch difference is significant at the 32σ level. Assuming a circular orbit the orbital fit to the RV data produced very large χ2-values or the RV data are incompatible with the photometric ephemeris.
Therefore we tried fitting an eccentric orbit to the RV data. The results are quite satisfactory:  . The orbit was found to have a slight eccentricity: e = 0.0700 ± 0.0017. The results of this fit can be found in Table 4.
. The orbit was found to have a slight eccentricity: e = 0.0700 ± 0.0017. The results of this fit can be found in Table 4.
Figure 3 shows the RV measurements – after correcting for the RV offset and subtracting the systemic radial velocity – phase folded to the orbital period (upper panel), along with the RV residuals (lower panel).
Zakamska et al. (2011) found that a precise estimation of eccentricity requires that the radial velocity curve should have a S/N of 40, and the individual RV measurements should have a precision better than 1%. These requirements are fulfilled in our analysis. Their Eq. (7) gives an estimate of the precision of the eccentricity determination, i.e., 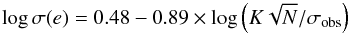 (1)where σ(e) is the expected precision on eccentricity, N = 12 is the number of the RV data points, σobs = 0.046 km s-1 is their average (median) uncertainty. Substituting our values, we get σ(e) = 0.011 and thus our eccentricity determination and its error bar are reliable. The estimate of Zakamska et al. (2011) is the result of an average error estimate based only on RV, in our case the joint RV and light-curve fit yielded a smaller uncertainty range for the eccentricity (Sect. 3.4). The relatively large K/σobs ratio enables us to achieve the aforementioned precision in the eccentricity.
(1)where σ(e) is the expected precision on eccentricity, N = 12 is the number of the RV data points, σobs = 0.046 km s-1 is their average (median) uncertainty. Substituting our values, we get σ(e) = 0.011 and thus our eccentricity determination and its error bar are reliable. The estimate of Zakamska et al. (2011) is the result of an average error estimate based only on RV, in our case the joint RV and light-curve fit yielded a smaller uncertainty range for the eccentricity (Sect. 3.4). The relatively large K/σobs ratio enables us to achieve the aforementioned precision in the eccentricity.
 |
Fig. 2 Finding chart and contamination source map for CoRoT-33. Red numbers denote stars whose contribution to the observed flux was taken into account; yellow numbers denote stars whose contamination was checked but was found negligible. Star with number 0 corresponds to CoRoT-33. |
 |
Fig. 3 Upper panel: phase-folded RV measurements of CoRoT-33. Red circles represent the HARPS-measurements while green circles are the data points obtained by FIES-instrument. Black solid line represents the eccentric orbit fit. The RV points and the fit is shifted by the γ-velocity of the system. Lower panel: it shows the residuals of the fit. Vertical lines on the data points indicate their error bars. |
3.2. Spectral analysis of the host star
We determine the spectroscopic parameters of the host star using the coadded HARPS and FIES spectra. The S/N of the coadded data is relatively low, about 15 and 30 per pixel at 5500 Å for HARPS and FIES, respectively, owing to the low S/N of each individual spectrum
We used the Spectroscopy Made Easy package (SME), version 4.1.2 (Valenti & Piskunov 1996; Valenti & Fischer 2005) along with Atlas 12 or MARCS 2012 model atmospheres (Kurucz 2013; Mészáros et al. 2012) to determine the fundamental photospheric parameters iteratively. SME fits the observed spectrum directly to the synthesized model spectrum and minimizes the discrepancies using a nonlinear least-squares algorithm. The SME utilizes input from the VALD database (Piskunov et al. 1995; Kupka et al. 1999). The uncertainties per measurement using SME based on a sample of more than 1000 stars was found by Valenti & Fischer (2005) to be 44 K for the effective temperature Teff, 0.06 dex for the surface gravity log g∗, and 0.03 dex for the metallicity [M/H]. This is in a statistical sense and somewhat optimistic. It was found from Valenti & Fischer (2005) that the scatter was systematically larger with an uncertainty in log g∗ of 0.1 dex and a scatter that occasionally could reach 0.3 dex. Fridlund et al. (in prep.) have, in a systematic study of the CoRoT exoplanet host stars, confirmed these numbers. Furthermore, the errors in Teff are also affected by the problems with determining the shape of the Balmer lines accurately enough, as pointed out by Fuhrmann in a series of papers (see, e.g., Fuhrmann et al. 2011, and references therein; also Fridlund et al., in prep.).
Torres et al. (2012) reported SME overestimates log g and correlates with Teff and [Fe/H]; see also Brewer et al. (2015) that this issue is eliminated. Therefore, we carried out an independent analysis of the spectrum using customized IDL software suite to fit the composite HARPS and FIES spectra with a grid of theoretical model spectra from Castelli & Kurucz (2004), Coelho et al. (2005), and Gustafsson et al. (2008), using spectral features that are sensitive to different photospheric parameters. Briefly, we used the wings of the Balmer lines to estimate the effective temperature of the star, and the Mg i 5167, 5173, and 5184 Å, the Ca i 6162 and 6439 Å, and the Na i D lines to determine log g∗. The iron abundance [Fe/H] and microturbulent velocity vmicro was derived by applying the method described in Blackwell & Shallis (1979) on isolated Fe i and Fe ii lines. We adopted the calibration equations for Sun-like dwarf stars from Doyle et al. (2014) to determine the macroturbulent velocity, vmacro. The projected rotational velocity vsini∗ was measured by fitting the profile of several clean and unblended metal lines.
The two analyses provided consistent results well within the errors bars, regardless of the method and spectrum used. The final adopted values – obtained as the weighted mean of the independent determinations – are listed in Table 4. We found Teff = 5225 ± 80 K, log g∗ = 4.4 ± 0.1 (cgs), vsini∗ = 5.7 ± 0.4 km s-1 and a considerably high iron content: [Fe/H] = +0.44 ± 0.10. Using the Straizys & Kuriliene (1981) calibration scale for dwarf stars, the effective temperature of CoRoT-33 translates to a G9 V spectral type.
3.3. Estimation of stellar parameters
The usual way to determine fundamental stellar parameters is to combine theoretical isochrones along with the measured mean density of the star, stellar metallicity and effective surface temperature. The mean density can be obtained from transit duration, the period and the impact parameter (e.g. Roberts 1899; Mochnacki 1981; Seager & Mallén-Ornelas 2003; Winn 2010). Stellar models are then selected that are able to reproduce the observed quantities. However, this method was found to be inadequate in our case because we have a grazing transit (see Sect. 3.4), and as a consequence, a low-transit depth-to-noise ratio.
Therefore the effective temperature, metallicity and log g∗ of the star were used to estimate the stellar mass and radius. We used the analytical stellar evolutionary tracks of Hurley et al. (2000) which have about 2% error relative to detailed numerical models, but are computationally fast. This yielded Mstar = 0.86 ± 0.04M⊙ and 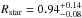 R⊙ for the stellar mass and radius, respectively. The age of the star is quite uncertain, but the object is definitely not young. This is supported by the fact that we did not find the presence of lithium in the spectrum. The lower age limit is 4.6 Gyr and, most likely the star has an age of 11 Gyr (see the derived stellar parameters in Table 4).
R⊙ for the stellar mass and radius, respectively. The age of the star is quite uncertain, but the object is definitely not young. This is supported by the fact that we did not find the presence of lithium in the spectrum. The lower age limit is 4.6 Gyr and, most likely the star has an age of 11 Gyr (see the derived stellar parameters in Table 4).
As a sanity check we calculated the stellar radius independently of the stellar models. If the stellar rotational axis is perpendicular to the orbital plane of the brown dwarf, then i∗ = 85.5° (cf. Sect. 3.4). Assuming that the 8.936 days modulation of the light curve is the stellar rotational period (cf. Sect. 3.5), then the stellar radius can be computed from 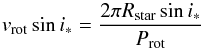 (2)resulting in Rstar = 1.06 ± 0.09R⊙. This is well within the uncertainty range of isochrone-based value of
(2)resulting in Rstar = 1.06 ± 0.09R⊙. This is well within the uncertainty range of isochrone-based value of 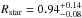 R⊙.
R⊙.
3.4. Transit light-curve analysis
To measure the transit parameters, we removed the stellar variability from the light curve using the following procedure. First, we applied a median filtering to replace the outliers. We then fit the flux variations in a narrow vicinity of the out-of-transit data (separately from transit to transit) with a parabola. All points in and out of transit were divided by the corresponding parabola. The width of the window which defined the “vicinity of the transit” was found by visual inspection after assuming various trial lengths: 1D, 1.5D, 2D, etc. up to 6D where D is the transit duration. A ± 2D window around each transit center was found to be the most appropriate.
The folded light curve using values binned by 201 s can be seen in Fig. 4.
The modeling of the transit light curve is challenging because of the faintness of the host star and small transit depth which result in a low S/N (transit depth/average noise level is ~1). We used Transit Light Curve Modeling Code (TLCM, written by SzCs) which utilizes the Mandel & Agol (2002) model to describe the transit light-curve shape. A genetic algorithm was used to optimize the fit (Geem et al. 2001) and the error estimation was carried out using a simulated annealing chain of 105 steps, starting from the best solution we found with the genetic algorithm procedure.
When scaled semi-major axis (a/Rstar) is treated as a free parameter, one gets the stellar mean density by rewriting Kepler’s 3rd law, 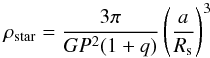 (3)where q = MBD/Mstar is the mass ratio. We find the star would have ρstar ~ 29 g cm-3 which is incompatible with the observed spectral type of G9V. The object G9V should have a mean density of about 1.27 g cm-3. This fit also leads to 0.44 Jupiter-radii for the brown dwarf which results in a mean density of ~834 g cm-3. This is unrealistically high as no brown dwarf is known to have a mean density higher 200 g cm-3 (cf. Table 1 and Ma & Ge 2014). These results are independent of how limb darkening is treated. In our case we used a quadratic limb darkening law fixed to values based on Sing’s (2010) tables. We also modeled the light curve allowing the limb darkening to vary as well as fixing one of the two limb darkening coefficients and allowing the other to be a free parameter.
(3)where q = MBD/Mstar is the mass ratio. We find the star would have ρstar ~ 29 g cm-3 which is incompatible with the observed spectral type of G9V. The object G9V should have a mean density of about 1.27 g cm-3. This fit also leads to 0.44 Jupiter-radii for the brown dwarf which results in a mean density of ~834 g cm-3. This is unrealistically high as no brown dwarf is known to have a mean density higher 200 g cm-3 (cf. Table 1 and Ma & Ge 2014). These results are independent of how limb darkening is treated. In our case we used a quadratic limb darkening law fixed to values based on Sing’s (2010) tables. We also modeled the light curve allowing the limb darkening to vary as well as fixing one of the two limb darkening coefficients and allowing the other to be a free parameter.
The transit depth is 0.28%, much shallower than the approximately 1% for a central transit of a Jupiter-sized brown dwarf around a late G-type star. The contamination by other stars in the photometric aperture does not explain the shallow transit depth. No additional contaminating source was revealed by the spectrum of the host star. The transit curve is V-shaped and the transit duration is just ~1.4 h, much shorter than the expected ~3 h for a centrally transiting short-period substellar object. This suggests that we have a grazing eclipse and the transiting object crosses the apparent stellar disk on a chord shorter than the diameter of the star.
The transit duration is (cf. Seager & Mallén-Ornelas 2003; Winn 2010): 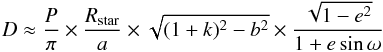 (4)where D is the measured transit duration (D = 1.4 ± 0.1 h), P is the orbital period, e is the eccentricity, ω is the argument of the periastron, k is the radius ratio and b is the impact parameter. All parameters are known from photometry or from spectroscopy, except k and b. Since the radius ratio must be positive we have the requirement of k> 0. Substituting the measured values, we get that this requirement is fulfilled only if b> 0.91. This kind of a high impact parameter means we must be dealing with a grazing transit scenario.
(4)where D is the measured transit duration (D = 1.4 ± 0.1 h), P is the orbital period, e is the eccentricity, ω is the argument of the periastron, k is the radius ratio and b is the impact parameter. All parameters are known from photometry or from spectroscopy, except k and b. Since the radius ratio must be positive we have the requirement of k> 0. Substituting the measured values, we get that this requirement is fulfilled only if b> 0.91. This kind of a high impact parameter means we must be dealing with a grazing transit scenario.
 |
Fig. 4 Light-curve solution (solid red line) and phase-folded, binned data points (black circles) of CoRoT-33b transits. Lower panel shows the residuals of the fit. Note that transit depth is only 0.28% on an R = 14.25 mag star. |
We conclude that the low S/N of the transit events prevents us from determining the transit shape with sufficient accuracy. We thus need to apply a penalty function (one may call a “prior”) to force the light-curve solution to converge to the right values: 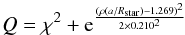 (5)and we minimized Q rather than χ2 of the light-curve fit. Here ρ represents the mean density of the star calculated for every iteration step of the fit via Eq. (3). The values 1.269 for the mean density and 0.210 for the width of the distribution are the mean density of the star and its uncertainty (in g cm-3), derived from the stellar mass and radius obtained in Sect. 3.2.
(5)and we minimized Q rather than χ2 of the light-curve fit. Here ρ represents the mean density of the star calculated for every iteration step of the fit via Eq. (3). The values 1.269 for the mean density and 0.210 for the width of the distribution are the mean density of the star and its uncertainty (in g cm-3), derived from the stellar mass and radius obtained in Sect. 3.2.
In addition to the low S/N, the impact parameter is high, and it is difficult to fit the limb darkening coefficients if the impact parameter is larger than ~0.85. Since the brown dwarf only crosses a fraction of the stellar disk, the transit center is no longer flat-bottomed and the inner contact points disappear (Müller et al. 2013; Csizmadia et al. 2013).
 |
Fig. 5 Window function of CoRoT-33. |
Another difficulty is connected to the fact that our theoretical knowledge of limb darkening is very poor close to the limb of the star. For instance, based on 38 Kepler light curves of transiting objects (12 of them are grazing), Müller et al. (2013) established that the quadratic limb darkening coefficients have a larger disagreement from the theoretically predicted values of Claret & Bloemen (2011) than the linear limb darkening coefficents2. Difficulties in the theoretical limb darkening laws occur mostly at the limb because of the quadratic term.
This is further illustrated by the fact that Claret & Bloemen (2011) and Sing (2010) used a plane-parallel stellar atmosphere model. When a more realistic spherically symmetric model is used, Neilson & Lester (2013) found a fast drop in the intensity close to the limb and the very edge of the star is predicted to be much darker than in Claret & Bloemen’s model (for comparison of the plane-parallel and spherically symmetric models, see Figs. 2−5 of Neilson & Lester 2013). Since none of these new models have been checked against a large sample of eclipsing binaries and transiting objects covering a wide range of stellar temperatures, it is too early to accept these as a final description of the limb darkening law. In addition, these theoretical models do not take the stellar spots and faculae into account which can modify the observable limb darkening coefficients (Csizmadia et al. 2013). We should note that we can see evidence of the presence of spots on CoRoT-33, thus it is an active star.
Therefore we carried out two light-curve fits with the Transit Light Curve Modeling Code (TLCM). During the fits, our free parameters were the scaled semimajor axis, the impact parameter3, the radius ratio and the epoch. The limb darkening combinations u+ = ua + ub and u− = ua − ub were fitted once (cf. Csizmadia et al. 2013 and Espinoza & Jordán 2015), and then for a second calculation they were fixed at theoretical values of Sing (2010). Eccentricity and argument of periastron could vary only within the limits of their uncertainties.
In the case of the adjusted limb darkening coefficients, the values of the coefficients are not constrained at all, but their uncertainties are large because of the low amplitude/noise ratio and the grazing transit. One cannot decide on a preferred solution based on the quality-parameter Q alone. Taking into account that the fixed limb darkening coefficient solution contains two less free parameters, we have chosen that solution for subsequent discussion in the paper.
Then a joint fit of RV- and light-curve data by Exofast (Eastman et al. 2013) with adjusted limb darkening coefficients was carried out. This confirmed our solution in Table 4. The parameters of this brown dwarf should be refined in the future using better photometric measurements obtained with larger telescopes.
The fit is shown in Table 4 and Fig. 4.
Results of three light-curve solutions of CoRoT-33.
3.5. Stellar variability analysis
The light curve of CoRoT-33 exhibits periodic and quasiperiodic flux variations with a peak-to-peak amplitude of about 3% (Fig. 1, upper panel). The Lomb-Scargle periodogram of the light curve is shown in Fig. 1. The strongest peak occurs at ν = 0.1117 d-1 (P = 8.95 d). Toward higher frequencies, there are two additional significant peaks at ν = 0.2248 d-1 (P = 4.44 d) and ν = 0.3337 d-1 (P = 3.00 d). The dominant peak is consistent with the expected rotational period, Prot of the star calculated using the spectroscopically measured rotational velocity and stellar radius. Therefore, this signal is most likely due to spots since CoRoT-33 should have a modest level of magnetic activity given its relatively fast rotation rate. Interestingly, this rotational period is ~3/2 × Porb. The other two peaks correspond to the first and second rotational harmonics (Prot/2, Prot/3, respectively). This probably reflects a complex pattern on the stellar surface. For instance, Prot/2 can result from two spot groups on opposite sides of the star.
Following the guidelines described in McQuillan et al. (2013) and revised in McQuillan et al. (2014), we use the autocorrelation function (ACF) to confirm these results. The ACF of the CoRoT-33 light curve shows a strong correlation peak at the rotational period of approximately nine days, consistent with the Lomb-Scargle periodogram, followed by a sequence of additional local maxima at integer multiples of this value. This is the result of the viewing geometry which repeats after multiple rotations (Fig. 1, lower panel). We estimate the position of the peaks by fitting Gaussian functions to the sequence of ACF maxima, and define the rotation period as the slope of a straight-line fit to the ACF peak positions as a function of peak numbers. This yields a stellar rotation period of Prot = 8.936 ± 0.015 days.
We also investigate the periodicities in the light curve using the package MUFRAN developed by Kolláth (1990). This software is an efficient tool for detecting periodic patterns in time series and is based on the Fourier transform.
Owing to temporal gaps in the data some false frequencies (aliases) can appear in the Fourier power spectrum. These alias frequencies are centered on the real signals offset from those peaks as indicated by the spectral window function of the Fourier transform. The spectral window (Fig. 5) indicates a negligible aliasing caused by the data sampling.
The Fourier amplitude spectrum of the whole data set is shown in Fig. 6 for this wide interval. The multiple peaks near 14 c/d are artifacts due to scattered earthshine arising from the 103 min orbit of the CoRoT satellite. For better visibility, the low-frequency part of the amplitude spectrum is shown in the insert of Fig. 6. This Fourier analysis confirmed the 8.936 day rotational period and the presence of its harmonics. The period analysis was carried out separately for the first and second half of the data set, too, and it showed that the main frequencies do not change with time.
 |
Fig. 6 Fourier amplitude spectrum of the light curve of CoRoT-33. Frequencies are in cycle/day units. The insert shows a zoom into the low-frequency part. |
3.6. Search for beaming effect
One can ask whether one of the frequencies in the Fourier spectra is related to beaming effect (Zucker et al. 2007). Mazeh & Faigler (2010) cleaned and binned the light curve to 100 points to see this effect in CoRoT-3. Unfortunately, we cannot follow their approach. We can estimate the magnitude of this effect using their formula: 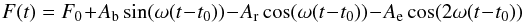 (6)where ω = 2π/Porbital, and Ab, Ar, Ae are the amplitudes of the beaming effect, the variation coming from reflected light and from the ellipsoidal shape of the star. All these effects act on the same time-scale, therefore we see a periodic signal at the orbital period and its half value. Using the formulae of Mazeh & Faigler (2010), we expect Ab = 94 ppm, Ar = 9 ppm, and Ae = 54 ppm for a total peak-to-peak amplitude of 231 ppm. Since the eccentricity is small, we can neglect its effect. Notice that these estimates are uncertain by several percent (Mazeh & Faigler 2010).
(6)where ω = 2π/Porbital, and Ab, Ar, Ae are the amplitudes of the beaming effect, the variation coming from reflected light and from the ellipsoidal shape of the star. All these effects act on the same time-scale, therefore we see a periodic signal at the orbital period and its half value. Using the formulae of Mazeh & Faigler (2010), we expect Ab = 94 ppm, Ar = 9 ppm, and Ae = 54 ppm for a total peak-to-peak amplitude of 231 ppm. Since the eccentricity is small, we can neglect its effect. Notice that these estimates are uncertain by several percent (Mazeh & Faigler 2010).
For an albedo of 0.1 and 0.9, the equilibrium temperature of the brown dwarf object would be between 1400−800 K in this system. Baraffe et al. (2003) predicts a surface temperature of 1100−1200 K for a brown dwarf with a mass and age consistent with our object. Thus the brown dwarf contributes only 0.2 ppm to the observed visible light so it can be neglected.
Using the approximate formula of Aigrain et al. (2009), we get that the two hours average noise level of CoRoT at the magnitude of CoRoT-33 is about 365 ppm (not taking the aging of the CCD detector into account). This means that we have to apply very strong binning to see the effect. To detect this signal at a S/N of 3 we had to apply a binning of two days. Therefore we choose a different approach from that of Mazeh & Faigler (2010); namely we utilize the Fourier-spectrum.
The cleaned light curve was taken again and a five-point median-filtering was carried out. We discovered a significant peak at 5.93 ± 0.32 days with an amplitude of 318 ppm in the Fourier-spectrum after a cleaning process. This peak is significant at the 13σ level (its significance was estimated by using Eq. (21) of Kjeldsen & Frandsen 1992). Its amplitude is 50% bigger than our expectation for the peak at the orbital period, but the expectation is also uncertain by several percent. Although this peak is quite close to the orbital period, it can also be identified as a harmonic of the rotational period of the star; the period ratio of this peak and the stellar rotational period is exactly 1.5. Further study is required to separate the stellar rotational modulation and the beaming effects.
3.7. A search for occultations
A brown dwarf in a close-in orbit may be occulted by the parent star (e.g. Winn 2010) which could be helpful to constrain the impact parameter and other properties of the system with higher accuracy. We searched for these kinds of occultations of the brown dwarf in the light curve of CoRoT-33 using a Bayesian model selection (e.g. Kass & Raftery 1995; Gregory 2010), wich are similar to the approaches used in Parviainen et al. (2013; 2014) and Gandolfi et al. (2015). The stellar variability was taken into account using Gaussian processes (Roberts et al. 2013; Gibson et al. 2011; Rasmussen et al. 2006). The nonzero orbital eccentricity means that the impact parameter for the occultation, bo, can be significantly different than the impact parameter for the transit, bt, or there might be no occultation. The technical details of this search are given in the Appendix. Our analysis was unable to find the occultation signal. The missing occultation signal can also be consistent with Baraffe et al.’s (2003) models.
4. Tides and stellar rotational properties
The rotation period is small for a G9V star of its age. The braking associated with the activity of a G9V star is not as efficient as it should be if we take the single-star scenario of Bouvier et al. (1997) or Mamajek & Hillenbrand (2008). Because of the heavy companion orbiting the star at a short distance, the tidal torques on the star are strong enough to accelerate the stellar rotation. Several factors concur to make this system one of the best suitable for the study of the interplay of magnetic braking and tidal evolution: the high mass of CoRoT-33b, the short distance from it to the star, and the age of the system.
The simulations done by Ferraz-Mello et al. (2015) show that in a system like CoRoT-33, the magnetic braking may be very efficient in the beginning and this drives the rotational period to a value somewhat larger than the current observed stellar rotational period, when braking and tidal evolution equilibrate themselves. Subsequently, the system evolves losing energy, and the companion orbit spirals down toward the star and both the orbital period of the companion and the rotation period of the star slowly decrease for the remaining life of the system, and it can possibly reach such commensurability just by chance. The fact that the orbital period and the stellar rotation period are strikingly close to the 2/3 ratio is not predicted in usual spin-orbit dynamical theories. Béky et al. (2014) listed six systems with a hot Jupiter where the planet and the star exhibit similar synchronization between these periods. They consider that the stellar differential rotation profile may happen to include a period at some latitude that is commensurable to the planetary orbit. These influence the displacement of the star features responsible for the periodic variation of the light of the star. The quality of our characterization of CoRoT-33 is in favors of it playing a key role in the study of these sorts of interactions and their influence on the tidal evolution of the system.
5. Conclusions
We report the detection of a transiting 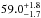 Jupiter-mass brown dwarf that orbits a G9V star in ~5.82 days. This is the 10th transiting object in the so-called brown dwarf desert not counting the transiting double brown dwarf system 2M0535-05 here). This desert is starting to be populated by more and more objects in recent years. The radius of the brown dwarf is 1.10 ± 0.53 Jupiter radii and its mean density is 55 ± 29 g cm-3. The object is close to the 65 MJup limit which separates the lower mass, deuterium-burning brown dwarfs from the higher mass, lithium-burning brown dwarfs. The host star seems to be an evolved, old, metal-rich star. The radius of the brown dwarf is not known to high precision because of a grazing transit. On the other hand, the mass is measured with higher accuracy from the RV observations, and its mass uncertainty is dominated by the uncertainty in the stellar mass. Better photometric precision using larger telescopes is required to improve the radius and thus density determination.
Jupiter-mass brown dwarf that orbits a G9V star in ~5.82 days. This is the 10th transiting object in the so-called brown dwarf desert not counting the transiting double brown dwarf system 2M0535-05 here). This desert is starting to be populated by more and more objects in recent years. The radius of the brown dwarf is 1.10 ± 0.53 Jupiter radii and its mean density is 55 ± 29 g cm-3. The object is close to the 65 MJup limit which separates the lower mass, deuterium-burning brown dwarfs from the higher mass, lithium-burning brown dwarfs. The host star seems to be an evolved, old, metal-rich star. The radius of the brown dwarf is not known to high precision because of a grazing transit. On the other hand, the mass is measured with higher accuracy from the RV observations, and its mass uncertainty is dominated by the uncertainty in the stellar mass. Better photometric precision using larger telescopes is required to improve the radius and thus density determination.
The statistical analysis of 65 brown dwarf companions to stars with orbital period less than 100 days by Ma & Ge (2014) showed that their host stars are not metal rich stars. This may be related to a different formation scenario of brown dwarfs compared to giant planets. The host stars of giant planets seem to be more metal rich (Johnson et al. 2010). However, CoRoT-33 is metal rich with [Fe/H] = +0.44 ± 0.10 and its abundance may exceed the previous record holder, HAT-P-13 with [Fe/H] = 0.41 ± 0.08 (Bakos et al. 2009; Ma & Ge 2014)4.
The light curve of CoRoT-33 shows a rotational modulation with a period of 8.936 d with a peak-to-peak amplitude of ~3%. This measured rotational period agrees with the calculated value based on the vsini∗ measurement and its stellar radius from isochrones (assuming i∗ ≈ iBD). The Fourier spectrum is complex, making the target ideal for future studies of spot activity on this star. In particular, multicolor photometry using large telescopes can help to determine the spot temperatures.
The rotational period of the star is very close to the 2:3 commensurability with the orbital period of the companion brown dwarf and this system is an interesting test case for checking and calibrating theories of the physical interactions between one star and a close-in companion. This relatively old system shows an eccentric orbit; the study of the tidal evolution of this system (Ferraz-Mello et al. 2015) shows that because of the distance between the brown dwarf and the star (0.0626 AU), an existing initial eccentricity is not damped to zero during the stellar lifetime, however, the presently observed rotational period of the star cannot be explained without taking the interplay between magnetic braking of the star and tidal forces into account.
One can assume that close-in hot Jupiters and brown dwarfs have the same transit detection bias since they both have approximately the same radius. Therefore, the ratio of the number of these detected systems should reflect the respective number frequencies of these objects. Until now, three brown dwarfs (CoRoT-3b, -15b and 33b) have been detected from the CoRoT data, and 21 hot and normal Jupiters (CoRoT-1b, -2b, -4b, -5b, -6b, -9 – -14b, 16b – -21b, -23b, 25b – -29b) most with periods P< 10 days5. The relative frequency, based on the CoRoT-sample and hence the observational biases are removed, is of ≈14%, but one has to take into account that so far we have only a small sample statistic.
If we take all transit surveys, then the brown dwarf/hot Jupiter ratio falls down to 0.05%. For instance, the WASP survey has detected one brown dwarf (see Table 1) and 96 hot Jupiters. HAT-P-survey has detected 33 hot Jupiters and none with a mass exceeding 8 MJup; there is no transiting brown dwarf in the HAT-P-sample (see also footnote 4). It is not well known how the targets for follow-up and the stellar samples are selected in these surveys. Better statistics should come from Kepler once the follow-up measurements for the transit candidates are completed which may resolve the discrepancy between ground-based and CoRoT observations. A major factor can be that ground-based surveys are biased for the detection of transits smaller than 1%.
 |
Fig. 7 Occurrence rate of brown dwarfs as companions to solar-like stars vs. orbital separation (a). Horizontal lines denote the found occurrence rates and the orbital separation range investigated while vertical lines denote the error bars. Different colors mark different studies; black is Metchev & Hillenbrand (2009); blue is Lafreniére et al. (2007), Grether & Lineweaver (2006), orange is Sahlmann et al. (2011), brown is Wittenmyer et al. (2009), violet is Patel et al. (2007), red is this study. These rather rough estimates indicate a tendency: the occurrence rate increases with increasing orbital separations. |
The true occurrence rate of hot Jupiters is 1.2 ± 0.4% around FGK dwarf stars for periods P< 10 days (Wright et al. 2012). Thus, the relative frequency of brown dwarfs to hot Jupiters can be scaled to the true frequency which means that the actual occurrence rate of brown dwarfs as companions to FGK dwarfs would be ~0.2% in the short period (P< 10 days) range. This is much smaller than the frequency rate of brown dwarfs as FGK companions at larger distance (see Introduction). One can plot the different brown dwarf occurrence rate estimates mentioned in the Introduction and determined here as a function of the star-companion distance. The result is shown in Fig. 7. A fit to those data yielded that the brown dwarf occurrence rate (f) around FGK dwarfs can be characterized roughly as 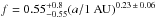 , where a is the semimajor axis of the orbit. This result is not robust yet because the occurrence rate estimates suffer from small number statistics, but a tendency might be visible already. More observational studies are needed to establish the occurrence rate-orbital separation relationship for solar-like star+brown dwarf pairs.
, where a is the semimajor axis of the orbit. This result is not robust yet because the occurrence rate estimates suffer from small number statistics, but a tendency might be visible already. More observational studies are needed to establish the occurrence rate-orbital separation relationship for solar-like star+brown dwarf pairs.
The early indication is that the occurrence rate of close-in brown dwarf (P< 10 days) is six times smaller than that of hot Jupiters in the same period range. It is not clear whether this relative occurrence rate is a consequence of the primordial conditions (i.e., much fewer brown dwarfs were formed in the protoplanetary disk than giant planets), or is caused by the higher efficiency of engulfing the companion by the host stars due to fast spiralization, as Armitage & Bonnell (2002) presumed. It is also possible that observational biases act: for instance, CoRoT’s stellar sample or its follow-up strategy or its higher photometric precision than ground-based surveys were simply more sensitive to brown dwarfs.
For larger sized planets, the planet-frequency decreases for shorter periods (Dong & Zhu 2013). The brown dwarfs seems to follow the same pattern, too, but we think there is an indication that the frequency of close-in brown dwarfs drops more steeply than that of close-in giant planets. However, further detection studies are needed to establish the true frequency of close-in brown dwarfs.
See at http://www.johnstonsarchive.net/astro/browndwarflist.html). The DwarfArchive.org project, maintained by C. Gelino, D. Kirkpatrick, M. Cushing, D. Kinder, A. Burgasser (http://spider.ipac.caltech.edu/staff/davy/ARCHIVE/index.shtml) tabulates 1281 L, T and Y dwarfs but it does not contain information about the masses and radii of the catalogued objects. The Johnston’s catalogue reports radius values for 191 brown dwarfs, but most of these were obtained by several different and often indirect methods, e.g. model-fitting to the spectral energy distributions. Radii of brown dwarfs measured by direct methods are listed in Table 1.
Their limb darkening formula that we also use is I = I0 − u1(1 − μ) − u2(1 − μ)2, where I0 is the intensity at the center of the apparent stellar disk, u1,u2 are the linear and quadratic limb darkening coefficients, respectively; μ = cosγ; and γ is the angle between the line of sight and the surface normal vector at the stellar surface point.
The brown dwarf HAT-P-13c is not transiting, it was detected by RV (Bakos et al. 2009).
Acknowledgments
The team at IAC acknowledges support by grant AYA2012-39346-C02-02 of the Spanish Secretary of State for R&D&i (MICINN). R.A. acknowledges the Spanish Ministry of Economy and Competitiveness (MINECO) for the financial support under the Ramón y Cajal program RYC-2010-06519. This research has made use of the ExoDat database, operated at LAM-OAMP, Marseille, France, on behalf of the CoRoT/Exoplanet program. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research has made use of NASA’s Astrophysics Data System. L. Szabados was supported by the ESTEC Contract No. 4000106398/12/NL/KML. The first author thanks the Hungarian OTKA Grant K113117. The German CoRoT Team (TLS and the University of Cologne) acknowledges DLR grants 50 OW 204, 50 OW 0603 and 50QP07011. This research has benefited from the M, L, T, and Y dwarf compendium housed at DwarfArchives.org. H.P. has received support from the Leverhulme Research Project grant RPG-2012-661. A.S. is supported by the European Union under a Marie Curie Intra-European Fellowship for Career Development with reference FP7-PEOPLE-2013-IEF, number 627202 and by Fundação para a Ciência e a Tecnologia (FCT) through the research grant UID/FIS/04434/2013. J.M.A. acknowledges support by CNES grant 251091. The prompt and valuable report of an anonymous referee is acknowledged.
References
- Aigrain, S., Pont, F., Fressin, F., et al. 2009, A&A, 506, 426 [Google Scholar]
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, D. R., Collier Cameron, A., et al. 2011, ApJ, 726, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J., & Bonnell, I. A. 2002, MNRAS, 330, 11 [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2007, in AIP Conf. Ser. 895, eds. C. Dumitrache, N. A. Popescu, M. D. Suran, & V. Mioc, 201 [Google Scholar]
- Bakos, G. Á., Howard, A. W., Noyes, R. W., et al. 2009, ApJ, 707, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 2002, A&A, 382, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., et al. 2003, A&A, 402, 701 [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béky, B., Holman, M. J., Kipping, D. M., & Noyes, R. W. 2014, ApJ, 788, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., & Shallis, M. J. 1979, MNRAS, 186, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Bonomo, A. S., Chabaud, P. Y., Deleuil, M., et al. 2012, A&A, 547, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonomo, A. S., Sozzetti, A., Santerne, A., et al. 2015, A&A, 575, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Deleuil, M., Guillot, T., et al. 2011a, A&A, 525, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Bonomo, A. S., Santerne, A., et al. 2011b, A&A, 533, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Forestini, M., & Allain, S. 1997, A&A, 326, 1023 [NASA ADS] [Google Scholar]
- Brewer, J. M., Fischer, D. A., Basu, S., Valenti, J. A., & Piskunov, N. 2015, ApJ, 805, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Bakos, G. A., Hartman, J. D., et al. 2010, ApJ, 720, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, ArXiv e-prints [arXiv:astro-ph/0405087] [Google Scholar]
- Chabrier, G., Baraffe, I., & Plez, B. 1996, ApJ, 459, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Johansen, A., Janson, M., & Rafikov, R. 2014, in Protostars & Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & Th. Henning (University of Arizona Press), 619 [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coelho, P., Barbuy, B., Meléndez, J., et al. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csizmadia, Sz., Pasternacki, T., Dreyer, C., et al. 2013, A&A, 549, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deleuil, M., Deeg, H. J., Alonso, R., et al. 2008, A&A, 491, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deleuil, M., Meunier, J. C., Moutou, C., et al. 2009, AJ, 138, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, R. F., Damiani, C., Deleuil, M., et al. 2013, A&A, 551, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Montagnier, J. L., Bonomo, A. A., et al. 2014, A&A, 572, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dong, S., & Zhu, Zh.-H. 2013, ApJ, 778, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, A. P., Davies, G. R., Smalley, B., et al. 2014, MNRAS, 444, 3592 [NASA ADS] [CrossRef] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J., Gaudi, B. S., & Agol, E. 2013, PASP, 125, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., & Jordán, A. 2015, MNRAS, 450, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraz-Mello, S., Tadeu dos Santos, M., Folonier, H., et al. 2015, ApJ, 807, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Frandsen, S., & Lindberg, B. 1999, in Astrophysics with the NOT, Proceedings, eds. H. Karttunen, & V. Piirola (Piikkio, Finland: University of Turku), 71 [Google Scholar]
- Fuhrmann, K., Chini, R., Hoffmeister, V. H., et al. 2011, MNRAS, 411, 2311 [NASA ADS] [CrossRef] [Google Scholar]
- Gandolfi, D., Parviainen, H., Deeg, H. J., et al. 2015, A&A, 576, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gardes, B., Chabaud, P. Y., & Guterman, P. 2011, Proc. of the 2nd CoRoT Symposium, 119 [Google Scholar]
- Geem, Z. W., Kim, J. H., & Lonatathan, G. V. 2001, Simulation, 76, 60 [CrossRef] [Google Scholar]
- Gibson, N. P.Aigrain, S., Roberts, S., et al. 2011, MNRAS, 419, 2683 [Google Scholar]
- Gregory, Ph. 2010, Bayesian Logical Data Analysis for the Physical Sciences (Cambridge University Press) [Google Scholar]
- Grether, D., & Lineweaver, Ch. H. 2006, ApJ, 640, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W. & Crepp, J. R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Apps, K., Gazak, J. Z., et al. 2011, ApJ, 730, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, J. Am. Stat. Assoc., 90, 773 [Google Scholar]
- Kjeldsen, H., & Frandsen, S. 1992, PASP, 104, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Kolláth Z. 1990, Occasional Technical Notes, Konkoly Obs., Budapest, No. 1, http://www.konkoly.hu/Mitteilungen/Mitteilungen.html#TechNotes [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., et al. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kurucz, R. L. 2013, Astrophysics Source Code Library, [record ascl:1303.024] [Google Scholar]
- Lafreniére, D., Doyon, R., Marois, Ch., et al. 2007, ApJ, 670, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, B., & Ge, J. 2014, MNRAS, 439, 2781 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E., & Hillenbarnd, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mazeh, T., & Faigler, S. 2010, A&A, 521, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metchev, S. A., & Hillenbrand, L. A. 2009, ApJS, 181, 62 [NASA ADS] [CrossRef] [Google Scholar]
- McQuillan, A., Aigrain, S., & Mazeh, T. 2013, MNRAS, 432, 1203 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mészáros, Sz., Allen de Prieto, C., Edvardsson, B., et al. 2012, AJ, 144, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Mochnacki, S. W. 1981, ApJ, 245, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Bonomo, A. S., Bruno, G., et al. 2013, A&A, 558, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. M., Huber, K. F., Czesla, S., et al. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., & Lester, J. B. 2013, A&A, 556, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parviainen, H., Deeg, H. J., & Belmonte, J. A. 2013, A&A, 550, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parviainen, H., Gandolfi, D., Deleuil, M., et al. 2014, A&A, 562, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasternacki, T., Bordé, P., & Csizmadia, Sz. 2011, Proc. of the 2nd CoRoT Symp., 117 [Google Scholar]
- Patel, S. G., Vogt, S. S., Marcy, G. W., et al. 2007, ApJ, 665, 744 [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., et al. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Rasmussen, C. E., & Williams, Ch. 2006, Gaussian processes (The MIT Press) [Google Scholar]
- Roberts, A. 1899, ApJ, 10, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, S., Osborne, M., Ebden, M., et al. 2013, Phil. Trans. A. Math. Phys. Eng. Sci., 371, 20110550 [Google Scholar]
- Sahlmann, J., Ségransan, D., Queloz, D., et al. 2011, A&A, 525, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D., 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K. 2010, A&A, 510, A21 [Google Scholar]
- Siverd, R. J., Beatty, T. G., Pepper, J., et al. 2012, ApJ, 761, 123 [Google Scholar]
- Spiegel, D. S., Burrows, A., & Milsom, J. A. 2011, ApJ, 727, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Straizys, V., & Kuriliene, G. 1981, Ap&SS, 80, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Surace, C., Alonso, R., Barge, P., et al. 2008, in SPIE Conf. Ser., 7019, 3 [Google Scholar]
- Stassun, K. G., Mathieu, R. D., & Valenti, J. A. 2006, Nature, 440, 311 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Telting, J. H., Avila, G., Buchhave, L., et al. 2014, Astron. Nach., 335, 41 [Google Scholar]
- Torres, G., Fischer, D. A., Sozzetti, A., et al. 2012, ApJ, 757, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Fischer, D. A., 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Valenti, J. A., & Piskunov, N., 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt, S. S., Butler, R. P., Marcy, G. W., et al. 2002, ApJ, 568, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N. 2010, ArXiv e-prints [arXiv:1001.2010] [Google Scholar]
- Wittenmyer, R. A., Endl, M., Cochran, W. D., et al. 2009, AJ, 137, 3529 [Google Scholar]
- Wright, J. T., Marcy, G. W., Howard, A. W., et al. 2012, ApJ, 753, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Zakamska, N. L., Pan, M., & Ford, E. B. 2011, MNRAS, 410, 1895 [NASA ADS] [Google Scholar]
- Zucker, S., Mazeh, T., & Tal, A. 2007, ApJ, 670, 1326 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Bayesian model selection
Here we describe our methodology which was used for searching the possible occultation of the brown dwarf.
We consider two models, M0 without an occultation signal and M1 with an occultation signal. We also use the Bayes factor B10, the ratio of the Bayesian evidences ZM, to assess whether the occultation model is significantly preferred over the non-occultation model. The evidence ZM for a model M is calculated by marginalizing the posterior probability over the model parameter space, 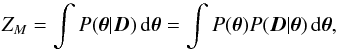 (A.1)where θ is the model-specific parameter vector, D is the observational data, P(θ | D) is the posterior probability density, P(θ) is the prior density, and P(D | θ) is the likelihood for the observational data.
(A.1)where θ is the model-specific parameter vector, D is the observational data, P(θ | D) is the posterior probability density, P(θ) is the prior density, and P(D | θ) is the likelihood for the observational data.
We assume the photometric noise to be normally distributed, and express the likelihood as 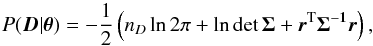 (A.2)where nD is the number of data points, Σ is the covariance matrix, and r is the observed-measured residual vector. The covariance matrix elements are defined by the Gaussian process (GP) covariance kernel, k(xi,xj,φ), where x are input parameter vectors for each data point, and φ is a kernel hyperparameter vector.
(A.2)where nD is the number of data points, Σ is the covariance matrix, and r is the observed-measured residual vector. The covariance matrix elements are defined by the Gaussian process (GP) covariance kernel, k(xi,xj,φ), where x are input parameter vectors for each data point, and φ is a kernel hyperparameter vector.
We only use one GP input parameter, mid-exposure time. We decided not to marginalize over the GP hyperparameters (we fix them to values optimized to the light-curve), but we did decide to use two different GP kernels to assess the sensitivity of our analysis on the choice of kernel. The two kernels used were the squared exponential (SE) kernel  (A.3)and the exponential (E) kernel
(A.3)and the exponential (E) kernel 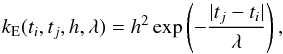 (A.4)where t is the mid-exposure time, h is the output scale, and λ is the input scale. The SE kernel leads to infinitely-differentiable smooth functions, while the E kernel leads to once-differentiable functions allowing for sharper changes (which is a more realistic choice considering the noise properties of CoRoT light curves).
(A.4)where t is the mid-exposure time, h is the output scale, and λ is the input scale. The SE kernel leads to infinitely-differentiable smooth functions, while the E kernel leads to once-differentiable functions allowing for sharper changes (which is a more realistic choice considering the noise properties of CoRoT light curves).
Parameterization and priors
We construct the priors for the orbital parameters and radius ratio based on the corresponding marginal posteriors from the transit and RV modeling, which leaves the surface flux ratio as the only truly unconstrained parameter.
In parallel with the main model selection analysis, we carry out a more explorative occultation search by mapping the B10-space as a function of sliding prior on ω. This corresponds roughly to making n model comparisons for a set of propositions, each differing in the prior set on ω. We use an uniform prior defined by its center and width, and let the prior center slide from 0 to 2π.
Appendix B: Results
We did not find support for the occultation model over the no-occultation model when we constrain ω using a prior based on RV and transit modelling. The geometry, ω ~ 180°, combined with the high impact parameter makes the detection of even a very strong signal unlikely.
The mapping of B10 as a function of ω results in a tentative occultation signal candidate near 270°, as shown in Fig. B.1. The result is curious, since this is the only geometry where an occultation could in theory be detected, while a false signal of instrumental or astrophysical origin could present itself anywhere in ω-space. However, the small number of orbits covered combined with the faintness of the signal candidate makes this impossible to confirm. If the occultation signal were to be real, it would be discrepant with the RV observations. This could be alleviated if the RV observations were to contain an unknown noise source, but the increase in the uncertainty per RV observation would need to be around 0.2−0.3 km s-1.
 |
Fig. B.1 Differences between the M0 and M1 log posterior samples with the SE kernel (corresponding to the log posterior ratios) for a set of 15 000 posterior samples mapped as a function of argument of periastron (angle). A uniform prior from 0 to 2π has been set on ω, and all the parameters have been drawn from their corresponding priors. The shown value, sample log posterior difference, does not correspond to the Bayesian evidence Z, but is used as an explorative tool. The radial spread in the difference between ω values of π and 2π is explained by the orbital geometry. The occultation signals are stronger within this interval than on the other half, and the data is able to exclude these signals leading to small log posterior ratio. The occultation signals between ω of 0 and π are too faint to be excluded by the data, and the with-occultation corresponds to the occultation model within uncertainties. |
The two GP kernels yield very similar results, meaning our analysis is not sensitive to the choice of the GP kernel.
All Tables
All Figures
 |
Fig. 1 Upper panel: full CoRoT light curve of CoRoT-33. The gray points represent the median-normalized raw data points after a 5-point width median filtering. We only used data points with flag “0” for this curve. The red line is a convolution of the raw light curve with a Savitzky-Golay filter that enhances the light-curve variations. Middle panel: Lomb-Scargle periodogram of the light curve of CoRoT-33. The horizontal dashed line denotes the 0.01% false-alarm probability (Scargle 1982). The vertical red line marks the rotation period of the star. Lower panel: autocorrelation function (ACF) of light curve, following the subtraction of the best fitting transit model. The red dashed line marks the peak corresponding to the rotation period of CoRoT-33 (see Sect. 3.5). |
| In the text | |
 |
Fig. 2 Finding chart and contamination source map for CoRoT-33. Red numbers denote stars whose contribution to the observed flux was taken into account; yellow numbers denote stars whose contamination was checked but was found negligible. Star with number 0 corresponds to CoRoT-33. |
| In the text | |
 |
Fig. 3 Upper panel: phase-folded RV measurements of CoRoT-33. Red circles represent the HARPS-measurements while green circles are the data points obtained by FIES-instrument. Black solid line represents the eccentric orbit fit. The RV points and the fit is shifted by the γ-velocity of the system. Lower panel: it shows the residuals of the fit. Vertical lines on the data points indicate their error bars. |
| In the text | |
 |
Fig. 4 Light-curve solution (solid red line) and phase-folded, binned data points (black circles) of CoRoT-33b transits. Lower panel shows the residuals of the fit. Note that transit depth is only 0.28% on an R = 14.25 mag star. |
| In the text | |
 |
Fig. 5 Window function of CoRoT-33. |
| In the text | |
 |
Fig. 6 Fourier amplitude spectrum of the light curve of CoRoT-33. Frequencies are in cycle/day units. The insert shows a zoom into the low-frequency part. |
| In the text | |
 |
Fig. 7 Occurrence rate of brown dwarfs as companions to solar-like stars vs. orbital separation (a). Horizontal lines denote the found occurrence rates and the orbital separation range investigated while vertical lines denote the error bars. Different colors mark different studies; black is Metchev & Hillenbrand (2009); blue is Lafreniére et al. (2007), Grether & Lineweaver (2006), orange is Sahlmann et al. (2011), brown is Wittenmyer et al. (2009), violet is Patel et al. (2007), red is this study. These rather rough estimates indicate a tendency: the occurrence rate increases with increasing orbital separations. |
| In the text | |
 |
Fig. B.1 Differences between the M0 and M1 log posterior samples with the SE kernel (corresponding to the log posterior ratios) for a set of 15 000 posterior samples mapped as a function of argument of periastron (angle). A uniform prior from 0 to 2π has been set on ω, and all the parameters have been drawn from their corresponding priors. The shown value, sample log posterior difference, does not correspond to the Bayesian evidence Z, but is used as an explorative tool. The radial spread in the difference between ω values of π and 2π is explained by the orbital geometry. The occultation signals are stronger within this interval than on the other half, and the data is able to exclude these signals leading to small log posterior ratio. The occultation signals between ω of 0 and π are too faint to be excluded by the data, and the with-occultation corresponds to the occultation model within uncertainties. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.