| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 15 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201423781 | |
| Published online | 13 November 2015 | |
Emergence of non-twisted magnetic fields in the Sun: Jets and atmospheric response
1 Reasearch Center for Astronomy and Applied Mathematics, Academy of Athens, 4 Soranou Efessiou Str., 11527 Athens, Greece
e-mail: psyntelis@phys.uoa.gr
2 Section of Astrophysics, Astronomy and Mechanics, Department of Physics, University of Athens, Panepistimiopolis, Zografos, 15784 Athens, Greece
3 School of Mathematics and Statistics, St. Andrews University, St. Andrews, KY16 9SS, UK
Received: 7 March 2014
Accepted: 8 August 2015
Aims. We study the emergence of a non-twisted flux tube from the solar interior into the solar atmosphere. We investigate whether the length of the buoyant part of the flux tube (i.e. λ) affects the emergence of the field and the dynamics of the evolving magnetic flux system.
Methods. We perform three-dimensional (3D), time-dependent, resistive, compressible magnetohydrodynamic (MHD) simulations using the Lare3D code.
Results. We find that there are considerable differences in the dynamics of the emergence of a magnetic flux tube when λ is varied. In the solar interior, for larger values of λ, the rising magnetic field emerges faster and expands more due to its lower magnetic tension. As a result, its field strength decreases and its emergence above the photosphere occurs later than in the smaller λ case. However, in both cases, the emerging field at the photosphere becomes unstable in two places, forming two magnetic bipoles that interact dynamically during the evolution of the system. Most of the dynamic phenomena occur at the current layer, which is formed at the interface between the interacting bipoles. We find the formation and ejection of plasmoids, the onset of successive jets from the interface, and the impulsive heating of the plasma in the solar atmosphere. We discuss the triggering mechanism of the jets and the atmospheric response to the emergence of magnetic flux in the two cases.
Key words: Sun: activity / Sun: interior / Sun: magnetic fields / magnetohydrodynamics (MHD) / methods: numerical
© ESO, 2015
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0),
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0),
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Active region formation and dynamic phenomena on the Sun have been associated with magnetic flux emergence from both a theoretical and observational perspective (e.g. Parker 1955; Tsinganos 1980; Priest 1982; Zwaan 1985; Shibata 1999; Archontis et al. 2004; Schrijver 2009). In numerical flux emergence models, a typical initial condition for the subphotospheric magnetic field is a twisted magnetic flux tube, which undergoes a buoyant rise towards the solar surface.
The buoyant rise is initiated by removing plasma density along the flux tube axis in a Gaussian manner (Δρ ∝ exp(−y2/λ2)). The length of the buoyant part of the flux tube (commonly denoted by λ) is an important parameter that affects the emergence of the flux tube and the following dynamics. For instance, Fan (2001) performed an experiment of a flux tube with λ = 20 (i.e. ≈3 Mm), which emerged into the solar atmosphere. Manchester et al. (2004), used the same initial conditions as Fan (2001), but with half the length of the buoyant section of the flux tube (λ = 10). They found that the decrease in λ results in more efficient plasma draining. In addition, they found the formation of a new flux rope at the low atmosphere due to the shearing and reconnection of the fieldlines across the polarity inversion line (PIL). Archontis & Hood (2010) studied the effect of different field strengths, twist, and λ to the formation of magnetic tails. For a highly twisted flux tube with high field strength, located at the upper convection zone, they changed the buoyant part of the flux tube from λ = 10 to λ = 20. This resulted in less magnetic tension on field lines of the higher λ during the initial emergence, leading to relatively faster emergence.
Another parameter that plays a major role in the emergence and the dynamics of flux tubes is the twist of the magnetic field. In many twisted flux tube models (e.g. Fan 2001; Magara & Longcope 2003; Archontis et al. 2005), the field lines wind about the axis of the tube in a uniform manner. A common setup for such axisymmetric flux tubes is to assume that the flux tube has a component of its magnetic field along its axis (Baxis) and an azimuthal component that is proportional to Baxis (i.e. Bφ ∝ αBaxis). This parameter α measures the twist of the magnetic field per unit of length. It also defines the pitch angle between the magnetic field vector and the axis of the flux tube. Highly twisted flux tubes with pitch angle greater than 45° would become kink unstable (Linton et al. 1996; Fan et al. 1999).
Concerning the ability of low-twist magnetic fields to emerge above the photosphere, simulations have indicated that the flux tubes can become fragmented into two counter-rotating vortices during their emergence (Schuessler 1979). This fragmentation can be suppressed by the addition of a sufficient amount of twist (e.g. Moreno-Insertis & Emonet 1996). On the other hand, by performing simulations with different perturbations of specific entropy in the flux tube, Abbett et al. (2000) found that even when the twist of the initial tube is not sufficient, the tube can remain coherent provided it has sufficiently large curvature at its rising apex. Abbett et al. (2001) found that the Coriolis force also suppresses the degree of fragmentation of the apex of the emerging flux tube. Also, if the magnetic field is much stronger than the equipartition value of the magnetic field in the convection zone, the buoyancy force dominates over the convective downdrafts, and the flux tube can emerge unimpeded (Fan et al. 2003). Failed emergence of flux tubes with low twist have been reported in several studies. Murray et al. (2006) performed experiments of flux tubes with λ = 20, for different values of twist (α = 0.1−0.4) and found that the highly twisted flux tube (α = 0.4) emerged into the atmosphere forming a bipolar region on the photosphere. Flux tubes with intermediate twist (α = 0.2) emerged forming two bipolar regions (like the “sea serpent” configuration) on the photosphere. Weakly twisted flux tubes (α = 0.1) failed to emerge above the photosphere. Instead, they continued to expand horizontally inside the solar interior. Toriumi & Yokoyama (2011) also studied the emergence of flux tubes with λ = 20 (and similar initial conditions to Murray et al. 2006) for a wider range of twists (α = 0.05−0.5) and found similar results to Murray et al. (2006). Those results indicate that weakly twisted flux tubes struggle to emerge above the photosphere.
The effect of λ (which affects the curvature of the emerging part of flux tube) on the emergence of weakly twisted flux tubes was studied by Archontis et al. (2013). They used similar initial conditions to Murray et al. (2006) and Toriumi & Yokoyama (2011) for a flux tube with α = 0.1, but assumed half the length of the buoyant part of the flux tube (λ = 10). In this case, the weakly twisted flux tube did not fail to emerge above the photophere. Instead, the flux tube formed two bipolar regions on the photosphere (similar to the α = 0.2 case of Murray et al. 2006). Above the two bipoles, the expanding magnetic field formed two magnetic lobes. The interaction of the lobes triggered several reconnection jets and created an envelope field that confined them. The shearing motion and reconnection of field lines along the PIL led to the formation of a highly twisted flux rope, which remained at the low atmosphere during the running time of the simulation.
In this paper, we advance the work by Archontis et al. (2013) on the emergence of weakly twisted fields by adding two key elements: firstly, we use a non-twisted flux tube and secondly, we study the effect of λ on the overall dynamics of the emerging flux system. The use of a non-twisted flux tube (α = 0) is chosen because non-twisted fields are more susceptible to distortion and/or fragmentation and, consequently, to an overall failed emergence. Furthermore, we want to examine whether the emergence of a non-twisted magnetic field can create twisted magnetic structures in the solar atmosphere, similar to the post-emergence flux ropes formed at the weakly twisted case by Archontis et al. (2013).
This paper is organized in the following manner. In Sect. 2 we describe the initial conditions of the experiments. In Sect. 3, we study the case of λ = 10 in terms of its initial emergence, the dynamics of the interaction between the formed magnetic bipoles, the coronal response, and the energy and flux transfer into the atmosphere. In Sect. 4, we study the λ = 5 case with respect to the same aspects and compare the results with the λ = 10 case. In Sect. 5, we summarize the results.
 |
Fig. 1 a) Initial stratification of the atmosphere (temperature (T), density (ρ), magnetic pressure (Pm), and gas pressure (Pg)). b) Instability term at the center of the EFR and c) at the center of the bipole at y = 4.8 Mm. |
2. Initial conditions and numerical code
 |
Fig. 2 a) Magnetogram at the mid-photosphere (z = 0.8 Mm) at t = 169 min. For simplicity, we call A, D the outer polarities and B, C the inner polarities. b) Field lines traced from the bipoles at t = 169 min. |
In order to study the emergence and evolution of the non-twisted flux tube, we solve the 3D time-dependent, resistive, compressible magnetohydrodynamic (MHD) equations in Cartesian geometry. We use the Lare3D code of Arber et al. (2001) to solve numerically the equations. The equations in dimensionless form are  where ρ, v, B, and P are density, velocity vector, magnetic field vector, and gas pressure. Gravity is included. We use constant explicit resistivity (η) such that the magnetic Reynolds number is Rm = 100. We assume perfect gas specific heat of γ = 5/3. Viscous heating Qvisc and Joule dissipation Qjoule are also included.
where ρ, v, B, and P are density, velocity vector, magnetic field vector, and gas pressure. Gravity is included. We use constant explicit resistivity (η) such that the magnetic Reynolds number is Rm = 100. We assume perfect gas specific heat of γ = 5/3. Viscous heating Qvisc and Joule dissipation Qjoule are also included.
The dimension constants we use are, density ρc = 1.67 × 10-7 g cm-3, temperature Tc = 5100 K, pressure Pc = 7.16 × 103 erg cm-3, length Hc = 180 km and magnetic field strength Bc = 300 G. From the above units we get velocity v0 = 2.1 km s-1 and time t0 = 85.7 s The numerical box consists of an adiabatically stratified subphotospheric layer at −3.6 Mm ≤ z< 0 Mm, an isothermal photospheric-chromospheric layer at 0 Mm ≤ z< 1.9 Mm, a transition region at 1.9 Mm ≤ z< 3.2 Mm and an isothermal coronal at 3.2 Mm ≤ z< 25.2 Mm.
We assume to have a field-free atmosphere in hydrostatic equilibrium. The initial distribution of temperature (T), density (ρ), gas (Pg) and magnetic (Pm) pressure is shown in Fig. 1a.
For the initial magnetic field, we assume a horizontal cylindrical non-twisted magnetic flux tube located at 2.1 Mm below the photosphere. The axis of the flux tube is oriented along the y-direction, so the transverse direction is along x and height is in the z-direction.
The axial field of the tube is  (6)where R = 450 km is a measure of the tube’s radius and r the radial distance from the tube axis. In order to make the flux tube to emerge, we assume a density distribution similar to the work by Archontis et al. (2004), which makes the middle part of the flux tube less dense and thus buoyant. The density deficit is
(6)where R = 450 km is a measure of the tube’s radius and r the radial distance from the tube axis. In order to make the flux tube to emerge, we assume a density distribution similar to the work by Archontis et al. (2004), which makes the middle part of the flux tube less dense and thus buoyant. The density deficit is  (7)where p is the external pressure and pt is the pressure within the flux tube (magnetic plus gas). The parameter λ is the length scale of the buoyant part of the flux tube. In our numerical experiments, we use λ = 5 (0.9 Mm) and λ = 10 (1.8 Mm). The field strength of the flux tube is B0 = 2780 G.
(7)where p is the external pressure and pt is the pressure within the flux tube (magnetic plus gas). The parameter λ is the length scale of the buoyant part of the flux tube. In our numerical experiments, we use λ = 5 (0.9 Mm) and λ = 10 (1.8 Mm). The field strength of the flux tube is B0 = 2780 G.
The computational box has a size of 28.8 × 28.8 × 28.8 Mm in the x, y, z directions, in a 457 × 457 × 457 grid. The resolution is such that, in the sites with steep field gradients (e.g. current layers), the magnetic Reynolds number is (on average) larger than the effective Reynolds number. This indicates that the explicit resistivity dominates numerical effects. We assume open boundary conditions in the x direction, periodic boundary conditions y direction, and a wave damping zone for z> 26 Mm, which decays exponentially the velocity, gas pressure and density fluctuations.
3. Case of λ =10
In this section we describe the λ = 10 case. We study the emergence of the flux tube through the highly stratified atmosphere and the onset of the associated dynamic phenomena in the EFR.
3.1. Initial emergence of the flux tube
As the magnetic field emerges from the solar interior, the flux tube reaches the photosphere where it becomes compressed. In order for the flux tube to emerge above the photosphere, it has to satisfy the buoyancy instability criterion (Acheson 1979; Archontis et al. 2004)  (8)where Hp is the pressure scale-height, B is the magnitude of the magnetic field, γ = 5/3 is the specific heats ratio, β is the plasma parameter, δ = −0.4 is the superadiabatic excess and k are the perturbation wavenumbers, where k∥ and k⊥ are the horizontal components parallel and vertical to the magnetic field, and kz is the vertical component. To calculate these wavenumbers, we measure the size of the flux tube sections below the photosphere. We find lx ≈ 0.5 Mm and ly ≈ 1.4 Mm and approximately the radius of the tube as the vertical width lz ≈ 0.45 Mm. These estimates are taken at t = 154 min. The corresponding wavevector components are k∥ ≈ 4.5 × 10-8 cm-1, k⊥ ≈ 1.2 × 10-7 cm-1 and kz ≈ 1.4 × 10-7 cm-1. Since the wavevector term in the instability criterion is small (4.6 × 10-15 cm-2) in comparison to the β term (which has minimum values of 10-12), we neglect it, and after dividing the inequality with its right part, we get approximately:
(8)where Hp is the pressure scale-height, B is the magnitude of the magnetic field, γ = 5/3 is the specific heats ratio, β is the plasma parameter, δ = −0.4 is the superadiabatic excess and k are the perturbation wavenumbers, where k∥ and k⊥ are the horizontal components parallel and vertical to the magnetic field, and kz is the vertical component. To calculate these wavenumbers, we measure the size of the flux tube sections below the photosphere. We find lx ≈ 0.5 Mm and ly ≈ 1.4 Mm and approximately the radius of the tube as the vertical width lz ≈ 0.45 Mm. These estimates are taken at t = 154 min. The corresponding wavevector components are k∥ ≈ 4.5 × 10-8 cm-1, k⊥ ≈ 1.2 × 10-7 cm-1 and kz ≈ 1.4 × 10-7 cm-1. Since the wavevector term in the instability criterion is small (4.6 × 10-15 cm-2) in comparison to the β term (which has minimum values of 10-12), we neglect it, and after dividing the inequality with its right part, we get approximately: 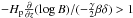 . We refer to the left side of this equation as the “instability term”.
. We refer to the left side of this equation as the “instability term”.
At the center (around x = 0,y = 0,z = 0) of the EFR, the field magnitude decreases as the flux tube expands. At the areas sideways of the center, along the y-direction, the field is compressed, leading to a smaller gradient of the magnetic field and a lower β. This makes the instability term greater than 1 in these areas, while it remains below unity around the center of the EFR. Thus, the flux tube does not emerge at the center of the EFR, but it forms two side bipoles, as shown in Fig. 2a. In Figs. 1b, c we plot the temporal evolution of the instability term at two positions in the numerical box. In Fig. 1b, we calculate the instability term at the center of the EFR. We confirm that the field does not emerge at this region (Fig. 2a). The flux tube becomes unstable at two areas along the flux tube axis, at (x,y) = (0, ± 4.8 Mm). There, the instability term becomes greater than 1 (Fig. 1c, calculated at y = 4.8 Mm). This leads to the emergence of two bipolar regions.
At t = 169 min (Fig. 2a), the two bipoles have emerged into the photosphere. Hereafter, we refer to polarities A, D as outer polarities, and B, C as inner polarities. During the evolution, the polarities at each bipoles expand along the y-direction. At the photosphere, the fieldlines that join the two polarities of each bipole are almost horizontal due to the absence of twist. If the flux tube was twisted, we would have detected magnetic “tails” on the two sides of the PIL in each bipole (e.g. López Fuentes et al. 2000; Chandra et al. 2009). As the magnetic field rises above the photosphere, the magnetized volume of each bipole expands and the attached magnetic field lines form two magnetic bipoles (Fig. 2b).
3.2. Interaction of the magnetic bipoles
In the following, we study the effect of the interaction of the magnetic bipoles on the solar atmosphere. Firstly, we focus on the formation of plasmoids and jets, and secondly on the transfer of plasma and flux into the solar atmosphere.
3.2.1. Jets and plasma transfer
After t = 171 min, the two magnetic bipoles come into contact and a current layer is formed at their interface. Eventually, the long and thin current layer becomes subject to the tearing mode instability. Thus, plasmoids are formed within the interface and later on they are ejected out of it. This induces inflows towards the interface and initiates effective reconnection of the oppositely directed fieldlines of the bipoles into contact. The dynamics of plasmoids in a similar configuration (i.e. interaction between two individual twisted flux tubes) was studied by Archontis et al. (2007). Figure 3 shows the overall topology of the fieldlines at a later stage of the evolution, when two new magnetic flux systems (apart from the two magnetic bipoles) have been developed. More precisely, reconnected fieldlines join the two outer polarities forming the envelope field (Fig. 3, orange lines) and reconnected fieldlines join the inner polarities forming an arcade-like structure (Fig. 3, red lines). Because of the emergence of the field and the gravitational draining of the plasma, low-atmosphere material accumulates at the interface, filling the area with cool and dense plasma (Fig. 3, green color around interface in the yz-plane).
In Fig. 4a, we plot the temporal evolution of maximum (black) and minimum (red) Vz above the photosphere. Up to t ≈ 240 min we find moderate upflows/downflows (5–10 km s-1) due to the emergence of the two bipoles and the draining of the plasma at the periphery of the magnetic bipoles respectively. The first major upflow occurs at t = 242 min (marked with a vertical dashed line). This is associated with the ejection of a plasmoid from the interface current layer into the corona. The ejection is driven by the tension of the reconnected fieldlines at the interface. The ejected plasmoid is cool (≈ 105 K) and dense (1−2 orders of magnitude heavier than the background plasma in the corona). During the evolution of the system, several plasmoids are formed and eventually being ejected from the 3D interface. The ejection of the plasmoids is followed by (fast) reconnection of fieldlines at the interface and the emission of a series of bi-directional flows (jets). The occurence of the bi-directional jets is shown in Fig. 4a for t ≥ 242 min.
 |
Fig. 3 Grayscale: Bz component of the magnetic field at the mid-photosphere (z = 0.9 Mm), ranging from −40 G to 40 G. Colored scale: density at yz-midplane, ranging from 1.7 × 10-14 g cm-3 (red) to 1.7 × 10-16 g cm-3 (blue). The lines correspond to fieldlines connecting the bipoles (blue), fieldlines of the arcade (red) and fieldlines of the envelope field (orange). Time is t = 250 min. |
Figure 4b shows the maximum temperature and density around the locations of maximum Vz. We find that the temperature evolution of the temperature is also highly impulsive. In fact, there is a very good temporal correlation between the bi-directional flows and the sudden temperature enhancements, which is an indication of a reconnection-driven plasma acceleration at the interface. The impulsive behavior shows that there are many jets, which are emitted from the interface, during the interaction of the magnetic bipoles. The first three high-speed jets occur in the period t ≈ 240−260 min. They have temperatures in the range 1−1.5 MK and densities between 10-16−10-15 g cm-3 (Fig. 4b) and, thus, they might account for soft X-ray jets. The following jets (for t ≥ 260 min) are (in general) less energetic, with velocities up to ≈50 km s-1 (with an exception, at t ≈ 295 min, where Vz ≈ 100 km s-1) and temperatures lower than 1 MK. The general decay of the onset of high-speed jets is due to the gradual decrease in the available flux and energy of the system that drives the ejections. The available energy comes only from the emerging magnetic field. Thus, this energy is limited and it unavoidably becomes exhausted.
 |
Fig. 4 a) Temporal evolution of maximum (black) and minimum (red) Vz above the photosphere. Vertical dashed lines correspond to the emission of the bi-directional jets at t = 242,248,257 min. b) Maximum temperature (black) and density (blue) around the locations of maximum Vz. |
 |
Fig. 5 The Vz component of the velocity field on the yz-midplane. Field lines show the projection of the full magnetic field vector onto that plane. a) Prior to plasmoid ejection at t = 242 min. b) Jet ejection at t = 248 min. |
Figure 5a is a close-up of the interface showing the upward motion of the plasmoid before the onset of the first bi-directional jet. The colorscale shows the vertical component of the velocity field and the overplotted fieldlines (black lines) show the projected magnetic field vector onto the plane. The fieldlines reveal the existence of the plasmoid (magnetic “island” in the 2D plane) at the interface. The upflow (red color) illustrates the upward motion (ejection) of the plasmoid at t = 242 min. The topology of the fieldlines show that the ejection is indeed driven by the tension of the V-shaped reconnected fieldlines underneath the plasmoid. The downward product of reconnection is the emission of a weaker downflow (blue color) and the formation of the O-shaped arcade.
Figure 5b shows the emission of a strong bi-directional jet after the expulsion of the plasmoid out of the interface. Now, the fieldlines from the interacting bipoles come into direct contact (since the plasmoid in between them has been disposed) at the interface and reconnect. This is reminiscent of the plasmoid-induced reconnection scenario, suggested by Yokoyama & Shibata (1994). The V-like reconnected fieldlines, which are released upwards, accelerate the reconnection outflow (jet). The downward-released fieldlines are added to the arcade, which thus, undergoes an apparent rising motion and it grows in size.
Figure 6a–c show the plasma dynamics during the emission of the reconnection jet at t = 248 min. The bi-directional flow starts at a coronal height (z ≈ 4.5 Mm). The upward reconnection flow runs with a velocity of 190 km s-1 and it carries relatively dense and hot (≥1.0 MK) plasma into the corona (6a, 6b). It reaches a height of ≈10 Mm, where it collides with the envelope field and it is diverted into two side flows, which run with velocities of ≈68 km s-1. Figure. 6c is a close-up of the reconnection region showing clearly the inflows towards the reconnection site, which are enhanced after the ejection of the plasmoid, and the profound hot, bi-directional jet driven by reconnection.
 |
Fig. 6 Density a) and temperature (b), c)) distribution at the vertical yz-midplane. Overplotted is the projection of the velocity field vector onto the plane. Bottom: a close-up of the reconnection site. |
3.2.2. Undulation of the PIL, fieldline topology and structure of the jets
 |
Fig. 7 a)Bz component of the magnetic field at the mid-photosphere (z = 0.9 Mm), with the velocity field overplotted at t = 243 min and b)t = 286 min. c) Fieldlines traced around the center of the EFR at t = 243 min, showing the arcade. Overplotted is the full magnetic field vector colored by the Bz component of the field at z = 0.9 Mm. Red is positive and blue is negative. The red rectangular inset marks the same region as the one in b). d) Fieldlines at t = 286 min, showing the deformation of the PIL. e) Isosurface of Vz> 60 km s-1 showing the V-shaped jet at t = 248 min. f) The emission of several jets at t = 286 min (isosurface of Vz> 60 km s-1). |
 |
Fig. 8 Visualization of the heating term (H) at t = 268 min for plasma having temperatures between a) 0.01−1 MK and b) 1−10 MK. |
One of the interesting features in this experiment is the evolution of the arcade structure at the interface. To study this, we firstly show the temporal evolution of the Bz distribution at the middle of the photosphere (Figs. 7a, b). Initially (Fig. 7a, t = 243 min), the inner polarities collide and the PIL in between them becomes almost perfectly aligned with the x-axis at the center of the emerging flux region. However, later we find that the PIL adopts an undulating shape (Fig. 7b, t = 286 min). The overplotted velocity field on this plane shows that the deformation of the PIL is associated with plasma motions along the y-axis, towards the PIL. A similar deformation was reported in the work by Archontis & Hood (2010): the tails of the magnetic field on the two sides of the PIL suffered by converging flows (inflows), which were produced due to the rapid expansion of the field above the photosphere. Here, we find that a similar process is at work. The finger-like segments, which are developed across the PIL, are sites with low density and pressure. At this height (z = 0.9 Mm), the magnetic field is also weak and the kinetic energy density is such that the magnetic field is advected towards the PIL. The low pressure at various points is produced due to the rapid ejection of several dense plasmoids from along the interface. The plasma then moves towards the low-pressure areas (inflows), deforming the PIL.
Figure 7c shows the 3D topology of the fieldlines around the arcade before the deformation (t = 243 min). Overplotted is the full magnetic field vector at the photosphere, colored by the vertical (Bz) component (red is positive, blue is negative). The arcade consists of fieldlines that join the inner polarities all along the PIL. The fieldines have been traced from random positions within the two inner polarities. We note that the fieldlines of the arcade towards its two ends (along the x-direction) are more inclined than the fieldlines at the middle of the arcade. This is due to the fan-like shape of the interacting fieldlines of the two magnetic bipoles. We also note the cusp-like shape at the top of the arcade’s fieldlines. This indicates the occurrence of reconnection above them. Left and right from the arcade, we find expanding fieldlines that belong to the interacting bipoles. Envelope fieldlines are not shown in this figure.
Figure 7d shows the topology of the fieldlines around the deformed PIL at t = 286 min. We note that after the deformation, the magnetic fieldlines becomes highly twisted all along the PIL. Some segments of the PIL are now oriented along the y-axis. For instance, the segment which is outlined by the red rectangular inset in Fig. 7d, is the same with the segment around x = −0.5 Mm and between y = −1 Mm and y = 1 Mm in Fig. 7b. Now, the relative motion of the inflows on the two sides of this segment induce a shearing (Fig. 7b, motions towards negative y-axis and positive y-axis around x = −0.3 Mm, as the positive (negative) inner polarity moves towards the negative (positive) polarity). The sheared and oppositely directed fieldlines across the PIL’s segment reconnect, producing a small twisted flux rope and a reconnection jet. This process occurs at several (similar) segments along the PIL, providing an additional source of twist for the fieldlines around the PIL and triggering the onset of more jets at the interface. Thus, we find that the deformation of the PIL leads to the parallel emission of new jets from the interface. The highly intermittent evolution of Vz for t> 280 min in Fig. 4a is due to this effect.
The 3D structure of the emitted jets before and after the deformation of the PIL is shown in Figs. 7e, f. In Fig. 7e we show the 3D structure of the t = 248 min jet, by visualizing the total velocity field as an isosurface (red color) with V> 60 km s-1. At low heights, the reconnection upflow has the shape of a sharp wedge with its length oriented vertically, above the reconnection site. At larger heights, it becomes confined by the envelope field and becomes diverted into two lateral flows, following the reconnected fieldlines. Thus, the overal configuration of the upward jet adopts a V-like shape. The magnetic fieldlines (white), which have been traced from within the lateral parts of the jet illustrate the envelope field. We also identify the two magnetic bipoles and the arcade underneath the reconnection site. At this time of the evolution, the downward reconnection jet is much weaker and, thus, it appears as a horizontal ribbon-like structure just above the arcade. Overplotted is the full magnetic field vector (horizontal cut) at z = 0.9 Mm.
In Fig. 7f, we visualize the total velocity field as an isosurface with V> 60 km s-1 at t = 311 min. The striking difference is the appearance of several jets (here, four jets) from the interface. All the upward jets have similar V-like shapes. The parallel emission of several hot jets from the interface starts after the deformation of the PIL and it is followed by intermittent heating of the plasma at the interface. The latter is discussed more in the following section.
3.2.3. Intermittent heating at the solar atmosphere
To study how much and where the dense plasma is heated during the emission of the jets, we calculate the term:  (9)We do the calculation for temperatures in the range of 0.01−1 MK and 1−10 MK, as a preliminary attempt to separate the cooler (i.e. <1 MK) from the hotter component of the plasma (i.e. >1 MK). Hereafter, for simplicity, we call this term the “heating term”. Figure 8 shows the heating term after the emission of the first four successive jets (i.e. at t = 268 min), during which the temperature enhancement of the associated plasma is more pronounced (see Fig. 4b).
(9)We do the calculation for temperatures in the range of 0.01−1 MK and 1−10 MK, as a preliminary attempt to separate the cooler (i.e. <1 MK) from the hotter component of the plasma (i.e. >1 MK). Hereafter, for simplicity, we call this term the “heating term”. Figure 8 shows the heating term after the emission of the first four successive jets (i.e. at t = 268 min), during which the temperature enhancement of the associated plasma is more pronounced (see Fig. 4b).
In the lower temperature regime (Fig. 8a), we find that heating is more evident in a fan-like arcade, which extends (vertically) from the chromosphere to the low corona. The arcade is formed by the reconnected fieldlines, which are released downwards, after the onset of the jets at the interface. The fan-like shape is formed naturally due to the 3D lateral expansion of the interacting magnetic bipoles and it is in agreement with the 3D shape of the arcade shown in Fig. 7c.
In the higher temperature regime (Fig. 8a), the heating is not smoothly distributed across the arcade, but it is much more intermittent. There are four small scale (<1 Mm) brightenings, which all occur within the area between the chromosphere and the transition region. These brightenings occur exactly under the reconnection sites of the four bi-directional jets, which were emitted during the t = 240−260 min period. The reconnection, which triggers the jets, occurs mainly in the corona. However, the downward jet(s) collide with the top of the arcade forming a termination shock. There, the plasma is compressed locally at high temperatures, causing heating of the dense material.
A very similar process, regarding the intermittent heating, was reported in recent more realistic simulations (radiative transfer, MHD) numerical experiments (Archontis & Hansteen 2014). In those simulations, small-scale flaring activity was produced at the current sheets between interacting magnetic loops. The small flares were triggered by plasmoid-induced reconnection at the interface current layers. In the present work, we are witnessing an analogous process: patchy reconnection associated with the ejections of plasmoids leads to plasma heating, which resembles the onset of nano-micro flares in the model by Archontis & Hansteen (2014). The present model does not include all the necessary energy terms (radiative transfer, heat conduction, radiation, etc.) for a complete treatment of the thermodynamical behavior of the system. The lack of these terms affects the estimated value of temperature (e.g. of the jets) in the present experiments.
 |
Fig. 9 a) Temporal evolution of the Poynting flux. Solid lines show the emergence term, Femergence, and dashed lines show the shearing term, Fshear. b) The unsigned magnetic flux Φxy. c) The axial flux for the bipole’s center in the positive y-direction (bipole AB). d) Flux difference ΔΦxz. The dashed vertical line marks the initiation of the undulation of the PIL and the dotted vertical lines show the times for the onset of the hight-speed jets. |
3.2.4. Energy transfer and magnetic flux
To study the transfer of flux into the solar surface and above, we first calculate the Poynting flux. We split it into the “emergence term”, which is the part of flux representing the direct emergence of the magnetic field, and the “shear term”, which represents the flux due to the horizontal motions (Kusano et al. 2002; Magara & Longcope 2003):  We calculate these fluxes at the mid-photosphere (z0 = 0.8 Mm), the base of the transition region (z0 = 2 Mm) and the low corona (z0 = 3.2 Mm).
We calculate these fluxes at the mid-photosphere (z0 = 0.8 Mm), the base of the transition region (z0 = 2 Mm) and the low corona (z0 = 3.2 Mm).
In Fig. 9a, we plot the emergence term (solid line) and the shearing term (dashed line). At the mid-photosphere (black), we find the emergence term to be greater than the shearing term between t = 140−155 min, as expected during the beginning of the emergence. The shearing term becomes greater than the emergence term, when the inner polarities collide. Owing to this collision, plasma is pushed sideways along the PIL and towards the x-direction, contributing to the shearing term (e.g. Fig. 7a, flows along the PIL). Both terms reach their maximum value at t ≈ 200 min and soon thereafter start to decrease. The drop in the two terms is due to the fact that the dynamical emergence and expansion of the field becomes less pronounced at the later stage of the evolution of the system. At larger heights (blue lines), we find that the shearing term is more dominant due to the expansion of the field.
To study the vertical flux transfered at the same heights, we calculate the unsigned magnetic flux through the xy-plane,  (12)At the photosphere, Φxy increases monotonically until t = 255 min (Fig. 9b, black line). The drop of the flux thereafter is evidence of flux cancellation at the photosphere, even during the deformation of the PIL after t = 260 min. Measuring Φxy at larger heights (red and blue lines) shows that less vertical flux is transported higher, as expected.
(12)At the photosphere, Φxy increases monotonically until t = 255 min (Fig. 9b, black line). The drop of the flux thereafter is evidence of flux cancellation at the photosphere, even during the deformation of the PIL after t = 260 min. Measuring Φxy at larger heights (red and blue lines) shows that less vertical flux is transported higher, as expected.
We also calculate the normalized axial flux through the xz-plane at a position y0, from the heights (z0) up to the top of the numerical box (zmax), i.e.  (13)We calculate this axial flux at y0 = ± 6 Mm, which are located around the center of the bipoles. We find the same flux at both locations, meaning that the same amount of axial flux emerges at both bipoles. In Fig. 9c, we plot this flux for the bipole center in the positive y-direction. An interesting result is that for each bipole, only 12% of the initial axial flux emerges above the photosphere (black line). From this, only 7.5% gets above the corona (blue line). Adding the axial flux of the two bipoles, a sum of 24% of the initial flux emerges above the photosphere and 15% above the corona. Thus, this study shows that non-twisted subphotospheric fields with these characteristics are not capable of transfering a considerable amount of flux above the photosphere.
(13)We calculate this axial flux at y0 = ± 6 Mm, which are located around the center of the bipoles. We find the same flux at both locations, meaning that the same amount of axial flux emerges at both bipoles. In Fig. 9c, we plot this flux for the bipole center in the positive y-direction. An interesting result is that for each bipole, only 12% of the initial axial flux emerges above the photosphere (black line). From this, only 7.5% gets above the corona (blue line). Adding the axial flux of the two bipoles, a sum of 24% of the initial flux emerges above the photosphere and 15% above the corona. Thus, this study shows that non-twisted subphotospheric fields with these characteristics are not capable of transfering a considerable amount of flux above the photosphere.
Owing to the non-twisted magnetic field in our initial conditions, there is only positive By at the beginning of the simulation. The emergence and expansion of the field forms the Bx and Bz components. In our configuration, negative By component at the xz-midplane could be formed through reconnection. This component is part of the arcade’s magnetic field lines. In order to estimate how much negative By is created on this plane, we calculate the normalized flux difference:  (14)Here ΔΦxz measures only the flux of negative By through the xz-midplane, from a height z0 up to the top of the numerical box zmax, normalized by the initial positive flux before the emergence. So, ΔΦxz indicates how much of the initially positive flux is transformed into negative flux, through reconnection. This calculation is valid only at the xz-midplane and due to the absence of twist.
(14)Here ΔΦxz measures only the flux of negative By through the xz-midplane, from a height z0 up to the top of the numerical box zmax, normalized by the initial positive flux before the emergence. So, ΔΦxz indicates how much of the initially positive flux is transformed into negative flux, through reconnection. This calculation is valid only at the xz-midplane and due to the absence of twist.
Figure 9d shows above the mid-photoshere (black line), flux difference increases after t = 170 min. This is due to reconnection at the interface. This leads to the formation of new fieldlines that point in the negative y-direction, joining the two inner polarities, and forming the arcade. We find that ΔΦxz increases rapidly after the major ejections (dotted vertical lines), peaking after the t = 240−260 min series of jets. This maximum shows that 2.6% of the initial By flux of the system is transformed into negative By. In the corona (blue line), we only find 0.3% of the flux. As a result, most of the post-reconnection flux at the interface resides between the photosphere and the low corona.
After t = 260 min (vertical dashed line), we find that ΔΦxz starts to decrease drastically. This is when the deformation of the PIL starts to occur (Figs. 7b, d). At this moment, the interface cannot be studied by using the 2D vertical xz-midplane, and ΔΦxz does not represent an accurate measurement of the normalized flux difference. This happens because, as we described previously, the field lines of the arcade follow the deformation of the PIL (Fig. 7d). Thus, some of the field lines which were previously perpendicular to the interface, they are now pointing towards the x-direction due to the undulation (e.g. Fig. 7b, lines around x = ± 0.3 Mm would tend to be parallel to the x-axis). As a result, their By (Bx) component decreases (increases), and consequently, ΔΦxz decreases. Also, the field lines that do not rotate, tend to move away from the xz-plane due to the flows in the y-direction (e.g. around the EFR center, PIL position is located x = 0, y ≈ 1.3 Mm). This further decreases By on the xz-midplane, and contributes to the decrease in ΔΦxz.
 |
Fig. 10 First row: z component of the forces along the vertical direction (x = 0, y = 0) at t = 3 min, for a) λ = 10 and b) λ = 5. Second row: temporal evolution of c) z-component of the magnetic tension and d) magnetic pressure, measured at the center of the flux tubes. We plot the quantities until the flux tubes reach the photosphere. |
4. Case of λ = 5 and comparison with λ = 10
In the following, we describe the emergence of the non-twisted flux tube with λ = 5, and make a comparison to the λ = 10 case.
4.1. Emergence from the solar interior to the photosphere
 |
Fig. 11 Forces and flux tube cross sections of λ = 10 and λ = 5, before they reach the photosphere (at t = 26 min and at t = 34 min respectively). (a), d)) Pmag of the flux tubes at the y = 0 cross section. The solid white lines (horizontal and vertical) pass through the flux tubes centers. Black Pmag contours have the same values in both panels. Vertical white dashed lines mark the position of the flux tube’s outer part. (b), e)) z-component of forces along the vertical direction through the flux tube’s center (direction marked with the vertical solid white line in (a), d))). Green is gas pressure force minus gravity force, orange is magnetic pressure force, red is magnetic tension force and black the total force. (c),f)) The x-component of forces along the horizontal direction through the flux tube’s center (direction marked with the horizontal solid white line in (a), d))). |
In the following, we firstly show the differences between the two λ cases when both flux tubes are located in the solar interior. In our experiments we apply a density deficit perturbation, which is practically controlled by λ (Eq. (7)). In order to study how different λ affects the initial emergence from the solar interior to the photosphere, we examine the cross section of the flux tubes at the vertical xz-midplane (i.e. y = 0). There, both flux tubes are equally buoyant (same Δρ in Eq. (7), since the pressure balance terms are the same for both cases).
At t = 0 min, the two flux tubes have equal forces applying to them (at y = 0) along the vertical z-axis. In Figs. 10a, b we plot for λ = 10 and λ = 5 respectively the z-component of the forces along the z-axis at t = 3 min. We find that: (i) the gas pressure force minus the gravitational force (green line) and (ii) the magnetic pressure force (orange line) are approximately equal in both cases. On the other hand, the magnetic tension force (red line) shows a distinctive difference from the beginning of the emergence. For λ = 5, the tension is higher because the apex of the buoyant part of the tube is more convex. Thus, the lower tension case experiences higher total force (black), making the flux tube to reach the photosphere faster than the one with higher tension and lower total force. Indeed, by comparing the apex positions of the flux tubes, we find that the λ = 10 flux tube reaches the photosphere at t = 26 min while the λ = 5 at t = 34 min. Figure 10c shows the temporal evolution of the z-component of the magnetic tension at the center of the flux tubes, until the flux tubes reach the photosphere. We find that the tension is up to 3 times higher for smaller λ (dashed line) throughout the initial emergence. As a result, the high tension of smaller λ continuously decelerates the emergence of the flux tube.
This faster emergence of the higher λ flux tube, causes it to expand more in the vertical direction. Therefore, it leads to a faster drop of its gas and magnetic pressure in comparison to that of λ = 5. In Fig. 10d, we plot the magnetic pressure Pm at the center of the flux tubes. We plot this quantity until the moment each flux tube reaches the photosphere. Indeed we find that for λ = 5 (dashed line), the flux tube has higher magnetic pressure at its center than for λ = 10 (solid line).
Figures 11a and d show the magnetic pressure at the xz-midplane (for λ = 10 and λ = 5, respectively) when the flux tubes reach the photosphere (at different times). The solid white lines indicate the vertical and horizontal directions through the flux rope’s center. As we showed before, the faster vertical emergence leads to lower internal pressure for the higher λ flux tube. This is apparent again by examining the z and x components of the forces along the vertical and horizontal direction through the center of the flux tube (Figs. 11b, c for λ = 10 and Figs. 11e, f for λ = 5).
Along the vertical direction, the comparison of the forces (Figs. 11b, e) shows again that the magnetic tension is higher for λ = 5. We find that both the gradient of gas (green line) and magnetic pressure (orange line) are lower for λ = 10, indicating the faster drop of pressure due to the faster emergence.
The comparison of the horizontal expansion of the flux tubes (dashed lines in Figs. 11a, d) indicates that λ = 10 expands more. Indeed, the x-component of the total force in the horizontal direction (black line Figs. 11c, f) shows that total force is higher for λ = 10. The forces that mainly act on the flux tube in the horizontal direction are the outward magnetic pressure, trying to expand the flux tube, and the inward gas pressure. In our initial flux tube, we have no twist, so initially there is no tension in the transverse direction. Still some inward tension is developed (red lines) due to the expansion of the flux tube and possibly due to internal reconnection of the field lines during this initial emergence.
An important result arises from the interior of the flux tubes during the initial emergence. Notice the contours in Figs. 11a, d. It is apparent that the λ = 5 case emerges coherently. On the other hand, the λ = 10 case develops two minor lobes in its interior. The lobes are formed as the center of the emerging flux rope starts to split in two parts. This also affects the plasma density in these regions. Density becomes lower in the vicinity of the lobes (due to higher magnetic pressure) and higher in the center of the flux rope (where the magnetic pressure drops). As a result we find outward directed gas pressure force (i.e. towards the lobes) in the interior of the λ = 10 flux tube (around −0.4 Mm <x< 0.4 Mm, Fig. 11c).
A similar behavior has been reported in previous studies of emerging flux tubes (e.g. Schuessler 1979; Longcope et al. 1996; Moreno-Insertis & Emonet 1996). Those studies showed that the cross section of rising flux tube was distorted through the interaction with the background non-magnetized medium. More precisely, they found that the emerging flux tube displaced the plasma above it and forced it to flow from the apex to the flanks of the tube. This created a drag that deformed the cross section of the flux tube and eventually created two counter-rotating vortices. In our numerical simulations (e.g. λ = 10 case) the appearance of the two minor lobes just before the flux rope reaches the photosphere (Fig. 11a). On the other hand, it seems that in the λ = 5 case this lobe formation is inhibited and the flux rope emerges as a whole, without distortion (Fig. 11d).
To further investigate the possible role of λ in the coherence of the flux tube during the emergence in the solar interior, we also performed simulations for λ = 15 and λ = 20. In Fig. 12 we plot the magnetic pressure of the cross section of the flux tubes on the xz-midplane before the flux tubes reach the photosphere, for each λ. The black contours show Pmag. To do a closer comparison between the different λ cases, we show the same value of Pmag. The contours of Pmag indicate that lower λ results in more coherent flux tubes that carry higher magnetic pressure flux at the photosphere (see dark red color inside the flux tubes). Also, we find that flux tubes with higher λ are more susceptible to splitting into two lobes. Indeed, the λ = 20 case (Fig. 12d) develops two very distinctive lobes, while in the λ = 10 (Fig. 12b) those lobes are marginally separated (the dark red region is more elongated rather than separated). This splitting is caused (in a similar manner to the afore-mentioned studies) by plasma flow from the apex to the flanks. This flow creates an aerodynamic gas pressure difference below the regions where we find the maximum horizontal expansion (around z = −1 Mm). Then, the pressure difference drives plasma motions. To illustrate this, we overplot the contours of the y-component of vorticity (gray contours in Fig. 12). We indeed find two counter rotating plasma flows along the flanks of the flux tubes. We note that the same vorticity values (for instance the second contour from inside out) are located deeper into the flux rope for larger λ. This signifies the presence of stronger gas-pressure driven plasma flows, which eventually deform the flux tubes. We find that lower tension along the flux tube axis (higher λ) results in more pronounced splitting of the flux tube. We should also mention (not shown here) that the flux tubes with λ = 15 and λ = 20 failed to emerge above the photosphere during the running time of our simulations.
 |
Fig. 12 Cross sections of Pmag at the xz-midplane for a) λ = 5; b) λ = 10; c) λ = 15; d) λ = 20. Purple is zero and dark red is 3.6 × 104 erg cm-3. Black lines are Pmag contours (same contour values for all images). Gray contours are the y-component of vorticity (same contour values for all images). Solid lines are positive values and dashed lines are negative values. |
We now focus on the λ = 5,10 cases, which eventually emerge above the photosphere. We have found that the higher tension flux tube reaches the photosphere later and with lower expansion. Consequently, the flux tube with higher tension reach the photosphere with higher magnetic pressure (i.e. higher magnitude of magnetic field) and lower plasma β. This has very important consequences on flux emergence at and above the solar surface. We find that the λ = 5 flux tube satisfies the instability criterion (Eq. (8)) earlier due to its higher magnitude of magnetic field and the lower β. Since the emerging field is non-twisted, it spreads horizontally and it becomes buoyantly unstable at two regions (similar to the λ = 10 case), forming two bipoles. A main difference compared to the λ = 10 case is that these bipoles appear at the photosphere earlier, (at t = 66 min, t = 154 min for λ = 10) and at a shorter distance (at y = ± 1.8 Mm, y = 4.9 Mm for λ = 10).
In the following sections we are going to highlight how the higher tension tube eventually goes through a more dynamic emergence and transfers more Poynting and axial flux above the photosphere than the lower tension tube.
 |
Fig. 13 a) Temporal evolution of maximum (black) and minimum (red) Vz above the photosphere. The vertical dashed lines correspond to the plasma ejections at t = 114, 120, 132 min. b) Maximum temperature and density around the locations of maximum Vz. |
4.2. Jet and associated plasma dynamics
 |
Fig. 14 a) Fieldline topology at the vertical yz-midplane, showing the plasmoid(s) at the interface (at t = 108 min). The horizontal cut shows the Bz component of the magnetic field at the photosphere, and the purple-green colorscale shows density in the yz-midplane. The fieldlines are colored according to the values of By. b) Isosurface of V> 60 km s-1 showing the t = 114 min jet. White fieldlines show the stretch of the envelope field by the ejection. Overplotted is the full magnetic vector colored by the Bz component of the field at z = 0.9 Mm. |
The dynamics of the jets depends on the magnetized plasma properties at the interface. We find that for λ = 5, the gradient of the magnetic field across the interface is much higher. The resulting current sheet is 3−5 times stronger. This leads to different characteristics (e.g. higher plasma temperatures) for the produced plasma jets.
Figure 13a shows the emission of three high-speed (200−600 km s-1) bi-directional jets from the interface, followed by lower speed jets (<100 km s-1 after t ≈ 135 min). The absolute values of the speeds of these jets are, on average, higher than in the λ = 10 case. This is due to the higher field strength (and lower plasma β) of the magnetized material within and around the interface. However, it is worthwhile mentioning that in both cases the speeds of the reconnection jets are comparable to the local Alfvén speed, as expected from the theory of reconnection. In this manner, we find that the speeds of the jets in the two cases are similar (determined by the Alfvén speed).
Regarding the heating due to reconnection-driven jets, the plasma of the upward jets has a higher temperature in the λ = 5 case. This is shown in Fig. 13b, which illustrates the temporal evolution of the maximum temperature at the sites of maximum Vz. The temperature can reach values up to 15 MK (first jet). The following jets have progressively lower temperatures. In general, the temperature increases by a factor of 1 /β. As we discussed earlier, plasma-β around the reconnection site is higher when λ is smaller. In the time period after the onset of the jets (i.e. t> 240 min for λ = 10, t> 105 min for λ = 5), we calculated that (on average) β ≈ 0.015 for λ = 5 and β ≈ 0.17 for λ = 5. This explains the differences in the temperature of the jets when λ is varied.
The corresponding density evolution shows a very good correlation with the temperature variations (maxima of temperature and minima of density occur at the same time). In comparison to the λ = 10 case, the density variations lie (on average) in the same regime 10-16−10-14 g cm-3. Thus, in both cases, the jets bring dense plasma into the solar atmosphere.
4.3. Fieldline topology and 3D structure of the jets
In both cases, the process that leads to the onset of the jets is similar. Namely, the interaction of the two bipoles leads to the formation of a strong current layer at the interface. The current layer becomes subject to the tearing-mode instability and plasmoid-induced reconnection leads to the emission of hot and high-speed jets. Hereafter, to avoid repetition, we describe briefly only the topology during the first jet.
Figure 14 shows the fieldline topology at t = 108 min, a few minutes before the emission of the first jet. The vertical midplane shows plasma density (blue-red colorscale), and the horizontal slice is Bz at the photosphere (black-white). We note that now the fieldlines are colored by the By component of the magnetic field. In our non-twisted configuration, the succession of positive and negative By highlights the locations of the plasmoid(s) and the arcade. At this time, one plasmoid has already been ejected upwards and another one has been formed at lower heights within the interface. The ejected plasmoid has collided with the envelope field and, consequently, it undergoes severe deformation. The ejection of the plasmoid is confined by the downward tension of the envelope fieldlines. The other plasmoid is ejected soon thereafter and it is also trapped by the closed ambient fieldlines.
After the ejection of the plasmoids, several jets are emitted from the interface. Figure 14b shows the 3D structure of the first jet at t = 114 min. The upward reconnection jet adopts a V-like shape (similar to the λ = 10 case). During its emission, the fast jet stretches the ambient field vertically but it does not break out. The jet is diverted into two lateral flows, which are running along the reconnected fieldlines of the envelope field. This leads to an apparent heating of the envelope fieldlines that join the outer polarities of the system.
Just underneath the upward V-like jet, there is another fast jet, which is less extensive and it adopts an inverse V-like configuration. It extends downwards until the top of the arcade, which is formed by the O-like fieldlines that are rooted to the minor polarities of the system. The jet compresses the plasma at the top of the arcade and heats it to ≈15 MK. The further evolution of the system is qualitatively similar to the λ = 10 case. For instance, the emission of several plasmoids from the interface leads to the onset of a series of jets, which can exist in parallel (e.g. like in Fig. 7f). Also, we find that the PIL undergoes deformation, developing horizontal undulations, around the center of the EFR, after t = 119 min.
4.4. Energy transfer and magnetic flux
 |
Fig. 15 a) Temporal evolution of the Poynting flux. Solid lines show the emergence term, Femergence, and dashed lines show the shearing term, Fshear. b) The unsigned magnetic flux Φxy. c) The axial flux for the bipole’s center in the positive y-direction (bipole AB) (solid). Dashed lines stand for the axial flux of λ = 10. d) Flux difference ΔΦxz. The dashed vertical line indicates then beginning of the undulation of the PIL and the dotted vertical lines indicate the times of the onset of high-speed jets from the interface. |
In Fig. 15a, we plot the shearing (dashed) and emergence (solid) term of Poynting flux, above the mid-photosphere (black), transition region (red) and the corona (blue). Energy is injected above the photosphere after t = 60 min, much sooner than the t = 140 min of λ = 10, due to the faster emergence of the flux tube above the photosphere. One difference between the two case is that more energy is injected into the atmosphere in the smaller λ case. Indeed, the emergence term in λ = 5 is 4.2 times higher that the one in λ = 10, while the shearing term is 2.4 times higher. This is because the emerging field with larger tension (i.e. λ = 5 case) brings stronger magnetic field at the photosphere and evolves/expands more dynamically (e.g. faster) in the solar atmosphere, as we showed in the previous sections. As a result, more flux/energy is transfered into the outer atmospheric layer, when the subphotospheric emerging field has larger tension. Therefore, our experiments reveal that this specific parameter of the subphotospheric emerging field is important towards understanding the dynamics of the emergence at and above the solar surface.
The unsigned flux, Φxy (Fig. 15b), indicates that more flux is injected into when λ is small. The maximum of the flux above the mid-photosphere (black), transition region (red) and corona (red) is 1.8 times larger the corresponding flux of λ = 10. We also find evidence of flux cancellation at the photosphere (after t = 120 min). We find a less profound decrease of flux above the transition region, while it is not clearly apparent above the corona. In Fig. 15c we plot the normalized axial flux of one bipole (the bipole that is located in the positive y-direction) above different atmospheric heights (solid lines). For comparison, we plot with dashed lines the λ = 10 values above the same heights. Above the mid-photosphere, we find that 26% of the initial axial flux emerges and from it 16% is located above the corona. Adding the axial flux of the two bipoles, we find that 52% of the initial axial flux emerges above the photosphere, which is 1.5 times the λ = 10 axial flux. Above the corona, we find 32% of the axial flux to emerge, which is 2.4 times larger than in the λ = 10 case.
These differences are caused by the emergence of stronger magnetic field in the lower λ (higher tension) case. This results in transfer of more flux and energy into the solar atmosphere. However, we note that in both cases 2/3 of the initial axial flux remain below the corona and only half of the axial flux emerges above the photosphere. Therefore, we find that in the cases under study a large amount of axial flux either stays at the photosphere or even submerges.
We also calculate the flux difference ΔΦxz. Above the photosphere (Fig. 15d, black line), ΔΦxz increases rapidly after the first ejection (dotted vertical line). Its maximum, at t = 120 min stands for 5% of the initial flux being transformed into negative By. This flux difference contains both the arcade and the plasmoid’s By. During the upward motion of the plasmoid(s), some of the plasmoid’s lines reconnect with envelope fieldlines. Part of this flux is added to the arcade, contributing positive to ΔΦxz, and part of it enhances the envelope field, contributing negative to ΔΦxz. We find that overall, ΔΦxz decreases as the plasmoid(s) moves upwards. The vertical dashed line indicates the start of the deformation of the PIL. Again, as in λ = 10, ΔΦxz decreases as the arcade follows the PIL undulation. As we mentioned in Sect. 3.2.4, ΔΦ indicates the transformation of flux through reconnection. Thus, we find increased reconnection along the lobe interface in the smaller λ case.
5. Summary and discussion
In the present work we studied the emergence of a non-twisted flux tube in a highly stratified atmosphere. The parameter we varied in our experiments was the buoyant part of the flux tube (λ).
We examined the initial emergence stage (below the photosphere). We found that the magnetic tension of the emerging part of the rising flux tube (smaller tension for higher λ) has a significant effect on the emergence process. More precisely, the λ = 10 tube is distorted into two smaller lobes. For λ = 5, the tube emerges in a more coherent manner. Moreover, smaller tension leads to higher upwards total force. As a result, in the λ = 10 case, the tube reaches the photosphere earlier and expands more horizontally, while it is still within the subphotospheric region. This faster emergence/expansion drops the flux tube’s internal magnetic pressure faster λ = 10. Subsequently, the higher λ (smaller tension) case reaches the photosphere having smaller magnitude of the magnetic field. Eventually, this difference in the magnitude of the magnetic field, makes the smaller λ (higher | B |) to emerge above the photosphere faster, although it reaches the photosphere later than the higher λ case. In both cases, the initial flux tube becomes buoyant in two positions along the tube’s length, forming two aligned bipoles at the photosphere. Since the λ = 5 emerges first, the horizontal distance between the two bipoles at the photosphere is smaller.
Simulations with λ = 15,20 indicated that distortion becomes more intense for higher λ. The origin of this distortion seems to be similar to the ones described by e.g. Schuessler (1979), Longcope et al. (1996), Moreno-Insertis & Emonet (1996). Flows at the flanks of the emerging flux tube increase the plasma vorticity locally. It is likely that the drag forces at the flanks of the flux tube cause the distortion. Although the results presented here are preliminary, we do find indications that the convex apex of the emerging flux tube helps the magnetic field to rise coherently. A full analysis with different magnetic field strengths, initial depths of the flux tubes and various twists is necessary for further conclusions.
The magnetic bipoles interact and reconnect at the interface between them, forming an envelope field and an arcade. We find that the interface current sheet is ≈5 times higher when λ = 5 which leads to more effective (faster) reconnection. From the interface current sheet, cool plasmoids are initially ejected, followed by several reconnection jets which are running with speeds comparable to the local Alfvén speed. All upward jets are confined by the envelope field and adopt a V-like shape. The downward jets compress the plasma at the top of the arcade and heat it to a few MK. The heating occurs in an intermittent manner due to the parallel emission of the jets at the interface. A similar process has been reported in more realistic experiments regarding the onset of nano-micro flares by Archontis & Hansteen (2014).
We have also found that the value of λ has implications on the energy and flux input into the atmosphere. Indeed, the emergence and shearing term of the Poynting flux are 4.2 and 2.4 times higher in λ = 5. The former is due to the faster emergence and the latter is due to more pronounced horizontal flows (along the PIL) at the interface. The vertical flux transfer is 1.8 times larger in λ = 5. In λ = 5 (λ = 10), 52% (30%) of the initial axial flux is transfered above the photosphere, and 24% (15%) above the low corona. The increased energy and flux transfer for smaller λ occurs as in this case stronger magnetic field is brought at the photosphere. This causes an overall faster and more dynamical evolution in the solar atmosphere.
In our aligned bipole configuration, we noticed that after the plasmoid ejections the PIL starts to gradually deform. The eruptions induce a total pressure deficit (at various locations) along the PIL. The flows towards the low-pressure regimes deform the PIL, forming finger-like features that are mainly oriented along the y-axis (transverse to the PIL). This makes the post-reconnection arcade to become a highly curved structure consisting of twisted fieldlines.
Previous studies that compared cases with different λ (e.g. Manchester et al. 2004; Archontis & Hood 2010) showed that the buoyant part of a twisted flux tube affects the eruption of newly formed flux ropes, which are triggered by shearing and reconnection within the emerging flux region. In the present study,
we investigated the effect of λ on the emergence of a non-twisted field. Although the initial magnetic field configuration and initial conditions in our experiments are idealized, the configuration of the emerging field at the photosphere and the subsequent dynamical evolution become very complex. The emission of several jets from the same interface and the intermittent heating of the plasma at different atmospheric heights is just one example of the arisen complexity. Therefore, this parametric study showed that the variation of only one parameter of the system can affect the dynamics of the system considerably. More work is needed to investigate the dynamics of the jets and the atmospheric response to the emergence of magnetic fields from the interior of the Sun.
Acknowledgments
The authors would like to thank the anonymous Referee and the Editor for their valuable comments which helped to improve the manuscript. The authors acknowledge support by the EU (IEF-272549 grant) and the Royal Society. The present research has been co-financed by the European Union (European Social Fund-ESF) and Greek national funds through the Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF) – Research Funding Program: Thales. Investing in knowledge society through the European Social Fund. This research has also been carried out in the frame of the research program of the RCAAM of the Academy of Athens and has been co-financed by the Program “IKY Scholarships” of the Greek national funds through the Operational Program Education and Lifelong Learning of the NSRF through the European Social Fund of ESPA 2007-2013. Finally, the work reported in this article was additionally supported by the SOLARNET project, funded by the European Commisions FP7 Capacities Program, under the Grant Agreement 312495. The simulations were performed on the STFC and SRIF funded UKMHD cluster, at the University of St Andrews.
References
- Abbett, W. P., Fisher, G. H., & Fan, Y. 2000, ApJ, 540, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Abbett, W. P., Fisher, G. H., & Fan, Y. 2001, ApJ, 546, 1194 [NASA ADS] [CrossRef] [Google Scholar]
- Acheson, D. J. 1979, Sol. Phys., 62, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Arber, T., Longbottom, A., Gerrard, C., & Milne, A. 2001, J. Comp. Phys., 171, 151 [Google Scholar]
- Archontis, V., & Hansteen, V. 2014, ApJ, 788, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Archontis, V., & Hood, A. W. 2010, A&A, 514, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Archontis, V., Moreno-Insertis, F., Galsgaard, K., Hood, A., & O’Shea, E. 2004, A&A, 426, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Archontis, V., Moreno-Insertis, F., Galsgaard, K., & Hood, A. W. 2005, ApJ, 635, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Archontis, V., Hood, A. W., & Brady, C. 2007, A&A, 466, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Archontis, V., Hood, A. W., & Tsinganos, K. 2013, ApJ, 778, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Chandra, R., Schmieder, B., Aulanier, G., & Malherbe, J. M. 2009, Sol. Phys., 258, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y. 2001, ApJ, 554, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y., Zweibel, E. G., Linton, M. G., & Fisher, G. H. 1999, ApJ, 521, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y., Abbett, W. P., & Fisher, G. H. 2003, ApJ, 582, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Kusano, K., Maeshiro, T., Yokoyama, T., & Sakurai, T. 2002, ApJ, 577, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Linton, M. G., Longcope, D. W., & Fisher, G. H. 1996, ApJ, 469, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., Fisher, G. H., & Arendt, S. 1996, ApJ, 464, 999 [NASA ADS] [CrossRef] [Google Scholar]
- López Fuentes, M. C., Demoulin, P., Mandrini, C. H., & van Driel-Gesztelyi, L. 2000, ApJ, 544, 540 [Google Scholar]
- Magara, T., & Longcope, D. W. 2003, ApJ, 586, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, IV, W., Gombosi, T., DeZeeuw, D., & Fan, Y. 2004, ApJ, 610, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno-Insertis, F., & Emonet, T. 1996, ApJ, 472, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, M. J., Hood, A. W., Moreno-Insertis, F., Galsgaard, K., & Archontis, V. 2006, A&A, 460, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1955, ApJ, 121, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R. 1982, Solar magneto-hydrodynamics (Dordrecht, Holland, Boston, Hingham: D. Reidel Pub. Co), 74 [Google Scholar]
- Schrijver, C. J. 2009, Adv. Space Res., 43, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Schuessler, M. 1979, A&A, 71, 79 [NASA ADS] [Google Scholar]
- Shibata, K. 1999, Ap&SS, 264, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Toriumi, S., & Yokoyama, T. 2011, ApJ, 735, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Tsinganos, K. C. 1980, ApJ, 239, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Yokoyama, T., & Shibata, K. 1994, ApJ, 436, L197 [NASA ADS] [CrossRef] [Google Scholar]
- Zwaan, C. 1985, Sol. Phys., 100, 397 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 a) Initial stratification of the atmosphere (temperature (T), density (ρ), magnetic pressure (Pm), and gas pressure (Pg)). b) Instability term at the center of the EFR and c) at the center of the bipole at y = 4.8 Mm. |
| In the text | |
 |
Fig. 2 a) Magnetogram at the mid-photosphere (z = 0.8 Mm) at t = 169 min. For simplicity, we call A, D the outer polarities and B, C the inner polarities. b) Field lines traced from the bipoles at t = 169 min. |
| In the text | |
 |
Fig. 3 Grayscale: Bz component of the magnetic field at the mid-photosphere (z = 0.9 Mm), ranging from −40 G to 40 G. Colored scale: density at yz-midplane, ranging from 1.7 × 10-14 g cm-3 (red) to 1.7 × 10-16 g cm-3 (blue). The lines correspond to fieldlines connecting the bipoles (blue), fieldlines of the arcade (red) and fieldlines of the envelope field (orange). Time is t = 250 min. |
| In the text | |
 |
Fig. 4 a) Temporal evolution of maximum (black) and minimum (red) Vz above the photosphere. Vertical dashed lines correspond to the emission of the bi-directional jets at t = 242,248,257 min. b) Maximum temperature (black) and density (blue) around the locations of maximum Vz. |
| In the text | |
 |
Fig. 5 The Vz component of the velocity field on the yz-midplane. Field lines show the projection of the full magnetic field vector onto that plane. a) Prior to plasmoid ejection at t = 242 min. b) Jet ejection at t = 248 min. |
| In the text | |
 |
Fig. 6 Density a) and temperature (b), c)) distribution at the vertical yz-midplane. Overplotted is the projection of the velocity field vector onto the plane. Bottom: a close-up of the reconnection site. |
| In the text | |
 |
Fig. 7 a)Bz component of the magnetic field at the mid-photosphere (z = 0.9 Mm), with the velocity field overplotted at t = 243 min and b)t = 286 min. c) Fieldlines traced around the center of the EFR at t = 243 min, showing the arcade. Overplotted is the full magnetic field vector colored by the Bz component of the field at z = 0.9 Mm. Red is positive and blue is negative. The red rectangular inset marks the same region as the one in b). d) Fieldlines at t = 286 min, showing the deformation of the PIL. e) Isosurface of Vz> 60 km s-1 showing the V-shaped jet at t = 248 min. f) The emission of several jets at t = 286 min (isosurface of Vz> 60 km s-1). |
| In the text | |
 |
Fig. 8 Visualization of the heating term (H) at t = 268 min for plasma having temperatures between a) 0.01−1 MK and b) 1−10 MK. |
| In the text | |
 |
Fig. 9 a) Temporal evolution of the Poynting flux. Solid lines show the emergence term, Femergence, and dashed lines show the shearing term, Fshear. b) The unsigned magnetic flux Φxy. c) The axial flux for the bipole’s center in the positive y-direction (bipole AB). d) Flux difference ΔΦxz. The dashed vertical line marks the initiation of the undulation of the PIL and the dotted vertical lines show the times for the onset of the hight-speed jets. |
| In the text | |
 |
Fig. 10 First row: z component of the forces along the vertical direction (x = 0, y = 0) at t = 3 min, for a) λ = 10 and b) λ = 5. Second row: temporal evolution of c) z-component of the magnetic tension and d) magnetic pressure, measured at the center of the flux tubes. We plot the quantities until the flux tubes reach the photosphere. |
| In the text | |
 |
Fig. 11 Forces and flux tube cross sections of λ = 10 and λ = 5, before they reach the photosphere (at t = 26 min and at t = 34 min respectively). (a), d)) Pmag of the flux tubes at the y = 0 cross section. The solid white lines (horizontal and vertical) pass through the flux tubes centers. Black Pmag contours have the same values in both panels. Vertical white dashed lines mark the position of the flux tube’s outer part. (b), e)) z-component of forces along the vertical direction through the flux tube’s center (direction marked with the vertical solid white line in (a), d))). Green is gas pressure force minus gravity force, orange is magnetic pressure force, red is magnetic tension force and black the total force. (c),f)) The x-component of forces along the horizontal direction through the flux tube’s center (direction marked with the horizontal solid white line in (a), d))). |
| In the text | |
 |
Fig. 12 Cross sections of Pmag at the xz-midplane for a) λ = 5; b) λ = 10; c) λ = 15; d) λ = 20. Purple is zero and dark red is 3.6 × 104 erg cm-3. Black lines are Pmag contours (same contour values for all images). Gray contours are the y-component of vorticity (same contour values for all images). Solid lines are positive values and dashed lines are negative values. |
| In the text | |
 |
Fig. 13 a) Temporal evolution of maximum (black) and minimum (red) Vz above the photosphere. The vertical dashed lines correspond to the plasma ejections at t = 114, 120, 132 min. b) Maximum temperature and density around the locations of maximum Vz. |
| In the text | |
 |
Fig. 14 a) Fieldline topology at the vertical yz-midplane, showing the plasmoid(s) at the interface (at t = 108 min). The horizontal cut shows the Bz component of the magnetic field at the photosphere, and the purple-green colorscale shows density in the yz-midplane. The fieldlines are colored according to the values of By. b) Isosurface of V> 60 km s-1 showing the t = 114 min jet. White fieldlines show the stretch of the envelope field by the ejection. Overplotted is the full magnetic vector colored by the Bz component of the field at z = 0.9 Mm. |
| In the text | |
 |
Fig. 15 a) Temporal evolution of the Poynting flux. Solid lines show the emergence term, Femergence, and dashed lines show the shearing term, Fshear. b) The unsigned magnetic flux Φxy. c) The axial flux for the bipole’s center in the positive y-direction (bipole AB) (solid). Dashed lines stand for the axial flux of λ = 10. d) Flux difference ΔΦxz. The dashed vertical line indicates then beginning of the undulation of the PIL and the dotted vertical lines indicate the times of the onset of high-speed jets from the interface. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


