| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201526401 | |
| Published online | 27 October 2015 | |
Bayesian least squares deconvolution
1
Instituto de Astrofísica de Canarias, 38205, La Laguna, Tenerife, Spain
e-mail: aasensio@iac.es
2
Departamento de Astrofísica, Universidad de La
Laguna, 38205, La
Laguna, Tenerife,
Spain
3
Université de Toulouse, UPS-OMP, Institut de Recherche en
Astrophysique et Planétologie, 31400
Toulouse,
France
4
CNRS, Institut de Recherche en Astrophysique et
Planétologie, 14 avenue Édouard
Belin, 31400
Toulouse,
France
Received: 24 April 2015
Accepted: 12 September 2015
Aims. We develop a fully Bayesian least squares deconvolution (LSD) that can be applied to the reliable detection of magnetic signals in noise-limited stellar spectropolarimetric observations using multiline techniques.
Methods. We consider LSD under the Bayesian framework and we introduce a flexible Gaussian process (GP) prior for the LSD profile. This prior allows the result to automatically adapt to the presence of signal. We exploit several linear algebra identities to accelerate the calculations. The final algorithm can deal with thousands of spectral lines in a few seconds.
Results. We demonstrate the reliability of the method with synthetic experiments and we apply it to real spectropolarimetric observations of magnetic stars. We are able to recover the magnetic signals using a small number of spectral lines, together with the uncertainty at each velocity bin. This allows the user to consider if the detected signal is reliable. The code to compute the Bayesian LSD profile is freely available.
Key words: stars: magnetic field / stars: atmospheres / line: profiles / methods: data analysis
© ESO, 2015
1. Introduction
The phenomena taking place in the atmospheres of solar-type stars is controlled by magnetic fields. One of the most straightforward ways of detecting and measuring such magnetic fields is through spectropolarimetry. The observation of the intensity (Stokes I), linear polarization (Stokes Q and U), and circular polarization (Stokes V) allows us to remotely infer the strength and orientation of magnetic fields.
During the last decades, we have been able to detect magnetic fields in cool stars. The first efforts 8 detected the presence of polarimetric signals in the most active of them. In these cases, it was necessary to reach a very high polarimetric sensitivity to detect these signals in individual spectral lines. In general, however, the polarization level in almost all cool stars is below our detection limit and we require post-processing techniques to enhance the detection rate. The first solution to this problem was the development of multiline techniques 24; 25, which averaged many photospheric spectral lines to improve the effective polarimetric sensitivity. This technique works under the assumption that noise is uncorrelated and adds up to zero when many spectral lines are summed. Meanwhile, the spectral line itself presents correlations that will make it appear above the noise after adding many spectral lines. This idea was later improved with the introduction of the least squares deconvolution technique LSD; 9, which has facilitated the detection of polarimetric signals in a wide variety of stars and the generation of a set of interesting surveys for the detection of magnetic fields in different stellar types e.g., 28; 14; 16.
Recently, the LSD method has been critically analyzed by 11, who pointed out the difficulties in the interpretation of the final LSD profile in terms of a normal spectral line. In recent years, several variations of the LSD method have been presented. These methods try to overcome some of the fundamental problems with LSD. For instance, 27 suggested introducing an improvement to deal nonlinearly with the presence of blends in spectral lines, much closer to what really happens during the formation of the spectral line. 5 and 15 generalized LSD to account for the deviations from the assumption of a single common profile for all spectral lines. This was done by using the principal component analysis (PCA) decomposition of all the considered lines and truncating the decomposition to get rid of the noise. 26 introduced the idea of multiline Zeeman signatures as detectors of the presence of magnetic fields. Finally, 11 introduced multiprofile LSD, a generalization of LSD that models each spectral line as the linear addition of several profiles, very similar to the PCA approach. These authors also discuss a simple modification of LSD to regularize the solution using a first-order Tikhonov regularization, which favors smooth solutions.
In this paper we treat the LSD from a Bayesian perspective and consider the use of a flexible prior for the expected LSD profile. This introduces a regularization that automatically adapts to the data. The method is fast and competitive in computing time with LSD. Given that the method we propose is fully Bayesian, one of the main advantages is that we are able to give sensible error bars to the detection of LSD signatures.
2. Bayesian LSD
The LSD technique is based on assuming that the circular polarization profiles of a set of selected spectral lines from a star correspond to a common basic Zeeman signature. The spectral shape of this signature does not change and only the amplitude is modified from line to line. The validity of this approximation is based on two assumptions. First, the line has to be in the so-called weak field regime, which happens when the magnetic field is sufficiently weak so that the Zeeman splitting is smaller than the Doppler width of the spectral line. Second, the line has to be weak so that no saturation effects are detected. Under these simplifying assumptions, the radiative transfer equation can be solved analytically and it can be demonstrated that the Stokes V profile is proportional to the wavelength derivative of the intensity profile e.g., 13. In this case 9 demonstrated that it is possible to write the Stokes V profile for line i as 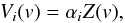 (1)where v is the displacement with respect to the central wavelength of the line in velocity units and αi is a proportionality constant that depends on the properties of the line. 9 also showed that these constants are αi = λidigi, with λi the central wavelength of the line, di the depth of the line, and gi the effective Landé factor of the line.
(1)where v is the displacement with respect to the central wavelength of the line in velocity units and αi is a proportionality constant that depends on the properties of the line. 9 also showed that these constants are αi = λidigi, with λi the central wavelength of the line, di the depth of the line, and gi the effective Landé factor of the line.
With a model for all the lines at hand, we can write the generative model. It states how a given observed spectral line is modeled in terms of some parameters. We assume that we observe Nlines spectral lines, each one sampled at Nv velocity positions. Then, we model our measurements with 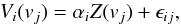 (2)which indicates that our measured Stokes V profile at a given velocity position and for a certain spectral line is just a weight times the common signature at this very same velocity with some added noise, ϵij. This noise can potentially be different for all velocity positions of all the spectral lines and can even accommodate the more general case in which there is nonzero correlation between different pixels. We note that the generative model can be written in matrix notation as
(2)which indicates that our measured Stokes V profile at a given velocity position and for a certain spectral line is just a weight times the common signature at this very same velocity with some added noise, ϵij. This noise can potentially be different for all velocity positions of all the spectral lines and can even accommodate the more general case in which there is nonzero correlation between different pixels. We note that the generative model can be written in matrix notation as 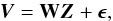 (3)where the matrix W is given by
(3)where the matrix W is given by ![\begin{equation} \mathbf{W} = \left[ \begin{array}{ccccc} \alpha_1 & 0 & 0 & 0 & \cdots \\ \alpha_2 & 0 & 0 & 0 & \cdots \\ \alpha_3 & 0 & 0 & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots\\ 0 & \alpha_1 & 0 & 0 & \cdots \\ 0 & \alpha_2 & 0 & 0 & \cdots \\ 0 & \alpha_3 & 0 & 0 & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots\\ \end{array} \right] . \end{equation}](/articles/aa/full_html/2015/11/aa26401-15/aa26401-15-eq19.png) (4)In other words, the matrix elements are given by Wij = αjδj,imodj.
(4)In other words, the matrix elements are given by Wij = αjδj,imodj.
2.1. Standard LSD
It is very simple to obtain the standard LSD method in a Bayesian framework. To this end, we let the observations V represent the Stokes V profiles of line i at wavelength j ordered as V = [ V1(v1),V2(v1),V3(v1),...,V1(v2),V2(v2),... ] T. Likewise, we define the Z vector as the sampled common signature, given by Z = [ Z(v1),Z(v2),... ] T. With these definitions, we can apply the Bayes theorem to obtain the probability distribution for the common signature given all the observed data 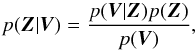 (5)where p(Z | V) is the posterior distribution for the common signature given the observations, p(V | Z) is the likelihood or sampling distribution (that gives the probability of getting a set of observed spectral lines conditioned on a common signature), p(Z) is the prior distribution for the common signature (that encodes all the a priori information we have for Z(v)). Finally, p(V) is the marginal likelihood or evidence that normalizes the posterior to make it a proper probability distribution. Given that the marginal likelihood does not depend on Z, it is usual to drop it.
(5)where p(Z | V) is the posterior distribution for the common signature given the observations, p(V | Z) is the likelihood or sampling distribution (that gives the probability of getting a set of observed spectral lines conditioned on a common signature), p(Z) is the prior distribution for the common signature (that encodes all the a priori information we have for Z(v)). Finally, p(V) is the marginal likelihood or evidence that normalizes the posterior to make it a proper probability distribution. Given that the marginal likelihood does not depend on Z, it is usual to drop it.
Even though the equations are valid for the general correlated case, we assume for simplicity that the noise is uncorrelated and with variance 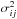 for line i at velocity point j. Under this assumption, the likelihood can be written as
for line i at velocity point j. Under this assumption, the likelihood can be written as 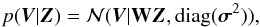 (6)where
(6)where 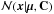 represents a multivariate Gaussian distribution for variable x with mean vector μ and covariance matrix C. The vector σ2 contains all the variances ordered exactly as in the case of V. We note that if all pixels share the same noise variance, equal to
represents a multivariate Gaussian distribution for variable x with mean vector μ and covariance matrix C. The vector σ2 contains all the variances ordered exactly as in the case of V. We note that if all pixels share the same noise variance, equal to 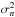 , the likelihood simplifies to
, the likelihood simplifies to 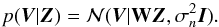 (7)If we assume that all Z(v) profiles are equally probable a priori, the posterior probability for Z(v) is
(7)If we assume that all Z(v) profiles are equally probable a priori, the posterior probability for Z(v) is 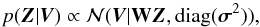 (8)where the posterior distribution is now seen as a distribution with respect to Z. Equation (8) represents the full probabilistic LSD solution. Given the special structure of the matrix W, it is very simple to compute the maximum a posteriori point estimate (the one that maximizes the posterior distribution) and one ends up with the known LSD result of Donati et al.1997; see also 26:
(8)where the posterior distribution is now seen as a distribution with respect to Z. Equation (8) represents the full probabilistic LSD solution. Given the special structure of the matrix W, it is very simple to compute the maximum a posteriori point estimate (the one that maximizes the posterior distribution) and one ends up with the known LSD result of Donati et al.1997; see also 26: 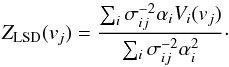 (9)
(9)
2.2. Bayesian hierarchical model
From the Bayesian point of view, the classical LSD method is just the maximum a posteriori solution to the inference problem when flat priors are used for the common signature Z(v). In other words, the value of Z(v) at one velocity position does not depend at all on the value at different velocity positions. This assumption does not capture some knowledge that we have from the physics of the problem. We know that there must be some correlation between different velocity positions because the Stokes V profile are a consequence of the combined solution of the radiative transfer equation and the statistical equilibrium equations on the stellar atmosphere. The emission and absorption properties of the atmosphere inherently introduce correlation between different velocity bins. One consequence of this is the typical smooth shape of the Z(v) profile, that we should somehow force in our solution.
 |
Fig. 1 Examples of functions extracted from GP priors with a squared exponential (solid lines) and Matérn with ν = 3 / 2 covariance functions. In both cases, σZ = 1 and different values of λZ are used. We note that λZ acts as a scale over which the function varies. The functions extracted from the Matérn covariance function have a rougher behavior than those of the squared exponential one. |
In the Bayesian framework, we impose this condition by introducing a suitable prior distribution. A very convenient way to do it is by using a Gaussian process GP; 23. Generally, a GP is a distribution over the subspace of functions that fulfill certain conditions. From the technical point of view, once a function is sampled at a finite number of points, a GP for the function Z(v) is defined by the following multivariate normal distribution: 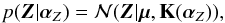 (10)where μ is the mean of the distribution, which is usually set to zero, and K(αZ) is the covariance matrix, that depends on a set of parameters αZ. The GPs are then defined by the specific covariance matrix. Instead of writing the full matrix, it is customary to define a function (the covariance function) that gives the value of the matrix elements. This covariance function has to fulfill certain conditions so that the ensuing covariance matrix is proper (for instance, the covariance matrix has to be symmetric). Widespread covariance functions are the squared exponential,
(10)where μ is the mean of the distribution, which is usually set to zero, and K(αZ) is the covariance matrix, that depends on a set of parameters αZ. The GPs are then defined by the specific covariance matrix. Instead of writing the full matrix, it is customary to define a function (the covariance function) that gives the value of the matrix elements. This covariance function has to fulfill certain conditions so that the ensuing covariance matrix is proper (for instance, the covariance matrix has to be symmetric). Widespread covariance functions are the squared exponential, ![\begin{equation} K_{ij}(\sigma_Z,\lambda_Z) = \sigma_Z^2 \exp \left[ -\frac{(v_i-v_j)^2}{2 \lambda_Z^2}\right], \end{equation}](/articles/aa/full_html/2015/11/aa26401-15/aa26401-15-eq49.png) (11)or the Matérn class of covariance functions,
(11)or the Matérn class of covariance functions, 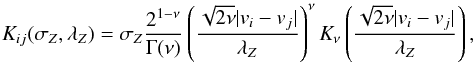 (12)where Kν(x) is the modified Bessel function see 1 and ν is a real number controlling the roughness of the resulting functions. Matérn covariance functions converge to the squared exponential covariance function when ν → ∞. Other covariance functions can be found in 23. Figure 1 shows samples from a squared exponential GP prior with σZ = 1 and different values of λZ. In the case of the squared exponential covariance function, one can see that the functions are smooth and the value of λZ defines the rate of variability.
(12)where Kν(x) is the modified Bessel function see 1 and ν is a real number controlling the roughness of the resulting functions. Matérn covariance functions converge to the squared exponential covariance function when ν → ∞. Other covariance functions can be found in 23. Figure 1 shows samples from a squared exponential GP prior with σZ = 1 and different values of λZ. In the case of the squared exponential covariance function, one can see that the functions are smooth and the value of λZ defines the rate of variability.
The two covariance functions described in the previous paragraph are stationary 23, because they only depend on the difference vi − vj, so that they are translation invariant. The experiments carried out in Sects. 3 and 4 demonstrate that these covariance functions do a good job. Although we do not pursue this objective here, it is possible to work with nonstationary covariance functions that are more localized and could possibly explain some features in some specific velocity bins better similar to the work of 6.
A GP prior introduces the parameters αZ into the inference. These parameters of the prior are termed hyperparameters and have to be considered in the posterior distribution. This is the reason why the inference model is hierarchical. Therefore, the posterior distribution of the hierarchical model is now given by 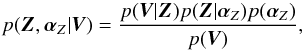 (13)where we have added a hyperprior, p(αZ), for the hyperparameters. Given that the hyperparameters are of no interest for obtaining the common signature, they should be marginalized (integrated) from the posterior so that we obtain the posterior distribution for Z:
(13)where we have added a hyperprior, p(αZ), for the hyperparameters. Given that the hyperparameters are of no interest for obtaining the common signature, they should be marginalized (integrated) from the posterior so that we obtain the posterior distribution for Z: 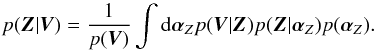 (14)This integral cannot be computed in closed form in general. For this reason, we pursue here a Type-II maximum likelihood (ML) solution 4, also known as empirical Bayes or maximum marginal likelihood. This method is used for the analytical treatment of hierarchical models in which the posterior distribution is intractable. The strategy is to compute the marginal posterior for the hyperparameters,
(14)This integral cannot be computed in closed form in general. For this reason, we pursue here a Type-II maximum likelihood (ML) solution 4, also known as empirical Bayes or maximum marginal likelihood. This method is used for the analytical treatment of hierarchical models in which the posterior distribution is intractable. The strategy is to compute the marginal posterior for the hyperparameters, 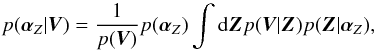 (15)and assume that this distribution is strongly peaked. Under this condition the set of hyperparameters
(15)and assume that this distribution is strongly peaked. Under this condition the set of hyperparameters 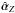 can be obtained that maximize the marginal posterior p(αZ | V) and use a Dirac delta function as prior distribution:
can be obtained that maximize the marginal posterior p(αZ | V) and use a Dirac delta function as prior distribution: 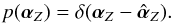 (16)In such a case, the integral in Eq. (14) can be trivially carried out, so that we find
(16)In such a case, the integral in Eq. (14) can be trivially carried out, so that we find 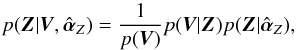 (17)where we make explicit in the posterior for Z that we are conditioning on a specific value of the hyperparameters.
(17)where we make explicit in the posterior for Z that we are conditioning on a specific value of the hyperparameters.
The advantage of following this Type-II ML approach is that the solution becomes analytical. Making use of the definition of the likelihood of Eq. (6) and the prior of Eq. (10) with μ = 0 and applying standard properties of the multivariate Gaussian distribution, we find 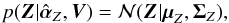 (18)where
(18)where ![\begin{eqnarray} \label{eq:posteriorMeanCovZ} \Sigmabold_Z &=& \left[ \mathbf{K}(\alphabold_Z)^{-1} + \mathbf{W}^T \mathrm{diag} \left( \frac{1}{\sigmabold^2} \right) \mathbf{W} \right]^{-1} \nonumber \\ \mubold_Z &=& \Sigmabold_Z \mathbf{W}^T \mathrm{diag} \left( \frac{1}{\sigmabold^2} \right) \vec{V}. \end{eqnarray}](/articles/aa/full_html/2015/11/aa26401-15/aa26401-15-eq65.png) (19)Likewise, the marginal posterior for αZ is
(19)Likewise, the marginal posterior for αZ is 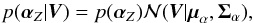 (20)with
(20)with 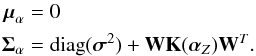 (21)The objective now is to obtain the value of
(21)The objective now is to obtain the value of 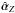 that maximizes Eq. (20). This is easier if one takes logarithms, ending up with the maximization of
that maximizes Eq. (20). This is easier if one takes logarithms, ending up with the maximization of 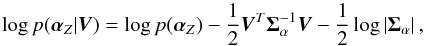 (22)where
(22)where 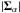 is the determinant of the matrix.
is the determinant of the matrix.
From a technical point of view, the calculation of the inverse and the determinant is computationally heavy because matrix Σα is of size NlinesNv × NlinesNv, which is very large in practical applications. However, it is possible to efficiently accelerate the computation using the Woodbury matrix identity 18, so that ![\begin{eqnarray} \label{eq:inverseSigma} \Sigmabold_\alpha^{-1} & = &\mathrm{diag}\left( \frac{1}{\sigmabold^2} \right) \nonumber \\ &&\hspace*{-5.5mm} - \mathrm{diag}\left( \frac{1}{\sigmabold^2} \right) \mathbf{W} \left[ \mathbf{K}(\alphabold_Z)^{-1} + \mathbf{W}^T \mathrm{diag}\left( \frac{1}{\sigmabold^2} \right) \mathbf{W} \right]^{-1} \mathbf{W}^T \mathrm{diag}\left( \frac{1}{\sigmabold^2} \right)\cdot \end{eqnarray}](/articles/aa/full_html/2015/11/aa26401-15/aa26401-15-eq72.png) (23)In this case, it is only necessary to obtain the inverse of the Nv × Nv matrix K(αZ) and of the matrix inside brackets, which is again of size Nv × Nv. These matrices are of a much smaller size than Σα and the inversion is much less time consuming. Likewise, using the matrix determinant lemma, we find
(23)In this case, it is only necessary to obtain the inverse of the Nv × Nv matrix K(αZ) and of the matrix inside brackets, which is again of size Nv × Nv. These matrices are of a much smaller size than Σα and the inversion is much less time consuming. Likewise, using the matrix determinant lemma, we find 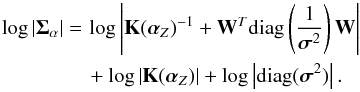 (24)The inverse of the matrix inside brackets can be efficiently computed using the Cholesky decomposition, which also gives the logarithm of the determinant as a subproduct.
(24)The inverse of the matrix inside brackets can be efficiently computed using the Cholesky decomposition, which also gives the logarithm of the determinant as a subproduct.
 |
Fig. 2 Examples of two different shapes of Z(v) and how they are recovered using LSD (green curve) and Bayesian LSD (mean shown in blue and credibility intervals as blue shaded regions). The original true Z(v) is shown in red. The experiments use the Matérn covariance function with ν = 3 / 2. |
 |
Fig. 3 Results of applying the LSD (green curve) and Bayesian LSD (blue curve showing the mean and blue regions showing the credibility intervals) to observations of II Peg, both for Stokes I (left panel) and V (right panel). The experiments use the Matérn covariance function with ν = 3 / 2. The green and blue curves overlap almost exactly in the left panel when increasing the number of considered spectral lines. |
As a final remark, we note that many of the terms in Eq. (23) do not change during the optimization with respect to the hyperparameters. They can be precomputed at the beginning of the optimization and only the term inside brackets in Eq. (23) needs to be recomputed when the hyperparameters are changed.
3. Synthetic experiments
The first test of the method is done with synthetic data. We generate two artificial Z(v) profiles, which are given by ![\begin{eqnarray} Z_1(v) &=& \exp \left[ -v^2 \right] \nonumber \\[2mm] Z_2(v) &=& \exp \left[ -v^2 \right] + \frac{1}{5} \exp \left[ -(v-2.5)^2 \right]. \end{eqnarray}](/articles/aa/full_html/2015/11/aa26401-15/aa26401-15-eq75.png) (25)For convenience, both profiles are normalized to 1 / 2 amplitude, multiplied by randomly generated α coefficients (with zero mean and unit variance) and then noise with diagonal covariance with variance σ2 = 1 is added to all the synthetic observations. A maximum of 200 synthetic spectral lines are used in both the standard LSD and the Bayesian LSD algorithms. For a single line, the signal-to-noise ratio equals S/N = 1 / 2. In the presence of noise, it is expected that adding Nlines spectral lines would increase the S/N in proportion to
(25)For convenience, both profiles are normalized to 1 / 2 amplitude, multiplied by randomly generated α coefficients (with zero mean and unit variance) and then noise with diagonal covariance with variance σ2 = 1 is added to all the synthetic observations. A maximum of 200 synthetic spectral lines are used in both the standard LSD and the Bayesian LSD algorithms. For a single line, the signal-to-noise ratio equals S/N = 1 / 2. In the presence of noise, it is expected that adding Nlines spectral lines would increase the S/N in proportion to 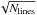 . Figure 2 shows how both estimations approach the true common signature (represented in red). The Bayesian LSD result is using a Matérn covariance function with ν = 3 / 2. The standard LSD method gives the green estimation. Given that no correlation is imposed between velocity bins, it can be seen that a large oscillation produced by noise remains even when adding 200 lines.
. Figure 2 shows how both estimations approach the true common signature (represented in red). The Bayesian LSD result is using a Matérn covariance function with ν = 3 / 2. The standard LSD method gives the green estimation. Given that no correlation is imposed between velocity bins, it can be seen that a large oscillation produced by noise remains even when adding 200 lines.
The mean of the marginal posterior for the common signature, given by μZ in Eq. (19), is represented in blue. One of the obvious advantages of working in a Bayesian framework is that the solution is given in terms of a probability distribution. This allows us to compute the probability distribution for each velocity point. They are obtained by marginalizing out all the variables in Eq. (18) except for the value of Z(vj) at the velocity bin j of interest. Using the special properties of the Gaussian distribution, these distributions are just one-dimensional Gaussian distributions with variance equal to the (j,j) element of matrix ΣZ. We represent the distribution at each velocity point using the 68%, 95%, and 99% credibility intervals with blue shaded regions.
Several properties of the Bayesian LSD solution are worth mentioning. First, the mean of the solution is very smooth. This is a consequence of the strong regularization introduced by the GP prior with squared exponential covariance function. Other covariance functions that give a less smooth solution can also be used. Second, the covariance function is stationary (it only depends on v − v′) so that we find some variability in the inferred solution when approaching the continuum because the scale of variation λZ is the same for all the velocity bins. Many other covariance functions can be used to diminish this behavior. Third, the true solution is always inside the credibility intervals. Fourth, the marginal posterior of Eq. (14) can be used as a suitable distribution to carry out the modeling of the LSD profile. Using this distribution instead of the usual least squares solution (which assumes a diagonal covariance) makes the fitting much more robust.
4. Real data
The previous section demonstrates that Bayesian LSD can recover a much more robust common signature from the observations, even when it is quite complex. In the following, we apply the method to real observations. We consider three different cases that are representative of what one can encounter in typical observations. The case of II Peg is representative of a very strong signal that can even be detected in individual lines. The case of HR1099 is representative of a very complex common signature. Finally, 18 Sco is representative of a very weak signal in which, even taking into account thousands of lines, the final signal is very close to the noise level. Public spectropolarimetric data for these three targets were downloaded from the PolarBase data base 22.
4.1. II Peg
II Peg is a very active RS CVn binary system where a system of starspots has been mapped on the K1IV primary component. The spot system usually covers up to 40% of the surface 3. The observations were carried out in July 2005 with the ESPaDOnS spectropolarimeter 10. Using a total integration time of one hour, the peak signal-to-noise ratio of the original Stokes V spectrum (achieved at wavelengths around 780 nm) is close to 1000 per wavelength bin. In agreement with the vast majority of published studies based on ESPaDOnS data, the S/N used here is the one computed from the Stokes I spectrum obtained by adding up the four polarimetric exposures combined to produce the Stokes V spectrum. For such an extremely active target, this noise level is sufficiently low to detect Zeeman signatures in a number of individual spectral lines formed in the photosphere and chromosphere 19. Here, we use a list of about 7400 spectral lines computed from a local thermodynamical equilibrium (LTE) atmospheric model matching the spectral type of the primary component of II Peg 12, keeping only photospheric lines deeper than 40% of the continuum level.
Figure 3 shows the improvement in the detection of the common signature Z(v) when the number of lines that are considered increases. The left panel shows the common signature in Stokes I, while the right panel displays the results for Stokes V. The lines that we have considered have been ordered on decreasing value of the weights αi. Therefore, the panels with only seven lines are obtained by considering the lines that produce the largest Zeeman signal. The LSD profile is shown in green, while the mean of the Bayesian LSD detection is shown in blue, with the credibility intervals at 68%, 95%, and 99% levels displayed in different gradations of blue. For the case of II Peg, the signature is detected at a very high signal-to-noise ratio with only seven lines (0.1% of the total number of lines considered in the line list). The Bayesian LSD approach leads to a much smoother profile than the LSD does. The presence of credibility intervals is of relevance for discarding features like the one found at v ≈ −85 km s-1, which is compatible with zero in the Bayesian LSD case. Increasing the number of spectral lines produces a convergence of the Bayesian LSD and the standard LSD profiles, which is especially relevant in Stokes V.
4.2. HR 1099
Similarly to II Peg, HR 1099 is one of the most active RS CVn systems, with both components of the binary association clearly visible in high resolution spectra (while the primary alone is seen in observations of II Peg). The projected rotational velocity has been measured to be vsini = 41 ± 0.5 km s-17. The magnetic structure of its active subgiant has been investigated in detail by 20 using Zeeman Doppler Imaging, showing the presence of large and axisymmetric regions with the magnetic field being azimuthal. Additionally, 20 also found clues for the presence of a differential rotation, much weaker than in the case of the Sun. The observation considered here was taken with ESPaDONS in August 2005.
The line list used here is the same as the one previously employed for II Peg, providing us with a good match to the photospheric characteristics of the evolved primary component, while the secondary is a much less active G5 main-sequence star.
The presence of several magnetized regions that also change with time produces Zeeman signals of large complexity. Figure 4 shows the inferred common signature for HR 1099, both for Stokes I (left panel) and for Stokes V (right panel). Several magnetic components are detected around −65 (which is roughly the radial velocity of the secondary star at that time), 20, and 40 km s-1 (originating from the surface of the primary star of the system). These detections in Stokes V are also consistent with what is found in Stokes I. When only the seven most magnetically sensitive lines are considered, the mean of the Bayesian LSD profile for Stokes V is very smooth with the dashed regions marking the large uncertainty. A large part of the noise that is intrinsic to the standard LSD profile is absent. With only 74 lines, the feature at positive relative velocities clearly appears. The quality of the detection increases drastically when considering more than 10% of the lines of the line list. However, it is interesting to note that the uncertainty in the continuum regions does not decrease much when using 10% or 100% of the lines (third and fourth panels). In the presence of only pure random errors with constant variance, this uncertainty should be reduced roughly in proportion to 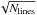 . However, the assumption of constant variance in these observations is not correct because the S/N changes greatly throughout the ESPaDOnS spectrum, being much lower at the borders of individual spectral orders and also near the boundaries of the spectral domain of the instrument. This leads to a slower decrease in the final uncertainty. It is important to point out that our Bayesian LSD method is able to take this into account and the ensuing final uncertainties do not decrease in such a proportion. The immediate consequence of this is that we could be missing very weak signals owing to the presence of systematic errors.
. However, the assumption of constant variance in these observations is not correct because the S/N changes greatly throughout the ESPaDOnS spectrum, being much lower at the borders of individual spectral orders and also near the boundaries of the spectral domain of the instrument. This leads to a slower decrease in the final uncertainty. It is important to point out that our Bayesian LSD method is able to take this into account and the ensuing final uncertainties do not decrease in such a proportion. The immediate consequence of this is that we could be missing very weak signals owing to the presence of systematic errors.
4.3. 18 Sco
18 Sco (HD 146233) is known to be one of the best solar twins among bright stars 17. In spite of its relatively low activity level, its surface magnetic field was detected by 21 using high S/N observations. The Stokes V spectrum analyzed here was obtained with the NARVAL spectropolarimeter 2 in July 2008. This observation is extracted from the time-series presented by 21. Our line list is also identical to the one used in the same study. The LTE model from 12 was computed for a G2 spectral type, leading to a total of about 3700 photospheric spectral lines deeper than 40% of the continuum.
The inferred common signature for 18 Sco is shown in Fig. 5 for an increasing number of spectral lines. Even when the full line list is considered, only a marginal detection of circular polarization is possible at the radial velocity of the star. This is an example in which having credibility intervals for each velocity bin is crucial. The oscillations detected by the standard LSD method fall inside the uncertainty region obtained from the Bayesian LSD method, although in this case the mean is much smoother.
5. Conclusions
We have described a fully Bayesian least squares deconvolution method which relies on a Gaussian process prior to regularizing the spectral shape of the common signature. Two obvious advantages emerge from this Bayesian approach. First, the final answer to the problem is in the form of a probability distribution. This allows the user to check whether the detected signals are relevant or just a consequence of fluctuations of random and/or systematic effects. Additionally, given that we also compute the covariance matrix of the ensuing probability distribution (taking into account possible correlations among all velocity bins), it can be used in inversion codes that fit the Bayesian LSD profile to estimate the stellar magnetic field. This introduces a strong regularization that avoids fitting spurious effects. Examples of this are features of the LSD profiles that are close to the noise level or systematic effects like interference fringes. Second, the hierarchical approach using a GP prior automatically adapts to the complexity of the spectral profile. The solution for very noisy velocity bins (for instance, close to the continuum) is very smooth and the noise is never overfitted. This automatic adaptation to the signal is allowed owing to the inclusion of the two hyperparameters of the GP prior. They are easily inferred from the data.
By taking advantage of standard linear algebra identities and techniques for working with sparse matrices, the Bayesian LSD common signature can be computed very quickly, in a matter of a few seconds for thousands of spectral lines. The code for computing the Bayesian LSD profile is freely available1.
Acknowledgments
Financial support by the Spanish Ministry of Economy and Competitiveness through projects AYA2010–18029 (Solar Magnetism and Astrophysical Spectropolarimetry) and Consolider-Ingenio 2010 CSD2009-00038 are gratefully acknowledged. A.A.R. also acknowledges financial support through the Ramón y Cajal fellowships. This research has made use of NASA’s Astrophysics Data System Bibliographic Services.
References
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical Functions (New York: Dover) [Google Scholar]
- Aurière, M. 2003, in EAS Pub. Ser. 9, eds. J. Arnaud, & N. Meunier, 105 [Google Scholar]
- Berdyugina, S. V., Jankov, S., Ilyin, I., Tuominen, I., & Fekel, F. C. 1998, A&A, 334, 863 [NASA ADS] [Google Scholar]
- Bishop, C. M. 1996, Neural networks for pattern recognition (Oxford University Press) [Google Scholar]
- Carroll, T. A., Kopf, M., Ilyn, I., & Strassmeier, K. G. 2008, Astron. Nachr., 328, 1043 [Google Scholar]
- Czekala, I., Andrews, S. M., Mandel, K. S., Hogg, D. W., & Green, G. M. 2015, ApJ, 812, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F. 1999, MNRAS, 302, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Semel, M., & Rees, D. E. 1992, A&A, 265, 669 [NASA ADS] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & CollierCameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Catala, C., Landstreet, J. D., & Petit, P. 2006, in ASP Conf. Ser. 358, eds. R. Casini, & B. W. Lites, 362 [Google Scholar]
- Kochukhov, O., Makaganiuk, V., & Piskunov, N. 2010, A&A, 524, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Kluwer Academic Publishers) [Google Scholar]
- Marsden, S. C., Petit, P., Jeffers, S. V., et al. 2014, MNRAS, 444, 3517 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, M. J., Asensio Ramos, A., Carroll, T. A., et al. 2008, A&A, 486, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Hervé, A., Bouret, J.-C., et al. 2015, A&A, 575, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, J., & Ramírez, I. 2007, ApJ, 669, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Petersen, K. B., & Pedersen, M. S. 2012, The Matrix Cookbook, version 20121115 [Google Scholar]
- Petit, P. 2006, in ASP Conf. Ser. 358, eds. R. Casini, & B. W. Lites, 335 [Google Scholar]
- Petit, P., Donati, J.-F., Wade, G. A., et al. 2004, MNRAS, 348, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Petit, P., Louge, T., Théado, S., et al. 2014, PASP, 126, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. I. 2005, Gaussian Processes for Machine Learning, Adaptive Computation and Machine Learning (The MIT Press) [Google Scholar]
- Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
- Semel, M., & Li, J. 1996, Sol. Phys., 164, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Semel, M., Ramírez Vélez, J. C., Martínez González, M. J., et al. 2009, A&A, 504, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sennhauser, C., Berdyugina, S. V., & Fluri, D. M. 2009, A&A, 507, 1711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Grunhut, J. H., & MiMeS Collaboration 2012, in Circumstellar Dynamics at High Resolution, eds. A. C. Carciofi, & T. Rivinius, ASP Conf. Ser., 464, 405 [Google Scholar]
All Figures
 |
Fig. 1 Examples of functions extracted from GP priors with a squared exponential (solid lines) and Matérn with ν = 3 / 2 covariance functions. In both cases, σZ = 1 and different values of λZ are used. We note that λZ acts as a scale over which the function varies. The functions extracted from the Matérn covariance function have a rougher behavior than those of the squared exponential one. |
| In the text | |
 |
Fig. 2 Examples of two different shapes of Z(v) and how they are recovered using LSD (green curve) and Bayesian LSD (mean shown in blue and credibility intervals as blue shaded regions). The original true Z(v) is shown in red. The experiments use the Matérn covariance function with ν = 3 / 2. |
| In the text | |
 |
Fig. 3 Results of applying the LSD (green curve) and Bayesian LSD (blue curve showing the mean and blue regions showing the credibility intervals) to observations of II Peg, both for Stokes I (left panel) and V (right panel). The experiments use the Matérn covariance function with ν = 3 / 2. The green and blue curves overlap almost exactly in the left panel when increasing the number of considered spectral lines. |
| In the text | |
 |
Fig. 4 Same as Fig. 3 for HR1099. |
| In the text | |
 |
Fig. 5 Same as Fig. 3 for 18 Sco. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


