| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201526785 | |
| Published online | 18 September 2015 | |
Determination of plasma parameters in solar zebra radio sources
1
Astronomical Institute, Academy of Sciences of the Czech
Republic,
251 65
Ondřejov,
Czech Republic
e-mail:
karlicky@asu.cas.cz
2
Radiophysical Research Institute of St.-Petersburg State
University, 198504
St.-Petersburg,
Russia
Received: 19 June 2015
Accepted: 2 August 2015
Aims. We present a new method for determining the magnetic field strength and plasma density in the solar zebra radio sources.
Methods. Using the double plasma resonance (DPR) model of the zebra emission, we analytically derived the equations for computing the gyroharmonic number s of selected zebra lines and then solved these equations numerically.
Results. The method was successfully tested on artificially generated zebras and then applied to observed ones. The magnetic field strength and plasma density in the radio sources were determined. Simultaneously, we evaluated the parameter Lnb = 2Lb/ (2Ln − Lb), where Ln and Lb are the characteristic scale-heights of the plasma density and magnetic field strength in the zebra source, respectively. Computations show that the maximum frequency of the low-polarized zebras is about 8 GHz, in very good agreement with observations. For the high-polarized zebras, this limit is about four times lower. Microwave zebras are preferentially generated in the regions with steep gradients of the plasma density, such as in the transition region. In models with smaller density gradients, such as those with a barometric density profile, the microwave zebras cannot be produced owing to the strong bremsstrahlung and cyclotron absorptions. We also show that our DPR model is able to explain the zebras with frequency-equidistant zebra lines.
Key words: Sun: flares / Sun: radio radiation
© ESO, 2015
1. Introduction
Studies of the fine structure of solar microwave bursts with zebra patterns (zebras for short) are very important for refining both the zebra-generation mechanism and the diagnostics of the flare coronal plasma. In radio spectra, the zebras look like simultaneously excited waves at closely spaced, nearly equidistant frequencies, see examples in the following. Zebras are observed in a broad range of frequencies from the metric range to microwaves (Slottje 1972); in some cases up to 7.5 GHz (Chernov et al. 2012).
Many models explaining zebras have been proposed (Rosenberg 1972; Kuijpers 1975; Zheleznyakov & Zlotnik 1975; Chernov 1976, 1990; LaBelle et al. 2003; Kuznetsov & Tsap 2007; Bárta & Karlický 2006; Ledenev et al. 2006; Laptukhov & Chernov 2009; Tan 2010; Karlický 2013). But most of them do not explain all observed features of zebras: the frequency range, bandwidth, polarization, number and frequency separation of zebra lines, their time variations and the high-frequency limit. Moreover, it is still debated whether all zebras are of the same physical origin or if zebras are generated by several different mechanisms (Tan et al. 2014). For a review and comparison of zebra models, see Chernov (2011).
Among all proposed mechanisms, the most promising one is that based on the double plasma resonance (DPR; Zheleznyakov & Zlotnik 1975; Zlotnik 2013). This model assumes that the zebra line emission is generated at locations where the upper-hybrid frequency fup equals multiples of the electron-cyclotron frequency fb.
In this paper we start from our DPR model (Yasnov & Karlický 2015). We extend this model and propose a new diagnostic method that enables determining the magnetic field strength and the plasma density in the zebra radio source. In the advanced version of this model, we explain the high-frequency limit of microwave zebras. We also successfully model the zebras with equidistant zebra lines. We note that this type of zebras is usually considered as the main argument in favour of the zebra model based on Bernstein modes (Chiuderi et al. 1973).
This paper is organized as follows: in Sect. 2 we present our new diagnostic method. Tests of this method on artificially generated zebras and its application on observed zebras are reported in Sects. 3 and 4. The following Sects. 5–7 are devoted to the high-frequency limit of microwave zebras, zebras with equidistant zebra lines, and zebras in the model with the barometric density profile. Finally, we conclude in Sect. 8.
2. Determining the plasma parameters
Zebras are commonly used for diagnostics of plasma parameters in their radio sources. In the DPR model, the main problem is determining the number of the gyro-frequency harmonic s that corresponds to a selected zebra line. Namely, in this model the frequency f of the zebra line emission can be expressed as 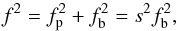 (1)where fp is the electron plasma frequency and fb is the electron gyro-frequency. This relation gives
(1)where fp is the electron plasma frequency and fb is the electron gyro-frequency. This relation gives 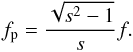 (2)Now, similarly as in Zheleznyakov & Zlotnik (1975), we write
(2)Now, similarly as in Zheleznyakov & Zlotnik (1975), we write 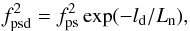 (3)where Ln = (dn/ dl)-1n is the characteristic density scale, fps and fpsd are the plasma frequencies at heights in the solar atmosphere corresponding to s and sd gyroharmonics, and ld is the spatial distance between the gyroharmonic sources. Similarly, we use fs and fsd for frequencies and fbs and fbsd for gyro-frequencies in these sources. Thus, we can write
(3)where Ln = (dn/ dl)-1n is the characteristic density scale, fps and fpsd are the plasma frequencies at heights in the solar atmosphere corresponding to s and sd gyroharmonics, and ld is the spatial distance between the gyroharmonic sources. Similarly, we use fs and fsd for frequencies and fbs and fbsd for gyro-frequencies in these sources. Thus, we can write ![\begin{eqnarray} &&f_{\rm sd}^2-f_{\rm s}^2 = f_{\rm psd}^2-f_{\rm ps}^2+f_{\rm bsd}^2-f_{\rm bs}^2 = \nonumber \\ &&f_{\rm ps}^2\left[\exp(-l_{\rm d}/L_{\rm n}) -1\right] + f_{\rm sd}^2/s_{\rm d}^2-f_{\rm s}^2/s^2 = \nonumber \\ &&f_{\rm s}^2\left[(s^2-1)/s^2\right] \left[\exp(-l_{\rm d}/L_{\rm n})-1\right] + f_{\rm sd}^2/s_{\rm d}^2-f_{\rm s}^2/s^2. \end{eqnarray}](/articles/aa/full_html/2015/09/aa26785-15/aa26785-15-eq21.png) (4)Using the ratio of squares of zebra line frequencies
(4)Using the ratio of squares of zebra line frequencies 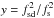 , the equation can be rewritten to
, the equation can be rewritten to ![\begin{eqnarray} y - 1 = \left[(s^2 -1)/s^2\right] \left[\exp(-l_{\rm d}/L_{\rm n})-1\right] + y/s_{\rm d}^2- 1 /s^2, \end{eqnarray}](/articles/aa/full_html/2015/09/aa26785-15/aa26785-15-eq23.png) (5)whose solution is
(5)whose solution is 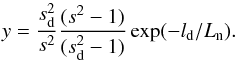 (6)Now, we apply this equation to two levels with s1 and s2, where Δs = s2 − s1. Then we have a set of two equations as
(6)Now, we apply this equation to two levels with s1 and s2, where Δs = s2 − s1. Then we have a set of two equations as 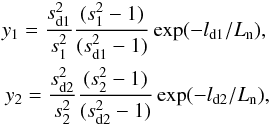 (7)where ld1 is the spatial distance between source heights corresponding to harmonic numbers s1 and sd1 = s1 + d, and ld2 is the distance between source heights corresponding to harmonic numbers s2 and sd2 = s2 + d.
(7)where ld1 is the spatial distance between source heights corresponding to harmonic numbers s1 and sd1 = s1 + d, and ld2 is the distance between source heights corresponding to harmonic numbers s2 and sd2 = s2 + d.
In agreement with Zheleznyakov & Zlotnik (1975), we assume that the distance ld can be computed from the formula 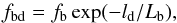 (8)where Lb = (dB/ dl)-1B is the characteristic magnetic field scale. Now, from the square root of Eq. (3) with the use of Eq. (2), we have
(8)where Lb = (dB/ dl)-1B is the characteristic magnetic field scale. Now, from the square root of Eq. (3) with the use of Eq. (2), we have 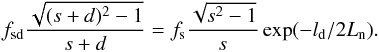 (9)Dividing now Eqs. (9) by (8), and considering Eq. (1), we can write
(9)Dividing now Eqs. (9) by (8), and considering Eq. (1), we can write 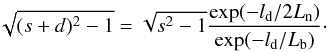 (10)The distance ld is then
(10)The distance ld is then 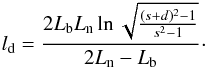 (11)We note that the sign of the distance ld is given by the sign of the natural logarithm (d can be positive or negative) and the sign of the term 2Ln − Lb.
(11)We note that the sign of the distance ld is given by the sign of the natural logarithm (d can be positive or negative) and the sign of the term 2Ln − Lb.
Now inserting Eq. (11) into the set of Eqs. (7), we obtain 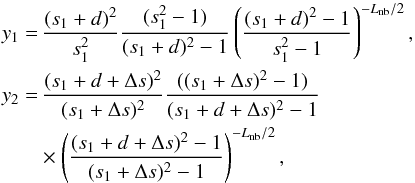 (11)where we use Lnb = 2Lb/ (2Ln − Lb). In these two equations there are two unknown variables (s1 and Lnb), whose values are obtained numerically using Mathematica. Then knowing s1 for specific zebra line and using Eqs. (1) and (2) and those defining the electron plasma fp and electron gyro-frequency fb, the magnetic field strength B and electron plasma density ne in the zebra radio source can be calculated.
(11)where we use Lnb = 2Lb/ (2Ln − Lb). In these two equations there are two unknown variables (s1 and Lnb), whose values are obtained numerically using Mathematica. Then knowing s1 for specific zebra line and using Eqs. (1) and (2) and those defining the electron plasma fp and electron gyro-frequency fb, the magnetic field strength B and electron plasma density ne in the zebra radio source can be calculated.
3. Test of the method
 |
Fig. 1 Electron density and temperature profiles as a function of height in the solar atmosphere according to Selhorst et al. (2008). |
We verified the method using artificially generated zebras. For this purpose, we considered the DPR (double plasma resonance) zebra model proposed by Yasnov & Karlický (2015), see also Yasnov (2014). In this model the density of the solar atmosphere is taken as in Selhorst et al. (2008), see Fig. 1. In the following, these densities are multiplied by the parameter nadd to determine effects of their changes. The magnetic field has the form of an arcade. This magnetic arcade is produced by two oppositely oriented magnetic dipoles located at y = −d/ 2 and y = d/ 2 and submerged under the photosphere at a depth of r0 = 30 Mm. We chose the magnetic dipole strength and dipole distance d in such a way that the magnetic field strength at the photosphere at the dipole axes is Bph = 3000 Gauss (G) and simultaneously the magnetic field strength at the photosphere in the middle between these dipoles (y = 0) is Bnls = 25 G.
Using this model, we computed the gyro-harmonic number s, heights in the solar atmosphere and frequencies of zebra lines of the artificial radio spectrum (Table 1). Then this spectrum was analysed with the method described in the previous section. We solved Eqs. (11), and the results of s1 are added in Table 1. We solved for all zebra lines separately. With this procedure, the number of s1 is lower than that of s. The table shows that the values of s1 agree very well with s.
Simultaneously, we computed the parameter Lnb. Its value is Lnb = −1.982 ± 0.007, which agrees very well with that estimated with our model (Lnb ≈ −2). In the model, the electron density decreases sharply in the zebra line regions and the magnetic field is nearly constant, that is, Ln ≪ Lb. For example, in the generation region of the gyro-harmonics 9−12, the model value of Ln/Lb is −0.0038, which corresponds to Lnb = −1.985. The negative value of Ln/Lb is given by the small positive gradient of the magnetic field and the negative gradient of the electron density.
These results show the effectiveness of the method for microwave zebras.
Parameters of zebra lines for Bph = 3000 G, Bnls = 25 G, nadd = 1, and y = 0.
Parameters of zebra lines (the same as in Table 1) for Bph = 3000 G, Bnls = 100 G, nadd = 1, and y = d/2.
Another test of the procedure was made for zebras at lower frequencies. We computed the model with the parameters Bph = 3000 G, Bnls = 100 G, nadd =1, and y = d/ 2. While in the previous case the zebra was generated in a relatively narrow area around the transition region, in this new case, zebras are generated at high altitudes and in a large area (about 100 Mm) in the solar atmosphere. The results are shown in Table 2 and agree well for parameters s1 and s. The difference between them is lower than 0.5. As a result of the spatially extended zebra source, the agreement between s1 and s is poorer than in the previous case, but still reasonable.
In this case, the computed parameter Lnb = 0.206 ± 0.003, that is, Ln/Lb ≃ 5.35. In the regions of zebra lines generation, the magnetic field decreases more strongly in the model than the electron density, that is, Ln/Lb> 1. In the model, the estimated values of Ln/Lb are lower than computed. For example, for the regions with gyro-harmonics 10−15, the parameter Ln/Lb ≃ 4.38. This means that in the metric range, where the generation region of zebras is more spatially extended than in the decimetric range, the precision of computation of Lnb is lower than in the decimetric range, but it is still good.
4. Applications to observed microwave zebras
 |
Fig. 2 Left panel: example of the zebra pattern observed by the Ondřejov radiospectrograph during the solar flare on 14 February 1999. Right panel: radio flux profile along the frequency at 12:08:57.7 UT. |
We first analyse the zebra observed by the Ondřejov radiospectrograph (Jiřička & Karlický 2008) during the flare on 14 February 1999 (Fig. 2). As can be seen here, at 12:08:57.7 UT the zebra lines were observed at 1.535, 1.56, 1.585, 1.61, 1.64, 1.67, 1.70, 1.73, 1.76, 1.80, 1.84, and 1.88 GHz. The solution of Eqs. (11) gives the gyro-harmonic number s1 = 32 and the parameter Lnb = 0.905 for the zebra line at the lowest frequency (1.535 GHz). The other zebra lines correspond to the gyro-harmonic numbers decreasing from 31 (1.56 GHz) to 21 (1.88 GHz). Now, assuming the radio emission of the zebra at the frequency of upper-hybrid waves, this gives the plasma density and magnetic field strength in the zebra-line source with s1 = 32 as ne = 2.8 × 1010 cm-3 and B = 17.1 G, respectively. The intermittent frequency drift of zebra lines in Fig. 2 is probably caused by the plasma turbulence, as proposed by Karlický (2014).
 |
Fig. 3 Left panel: example of the zebra pattern observed by the Ondřejov radiospectrograph during the solar flare on 6 June 2000. Right panel: radio flux profile along the frequency at 15:43:12.6 UT. |
As a second example, we analysed the zebra shown in Fig. 3. Here, at 15:43:12.6 UT the zebra lines were observed at 3.60, 3.65, 3.70, 3.76, 3.83, 3.90, 3.97, and 4.04 GHz. For the zebra line at the lowest frequency (3.6 GHz), the solution of Eq. (11) gives the gyroharmonic number s1 = 34 and the parameter Lnb = 1.021. The other zebra lines correspond to the gyroharmonic numbers decreasing from 33 (3.65 GHz) to 27 (4.04 GHz). Thus, for the emission in the double upper-hybrid frequency (for this assumption, see below) the plasma density and magnetic field strength in the zebra-line source with s1 = 34 is ne = 3.99 × 1010 cm-3 and B = 18.9 G, respectively.
5. High-frequency limit of microwave zebras
There are no zebras observed above 8 GHz (Tan 2010). Furthermore, Tan et al. (2014) mentioned only one zebra in the 7−8 GHz range. Therefore, we explain this high-frequency limit using our model. In our model we compute not only the zebra-line frequencies, but also the optical thicknesses of the zebra-line emissions considering the cyclotron and bremsstrahlung absorptions. For details, see Yasnov & Karlický (2015).
We here took the model parameters to be Bph = 2000 G and Bnls = 10, 20, and 100 G. We defined the high-frequency limit of the zebra emission as the zebra-line frequency where the optical thickness is still lower than one and at the following zebra line (with higher frequency) the optical thickness is greater than one. We considered two cases of zebras; a) low-polarized zebras, that is, those generated at the double upper-hybrid frequency; and b) high-polarized zebras generated at the upper-hybrid frequency.
Varying the plasma density in our model by the nadd parameter, we first computed the high-frequency limit for the low-polarized zebras, see Fig. 4. We note that a further increase of the parameter nadd does not change the limit. Even the change of the parameter r0, which changes the magnetic field gradient in the model essentially, the limit remains similar. Figure 4 shows that the results are practically independent of Bnls and the magnetic field structure (the parameter r0). Furthermore, Fig. 4 shows that the limit frequency for the low-polarized zebras is about 8.5 GHz, which agrees well with observations.
The same computations were made for the high-polarized zebras. We took the model parameters to be Bph = 2000 G, Bnls = 10 G and r0 = 30 Mm. The results are shown in Fig. 5. In this case, the maximum is at about 2 GHz, which is four times lower than for the low-polarized zebras. Namely, the optical thickness due to the bremsstrahlung absorption is inversely proportional to the square of the frequency. That is why the optical thickness of the same levels in the atmosphere is four times lower for double frequency. This last result shows that the zebras observed at frequencies above 2 GHz are probably generated at the double upper-hybrid frequency. This confirms our assumption made in estimating the plasma density and the magnetic field strength in the analysis of the zebra shown in Fig. 3.
 |
Fig. 4 High-frequency limit as a function of the parameter nadd for lowly polarized zebras with the model parameter Bph = 2000 G. The upper part with Bnls = 10 G and r0 = 30 Mm, the middle part with Bnls = 20 G and r0 = 30 Mm, and the bottom part with Bnls = 100 G and r0 = 7 Mm. |
6. Zebras with equidistant zebra lines
There are microwave zebras with equidistant zebra lines, which are usually interpreted in the zebra model based on Bernstein modes (Tan et al. 2014). However, this model has several drawbacks: a) it generates mainly extraordinary waves; b) the growth rate of these modes is much lower than that of the upper-hybrid waves; and c) the radio emission generated by non-linear interactions of Bernstein modes is very narrow-directional and thus has a low probability to be observed. Therefore, we simulated these zebras within our DPR model.
We considered the model of Selhorst et al. (2008), where the plasma density sharply decreases in the transition region. Microwave zebras generated in this region are thus produced in very spatially limited areas. This can lead to generation of the microwave zebras with equidistant zebra lines in the DPR model. An example of such a zebra with equidistant frequencies is shown in Fig. 6. We assumed the radio emission to be generated at the double upper-hybrid frequency and the model parameters to be Bph = 2000 G, Bnls = 10 G, nadd = 8 and r0 = 30 Mm. This figure only shows the emission for an optical thickness lower than one. In the interval of the parameter s = 50−120, the frequency separation of zebra-line frequencies is nearly constant. This is not a unique example, similar examples can be easily simulated by varying the model parameters. The only important aspect is the sharp decrease of the plasma density in the region of the zebra generation. This simulation shows that the zebras with equidistant zebra lines can be explained in the DPR model.
7. Zebras in models with the barometric density profile
All our computations show that the most important parameter necessary to generate microwave zebras is the plasma density profile.
For comparison with the results presented here and in Yasnov & Karlický (2015), we considered the barometric model of densities in the solar atmosphere as 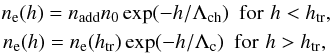 where h is the height in the solar atmosphere, htr means the height of the transition region, nadd is the multiplication factor, n0 and ne(htr) are the density at h = 0 and at the transition region, Λch and Λc are the scale-heights in the chromosphere and corona (Λ [m] = 50 T [K]), respectively. The temperature in the chromosphere and in the corona is taken to be Tch = 104 K and Tc = 106 K. The height of the transition region is close to that in the model of Selhorst et al. (2008), used in our zebra model (htr = 2.9 Mm). To have the density in the low corona in the barometric model the same as in our model, the density n0 is taken as n0 = 1.5 × 1012 cm-3. The density profile, the upper-hybrid frequency profile and the electron gyro-frequency harmonic profiles for the magnetic field parameters Bph = 2000 G, Bnls = 50 G, y = 0 and r0 = 30 Mm are shown in Fig. 7.
where h is the height in the solar atmosphere, htr means the height of the transition region, nadd is the multiplication factor, n0 and ne(htr) are the density at h = 0 and at the transition region, Λch and Λc are the scale-heights in the chromosphere and corona (Λ [m] = 50 T [K]), respectively. The temperature in the chromosphere and in the corona is taken to be Tch = 104 K and Tc = 106 K. The height of the transition region is close to that in the model of Selhorst et al. (2008), used in our zebra model (htr = 2.9 Mm). To have the density in the low corona in the barometric model the same as in our model, the density n0 is taken as n0 = 1.5 × 1012 cm-3. The density profile, the upper-hybrid frequency profile and the electron gyro-frequency harmonic profiles for the magnetic field parameters Bph = 2000 G, Bnls = 50 G, y = 0 and r0 = 30 Mm are shown in Fig. 7.
 |
Fig. 5 High-frequency limit as a function of the parameter nadd for highly polarized zebras with the model parameters Bph = 2000 G, Bnls = 10 G, and r0 = 30 Mm. |
 |
Fig. 6 Selected zebra-line emission frequencies (points) as a function of the parameter s for the lowly polarized zebras with the model parameters Bph = 2000 G, Bnls = 10 G, nadd = 8, y = 0 and r0 = 30 Mm. The straight line is added for comparison. |
 |
Fig. 7 Upper panel: plasma density in the barometric model as a function of height. Bottom panel: corresponding upper-hybrid frequency profile (thick line) and examples of the gyro-frequency harmonic profiles (thin lines). |
Computations made with Bph = 2000 G, Bnls = 50, and 10 G and in the interval of the parameter nadd = 0.01−1 show that microwave zebras cannot be observed in this case due to the strong bremsstrahlung absorption. The same result was obtained for Bph = 3000 G. An example of the results of computations for Bph = 2000 G, Bnls = 10 G, and nadd = 1 is shown in Table 3, where s means the harmonic number, h is the height of the zebra-line source, fup is the upper-hybrid frequency, and τ is the optical thickness. As can be seen here, the optical thickness is greater than one everywhere, especially at higher frequencies.
Because in the barometric model an area of the zebra generation is larger than in the model of Selhorst et al. (2008), it is reasonable to make computations in the model with a higher gradient of the magnetic field, which can be made by decreasing the parameter r0. We made these computations with the parameters Bph = 2000 G, Bnls = 100 G, nadd = 1, and r0 = 1 Mm. In this case, the magnetic field in the transition region is about 25 G. Results are summarized in Table 4. In this model the zebra lines with s< 8 do not exist. Table 4 shows that in this model the optical thickness is greater than one in all zebra lines. We note that for lower densities in the model, for example, for nadd = 0.1, the heights are higher and the zebra emission frequencies lower.
In Fig. 8 we present the optical thickness of the emission layer with f = fp in the chromosphere with the barometric density profile, considering the cyclotron and bremsstrahlung absorptions in the higher lying layers. It shows that generation of microwave zebras is impossible in the model with the standard barometric density profile. The generation of zebras needs models with a much steeper density profile, for example, the model of Selhorst et al. (2008).
Parameters of zebra lines for Bph = 2000 G, Bnls = 10 G, nadd = 1, r0 = 30 Mm and y = 0.
Parameters of zebra lines (the same as in Table 3) for Bph = 2000 G, Bnls = 100 G, nadd = 1, r0 = 1 Mm and y = 0.
The presented optical thicknesses are valid for all types of zebra models.
 |
Fig. 8 Optical thickness τ for the emission layer with f = fp for the parameters nadd = 1 (upper part) and nadd = 0.01 (bottom part). |
8. Conclusions
Using the double plasma resonance (DPR) model of zebras, we presented a new method for determining the number gyro-harmonics s of the selected line of microwave zebras. It enables computing the magnetic field strength and plasma density in the radio source of this zebra line. Furthermore, the parameter Lnb = 2Lb/ (2Ln − Lb), where Ln and Lb are the characteristic scale-heights of the plasma density and magnetic field in the zebra source, respectively, can be evaluated.
The method was successfully tested using artificially generated zebras in the model of Yasnov & Karlický (2015). In all tests the method showed high precision in determining the parameter s in broad intervals of the model parameters. It is important to mention that the method precision was high even for low values of s, where the emission frequency f essentially differs from the plasma frequency fp. This method was also applied to observed zebras, and the magnetic field strength and plasma density in the zebra source were determined.
We showed that the high-frequency limit of the low-polarized zebras is about 8 GHz, which agrees very well with observations. For the highly polarized zebras, this limit is about 2 GHz, which is four times lower than for the lowly polarized zebras. Namely, the optical thickness due to the bremsstrahlung absorption is inversely proportional to the square of the frequency. That is why the optical thickness of the same levels in the atmosphere is four times lower for the double frequency.
Furthermore, we showed that microwave zebras are preferentially generated in regions with steep gradients of the plasma density, for instance, in the transition region, as shown for example in the model of Selhorst et al. (2008). In models with smaller density gradients, such as the model with the barometric density profile, the microwave zebras are not generated owing to the strong bremsstrahlung and cyclotron absorptions.
Using this DPR model, we also successfully modelled zebras with equidistant zebra lines. We found that the most probable frequency range of this type of zebras is in the microwave range, which corresponds to the transition region, where is a steep gradient of the plasma density.
Acknowledgments
The authors thank the referee G. Chernov for useful comments. This research was supported by grant P209/12/0103 (GA CR) and EU FP7 project No. 606862 F-CHROMA.
References
- Bárta, M., & Karlický, M. 2006, A&A, 450, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chernov, G. P. 1976, Sov. Astron., 20, 449 [Google Scholar]
- Chernov, G. P. 1990, Sol. Phys., 130, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P., 2011, Fine Structure of Solar Radio Bursts, Astrophys. Space Sci. Lib., 375 [Google Scholar]
- Chernov, G. P., Sych, R. A., Meshalkina, N. S., Yan, Y., & Tan, C. 2012, A&A, 538, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiuderi, C., Giachetti, R., & Rosenberg, H. 1973, Sol. Phys., 33, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Jiřička, K., & Karlický, M. 2008, Sol. Phys., 253, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Karlický, M. 2013, A&A, 552, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karlický, M. 2014, A&A, 561, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuijpers, J. M. E. 1975, Ph.D. Thesis, Utrecht, Rijksuniversiteit [Google Scholar]
- Kuznetsov, A. A., & Tsap, Y. T. 2007, Sol. Phys., 241, 127 [NASA ADS] [CrossRef] [Google Scholar]
- LaBelle, J., Treumann, R. A., Yoon, P. H., & Karlický, M. 2003, ApJ, 593, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Laptukhov, A. I., & Chernov, G. P. 2009, Plasma Phys. Rep., 35, 160 [Google Scholar]
- Ledenev, V. G., Yan, Y., & Fu, Q. 2006, Sol. Phys., 233, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenberg, H. 1972, Sol. Phys., 25, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Selhorst, C. L., Silva-Válio, A., & Costa, J. E. R. 2008, A&A, 488, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slottje, C. 1972, Sol. Phys., 25, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, B. 2010, Astrophys. Space Sci., 325, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, B., Tan, C., Zhang, Y., Mészárosová, H., & Karlický, M. 2014, ApJ, 780, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Yasnov, L. V. 2014, Sol. Phys., 289, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Yasnov, L. V., & Karlický, M. 2015, Sol. Phys., 290, 2001 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V., & Zlotnik, E. Y. 1975, Sol. Phys., 44, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Zlotnik, E. Y. 2013, Sol. Phys., 284, 579 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameters of zebra lines (the same as in Table 1) for Bph = 3000 G, Bnls = 100 G, nadd = 1, and y = d/2.
Parameters of zebra lines for Bph = 2000 G, Bnls = 10 G, nadd = 1, r0 = 30 Mm and y = 0.
Parameters of zebra lines (the same as in Table 3) for Bph = 2000 G, Bnls = 100 G, nadd = 1, r0 = 1 Mm and y = 0.
All Figures
 |
Fig. 1 Electron density and temperature profiles as a function of height in the solar atmosphere according to Selhorst et al. (2008). |
| In the text | |
 |
Fig. 2 Left panel: example of the zebra pattern observed by the Ondřejov radiospectrograph during the solar flare on 14 February 1999. Right panel: radio flux profile along the frequency at 12:08:57.7 UT. |
| In the text | |
 |
Fig. 3 Left panel: example of the zebra pattern observed by the Ondřejov radiospectrograph during the solar flare on 6 June 2000. Right panel: radio flux profile along the frequency at 15:43:12.6 UT. |
| In the text | |
 |
Fig. 4 High-frequency limit as a function of the parameter nadd for lowly polarized zebras with the model parameter Bph = 2000 G. The upper part with Bnls = 10 G and r0 = 30 Mm, the middle part with Bnls = 20 G and r0 = 30 Mm, and the bottom part with Bnls = 100 G and r0 = 7 Mm. |
| In the text | |
 |
Fig. 5 High-frequency limit as a function of the parameter nadd for highly polarized zebras with the model parameters Bph = 2000 G, Bnls = 10 G, and r0 = 30 Mm. |
| In the text | |
 |
Fig. 6 Selected zebra-line emission frequencies (points) as a function of the parameter s for the lowly polarized zebras with the model parameters Bph = 2000 G, Bnls = 10 G, nadd = 8, y = 0 and r0 = 30 Mm. The straight line is added for comparison. |
| In the text | |
 |
Fig. 7 Upper panel: plasma density in the barometric model as a function of height. Bottom panel: corresponding upper-hybrid frequency profile (thick line) and examples of the gyro-frequency harmonic profiles (thin lines). |
| In the text | |
 |
Fig. 8 Optical thickness τ for the emission layer with f = fp for the parameters nadd = 1 (upper part) and nadd = 0.01 (bottom part). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


