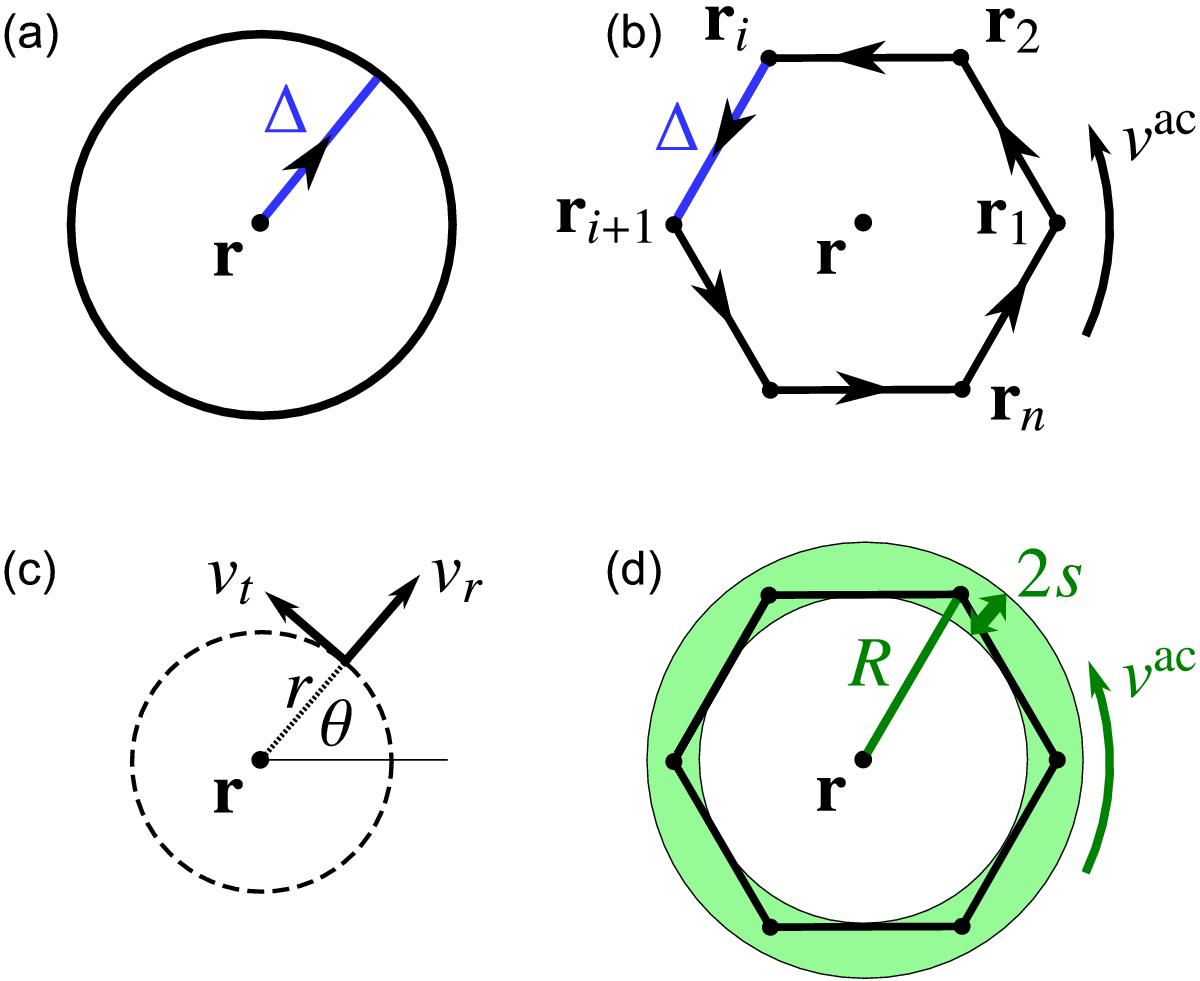
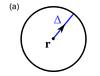
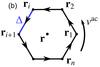
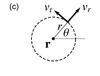
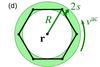
Measurement geometries for divergence- and vorticity-sensitive travel times and LCT velocities. a) The divergence-sensitive travel time τ^oi is obtained by measuring the travel-time difference between a central point r and a surrounding annulus of radius Δ. b) The vorticity-sensitive travel time τ^ac is obtained by measuring the travel-time differences τ^diff between adjacent points along a regular polygon surrounding r. The polygon consists of n points and has edges of length Δ. The points are situated on a circle of radius R = Δ/ [2sin(π/n)]. The travel time τ^ac is the average over the components τ^diff (see Eq. (3)). We obtain circulation velocities v^ac by multiplying τ^ac by a calibration factor. c) From LCT, we obtain the horizontal velocity components v_x and v_y. Given a reference point r, the LCT velocities can be expressed in 2D polar coordinates (r,θ) by the outward pointing radial velocity component v_r and the anticlockwise pointing tangential velocity component v_t. d) Using LCT velocities, we approximate v^ac by averaging the tangential velocity component v_t over the annulus shaded in green. The annulus is defined by its radius R and half-width s. We choose R = Δ for n = 6 and s = 2 Mm.