| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 25 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201424471 | |
| Published online | 01 September 2015 | |
The DICE calibration project Design, characterization, and first results
1 LPNHE, CNRS-IN2P3 and Universités Paris 6 and 7, 4 place Jussieu, 75252 Paris Cedex 05, France
e-mail: nicolas.regnault@lpnhe.in2p3.fr
2 Canada-France-Hawaii Telescope Corporation, Kamuela, HI 96743, USA
3 Research School of Astronomy and Astrophysics, Australian National University, ACT 2601, Australia
Received: 24 June 2014
Accepted: 26 May 2015
Aims. We describe the design, operation, and first results of a photometric calibration project, called DICE (Direct Illumination Calibration Experiment), aiming at achieving precise instrumental calibration of optical telescopes. The heart of DICE is an illumination device composed of 24 narrow-spectrum, high-intensity, light-emitting diodes (LED) chosen to cover the ultraviolet-to-near-infrared spectral range. It implements a point-like source placed at a finite distance from the telescope entrance pupil, yielding a flat field illumination that covers the entire field of view of the imager. The purpose of this system is to perform a lightweight routine monitoring of the imager passbands with a precision better than 5 per-mil on the relative passband normalisations and about 3 Å on the filter cutoff positions.
Methods. Prior to installation, the light source is calibrated on a spectrophotometric bench. As our fundamental metrology standard, we use a photodiode calibrated at the National Institute of Standards and Technology (NIST). The radiant intensity of each beam is mapped, and spectra are measured for each LED. All measurements are conducted at temperatures ranging from 0 °C to 25 °C in order to study the temperature dependence of the system. The photometric and spectroscopic measurements are combined into a model that predicts the spectral intensity of the source as a function of temperature.
Results. We find that the calibration beams are stable at the 10-4 level – after taking the slight temperature dependence of the LED emission properties into account. We show that the spectral intensity of the source can be characterised with a precision of 3 Å in wavelength, depending on how accurately we are able to calibrate the wavelength response of the mononochromator. In flux, we reach an accuracy of about 0.2 − 0.5% depending on how we understand the off-diagonal terms of the error budget affecting the calibration of the NIST photodiode. We describe how with a routine ≲ 60-mn calibration program, the apparatus is able to constrain the imager passbands at the targeted precision levels.
Key words: methods: data analysis / telescopes / techniques: photometric / instrumentation: miscellaneous
© ESO, 2015
1. Introduction
The measurement of the dark energy equation of state with type Ia supernovae (SNe Ia; see for recent examples: Suzuki et al. 2012; Betoule et al. 2014) sets very strong constraints on the accuracy of the flux calibration of the imagers used to infer the SN Ia luminosity distances. Indeed, mapping the relative variation in SN distances with redshift boils down to comparing fluxes measured at both ends of the visible spectrum. A key concern is therefore the control of the imager throughput as a function of wavelength. In practice, this means, on the one hand, controlling the intercalibration of the fluxes, measured in different passbands, and on the other hand, measuring and monitoring the passband shapes, in particular, the position of the filter fronts.
The best technique of passband intercalibration today relies on observations of stellar spectrophotometric standards, whose absolute spectral energy distribution (SED) is known with accuracy. The most reliable sets of standards are probably those that were established to calibrate the instruments mounted on-board HST (CALSPEC 2000). The CALSPEC flux scale is defined by the SED of three hot DA white dwarfs, as predicted by a non-local thermodynamical equilibrium (NLTE) model atmosphere code, itself tuned to the Balmer line profiles of each dwarf (Bohlin 2007; Rauch et al. 2013). The calibration of the HST STIS and NICMOS spectrographs obtained by observing these fundamental standards is then propagated to a larger network of redder and mostly fainter stars (Bohlin 2010; Bohlin et al. 2014).
This approach is robust, since it relies on more than one fundamental calibrator. It is also sound, since each CALSPEC release can be traced back to a well-identified series of HST observations and to a particular version of a stellar atmosphere model. However, even DA white dwarfs are complex objects, and the modelling systematics that affect the CALSPEC flux scale are difficult to estimate with precision.
Most recent supernova surveys have been anchored on the CALSPEC network. This was often implicit because people were using the SEDs of historical bright standards recalibrated with HST (Bohlin & Gilliland 2004a,b) when interpreting their magnitudes as fluxes (see e.g. Amanullah et al. 2010). A few projects, such as SNLS and SDSS, tried to explicitly tie their calibration to specific CALSPEC calibrators (Holtzman et al. 2008; Regnault et al. 2009). The calibration error budgets published by these authors were dominated by uncertainties introduced in the metrology chain that links the standard star observations to the science images. Recent work by Betoule et al. (2013) has shown, however, that it is now possible to transfer the CALSPEC flux scale with uncertainties comparable to the CALSPEC internal uncertainties (σg − i ~ 3 − 5 mmag).
To improve on the current cosmological measurements, future dark energy surveys will need to intercalibrate their passbands at a few per-mil, which is below the current estimates of the CALSPEC uncertainty budget. Since modern, ground-based imagers display repeatabilities of 1−3 mmag (Montalto et al. 2007), they can in theory be calibrated to this precision level. However, it is not obvious yet that this ambitious goal is within reach of the stellar calibration techniques presented above.
In this context, alternate calibration strategies have been proposed by several groups. Most have in common that they rely on laboratory flux standards instead of stellar models. Over the past two decades, flux metrology has indeed experienced dramatic improvements, moving from 1−2% source standards to detector standards accurate at the 0.1% level. In the visible, the metrology standards are generally silicon photodiodes, whose calibration can be traced back to the Primary Optical Watt Radiometer (POWR, Houston & Rice 2006), an electrical cryogenic substitution radiometer maintained by the National Institute of Standards and Technology (NIST) as the official implementation of the optical watt. To characterise the photodiodes provided to its end users, NIST maintains a sophisticated metrology chain (Larason & Houston 2008) involving intermediate light sources, notably the SIRCUS laser facility (Brown et al. 2006, 2000) and the Spectral Comparator Facility (SCF). With a calibrated photodiode in hand and the goal of calibrating another light detector, the end user has no choice but to build an intermediate light source to transfer the NIST flux scale to his own instrument. As a consequence, most alternatives to stellar calibration implement variations around the generic metrology chain presented in Fig. 1.
Among those, at least two groups have proposed to revisit the historical measurements of Hayes & Latham (1975) using modern flux metrology techniques. The goal is to compare the CALSPEC and NIST flux scales directly using bright standard stars. A first team is developing the ACCESS rocket-borne 40-cm telescope (Kaiser et al. 2010). The instrument is a spectrograph, sensitive from 350-nm to 1.7 μm and calibrated directly at the SIRCUS facility. The other team, comprising NIST scientists, is building a spectrophotometer at the focus of a 10-cm telescope, calibrated with an artificial source, which will target stars in the 0 <V< 5 magnitude range (e.g. McGraw et al. 2012). Both projects will rely on HST observations to bridge the gap between their magnitude range and the CALSPEC magnitude range. They will permit a direct comparison between the CALSPEC and NIST flux scales, which is an invaluable piece of information. This does not, however, relieve future surveys from monitoring their own instrument, in particular, from measuring their passbands in situ and checking for a possible evolution in the long term.
Today, the required accuracy on the positioning of the passband cut-offs is as low as a fraction of a nanometre. As an example, for SNLS, decreasing the uncertainty on r-band positioning from 3-nm to 2 Å decreases the uncertainty on w as much as adding 200 SNe Ia in the Hubble diagram. Passband models are usually built using pre-installation test-bench measurements of the imager optical components. This is not entirely satisfactory because filters may evolve over time. For this reason, nearly every modern survey has plans to build and operate a dedicated calibration source, able to follow the shape and normalisation of the imager passbands in real time. A precursor in this domain is the apparatus described in Doi et al. (2010). It consists in a movable light source, designed to inject quasi-monochromatic light into the optics of the SDSS 2.5-m telescope, and measure its effective passbands in situ. This system permitted to unveil significant variations in the blue part of the imager u band.
Stubbs & Tonry (2006) push the concept one step further by describing how an in-situ narrow-band illumination system can be used to transfer the calibration of a NIST photodiode to an astronomical imager. Implementations of the procedure sketched in their paper are the systems developed for the Mosaic imager on the CTIO 4-m Blanco telescope (Stubbs et al. 2007) and for the PanSTARRS GigaPixel imager (Stubbs et al. 2010). Another notable example, built along similar design principles, is the DECal system (Marshall et al. 2013) now installed in the dome of the Blanco Telescope to monitor and calibrate the DECam imager (DePoy et al. 2008). All these systems consist in a large diffusive screen placed in front of the telescope pupil and illuminated with monochromatic light, generated either by a lamp coupled to monochromators or by a tunable laser. So far, these projects have mostly focussed on in-situ measurements of the passband shapes. Stubbs et al. (2010) was able to perform a comparison between a stellar and an instrumental calibration, reporting a qualitative agreement of ~ 5% between both.
 |
Fig. 1 Generic metrology chain from POWR, the official implementation of the optical watt, which is maintained at NIST, to the telescope imagers. |
DICE1 was conceived by members of the SNLS collaboration, building upon the lessons learned working with the MegaCam wide field imager. It shares most of the goals of the projects described above, but differs in several points of its design. The primary goal of the DICE project is to implement the metrology chain sketched in Fig. 1, i.e. to transport the calibration carried by a NIST photodiode to the MegaCam imager and compare this calibration to CALSPEC. This includes performing a spectrophotometric calibration of the light source using the NIST photodiode as a metrology standard (Step 1 in Fig. 1), measuring the relative normalisations of the MegaCam passbands from series of calibration exposures taken with DICE (Step 2), and applying this calibration to observations of CALSPEC standards (Step 3).
This paper is the first in a series of three papers that will describe Steps 1, 2, and 3. For now, we focus on Step 1. We present the design and implementation of the DICE calibration sources (Sect. 2). We then concentrate on the spectrophotometric characterisation of the DICE sources in Sects. 3–5, on a dedicated test bench equipped with a photodiode calibrated at NIST. Spectrophotometry is notoriously difficult, and we had to develop specific methods to remain immune to the measurement systematics. In Sect. 6, we venture into the area that will be covered in the next DICE papers: we sketch briefly how a DICE source can be used to calibrate a broadband imager, and we estimate the precision of the calibration that can be obtained from DICE observations by propagating the Step 1 error budget established in this paper.We conclude in Sect. 7.
2. The DICE light source
The design of the DICE light source has been described in Juramy (2006), Barrelet & Juramy (2008), and Juramy et al. (2008). Two demonstrators have been built and installed. A first apparatus (SnDICE) was designed in 2007 for the MegaCam wide field imager (Boulade et al. 2003) which equips the 3.6-m Canada-France-Hawaii Telescope (CFHT). In 2011–2012, a second light source (SkyDICE) was built for the SkyMapper imager (Keller et al. 2007) with an improved design, building on the lessons learned with SnDICE. A third source was also built and kept at LPNHE for long-duration test-bench studies.
A key requirement that guided our design effort is that a calibration instrument must be as simple and easy to maintain as possible. Also, it must intrinsically be as stable as possible, with additional built-in redundancies that allow checking for long-term drifts of the intensity delivered into the telescope pupil. As a rule of thumb, we consider that to calibrate an instrument at the permil level, we must be able to measure and study any 1%0 drift of its response with a precision of 10% or better. This sets an ambitious stability goal on the light source of about 10-4. In the rest of this section, we present the most important aspects of the light source design.
2.1. Calibration beam
 |
Fig. 2 Left: DICE calibration beam. A DICE light source consists in a quasi-point source, located at a finite distance from the telescope pupil. Such a beam generates a quasi-uniform illumination of the focal plane. Right: science beam. The light from a distant source, such as a star, may be approximately modelled by a plane wave that fills the entire telescope aperture. Such a beam is focussed on a single point of the focal plane. |
Ideally, a calibration light source should mimic the science objects under study as much as possible. Since a supernova survey is dealing primarily with point sources (supernovae and field stars), we should try to generate quasi-parallel beams, covering the entirety of the primary mirror (see Fig. 2b). Such a beam would result in a spot on the focal plane, and we could use the photometry code used in the survey photometry pipeline to estimate its flux, thereby avoiding the systematic errors that arise from using different flux estimators.
Unfortunately, building a good artificial star turns out to be difficult. We therefore deliberately opted for a different design (Fig. 2a). SnDICE is a point source located in the dome a few metres away from the telescope primary mirror and close to the object plane. The source generates a conical, quasi-Lambertian beam, of aperture ~ 2o, so slightly larger than the telescope’s angular acceptance. Such an illumination results in an almost uniform focal-plane illumination.
As shown in Fig. 2, the calibration beam is radically different from the science beam. In particular, the angular distribution of the light rays that hit the various optical surfaces (e.g. the interference filters) is not comparable. However, this specific calibration beam has at least two very nice properties. First, no intermediate elements (folding mirror, window, screen, etc.) are present between the light emission zone and the primary mirror. As a consequence, the design stays very simple, and the system is expected to be stable in the long term. Second, the structure of the beam is much simpler than the science beam, in the sense that each pixel sees photons that came through a unique path. In other words, there is a one-to-one relationship between the focal plane elementary surface elements and the calibration beam elementary solid angles. It is therefore quite simple to predict the focal plane illumination, once one knows the beam radiant intensity map: the former follows from the latter from purely geometrical considerations, involving propagation of light in free space, and through the optics.
2.2. Light emitters
Narrow-spectrum light emitting diodes (LED) were chosen as light emitters. As shown later in this paper, LEDs are extremely stable, as long as they are fed with stable currents and operated at a stable temperature. It it is relatively easy today to build current sources that are stable at a few 10-5 over a temperature range of a few degrees, and the LED emission properties vary with temperature in a smooth and simple manner. One of the purposes of this paper is to show that one can build a LED-based light source, delivering beams whose stability can be controlled at the level of a few 10-4 over long durations.
 |
Fig. 3 Lower panels: (left) coverage of the MegaCam filters with SnDICE (2008). The central wavelengths of all LEDs are displayed with arrows. The shaded regions show the wavelength extension of each LED SED – within 7% of the spectrum peak. In 2007, no narrow spectrum LED with sufficiently high power was available around 700-nm and above 900-nm. Right: coverage of the SkyMapper filters with SkyDICE (2010). The position of about half of the LEDs were chosen so that they constrain the filter cutoffs well. The other LEDs were selected to fill the gaps between filter cutoffs with about one LED every 20/30-nm. Upper panels: (right) sampling from the near-UV to the near-IR achievable with the LEDs listed in the OSRAM and Roithner catalogs. Left: optimised sampling of the MegaCam passbands that can be implemented today with the LEDs available on the market. |
LEDs do not emit monochromatic light. The typical FWHM of a LED spectrum is about δλ/λ ~ 5−7% (i.e. 20-nm to 50-nm). This means that we need 20 to 25 LEDs to cover the entire visible spectrum – from 350-nm to 1100-nm. In Fig. 3, we show the sampling that could be obtained with the first prototype, which was built for MegaCam (Fig. 3a). We also show, for comparison, what could be achieved four years later with SkyDICE, our second prototype, built to calibrate SkyMapper (Fig. 3b). As can be seen, the diversity of LEDs available on the market improved very significantly in a few years. Today, by combining the catalogues of the three main LED manufacturers, it is theoretically possible to cover the entire spectral range of silicon imagers with about one LED every 10−20 nm (upper panel of Fig. 3b) or to design some sort of “optimal sampling” of the passbands (upper panel of Fig. 3a).
In this design, we chose to sacrifice wavelength precision in favour of high-stability illumination. This makes sense, since what one actually needs is a follow-up more than an absolute measurement of the filter cutoff positions. The filter transmissions are measured well prior to installation, and our goal is instead to monitor any drift over the life time of the instrument. One of the aims of this paper is to estimate how precisely one can locate a filter front with such an instrument, which delivers a coarse wavelength sampling. We show in Sect. 6 that excellent precision may be attained with a small number of exposures, as long as we can secure a precise model of the spectral intensity delivered by the light source.
As temperature increases, the LED emission efficiency drops by about 0.5%/°C, and the mean wavelength of the emitted light shifts redwards by as much as 0.1 Å/°C. We often refer to these variations as the “cooler-brighter” and “cooler-bluer” effects, respectively. As discussed in Sect. 3.2, these variations are generally linear and extremely reproducible. As a consequence, once each emitter has been characterised well, one only needs to implement a real-time follow-up of the source temperature to account for these effects.
The temperature variations induced by the LED itself are small, if detectable. Around 2007−2008, the typical power consumption of our LEDs operated at a low regime was of 50 to 100 mW. With the new generation of LEDs available today, it is closer to 10 mW. A large fraction of this power is dissipated as heat, but it is easy to build a heat sink able to absorb all of it. We have verified that if a LED is correctly glued to a radiator with a heat-conducting glue, no noticeable temperature elevation of the radiator itself can be detected. The only exceptions so far are less powerful LEDs (older models or UV LEDs), which have to be operated near their maximum power. For those emitters, we found typical radiator temperature elevations of about 0.1 °C, with a maximum of 0.2 °C for a UV LED, after an hour of operation).
2.3. Light source design
 |
Fig. 4 Design of the DICE LED head. The LED head is made of 8 aluminium blocks pierced with 24 holes corresponding to each of the 24 LED channels. Black masks are placed between each block to shape the beam and minimise the stray light. Each channel is equipped with an off-axis control photodiode that monitors the light delivered by the LED in real time. The photodiodes are placed on a board just behind the front face of the device. The LEDs are in thermal contact with an aluminium radiator, in order to dissipate waste heat and monitor the LED temperature. An additional central 25th channel delivers a pencil beam used to control the relative orientation of the device with respect to the telescope. |
The mechanical design of the light source is illustrated in Fig. 4. SnDICE and SkyDICE have very similar designs. SnDICE is a 150 mm × 150 mm × 300 mm modular box, made of eight almost identical anodised aluminium blocks, each pierced with 25 apertures to let the light through. The LEDs are located on the back of the device, about 260-mm from the front face. The calibration beams exit through ⌀ 9-mm apertures located on the front face of the device. This design permits conical 2° wide beams to be generated. SkyDICE, the second prototype, is shorter (150 mm × 150 mm × 227 mm) because it needs to generate wider (3°) beams to cover the larger (5.7 deg2) field of view of the imager. The modularity of the design allows us to adapt the aperture of the beam easily as a function of the imager field of view.
The light source implements 24 calibration channels, each generating a conical Lambertian beam, in order to cover the 350 nm <λ< 1100 nm spectral range as evenly as possible. The LED currents are chosen so that a beam generates about 1000 photoelectrons per second in each pixel. As the typical solid angle subtended by a pixel is about 10-12 sr, this means that the radiant intensity of the LED should generate of the order of 1015γ/ s/sr, which corresponds to about 0.5 mW/sr at 500-nm.
The source is attached to the dome of the telescope. It can rotate around an altitude and an azimuth axis, in order to control the alignment of the LED beams with the telescope axis. By moving the source and the telescope simultaneously, it is possible to illuminate nearly every region of the primary mirror.
A special LED channel, called the artificial planet is used to control the relative alignment of the device and the telescope. The planet light is generated by a wide spectrum LED covering all the filter passbands. The planet channel is equipped with a small ⌀ 10-mm convergent lens that transforms the isotropic LED beam into a quasi-parallel beam. Planet exposures produce a spot on the imager focal plane, along with ghosts, owing to internal reflexions between the optical components. The position of the planet spot is a direct measurement of the angle between the telescope optical axis and the planet beam. It is measured with a precision of about 3′′ (the FWHM of the spot itself being of about 20′′). This precision is slightly better than the precision of the motor axis encoders (0.0025 degree, 9′′).
2.4. Generation of the LED currents
The intensity of the light emitted by each LED is a function of the current injected into it. The LED currents are generated (and monitored in real time) by a custom-made backend board, connected to the illumination system with an analogue link. We attempted to build a current source that achieves an electrical stability better than 10-5 over a temperature range of a few degrees. It is classically implemented as a transistor current source driven by a programmable voltage level and stabilised with a negative feedback loop (see e.g. Horowitz & Hill 1989, p. 181). For redundancy, the feedback voltage level is also sampled at a rate of a few kHz by a LTC1608 16-bit ADC and logged for offline checks.
The accuracy and stability of this current source depends entirely on a few high-quality commercial components, used in the board, namely the voltage references of the ADC and DAC, the voltage division chains of the ADC and DAC, and the serial resistors. Extensive, long-duration tests of the generated currents show that they are stable at the 10-5-level (Fig. 7). As the characteristics of the components may have a small temperature dependence, the temperature of the backend board is monitored in real time during data-taking.
2.5. Redundancies
Redundant checks are an essential part of the design. No matter how stable the source is on a test bench, we need to prove that the light actually delivered during the calibration runs is not affected by unexpected fluctuations or long-term drifts. For this reason, several critical quantities are monitored in real time during operations.
The temperature of the LEDs is the most important of all of these. What is measured in practice is the temperature of the radiator on which all LEDs are glued with a thermally conductive glue. For this purpose, we use a PT1000 thermistor glued to the radiator. What we monitor with this probe does not strictly correspond to the temperature of the LED junctions. It is, however, a surprisingly good proxy, which allows us to empirically standardise each LED on a test bench and use these standardisation relations later during operations.
Another critical point is the stability of the current source itself. We characterise it with two observables. First, the temperature of the backend board, which may have an impact on the current generator, is monitored using a DS600 temperature sensor, mounted on the board itself. Second, the current actually delivered to the LED (in practice, the voltage drop across a resistor mounted in series with the LED) is also logged for offline checks.
Finally, we directly characterise the light actually delivered by the LED by placing an off-axis monitoring photodiode in each LED channel, close to the exit hole (see Fig. 5). We use 5.8 mm × 5.8 mm Centronic2 OSD35-7 photodiodes, covering the full wavelength range of the illumination system with good efficiency in the UV. These control photodiodes are mounted on a board located just behind the front panel of the instrument (see Fig. 4).
All these quantities are digitised on the backend board at a frequency that can be tuned (from 1 kHz to 32 kHz), so that one can study the possible sources of noise over a large band. The digital samples are stored in a 16 MB buffer that is read out on demand by the DAQ system (typically after each calibration frame).
 |
Fig. 5 Sketch of a calibration channel showing the emitting LED and the off-axis monitoring photodiode. |
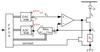 |
Fig. 6 Schematics of the current source. |
 |
Fig. 7 Relative variations in the LED current, measured as the voltage drop across a resistor in series with the LED and monitored over a duration of 3 weeks. During this period, the LED head was operated without interruption on our spectrophotometric test bench. During this run the temperature varied by about 5 °C. As can be seen, the current varies by a few 10-5 at most. |
Another miniaturised system, comprising a cooled, large area photodiode coupled to a ultra-low noise current amplifier has been built to monitor the light as it goes through the telescope optical path. It has not been used extensively in our analysis. We describe it in Appendix F.
2.6. Data acquisition
The DAQ and control system of these light sources run on a dedicated industrial PC (PC104), which can be installed a few metres away from the source. It is connected to the backend board with a USB link and to the telescope control system (TCS) with an ethernet link. In its current implementation, it hosts a lightweight server, which interacts with the TCS through a variant of the XML-RPC protocol. The server communicates with the backend electronics and relays the orders sent by the TCS. In particular, it controls the LED current and the LED head orientation motors, and it retrieves on demand the monitoring data stored on the backend board and sends them to the TCS so that they can be stored along with the calibration frames.
2.7. Operations
All calibration frames are taken during daytime in order not to interfere with the telescope observing schedule. This requires the dome to be dark, or requires monitoring the ambiant luminosity with the imager itself, complemented with an external device, such as one of the modules described in Appendix F. In practice, we have found that in the years 2008−2010, the dome of CFHT was very dark with a contamination lower than 0.05 ADU/s/pixel. For a 10 s exposure, with a typical level of ~5000 to 10 000 ADU, this yields a relative contamination by ambiant light of 5 × 10-5 to 10-4 at most. The enclosure of SkyMapper is slightly less light-tight, but the ambiant luminosity is also lower than 0.1 ADU/s, giving relative contaminations of a few 10-4. With such low contamination levels, we did not implement any correction at the pixel level. During a later series of calibration runs performed at the CFHT from January to August 2014, the dome was found to be significantly brighter, following the installation of venting apertures (several ADU/s/pixel). The ambient luminosity was then monitored by interlacing the calibration frames with dark dome exposures taken in the same position with the LED turned off. This nearly doubled the duration of a typical calibration run from ~50′ to 1 h 40′ (see Table 2 of Sect. 6.3).
A calibration run goes as follows. The telescope and dome motion are decoupled, and the telescope points inside the dome in the direction of the illumination device. The optical axes of both instruments are then aligned using the planet beam (see Sect. 2), as a guide. Once the alignment of both instruments is known, within an acceptable range, series of calibration exposures may be taken using the main LEDs.
Several types of calibration exposures may be taken. The stability of the readout electronics is studied with repeated exposures of the same LED, taking advantage of the 10-4 stability of the illumination system. The linearity of the imager is checked using illumination ramps (i.e. exposures of the same LED of longer and longer exposure time). Finally, one measures the instrument passbands with series of calibration frames taken with all the LEDs matching the passband under study.
As we see in Sect. 6, calibrating one single filter requires taking about four to eight exposures (each with a different LED), of one to ten seconds each. The length of a calibration sequence is therefore dominated by the imager readout time (40 s for MegaCam) and never exceeds ten minutes. As a result, it is possible to check the five to six filters that equip MegaCam or SkyMapper in less than one hour.
3. Spectrophotometric test bench: overview
 |
Fig. 8 Spectro-photometric test bench. Left panel: photometric bench. The photodiode is placed on a linear table and moved in planes parallel to the z-axis to map each LED beam. Right panel: a monochromator is inserted between the source and the photodiode. |
3.1. Goal
The primary goal of the test bench studies is to transfer the calibration carried by the NIST photodiode to the light source (arrow labelled 1 in Fig. 1). In practice this means that we want to characterise the emissivity of each LED using the NIST photodiode as our primary standard.
The physical quantity which describes the emissivity of a point source is its spectral intensity, 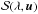 . It is defined as the power emitted by the source, per unit wavelength and per unit solid angle (at a given wavelength λ and in a given direction u). Since the properties of many types of LEDs are sensitive to temperature, we expect
. It is defined as the power emitted by the source, per unit wavelength and per unit solid angle (at a given wavelength λ and in a given direction u). Since the properties of many types of LEDs are sensitive to temperature, we expect  to also be a function of T:
to also be a function of T: 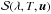 .
.
Our goal is to build a smooth model Ŝ(λ,T,u) of the LED’s true spectral intensity 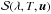 , which is valid in the temperature range 0 °C <T< + 25 °C and which is typical of what is measured in most telescope enclosures. Along with this model, we would like to build an uncertainty model to account for the finite precision of the test-bench measurements and the finite stability of the source. These two ingredients will then allow us to predict, with a known accuracy, the amount of calibration light delivered by the source for any real calibration exposure.
, which is valid in the temperature range 0 °C <T< + 25 °C and which is typical of what is measured in most telescope enclosures. Along with this model, we would like to build an uncertainty model to account for the finite precision of the test-bench measurements and the finite stability of the source. These two ingredients will then allow us to predict, with a known accuracy, the amount of calibration light delivered by the source for any real calibration exposure.
To build such a model, we need to accumulate enough measurements at temperatures typical of what is measured in a telescope enclosure. We also need to characterise the short-term and long-term stability of the source. In the next sections, we describe the test-bench configurations, the measurements that are taken, and the way we combine them to build a smooth estimate of the LED spectral intensities.
3.2. Test-bench setup
A sketch of the calibration test bench is shown in Fig. 8. The light source is placed on one end of a 2.5-m long optical table and mounted on an X-Y Kinetic Systems KVP-100 linear table, with a total stroke length of 150-mm.
A 1 cm2 Hamamatsu S2281 Si photodiode was purchased from NIST to be used as our primary standard. Following the NIST procedures, it is operated unbiased at room temperature3. Depending on the bench setup (see below), the photocurrents generated by the photodiode vary from a few nano-amperes (in photometric mode) down to a few pico-amperes (in spectroscopic mode). They are measured with a Keithley 6514 feedback picoammeter.
The calibrated photodiode is mounted on a KVP-100 X-Y linear table that allows for a stroke length of about 300-mm. A third motorisation permits moving it by about 1500-mm along the z-axis. The repeatability of the KVP-100 tables is of 1 μm, allowing us to control the relative positioning of the source and the detector very precisely.
The test bench is placed in a 2 m × 2 m × 3.5 m dark enclosure. The enclosure walls are insulated, and using a powerful air conditioning system, we manage to cool it down to a temperature of ~0 °C. The bench is not strictly speaking thermalised, since its temperature is neither regulated nor perfectly uniform within the whole volume. We compensate for this by monitoring the temperature of the key parts of the test bench using PT1000 thermistances or type-K thermocouples.
3.3. Assumptions
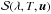 depends on four scalar parameters. This means that to pave the full parameter space, we need to accumulate a large number of spectra. However, we have verified on six LED models, chosen so as to cover the full spectral range and the full range of available LED technologies, that the spectra are essentially independent of the direction of emission u (see Appendix D for a full discussion).As a consequence, we assume that the spectral intensity of all the LEDs that equip the DICE light sources can be written as
depends on four scalar parameters. This means that to pave the full parameter space, we need to accumulate a large number of spectra. However, we have verified on six LED models, chosen so as to cover the full spectral range and the full range of available LED technologies, that the spectra are essentially independent of the direction of emission u (see Appendix D for a full discussion).As a consequence, we assume that the spectral intensity of all the LEDs that equip the DICE light sources can be written as 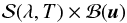 (1)where
(1)where 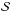 is the spectral intensity of the LED in a (arbitrary) reference direction, while ℬ(u) is a dimensionless function, which accounts for the variations in the beam intensity as a function of the angle of emission. Here, ℬ(u) is normalised to one in the reference direction.
is the spectral intensity of the LED in a (arbitrary) reference direction, while ℬ(u) is a dimensionless function, which accounts for the variations in the beam intensity as a function of the angle of emission. Here, ℬ(u) is normalised to one in the reference direction.
In what follows, we refer to 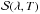 as the LED “spectrum”, keeping in mind that it is actually a spectral intensity. The dimensionless quantity ℬ(u) is called the “beam map”.
as the LED “spectrum”, keeping in mind that it is actually a spectral intensity. The dimensionless quantity ℬ(u) is called the “beam map”.
3.4. Photometric and spectroscopic measurements
The beam maps ℬ can be measured simply by intercepting the beam with a calibrated photodiode placed at a known distance from the source and moved with respect to the source, in order to sample the whole beam. The measurement of 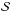 is a little more complex. We need to perform spectroscopic measurements by inserting a monochromator between the source and the calibrated photodiode.
is a little more complex. We need to perform spectroscopic measurements by inserting a monochromator between the source and the calibrated photodiode.
The calibration of the light source is therefore performed in two distinct steps. First, we simply map the radiant intensity of each calibration beam by moving the standard photodiode in a series of planes orthogonal to the z-axis. These calibration sequences, called hereafter “photometric calibration sequences”, are performed at about 10 to 15 different temperatures, ranging between ~ 0 °C and ~ 25 °C. They allow us to study how the intensity delivered by each LED varies with temperature and how the intensity varies with the direction of emission (beam map). They also permit us to assess the stability of the source. The analysis of this dataset is discussed in Sect. 4.
In a second step, we insert a Digikröm DK240 Czerny-Turner monochromator between the light source and the calibrated photodiode. The LEDs are positioned in turn in front of the monochromator entrance slit, while the photodiode senses the intensity that comes out of the exit slit. These measurements are performed at about ten distinct temperatures between 0 °C and room temperature. This spectroscopic dataset, combined with the photometric measurements described above, allows us to derive smooth models of the LED spectral intensity. The spectroscopic measurements are described in Sect. 5 with additional details given in Appendix C.
4. Photometric calibration of the light source
The goal of the photometric calibration studies is to determine the absolute normalisation of the LED spectral intensities 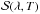 and also to measure the beam maps ℬ(u) (see Sect. 3.3). In this configuration of the bench, the calibrated photodiode samples directly the beam light (left panel of Fig. 8). The photocurrent registered with the Keithley 6514 picoammeter can then be written as the product of two simple quantities:
and also to measure the beam maps ℬ(u) (see Sect. 3.3). In this configuration of the bench, the calibrated photodiode samples directly the beam light (left panel of Fig. 8). The photocurrent registered with the Keithley 6514 picoammeter can then be written as the product of two simple quantities: 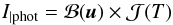 (2)where ℬ(u) is the beam map defined in Sect. 3.3, T is the LED temperature (or at least a proxy for it), and
(2)where ℬ(u) is the beam map defined in Sect. 3.3, T is the LED temperature (or at least a proxy for it), and 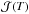 the photocurrent generated when the photodiode is placed at a specific reference position r0 with respect to the source. At this reference position, ℬ is conventionally set to 1, the photodiode subtends a solid angle δΩ0, and we have
the photocurrent generated when the photodiode is placed at a specific reference position r0 with respect to the source. At this reference position, ℬ is conventionally set to 1, the photodiode subtends a solid angle δΩ0, and we have 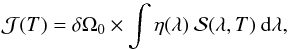 (3)where η(λ) is the photodiode efficiency reported by NIST. The main difficulty is to control the relative positions and orientations of the photodiode with respect to the source.
(3)where η(λ) is the photodiode efficiency reported by NIST. The main difficulty is to control the relative positions and orientations of the photodiode with respect to the source.
Since acquiring detailed beam maps is time consuming (~30 to 60 min per map), we optimise the photometric measurements as follows. In a first series of measurements, we concentrate on a few specific beam locations, keeping the photodiode fixed, while varying the bench temperature. These sequences, called “minimaps” are much faster to acquire (about 260 s) and yield about ten independent measurements of each selected beam location (in particular, the central region of the beam, taken as a reference). They are targeted at measuring 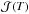 for each LED, i.e. the relative variations in the LED emission with temperature. The analysis of the minimaps is presented in Sect. 4.1 below.
for each LED, i.e. the relative variations in the LED emission with temperature. The analysis of the minimaps is presented in Sect. 4.1 below.
We also realise fine-grained maps of the calibration beams at two or three temperatures, keeping the temperature of the bench as constant as possible during data taking. From this data, we obtain the ℬ(u) maps described above, and we verify that these maps are stable with temperature (see Sect. 4.3). Such measurements are taken at several distances to the source, in order to verify the projectivity of the beam against scattered light and to check that we control the LED-source geometry well.
4.1. Minimaps: LED emission versus temperature
In most cases, the LED emissivity decreases with temperature. We refer to this as the “cooler-brighter” relation already mentioned above. It generally obeys a linear law: 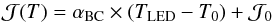 (4)where
(4)where 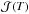 is the photodiode current defined above, T a proxy for the LED temperature, typically the temperature of the LED radiator, and T0 is an arbitrary temperature pivot.
is the photodiode current defined above, T a proxy for the LED temperature, typically the temperature of the LED radiator, and T0 is an arbitrary temperature pivot.
 |
Fig. 9 Top panel: cooler-brighter relation measured from 13 minimaps for a Roithner-Lasertechnik APG2C1-690 emitter, mounted on SkyDICE. Bottom panel: residuals. The small black error bars display the uncertainties on the minimap measurements (combined). The larger grey error bars take the measurement repeatability between maps into account (i.e. over time scales of one hour). |
 |
Fig. 10 Cooler-brighter slopes for the SkyDICE LEDs. The various LED technologies are coded with different symbols (see Appendix A for details). The amplitude of the effect is similar for all LEDs at about 0.5% /°C. For two LEDs, which are operated at very low currents, we actually observe a “brighter-warmer” relation. |
Ten to fifteen minimaps are taken for each LED at temperatures ranging from 0 °C to 25 °C. The cooler-brighter law is fitted on the measurements of the central region of the beam. An example of the fit, along with the residuals to the linear law, is shown in Fig. 9 for one of the LEDs that equips SkyDICE.
Our determinations of the LED radiant intensities at 25 °C and of the cooler-brighter slopes are reported in Tables A.1 and A.2 for SnDICE and SkyDICE, respectively. Whenever possible, the SkyDICE LEDs have been tuned to deliver of the order of 0.1 mW/sr. On the test bench, placing the 1 cm2 NIST photodiode about 2 m away from the source, this translates into typical photodiode currents of a few 103 pA, as shown in Fig. 9. Such a current level is easily measured with a picoammeter. In Fig. 10 we summarise the intensity of the cooler-brighter effect for all the LEDs mounted on SkyDICE. On average, it is slightly lower than 0.5%/°C for all LEDs (regardless of the LED technology), except for two blue InGaN emitters that can reach over 1%/°C. We notice that two LEDs emitting around 500-nm actually exhibit a warmer-brighter relation. It may be because the nominal currents that were chosen for these LEDs are below the normal range recommended by the vendor. What matters for our application is that the effect is well measured and reproducible.
Only one of the LEDs mounted on SkyDICE clearly displays small deviations from a linear cooler-brighter law. It is a Golden Dragon LED of type LD W5AM, emitting at ~ 450-nm. The intensity of the effect is small (≲ 0.2% peak-to-peak over the full temperature range), and we model it with a second-order polynomial. For all the other LEDs, it is not possible with the data in hand to distinguish between small deviations from linearity from the bench or source instabilities.
Special care has been taken into evaluating the measurement repeatability empirically on various time scales. The black error bars in the lower panel of Fig. 9 display the empirical variability of the central beam region, measured on each single minimap (i.e. over about 260 s). It is about 0.1 pA (about 5 nW/sr) and depends slightly on whether the cooling system is on or off. When combining the ten minimap measurements together, it represents a negligible contribution to the flux uncertainty: about 1.5 nW/sr, for a nominal flux of about 0.1 mW/sr, i.e. a few 10-5. The grey error bars in the same figure represent the map-to-map variability. This contribution depends on the LEDs, so we attribute it to some longer term-variability of the source, and to a minor extent, to some additional variability of the bench. We model it with a noise pedestal σint, adjusted iteratively to obtain a reduced χ2 of unity. For most LEDs, it represents a little less than 5 × 10-4 of the LED nominal flux. For the two faintest UV LEDs, it is slightly larger (2 × 10-3).
4.2. Long-term stability of the DICE illumination device
 |
Fig. 11 Upper panel: variations in the source temperature over a 3-week run designed to test the system stability. Middle panel: black triangles: relative variations of the raw flux delivered by the source. Blue lower triangles: relative variations in the flux after correction for the cooler-brighter effect. Red upper triangles: relative variations in the flux after correction by the control photodiode measurements. Lower panel: zoom on the corrected flux baselines. |
In the previous section, we have shown, from the study of the residuals to the brighter-cooler law, that the source is stable at the level of a few 10-4 (rms) over the duration of a calibration run (i.e. 24 h). Since the stability of the light source is a critical aspect of the design, it has been checked over longer durations (i.e. weeks). For these tests, the bench was configured in photometric mode, and repeated minimaps of each calibration channel were acquired. The system cycles through all LEDs over and over again for a little more than three weeks. The tests were performed at room temperature, each LED being fed with its nominal current. All the auxiliary quantities (LED temperature, backend board temperature, control photodiode current, etc.) were logged, along with the NIST photodiode measurements.
 |
Fig. 12 Red histogram: stability of the LED flux (i.e. the NIST photodiode current) after correction for the cooler-brighter effect (and for the backend board temperature variations). Blue histogram: stability of the LED channels after correction for the control photodiode measurements. The two outliers above 5 × 10-3 are LEDs in the blue histogram that correspond to channels that are intrinsically unstable. The outliers in the red histogram correspond to the same LEDs, plus one LED whose control photodiode is faulty. |
Figure 11 shows the flux baseline that was acquired for a typical LED, along with the LED temperatures. Significant, anti-correlated variations of the temperature (~ 5 °C) and the LED flux (~2%) are noticeable over the course of the run. This is the consequence of the cooler-brighter relation studied in the previous section.
We can take advantage of the cooler-brighter effect to predict the variations in the LED flux, since we monitor the temperature of the LED radiator TLED. We also measure the temperature of the backend board that generates the LED currents, Tbb, which has been found to correlate slightly with the LED flux for some channels. We use these two variables to predict the variations in the LED flux over the long run: 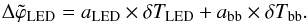 (5)We find that TLED and Tbb permit parametrizing most of the variations in the LED flux over time as shown in Fig. 11. We show the residual dispersions attained over three weeks of continuous monitoring in Fig. 12. It is in the range
(5)We find that TLED and Tbb permit parametrizing most of the variations in the LED flux over time as shown in Fig. 11. We show the residual dispersions attained over three weeks of continuous monitoring in Fig. 12. It is in the range  (rms) with a median value of 6 × 10-4 (rms). Only two LEDs are less stable than 5 × 10-3. One is a UV LED (340-nm) with a large threshhold voltage (about 5V). Such voltages are slightly higher than what our current source was designed for, and it seems to become less stable in this regime. Fortunately, the modern UV LEDs on the market require lower threshhold voltages, so we should not have to deal with this problem in the future. The other unstable LED, a red APG2C1-760 distributed by Roithner-Lasertechnik, has displayed a true instability during the run, its flux jumping by almost 2% about two weeks after the beginning of the operations. This behaviour has not been explained yet and has not been seen with any other LED. It has no counterpart on the monitoring data, besides the LED control photodiode placed close to the exit hole (see Appendix B).
(rms) with a median value of 6 × 10-4 (rms). Only two LEDs are less stable than 5 × 10-3. One is a UV LED (340-nm) with a large threshhold voltage (about 5V). Such voltages are slightly higher than what our current source was designed for, and it seems to become less stable in this regime. Fortunately, the modern UV LEDs on the market require lower threshhold voltages, so we should not have to deal with this problem in the future. The other unstable LED, a red APG2C1-760 distributed by Roithner-Lasertechnik, has displayed a true instability during the run, its flux jumping by almost 2% about two weeks after the beginning of the operations. This behaviour has not been explained yet and has not been seen with any other LED. It has no counterpart on the monitoring data, besides the LED control photodiode placed close to the exit hole (see Appendix B).
We have developed an alternate and redundant standardisation method that relies on the direct measurements of the LED fluxes performed with the off-axis control photodiodes. Since the photodiode currents are digitised on the backend board, we also include the backend temperature in the standardisation relation: 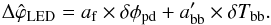 (6)Again, we observe very low residual dispersions of the standardised flux (
(6)Again, we observe very low residual dispersions of the standardised flux (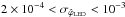 ) (rms) with a median value of 4 × 10-4 (rms), as shown in Fig. 12. Again, there are a few outliers: the two LEDs discussed above, as well as a third LED whose control photodiode seems to be malfunctioning. These channels still display repeatabilities that are better than 1% over weeks.
) (rms) with a median value of 4 × 10-4 (rms), as shown in Fig. 12. Again, there are a few outliers: the two LEDs discussed above, as well as a third LED whose control photodiode seems to be malfunctioning. These channels still display repeatabilities that are better than 1% over weeks.
We plan to extend the duration of these intensive stability tests to longer durations of the order of a few months. In a near future, we will also re-calibrate the sources that are currently in operation (SnDICE at CFHT and SkyDICE at SSO). This will allow us to check the stability of their calibration over durations of a few years.
As a conclusion, we have built a calibrated source that is intrinsically stable at the 10-2-level. The fluctuations of the light delivered by each LED can be parametrised as a function of simple auxiliary observables, notably the temperature of the LED radiator, TLED. Using two independent methods (one based on monitoring TLED and another based on the measurements performed with the off-axis control photodiodes), we have shown that we can correct for the variations of the source at the level of a few 10-4. During operations, we generally choose to use the temperature method as our primary standardisation technique and to use the control photodiode for redundancy checks. The photodiode and temperature probes are read before and after each calibration exposure, therefore either of the two techniques can be used for each exposure. Since both methods give similar results, they can be interchanged in the future.
 |
Fig. 13 Beam map of LED LVW5AM (OSRAM, Golden Dragon® series) mounted on the SkyDICE device. |
Because of its stability, our light source qualifies as a “standard light source”. Once calibrated, it may be used to disseminate a flux calibration to remote locations.
4.3. Beam maps: LED emission versus direction
We now describe how we derive fine-grained beam maps (ℬ) from the detailed photometric scans realised at nearly constant temperature (Fig. 13). We have found that the relative variations in the LED emissivity with direction are small (1% at most) and smooth. They sometimes display a complicated shape, which does not suggest an analytic parametrisation. We therefore develop them on the basis of splines: 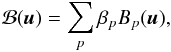 (7)and we fit for the β parameters. The main source of systematics here is the determination of δΩ, i.e. the control of the test-bench geometry.
(7)and we fit for the β parameters. The main source of systematics here is the determination of δΩ, i.e. the control of the test-bench geometry.
The stability of the beam maps themselves has been studied in detail over long durations. The temperature fluctuations may indeed dilate the metal, hence slightly change the relative positioning of the LED with respect to the masks and pieces of baffles that shape the beam. We have found that the fluctuations of the map profiles are always lower than 5 × 10-4.
 |
Fig. 14 Upper panel: comparison between a typical LED spectrum (SkyDICE Golden Dragon LV W5AM) and the fitted model (red line). Bottom panel: residuals. |
5. Spectroscopic calibration of the light source
We now turn to the determination of the LED spectra. This requires additional measurements, which are performed on our spectroscopic test bench (see right panel of Fig. 8). This bench is similar to the photometric test bench described above, except for the presence of a Czerny-Turner type monochromator, inserted between the LED source and the calibrated photodiode. In this configuration, the photocurrent generated by the photodiode is then given by ![\begin{equation} I_{|\mathrm{spec}} = \left[\eta(\lambda) \cdot T_{\rm m}(\lambda) \cdot {\cal S}(\lambda, T)\right] \otimes W_{\rm m}(\lambda) \label{eqn:i_spec} \end{equation}](/articles/aa/full_html/2015/09/aa24471-14/aa24471-14-eq92.png) (8)where η(λ) is the photodiode efficiency reported by NIST, Tm(λ) and Wm(λ) are the transmission and the spectral response of the monochromator, respectively.
(8)where η(λ) is the photodiode efficiency reported by NIST, Tm(λ) and Wm(λ) are the transmission and the spectral response of the monochromator, respectively.
The key point here is the control of the monochromator calibration. From the equation above, we see that we need to check (1) the wavelength calibration of the monochromator; (2) its transmission Tm(λ); and (3) its spectral response, Wm(λ). This work is described in detail in Appendix C and briefly summarised in Sect. 5.3.1 below.
 |
Fig. 15 Spectral intensity surfaces Ŝ(λ,T) for two SkyDICE LEDs. The model incorporates the cooler-brighter and cooler-bluer effects. |
5.1. Modelling the LED spectra
Our goal is to build a smooth model of the LED spectral intensities as a function of wavelength and temperature. We choose to develop this model on the basis of two-dimensional B-splines: 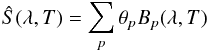 (9)where the Bp(λ,T) functions are two-dimensional splines of order 3 to describe the wavelength variations, and order 2 to model the temperature variations. We use three nodes placed every 10 °C to describe the temperature and O(100) nodes, placed every 2-nm to capture the spectral shapes.
(9)where the Bp(λ,T) functions are two-dimensional splines of order 3 to describe the wavelength variations, and order 2 to model the temperature variations. We use three nodes placed every 10 °C to describe the temperature and O(100) nodes, placed every 2-nm to capture the spectral shapes.
Because the uncertainty on the absolute normalisation of the monochromator transmission is difficult to assess, we decided to fit for the (unknown) normalisation fs of each spectrum measurement s. This means that the only piece of information we extract from the spectroscopic measurements is related to the spectrum shapes and not the spectrum normalisations. Our model of the photodiode current (Eq. (8) above) becomes ![\begin{equation} I_{|\mathrm{spec}} = f_s \times \sum_p \theta_p\ \left[\eta(\lambda) \cdot T_{\rm m}(\lambda) \cdot {B}_p(\lambda, T)\right] \otimes W_{\rm m} (\lambda) \label{eqn:i_spec_developed} . \end{equation}](/articles/aa/full_html/2015/09/aa24471-14/aa24471-14-eq101.png) (10)By construction, there is a perfect degeneracy between the
(10)By construction, there is a perfect degeneracy between the 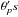 and the
and the 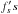 . We break it by requiring that the absolute normalisation of the Ŝ models is determined by the photometric measurements (performed without a monochromator). In practice, this is done by adding the following term to the fit χ2:
. We break it by requiring that the absolute normalisation of the Ŝ models is determined by the photometric measurements (performed without a monochromator). In practice, this is done by adding the following term to the fit χ2: 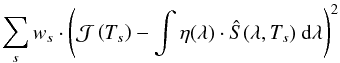 (11)where
(11)where 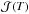 is the photocurrent measured in a reference position, as defined in Sect. 4. With this approach, the uncertainty affecting the monochromator transmission is entirely absorbed, and the absolute normalisation of the LED spectral intensity models is set exclusively by the photometric measurements.
is the photocurrent measured in a reference position, as defined in Sect. 4. With this approach, the uncertainty affecting the monochromator transmission is entirely absorbed, and the absolute normalisation of the LED spectral intensity models is set exclusively by the photometric measurements.
We estimate the LED spectral intensities by fitting the model above on the photodiode current measurements and marginalizing on the fs nuisance parameters.
5.2. Results
The spectral intensity of the SnDICE and SkyDICE LEDs, 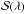 , have been reconstructed using the method described above, combining the spectroscopic and photometric data. On average, about 15 spectra and a similar number of minimaps have been taken for each LED at temperatures ranging from 2 °C to 25 °C. In Fig. 14 we show a comparison between the model and a typical spectrum. Figure 15 shows the spectral intensity surfaces obtained for typical blue and red LEDs. These models summarise the behaviour of the source. Their normalisation is set by the photometric dataset. By construction they incorporate the cooler-brighter and cooler-bluer effects. Once we know the operating temperature and the distance between the source and the telescope aperture, we can predict the spectral intensity delivered on the primary mirror.
, have been reconstructed using the method described above, combining the spectroscopic and photometric data. On average, about 15 spectra and a similar number of minimaps have been taken for each LED at temperatures ranging from 2 °C to 25 °C. In Fig. 14 we show a comparison between the model and a typical spectrum. Figure 15 shows the spectral intensity surfaces obtained for typical blue and red LEDs. These models summarise the behaviour of the source. Their normalisation is set by the photometric dataset. By construction they incorporate the cooler-brighter and cooler-bluer effects. Once we know the operating temperature and the distance between the source and the telescope aperture, we can predict the spectral intensity delivered on the primary mirror.
Summary of the test bench systematics.
As can be seen in Fig. 15, the cooler-bluer effect does not have the same intensity for all LEDs. In Fig. 16 we report the variations in the mean spectrum wavelength as a function of temperature (estimated from the model, for all the LEDs that equip SkyDICE). On average, the effect is about 1 Å/°C. A trend is clearly visible, indicating that the red LEDs are more sensitive to the effect than the blue LEDs. The two LEDs that have been found to exhibit a warmer-brighter behaviour (Sect. 4.1) also follow a warmer-bluer relation.
 |
Fig. 16 Cooler-bluer slopes measured on the SkyDICE spectra. |
The spectral intensity models are affected by uncertainties owing to the finite number of spectra and flux measurements. These uncertainties are statistical in nature, but behave as systematics in any subsequent analysis relying on these spectral intensity models. For this reason, we are careful to propagate them in an exact way (i.e. including the off-diagonal terms). They are derived from the covariance matrix of the spectral intensity fit presented in the previous section. We find that with the datasets in hand, the relative uncertainties on the LED broadband fluxes predicted with the spectral intensity model are below 0.05%.
5.3. Test-bench systematics
We now examine the systematic uncertainties that have an impact on our spectral intensity models, Ŝ(λ,T). We identify three main sources of systematics: the wavelength calibration of the monochromator, the transmission of the same monochromator, and the accuracy of the NIST photodiode efficiency η(λ).
5.3.1. Monochromator
Wavelength calibration.
The wavelength calibration of the device is checked (at several temperatures), using a series of calibration lamps, notably a sodium lamp and a polymetallic lamp. From this dataset we obtain a correction to the calibration given by the manufacturer. This correction does not exceed 0.1-nm in amplitude. We find a small linear dependence of the wavelength calibration with temperature (see Table C.1) of about 0.025 nm/°C, which is taken into account. The dominant systematics affecting the wavelength calibration is related to the positioning uncertainty of the source with respect to the monochromator entrance slit. We found that this contribution never exceeds 0.1-nm. Given the limited precision of the alignment procedure and the small number of calibration runs, we conservatively set the wavelength calibration systematics to 0.3-nm (see Table 1).
 |
Fig. 17 Upper panel: efficiency (in A/W) of the Hamamatsu S2281 photodiode calibrated at NIST, purchased for this project. Bottom panel: black points: uncertainties reported by NIST (in percentage); dashed red line: diagonal elements of the “worst case” interpretation of the NIST error budget, as discussed in Sect. 5.3.2; dashed blue line: diagonal elements of the “best case” interpretation of the NIST ERROR budget discussed in the same section. |
Transmission.
The transmission of the monochromator, Tm(λ), is measured at several discrete wavelengths. For Czerny-Turner designs, it is relatively easy to compute the global shape of Tm(λ), as a function of two specific angles: the so-called “Ebert angle” αE, which depends on the optical design of the device, and the “blaze angle” ϵblaze | i of each grating i being used. We use these continuous models (one for each grating) fitted on the discrete transmission measurements as our estimates of the monochromator transmission (see Fig. C.1). At first order, Tm(λ) only depends on the ϵblaze parameter. The uncertainty on the monochromator transmission is estimated by propagating the uncertainties on our estimates of the ϵblaze angles. They are reported in Table 1.
The method used to extract the LED spectrophotometric models (Eqs. (10) and (11)) ensures that the model normalisation only depends on the photometric measurements (without the monochromator). This means that the uncertainties on the monochromator transmission have no impact on the LED-to-LED calibration and may only affect the spectrum shapes. To fix ideas, we find that varying the Ebert angle by one degree has an impact on the spectrum mean wavelength (⟨λ⟩ = ∫λS(λ)dλ/∫S(λ)dλ), which is lower than 1 Å. We also find that altering the monochromator transmission model around 550-nm, as suggested by the residuals of Fig. C.1, results in a shift in wavelength that is also lower than 1 Å.
5.3.2. NIST
The calibration of the NIST photodiode is itself uncertain. NIST provides its clients with an error budget and reports uncertainties of about ~ 0.2% between 400-nm and 950-nm and up to 1% in the UV and near-IR (Fig. 17). We expect a fraction of the uncertainties affecting measurements at different wavelengths to be correlated. And since we are primarily interested in the relative calibration of our passbands, it is essential for us to account for these off-diagonal terms. As of today, we have not been able to obtain this information from NIST. We therefore built two different error models, depending on how we choose to interpret the NIST uncertainties.
In the “best case scenario”, we assume that what is uncertain in the photodiode efficiency is primarily a grey scale. This means that the NIST uncertainties are positively fully correlated. Since our goal is to measure the relative normalisation of the imager passbands, this would be an ideal situation, because the uncertainty on the global flux scale cancels out when comparing two different passbands.
In the “worst case scenario”, we assume that there is a “colour uncertainty” affecting the efficiency reported by NIST. This can be modelled with two random variables αNIST and βNIST, of variance σα and σβ, and such that 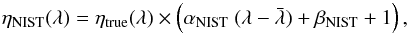 (12)where σα and σβ are chosen so that the uncertainties computed from the equation above stay compatible with the error budget reported by NIST, and
(12)where σα and σβ are chosen so that the uncertainties computed from the equation above stay compatible with the error budget reported by NIST, and 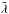 is a pivot value (chosen to be
is a pivot value (chosen to be 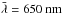 ). Their values are listed in Table 1.
). Their values are listed in Table 1.
This model is of course a little extreme because it assumes a correlation length that spans the entire visible range. This would mean that the uncertainty reported by NIST lies with POWR, the primary flux standard. This is not the case, since for the first steps of its metrology chain, NIST reports uncertainties of a few 10-4, about one order of magnitude lower. It is more likely that the main fraction of the uncertainty budget is introduced in the last step at the SCF facility, and it is difficult to see how SCF could introduce error with an infinite correlation length in wavelength. However, in the present state of our knowledge, exploring these two extreme cases is the best we can do, because they bracket the true uncertainties.
5.3.3. Propagating the bench systematics
The test bench systematics affect how we reconstruct the LED spectral intensities (Ŝ). They may, for example, shift the Ŝ(λ) models in wavelength or distort their shape, and this must be accounted for. Regardless of the propagation method we choose, we need to quantify how the bench errors change the reconstructed LED spectral intensities, Ŝ(λ,T). To do this, we compute the derivatives of the Ŝ(λ,T) models with respect to all the identified systematics. This is done by shifting each term of the systematics vector in turn and re-determining the model parameters as described in Sect. 5.1 above. They are used to propagate the test-bench systematics (see Sect. 6 and Appendix E for details).
5.4. Conclusion
At this stage, we have modelled the emissivity of each LED as a smooth function that predicts the spectral intensity of the beam in any given direction and at any temperature. The bench statistical uncertainties were encoded into the covariance matrices of the θ parameters. The main systematics were quantified. They come primarily from our calibration of the monochromator and from the error budget reported at NIST. How they will be propagated in the final analysis is discussed in Sect. 6 and Appendix E.
We now have all we need to measure the transmission of an imager from series of calibration frames taken with these light sources. This is the subject of the next section.
6. Discussion: calibrating broadband observations
We have built a very stable (0.01%) light source and characterised it on a test bench with an accuracy of ~0.3 nm in wavelength and ~ 0.1% in flux. Now the question is how we use it to calibrate a real imager. And first of all: what do we need to measure in order to calibrate an imager?
6.1. Transmissions
Passbands are known long before the first star light hits the focal plane. The transmissions of all optical components and the quantum efficiency curves of the detectors are measured before assembly. These measurements are combined to build a synthetic passband model: 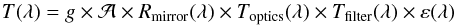 (13)where ε(λ) is the quantum efficiency of the CCD, g is the gain of its readout chain,
(13)where ε(λ) is the quantum efficiency of the CCD, g is the gain of its readout chain, 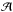 is the area of the mirror, and the other terms are the various transmissions and reflectivities of the optical elements. Note that T(λ) is a dimensioned quantity: here it has units of ADU/γ/m2.
is the area of the mirror, and the other terms are the various transmissions and reflectivities of the optical elements. Note that T(λ) is a dimensioned quantity: here it has units of ADU/γ/m2.
The absolute normalisation of T(λ) varies with time and must be monitored: the gain g of the readout electronics may fluctuate by a few per-mil on timescales of a few hours; also, alterations of the optical surfaces (dust deposits, ageing of the coatings, etc.) slowly degrade the transmission of the instrument by as much as 5−10% per year. The resulting attenuation of the telescope transmission is slightly wavelength dependent. Therefore, the relative normalisation of the passbands with respect to each other may itself vary by a few percentage points per year. The main purpose of calibration is therefore to monitor these variations. In most applications, what we need to measure is the evolution of the relative normalisation of the passbands with respect to each other.
The shape of the passbands is not expected to vary very significantly over time. This is a design requirement. However, several studies have reported evidence of slow evolution of the passband shape. For example, Doi et al. (2010) report a 30% decrease in the short-wavelength side of the SDSS 2.5-m u-band channels, probably due to ageing of the CCD anti-reflective coatings. Another example can be found in Betoule et al. (2013), who show hints that the red fronts of the r-band and i-bands that equips MegaCam are about 8-nm off with respect to the scans provided by the manufacturer (resulting in a disagreement of 4 nm on the filter mean wavelength). In this case, there is indirect evidence that this evolution of the passbands took place in an early phase of the life of the instrument. There is therefore a strong incentive for future surveys to monitor the shape of their effective passbands.
6.2. Constraining passbands
Instead of measuring the filter transmissions again with a monochromatic beam, the DICE strategy consists in taking the (known) synthetic passbands as a starting point and in constraining small alterations to these passbands from series of measurements.
The broadband flux of an astrophysical object is primarily sensitive to (1) the normalisation of the passband and (2) the position (in wavelength) of the blue and red filter cutoffs. These three quantities are therefore what should be monitored in the long run. To do this, we alter the synthetic passband model T(λ) presented in Eq. (13) to allow for a different normalisation and for small (potential) variations in the filter cutoffs. The latter is done by composing T(λ) with a linear function that shifts and stretches (or dilates) λ around the filter mean wavelength: 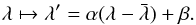 (14)In practice, we reparametrise the function above, so that it depends directly on the filter cutoff displacements, denoted δλblue and δλred hereafter. This way, one can shift each front easily, and they are essentially independent of the other, as shown in Fig. 18.
(14)In practice, we reparametrise the function above, so that it depends directly on the filter cutoff displacements, denoted δλblue and δλred hereafter. This way, one can shift each front easily, and they are essentially independent of the other, as shown in Fig. 18.
 |
Fig. 18 Distortion of the red and blue fronts of the SkyMapper g and r passbands, respectively. |
By doing so, we reduce our problem to fitting only three parameters per filter: a normalisation, 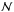 , and two filter front displacements. For an imager equipped with N (typically 5) filters, we end up with 3 × N calibration parameters, which we group in a single vector, noted ϑt:
, and two filter front displacements. For an imager equipped with N (typically 5) filters, we end up with 3 × N calibration parameters, which we group in a single vector, noted ϑt: 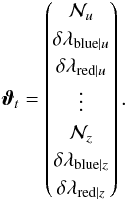 (15)To constrain these unknowns, we build a model that predicts the flux registered on the focal plane. These predictions are built from the LED spectral intensity estimates Ŝl(λ,T), derived in Sect. 5, and the re-parametrised passbands that we denote as Tb(λ,ϑt). The model simply writes as
(15)To constrain these unknowns, we build a model that predicts the flux registered on the focal plane. These predictions are built from the LED spectral intensity estimates Ŝl(λ,T), derived in Sect. 5, and the re-parametrised passbands that we denote as Tb(λ,ϑt). The model simply writes as 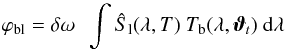 (16)where δω is the solid angle covered by a focal plane pixel or superpixel (about 10-12 sr for a single pixel, and 10-8 sr for a typical 128 × 128 superpixel). Comparing measurements of the calibration flux performed with the imager with the predicted flux ϕbl yields constraints on ϑt.
(16)where δω is the solid angle covered by a focal plane pixel or superpixel (about 10-12 sr for a single pixel, and 10-8 sr for a typical 128 × 128 superpixel). Comparing measurements of the calibration flux performed with the imager with the predicted flux ϕbl yields constraints on ϑt.
The details of the method are described in Appendix E. Classically, it consists in minimising a χ2 function built from the model above and the flux measurements. We are careful to propagate the effect of the identified uncertainties to the final estimates. The statistical uncertainties affecting the LED spectral intensity models are accounted for. The systematics, those related to the test bench measurements, as well as those affecting the flux measurements on site, are incorporated into the fit as nuisance parameters and marginalised over.
6.3. Lightweight calibration runs
The system has been designed to be run in routine mode every day or so. During a typical calibration run, each passband is sampled with the corresponding LEDs. Figure 3 shows that the typical u(v)griz passbands are covered by three to nine LEDs, depending on their extension in wavelength, with the filter cut-ons and cut-offs sampled by one or two LEDs4. In Table 2, we estimate the number of exposures that have to be taken during typical calibration runs for various designs and the time requested to complete these runs. Conservatively taking about one minute per exposure, plus 20 min for the overheads (filter changes, alignment of the source, and the telescope, etc.), we find that a typical run requires a little less than one hour of daytime. This calibration program is short enough to be run every day or so just after and/or before telescope operations.
Significant gains in precision can be obtained by combining several calibration runs. Indeed, if the normalisation of the passbands does change slightly from one night to the next, the position of the filter cut-offs is not expected to move in a measurable way overnight. As a consequence, we will typically fit for one normalisation per filter and per run, but only one position parameter for each filter cut-off. This represents ~ Nbands × Nruns + 2 × Nbands (e.g. 60 parameters for 10 MegaCam calibration runs and 135 parameters for 25 runs). As shown below, this allows us to improve the precision on all calibration parameters sizeably, at the price of a slightly more complex procedure.
6.4. Simulated datasets
To conclude, we assess the quality of the constraints that can be obtained from series of calibration runs of the type described above. The main goal here is to show that the problem is well constrained and to give estimates of the uncertainty budget. These estimates are derived from the quantitative analysis of the accuracy of the source test bench calibration (Sect. 5). These are lower bounds, because we do not discuss the uncertainties associated with the imager measurements of the calibration light in detail. Based on preliminary analyses of the calibration frames taken with MegaCam and SkyMapper, we assume that they are of about 0.5% (uncorrelated).
Typical MegaCam and SkyMapper calibration runs.
We generate synthetic flux measurements, using MegaCam/ SkyMapper passband models as follows. We first simulate realistic test bench datasets, by modelling the “true” LED spectral intensities Strue(λ,T) with Gaussians of width σ ~ 15-nm, normalised to a radiant intensity of 0.1 mW/sr, and emulating the true SnDICE and SkyDICE coverage. We estimate the LED spectral intensities with the methods described in Sects. 4 and 5. We use the “true” (Gaussian) spectra to generate the broadband fluxes and the reconstructed spectral intensity models Ŝ(λ,T) to estimate the calibration parameters. The calibration parameters ϑt are estimated following the method described in Sect. 6.2 and Appendix E (using the reconstructed LED spectral intensity models). The method yields the full stat+syst covariance matrix of the calibration parameters, and we report the diagonal elements as a function of the number of calibration runs.
The quality of the constrains on ϑt is a function of the quality of the flux measurements performed on site, but also of how we manage to sample each filter. We therefore study not only what may be obtained with the sources already in place, but also what could be done with optimised designs, such as those discussed in Appendix A. All designs involve the same number of LEDs (24), so that the duration of the corresponding calibration runs is similar to what is reported in Table 2.
 |
Fig. 19 Upper panel: uncertainties in nanometres on the blue (blue triangles) and red (red crosses) cut-offs of the MegaCam passbands, after 20 calibration runs. Grey points: the same, for an optimised design such as the one described in Appendix A. Lower panel: the same, for SkyMapper. |
Filter cutoffs.
The precision on the filter cut-off positions only slightly depends on the number of runs that are combined into the calibration fit. In five to ten runs, depending on the quality of the cut-off coverage, it hits a systematics floor of about 0.3-nm, where the dominant systematics here is the precision of the monochromator wavelength calibration. It affects all the filter cut-off estimates performed with a given source.
In Fig. 19 we show, for SnDICE (MegaCam), SkyDICE (SkyMapper), and their associated optimised designs, the uncertainties on the filter cut-off positions obtained by combining about 20 calibration runs. SkyDICE is very close to an optimal design, and it can constrain the SkyMapper filter cut-offs extremely well. On the other hand, SnDICE suffers from its identified lack of coverage around 700-nm. In particular, it yields only marginal constraints on the red cutoff of MegaCam r-band.
Passband normalisations.
The uncertainties on the normalisation of the MegaCam and SkyMapper passbands (relative to r) improve sizeably with the number of runs, as shown in Fig. 20. In one run, we are able to reach a sub-percent accuracy. After about ten calibration runs, the uncertainty is divided by two, below 0.5% in all bands.
 |
Fig. 20 Uncertainty on the MegaCam i-band normalisations, relative to the r-band, as a function of the number of calibration runs. The uncertainty level actually depends on how we interpret the NIST error budget colour uncertainty (black line) or gray scale uncertainty (dashed red line) – see Sect. 5.3 for details. The grey lines show the calibration uncertainties obtained with an optimised filter sampling (see Appendix A). |
The level of the systematics floor depends on how we interpret the NIST uncertainties. In the “best case scenario” discussed in Sect. 5.3.2, in which the NIST uncertainties are interpreted as a grey-scale uncertainty, the impact of the NIST error budget is small, and we are able to reach uncertainties of 0.3% or below. In the other scenario, where the NIST errors are negatively correlated, the error floor can be significantly higher.
 |
Fig. 21 Upper panel: uncertainty on the MegaCam passband normalisation (relative to r) obtained when combining 20 SnDICE runs. Lower panel: the same, for SkyMapper. |
Figure 21 summarises the normalisation uncertainties for SnDICE (MegaCam) and SkyDICE. The true uncertainties are somewhere in the grey band, probably closer to the “best-case scenario” line. This shows that neither our design choices nor the finite precision of the test bench measurements may limit the precision of the calibration that we will obtain from such measurements. All essentially depends on how accurately we can measure the calibration flux delivered on the focal plane.
7. Conclusion
We have presented the concept and performances of a stable LED-based calibrated light source, designed for the photometric calibration of wide field imagers. The design has been deliberately kept as simple as possible. The light is generated by a series of 24 narrow spectrum LEDs chosen to cover the imager spectral range. Each LED implements a point source, generating a conical beam, which yields a uniform illumination of the focal plane. No intermediate optical surface is present between the LED emission zone and the telescope primary mirror. This makes the hardware very stable and easy to maintain in the long run.
In this paper, we have described the first step of our calibration program in detail (labelled 1 on Fig. 1): the transfer of the NIST flux scale to the light source itself. The emissivity of each LED is characterised by its spectral intensity, i.e. the emitted power per unit solid angle and per unit wavelength. The LED spectral intensities are measured on a spectrophotometric test bench, using a monochromator and a Hamamatsu S2281 photodiode calibrated at NIST. The test bench data are combined into a spectral intensity model that captures the variations in the LED emissivity as a function of temperature (the so-called “brighter-cooler” and “bluer-cooler” effects). This model is then used on site to predict the light actually delivered by the source at a given temperature.
The source is intrinsically stable at the level of ≲ 1%. It is equipped with several monitoring systems to control its stability during operations. We have shown that if we monitor either the temperature of the LEDs or directly the light emitted by the LED, we can control the relative variations in the calibration light with a precision that ranges from a few 10-4 for the best channels to about 10-3. This means that we have built a source that is as stable as the silicon photodiodes used to disseminate the NIST flux scale. This source can then be used to calibrate other light detectors (e.g. astronomical imagers).
In the last section of this introductory paper, we sketched the second step in our calibration program (labelled 2 in Fig. 1) in order to give a complete picture of the system and its main use case. We described how we extract simultaneously the relative normalisation of the telescope passbands and the position of the passband cutoffs from a relatively small number of non-monochromatic calibration exposures (4 to 9, depending on the passband width). All the uncertainties, either those related to the test bench measurements or those affecting the flux measurements performed on site, can be propagated to the final result (including the non-diagonal terms).
As an illustration, we quantified the impact of the test bench systematics on the calibration parameters. Regarding the filter normalisations (relative to the r-band), we showed that the systematics floor is well below 0.5%. The exact value actually depends on how we interpret the NIST error budget. This is an important point that will have to be clarified in the future. Regarding the passband cutoffs, we have shown that, although the source is not monochromatic, the constraints we obtain are essentially limited by the accuracy on the wavelength calibration of our monochromator.
As of today, more than 30 calibrations runs have been accumulated with MegaCam, about ten of them, in conjunction with direct observations of CALSPEC standards. The analysis of this dataset is ongoing. It constitutes the next step in our calibration programme, and it will be described in upcoming papers, currently in preparation.
Paper 2 will be devoted to analysing the calibration exposures, in particular determining the passband normalisations and cutoffs, as described in Sect. 6 (Step 2 of Fig. 1). A specific analysis pipeline is being developed for this purpose. The pre-processing stage (e.g. bias subtractions, gain equalization, etc.) is extremely similar to what is implemented in a classical image processing framework. The downstream operations are more specific: the goal is to measure the irradiance delivered on the focal plane by an extended beam, and one has to deal with non-standard foreground effects, such as (1) the diffraction patterns caused by dust and optical defects in the light path; (2) the angular distribution of the beam on the MegaCam interference filters; and (3) stray light (or ghosts) coming from reflections within the telescope optics. Our experience with the MegaCam imager has shown that ghost contamination can be as high as 20% in some regions of the focal plan. This effect is chromatic and can therefore affect the relative calibration of bands. How we deal with it has been the central topic of this paper.
Paper 3 will describe Step 3 of our calibration programme, i.e. the comparison between the NIST and CALSPEC flux scales, using the observations of the CALSPEC objects, taken in conjunction with the SnDICE2 calibration runs. There are two main difficulties: one is the control of the atmospheric transmission at the time of the observations. We deal with this by carefully scheduling the observations, along with using a semi-empirical model of the atmosphere, trained on observations performed at the UH 2.2-m with the SNIFS instrument. (Some of these observations were taken in conjunction with the MegaCam observations of the CALSPEC standards.) The other difficulty resides in assessing the systematic differences between calibrations obtained from flat field exposures, on one hand, and point source measurements, on the other. Low-angle scattering of light within the telescope optics is the main effect that has to be understood.
For now, we have fulfilled the first step of our programme, which is to demonstrate that it is possible to build LED-based sources, to characterise them spectrophotometrically with an accuracy of a few 10-4 in flux and 3 Å in wavelength, and to control their behaviour in the long run. The DICE sources can be used to disseminate a NIST-based calibration to a telescope.
Acknowledgments
This work was supported by CNRS/IN2P3, the CFHT Corporation, the “Programme National Cosmologie et Galaxies” (PNCG), and the Université Pierre et Marie Curie. The authors acknowledge funding from the Émergence-UPMC-2009 research programme. PFR received a Ph.D. grant from Émergence-UPMC-2009. We are indebted to Philippe Bailly, Julien Coridian, Colette Goffin, Hervé Lebbolo, Philippe Repain, Alain Vallereau, and Daniel Vincent from the LPNHE staff, who helped build the DICE light sources and the associated test bench. The authors wish to thank the CFHT Corporation and its staff for the precious advice and continuous support. We are particularly grateful to Gregory Barrick, Tom Benedict, Kevin Ho, Derrick Salmon, Jim Thomas and Christian Veillet for their help before, during and after the SnDICE installation. The SkyDICE project was supported by the Research School of Astronomy and Astrophysics (RSAA) at Australian National University. We are thankful to Daniel Bayliss, Gabe Bloxham, Peter Conroy, Bill Roberts, Brian Schmidt, Denise Sturgess, Annino Vaccarella, Peter Verwayen, and Colin Vest, for their support during the design and installation effort.
References
- Amanullah, R., Lidman, C., Rubin, D., et al. 2010, ApJ, 716, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Barrelet, E., & Juramy, C. 2008, Nucl. Instrum. Meth. Phys. Res. A, 585, 93 [Google Scholar]
- Betoule, M., Marriner, J., Regnault, N., et al. 2013, A&A, 552, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 315 [Google Scholar]
- Bohlin, R. C. 2010, AJ, 139, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., & Gilliland, R. L. 2004a, AJ, 128, 3053 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., & Gilliland, R. L. 2004b, AJ, 127, 3508 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Gordon, K. D., & Tremblay, P.-E. 2014, PASP, 126, 711 [NASA ADS] [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 72 [Google Scholar]
- Brown, S. W., Eppeldauer, G. P., & Lykke, K. R. 2000, Metrologia, 37, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, S. W., Eppeldauer, G. P., & Lykke, K. R. 2006, Appl. Opt., 45, 8218 [NASA ADS] [CrossRef] [Google Scholar]
- CALSPEC 2000, Calspec, http://www.stsci.edu/hst/observatory/cdbs/calspec.html [Google Scholar]
- DePoy, D. L., Abbott, T., Annis, J., et al. 2008, in SPIE Conf. Ser., 7014, 0 [Google Scholar]
- Doi, M., Tanaka, M., Fukugita, M., et al. 2010, AJ, 139, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, D. S., & Latham, D. W. 1975, ApJ, 197, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Holtzman, J. A., Marriner, J., Kessler, R., et al. 2008, AJ, 136, 2306 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, P., & Hill, W. 1989, The Art of Electronics – 2nd edn. (Cambridge University Press) [Google Scholar]
- Houston, J. M., & Rice, J. P. 2006, Metrologia, 43, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Juramy, C. 2006, Thesis, Université Pierre et Marie Curie – Paris VI [Google Scholar]
- Juramy, C., Barrelet, E., Schahmaneche, K., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Kaiser, M. E., McCandliss, S. R., Pelton, R., et al. 2010, in Hubble after SM4, Preparing JWST, The 2010 STScI Calibration Workshop [Google Scholar]
- Keller, S. C., Schmidt, B. P., Bessell, M. S., et al. 2007, PASA, 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Larason, T. C., & Houston, J. M. 2008, NIST Special Publication 250.1 [Google Scholar]
- Marshall, J. L., Rheault, J.-P., DePoy, D. L., et al. 2013, ArXiv e-prints [arXiv:1302.5720] [Google Scholar]
- McGraw, J. T., Zimmer, P. C., Zirzow, D. C., et al. 2012, in SPIE Conf. Ser., 8450 [Google Scholar]
- Montalto, M., Piotto, G., Desidera, S., et al. 2007, A&A, 470, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Werner, K., Bohlin, R., & Kruk, J. W. 2013, A&A, 560, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Regnault, N., Conley, A., Guy, J., et al. 2009, A&A, 506, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stubbs, C. W., & Tonry, J. L. 2006, ApJ, 646, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Stubbs, C. W., Slater, S. K., Brown, Y. J., et al. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 373 [Google Scholar]
- Stubbs, C. W., Doherty, P., Cramer, C., et al. 2010, ApJS, 191, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, N., Rubin, D., Lidman, C., et al. 2012, ApJ, 746, 85 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: LED selection
SnDICE LEDs.
We now give additional information about the calibration LEDs used for SnDICE. In the wavelength range 400 nm <λ< 630 nm, we use a series of high-intensity LEDs, manufactured by OSRAM Semiconductors GmbH and marketed under the name Golden Dragon. The Golden Dragon LEDs are flat top InGaN (up to ~ 550 nm) and InGaIP (beyond ~ 550 nm) emitters, able to deliver up to a few hundred milliwatts at maximum current. This is actually far more than what is needed. At the telescope, they are therefore operated on a low regime and emit about ~ 0.5 mW/sr.
At longer wavelengths, we use AlGaAs LEDs, manufactured by Marubeni America Corporation (SMC series). These components are much less powerful, delivering a maximum of ten milliwatts. They nevertheless suit our needs perfectly, as we only need a fraction of this illumination.
In the UV, the LEDs that were available on the market in 2007 were unfortunately much less powerful. We selected a series of components manufactured by Seoul Semiconductors. They all emit a maximum of a few 10-2 mW per steradian. As a consequence, SnDICE requires very long exposures (hundreds of seconds) to accumulate enough flux in the MegaCam u-band.
Figure A.1 shows the SnDICE LED mother board. The Golden Dragon LEDs are the flat top components mounted in white packaging. The Marubeni emitters are the flat top LEDs, on the left. Whenever possible, we tried to choose flat top devices, which are Lambertian emitters with a very good approximation. All the blue LEDs procured from Seoul Semiconductors have either a flat (D8, D21) or hemispheric (D4, D14, D16, D24) protection. They are nevertheless quasi-Lambertian emitters in the angular range we are considering (± 1°).
 |
Fig. A.1 SnDICE LEDs mounted on their front-end board. The characteristics of all LEDs are summarised in Table A.1. The central LED in slot D0 is used to generate the planet beam. The flat-top LEDs mounted in a white packaging are the high-intensity OSRAM Golden Dragon. The remaining slots host lower intensity LEDs purchased from Marubeni and Seoul Semiconductors. They cover the redder wavelength range. |
The wavelength coverage of the MegaCam passbands is shown in Fig. 3a and discussed earlier in this paper. It is not very satisfactory, mainly because of the gap around 700-nm, which leaves the red cutoff of the r-band and the blue cutoff the i-band unconstrained. SnDICE was designed in 2007, and the LED diversity was not then what it is today. However, the SnDICE coverage was considered perfectly adequate for tests and feasibility studies.
The types and properties of the LEDs that equip SnDICE are summarised in Table A.1. We report the coefficients that characterise the brighter-cooler and bluer-cooler relations. As can be seen, the mean wavelength of the LED spectra vary typically by 1 Å/°C (note however, that some LEDs seem to display an inverse behaviour). The importance of the flux variations as a function of temperature varies from LED to LED, from a fraction of one percentage point per degree up to 3%/°C for the UV LEDs. Again, one LED seems to display a different behaviour, at least at the nominal current at which it is operated. These relations are (1) well measured and (2) very reproducible, which is all that matters for our application.
Summary of the SnDICE LED characteristics.
SkyDICE LEDs.
The SkyDICE source was designed about three years later. At that time, the LED market had literally exploded, and a much higher diversity of narrow spectrum LEDs was then available. Figure 3b shows the resulting sampling of the SkyMapper filters. As discussed earlier in this paper, this coverage is much better, although the LED density in the blue part of the spectrum could be improved, in order to obtain tighter constrains on the narrow u- and v-bands.
Summary of the SkyDICE LED characteristics.
The types and properties of the SkyDICE LEDs are summarised in Table A.2. Again, in the visible, we use InGaN and InGaAlP Golden Dragon components. In the IR, we use a new family of high-intensity GaAlAs LEDs distributed by Roithner Lasertechnik GmbH. Finally, in the UV, down to ~ 360-nm, the situation has improved considerably in terms of emitted power. In this region, we rely on a series of InGaN LEDs from Roithner Lasertechnik.
These new-generation LEDs are more powerful than their SnDICE counterparts, and they have to be operated at even lower currents. Again, the parameters of the brighter-cooler and bluer-cooler relations are reported in Table A.2. They are similar in magnitude to what was measured with SnDICE. As mentioned earlier in this paper, the amplitude of these effects do strongly depend on the LED technology and mean wavelength.
 |
Fig. B.1 Time series registered during a long duration test of a a Roithner-Lasertechnik APG2C1-760 LED mounted on a DICE source. After 18 days of operations, the flux registered by the NIST photodiode (upper left panel) suddenly increased by almost 2%. Only a fraction of this variation was detected by the internal off-axis control photodiode (upper right panel). The other panels display the timeline of the other quantities monitored by the backend electronics: the LED temperature (middle left panel), the backend board temperature (middle right panel), the LED current (lower right panel), and the board reference tension (lower right). No corresponding glitch can be observed on these quantities. |
Optimised designs.
The diversity of narrow spectrum LEDs continues to improve at a rapid pace (see upper right panel of Fig. 3). A quick glance at the Roithner and OSRAM catalogues shows that there are about 50 LEDs covering the wavelength range 245 nm <λ< 1100 nm, allowing us to sample the imager wavelength range with almost one LED every 10 to 20-nm. One may therefore wonder whether it is feasible to design a calibration source that would sample the imager response in some kind of “optimal” way.
There are many ways to define optimality. We seek to identify the set of LEDs that would allow us to obtain the best constraints on the model described in Sect. 6 after one single calibration run. We proceed as follows. We first identify the LED positions that would yield the best constraints on the filter fronts: these are the positions that maximise the derivatives of the ϕbl model as a function of the filter cutoff displacements δλb and δλr. We match these positions as precisely as possible using the LEDs available on the market. In general, we are able to find a LED within 10 nm of the optimal position. It is possible to play on the diversity of LEDs of the same model to reach optimality even better. Finally, we cover the gaps between the filter fronts as densely as possible, with about one LED every 25-nm.
For MegaCam, this procedure yields the coverage shown in the upper panel (left) of Fig. 3. The dotted lines show our “optimal” positions. The blue bands show the peak emission of the spectra (± 5% of the peak position). The LEDs available in the OSRAM and Roithner catalogues are indicated with arrows. In practice, we have seen on simulations that the optimal design (dotted lines) and its actual implementation (arrows) are nearly indistinguishable in terms of performances. For SkyMapper, we have not been able to identify a design that would give constraints significantly better than those obtained from the current source.
In Sect. 6, we systematically compare the performances of the existing DICE sources with these optimised designs. In particular, we show that, although SnDICE is far from optimality, SkyDICE is nearly optimal, except for the narrow SkyMapper v-band.
Appendix B: Glitch observed on a APG2C1-760
In Sect. 4, we mentioned a 2% glitch observed on a Roithner-Lasertechnik APG2C1-760 LED during a long-duration test. In Fig. B.1 we show the timelines registered by the source and the bench sensors. We see in the upper left-hand panel that after about two weeks of uninterrupted operation, the LED flux suddenly increased by almost two percent. This increase was detected by the off-axis control photodiode that monitors the LED flux (upper right panel). However, for a reason that is not fully understood, it registered only a fraction of the variation (~ 1%).
The other panels of Fig. B.1 display the timelines of the source parameters, monitored along with the LED flux: the LED temperature, the temperature of the backend board, the LED current, and the reference tension of the electronics. No corresponding glitch was registered on any of these quantities.
As of today, we have no clear explanation for this phenomenon. It may be due to a sudden variation in the structure of the LED junction. We have not been able to observe any similar event in any of our subsequent long duration tests. In any case, should such an event occur during operations, it would be detectable by the off-axis control photodiode, and the corresponding LED would not be used in subsequent operations (until recalibration of the source).
Appendix C: Spectroscopic calibration bench
Test bench setup and operations
The test bench setup is presented in Fig. 8. The monochromator is operated in a slightly non-standard way, in the sense that the LEDs are not placed just in front of the entrance slit, but at a distance of 270 mm. Since the LED emissive zone is very small, the light that enters the monochromator is a quasi-pencil beam, with an angle distribution less than 0.2° wide.
The value of the mean angle of the incident beam is defined by the relative positioning of the LED and the entrance slit. We (conservatively) estimate a positioning error of the LED head with respect to the monochromator of about 1 mm. This translates into an uncertainty on the incident beam angle of 0.2°.
The output is a larger beam, convolved with the monochromator response. At the level of the photodiode, it produces an illumination of width 4 mm and height 6 mm with an extended penumbra zone. It is almost entirely contained in the S2281 NIST photodiode used to measure it. Since we were concerned that there could be chromatic flux losses affecting the measurements, the beam was scanned spatially and in wavelength in order to check for diffuse light and parasitic reflexions. We found that the flux loss is essentially constant (0.5%) as a function of wavelength in the 400 nm <λ< 800 nm range. It then increases up to 1% for redder wavelengths. The LED SED being narrow, the shapes of the measured spectra are not affected by this effect.
The size of the entrance and output slits define the monochromator wavelength passband – through the dispersion relation. The latter has been remeasured by studying images of monochromatic sources with various slits apertures. We find 3.2 ± 0.11 nm per millimetre aperture in accordance with the manufacturer indications. We set the slit openings to 625 μm and the monochromator step to 2 nm for optimal sampling, during the full calibration process. This choice is a trade-off between fineness of sampling and S/N (which is critical for UV LEDs).
Apart from the grating and picoammeter range, which differ for each LED, the measurement protocol is the same for all calibration channels. The temperature is set to the desired value, and we let the bench thermalise. Each LED is positioned in front of the entrance slit, and a fast wavelength scan is performed in order to check the SED extension. Each spectrum is then sampled every 2 nm. At each step, we alternate measurements of the dark current and the LED flux. Spectra are obtained at least at six different temperatures ranging from 0 °C to 25 °C.
Wavelength Calibration.
The monochromator does not come with a temperature-dependent wavelength calibration. During the tests, the monochromator temperature has been found to vary between 5 °C and 25 °C. (The bench is never fully thermalised, and the monochromator is always slightly warmer than the LEDs.) It is therefore essential to check for potential temperature-dependent effects. The absolute wavelength calibration of the monochromator was determined at 25 °C, 18 °C and 13 °C using two calibration lamps: one Cd lamp and one Hg lamp. We have found a small wavelength offset, Δλ, that varies slightly as a function of the temperature of the monochromator, TM: 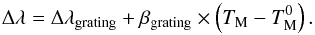 (C.1)The values of Δλgrating and βgrating are reported in Table C.1. This correction was applied to all wavelength measurements. The final wavelength calibration error is classically derived by propagating the uncertainties on Δλgrating s and βgrating and on the monochromator temperature (σTM ~ 1 °C). We find that it never exceeds 1 Å (for UV LEDs).
(C.1)The values of Δλgrating and βgrating are reported in Table C.1. This correction was applied to all wavelength measurements. The final wavelength calibration error is classically derived by propagating the uncertainties on Δλgrating s and βgrating and on the monochromator temperature (σTM ~ 1 °C). We find that it never exceeds 1 Å (for UV LEDs).
Absolute wavelength calibration offsets.
Transmission.
The monochromator transmission is a rapidly varying function of λ. It cannot be considered to be flat on the scale of one single LED spectrum, so it has to be measured precisely. To perform this measurement, we placed a 800 μm wide mask in front of the monochromator entrance slit, at a distance of about 1 cm. The latter was opened slightly wider than in normal operations (1 mm instead of 625 μm), so that it contains a large, constant fraction of the beam.
The transmission of the monochromator at a given wavelength λ can then be estimated using a LED emitting in that wavelength range, by measuring the ratio between the flux measured with the monochromator φ(λ,LED) and the flux without it: 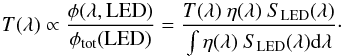 (C.2)The monochromator transmission can be modelled knowing the groove spacing (1200 g/mm). It is a simple function of the blaze angle (ϵ), the Ebert angle (α), and the focal distance f:
(C.2)The monochromator transmission can be modelled knowing the groove spacing (1200 g/mm). It is a simple function of the blaze angle (ϵ), the Ebert angle (α), and the focal distance f: 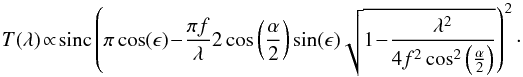 (C.3)Figure C.1 shows the measurements performed over the full wavelength range of grating #2 (500 nm). It shows excellent agreement of the model and the observations. For example, for this grating, a fit of the model yields θblaze = 18.1 ± 0.28° and θebert = 16.6 ± 1°, in remarkable agreement with the constructor data.
(C.3)Figure C.1 shows the measurements performed over the full wavelength range of grating #2 (500 nm). It shows excellent agreement of the model and the observations. For example, for this grating, a fit of the model yields θblaze = 18.1 ± 0.28° and θebert = 16.6 ± 1°, in remarkable agreement with the constructor data.
 |
Fig. C.1 Top panel: model (dark line) and measurements (triangles) of monochromator grating #2. Bottom panel: fit residuals (same units as top panel). |
Our transmission model does not include the reflectivities of the four mirrors that are inside the monochromator. Inspecting the residuals of Fig. C.1, we see a dip around 550 − 600 nm that could be the signature of Al reflectivity. Incorporating an Al reflectivity function (at the fourth power because there are four mirrors) into the transmission model does not improve the fit significantly. We find, however, that correcting locally for the dip has a negligible impact on the spectrum shape (less than 1 Å for the mean wavelength). We therefore use the model as it is and consider that the uncertainties it carries essentially have no impact on the spectrum shapes.
Appendix D: Isotropy of the LED illumination
In this section, we report on a study conducted to look for a possible dependence between the LED spectra and the direction of emission, u. We know already that the beam intensities vary by about 1−2% as a function of u. These non-uniformities are measured, as described in Sects. 3.4 and 4.3, and the resulting beam maps are included in the source emissivity model. Now, we want to verify that the shape of the source spectrum also does not depend on the direction of emission.
In principle, we do not expect a large effect. Indeed, the process that generates the LED light takes place everywhere in the junction. For small angles, the photon generation and extraction mechanisms are the same. However, we cannot exclude effects induced by the LED packaging or possibly interferences taking place within the junction.
This work was initiated after the DICE sources had been installed on site. As a consequence, it was not performed on the real sources, but on a small model built by gluing a selection of LEDs on a radiator, and connecting them to a laboratory current source. This system is slightly less stable in flux than the real DICE sources (0.1% stability). However, it is stable enough for our purpose.
Our selection of LEDs is listed in Table D.1. They are chosen so as to cover the full spectral range of DICE (3800 Å <λ< 9500 Å). Also, we tried to probe as many technologies and packaging types as possible. All these LEDs are narrow-spectrum emitters with typical smooth spectra (Fig. D.1). There is one exception: the reddest LED (SFH4203) that displays sharp features probably due to fringing within the substrate. For this LED, we expect a more pronounced dependence of the spectrum shape on the emission angle.
 |
Fig. D.1 All panels show the superposition the LED spectrum models, fitted on each run. Each model therefore corresponds to a specific angle of incidence. Except for the IR emitter (SFH4203), the spectra at various angles can barely be distinguished from each other. The insets show the spectrum average wavelength ⟨λ⟩ = ∫λS(λ)dλ/∫S(λ)dλ computed on each run. This quantity varies by less than 1 Å (peak-to-peak) over a ~ 15° range. Except for SFH4203, these variations are likely to be due to residual temperature effects, which not well accounted for by the crude model used for this study. |
The source model is mounted on a support that can rotate around a vertical axis, and the LED light is injected at various angles wwith respect to the direction of normal emission into the Digikröm DK240 monochromator that equips the bench. A photodiode, read out with a Keithly picoammeter, is placed at the exit slit of the monochromator.
LED models tested for isotropy.
Information about the dataset accumulated with this setup can be found in Table D.1. For each LED, series of consecutive spectra are taken at four to eight different angles, spanning a range of about ± 8 degrees, around the direction of normal emission. This range is chosen to be deliberately larger than the 1° field of view of MegaCam in order to enhance our chances of detecting an effect. This dataset represents hundreds of spectra per LED, taken over the course of several weeks. Incidentally, it allowed us to check the stability of the LED spectra over long periods of time.
We call run a series of consecutive spectra taken at a same angle. Each single run is analysed independently from the others. The only piece of information shared from one run to another is the measurement of the dark current, performed during dedicated data-gathering sessions. The analysis consists in extracting from each run an average spectrum template Ŝ(λ), modelled in practice as a series of 1-nm-wide bins. If the temperature was constant with a precision of a tenth of a degree, its effect on the spectral shapes (the cooler-bluer effect) could be neglected, and the model could be obtained simply by averaging the flux measurements in each single bin.
In fact, the temperature has been found to vary by up to a few degrees during each single run. As a consequence, spectra taken at different angles were taken at slightly different temperatures. This induces spectrum-shape variations that are independent of the effect we are looking for. To account for this, we fit the following (temperature dependent) model on each run: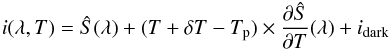 where i(λ,T) is the measured photocurrent, idark the dark current, T the bench temperature reported by the bench DAQ at the time of measurement, Tp a median pivot temperature common to all the runs performed with a given LED and reported in Table D.1, δT an offset introduced to account for the fact that T lags by a fraction of a degree on the real LED temperature. Here, Ŝ(λ) is the average LED spectrum at the pivot temperature, ∂Ŝ/∂T(λ) corresponds to the (binned) derivatives of the spectrum with respect to temperature, and idark is measured independently. Therefore, the parameters that are fitted are Ŝ, ∂Ŝ/∂T, and the δT offsets. This model has slight degeneracies, which we break by adding constraints to the χ2 of the form (δT/σ)2 with σ ~ 0.1 °C.
where i(λ,T) is the measured photocurrent, idark the dark current, T the bench temperature reported by the bench DAQ at the time of measurement, Tp a median pivot temperature common to all the runs performed with a given LED and reported in Table D.1, δT an offset introduced to account for the fact that T lags by a fraction of a degree on the real LED temperature. Here, Ŝ(λ) is the average LED spectrum at the pivot temperature, ∂Ŝ/∂T(λ) corresponds to the (binned) derivatives of the spectrum with respect to temperature, and idark is measured independently. Therefore, the parameters that are fitted are Ŝ, ∂Ŝ/∂T, and the δT offsets. This model has slight degeneracies, which we break by adding constraints to the χ2 of the form (δT/σ)2 with σ ~ 0.1 °C.
 |
Fig. D.2 Broadband flux sensitivity (Δ) to emission-angle-dependent spectrum variations as a function of the red-cutoff of a rectangular broadband filter. |
In Fig. D.1, we show the reconstructed LED models at their respective pivot temperatures for all the angles studied. For all LEDs that emit in the visible, the spectra taken at different angles are virtually indistinguishable. In the corresponding insets, we show the variations in the LED mean wavelengths ⟨λ⟩, which are found to be stable at better than 1 Å over an angular range that is much greater than the acceptance of MegaCam.
The situation is different for the IR emitter, (SFH4203). We see “spectral features” whose positions and relative amplitudes depend on the angle of emission. The question is how this affects the passband measurements.
Following the analysis sketched in Sect. 6, the bench spectra are combined with a (parametrised) passband model to predict broadband fluxes,  (D.1)which are then compared with the fluxes measured directly on the calibration frames. An estimate of how much the LED broadband flux varies over a 1° angle (which is precisely the size of the MegaCam focal plane) is
(D.1)which are then compared with the fluxes measured directly on the calibration frames. An estimate of how much the LED broadband flux varies over a 1° angle (which is precisely the size of the MegaCam focal plane) is 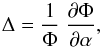 (D.2)where α is the direction of emission.
(D.2)where α is the direction of emission.
We use a rectangular filter to compute the broadband LED fluxes from the spectrum models fitted on each run. Here, Δ is computed numerically from the broadband fluxes at a given angle and the broadband flux at a reference angle. We vary the filter cutoff with respect to the LED spectrum in order to explore all the configurations. In Fig. D.2, we show the value of Δ as a function of the red filter cutoff for two of our LEDs. When the red filter cutoff moves towards the redder wavelengths, the LED spectrum is fully encompassed by the filter shape, and the broadband flux becomes independent of the LED spectral shape. On the other hand, when the cutoff moves towards bluer wavelengths, we explore the region where only a fraction of the LED light is integrated by the filter. This is the regime that constrains the filter cutoff positions.
For a normal LED (left), we see that Δ is of the order of 10-4. Only in the regime where a small fraction of the LED spectrum tail overlaps the filter do we observe small (but not significant) deviations around 0.1%. Conversely, for the IR-LED SFH4203, we observe that the spectrum shape variations induce variations in the broadband fluxes of about 0.5%. We conclude that except for one LED model, for which an effect was easily detected, no emission-angle dependent variation in the LED spectra could be seen over a range of angles of the order of ± 8°.
Appendix E: Constraining passbands (details)
We now explain the estimation of the calibration parameters from series of DICE measurements (Sect. 6). The predicted flux registered on the focal plane is given by Eq. (16), which can be rewritten in matrix form: 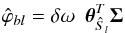 (E.1)where δω is the solid angle covered by the focal plane pixel or superpixel,
(E.1)where δω is the solid angle covered by the focal plane pixel or superpixel, 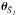 are the parameters of the LED spectral intensity model Ŝl(λ), and Σ is a vector whose components are the integrals of the basis functions defined in Sect. 5, convolved with the telescope transmission Tb(λ):
are the parameters of the LED spectral intensity model Ŝl(λ), and Σ is a vector whose components are the integrals of the basis functions defined in Sect. 5, convolved with the telescope transmission Tb(λ): 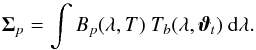 (E.2)The calibration parameters ϑt are determined by minimizing a χ2 built from the measurements of the LED calibration light observed through the different telescope passbands φbl, and from the corresponding predictions
(E.2)The calibration parameters ϑt are determined by minimizing a χ2 built from the measurements of the LED calibration light observed through the different telescope passbands φbl, and from the corresponding predictions 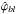 . If we note R the vector of residuals, this χ2 writes as
. If we note R the vector of residuals, this χ2 writes as 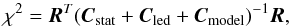 (E.3)where Cstat is the covariance matrix of the flux measurement uncertainties. It will be discussed in detail in the next paper of the series. Here, Cled accounts for the LED intrinsic variabilities and Cmodel accounts for the model uncertainties. The elements of Cmodel are propagated from the covariance matrix of the spectral intensity model parameter, Cθ:
(E.3)where Cstat is the covariance matrix of the flux measurement uncertainties. It will be discussed in detail in the next paper of the series. Here, Cled accounts for the LED intrinsic variabilities and Cmodel accounts for the model uncertainties. The elements of Cmodel are propagated from the covariance matrix of the spectral intensity model parameter, Cθ: 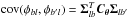 .
.
Since ϕbl is not a linear function of ϑt we linearise it: 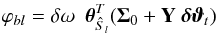 (E.4)at each minimisation step. Here, Σ0 is the “current” value of the Σ vector at a given step, and Y is a matrix containing its derivatives with respect to the calibration parameters. Both are computed numerically, the full minimisation taking a little less than five seconds on a laptop.
(E.4)at each minimisation step. Here, Σ0 is the “current” value of the Σ vector at a given step, and Y is a matrix containing its derivatives with respect to the calibration parameters. Both are computed numerically, the full minimisation taking a little less than five seconds on a laptop.
Systematics.
The systematics we have to consider come from two main sources. First, we have the uncertainties that affect the test-bench measurements. Those have been discussed in Sect. 5 and summarised as seven parameters listed in Table 1. We group them into a vector ηb, which comes along with a (diagonal) covariance matrix Cb. These bench systematics have an impact on our estimates of the LED spectral intensities, Ŝl(λ), and therefore on our broadband flux predictions, ϕbl.
Second, the calibration measurements performed with the imager are themselves affected by several systematics. They include uncertainties on (1) the LED temperature; (2) the positioning of the source with respect to the telescope; (3) systematic drifts of the readout electronics during the data-taking sequence; and (4) contamination of the calibration frames by stray light, in particular the ghosts generated by parasitic reflections on the optical surfaces. The most problematic ones are those which are wavelength dependent, in particular the ghost contamination, which is higher when illuminating the telescope with LEDs close to the filter cutoff. These contributions will be discussed and quantified in detail in Paper II. We will leave them aside for now. Our purpose is to describe the propagation method and to evaluate the impact of the bench systematics.
All the contributions listed above are included as nuisance parameters into the calibration fit described in Sect. 6.2, and marginalised over, using their uncertainty estimates (encoded in matrix Cb) as priors in the χ2 – this is the most direct and exact way to compute their contribution to the total error budget. This means that we minimise the following χ2: 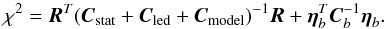 (E.5)Again, the fit is non-linear, and the model is linearised at each step, as follows:
(E.5)Again, the fit is non-linear, and the model is linearised at each step, as follows: 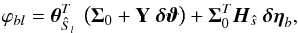 (E.6)which is the equivalent of Eq. (E.4), with the systematics. The fit with systematics is very fast, and takes seconds on a standard laptop.
(E.6)which is the equivalent of Eq. (E.4), with the systematics. The fit with systematics is very fast, and takes seconds on a standard laptop.
Covariances.
 |
Fig. E1 Correlation matrix yielded by the passband (syst. included). We note the strong positive correlations between the filter fronts. This is because the all uncertainties on the filter front positions are dominated by the wavelength calibration of the bench monochromator. |
The test bench systematics are shared by all LEDs. As a result, we expect them to introduce sizeable off-diagonal terms in the covariance matrix of the calibration parameters. The calibration fit described above yields the full (stat+syst) covariance matrix of the calibration parameters, ϑt. In Fig. E1, we show a typical correlation matrix obtained from the fit of ten (simulated) calibration runs. The matrix elements labelled 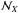 are related to the filter normalisation (relative to the r-filter normalisation). The elements labelled δλX are the filter cutoff displacements. The matrix presented here corresponds to the “best case scenario” presented in Sect. 5.3.2 and to where the NIST uncertainties are all fully positively correlated (best case scenario). The band-to-band correlations of the filter normalisations are essentially negligible, while the filter’s front displacements are all positively correlated. Indeed, they all share the uncertainty on the monochromator wavelength calibration, which is the dominant contribution to their error budget.
are related to the filter normalisation (relative to the r-filter normalisation). The elements labelled δλX are the filter cutoff displacements. The matrix presented here corresponds to the “best case scenario” presented in Sect. 5.3.2 and to where the NIST uncertainties are all fully positively correlated (best case scenario). The band-to-band correlations of the filter normalisations are essentially negligible, while the filter’s front displacements are all positively correlated. Indeed, they all share the uncertainty on the monochromator wavelength calibration, which is the dominant contribution to their error budget.
Appendix F: Cooled Large Area Photodiodes
The time between two test-bench recalibrations of the illumination system is expected to be long – several years at least. For this reason, it is recommended to install a calibrated photodiode on site that can measure the light actually delivered by the device and monitor any unexpected drift in the calibration beam. A solution would be to install in the dome, or even directly on the telescope, a calibrated photodiode procured from NIST coupled with a picoammeter. The typical irradiance of the calibration beam close to the focal plane is about 0.5 nW cm-2. A typical photodiode that can be procured from NIST, such as the Hamamatsu S2281 with an active area of 1 cm-2 and a sensitivity of 0.3 A W-1 at 555 nm, would generate a current of 150 pA, which can be easily measured using a commercial picoammeter. This solution is nevertheless expensive and not very practical, because the photodiode and picoammeter are quite sizeable.
The DICE team has developed miniaturised modules comprising a Hamamatsu S3477-04 photodiode coupled with an ultra-low noise current amplifier implemented as a custom-made ASIC. Each module is connected with an analogue link to a small backend electronics whose main purpose is to digitise the photodiode current and store it in a buffer. Thanks to their small size (100 mm × 100 mm × 15 mm), these modules can be fixed directly on the telescope, close enough to the calibration beam to intercept it. One experimental CLAP module has been installed for tests inside MegaPrime in front of the filter jukebox. Besides demonstrating that this miniaturised low-cost monitoring solution works, our goal is to investigate whether we could gain in precision by polarising the photodiode in reverse and operating it in photoelectric mode, as recommended by all photodiode makers. This would have the advantage of increasing the sensitivity of the detector, at the expense of having a stronger dark current.
The S3477-04 is slightly smaller than the S2281 (5.8 mm × 5.8 mm) and has a similar sensitivity. It is coupled to a small Peltier effect, which allows one to operate it around –20 °C, hence reducing the dark current very significantly when the photodiode is polarised in reverse. NIST does not provide a calibration service for this type of detector, so we have to calibrate it ourselves, using a NIST photodiode as a primary standard and a DICE apparatus as an intermediate light source.
All Tables
All Figures
 |
Fig. 1 Generic metrology chain from POWR, the official implementation of the optical watt, which is maintained at NIST, to the telescope imagers. |
| In the text | |
 |
Fig. 2 Left: DICE calibration beam. A DICE light source consists in a quasi-point source, located at a finite distance from the telescope pupil. Such a beam generates a quasi-uniform illumination of the focal plane. Right: science beam. The light from a distant source, such as a star, may be approximately modelled by a plane wave that fills the entire telescope aperture. Such a beam is focussed on a single point of the focal plane. |
| In the text | |
 |
Fig. 3 Lower panels: (left) coverage of the MegaCam filters with SnDICE (2008). The central wavelengths of all LEDs are displayed with arrows. The shaded regions show the wavelength extension of each LED SED – within 7% of the spectrum peak. In 2007, no narrow spectrum LED with sufficiently high power was available around 700-nm and above 900-nm. Right: coverage of the SkyMapper filters with SkyDICE (2010). The position of about half of the LEDs were chosen so that they constrain the filter cutoffs well. The other LEDs were selected to fill the gaps between filter cutoffs with about one LED every 20/30-nm. Upper panels: (right) sampling from the near-UV to the near-IR achievable with the LEDs listed in the OSRAM and Roithner catalogs. Left: optimised sampling of the MegaCam passbands that can be implemented today with the LEDs available on the market. |
| In the text | |
 |
Fig. 4 Design of the DICE LED head. The LED head is made of 8 aluminium blocks pierced with 24 holes corresponding to each of the 24 LED channels. Black masks are placed between each block to shape the beam and minimise the stray light. Each channel is equipped with an off-axis control photodiode that monitors the light delivered by the LED in real time. The photodiodes are placed on a board just behind the front face of the device. The LEDs are in thermal contact with an aluminium radiator, in order to dissipate waste heat and monitor the LED temperature. An additional central 25th channel delivers a pencil beam used to control the relative orientation of the device with respect to the telescope. |
| In the text | |
 |
Fig. 5 Sketch of a calibration channel showing the emitting LED and the off-axis monitoring photodiode. |
| In the text | |
 |
Fig. 6 Schematics of the current source. |
| In the text | |
 |
Fig. 7 Relative variations in the LED current, measured as the voltage drop across a resistor in series with the LED and monitored over a duration of 3 weeks. During this period, the LED head was operated without interruption on our spectrophotometric test bench. During this run the temperature varied by about 5 °C. As can be seen, the current varies by a few 10-5 at most. |
| In the text | |
 |
Fig. 8 Spectro-photometric test bench. Left panel: photometric bench. The photodiode is placed on a linear table and moved in planes parallel to the z-axis to map each LED beam. Right panel: a monochromator is inserted between the source and the photodiode. |
| In the text | |
 |
Fig. 9 Top panel: cooler-brighter relation measured from 13 minimaps for a Roithner-Lasertechnik APG2C1-690 emitter, mounted on SkyDICE. Bottom panel: residuals. The small black error bars display the uncertainties on the minimap measurements (combined). The larger grey error bars take the measurement repeatability between maps into account (i.e. over time scales of one hour). |
| In the text | |
 |
Fig. 10 Cooler-brighter slopes for the SkyDICE LEDs. The various LED technologies are coded with different symbols (see Appendix A for details). The amplitude of the effect is similar for all LEDs at about 0.5% /°C. For two LEDs, which are operated at very low currents, we actually observe a “brighter-warmer” relation. |
| In the text | |
 |
Fig. 11 Upper panel: variations in the source temperature over a 3-week run designed to test the system stability. Middle panel: black triangles: relative variations of the raw flux delivered by the source. Blue lower triangles: relative variations in the flux after correction for the cooler-brighter effect. Red upper triangles: relative variations in the flux after correction by the control photodiode measurements. Lower panel: zoom on the corrected flux baselines. |
| In the text | |
 |
Fig. 12 Red histogram: stability of the LED flux (i.e. the NIST photodiode current) after correction for the cooler-brighter effect (and for the backend board temperature variations). Blue histogram: stability of the LED channels after correction for the control photodiode measurements. The two outliers above 5 × 10-3 are LEDs in the blue histogram that correspond to channels that are intrinsically unstable. The outliers in the red histogram correspond to the same LEDs, plus one LED whose control photodiode is faulty. |
| In the text | |
 |
Fig. 13 Beam map of LED LVW5AM (OSRAM, Golden Dragon® series) mounted on the SkyDICE device. |
| In the text | |
 |
Fig. 14 Upper panel: comparison between a typical LED spectrum (SkyDICE Golden Dragon LV W5AM) and the fitted model (red line). Bottom panel: residuals. |
| In the text | |
 |
Fig. 15 Spectral intensity surfaces Ŝ(λ,T) for two SkyDICE LEDs. The model incorporates the cooler-brighter and cooler-bluer effects. |
| In the text | |
 |
Fig. 16 Cooler-bluer slopes measured on the SkyDICE spectra. |
| In the text | |
 |
Fig. 17 Upper panel: efficiency (in A/W) of the Hamamatsu S2281 photodiode calibrated at NIST, purchased for this project. Bottom panel: black points: uncertainties reported by NIST (in percentage); dashed red line: diagonal elements of the “worst case” interpretation of the NIST error budget, as discussed in Sect. 5.3.2; dashed blue line: diagonal elements of the “best case” interpretation of the NIST ERROR budget discussed in the same section. |
| In the text | |
 |
Fig. 18 Distortion of the red and blue fronts of the SkyMapper g and r passbands, respectively. |
| In the text | |
 |
Fig. 19 Upper panel: uncertainties in nanometres on the blue (blue triangles) and red (red crosses) cut-offs of the MegaCam passbands, after 20 calibration runs. Grey points: the same, for an optimised design such as the one described in Appendix A. Lower panel: the same, for SkyMapper. |
| In the text | |
 |
Fig. 20 Uncertainty on the MegaCam i-band normalisations, relative to the r-band, as a function of the number of calibration runs. The uncertainty level actually depends on how we interpret the NIST error budget colour uncertainty (black line) or gray scale uncertainty (dashed red line) – see Sect. 5.3 for details. The grey lines show the calibration uncertainties obtained with an optimised filter sampling (see Appendix A). |
| In the text | |
 |
Fig. 21 Upper panel: uncertainty on the MegaCam passband normalisation (relative to r) obtained when combining 20 SnDICE runs. Lower panel: the same, for SkyMapper. |
| In the text | |
 |
Fig. A.1 SnDICE LEDs mounted on their front-end board. The characteristics of all LEDs are summarised in Table A.1. The central LED in slot D0 is used to generate the planet beam. The flat-top LEDs mounted in a white packaging are the high-intensity OSRAM Golden Dragon. The remaining slots host lower intensity LEDs purchased from Marubeni and Seoul Semiconductors. They cover the redder wavelength range. |
| In the text | |
 |
Fig. B.1 Time series registered during a long duration test of a a Roithner-Lasertechnik APG2C1-760 LED mounted on a DICE source. After 18 days of operations, the flux registered by the NIST photodiode (upper left panel) suddenly increased by almost 2%. Only a fraction of this variation was detected by the internal off-axis control photodiode (upper right panel). The other panels display the timeline of the other quantities monitored by the backend electronics: the LED temperature (middle left panel), the backend board temperature (middle right panel), the LED current (lower right panel), and the board reference tension (lower right). No corresponding glitch can be observed on these quantities. |
| In the text | |
 |
Fig. C.1 Top panel: model (dark line) and measurements (triangles) of monochromator grating #2. Bottom panel: fit residuals (same units as top panel). |
| In the text | |
 |
Fig. D.1 All panels show the superposition the LED spectrum models, fitted on each run. Each model therefore corresponds to a specific angle of incidence. Except for the IR emitter (SFH4203), the spectra at various angles can barely be distinguished from each other. The insets show the spectrum average wavelength ⟨λ⟩ = ∫λS(λ)dλ/∫S(λ)dλ computed on each run. This quantity varies by less than 1 Å (peak-to-peak) over a ~ 15° range. Except for SFH4203, these variations are likely to be due to residual temperature effects, which not well accounted for by the crude model used for this study. |
| In the text | |
 |
Fig. D.2 Broadband flux sensitivity (Δ) to emission-angle-dependent spectrum variations as a function of the red-cutoff of a rectangular broadband filter. |
| In the text | |
 |
Fig. E1 Correlation matrix yielded by the passband (syst. included). We note the strong positive correlations between the filter fronts. This is because the all uncertainties on the filter front positions are dominated by the wavelength calibration of the bench monochromator. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


