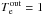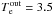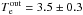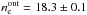| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424386 | |
| Published online | 03 September 2015 | |
X-ray observations of the hot phase in Sagittarius A*
1 N. Copernicus Astronomical Center, Bartycka 18, 00-716 Warsaw, Poland
e-mail: agata@camk.edu.pl
2 Warsaw University Observatory, Al. Ujazdowskie 4, 00-478 Warsaw, Poland
e-mail: pmroz@camk.edu.pl
3 Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
e-mail: M.Moscibrodzka@astro.ru.nl
Received: 12 June 2014
Accepted: 5 July 2015
Context. We analyse 134 ks Chandra ACIS-I observations of the Galactic Centre (GC) performed in July 2011. The X-ray image with the field of view 17′ × 17′ contains the hot plasma surrounding the Sgr A*. The obtained surface brightness map allows us to fit the Bondi hot accretion flow to the innermost hot plasma around the GC.
Aims. Contrary to the XMM-Newton data where a strong 6.4 keV iron line was observed andinterpreted as a reflection from molecular clouds, we search here for the diffuse X-ray emission with prominent 6.69 keV iron line. We found a surface brightness profile that allowed us to determine the stagnation radius of the flow around Sgr A*.
Methods. We fitted spectra from the region up to 5′′ from Sgr A* using a thermal bremsstrahlung model and four Gaussian profiles responsible for Kα emission lines of Fe, S, Ar, and Ca. The X-ray surface brightness profile up to 3′′ from Sgr A* found in our data image was successfully fitted with the dynamical model of Bondi spherical accretion.
Results. We show that the temperature of the hot plasma derived from our spectral fitting is of the order of 2.2−2.7 keV depending on the choice of background. By modelling the surface brightness profile, we derived the temperature and number density profiles in the vicinity of the black hole. The best fitted model of spherical Bondi accretion shows that this type of flow works only up to 3′′ and implies that the outer plasma density and temperature are 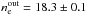 cm-3 and
cm-3 and 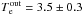 keV, respectively.
keV, respectively.
Conclusions. We show that the Bondi flow can reproduce observed surface brightness profiles up to 3′′ from Sgr A* in the Galactic centre. This result strongly suggests the position of stagnation radius in the complicated dynamics around GC. The temperature at the outer radius of the flow is higher by 1 keV than the value found by our spectral fitting of thermal plasma within the circle of 5′′. The Faraday rotation computed from our model towards the pulsar PSR J1745-2900 near the GC agrees with the observed one, recently reported. We speculate here that the emission lines observed in spectra up to 5′′ can be interpreted as the reflection of the radiation from two-phase regions occurring at distances between 3 − 5′′ of the flow. The hot plasma in Sgr A* illuminated in the past by a strong radiation field may be a seed for thermal instabilities and eventual strong clumpiness.
Key words: Galaxy: center / ISM: individual objects: Sgr A* / X-rays: general / X-rays: ISM
© ESO, 2015
1. Introduction
The central region of the Milky Way hosts a supermassive black hole (BH) with well-established mass MBH = 4.4 × 106M⊙ (Genzel et al. 2010) at a distance R = 8.4 kpc. The surroundings of the black hole are unique. It contains a number of relatively cold molecular clouds (Zhao et al. 2009) located within 15′ from Sgr A*, and a hot plasma of temperature around 2 keV situated within a few arcmin (Baganoff et al. 2003). Both phases of the gas show X-ray emission with a prominent iron Kα line,which may arise from the reflection of hard radiation emitted at the very centre of the Galaxy nucleus.
The cold phase emits a neutral Fe Kα line at energy 6.4 keV, as in the case of molecular clouds reported recently by Ponti et al. (2010). These cold clouds situated at the distance of 30−60 pc from the Galactic centre (GC), are well resolved by the XMM-Newton satellite, enabling proper studies of their velocities and the nature of the reflected continuum. Tracing history of fluorescent reflection, it is possible to capture historic luminosity variations of Sgr A* (Yu et al. 2011).
The hot phase emits the Fe Kα line at energy 6.690 keV, indicating that iron atoms are in helium-like ionization state. X-ray emission from a diffuse hot gas has been observed in extended regions around the GC (Park et al. 2004; Muno et al. 2004). Particularly, it appears to be concentrated within the central 2−3 pc eastwards from Sgr A*, named Sgr A East, and most probably is caused by a young supernova remnant (SNR; Maeda et al. 2002). Additionally, the hot phase lies on the line of sight toward Sgr A* and it may accrete on the supermassive black hole in the form of spherical Bondi accretion or radiatively inefficient accretion flow (RIAF). The dynamical model of the accretion on the GC is still not well established since it is clearly seen that this region may be a mixture of hot plasma with cold clouds i.e. a mini-spiral region (Zhao et al. 2010). The accretion of hot plasma fed by stars due to mass and energy exchange was proposed by Shcherbakov & Baganoff (2010) to explain the observed surface brightness profile. On the other hand, Czerny et al. (2013) constructed a model of multiple accretion events caused by cold clouds to trigger the Sgr A* activity. Such a hot and cold two-phase medium can be formed from the thermal instability caused by irradiation with hard X-rays from the GC, as was recently shown by Różańska et al. (2014). Thermally unstable clouds can be located close to the centre at 0.008−0.2 pc, i.e. within 5′′, and they can survive hundreds years. The radiation reflected from these clouds can produce a hot iron line in that region.
Since the extension of the hot gas is an order of magnitude lower than of the cold phase, Chandra and Suzaku satellites are better for detailed studies of those regions (e.g. Maeda et al. 2002; Koyama et al. 2007; Wang et al. 2013, and references therein). Recently, Wang et al. (2013) have reported the results of the spectral fitting of the longest 3 Ms Chandra observations of the 1.5′′ circular region around Sgr A*, and the spectrum presented in this paper is the most detailed ever published. However, the surface brightness profile from the dynamical model is not fitted in this paper. The authors fit model spectrum computed as a thermal emission from the distribution of temperatures and densities according to the analytical formula appropriate for RIAF (see Sect. 4.2 in this paper).
The purpose of this paper is to study the hot plasma around Sgr A*. Analysing the X-ray image we aim to put constraints on the physical parameters of the hot phase, which is an important source of radiation from Sgr A*. We present archival Chandra ACIS-I observations of the GC made in July 2011 with a field of view of 17′ × 17′ containing both the Sgr A* and Sgr A East. The data were collected with three very short time intervals, one after another. Therefore, spectral and imaging coadding was very accurate.
From Chandra observations, we extracted the spectrum from one circular region around Sgr A* with a radius of 5′′. We performed detailed spectral analysis by fitting a thermal plasma with a strong Kα line from helium-like iron. Additionally, we fitted other emission lines seen in residuals from C, Ar, Ca, but the detection of the last two was marginal. Following Shcherbakov & Baganoff (2010), we extracted a surface brightness profile around Sgr A* within the radius of 10′′ with sub-pixel accuracy. We fitted the dynamical model of the hot Bondi accretion flow by Mościbrodzka et al. (2009) to this imaged emissivity profile. To make a fit, for each computed model we constructed the map of emission around GC convolved with the Chandra exposure map of ACIS-I chip. In our observations Sgr A* is located off-axis, and we constructed a point spread function (PSF) to account for this particular observation. Final models were convolved with normalized PSF before being compared to the data. We point out here, that only a basic spectral fitting is done in this paper owing to the short time exposure. In contrast to Wang et al. (2013), we do not compute the line emissivity from our model. Instead, we focus on modelling the sub-pixel surface brightness profile (see also Shcherbakov & Baganoff 2010).
The main result of the observed surface brightness profile modelling is the derivation of electron density and temperature profiles of the flow from 3′′ down to the black hole horizon. The best fitting model is for temperature and density at the outer flow radius 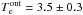 keV, and
keV, and 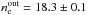 cm-3. Our fit is not valid outside 3′′ indicating the location of the stagnation radius of the dynamical flow around GC. Outside the stagnation radius, matter can possess outflow as was indicated in the RIAF model of Wang et al. (2013). The temperature at the outer flow radius is in good agreement with that derived from the spatially resolved spectral modelling presented in Wang et al. (2013), and then rejected by the RIAF model. In addition, Wang et al. (2013) considered the RIAF model, where the line emissivity was computed from the predicted RIAF temperature profile. This line fitted to the data indicated the outer plasma temperature to be 1 keV, which is lower than in our model. In this paper we compare the temperature and density profiles implied for both models, RIAF and Bondi.
cm-3. Our fit is not valid outside 3′′ indicating the location of the stagnation radius of the dynamical flow around GC. Outside the stagnation radius, matter can possess outflow as was indicated in the RIAF model of Wang et al. (2013). The temperature at the outer flow radius is in good agreement with that derived from the spatially resolved spectral modelling presented in Wang et al. (2013), and then rejected by the RIAF model. In addition, Wang et al. (2013) considered the RIAF model, where the line emissivity was computed from the predicted RIAF temperature profile. This line fitted to the data indicated the outer plasma temperature to be 1 keV, which is lower than in our model. In this paper we compare the temperature and density profiles implied for both models, RIAF and Bondi.
Fitting the canonical model of thermal bremsstrahlung plus the Gaussian profiles for all lines indicates temperatures for the plasma around Sgr A* in the 2.2–2.7 keV range, depending on the choice of background. Again, these values are lower than those obtained by Wang et al. (2013) with the same model for the 1.5′′ Sgr A* spectral fitting, but higher than the 1 keV temperature derived when they used the RIAF emissivity profile. The equivalent width (EW) of the iron line we find is in the 0.9−1.2 keV range. Within the uncertainties, our EW of the iron line is consistent with that estimated by Wang et al. (2013) at the 1σ confidence level. Since the result is degenerated according to plasma temperature and warm absorption, the broad-band spectra are needed to discriminate between the models.
In addition, we calculated the Faraday rotation (RM) towards the Galactic centre and towards the pulsar located at 3′′ in the projected distance away from the GC. The first result matches with observations (Marrone et al. 2007) only with additional assumption of the very weak magnetic field, while the second result agrees with the recently observed value very well (Eatough et al. 2013).
Our paper shows that Bondi accretion can nicely represent the hot phase accretion on the GC up to 3′′. We argue that the radiation originating from the very close vicinity of Sgr A*, illuminating external zones of the Bondi flow may produce a two-phase medium when all lines are created. The exact distance of such clumps and their lifetimes are given in Różańska et al. (2014). The temperature of such clouds varies from log(T) = 5.5 − 7.5 in units of kelvin, and the warm clouds have longer lifetimes than the cold clouds. We postulate here that they can be responsible for the formation of an iron line at energy 6.7 keV, seen in the Chandra data. Better data are needed to fully confirm this hypothesis.
The structure of the paper is as follows: in Sect. 2 we present the details of data extraction that resulted in obtaining images, the brightness profile, and spectra of hot plasma in the neighbourhood of the GC. Section 3 contains results of spectral fitting, while Sect. 4 shows the results of surface brightness profile fitting in the vicinity of Sgr A*. Discussion and conclusions are presented in Sect. 5.
2. Observations
The Chandra X-Ray Observatory has observed the central regions of the Galaxy multiple times. For our analysis, we have selected three observations carried out in July 2011. the longest unpublished observations available in the Chandra archive. They were performed for a very similar period of time, allowing us to avoid significant changes with time and astrometry. Table 1 presents identification numbers, starting dates, and exposure times of the observations. All of them were done using ACIS-I spectrometer with the field of view 17′ × 17′. It corresponds to the region of 40 × 40 pc in the centre of our Galaxy. The pointing coordinates were 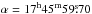 ,
, 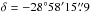 , and were
, and were 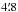 away from Sgr A*.
away from Sgr A*.
Chandra satellite observation log.
2.1. Data reduction
All subsequent analysis was performed using CIAO 4.4 software1, and CALDB version 4.5.3.
We started our analysis by processing individual observations. The corrections for charge transfer inefficiency, bad pixel removal, and background flaring were done in the whole energy band, 0.5−8.0 keV. The lc_sigma_clip tool was used to clip the data that deviates from the mean by more than 2 sigma. In order to minimize the influence of the molecular cloud variability we made two tests: i) point sources were removed from the ACIS-I2 CCD chip, where diffuse emission was marginal, filtering counts to the 0.5−8 keV energy band and ii) photons with energy from 7 to 10 keV in the whole ACIS-I field of view were considered. In both cases similar good time intervals (GTI) were obtained. Hereafter we use the GTI found in case (i) as they set more stringent limits. For all observations the light curves are of good quality and the background flaring is insignificant. Finally, we choose GTI = 134.77 ks, which covers 86% of the total exposure time.
Although the telescope was pointed at the same target during all the observations, we found a small shift between three images (a few arcsec). In order to correct the absolute astrometry of the data, we searched for point sources using the wavdetect tool. Fifty-three bright sources were found and their coordinates were obtained from the SIMBAD astronomical database2. Subsequently we applied minor corrections to the WCS using the reproject_aspect script, which calculates the shift between the wavdetect output and the absolute coordinates from a catalogue.
 |
Fig. 1 Flux image of the GC in the 0.5−8 keV energy range (upper panel). Sgr A* is marked with a black cross. A few brightest filaments reported by Johnson et al. (2009) are marked with small white ellipses and labelled following the names given in the previous detection. The large green ellipse shows the region used for background spectrum extraction (distant background, see Sect. 2.4 for details). The bottom panel shows the flux image of the GC in the energy range of 6.3−7.0 keV, where the iron line is created. The emission presented here is the Kα line emission after subtracting the continuum flux. The flux is presented in asinh scale, since it behaves well for negative count rate values that might originate during the subtraction process. |
2.2. Images in continuum and in Kα iron line bandpass
We regraded event files to a common tangent point with reproject_events and we merged them using dmmerge. A similar procedure was applied to the images, except that the reproject_image and dmimgcalc scripts were used instead. We created exposure-corrected image in the 0.5−8 keV energy band using the fluximage script. The flux image is presented in the upper panel of Fig. 1; the position of Sgr A* is marked by the black cross. In this figure we have also indicated and named the brightest filaments reported by Johnson et al. (2009). Nevertheless, our total exposure time was too short to make spectral analysis of these filaments or to discover new ones, so we do not proceed with their analysis. However, by merging the three observations we obtained enough counts to study the hot extended plasma around Sgr A*. Since the Chandra X-ray observatory has the best spatial resolution among all currently working satellites, in Sect. 4 we present the analysis of the surface brightness profile around Sgr A* with 1′′ scale resolution.
Since we were interested in the spatial distribution of the ionized iron Kα line, additional images were created in the 4.5−6.3 keV (the continuum) and 6.3−7.0 keV (broad line) energy bands. The former was subtracted from the line image with a normalization factor of 0.12. This constant was calculated on the assumption that the continuum emission is modelled by an absorbed power-law function with photon index Γ = 3 and hydrogen column density NH = 1023 cm-2. The continuum spectrum was modelled using Sherpa3 (Freeman et al. 2001) and simulated with the fake_pha command. The response matrix and effective area files were created with mkacisrmf and mkwarf (sample RMFs and ARFs were also taken from CALDB, and a similar value was obtained). The normalization factor is simply the ratio of the flux in the line to the flux in the continuum energy band.
The image in iron line emission after subtracting the continuum image is presented in the bottom panel of Fig. 1. The majority of point sources and diffuse emission around Sgr A* are properly subtracted. Some faint molecular clouds remained after subtraction because the emission from the cold Fe line overlaps the broad line energy band (Ponti et al. 2010). We constructed the flux image in the Kβ line, but the emission was negligible.
Figure 1 (bottom panel) is presented in the asinh (the inverse hyperbolic sine) scale. In the case of a high count rate this scale is practically logarithmic; for low values it changes linearly. It is especially useful in subtracted images, i.e. the iron line, as it behaves well for negative count rate values which might be present.
2.3. Sgr A* surface brightness profile
The surface brightness profile can be constructed in counts per pixel squared as a function of distance from the BH. This was previously done for much longer observations (Shcherbakov & Baganoff 2010) with an exposure time of 953 ks.
Here, we repeat this analysis for our data, but we fit them with a different model (see below Sect. 4). The size of Chandra pixel is 0.5′′, but the position of the satellite over the duration of observation can be determined with a 0.1′′ accuracy by comparing the data with the known positions of bright point sources.
As noted by Shcherbakov & Baganoff (2010) we can achieve the pixel resolution accuracy in the surface brightness profile by knowing the orientation of the detector pixels at the given time.
 |
Fig. 2 X-ray image of the 10′′ region around Sgr A* (circle). The surface brightness profile was extracted integrating counts over annuli from 0 to 10′′. The influence of point sources was rejected as shown in the image. |
 |
Fig. 3 Vicinity of the black hole up to 10′′ from Sgr A*. Red points with errors represent the observed profile, and are connected by continuous line. The black long-dashed line is the normalized PSF. Two models convolved with PSF are also presented: green dotted line for |
In Fig. 2 we show the pixel image of the close vicinity of the GC. It was necessary to exclude some point-like features in the Sgr A* neighbourhood because they broke spherical symmetry around the source. In order to obtain a radial profile, the net counts in a set of concentric annuli around Sgr A* were measured with the dmextract tool. The width of annuli is 0.25′′, the radius of the outer annulus is 10′′, and is marked in Fig. 2 by a black circle. The radial profile monotonically decreases in the whole range of radii. The final profile of the surface brightness with errors is presented in Fig. 3 by red points.
To make any further analysis of the brightness profile on the subpixel scale, we have to account for the PSF appropriate for the Chandra X-ray telescope. Any model fitted to the profile has to be convolved with the PSF. To construct the ACIS-I PSF for our observation we used the Chandra ray-tracing program, ChaRT4, to simulate the Sgr A* (point source) photons scattered by the Chandra mirrors, and the MARX5 software version 4.5.0 to project the simulated rays onto the detector plane. The MARX output was used to extract the PSF profile for convolution with our model spectra. ChaRT requires the position of the point source on the chip, exposure time, and the point source spectrum to run the simulations. For these we used the position of Sgr A* in our stacked observation, total GTI exposure, and the best fitting model to the innermost region of Sgr A* (5′′, Table 2). The normalized PSF constructed for our particular observation is presented in Fig. 3 by black crosses and a long-dashed line. The PSF is wider than in the paper by Shcherbakov & Baganoff (2010) because Sgr A* was slightly off-axis in our observations.
2.4. Extraction of the spectrum
We have extracted spectra from regions where the emission of the line was the highest, especially from the region around Sgr A*. Sgr A East region is treated separately and it will be presented in a forthcoming paper.
Best fit parameters for the 5′′ region around SgrA*.
For the purpose of this work, the spectrum from the circular region of the radius of 5′′ around Sgr A* was extracted and analysed in detail. This was done to see how far from the BH the iron line emission is crucial, and to estimate the temperature at the outer radius of the dynamical flow, which is independently derived while the surface brightness profile is fitted as presented in Sect. 4.1.
Prior to creating the spectrum, a few point-like sources were excluded since they might contaminate the results. The spectrum was obtained with the specextract script for each observation independently and merged with the combine_spectra tool. We consider two different regions for background: a distant region marked as a green ellipse in the upper panel of Fig. 1, and a local region defined as an annulus between 6′′ − 18′′ around the 5′′ source region. The distant background region does not contain any point sources, and the diffuse emission is negligible inside the ellipse. In the case of local background the possible point source contamination was investigated and corrected for during the data reduction process. After background subtraction from 5′′ source, there are 2937 and 2358 photons in the 0.5−8 keV band for the case of distant and local backgrounds, respectively. A full description of our spectral analysis is presented below in Sect. 3.
 |
Fig. 4 Modelling of the spectrum extracted from the 5′′ circular region around the Sgr A*. Both panels present fits with the distant background. The upper panel shows a model consisting of Galactic absorption (tbabs), thermal bremsstrahlung, and one Gaussian line to account for the iron emission. The lower panel shows a model with three additional Gaussian lines for the S, Ar, and Ca emission. |
3. Spectral fitting
The spectral fitting of the data was performed with the Sherpa 4.4 fitting package. In all plots presented in this section, the data were grouped requiring the signal-to-noise ratio S/N = 5 for presentation purposes only. All errors on the spectral parameters correspond to the 68% confidence level (1σ) for one significant parameter.
In the first step, considering case A (distant background), we rejected the simple background subtraction process. Instead, the source region and corresponding background were modelled simultaneously using the CSTAT statistics. We used a phenomenological model composed of a thermal bremsstrahlung emission (bremss) to describe the continuum, and a Gaussian profile to account for the iron Kα line emission. The total model was multiplied by warm Galactic absorption (tbabs). The background data were parametrized with a power-law model. Resulting fit parameters are presented in Table 2 in the first row. Figure 4 (upper panel) shows the data and the best fit model together with residuals. The fit resulted in CSTAT = 1759 for 1019 deg of freedom (d.o.f.). The residuals below 4 keV hint at the presence of additional emission lines detected e.g. by Wang et al. (2013).
In the second step, using the same source/background regions statistics, we add three fit Gaussian profiles to the model to account for the S, Ar, and Ca emission lines reported by Wang et al. (2013). The widths of these additional lines were fixed at σ = 10-5 keV. Certain residuals around the energy of the S line were also visible in the background data, and thus the S line was added to the background model (again with σ fixed at 10-5 keV). These changes resulted in CSTAT = 1696 for 1007 d.o.f., a decrease in the temperature of the plasma, and an increase in the column density of the absorber.
Further improvement to the fit quality was obtained by adjusting the curvature of the background model, i.e. replacing the simple power-law model with a third-degree polynomial, and adding a Gaussian with negative normalization to account for a feature visible below 1 keV. These updates did not affect the values of plasma temperature or the column density, but they led to a substantial decrease in the fit statistics, CSTAT = 1254 for 1011 d.o.f. The best fit parameters are shown in the second row of Table 2. The data and best fit model are presented in Fig. 4, lower panel.
We investigated if the change in the values of the NH (from 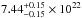 cm-2 to
cm-2 to 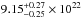 cm-2) and kT (from
cm-2) and kT (from 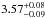 keV to
keV to 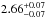 keV) could be due to a degeneracy between these two parameters. We found that at each step we are able to find both a low-NH high-kT solution, and a high-NH low-kT solution with the statistics that differed only by ΔCSTAT = 5–32 (for d.o.f. changing from 1019 to 1007, respectively), with the high-NH low-kT solution always with the lower CSTAT. We interpret it as an indication that these two parameters are indeed degenerate in our modelling, with a slight hint towards the high-NH low-kT solution.
keV) could be due to a degeneracy between these two parameters. We found that at each step we are able to find both a low-NH high-kT solution, and a high-NH low-kT solution with the statistics that differed only by ΔCSTAT = 5–32 (for d.o.f. changing from 1019 to 1007, respectively), with the high-NH low-kT solution always with the lower CSTAT. We interpret it as an indication that these two parameters are indeed degenerate in our modelling, with a slight hint towards the high-NH low-kT solution.
Table 2 also shows the best-fit model parameters for two additional fits with total model tbabs + bremss + 4 lines, using the default Sherpa statistic (chi2gehrels), and background subtracted data grouped requiring that S/N = 3. We performed these fits in order to check how different ways of treating the background affect our analysis. The third and fourth rows of the table presents results obtained using the local and distant backgrounds, respectively. The corresponding plots are presented in Fig. 5.
The change of the statistics does not change the results if the same (distant) background is used. All model parameters are consistent within their uncertainties. In the case with the local background, we observe a further decrease in the plasma temperature to a value 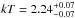 keV and increase in the absorbing column,
keV and increase in the absorbing column, 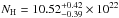 cm-2; these values are not consistent at the 2σ level with the estimates from the other models including all four emission lines.
cm-2; these values are not consistent at the 2σ level with the estimates from the other models including all four emission lines.
We conclude that the continuum is well fitted by a thermal bremsstrahlung model indicating temperatures for the plasma around Sgr A* in the 2.2–2.7 keV range, depending on the choice of background. These values are lower than those obtained by Wang et al. (2013) with the same model for the 1.5′′ Sgr A* spectrum; they quote 3.5(3.0,4.0) keV. The EW of the iron line we find is in the 0.9−1.2 keV range, but its uncertainties are high owing to the uncertainty in deriving the relative contribution of the continuum and line, the number of model parameters, and the quality of the data. Within the uncertainties, our EW is consistent with that estimated by Wang et al. (2013) at the 1σ confidence level (EW = 691(584,846) eVs). Our data are of not sufficient quality to study the Fe line properties (e.g. its evolution with the distance from Sgr A*) in detail, and for this purpose we refer to the work of Wang et al. (2013). The absorbing column in Wang et al. (2013), 10.1(9.4,11.1) × 1022 cm-2, is also consistent with our results at the 1σ confidence level. We note, however, that this value of NH is inconsistent with the absorbing column they find for the flaring Sgr A* spectrum, and based on this result they tend to discard this phenomenological fitting as unphysical and continue with the development of their RIAF model where they find plasma temperature ~1 keV. Our value of kT is intermediate between those of Wang et al. (2013) resulting from their phenomenological and RIAF models. However, in the following, we show an alternative to the Wang et al. (2013) fitting of the surface brightness profile. Instead of computing emissivity from the gas with temperature and density profile analytical expressions, which mimic the RIAF dynamical model as done by Wang et al. (2013), we fit the dynamical Bondi flow directly to the luminosity map without any profile functions.
 |
Fig. 5 Results of spectral fitting of the 5′′ region: upper panel for distant background, lower panel for annulus 6′′ − 18′′. The total model marked with a solid red line is a sum of Galactic absorption (tbabs), thermal bremsstrahlung, and four Gaussian lines for Fe, S, Ar, and Ca emission. |
4. Hot flow around Sgr A*
Chandra ACIS-I camera spatially resolves the close vicinity of the central supermassive black hole and the observations constrain the model of hot plasma around Sgr A*. Previously, Shcherbakov & Baganoff (2010) have analysed 953 ks Chandra data and they have fitted the model of hot plasma interacting with stars up to 5′′ from the Sgr A* complex. They have provided density and temperature radial profiles of the hot plasma at the outer radius of the flow to be equal: T = 2 keV and ne = 60 cm-3. More recently, Wang et al. (2013) have reported 3 Ms observations of Sgr A*, where they concluded that the RIAF model, when the spectrum is fitted by calculating emissivity from RIAF temperature and density profiles, provides an excellent spectral fit indicating the plasma temperature to be 1 keV. Unfortunately, the authors did not fit surface brightness profile to the data.
In the data that we extracted, the collected counts per pixel square are above 30 in the centre and ~3 at 10′′ (Fig. 2 red line). Below we present the fit to the surface brightness profile with the model of the hot Bondi flow. The purpose of our studies is to show to which extent the Bondi flow works. In principle, in the very centre star influence can be inefficient as discussed by Shcherbakov & Baganoff (2010). In any of such models or the RIAF model with outflow, there is a stagnation radius that indicates the border between the matter inflowing or outflowing from the very centre. At the stagnation radius the Bondi flow stops being valid, as we show in the section below.
4.1. Dynamical model of the hot accretion flow
We compute the model brightness profile based on a standard spherical accretion flow theory (Bondi 1952). The plasma density, temperature, and velocity radial profiles are obtained by solving the general Bondi equations (the conservation equations given in Shapiro & Teukolsky 1983, Eqs. (G.21) and (G.22)).
In particular we solve the following Bernoulli equation, 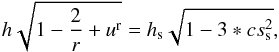 (1)where fluid enthalpy is h = 1/(1 − cs2/ (γad − 1)), cs is the speed of sound, ur is the fluid velocity, and the right-hand side is the integration constant, found by taking the h and cs at the sonic radius, denoted with underscore s. The speed of sound at the sonic radius rs is given by
(1)where fluid enthalpy is h = 1/(1 − cs2/ (γad − 1)), cs is the speed of sound, ur is the fluid velocity, and the right-hand side is the integration constant, found by taking the h and cs at the sonic radius, denoted with underscore s. The speed of sound at the sonic radius rs is given by 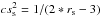 (see Eq. (G17) in Shapiro & Teukolsky 1983). The adiabatic index is assumed to be γad ≈ 5/3. Although we use equations that generalize Bondi equations for the Schwarzschild spacetime, our solutions at large distances from the black hole naturally converge to the classical Bondi solution.
(see Eq. (G17) in Shapiro & Teukolsky 1983). The adiabatic index is assumed to be γad ≈ 5/3. Although we use equations that generalize Bondi equations for the Schwarzschild spacetime, our solutions at large distances from the black hole naturally converge to the classical Bondi solution.
The above Bondi model has two free parameters (except γad, which is fixed in our model): density 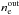 and temperature of plasma
and temperature of plasma 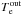 , both at the outer radius Rout ≥ 10′′. These variables are assumed to be far away from the black hole, and so they are equivalent to the “infinity” values (i.e.
, both at the outer radius Rout ≥ 10′′. These variables are assumed to be far away from the black hole, and so they are equivalent to the “infinity” values (i.e. 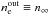 ,
, 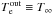 ). The mass accretion rate onto the black hole in the Bondi models in the units of g s-1 is
). The mass accretion rate onto the black hole in the Bondi models in the units of g s-1 is 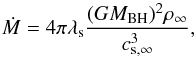 (2)where λs is a function of adiabatic index γad (for our γad ≈ 5/3, λs = 0.25). We integrate the model equations from Rout down to the black hole horizon. The list of models explored in this work is given in Table 3.
(2)where λs is a function of adiabatic index γad (for our γad ≈ 5/3, λs = 0.25). We integrate the model equations from Rout down to the black hole horizon. The list of models explored in this work is given in Table 3.
To create synthetic brightness profiles, we first generate images of the inner region of the GC 20′′ × 20′′ using a ray tracing method. Our scheme performs radiation transfer through the three-dimensional spherically symmetric accretion flow model and records the radiation flux density at each of the detector pixels. In our modelling, we assume that the X-ray radiation is produced by bremsstrahlung. We solve the radiation transfer equation along many rays, using the following bremsstrahlung emissivity function: 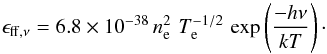 (3)The plasma absorptivity is also taken into account and it is derived from Kirchhoff’s law of thermal radiation, αff,ν = ϵff,ν/Bν, where Bν is the Planck function.
(3)The plasma absorptivity is also taken into account and it is derived from Kirchhoff’s law of thermal radiation, αff,ν = ϵff,ν/Bν, where Bν is the Planck function.
To convert the theoretical flux to counts detected by ACIS-I Chandra CCD, the model fluxes are convolved with the instrument response. The total number of counts detected during the exposure time Texp is 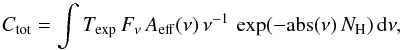 (4)where ν is a frequency corresponding to energies from 0.5 up to 8 keV. Additionally, we assume that absorption also takes place in the ISM between the outer boundary of accretion model and the detector. Hence, we multiply the flux by additional exponential function, and NH = 1023 cm-2 is a typical column density of the ISM. Effective area of the instrument Aeff(ν) and absorption coefficient in the ISM abs(ν) are energy dependent; we adopt the same dependencies as in Shcherbakov & Baganoff (2010, priv. comm.).
(4)where ν is a frequency corresponding to energies from 0.5 up to 8 keV. Additionally, we assume that absorption also takes place in the ISM between the outer boundary of accretion model and the detector. Hence, we multiply the flux by additional exponential function, and NH = 1023 cm-2 is a typical column density of the ISM. Effective area of the instrument Aeff(ν) and absorption coefficient in the ISM abs(ν) are energy dependent; we adopt the same dependencies as in Shcherbakov & Baganoff (2010, priv. comm.).
The final modelled emissivity profiles are obtained by mapping the square images (20′′ × 20′′) onto 40 concentric rings (the same used to extract the data). The total count rate collected on each ring is divided by that ring area (in units of pixels).
Thus computed profiles have to be convolved with the PSF derived for our particular observation in Sect. 2.3. Examples of convolved models of Bondi hot accretion are shown in Fig. 6 by dotted and short-dashed lines for two outer temperatures equal to 1 and 3.5 keV, respectively. As a fitting procedure, we have computed a grid of models with different temperatures and densities in the ranges of:  keV,
keV, 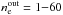 cm-3 (see Table 3).
cm-3 (see Table 3).
4.2. Best model of the surface brightness profile
We fit the model emissivity profile from the Bondi accretion flow convolved with instrument response and with the PSF to the observed surface brightness profile. In Fig. 3 (lower panel) the residuals of fitting up to 10′′ are shown. The fit is not statistically acceptable, showing that the uniform Bondi flow is not a good representation for the hot plasma at distances up to 10′′ from Sgr A*. In a previous analysis by Shcherbakov & Baganoff (2010) a dynamical model of the hot plasma interacting with stars was fitted to the surface brightness profile up to the 5′′ from GC. Additionally, Wang et al. (2013) pointed out that Bondi accretion flow ends at radius ~3.6 × 105RSchw which is 3.8′′ in the case of the M = 4.4 × 106M⊙ black hole.
 |
Fig. 6 Surface brightness profile up to 3′′ from Sgr A*. Red points represent the observed profile, and are connected by a continuous line. The best fit model with |
For this reason, we restricted our modelling to smaller radii and obtained a good fit up to 3′′ from Sgr A*. The best theoretical fit profile is shown with a dashed line in the upper panel of Fig. 6, and the parameters of the spherical accretion model are 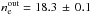 cm-3 and
cm-3 and 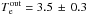 keV. The corresponding integrated mass accretion rate is Ṁ = 1.3 × 10-6M⊙ yr-1. The reduced χ2 of our best fit is 1.19. Residuals are presented in the lower panel of Fig. 6. All data points are within 2 sigma from the model.
keV. The corresponding integrated mass accretion rate is Ṁ = 1.3 × 10-6M⊙ yr-1. The reduced χ2 of our best fit is 1.19. Residuals are presented in the lower panel of Fig. 6. All data points are within 2 sigma from the model.
From the best fitting model we can estimate profiles of temperature and density of the hot plasma. We present them in Fig. 7 with solid lines. As a result of our fitting we found the values of density and temperature at the distance of 1.5′′ to be ne = 29.2 cm-3 and Te = 4.8 keV, respectively. These values are different to those obtained by Shcherbakov & Baganoff (2010) (ne = 130 cm-3 and Te = 2 keV).
The mass accretion rate from our Bondi best fit model is 10−1000 times larger than the mass accretion rate limits set by the measurements of the Faraday rotation near the central black hole 10-9<Ṁ< 10-7M⊙ yr-1 (Bower et al. 2005; Marrone et al. 2006, 2007). Nevertheless, the derived mass accretion rate is always model dependent and the direct comparison is meaningless. The above limits computed by Marrone et al. (2006, see Eq. (8) in this paper), strongly depend on how the Faraday rotation measure (RM) relates to the accretion flow and magnetic field projected on the line of integration. To avoid any inaccuracies, we present here RM computed from our models according to the formula RM 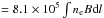 , where electron density ne is in cm-3, the path length dl in pc, and the magnetic field B in Gauss (Gardner & Whiteoak 1966); this last parameter is defined by standard formula B2 = 8πPgas/β, where β is the plasma parameter.
, where electron density ne is in cm-3, the path length dl in pc, and the magnetic field B in Gauss (Gardner & Whiteoak 1966); this last parameter is defined by standard formula B2 = 8πPgas/β, where β is the plasma parameter.
There is no direct constraint on the magnetic field value in Sgr A*, and so we consider the cases of moderate and very weak magnetic fields. We present RM computed towards the GC from all our models in Table 3. Column 5 is for β = 1 (magnetic field in equipartition with the gas), while Col. 6 is for β = 107. For β = 1, RMGC for the best fitted model does not agree with measured value RM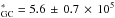 rad/m2 (Marrone et al. 2007); however, it does fully agree if we assume that the magnetic field in the radial direction is very weak, i.e. β = 107. We therefore admit that our best fit model is not well constrained within approximately 100RSchw or that the magnetic field in radial direction is very weak. When we start the integration of our model from 5 × 10-3′′ (which corresponds to the distance of 464 Rschw), the result is RMGC = 6.91 × 105 rad/m2 with the magnetic field being in equipartition. In this case, our result agrees quite well with the observations, especially those in Marrone et al. (2006; Fig. 4), where the integration of models was typically done from 300 Rschw, and then compared to the data.
rad/m2 (Marrone et al. 2007); however, it does fully agree if we assume that the magnetic field in the radial direction is very weak, i.e. β = 107. We therefore admit that our best fit model is not well constrained within approximately 100RSchw or that the magnetic field in radial direction is very weak. When we start the integration of our model from 5 × 10-3′′ (which corresponds to the distance of 464 Rschw), the result is RMGC = 6.91 × 105 rad/m2 with the magnetic field being in equipartition. In this case, our result agrees quite well with the observations, especially those in Marrone et al. (2006; Fig. 4), where the integration of models was typically done from 300 Rschw, and then compared to the data.
For the parameter β = 107, the magnetic field in the centre of the flow is B = 5 × 10-2 Gauss, which is not in agreement with recent findings that the strength of B in GC is around a hundred gauss (Eatough et al. 2013). Nevertheless, this value was given by authors after they have measured RM toward the pulsar PSR J1745-2900 near the GC. Since all model computations are not precise very close to the black hole, we decided to compare the modelled RM towards the above pulsar, located 3′′ in the projected distance from the black hole. This value was reported recently as equal to RM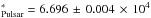 rad/m2 (Eatough et al. 2013). We project our density profile and magnetic field in the direction of the pulsar and compute modelled RMPulsar in the case of β = 1 and β = 100. We present the results in Table 3, Cols. 7 and 8, respectively.
rad/m2 (Eatough et al. 2013). We project our density profile and magnetic field in the direction of the pulsar and compute modelled RMPulsar in the case of β = 1 and β = 100. We present the results in Table 3, Cols. 7 and 8, respectively.
The RMPulsar for the best fitted model agrees very well with the observed value for β = 1. For this value of the β parameter the magnetic field towards Sgr A* is B = 157 Gauss, from our best fitted model. We conclude, that our model density and temperature profiles, and hence mass accretion rate of about 10-6M⊙ yr-1 around 3′′ are consistent with the RM measured toward the GC pulsar. It is possible that the mass accretion rate is reduced at distances closer to the black hole. However, these outflows cannot be accounted for in our simple spherically symmetric model that is fitted to a spherically averaged brightness profile.
For comparison, Fig. 7 also shows the radial profiles of temperature and gas number density from analytical radiativelly inefficient accretion flow (RIAF) models (Shapiro et al. 1976; Rees et al. 1982). In such models the density profile is given by n ~ r(− 3/2 + s); if the s parameter is positive here, then the RIAF launches an outflow. In Fig. 6 (lower panel), we plot the density profile for s = 0 (no outflow) and s = 1 with big and small dots, respectively. The density normalization is arbitrary. In RIAF the temperature profile follows T ~ r− θ where the parameter 0 <θ< 1 (upper panel). Typically in RIAF θ = 1, i.e. the temperature has a virial profile (Wang et al. 2013). In Bondi spherical accretion below the sonic point the density profile follows the same radial dependency as in RIAF without the outflow (i.e. s = 0), and the temperature is virial. However, the Bondi solutions at large radii naturally connect to constant values, and both density and temperature profiles deviate from the n ~ r− 3/2 and T ~ r-1 laws, although there is no outflow in this solution.
Our result does not contradict other accretion flow models considered in the case of Sgr A*. It shows the position of the stagnation radius to be at 3′′. Outside this distance, our derived profiles may not work.
 |
Fig. 7 Temperature and density profiles around Sgr A* for our best fitted model |
5. Conclusions
In this paper we presented 134 ks Chandra ACIS-I observations of the GC containing the Sgr A* region. After analysing flux images in the continuum (0.5–8 keV) and iron line (6.3–7.0 keV) bandpasses, we have extracted the spectrum of the 5′′ circular region around Sgr A*. Our spectral model consists of a thermal plasma for the continuum plus Gaussian profiles for the Kα emission of Fe, S, Ar, and Ca lines. The continuum is well fitted by a thermal bremsstrahlung emission indicating temperatures for the plasma around Sgr A* in the 2.2–2.7 keV range, depending on the choice of background. The corresponding absorbing column densities towards the source are 10.5–9.2 × 1022 cm-2, and the corresponding EWs of FeKα line are 1.19–0.91 keV. Our spectral fitting indicates a temperature that is lower (by about 0.5 keV) than the value obtained by Wang et al. (2013) with the same model. Nevertheless, the strength of the iron line is consistent with the value reported by Wang et al. (2013) at the 1σ confidence level.
Furthermore, we studied the brightness profile of the hot plasma in the vicinity of the Sgr A* black hole. We found that the classical Bondi accretion can reproduce the observed brightness profile up to 3′′. This result implies strong constraints on the position of the stagnation point always thought to be present in the complicated flow around Sgr A*. The best fit model for the surface brightness profile requires that the hot plasma outside the flow should have temperature Te = 3.5 ± 0.3 keV and density ne = 18.3 ± 0.1 cm-3.
Sgr A* has recently been resolved down to 1.5′′ and studied by Wang et al. (2013). They have reported an X-ray image of the source based on a 3 Ms Chandra observation. The best fitted model was RIAF, but they did not show any resulting temperature and density profiles. Only a general description for the temperature dependence on the distance was given as T ∝ r− θ, where θ ≳ 0.6. Additionally, they concluded from the weak line of H-like iron Fe XXVI that the amount of gas at temperatures ~9 keV is very small. Our temperature profile predicts the temperature of 9 keV at the distance 0.4′′ from the black hole. Such plasma would have number density equal to 70 cm-3. Both temperature profiles, RIAF and Bondi, agree up to 0.1′′, as can be seen in Fig. 7. However, the Bondi flow that we fitted predicts a higher density by one order of magnitude.
All models show different temperatures at the outer parts of the flow Te = 1,2, and 3.5 keV respectively in the RIAF model (Wang et al. 2013), hot plasma fed by stars (Shcherbakov & Baganoff 2010), and the only Bondi flow reported in this paper. Additionally, our spectral fitting and that done by Wang et al. (2013) indicates slightly different temperatures (2.7 and 3.5, respectively). These results show a big complexity of matter structure around Sgr A*, and additional indications should be taken into account when studying hot plasma in this region. For instance, Wang et al. (2013) also found the He-like Fe Kα line. Therefore, we argue that up to 3′′ Bondi flow works, but hot matter that is farther away may be in the form of a two-phase medium. We speculate that the Fe Kα line emission at 6.69 keV can be attributed to the reflection from clouds of the warm gas. This illuminated radiation originates from the very innermost nucleus and, depending on the luminosity state of Sgr A*, can provide strong clumpiness and trigger the formation of such hot clouds, as proposed by Różańska et al. (2014). However, it is critically important to confirm that the Bondi model fitted here does not overpredict the strength of the FeXXVI line. Wang et al. (2013) concluded that because of the weakness of the FeXXVI line, there must be a little gas at temperatures larger than 9 keV. In our Bondi model the gas temperature reaches 9 keV at 0.4′′ (compared to 0.1′′ in the RIAF model). If the strength of this line computed from our best fitted model of Bondi flow disagrees with the observed value, this may rule out our model despite its agreement with the surface brightness profile. To fully check our predictions we plan to construct thermal plasma model. In addition, better spectra will be needed for this kind of analysis.
The mass accretion rate from our Bondi best fit model is 1.3 × 10-6M⊙ yr-1. This is out of the range of accretion rates predicted from measurements of the Faraday rotation (RM; Marrone et al. 2007). Nevertheless, we point out that the derived mass accretion rate limits are always model dependent. In particular, we can modify the resulting accretion rate by changing the structure and strength of a magnetic field. For our best fitted model the computed RMGC agrees with the observed value toward the Galactic centre with the assumption of a very weak radial magnetic field. Moreover, RMPulsar computed from the best fit model towards the pulsar PSR J1745-2900 located at a 3′′ projected distance from GC is in very good agreement with observations assuming a moderate magnetic field, β = 1. This result clearly shows that any limitation on the accretion rate from the Faraday rotation strongly depends on the model and orientation of the magnetic field. We admit that the best way to compare the accretion model to the Faraday rotation measure is not by comparing accretion rates, but by self-consistent calculations of RM from the model.
The temperature and density profiles resulting from our fitting put constraints on the physical conditions in the vicinity of the GC. It may provide information on the value of the gas pressure of the hot plasma. Together with radiation pressure taken from observed luminosity states of Sgr A* we can estimate the size of the thermal instability and eventual cloud formation in this region (Różańska et al. 2014). Such a multi-phase complex structure is observed in our GC (for review, see Cox 2005). This structure is important because it feeds the central black hole and because there is the possibility of an accompanying outflow.
To study any possible outflow related to the Sgr A* accretion, we should search for spatially resolved regions of the hot plasma farther away from the Sgr A* region where the line emission is prominent. For example, strong iron Kα line emission detected in our observations occurs in the Sgr A East region. The origin of this emission is strongly affected by the SNR, and a more advanced spectral model should be used to describe the emerging spectra. We address these studies in a forthcoming paper.
Acknowledgments
We thank Roman Shcherbakov for providing Chandra ACIS-I effective area responce function. This research was supported by Polish National Science Center grants No. 2011/03/B/ST9/03281, 2013/10/M/ST9/00729, and by Ministry of Science and Higher Education grant W30/7.PR/2013. It has received funding from the European Union Seventh Framework Programme (FP7/2007−2013) under grant agreement No. 312789.
References
- Baganoff, F. K., Maeda, Y., Morris, M., et al. 2003, ApJ, 591, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bower, G. C., Falcke, H., Wright, M. C., & Backer, D. C. 2005, ApJ, 618, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, D. P. 2005, ARA&A, 43, 337 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Czerny, B., Kunneriath, D., Karas, V., & Das, T. K. 2013, A&A, 555, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eatough, R. P., Falcke, H., Karuppusamy, R., et al. 2013, Nature, 501, 391 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Freeman, P., Doe, S., & Siemiginowska, A. 2001, in Astronomical Data Analysis, eds. J.-L. Starck, & F. D. Murtagh, SPIE Conf. Ser., 4477, 76 [Google Scholar]
- Gardner, F. F., & Whiteoak, J. B. 1966, ARA&A, 4, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, Rev. Mod. Phys., 82, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, S. P., Dong, H., & Wang, Q. D. 2009, MNRAS, 399, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, K., Uchiyama, H., Hyodo, Y., et al. 2007, PASJ, 59, 237 [NASA ADS] [Google Scholar]
- Maeda, Y., Baganoff, F. K., Feigelson, E. D., et al. 2002, ApJ, 570, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2006, ApJ, 640, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2007, ApJ, 654, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., Gammie, C. F., Dolence, J. C., Shiokawa, H., & Leung, P. K. 2009, ApJ, 706, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Muno, M. P., Baganoff, F. K., Bautz, M. W., et al. 2004, ApJ, 613, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Park, S., Muno, M. P., Baganoff, F. K., et al. 2004, ApJ, 603, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Terrier, R., Goldwurm, A., Belanger, G., & Trap, G. 2010, ApJ, 714, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., Begelman, M. C., Blandford, R. D., & Phinney, E. S. 1982, Nature, 295, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Różańska, A., Czerny, B., Kunneriath, D., et al. 2014, MNRAS, 445, 4385 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black holes, white dwarfs, and neutron stars: The physics of compact objects [Google Scholar]
- Shapiro, S. L., Lightman, A. P., & Eardley, D. M. 1976, ApJ, 204, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Shcherbakov, R. V., & Baganoff, F. K. 2010, ApJ, 716, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Q. D., Nowak, M. A., Markoff, S. B., et al. 2013, Science, 341, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Y.-W., Cheng, K. S., Chernyshov, D. O., & Dogiel, V. A. 2011, MNRAS, 411, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J.-H., Blundell, R., Moran, J. M., et al. 2010, ApJ, 723, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J.-H., Morris, M. R., Goss, W. M., & An, T. 2009, ApJ, 699, 186 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Flux image of the GC in the 0.5−8 keV energy range (upper panel). Sgr A* is marked with a black cross. A few brightest filaments reported by Johnson et al. (2009) are marked with small white ellipses and labelled following the names given in the previous detection. The large green ellipse shows the region used for background spectrum extraction (distant background, see Sect. 2.4 for details). The bottom panel shows the flux image of the GC in the energy range of 6.3−7.0 keV, where the iron line is created. The emission presented here is the Kα line emission after subtracting the continuum flux. The flux is presented in asinh scale, since it behaves well for negative count rate values that might originate during the subtraction process. |
| In the text | |
 |
Fig. 2 X-ray image of the 10′′ region around Sgr A* (circle). The surface brightness profile was extracted integrating counts over annuli from 0 to 10′′. The influence of point sources was rejected as shown in the image. |
| In the text | |
 |
Fig. 3 Vicinity of the black hole up to 10′′ from Sgr A*. Red points with errors represent the observed profile, and are connected by continuous line. The black long-dashed line is the normalized PSF. Two models convolved with PSF are also presented: green dotted line for |
| In the text | |
 |
Fig. 4 Modelling of the spectrum extracted from the 5′′ circular region around the Sgr A*. Both panels present fits with the distant background. The upper panel shows a model consisting of Galactic absorption (tbabs), thermal bremsstrahlung, and one Gaussian line to account for the iron emission. The lower panel shows a model with three additional Gaussian lines for the S, Ar, and Ca emission. |
| In the text | |
 |
Fig. 5 Results of spectral fitting of the 5′′ region: upper panel for distant background, lower panel for annulus 6′′ − 18′′. The total model marked with a solid red line is a sum of Galactic absorption (tbabs), thermal bremsstrahlung, and four Gaussian lines for Fe, S, Ar, and Ca emission. |
| In the text | |
 |
Fig. 6 Surface brightness profile up to 3′′ from Sgr A*. Red points represent the observed profile, and are connected by a continuous line. The best fit model with |
| In the text | |
 |
Fig. 7 Temperature and density profiles around Sgr A* for our best fitted model |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.