EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 580 (August 2015) A&A, 580 (2015) A74 Full HTML
Free Access
Issue
A&A
Volume 580, August 2015
Article Number A74
Number of page(s) 7
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201525932
Published online 05 August 2015

© ESO, 2015

1. Introduction

The breakthrough developments of Cherenkov telescopes in the past decade have enabled exploration in the very-high-energy (VHE; E> 100 GeV) γ-ray sky with angular resolution better than 0.1° and unprecedented sensitivity. Observations with the current generation of Cherenkov telescopes (H.E.S.S., MAGIC, and VERITAS) of the Galactic plane have revealed a population of supernova remnants (SNRs) radiating in VHE γ-rays. This radiation is the signature that particles are accelerated to multi-TeV energies in SNRs.

VHE observations, combined with longer wavelength information, have been used to probe the nature (hadrons or leptons) and the energy properties (energetics and maximum energy) of those accelerated particles in order to investigate the origin of Galactic cosmic rays (CRs).

The list of VHE sources associated with a SNR has been steadily growing in the past decade and a dozen detections have been reported so far (see, for example, the TeV online catalog TeVCat1 or the catalog of high-energy observations of Galactic SNRs2). This sample could be described in two main categories: 1) a population of young objects (t ≲ 5 kyr) where the emission is probably associated with the SNR shell and 2) a group of older SNRs (t> 10 kyr) that are mostly radiating through their interaction with the surrounding molecular clouds (e.g., W28, IC443).

For several objects in the first group with large angular size (RSNR> 0.25°), the VHE emission is spatially resolved and exhibits a shell-type morphology that is spatially coincident with the shock front of the SNR. The members of this VHE shell SNR club are RX J1713.7−3946 (Aharonian et al. 2004), RX J0852.0−4622 (Aharonian et al. 2007b), RCW 86 (Aharonian et al. 2009), SN 1006 (Acero et al. 2010), and HESS J1731−347 (Abramowski et al. 2011). In those objects, the γ-ray emission allows us to probe the population of high-energy particles directly at the shock where the acceleration is taking place. Those objects also share many similarities. For example, they are evolving in low-density ambient medium (<1 cm-3) and are bright X-ray synchrotron emitters (see Sect. 3.3 and Table 2 for references).

The VHE emission can be produced either from the inverse Compton (IC) scattering of electrons off the ambient photon field or in interactions of hadrons with ambient matter. Understanding the nature of the γ-ray emission based solely on the VHE observations is a difficult task because both mechanisms produce similar spectra in the VHE regime. The Large Area Telescope (LAT) onboard the Fermi Gamma-ray Space Telescope is operating in the high-energy (HE; 0.1 <E< 100 GeV) γ-ray domain, a crucial energy range where the spectral signatures of the leptonic and hadronic scenario differ. The hadronic emission in a case with an 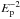Ep-2\hbox{$E_{\rm p}^{-2}$} proton spectrum produces approximately an 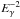Eγ-2\hbox{$E_{\gamma}^{-2}$} spectrum in the GeV regime3. 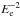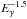In the case of IC emission, an Ee-2\hbox{$E_{\rm e}^{-2}$} electron population translates into a spectrum with a slope Eγ-1.5\hbox{$E_{\gamma}^{-1.5}$}.

Joint studies of the HE/VHE emission in a multiwavelength context (including radio and X-ray observations) are providing new means to disentangle the different scenarios. The best example so far is the case of RX J1713.7−3946, one of the brightest SNRs in the VHE γ-ray sky and considered as one of the prototypes of an efficient CR accelerator. The observations with Fermi-LAT of RX J1713.7−3946 have revealed a hard spectrum at HE with a photon index Γ = 1.50 ± 0.11stat (Abdo et al. 2011), which tends to be incompatible with purely hadronic models (e.g., Ellison et al. 2010; Zirakashvili & Aharonian 2010). A similarly hard index (Γ ~ 1.4 ± 0.2stat; Yuan et al. 2014) was found for RCW 86.

For RX J0852.0−4622, HE γ-rays were detected in spatial coincidence with the SNR, and the resulting HE spectrum was found to be hard (although systematic errors are rather large) with a spectral index of Γ = 1.85 ± 0.06stat ± 0.18sys (Tanaka et al. 2011). However, we note that a fraction of the HE emission seen by Fermi-LAT from RX J0852.0−4622 could be associated with the pulsar wind nebula (PWN) surrounding PSR J0855−4644, which would harden the spectral slope. This PWN is in spatial coincidence with the southeastern shell of the SNR and is seen in X-rays (Acero et al. 2013) and possibly VHE γ-rays (Paz Arribas et al. 2012).

For HESS J1731−347 and SN 1006, no Fermi-LAT source is listed at the position of the two SNRs in the third Fermi catalog (3FGL4, Acero et al. 2015). SN 1006 has been studied using 3.5 years of Fermi-LAT P7V6 data by Araya & Frutos (2012), and no detection was reported. An upper limit was reported (assuming a point source) on a wide energy range (500 MeV to 100 GeV) that is not optimized for constraining the models. The last object of the VHE SNR club, HESS J1731−347, was studied in the HE domain with 3.5 years of Fermi-LAT P7V6 data by Yang et al. (2014), and no detection was reported.

With the advent of the new Fermi-LAT reprocessed data (P7REP), which provide improved sensitivity and angular resolution (see Sect. 2), together with a new Galactic diffuse model, we investigate, with six years of data, the HE counterpart of the two TeV shell SNRs (SN 1006 and HESS J1731−347) that have not yet been detected. In Sect. 2 we present the data analysis, while in Sect. 3 we discuss the implication of the results with respect to the nature of the γ-ray emission and investigate the general class properties of the TeV shell SNRs.

2. γ-ray observations with Fermi-LAT

2.1. Data analysis

The Fermi Large Area Telescope (LAT) is a γ-ray telescope operating from 20 MeV to energies greater than 300 GeV. A description of the instrument and of its performance is presented in Atwood et al. (2009). In operation since August 2008, the LAT provides the most sensitive all-sky survey in the HE γ-ray regime (Ackermann et al. 2012).

The analysis presented here was carried out with six years of data from August 4, 2008 to August 4, 2014 using the LAT reprocessed Pass 7 data (P7REP). A detailed description of the reprocessed data can be found in Bregeon et al. (2013). This reprocessing results in several improvements in the quality of LAT data. Among them, the point-spread function (PSF) is significantly improved above a few GeV (~25% smaller above 10 GeV), and the significance of detection and precision of measured photon flux is increased slightly for most sources and more strongly for sources with hard spectra, as could be the case for some young SNRs.

The P7REP SOURCE class events and the Instrument Response Functions (IRFs) P7REP_SOURCE_V15 were used for this study. We selected only events with energies greater than 3 GeV as a compromise between statistics and background from the diffuse Galactic emission, and zenith angles smaller than 100° to reduce contamination from the Earth limb (Abdo et al. 2009). Time intervals when the rocking angle was more than 52° and when the Fermi satellite was within the South Atlantic Anomaly were also excluded. The Fermi Science Tools5 v9r31p1 and the corresponding Galactic diffuse background (gll_iem_v05_rev1.fit) and extragalactic isotropic background (iso_source_v05.txt) were used.

In addition to the diffuse backgrounds, the model of the region of interest contains the 3FGL sources within a 10° radius of the SNR positions. Using this model, we computed residual test statistic (TS) maps to search for additional background sources. The residual TS map is obtained by computing the TS value for an additional point source at each point of the grid in excess of a given model for the region of interest (see Sect. 3.1 of Nolan et al. 2012,for a more detailed description of the concept of residual TS maps). The positions of the excesses (with a threshold in residual TS of 25) were used as seeds to define the position of additional γ-ray sources not present in 3FGL.

With six years of P7REP data, we investigated the GeV counterparts of those two SNRs using a binned likelihood fit on a 7° × 7° region of interest. Both SNRs are approximately 0.5° in diameter and, for the energy range considered here, should be considered as spatially extended sources for Fermi-LAT. Therefore they were modeled using morphological templates derived from the H.E.S.S. excess maps. The energy threshold for these excess maps is 240 GeV and 500 GeV for HESS J1731−347 and SN 1006, respectively (Acero et al. 2010; Abramowski et al. 2011). Although SN 1006 is located at high Galactic latitude (ℓ = 14.6°) and is not as affected by the Galactic diffuse emission as HESS J1731−347, the same energy threshold (E> 3 GeV) was used for both SNRs for the sake of comparison.

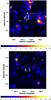thumbnail Fig. 1

Residual test statistic (TS) maps for E> 3 GeV in a 4° × 4° region for HESS J1731−347 (top) and SN 1006 (bottom). The background model is described in Sect. 2 and the SNRs are not included. The point sources included in the model are represented by diamonds (3FGL sources) and crosses (additional background sources). The H.E.S.S. significance contours of HESS J1731−347 (Abramowski et al. 2011) and SN 1006 (Acero et al. 2010) are shown in white in the panels. The source HESS J1729−345 seen near the SNR HESS J1731−347 is shown on the TS map (top) but is not included in the morphological template used to derive upper limits. No Fermi-LAT sources are detected in the vicinity of SN 1006.

2.2. Results: HESS J1731−347

Using the model presented in the previous section (diffuse models+3FGL sources), we generated a TS map of the region to search for new background sources. Based on the TS map, two additional background point sources (PS-SE and PS-NW, see Fig. 1) at the Galactic positions ℓ,b = (354.34°, −1.11°) and (352.93°, −0.30°) were detected with TS = 41.19 and 31.22, respectively.

We generated the residual TS map with a model that includes these two new sources but not SNR HESS J1731−347. This residual TS map is shown in Fig. 1 along with the positions of the 3FGL sources and the newly added background sources. No significant excess γ-ray emission is observed in the region of the SNR. Within the SNR contours, the maximum TS value is 6.4.

To investigate the γ-ray emission under the extended source assumption, we added the H.E.S.S. template to the model using a power-law spectral model. The TS value of the SNR derived from the binned likelihood fit is 2.58/2.55/2.28, assuming a spectral index of 1.5, 2.0, and 2.5, respectively.

Table 1

Fermi-LAT test statistics (TS) values obtained using the H.E.S.S. morphological templates.

thumbnail Fig. 2

Broadband spectral energy distributions (SEDs) for the SNR HESS J1731−347 (top) and SN 1006 (bottom). A purely leptonic (blue solid) and a hadronic (red solid) scenario are shown in the test particle case (se,p = 2.0). The red dashed line shows the steepest hadronic spectral slope compatible with the data, respectively sp = 1.5 and 1.7 for HESS J1731−347 and SN 1006. The H.E.S.S. data points for the top and bottom panels are extracted from Abramowski et al. (2011) and Acero et al. (2010), respectively, and the Fermi-LAT 95% confidence level upper limits are derived assuming a spectral index of 2.0.

To derive upper limits for this extended source, we used the H.E.S.S. morphological template of the SNR alone (the nearby source HESS J1729−345, contours shown in Fig. 1, is not included). A power-law spectral distribution with a fixed spectral index of 2.0 was assumed. Upper limits at 95% confidence level (CL) were derived using a Bayesian method implemented in the Python tool IntegralUpperLimit provided in the Fermi science tools. The energy bands 3−30 GeV and 30−300 GeV were chosen as the best compromise between statistics and contamination from the diffuse Galactic emission. The resulting limits (listed in Table 1) are shown in Fig. 2 with the H.E.S.S. spectral data points. In the most constraining energy bin (3−30 GeV), changing the spectral index to 1.5 or 2.5 alters the results by 10% to 20% (see Table 1).

While the analysis was carried out for E> 3 GeV in order to minimize the impact of the Galactic diffuse emission, its contribution in the Galactic plane is non-negligible even at these high energies. To estimate the associated systematic uncertainty, we applied the procedure used in several Fermi analyses of Galactic sources (e.g. the second Fermi-LAT catalog of γ-ray pulsars, Abdo et al. 2013). In this procedure the best-fit value of the normalization of the Galactic diffuse component is increased/decreased by 6%6, and the flux is srecomputed with the latter normalization parameter kept frozen. As we are dealing with upper limits, we decreased the normalization of the Galactic diffuse emission by 6% (the residuals are thus higher), froze this parameter, and recomputed the upper limit. The resulting upper limit is 1.68 × 10-12 erg cm-2 s-1 in the 3−30 GeV energy range (a ~2% increase in comparison with the value in Table 1), while the upper limit in the 30−300 GeV energy bin was unchanged.

2.3. Results: SN 1006

The same procedure, described in Sect. 2.2, is applied to the region of SN 1006. No background sources were detected on top of the standard model (diffuse emission+3FGL sources). The resulting residual TS map in shown in Fig. 1, and no significant emission is detected within the contours of the SNR. Using the H.E.S.S. morphological template of SN 1006, the TS value from the likelihood fit is very small (TS = 0.95). Owing to the bipolar morphology of SN 1006, both limbs were tested independently by splitting the H.E.S.S. template into two regions. Since both regions are separated by ~0.5°, the Fermi-LAT PSF above a few GeV is sufficient to disentangle the contribution from both limbs. The resulting TS from the northeastern and southwestern limbs are 0.13 and 0.91, respectively, for a spectral index of 2.0.

Because of the low significance of SN 1006 using six years of P7REP data, we do not expect any significant detection in the coming years. Upper limits using the morphological template for the whole SNR and for the two limbs are derived in the 3−30 GeV and 30−300 GeV energy bands and are reported in Table 1. The limits for the whole SNR, together with the H.E.S.S. data, are shown in Fig. 2. As SN 1006 lies 14° above the Galactic plane, we expect the contribution from the Galactic diffuse emission above 3 GeV to be negligible. We applied the same test as in the previous section for a systematic effect related to the Galactic diffuse emission normalization, and the upper limits remained unchanged.

3. Discussion

To investigate the nature of the γ-ray emission from both SNRs, we focused on the HE upper limits derived in the previous section and the VHE data collected in the literature. The data are then compared with a simple one-zone static model where the particles (electrons and protons) are described by a power law with an exponential cutoff7 of the form 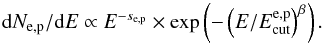dNe,p/dE∝E−se,p×exp(−(E/Ecute,p)β).\begin{equation} \mathrm{d} N_{\rm e,p}/\mathrm{d}E \propto E^{-s_{\rm e,p}} \times \exp\left(- \left(E/E_{\rm cut}^{\rm e,p}\right)^{\beta} \right). \label{expcut} \end{equation}(1)The sharpness of the cutoff is represented by the factor β. In most of the literature, an exponential cutoff is assumed (β = 1.0), which we use throughout this study for the sake of comparison. However, we note that a broader cutoff with β = 0.5 can also reproduce the multiwavelength data fairly well, in particular the low-energy part of the VHE spectra (see Liu et al. 2008; Li et al. 2011,for an example on RX J1713.7−3946).

The γ-ray emission from the π0 decay is calculated following the method of Huang et al. (2007) where accelerated protons and helium nuclei collide with the interstellar medium with standard composition. The IC emission is derived from the scattering on the cosmic microwave background (CMB) and the local interstellar infrared radiation field derived from Porter et al. (2006). A lower limit to the distance of HESS J1731−347 of 3.2 kpc was derived in Abramowski et al. (2011). In the following discussion the distance is fixed to 3.2 kpc, and therefore the electrons and protons energy budget (We and Wp) should be viewed as lower limits. The distances to the other SNRs are listed in Table 2.

Table 2

Summary of the physical properties of the known TeV shell morphology SNRs.

3.1. Constraints on emission model for HESS J1731−347

The Fermi-LAT upper limits reported in Sect. 2 are shown in Fig. 2 with respect to the H.E.S.S. data points. In a purely hadronic scenario, both the HE and VHE emission result from the π° decay. In the test particle case with a proton spectrum index sp = 2.0 (illustrated in Fig. 2), the purely hadronic scenario is excluded by the Fermi-LAT upper limits. To quantify to what extent we can exclude this hadronic scenario, we compared the log-likelihood (L0) obtained when the SNR flux is frozen to the hadronic case, to the log-likelihood (L1) given by the fit of the SNR when the flux is left free. In both cases, the log-likelihoods are computed using Fermi data, i.e. in the 3−300 GeV range, and the photon spectral index was fixed to 2. For L0, the SNR flux is frozen to a value of 10.21 × 10-10 cm-2 s-1 in the 3−300 GeV band, which corresponds to the flux in the purely hadronic case where sp = 2.0 that connects to the H.E.S.S. data points.

The resulting ΔL = (L1−L0) is 14.68 for one additional degree of freedom, so we conclude that the hadronic test particle scenario is excluded at the ~5.4σ confidence level. To accommodate the HE upper limit and the VHE data in a hadronic model, a proton slope sp ≤ 1.5 is required (see Fig. 2).

In several aspects (age, bright X-ray synchrotron emission, low-density ambient medium, VHE luminosity) HESS J1731−347 is very similar to RX J1713.7−3946 (see Table 2). Our Fermi-LAT analysis has shown that HESS J1731−347 has very similar properties at HE to RX J1713.7−3946, whose measured photon index is 1.5 ± 0.1. It is therefore likely that the dominant emission mechanism in γ-ray for HESS J1731−347 is similar to the case of RX J1713.7−3946 (i.e., leptonic-dominated).

3.2. Constraints on emission model for SN 1006

The upper limits derived for SN 1006 by Araya & Frutos (2012) were not constraining enough to be able to disentangle the different emission scenarios that are possible. We also note that SN 1006 was modeled as a point source in their study. While this is a reasonable assumption for Fermi-LAT in the 100 MeV energy range, the radius of the SNR (R = 0.25°) becomes non-negligible in comparison with the PSF above a few GeV. In consequence, the value of the upper limits for SN 1006 can be artificially low when the point source hypothesis is used.

Here, with six years of P7 reprocessed data and assuming an extended source hypothesis (the H.E.S.S. template), we show in Fig. 2 the first constraining upper limits at HE. As for HESS J1731−347, we compared the log-likelihoods in a scenario where the 3−300 GeV flux is fixed to the hadronic hypothesis (2.19 × 10-10 cm-2 s-1, Fig. 2) and a scenario in which the flux normalization is left free. With a ΔL = 17.13, the hadronic scenario is excluded at a 5.8σ confidence level. The steepest hadronic spectral slope compatible with the HE upper limit and the VHE data points gives sp ≤ 1.7 (Fig. 2).

When using the H.E.S.S. template to model only the southwest rim of the SNR, we find no evidence of HE emission. While the synchrotron cut-off frequency is slightly higher in the northeast rim (Miceli et al. 2009), the southwest rim is of high interest to study the hadronic scenario as this region is the only one in the SNR where we have evidence of efficient particle acceleration at the shock (traced by the non-thermal X-rays), dense target densities (traced by the HI observations), and proof of the interaction between the shock and the cloud (shock front is curved inwards in this region) as reported by Miceli et al. (2014). However, this interaction region represents a small angular fraction of the whole SNR and requires detailed HE and VHE spatially resolved spectroscopy that is at the limit of the capacities of current generation instruments.

3.3. Source class comparison at HE and VHE

To understand the underlying emission mechanism at HE and VHE, we investigate and compare the γ-ray properties of the members of the class. Among those properties, the photon spectral index observed at HE is a key ingredient for distinguishing between a test particle leptonic and hadronic scenario. The HE and VHE spectral index of the five SNRs considered here are listed in Table 2. We note that in a simple one-zone leptonic model, the slope of the electron population is in part constrained from the radio to X-ray synchrotron radiation. However, because there are usually no data between the radio and the X-ray data points, the slope and the synchrotron cutoff frequency can be degenerate parameters, in particular if synchrotron cooling effects are significant and if curvature is allowed in the particle spectrum. In the case of RX J1713.7−3946, RX J0852.0−4622, and RCW 86, which were detected in the Fermi-LAT data, the electron slope can actually be fitted over a wider energy range using GeV to TeV data, thus giving better leverage on the electron slope and reducing the impact of the aforementioned caveats. In the two cases where Fermi-LAT upper limits are reported, the electron slope can be regarded as an upper limit (i.e., the steepest slope allowed by the Fermi-LAT upper limits).

For the five SNRs considered, all show, or are compatible with hard HE spectral indices (1.4 < Γ < 1.8) that exclude the standard hadronic test particle scenario. All photon indices (except for RX J0852.0−4622) are compatible with a test-particle leptonic-dominated scenario where the electron slope is se = 2.0, which translates into a photon spectral index of 1.5. For RX J0852.0−4622, the slightly higher HE photon index (1.85 ± 0.06stat ± 0.18syst, Tanaka et al. 2011) could be due to a deviation from the test particle case, a mix of hadronic and leptonic contributions or a possible contamination from the pulsar wind nebula seen around PSR J0855−4644 (Acero et al. 2013) that is located right on the southeastern part of the SNR shell.

Theoretical possibilities for explaining a hard spectral index (ΓHE< 2.0) within a hadronic scenario include back reaction effects (Berezhko & Völk 2006; Zirakashvili & Aharonian 2010) or shock-cloud interaction (Inoue et al. 2012; Gabici & Aharonian 2014). However, in young SNRs where the hadronic hypothesis is preferred, the measured spectral indices are softer than or equal to 2.0 as in Cassiopeia A (2.0 ± 0.1stat ± 0.1syst, Abdo et al. 2010) and Tycho (2.3 ± 0.2stat ± 0.1syst, Giordano et al. 2012).

This similarity of hard photon spectral indices in our SNR sample tends to point toward a common leptonic-dominated scenario for the HE and VHE γ-ray emission. We note that while this is probably true when looking at the spectrum averaged on the whole SNR, there could be some smaller subregions (e.g., dense clumps) where the hadronic mechanism could significantly contribute to the local γ-ray emission.

Based on the model parameters compiled from the leptonic model fits in the literature, the SEDs in HE and VHE γ-rays in luminosity space of the five shell SNRs are presented in Fig. 3. In addition to a similar HE spectral index, this comparison plot reveals a striking similarity in terms of peak luminosity and spectral shape for the SNRs considered in this sample. This similarity is highlighted when compared with the SED of the SNR W44 where the evidence of hadronic emission is secure (detection of the π° decay feature, the smoking-gun evidence of hadronic emission, in the <100 MeV energy range: Ackermann et al. 2013). The γ-ray luminosity of SN 1006 in Fig. 3 is lower than for other SNRs. This is probably related to the SNR bipolar morphology and the reduced surface for efficient particle acceleration. If we correct for this effect by a renormalization factor of 0.2 as discussed in Berezhko et al. (2009), the peak luminosity is comparable to other SNRs.

This similar γ-ray luminosity in Fig. 3 was not a priori expected given the fact that our sample is composed of different types of SN explosion and ages ranging from 1 to 6 kyr (see Table 2). Nevertheless, the sources in our sample share an important characteristic that could explain part of this γ-ray similarity. This characteristic is that the SNRs have evolved for most of their life in a low-density ambient medium (see Table 2), which allowed them to maintain a high shock velocity over a long period of time and therefore efficiently accelerate particles to high energies. In this low-density ambient medium, the γ-ray emission is dominated by the leptonic mechanism in which the main source of the photon field, the CMB, is common to all the SNRs. We note that this low-density argument is likely an oversimplification in the case of RCW 86. This object probably exploded in a low-density cavity blown by the wind of a single degenerate system, and only recently have parts of the shock started to interact with the border of the cavity (Williams et al. 2011; Broersen et al. 2014). As a result, the thermal X-rays (tracing the shocked ISM) and the non-thermal X-ray emission (tracing the high-energy particles) do not stem exactly from the same region. A similar caveat applies in the case of RX J1713.7−3946 and HESS J1731−347, which are surrounded by molecular clouds (Fukui et al. 2012; Fukuda et al. 2014) with possible interactions in some regions of RX J1713.7−3946.

It is surprising that RCW 86, where part of the shock emits thermal X-rays that trace ambient medium densities of ~0.5 cm-3, shows a similar HE spectral index to RX J1713.7−3946 where no thermal X-ray emission has been detected so far and where the density upper limit is very constraining (<0.02 cm-3, Cassam-Chenaï et al. 2004). Because of the density difference, we could have expected a higher fraction of hadronic emission in RCW 86 and thus a steeper spectral index at HE. We emphasize that this possible hadronic contribution on small scales is at the sensitivity and angular resolution limit of current-generation instruments. We particularly anticipate the next generation of Cherenkov telescope CTA to carry out spatially resolved spectroscopy on a wide energy range to test those predictions.

thumbnail Fig. 3

Intrinsic spectral energy distribution for all the members of the TeV shell SNR club in the GeV-TeV energy range. For the sake of comparison, the SED from the SNR W44 (age ~20 kyr), where the evidence of hadronic emission is secure, is shown by the dashed line. The corresponding parameters used to produce this figure are shown in Table 2 except for W44 where the broken power-law model from Ackermann et al. (2013) is used.

4. Summary and conclusion

Using six years of P7REP data of the Fermi-LAT telescope, we have studied the HE counterparts of the SNRs HESS J1731−347 and SN 1006. Although both objects are not detected at those energies, we report new upper limits that can rule out, at a confidence level >5σ, a standard hadronic emission scenario (sp = 2.0) as the main mechanism for HE and VHE γ-ray emission. Given that there is no hint of detection in those six years of data, we do not expect a detection with Fermi-LAT in the years to come.

With this study, we now have a complete view of HE and VHE emission of the five TeV shell SNRs. All objects show hard spectral indices at HE (1.4 < Γ < 1.8) that can simply be explained in a standard leptonic dominated scenario. While the SNRs are from different types of SNe (core collapse and Type Ia), have ages ranging from 1 to 6 kyrs, and are evolving in different ambient media, they all show a surprisingly similar HE and VHE luminosity.

We emphasize that the likelihood that the HE and VHE emissions are dominated by leptonic emission does not rule out efficient hadrons acceleration in those TeV shell SNRs. However, owing to the low-density ambient medium on average, the hadrons do not encounter high enough target densities to produce a level of hadronic flux that can compete with the leptonic emission from the whole SNR. We note that in certain localized regions of those SNRs, the shock probably encounters enhanced densities and that locally the hadronic contribution might become important. The next generation of Cherenkov telescopes such as CTA will provide the necessary angular resolution to carry out detailed spatially resolved spectroscopy, which might unveil different emission mechanisms depending on the regions. We anticipate that this will bring a shift in paradigm from “Is the γ-ray emission leptonic or hadronic dominated?” to “In which region of the SNR is the emission leptonic or hadronic dominated?”. This evolution might be comparable to the question about the nature of the X-ray emission of SN 1006 in the 80s (see Becker et al. 1980, and reference therein) which debated whether the emission was Crab-like (power law) or Tycho-like (thermal). The ASCA satellite with an improved energy range, sensitivity, and angular resolution has revealed that both emission mechanisms co-exist but with a different spatial distribution (Koyama et al. 1995).

3

Assuming that the cutoff energy in the particle population is beyond the HE regime.

4

The 3FGL uses 4 years of P7 reprocessed data.

6

The specific value of 6% represents the 1.5σ deviation in the distribution of Galactic diffuse normalization parameters from all the fits in the second catalog of pulsar (Abdo et al. 2013).

7

We note that in all the cases, except RX J1713.7−3946, the statistics at HE and VHE are not sufficient for measuring the shape of the cutoff.

Acknowledgments

The Fermi-LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT, as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana, the Istituto Nazionale di Fisica Nucleare, and the Istituto Nazionale di Astrofisica in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase from the following agencies is also gratefully acknowledged: the Instituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Phys. Rev. D, 80, 122004 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 710, L92 [NASA ADS] [CrossRef] [Google Scholar]
  3. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 734, 28 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
  5. Abramowski, A., Acero, F., Aharonian, F., et al. 2011, A&A, 531, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Acero, F., Ballet, J., & Decourchelle, A. 2007, A&A, 475, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Acero, F., Pühlhofer, G., Klochkov, D., et al. 2009, ArXiv e-prints [arXiv:0907.0642] [Google Scholar]
  8. Acero, F., Aharonian, F., Akhperjanian, A. G., et al. 2010, A&A, 516, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Acero, F., Gallant, Y., Ballet, J., Renaud, M., & Terrier, R. 2013, A&A, 551, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
  11. Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ackermann, M., Ajello, M., Allafort, A., et al. 2013, Science, 339, 807 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  13. Aharonian, F. A., Akhperjanian, A. G., Aye, K.-M., et al. 2004, Nature, 432, 75 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007a, A&A, 464, 235 [Google Scholar]
  15. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007b, ApJ, 661, 236 [NASA ADS] [CrossRef] [Google Scholar]
  16. Aharonian, F., Akhperjanian, A. G., de Almeida, U. B., et al. 2009, ApJ, 692, 1500 [NASA ADS] [CrossRef] [Google Scholar]
  17. Allen, G. E., Chow, K., DeLaney, T., et al. 2015, ApJ, 798, 82 [Google Scholar]
  18. Araya, M., & Frutos, F. 2012, MNRAS, 425, 2810 [NASA ADS] [CrossRef] [Google Scholar]
  19. Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
  20. Becker, R. H., Szymkowiak, A. E., Boldt, E. A., Holt, S. S., & Serlemitsos, P. J. 1980, ApJ, 240, L33 [NASA ADS] [CrossRef] [Google Scholar]
  21. Berezhko, E. G., & Völk, H. J. 2006, A&A, 451, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Berezhko, E. G., Ksenofontov, L. T., & Völk, H. J. 2009, A&A, 505, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Bocchino, F., Vink, J., Favata, F., Maggio, A., & Sciortino, S. 2000, A&A, 360, 671 [NASA ADS] [Google Scholar]
  24. Bregeon, J., Charles, E., & Wood M., et al. 2013, ArXiv e-prints [arXiv:1304.5456] [Google Scholar]
  25. Broersen, S., Chiotellis, A., Vink, J., & Bamba, A. 2014, MNRAS, 441, 3040 [NASA ADS] [CrossRef] [Google Scholar]
  26. Cassam-Chenaï, G., Decourchelle, A., Ballet, J., et al. 2004, A&A, 427, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Ellison, D. C., Patnaude, D. J., Slane, P., & Raymond, J. 2010, ApJ, 712, 287 [NASA ADS] [CrossRef] [Google Scholar]
  28. Ferrand, G., & Safi-Harb, S. 2012, Adv. Space Res., 49, 1313 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fesen, R. A., Kremer, R., Patnaude, D., & Milisavljevic, D. 2012, AJ, 143, 27 [NASA ADS] [CrossRef] [Google Scholar]
  30. Fukuda, T., Yoshiike, S., Sano, H., et al. 2014, ApJ, 788, 94 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fukui, Y., Sano, H., Sato, J., et al. 2012, ApJ, 746, 82 [NASA ADS] [CrossRef] [Google Scholar]
  32. Gabici, S., & Aharonian, F. A. 2014, MNRAS, 445, L70 [NASA ADS] [CrossRef] [Google Scholar]
  33. Giordano, F., Naumann-Godo, M., Ballet, J., et al. 2012, ApJ, 744, L2 [Google Scholar]
  34. Huang, C.-Y., Park, S.-E., Pohl, M., & Daniels, C. D. 2007, Astropart. Phys., 27, 429 [NASA ADS] [CrossRef] [Google Scholar]
  35. Inoue, T., Yamazaki, R., Inutsuka, S.-I., & Fukui, Y. 2012, ApJ, 744, 71 [NASA ADS] [CrossRef] [Google Scholar]
  36. Katsuda, S., Tsunemi, H., & Mori, K. 2008, ApJ, 678, L35 [NASA ADS] [CrossRef] [Google Scholar]
  37. Katsuda, S., Petre, R., Long, K. S., et al. 2009, ApJ, 692, L105 [NASA ADS] [CrossRef] [Google Scholar]
  38. Koyama, K., Petre, R., Gotthelf, E. V., et al. 1995, Nature, 378, 255 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lemoine-Goumard, M., Renaud, M., Vink, J., et al. 2012, A&A, 545, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Li, H., Liu, S., & Chen, Y. 2011, ApJ, 742, L10 [NASA ADS] [CrossRef] [Google Scholar]
  41. Liu, S., Fan, Z.-H., Fryer, C. L., Wang, J.-M., & Li, H. 2008, ApJ, 683, L163 [NASA ADS] [CrossRef] [Google Scholar]
  42. Miceli, M., Bocchino, F., Iakubovskyi, D., et al. 2009, A&A, 501, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Miceli, M., Bocchino, F., Decourchelle, A., et al. 2012, A&A, 546, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Miceli, M., Acero, F., Dubner, G., et al. 2014, ApJ, 782, L33 [NASA ADS] [CrossRef] [Google Scholar]
  45. Moriguchi, Y., Tamura, K., Tawara, Y., et al. 2005, ApJ, 631, 947 [NASA ADS] [CrossRef] [Google Scholar]
  46. Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
  47. Paz Arribas, M., Schwanke, U., Sushch, I., et al. 2012, Proc. 32rd ICRC, 7, 140 [Google Scholar]
  48. Porter, T. A., Moskalenko, I. V., & Strong, A. W. 2006, ApJ, 648, L29 [NASA ADS] [CrossRef] [Google Scholar]
  49. Sollerman, J., Ghavamian, P., Lundqvist, P., & Smith, R. C. 2003, A&A, 407, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Tanaka, T., Allafort, A., Ballet, J., et al. 2011, ApJ, 740, L51 [NASA ADS] [CrossRef] [Google Scholar]
  51. Tian, W. W., Leahy, D. A., Haverkorn, M., & Jiang, B. 2008, ApJ, 679, L85 [NASA ADS] [CrossRef] [Google Scholar]
  52. Tian, W. W., Li, Z., Leahy, D. A., et al. 2010, ApJ, 712, 790 [NASA ADS] [CrossRef] [Google Scholar]
  53. Williams, B. J., Blair, W. P., Blondin, J. M., et al. 2011, ApJ, 741, 96 [NASA ADS] [CrossRef] [Google Scholar]
  54. Winkler, P. F., Gupta, G., & Long, K. S. 2003, ApJ, 585, 324 [NASA ADS] [CrossRef] [Google Scholar]
  55. Yang, R.-z., Zhang, X., Yuan, Q., & Liu, S. 2014, A&A, 567, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Yuan, Q., Liu, S., Fan, Z., Bi, X., & Fryer, C. L. 2011, ApJ, 735, 120 [NASA ADS] [CrossRef] [Google Scholar]
  57. Yuan, Q., Huang, X., Liu, S., & Zhang, B. 2014, ApJ, 785, L22 [NASA ADS] [CrossRef] [Google Scholar]
  58. Zirakashvili, V. N., & Aharonian, F. A. 2010, ApJ, 708, 965 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Fermi-LAT test statistics (TS) values obtained using the H.E.S.S. morphological templates.

In the text
Table 2

Summary of the physical properties of the known TeV shell morphology SNRs.

In the text

All Figures

thumbnail Fig. 1

Residual test statistic (TS) maps for E> 3 GeV in a 4° × 4° region for HESS J1731−347 (top) and SN 1006 (bottom). The background model is described in Sect. 2 and the SNRs are not included. The point sources included in the model are represented by diamonds (3FGL sources) and crosses (additional background sources). The H.E.S.S. significance contours of HESS J1731−347 (Abramowski et al. 2011) and SN 1006 (Acero et al. 2010) are shown in white in the panels. The source HESS J1729−345 seen near the SNR HESS J1731−347 is shown on the TS map (top) but is not included in the morphological template used to derive upper limits. No Fermi-LAT sources are detected in the vicinity of SN 1006.
In the text
thumbnail Fig. 2

Broadband spectral energy distributions (SEDs) for the SNR HESS J1731−347 (top) and SN 1006 (bottom). A purely leptonic (blue solid) and a hadronic (red solid) scenario are shown in the test particle case (se,p = 2.0). The red dashed line shows the steepest hadronic spectral slope compatible with the data, respectively sp = 1.5 and 1.7 for HESS J1731−347 and SN 1006. The H.E.S.S. data points for the top and bottom panels are extracted from Abramowski et al. (2011) and Acero et al. (2010), respectively, and the Fermi-LAT 95% confidence level upper limits are derived assuming a spectral index of 2.0.
In the text
thumbnail Fig. 3

Intrinsic spectral energy distribution for all the members of the TeV shell SNR club in the GeV-TeV energy range. For the sake of comparison, the SED from the SNR W44 (age ~20 kyr), where the evidence of hadronic emission is secure, is shown by the dashed line. The corresponding parameters used to produce this figure are shown in Table 2 except for W44 where the broken power-law model from Ackermann et al. (2013) is used.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.