| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201526331 | |
| Published online | 03 July 2015 | |
The photospheric solar oxygen project
III. Investigation of the centre-to-limb variation of the 630 nm [O I]-Ni I blend
1
GEPI, Observatoire de Paris, PSL Resarch University, CNRS, Univ. Paris Diderot, Sorbonne Paris Cité,
place
Jules Janssen,
92195
Meudon,
France
e-mail:
Elisabetta.Caffau@obspm.fr
2
Zentrum für Astronomie der Universität Heidelberg,
Landessternwarte, Königstuhl 12,
69117
Heidelberg,
Germany
3
Leibniz-Institut für Astrophysik Potsdam,
An der Sternwarte 16,
14482
Potsdam,
Germany
4
National Solar Observatory, Tucson, AZ
85726,
USA
5
LESIA, Observatoire de Paris, PSL Resarch University,
CNRS, Univ. Pierre et Marie Curie,
Univ. Paris Diderot, Sorbonne Paris Cité, Sorbonne Univertités, place Jules
Janssen, 92195
Meudon Cedex,
France
6
Kiepenheuer-Institut für Sonnenphysik,
Schöneckstraße 6, 79104
Freiburg,
Germany
7
Max-Planck-Institute for Solar System Research,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
Received: 16 April 2015
Accepted: 15 May 2015
Context. The solar photospheric abundance of oxygen is still a matter of debate. For about ten years some determinations have favoured a low oxygen abundance which is at variance with the value inferred by helioseismology. Among the oxygen abundance indicators, the forbidden line at 630 nm has often been considered the most reliable even though it is blended with a Ni i line. In Papers I and II of this series we reported a discrepancy in the oxygen abundance derived from the 630 nm and the subordinate [O I] line at 636 nm in dwarf stars, including the Sun.
Aims. Here we analyse several, in part new, solar observations of the centre-to-limb variation of the spectral region including the blend at 630 nm in order to separate the individual contributions of oxygen and nickel.
Methods. We analyse intensity spectra observed at different limb angles in comparison with line formation computations performed on a CO5BOLD 3D hydrodynamical simulation of the solar atmosphere.
Results. The oxygen abundances obtained from the forbidden line at different limb angles are inconsistent if the commonly adopted nickel abundance of 6.25 is assumed in our local thermodynamic equilibrium computations. With a slightly lower nickel abundance, A(Ni) ≈ 6.1, we obtain consistent fits indicating an oxygen abundance of A(O) = 8.73 ± 0.05. At this value the discrepancy with the subordinate oxygen line remains.
Conclusions. The derived value of the oxygen abundance supports the notion of a rather low oxygen abundance in the solar photosphere. However, it is disconcerting that the forbidden oxygen lines at 630 and 636 nm give noticeably different results, and that the nickel abundance derived here from the 630 nm blend is lower than expected from other nickel lines.
Key words: Sun: abundances / stars: abundances / hydrodynamics
© ESO, 2015
1. Introduction
Although oxygen is the third most abundant element in the Sun (after hydrogen and helium), its precise abundance is currently under discussion. Very early on, Sedlmayr (1974) derived a rather low oxygen abundance in comparison to the accepted value at the time, and attributed the difference to the important role of departures from local thermodynamic equilibrium (LTE) for the oxygen infrared triplet at 777 nm. The debate gained momentum thanks to the pioneering works of Kiselman & Nordlund (1995), Allende Prieto et al. (2001), Holweger (2001), and Asplund et al. (2004) who were the first to apply hydrodynamical simulations (hereafter 3D models) to the determination of the solar oxygen abundance. Their results advocated a downward revision of the solar oxygen abundance, and therefore of the solar metallicity Z, which now appears to be in conflict with the helioseismic data (see Basu & Antia 2008, for a review of the topic). In the last ten years much effort has been dedicated to confirming or dismissing the downward revision of the solar oxygen abundance (Asplund et al. 2004, 2009). Pereira et al. (2009b) analysed the [OI] line; they put A(Ni) = 6.22 and derived A(O) = 8.64 from their centre-disc spectrum. Ayres et al. (2006) investigated the infrared lines of CO while Ayres (2008) analysed the [OI] line at 630 nm, both indicating a “high” oxygen abundance. Centeno & Socas-Navarro (2008) also analysed the [OI] line at 630 nm and derived a high value, A(O) = 8.86 ± 0.07. Socas-Navarro & Norton (2007) analysed the oxygen triplet deriving a “low” NLTE oxygen abundance. Socas-Navarro (2015) investigated the [OI] line with the support of an empirical three dimensional model, obtaining a high A(O), but with a large uncertainty and with the possibility of deriving a low oxygen abundance by slightly changing the model. This paper is particularly interesting because it shows the limiting factors of the models we use.
Our project aims at investigating the oxygen indicators in the solar spectrum and deriving the solar oxygen abundance based on a CO5BOLD 3D model of the solar atmosphere. In a previous paper of this series (Caffau et al. 2008, hereafter Paper I), we derived a measure of the solar oxygen abundance from an ensemble of atomic lines. Among the lines employed in that investigation the two [OI] lines at λ = 630 nm and 636 nm were singled out as potentially problematic. The abundance we derived from the two lines differed by 0.1 dex, both when using the 3D model and when using the 1D Holweger-Müller solar model (Holweger 1967; Holweger & Müller 1974, hereafter HM). This is certainly a good reason to investigate these lines further. In addition, the [OI] lines, and in particular the stronger 630 nm line, have often been considered the best indicators of the oxygen abundance, given that they are weak and formed in conditions of LTE. When using other atomic lines to determine the solar oxygen abundance, one is forced to introduce an additional uncertainty related to the computation of the NLTE corrections, which stems from our lack of knowledge of the efficiency of excitation and ionisation of oxygen by collisions with hydrogen atoms. Only for a few atoms do we know the cross sections of inelastic collisions with neutral hydrogen from either experiments or quantum-mechanical computations. The use of the Drawin approximation (Drawin 1969; Steenbock & Holweger 1984) has been seriously criticised by Barklem et al. (2011). For further discussion on this point see also Steffen et al. (2015). We estimated the abundance uncertainty due to this unknown parameter as about 0.03 dex (Paper I). If one could reliably determine the oxygen abundance from the forbidden lines, the role of hydrogen collisions could be constrained by requiring that forbidden and permitted lines yield the same abundance.
We investigated in Caffau et al. (2013, Paper II) the forbidden lines in a sample of stars from high-quality spectra and concluded that the disagreement in the oxygen abundance derived from the two [OI] lines is generally evident in dwarf stars, while it vanishes in giants.
In the present investigation we exploit observations of solar intensity spectra at different limb angles to put additional constraints on the abundance analysis of the forbidden oxygen line at 630 nm.
2. Atomic data and model atmospheres
For the forbidden oxygen line and for the Ni i line we employ the same atomic data as used in Paper I. The adopted f-values are from Storey & Zeippen (2000). The damping parameters have no influence on the profile of these weak lines.
Our analysis is based on a 3D model atmosphere computed with the CO5BOLD code (Freytag et al. 2012). The box-size of the CO5BOLD 3D solar model atmosphere is 5.6 × 5.6 × 2.25 Mm, with a resolution of 140 × 140 × 150. The simulation covers a range in time of 2.1 h, represented by 20 snapshots; this time interval corresponds to 25 periods of the solar 5 min oscillations and about 18 convective turn-over times. The snapshots were taken at equal time intervals and were selected to provide a good representation of the statistical properties of the complete temporal sequence obtained in the CO5BOLD run. The model has been described in Caffau et al. (2011) and used for the chemical investigation of the photospheric solar abundance of several elements. The spectrum synthesis code employed is Linfor3D1. The spectra are calculated for the same μ inclinations as the observed spectra, and for four values of azimuthal angles. The spectrum corresponding to each μ-value is an average over all surface elements, all azimuthal directions, and all time snapshots.
3. Observations
We analysed five sets observations from
-
Hinode (five disc positions);
-
the Swedish Solar Telescope, SST (four disc positions);
-
the McMath-Pierce Solar Telescope, Kitt Peak (six disc positions);
-
the Vacuum Tower Telescope, VTT (five disc positions);
-
THEMIS (eight disc positions).
We think that all of these observations are extremely useful to the discussion of the solar oxygen problem. However, two sets clearly stand out for different reasons: the Hinode observations, taken from space, are not contaminated by any telluric feature; the VTT data are of higher spectral resolution than any other data set. The Kitt Peak and the SST observations are of similar quality, although the latter ones have higher signal-to-noise ratios (S/Ns). The THEMIS observations present some difficulty in the determination of the continuum. In the following, each set of observations is discussed in a dedicated section.
We restrict our analysis to the spectra at μ> 0.2 for all observed sets of spectra for the following reasons. At smaller μ-values sphericity effects become large enough to influence the computed line shapes. The most extreme limb spectra are formed in more external regions of the solar photosphere, and more so for oxygen than for nickel (see Figs. 1 and 2, respectively). The thermal structure and velocity fields of these external low-density layers of the atmosphere are more difficult to model correctly, since they are more sensitive to the upper boundary condition of the simulation box.
3.1. Hinode data
Hinode (JAXA/NASA) observations were obtained with the Solar Optical Telescope (SOT, 50 cm aperture) and the spectro polarimeter (SP) using a thin slit of 0.3 arcsec × 160 arcsec. Details of the solar granulation are clearly visible (granules, intergranules). Observations were performed at ten locations along the solar equator with the slit orthogonal to the equator direction so that pixels along the slit are seen at a mostly constant heliocentric direction, cosine μ. In fact, there is a small μ variation along the slit because pixels at the end of the slit (± 80′′) do not exactly have the μ of the slit centre, but it is a small effect. The resolution provided by the spectrograph is about 200 000 so that the spectra exhibit resolved features of 3 pm at 630 nm. The sampling is 2 pm. The SP is usually centred on the Fe i 630.15 and 630.25 nm lines, but it is possible to move the spectral coverage slightly to [O I] 630.03 nm and Fe i 630.15 nm. The CCD provided spectral images of 112 × 512 pixels corresponding to a spectral/spatial field of 0.23 nm × 160 arcsec. Individual images have a S/N of 1000 in the continuum. For each position along the equator, a small scan along 24 arcsec was made in the equatorial direction, which is the reason why we selected only the central part of the scan to stay at constant μ along the equator. Two sides of the CCD were exposed (1.6 s exposure time) and we used both. All Stokes parameters were recorded (full Stokes mode I, Q, U, V), but we selected only intensities, I. However, the full Stokes mode allowed us to check on the Fe i 630.15 nm line (Lande factor 1.67) that only a few pixels were affected by magnetic fields of the solar network. The curvature of lines was corrected by a parabolic fit derived from the strong Fe i 630.15 nm line close to the [O I] 630.03 nm line with flat-field data. Then, a summation was done in the spatial direction along the slit to get high precision spectra for various μ-values with a final nominal S/N of 20 000 in the continuum.
3.2. SST data
These spectra were observed at the Swedish Solar Telescope in May 2007. They are described in Pereira et al. (2009a) and analysed in Pereira et al. (2009b). The observations were taken with slit width of 0.11 arcsec, the spectral resolving power is 200 000, the four μ-values used are 0.999, 0.793, 0.608, and 0.424.
3.3. McMath-Pierce data (WCL)
The observational data consists of solar intensity spectra for nine heliocentric angles θ (μ = 1.00, 0.87, 0.66, 0.48, 0.35, 0.25, 0.17, 0.12, 0.10), observed with the McMath-Pierce Solar Telescope at Kitt Peak, using the rapid scan double-pass spectrometer (see Livingston et al. 2007, and references therein) in single-pass mode. The observations were taken on September 14, 2006; the local time was about 09h30m to 10h30m. The resolution was set by the slit width: 0.06 mm entrance, 0.1 mm exit. This yields a spectral resolving power of about 90 000. The scan length, in wavelength, is 2048 points. The image scale is 2.̋5 mm-1. The slit was set parallel to the nearest limb.
The setting was fixed in order to observe the two oxygen forbidden lines at 630 nm and 636 nm. The observations were performed on the north-south axis in the sky, from solar centre to limb. For each line we obtained two spectra for any μ-value off-centre, and four spectra of the intensity at disc-centre. Each observation freezes the solar five-minute oscillations, covering a shorter interval of time. Effective exposure time was 100 s for μ ≥ 0.25 (ten scans of 10 s), and 200 s for μ ≤ 0.17 (twenty scans of 10 s). We summed the spectra at equal μ to improve the S/N. No wavelength calibration source was observed and we used the available telluric lines to perform the wavelength calibration. The positions of the telluric lines were measured on the high-resolution, high S/N, solar spectra of the disc-centre atlas of Neckel & Labs (1984), assuming a linear dispersion relation. We will refer to this set of observations as WCL data.
3.4. VTT data
The VTT data were obtained on Tenerife, Canary Islands, with the new prototype instrument LARS (Lars is an absolute reference spectrograph). The set-up is based on the high-resolution vertical Echelle spectrograph of the VTT and employs a laser frequency comb (LFC) wavelength calibration source (see e.g. Murphy et al. 2007; Wilken et al. 2012; Steinmetz et al. 2008) and a single-mode fibre feed (SMFF). The wavelength calibration obtained from the LFC is accurate to 1 m s-1. Light from the VTT focal plane is coupled to the fibre from a circular field of view (FOV) with a diameter of 10 arcsec on the sky. Flat fields are obtained with a fibre-coupled continuum lamp, resulting in an excellent gain-table correction. The set-up provides a spectral purity and fidelity that is, to the best of our knowledge, not attainable with any other instrument currently available for solar observations. An early version of the instrument is described by Doerr et al. (2012a,b) and by Probst et al. (2015).
The spectra used in this work were obtained during several campaigns in the testing and commissioning phase of the instrument in August and December 2013 and in March and July 2014. Repeated observations were carried out at disc-centre and at heliocentric angles corresponding to μ = {0.8,0.6,0.4,0.3,0.2}, but only the data for μ = 1.0...0.3 were used. Individual observations ran between 15 and 30 min, depending on the observing conditions. Seeing usually was moderate to bad which is, however, not important as the instrument was fed with the spatial average of a 10 arcsec FOV in all cases. We took some care to avoid regions with magnetic activity by monitoring G-Band context images and calcium II K full-disc images provided by the ChroTel telescope in real-time (Kentischer et al. 2008). The absolute pointing accuracy of the VTT is better than 5 arcsec and was checked frequently and adjusted if necessary.
All spectra were corrected for dark-current, and the gain-table obtained from the continuum lamp was applied. Residual spectral slopes were corrected by fitting a second-order polynomial to selected high-points in our spectra and to the corresponding points in the Kitt Peak Fourier Transform Spectrometer (FTS) disc-centre spectrum as provided by Neckel (1999). The ratio of both polynomials gave the correction factor that was applied to our spectra to force their continuum to be identical with that of the FTS spectrum. The wavelength calibration was derived from the LFC calibration spectra. The laser lines are completely unresolved by the spectrograph and can be used to measure its instrumental profile (IP). From the full width at half maximum (FWHM) of the IP, we derived a spectral resolution between 600 000 and 750 000 for these observations, depending somewhat on the alignment of the SMFF, which was changed between the individual observing campaigns.
The calibrated spectra were interpolated to an equidistant wavelength scale of 1 mÅ pixel-1 (native sampling is 2.73 mÅ pixel-1). The LFC calibration naturally removes the effect of any instrumental drift and the radial velocity of each observed spectrum was subtracted, resulting in a wavelength scale that is defined in the solar reference frame. All spectra measured at the same heliocentric angle were then summed to increase the S/N. The S/N was measured in the continuum at 6300 Å and it reaches a value of 6900 for the disc-centre spectra. Table 1 provides a census of the calibrated spectra that are used in this work.
Census of the VTT data.
3.5. THEMIS data
THEMIS observations were obtained with the eight-metre spectrograph in classical spectroscopic mode using a thin slit of 0.5 arcsec × 120 arcsec. However, the seeing was never better than 1 to 2 arcsec, so that details of the solar granulation are not visible. Several scans along the solar radius were performed with the slit orthogonal to the radius direction (so that pixels along the slit are seen at almost constant μ). The interference order was 36 and was selected by the predisperser spectrograph. The final resolution provided by the eight-metre spectrograph is about 300 000 so that the spectra exhibit resolved features of 2 pm at 630 nm. The CCD provides spectral images of 512 × 512 pixels corresponding to a spectral/spatial field of 0.5 nm × 120 arcsec with exposure time of 100 ms. Individual images have a S/N of 250 in the continuum. For each position of the slit on the sun, 360 images were recorded and summed to improve the S/N to about 5000. The curvature of lines was corrected by a parabolic fit derived from the strong Fe i 630.15 nm line close to the [O I] 630 nm line with flat-field data. Then, a summation was done in the spatial direction of the slit to get high-precision spectra for various μ-values with a final S/N of 100 000 in the continuum.
Eight positions on the solar disc are observed, at μ = {1.00,0.96,0.88,0.72,0.66,0.48,0.35,0.25}.
4. Data analysis
In our previous analysis of the solar oxygen abundance based on high-resolution, high S/N, central intensity and flux spectra (Paper I), we found that the oxygen abundance A(O) from the 630 nm line is 0.1 dex lower than the value obtained from the 636 nm line. It is known that the 630 nm line is blended with a Ni i line, whose log gf has been well determined (Johansson et al. 2003). On the other hand the 636 nm line, which is weaker than the other [OI] line, lies on the red wing of a Ca i autoionisation line, and is blended with CN molecular lines, whose log gf are more uncertain. From these considerations one should give preference to the A(O) determination from the 630 nm line, and for this reason we concentrate on this line in the present work.
The two forbidden lines are very similar from the point of view of atomic data, and are formed in the same atmospheric layers. Based on the 3D model, we computed the contribution function for the equivalent width (EW) of the [OI] 630 nm line at the various μ-values of the Kitt Peak intensity spectra with the spectral synthesis code Linfor3D. These are shown in Fig. 1. As μ decreases, the contribution function becomes broader and the peak moves to higher photospheric layers. For μ = 1.0 the maximum value of the contribution function is at log τ630 nm = −0.6 and has a FWHM of 1.2 in log τ; for μ = 0.25 the maximum is at –1.0 and the FWHM 1.5 in log τ. The spectra at different limb angles sample slightly different thermodynamic conditions at which the 630 nm blend is formed. In principle, different spectral lines probe different atmospheric layers, and show a different centre-to-limb variation. This can help to disentangle the contribution of oxygen and nickel to the total EW of the blend. In Fig. 2, the contribution function of the EW is shown for the Ni contribution. The similarity of the μ-dependence of the contribution functions of oxygen (Fig. 1) and nickel (Fig. 2) already indicates that it is still a difficult task.
 |
Fig. 1 Contribution function of the EW of the pure [OI] 630 nm line for various μ-angles as a function of monochromatic optical depth in the continuum. The μ-values are given at the top of the panel, the curves are plotted alternating as solid and dashed lines. The ones peaking at higher optical depth correspond to higher μ-values. |
The feature we investigate is a O-Ni blend. The observed spectra at disc-centre agree in that the EW of the blend is of the order of 0.47 pm. It is clear that the derived abundances of oxygen and nickel are related: any increase in A(O) implies a decrease in A(Ni) and vice-versa. A high oxygen abundance has to be associated with a low Ni abundance (a high A(O) implies a high contribution to the EW of the blend due to oxygen so that the fraction of EW left for Ni is small, implying a low A(Ni)) and a low A(O) to a high A(Ni). The situation is summarised in Fig. 3, where we present the relative abundances of oxygen and nickel for a given range in EW based on 3D analysis.
 |
Fig. 3 Oxygen and nickel abundances derived in the past years. The grey bar is the presently discussed range of the solar Ni abundance. Red symbols mean disc-integrated spectrum, green symbols disc centre. Stars indicate theoretical models, squares the HM model. The round dot of Centeno08: in the work a sun-spot spectrum is used. The dashed lines are lines of constant EW for disc centre, solid for disc-integrated light. This figure is an updated version of the one shown by Ludwig et al. (2010). The big green-blue star represents the result of this investigation. The horizontal dotted line at A(Ni) = 6.23 represents values from Grevesse & Sauval (1998); the horizontal dot-dashed line at A(Ni) = 6.17 the value from Scott et al. (2009); the horizontal dot-dashed line at A(Ni) = 6.20 the value from Scott et al. (2015). |
4.1. Line profile fitting
We determine the oxygen abundance of the [OI] line at 630 nm from line profile fitting. In this way we take into account the line strength and the line shape at the same time. As in Bonifacio & Caffau (2003), we fitted the line profile interpolating in a grid of synthetic spectra. To use the complete information, we simultaneously fitted all the limb angles of the solar intensity profiles, discarding the spectra closest to the limb. The same method is also used to analyse the O i triplet lines and is extensively explained in Steffen et al. (2015). The previous analysis of this [OI] line by Pereira et al. (2009b) focused only on the centre-disc spectrum for the line profile fitting procedure.
To fit the observed spectra with the grid of 3D spectra, we must normalise the wings of the [OI] line to unity because the 3D synthetic spectra contain only the lines of oxygen and nickel. No molecular or other line contributions that would prevent normalised spectra from going to unity are considered in the spectrum synthesis. To try to be as objective as possible, and to avoid a subjective normalisation of the spectra, we select two ranges that are not contaminated by lines on the red and on the blue side of the [OI] line, and use these two ranges to pseudo-normalise the spectra at all μ-angles. Using this procedure, there are between 10 and 18 free fitting parameters (A(O), A(Ni), and wavelength shift and continuum level for each of the spectra, observed at four to eight μ-values). We find that the fits are not always very robust. The minimum of the χ2 is not narrow and in the region of the best A(O) and A(Ni) values there are several local minima. By changing the input parameters, the values we derive for A(O) and A(Ni) are not always the same but fall in a limited range spanning ≲ 0.02 dex. We restricted the fit to reasonable values of oxygen abundance (8.6 ≤ A(O) ≤ 8.85) and nickel abundance (5.85 ≤ A(Ni) ≤ 6.35).
Another problem that needs to be mentioned is that we did not apply any instrumental broadening to the synthetic profile (which would correspond to about 0.5 km s-1 for the VTT data and 1.5 km s-1 for Hinode spectrum) because it is already as broad as or slightly broader than the observed one even without any extra broadening. The problem is visible in Fig. 4 where two VTT profiles, observed at centre-disc and at μ = 0.4, respectively, are compared to a synthetic profile with the oxygen and nickel abundances of A(O) = 8.72 and A(Ni) = 6.17. From the figure it is clear that the agreement is worse towards the limb.
 |
Fig. 4 VTT observations with a resolving power of 700 000 (black circles) compared to the 3D synthetic profile (solid red) at μ = 0.4 (top) and at disc-centre (bottom). Below each profile the residual (× 10, displaced by + 0.94) is shown. |
The five sets of observations provide A(O) and A(Ni) in limited ranges. The results are summarised in Table 2. When we average the results we obtain 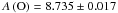 and A(Ni) = 6.096 ± 0.049. If we restrict our average to the data of Hinode, VTT, and SST, which we think are of higher quality, we obtain:
and A(Ni) = 6.096 ± 0.049. If we restrict our average to the data of Hinode, VTT, and SST, which we think are of higher quality, we obtain: 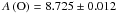 and A(Ni) = 6.122 ± 0.034, the uncertainty being the observed-to-observed scatter. This latter value for the Ni abundance is in agreement with the value of A(Ni) = 6.17 ± 0.02 from Scott et al. (2009) and in reasonable agreement with A(Ni) = 6.20 ± 0.04 from Scott et al. (2015), who used an improved 3D solar model atmosphere with respect to Scott et al. (2009). Our nickel abundance is almost within one σ of the Scott et al. (2009) and of the Scott et al. (2015) results.
and A(Ni) = 6.122 ± 0.034, the uncertainty being the observed-to-observed scatter. This latter value for the Ni abundance is in agreement with the value of A(Ni) = 6.17 ± 0.02 from Scott et al. (2009) and in reasonable agreement with A(Ni) = 6.20 ± 0.04 from Scott et al. (2015), who used an improved 3D solar model atmosphere with respect to Scott et al. (2009). Our nickel abundance is almost within one σ of the Scott et al. (2009) and of the Scott et al. (2015) results.
Summary of the results of the line-profile fitting.
4.1.1. Hinode data
We investigated the possibility of scattered light, but it does not seem to be a problem for the Hinode observations. The comparison of the Hinode centre-disc spectrum with the Neckel centre-disc data gives a perfect agreement (see Fig. 5).
 |
Fig. 5 Comparison of the Hinode centre-disc observation (dashed red) with the Neckel centre-disc spectrum (solid black); the agreement is very good. The Neckel spectrum has been broadened by 2 km s-1 for comparison with the Hinode observation. In the lower panel the residual (× 100) is shown. |
We fitted the five observed spectra corresponding to μ-values of 0.99, 0.95, 0.86, 0.70, and 0.38 for two sets of Hinode data. The best fit of the five μ-values gave A(O) = 8.71 and A(Ni) = 6.16 (see Fig. 6).
 |
Fig. 6 Fitted 3D line profiles for the five μ-values (red) compared to the Hinode observed spectra (black). From the simultaneous fit we derive A(O) = 8.71 and A(Ni) = 6.16. Below each profile the residual (× 10, displaced by +0.94) is shown. |
4.1.2. SST data
The best fit of the four μ-values gave A(O) = 8.73 and A(Ni) = 6.13 (see Fig. 7). The fit looks good and the result is in agreement with the values derived from the other observed spectra. The spectra show no signs of scattered light.
 |
Fig. 7 Fitted 3D line profiles for the four μ-values (red) compared to the SST observed spectra (black). From the simultaneous fit we derive A(O) = 8.73 and A(Ni) = 6.13. Below each profile the residual (× 10, displaced by +0.94) is shown. |
4.1.3. WCL data
We compared the WCL observed spectra at μ = 1.0 to the solar atlases of Delbouille et al. (1973) and Neckel & Labs (1984) and discovered that our WCL disc-centre spectrum has a smaller EW (by roughly 4%) than in both high-resolution solar atlases. This could be due to scattered light in the spectrograph, solar activity, or some other unknown effect. We corrected the data by this factor, assuming that the scattered light affects the spectra at all μ-angles in the same way. We restricted the line profile fitting to the six spectra with μ> 0.2. Using this procedure, we fitted the observed spectra with 14 free parameters (A(O), A(Ni), and wavelength shift and continuum level for each of the six spectra) and obtained A(O) = 8.74 and A(Ni) = 6.10 (see Fig. 8).
 |
Fig. 8 Fitted 3D line profiles for the six μ-values (red) compared to the WCL observed spectra (black). From the fit we derive A(O) = 8.74 and A(Ni) = 6.10. Below each profile the residual (× 5, displaced by +0.94) is shown. |
4.1.4. VTT data
We find no evidence for a contamination by scattered light in these spectra.
We note that we are not able to fit the high-quality VTT spectra because our synthetic profiles are too broad. We therefore decided to broaden the observed profiles and we were able to obtain a very good fit (see Fig. 9 for an example). The required extra broadening is μ-dependent: 1.3, 1.7, 1.8, and 1.9 km s-1 for μ positions 1.0, 0.8, 0.6, and 0.4, respectively. In this way we derive A(O) = 8.74 and A(Ni) = 6.08. With five μ-values, the most extreme limb component, μ = 0.3, required an extra broadening of 1.9 km s-1 . In this case we derive A(O) = 8.72 and A(Ni) = 6.12 (see Fig. 9). The oxygen and nickel abundances we derive in the two cases are very similar, but we prefer to use the case with four μ-values because the agreement with the observed data is better.
 |
Fig. 9 Fitted 3D line profiles for five μ-values (red) compared to the VTT observed spectra (black). From this fit we derive A(O) = 8.72 and A(Ni) = 6.12. Below each profile the residual (× 10, displaced by + 0.94) is shown. |
4.1.5. THEMIS data
As we did in the previous cases, we compared the observed line profile of the disc-centre spectrum to the solar atlases of Delbouille et al. (1973) and Neckel & Labs (1984). From this comparison we estimate a scattered light fraction of about 4%. The quality of the THEMIS spectra is inferior to that of the other sets of observations, so that the continuum is difficult to define. This could be due to a not entirely successful flat-field correction of the data. From the fit shown in Fig. 10 we obtain A(O) = 8.76 and A(Ni) = 6.02, but the fit is not as good as for the other observations.
 |
Fig. 10 Fitted 3D line profiles at the eight μ-values (red) compared to the THEMIS observed spectra (black). From the fit we derive A(O) = 8.76 and A(Ni) = 6.02. Below each profile the residual (× 5, displaced by +0.94) is shown. |
4.1.6. Monte Carlo tests
We investigated the role of the S/N on the uncertainty in the abundance determination. We performed two different Monte Carlo simulations. In the first, we injected Poisson noise in the synthetic spectra with parameters A(O) = 8.66 and A(Ni) = 6.25. We considered the five μ-values of the Hinode data, 1.00, 0.95, 0.86, 0.70, and 0.38. The results are presented in Table 3. The uncertainties in the Table are fit-to-fit scatter for three cases of noise injection of S/N of 800, 400, and 300. We can consider these uncertainties as the statistical error in the abundance determinations related to Poisson noise. Owing to the high-quality spectra we work with, we suggest an uncertainty of 0.02 dex and 0.04 dex for the derived abundance of oxygen and nickel, respectively.
1000 Monte Carlo simulations on synthetic spectra.
We then took the observed Hinode spectra, slightly degrading their quality by injecting noise, but obtaining a plausible different “realisation” of an observation in order to verify whether the result is consistent with the previous exercise of the Monte Carlo simulation over synthetic profiles. This Monte Carlo simulation consists of 1000 events where Poisson noise is injected into the five Hinode observed spectra. The results are presented in Table 4. We see that the scatter within the realisations for oxygen is twice the value derived from synthetic spectra, which is expected because we start from an observed spectrum. For Ni the fit-to-fit scatter is about a factor of three larger than in the case of the synthetic spectra. Nickel seems to be more difficult to derive from observed spectra because the line is weaker, or perhaps because there are uncertainties in the wavelengths of the Ni isotopic components (see Rosberg et al. 1993). The results of the Monte Carlo tests give an indication that the systematics dominate the error budget.
1000 Monte Carlo simulations on the Hinode spectra.
5. Discussion
5.1. The blending nickel line
In the previous sections we have discussed the role of the nickel blend in terms of the Ni abundance. However, we believe it is unlikely that a re-analysis of the solar Ni abundance will result in a large downward revision. The recent result of Scott et al. (2015), who find A(Ni) = 6.20 ± 0.04, corroborates this notion. For the meteoritic nickel abundance, Lodders (2003) recommends A(Ni) = 6.22 ± 0.03, thus a nickel abundance as low as around 6.00 (THEMIS) would be in stark disagreement with the meteoritic nickel abundance. Likewise, such a revision cannot be due to errors in the f-value of the Ni i line, which is known with an uncertainty of only 14% (Johansson et al. 2003), i.e. 0.06 dex in logarithmic abundance. On the other hand, we note that the Ni line has a rather high excitation energy (4.266 eV) and that no calculations exist concerning the deviations from LTE for Ni. NLTE effects may produce a line weaker than predicted by our LTE computations. However, Scott et al. (2009) obtained a rather homogeneous Ni abundance in LTE from all Ni i lines used in their analysis, which would make strong departures from LTE for the blending Ni line rather surprising. Computations on a Fe i line with similar atomic properties provided by Lyudmila Mashonkina (priv. comm.) suggest that the NLTE correction of the Ni i line cannot be the solution to the problem.
We consider here a Ni abundance of about 6.1 dex, which – taking into account the uncertainty in the oscillator strength of the Ni line – is perfectly consistent with the Scott et al. (2009) result. We would like to emphasise that a low contribution of nickel to the 630 nm blend corresponding to A(Ni) ≈ 6.1 is also clearly compatible with previous findings. Combining the result of Allende Prieto et al. (2001), log gfϵNi = 3.94, with the presently accepted value of the oscillator strength (log gfNi = −2.11) results in a nickel abundance of 6.05. We note that Allende Prieto et al. (2001) and also Scott et al. (2009) applied the same 3D model atmosphere in their analyses, but Scott et al. arrived at a significantly higher nickel abundance from the unblended Ni lines. Melendez & Asplund (2008) used the [OI] line at 557.34 nm to obtain an oxygen abundance of 8.71 ± 0.07, which is in reasonable agreement with our result for the two other forbidden lines within the uncertainties. Ayres (2008) analysed the 630 nm blend with a single snapshot from the same solar CO5BOLD model as used in this work. He obtains A(O) = 8.81 ± 0.04 and A(Ni) = 6.08 (he states a ≈ 30% smaller Ni abundance than the value given by Grevesse & Sauval 1998 which is 6.23 ± 0.04) adopting a rather large EW for the feature at disc-centre of 0.476 pm, and applying corrections to the model to reproduce the measured continuum intensity at the wavelength of the blend. While his result is certainly at the high end at the presently discussed oxygen abundances, again, the contribution to the blend by nickel is small.
5.2. The role of the centre-to-limb variation
One should bear in mind that the purpose of this work was to investigate the line formation in the solar photosphere at different limb-angles. In this respect the data we used are unique, but not all these spectra have the high quality of the traditional solar atlases. As we pointed out above, the equivalent widths (EWs) of the two WCL and THEMIS disc-centre spectra of the 630 nm line are smaller than the ones of the largely used disc-centre solar atlases (Delbouille et al. 1973; Neckel & Labs 1984). However, we argue that our observations in their ensemble are surely sufficient to allow a differential study of the centre-to-limb variation of the forbidden oxygen feature.
As pointed out in Sect. 4.1.4, the synthetic profiles are too broad when compared to high-quality data of extremely high spectral resolution. The extra broadening in the synthetic spectra could indicate a velocity field in the hydrodynamical model that is too strong. This effect is most evident in the VTT observation owing to their high resolution, but the effect that the FWHM of the observed spectrum becomes increasingly smaller than in the synthesis towards the limb is visible in the SST (see Fig. 7) and THEMIS data as well (see Fig. 10).
6. Conclusions
Our results can be summarised as follows:
-
1.
The oxygen abundance we derive from the 630 nm blend is A(O) = 8.73 ± 0.02 ± 0.05 (with error estimates from the scatter of the different observations and the Monte Carlo simulations).
-
2.
The above oxygen abundance from the 630 nm feature is inconsistent with a Ni abundance of 6.25 and the assumption of LTE: we advocate a lower contribution of the Ni line to the blend corresponding to a nickel abundance of 6.11 ± 0.04, or log gfϵNi = 4.00.
-
3.
The synthetic line profile we obtain from the 3D model is broader than expected, and this is particularly evident in comparison with the VTT observations with the highest spectral resolving power of 700 000. This effect, which is not seen for other lines, can be due to an overly large velocity field in the model atmosphere, although this effect may also indicate errors in the adopted atomic line wavelength difference between the two components of the [OI]+Ni i blend.
-
4.
The observed spectra at the lowest limb angles (μ< 0.2) are not reproduced satisfactorily by our computations. We speculate that this problem is due to the solar model that is neither taking into account sphericity effects nor a chromosphere.
-
5.
On the other hand, the synthetic spectra reproduce most of the observed data for μ> 0.2 very well, even though the agreement between observed and synthetic spectra deteriorates somewhat towards the limb.
-
6.
With the low oxygen abundance we derive in this work from the [OI] line at 630 nm, the discrepancy of about 0.1 dex with the oxygen abundance derived from the [OI] 636 nm line in Paper I and discussed in Paper II is reduced to 0.06 dex due to a lower A(Ni), but remains unexplained.
Acknowledgments
This project was funded by FONDATION MERAC. We are grateful to Lyudmila Mashonkina for providing us with results of her NLTE computations of an Fe i line that should be analogous to the Ni i line discussed in the present paper. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organised at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway). The LARS instrument at the VTT was funded by the “Senatsauschuss Wissenschaft” of the Leibniz-Gemeinschaft, Germany. E.C. and H.G.L. acknowledge financial support by the Sonderforschungsbereich SFB881 “The Milky Way System” (subprojects A4) of the German Research Foundation (DFG). E.C. and P.B. acknowledge support from Programme National de Physique Stellaire of the Institut National des Sciences de l’Univers of CNRS.
References
- Allen de Prieto, C., Lambert, D. L., & Asplund, M. 2001, A&A, 556, 63 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., Allen de Prieto, C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R. 2008, ApJ, 686, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R., Plymate, C., & Keller, C. U. 2006, ApJS, 165, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Belyaev, A. K., Guitou, M., et al. 2011, A&A, 530, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Basu, S., & Antia, H. M. 2008, Phys. Rep., 457, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., & Caffau, E. 2003, A&A, 399, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2008, A&A, 488, 1031 [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Malherbe, J.-M., et al. 2013, A&A, 554, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Centeno, R., & Socas-Navarro, H. 2008, ApJ, 682, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Delbouille, L., Roland, G., & Neven, L. 1973, Atlas photométrique du spectre solaire de λ3000 à λ10000 (Liège: Université de Liège, Institut d’Astrophysique) [Google Scholar]
- Doerr, H.-P., Steinmetz, T., Holzwarth, R., Kentischer, T., & Schmidt, W. 2012a, Sol. Phys., 280, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Doerr, H.-P., Kentischer, T. J., Steinmetz, T., et al. 2012b, Proc. SPIE, 8450, 84501 [CrossRef] [Google Scholar]
- Drawin, H. W. 1969, Z. Phys., 228, 99 [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Computat. Phys., 231, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Holweger, H. 1967, Z. Astrophys., 65, 365 [Google Scholar]
- Holweger, H. 2001, in Joint SOHO/ACE workshop Solar and Galactic Composition, AIP Conf. Proc., 598, 23 [Google Scholar]
- Holweger, H., & Müller, E. A. 1974, Sol. Phys., 39, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, S., Litzén, U., Lundberg, H., & Zhang, Z. 2003, ApJ, 584, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Kentischer, T. J., Bethge, C., Elmore, D. F., et al. 2008, Proc. SPIE, 7014, 701413 [CrossRef] [Google Scholar]
- Kiselman, D., & Nordlund, A. 1995, A&A, 302, 578 [Google Scholar]
- Livingston, W., Wallace, L., White, O. R., & Giampapa, M. S. 2007, ApJ, 657, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Ludwig, H.-G., Caffau, E., Steffen, M., et al. 2010, IAU Symp., 265, 201 [NASA ADS] [Google Scholar]
- Melendez, J., Asplund, M. 2008, A&A, 490, 817 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Murphy, M. T., Udem, T., Holzwarth, R., et al. 2007, MNRAS, 380, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H. 1999, Sol. Phys., 184, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H., & Labs, D. 1984, Sol. Phys., 90, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira, T. M. D., Kiselman, D., & Asplund, M. 2009a, A&A, 507, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Asplund, M., & Kiselman, D. 2009b, A&A, 508, 1403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Probst, R. A., Wang, L., Doerr, H.-P., et al. 2015, New J. Phys., 17, 023048 [NASA ADS] [CrossRef] [Google Scholar]
- Rosberg, M., Litzen, U., & Johansson, S. 1993, MNRAS, 262, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, P., Asplund, M., Grevesse, N., Sauval, A. J. 2009, ApJ, 691, 119 [Google Scholar]
- Scott, P., Asplund, M., Grevesse, N., Bergemann, M., & Sauval, A. J. 2015, A&A, 573, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sedlmayr, E. 1974, A&A, 31, 23 [Google Scholar]
- Socas-Navarro, H. 2015, A&A, 577, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H., & Norton, A. A. 2007, ApJ, 660, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, M., Prakapavičius, D., Caffau, E., et al. 2015, A&A, submitted [Google Scholar]
- Steinmetz, T., Wilken, T., Araujo-Hauck, C., et al. 2008, Science, 321, 1335 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [Google Scholar]
- Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., & Holweger, H. 2004, A&A, 414, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilken, T., Curto, G. L., Probst, R. A., et al. 2012, Nature, 485, 611 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Contribution function of the EW of the pure [OI] 630 nm line for various μ-angles as a function of monochromatic optical depth in the continuum. The μ-values are given at the top of the panel, the curves are plotted alternating as solid and dashed lines. The ones peaking at higher optical depth correspond to higher μ-values. |
| In the text | |
 |
Fig. 2 Like Fig. 1 but for the blending Ni i line at 630 nm. |
| In the text | |
 |
Fig. 3 Oxygen and nickel abundances derived in the past years. The grey bar is the presently discussed range of the solar Ni abundance. Red symbols mean disc-integrated spectrum, green symbols disc centre. Stars indicate theoretical models, squares the HM model. The round dot of Centeno08: in the work a sun-spot spectrum is used. The dashed lines are lines of constant EW for disc centre, solid for disc-integrated light. This figure is an updated version of the one shown by Ludwig et al. (2010). The big green-blue star represents the result of this investigation. The horizontal dotted line at A(Ni) = 6.23 represents values from Grevesse & Sauval (1998); the horizontal dot-dashed line at A(Ni) = 6.17 the value from Scott et al. (2009); the horizontal dot-dashed line at A(Ni) = 6.20 the value from Scott et al. (2015). |
| In the text | |
 |
Fig. 4 VTT observations with a resolving power of 700 000 (black circles) compared to the 3D synthetic profile (solid red) at μ = 0.4 (top) and at disc-centre (bottom). Below each profile the residual (× 10, displaced by + 0.94) is shown. |
| In the text | |
 |
Fig. 5 Comparison of the Hinode centre-disc observation (dashed red) with the Neckel centre-disc spectrum (solid black); the agreement is very good. The Neckel spectrum has been broadened by 2 km s-1 for comparison with the Hinode observation. In the lower panel the residual (× 100) is shown. |
| In the text | |
 |
Fig. 6 Fitted 3D line profiles for the five μ-values (red) compared to the Hinode observed spectra (black). From the simultaneous fit we derive A(O) = 8.71 and A(Ni) = 6.16. Below each profile the residual (× 10, displaced by +0.94) is shown. |
| In the text | |
 |
Fig. 7 Fitted 3D line profiles for the four μ-values (red) compared to the SST observed spectra (black). From the simultaneous fit we derive A(O) = 8.73 and A(Ni) = 6.13. Below each profile the residual (× 10, displaced by +0.94) is shown. |
| In the text | |
 |
Fig. 8 Fitted 3D line profiles for the six μ-values (red) compared to the WCL observed spectra (black). From the fit we derive A(O) = 8.74 and A(Ni) = 6.10. Below each profile the residual (× 5, displaced by +0.94) is shown. |
| In the text | |
 |
Fig. 9 Fitted 3D line profiles for five μ-values (red) compared to the VTT observed spectra (black). From this fit we derive A(O) = 8.72 and A(Ni) = 6.12. Below each profile the residual (× 10, displaced by + 0.94) is shown. |
| In the text | |
 |
Fig. 10 Fitted 3D line profiles at the eight μ-values (red) compared to the THEMIS observed spectra (black). From the fit we derive A(O) = 8.76 and A(Ni) = 6.02. Below each profile the residual (× 5, displaced by +0.94) is shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


