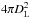| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526105 | |
| Published online | 29 June 2015 | |
The origin of the far-infrared continuum of z ~ 6 quasars
A radiative transfer model for SDSS J1148+5251
1 INAF–Osservatorio Astronomico di Roma, via di Frascati 33, 00090 Roma, Italy
e-mail: raffaella.schneider@oa-roma.inaf.it
2 INAF–Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
3 Kapteyn Astronomical Institute, Landleven 12, 9747 AD Groningen, The Netherlands
Received: 16 March 2015
Accepted: 5 May 2015
Context. Understanding the history of formation of z > 6 quasars is a major challenge to theoretical models. Physical insights on the connection between the central black hole and its host galaxy can be gained by means of the quasar infrared properties.
Aims. Here we investigate the origin of the far-infrared continuum of SDSS J1148+5251, using it as a prototype for the more general class of high-luminosity high-redshift quasars.
Methods. We run the radiative transfer code TRADING to follow the transfer of radiation from the central source and from stellar sources through the dusty environment of the host galaxy. We adopt simple models for the central source, including all the radiation that can travel beyond the dusty torus. The radiation from stellar sources is modelled using the code PÉGASE. The model is based on the output of the semi-analytical merger tree code, GAMETE/QSOdust, which lets us predict the evolution of the host galaxy and of its nuclear black hole, following the star formation history and chemical evolution – including dust – in all the progenitor galaxies of SDSS J1148+5251.
Results. We find that the radiation emitted by the central source, which dominates the observed spectral energy distribution from UV/optical to near- and mid-infrared wavelengths, can also provide an important source of heating for the dust distributed in the host galaxy, powering at least 30% and up to 70% of the observed far-infrared emission at rest-frame wavelengths [20−1000] μm. The remaining fraction is contributed by stellar sources and can only be achieved if the host galaxy is able to sustain a star formation rate of ≈900 M⊙/yr at z = 6.4. This points to a co-evolution scenario where, during their hierarchical assembly, the first super-massive black holes and their host galaxies grow at the same pace until the black hole reaches a mass of ~2 × 108 M⊙; it then starts growing faster than its host, reaching the bright quasar phase when the black hole and stellar mass fall within the scatter of the scaling relation observed in local galaxies. This same evolutionary scenario has been recently shown to explain the properties of a larger sample of 5 < z < 6.4 quasars, with the implication that current dynamical mass measurements may have missed an important fraction of the host galaxy stellar mass.
Conclusions. We conclude that the far-infrared luminosity of high-z quasars is a sensitive tracer of the rapidly changing physical conditions in the host galaxy. Quasars appear far-infrared bright when the host galaxy can still sustain strong starbursts, with star formation rates 100 M⊙/yr <SFR < 1000 M⊙/yr, and progressively dim as large quasar-driven outflows deplete the host galaxy of its gas content, damping star formation and leaving the central source as the only source of dust heating.
Key words: quasars: supermassive black holes / galaxies: ISM / galaxies: stellar content / galaxies: evolution / dust, extinction / radiative transfer
© ESO, 2015
1. Introduction
The first comprehensive far-infrared (FIR) investigations into optically selected low-z active galactic nuclei (AGNs) were made using Infrared Astronomical Satellite (IRAS) and Infrared Space Observatory (ISO) data, supplemented with SCUBA and IRAM data at longer wavelengths (see e.g. Haas et al. 2000, 2003). A variety of different spectral energy distribution (SED) shapes were observed, suggesting that the mid-infrared (MIR) and FIR emission originate from dust components whose heating mechanisms may be different (Haas et al. 2000). In particular, while in all sources the MIR emission could be powered by the central AGN, the relative role of starbursts and AGN in powering the FIR emission was hard to establish, although Haas et al. (2003) proposed that quasars with the largest FIR luminosities (LFIR ≥ 1013−1014 L⊙) favour a strongly dominating AGN contribution.
Progress in the field was enabled by observations with the Spitzer Space Telescope, using MIR polycyclic aromatic hydrocarbon (PAH) emission features as tracers of star formation in quasar host galaxies (Schweitzer et al. 2006; Netzer et al. 2007; Lutz et al. 2008). Indeed, the main MIR PAH emission features at 6.2, 7.7, 8.6, and 11.3 μm have been extensively used as extragalactic star formation indicators because of their presence in star-forming environments with a wide range of physical conditions and their absence in the proximity of AGNs. While the calibration between the PAH luminosity and the star formation rate depends on the physical properties of the interstellar medium, PAH emission is sufficiently strong to be less easily outshone by the AGN emission, unlike Hα or the 24 μm continuum. Netzer et al. (2007) applied this technique to local quasars; comparing the average SEDs of groups of quasars that differ in their FIR luminosity, they were able to derive a SED for the pure AGN, after subtraction of the host star formation. Lutz et al. (2008) have extended the study to a sample of mm-detected quasars at 1.8 ≤ z ≤ 2.8, showing that these sources follow the same correlation between the PAH luminosity and the rest-frame FIR emission inferred for local quasars. For mm-bright quasars, this provides strong evidence for intense star formation rates in their hosts, sometimes exceeding 1000 M⊙/yr. However, the mm-faint end of this quasar population may contain pure AGNs, with no strong host star formation, and the observed weak rest frame FIR emission appears consistent with pure AGN-heated dust (Lutz et al. 2008).
The launch of the Herschel Space Observatory has enabled us to directly observe the galaxy rest-frame FIR emission. Using large samples of type 1 and type 2 AGN in the Herschel Multi-tiered Extragalactic Survey (HerMES) fields observed with SPIRE at 250, 350, and 500 μm, Hatziminaoglou et al. (2010) showed that quasars out to z ~ 4 have the same FIR colours as star-forming galaxies and that a starburst was always needed to reproduce the FIR emission (see also Elbaz et al. 2010). By matching a sample of 24 μm – selected quasars in the Spitzer Wide-area InfraRed Extragalactic Survey to HerMES, Dai et al. (2012) collected 32 quasars with 0.5 ≤ z< 3.6 with SPIRE data. These FIR-detected quasars show cold dust emission with LFIR in the range 1011.3−1011.5 L⊙, dust masses of 108−109 M⊙, and temperatures from 18 K to 80 K, similar to ULIRGs and (sub)mm detected quasars. They find that the FIR properties cannot be predicted from shorter wavelengths, because at rest-frame frequencies 0.3−20 μm FIR-detected quasars have similar SEDs of FIR-undetected quasars at comparable redshifts. Assuming that star formation powers the FIR emission, about 40% of the sample requires SFR> 1000 M⊙/yr; however, for some quasars the derived star formation rates (SFRs) are >5000 M⊙/yr, which is unlikely and may imply a non-negligible contribution from the AGN. Multi-components SED fits of a much larger sample of 250 μm selected galaxies from HerMES with Spitzer/InfraRed Spectrograph spectra show, however, that the presence of a starburst is necessary to account for the total FIR emission, and that the presence of an AGN has no noticable effect on the FIR properties of the host galaxy (Feltre et al. 2013).
Similar studies have recently been applied to 69 quasars at z> 5 by Leipski et al. (2014), who have presented SEDs covering the rest-frame wavelengths from 0.1 μm to ~80 μm, including Spitzer and Herschel observations. At rest-frame wavelengths ≥50 μm, the SEDs of the ten sources that have been detected in at least four of the five Herschel bands (with PACS at 100 and 160 μm, and with SPIRE at 250, 350, and 500 μm) are completely dominated by a luminous cold dust component with 47 K ≤ TFIR ≤ 60 K and LFIR ~ 1013 L⊙. The origin of the FIR component is further analysed by stacking the SEDs of Herschel-detected (10 objects detected at 160, 250, and 350 μm), partly Herschel-detected (14 objects detected at 100 and/or 160 μm) and Herschel-non-detected sources (33 objects). At rest-frame wavelengths λ ≤ 15 μm, the average SEDs of the Herschel-detected and partly Herschel-detected subsamples appear very similar, but partly detected sources show a substantial drop in their average SED at longer wavelengths. The fact that some optical and MIR luminous quasars show FIR emission and others do not is interpreted as an indication that star formation is the dominant driver for the additional FIR component observed in Herschel-detected quasars.
All the above studies adopt physically motivated multi-component SED fitting techniques that miss, however, the energy balance between the various components. A notable exception is the work by Dwek et al. (2007), who have made a simple decomposition of the observed SED of SDSS J1148 into different components. They used a simple screen model with a Galactic extinction law to calculate the spectrum of the escaping stellar radiation, choosing the magnitude of the extinction so that the total reradiated FIR emission was equal to the total energy absorbed by the dust. In this way they estimated that the inferred FIR luminosity of 4.6 × 1013 L⊙ could be powered by star formation, but that it requires a continuous star formation rate of 2500 M⊙/yr for 400 Myr with a top-heavy initial mass function (IMF).
Here we attempt to make a step forward by using a detailed radiative transfer (RT) model to follow the contribution of the host star formation and the central AGN to dust heating. Our aim is to assess to what extent the observed SEDs of z ~ 6 quasars in the rest-frame FIR can place constraints on current scenarios for the formation and evolution of the first super-massive black holes (SMBHs) and their host galaxies.
Information on the star formation rate, the nature of the stellar populations, and the mass of gas and dust of the host galaxy are obtained using the data-constrained semi-analytical merger tree model, GAMETE/QSOdust (Valiante et al. 2011, 2012, 2014). This model allows the star formation history and the mass growth of the nuclear black hole (BH) to be followed in all the progenitor galaxies that contribute to the hierarchical build-up of z ~ 6 quasars. Valiante et al. (2011) show that when the model is applied to SDSS J1148+5251 (hereafter SDSS J1148), one of the best-studied quasars at z = 6.4, the observed properties of the quasar (BH, gas and dust masses, SFR, stellar mass) are reproduced provided that distinct evolutionary paths are followed. This same conclusion has been recently confirmed to hold for a larger sample of quasars at 5 < z < 6.4 (Valiante et al. 2014) that share a common formation scenario: in all the progenitor galaxies of the final host dark matter halo, stars form according to a standard, Salpeter-like IMF via quiescent star formation and efficient merger-driven bursts. At the same time, the central BH grows via gas accretion and mergers with other BHs. When the BH mass reaches a threshold value of 2 × 108−109 M⊙, a strong energy-driven wind starts to clear up the interstellar medium of dust and gas through a large outflow, damping the star formation rate and un-obscuring the line of sight toward the quasar. Although the estimated outflow rates can be as large as a few 1000 M⊙/yr, in agreement with current observational constraints (Maiolino et al. 2012; Cicone et al. 2015), the final star formation rates are comparably large, ~600–2000 M⊙/yr, due to intense merger-driven bursts. As a result, all the quasars host galaxies are characterized by final stellar masses in the range (4–6) ×1011 M⊙, a factor of 3–30 larger than the upper limits allowed by the observed dynamical and molecular gas masses.
Although large uncertainties still affect dynamical mass measurements in these high-z galaxies, one possible solution to this so-called stellar mass crisis would be to assume that the cold gas is converted into stars at a smaller efficiency than adopted by the scenario described above. In this way, the BH grows faster than the host galaxy and when it reaches a final mass of ~109 M⊙, the stellar mass is still 1010−1011 M⊙ (Valiante et al. 2014). However, in order to reproduce the observed chemical properties of the host galaxy, in particular the dust mass, the stars must form according to a top-heavy IMF, with a characteristic mass of 5 M⊙, that allows maximization of the stellar metal and dust yield (Valiante et al. 2011). More importantly, the final SFRs are <100 M⊙/yr, significantly smaller than in the standard model.
It is clear that the two scenarios discussed above result in very different predictions on the relative role of the AGN and star formation as the powering sources of the FIR emission. Hence, any attempt to gain a deeper understanding of the origin of the FIR emission in high-z quasars may provide important insights into the co-evolution of the first SMBHs and their host galaxies.
The paper is organized as follows: in Sect. 2 we give a short description of the main features of the semi-analytical model GAMETE/QSOdust and we present the standard scenario for SDSS J1148 at z = 6.4, using this quasar as a prototype for the general class of high-z quasars; in Sect. 3 we describe the numerical set-up and the radiative transfer model; in Sects. 4–6, we present the adopted model for the spectrum emitted by the central AGN and by the stars, and the assumed spatial distribution of the dust in the host galaxy; in Sect. 7 we illustrate and critically discuss our main results, and in Sect. 8 we draw our conclusions.
For consistency with previous works (Valiante et al. 2011, 2014), we adopt a Lambda Cold Dark Matter (ΛCDM) cosmology with Ωm = 0.24, ΩΛ = 0.76, Ωb = 0.04, and H0 = 73 km s-1 Mpc-1. The age of the Universe at a redshift z = 6.4 is 900 Myr and the model and observations are scaled using the luminosity distance at this redshift, 64.5 Gpc.
2. Modelling the evolution of high-redshift quasars
In this section we give a brief presentation of the best-fit models for the formation and evolution of the quasar J1148 obtained by means of the semi-analytical code GAMETE/QSOdust (Valiante et al. 2011, 2012, 2014). We focus here only on those features that are particularly relevant for the present study and address the interested reader to Valiante et al. (2011) for a comprehensive description of the code.
Dark matter and BH evolution High-z quasars are likely to reside in dark matter (DM) halos with masses ~1012−1013 M⊙ (Fan et al. 2004; Volonteri & Rees 2006; Valiante et al. 2012; Fanidakis et al. 2013). Here we assume that J1148 is hosted by a 1013 M⊙ DM halo at z = 6.4 whose evolution, backward in time, is simulated using a binary Monte Carlo merger tree algorithm (Valiante et al. 2011). To save computational time, we only resolve dark matter halos with a virial temperature Tvir > 104 K that can cool through hydrogen Lyman-α emission; in the first star-forming halos we plant BH seeds with a mass of 104h-1 M⊙ and stop populating newly virialized halos once their mass falls below the mass of a 4σ halo at the same redshift. We then follow the subsequent evolution of these BH seeds as they grow through mergers and gas accretion. In our formulation, gas accretion onto the central BH is Eddington-limited and regulated by the Bondi-Hoyle accretion rate, with a constant efficiency parameter, α ~ 200, set to reproduce the observed BH mass of J1148 of ~3 × 109 M⊙ (Barth et al. 2003; Willott et al. 2003).
BH feedback and outflow rates The gas content within each progenitor galaxy is regulated by infall and outflow rates as well as by the rate of star formation and of returned gas at the end of stellar evolution. Gas outflows can be powered by supernova explosions and BH feedback; the relative importance of these two physical processes depends on the evolutionary phase of each progenitor galaxy. At redshifts 6.4 < z < 8, the dominant effect is AGN feedback, since BH-driven outflows have already significantly depleted the gas content of the host galaxy, leading to a down-turn of the star formation rate (see Figs. 3 and 4 in Valiante et al. 2012). It is important to stress that, despite the very schematic implementation of AGN feedback (described as energy-driven winds), the predicted outflow rate at z = 6.4 is in good agreement with the massive gas outflow rate of ~3500 M⊙/yr detected by Maiolino et al. (2012) and Cicone et al. (2015) through IRAM PdBI observations of the [CII] 158 μm line in the host galaxy of J1148 (Valiante et al. 2012).
Star formation law The evolution of the stellar content of the host galaxy has been investigated adopting different prescriptions for the SFR. The star formation rate can occur through a quiescent mode by converting a given fraction of cold gas into stars on the galaxy dynamical time or by means of merger-induced starbursts with enhanced efficiencies in the so-called bursting mode (see Valiante et al. 2011). The relative importance of these two modes of star formation depends on the mass ratio of the progenitor merging galaxies, μ. In equal-mass mergers, when μ → 1 the starbursts are maximally efficient and the star formation rate can be up to 80 times greater than in the quiescent mode (see Table 2 in Valiante et al. 2011 for the numerical values of the parameters). All the models that we have explored predict a tight co-evolution of the nuclear BH and stellar content of the host galaxies in the first 600-700 Myr. However, at z < 8, when the mass of the nuclear BH has grown to ~108 M⊙ and AGN feedback starts to affect the gas content of the host galaxy, the rate of star formation is very sensitive to the adopted star formation efficiency. As a result, the final star formation rates and stellar masses can increase from SFR ~ 70 M⊙/yr and M⋆ ~ 3 × 1010 M⊙ (for the models that adopt the lowest star formation efficiency) to SFR ~ 900 M⊙/yr and M⋆ ~ 4 × 1011 M⊙ (when the highest star formation efficiency is considered). In the first case, the final stellar mass is within the limits allowed by measurements of the dynamical mass within the central 2.5 kpc of the host galaxy obtained by means of the resolved CO emission (Walter et al. 2004). Conversely, in the second case the final stellar mass is closer to the value that would be implied by the nuclear SMBH mass of J1148 if the local BH-stellar mass relation were assumed to hold at these very high redshifts (see Fig. 3 in Valiante et al. 2011). We return to this point in Sect. 8.
 |
Fig. 1 Rest-frame SED of J1148 compared to the SED of the central source adopted in our models (solid lines for the face-on view, dashed lines for the edge-on view). Model A SED is from model t0.1_p1_q6_oa50_1pC11_8 of Stalevski et al. (2012); models B and C are from models N2.5_a-2.00_theta60_Rout150_tauV80 and N2.5_a-0.50_theta60_Rout150_tauV80, respectively, of Hönig & Kishimoto (2010). For clarity, we show the SED of the stars only in the right panel (shaded region). This is computed with PÉGASE using the output of the GAMETE/QSOdust standard IMF model (see Sect. 5). |
Chemical enrichment The enrichment of the ISM is followed taking into account the release of heavy elements and dust grains by asymptotic giant branch (AGB) stars and supernovae (SN), assuming mass and metal-dependent yields (Valiante et al. 2009). We do not adopt the instantaneous recycling approximation, hence we take into account stellar evolution on the characteristic stellar lifetimes. The mass of dust is computed following the cycling of dust in the interstellar medium, taking into account grain destruction in the hot diffuse phase of the interstellar medium by interstellar shocks and grain-growth in dense molecular clouds (de Bennassuti et al. 2014; Valiante et al. 2014). Indeed, Valiante et al. (2011) show that for the adopted dust yields, stellar sources can produce up to ≈3 × 107 M⊙ of dust as a result of the balance between dust production and dust destruction by the combined effect of astration and interstellar SN shocks. This is approximately a factor ten smaller than the dust mass inferred by fitting the observed rest-frame FIR-emission1.
Efficient grain growth in dense interstellar clouds must be invoked to reproduce the observed dust mass (Michałowski et al. 2010; Valiante et al. 2011). This mechanism requires, however, that enough gas-phase metals are available to fuel grain growth (de Bennassuti et al. 2014; Valiante et al. 2014).
Selected models The detailed analysis done by Valiante et al. (2011) convincingly showed that if the stars are formed with a Larson IMF,
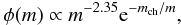 the chemical properties inferred from observations of J1148 host galaxy require that either (i) the stars are formed with a characteristic stellar mass of mch = 0.35 M⊙ (standard IMF) and with high-efficiency or that (ii) the stars are formed with a characteristic stellar mass of mch = 5 M⊙ (top-heavy IMF) but with low-efficiency (see Table 2 and Fig. 7 in Valiante et al. 2011).
the chemical properties inferred from observations of J1148 host galaxy require that either (i) the stars are formed with a characteristic stellar mass of mch = 0.35 M⊙ (standard IMF) and with high-efficiency or that (ii) the stars are formed with a characteristic stellar mass of mch = 5 M⊙ (top-heavy IMF) but with low-efficiency (see Table 2 and Fig. 7 in Valiante et al. 2011).
As we have discussed above, the two models predict different star formation rates and UV luminosities, hence FIR emission. Using the population synthesis code PÉGASE (see section 5 and references therein) and assuming that the stars form in a 50 Myr burst with solar metallicity, we estimate that (i) a SFR of 1 M⊙/yr leads to a FIR luminosity in the wavelength range [8−1000] μm of 1.08 × 1010 L⊙ for mch = 0.35 M⊙ and (ii) of 2.89 × 1010 L⊙ for mch = 5 M⊙. Although the star formation history that characterize the evolution of the simulated quasar is more complex and cannot be approximated by a single 50 Myr burst, these conversion factors can provide a rough estimate of the FIR luminosities contributed by the stars. Given the predicted SFRs at z = 6.4, we find LFIR,⋆ ~ 1013 L⊙ and LFIR,⋆ ~ 2 × 1012 L⊙ for the standard and top-heavy IMF models, respectively. In the same wavelength range, a χ2 fit to the observed points of J1148 (see Fig. 1) leads to a luminosity of LFIR,obs = 3.3 × 1013 L⊙ (see footnote 1), close to that obtained by star formation in the host for a standard IMF model. Hence, in what follows we will adopt the standard IMF model as input to the radiative transfer calculations, and we discuss in Sect. 7 the implications of our results for the other model.
3. Modelling the spectral energy distribution
The observed SED of J1148 is shown in Fig. 1. Data points come from the Sloan Digital Sky Survey (Fan et al. 2003), Subaru Telescope (Iwamuro et al. 2004), and Spitzer (Jiang et al. 2006; Hines et al. 2006) as reported in Table 1 of Leipski et al. (2010), to which flux densities at 70, 100, 160, 250, 350, and 500 μm from Herschel were added, fully sampling the peak of the rest-frame FIR emission (Leipski et al. 2013).
 |
Fig. 2 Schematic representation of the adopted geometry, assuming two different inclination angles between the polar axis of the torus and of the host galaxy (i = 0, left panel, and i = 20°, right panel). |
In the optical, the SED shows the typical power-law (close to Fν ∝ ν0.5) of unreddened type 1 quasar, emitted by the accretion disk around the central BH. Thus the quasar can be considered as seen perpendicularly to the dusty torus surrounding the accretion disk (i.e. it is seen face-on). This dust-free view can be used to estimate the bolometric luminosity of the accretion disk, by using a template SED that extends outside of the optical wavelengths: we found a bolometric luminosity of 1.6 × 1014 L⊙ for the intrinsic SED used in the radiative transfer models of Stalevski et al. (2012).
The radiation travelling along directions close to edge-on passes through the torus and heats the dust to high temperatures, producing thermal radiation in the NIR. The mean quasar SED derived by Richards et al. (2006) for type 1 quasars observed by SDSS and Spitzer does show a NIR bump, but this template is unable to predict the larger output observed in this wavelength range from high-luminosity, high-redshift quasars such as J1148 (see Fig. 7 in Leipski et al. 2013). Beyond 20 μm, the emission comes from relatively colder dust in the quasar’s host (outside of the dusty torus). As discussed in Sect. 1, the FIR emission is generally believed to be heated by star formation in the host; however, we cannot exclude that the radiation emitted by or escaping from the dusty torus of the quasar can provide an additional, non-negligible contribution. Indeed, this is what we intend to assess with a detailed radiative transfer calculation.
We model the SED using the 3D Monte Carlo Radiative Transfer code TRADING (Bianchi 2008). The code has been developed to study dust extinction and emission in dusty spiral galaxies (see e.g. Bianchi & Xilouris 2011; Holwerda et al. 2012), but it has a general structure and can be easily adapted to other astrophysical contexts. In particular, the code uses an adaptive grid to sample the dust distribution at different scales in environments of different densities. Despite this ability, a full radiative transfer model from the sub-pc scale of the dusty torus up to the kpc scales of the host galaxy is still computationally too expensive. Thus, we are forced to make a few simplyifing assumptions:
-
(i)
For the central source, we adopt the SED obtained bydedicated, external, models for the transfer of the radiation fromthe accretion disk through the dusty torus. We present the threedifferent models that we have explored in Sect. 4.
-
(ii)
For the stellar sources in the host galaxy, we adopt the SED computed with the PÉGASE population synthesis model using as input the star formation histories, age, and metallicities of the stellar populations predicted by GAMETE/QSOdust. Similarly, GAMETE/QSOdust allows the mass of gas and dust in the host to be estimated. The stellar SED and the adopted spatial distributions of star, gas, and dust are presented in Sects. 5 and 6.
-
(iii)
Using TRADING, we follow the transfer of radiation from the central source (accretion disk and dusty torus) and from stellar sources through the dusty environment of the host galaxy. As is customary for RT models in a dusty galaxy, we consider the transfer of radiation only for λ > 912 Å assuming that ionizing radiation will be intercepted entirely by the neutral hydrogen in the host.
4. The central source
Several models for the radiation emitted by the dusty torus that surrounds the accretion disk are available in the literature. These often rely on different methods and might result in contradictory and/or non-unique solutions when fitted to the data (see Hönig 2012 for an overview). In this work, our intent is not to determine the internal properties of the torus but rather to explore central source models that provide a reasonable agreement with the observed SED at NIR/MIR wavelengths and study their impact on the FIR emission. To this aim we have selected three alternative models extracted from two different libraries available in the literature: a model from Stalevski et al. (2012) that was computed using a Monte Carlo radiative transfer code similar to TRADING (model A), and two models from the library of Hönig & Kishimoto (2010). The first of these (model B) provides an equally good agreement to the observed NIR emission as model A, but with different physical and geometrical torus properties. The second (model C) is similar to the SED that has been recently used to fit the MIR emission of a sample of high-z FIR-luminous quasars, including J1148, by Leipski et al. (2013). In addition, these two classes of models predict very different dusty torus optical depths and this lets us explore how this difference affects the contribution of the central source to the heating of dust in the host galaxy.
Model A The first SED is taken from the simulations of Stalevski et al. (2012), which were computed using the radiative transfer code SKIRT (Baes et al. 2011)2. The torus is simulated as a two-phase medium with half-opening angle of θh = 40°, so that dust is present for 40° ≤ θ ≤ 140°, with θ the polar angle from the torus vertical axis. When the torus is seen at inclinations θ<θh, the light from the accretion disk is seen unattenuated (see the schematic representation in Fig. 2). Since these models include the radiation directly emitted from the accretion disk, it is straightforward to normalize the dust-free face-on SEDs to the observed optical data of J1148. The database was then searched for template spectra that best matched the infrared data. It was found that models that match the observed data at λ > 10 μm result in dust emission that is too high at shorter wavelengths. Conversely, a few dusty torus models with relatively low optical depth can roughly reproduce the observations at 1 μm ≤ λ ≤ 10 μm. The model selected is the one that passes through the data at 3.2 μm without exceeding the observed flux at wavelengths λ > 10 μm and is shown in the left panel of Fig. 1. The solid line is the face-on SED of the accretion disk (i.e. the emission in directions within the polar cone, θ<θh) and the dashed line is the edge-on SED (i.e. the emission in directions outside the polar cone, θ>θh). We note that since the SED along directions that intersect the dusty torus depends on the viewing angle, for the sake of simplicity we adopt the solid-angle average as the edge-on SED of the central source. Comparing the solid and dashed lines in the figure, we note that the SED in the NIR is almost isotropical and that a fraction of the optical luminosity from the accretion disk is able to escape the dusty torus even along the edge-on direction. These features are due to the moderate opacity of the torus which limits dust self-absorption. Indeed, for the selected model, the optical depth at 9.7 μm in the equatorial direction (θ = 90°) and assuming a homogeneous dust distribution in the torus is τ9.7 = 0.1. This is also evident from the prominent silicate emission feature at 10 μm. At longer wavelengths, the SED of the central source rapidly drops.
Model B The second model for the central source was taken from the CAT3D models of Hönig & Kishimoto (2010), where Monte Carlo simulations of individual clouds are combined with a statistical approach to compute the torus emission3. These models do not include the direct light from the accretion disk, but only the radiation that has been absorbed/emitted or scattered by the dusty torus. Following Leipski et al. (2013), we added a template to model the accretion disk emission in the UV/optical band. We adopt the Stalevski et al. (2012) spectrum for the face-on direction, with luminosity scaled to the UV/optical data. We note, however, that scaling a CAT3D model to the observations of a quasar of known distance already implies an estimate of its bolometric luminosity. In addition, the accretion disk template of Hönig & Kishimoto (2010) is different from that of Stalevski et al. (2012); we comment on these issues in Sect. 7. We selected the dusty torus model that, together with the accretion disk template, more closely fits the data at 1 μm ≤ λ ≤ 10 μm. The result is shown in the central panel of Fig. 1. The dusty torus model is characterized by a half-opening angle of θh = 60°. However, since in these models the opening angle is not defined as a sharp boundary between the dust-free polar cone and the torus, but rather as a transition parameter, both the face-on and the edge-on SEDs are derived by averaging over the solid angle within and outside the polar cone. The figure shows that in this second model for the central source (hereafter, model B) the emission is less isotropic than in the previous case. Compared to model A, the radiation along edge-on directions at λ < 1 μm is negligible. Although this might be due to the missing information about the attenuated accretion disk light in CAT3D spectra, it is compatible with the larger opacity of the selected dusty torus, which is characterized by a mean optical depth of τ9.7 ~ 17 in the equatorial direction. Accordingly, we assumed complete obscuration – i.e. no edge-on emission – in our optical/UV template.
 |
Fig. 3 Maps of 7 kpc × 7 kpc regions representing the radiation emitted at 40 μm in the face-on direction for model A. In the left panel the only source of radiation is the central one. The right panel shows the full model where both the central source and the stars embedded in the clouds contribute to dust heating. |
Model C The central source templates presented so far have been selected to reproduce the NIR bump at 1 μm ≤ λ ≤ 10 μm with torus emission. However, the exact nature of this emission poses a challenge to most torus models4 and it is often taken into account by including an additional hot dust component at the inner edge of the torus (Hönig 2012). In view of this, Leipski et al. (2013, 2014) model the NIR bumps with hot dust black-body spectra and select torus models that fit the observed data at longer wavelengths in the MIR. Following this strategy, we select a third model for the central source from Hönig & Kishimoto (2010) templates, which we show in the right panel of Fig. 1 (hereafter, model C). We do not include, however, the component for the NIR bump; we discuss the effects of this omission in Sect. 7. The face-on and edge-on SEDs have been obtained as for the second model discussed above and for the same torus half-opening angle of θh = 60°. We note that the two dusty torus models selected from the Hönig & Kishimoto (2010) templates (models B and C) have the same mean optical depth and cloud properties. The only difference is the adopted power law index of the radial dust cloud distribution, which is flatter in model C. This is consistent with having a stronger emission at longer wavelengths as the clouds are expected to be colder, on average.
The derived non-ionizing luminosities of the three models for the central source that are used for the radiative transfer calculations are Lcentral = 7.0, 6.2, and 5.4 × 1013 L⊙ for model A, B, and C, respectively.
5. The stellar spectral energy distribution
As explained in Sect. 2, the properties of the host galaxy are inferred from the output of the semi-analytical code GAMETE/QSOdust (Valiante et al. 2011, 2012, 2014). This code allows the simulation of a large number of independent hierarchical histories for the DM halo that host J1148 at z = 6.4. Hence, the values for the star formation rate and total stellar mass for the selected model that we have quoted in Sect. 2 and that we give here for convenience represent the average among 50 independent merger trees, with the errors showing the associated 1σ dispersion.
At z = 6.4 the selected standard IMF model predicts a star formation rate of SFR = (895 ± 800) M⊙/yr and a total stellar mass of M⋆ = (3.8 ± 1.2) × 1011 M⊙ (Valiante et al. 2011, 2014). The large dispersion around the mean SFR is due to sensible variations of the merger rates and the effects of AGN feedback predicted by the different hierarchical histories.
To compute the SED of the stars in the host galaxy of J1148 we use the public code PÉGASE v2.05 (Fioc & Rocca-Volmerange 1997) that allows the reconstruction of the SED of stars that form with arbitrary star formation history, IMF, and metallicity. The result is shown in the right panel of Fig. 1, where we plot the SED produced by the average star formation history (solid black line) and the shaded region illustrates the range of SED associated with star formation histories that lie within 1σ of the average.
Even though all the star formation histories predict a peak in the star formation rate at 7 < z < 9 (see Fig. 4 in Valiante et al. 2014), the z = 6.4 SED is largely dominated by stars formed in the last <100 Myr of the evolution of the host because the luminosity of the stars formed at the peak of star formation has already faded away. As expected for an optically bright quasar, Fig. 1 shows that the radiation emitted by the stars at optical and NIR wavelengths is always largely subdominant with respect to that produced by the accretion disk and dusty torus.
In the radiative transfer model, stellar radiation is assumed to be emitted isotropically. The non-ionizing luminosity is L⋆ = (1.5 ± 1.3) × 1013 L⊙, for the mean and ± 1σ SFRs, respectively. The adopted spatial distribution for the gas, dust, and stars in the host galaxy is presented in the next section.
 |
Fig. 4 SED of J1148 obtained by the radiative transfer calculation for the different inputs for the central source (models A, B, and C) presented in Fig. 1. The solid lines show the results including the central source and the stellar component, with the shaded region illustrating the variations of the stellar SED induced by the 1σ scatter of the SFR (see the left panel of Fig. 1). The dashed lines show the results obtained using only the central source. |
6. The dust distribution in the host galaxy
The radiative transfer is computed after distributing dust within a cubic volume centred on the central source. Two dust-free regions are included in the cube: (i) a central sphere of radius 600 pc, since the adopted SED for the central source already takes into account radiative transfer through the dusty torus at these scales6; and (ii) a cone that is the extension of the opening cone of the dusty torus, 2θh, so that the radiation exiting the dusty torus unabsorbed is not further absorbed by the host and maintains the observed spectral slope in the optical. We note that we also explore the possibility that the polar axis of the dusty torus is inclined by an angle i > 0 with respect to the polar axis of the host galaxy (see Fig. 2). However, since J1148 is classified as a type 1 quasar, i ≪ θh so that most of the lines of sight to the accretion disk are dust-free.
At z = 6.4 the selected model predicts a molecular gas mass of MH2 = (3.1 ± 2.8) × 1010 M⊙ and a total dust mass of Mdust = (3.2 ± 2.9) × 108 M⊙. Since the dominant contribution to dust enrichment comes from grain growth in dense molecular clouds, almost all of the final dust mass is associated with molecular gas (Valiante et al. 2014). Hence, we distribute the dust mass solely in spherical, homogeneous clouds simulating dust associated with molecular gas. As in Bianchi (2008), we adopt a cloud radius of about 100 pc, which is covered by about five cells of the adaptive grid in the standard resolution settings. With this clumpy distribution, we minimize the extinction of radiation from the central source and maximize that from the stellar component since, as we see below, we assume the stars to be embedded in the clouds.
Interferometric observations of J1148 reveal CO emission within 2.5 kpc from the quasar’s centre, which corresponds to about 2.3 × 1010 M⊙ of molecular hydrogen (Walter et al. 2004). From these observations, we derive a molecular gas surface density of about 1200 M⊙/pc2, which we assume to represent the surface density of the individual clouds. Such high surface density clouds are not unrealistic for quasar host galaxies at high redshifts. In fact, CO excitation analyses show that the observed transitions can be modelled with a single gas component with density nH2 ~ 103.6−104.3 cm-3 and temperature T ~ 40−60 K, suggesting that the emission comes from a very compact and central region of the host (see Carilli & Walter 2013 and references therein).
Clouds are distributed homogeneously within a radius of 3.0 kpc, so that the average surface density within 2.5 kpc from the quasar’s is similar to the observed value. To be consistent with the radiative transfer models for the central source, we use the Milky Way (MW) dust composition of Draine (2003). For simplicity, we consider the mean extinction and emission properties of the models, i.e. we adopt a single grain of mean properties rather than a full distribution of grain sizes and materials. We also assume thermal equilibrium emission. We will discuss the effects of these assumptions later.
Given the average molecular gas mass predicted by the model, we end up by having ~850 clouds, each one having a molecular gas mass of 3.6 × 107 M⊙. The average gas-to-dust ratios of the clouds is G/D ~ 100, comparable to the value for the moderately dense interstellar medium of the Milky Way (Jenkins 2009). As a result, the optical depth of the clouds along the diameter in the V-band is very large, τV ~ 99, for Draine (2003) dust composition. Thus, some edge-on lines of sight could be severely attenuated in the optical/MIR.
Finally, stellar radiation is assumed to be emitted at the centre of each cloud. Given the high optical depth of clouds, the stellar radiation is entirely absorbed within each cloud. Thus, the stellar contribution to dust emission in all the models should be considered as an upper limit.
7. Results and discussion
A qualitative picture of the results of the RT calculation is presented in Fig. 3, which shows maps of the radiation emitted at 40 μm in the face-on direction for model A. Owing to the large optical depth of the dusty clouds in the host galaxy, the central source is able to illuminate and heat only the surface of the closest clouds (left panel); the most distant clouds appear to contribute to the FIR only when the dust is heated by the stellar radiation (right panel).
 |
Fig. 5 Left panel: reconstructed full face-on SED of the adopted CAT3D models, adding to the dusty torus SED (red solid line for model B and green solid line for model C) a dust-free view of the Hönig & Kishimoto (2010) intrinsic SED of the accretion disk. The dotted line is the SED of the accretion disk scaled to the observed optical/UV datapoints. Central panel: SEDs for models A (blue) and B (red) using the central source only and adopting two different inclination angles of the polar axis of the torus with respect to that of the host: i = 0 (dashed lines) and 20° (dotted lines). Right panel: SEDs for model A but with dust mass reduced by a factor of 10 (dashed line), and by using the original dust mass but increasing the resolution and adopting a full grain size distribution plus stochastic heating (dotted line). The solid line is the reference model from the left panel of Fig. 4. |
More quantitatively, the full SED of J1148 in the face-on direction is shown in Fig. 4, where each panel represents the results of the RT calculation adopting one of the central source models described in Sect. 4. The solid lines show the predicted SED when both the radiation from the central source and from the stars contribute to heating the dust in the host galaxy, powering the FIR emission. As indicated by the shaded regions, which account for the 1σ variation on the SFR among different hierarchical histories of the host galaxy (see the right panel of Fig. 1), the radiation from stellar sources affects the SED only at λ > 10 μm; at lower wavelengths, the emission is entirely dominated by the central source. Even though it is not possible to separate the two contributions from the FIR SED (the dust emission depending in a non-linear way on the radiation absorbed by the dust from each type of source), we can have a clue to their relative importance by comparing the above results with the RT calculation when the dust in the host galaxy is heated only by the central source (dashed line in each panel).
For model A, the observed FIR emission is marginally consistent with dust heated only by the central source. Integrating7 the dashed line shown in the left panel of Fig. 4, we find that the luminosity in the wavelength range [20−1000] μm is LFIR,central = 2.3 × 1013 L⊙, where instead the luminosity of the full model including stellar sources (shaded region) is in the range LFIR,TOT = (2.5−4.7) × 1013 L⊙. Comparing these figures with the FIR luminosity inferred from the observational data, LFIR,obs = 3.3 × 1013 L⊙ (see Sect. 2), we conclude that LFIR,AGN = 0.7 LFIR,obs and that the radiation emitted by the central source in model A dominates the heating of the dust which powers the FIR emission.
For model B (central panel of Fig. 4) the contribution of the central source to the FIR SED is smaller, but still significant: we find LFIR,central = 1.1 × 1013 L⊙ (dashed line) and LFIR,TOT = (1.3−3.7) × 1013 L⊙ (shaded region). Thus, we conclude that the central source contribute to about 30% of the FIR emission, LFIR,AGN = 0.33 LFIR,obs.
Results for model C (right panel) appear to be similar, with LFIR,central = 1.5 × 1013 L⊙ (dashed line) and LFIR,TOT = (1.7−4.1) × 1013 L⊙ (shaded region). Hence, we find that LFIR,AGN = 0.45 LFIR,obs. However, in this case, the contribution of the central source to the observed FIR emission is not only the result of dust heating in the host galaxy, but also directly through its intrinsic, unattenuated, SED. For our particular choice among the Hönig & Kishimoto (2010) models and normalization, the direct light accounts for more than half of the central source contribution to the FIR output. However, because of the rapid decrease of the SED with wavelength, alternative choices for model C (and different normalizations) might result in widely different contributions of the central source to the FIR SED. For example, in the model chosen by Leipski et al. (2013), the FIR output of direct light from the central source is about 20% of the total, similar to our choice here; in the updated model of Leipski et al. (2014), the contribution is only 5%.
The results of the RT calculation show that the contribution of dust heating from the central source can range from moderate to significant, LFIR,AGN = (0.33−0.70) LFIR,obs depending on the adopted models and templates for the central source. This affects the determination of the SFR from the FIR luminosity and our ability to constrain the connection between the BH and its host galaxy from the IR properties of quasars. In what follows, we discuss some critical aspects of the radiative transfer model and how these might affect the results presented above.
Limitations and uncertainties of the central source models Among the many different models proposed in the literature, here we have explored three different templates for the radiation emitted by the dusty torus that surrounds the nuclear BH accretion disk. From a methodological point of view, the Stalevski et al. (2012) library, from which we have selected model A, is the most suitable to be used as a central source of radiation in our RT model. In fact, it includes the radiation emitted by the accretion disk, so that the predicted dust-free face-on SED can be easily normalized to match the observed UV/optical data points (see Sect. 4). Conversely, using the CAT3D library, from which we have selected models B and C, is more challenging. This can be seen in the left panel of Fig. 5, where we have reconstructed the full face-on view of the original CAT3D models, adding to the selected dusty torus SED (models B and C) the original template used by Hönig & Kishimoto (2010) for the accretion disk. It is evident that the original accretion disk template does not show the same spectral slope as the data. Hönig & Kishimoto (2010) claim that in their models the actual shape of the spectrum is much less important than the total luminosity. Indeed, scaling their accretion disk template to the optical/UV data in the range [0.1−1] μm (dotted line), we derive a bolometric luminosity of 1.0 × 1014 L⊙, which falls within the estimates reported in Sect. 3. However, this is not the intrinsic bolometric luminosity corresponding to the dusty torus template models B and C shown in Fig. 4. In fact, scaling the CAT3D models to observations of a quasar of known luminosity distance allows us to determine the physical scale of the sublimation radius (i.e. the inner edge of the dusty torus) and thus the bolometric luminosity intrinsic to each template8. For the dusty torus model B, the bolometric luminosity estimated in this way is smaller, 8.2 × 1013 L⊙. The reconstructed face-on SED corresponding to this luminosity (solid line in the left panel of Fig. 5) is marginally consistent with the optical/UV data. We note that now the dusty torus model B does not reproduce the NIR data as it used to in the central panels of Figs. 1 and 4 because model B was originally selected in combination with the UV/optical template of Stalevski et al. (2012), which – following the flatter slope of the observed optical/UV data – extends to 5 μm and contributes to the NIR.
More critical is the problem for the dusty torus model C (dashed line in the left panel of Fig. 5). The bolometric luminosity derived, after scaling to match the MIR data, is 5 × 1013 L⊙, definitely lower than the value predicted by observations. Conversely, if the model was scaled to the optical/UV observations (i.e. if the dashed line in Fig. 5 was made to coincide with the dotted line), the MIR prediction would be higher than the data9.
The results shown in the left panel of Fig. 5 suggest that choosing independent templates for the optical/UV emission of the accretion disk and for the dusty torus, as we have done for the central source models B and C, does not ensure that the heating source in the RT model is compatible with the observations. We note that this same approach has been recently followed by Leipski et al. (2013, 2014) and was applied by Barnett et al. (2015) to the SED of the most distant quasar at z = 7.1.
We also note that a similar problem affects the black-body template used by Leipski et al. (2013) to fit the observed NIR peak of high-z quasar spectra (see also footnote 4 in Sect. 4), which is thought to arise from the radiation emitted by hot dust at the boundary between the accretion disk and the torus: in a consistent RT model, this emission should be included as an additional heating source, and would thus alter the dusty torus SED in ways that are difficult to predict without running a dedicated RT computation.
Based on the above considerations, we can reject model C and conclude that only dusty torus SEDs peaking in the NIR (and thus reproducing the observed bump) are acceptable, in that they are based on intrinsic accretion disk luminosities that can be reconciled with the observations.
Dependence on the inclination angle i The results discussed above do not change significantly if we allow for a moderate disalignment between the polar axis of the dusty torus and the polar axis of the host galaxy. This is illustrated by the central panel of Fig. 5, where we show the predicted SEDs for models A and B using the central source only and adopting two different inclination angles. When i = 20° (see also the geometric scheme in Fig. 2), the FIR luminosity contributed by the central source in model A increases only slightly, to LFIR,central = 2.4 × 1013 L⊙. This is a consequence of the relatively low optical depth of the dusty torus in this model. Indeed, the left panel of Fig. 1 shows that there is a significant fraction of the radiation emitted by the accretion disk that is able to escape the dusty torus in the edge-on direction both at MIR and optical wavelengths; these two components almost equally contribute to dust heating and their effect is not sensitive to the inclination angle of the dusty-torus. In fact, when i> 0 the dusty clouds in the host galaxy will be exposed to a smaller fraction of the radiation escaping the torus in the edge-on direction, 1−sin2(i/ 2)/(2−sin2θh), but – at the same time – will intercept a fraction sin2(i/ 2)/(2−sin2θh) of the radiation emitted by the accretion disk in the face-on direction, which is unattenuated by the dusty torus. These two components partly compensate, leading to a negligible effect of the inclination angle on the FIR emission. Given the larger optical depth of the dusty torus, in model B the net effect of the disalignment i is larger (see the central panel of Fig. 5). The unattenuated UV/optical radiation from the accretion disk now intercepts the dusty clouds distributed within a solid angle sin2(i/ 2)/(2−sin2θh). As a result, the contributions of the central source to the FIR luminosity increase to LFIR,central = 1.5 × 1013 L⊙, contributing to 0.45 of LFIR,obs.
Dependence on the dust mass and composition In the right panel of Fig. 5, we show the predicted SED assuming the same heating sources as for model A, but with a factor of 10 smaller dust mass, 3.1 × 107 M⊙ (dashed line). In this case, both the amplitude and frequency of the thermal dust emission associated with the host galaxy shift to lower values as the clouds are more transparent and the dust temperature is larger. Hence, although dust mass estimates derived by fitting the observed FIR emission are plagued by a number of uncertainties, our RT model shows that published values have not been severely over-estimated. Similarly, the mass-averaged dust temperatures computed by the RT calculations are ⟨ Td ⟩ = 56 and 52 K for models A and B, respectively; these values are very close to the dust temperature estimated from the observed data points assuming optically thin dust emission (see Sect. 2).
Throughout the analysis, we have adopted the average Draine (2003) dust model for which k(λ) = k0 (250 μm /λ)β with k0 = 4 cm2/ gr and β = 2.08 (Bianchi 2013). Even at FIR wavelengths, some of the features predicted by the RT calculation may be affected by the adopted dust properties. Indeed, none of the three models shown in Fig. 4 can fully account for the observations at λ ≥ 100 μm. The excess emission could be accounted for by dust emissivity with a flatter spectral index, as predicted by SN dust models (Bianchi & Schneider 2007) and as suggested by the fits of the FIR modified black body in Leipski et al. (2013). However, the same excess could be the result of dust further out of the source or of passively heated clouds (without sources in them), which we have not considered. We note also that, by analysing the optical near-IR spectra of 33 quasars with redshifts 3.9 ≤ z ≤ 6.4, Gallerani et al. (2010) find that their mean extinction curve deviates from that of the Small Magellanic Cloud, which has been shown to reproduce the dust reddening of most quasars at z< 2.2. This may be an indication of different dust properties at high redshift.
Finally, we have checked that increasing the resolution by a factor of 4 (100 pc covered by about 20 cells of the adaptive grid) does not affect our results. Similar conclusions hold for models where we have taken into account the full distribution of grain sizes and materials (rather than a single grain with mean properties), and the effects of stochastic heating (rather than thermal equilibrium emission). All the test runs show differences with respect to our reference models that are smaller than the photometric errors at λ> 30 μm (see the dotted line in the right panel of Fig. 5).
8. Conclusions
One of the main motivations of the present study was to explore to what extent the FIR properties of high-z quasars can help constrain current scenarios for the coevolution of the BH and its host galaxy in the first Gyr of cosmic evolution.
In FIR luminous high-z quasars, such as the z = 6.4 quasar SDSS J1148 that we have selected as a representative case, the observed FIR emission is generally attributed to an ongoing strong starburst in the host galaxy, with inferred star formation rates that can range from ~1000 M⊙/yr up to ~3700 M⊙/yr (see Table 1 in Valiante et al. 2014). However, these figures can only provide a loose upper limit on the star formation rate. In fact, by means of a detailed RT calculation, we show that
-
the radiation emitted by the central source, which dominates theobserved SED from the UV/optical to near- and mid-IRwavelengths, provides an important source of heating for the dustdistributed in the host galaxy, powering at least30% and up to 70% of the observedFIR emission;
-
the FIR SED of SDSS J1148 can only be reproduced by models where the star formation rate in the host galaxy at z = 6.4 is as large as SFR ~ 900 M⊙/yr, as predicted by the selected standard IMF model (Valiante et al. 2011). In fact, a top-heavy IMF model with reduced star formation efficiencies predicts a SFR at z = 6.4 of only 66 ± 59 M⊙/yr, too small to supply the required heating, in addition to the heating of the central source, and to power the observed FIR emission.
Hence, we conclude that our analysis supports a scenario for the co-evolution of the first SMBHs and their host galaxies where, during their hierarchical assembly, the evolutionary tracks followed by the systems in the MBH−Mstar plane approach the local relation from the bottom (see Fig. 5 in Valiante et al. 2014): during the first period of evolution, at redshifts 8−10 <z< 30, in all the progenitor galaxies, stars form according to a standard Salpeter-like IMF via quiescent star formation and merger-driven bursts. At the same time, the nuclear BHs grow through mergers with other BHs and gas accretion; hence BHs and their host galaxies grow hand-in-hand, in a symbotic way (Volonteri 2012). At 5−6.4 ≤ z ≤ 8−10; however, the BH starts growing faster than the stellar bulge and the predicted MBH−Mstar evolution progressively steepens, falling within the observed scatter of the local relation. This scenario implies that current dynamical mass measurements may have missed an important fraction of the host galaxy stellar mass.
It is important to note that the transition between the starburst-dominated stage and the quasar-dominated stage of the evolution is regulated by the effects of BH feedback: for the quasars that we have investigated, we find that when the nuclear BH masses have grown to ~2 × 108−109 M⊙, strong AGN-driven outflow rates of (4−6) × 103 M⊙/yr damp the star formation rate and un-obscure the line of sight toward the quasar. At these large outflow rates, the host galaxies would be completely depleted of their gas content in less than 20 Myr, shutting down both the star formation rate and the BH activity; as a result, we predict the active and bright quasar phase to last ~107 yr (Valiante et al. 2014). During this relatively short phase, the FIR luminosity is expected to respond to the rapidly changing physical conditions in the host galaxy. Our analysis suggest that FIR-luminous quasars are likely tracing a phase of the evolution where the gas content in the host galaxy can still sustain strong starbursts, with 100 M⊙/ yr <SFR< 1000 M⊙/yr. When the conditions in the ISM are such that the star formation rate falls below <100 M⊙/yr, the FIR emission can only be powered by dust heating from the central source, and we expect a stronger correlation between the UV/optical, NIR/MIR and the residual FIR luminosities.
It is interesting to note that this results resonate with the recent analysis by Leipski et al. (2013, 2014), where the authors find that the average SED of quasars z> 5 with Herschel detections, including SDSS J1148, are preferentially found at the high luminosity end of their sample (for LUV/opt and in particular for LNIR). Moreover, as discussed in Sect. 1, they also find that some optical and MIR luminous quasars do show FIR emission and others do not. This is an indication that star formation is the dominant driver for the additional FIR component observed in their Herschel-detected sources. Following a similar approach, Barnett et al. (2015) has recently analysed the SED of quasar ULAS J1120+0641 at z = 7.1. This object has been detected by Herschel PACS at 100 and 160 μm, but not by Herschel SPIRE at 250, 350, and 500 μm, hence it would be a member of the partly Herschel-detected objects, according to the classification by Leipski et al. (2014). On average, these sources are optically luminous AGN with strong NIR and MIR emission, but do not show a bright FIR emission, consistent with the idea that the central source is likely contributing significantly, if not predominantly, to the FIR emission. Using local scaling relations, Barnett et al. (2015) estimate a star formation rate in the range 60−270 M⊙/yr from the [CII] line luminosity and the 158 μm continuum luminosity and conclude that, at the time of observation, the BH was growing in mass 100 times faster than the stellar bulge. This is consistent with the idea that the source was likely caught in action when the quasar-driven wind had already significantly depleted the host galaxy of its gas content, suppressing star formation.
Our results are in good agreement with another study done on the same object by Li et al. (2008). By applying a 3D radiative transfer code to a hydrodynamical simulation, these authors show that the observed SED and inferred dust properties of SDSS J1148 request vigorous star formation in the merging progenitors and a substantial contribution to dust heating and the FIR luminosity from the AGN. They also suggest that the quasar host should have already built up a large stellar population by z ~ 6, in agreement with our best-fit evolutionary scenario described above. Our study, which is based on a semi-analytical code, complements these previous findings allowing an exploration of a larger parameter space (in terms of stellar IMF and star formation history) and a more sophisticated treatment of the chemical enrichment of the ISM by dust and metals.
Assuming that the dust is optically thin and that it radiates as a “grey-body”, the mass of dust can be computed as
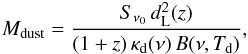 where κd(ν) = κ0(ν/ν0)β is the opacity coefficient per unit dust mass, B(ν,Td) is the Planck function for a dust temperature Td, and dL is the luminosity distance to the source. Using a χ2 fit to the observed points at λ ≥ 160 μm (see Sect. 3) and the average dust properties of Draine (2003), which we adopt for the present study, we estimate a dust mass Mdust = 3.6 × 108 M⊙, a dust temperature Td = 56 K, and a total FIR luminosity LFIR,obs = 3.3 × 1013 L⊙.
where κd(ν) = κ0(ν/ν0)β is the opacity coefficient per unit dust mass, B(ν,Td) is the Planck function for a dust temperature Td, and dL is the luminosity distance to the source. Using a χ2 fit to the observed points at λ ≥ 160 μm (see Sect. 3) and the average dust properties of Draine (2003), which we adopt for the present study, we estimate a dust mass Mdust = 3.6 × 108 M⊙, a dust temperature Td = 56 K, and a total FIR luminosity LFIR,obs = 3.3 × 1013 L⊙.
Stalevski et al. (2012) models are available at: https://sites.google.com/site/skirtorus
CAT3D models are available at: http://www.sungrazer.org/CAT3D.html.
For a bolometric luminosity of 1011 L⊙, Stalevski et al. (2012) adopt an external radius of the dusty torus of 15 pc. Scaling to the bolometric luminosity of J1148, Lbol = 1.6 × 1014 L⊙, and assuming flux conservation, the radius is 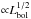 and we infer a radius of 600 pc.
and we infer a radius of 600 pc.
See Sect. 4.1 of Hönig & Kishimoto (2010) and the documentation on the dedicated webpage.
Browsing the Stalevski et al. (2012) dataset we find similar results: if we assign the models the same bolometric luminosity as derived from the optical/UV data, then models peaking in the NIR might reproduce the observed NIR data, while models peaking in the MIR have a larger luminosity.
Acknowledgments
We thank the anonymous Referee for the insightful comments, Sebastian Hönig, Christian Leipski and Dominik Riechers for the kind clarifications about their work. R.S. and R.V. acknowledge the support and hospitality of the INAF/Osservatorio Astrofisico di Arcetri during part of the work. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement No. 306476. S. Salvadori acknowledges the support from the Netherlands Organisation for Scientific Research (NWO), VENI grant 639.041.233
References
- Baes, M., Verstappen, J., De Looze, I., et al. 2011, ApJS, 196, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Barnett, R., Warren, S. J., Banerji, M., et al. 2015, A&A, 575, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barth, A. J., Martini, P., Nelson, C. H., & Ho, L. C. 2003, ApJ, 594, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S. 2008, A&A, 490, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S. 2013, A&A, 552, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., & Xilouris, E. M. 2011, A&A, 531, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carilli, C., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cicone, C., Maiolino, R., Gallerani, S., et al. 2015, A&A, 574, 14 [Google Scholar]
- Deo, R. P., Richards, G. T., Nikutta, R., et al. 2011, ApJ, 729, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Y. S., Bergeron, J., Elvis, M., et al. 2012, ApJ, 753, 33 [NASA ADS] [CrossRef] [Google Scholar]
- de Bennassuti, M., Schneider, R., Valiante, R., & Salvadori, S. 2014, MNRAS, 445, 3039 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Galliano, F., & Jones, A. P. 2007, ApJ, 662, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Hwang, H. S., Magnelli, B., et al. 2010, A&A, 518, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fan, X., Strauss, M. A., Schneider, D. P., et al. 2003, ApJ, 125, 1649 [Google Scholar]
- Fan, X., Hennawi, J. F., Richards, G. T., et al. 2004, AJ, 128, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Fanidakis, N., Macció, A. V., Baugh, C. M., Lacey, C. G., & Frenk, C. S. 2013, MNRAS, 436, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Feltre, A., Hatziminaoglou, E., Fritz, J., & Franceschini, A. 2012, MNRAS, 426, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Feltre, A., Hatziminaoglou, E., Hernán-Caballero, A., et al. 2013, MNRAS, 434, 2426 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volemrange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Gallerani, S., Maiolino, R., Juarez, Y., et al. 2010, A&A, 523, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haas, M., Müller, S. A. H., Chini, R., et al. 2000, A&A, 354, 453 [NASA ADS] [Google Scholar]
- Haas, M., Klaas, U., Müller, S. A. H., et al. 2003, A&A, 402, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatziminaoglou, E., Omont, A., Stevens, J. A., et al. 2010, A&A, 518, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. 2012, Proc. Torus Workshop, held 5 December, at University of Texas, San Antonio, 157 [Google Scholar]
- Hönig, S., & Kishimoto, M. 2010, A&A, 523, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holwerda, B. W., Bianchi, S., Böker, T., et al. 2012, A&A, 541, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hines, D. C., Krause, O., Rieke, G. H., et al. 2006, ApJ, 641, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamuro, F., Kimura, M., Eto, S., et al. 2004, ApJ, 614, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, L., Fan, X., Hines, D. C., et al. 2006, AJ, 132, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Leipski, C., Meisenheimer, K., Klaas, U., et al. 2010, A&A, 518, L34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leipski, C., Meisenheimer, K., Walter, F., et al. 2013, ApJ, 772, 103L [NASA ADS] [CrossRef] [Google Scholar]
- Leipski, C., Meisenheimer, K., Walter, F., et al. 2014, ApJ, 785, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Hopkins, P. F., Hernquist, L., et al. 2008, ApJ, 678, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Sturm, E., Tacconi, L. J., et al. 2008, ApJ, 684, 853 [Google Scholar]
- Maiolino, R., Gallerani, S., Neri, R., et al. 2012, MNRAS, 425, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H., Lutz, D., Schweitzer, M., et al. 2007, ApJ, 666, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Schweitzer, M., Lutz, D., Sturm, E., et al. 2006, ApJ, 649, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Stalevski, M., Fritz, J., Baes, M., et al. 2012, MNRAS, 420, 2756 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, R., Schneider, R., Bianchi, S., & Andersen, A. C. 2009, MNRAS, 397, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, R., Schneider, R., Salvadori, S., & Bianchi, S. 2011, MNRAS, 416, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, R., Schneider, R., Maiolino, R., Salvadori, S., & Bianchi, S. 2012, MNRAS, 427, L60 [NASA ADS] [Google Scholar]
- Valiante, R., Schneider, R., Salvadori, S., & Gallerani, S. 2014, MNRAS, 444, 2442 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M. 2012, Science, 337, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., & Rees, M. J. 2006, ApJ, 650, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Carilli, C., Bertoldi, F., et al. 2004, ApJ, 615, L17 [CrossRef] [Google Scholar]
- Willott, C. J., McLure, R. J., & Jarvis, M. J. 2003, ApJ, 587, L15 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Rest-frame SED of J1148 compared to the SED of the central source adopted in our models (solid lines for the face-on view, dashed lines for the edge-on view). Model A SED is from model t0.1_p1_q6_oa50_1pC11_8 of Stalevski et al. (2012); models B and C are from models N2.5_a-2.00_theta60_Rout150_tauV80 and N2.5_a-0.50_theta60_Rout150_tauV80, respectively, of Hönig & Kishimoto (2010). For clarity, we show the SED of the stars only in the right panel (shaded region). This is computed with PÉGASE using the output of the GAMETE/QSOdust standard IMF model (see Sect. 5). |
| In the text | |
 |
Fig. 2 Schematic representation of the adopted geometry, assuming two different inclination angles between the polar axis of the torus and of the host galaxy (i = 0, left panel, and i = 20°, right panel). |
| In the text | |
 |
Fig. 3 Maps of 7 kpc × 7 kpc regions representing the radiation emitted at 40 μm in the face-on direction for model A. In the left panel the only source of radiation is the central one. The right panel shows the full model where both the central source and the stars embedded in the clouds contribute to dust heating. |
| In the text | |
 |
Fig. 4 SED of J1148 obtained by the radiative transfer calculation for the different inputs for the central source (models A, B, and C) presented in Fig. 1. The solid lines show the results including the central source and the stellar component, with the shaded region illustrating the variations of the stellar SED induced by the 1σ scatter of the SFR (see the left panel of Fig. 1). The dashed lines show the results obtained using only the central source. |
| In the text | |
 |
Fig. 5 Left panel: reconstructed full face-on SED of the adopted CAT3D models, adding to the dusty torus SED (red solid line for model B and green solid line for model C) a dust-free view of the Hönig & Kishimoto (2010) intrinsic SED of the accretion disk. The dotted line is the SED of the accretion disk scaled to the observed optical/UV datapoints. Central panel: SEDs for models A (blue) and B (red) using the central source only and adopting two different inclination angles of the polar axis of the torus with respect to that of the host: i = 0 (dashed lines) and 20° (dotted lines). Right panel: SEDs for model A but with dust mass reduced by a factor of 10 (dashed line), and by using the original dust mass but increasing the resolution and adopting a full grain size distribution plus stochastic heating (dotted line). The solid line is the reference model from the left panel of Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.