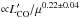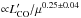| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 4 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526062 | |
| Published online | 19 June 2015 | |
Research Note
CO luminosity – line-width correlation of submillimeter galaxies and a possible cosmological application
1 National Tsing Hua University, No. 101, Section 2, Kuang-Fu Road, Hsinchu, Taiwan 30013, ROC
e-mail: tomo@phys.nthu.edu.tw
2 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Denmark
e-mail: sune@dark-cosmology.dk
Received: 10 March 2015
Accepted: 21 April 2015
Context. A possible correlation between CO luminosity (LCO) and its line width (FWHM) has been suggested and denied in the literature. Such claims were often based on a small or heterogeneous sample of galaxies, hence were inconclusive.
Aims. We aim to prove or disprove the LCO-FWHM correlation.
Methods. We compiled a large sample of sub-mm galaxies at z> 2 from the literature and investigated the L′CO-FWHM relation.
Results. After carefully evaluating the selection effects and uncertainties, such as inclination and magnification via gravitational lensing, we show that a weak but significant correlation exists between LCO and FWHM. We also discuss a feasibility to measure the cosmological distance using the correlation.
Key words: methods: observational / distance scale / submillimeter: galaxies
© ESO, 2015
1. Introduction
A possible correlation between CO luminosity ( ) and its line width at high z has been suggested in the literature. Bothwell et al. (2013) observed 32 sub-mm galaxies (SMG) at 1.2 <z< 4.1 in 12CO and suggested a correlation between CO luminosity and line width (FWHM) in high-redshift starbursts, probably relating to baryon-dominated gas dynamics within the regions probed (see their Fig. 5). Using 15 SMG at z = 2−4 with known lens magnifications, Harris et al. (2012) show that the SMGs fall close to a power law with small scatter in the CO luminosity and line width (FWHM) plane (see their Fig. 7).
) and its line width at high z has been suggested in the literature. Bothwell et al. (2013) observed 32 sub-mm galaxies (SMG) at 1.2 <z< 4.1 in 12CO and suggested a correlation between CO luminosity and line width (FWHM) in high-redshift starbursts, probably relating to baryon-dominated gas dynamics within the regions probed (see their Fig. 5). Using 15 SMG at z = 2−4 with known lens magnifications, Harris et al. (2012) show that the SMGs fall close to a power law with small scatter in the CO luminosity and line width (FWHM) plane (see their Fig. 7).
Bright SMGs are often gravitationally-lensed. Such relation between  and FWHM can be used to estimate magnification factor (μ). Indeed, Harris et al. (2012) used the relation to estimate luminosity of SMGs with unknown μ. Fu et al. (2013) also used this relation to estimate a small μ (~1.8) of merging galaxies at z = 2.3 to conclude that their star formation rate was 2000 M⊙ yr-1 (see their Fig. S7). Similarly, Riechers et al. (2013) used the relation to estimate μ (1.5 ± 0.7) for a starburst galaxy at z = 6.34, finding its SFR of 2900 M⊙ yr-1.
and FWHM can be used to estimate magnification factor (μ). Indeed, Harris et al. (2012) used the relation to estimate luminosity of SMGs with unknown μ. Fu et al. (2013) also used this relation to estimate a small μ (~1.8) of merging galaxies at z = 2.3 to conclude that their star formation rate was 2000 M⊙ yr-1 (see their Fig. S7). Similarly, Riechers et al. (2013) used the relation to estimate μ (1.5 ± 0.7) for a starburst galaxy at z = 6.34, finding its SFR of 2900 M⊙ yr-1.
Conversely, Carilli & Walter (2013) examined the relation using a much larger sample and found no significant correlation between  and FWHM (see their Fig. 5). However, their sample was heterogeneous because it included various types of galaxies, such as SMM, QSO, radio galaxies, and 24 μm sources. Therefore, the existence of
and FWHM (see their Fig. 5). However, their sample was heterogeneous because it included various types of galaxies, such as SMM, QSO, radio galaxies, and 24 μm sources. Therefore, the existence of  -FWHM correlation is still controversial.
-FWHM correlation is still controversial.
In this paper, we compile a larger sample of z> 2 galaxies with CO detection from the literature, to re-examine the  -FWHM correlation at high z. We carefully examine various sources of possible uncertainties, such as different types of galaxies, luminosity conversion from different CO transitions, and errors in estimating μ. Unless otherwise stated, we adopt a cosmology with (h,Ωm,ΩΛ) = (0.7,0.3,0.7).
-FWHM correlation at high z. We carefully examine various sources of possible uncertainties, such as different types of galaxies, luminosity conversion from different CO transitions, and errors in estimating μ. Unless otherwise stated, we adopt a cosmology with (h,Ωm,ΩΛ) = (0.7,0.3,0.7).
Correlation between 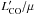 and FWHM for various samples.
and FWHM for various samples.
2. Sample
Our sample is based on the updated version of the supplemental table of Carilli & Walter (2013), which contains all published CO line measurements at z> 2 as of December 31, 2012. The updated version also includes some sub-mm sources published in 2013. We created a large sample of high-z sub-mm galaxies by adding 32 sources observed by Bothwell et al. (2013). In total, our sample contains 195 galaxies that were detected at least in one CO transition, with a measured FWHM.
3. Analysis
We compute  using the standard definition
using the standard definition 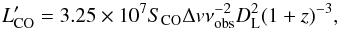 (1)where SCOΔv is the velocity integrated line flux,
(1)where SCOΔv is the velocity integrated line flux, 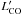 is the line luminosity in K Km s-1 pc2, νobs is the observed central frequency of the line, and DL the luminosity distance in Mpc.
is the line luminosity in K Km s-1 pc2, νobs is the observed central frequency of the line, and DL the luminosity distance in Mpc.
If the molecular gas emission comes from thermalized, optically thick regions,  is constant for all J levels. However, in reality, the ratio of
is constant for all J levels. However, in reality, the ratio of 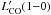 to higher order
to higher order 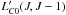 depends on temperature and density. We use average ratio of
depends on temperature and density. We use average ratio of  /
/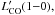 provided in Table 4 of Bothwell et al. (2013), to calculate
provided in Table 4 of Bothwell et al. (2013), to calculate 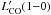 from higher order CO observations. Higher redshift galaxies are often observed only at mid-to-high-J CO transitions. We discuss uncertainties associated with this conversion in Sect. 4 in detail.
from higher order CO observations. Higher redshift galaxies are often observed only at mid-to-high-J CO transitions. We discuss uncertainties associated with this conversion in Sect. 4 in detail.
 |
Fig. 1 Correlation between |
It is always a concern with high-z objects that they might be gravitationally magnified. Submillimeter galaxies are not an exception, so 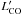 also needs to be corrected for a magnification factor (μ), when the galaxy is magnified by a gravitational lens. We collected μ values from the literature whenever available. However, since μ must be estimated from detailed modeling of the lens potential, a reliable measurement is not always available. We examine how the correlation depends on the availability and amplitude of μ in Sect. 4, but to be brief, they do not change our main results. Most likely, majority of galaxies with missing μ are not strongly magnified; otherwise, a lens galaxy would have been detected and μ would have been estimated. We present
also needs to be corrected for a magnification factor (μ), when the galaxy is magnified by a gravitational lens. We collected μ values from the literature whenever available. However, since μ must be estimated from detailed modeling of the lens potential, a reliable measurement is not always available. We examine how the correlation depends on the availability and amplitude of μ in Sect. 4, but to be brief, they do not change our main results. Most likely, majority of galaxies with missing μ are not strongly magnified; otherwise, a lens galaxy would have been detected and μ would have been estimated. We present 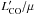 , whenever μ is available hereafter.
, whenever μ is available hereafter.
4. Results
4.1. L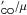 -FWHM correlation
-FWHM correlation
In Fig. 1, we plot CO line width FWHM against 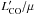 for all galaxies in our sample. The solid line is the best-fit power law, which is
for all galaxies in our sample. The solid line is the best-fit power law, which is 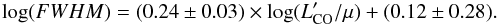 (2)The significance of the non-zero slope is 8.7σ. Spearman’s correlation coefficient is 0.55 with a p value of 1.7 × 10-16. Kendall’s correlation coefficient is similarly significant as shown in Table 1. Errors on each point are small thanks to the large number of galaxies in our sample. The median values increase with increasing
(2)The significance of the non-zero slope is 8.7σ. Spearman’s correlation coefficient is 0.55 with a p value of 1.7 × 10-16. Kendall’s correlation coefficient is similarly significant as shown in Table 1. Errors on each point are small thanks to the large number of galaxies in our sample. The median values increase with increasing 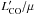 . These results show that there is a weak, but very significant correlation between
. These results show that there is a weak, but very significant correlation between 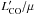 and FWHM.
and FWHM.
The presence of such a correlation is not surprising, because 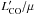 is sensitive to the total mass of molecular gas, while the FWHM is sensitive to dynamical mass. The relation is similar to the Tully-Fisher relation, which is also a power law, in the local Universe (Tully & Fisher 1977). A large scatter around the relation is also expected because of the inclination effect, along with the unknown μ for a subset of galaxies. We measured a dispersion around the best-fit line of 43%, which is consistent with what one expects from randomly oriented thin disks (45%), suggesting μ is close to 1 for most of the galaxies with unknown μ.
is sensitive to the total mass of molecular gas, while the FWHM is sensitive to dynamical mass. The relation is similar to the Tully-Fisher relation, which is also a power law, in the local Universe (Tully & Fisher 1977). A large scatter around the relation is also expected because of the inclination effect, along with the unknown μ for a subset of galaxies. We measured a dispersion around the best-fit line of 43%, which is consistent with what one expects from randomly oriented thin disks (45%), suggesting μ is close to 1 for most of the galaxies with unknown μ.
4.2. Uncertainty in converting different transitions
We tested that conversions from different CO transitions can mimic the correlation. In Fig. 1, we used different symbols for different CO transitions (4−3, 3−2, 2−1, and 1−0). In Table 1, we show the correlation coefficients for them. For CO(4−3), we do not see a positive correlation, while we see weak correlations for the other transitions. It is reassuring to see the correlations within single CO transitions, because they cannot be due to errors in the transition conversion. The reason we do not see a positive correlation for the CO(4−3) transition is not clear, but we point out that this is the smallest subsample and that since a single transition only spans a narrow redshift range (and thus, a narrow luminosity range), it is difficult to examine a correlation with a small sample in a single transition. It will be necessary to repeat this test using the wider frequency coverage of ALMA. On the other hand, we see significant correlations in all cases where we exclude a certain CO transition from the sample. These tests suggest that the  -FWHM correlation is not an artifact of CO order conversions.
-FWHM correlation is not an artifact of CO order conversions.
4.3. Dependence on magnification
In our sample, 85 galaxies have known μ, while the other 110 galaxies have not. We should first note that many sub-mm galaxies with unknown μ are probably not strongly magnified, or we would have seen the lens galaxy/cluster and measured μ. With this in mind, we still test that an unknown μ can mimic the correlation. In Fig. 1, we show two extreme samples of galaxies, those with μ> 3 in cyan, and those with unknown μ in green. There is no apparent deviation from the best-fit relation, except that more μs are unknown at higher redshift. In Table 1, we separate the sample into those with known μ and those with unknown μ, both of which show a significant correlation. Because brighter sub-mm galaxies are more likely to be lensed (owing to the steep luminosity function), the correction to unknown μ will steepen the correlation; i.e., the correlation will not disappear with the correction. It is reassuring to see a positive correlation using many sub-mm galaxies with unknown μ.
 |
Fig. 2
|
4.4. Dependence on galaxy types
We also separate the sample according to galaxy types in Table 1 and Fig. 1. Unfortunately, 24 μm sources and BzK galaxy samples are too small to examine the correlation. Both sub-mm galaxies (SMG) and QSOs have a significant correlation, with sub-mm galaxies having a greater significance.
4.5. Redshift dependence
Next we examine whether the  -FWHM correlation changes with redshift. Unfortunately, owing to the flux limits of the telescopes, the higher redshift sample includes more luminous sources, while lower redshift sources have smaller luminosity due to volume effects. With this limitation in mind, we separated the sample into high (z> 3) and low (z ≤ 3) redshift samples in Fig. 2. The best-fit lines to each sample agree with each other within the errors, which is consistent with no significant redshift evolution. The slopes are also consistent with each other and with that of the full sample in Fig. 1.
-FWHM correlation changes with redshift. Unfortunately, owing to the flux limits of the telescopes, the higher redshift sample includes more luminous sources, while lower redshift sources have smaller luminosity due to volume effects. With this limitation in mind, we separated the sample into high (z> 3) and low (z ≤ 3) redshift samples in Fig. 2. The best-fit lines to each sample agree with each other within the errors, which is consistent with no significant redshift evolution. The slopes are also consistent with each other and with that of the full sample in Fig. 1.
A concern for any low-level CO transition is that CMB temperature becomes higher at the highest redshift end. For example, the CMB temperature at z = 6 is ~19 K, which is higher than the temperature needed to excite the CO(2−1) line (16.6 K). Fortunately at high redshift, ALMA can only observe higher excitation lines, which are less affected. At z> 6, only CO(6−5) (Te = 116.16 K) and higher excitations can be observed with ALMA. The relation would still be valid at lower redshift (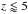 ). However, the effect of the higher CMB temperature needs to be examined carefully at higher redshifts.
). However, the effect of the higher CMB temperature needs to be examined carefully at higher redshifts.
Although we did not find any sign of redshift evolution, we also note that it is expected that the gas fraction in a galaxy increases as a function of redshift. Therefore, it is important to repeat this test when a larger sample becomes available in the future.
4.6. Estimating gravitational magnification using the L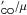 -FWHM relation
-FWHM relation
If we assume the 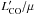 -FWHM relation, Eq. (2) can be used to estimate μ. We rewrite the equation as
-FWHM relation, Eq. (2) can be used to estimate μ. We rewrite the equation as  (3)The units for
(3)The units for  and FWHM are K Km s-1 pc2 and Km s-1, respectively. The equation can be useful when, for example, a sub-mm galaxy is detected behind a galaxy cluster and subject to gravitational magnification, but the detailed lens model is not available. Using Eq. (3), one can estimate μ, hence intrinsic luminosities of the sub-mm galaxy.
and FWHM are K Km s-1 pc2 and Km s-1, respectively. The equation can be useful when, for example, a sub-mm galaxy is detected behind a galaxy cluster and subject to gravitational magnification, but the detailed lens model is not available. Using Eq. (3), one can estimate μ, hence intrinsic luminosities of the sub-mm galaxy.
5. Discussion
5.1. A possible cosmological application
If the correlation is independent of redshift, the luminosity distance to CO-emitting galaxies can in principle be measured by estimating  from FWHM. Such a distance measure would be useful because already now, galaxies at z ~ 6 have been detected in CO with ALMA (Riechers et al. 2013; Wang et al. 2013). This method can be used up to such a high redshift, where it is difficult for other distance measures to reach. Here we assess whether such an approach could be feasible.
from FWHM. Such a distance measure would be useful because already now, galaxies at z ~ 6 have been detected in CO with ALMA (Riechers et al. 2013; Wang et al. 2013). This method can be used up to such a high redshift, where it is difficult for other distance measures to reach. Here we assess whether such an approach could be feasible.
In Figs. 1 and 2,  is computed with a cosmology; (ΩM,ΩΛ,h) = (0.3,0.7,0.7). Therefore, we need to calibrate the correlation by using CO-detected galaxies with a measured distance from another method. This, however, is difficult because CO detected galaxies are mostly at very high redshifts where other distance measures cannot easily reach.
is computed with a cosmology; (ΩM,ΩΛ,h) = (0.3,0.7,0.7). Therefore, we need to calibrate the correlation by using CO-detected galaxies with a measured distance from another method. This, however, is difficult because CO detected galaxies are mostly at very high redshifts where other distance measures cannot easily reach.
There are a number of ways to calibrate the distances, but here we use a method often used to calibrate gamma ray bursts. We use an empirical formula for the luminosity distance as a function of redshift based on 192 Type-Ia supernovae at 0.168 <z< 1.755 (DL/ 1027 cm = 6.96z1.79 + 14.79z1.02; Eq. (1) of Tsutsui et al. 2009). This empirical formula does not assume any cosmology, but just that the Type-Ia supernovae are standard candles. We use the formula to assign luminosity distances to our sub-mm galaxies at z ≤ 3, and thus to calibrate our  -FWHM correlation. Then, we apply the
-FWHM correlation. Then, we apply the  -FWHM correlation to measure luminosity distances to the z> 3 sub-mm galaxies.
-FWHM correlation to measure luminosity distances to the z> 3 sub-mm galaxies.
The results are shown in Fig. 3. Along with the data points, we plot three different cosmological models with (ΩM,ΩΛ) = (0.3,0.7), (0.3, 0.0), and (1.0, 0.0). At this stage, it is clear that the scatter is more than an order of magnitude larger than needed to obtain meaningful constraints on the cosmological parameters.
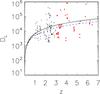 |
Fig. 3 Luminosity distance in Mpc against z. The red circles and black triangles are our CO samples separated at z = 3. The black dots are 192 supernovae used to calibrate our low-z sample. The black solid, green dotted, and blue-dashed lines are (ΩM,ΩΛ) = (0.3,0.7), (0.3, 0.0), and (1.0, 0.0), respectively. |
5.2. Sources of scatter in the relation, and prospects for reducing it
The scatter around the  -FWHM correlation (43%) is consistent with what is expected from randomly oriented disks, so if most sub-mm galaxies are rotating spiral-like galaxies, then the largest uncertainty is likely to come from the unknown inclinations. With the full operational array, ALMA’s spatial resolution will be as good as 0.037 at 110 GHz (for CO observation) in the extended configuration. At z ~ 6, this corresponds to 0.2 kpc, which is sufficient to resolve sub-mm galaxies, which typically extend over several kpc (Wang et al. 2013; De Breuck et al. 2014). With such observations, it will also be possible to exclude mergers and pressure-supported galaxies, which may be causing some of the extreme outliers from the relation, and to select samples of rotationally dominated galaxies. Furthermore, because the inclination is a random effect and its distribution is known (with ⟨ sini ⟩ ~ 0.79 and 1σ ~ 0.22), one can statistically correct for the effect. For the Tully-Fisher relation, for example, it has been shown that even when no information on the inclination is available, by using maximum likelihood estimation, the true relation can be recovered with only a 1.5 times larger
-FWHM correlation (43%) is consistent with what is expected from randomly oriented disks, so if most sub-mm galaxies are rotating spiral-like galaxies, then the largest uncertainty is likely to come from the unknown inclinations. With the full operational array, ALMA’s spatial resolution will be as good as 0.037 at 110 GHz (for CO observation) in the extended configuration. At z ~ 6, this corresponds to 0.2 kpc, which is sufficient to resolve sub-mm galaxies, which typically extend over several kpc (Wang et al. 2013; De Breuck et al. 2014). With such observations, it will also be possible to exclude mergers and pressure-supported galaxies, which may be causing some of the extreme outliers from the relation, and to select samples of rotationally dominated galaxies. Furthermore, because the inclination is a random effect and its distribution is known (with ⟨ sini ⟩ ~ 0.79 and 1σ ~ 0.22), one can statistically correct for the effect. For the Tully-Fisher relation, for example, it has been shown that even when no information on the inclination is available, by using maximum likelihood estimation, the true relation can be recovered with only a 1.5 times larger
statistical error than when inclinations are known with zero uncertainty (Obreschkow & Meyer 2013). As a reference, using the Tully-Fisher relation, Sakai et al. (2000) obtained H0 = 71 ± 4 (random) ±7 (systematic), i.e., 6% and 10% of the statistical and systematic errors, respectively.
Another possible source of scatter is calibration errors, because even state-of-the art sub-mm telescopes can only be calibrated to 10% at best for individual observations. Such errors are also expected to improve drastically as large, homogeneous statistical samples become available from ALMA, because the error on the median reduces with 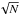 . In a sample of 10 000 sub-mm galaxies, for example, the statistical error on the median will reduce to 1%. This assumes the calibration error is random. If there is a systematic calibration error we are unaware of, this error will be added to the distance measurement.
. In a sample of 10 000 sub-mm galaxies, for example, the statistical error on the median will reduce to 1%. This assumes the calibration error is random. If there is a systematic calibration error we are unaware of, this error will be added to the distance measurement.
Another possible source of scatter in the relation that will be decreased in future ALMA surveys, is conversions between CO transitions. In such samples, it will be possible to study galaxies in the same transition as a function of redshift or as subsets of galaxies with well-constrained transition conversions. Once the observational and systematic errors have been lowered enough to measure the intrinsic scatter of the relation, it will be necessary to assess its possible cosmological applications. At the moment, it is impossible to tell.
Acknowledgments
We greatly appreciate the anonymous referee, whose insightful comments helped in improving the paper significantly. We acknowledge the support by the Ministry of Science and Technology of Taiwan through grant NSC 103-2112-M-007-002-MY3. The Dark Cosmology Centre is funded by the Danish National Research Foundation.
References
- Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Breuck, C., Williams, R. J., Swinbank, M., et al. 2014, A&A, 565, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fu, H., Cooray, A., Feruglio, C., et al. 2013, Nature, 498, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. I., Baker, A. J., Frayer, D. T., et al. 2012, ApJ, 752, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Obreschkow, D., & Meyer, M. 2013, ApJ, 777, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
- Sakai, S., Mould, J. R., Hughes, S. M. G., et al. 2000, ApJ, 529, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Tsutsui, R., Nakamura, T., Yonetoku, D., et al. 2009, J. Cosmol. Astropart. Phys., 8, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Wang, R., Wagg, J., Carilli, C. L., et al. 2013, ApJ, 773, 44 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Correlation between |
| In the text | |
 |
Fig. 2
|
| In the text | |
 |
Fig. 3 Luminosity distance in Mpc against z. The red circles and black triangles are our CO samples separated at z = 3. The black dots are 192 supernovae used to calibrate our low-z sample. The black solid, green dotted, and blue-dashed lines are (ΩM,ΩΛ) = (0.3,0.7), (0.3, 0.0), and (1.0, 0.0), respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.