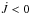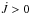| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526042 | |
| Published online | 23 June 2015 | |
Angular momentum redistribution by mixed modes in evolved low-mass stars⋆
I. Theoretical formalism
1 LESIA, Observatoire de Paris, PSL Research University, CNRS, Université Pierre et Marie Curie, Université Denis Diderot, 92195 Meudon, France
e-mail: kevin.belkacem@obspm.fr
2 Institut d’Astrophysique Spatiale, CNRS, Université Paris XI, 91405 Orsay Cedex, France
3 Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
4 Institut d’Astrophysique et de Géophysique, Université de Liège, Allée du 6 Août 17, 4000 Liège, Belgium
5 Laboratoire AIM Paris-Saclay, CEA/DSM-CNRS-Université Paris Diderot, IRFU /SAp, Centre de Saclay, 91191 Gif-sur-Yvette Cedex, France
Received: 6 March 2015
Accepted: 15 May 2015
Seismic observations by the space-borne mission Kepler have shown that the core of red giant stars slows down while evolving, requiring an efficient physical mechanism to extract angular momentum from the inner layers. Current stellar evolution codes fail to reproduce the observed rotation rates by several orders of magnitude and instead predict a drastic spin-up of red giant cores. New efficient mechanisms of angular momentum transport are thus required. In this framework, our aim is to investigate the possibility that mixed modes extract angular momentum from the inner radiative regions of evolved low-mass stars. To this end, we consider the transformed Eulerian mean (TEM) formalism, which allows us to consider the combined effect of both the wave momentum flux in the mean angular momentum equation and the wave heat flux in the mean entropy equation as well as their interplay with the meridional circulation. In radiative layers of evolved low-mass stars, the quasi-adiabatic approximation, the limit of slow rotation, and the asymptotic regime can be applied for mixed modes and enable us to establish a prescription for the wave fluxes in the mean equations. The formalism is finally applied to a 1.3 M⊙ benchmark model, representative of observed CoRoT and Kepler oscillating evolved stars. We show that the influence of the wave heat flux on the mean angular momentum is not negligible and that the overall effect of mixed modes is to extract angular momentum from the innermost region of the star. A quantitative and accurate estimate requires realistic values of mode amplitudes. This is provided in a companion paper.
Key words: waves / stars: oscillations / stars: evolution / stars: interiors / stars: rotation
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Rotation has important consequences on stellar evolution. In particular, it induces meridional circulations, as well as shear and baroclinic instabilities, which contribute to the redistribution of angular momentum and to the mixing of chemical elements (see for instance Talon 2008; Maeder 2009; Mathis 2013; Palacios 2013, for comprehensive reviews). Except for the Sun, the observational constraints remained sparse until the advent of the space-borne missions CoRoT (Baglin et al. 2006a,b; Michel et al. 2008) and Kepler (Borucki et al. 2010; Bedding et al. 2010; Chaplin et al. 2011). These were mainly constraints on the efficiency of the transport of chemicals (e.g., Charbonnel & Zahn 2007) provided by observations of surface abundances.
Based on seismic measurements, Beck et al. (2012) and Deheuvels et al. (2012, 2014) brought stringent observational constraints on the rotation profiles in the innermost layers of subgiant stars observed by Kepler. They concluded that the core of subgiant stars spins up, while their envelope decelerates. Their core rotates about three to ten times faster than the envelope, depending on the evolutionary state of the star. On the other hand, Mosser et al. (2012) analysed a sample of about 300 red-giant stars observed by Kepler and found that, surprisingly, the mean core rotation rate decreases significantly during the red-giant phase.
Current models of red-giant stars including angular momentum redistribution processes are unable to explain such low core rotation rates in subgiant and red giant stars. They are also unable to explain the deceleration of the core during the ascent of the red-giant branch. Indeed, Eggenberger et al. (2012), Marques et al. (2013), and Ceillier et al. (2013) computed stellar models with transport of angular momentum by both meridional circulation and shear instabilities, concluding that these processes cannot explain the observed rotation profiles. The authors emphasised the need for an additional physical mechanism to do so. Along the same lines, Cantiello et al. (2014) included the rotationally induced circulations and shear instabilities together with the effect of a magnetic field generated through the Tayler-Spruit dynamo (Spruit 1999, 2002) and reached the same conclusion. However, a recent work by Rüdiger et al. (2015) has shown that magneto-rotational instabilities of a toroidal magnetic field could explain the angular momentum redistribution in subgiants and early red giants (see also Maeder & Meynet 2014). Internal gravity waves1 can also transport angular momentum (e.g., Press 1981) and it has been demonstrated that they could explain the nearly flat rotation profile in the inner radiative zone of the Sun (Charbonnel & Talon 2005). While this process is still to be investigated for subgiant and red giant stars, Fuller et al. (2014) have found that internal gravity waves are likely to couple the convective region and the upper radiative region, but not the innermost layers. Hence, the question remains open, and we still need an efficient physical mechanism that explains the slow-down in the core of evolved low-mass stars.
Our aim in this paper is to investigate the influence of normal modes (more precisely, mixed modes) on the core rotation of subgiant and red giant stars. Angular momentum can be transferred through energy exchanges between the oscillations and the mean flow, which results in a modification of the rotation profile. Non-radial modes in subgiants and red giants have two interesting properties. Firstly, they have large amplitudes both in the outer layers and in the core of the star so that they are efficiently excited by turbulent convection while having a non-negligible effect on the innermost layers. Secondly, their amplitudes can be inferred, since they have been observed by CoRoT and Kepler (e.g., Bedding et al. 2011; Mosser et al. 2011; Chaplin & Miglio 2013). It is possible, therefore, to provide not only qualitative but also quantitative estimates of the angular momentum transport.
The problem of the redistribution of angular momentum by progressive waves and normal modes has been considered for a long time from a theoretical point of view. For modes, the pioneer work of Ando (1983) addressed the question of the interaction of wave and rotation through wave momentum stresses in the mean angular momentum equation. Following this work, efforts have been made to theoretically address the problem of the redistribution of angular momentum in classical pulsators by unstable modes (e.g., Ando 1986; Lee & Saio 1993; Lee 2007; Townsend & MacDonald 2008; Townsend 2014). Nevertheless, a quantitative estimate is difficult to make since it remains a challenge to predict the amplitude of modes in classical pulsators (see, however, Lee et al. 2014). In parallel, Press (1981), Zahn et al. (1997), Kumar et al. (1999), Mathis et al. (2008, 2013) have considered the interaction of the wave with the mean flow for progressive internal gravity waves (IGW) with a slightly different formalism. Nevertheless, all these works mainly focused on the effect of waves on the mean angular momentum equation and neglected their effects on the mean energy equation.
In contrast, the interaction between waves/modes and meridional circulations has been extensively studied in geophysical flows in the 60 s and 70 s in the context of middle atmosphere dynamics (e.g., Andrews et al. 1987; Holton 1992). Andrews & McIntyre (1976, 1978b) proposed the transformed Eulerian mean formalism (TEM) to account for the interaction between waves and the mean flow in a general way. That allowed them to demonstrate the non-acceleration theorem: if the waves are steady, conservative, and of small amplitudes, the mean flow is not accelerated. In the present series of papers, we adopt this formalism and adapt it to model angular momentum transport by mixed modes in stars. In this paper, which is the first of the series, we establish the formalism and discuss numerical results for a benchmark model. In a companion paper (Belkacem et al. 2015, hereafter Paper II) we consider realistic mode amplitudes to quantitatively estimate the efficiency of the angular momentum transport by modes along the evolution of low-mass stars.
This paper is organised as follows: Sect. 2 introduces the mean flow equations. Section 3 discusses the transformed Eulerian mean (TEM) formalism and its particular form in the case of stellar shellular rotation. In Sect. 4, we model the wave fluxes for mixed modes. In Sect. 5, the rate of angular momentum transport is computed numerically for a benchmark model of an evolved 1.3 M⊙ star, representative of CoRoT and Kepler observations. Section 6 is dedicated to discussions and conclusions.
2. Preliminary remarks on the wave mean-flow equations
In this section, we derive the equations that describe the interaction between the mean flow and waves. We use an Eulerian averaging process to derive the equations of the mean flow. It allows us to discuss the coupling between waves and the meridional circulation as well as the role of the wave heat flux.
The continuity, momentum, and energy equations in an inertial frame can be written as 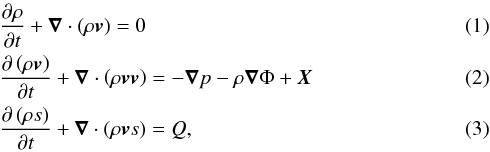 where ρ is the density, v the velocity field, p the pressure, s the specific entropy, Φ the gravitational potential, X is a non-conservative mechanical forcing (e.g., turbulent dissipation), and Q represents heating or cooling terms.
where ρ is the density, v the velocity field, p the pressure, s the specific entropy, Φ the gravitational potential, X is a non-conservative mechanical forcing (e.g., turbulent dissipation), and Q represents heating or cooling terms.
The azimuthal component of Eq. (2) can be written in a form that represents the conservation of specific angular momentum: 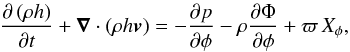 (4)where the specific angular momentum is h = ϖvφ = ϖ2 Ω, with Ω representing the angular velocity, ϖ = rsinθ, and vφ the azimuthal component of the velocity field.
(4)where the specific angular momentum is h = ϖvφ = ϖ2 Ω, with Ω representing the angular velocity, ϖ = rsinθ, and vφ the azimuthal component of the velocity field.
A given field can be decomposed into a mean part and a perturbation. The perturbation is associated with linear non-radial waves. More precisely, for a given field A, we have 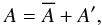 (5)where
(5)where 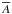 is the Eulerian-mean azimuthal average
is the Eulerian-mean azimuthal average 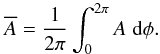 (6)Introducing the decomposition given by Eq. (5) into Eqs. (1), (3), and (4) and azimuthal averaging them, we obtain the following system:
(6)Introducing the decomposition given by Eq. (5) into Eqs. (1), (3), and (4) and azimuthal averaging them, we obtain the following system: 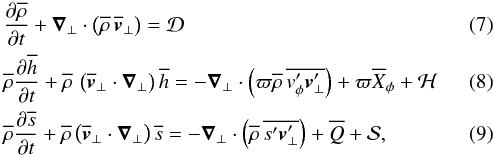 with
with 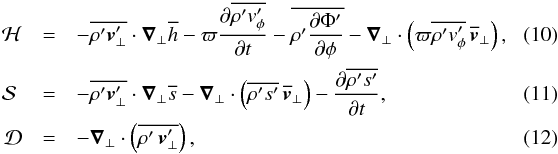 and ∇⊥, ∇⊥·(), v⊥ are the gradient, divergence, and velocity vector in the meridional plane, respectively. They are defined by
and ∇⊥, ∇⊥·(), v⊥ are the gradient, divergence, and velocity vector in the meridional plane, respectively. They are defined by 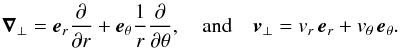 (13)The terms involving the density perturbation (ρ′) are generally considered to be small (e.g., Ando 1983; Unno et al. 1989). This is particularly the case for low-frequency waves (σR ≪ N, where σR is the wave frequency and N the buoyancy frequency) where the anelastic approximation applies (e.g., Dintrans & Rieutord 2001). Therefore, we neglect the terms
(13)The terms involving the density perturbation (ρ′) are generally considered to be small (e.g., Ando 1983; Unno et al. 1989). This is particularly the case for low-frequency waves (σR ≪ N, where σR is the wave frequency and N the buoyancy frequency) where the anelastic approximation applies (e.g., Dintrans & Rieutord 2001). Therefore, we neglect the terms 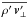 ,
, 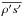 , and
, and 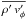 in Eqs. (10) to (12). In addition, we use the Cowling approximation by neglecting the perturbation of the gravitational potential, so that Eqs. (7) to (9) become
in Eqs. (10) to (12). In addition, we use the Cowling approximation by neglecting the perturbation of the gravitational potential, so that Eqs. (7) to (9) become 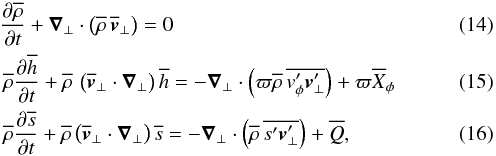 where the effect of waves now appears through the wave momentum flux in the mean angular momentum equation, Eq. (15)and the wave heat flux in the mean entropy equation, Eq. (16).
where the effect of waves now appears through the wave momentum flux in the mean angular momentum equation, Eq. (15)and the wave heat flux in the mean entropy equation, Eq. (16).
However, the mean specific entropy 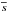 and mean specific angular momentum
and mean specific angular momentum 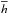 are not independent. They are connected by the baroclinic equation (also known as the thermal wind balance equation), obtained by taking the curl of the hydrostatic equilibrium equation:
are not independent. They are connected by the baroclinic equation (also known as the thermal wind balance equation), obtained by taking the curl of the hydrostatic equilibrium equation: 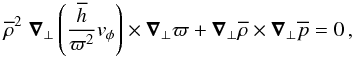 (17)together with the equation of state
(17)together with the equation of state 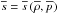 .
.
Therefore, we must solve the complete set of Eqs. (14)to (17)to compute the effect of waves on the mean flow, including both wave stresses in the mean angular momentum equation, Eq. (15), and the wave heat flux in the mean entropy equation, Eq. (16). However, the effect of the wave heat flux is often neglected in the literature related to transport of angular momentum in stars by waves (e.g., Press 1981; Ando 1983; Lee & Saio 1993; Zahn et al. 1997; Kumar et al. 1999; Pantillon et al. 2007; Mathis et al. 2013; Townsend 2014).
It is potentially misleading to overlook the effect of the wave heat flux. To illustrate this point, we consider the extreme case of a conservative and stationary wave field. Under these assumptions, the non-acceleration theorem states that the mean flow is not accelerated by waves, although the wave momentum and heat fluxes defined in Eqs. (15)and (16)do not vanish. In other words, the wave fluxes of heat and momentum produce a meridional circulation that cancels their tendency to affect the mean flow. Indeed, the wave momentum and wave heat fluxes are not independent and, in the presence of wave forcing, the meridional circulation must ensure that 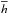 and
and 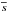 satisfy the baroclinic equation.
satisfy the baroclinic equation.
Consequently, both the wave momentum and wave heat fluxes must be considered to account for the effect of waves on the mean flow. To do so, we adopt in the following section the TEM formalism introduced by Andrews & McIntyre (1976, 1978b).
3. Transformed Eulerian mean equations
3.1. Formalism
The wave heat flux 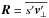 can be split into a component along an isentropic surface, the skew flux, and a component perpendicular to it. Following Vallis (2006),
can be split into a component along an isentropic surface, the skew flux, and a component perpendicular to it. Following Vallis (2006), 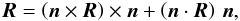 (18)with
(18)with 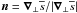 . The divergence of the skew flux can be rewritten as
. The divergence of the skew flux can be rewritten as ![\begin{eqnarray} \label{split_div_flux} \vec \nabla_\bot \cdot \left[\left( \vec n \times \vec R \right) \times \vec n \right] &=& \vec \nabla_\bot \cdot \left( \frac{ \vec \nabla_\bot \overline{s} \times \vec R }{\vert \vec \nabla_\bot \overline{s} \vert^2} \times \vec \nabla_\bot \overline{s} \right) \nonumber \\ &=& \left( \vec \nabla_\bot \times \frac{\vec \nabla_\bot \overline{s} \times \vec R}{\vert \vec \nabla_\bot \overline{s} \vert^2} \right) \cdot \vec \nabla_\bot \overline{s} \nonumber \\ &=& \tilde{\vec \vt}\cdot \vec \nabla_\bot \overline{s} , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq40.png) (19)where we used the relation ∇·(a × ∇α) = ∇α·(∇ × a), valid for any scalar α and vector a.
(19)where we used the relation ∇·(a × ∇α) = ∇α·(∇ × a), valid for any scalar α and vector a.
Equation (19) shows that the skew flux behaves like an advection by the velocity 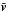 . The main motivation underlying the TEM is thus to incorporate the advective part of the wave heat flux into the mean meridional velocity field (
. The main motivation underlying the TEM is thus to incorporate the advective part of the wave heat flux into the mean meridional velocity field (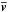 ).
).
The residual meridional circulation is thus defined by 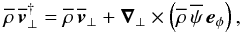 (20)where the stream function
(20)where the stream function 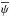 is defined, from Eq. (19), by
is defined, from Eq. (19), by ![\begin{eqnarray} \label{def_psi_general} \overline{\psi} = \frac{\vec \nabla_\bot \overline{s} \times \vec R}{\vert \vec \nabla_\bot \overline{s} \vert^2} \cdot \vec e_\phi= \frac{1}{\vert \vec \nabla_\bot \overline{s} \vert^2} \left[\left(\derivp{\overline{s}}{r}\right) \, \overline{\vt_\theta^\prime s^\prime} - \frac{1}{r} \left(\derivp{\overline{s}}{\theta}\right) \, \overline{\vt_r^\prime s^\prime} \right] . \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq48.png) (21)We note that the definition for ψ given in Eq. (21) is not unique (see Plumb & Ferrari 2005; Vallis 2006, for details).
(21)We note that the definition for ψ given in Eq. (21) is not unique (see Plumb & Ferrari 2005; Vallis 2006, for details).
Inserting Eqs. (20) and (21) into Eq. (14) to Eq. (16), we have
![\begin{eqnarray} && \label{continuity_eulerian_final} \derivp{\overline{\rho}}{t} + \vec \nabla_\bot \cdot \left( \overline{\rho} \, \overline{\vec \vt}_\bot^{\dag} \right) = 0 \\[2mm] &&\label{momentum_eulerian_final} \overline{\rho} \derivp{\overline{h}}{t} + \overline{\rho} \, \left( \overline{\vec \vt}_\bot^{\dag} \cdot \vec \nabla_\bot \right) \overline{h} = - \vec \nabla_\bot \cdot \left( \overline{\rho} \, \vec F \right) + \varpi \overline{X}_\phi \\[2mm] &&\label{energy_eulerian_final} \overline{\rho} \derivp{\overline{s}}{t} + \overline{\rho}\left( \overline{\vec \vt}_\bot^{\dag} \cdot \vec \nabla_\bot \right) \overline{s} = - \vec \nabla_\bot \cdot \left( \overline{\rho}\, \vec G \right) + \overline{Q} , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq50.png) where the components of the vectors F and G are given by
where the components of the vectors F and G are given by 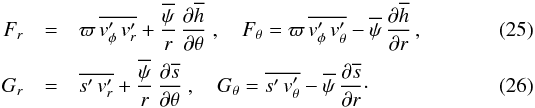 Equation (17)is left unmodified.
Equation (17)is left unmodified.
Finally, when F and G are specified, the residual velocity 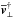 becomes part of the solution of Eqs. (22)to (24)together with Eq. (17). They are strictly equivalent to Eqs. (14)–(16), but present several conceptual and practical advantages:
becomes part of the solution of Eqs. (22)to (24)together with Eq. (17). They are strictly equivalent to Eqs. (14)–(16), but present several conceptual and practical advantages:
-
The TEM equations enable distinguishing the advective anddiffusive parts of the wave heat flux and incorporating theadvective component in the mean velocity field.
-
Andrews & McIntyre (1978b) showed that
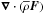 and
and 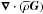 only depend on wave dissipation and non-steady terms. It is the non-acceleration theorem. Therefore, the TEM makes the adiabatic and non-adiabatic contributions of waves more explicit, the latter being able to modify the mean flow.
only depend on wave dissipation and non-steady terms. It is the non-acceleration theorem. Therefore, the TEM makes the adiabatic and non-adiabatic contributions of waves more explicit, the latter being able to modify the mean flow. -
Finally, depending upon the considered problem, the TEM formalism allows us to gather in a single equation and in the single term F both the wave momentum and wave heat fluxes. It explicitly shows that wave momentum fluxes and wave heat fluxes do not influence the mean flow separately, but only in the combination given by F. For instance, in the quasi-geostrophic approximation G ≈ 0 so that the term F (the Eliassen-Palm flux) is the only wave contribution to the problem. As we will show in the companion paper, we are in the same situation for mixed modes in the limit of shellular rotation, in which the radial component of G can be neglected.
3.2. Equation for the mean angular momentum: shellular rotation
Following the work of Zahn (1992), Maeder & Zahn (1998), Mathis & Zahn (2004) (see also Maeder 2009, for an extensive discussion), shellular rotation has been an approximation widely used in 1D stellar evolutionary codes. It is based on the assumption that turbulence is highly anisotropic in stellar radiative zones (e.g., Talon & Zahn 1997; Maeder 2003; Mathis et al. 2004); it is much stronger in the horizontal than in the vertical direction. Accordingly, efficient horizontal turbulent viscosity ensures that the angular velocity is almost constant on isobars. We then consider the TEM equations in this framework.
Given that the specific angular momentum is defined by 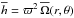 , we introduce the following decomposition
, we introduce the following decomposition 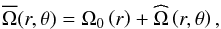 (27)with
(27)with 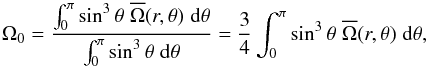 (28)where, with the shellular approximation,
(28)where, with the shellular approximation,  . The scalar quantities are developed as
. The scalar quantities are developed as 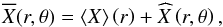 (29)with
(29)with 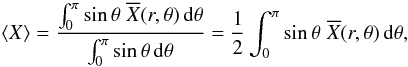 (30)and the velocity field equals to
(30)and the velocity field equals to 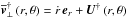 , where ṙ comes from the contraction or dilatation of the star and U† is the residual meridional circulation.
, where ṙ comes from the contraction or dilatation of the star and U† is the residual meridional circulation.
The various physical quantities are expanded in Legendre polynomials
![\begin{eqnarray} &&\label{def_vitesse} \vec U^{\dag} \left(r,\theta\right) = \sum_\ell \left[U_\ell^{\dag} (r) \, P_\ell (\cos \theta) \, \vec e_r+ V^{\dag}_\ell (r) \deriv{P_\ell (\cos \theta)}{\theta} \, \vec e_\theta \right] \\ &&\widehat{\Omega} \left(r,\theta\right) = \sum_\ell \Omega_\ell Q_\ell \left(\cos \theta\right) \\ &&\label{def_scalar2} \widehat{X} \left(r,\theta\right) = \sum_\ell X_\ell (r) P_\ell \left(\cos \theta\right) , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq68.png) where Qℓ = Pℓ − δℓ,0 + δℓ,2/ 5 (see Mathis & Zahn 2004), and, for slow to moderate rotation, we assume that
where Qℓ = Pℓ − δℓ,0 + δℓ,2/ 5 (see Mathis & Zahn 2004), and, for slow to moderate rotation, we assume that 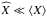 .
.
Following these assumptions, the specific entropy is nearly constant on isobars and the stream function 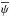 (Eq. (21)) becomes at dominant order
(Eq. (21)) becomes at dominant order 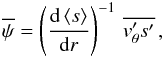 (34)which is the same expression as for geostrophic flows (e.g., Holton 1992).
(34)which is the same expression as for geostrophic flows (e.g., Holton 1992).
Introducing Eqs. (31)–(33) into Eq. (23), horizontal averaging, neglecting the time-variation of the density, and using the expression of the residual stream function given by Eq. (34), we obtain, at dominant order, ![\begin{eqnarray} \label{shellular_omega_r} \left< \rho \right> \deriv{\left(r^2 \Omega_0\right)}{t} = -\frac{1}{r^2} \derivp{}{r} \left[r^2 \left( \mathcal{F}_{\rm circ} + \mathcal{F}_{\rm shear} + \mathcal{F}_{\rm waves} \right) \right] \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq72.png) (35)with the fluxes defined by
(35)with the fluxes defined by
![\begin{eqnarray} &&\label{shellular_omega_r_advection} \mathcal{F}_{\rm circ} = -\frac{1}{5} \left< \rho \right> r^2 \Omega_0 \, U_2^{\dag} \\ &&\label{shellular_omega_r_shear} \mathcal{F}_{\rm shear} = -\left< \rho \right> \nu\ind{v} r^2 \derivp{\Omega_0}{r} \\ &&\label{shellular_omega_r_wave} \mathcal{F}_{\rm waves} = \left< \rho \right> \left< \varpi \left[\overline{\vt_\phi^\prime \, \vt_r^\prime} + 2 \cos \theta \, \Omega_0 \, \overline{\vt_\theta^\prime s^\prime} \left(\deriv{\left< s\right>}{r}\right)^{-1} \right] \right> . \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq73.png) The turbulent stresses are described by an anisotropic eddy viscosity denoted νv and νh for the vertical and horizontal component, respectively (see Zahn 1992; Mathis & Zahn 2004, for details). We also note that we introduced the Lagrangian derivative d/dt = ∂/∂t + ṙ∂/∂r.
The turbulent stresses are described by an anisotropic eddy viscosity denoted νv and νh for the vertical and horizontal component, respectively (see Zahn 1992; Mathis & Zahn 2004, for details). We also note that we introduced the Lagrangian derivative d/dt = ∂/∂t + ṙ∂/∂r.
Under the assumptions used for Eq. (35), we obtain for the entropy equation 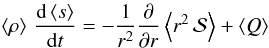 (39)with
(39)with 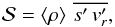 (40)and
(40)and 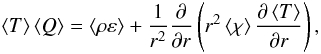 (41)where T is the temperature, ε is the nuclear energy generation rate, and χ is the thermal conductivity (see, e.g., Sect. 6 of Mathis & Zahn 2004; and also Maeder & Zahn 1998). This expresses energy conservation on a level surface. To obtain Eq. (39), we used Eq. (34) and assumed that the horizontal derivative of entropy is negligible at dominant order.
(41)where T is the temperature, ε is the nuclear energy generation rate, and χ is the thermal conductivity (see, e.g., Sect. 6 of Mathis & Zahn 2004; and also Maeder & Zahn 1998). This expresses energy conservation on a level surface. To obtain Eq. (39), we used Eq. (34) and assumed that the horizontal derivative of entropy is negligible at dominant order.
3.3. Discussion
As mentioned in Sect. 2, transport of angular momentum by waves in stars has been extensively studied, but often ignoring the effect of the wave heat flux (e.g., Press 1981; Ando 1983; Lee & Saio 1993; Zahn et al. 1997; Kumar et al. 1999; Townsend 2014). Following the work of Bretherton (1969), Pantillon et al. (2007) have also considered an additional wave contribution in the momentum equation, equal to 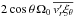 in our notation (see also Lee 2008; Mathis 2009). This term corresponds to a Lagrangian correction that can be understood as follows: on the typical time-scale of the momentum transport by waves (the modal period, for example), rotation advects a wave-related momentum flux. This term arises naturally in Lagrangian mean wave-flow theories such as the generalized Lagrangian mean (GLM) formulation by Andrews & McIntyre (1978a) (see also Grimshaw 1984; Lee 2013).
in our notation (see also Lee 2008; Mathis 2009). This term corresponds to a Lagrangian correction that can be understood as follows: on the typical time-scale of the momentum transport by waves (the modal period, for example), rotation advects a wave-related momentum flux. This term arises naturally in Lagrangian mean wave-flow theories such as the generalized Lagrangian mean (GLM) formulation by Andrews & McIntyre (1978a) (see also Grimshaw 1984; Lee 2013).
For linear waves, one can show that this Lagrangian term can be recovered from the TEM equations if one assumes that the Lagrangian perturbation of entropy vanishes (i.e. δs = 0). The wave flux in the mean angular momentum equation (Eq. (35)) is 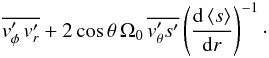 (42)We can then express the entropy Eulerian perturbation in terms of the Lagrangian perturbation at first order: δs = s′ + ξr d⟨s⟩/dr, where ξr is the wave displacement. Using Eq. (45) and the expression for the wave velocity v′ = i(σR + mΩ0)ξ − ϖ(ξ·∇Ω0) eφ (where σR is the modal frequency), we obtain
(42)We can then express the entropy Eulerian perturbation in terms of the Lagrangian perturbation at first order: δs = s′ + ξr d⟨s⟩/dr, where ξr is the wave displacement. Using Eq. (45) and the expression for the wave velocity v′ = i(σR + mΩ0)ξ − ϖ(ξ·∇Ω0) eφ (where σR is the modal frequency), we obtain 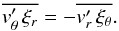 (43)Therefore, if the entropy Lagrangian perturbation vanishes (i.e. δs = 0), the term (42) becomes
(43)Therefore, if the entropy Lagrangian perturbation vanishes (i.e. δs = 0), the term (42) becomes 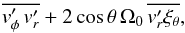 (44)which is the expression given in Pantillon et al. (2007) as claimed. Finally, Eq. (44) shows that the Lagrangian correction introduced by Pantillon et al. (2007), Lee (2008), Mathis (2009) is recovered from the TEM equations. In this framework, it can be understood as originating from the wave heat source term in the mean entropy equation.
(44)which is the expression given in Pantillon et al. (2007) as claimed. Finally, Eq. (44) shows that the Lagrangian correction introduced by Pantillon et al. (2007), Lee (2008), Mathis (2009) is recovered from the TEM equations. In this framework, it can be understood as originating from the wave heat source term in the mean entropy equation.
However, the contribution related to the entropy Lagrangian perturbation is not negligible (see the results presented in Sect. 5.2 below). Therefore, it is not enough to consider the wave flux in the mean angular momentum given by Eq. (44).
4. Modelling the wave fluxes: the case of mixed modes in evolved low-mass stars
In this section, we focus on the transport of angular momentum by mixed normal modes in the radiative region of evolved low-mass stars (i.e. subgiants and red giants). These modes have a dual nature; they behave as acoustic modes in the upper layers and as gravity modes in the inner layers. Therefore, they are detectable at the stellar surface while providing information on the innermost regions. They have been detected in several thousands of evolved stars (e.g., Bedding et al. 2011; Mosser et al. 2012, 2014) and have provided a wealth of information on the core of red giants (e.g., Mosser et al. 2012). These modes must not be confused with progressive gravity waves, often called internal gravity waves in the literature.
4.1. Simplifying approximations
We restrict ourselves to the case of strictly shellular rotation (see Sect. 3.2). Moreover, we focus on the inner radiative regions since our aim in this series of papers is to investigate the transport of angular momentum in the core of evolved low-mass stars. These restrictions allow us to use several approximations to describe the wave field:
-
1.
The quasi-adiabatic approach: it consists of neglecting thedifference between adiabatic and non-adiabatic eigenfunctionsin the full wave equations. This approximation is valid when thelocal thermal time-scale is much longer than the modal period.This is the case in the radiative region of evolved low-mass stars.
-
2.
The low-rotation limit: we assume that the modal period is much shorter than the rotation period. This is justified by recent inferences of the rotation in the core of subgiants (Deheuvels et al. 2012, 2014) and red giants (Mosser et al. 2012) using seismic constraints from Kepler.
-
3.
The asymptotic limit: finally, we use an asymptotic description for gravity modes (e.g., Dziembowski et al. 2001; Godart et al. 2009), which is valid for mixed modes in the inner radiative region of subgiants and red giants (e.g., Goupil et al. 2013).
4.2. Derivation of the wave fluxes
We assume that the perturbations consist of non-radial oscillations such that, for any perturbed variable f′, we have 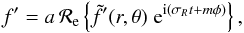 (45)where ℛe denotes the real part, a is the amplitude, and σR is the real frequency (so that non-adiabatic effects are neglected). The amplitude is considered as statistically constant in time since we deal with solar-like oscillations resulting from a balance between mode driving and damping (see Samadi 2011, for details).
(45)where ℛe denotes the real part, a is the amplitude, and σR is the real frequency (so that non-adiabatic effects are neglected). The amplitude is considered as statistically constant in time since we deal with solar-like oscillations resulting from a balance between mode driving and damping (see Samadi 2011, for details).
We now consider the equations governing non-radial and non-adiabatic oscillations in the presence of rotation (e.g., Eqs. (36.12) to (36.15) of Unno et al. 1989). For sake of simplicity, tildes, bars, and brackets will be dropped from now on unless necessary. The equations are ![\begin{eqnarray} \label{eq1} &&\derivD{\vec \vt_\bot^\prime}{t} - \frac{2 h}{\varpi^2} \vt_\phi^\prime \nabla_\bot \varpi = -\frac{1}{\rho} \nabla_\bot p^\prime + \frac{\rho^\prime}{\rho^2} \nabla_\bot p \\[2mm] \label{eq2} && \derivD{\vt_\phi^\prime}{t} +\frac{1}{\varpi} \vec \vt_\bot^\prime\cdot \nabla_\bot h = -\frac{{\rm i} m}{\varpi} \frac{p^\prime}{\rho} \\[2mm] \label{eq3} &&\derivD{}{t} \left(\frac{\rho^\prime}{\rho}-\frac{p^\prime}{\Gamma_1 p} +\rho_T \frac{\delta s}{c_p} \right) = - \vec \vt_\bot^\prime \cdot \vec A \\[2mm] \label{eq4} &&\derivD{\rho^\prime}{t} + \nabla_\bot \cdot \left(\rho \vec \vt_\bot^\prime \right) + \frac{{\rm i} m \rho}{\varpi} \vt_\phi^\prime = 0 , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq96.png) where Γ1 = (∂lnp/∂lnρ)s, ρT = −(∂lnρ/∂lnT)p, and
where Γ1 = (∂lnp/∂lnρ)s, ρT = −(∂lnρ/∂lnT)p, and 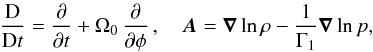 (50)so that N2 = ρ-1∇p·A.
(50)so that N2 = ρ-1∇p·A.
Given the assumption that the mode amplitude is statistically constant in time, Eqs. (46) to (49) reduce to 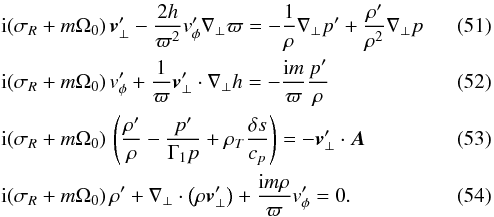 Using Eqs. (51) to (54) and the assumptions detailed in Sect. 4.1, and after stirring vigorously as detailed in Appendix A, we obtain for a mode of a given angular degree ℓ and azimuthal order m an expression of the form
Using Eqs. (51) to (54) and the assumptions detailed in Sect. 4.1, and after stirring vigorously as detailed in Appendix A, we obtain for a mode of a given angular degree ℓ and azimuthal order m an expression of the form ![\begin{eqnarray} \label{final_F_waves} &&\!\!-\frac{1}{r^2} \derivp{}{r} \left( r^2 \mathcal{F}_{\rm waves} \right) = \\ &&a_{\ell,m}^{2} \left[\mathcal{A}_{\ell}^m \; \derivp{^2\left(r^2 \Omega_0 \right)}{r^2} +\mathcal{B}_{\ell}^m \; \derivp{\left(r^2 \Omega_0 \right)}{r} + \mathcal{C}_{\ell}^m \; r^2 \Omega_0 + m \hat \sigma \, \mathcal{D}_{\ell}^m \right] \nonumber , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq104.png) (55)where
(55)where 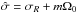 and the coefficients
and the coefficients 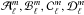 are given by Eqs. (A.24) to (A.27), respectively. The amplitude aℓ,m corresponds to the amplitude of a mode of angular degree ℓ, and azimuthal order m.
are given by Eqs. (A.24) to (A.27), respectively. The amplitude aℓ,m corresponds to the amplitude of a mode of angular degree ℓ, and azimuthal order m.
The derivation of the wave fluxes in Eq. (39) is more direct. Using the asymptotic expression for the Lagrangian perturbation of entropy given by Eq. (A.21), we obtain 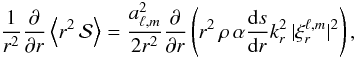 (56)where
(56)where ![\begin{eqnarray} \label{alpha_main} &\alpha = -\frac{L}{4 \pi r^2 \rho T} \left( \frac{\nabla_{\rm ad}}{\nabla}-1 \right) \, \left(\deriv{s}{r}\right)^{-1}\\[2mm] \label{kr2_main} &k_r^2 \simeq \frac{\ell(\ell+1)}{r^2} \, \left(\frac{N^2}{\sigma_R^2}-1\right) , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq109.png) with L being the luminosity, N the buoyancy frequency, ∇ and ∇ad the actual and adiabatic temperature gradients, respectively.
with L being the luminosity, N the buoyancy frequency, ∇ and ∇ad the actual and adiabatic temperature gradients, respectively.
5. Case of an evolved 1.3 M⊙ star
The aim of this section is to qualitatively discuss the effect of mixed modes on the mean angular momentum profile within the TEM framework. To this end, we consider a stellar model for an evolved 1.3 M⊙ star that is representative of the oscillating red giant stars observed by CoRoT and Kepler. A quantitative estimate as well as a discussion of the effect of mixed modes throughout the evolution is given in Paper II.
5.1. Computing the benchmark model
 |
Fig. 1 Rotation rate normalised by its central value (solid line) and buoyancy frequency normalised by its maximum value (dashed dots lines) versus normalised radius for the model described in Sect. 5.1 (logarithmic scale in both axes). |
The equilibrium model was computed with the stellar evolution code CESTAM (Marques et al. 2013). The atmosphere was computed assuming a grey Eddington approximation. Convection was included according to Canuto et al. (1996), with a mixing-length parameter α = 0.67. The initial chemical composition was the solar composition of Asplund et al. (2005), with a helium mass fraction Y = 0.261 and metallicity Z = 0.0138, and diffusion was not included. We used the OPAL equation of state (Rogers et al. 1996) and opacities (Iglesias & Rogers 1996), complemented, at T< 104 K, by the Alexander & Ferguson (1994) opacities. We adopted the NACRE nuclear reaction rates (Angulo et al. 1999) except for the 14N + p reaction, where we used the reaction rates of Imbriani et al. (2004). The model was computed without rotation.
To obtain a rotation profile as realistic as possible, we computed an equivalent model with rotation (using the procedure described in Marques et al. 2013) and rescaled the rotation profile to gain a core rotation rate Ωc/ (2π) = 1 μHz. This value is consistent with the mean central rotation rate of evolved low-mass stars derived from Kepler observations (see Mosser et al. 2012; Deheuvels et al. 2014). The resulting rotation profile and buoyancy frequency are shown in Fig. 1. Consistently with the slow rotation limit we consider, this procedure is equivalent to assuming that rotation has a negligible effect on the star equilibrium structure. The equivalent model including rotation was computed using the same input physics and parameters as the model without rotation. It has a radius as close as possible to the radius of the model without rotation and is in the same evolutionary phase. The main characteristics of the models are given in Table 1.
Characteristics of the models computed with rotation and without rotation for comparison.
Finally, we used the ADIPLS code for adiabatic oscillations (Christensen-Dalsgaard 2008, 2011) to compute eigenfunctions and eigenfrequencies. The effect of rotation was also neglected in computing the eigenfunctions and eigenfrequencies.
5.2. Effect of prograde and retrograde mixed modes
We will show in Paper II that the wave fluxes in the mean energy equation, Eq. (39), is negligible. Therefore, within the TEM formalism, the contribution of the mixed modes to the mean flow consists entirely of the wave flux in the mean angular momentum equation (see Eq. (35)). Thus, for ease of notation, we define the rate of temporal variation of the mean specific angular momentum induced by mixed modes by 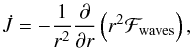 (59)where we recall that ℱwaves is given by Eq. (38). Note that
(59)where we recall that ℱwaves is given by Eq. (38). Note that 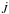 is normalised so that for a given mode of angular degree ℓ and azimuthal order m one has
is normalised so that for a given mode of angular degree ℓ and azimuthal order m one has 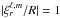 at the photosphere.
at the photosphere.
Computing 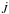 as described in Sect. 4.2 leads to the conclusion that prograde modes (m< 0) extract angular momentum in the regions near the maximum of the buoyancy frequency and the maximum of the rotation rate, therefore slowing down the core. Conversely, the retrograde modes (m> 0) tend to spin up the core. This is illustrated in Fig. 2 (top and middle panels) for the sectoral modes ℓ = 2, m = { − 2, + 2 } at the frequency νR = σR/ (2π) = 300.9 μHz, but this conclusion is valid for the other modes as well. When we consider unstable modes, the opposite situation is found, that is, the retrograde modes extract angular momentum (e.g., Ando 1986; Lee & Saio 1993; Townsend & MacDonald 2008; Townsend 2014; Lee et al. 2014). In this case, the wave stresses in the mean angular momentum equation are dominated by transient terms.
as described in Sect. 4.2 leads to the conclusion that prograde modes (m< 0) extract angular momentum in the regions near the maximum of the buoyancy frequency and the maximum of the rotation rate, therefore slowing down the core. Conversely, the retrograde modes (m> 0) tend to spin up the core. This is illustrated in Fig. 2 (top and middle panels) for the sectoral modes ℓ = 2, m = { − 2, + 2 } at the frequency νR = σR/ (2π) = 300.9 μHz, but this conclusion is valid for the other modes as well. When we consider unstable modes, the opposite situation is found, that is, the retrograde modes extract angular momentum (e.g., Ando 1986; Lee & Saio 1993; Townsend & MacDonald 2008; Townsend 2014; Lee et al. 2014). In this case, the wave stresses in the mean angular momentum equation are dominated by transient terms.
We have also found that, despite an important rotation gradient in the hydrogen burning shell, the dominant contribution to the angular momentum transport comes from the term 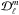 so that, from Eq. (55) and for a mode of a given angular and azimuthal degree, we can write
so that, from Eq. (55) and for a mode of a given angular and azimuthal degree, we can write 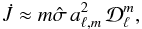 (60)where
(60)where 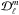 is given by Eq. (A.27).
is given by Eq. (A.27).
To proceed, we considered the sum of the contributions of a prograde and a retrograde mixed modes to the mean angular momentum profile. In the absence of rotation, both prograde and retrograde modes transport angular momentum, but the sum vanishes so that there is no net transport. Including rotation, the net transport of angular momentum is a small residual (see Fig. 2 bottom panel). The asymmetry between prograde and retrograde modes arises from the Doppler shift terms in the mode frequencies (i.e., 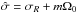 ). More precisely, the dominant term of Eq. (60) comes from the first term of
). More precisely, the dominant term of Eq. (60) comes from the first term of 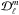 in Eq. (A.27). This term originates in the second term of Eq. (38), thus from the wave heat flux. To illustrate it, we added a prograde and retrograde mode, expand in Ω0/σR, and only kept the leading term to obtain
in Eq. (A.27). This term originates in the second term of Eq. (38), thus from the wave heat flux. To illustrate it, we added a prograde and retrograde mode, expand in Ω0/σR, and only kept the leading term to obtain 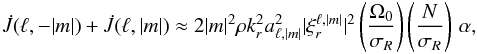 (61)which is negative, since the term α (see Eq. (57)) is negative. The sum of the contributions of prograde and retrograde mixed modes thus implies an extraction of angular momentum. Nonetheless, in the regions where the contribution of the prograde mode has nodes, the contribution of the retrograde mode dominates due to the second and third terms of
(61)which is negative, since the term α (see Eq. (57)) is negative. The sum of the contributions of prograde and retrograde mixed modes thus implies an extraction of angular momentum. Nonetheless, in the regions where the contribution of the prograde mode has nodes, the contribution of the retrograde mode dominates due to the second and third terms of 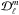 in Eq. (A.27). It therefore results in a complex situation where there is a spatial alternation between regions where mixed modes decrease and increase the mean momentum, as shown in Fig. 2 (bottom panel). However, before reaching a conclusion, we have to consider the collective effect of mixed modes.
in Eq. (A.27). It therefore results in a complex situation where there is a spatial alternation between regions where mixed modes decrease and increase the mean momentum, as shown in Fig. 2 (bottom panel). However, before reaching a conclusion, we have to consider the collective effect of mixed modes.
 |
Fig. 2 Rate of angular momentum transport by mixed modes ( |
5.3. Collective influence of mixed mode
Oscillation spectra of low-mass evolved stars exhibit quasi-periodic patterns with periods that correspond to the large separation as depicted in Fig. 3 (top panel). Each pattern is made of p-dominated mixed modes separated by several g-dominated modes. It is therefore instructive to consider the collective effect of mixed modes on the mean angular momentum.
We selected a range of modes, shown in red in Fig. 3 (top panel), and computed the total contribution to 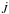 by summing the contribution of all modes belonging to this range, including the different values of the azimuthal order m for each mode. Given the spatial shift between the consecutive mixed modes, the summation induces a smoothing of
by summing the contribution of all modes belonging to this range, including the different values of the azimuthal order m for each mode. Given the spatial shift between the consecutive mixed modes, the summation induces a smoothing of 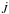 , as shown by Fig. 3 (bottom panel). The collective effect of mixed modes is to decrease the mean angular momentum and thus to slow down the core rotation of the star.
, as shown by Fig. 3 (bottom panel). The collective effect of mixed modes is to decrease the mean angular momentum and thus to slow down the core rotation of the star.
Nevertheless, we emphasise that to realistically compute the effect of the modes on the mean angular momentum profile, we need to consider all modes with realistic individual amplitudes This is the scope of Paper II.
 |
Fig. 3 Top panel: mode inertia versus mode frequencies for angular degrees ℓ = 0 and ℓ = 2. Mode inertias are computed by integrating the squared eigendisplacement over the stellar mass. Bottom panel: same as Fig. 2, except that |
6. Conclusion
Our aim here was to establish a formalism allowing us to calculate the transport of angular momentum by mixed modes in the inner radiative region of evolved low-mass stars. We thus considered the transformed Eulerian mean (TEM) formalism that allowed us to take into account the combined effect of both the wave momentum flux in the mean angular momentum equation and the wave heat flux in the mean energy equation. Indeed, the effect of the wave heat flux on the mean flow is generally neglected in the context of angular momentum transport by waves in stars. Here, the TEM allows us to include its impact on the mean angular momentum in a relatively simple way.
Given the important contraction of the core and expansion of the envelope of low-mass stars after the main sequence, a strong radial rotation gradient appears. This was taken into account by adopting the shelullar approximation. While a two-dimensional treatment is certainly desirable and more accurate (e.g., Espinosa Lara & Rieutord 2013), this approximation provides a first approach of the problem while keeping it tractable.
Subsequently, the wave field has been modelled so as to account for the transport of angular momentum by mixed modes. We limited our investigation to the inner radiative regions. Thus, several simplifications are justified; the low-frequency limit (i.e. 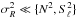 ), the quasi-adiabatic approach (the local thermal time-scale is higher than the modal period), and the low-rotation limit as suggested by recent asteroseismic observations (Deheuvels et al. 2012; Mosser et al. 2012). It allowed us to obtain an explicit expression of the wave-related terms appearing in the mean angular momentum equation.
), the quasi-adiabatic approach (the local thermal time-scale is higher than the modal period), and the low-rotation limit as suggested by recent asteroseismic observations (Deheuvels et al. 2012; Mosser et al. 2012). It allowed us to obtain an explicit expression of the wave-related terms appearing in the mean angular momentum equation.
Then, the formalism was applied to a benchmark model of a 1.3 M⊙ evolved star. We found that the influence of the wave heat flux on the mean angular momentum is not negligible and even dominant when considering the sum of prograde and retrograde modes. In addition, we showed that the overall effect of mixed modes is to extract angular momentum in the innermost radiative layers.
Nevertheless, more realistic estimates of mode amplitudes are required for a more quantitative determination of the amount of angular momentum transported by mixed modes. The second paper of this series is dedicated to this.
Online material
Appendix A: Derivation of the wave flux in the mean angular momentum equation (Eq. (35))
We assume that the perturbations consist in non-radial oscillations and that they behave linearly as exp[i(σt + mφ)], where σ is the modal frequency, t the time, and m the azimuthal degree. Consequently, for a given quantity f, its perturbation can be written 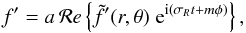 (A.1)where a is the amplitude, σR the real part of the frequency σ, and ℛe stands for the real value. From Eq. (A.1) one immediately deduces a relation for squared quantities that reads
(A.1)where a is the amplitude, σR the real part of the frequency σ, and ℛe stands for the real value. From Eq. (A.1) one immediately deduces a relation for squared quantities that reads 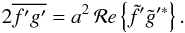 (A.2)One can then express the Eulerian perturbation of the entropy in terms of the Lagrangian one, using δs = s′ + ξrd⟨s⟩/dr, where ξr is the radial component of the wave displacement. It allows us to rewrite the divergence of the wave flux in the momentum equation (see Eq. (39)) such as
(A.2)One can then express the Eulerian perturbation of the entropy in terms of the Lagrangian one, using δs = s′ + ξrd⟨s⟩/dr, where ξr is the radial component of the wave displacement. It allows us to rewrite the divergence of the wave flux in the momentum equation (see Eq. (39)) such as 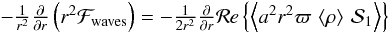 (A.3)with
(A.3)with ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{S1_app} \mathcal{S}_1 = \tilde{\vt}_r^\prime \tilde{\vt}_\phi^{\prime \ast} - 2 \cos \theta \, \Omega_0 \left[\tilde{\vt}_\theta^{\prime} \tilde{\xi}_r^{\prime \ast} - \tilde{\vt}_\theta^{\prime} \delta s^{\ast} \left(\deriv{\left< s\right>}{r}\right)^{-1} \right] \, \cdot \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq153.png) (A.4)In the following, our objective is to provide a general expression of Eq. (A.3) using the full set of equations governing waves. Note that in the following, the tilde will be omitted for the perturbation as well as overbar and brackets for the unperturbed quantities.
(A.4)In the following, our objective is to provide a general expression of Eq. (A.3) using the full set of equations governing waves. Note that in the following, the tilde will be omitted for the perturbation as well as overbar and brackets for the unperturbed quantities.
Appendix A.1: Using the full wave equations for expressing Eq. (A.4)
In this subsection, we aim to express the correlation products appearing in Eq. (A.4) using the set of Eq. (51) to Eq. (54).
Appendix A.1.1: Derivation of the first term of Eq. (A.4)
First, Eqs. (52) and (53) are inserted into (54), and an integration by part is performed. Second, Eqs. (51) to (53) are used as well as the relation 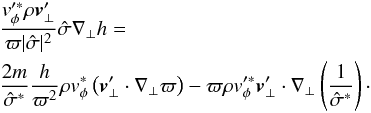 (A.5)Finally, taking the real part and considering that the imaginary part of the frequency vanishes (σI = 0) since we consider steady waves (see Sect. 4.2), one gets
(A.5)Finally, taking the real part and considering that the imaginary part of the frequency vanishes (σI = 0) since we consider steady waves (see Sect. 4.2), one gets ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{moment_app} &&\!- \nabla_\bot \cdot \left[\rho \varpi\overline{ \vec \vt_\bot^\prime \vt_\phi^\prime} \right] = - \frac{m\rho}{ 2} \left[\frac{\left(\vec \vt_\bot^\prime \cdot \rho^{-1} \vec \nabla_\bot p \right) \vec \vt_\bot^{\prime \ast} \cdot \vec A}{\hat \sigma^2} \right]_I \nonumber \\ &&\quad - \frac{m\rho}{2 \varpi} \left( \frac{\rho \varpi^2}{m^2 \Gamma_1 p} - \frac{1}{\hat \sigma^2} \right) \left[\hat \sigma \vec \vt_\bot^\prime \vt_\phi^{\prime \ast} \right] _R\cdot \vec \nabla_\bot h \nonumber \\ &&\quad - \frac{\rho}{2} \left[\frac{\left( \vec \vt_\bot^\prime \cdot \vec A + \vec \vt_\bot^\prime \cdot \vec \nabla_\bot \right) \left(\vec \vt_\bot^{\prime \ast} \cdot \vec \nabla_\bot h \right)}{\hat \sigma }\right]_I + \frac{\rho \varpi}{2} \left[\vt_\phi^{\prime \ast} \hat \sigma \rho_T \frac{\delta s}{c_p} \right]_I\nonumber \\ &&\quad + \frac{m \rho}{2} \left[\frac{\left(\vec \vt_\bot^{\prime} \cdot \rho^{-1} \vec \nabla_\bot p \right) \rho_T \delta s^{\ast}/c_p }{\hat \sigma}\right]_R , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq156.png) (A.6)where we introduced the notation
(A.6)where we introduced the notation 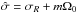 , ρT = −(∂lnρ/∂lnT)p, and the subscripts I and R denote the imaginary and real part, respectively. Note that this expression corresponds to Eq. (36.16) of Unno et al. (1989) and was first derived by Ando (1983).
, ρT = −(∂lnρ/∂lnT)p, and the subscripts I and R denote the imaginary and real part, respectively. Note that this expression corresponds to Eq. (36.16) of Unno et al. (1989) and was first derived by Ando (1983).
To go further, we assume shellular rotation and that the equilibrium state is not deformed by rotation. Moreover, integration over the solid angle is performed so that it finally gives 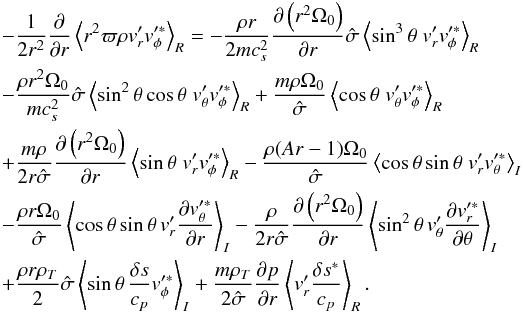 (A.7)
(A.7)
Appendix A.1.2: Derivation of the second term of Eq. (A.4)
We start from Eq. (52), which immediately gives 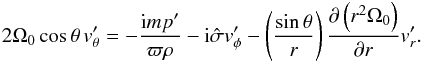 (A.8)Equation (A.8) is further multiplied by
(A.8)Equation (A.8) is further multiplied by 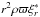 and radial derivation is performed to give
and radial derivation is performed to give ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{C3} && \frac{1}{r^2} \derivp{}{r} \left( 2 \Omega_0 r^2 \varpi \rho \cos \theta \vt_\theta^{\prime} \xi_r^{\prime \ast} \right) = - {\rm i} m \left[\frac{p^\prime}{r^2} \derivp{\left(r^2 \xi_r^{\ast}\right)}{r} + \xi_r^{\ast} \derivp{p^\prime}{r}\right] \nonumber \\ &&\quad \quad - {\rm i} \varpi \rho \hat \sigma \left( \vt_\phi^\prime \derivp{\xi_r^{\ast}}{r} + \xi_r^{\ast} \derivp{\vt_\phi^\prime}{r}\right) - \rho \sin^2\theta \derivp{^2\left(r^2 \Omega_0\right)}{r^2} \vt_r^\prime \xi_r^{\ast} \nonumber \\ &&\quad \quad - \rho \sin^2\theta \derivp{\left(r^2 \Omega_0\right)}{r} \left[\left( \frac{2}{r} + \derivp{\ln \rho}{r} \right) \vt_r^\prime \xi_r^{\ast} + \left( \vt_r^\prime \derivp{\xi_r^{\ast}}{r} + \xi_r^{\ast} \derivp{\vt_r^\prime}{r} \right)\right] \nonumber \\ &&\quad \quad - {\rm i} \sin \theta \rho \hat \sigma \vt_\phi^\prime \xi_r^{\ast} \left[1 + \derivp{\ln \rho}{\ln r} + \frac{2\sigma_R}{\hat \sigma} + \frac{m}{r \hat \sigma} \derivp{ \left(r^2\Omega_0\right)}{ r} \right] \cdot \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq163.png) (A.9)Now one needs to express both the perturbation of pressure and its radial derivative. To this end, we use Eqs. (53) and (54) as well as Eqs. (51) to (53) to get
(A.9)Now one needs to express both the perturbation of pressure and its radial derivative. To this end, we use Eqs. (53) and (54) as well as Eqs. (51) to (53) to get 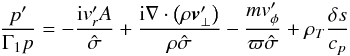 (A.10)and
(A.10)and ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{gradp_prime} &&\derivp{p^\prime}{r} = - {\rm i} \left[\rho \hat \sigma - \frac{\sin^2\theta}{m c_s^2} \derivp{p}{r} \derivp{\left( r^2 \Omega_0 \right)}{r} - \frac{A}{\hat \sigma} \derivp{p}{r} \right] \vt_r^\prime \\ &&\!+ \left[2 \rho \Omega_0 \sin \theta - \frac{\varpi \hat \sigma}{m c_s^2} \derivp{p}{r} \right] \vt_\phi^\prime + 2 {\rm i} \derivp{p}{r} \frac{r \sin \theta \cos \theta \Omega_0}{m c_s^2} \vt_\theta^\prime \nonumber - \rho_T \derivp{p}{r} \frac{\delta s}{c_p} \cdot \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq165.png) (A.11)Finally, inserting Eqs. (A.11) and (A.10) into Eq. (A.9), integrating over the solid angle and taking the real part gives
(A.11)Finally, inserting Eqs. (A.11) and (A.10) into Eq. (A.9), integrating over the solid angle and taking the real part gives ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{second_S1_eq} &&\frac{1}{2 r^2} \derivp{}{r} \mathcal{R}_{\rm e} \left< 2 \Omega_0 r^2 \varpi \rho \cos \theta \vt_\theta^{\prime} \xi_r^{\prime \ast} \right>_R = \nonumber \\ && \frac{\rho}{2} \Bigg[A r + 3 + \frac{m}{r \hat \sigma} \derivp{ \left(r^2\Omega_0\right)}{ r} \Bigg] \left<\sin \theta\; \vt_\phi \vt_r^{\ast}\right>_R - \frac{m \rho_T}{2 \hat \sigma}\derivp{p}{r} \left< \frac{\delta s}{c_p} \vt_r^{\ast}\right>_R \nonumber \\ &&\!+ \frac{m \rho c_s^2}{2 r^3 \hat \sigma} \left<\frac{1}{\sin \theta} \derivp{\left(\sin \theta \vt_\theta \right)}{\theta}\; \derivp{\left(r^2 \xi_r^{\ast}\right)}{r}\right>_R \!+\! \frac{m}{2 r^2} \rho_T \Gamma_1 p \, \left< \frac{\delta s}{c_p} \derivp{\left( r^2 \xi_r^{\ast}\right)}{r}\right>_I \nonumber \\ &&\!+ \frac{\rho r}{2} \hat \sigma \left< \sin \theta \left[\vt_\phi^\prime \derivp{\xi_r^{\ast}}{r} + \derivp{\vt_\phi^\prime}{r} \xi_r^{\ast}\right] \right>_I - \frac{m^2 \rho c_s^2}{2 r^3 \hat \sigma} \left< \frac{1}{\sin \theta} \vt_\phi^\prime \derivp{\left(r^2 \xi_r^{\ast}\right)}{r} \right>_I \nonumber \\ &&\!- \frac{ \rho \Omega_0}{\hat \sigma} \frac{1}{\Gamma_1} \derivp{\ln p}{\ln r} \left< \cos \theta \sin \theta \; \vt_\theta^\prime \vt_r^{\ast} \right>_I . \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq166.png) (A.12)
(A.12)
Appendix A.1.3: Derivation of the third term of Eq. (A.4)
The derivation is similar to the previous subsection, it gives ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{third_S1_eq} &&\!- \frac{1}{2 r^2} \derivp{}{r} \left< 2 \Omega_0 r^2 \varpi \rho \cos \theta \vt_\theta^{\prime} \xi_s^{\prime \ast} \right>_R = \frac{m \rho}{2} \hat \sigma \left[1-\frac{A}{\rho \hat \sigma^2 }\derivp{p}{r}\right] \left< \vt_r^\prime \xi_s^{\ast} \right>_R \nonumber \\ &&\! -\frac{\rho}{2} \hat \sigma \left[Ar+3+\frac{m}{r \hat \sigma} \derivp{\left(r^2 \Omega_0\right)}{r}\right] \left< \sin \theta \, \vt_\phi^\prime \xi_s^{\ast} \right>_I \nonumber \\ &&\!+ \frac{\rho}{2} \left[(Ar+2) \frac{1}{r} \derivp{\left(r^2 \Omega_0\right)}{r} + \derivp{^2 \left(r^2 \Omega_0\right)}{r^2} \right] \left< \sin^2\theta \, \vt_r^\prime \xi_s^{\ast} \right>_R \nonumber \\ &&\!+ \frac{\rho}{2} \derivp{\left(r^2 \Omega_0\right)}{r} \left< \sin^2 \theta \, \left( \vt_r^\prime \derivp{\xi_s^{\ast}}{r} + \xi_s^{\ast} \derivp{\vt_r^\prime}{r} \right) \right>_R \nonumber \\ &&\!- \frac{\rho r}{2} \hat \sigma \, \left< \sin \theta \, \left( \vt_\phi^\prime \derivp{\xi_s^{\ast}}{r} + \xi_s^{\ast} \derivp{\vt_\phi^\prime}{r} \right) \right>_I + \frac{m A \Gamma_1 p}{2r^2 \hat \sigma}\left< \vt_r^\prime \derivp{\left(r^2 \xi_s^{\ast}\right)}{r} \right>_R \nonumber \\ &&\!- \frac{m c_s^2}{2 r^2 \hat \sigma} \left< \vec \nabla_\bot \cdot \left(\rho \vec \vt_\bot\right) \derivp{\left(r^2 \xi_s^{\ast}\right)}{r} \right>_R + \frac{m^2 \rho c_s^2}{2 r^3 \hat \sigma} \left< \frac{1}{\sin \theta} \; \vt_\phi \derivp{\left(r^2 \xi_s^{\ast}\right)}{r} \right>_I \nonumber \\ &&\!- \frac{r \Omega_0}{c_s^2} \derivp{p}{r} \, \left< \sin \theta \cos \theta \, \vt_\theta^\prime \xi_s^{\ast} \right>_R , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq167.png) (A.13)where we have introduced the notations
(A.13)where we have introduced the notations 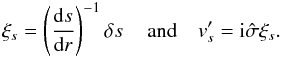 (A.14)
(A.14)
Appendix A.2: The case of low rotation and frequency limit
As described in the main text (see Sect. 4.2) we restrict ourselves in the limit of low rotation (i.e. σR ≫ Ω0) and low frequency (i.e. σR ≪ N, where N is the buoyancy frequency). Those approximations will permit us to derive tractable expressions for Eqs. (A.7), (A.12), and (A.13). To this end, the first step consists in considering the wave equations without rotation and introducing them into Eqs. (A.7), (A.12), and (A.13). This is equivalent in considering a first-order development in term of rotation for Eq. (A.4).
Projection onto the spherical harmonics is thus performed in the limit of low rotation. For one normal mode of a given m and ℓ, the eigen-displacement and velocity can be decomposed such as 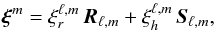 (A.15)where (Rieutord 1987)
(A.15)where (Rieutord 1987) 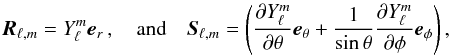 (A.16)so that
(A.16)so that 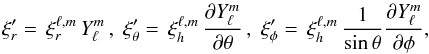 (A.17)and
(A.17)and 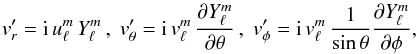 (A.18)where we used
(A.18)where we used 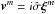 .
.
In the non-rotating limit and providing the decomposition given by Eq. (A.15), using Eqs. (51) to (54), 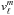 can be expressed as a function of
can be expressed as a function of 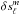 and
and 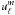 only through the relation
only through the relation ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{vellm_norot} \vt_\ell^m = r \, \mathcal{G} \, \left[\sigma_R \rho_T \frac{\delta s_{\ell}^m}{c_p} -\frac{1}{r^2} \deriv{\left( r^2 u_\ell^m\right)}{r} - \frac{u_\ell^m}{\Gamma_1} \deriv{\ln p}{r}\right] \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq178.png) (A.19)with
(A.19)with ![\appendix \setcounter{section}{1} \begin{eqnarray} \mathcal{G} = \frac{c_s^2}{r^2 \, \sigma_R^2} \left[1- \frac{S_\ell^2}{\sigma_R^2} \right]^{-1} , \; {\rm and} \quad S_\ell^2 = \ell(\ell+1) \, \frac{c_s^2}{r^2} . \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq179.png) (A.20)To go further, in the asymptotic, quasi-adiabatic limit (σR ≪ N),
(A.20)To go further, in the asymptotic, quasi-adiabatic limit (σR ≪ N), 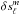 is a function of
is a function of 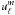 (or equivalently
(or equivalently 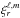 ) so that
) so that 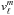 depends only on
depends only on 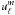 . It reads (see Godart et al. 2009, for details)
. It reads (see Godart et al. 2009, for details) 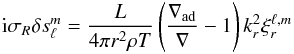 (A.21)and
(A.21)and 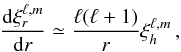 (A.22)where L is the luminosity, T the temperature, ρ the density, ∇ the temperature gradient, and ∇ad the adiabatic temperature gradient.
(A.22)where L is the luminosity, T the temperature, ρ the density, ∇ the temperature gradient, and ∇ad the adiabatic temperature gradient.
Finally, after projection onto the spherical harmonics and using Eqs. (A.19), (A.21), and (A.22), one obtains for a mode of a given angular degree (ℓ) and azimuthal degree (m) an expression of the form ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{final_F_waves_app} &&\!-\frac{1}{r^2} \derivp{}{r} r^2 \mathcal{F}_{\rm waves} = \\ &&a_{\ell,m}^{2} \left[\mathcal{A}_{\ell}^m \; \derivp{^2\left(r^2 \Omega_0 \right)}{r^2} +\mathcal{B}_{\ell}^m \; \derivp{\left(r^2 \Omega_0 \right)}{r} + \mathcal{C}_{\ell}^m \; r^2 \Omega_0 + m \hat \sigma \, \mathcal{D}_{\ell}^m \right] \nonumber , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq183.png) (A.23)with
(A.23)with ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{coeffAf} &&4 \pi \, \mathcal{A}_{\ell,m} = \frac{\rho \alpha k_r^2}{2} \, K_1 \, \vert \xi_r^{\ell,m} \vert^2 , \\ \label{coeffBf} &&\frac{4 \pi \mathcal{B}_{\ell,m}}{\rho k_r^2 \vert \xi_r^{\ell,m} \vert^2} = \frac{1}{2} \alpha \, \left(A+2 \zeta_1+\deriv{}{r}\ln\left[r^2 \zeta_2 \right]\right) \, K_1 \\ &&\quad \quad \quad \quad \quad +\frac{ r^2 \sigma_R \hat \sigma}{2 c_s^2} \mathcal{G} \zeta_0 K_1 + \frac{m^2}{2} \alpha \mathcal{G} \zeta_3 - \frac{\sigma_R}{\hat \sigma} \mathcal{G} \zeta_0 \left( m^2 + \frac{K_0}{2} \right) \nonumber \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq184.png)
![\appendix \setcounter{section}{1} \begin{eqnarray} \label{coeffCf} &&\frac{4 \pi \, \mathcal{C}_{\ell,m}}{\rho k_r^2 \vert \xi_r^{\ell,m} \vert^2} = - \frac{\sigma_R}{\hat \sigma}\frac{1}{\Gamma_1 p}\deriv{p}{r} \mathcal{G} K_2 \left( \zeta_0 - \alpha \zeta_3 \right) \\ &&\quad \quad \quad \quad \quad +\frac{\sigma_R}{\hat \sigma} \mathcal{G} \zeta_0 K_2 \, \left[\frac{\left(Ar-1\right)}{r} + \deriv{}{r}\ln \left(r \mathcal{G} k_r^2 \zeta_0\right) + \zeta_1 \right] \, , \nonumber \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq185.png) (A.26)and
(A.26)and ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{coeffDf} &&\frac{4 \pi \, \mathcal{D}_{\ell,m}}{\rho k_r^2 \vert \xi_r^{\ell,m} \vert^2} = \frac{\alpha}{2} \left[1 - \frac{A}{\rho \hat \sigma^2} \deriv{p}{r} \right] \\[3mm] &&\quad \quad \quad\; - \frac{r^2}{2} \mathcal{G} \zeta_0 \left[A+\frac{1}{r}+\zeta_1+\deriv{}{r}\ln\left(r\mathcal{G} k_r^2 \zeta_0\right) -\frac{1}{\Gamma_1} \deriv{\ln p}{r} \right] \nonumber \\[3mm] && \quad \quad \quad\;+ \frac{r^2}{2} \mathcal{G} \alpha \zeta_3 \left[A +\frac{3}{r}+2 \zeta_1+\deriv{}{r}\ln\left(r\mathcal{G} \sigma_R \zeta_3 \right) + \deriv{}{r}\ln\left(\zeta_2\right) \right] ,\nonumber \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq186.png) (A.27)where for Eq. (A.27) we use the approximation
(A.27)where for Eq. (A.27) we use the approximation 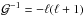 obtained in the limit
obtained in the limit 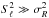 , and
, and ![\appendix \setcounter{section}{1} \begin{eqnarray} \alpha\, &=& -\frac{L}{4 \pi r^2 \rho T} \left( \frac{\nabla_{\rm ad}}{\nabla}-1 \right) \, \left(\deriv{s}{r}\right)^{-1} \nonumber \\[3mm] \zeta_0 &=& \alpha \frac{\rho_T}{c_p} \left(\deriv{s}{r}\right)\; ; \quad \zeta_1 = \frac{\ell(\ell+1)}{r} \frac{\xi_h^{\ell,m}}{\xi_r^{\ell,m}} \nonumber \\[3mm] \zeta_2 &=& \frac{\alpha k_r^2}{\sigma_R}\; ; \quad \zeta_3 = \frac{2}{r} + \zeta_1 + \frac{1}{\Gamma_1} \deriv{\ln p}{r} \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq189.png) (A.28)
(A.28)
as well as
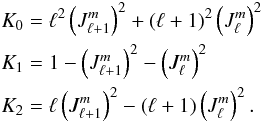 (A.29)Finally, we note that the normalization condition for spherical harmonics is
(A.29)Finally, we note that the normalization condition for spherical harmonics is 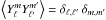 , where δ is the Kronecker symbol. Note also that the following relation have been used
, where δ is the Kronecker symbol. Note also that the following relation have been used 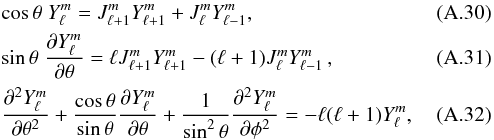 where
where ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{defs_coeffs} J_\ell^m = \left[\frac{\ell^2-m^2}{(4\ell^2-1)}\right]^{1/2} , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26042-15/aa26042-15-eq194.png) (A.33)if ℓ> | m |, and
(A.33)if ℓ> | m |, and 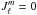 otherwise.
otherwise.
Acknowledgments
We acknowledge the ANR (Agence Nationale de la Recherche, France) program IDEE (n° ANR-12-BS05-0008) “Interaction Des Étoiles et des Exoplanètes” as well as financial support from “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, France. R.M.O. aknowledges funding for the Stellar Astrophysics Centre, provided by The Danish National Research Foundation, and funding for the ASTERISK project (ASTERoseismic Investigations with SONG and Kepler) provided by the European Research Council (Grant agreement No.: 267864).
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Ando, H. 1983, PASJ, 35, 343 [Google Scholar]
- Ando, H. 1986, A&A, 163, 97 [NASA ADS] [Google Scholar]
- Andrews, D. G., & McIntyre, M. E. 1976, J. Atmos. Sci., 33, 2031 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, D. G., & McIntyre, M. E. 1978a, J. Fluid Mech., 89, 609 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Andrews, D. G., & McIntyre, M. E. 1978b, J. Atmos. Sci., 35, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, D. G., Holton, J. R., & Leovy, C. B. 1987, Middle atmosphere dynamics (Academic Press) [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006a, in ESA SP 1306, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 33 [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006b, in 36th COSPAR Scientific Assembly, COSPAR Meet., 36, 3749 [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Huber, D., Stello, D., et al. 2010, ApJ, 713, L176 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Belkacem, K., Marques, J. P., Goupil, M. J., et al. 2015, A&A, 579, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bretherton, F. P. 1969, Quart. J. Roy. Meteorol. Soc., 95, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Mankovich, C., Bildsten, L., Christensen-Dalsgaard, J., & Paxton, B. 2014, ApJ, 788, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Ceillier, T., Eggenberger, P., García, R. A., & Mathis, S. 2013, A&A, 555, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Kjeldsen, H., Christensen-Dalsgaard, J., et al. 2011, Science, 332, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charbonnel, C., & Zahn, J.-P. 2007, A&A, 467, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christensen-Dalsgaard, J. 2008, Ap&SS, 316, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2011, Astrophysics Source Code Library [record ascl : 1109.002] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dintrans, B., & Rieutord, M. 2001, MNRAS, 324, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A., Gough, D. O., Houdek, G., & Sienkiewicz, R. 2001, MNRAS, 328, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2013, A&A, 552, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuller, J., Lecoanet, D., Cantiello, M., & Brown, B. 2014, ApJ, 796, 17 [Google Scholar]
- Godart, M., Noels, A., Dupret, M.-A., & Lebreton, Y. 2009, MNRAS, 396, 1833 [NASA ADS] [CrossRef] [Google Scholar]
- Goupil, M. J., Mosser, B., Marques, J. P., et al. 2013, A&A, 549, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grimshaw, R. 1984, Ann. Rev. Fluid Mech., 16, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Holton, J. R. 1992, An introduction to dynamic meteorology (Academic Press) [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2004, A&A, 420, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kumar, P., Talon, S., & Zahn, J.-P. 1999, ApJ, 520, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, U. 2007, in Active OB-Stars: Laboratories for Stellare and Circumstellar Physics, eds. A. T. Okazaki, S. P. Owocki, & S. Stefl, ASP Conf. Ser., 361, 45 [Google Scholar]
- Lee, U. 2008, Commun. Asteroseismol., 157, 203 [NASA ADS] [Google Scholar]
- Lee, U. 2013, PASJ, 65, 122 [NASA ADS] [Google Scholar]
- Lee, U., & Saio, H. 1993, MNRAS, 261, 415 [Google Scholar]
- Lee, U., Neiner, C., & Mathis, S. 2014, MNRAS, 443, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2003, A&A, 399, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars, Physics, Formation and Evolution of Rotating Stars: Astronomy and Astrophysics Library (Berlin, Heidelberg: Springer) [Google Scholar]
- Maeder, A., & Meynet, G. 2014, ApJ, 793, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S. 2009, A&A, 506, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S. 2013, in Lect. Notes Phys. 865, eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green (Berlin: Springer Verlag), 23 [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Palacios, A., & Zahn, J.-P. 2004, A&A, 425, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Talon, S., Pantillon, F.-P., & Zahn, J.-P. 2008, Sol. Phys., 251, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S., Decressin, T., Eggenberger, P., & Charbonnel, C. 2013, A&A, 558, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michel, E., Baglin, A., Auvergne, M., et al. 2008, Science, 322, 558 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mosser, B., Barban, C., Montalbán, J., et al. 2011, A&A, 532, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Benomar, O., Belkacem, K., et al. 2014, A&A, 572, L5 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Palacios, A. 2013, EAS Pub. Ser., 62, 227 [Google Scholar]
- Pantillon, F. P., Talon, S., & Charbonnel, C. 2007, A&A, 474, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plumb, R. A., & Ferrari, R. 2005, J. Phys. Oceanogr., 35, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H. 1981, ApJ, 245, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M. 1987, Geophys. Astrophys. Fluid Dyn., 39, 163 [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G., Gellert, M., Spada, F., & Tereshin, I. 2015, A&A, 573, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi, R. 2011, in Lect. Notes Phys. 832, eds. J.-P. Rozelot, & C. Neiner (Berlin: Springer Verlag), 305 [Google Scholar]
- Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S. 2008, in EAS PS 32, eds. C. Charbonnel, & J.-P. Zahn, 81 [Google Scholar]
- Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749 [Google Scholar]
- Townsend, R. 2014, in IAU Symp. 301, eds. J. A. Guzik, W. J. Chaplin, G. Handler, & A. Pigulski, 153 [Google Scholar]
- Townsend, R., & MacDonald, J. 2008, in IAU Symp. 250, eds. F. Bresolin, P. A. Crowther, & J. Puls, 161 [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars, 2nd edn. (University of Tokyo Press) [Google Scholar]
- Vallis, G. K. 2006, in Atmospheric and Oceanic Fluid Dynamics (Cambridge University Press), 745 [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zahn, J.-P., Talon, S., & Matias, J. 1997, A&A, 322, 320 [Google Scholar]
All Tables
Characteristics of the models computed with rotation and without rotation for comparison.
All Figures
 |
Fig. 1 Rotation rate normalised by its central value (solid line) and buoyancy frequency normalised by its maximum value (dashed dots lines) versus normalised radius for the model described in Sect. 5.1 (logarithmic scale in both axes). |
| In the text | |
 |
Fig. 2 Rate of angular momentum transport by mixed modes ( |
| In the text | |
 |
Fig. 3 Top panel: mode inertia versus mode frequencies for angular degrees ℓ = 0 and ℓ = 2. Mode inertias are computed by integrating the squared eigendisplacement over the stellar mass. Bottom panel: same as Fig. 2, except that |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.