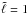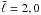| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201525734 | |
| Published online | 10 July 2015 | |
Pulsations of rapidly rotating stars
II. Realistic modelling for intermediate-mass stars
1 Stellar Astrophysics Centre, Department of Physics and AstronomyAarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: rhita-maria.ouazzani@phys.au.dk
2 Astronomy Unit, Queen Mary University of London, Mile End Road, London, E1 4NS, UK
3 Institut d’Astrophysique et de Géophysique de l’Université de Liège, Allée du 6 Août 17, 4000 Liège, Belgium
Received: 26 January 2015
Accepted: 4 May 2015
Context. Very high precision seismic space missions such as CoRoT and Kepler provide the means for testing the modelling of transport processes in stellar interiors. For some stars, such as δ Scuti, γ Doradus, and Be stars, the observed pulsation spectra are modified by rotation to such an extent that it prevents any fruitful interpretation.
Aims. Our aim is to characterise acoustic pulsation spectra of realistic stellar models in order to be able to interpret asteroseismic data from such stars.
Methods. The 2D oscillation code ACOR, which treats rotation in a non-perturbative manner, is used to study pulsation spectra of highly distorted evolved models of stars. Two-dimensional models of stars are obtained by a self-consistent method that distorts spherically averaged stellar models a posteriori, at any stage of evolution, and for any type of rotation law.
Results. Four types of modes are calculated in a very dense frequency spectrum, among which are island modes. The regularity of the island modes spectrum is confirmed and yields a new set of quantum numbers, with which an échelle diagram can be built. Mixed gravito-acoustic modes are calculated in rapidly rotating models for the first time.
Key words: asteroseismology / stars: rotation / stars: variables: delta Scuti / stars: interiors / methods: numerical / stars: early-type
© ESO, 2015
1. Introduction
Rapid stellar rotation introduces a number of phenomena that considerably complicate the modelling of stars and the study of their pulsation modes. On the one hand, centrifugal acceleration reduces local gravity, mimicking a lower mass. On the other hand, rotation induces meridional circulation (Eddington 1925) and shear and baroclinic instabilities (Mathis & Zahn 2004), which contribute to the mixing of chemical elements. Although crucial for modelling stellar structure and evolution, the problem of transport of angular momentum inside stars has not yet been fully understood.
As shown with great success for evolved low mass stars, asteroseismology is a very efficient tool for constraining the internal structure of stars. Unfortunately, for intermediate mass stars, because they do not undergo magnetic braking, rapid rotation comes into play and makes the interpretation of their seismic spectra much more delicate. Fast rotation is known to have a strong impact on stellar pulsations: the centrifugal force distorts the pulsations cavity and the Coriolis force modifies the dynamic of modes. The impact of fast rotation on observational frequency spectra is still poorly understood, and some questions need to be answered: what are the modes corresponding to each observed frequency? Which cavity inside the star do they probe? How can the physics inside this cavity be extracted? All these questions call for realistic modelling.
For slow rotators, the effect of rotation is taken into account as a small perturbation of pulsations (see e.g. Ledoux 1951 for first-order effects; the second-order effects were first explored by Vorontsov 1981, 1983, see also Dziembowski & Goode 1992; and we refer to Soufi et al. 1998 for third-order effects). But these methods, although elegant and simple to use, have their limitations (Reese et al. 2006; Suárez et al. 2010); they fail to adequately model the effects of rapid rotation in stars that show very high surface velocities, such as δ Scuti and Be stars, and also fail to model the impact of the Coriolis force on gravity modes in stars whose surface rotates slowly, but in which the pulsation periods are of the same order as their rotation period (Prot ~ Posc), such as SPB or γ Doradus stars
This is important for many stars in the CoRoT and Kepler fields of observation. Hence, if one aims at correctly extracting the internal structure from seismic observations, they need to correctly describe the effects of rotation on pulsations. In that context, the aim of this article is to investigate synthetic seismic spectra of such stars for any type of rotation profile Ω(r,θ), differential both in radius r and co-latitude θ, and to propose new seismic diagnostics in order to interpret their seismic observations.
In a previous paper, Roxburgh (2006) presented self-consistent 2D models of main-sequence stars where the angular velocity is differential both in depth and in latitude, and for different stages of evolution. The adiabatic oscillations of stars are only governed by the acoustic structure of the star, i.e. the hydrostatic structure: density, pressure, gravity, and adiabatic exponent. The pulsations do not depend on whether the star is in thermal equilibrium. The self-consistent method allows such an acoustic structure to be determined.
In the first paper (Ouazzani et al. 2012, hereafter Paper I), we presented the Adiabatic Code of Oscillation including Rotation (ACOR) and its results for a 2D polytropic model. Here, we report on pulsation modelling of an evolved distorted model of an intermediate mass star, typical of a δ Scuti star. Section 2 introduces the method applied to obtain distorted models of stars following Roxburgh (2006). Section 3 is dedicated to the pulsation modelling with an emphasis on how the ACOR code was improved in order to compute the pulsations of realistic distorted stellar models. In Sect. 4 we present an application to a typical model of intermediate mass star. Finally, Sect. 5 reports on regularities revealed in the theoretical pulsation spectrum of the model, and conclusions are given in Sect. 6.
2. Self-consistently distorted model
Stellar evolution in two dimensions has yet to be modelled. Progress is being made in this field, for instance by the ESTER project (for Evolution STEllaire en Rotation, Rieutord 2007; Espinosa Lara & Rieutord 2013). The ultimate goal of the ESTER project is to solve the hydrodynamics equations in two dimensions along with the chemical evolution. Currently ESTER can only model the steady state with regard to evolution, the central chemical composition being specified ad hoc.
An alternative to this approach is to calculate spherically averaged stellar evolution models, then distort the models a posteriori using a self-consistent method. The first self-consistent model was developed for rapidly rotating polytropes and white dwarfs by James (1964), see also Hurley & Roberts (1964), closely followed by a two-zone model by Monaghan & Roxburgh (1965) and two-zone models for rapidly rotating main-sequence stars by Roxburgh et al. (1965). In parallel, Ostriker & Mark (1968) developed and used such an approach to compute uniformly and differentially rotating polytropic stellar models. The method was then improved by including more realistic input physics (Jackson 1970), but only applied to massive stars because convergence problems arose when dealing with low mass stars owing to the high concentration of the central mass (Clement 1978). Jackson et al. (2004) and MacGregor et al. (2007) solved this problem and successfully applied the method to intermediate mass stars. In their models, the only remaining limitation is the chemical homogeneity and conservative laws of rotation.
We present here such an approach based on a method established by Roxburgh (2006) which allows the computation of non-homogeneous, fully differentially rotating stellar models. It consists of building the 2D acoustic structure of a rotating star in hydrostatic equilibrium starting with spherical profiles of the structural quantities using an iterative scheme.
2.1. Acoustic structure
We note that the adiabatic pulsations of stars are solely governed by their acoustic (i.e. hydrostatic) structure: the internal density ρ, pressure p, and gravity ∇Φ, together with the adiabatic exponent Γ1. As shown in Roxburgh (2006), for rotating stars the 2D hydrostatic structure ρ(r,θ), P(r,θ), and gravitational potential Φ(r,θ) are determined solely by the angular velocity profile Ω(r,θ), the density ρm(r) = ρ(r,θm), and the surface pressure Ps along any one angle θm. The adiabatic exponent Γ1(r,θ) is determined from ρ(r,θ), P(r,θ), and the 2D hydrogen profile X(r,θ). If we assume a particular model of chemical elements transport (which is the case in this work: X is constant on surfaces of constant entropy) then it is sufficient to have Xm(r) along θm. The method then consists of generating acoustic models of rotating stars with any Ω(r,θ) by considering that the radial density and hydrogen abundance along the angle θm take the values from a spherically averaged model, yielded by 1D evolution modelling. The reference angle θm is taken here as the root of the second-order Legendre polynomial: 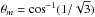 .
.
The scheme is the following:
-
1.
Take as an initial estimate ρ(r,θ) = ρm(r).
-
2.
Solve the Poisson equation
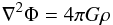 (1)for Φ(r,θ) given ρ(r,θ), together with the proper boundary conditions. This is done by expanding Φ(r,θ) and ρ(r,θ) into a series of Legendre polynomials. The density decomposition is found by imposing that ρ(r,θ) = ρ(ri,θj) at each grid point (ri,θj). Given that, the coefficients of the gravitational potential expansion are determined from an integral representation of the solution of the Poisson equation and the upper boundary condition projected onto the Legendre polynomials (for a detailed solution, see Roxburgh 2004).
(1)for Φ(r,θ) given ρ(r,θ), together with the proper boundary conditions. This is done by expanding Φ(r,θ) and ρ(r,θ) into a series of Legendre polynomials. The density decomposition is found by imposing that ρ(r,θ) = ρ(ri,θj) at each grid point (ri,θj). Given that, the coefficients of the gravitational potential expansion are determined from an integral representation of the solution of the Poisson equation and the upper boundary condition projected onto the Legendre polynomials (for a detailed solution, see Roxburgh 2004). -
3.
Solve the curl of the hydrostatic equilibrium
![\begin{eqnarray} \vec{curl} \left(\rho \left[{\vec \nabla} \Phi - \Omega^2 {\vec \varpi} \right] \right) = {\vec 0} \label{curlHE} \end{eqnarray}](/articles/aa/full_html/2015/07/aa25734-15/aa25734-15-eq26.png) (2)for ρ(r,θ) given Φ(r,θ) from step 2, where ϖ = (rsinθ,rcosθ,0) is the vectorial distance from the rotation axis. This is done in two steps: first, we look for the characteristic curves r(θ) along which the partial differential equation is an ordinary differential equation (ODE), and then solve Eq. (2) as an ODE along these curves (for a detailed solution, see Roxburgh 2006).
(2)for ρ(r,θ) given Φ(r,θ) from step 2, where ϖ = (rsinθ,rcosθ,0) is the vectorial distance from the rotation axis. This is done in two steps: first, we look for the characteristic curves r(θ) along which the partial differential equation is an ordinary differential equation (ODE), and then solve Eq. (2) as an ODE along these curves (for a detailed solution, see Roxburgh 2006). -
4.
Then this density profile is injected at step 2, and steps 2 and 3 are iterated until convergence of the equatorial and the polar radii.
-
5.
The characteristic curves turn out to be the isobars. Once the characteristic curves are determined, all we need is the value of P along a radius at any angle θ and P(r,θ) is constant along the characteristic curves.
-
6.
To determine the 2D profile of the adiabatic exponent given P(r,θ) and ρ(r,θ), we assume that X(r,θ) is constant on isobars (justification for this assumption follows in Sect. 2.2). We then solve the equation of state for Γ1 = Γ1(P,ρ,Xm), Xm being the value of the hydrogen mass fraction at the reference angle θm. This gives Γ1 along the isobars. For further details we refer to Roxburgh (2006).
2.2. Discussion
For the algorithm to converge, several approximations must be assumed, the first of which concerns the structure of surface layers. In stars that are differentially rotating, the fluid is baroclinic. This means that surfaces of constant pressure do not correspond to surfaces of constant density. Hence the solution of the algorithm presented in the previous section may have ρ = 0 on surfaces of P> 0. For the solution to be well behaved at the surface, we need curl(Ω2ϖ) = 0 in the surface layers. This is ensured by taking Ω as constant in the outer layers of the star.
Moreover, in this region of low density and pressure, the meridional circulation driven by the rotation can become very large, and induce small-scale turbulence. We assume here that the time scale of the circulation is very small in these layers, so that transport of angular momentum is rapid, and the system reaches a steady state (Ω constant near the surface).
Finally, in order to retrieve the adiabatic exponent Γ1, we have assumed that the hydrogen mass fraction X is constant on isobars. However, in the fully ionised interior of most stars where, due to nuclear reactions, X differs from its initial value X0, the values of Γ1 are only weakly dependent on X. On the other hand, in the outer layers where Γ1 can vary considerably and in the absence of diffusion, X is unchanged from its initial value X0. Therefore, X constant on isobars seems to be a reasonable assumption here.
3. Pulsation modelling
As mentioned above, for the computation of pulsations we only require the hydrostatic structure of the star and not the thermal structure. We compute the oscillation modes as the adiabatic response of the structure to small perturbations, i.e. of the density, pressure, gravitational potential, and velocity field, using the Eulerian formalism.
The ACOR code was developed for this purpose and is presented in Paper I. Here we report on new improvements that were necessary to implement in order to compute the pulsations of non-barotropic models of stars, which present steeper gradients around the poles than near the equator.
3.1. A new coordinate system
The method reported in Sect. 2 yields a 2D stellar model which quantities are expressed on the characteristic curves (isobars). In order to avoid potential uncertainties caused by interpolation, the idea is to keep the structural quantities expressed on the isobars in as many internal layers as possible when computing the pulsations of such models. Nevertheless, to simplify boundary conditions – at the centre, where the eigenfunctions should behave spherically, and at infinity, where the gravitational potential should vanish – a new hybrid coordinate system is proposed. The new radial coordinate ζ is expressed as a bijective, monotonic, and continuously differentiable function of the radius r. From spherical coordinates at the centre, the system progressively matches isobars, and from the distorted stellar surface becomes spherical again outside the star. Therefore, we adopted a multidomain approach, which consists in dividing the physical space into three domains whose boundaries correspond to the model’s discontinuities: one central domain V0 whose upper boundary is included in the convective core, one domain V1 that encloses the stellar surface, and one external domain V2 that is bounded by the stellar surface and an external sphere.
DomainV0 from ζ = 0 to ζ = xc,eq
Here xc,eq is the ratio of the radius at the edge of the convective core over the total radius of the star, both at equator (see Fig. 1 the inner domain, encircled by the red boundary). In Paper I, where polytropic structural models were treated, the bijective transformation continuously goes from spherical at the centre to matching the stellar surface without intermediately adopting the isobars. In the case of a non-barotropic model of star, isobars are closer to each other at the poles than at the equator. To ensure continuity of ∂ζr over the boundary ζ = xc,eq, ∂ζr should depend on the latitude when ζ goes to xc,eq. Hence, the following transformation has been developed, ![\begin{eqnarray} \label{Eq_zeta_centre} \forall \, \zeta_{\rm c} &=& \zeta/{x_{\rm c,eq}} \, \in \, \left[0;1\right] \, , \forall \, \theta \, \in \, \left[0;\pi\right] \, , \\ x(\zeta,\theta) & =& {x_{\rm c,eq}} \, \left[\zeta_{\rm c} \, + \, \frac{5 \zeta_{\rm c}^3-3\zeta_{\rm c}^5}{2} \, \left( \frac{x_{\rm c} (\theta)}{x_{\rm c,eq}} - 1 \right) \right. \nonumber \\ &&\qquad\quad\ \ \, + \, \left. \frac{\zeta_{\rm c}^5-\zeta_{\rm c}^3}{2} \, \left( \frac{1}{x_{\rm c,eq}} \, \frac{\partial x_{\rm c}}{\partial \zeta}(\theta) - 1 \right) \right], \nonumber \end{eqnarray}](/articles/aa/full_html/2015/07/aa25734-15/aa25734-15-eq45.png) (3)where x is the fractional radius (r/R), and ∂xc/∂ζ is the derivative of x with respect to ζ at ζ = xc,eq. The first term in brackets enforces a spherical behaviour for x(ζ,θ) near the center, the second term allows to match the isobar xc(θ) located at ζc = 1, and the last term ensures that the derivative of x(ζ,θ) at ζc = 1 matches ∂ζxc(θ). We chose the simplest functions that fulfilled the constraints. Odd polynomials of ζc were chosen because they go faster toward zero at the centre. In practice, xc,eq can take any value smaller than the actual fractional radius of the μ gradient location, both for low mass and massive stars.
(3)where x is the fractional radius (r/R), and ∂xc/∂ζ is the derivative of x with respect to ζ at ζ = xc,eq. The first term in brackets enforces a spherical behaviour for x(ζ,θ) near the center, the second term allows to match the isobar xc(θ) located at ζc = 1, and the last term ensures that the derivative of x(ζ,θ) at ζc = 1 matches ∂ζxc(θ). We chose the simplest functions that fulfilled the constraints. Odd polynomials of ζc were chosen because they go faster toward zero at the centre. In practice, xc,eq can take any value smaller than the actual fractional radius of the μ gradient location, both for low mass and massive stars.
Domain V1 from ζ = xc,eq to ζ = 1 In this domain, constant ζ corresponds to the isobars, with ζ = x(θm). The value of x(ζ,θ) is determined by the characteristic equation.
 |
Fig. 1 Coordinate system used in ACOR. V0 corresponds to a region inside the convective core, V1 extends from a boundary inside the convective core to the stellar surface, and V2 encompasses the star. |
Domain V2 from ζ = 1 to ζ = 2 In V2 the coordinate system goes gradually from the distorted stellar surface to a sphere. A new transformation is proposed that ensures the continuity of r and ∂ζr at the surface of the star ζ = 1. The same mathematical form as for Eq. (3) applies here, except that Eq. (4) is not taken in zero, and so there is no need for odd polynomials. The simplest form which fulfils the constrains is: ![\begin{eqnarray} \label{Eq_zeta_ext} &&\forall \, \zeta \, \in \, \left[1;2\right] \, , \forall \, \theta \, \in \, \left[0;\pi\right], \\ && x(\zeta,\theta) \, = \, \zeta \, + \, \left(2 \zeta^3-9 \zeta^2+12 \zeta -4\right) \, \left( {x_{\rm s}(\theta)} - 1 \right) \nonumber \\ &&\hspace*{17mm}+ \, \left(\zeta^3-5 \zeta^2+8 \zeta-4\right) \, \left( \frac{{\rm d} x_{\rm s}}{\rm d \zeta}(\theta) - 1 \right) \nonumber . \end{eqnarray}](/articles/aa/full_html/2015/07/aa25734-15/aa25734-15-eq58.png) (4)In the two domains V0 and V2 where the coordinate system does not rely on isobars, the structural quantities are interpolated on the new grid (ζ,θ) by the help of cubic polynomial interpolation over two grid points.
(4)In the two domains V0 and V2 where the coordinate system does not rely on isobars, the structural quantities are interpolated on the new grid (ζ,θ) by the help of cubic polynomial interpolation over two grid points.
3.2. Pulsation computations
These computations consist in solving the hydrodynamics equations perturbed by Eulerian fluctuations, by direct integration of the 2D problem. The numerical method is based on a spectral multidomain method which expands the angular dependence of eigenfunctions into spherical harmonics series, and whose radial treatment is particularly well adapted to the behaviour of equilibrium quantities in evolved models (at the interface of convective and radiative regions, and at the stellar surface). The radial differentiation is made by means of a sophisticated finite difference method, which is accurate up to the fifth order in terms of the radial resolution (developed by Scuflaire et al. 2008).
This code has been validated by comparison with the results of Reese et al. (2006) for polytropic models. The agreement between the two codes is excellent. All details concerning the ACOR code are given in Paper I.
4. An example: M = 2 M⊙, Xc = 0.35, Ω = Ω(r)
4.1. Stellar model
As an illustrative example we take Ω = Ωsω(x) as a function only of radius x = r/R0, where ω(x), shown in Fig. 2, decreases from a value of 3 in a central core to 1 in the outer envelope, and has continuous derivatives. As mentioned in Sect. 2.2, with Ω constant in the outer layers the solution is well behaved at the surface. For the spherically averaged model we took a star of 2 M⊙ with an initial composition X = 0.72, Z = 0.02, evolved to the stage where Xc = 0.35. The average centrifugal force 2Ω2r/ 3 was added to the hydrostatic equation, the remaining equations being those of spherical stars. The dimensionless angular velocity ω(x) was taken as fixed throughout the evolution and Ωs determined by requiring conservation of angular momentum for the star as a whole. The initial model had radius R ≃ 2.5 R⊙ and Ωs = 4.3 × 10-5 rad s-1 corresponding to an equatorial velocity of ≃80 km s-1. The star was evolved to a central hydrogen abundance Xc = 0.35, at which stage Ωs = 1.296 × 10-4 rad s-1.
The models were produced using the STAROX evolution code (see Roxburgh 2008) with the OPAL2001 equation of state (Rogers & Nayfonov 2002), OPAL GN93 Iglesias & Rogers (1996) and Alexander & Ferguson (1994) opacities, NACRE (Angulo et al. 1999) nuclear reaction rates, and a radial mesh in mass with N = 2000 points. The spherically averaged model was taken to represent the 2D model along the angle 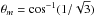 , and the procedure described in Sect. 2.1 followed to produce the 2D model. The angular mesh had Nj = 240 points and the mesh in domain V2 for solving Poisson’s equation had Nk = 500 points. The flatness of the model 1−Rpol/Req ≃ 0.25, the equatorial rotational velocity Veq = 282.3 km s-1, and the ratio of centrifugal force to gravity at the surface equator
, and the procedure described in Sect. 2.1 followed to produce the 2D model. The angular mesh had Nj = 240 points and the mesh in domain V2 for solving Poisson’s equation had Nk = 500 points. The flatness of the model 1−Rpol/Req ≃ 0.25, the equatorial rotational velocity Veq = 282.3 km s-1, and the ratio of centrifugal force to gravity at the surface equator 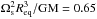 .
.
 |
Fig. 2 Radial profile of the rotation angular velocity scaled by the equatorial angular velocity at the surface. Ω is constant on isobars but differential in the normal direction. Therefore, the model is not barotropic. |
4.2. The pulsation modes
Given the rotation velocity (Ω = 0.81Ωk at the surface, where 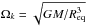 ) a convergence study found that 40 spherical harmonics were necessary in the spectral expansion of eigenmodes. In the present article we confine our analysis to axisymmetric modes, although there is no restriction to such modes in the ACOR code. Odd and even modes with m = 0 are presented here. The parity of a mode p is given by p = (ℓ + | m |) mod 2. Therefore, modes with p = 0 are called even modes, and modes with p = 1 odd modes. For axisymmetric modes, odd modes (resp. even) are expanded on spherical harmonics series with only odd (resp. even) values of angular degree ℓ.
) a convergence study found that 40 spherical harmonics were necessary in the spectral expansion of eigenmodes. In the present article we confine our analysis to axisymmetric modes, although there is no restriction to such modes in the ACOR code. Odd and even modes with m = 0 are presented here. The parity of a mode p is given by p = (ℓ + | m |) mod 2. Therefore, modes with p = 0 are called even modes, and modes with p = 1 odd modes. For axisymmetric modes, odd modes (resp. even) are expanded on spherical harmonics series with only odd (resp. even) values of angular degree ℓ.
In this study, we have computed axisymmetric eigenmodes with frequencies ranging from 250 μHz to 750 μHz (10–30Ωk); by scanning the frequency interval we made sure that all the axisymmetric modes with contributions up to ℓ = 80 are found. The resulting pulsation spectrum presents around 800 modes, which on average corresponds to one mode every 0.63 μHz. It is shown in Fig. 3, where we have simulated each frequency peak by a Lorentzian of width 0.05 μHz and height 1. The quantity on the y-axis of that graph has no significance. The different amplitudes are to be attributed to the fact that when two frequencies are closer than 0.05 μHz, their amplitudes add up.
 |
Fig. 3 Simulated spectrum of axisymmetric modes for the model presented Sect. 4; it contains the eigenfrequencies of odd and even island modes (in blue and red, respectively), as well as modes trapped only in the μ gradient, chaotic modes, and whispering-gallery modes in grey. |
Fast rotation drastically modifies the geometry of the pulsation modes; their geometric structure determines their visibility, as well as the region they probe. Therefore, a correct characterisation of the geometry of different modes is important for the asteroseismology of fast rotators. The geometry of each of the 800 modes have been visualised (based on their kinetic energy in a meridional plane) allowing a careful characterisation. Depending on the region of the frequency spectrum explored by our computations, four geometric classes are found.
At low frequency, we mostly find modes trapped in the region of sharp variation of the mean molecular weight, characterised by a sharp feature in the Brunt-Väisälä frequency. These modes are counterparts of high-order g-modes in the rapidly rotating case. As in the non-rotating case, their wave number is proportional to 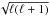 . Therefore, since we include components with ℓ up to 80 here, g-modes with high ℓ components are very numerous, even in the high frequency range. Their amplitude is confined around the central region, they have negligible amplitude in outer layers, and we expect them to undergo radiative damping; therefore, they should not be detected observationally.
. Therefore, since we include components with ℓ up to 80 here, g-modes with high ℓ components are very numerous, even in the high frequency range. Their amplitude is confined around the central region, they have negligible amplitude in outer layers, and we expect them to undergo radiative damping; therefore, they should not be detected observationally.
At higher frequency, we find whispering-gallery modes, chaotic modes, and island modes such as those computed in homogeneous models of stars by Lignières et al. (2006). Whispering-gallery modes are the counterpart of high degree acoustic modes in the rapidly rotating case. They probe the outer layers of the star, but as they show very low visibility factors, they might not be detected.
Chaotic modes have no counterparts in the non-rotating case. They have been computed only in very high rotating models of stars (Lignières & Georgeot 2009). Their spatial distribution does not show a simple symmetry. They have significant amplitude in the whole of the stellar interior. The lack of symmetry should result in a low cancellation factor. Therefore, these modes are expected to be detected observationally.
Whispering-gallery and chaotic modes correspond, respectively, to high and intermediate values of ℓ− | m | at zero rotation (Lignières et al. 2006).
Island modes are counterparts of low degree acoustic modes in the rapidly rotating case. They probe outer layers of the star, and present good geometric visibility factors. Therefore they should be easily detected observationally. The geometry of such a mode is presented in Fig. 4 with the distribution of kinetic energy of the mode in a meridional plane. As mentioned in Reese et al. (2008), if their non-rotating counterpart is characterised by the known quantum numbers (n,ℓ,m), the geometry of these island modes follows a different distribution characterised by a new set of quantum numbers 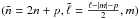 , where p indicates the mode’s parity. The two new quantum numbers
, where p indicates the mode’s parity. The two new quantum numbers 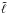 and
and 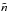 correspond respectively to the number of nodes along and perpendicular to the ray path (Fig. 4), see Reese et al. (2008, 2009b).
correspond respectively to the number of nodes along and perpendicular to the ray path (Fig. 4), see Reese et al. (2008, 2009b).
 |
Fig. 4 Kinetic energy ρ | vpuls | 2 in a meridional plane, of an |
Some island modes in the explored frequency range are found to be mixed, i.e. they behave as pressure modes in the envelope and gravity modes near the core. In Fig. 5 we give the geometry distribution of a mixed mode in a meridional plane, illustrated by the kinetic energy divided by the square root of the density and multiplied by the square of the distance to the axis. Mixed non-radial modes have been theoretically known since Osaki (1975) discovered them in a non-rotating model of a 10 M⊙ star on the main sequence. For the first time, we show that such gravito-acoustic mixed modes are present in the theoretical spectrum of rapidly rotating stellar models too. Indeed, as a star evolves, the Brunt-Väisälä frequency, i.e. the maximum frequency of trapped g-modes, increases owing to the increasing core density. Therefore, the frequencies of g-modes become comparable to those of p modes, and some of them adopt a mixed character. These mixed modes are very useful because, unlike pure g-modes, they have large enough surface amplitudes to be detected and yet are sensitive to the structure of the core. In the space photometry era, these mixed modes have been intensively observed in evolved solar-type stars, first with CoRoT (Deheuvels et al. 2010) and with Kepler (e.g. Campante et al. 2011; Mathur et al. 2011). These modes enabled one to probe the structure of the core of subgiants (Deheuvels & Michel 2011) and red giants (Beck et al. 2011; Mosser et al. 2011), thus making it possible to discriminate between evolutionary scenarios (shell hydrogen or core helium burning, see e.g. Mosser et al. 2012). The detection of mixed modes that are split by rotation also allow the rotation rate of stars to be probed even in their deepest interior (Beck et al. 2012; Deheuvels et al. 2012). The situation of fast rotating intermediate mass stars is much less favourable, not only because they are not solar-like pulsators, but also because the impact of rapid rotation on their spectra has been poorly modelled. Once stellar and pulsations models are adapted to such an impact, the use of mixed modes as a probe for the interior of rapidly rotating stars now seems reachable in the near future.
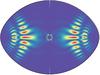 |
Fig. 5 Kinetic energy divided by the square root of the density and multiplied by the square of the distance to the axis in a meridional plane, for an axisymmetric mixed island mode of |
5. Island mode regularity
Low 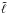 island modes are expected to be the most visible modes in the seismic spectra of rapidly rotating stars since they are the rotating counterparts to modes with low ℓ values. Their frequency organisation has been studied in Lignières et al. (2006) in non-distorted polytropic models (of index n = 3), Lignières & Georgeot (2008, 2009) using ray dynamics in polytropic models, Reese et al. (2008) in fully distorted polytropic models, Reese et al. (2009a) for homogeneous models distorted using the SCF method (MacGregor et al. 2007), and Pasek et al. (2012) who have developed an semi-analytic formula for their spectrum under the Cowling approximation, and neglecting the Coriolis force.
island modes are expected to be the most visible modes in the seismic spectra of rapidly rotating stars since they are the rotating counterparts to modes with low ℓ values. Their frequency organisation has been studied in Lignières et al. (2006) in non-distorted polytropic models (of index n = 3), Lignières & Georgeot (2008, 2009) using ray dynamics in polytropic models, Reese et al. (2008) in fully distorted polytropic models, Reese et al. (2009a) for homogeneous models distorted using the SCF method (MacGregor et al. 2007), and Pasek et al. (2012) who have developed an semi-analytic formula for their spectrum under the Cowling approximation, and neglecting the Coriolis force.
The first difficulty with studying the spectrum of island modes is to be able to identify them among all the other type of modes present in the spectra of rapidly rotating stars (chaotic and whispering-gallery modes). This was done by finding a few island modes in the high frequency regime, identifying their spatial geometry (i.e. 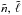 , m is fixed) determining their frequency spacings, and then visually checking the modes to see which frequencies are around the expected one.
, m is fixed) determining their frequency spacings, and then visually checking the modes to see which frequencies are around the expected one.
5.1. Asymptotic frequencies
Reese et al. (2008) suggested a new asymptotic formula for island modes, 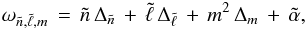 (5)which they have tested for the SCF homogeneous models. Based on our synthetic spectrum of axisymmetric modes we were able to determine the parameters
(5)which they have tested for the SCF homogeneous models. Based on our synthetic spectrum of axisymmetric modes we were able to determine the parameters 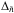 ,
, 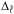 , and
, and 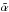 of this asymptotic formula based on a fit on our frequency spectrum. This fit has been carried out for the fully rotating 2D model, as well as for the spherical non-rotating model corresponding to the structural quantities of the 2D model at the latitude
of this asymptotic formula based on a fit on our frequency spectrum. This fit has been carried out for the fully rotating 2D model, as well as for the spherical non-rotating model corresponding to the structural quantities of the 2D model at the latitude 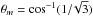 . The results are shown in Table 1.
. The results are shown in Table 1.
In order to highlight this regularity, one can also plot what we call an échelle diagram which is the spectrum folded about the spacing 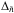 . The result is shown in Fig. 6, which gives the échelle diagram for axisymmetric island modes of different parity and for
. The result is shown in Fig. 6, which gives the échelle diagram for axisymmetric island modes of different parity and for 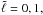 and 2. For a given parity, the mode frequencies line up along ridges of given
and 2. For a given parity, the mode frequencies line up along ridges of given 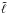 values. This feature is of course not surprising as island modes are acoustic modes, and once the shape of their cavity is known, their spectrum is determined by the stratification of the fluid in the cavity.
values. This feature is of course not surprising as island modes are acoustic modes, and once the shape of their cavity is known, their spectrum is determined by the stratification of the fluid in the cavity.
 |
Fig. 6 Échelle diagram for axisymmetric island modes of different degree |
As pointed out in non-rotating models of evolved low mass stars, when acoustic modes acquire a gravity contribution during an avoided crossing for instance, their frequencies have the tendency to deviate from the regular pattern defined by the large spacing. That is what is causing the deviation at low frequency in Fig. 6, where the corresponding eigenmodes clearly show trapping in the μ gradient region. For instance, the lowest frequency mode on the odd 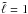 ridge is the mixed mode whose kinetic energy distribution is given in Fig. 5.
ridge is the mixed mode whose kinetic energy distribution is given in Fig. 5.
5.2. Theoretical Large Separation
In previous works of full modelling (Reese et al. 2008, 2009b) the hypothesis that the pseudo-large separation 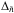 is a measure of the travel time in the island modes cavity was mentioned, but never actually tested. The difficulty here is to find the ray path for island modes geometry. The approach adopted consists in finding the underlying ray path for our model based on the topology of the 2D eigenfunctions. For the sake of simplicity, we assume that the underlying ray path corresponds to the local maxima of the pressure perturbation for an
is a measure of the travel time in the island modes cavity was mentioned, but never actually tested. The difficulty here is to find the ray path for island modes geometry. The approach adopted consists in finding the underlying ray path for our model based on the topology of the 2D eigenfunctions. For the sake of simplicity, we assume that the underlying ray path corresponds to the local maxima of the pressure perturbation for an 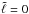 island mode. This yields the μ(ζ) curve plotted in red in Fig. 7, where μ = cosθ and ζ the pseudo-radial coordinate. The theoretical large separation is then given by
island mode. This yields the μ(ζ) curve plotted in red in Fig. 7, where μ = cosθ and ζ the pseudo-radial coordinate. The theoretical large separation is then given by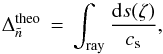 (6)where cs is the sound speed along the ray, and ds corresponds to the arclength along the ray. This a method allowed us to determine a theoretical large frequency separation of
(6)where cs is the sound speed along the ray, and ds corresponds to the arclength along the ray. This a method allowed us to determine a theoretical large frequency separation of 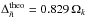 , which is compatible with the large separation computed from the theoretical seismic spectrum by averaging the individual values
, which is compatible with the large separation computed from the theoretical seismic spectrum by averaging the individual values 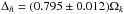 , but not within the dispersion.
, but not within the dispersion.
This is a rough estimate of the inverse of the travel time on the island modes ray paths, but this confirms that this new spacing 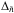 is an equivalent of the large separation Δν of acoustic modes without rotation. Once island modes are identified in the spectrum,
is an equivalent of the large separation Δν of acoustic modes without rotation. Once island modes are identified in the spectrum, 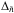 allows the sound speed profile to be constrained in the outer radiative envelope of these rapidly rotating intermediate-mass stars. The other way around, in theoretical studies, it can also be of great help in order to track island modes in synthetic spectra by pointing toward the right pattern.
allows the sound speed profile to be constrained in the outer radiative envelope of these rapidly rotating intermediate-mass stars. The other way around, in theoretical studies, it can also be of great help in order to track island modes in synthetic spectra by pointing toward the right pattern.
Most of the uncertainty of this method lies in the determination of the ray path from the eigenfunctions of the modes. Of course the most accurate way to compute the ray path is by actually studying the dynamics of acoustics rays (as is done in Lignières & Georgeot 2009, for polytropes), but so far it has never been done in a realistic model, and without making certain assumptions, such as that the Coriolis force does not affect acoustic-ray dynamics very much (Reese et al. 2006, have shown that its effects are weak even on relatively low radial orders), and the Cowling approximation. The presence of mixed modes in our spectrum of a realistic mid-main-sequence model requires one to drop these assumptions. We leave this study for future work.
6. Conclusions
A new modelling chain which computes non-radial adiabatic pulsations in rapidly rotating distorted models of stars has been presented. The first step consists in building a distorted stellar model starting with a spherically averaged one for arbitrary rotation laws (Roxburgh 2006). The second step is the computation of its stellar pulsations by fully accounting for the impact of centrifugal distortion and for the effect of the Coriolis force on mode dynamics (using the 2D non-perturbative oscillation code ACOR, see Paper I). In rotationally distorted stars, the structural gradients are steeper near the poles than near the equator. To handle this, a new coordinate system was developed that greatly simplifies the computations, and disminishes numerical sources of uncertainties, which allowed us to compute for the first time the synthetic spectrum of a realistic distorted model of a non-homogeneous star evolved on its main sequence.
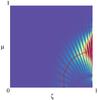 |
Fig. 7 Kinetic energy distribution of an |
This approach has been applied to a 2 M⊙ star evolved midway on its main sequence (Xc = 0.35). The simulations yield a wealth of modes with a spectrum denser than its non-rotating counter-part. Four types of modes have been computed, among which island modes that are expected to be the most visible ones. The regularity of island modes is confirmed in the general case of non-barotropic stratified stellar models. In particular the spectrum is organised around the large spacing 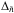 , and it is possible to build échelle diagrams for island modes. Once the shape of the cavity is correctly defined, it is possible to retrieve a theoretical value of this large spacing as the inverse of the travel time along the mode path that is compatible with the value computed from the spectrum.
, and it is possible to build échelle diagrams for island modes. Once the shape of the cavity is correctly defined, it is possible to retrieve a theoretical value of this large spacing as the inverse of the travel time along the mode path that is compatible with the value computed from the spectrum.
Moreover, we have shown that, just like their non-rotating counterparts, the island modes can be involved in avoided crossings with modes trapped near the core. Such mixed modes (in the sense of gravito-acoustic modes) deviate from the regular pattern defined by the large spacing  .
.
Finally, several seismic diagnostics based on these island modes arise. The large spacing of the island-mode spectrum is related to the stratification of the star in the outer radiative envelope. The deviation from the regular spacing due to avoided crossings should allow the evolutionary status of the star to be constrained.
Acknowledgments
R.M.O. thanks D. Reese and F. Lignieres for fruitful discussions, as well as J. Christensen-Dalsgaard for careful reading which helped to improve the manuscript. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant DNRF106). The research is supported by the ASTERISK project (ASTERoseismic Investigations with SONG and Kepler) funded by the European Research Council (Grant agreement No. 267864). I.W.R. gratefully acknowledges support from the Leverhulme Foundation under grant EM-2012-035/4.
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Campante, T. L., Handberg, R., Mathur, S., et al. 2011, A&A, 534, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clement, M. J. 1978, ApJ, 222, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., & Michel, E. 2011, A&A, 535, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Bruntt, H., Michel, E., et al. 2010, A&A, 515, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A., & Goode, P. R. 1992, ApJ, 394, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1925, The Observatory, 48, 73 [NASA ADS] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2013, A&A, 552, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurley, M., & Roberts, P. H. 1964, ApJ, 140, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, S. 1970, ApJ, 161, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, S., MacGregor, K. B., & Skumanich, A. 2004, ApJ, 606, 1196 [NASA ADS] [CrossRef] [Google Scholar]
- James, R. A. 1964, ApJ, 140, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, P. 1951, ApJ, 114, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Lignières, F., & Georgeot, B. 2008, Phys. Rev. E, 78, 016215 [NASA ADS] [CrossRef] [Google Scholar]
- Lignières, F., & Georgeot, B. 2009, A&A, 500, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lignières, F., Rieutord, M., & Reese, D. 2006, A&A, 455, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacGregor, K. B., Jackson, S., Skumanich, A., & Metcalfe, T. S. 2007, ApJ, 663, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S., & Zahn, J. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Handberg, R., Campante, T. L., et al. 2011, ApJ, 733, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Monaghan, J. J., & Roxburgh, I. W. 1965, MNRAS, 131, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Barban, C., Montalbán, J., et al. 2011, A&A, 532, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osaki, J. 1975, PASJ, 27, 237 [NASA ADS] [Google Scholar]
- Ostriker, J. P., & Mark, J. 1968, ApJ, 151, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Ouazzani, R.-M., Dupret, M.-A., & Reese, D. R. 2012, A&A, 547, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasek, M., Lignières, F., Georgeot, B., & Reese, D. R. 2012, A&A, 546, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reese, D., Lignières, F., & Rieutord, M. 2006, A&A, 455, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reese, D., Lignières, F., & Rieutord, M. 2008, A&A, 481, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reese, D. R., MacGregor, K. B., Jackson, S., Skumanich, A., & Metcalfe, T. S. 2009a, A&A, 506, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reese, D. R., Thompson, M. J., MacGregor, K. B., et al. 2009b, A&A, 506, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M. 2007, ArXiv e-prints [arXiv:astro-ph/0702384] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Roxburgh, I. W. 2004, A&A, 428, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I. W. 2006, A&A, 454, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I. W. 2008, Ap&SS, 316, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Roxburgh, I. W., Griffith, J. S., & Sweet, P. A. 1965, Z. Astrophys., 61, 203 [Google Scholar]
- Scuflaire, R., Montalbán, J., Théado, S., et al. 2008, Ap&SS, 316, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Soufi, F., Goupil, M. J., & Dziembowski, W. A. 1998, A&A, 334, 911 [NASA ADS] [Google Scholar]
- Suárez, J. C., Goupil, M. J., Reese, D. R., et al. 2010, ApJ, 721, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Vorontsov, S. V. 1981, Sov. Astron., 25, 724 [NASA ADS] [Google Scholar]
- Vorontsov, S. V. 1983, Sol. Phys., 82, 379 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Coordinate system used in ACOR. V0 corresponds to a region inside the convective core, V1 extends from a boundary inside the convective core to the stellar surface, and V2 encompasses the star. |
| In the text | |
 |
Fig. 2 Radial profile of the rotation angular velocity scaled by the equatorial angular velocity at the surface. Ω is constant on isobars but differential in the normal direction. Therefore, the model is not barotropic. |
| In the text | |
 |
Fig. 3 Simulated spectrum of axisymmetric modes for the model presented Sect. 4; it contains the eigenfrequencies of odd and even island modes (in blue and red, respectively), as well as modes trapped only in the μ gradient, chaotic modes, and whispering-gallery modes in grey. |
| In the text | |
 |
Fig. 4 Kinetic energy ρ | vpuls | 2 in a meridional plane, of an |
| In the text | |
 |
Fig. 5 Kinetic energy divided by the square root of the density and multiplied by the square of the distance to the axis in a meridional plane, for an axisymmetric mixed island mode of |
| In the text | |
 |
Fig. 6 Échelle diagram for axisymmetric island modes of different degree |
| In the text | |
 |
Fig. 7 Kinetic energy distribution of an |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.