| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201525665 | |
| Published online | 30 June 2015 | |
Spectrophotometric analysis of gamma-ray burst afterglow extinction curves with X-Shooter⋆,⋆⋆
1 Faculty of Mathematics and Physics, University of Ljubljana, Jadranska ulica 19, 1000 Ljubljana, Slovenia
e-mail:
jure.japelj@fmf.uni-lj.si
2 INAF, Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate, Italy
3 GEPI-Observatoire de Paris Meudon. 5 Place Jules Janssen, 92195 Meudon, France
4 APC, Astroparticule et Cosmologie, Univ. Paris Diderot, CNRS/IN2P3, CEA/Irfu, Obs. de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
5 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
6 Centre for Astrophysics and Cosmology, Science Institute, University of Iceland, Dunhagi 5, 107 Reykjavík, Iceland
7 INAF–Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
8 ASI–Science Data Center, via del Politecnico snc, 00133 Rome, Italy
9 Astronomical Institute Anton Pannekoek, University of Amsterdam, PO Box 94249, 1090 GE Amsterdam, The Netherlands
10 ARI – Liverpool John Moores University, IC2 Liverpool Science Park, 146 Brownlow Hill, Liverpool, L3 5RF, UK
11 European Southern Observatory, Alonso de Coórdova 3107, Vitacura, Casilla 19001, Santiago 19, Chile
12 Unidad Asociada Grupo Ciencias Planetarias (UPV/EHU, IAA-CSIC), Departamento de Física Aplicada I, E.T.S. Ingeniería, Universidad del País Vasco (UPV/EHU), Alameda de Urquijo s/n, 48013 Bilbao, Spain
13 Ikerbasque, Basque Foundation for Science, Alameda de Urquijo 36-5, 48008 Bilbao, Spain
14 Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la Astronomía s/n, 18008 Granada, Spain
15 Department of Physics and Astronomy, University of Leicester, University Road, Leicester LE1 7RH, UK
Received: 15 January 2015
Accepted: 11 March 2015
We use gamma-ray burst (GRB) afterglow spectra observed with the VLT/X-Shooter spectrograph to measure rest-frame extinction in GRB lines-of-sight by modelling the broadband near-infrared (NIR) to X-ray afterglow spectral energy distributions (SEDs). Our sample consists of nine Swift GRBs, of which eight belong to the long-duration and one to the short-duration class. Dust is modelled using the average extinction curves of the Milky Way and the two Magellanic Clouds. We derive the rest-frame extinction of the entire sample, which fall in the range 0 ≲ AV ≲ 1.2. Moreover, the SMC extinction curve is the preferred extinction curve template for the majority of our sample, a result that is in agreement with those commonly observed in GRB lines of sights. In one analysed case (GRB 120119A), the common extinction curve templates fail to reproduce the observed extinction. To illustrate the advantage of using the high-quality, X-Shooter afterglow SEDs over the photometric SEDs, we repeat the modelling using the broadband SEDs with the NIR-to-UV photometric measurements instead of the spectra. The main result is that the spectroscopic data, thanks to a combination of excellent resolution and coverage of the blue part of the SED, are more successful in constraining extinction curves and therefore dust properties in GRB hosts with respect to photometric measurements. In all cases but one the extinction curve of one template is preferred over the others. We show that themodelled values of the extinction AV and the spectral slope, obtained through spectroscopic and photometric SED analysis, can differ significantly for individual events, though no apparent trend in the differences is observed. Finally we stress that, regardless of the resolution of the optical-to-NIR data, the SED modelling gives reliable results only when the fit is performed on a SED covering a broader spectral region (in our case extending to X-rays).
Key words: gamma-ray burst: general / dust, extinction
Based on observations collected at the European Southern Observatory, Paranal, Chile, under programs 084.A-0260(B), 085.A-0009(B), 088.A-0051(B), 089.A-0067(B) and 091.C-0934(C).
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Dust plays a central role in the astrophysical processes of interstellar medium and in the formation of stars (e.g. Mathis 1990; Draine 2003). Its obscuring effects can introduce large uncertainties to the interpretation of astronomical observations, but at the same time offer us the means to study its physical properties. For example, the attenuation of light as a function of wavelength, or extinction curve, is strongly dependent on the composition and size distribution of the dust grains. The origin and properties of dust are still poorly known, especially at cosmological distances, where a unique probe of dust can be found in gamma-ray bursts (GRBs).
These violent explosions originate in galaxies at cosmological distances (e.g. Bloom et al. 1998; Jakobsson et al. 2012). As they are usually accompanied by bright optical and X-ray afterglow emission (e.g. Kann et al. 2011), they can be used as a powerful tool to study environments at different stages of the Universe’s evolution. According to the standard theory (e.g. Gehrels et al. 2009; Gomboc 2012), GRB afterglows are a result of an interaction between highly relativistic ejecta, produced in the progenitor’s explosion, and an interstellar medium. The resulting emission is of a synchrotron nature, which in its simplest case, has a power-law dependence in both time and frequency (e.g. Sari et al. 1998). The deviation from a simple power law is then attributed to the absorption and scattering of light by dust grains (e.g. Kann et al. 2006, 2011). GRB afterglow emission is thus better suited for studying the extinction, as compared to more complex spectra of quasars or galaxies. Modelling of afterglow spectral energy distribution (SED) in the optical-to-X-ray spectral range provides us with information regarding the intrinsic afterglow spectrum and properties of the intervening dust. The dust properties in random lines-of-sight (LOS) in high-redshift galaxies are not known a priori, therefore representative extinction curves are usually assumed in the modelling. Best studied and widely adopted are the average extinction curves observed in the Milky Way (MW; Cardelli et al. 1989; Pei 1992; Fitzpatrick & Massa 2007), Large Magellanic Cloud (LMC; Pei 1992; Gordon et al. 2003), and Small Magellanic Cloud (SMC; Prevot et al. 1984; Pei 1992; Gordon et al. 2003). The three curves differ in their UV slope (steepest in the SMC and shallowest in MW curve) and the prominence of the 2175 Å bump feature, the latter being the strongest in the MW-type and disappearing in the SMC-type dust.
Afterglow SED modelling, either limited to the near-infrared to ultraviolet (NIR-UV; e.g. Galama & Wijers 2001; Stratta et al. 2004; Kann et al. 2006, 2010; Liang & Li 2010) or extended to the X-ray spectral range (Schady et al. 2007, 2010; Greiner et al. 2011), has revealed systems with mostly low LOS extinction where the extinction is preferentially described with the SMC-type dust. Studies dedicated to subsamples of more extincted afterglows (Krühler et al. 2011; Zafar et al. 2012; Perley et al. 2013; Fynbo et al. 2014) indicate that some SEDs show signatures of the 2175 Å absorption feature. To get a clear and unbiased picture of the extinction properties, Covino et al. (2013) analysed the SEDs of a complete sample of GRBs, which are not biased towards optically bright events (Salvaterra et al. 2012; Melandri et al. 2012). They find that ~50% of the afterglows are found within lines-of sight of low extinction (AV< 0.4 mag) and only ~13% are heavily extincted (AV> 2 mag).
Most of the extinction studies have been done using photometric SEDs. An accurate extinction measurement requires simultaneous high-quality data in a broad spectral range from NIR to X-rays. Examples of reliable studies of homogeneous data sets are those using the observations done with the GROND1 instrument (Greiner et al. 2008), whose capability to simultaneously observe in seven bands in the NIR-UV is especially well suited for SED studies (Greiner et al. 2011; Krühler et al. 2011).
Extinction studies could be improved by using spectroscopic instead of photometric SEDs. Zafar et al. (2011, hereafter Z11) studied a sample of 41 optical afterglow spectra obtained mostly with FORS2 (VLT). They show that the SEDs with prominent 2175 Å absorption are among the most extincted with AV> 1.0, while the events with SMC-type dust have low extinction (AV< 0.65). This led them to conclude that the low detection rate of afterglows with LMC or MW-type dust is more likely due to observational bias against dusty LOS than due to the MW-type dust to be rare in high redshift environments. While of a limited spectral coverage, the spectroscopic SEDs allowed them to prove convincingly that the afterglow spectra are indeed consistent with a simple synchrotron model.
In this work we take the next step in the SED modelling using the afterglow spectra obtained with the X-Shooter instrument (Vernet et al. 2011). The X-Shooter is a state-of-the-art intermediate resolution spectrograph, mounted on the VLT, which simultaneously covers a broad spectral range with three spectroscopic arms: ultraviolet (UVB; ~3000–5500 Å), visible (VIS; ~5500–10 000 Å) and NIR (~10 000–25 000 Å). The large spectral coverage of X-Shooter spectra offers us a unique opportunity to apply a detailed extinction curve analysis. The power of X-Shooter in extinction curve studies was illustrated by the recent observation of GRB 140506A, whose afterglow spectrum revealed a unique extinction signature: a very strong flux drop below ~4000 Å (in the GRB’s rest system) is unprecedented in the study of GRB environment and has been found only in a few other LOS to other types of objects so far (Fynbo et al. 2014). Our aim is to use afterglow spectra acquired with the X-Shooter instrument to derive the dust properties in the LOS of GRB host galaxies and to evaluate the applicability of the commonly used extinction curves in this type of analysis. The sample, data preparation, and analysis are presented in Sect. 2. Results and detailed discussion are given in Sects. 3 and 4, respectively. We summarise our conclusions in Sect. 5.
Throughout the paper the convention Fν(t) ∝ t− αν− β is adopted, where α and β are temporal and spectral afterglow slopes, respectively. Times are given with respect to GRB trigger time.
2. Data and analysis
2.1. Preparation of X-Shooter and X-ray spectra
As part of the X-Shooter GRB GTO program3, spectra for ~60 GRB afterglows have been acquired in the period between 2009 and 2014. From this sample, we selected those GRBs whose spectra, according to photometric observations of the afterglows, are not contaminated by supernova or host galaxy emission. We reduced and calibrated the spectra using version 2.0 of the X-Shooter data reduction pipeline (Goldoni et al. 2006; Modigliani et al. 2010); details are described in Fynbo et al. (in prep.). In particular, the instrument’s response function, required to flux-calibrate a spectrum, was obtained by comparing an observed spectrum of a spectrophotometric standard star with the tabulated values. Flux calibration of the X-Shooter spectra has to be robust for our science case. The observations of the standard stars used for the flux calibration are performed only once per night with a 5′′ wide slit and different binning than that used for the science spectra. Afterglow observations are done with much narrower slits, usually with 1.0′′, 0.9′′ and 0.9′′ for UVB, VIS and NIR spectra, respectively. Even if the sky conditions are the same when the standard star and afterglow are observed, a narrow slit loses much more light in the case where seeing is comparable to or larger than the slit width, which can be especially problematic because of the weak wavelength dependence of the seeing (Roddier 1981). Other potential problems are the loss of light in the case the slit is not positioned in the direction of the parallactic angle, and a faulty performance of the atmospheric dispersion correctors in the UVB and VIS spectroscopic arms, which have been disabled in Aug. 2012.
Presentation of the sample.
For these reasons, we cannot blindly rely on the instrument’s response function obtained in the calibration process and we therefore require multiwavelength photometric data of the studied objects to check and validate the flux calibration (see also Krühler et al., in prep.). Our sample is thus limited by the availability of multi-band photometric data in the literature. Photometric observations should be available at or near the epoch of X-Shooter spectra. We found that for several GRBs in the full X-Shooter sample not only the absolute flux level, but also the flux calibration as a function of wavelength did not match the photometric SED. Since it is extremely difficult to reliably account and correct for all the effects (either of observational or technical nature), which influence the calibration, we decided to work only with the spectra with flux calibration where, after applying a correction to the absolute flux calibration, the difference between the spectrum and photometry is less than 10% in all bands. The photometric data are used only to check the validity of the flux calibration. We do not use them to correct the slopes of the flux-calibrated spectra. Photometric observations in UV are seldom available around the X-Shooter epoch. The seeing for all but one event, as measured from the 2D trace of the spectra, is small enough that the slit losses as a function of wavelength at the blue part of the UVB arm should be negligible and therefore we trust the calibration of the bluest SED part. The seeing was bad during the observation of the GRB 100901A afterglow (FWHM ~ 1.5″), but in this case the UV photometric observations were available, confirming the calibration in the UV part of the SED is fine. In summary, a GRB was included in our sample if (i) multiwavelength photometric observations of its afterglow around the epoch of X-Shooter observation are available; (ii) its spectrum is not contaminated by host or supernova emission, and; (iii) the difference between the flux-calibrated spectrum and photometry is less than 10% in all bands. Our final sample consists of nine GRBs, eight of them belonging to the long and one to the short class4. The sample is presented in Table 1. In the future, more published light curve data will enable us to expand the analysis to a bigger sample.
The absolute flux calibration of the spectra in this sample was first fine-tuned with the photometric observations. We corrected spectra for the extinction originating in our Galaxy using Cardelli et al. (1989) extinction curve (assuming the ratio of total-to-selective extinction RV = 3.1) and Galactic extinction maps (Schlafly & Finkbeiner 2011). Regions of telluric absorption and strong absorption lines originating in the GRB host galaxies were masked out. We then rebinned the spectra in bins of widths 30–100 Å to reduce the noise and to guarantee a comparable weight of the optical and X-ray SED part. We performed the binning with the sigma-clipping algorithm: we rejected all data points within a binned interval that differ for more than three standard deviations from the mean of the points in the interval. Since the flux in the binning region is not constant (i.e. the spectra follow power laws), we paid special attention to avoid removing the tails of the binned region during the sigma-clipping. Because a large number of points were binned, we calculated the errors as an average of a standard deviation of binned points from the mean value σ/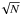 , where N is the number of binned data points. We cross-checked these values with a Monte Carlo simulation. We assumed the errors of the data points, as obtained in the reduction and calibration procedure, are Gaussian. We then resampled the data points in each interval for a thousand times and computed the 1σ equivalent of the resulting distribution of mean values. The errors, computed by the two methods, are comparable.
, where N is the number of binned data points. We cross-checked these values with a Monte Carlo simulation. We assumed the errors of the data points, as obtained in the reduction and calibration procedure, are Gaussian. We then resampled the data points in each interval for a thousand times and computed the 1σ equivalent of the resulting distribution of mean values. The errors, computed by the two methods, are comparable.
The reddest part (e.g. K band) of the NIR spectrum is seldom accurately flux calibrated. This is due mainly to the strong vignetting of the K band (Sect. 2.4.9 of the X-Shooter User Manual), which prevents a reliable sky subtraction especially for long exposure and faint sources. In addition, many observations were conducted with a special K-blocking filter5. For these reasons, only λ ≲ 20 000 Å part of the NIR spectra have been used in the analysis.
We took X-ray data from the Swift/XRT instrument (Burrows et al. 2005) from the online repository of X-ray afterglow spectra (Evans et al. 2009). The X-ray SED was built from the light curve in a time interval around the epoch at which the X-Shooter spectrum was taken: only a portion of the X-ray light curve without significant spectral evolution was considered. The mean time of the X-ray SED was computed as ∑ i(tiΔti)/ ∑ i(Δti), where ti is the mid-time of individual exposure and Δti is the exposure length. The light curve at the considered time interval was fitted with a power-law function: by knowing the slope, the X-ray SED was normalised by interpolation to the epoch of X-Shooter observations. The uncertainty of calculated normalisation is never greater ~10%; by varying the normalisation within this uncertainty for each analysed SED, we found that the best-fit parameters are consistent within errors. We rebinned X-ray channels to have at least 20 photons in each channel, which ensures that the data are roughly Gaussian and enables reliable use of χ2 statistics.
2.2. The SED modelling
In most cases, the optical-to-X-ray SED of the afterglow is studied hours to days after the GRB explosion (see Table 1) when the shape is expected to depend on the relative values of the cooling (νc), optical (νO), and X-ray (νX) frequencies (Sari et al. 1998). The SED can therefore be described with a power-law function Fν = F0ν− βOX (i.e. νc<νO or νc>νX) or, in case νO<νc<νX, by a broken power law, 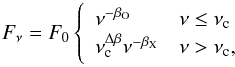 (1)where Δβ = βX−βO.
(1)where Δβ = βX−βO.
Results of the best-fit models of the broadband SEDs.
 |
Fig. 1 Rest-frame afterglow SED analysis of GRB 120815A. Broadband SED is shown in the left plot. Optical and X-ray data are plotted with black points, the best-fitted model is plotted with solid blue lines and the intrinsic afterglow spectrum with dashed-blue line. Zoomed part of the X-Shooter SED is shown in the right plot, where residuals to the best-fitted model are also shown. Vertical lines divide the spectral regions covered by the NIR, VIS, and UVB spectrograph arm. Orange points are photometric observations used to calibrate the absolute flux of the spectrum. References for photometric data points and details on the fitting procedure are reported in Sect. 3. Similar plots for other GRBs in our sample are shown in Figs. 2 and 3. |
The optical afterglow is attenuated because of light scattering by dust particles and can be accounted for in our observations by Fν,obs = Fν10− 0.4 Aλ, where Aλ is a wavelength-dependent extinction in the host galaxy frame. We assume extinction is dominated by dust in GRB hosts rather than being attenuated by intervening galaxies that happen to occur in the LOS between the GRB event and observers on Earth. There are known cases when other galaxies are found in the LOS (e.g. Sparre et al. 2014), however, in most cases, the host galaxy is the dominant absorption system (e.g. Vergani et al. 2009; Schady et al. 2010). The value of Aλ = AVf(λ;RV,...) is parametrised using the rest-frame extinction AV (extinction in the rest frame V-band, at 5500 Å) and the extinction curve f, which reflects the properties of dust in the LOS. We consider the average observed extinction curves of Milky Way (MW) and Large and Small Magellanic Clouds (LMC, SMC; Pei 1992) in the analysis. Initially we also considered the average extinction curve of starburst galaxies (Calzetti et al. 2000), but we find the starburst curve is inadequate in describing extinction in lines of sight of GRB hosts. In addition to being statistically unjustified, fits of starburst models for all events in our sample result in physically unreasonable best-fit parameters of β and AV. The conclusion that starburst models cannot describe dust in GRB lines of sight was also reached in other studies (e.g. Covino et al. 2013). This is not surprising as it is not expected that extinction in LOS to individual sources and galaxy integrated extinction properties are the same.
Fitting only the X-Shooter SED may result in a degenerate solution between the values of the spectral slope, β, and the visual extinction, AV, i.e. data could be successfully represented both by a shallow slope and high amount of extinction or a steep slope and low extinction. The problem can be resolved by constraining one of the parameters. We decided to constrain the spectral slope by including the X-ray part of the SED in the fit. By analysing a large afterglow sample, Z11 found that the difference between the optical and X-ray slope is very close to the theoretically predicted value of Δβ = 0.5 in the majority of cases. Nevertheless, we left the slope difference Δβ as a free parameter of our model. The photoelectric absorption of soft X-rays by metals is assumed to originate in the Galaxy and in the host galaxy at a known redshift z. Galactic equivalent neutral hydrogen column density 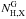 is taken from maps provided by Kalberla et al. (2005)6, while the value in the host galaxy line-of-sight NH,X is left as a free parameter of the model. Following the discussion of Watson et al. (2013) we assume solar abundances of Anders & Grevesse (1989).
is taken from maps provided by Kalberla et al. (2005)6, while the value in the host galaxy line-of-sight NH,X is left as a free parameter of the model. Following the discussion of Watson et al. (2013) we assume solar abundances of Anders & Grevesse (1989).
In principle, we do not know whether the spectral break is sharp as in Eq. (1) or the transition is more mild and smooth (e.g. Granot & Sari 2002; Uhm & Zhang 2014). Indeed, at least in one case the cooling break appears to be smooth: Filgas et al. (2011) found that multi-epoch SEDs of GRB 091127 can be described with a broken power law with a smooth spectral transition. We carefully evaluated the effect of the smoothness on our modelling of broadband SEDs with data of X-Shooter quality. We find that the available data cannot constrain the magnitude of the smoothness (i.e. the sharpness index in Eq. (1) in Filgas et al. 2011). Furthermore, if a break is very smooth and lies near the optical region, the values of other parameters (like AV and βO) obtained in the modelling are considerably affected and uncertain. This is not the case if the break is sharp. In the absence of better knowledge of the spectral smoothness, we assume that the breaks are sharp to reduce the possible systematic parameter errors.
For GRBs occurring at z ≳ 2, the host’s Lyα absorption line enters the X-Shooter observational window. To better constrain the UV slope of the extinction curve, we decided to include the modelling of the red wing of the Lyα line in our analysis. The Lyα line is characterised by its central wavelength λLyα, column density of the absorbing gas NHI and Doppler parameter b. As expected for the damped Lyman alpha absorbers, the fitting turned out to be very insensitive to the latter, therefore we fixed its value to b = 12.6 km s-1, which is the average Doppler parameter of GRB host galaxy absorption lines (de Ugarte Postigo et al. 2012). To model the Lyα line, we used the analytical approximation derived by Tepper-García (2006, 2007). The final model applied to the data and already corrected for Galactic extinction and photoelectric absorption can therefore be summarised as ![\begin{eqnarray} F_{\rm \nu,obs} = F_{\nu}\times10^{-0.4~A_{\lambda} }\times\exp[-N_{\rm H,X}\sigma(\nu)]\times\exp[-\tau_{\rm Ly\alpha}(\nu)], \end{eqnarray}](/articles/aa/full_html/2015/07/aa25665-15/aa25665-15-eq95.png) (2)where σ(ν) is a cross section for photoelectric absorption occurring from the gas in the host galaxy.
(2)where σ(ν) is a cross section for photoelectric absorption occurring from the gas in the host galaxy.
The SED fitting was carried out with the spectral fitting package XSPECv12.8 (Arnaud 1996). The analysis was done separately for (i) the X-Shooter spectrum; and (ii) the broadband SED including the X-Shooter and X-ray spectra. We also modelled a broadband SED with photometric data instead of the X-Shooter spectrum to compare the two types of analyses. Confidence intervals were computed at 90% confidence level following Avni (1976) and Cash (1976), with one parameter of interest. Confidence intervals were being computed independently for each model parameter. We did not investigate possible correlations of uncertainties between the model parameters. We considered a fit to be successful if the null probability (that is, the probability of getting a value of χ2 as large or larger than observed if the model is correct) was better than 10%. If the broken power law provided a better fit than a single power law, we used the F-test (with the probability of 5% as a threshold) to assess whether the improvement in the χ2 is statistically significant.
3. Results
Best-fitted model parameters for the SEDs of the GRBs in our sample are reported in Table 2. An example of the best model in the case of GRB 120815A is plotted in Fig. 1; plots corresponding to other GRBs are shown in Figs. 2 and 3. Detailed fitting results are outlined in Table A.1 and discussed in this section on a case by case basis.
In the following we report qualitative fitting information for each analysed SED in the sample. We also briefly discuss the compatibility of our SED results with the closure relations for each case, assuming models assembled by Racusin et al. (2009, Table 1). To simplify the discussion we do not consider structured jet models and models with continuous energy injection. For a detailed understanding of each event, we point to works dedicated to each GRB.
3.1. GRB 100219A
We obtained photometric data used for normalisation and photometric SED analysis from Thöne et al. (2013). The X-Shooter SED alone can be fitted by a single power law and SMC or LMC extinction curve. The fit is improved when we include X-ray data. The broadband SED can be fitted by a power law and all three extinction curves. The best fit is achieved with the LMC extinction curve. A broken power law does not improve the fit statistically, therefore we do not consider it further. This is a high-redshift GRB (z = 4.667), therefore we had to include the Lyα absorption to constrain the UV slope. The value of the log NHI = 21.0 ± 0.1 that we obtain in the fit is comparable within errors with the one derived by Thöne et al. (2013) from normalised spectrum (i.e. log NHI = 21.14 ± 0.15). Fixing the value to log NHI = 21.14 results in a bit worse χ2 statistics, but otherwise the other parameter values do not change.
For photometric SED, we only use filters not affected by host’s Lyα and Lyman forest. According to the statistics, broadband SED with photometric optical points is best fitted with a power law and MW curve. However, visual inspection shows that the optical SED part is better described with a power law and SMC or LMC extinction. The latter two give a comparable power-law slope and slightly lower extinction AV as that obtained with the X-Shooter broadband SED. A rather low reduced χ2 values are due to the small number of data points (both at optical and X-rays) included in the fit.
Optical light curve is characterised by several moderate rebrightenings (Mao et al. 2012). The X-Shooter spectrum is taken right after a bump peaking at ~20 ks. The light curve slope at the X-Shooter epoch is α ≈ 1.31 (Thöne et al. 2013). The case of an ISM environment and νc>νX seems to describe the optical light curve the best (α ~ 1.1, p ~ 2.5). At this point the X-ray light curve is in a transition from a shallow to steep (α ~ 2.9) phase, which is not seen in the optical (Thöne et al. 2013). If this is due to a geometrical effect (i.e. a jet break) rather than spectral evolution, our result is wrong. Because of a combination of the aforementioned bump and sparse data, it is hard to estimate the correction to normalisation of the X-ray spectrum due to a jet break. We approximately estimate that X-ray afterglow at the X-Shooter epoch would be a factor of 2 brighter in the absence of a jet break. After applying this correction and repeating the fit, we find that a single power law and the LMC-type extinction curve still describe the data the best, although the extinction (AV ≈ 0.26) and spectral slope (β ≈ 0.66) do change a bit, as expected.
3.2. GRB 100418A
We obtained photometric data used for normalisation and photometric SED analysis from de Ugarte Postigo et al. (in prep.). We obtained three afterglow spectra at ~0.4, 1.4 and 2.4 days after the burst. Because of the bad flux calibration of the first epoch spectra and possible contamination from host galaxy and supernova emission of the third epoch of observation, we only use the second epoch spectrum. The X-Shooter SED alone can be fitted by a single power law. However, the broadband SED requires a broken power-law shape. The difference in spectral slopes is Δβ = 0.31 ± 0.09. Fixing the spectral difference to Δβ = 0.5 significantly changes only βO, while other parameter values stay almost unchanged. The F-test probability (<1%) confirms that the model in which both spectral slopes are left free to vary is statistically better. While the χ2 statistics is similar for all three extinction types, visual inspection reveals that the SMC extinction curve provides the best fit to the blue part of the optical data.
The broadband SED with photometric optical points is fitted equally well with all three extinction curves and a broken power law. The best-fit slopes are comparable to the values obtained from the X-Shooter broadband SED fit, while extinction values are slightly higher (but within errors). The broadband fit with a single power law also describes the data well, however the F-test probability (<5%) confirms the broken power law improves the fit significantly.
Initially shallow evolution of the optical light curve was followed by a rebrightening, reaching its peak brightness at ~0.6 days (Marshall et al. 2011). The data from de Ugarte Postigo et al. (in prep.) suggest an optical late-time steepening of αO ~ 1.5, similar to the X-ray decay of αX ~ 1.4 in this late phase. Marshall et al. (2011) find a shallower optical steepening of αO ~ 1.1. In the latter case, the difference between the optical and X-ray light curve slopes cannot be explained within the standard model without a spectral break between the optical and X-ray region. On the other hand, the case of αO ~ 1.5 could be explained within a model of non-spreading uniform jet in a wind environment. We do not find any significant colour evolution in a few days around the X-Shooter epoch (de Ugarte Postigo et al., in prep.), which is in contradiction with the stellar wind environment scenario.
3.3. GRB 100814A
We obtained photometric data used for normalisation and photometric SED analysis from Nardini et al. (2014). We obtained three afterglow spectra at ~0.038, 0.089 and 4.1 days after the burst. Because of the discrepancy between flux calibrated spectra and photometric measurements at the first two epochs, we only analysed the spectrum taken 4.1 days after the burst. The X-Shooter SED alone can be fitted with a SMC extinction curve and a power-law intrinsic behaviour. Statistically there is no need for a spectral break. The LMC and MW curves fail to reproduce the data. The broadband SED is fitted well with a broken power law and the SMC or LMC extinction curve. However, the LMC clearly overpredicts the 2175 Å bump. We therefore prefer the SMC extinction curve as the best model to describe the data. The difference in spectral slopes is Δβ = 0.53 ± 0.08. Fixing the spectral difference to Δβ = 0.5 does not significantly change the results.
The broadband SED with photometric optical points is fitted equally well with all three extinction curves and a broken power law. The position of the spectral break is similar to the position obtained with the X-Shooter broadband SED, while the spectral slopes are different. The broadband fit with a single power law is bad (χ2/ d.o.f.> 3.0).
Optical afterglow light curve of GRB 100814A is characterised by a strong rebrightening at ~20 ks. At the X-Shooter epoch, the optical and X-ray light curves decay as α ≈ 2.25,2.30, respectively (Nardini et al. 2014). Our SED results are marginally consistent with the model of a spreading uniform jet. Light curve evolution in the optical prior to the X-Shooter epoch is chromatic, and the afterglow is becoming redder with time (Nardini et al. 2014). If the position of the cooling frequency is indeed between the optical and X-ray (as we find it to be), then this would suggest that the frequency is travelling towards higher frequencies.
3.4. GRB 100901A
We obtained photometric data used for normalisation and photometric SED analysis from Gomboc et al. (in prep.). The X-Shooter SED alone can be fitted by a single power-law spectrum. Broadband fit reveals the need for a spectral break between the optical and X-ray regions. The SMC extinction curve provides an excellent fit to the data, while the LMC and MW curves are completely inadequate to describe the SED. The difference in spectral slopes is Δβ = 0.56 ± 0.07. Fixing the spectral difference to Δβ = 0.5 does not significantly change the results.
The broadband SED with photometric optical points is fitted best with a broken power law. The model with SMC-type dust provides a marginally better fit than LMC- or MW-type dust. The values differ quite a lot from those obtained from X-Shooter broadband SED, owing to the unavailable NIR photometric observations.
The afterglow exhibits an extreme rebrightening phase at optical wavelengths (e.g. Hartoog et al. 2013; Gomboc et al., in prep.). The light curve at the time of the X-Shooter observation evolves practically achromatically with αO = 1.52 ± 0.05 and αX = 1.55 ± 0.05. None of the closure relations can simultaneously describe the observed spectral and temporal properties at late times.
3.5. GRB 120119A
We obtained photometric data for normalisation and photometric SED analysis from Morgan et al. (2014). We obtained two afterglow spectra at ~0.074 and 0.20 days after the burst. Because of the poor signal-to-noise ratio of the second epoch spectrum we only use the spectrum obtained at 0.074 days. This is the only case in our sample with a clear 2175 Å bump in the SED. In addition, the blue part of the SED is already affected by the red wing of the Lyα line. We cannot obtain a very good fit modelling the X-Shooter SED alone. The broadband SED is fitted best with a power law and LMC extinction curve. Even so, the LMC curve overpredicts the strength of the 2175 Å bump. A broken power law on a broadband data set (and X-Shooter data alone) results in an unphysical result of β2<β1. The Lyα line lies in the bluest part of the spectra, where the signal-to-noise ratio is very low. This is probably the main factor contributing to the overestimated value of log NHI = 23.4 ± 0.2 with respect to the value measured from the normalised spectra (e.g. log NHI = 22.5 ± 0.3; Vreeswijk et al., in prep.).
The broadband SED with photometric optical points is best fitted with a single power law and LMC extinction curve. Best-fit spectral slope is similar to that obtained with the X-Shooter broadband fit, while the extinction AV is slightly lower. Statistically there is no need for a spectral break in the fitted spectral region.
The early time light curve is characterised by colour evolution, possibly explained as a result of dust destruction (Morgan et al. 2014). At the X-Shooter epoch, the light curve evolution is achromatic in the optical-to-X-ray spectral range with α ~ 1.3. Spectral and temporal indices are consistent with the case of νC>νX and an ISM environment.
3.6. GRB 120815A
We obtained photometric data used for normalisation and photometric SED analysis from Krühler et al. (2013). The X-Shooter SED can be fitted with a broken power law and SMC extinction curve. Models with LMC and MW extinction curves are successful in reproducing the data, but the values of the post-break slopes are unrealistically steep (given the X-ray part of the SED). The broadband SED can only be fitted with a broken power law and an SMC extinction curve. This GRB originates at z = 2.358, and therefore we had to include the Lyα absorption to constrain the UV slope. The value of the log NHI = 22.3 ± 0.2 that we obtain is slightly larger than that derived by Krühler et al. (2013), who found log NHI = 21.95 ± 0.10. As discussed by Krühler et al. (2013), the Lyα line is contaminated by vibrationally excited H lines that form a continuum around this spectral region and cause the line to appear stronger. Not taking the H
lines that form a continuum around this spectral region and cause the line to appear stronger. Not taking the H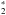 into account, the column density value of (contaminated) Lyα is log NHI ≈ 22.1, closer to our value. Fixing the value to log NHI = 22.1 in the modelling does not change the results (see Table A.1). The difference in spectral slopes is Δβ = 0.46 ± 0.07: fixing it to Δβ = 0.5 does not significantly change the results of the fitting.
into account, the column density value of (contaminated) Lyα is log NHI ≈ 22.1, closer to our value. Fixing the value to log NHI = 22.1 in the modelling does not change the results (see Table A.1). The difference in spectral slopes is Δβ = 0.46 ± 0.07: fixing it to Δβ = 0.5 does not significantly change the results of the fitting.
We did not use the g′-band photometric point in the photometric SED analysis because the measurement is affected by Lyα absorption. The broadband SED with photometric optical points is fitted best with a broken power law and SMC or LMC curve. Fit with a MW curve, on the other hand, is successful with a single power-law spectrum. In the latter case, the visual inspection reveals the model does not describe optical part of the SED very well. Best-fit host extinction is lower than that obtained from the X-Shooter broadband fit.
The light curve of GRB 120815A exhibits a smooth transition from shallow (α = 0.52 ± 0.01) to somewhat steeper (α = 0.86 ± 0.03) decay at ≈0.05 days after the burst (Krühler et al. 2013). Its behaviour is achromatic in the NIR-to-X-rays, implying an absence of spectral break in this spectral regime.
3.7. GRB 130427A
We obtained photometric data used for normalisation and photometric SED analysis from Perley et al. (2014). The X-Shooter SED alone can be fitted by a broken power law and all three extinction curves. The broadband SED also requires a broken power-law shape. While the reduced χ2 implies the SMC or LMC curve provide a fit of a similar quality, a visual inspection shows that the model with LMC-type dust fails to reproduce the data in the bluest X-Shooter region. We thus prefer the SMC curve with low host extinction as the case best describing the real conditions. The break is required to occur within the observable X-Shooter range. The difference in spectral slopes is Δβ = 0.31 ± 0.05. Fixing the spectral difference to Δβ = 0.5 results in statistically worse, yet still acceptable fit. Visual inspection reveals that the X-Shooter continuum in the case with fixed Δβ is not fitted that well. This fit also results in a shallower optical slope (βO ~ 0.2) and consequently higher extinction (AV ~ 0.35).
The broadband SED with photometric optical points is fitted best with a broken power law. All three extinction curves can be used in the modelling of the optical SED. Results are in agreement with the X-Shooter broadband SED fit and the SMC extinction curve.
The afterglow of GRB 130427A comes with a rich multiwavelength data set and has been analysed in detail. It has been interpreted either as a combination of a forward and reverse shock afterglow contributions rising from a wind (Laskar et al. 2013; Perley et al. 2014; Panaitescu et al. 2013) or ISM circumburst medium (Maselli et al. 2014). Regardless of the interpretation, the cooling frequency lies at νC > νX at the X-Shooter epoch. Therefore the break we observe in the SED is not the cooling break, but may be due to the contribution of both forward and reverse shock to the emission (Perley et al. 2014).
Overview of the quality of fit results.
3.8. GRB 130603B
This is the only short GRB in our sample. We obtained photometric data used for normalisation and photometric SED analysis from de Ugarte Postigo et al. (2014). The X-Shooter SED alone can be fitted by a broken power-law model and all three extinction curves. Broadband SED is modelled well with a broken power law and all three extinction curves. Visual inspection shows the LMC and MW-type curves do not reproduce the blue part of the SED that well, and therefore we prefer the SMC-type curve. A single power law fails to reproduce the SED. In this case, we included the K-band photometric observation in the fitting procedure: without this point the fitted pre-break slope would be too steep. However, we note that the NIR SED part cannot be modelled very well (see the residual plot in Fig. 3). The difference in spectral slopes is Δβ ~ 0.5; fixing the spectral difference to Δβ = 0.5 therefore does not change the results. A similar analysis has been done by de Ugarte Postigo et al. (2014). They also find a high extinction of AV ~ 0.9, albeit a bit lower than we find (AV ~ 1.2). They find a position of the spectral break to be near 1016 Hz, while our best fit prefers a value of ≈0.8 × 1015 Hz.
The broadband SED with photometric optical points is fitted best with a broken power law. All three extinction curves can be used in the modelling of the optical SED, although the MW curve seems to provide a slightly better fit than the other two curves. As in the X-Shooter broadband fit, the spectral break is found in the optical region. However, best-modelled extinction AV is found to be significantly lower.
Optical afterglow observations of the GRB 130603B are sparse. Optical and X-ray light curves appear to evolve achromatically after ~0.25 days, but are very different prior to that time (de Ugarte Postigo et al. 2014). During this time, a gradual steepening from α ≈ 1.4 to α ≈ 2.4 in X-rays implies an occurrence of a jet break (Fong et al. 2014). The complicated light curve behaviour prevents us from using the closure relations. We note that both Fong et al. (2014) and de Ugarte Postigo et al. (2014) find a spectral break between the optical and X-ray region, but at higher frequencies than we find.
3.9. GRB 130606A
We obtained photometric data used for normalisation and photometric SED analysis from Castro-Tirado et al. (2013) and Afonso et al. (2013). The fit to the X-Shooter part of the SED alone is not very well constrained. Broadband SED is well represented by a power law. No host extinction is necessary (AV < 0.01). This is a high-redshift GRB (z = 5.913), therefore we had to include the Lyα absorption to constrain the UV slope. The value of the log NHI = 19.9 ± 0.3 that we obtain in the fit agrees with that derived by Hartoog et al. (2014) (i.e. log NHI = 19.94 ± 0.01). Fixing the value to log NHI = 19.94 therefore does not change the results.
For photometric SED, we only use filters not affected by host’s Lyα and intergalactic medium absorption. The broadband SED with photometric optical points is fitted best with a single power law and negligible extinction (while upper limits are quite high, clearly no extinction is necessary to model the SED). The results are in agreement with those obtained from the X-Shooter broadband SED.
At the X-Shooter epoch the light curve of GRB 130606A decays achromatically with α ~ 1.9 both at optical and X-ray wavelengths (Castro-Tirado et al. 2013). Our spectral slope and temporal decay index are consistent within the case of νC > νX and wind circumburst environment.
4. Discussion
4.1. Spectroscopic vs. photometric SEDs
To show the advantage of using spectroscopic SEDs in dust analysis, we also modelled photometric SEDs7, using the photometric data shown in Figs. 2, 3 (but adding K-band magnitudes, where available). Because of a poor sampling in blue SED parts, we did not use photometric points contaminated by Lyα absorption. While the difference in the spectral slopes Δβ in the case of photometric SED studies is usually fixed to Δβ = 0.5, we leave it as a free parameter because the same prescription was used in the spectroscopic SED study and therefore the comparison between the two analyses is more genuine. The results are reported in Table A.1.
 |
Fig. 4 Comparison of best-fit parameters of extinction AV (left) and optical spectral index βO (right) obtained by fitting the broadband SED with photometric measurements and X-Shooter spectra. Dashed lines represent relations AV,Xshoot = AV,phot and βO,Xshoot = βO,phot. Filled and empty symbols represent the cases where the broadband SED is best described by a single or broken power law, respectively. |
 |
Fig. 5 Extinction and hydrogen equivalent column density values as a function of redshift for our sample. Long GRBs are plotted with empty red squares while the short GRB 130603B is given with a filled red square. Empty blue circles represent values obtained in a study of a complete sample of long GRBs (Covino et al. 2013). |
We find that the results of the modelling of photometric SEDs are similar in spectral shape to the results of modelling the spectroscopic SEDs. However, photometric SEDs can usually be modelled by more than one extinction curve: in most cases, we cannot strongly favour one of the models over the other two. Similar conclusions have been reached in other sample studies (e.g. Covino et al. 2013). The poor resolution of multicolour photometry is not sufficient to detect the smooth features in the SED that separate one extinction curve from another. This is in contrast to what is found in X-Shooter SED analysis. In four cases of our sample one extinction curve is strongly preferred according to the χ2 statistics. In four additional cases for which the best-fit models with different extinction curves are of a similar quality, the better coverage of the blue part of the X-Shooter SED allows us to distinguish the best extinction curve by visually inspecting the blue part of the SED, which is most sensitive to the modelling. In these four cases the SMC-type extinction curve matched the blue data well, while for the other two curves either the 2175 Å absorption was overestimated or the bluest SED part was overpredicted by the modelling (see Sect. 3 for details). The ability to distinguish between the different extinction curves is summarised in Table 3. In the spectroscopic analysis, we were thus able to single out the best model for all cases but GRB 130606A, whose LOS lacks a notable extinction in the first place.
Differences are also observed in the values of the best-fit parameters. Figure 4 compares the values of extinction AV and optical spectral index βO obtained from both types of analysis. The extinction values seem to be systematically larger in the spectroscopic analysis, while optical spectral indices do not show any preferential deviation. Fixing the difference in spectral slope to Δβ = 0.5, as it is usually done in these types of analyses (e.g. Greiner et al. 2011; Covino et al. 2013), does not signficantly reduce the differences. Because of rather large errors in the values derived from photometric analysis and small sample we cannot draw strong conclusions about possible trends in deviation. However, we emphasise that photometric SEDs used in the analysis cover a very broad wavelength region. The analysis of SEDs with less covered spectral range, which are still often used in SED modelling, would result in even greater differences from the spectroscopic analysis.
Equivalent hydrogen column densities were not constrained very well by fitting only the X-ray part of the SED (see Table A.1). The reason for this is the low signal-to-noise ratio of the X-ray spectrum: to minimise the error due to possible spectral evolution and uncertainties in temporal extrapolation, the X-ray SEDs were built from rather narrow time intervals. The broadband fit resulted in more constrained values of NH,X. We note that spectral slopes in the X-ray are systematically steeper (although still within the error) in the broadband with respect to the X-ray-only fits. On the other hand, the fit of the X-Shooter SED alone usually turned out very badly. This type of fit was both statistically acceptable (i.e. see Sect. 2.2) and resulted in similar parameter values as in the case of the broadband fit in only three cases. Thus, independent of the quality (resolution) of the optical-to-NIR data, the SED modelling is secure only when the fit is performed on a broader band SED.
4.2. Extinction and equivalent hydrogen column densities
The values of extinction (0 ≲ AV ≲ 1.2) and equivalent hydrogen column density (0.1 ≲ NH,X[1022 cm-2] ≲ 2; not including upper limits) that we find for our sample are similar to those found in GRB lines of sight (e.g. Zafar et al. 2011; Greiner et al. 2011; Watson & Jakobsson 2012; Campana et al. 2012; Covino et al. 2013). This is illustrated in Fig. 5 where we plot both quantities as a function of redshift and compare them to the Swift BAT6 complete GRB sample (Salvaterra et al. 2012; Covino et al. 2013). Most of the events are found to have low extinction (AV ≲ 0.3). GRBs 120119A and 130603B are moderately extinguished with AV ~ 1.1, which according to the complete Swift BAT6 sample places them into the top 20–25%. The short GRB 130603B has the highest extinction in the sample. Dust-to-gas ratios of our (long GRB) sample are low with respect to those of the Local Group, which is a well-known result (Stratta et al. 2004; Schady et al. 2010; Zafar et al. 2011). The ratio also appears to increase with redshift. Since the extinction does not evolve much with redshift (see Fig. 5), the evolution of the ratio is a consequence of the lack of low NH,X values at high redshifts (Watson et al. 2013; Covino et al. 2013). The reason for the preference of high NH,X values at high redshifts is not yet clear. Campana et al. (2012) claim that for high-redshift GRBs absorption by intervening systems in the GRB LOS contributes a great deal to the measured NH,X. Alternatively, Watson et al. (2013) claim that the absorption is intrinsic to the GRB environment and that the evolution of the (metal) gas column density reflects the evolution of cosmic metallicity. As already noted by de Ugarte Postigo et al. (2014), the dust-to-gas ratio of the short GRB 130603B is consistent with the Galactic, indicating that the explosion site for this event differs from a typical long GRB site.
4.3. Extinction curves
We find that the dust properties preferred for the GRB sight lines are those of SMC type, with six afterglow SEDs best fitted by the corresponding averaged extinction curve. Two are best described by the LMC curve and one (GRB 130606A) is found to have AV ~ 0. While the preference for the SMC-type of dust has been already observed in sample studies using photometric SEDs (e.g. Kann et al. 2010; Greiner et al. 2011; Covino et al. 2013) and the spectroscopic study of Z11, it is still interesting that the well-sampled and broadband X-Shooter SEDs can be modelled with this average extinction curve that well. The lack of the 2175 Å bump in all but one event (see below) is not surprising: Z11 found that the events with a notable 2175 Å feature all have rather high extinction values and that the preference for the SMC-type dust can be attributed to the observed GRBs being biased towards low extinction lines of sight. Indeed, most of our events have low measured extinction. If the total-to-selective extinction RV in the lines of sight in GRB hosts were larger than in the three assumed extinction curves, the curves would be flatter and the derived extinction higher. This type of extinction could occur if dust were being destroyed by a GRB and grains of smaller size are preferentially destroyed (Waxman & Draine 2000). However, while this dust may have been found in some events (Perley et al. 2008; Liang & Li 2010), as already emphasised in Sect. 2.2, we find that flat extinction curves inadequately describe the dust in all lines of sight of our GRB sample.
GRB 120119A is the only event in our sample with a clear 2175 Å absorption bump (see Fig. 6), the feature also observed in a few other afterglow spectra (Elíasdóttir et al. 2009; Prochaska et al. 2009; Zafar et al. 2012; Fynbo et al. 2014). In our analysis, the LMC template provided the best fit to the data for this GRB. Still, it is clear from Fig. 6 that the LMC overpredicts the strength of the 2175 Å bump. The failure to find a good model is not completely unexpected, since we are using merely average extinction curves. Different lines of sight in our Galaxy or in the two Magellanic Clouds have different extinction properties. There are known lines of sight in the Galaxy that have SMC-type dust and vice versa (e.g. see Elíasdóttir et al. 2009 for review). The analysis thus calls for a more detailed extinction model, like that introduced by Fitzpatrick & Massa (2007), where the strength of the bump as well as the UV extinction slope are free parameters of the model. The use of more general extinction curves in the X-Shooter SED analysis will be presented in a separate work (Zafar et al., in prep.). GRB 120119A is a perfect example with excellent data both in optical and X-ray frequency range that clearly shows the power of the X-Shooter data. A photometric SED can hardly differentiate between the three models, while the X-Shooter data allow us to extract much more detailed information about the dust.
 |
Fig. 6 Zoomed blue X-Shooter part of broadband SED fit of GRB 120119A. Several models are shown, indicating their failure to fully reproduce the data. |
4.4. Neutral hydrogen column densities
Four GRBs in the sample are at a redshift z ≳ 1.7 for which the red wings of the Lyα absorption line enter the X-Shooter observational window and influence the SED shape. The modelled hydrogen column density values for these bursts are given in Table 2. In two cases our values agree with those derived from normalised spectra (i.e. GRB 100219A – Thöne et al. 2013; GRB 130606A - Hartoog et al. 2014). In the cases of GRB 120815A (Krühler et al. 2013) and GRB 120119A (Vreeswijk et al., in prep.) we derive values that are slightly or significantly higher from those in the literature, respectively. In the case of GRB 120815A, the Lyα line is contaminated by vibrationally excited H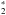 lines that form a continuum around this spectral region and cause the line to appear stronger (Krühler et al. 2013). The contribution of the H
lines that form a continuum around this spectral region and cause the line to appear stronger (Krühler et al. 2013). The contribution of the H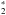 absorption has already been subtracted from the value of log NHI = 21.95 ± 0.15, reported by Krühler et al. (2013). Not taking the molecular hydrogen into account, they measure log NHI ~ 22.1, closer to our value.
absorption has already been subtracted from the value of log NHI = 21.95 ± 0.15, reported by Krühler et al. (2013). Not taking the molecular hydrogen into account, they measure log NHI ~ 22.1, closer to our value.
There are several possible reasons for the further discrepancy. Firstly, we normalised the spectra of the four GRB afterglows and fitted the Lyα lines: our best-fit NHI matches very well with the values from the literature. Secondly, our spectra are heavily binned. To check the dependency of the results on the bin size, we redid the modelling of the X-Shooter SED part but with smaller bin widths in the region around the line: the obtained value of the log NHI does not change significantly. We also fixed the log NHI to the values measured from the normalised spectra (see Table A.1 and Sect. 3). The results did not change significantly for GRBs 100219A and 130606A. In the case of GRB 120815A, the fit statistics was worse, but otherwise the parameter values did not significantly change. The case of GRB 120119A remains puzzling. The value of log NHI = 23.4 ± 0.2 found for GRB 120119A seems to be unrealistically high. While GRB lines of sight are characterised by generally high hydrogen column densities (Fynbo et al. 2009; Thöne et al. 2013), the measured values have never surpassed log NHI = 23.0. Indeed, the column density measured from the normalised spectrum is found to be 22.5 ± 0.3 (Vreeswijk et al., in prep.), but fixing this value in the fitting procedure cannot reproduce the blue part of the SED (see Fig. 6). The main reason for the discrepancy is probably due to a low signal-to-noise ratio of the spectral region in which the line lies (i.e. the bluest part of the spectrum). The uncertainty of our result is further enhanced by the shape of the extinction curves that in this case have proved to inadequately model the extinction.
 |
Fig. 7 Comparison of optical and X-ray spectral slopes for the cases where spectral break is found to lie in the analysed spectral range. Our values (empty red squares) are compared to the sample of Zafar et al. (2011) (filled black circles). Dashed line represents the relation βX = βO + 0.5, corresponding to a theoretical prediction in the case the observed break is the cooling break. The data point corresponding to GRB 130427A, for which the break probably does not correspond to a cooling break, is plotted with filled square. |
4.5. Standard afterglow model
While it is not the main goal of the paper, here we present a brief discussion of our results as analysed with respect to the standard afterglow theory. A spectral break is necessary to model the SEDs of six GRBs in our sample: GRB 100418A, 100814A, 100901A, 100815A, 130427A, and 130603B. An occurrence of a spectral break in the SED is not surprising: analysing a sample of ~40 afterglows, Z11 find that ~60% of SEDs have a spectral break lying somewhere between the optical and X-ray frequencies. Spectral slopes for the six GRBs, together with data of the sample presented by Z11, are plotted in Fig. 7. In four of our cases, the difference between pre- and post-break slopes of our GRBs is in agreement within errors with the theoretically predicted value of Δβ = 0.5, confirming that both optical and X-ray emission have a synchrotron origin and are produced by the same mechanism; similar conclusions were reached by Z11. Nevertheless, we find two exceptions to the expected behaviour. The SEDs of GRBs 100418A and 130427A are found to have a break with much shallower Δβ ~ 0.3. The afterglow of the GRB 130427A has been interpreted either as a combination of a forward and reverse afterglow contribution rising from a wind (Laskar et al. 2013; Perley et al. 2014; Panaitescu et al. 2013) or ISM circumburst medium (Maselli et al. 2014). Regardless of interpretation, the cooling frequency is found to lie above the X-ray frequency at X-Shooter epoch, suggesting that the break in SED is not because of the passing of the cooling frequency through the optical SED. This is supported by the fact that the measured change in spectral slopes differs from that predicted by the standard theory for the cooling break. The break we find may thus be because of the contribution of both forward and reverse shock to the emission (Perley et al. 2014). The case of GRB 100418A is harder to explain. Its optical afterglow is characterised by a strong bump, which is not seen in the X-rays; our spectrum is taken when the bump is still strong. A contribution of multiple components in the optical may be the cause of the shallow Δβ = 0.31 ± 0.09. Even greater discrepancy was found for GRB 080210A by Z11 and De Cia et al. (2011), for which the spectral difference is Δβ ~ 1. However we recall that we used a sharp spectral break in the fitting procedure (see Sect. 2.2). If the actual spectral transition is somewhat milder, occurring over several orders of magnitudes, the modelled spectral difference would be underestimated by using a sharp break. We also point to rather large uncertainties of optical spectral indices. This is because spectral breaks lie within or near the optical spectral region and consequently the spectral range needed to constrain the optical slopes is quite narrow.
We briefly checked the available afterglow light curves of the GRBs in our sample to see whether the relations between spectral and temporal indices are in agreement with theoretical expectations in the case of different physical models (e.g. Table 1 in Racusin et al. 2009). A detailed account on the consistency with closure relations for each burst is given in Sect. 3. While some cases can indeed be explained within one of the models’ predictions (e.g. 100814A and 130606A), most of the events are not consistent with closure relations. This is a known problem observed in other sample studies (e.g. Z11, Zaninoni et al. 2013) and probably reflects our ignorance of the hydrodynamic evolution of the outflow and the behaviour of the central engine.
5. Conclusions
We have presented a detailed SED analysis of a sample of GRB afterglows, observed with the VLT/X-Shooter spectrograph. Our aim was to model broadband afterglow SEDs, composed of the NIR-to-UV X-Shooter spectra and Swift/XRT X-ray observations, to infer dust properties along the lines of sight in GRB host galaxies. Only spectra with trustworthy flux calibration (i.e. for which the spectral slope matches that built from photometric measurements) were used in the analysis. The sample consists of nine GRBs: eight GRBs belong to the long and one to the short class.
The values of extinction (0 ≲ AV ≲ 1.2) and equivalent hydrogen column density (0.1 ≲ NH,X[1022 cm-2] ≲ 2) that we measure are commonly found in GRB sightlines (e.g. Covino et al. 2013). Six GRBs in the sample require a spectral break in the modelled spectral region. Interestingly, four breaks occur in the region covered by X-Shooter. Most of the events are best described by the SMC-type of dust.
We redid the modelling using the broadband SEDs with the NIR/UV photometric measurements to see whether there are any differences between using the two data sets in the analysis. The derived values of the extinction AV and spectral slope, obtained through spectroscopic and photometric SED analysis, for individual events can differ significantly, although no apparent trend in the differences is observed. More importantly, the spectroscopic data, especially with their excellent coverage of the blue SED part, can help us to constrain the dust properties (e.g. the extinction curve) much better than the photometric measurements. In addition, we show that independent of the quality (resolution) of the optical-to-NIR data, the SED modelling is secure only when the fit is performed on a SED covering broader spectral region (in our case, including X-rays).
We have demonstrated that spectra, obtained with X-Shooter, can be successfully used for a detailed SED analysis. The X-Shooter spectra with good flux calibration can be used to constrain extinction curves and can therefore improve our understanding of dust in the high redshift Universe. The study will be expanded when more photometric observations of afterglows become available in the future.
Online material
Appendix A: Fitting details
Fitting results.
Traditionally, GRBs are classified into a long or short class according to their observed duration (i.e. longer or shorter than ~2 s) and spectral properties (Kouveliotou et al. 1993). However, a reliable classification into the two classes, which correspond to different progenitor types, is usually more complicated (e.g. Zhang et al. 2009).
The filter blocks the spectral range above 2 μm and thus prevents the scattered light from K-band orders to contaminate the J- and H-band background (e.g. Vernet et al. 2011).
In general, in addition to the atomic hydrogen H i, provided by maps of Kalberla et al. (2005), a contribution of molecular hydrogen H2 should be taken into account when estimating Galactic X-ray absorption (Willingale et al. 2013). We ignore the molecular component to make our modelling of the X-ray spectra comparable to analyses of larger samples in previous studies (e.g. see Sect. 4.2 and Fig. 5), in which the H2 has not been considered. Nevertheless, we checked that taking the simplified model does not affect our global modelling, i.e. the values of spectral slopes and extinction.
Acknowledgments
A.d.U.P. acknowledges support from a Ramón y Cajal fellowship. The Dark Cosmology Centre is funded by the Danish National Research Foundation. This work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester.
References
- Afonso, P., Kann, D. A., Nicuesa Guelbenzu, A., et al. 2013, GRB Coordinates Network, 14807, 1 [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Avni, Y. 1976, ApJ, 210, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Djorgovski, S. G., Kulkarni, S. R., & Frail, D. A. 1998, ApJ, 507, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Salvaterra, R., Melandri, A., et al. 2012, MNRAS, 421, 1697 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1976, A&A, 52, 307 [NASA ADS] [Google Scholar]
- Castro-Tirado, A. J., Sánchez-Ramírez, R., Ellison, S. L., et al. 2013, ArXiv e-prints [arXiv:1312.5631] [Google Scholar]
- Covino, S., Melandri, A., Salvaterra, R., et al. 2013, MNRAS, 432, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- De Cia, A., Jakobsson, P., Björnsson, G., et al. 2011, MNRAS, 412, 2229 [NASA ADS] [CrossRef] [Google Scholar]
- de Ugarte Postigo, A., Fynbo, J. P. U., Thöne, C. C., et al. 2012, A&A, 548, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ugarte Postigo, A., Thöne, C. C., Rowlinson, A., et al. 2014, A&A, 563, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Elíasdóttir, Á., Fynbo, J. P. U., Hjorth, J., et al. 2009, ApJ, 697, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Filgas, R., Greiner, J., Schady, P., et al. 2011, A&A, 535, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fong, W., Berger, E., Metzger, B. D., et al. 2014, ApJ, 780, 118 [Google Scholar]
- Fynbo, J. P. U., Jakobsson, P., Prochaska, J. X., et al. 2009, ApJS, 185, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Krühler, T., Leighly, K., et al. 2014, A&A, 572, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galama, T. J., & Wijers, R. A. M. J. 2001, ApJ, 549, L209 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Ramirez-Ruiz, E., & Fox, D. B. 2009, ARA&A, 47, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Goldoni, P., Royer, F., François, P., et al. 2006, in SPIE Conf. Ser., 6269, 2 [Google Scholar]
- Gomboc, A. 2012, Contemporary Physics, 53, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Granot, J., & Sari, R. 2002, ApJ, 568, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2008, PASP, 120, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Krühler, T., Klose, S., et al. 2011, A&A, 526, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartoog, O. E., Wiersema, K., Vreeswijk, P. M., et al. 2013, MNRAS, 430, 2739 [NASA ADS] [CrossRef] [Google Scholar]
- Hartoog, O. E., Malesani, D., Fynbo, J. P. U., et al. 2014, ArXiv e-prints [arXiv:1409.4804] [Google Scholar]
- Jakobsson, P., Hjorth, J., Malesani, D., et al. 2012, ApJ, 752, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kann, D. A., Klose, S., & Zeh, A. 2006, ApJ, 641, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Klose, S., Zhang, B., et al. 2010, ApJ, 720, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Klose, S., Zhang, B., et al. 2011, ApJ, 734, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Greiner, J., Schady, P., et al. 2011, A&A, 534, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krühler, T., Ledoux, C., Fynbo, J. P. U., et al. 2013, A&A, 557, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laskar, T., Berger, E., Zauderer, B. A., et al. 2013, ApJ, 776, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, S. L., & Li, A. 2010, ApJ, 710, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, J., Malesani, D., D’Avanzo, P., et al. 2012, A&A, 538, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marshall, F. E., Antonelli, L. A., Burrows, D. N., et al. 2011, ApJ, 727, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Maselli, A., Melandri, A., Nava, L., et al. 2014, Science, 343, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1990, ARA&A, 28, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Melandri, A., Sbarufatti, B., D’Avanzo, P., et al. 2012, MNRAS, 421, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Modigliani, A., Goldoni, P., Royer, F., et al. 2010, in SPIE Conf. Ser., 7737, 28 [Google Scholar]
- Morgan, A. N., Perley, D. A., Cenko, S. B., et al. 2014, MNRAS, 440, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, M., Elliott, J., Filgas, R., et al. 2014, A&A, 562, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panaitescu, A., Vestrand, W. T., & Woźniak, P. 2013, MNRAS, 436, 3106 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Bloom, J. S., Butler, N. R., et al. 2008, ApJ, 672, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Levan, A. J., Tanvir, N. R., et al. 2013, ApJ, 778, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Cenko, S. B., Corsi, A., et al. 2014, ApJ, 781, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Prevot, M. L., Lequeux, J., Prevot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
- Prochaska, J. X., Sheffer, Y., Perley, D. A., et al. 2009, ApJ, 691, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Racusin, J. L., Liang, E. W., Burrows, D. N., et al. 2009, ApJ, 698, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Roddier, F. 1981, Progress in optics, vol. 19 (Amsterdam: North-Holland Publishing Co.), 281 [Google Scholar]
- Salvaterra, R., Campana, S., Vergani, S. D., et al. 2012, ApJ, 749, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schady, P., Mason, K. O., Page, M. J., et al. 2007, MNRAS, 377, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Schady, P., Page, M. J., Oates, S. R., et al. 2010, MNRAS, 401, 2773 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Sparre, M., Hartoog, O. E., Krühler, T., et al. 2014, ApJ, 785, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Stratta, G., Fiore, F., Antonelli, L. A., Piro, L., & De Pasquale, M. 2004, ApJ, 608, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Tepper-García, T. 2006, MNRAS, 369, 2025 [NASA ADS] [CrossRef] [Google Scholar]
- Tepper-García, T. 2007, MNRAS, 382, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Thöne, C. C., Fynbo, J. P. U., Goldoni, P., et al. 2013, MNRAS, 428, 3590 [NASA ADS] [CrossRef] [Google Scholar]
- Uhm, Z. L., & Zhang, B. 2014, ApJ, 780, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Vergani, S. D., Petitjean, P., Ledoux, C., et al. 2009, A&A, 503, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, D., & Jakobsson, P. 2012, ApJ, 754, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, D., Zafar, T., Andersen, A. C., et al. 2013, ApJ, 768, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Waxman, E., & Draine, B. T. 2000, ApJ, 537, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Zafar, T., Watson, D., Fynbo, J. P. U., et al. 2011, A&A, 532, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zafar, T., Watson, D., Elíasdóttir, Á., et al. 2012, ApJ, 753, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Zaninoni, E., Bernardini, M. G., Margutti, R., Oates, S., & Chincarini, G. 2013, A&A, 557, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, B., Zhang, B.-B., Virgili, F. J., et al. 2009, ApJ, 703, 1696 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Rest-frame afterglow SED analysis of GRB 120815A. Broadband SED is shown in the left plot. Optical and X-ray data are plotted with black points, the best-fitted model is plotted with solid blue lines and the intrinsic afterglow spectrum with dashed-blue line. Zoomed part of the X-Shooter SED is shown in the right plot, where residuals to the best-fitted model are also shown. Vertical lines divide the spectral regions covered by the NIR, VIS, and UVB spectrograph arm. Orange points are photometric observations used to calibrate the absolute flux of the spectrum. References for photometric data points and details on the fitting procedure are reported in Sect. 3. Similar plots for other GRBs in our sample are shown in Figs. 2 and 3. |
| In the text | |
 |
Fig. 2 SEDs and best-fitted models of the sample. For details, see caption in Fig. 1. |
| In the text | |
 |
Fig. 3 SEDs and best-fitted models of the sample. For details, see caption in Fig. 1. |
| In the text | |
 |
Fig. 4 Comparison of best-fit parameters of extinction AV (left) and optical spectral index βO (right) obtained by fitting the broadband SED with photometric measurements and X-Shooter spectra. Dashed lines represent relations AV,Xshoot = AV,phot and βO,Xshoot = βO,phot. Filled and empty symbols represent the cases where the broadband SED is best described by a single or broken power law, respectively. |
| In the text | |
 |
Fig. 5 Extinction and hydrogen equivalent column density values as a function of redshift for our sample. Long GRBs are plotted with empty red squares while the short GRB 130603B is given with a filled red square. Empty blue circles represent values obtained in a study of a complete sample of long GRBs (Covino et al. 2013). |
| In the text | |
 |
Fig. 6 Zoomed blue X-Shooter part of broadband SED fit of GRB 120119A. Several models are shown, indicating their failure to fully reproduce the data. |
| In the text | |
 |
Fig. 7 Comparison of optical and X-ray spectral slopes for the cases where spectral break is found to lie in the analysed spectral range. Our values (empty red squares) are compared to the sample of Zafar et al. (2011) (filled black circles). Dashed line represents the relation βX = βO + 0.5, corresponding to a theoretical prediction in the case the observed break is the cooling break. The data point corresponding to GRB 130427A, for which the break probably does not correspond to a cooling break, is plotted with filled square. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


