| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201525997 | |
| Published online | 05 June 2015 | |
Active galactic nuclei cores in infrared-faint radio sources
Very long baseline interferometry observations using the Very Long Baseline Array
1 Astronomisches Institut, Ruhr-Universität Bochum, Universitätsstr. 150, 44801 Bochum, Germany
e-mail: herzog@astro.rub.de
2 Macquarie University, Sydney, NSW 2109, Australia
3 CSIRO Astronomy and Space Science, Marsfield, PO Box 76, Epping, NSW 1710, Australia
4 Australian Astronomical Observatory, PO Box 915, North Ryde, NSW 1670, Australia
5 The Netherlands Institute for Radio Astronomy (ASTRON), Postbus 2, 7990 AA Dwingeloo, The Netherlands
6 University of Western Sydney, Locked Bag 1797, Penrith, NSW 2751, Australia
Received: 2 March 2015
Accepted: 31 March 2015
Context. Infrared-faint radio sources (IFRS) form a new class of galaxies characterised by radio flux densities between tenths and tens of mJy and faint or absent infrared counterparts. It has been suggested that these objects are radio-loud active galactic nuclei (AGNs) at significant redshifts (z ≳ 2).
Aims. Whereas the high redshifts of IFRS have been recently confirmed based on spectroscopic data, the evidence for the presence of AGNs in IFRS is mainly indirect. So far, only two AGNs have been unquestionably confirmed in IFRS based on very long baseline interferometry (VLBI) observations. In this work, we test the hypothesis that IFRS contain AGNs in a large sample of sources using VLBI.
Methods. We observed 57 IFRS with the Very Long Baseline Array (VLBA) down to a detection sensitivity in the sub-mJy regime and detected compact cores in 35 sources.
Results. Our VLBA detections increase the number of VLBI-detected IFRS from 2 to 37 and provide strong evidence that most – if not all – IFRS contain AGNs. We find that IFRS have a marginally higher VLBI detection fraction than randomly selected sources with mJy flux densities at arcsec-scales. Moreover, our data provide a positive correlation between compactness – defined as the ratio of milliarcsec- to arcsec-scale flux density – and redshift for IFRS, but suggest a decreasing mean compactness with increasing arcsec-scale radio flux density. Based on these findings, we suggest that IFRS tend to contain young AGNs whose jets have not formed yet or have not expanded, equivalent to very compact objects. We found two IFRS that are resolved into two components. The two components are spatially separated by a few hundred milliarcseconds in both cases. They might be components of one AGN, a binary black hole, or the result of gravitational lensing.
Key words: techniques: interferometric / galaxies: active / galaxies: high-redshift / galaxies: nuclei / radio continuum: galaxies
© ESO, 2015
1. Introduction
One of the most controversially discussed topics in current astrophysics is the question of how active galactic nuclei (AGNs) influence star forming activity in their host galaxies. This interaction is known as feedback, and both negative and positive feedback of the AGN have been proposed.
Negative AGN feedback is thought to be caused by the AGN heating or disrupting the surrounding gas and, by this, quenching star formation. This scenario consists of two consecutive phases and may be caused by a merger of two galaxies. In the first phase, which is called cold mode (or quasar mode; e.g. Kauffmann et al. 2003; Croton et al. 2006; Hardcastle et al. 2007), cold gas from the galaxies involved in the merger fuels the accretion accompanied by high star forming activity. Finally, the AGN heats or blows away the remaining gas and star formation ends. This represents the transition to the second phase, the so-called hot mode accretion (also known as radio mode; e.g. Narayan & Yi 1995). In this phase, the supermassive black hole (SMBH) can only accrete hot gas from the halo in so-called advection dominated accretion flows.
The accretion in the cold mode phase is radiatively efficient and observational evidence is difficult because of the highly obscured nucleus. In contrast, accretion in the hot mode phase is typically well below the Eddington limit and the accretion flow radiatively inefficient. In hot mode, AGN feedback is kinetic and the total energy output usually dominated by the mechanical power of the radio jets. Radio jets are associated with both accretion modes and the radio emission can be used to trace the mechanical jet power (e.g. Alexander & Hickox 2012 and references therein).
This scenario of negative AGN feedback is an important ingredient for the current preferred cosmological Λ cold dark matter (ΛCDM) model. In this model, negative AGN feedback is needed to make the number of massive and luminous galaxies in simulations consistent with the observed number (Springel et al. 2005; Croton et al. 2006).
Contrary to this widely accepted negative AGN feedback, examples have been found where AGN activity enhances star formation, i.e. showing a positive feedback (e.g. Klamer et al. 2004; Gaibler et al. 2012; Zinn et al. 2013; Karouzos et al. 2014). These observations are explained by the AGN jets propagating through the gas of the host galaxy, generating shocks that trigger the gravitational collaps of the gas and, by this, boost star formation.
One important class of object in studying AGN feedback processes is the class of high-redshift radio galaxies (HzRGs) since these galaxies can be observed out to high redshifts. HzRGs are very powerful radio-galaxies that contain significant emission both from a starburst activity and AGN activity. They are expected to be the progenitors of the most massive galaxies in the local universe (e.g. Seymour et al. 2007; De Breuck et al. 2010). Only around 200 of these objects – which are defined by z> 1 and L3 GHz> 1026 W Hz-1 – are known in the entire sky. However, a new class of object has recently been found that suggests a link to HzRGs: the class of infrared-faint radio sources.
1.1. Discovery and definition of infrared-faint radio sources
Infrared-faint radio sources (IFRS) are characterised by radio emission of the order of tenths to tens of mJy and associated deep near-infrared faintness. Norris et al. (2006) and Middelberg et al. (2008a) discovered these objects in the deep radio maps of the Australia Telescope Large Area Survey (ATLAS) in the Chandra Deep Field South (CDFS) and the European Large Area IR space observatory Survey South 1 (ELAIS-S1) as lacking infrared (IR) counterparts in the co-located Spitzer Wide-area Infrared Extragalactic Survey (SWIRE; Lonsdale et al. 2003). Zinn et al. (2011) defined two survey-independent criteria for the selection of IFRS:
-
(i)
S1.4 GHz/S3.6 μm> 500 and
-
(ii)
S3.6 μm< 30 μJy.
The high radio-to-IR flux density ratios, ensured by the first criterion, show that IFRS are clear outliers from the radio-to-IR correlation. The second criterion is equivalent to a distance selection and prevents ordinary objects at z ≲ 1.4 from being included in this class of object.
Based on the two selection criteria, Zinn et al. (2011) compiled a catalogue of 55 IFRS in the deep fields of the CDFS, ELAIS-S1, Spitzer extragalactic First Look Survey (xFLS), and the Cosmological Evolution Survey (COSMOS), based on the work by Norris et al. (2006), Middelberg et al. (2008a), and Garn & Alexander (2008). Later, IFRS were also found in the European Large Area IR space observatory Survey North 1 (ELAIS-N1) field by Banfield et al. (2011) and in the Lockman Hole field by Maini et al. (2013). Around 100 IFRS have been found in these deep fields, covering a total area of around 35 deg2.
Recently, Collier et al. (2014), for the first time, used a different approach and looked for IFRS in much shallower radio and IR data, which covered a much larger area compared to the deep fields mentioned above. Collier et al. used data from the Unified Radio Catalogue (URC; Kimball & Ivezić 2008; Kimball & Ivezic 2014) and from the all-sky Wide-Field IR Survey Explorer (WISE; Wright et al. 2010). Based on these data, Collier et al. compiled a catalogue of 1317 IFRS, all of them fulfilling both selection criteria from Zinn et al. (2011).
1.2. The properties of IFRS
Since the first detection of IFRS by Norris et al. (2006) it has been suggested that IFRS are radio-loud AGNs at significant redshifts (z ≳ 2). Different studies found evidence for this suggestion. Norris et al. (2007) and Middelberg et al. (2008b) presented very long baseline interferometry (VLBI) observations of IFRS and detected compact cores in two IFRS. Norris et al. used the Australian Long Baseline Array (LBA) and targeted two IFRS from the CDFS, out of which one was detected, showing a total VLBI flux density of 5.0 mJy at 1.6 GHz. The source was unresolved on VLBI scales and its size measured to be less than 0.03′′, corresponding to less than 260 pc at any redshift. Middelberg et al. also used the LBA and observed four IFRS from the ELAIS-S1 field at 1.6 GHz or 1.4 GHz. One out of these four IFRS was detected with a VLBI flux density of 12.5 mJy at 1.6 GHz. Based on a flux density of 7 mJy on the longest baselines, Middelberg et al. measured a lower limit on the brightness temperature of 3.6 × 106 K. Three IFRS were included in the sample observed with the Very Long Baseline Array (VLBA) in the CDFS by Middelberg et al. (2011a); however, they remained undetected. The two VLBI detections of IFRS showed that at least a fraction of IFRS contain AGNs.
Garn & Alexander (2008) and Huynh et al. (2010) found that obscured star forming galaxies cannot reproduce the characteristics of IFRS because IFRS clearly deviate from the radio-IR correlation, providing another hint for the AGN content in IFRS. Furthermore, Garn & Alexander and Huynh et al. presented the first spectral energy distribution (SED) modelling of IFRS and showed that 3C sources like 3C 273 are in agreement with the characteristics of IFRS if these sources are at redshifts z ≳ 2. Herzog et al. (2014) showed that the SED of their sample of IFRS can only be explained by radio-loud AGN templates.
A potential link between IFRS and HzRGs was first suggested by Huynh et al. (2010) based on the similarly high radio-to-IR flux density ratios. Middelberg et al. (2011b) showed that IFRS have steeper radio spectra1 (median spectral index α = −1.4) than the general radio source population (α = −0.86) and the AGN source population (α = −0.82), using data in the ELAIS-S1 field between 2.3 GHz and 8.4 GHz. Moreover, Middelberg et al. found that the radio spectrum of IFRS is even steeper than that of HzRGs (α = −1.02). Norris et al. (2011) pointed out that HzRGs are the only objects known at high redshifts that share the extreme radio-to-IR flux density ratios with IFRS. Based on this similarity and the deep IR faintness of IFRS, Norris et al. suggested that IFRS might follow the correlation between 3.6 μm flux density and redshift found for HzRGs (Seymour et al. 2007), similar to the K − z relation (Willott et al. 2003). Herzog et al. (2015) showed that the non-detection of IFRS in deep far-IR Herschel observations can only be explained by SED templates of HzRGs.
Collier et al. (2014) and Herzog et al. (2014) presented the first spectroscopic redshifts of IFRS and found all of 22 but one – which is most likely a misidentification or a star forming galaxy with an AGN – redshifts in the range 1.7 ≤ z ≤ 3.0, confirming the suggested high-redshift nature of IFRS. Furthermore, both studies found their data in agreement with the suggested correlation between near-IR flux density and redshift, indicating that most IFRS in deep fields – which were summarised by Zinn et al. (2011) and Maini et al. (2013) – might be at even higher redshifts.
1.3. Populations of IFRS found in deep and shallow surveys
Here, we consider the relationship between IFRS found in deep surveys of small area and those found in shallow all-sky surveys. First, all IFRS found in the various works mentioned above fulfil the – in some cases slightly changed – selection criteria by Zinn et al. (2011) and therefore qualify as IFRS. Maini et al. (2013) lowered the radio-to-IR flux density criterion and replaced the IR flux density criterion by an extension criterion. Others – like Norris et al. (2007) and Middelberg et al. (2008a) – required IFRS to be undetected at 3.6 μm without applying a radio-to-IR flux density criterion. Nevertheless, these IFRS, which were selected based on slightly different criteria, are close to fulfil the criteria by Zinn et al..
While the IFRS in deep fields usually have 1.4 GHz flux densities of tenths of mJy to a few mJy, the IFRS in the all-sky survey have median radio flux densities of several tens of mJy, some reaching even several hundred mJy. Similarly, each IFRS in the sample from Collier et al. (2014) provides an IR counterpart at 3.4 μm with a mean flux density of around 25 μJy, while a significant fraction of IFRS in deep fields has no IR counterpart in the even deeper 3.6 μm data. Thus, the median IFRS in deep fields is both radio and IR-fainter than the median IFRS in the shallower all-sky sample from Collier et al..
All spectroscopic redshifts of IFRS from both the deep fields and the shallow survey were found to be in the same redshift range 1.7 ≲ z ≲ 3.0. However, a selection effect putatively biases the observed spectroscopic redshift distribution of IFRS in the deep fields since the IFRS with known spectroscopic redshifts in these fields are the optically and IR brightest IFRS in that sample. Since their optical, IR, and radio properties are similar to those of the all-sky IFRS, it is expected that these IFRS represent the overlap between the fainter IFRS population in deep fields and the brighter all-sky IFRS population (Herzog et al. 2014).
It has been suggested by Collier et al. (2014) that their IFRS sample consists of the lowest-redshift IFRS while the IFRS found in deep fields are on average at higher redshifts. This suggestion is in agreement with the correlation between 3.6 μm flux density and redshift discussed by Norris et al. (2011), Collier et al., and Herzog et al. (2014). The overlapping spectroscopic redshifts found for both subsets are in agreement with this suggested unification, too.
Collier et al. (2014) could only set a lower limit of ~ 0.1 deg-2 for the sky density of IFRS with S1.4 GHz ≥ 7.5 mJy because of the non-uniform sensitivity of the WISE survey. In contrast, the sky density of IFRS in deep fields is of the order of a few per square degree and might reach 30 deg-2 (Zinn et al. 2011).
In this paper, we test the AGN content in IFRS based on VLBI observations with the VLBA of a large number of sources taken from the all-sky catalogue of IFRS (Collier et al. 2014). In Sect. 2, we describe our sample and the observing strategy. We discuss data calibration, imaging, flux measuring, and redshifts in Sect. 3. We analyse our data in Sect. 4 with respect to detection fraction (Sect. 4.1), compactness (Sect. 4.2), and individual sources (Sect. 4.3). We discuss the implications of our analysis in Sect. 5, and present our conclusions in Sect. 6. Throughout this paper, we use flat ΛCDM cosmological parameters ΩΛ = 0.7, ΩM = 0.3, H0 = 70 km s-1 Mpc-1 and the calculator by Wright (2006). We quote 1σ confidence intervals of binomial population proportions based on the Bayesian approach, following Cameron (2011).
2. Sample and observations
We selected all IFRS from the catalogue from Collier et al. (2014) which were located within 1 deg of a VLBA calibrator. This low angular separation between source and calibrator ensured the phase coherence required for VLBI observations. Since 1.4 GHz VLBI observations of the calibrators were not available, we required the calibrators to have a 2.3 GHz flux density of at least 0.2 Jy on a baseline of 5000 km. Out of the 1317 IFRS presented by Collier et al., 110 were found to provide a calibrator which fulfills the given conditions.
A VLBI detection provides unambiguous evidence for an AGN because compact radio emission in AGNs is a non-thermal process and results in brightness temperatures of more than 106 K to which our observations are sensitive. In contrast, compact radio emission in starburst galaxies, which is usually dominated by thermal free-free emission, is represented by brightness temperatures of around 104 K (e.g. Condon et al. 1991). Although brightness temperatures of 106 K can also be produced by very luminous radio supernovae (SNe; Huang et al. 1994; Smith et al. 1998), Kewley et al. (2000) showed that the probability for a VLBI-detected radio SN in a galaxy sample is very low. Therefore, a VLBI detection provides strong evidence for an AGN. However, it should be noted that the reverse is not true, i.e. the non-detection of a source in a VLBI observation does not imply the non-existence of an AGN. Instead, a VLBI non-detection implies significant extended emission compared to the compact core. The ratio of extended emission to core emission depends on beaming which can boost or suppress the compact core emission, AGN age, and the surrounding medium, affecting the brightness and extent of the diffuse radio lobes.
Since this is a detection experiment, the uv coverage is not critically important and a minimum number of six out of ten VLBA antennas was requested. Since the individual observations were short and independent of the weather conditions because of the observing frequency of 1.4 GHz, the observations were scheduled in filler time. Although the maps resulting from the data will be of rather poor quality, they will unambiguously resolve potential compact components.
Out of 110 proposed objects, 57 IFRS were observed in semester 14A in project BH197. The 57 observed IFRS were randomly selected based on the IFRS positions and available filler time at the VLBA. These observed sources have 1.4 GHz integrated flux densities between 11 mJy and 183 mJy in the NRAO VLA Sky Survey (NVSS; Condon et al. 1998). The VLBA observations were set to a bandwidth of 32 MHz in each of the eight basebands which were observed in dual polarisation at 1.4 GHz, resulting in a total data rate of 2048 Mbps.
Each of the 57 epochs had a total observing time of one hour. We decided to use two different approaches for the scan settings, depending on the distance between source and calibrator. If the separation between source and calibrator was less than 25′, we continuously pointed at the position in between IFRS and calibrator to prevent unnecessary nodding between the two sources. If the separation was more than 25′, we alternately observed the calibrator for 60 s and the source for 225 s, starting and ending with a scan on the calibrator. The resulting observing time on the IFRS was around 45 min. The data were correlated using the VLBA Distributed FX (DiFX) software correlator (Deller et al. 2007, 2011).
3. VLBA data calibration, optical properties, and redshifts
3.1. Data calibration, imaging, and flux measurement of the VLBA data
Calibration and imaging of the individual epochs was carried out based on a ParselTongue script. ParselTongue (Kettenis et al. 2006) is a Python-based interface to the Astronomical Image and Processing System2 (AIPS). The calibration and imaging strategy used here is very similar to the procedure described by Deller & Middelberg (2014). However, we calibrated the amplitudes using the technique suggested by VLBA Scientific Memo #37 (R. Craig Walker; Dec. 15, 2014).
In the pipeline, we loaded the data into AIPS and applied a priori flags and manual flags. We then corrected for ionospheric effects using the task TECOR, applied the latest earth orientation parameters, and corrected for parallactic angles, in the latter cases using the task CLCOR. Amplitudes were calibrated based on autocorrelation data using the task ACCOR. We corrected for primary beam effects using the task CLVLB, following the procedure outlined by Middelberg et al. (2013). Delay correction was carried out based on the calibrator, using the task FRING and a solution interval of 2 min. We applied a bandpass correction using the task BPASS. The new task ACSCL, implemented in AIPS in consequence of the flux density calibration errors described in the VLBA Scientific Memo #37, kept the calibrated autocorrelation values at unity. The flux density calibration was completed by using APCAL, calibrating the amplitudes based on system temperatures and gains. We used the AIPS/ParselTongue implementation of Pieflag (Middelberg 2006), dynspec-flagger, to automatically flag data affected by interference. Using the task CALIB, we performed one iteration of phase and amplitude self-calibration on the calibrator and applied the solution on the target. Finally, we imaged the UV data based on the task IMAGR into a map of 2048×2048 pixels with a pixel size of 1 milliarcsecond (mas) – matching the angular resolution of ~ 5 mas – using uniform weighting. In this step, we cleaned the dirty image in a given box, down to a flux of three times the root mean square (rms) or up to 500 iterations.
The mean synthesised beam size in our observations is 14.3 × 4.7 mas2. Because the linear scale is limited in a ΛCDM cosmology at redshifts 0.5 ≤ z ≤ 12 between 4 kpc/′′ and 8.5 kpc/′′, we were able to convert this beam size over this redshift range to an area of between 57 pc × 19 pc and 122 pc × 40 pc. The rms in the final maps is around 60 μJy beam-1, depending on the number of antennas. Of the 57 observations, 31, 21, 4, and 1 were carried out with 10, 9, 8, and 7 antennas, respectively. Since the longest VLBA baseline of 8611 km – between the stations Mauna Kea and St. Croix – was available in all observations, the east-west angular resolution of around 5 mas is similar for all 57 observations, whereas the north-south angular resolution varies slightly because of changing antenna availability. As an example, Fig. 1 shows the final map of IFRS F0398.
 |
Fig. 1 VLBA map of IFRS F0398. The source is slightly resolved with a peak flux density of 13.7 mJy beam-1 and an integrated flux density of 17.2 mJy. |
We measured the flux density of each component using the AIPS task JMFIT, setting a box of size of 40 pixels around the components. For a few sources, image artefacts resulted in unreasonable fluxes. In these cases, we manually measured flux densities using the task TVSTAT. Checks on control sources resulted in consistent flux measurements based on TVSTAT and JMFIT. For the brighter component in IFRS F0030, we measured the flux density using the blobcat package (Hales et al. 2012) because of the complex structure of this source. Following Deller & Middelberg (2014), we set a 6.75σ detection limit for all sources, corresponding to a mean detection sensitivity of around 450 μJy beam-1. Most of our sources are slightly resolved, but insufficiently resolved to determine the morphology. The resulting flux densities und flux density upper limits are summarised in Table 1. Since observations and data calibration are very similar to the approach taken by Deller & Middelberg who targeted more than 20 000 sources in their mJy Imaging VLBA Exploration (mJIVE) survey, we expect our flux densities to be of similar accuracy of 20%.
Component catalogue of 57 IFRS observed with the VLBA.
3.2. Optical properties and redshifts
Our sample was taken from the all-sky IFRS catalogue from Collier et al. (2014) who cross-matched their sources with the Sloan Digital Sky Survey (SDSS) DR9 (Ahn et al. 2012). For the purpose of this work, we cross-matched our sample of VLBA-observed IFRS to the recent SDSS DR10 (Ahn et al. 2014). 53 (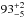 %) out of our IFRS are covered by SDSS DR10. Eleven (
%) out of our IFRS are covered by SDSS DR10. Eleven (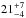 %) out of these 53 IFRS provide photometric counterparts which are all close to the sensitivity limit of SDSS.
%) out of these 53 IFRS provide photometric counterparts which are all close to the sensitivity limit of SDSS.
We used the software EAZY (Brammer et al. 2008) with the standard template set to derive photometric redshifts for our sources. Since most IFRS in the catalogue from Collier et al. (2014) are only detected in the WISE bands W1 (3.4 μm) and W2 (4.6 μm) – apart from the radio detections which are not used in the redshift fitting – measuring photometric redshifts is impossible for most of the IFRS in our sample. However, measuring photometric redshifts is possible for those IFRS with SDSS counterparts. For these eleven IFRS in our sample with SDSS counterparts, we obtained ten photometric redshifts using EAZY. As examples, we show the resulting fits for IFRS F0197 and F0273 in Fig. 2.
 |
Fig. 2 Resulting photometric redshift fit from EAZY for IFRS F0197 (left) and F0273 (right). The SED (orange line) shows the best fit template based on the peak redshift in the observer’s frame. Black dots with error bars represent photometric data points of the IFRS, whereas black triangles show the flux density of the fitted SED at the same wavelengths. The subplots in the upper right of both plots show the redshift-probability distribution. The redshift of the peak in the probability distribution is quoted below each subplot. |
The fitting of IFRS F0277 failed. Table 2 summarises the photometric redshifts and – where applicable – spectroscopic redshifts for our subsample of IFRS with SDSS DR10 counterparts.
Redshift information for those IFRS with SDSS DR10 detections.
Figure 3 shows the photometric redshifts as a function of the spectroscopic redshifts for the three IFRS in our sample for which SDSS DR10 provides spectroscopic redshifts.
 |
Fig. 3 Comparison of the photometric redshifts obtained from EAZY and the spectroscopic redshifts from SDSS DR10. The error bars show the 1σ uncertainties in the photometric redshifts as determined by EAZY. The solid line represents the positions of exact agreement between photometric and spectroscopic redshifts. |
Based on the SEDs resulting from the fitting of photometric redshifts, we find that most of our fitted IFRS are very blue. These characteristics can be explained by a Type I AGN in the optical. However, we stress that we might be significantly affected by selection bias since these IFRS are very close to the detection sensitivity of SDSS and SDSS is more sensitive to blue objects. Nevertheless, this study shows that at least some IFRS are very blue, non-dusty galaxies.
4. Analysis
4.1. VLBI detection fraction
In our VLBA observations, we detected 35 ( %) out of 57 observed IFRS, showing peak flux densities between 0.4 mJy beam-1 and 26.4 mJy beam-1 and integrated flux densities between 0.6 mJy and 40.4 mJy as listed in Table 1.
%) out of 57 observed IFRS, showing peak flux densities between 0.4 mJy beam-1 and 26.4 mJy beam-1 and integrated flux densities between 0.6 mJy and 40.4 mJy as listed in Table 1.
The detection of a source in VLBI observations with brightness temperatures above 106 K – which is reached for our VLBA observations – is an unambiguous sign for an AGN as discussed in Sect. 2. However, we note that the reverse is not true, i.e. the non-detection of a source in VLBI observations does not exclude the existence of an AGN. The detection of 35 out of 57 IFRS in our VLBA observations provides strong evidence that most – if not all – IFRS contain AGNs.
4.1.1. VLBI detection fraction compared to other samples
The detection fraction in our VLBA observations of  % down to a 6.75σ detection limit of ~ 0.45 mJy beam-1 is significantly higher than the detection fractions found by Garrington et al. (1999) or Deller & Middelberg (2014) who targeted large samples of sources from the Faint Images of the Radio Sky at Twenty centimetres (FIRST; Becker et al. 1995) survey in VLBI observations and detected 35% and 20%, respectively. However, the sensitivity of the respective VLBI observations and the sample selection criteria were different. Garrington et al. had a detection sensitivity between 1 mJy and 2 mJy and targeted FIRST sources with 1.4 GHz peak flux densities above 10 mJy, whereas Deller & Middelberg targeted all kinds of FIRST sources without any preselection at a varying detection sensitivity. In order to compare their detection fraction with that of Garrington et al., Deller & Middelberg cut their catalogue to FIRST sources with S1.4 GHz> 10 mJy beam-1 and to the VLBI detection sensitivity from Garrington et al.Deller & Middelberg found a detection fraction of 36% in that subsample, in agreement with the number from Garrington et al.
% down to a 6.75σ detection limit of ~ 0.45 mJy beam-1 is significantly higher than the detection fractions found by Garrington et al. (1999) or Deller & Middelberg (2014) who targeted large samples of sources from the Faint Images of the Radio Sky at Twenty centimetres (FIRST; Becker et al. 1995) survey in VLBI observations and detected 35% and 20%, respectively. However, the sensitivity of the respective VLBI observations and the sample selection criteria were different. Garrington et al. had a detection sensitivity between 1 mJy and 2 mJy and targeted FIRST sources with 1.4 GHz peak flux densities above 10 mJy, whereas Deller & Middelberg targeted all kinds of FIRST sources without any preselection at a varying detection sensitivity. In order to compare their detection fraction with that of Garrington et al., Deller & Middelberg cut their catalogue to FIRST sources with S1.4 GHz> 10 mJy beam-1 and to the VLBI detection sensitivity from Garrington et al.Deller & Middelberg found a detection fraction of 36% in that subsample, in agreement with the number from Garrington et al.
We followed the approach from Deller & Middelberg (2014) and compiled a subsample of our IFRS sample by including only those sources with an arcsec-scale 1.4 GHz flux density above 10 mJy beam-1, ending up with 56 IFRS. Setting our detection sensitivity to 1.5 mJy, we would have detected 25 (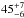 %) out of these 56 IFRS, i.e. a slightly higher fraction than those from Garrington et al. (1999) and Deller & Middelberg. Using a Fisher’s exact test (e.g. Wall & Jenkins 2012), we found a probability of 0.88 that our sample has a higher VLBI detection fraction than the sample from Deller & Middelberg.
%) out of these 56 IFRS, i.e. a slightly higher fraction than those from Garrington et al. (1999) and Deller & Middelberg. Using a Fisher’s exact test (e.g. Wall & Jenkins 2012), we found a probability of 0.88 that our sample has a higher VLBI detection fraction than the sample from Deller & Middelberg.
It is known that the radio source population at 1.4 GHz with flux densities above 1 mJy consists almost exclusively of AGNs (e.g. Condon et al. 2012, Fig. 11). This implies that the VLBI-observed subsamples from Garrington et al. (1999) and Deller & Middelberg (2014) and the sample presented in this work – all cut to 10 mJy and matched to the same sensitivity as discussed above – contain virtually only AGNs. Thus, based on the numbers given above, we find a tendency of a higher VLBI detection fraction for IFRS compared to the general AGN population.
Collier et al. (2014) discarded all objects from their IFRS catalogue which provided a spurious WISE counterpart to one of the radio lobes. It is unclear whether this selection criterion can explain the higher VLBI detection fraction of IFRS compared to the general AGN population. Apart from that, the only difference in selecting the objects of the general AGN sample and the IFRS sample is the application of the IFRS selection criteria from Zinn et al. (2011) mentioned in Sect. 1.1.
Figure 4 shows the VLBA detection fraction binned in the 3.4 μm flux density for our sample of IFRS.
 |
Fig. 4 Histogram of the VLBA detection and non-detection fraction, binned by the flux density at 3.4 μm. The horizontal lines show the overall detection and non-detection fraction of the observations presented in this work. 1σ confidence intervals are shown in grey. |
We do not find any evidence for a dependence of the VLBI detection fraction on the 3.4 μm flux density. We also tested the detection fraction against the arcsec-scale 1.4 GHz flux density, the radio-to-IR flux density ratio, and the WISE colour [W1-W2] and found no significant correlation.
Compact radio cores are detected in eight (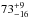 %) of the eleven IFRS with SDSS counterpart and in 24 (
%) of the eleven IFRS with SDSS counterpart and in 24 (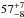 %) of the 42 IFRS covered by SDSS without SDSS counterpart. However, we do not consider this a significant difference (a) because these two subsamples are not flux-complete; (b) because of the non-uniform sensitivity of SDSS; and (c) because SDSS is biased towards detecting blue objects as discussed above.
%) of the 42 IFRS covered by SDSS without SDSS counterpart. However, we do not consider this a significant difference (a) because these two subsamples are not flux-complete; (b) because of the non-uniform sensitivity of SDSS; and (c) because SDSS is biased towards detecting blue objects as discussed above.
Three out of the eleven IFRS with SDSS counterpart are classified as “galaxy” in SDSS. We detected two (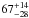 %) of these three galaxy-type IFRS in our VLBA observations. The other eight IFRS with SDSS counterpart are classified as “star” in SDSS. We note that this photometry-based classification is based on the extension of the object, i.e. objects classified as star are point-like, whereas extended objects are classified as galaxy. Out of these eight IFRS classified as star, we detected six (
%) of these three galaxy-type IFRS in our VLBA observations. The other eight IFRS with SDSS counterpart are classified as “star” in SDSS. We note that this photometry-based classification is based on the extension of the object, i.e. objects classified as star are point-like, whereas extended objects are classified as galaxy. Out of these eight IFRS classified as star, we detected six (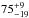 %) in our VLBA observations. Deller & Middelberg (2014) found a higher VLBI detection fraction for sources classified as star-like in SDSS. Our results are in agreement with this finding.
%) in our VLBA observations. Deller & Middelberg (2014) found a higher VLBI detection fraction for sources classified as star-like in SDSS. Our results are in agreement with this finding.
4.1.2. Dependence of the VLBI detection fraction on radio properties
Gigahertz peaked spectrum (GPS) and compact steep spectrum (CSS) sources are very compact AGNs and expected to be the earliest phases in the evolution of AGNs. GPS sources have a turnover frequency of around 1 GHz and are usually less than 1 kpc in size, whereas CSS sources are more extended with a size of a few kpc or a few tens of kpc. CSS sources are named for their steep radio spectra (α ≤ − 0.5; e.g. Randall et al. 2011).
Based on data at 6 cm, 20 cm, and 92 cm, Collier et al. (2014) classified 124 of their IFRS as CSS sources and 32 as GPS sources. Out of the 57 IFRS observed with the VLBA, five IFRS were classified as CSS sources and two as GPS sources. In our VLBA observations, we detected four out of five IFRS which were classified as CSS sources and both IFRS which were classified as GPS sources so that CSS/GPS sources have a higher detection rate (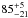 %) than the non-classified sources (
%) than the non-classified sources (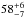 %).
%).
Collier et al. (2014) used the lower-resolution data of NVSS for the flux densities in their IFRS catalogue. They also listed the number of sources in the higher-resolution FIRST survey associated with the NVSS source. IFRS detected with more than one FIRST component are clearly extended radio galaxies and not GPS or CSS sources. Out of the 57 IFRS observed with the VLBA, 47 are associated with exactly one FIRST source, while ten IFRS are associated with two or three FIRST sources. Out of these ten IFRS with two or three FIRST counterparts, we detected one (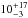 %) in our VLBA observations, whereas 34 (
%) in our VLBA observations, whereas 34 (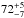 %) out of 47 IFRS with exactly one FIRST counterpart were detected with the VLBA. We found a statistically significantly higher VLBA detection fraction for IFRS with exactly one FIRST counterpart compared to the detection fraction of IFRS with more than one FIRST counterpart.
%) out of 47 IFRS with exactly one FIRST counterpart were detected with the VLBA. We found a statistically significantly higher VLBA detection fraction for IFRS with exactly one FIRST counterpart compared to the detection fraction of IFRS with more than one FIRST counterpart.
We also compared our VLBA detection fraction of IFRS with exactly one FIRST counterpart to the detection fraction found by Deller & Middelberg (2014) for the general radio source population. As described above, we matched the arcsec-scale radio flux density and the VLBA detection sensitivity to 10 mJy beam-1 and 1.5 mJy beam-1, respectively. We found a detection fraction of 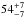 % for those IFRS with exactly one FIRST counterpart, compared to a detection fraction of 36% for the general radio source population above 10 mJy beam-1 measured by Deller & Middelberg. Thus, our sample of IFRS with exactly one FIRST counterpart is statistically different to the general radio source population, based on a probability of 0.01 in a Fisher’s exact test (e.g. Wall & Jenkins 2012) that the two samples are taken from the same parent population.
% for those IFRS with exactly one FIRST counterpart, compared to a detection fraction of 36% for the general radio source population above 10 mJy beam-1 measured by Deller & Middelberg. Thus, our sample of IFRS with exactly one FIRST counterpart is statistically different to the general radio source population, based on a probability of 0.01 in a Fisher’s exact test (e.g. Wall & Jenkins 2012) that the two samples are taken from the same parent population.
4.2. Compactness
We determined ratios of the integrated mas-scale flux density in the VLBA observations at 1.4 GHz to the integrated arcsec-scale flux density in NVSS at 1.4 GHz to fall between 0.86 and 0.014 for the IFRS detected in our VLBA observations. On average, this ratio, which we refer to as compactness, was 0.33 ± 0.23.
 |
Fig. 5 Histogram of the VLBA detections and non-detections, binned in the compactness at 1.4 GHz. Compactness is defined as the ratio of mas-scale flux density to arcsec-scale flux density. The vertical lines show the mean compactness – from left to right – of all VLBA-undetected IFRS, of all VLBA-observed IFRS, and of all VLBA-detected IFRS, respectively. The former two lines represent upper limits as indicated by the horizontal arrows. |
Figure 5 shows the number of detections binned by the compactness.
The mean compactness of our detected IFRS of 0.33 ± 0.23 is lower than that of the two former VLBI detections of IFRS where Norris et al. (2007) and Middelberg et al. (2008b) detected 88% and 58%, respectively, of the arcsec-scale flux density. This discrepancy may be due to small-number statistics or because our fluxes are measured on smaller scales than those from Norris et al. and Middelberg et al. The restoring beam of the LBA observations presented by Middelberg et al. was 51.7 mas × 23.6 mas, i.e. 17 times larger compared to the median beam of 14.3 mas × 4.7 mas in our VLBA observations. Norris et al. did not image their uv data because of the poor uv coverage, but their angular resolution was similar to that of Middelberg et al. Therefore, a lower fraction of detected flux in our VLBA observations could be expected.
4.2.1. Dependence of the compactness on the redshift
In the following, we tested our data against a potential correlation between redshift and compactness. SDSS DR10 provides spectroscopic redshifts for three out of our 57 IFRS. Two (z = 2.11 and z = 2.62) of those are undetected and one (z = 2.55) is detected in the VLBA observations. However, IFRS F0912 at z = 2.62 was observed for only ~ 25 min with the VLBA, resulting in a sensitivity only half that of the other sources. Since the number of objects in this subsample is too low to test our data, we extended our subsample by including those IFRS with photometric redshifts presented in Sect. 3.2.
Figure 6 shows the compactness as a function of the redshift for all ten VLBA-observed IFRS with redshift information.
 |
Fig. 6 Compactness as a function of redshift for those IFRS with redshift information. VLBA-detected IFRS are shown by crosses and the 6.75σ upper limits on the compactness of VLBA-undetected IFRS are shown by arrows. Three spectroscopic (red markers) and seven photometric (black markers) redshifts were used in this analysis. Note that the errors on the compactness are around 20%. |
The data do not provide compact objects at low redshifts, whereas compact objects were found at higher redshifts. The data suggest a possible correlation between compactness and redshift for IFRS. We tested the data using a Spearman rank correlation test (e.g. Wall & Jenkins 2012) and found a correlation coefficient between 0.66 and 0.52, indicating a positive correlation between redshift and compactness. A correlation coefficient of + 1 and −1 represents an ideal correlation and anticorrelation, respectively, whereas an uncorrelated data set is represented by a coefficient of 0. In our case, the probability that the two parameters are uncorrelated is between 0.019 and 0.063. The margin arises from the unknown compactnesses of the VLBA-undetected sources for which only upper limits are known. We determined this margin using a permutation test. Based on the strong positive correlation coefficients, we suggest a correlation between compactness and redshift for our sample of IFRS. When considering only the VLBA-detected sources, we found a correlation coefficient of 0.96 and a probability of 4.5 × 10-4 that the parameters are uncorrelated. We cautiously note that the putative positive correlation seems to be mainly based on the two highest-redshift IFRS in Fig. 6 which might be outliers. Therefore, we emphasise that this suggested correlation needs further testing.
4.2.2. Dependence of the compactness on the 1.4 GHz flux density
 |
Fig. 7 Compactness as a function of the arcsec-scale 1.4 GHz flux density. VLBA-detected IFRS are shown by crosses and the 6.75σ upper limits on the compactness of VLBA-undetected IFRS are shown by black arrows. The grey horizontal lines represent – from top to bottom – the mean compactness of all VLBA-detected IFRS, of all VLBA-observed IFRS, and all VLBA-undetected IFRS, respectively. The latter ones represent upper limits as indicated by grey arrows. The black line shows the minimal detectable compactness depending on the arcsec-scale flux density, based on an mean detection sensitivity of 450 μJy in our VLBA observations. |
Figure 7 shows the compactness as a function of the arcsec-scale 1.4 GHz flux density and includes detections and upper limits for the non-detections. We did not find compact radio-bright IFRS, whereas compact radio-faint IFRS are common in our sample. If we divide our sample at an arcsec-scale flux density of 60 mJy, we find twelve (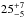 %) sources with compactnesses above 0.4 and 36 (
%) sources with compactnesses above 0.4 and 36 (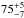 ) sources with compactnesses below 0.4 in the fainter subsample. At arcsec-scale flux densities above 60 mJy, we find nine (100-17%) sources with compactnesses below 0.4 and no (0+ 17%) source with a compactness above 0.4. This is in agreement with results from Deller & Middelberg (2014), who found a statistically significant anti-correlation between compactness and arcsec-scale 1.4 GHz flux density in their sample of randomly selected radio sources. We used a Spearman rank correlation test (e.g. Wall & Jenkins 2012) to test for putative correlations. However, because of the significant fraction of upper limits in this plot, we can only narrow down the correlation coefficient to a rather broad range. We found that the correlation coefficient is between 0.39 and −0.15. Based on this test, we cannot exclude either a positive or a negative correlation or a decorrelation.
) sources with compactnesses below 0.4 in the fainter subsample. At arcsec-scale flux densities above 60 mJy, we find nine (100-17%) sources with compactnesses below 0.4 and no (0+ 17%) source with a compactness above 0.4. This is in agreement with results from Deller & Middelberg (2014), who found a statistically significant anti-correlation between compactness and arcsec-scale 1.4 GHz flux density in their sample of randomly selected radio sources. We used a Spearman rank correlation test (e.g. Wall & Jenkins 2012) to test for putative correlations. However, because of the significant fraction of upper limits in this plot, we can only narrow down the correlation coefficient to a rather broad range. We found that the correlation coefficient is between 0.39 and −0.15. Based on this test, we cannot exclude either a positive or a negative correlation or a decorrelation.
4.3. Individual sources
In the following, we discuss three individual sources which are of particular interest.
4.3.1. F0398
The only VLBA-detected IFRS with spectroscopic redshift is F0398 at z = 2.55, showing an arcsec-scale 1.4 GHz integrated flux density of 62.9 mJy. This corresponds to a K-corrected 1.4 GHz rest-frame luminosity of 2.3 × 1027 W Hz-1, using the radio spectral index α = −0.72 between 20 cm and 92 cm from Collier et al. (2014). In our VLBA observations, the source – shown in Fig. 1 – is slightly resolved with a peak flux density of 13.7 mJy beam-1 and an integrated flux density of 17.2 mJy, corresponding to a luminosity of 6.3 × 1026 W Hz-1 on scales smaller than 146 pc × 43 pc. Based on this luminosity, F0398 can be classified as Fanaroff-Riley (FR; Fanaroff & Riley 1974) Type II. The source has a compactness of 0.283.
4.3.2. F0030
 |
Fig. 8 VLBA map of IFRS F0030. The brighter component (upper left) has a complex morphology and a flux density of 21.8 mJy. The second component (lower right) has a flux density of 6.0 mJy and is separated by |
A particularly interesting source is F0030 which has two spatially separated components in the VLBA map shown in Fig. 8. The first, brighter component shows a mas-scale flux density of 21.8 mJy (S/N = 55) and is spatially resolved with a complex morphology which is unique in our observations. The second component shows a flux density of 6.0 mJy (S/N = 46) and is separated by 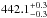 mas. The linear distance between both components is between 1.7 kpc and 3.8 kpc at any redshift in the range 0.5 ≤ z ≤ 12.
mas. The linear distance between both components is between 1.7 kpc and 3.8 kpc at any redshift in the range 0.5 ≤ z ≤ 12.
In order to obtain a rough spectral index of the components, we separately imaged the four lower-frequency basebands and the four higher-frequency basebands centred at 1.380 GHz and 1.508 GHz, respectively. Fluxes were measured as described in Sect. 3.1. We obtained spectral indices of −1.2 ± 1.2 and −1.2 ± 0.6 for component 1 and 2, respectively.
4.3.3. F0257
 |
Fig. 9 VLBA map of IFRS F0257. The brighter component (left) has a flux density of 5.7 mJy. The second component (right) has a flux density of 2.1 mJy and is separated by |
Source F0257 – shown in Fig. 9 – consists of two individual components. While the brighter component shows a flux density of 5.7 mJy (S/N = 77), the weaker component is 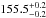 mas distant and shows less than half of the other component’s flux density (2.1 mJy beam-1, S/N = 36). This angular distance corresponds to a linear distance between 0.6 kpc and 1.3 kpc. We measured mas-scale radio spectral indices between 1.380 GHz and 1.508 GHz of −0.3 ± 0.4 and 0.2 ± 0.9, respectively, for component 1 and 2. Collier et al. (2014) measured an arcsec-scale radio spectral index of −0.6 between 6 cm, 20 cm, and 92 cm.
mas distant and shows less than half of the other component’s flux density (2.1 mJy beam-1, S/N = 36). This angular distance corresponds to a linear distance between 0.6 kpc and 1.3 kpc. We measured mas-scale radio spectral indices between 1.380 GHz and 1.508 GHz of −0.3 ± 0.4 and 0.2 ± 0.9, respectively, for component 1 and 2. Collier et al. (2014) measured an arcsec-scale radio spectral index of −0.6 between 6 cm, 20 cm, and 92 cm.
4.3.4. Could double component sources be a coincidence?
Sources F0030 and F0257 have both two compact components separated by 445 mas and 155 mas, respectively. In the following, we estimate the probability that two close by components are unrelated background sources. NVSS found 1.8 million radio sources in an area of 3 × 104 deg2, out of which less than 50% have compact cores detectable in VLBI observations (Deller & Middelberg 2014). This corresponds to a sky density of 1.8 × 10-6 arcsec-2. The probability of finding an additional unrelated source at a given position in an area of 0.5″ × 0.5″ is therefore of the order of 5 × 10-7. Thus, we can effectively rule out any chance that the two components found both in F0030 and F0257 are physically unrelated.
5. Discussion
Our observations increase the number of VLBI-detected IFRS from 2 to 37. Based on our detection fraction of  % and a reasonably large sample size, we find strong evidence that most – if not all – IFRS contain AGNs. This result confirms earlier studies by e.g. Garn & Alexander (2008), Middelberg et al. (2011b), and Herzog et al. (2014), who suggested compact cores in IFRS based on SED modelling, radio-to-IR flux density ratios, and emission lines in optical spectra. With higher sensitivity, we would have most likely detected more sources in our VLBA observations.
% and a reasonably large sample size, we find strong evidence that most – if not all – IFRS contain AGNs. This result confirms earlier studies by e.g. Garn & Alexander (2008), Middelberg et al. (2011b), and Herzog et al. (2014), who suggested compact cores in IFRS based on SED modelling, radio-to-IR flux density ratios, and emission lines in optical spectra. With higher sensitivity, we would have most likely detected more sources in our VLBA observations.
We also tested our data for different potential correlations in Sect. 4. Although not all of them are statistically significant, in the following, we explore the astrophysical consequences if these results are confirmed by subsequent observations and describe how these hypotheses can be tested.
In Sect. 4.2.2, we found a tendency that radio-brighter IFRS are less compact. Deller & Middelberg (2014) found the same behaviour when testing the general AGN population and argued that this anti-correlation might be explained by Doppler boosting effects as presented by Mullin et al. (2008). Mullin et al. studied a complete sample of narrow-line and broad-line radio galaxies and found an anti-correlation between radio luminosity and core prominence. They argued that higher-luminosity sources have higher boosting factors, associated with narrower boosting solid angles and a higher fraction of sources for which a Doppler suppressed core is seen. In contrast, lower-luminosity sources have lower boosting factors and wider solid angles, corresponding to a lower core supression fraction and a higher compactness.
We argue that another factor might contribute to the observed behaviour in our sample. It is known that AGNs evolve from very compact to extended objects by forming and expanding jets, associated with an increasing total luminosity. Namely, GPS sources are most compact and evolve into CSS sources and finally into the largest radio galaxies, FR Type I or II (e.g. O’Dea 1998; Snellen et al. 1999; Fanti 2009). Following this sequence, we would expect younger AGNs to be more compact than old AGNs.
We note that both effects might overlap since they both predict a lower compactness at higher luminosities. Based on the slightly higher VLBI detection fraction of IFRS – which is expected to be a result of higher compactnesses – compared to the general AGN population as found in Sects. 4.1.1 and 4.1.2, we suggest that IFRS are on average younger than the general AGN population. This would be in agreement with results by Middelberg et al. (2011b) and Collier et al. (2014) who found some IFRS to be GPS and CSS sources. The higher VLBI detection fraction for IFRS classified as GPS and CSS sources compared to non-classified IFRS reported in Sect. 4.1.2 also agrees with this reasoning.
We suggest that – at least some – IFRS are young AGNs. However, the sample presented by Collier et al. (2014) contains IFRS with different characteristics. IFRS, which are associated with more than one FIRST source, are clearly no GPS or CSS sources but extended radio galaxies. Those sources would be expected to be older and less compact than IFRS with exactly one FIRST counterpart. We found evidence for this expected behaviour in Sect. 4.1.2 based on a lower detection fraction for IFRS that are extended in arcsec-resolution images. We therefore suggest that these extended IFRS are on average older and more evolved than the VLBA-detected IFRS.
We found lower mean compactnesses of our VLBA-detected IFRS compared to the other two VLBI-detections of IFRS by Norris et al. (2007) and Middelberg et al. (2008b). In addition to the technical explanations given in Sect. 4.2, this discrepancy can also be explained by boosting effects. The IFRS from Norris et al. and Middelberg et al. are radio-fainter than the IFRS analysed in our work. Following the reasoning by Deller & Middelberg (2014) that brighter objects are more likely to be Doppler suppressed, lower compactnesses for our IFRS compared to the fainter IFRS from Norris et al. and Middelberg et al. could be expected.
In Sect. 4.2.1, we found a statistically significant correlation between redshift and compactness, with higher-redshift IFRS being more compact. Two arguments can explain this correlation. (a) Higher-redshift objects have a tendency to be younger than low-redshift versions of the same class of object. Combining the increasing luminosity of GPS and CSS sources with time and the boosting-related argument of decreasing compactness with luminosity, higher-redshift – and thus younger and fainter – IFRS would be expected to be more compact. (b) At higher redshifts, IFRS are more likely to be located in gas-rich environments as shown for high-redshift galaxies (Klamer et al. 2006). The higher gas density confines these objects and keeps them more compact.
These results are all in agreement with the scenario that IFRS are younger and therefore less luminous compared to the general AGN population, resulting in higher compactnesses and higher detection fractions. However, we stress that this putative connection between the age of IFRS and their VLBI properties is not statistically significant and needs further testing.
Alternatively, the slightly higher VLBI detection fraction of IFRS compared to the general AGN population could also be explained by a higher dust content of IFRS, making it harder for the jets to expand and resulting in a more compact object. However, no evidence has been found that IFRS are obscured by dust. On the contrary, Collier et al. (2014) and Herzog et al. (2014) argued that the IR faintness of IFRS is not caused by dust extinction. The SEDs resulting from our photometric redshift fitting presented in Sect. 3.2 also indicate that at least some IFRS are very blue and do not support the hypothesis that a significant fraction of IFRS is associated with dusty galaxies.
Future observations will help to test the hypotheses made in this work. In particular, additional VLBA observations – similar to the observations presented in this work – scheduled for semester 15A will increase the sample size of VLBI-observed IFRS, providing the basis for more robust tests.
We plan to match arcsec-resolution radio data at higher and lower frequencies, enabling the measurement of spectral indices and turnover frequencies of IFRS. This information will bring out a putative overlap between IFRS and GPS/CSS sources and provide further insights into the evolutionary status of IFRS (Herzog et al., in prep.).
Radio observations – exposing the intermediate-resolution morphologies of IFRS – could discriminate between the two mechanisms which may be responsible for the lower compactness of brighter objects: beaming and age. If beaming is the predominant cause for this effect, the radio-fainter IFRS should mainly be one-sided objects (core-jet) since a beaming effect is more likely to be seen for fainter objects as discussed above. In contrast, radio-brighter IFRS would be expected to show a more symmetric structure. However, if the anti-correlation between compactness and arcsec-scale radio flux density is mainly driven by the age of the objects, no difference in the morphology would be expected, although radio-brighter objects should be larger.
Two IFRS stand out from our sample since they were found to be composed of two mas-scale components, separated by a few hundred mas. There are four different explanations for those sources which we now discuss.
-
(i)
GPS/CSS double lobe sources: it is known that GPSand CSS double lobe sources can appear as separate com-ponents in VLBI observations (Snellenet al. 2003). In thatcase, the two components would be hot-spots inthe two jets and steep spectral indices would be ex-pected (e.g. Hovattaet al. 2014), while the VLBI-undetected core of the source would be between bothcomponents. GPS sources are usually smaller than 1[en-tity!#x2009!]kpc (O’Dea 1998),whereas CSS sources show extensions of a few to a few tens ofkpc (Fanti 2009; Randallet al. 2011).
-
(ii)
Compact core and jet of a GPS or CSS source: related to the first scenario, the two components could be the compact core of the AGN and a hot-spot in one jet. In that case, the spectral indices of both components can be different. While the hot-spot should provide a steep spectrum as discussed above, the core component would most likely provide a flat spectrum. However, the core spectrum could also be steep (Hovatta et al. 2014).
-
(iii)
Gravitational lensing: the appearence of two components can also be explained by gravitational lensing (e.g. Porcas 1998). In that case, the emission seen as two components would originate from one distant source whose emission is deflected by the gravitation of a nearby object. Therefore, similar spectral indices for the two components are expected. In F0030 and F0257, the two components are too close to find a potential gravitational lensing effect in optical images.
-
(iv)
Binary black hole: the two components could also be a binary black hole (e.g. Burke-Spolaor 2011). In that case, the spectral indices of the components could be flat or steep or mixed as discussed in (ii) for the compact core.
Based on the available data, we are not able to exclude any of those four different explanations because of the large error bars on the spectral indices. F0030 is unlikely to be a GPS source because of the linear size of more than 1.7 kpc. Following the correlation between intrinsic peak frequency and linear size of compact AGNs presented by O’Dea & Baum (1997), F0030 would be expected to show a rest-frame turn-over frequency of less than a few hundred MHz. Particularly, F0030 has different characteristics than the high-redshift (z = 5.774) steep spectrum source J0836+0054 (Petric et al. 2003; Frey et al. 2005). This RL quasar shows arcsec-scale properties (S1.4 GHz = 1.75 mJy, α = −0.8) similar to those of IFRS. However, in contrast to F0030, J0836+0054 has a second arcsec-scale radio component which was undetected in VLBI observations and is most likely associated with a lower-redshift galaxy.
6. Conclusion
We observed 57 IFRS with the VLBA and detected compact emission in 35 of them. Based on these observations, we draw the following conclusions.
-
We tested the hypothesis that IFRS contain AGNs. Ourobservations finally confirm the suggested compact cores in themajority of – if not all – IFRS, establishing IFRS as a new class ofAGN. Our data increase the number of VLBI-detected IFRS from2 to 37.
-
Our data suggest that radio-brighter IFRS are on average less compact. This finding agrees with the evolutionary scenario that young AGNs evolve by expanding jets, becoming radio brighter and less compact with time. However, boosting effects may play a role, too.
-
We found a marginal tendency for IFRS to show a higher VLBI detection fraction compared to randomly selected sources with mJy arcsec-scale flux densities, i.e. mainly AGNs. In our sample, the detection fraction is higher for IFRS with exactly one FIRST counterpart and for IFRS classified as GPS and CSS sources.
-
A statistically significant correlation between redshift and compactness was found in our data for IFRS with higher-redshift sources to be more compact. This is in agreement with higher-redshift sources being located in denser environments and having a tendency to be younger.
-
Two sources show two components each, separated by between 0.4 kpc and 3 kpc at any reasonable redshift. These components might be jet/jet or core/jet components of an AGN, a binary black hole, or arising from gravitational lensing.
All our findings are in agreement with the scenario that IFRS contain young AGNs which are in an early stage of their evolution. Their jets are not yet formed or expanded significantly, resulting in a very compact source. When evolving, the jets expand and the total radio fluxes of the sources increase, while the compactnesses decrease at the same time. We note that some IFRS already formed jets as known from arcsec-resolution maps.
Our analyses in this work were limited because of the low number of objects in relevant subsamples. Based on new data from VLBA observations of IFRS in semester 15A and planned lower-resolution observations, we are aiming at extending our study and further testing the hypotheses presented in this work.
Acknowledgments
A.T.D. acknowledges support from an NWO Veni Fellowship. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This work made use of the Swinburne University of Technology software correlator, developed as part of the Australian Major National Research Facilities Programme and operated under licence. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
References
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M., & Hickox, R. C. 2012, New A Rev., 56, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Banfield, J. K., George, S. J., Taylor, A. R., et al. 2011, ApJ, 733, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Burke-Spolaor, S. 2011, MNRAS, 410, 2113 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, E. 2011, PASA, 28, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Collier, J. D., Banfield, J. K., Norris, R. P., et al. 2014, MNRAS, 439, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Huang, Z.-P., Yin, Q. F., & Thuan, T. X. 1991, ApJ, 378, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Fomalont, E. B., et al. 2012, ApJ, 758, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- De Breuck, C., Seymour, N., Stern, D., et al. 2010, ApJ, 725, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., & Middelberg, E. 2014, AJ, 147, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Tingay, S. J., Bailes, M., & West, C. 2007, PASP, 119, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Brisken, W. F., Phillips, C. J., et al. 2011, PASP, 123, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Fanti, C. 2009, Astron. Nachr., 330, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Frey, S., Paragi, Z., Mosoni, L., & Gurvits, L. I. 2005, A&A, 436, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaibler, V., Khochfar, S., Krause, M., & Silk, J. 2012, MNRAS, 425, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Garn, T., & Alexander, P. 2008, MNRAS, 391, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Garrington, S. T., Garrett, M. A., & Polatidis, A. 1999, New A Rev., 43, 629 [Google Scholar]
- Hales, C. A., Murphy, T., Curran, J. R., et al. 2012, MNRAS, 425, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Herzog, A., Middelberg, E., Norris, R. P., et al. 2014, A&A, 567, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herzog, A., Norris, R. P., Middelberg, E., et al. 2015, A&A, accepted [Google Scholar]
- Hovatta, T., Aller, M. F., Aller, H. D., et al. 2014, AJ, 147, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Z. P., Thuan, T. X., Chevalier, R. A., Condon, J. J., & Yin, Q. F. 1994, ApJ, 424, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Huynh, M. T., Norris, R. P., Siana, B., & Middelberg, E. 2010, ApJ, 710, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Karouzos, M., Im, M., Trichas, M., et al. 2014, ApJ, 784, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kettenis, M., van Langevelde, H. J., Reynolds, C., & Cotton, B. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 497 [Google Scholar]
- Kewley, L. J., Heisler, C. A., Dopita, M. A., et al. 2000, ApJ, 530, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Kimball, A., & Ivezic, Z. 2014, ArXiv e-prints [arXiv:1401.1535] [Google Scholar]
- Kimball, A. E., & Ivezić, Ž. 2008, AJ, 136, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Klamer, I. J., Ekers, R. D., Sadler, E. M., & Hunstead, R. W. 2004, ApJ, 612, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Klamer, I. J., Ekers, R. D., Bryant, J. J., et al. 2006, MNRAS, 371, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Smith, H. E., Rowan-Robinson, M., et al. 2003, PASP, 115, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Maini, A., Prandoni, I., Norris, R. P., et al. 2013, A&A, submitted [Google Scholar]
- Middelberg, E. 2006, PASA, 23, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Middelberg, E., Norris, R. P., Cornwell, T. J., et al. 2008a, AJ, 135, 1276 [NASA ADS] [CrossRef] [Google Scholar]
- Middelberg, E., Norris, R. P., Tingay, S., et al. 2008b, A&A, 491, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Middelberg, E., Deller, A., Morgan, J., et al. 2011a, A&A, 526, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Middelberg, E., Norris, R. P., Hales, C. A., et al. 2011b, A&A, 526, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Middelberg, E., Deller, A. T., Norris, R. P., et al. 2013, A&A, 551, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mullin, L. M., Riley, J. M., & Hardcastle, M. J. 2008, MNRAS, 390, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Afonso, J., Appleton, P. N., et al. 2006, AJ, 132, 2409 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Tingay, S., Phillips, C., et al. 2007, MNRAS, 378, 1434 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Afonso, J., Cava, A., et al. 2011, ApJ, 736, 55 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P. 1998, PASP, 110, 493 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P., & Baum, S. A. 1997, AJ, 113, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Petric, A. O., Carilli, C. L., Bertoldi, F., et al. 2003, AJ, 126, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Porcas, R. W. 1998, in IAU Colloq. 164: Radio Emission from Galactic and Extragalactic Compact Sources, eds. J. A. Zensus, G. B. Taylor, & J. M. Wrobel, ASP Conf. Ser., 144, 303 [Google Scholar]
- Randall, K. E., Hopkins, A. M., Norris, R. P., & Edwards, P. G. 2011, MNRAS, 416, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Seymour, N., Stern, D., De Breuck, C., et al. 2007, ApJS, 171, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, H. E., Lonsdale, C. J., Lonsdale, C. J., & Diamond, P. J. 1998, ApJ, 493, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., Schilizzi, R. T., Miley, G. K., et al. 1999, New A Rev., 43, 675 [Google Scholar]
- Snellen, I. A. G., Mack, K.-H., Schilizzi, R. T., & Tschager, W. 2003, PASA, 20, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wall, J. V., & Jenkins, C. R. 2012, Practical statistics for astronomers, Cambridge Observing Handbooks for Research Astronomers (Leiden: Cambridge Univ. Press) [Google Scholar]
- Willott, C. J., Rawlings, S., Jarvis, M. J., & Blundell, K. M. 2003, MNRAS, 339, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L. 2006, PASP, 118, 1711 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, P.-C., Middelberg, E., & Ibar, E. 2011, A&A, 531, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zinn, P.-C., Middelberg, E., Norris, R. P., & Dettmar, R.-J. 2013, ApJ, 774, 66 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 VLBA map of IFRS F0398. The source is slightly resolved with a peak flux density of 13.7 mJy beam-1 and an integrated flux density of 17.2 mJy. |
| In the text | |
 |
Fig. 2 Resulting photometric redshift fit from EAZY for IFRS F0197 (left) and F0273 (right). The SED (orange line) shows the best fit template based on the peak redshift in the observer’s frame. Black dots with error bars represent photometric data points of the IFRS, whereas black triangles show the flux density of the fitted SED at the same wavelengths. The subplots in the upper right of both plots show the redshift-probability distribution. The redshift of the peak in the probability distribution is quoted below each subplot. |
| In the text | |
 |
Fig. 3 Comparison of the photometric redshifts obtained from EAZY and the spectroscopic redshifts from SDSS DR10. The error bars show the 1σ uncertainties in the photometric redshifts as determined by EAZY. The solid line represents the positions of exact agreement between photometric and spectroscopic redshifts. |
| In the text | |
 |
Fig. 4 Histogram of the VLBA detection and non-detection fraction, binned by the flux density at 3.4 μm. The horizontal lines show the overall detection and non-detection fraction of the observations presented in this work. 1σ confidence intervals are shown in grey. |
| In the text | |
 |
Fig. 5 Histogram of the VLBA detections and non-detections, binned in the compactness at 1.4 GHz. Compactness is defined as the ratio of mas-scale flux density to arcsec-scale flux density. The vertical lines show the mean compactness – from left to right – of all VLBA-undetected IFRS, of all VLBA-observed IFRS, and of all VLBA-detected IFRS, respectively. The former two lines represent upper limits as indicated by the horizontal arrows. |
| In the text | |
 |
Fig. 6 Compactness as a function of redshift for those IFRS with redshift information. VLBA-detected IFRS are shown by crosses and the 6.75σ upper limits on the compactness of VLBA-undetected IFRS are shown by arrows. Three spectroscopic (red markers) and seven photometric (black markers) redshifts were used in this analysis. Note that the errors on the compactness are around 20%. |
| In the text | |
 |
Fig. 7 Compactness as a function of the arcsec-scale 1.4 GHz flux density. VLBA-detected IFRS are shown by crosses and the 6.75σ upper limits on the compactness of VLBA-undetected IFRS are shown by black arrows. The grey horizontal lines represent – from top to bottom – the mean compactness of all VLBA-detected IFRS, of all VLBA-observed IFRS, and all VLBA-undetected IFRS, respectively. The latter ones represent upper limits as indicated by grey arrows. The black line shows the minimal detectable compactness depending on the arcsec-scale flux density, based on an mean detection sensitivity of 450 μJy in our VLBA observations. |
| In the text | |
 |
Fig. 8 VLBA map of IFRS F0030. The brighter component (upper left) has a complex morphology and a flux density of 21.8 mJy. The second component (lower right) has a flux density of 6.0 mJy and is separated by |
| In the text | |
 |
Fig. 9 VLBA map of IFRS F0257. The brighter component (left) has a flux density of 5.7 mJy. The second component (right) has a flux density of 2.1 mJy and is separated by |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


