| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201525873 | |
| Published online | 27 May 2015 | |
Precise mass and radius measurements for the components of the bright solar-type eclipsing binary star V1094 Tauri⋆
1
Astrophysics Group, Keele University,
Keele,
Staffordshire
ST5 5BG,
UK
e-mail:
p.maxted@keele.ac.uk, richard.hutcheon@btinternet.com
2
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge,
MA
02138,
USA
e-mail: gtorres@cfa.harvard.edu; rstefanik@cfa.harvard.edu
3
Physics Department, University of Arkansas,
Fayetteville, AR
72701,
USA
4
Department of Physics, University of Zagreb,
Bijenička cesta 32,
10000
Zagreb,
Croatia
5
Department of Physics, Gettysburg College, 300 North Washington Street,
Gettysburg, PA
17325,
USA
6
Niels Bohr Institute, Copenhagen University,
Juliane Maries Vej 30,
2100
Copenhagen Ø,
Denmark
Received: 11 February 2015
Accepted: 15 March 2015
Context. V1094 Tau is a bright eclipsing binary star with an orbital period close to nine days that contains two stars similar to the Sun.
Aims. Our aim is to test models of Sun-like stars using precise and accurate mass and radius measurements for both stars in V1094 Tau.
Methods. We present new spectroscopy of V1094 Tau, which we use to estimate the effective temperatures of both stars and to refine their spectroscopic orbits. We also present new, high-quality photometry covering both eclipses of V1094 Tau in the Strömgren uvby system and in the Johnson V-band.
Results. The masses, radii, and effective temperatures of the stars in V1094 Tau are found to be MA = 1.0965 ± 0.0040 M⊙, RA = 1.4109 ± 0.0058 R⊙, Teff,A = 5850 ± 100 K, MB = 1.0120 ± 0.0028 M⊙, RB = 1.1063 ± 0.0066 R⊙, and Teff,B = 5700 ± 100 K. An analysis of the times of mid-eclipse and the radial velocity data reveals apsidal motion with a period of 14 500 ± 3700 years.
Conclusions. The observed masses, radii, and effective temperatures are consistent with stellar models for an age ≈6 Gyr if the stars are assumed to have a metallicity similar to the Sun. This estimate is in reasonable agreement with our estimate of the metallicity derived using Strömgren photometry and treating the binary as a single star ([ Fe/H ] = −0.09 ± 0.11). The rotation velocities of the stars suggest that V1094 Tau is close to the limit at which tidal interactions between the stars force them to rotate pseudo-synchronously with the orbital motion.
Key words: binaries: eclipsing / stars: solar-type / stars: fundamental parameters / stars: individual: V1094 Tau
The table of the light curves shown in Fig. 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/578/A25
© ESO, 2015
1. Introduction
V1094 Tau (HD 284195) is a ninth-magnitude star that was discovered to be an eclipsing binary star by Kaiser (1994) using photographic photometry. The period quoted in that paper is incorrect and was later found to be the time between the secondary and primary minima. The correct period (P ≈ 8.988 d) was first given by Kaiser & Frey (1998), who also established that the orbit is eccentric, with the secondary minimum falling near phase 0.65. Observations of the times of mid-eclipse have continued since its discovery and have been analysed by Wolf et al. (2010), who claim to have detected apsidal motion with a period of 13 600 years and variations in these times of mid-eclipse with a period of about eight years and an amplitude of 200 s that they suggest may be due to a third body in the system.
The spectroscopic orbits of both stars have been measured to good accuracy by Griffin & Boffin (2003). No good light curves of the star were available at that time, but they were able to establish that the rotation of the stars is likely to be pseudo-synchronised with the orbital motion, that the masses are close to 1.1 M⊙ and 1.0 M⊙, and that the spectral types of the stars are approximately G0 and G3.
The techniques for measuring the masses and radii of the stars in eclipsing binaries, such as V1094 Tau to good accuracy (≈1%) independently of any stellar structure models, are now well established. To obtain masses and radii to this precision requires light curves of good quality that cover both eclipses and spectroscopic orbits with good phase coverage based on high-resolution spectroscopy. With data of this quality, it is possible to critically test stellar structure models, particularly if these mass and radius estimates can be complemented with reliable estimates for the effective temperatures of the stars and their metallicity (Torres et al. 2010). Compilations of such data have also been used to establish empirical relationships between mass, radius, effective temperature, etc. These empirical relationships can be used, for example, to estimate the mass of a star based on its observed density, effective temperature, and metallicity. These quantities are directly measurable for stars in transiting exoplanet systems (Enoch et al. 2010).
In this work we present the first high-quality light curves and the first high-resolution spectroscopy for V1094 Tau. We use these data to measure the masses and radii of the stars in this binary to better than 1%. We also make useful estimates of the effective temperatures of the stars and their metallicity based on Strömgren photometry.
2. Observations
2.1. Spectroscopy
V1094 Tau was observed with a Cassegrain-mounted echelle spectrograph attached to the 1.5-m Wyeth reflector at the Oak Ridge Observatory (Harvard, Massachusetts, USA). A total of 59 useful exposures were obtained between 1995 December and 1997 April at a resolving power of R ≈ 35 000. A single echelle order was recorded with an intensified photon-counting Reticon detector, giving 45 Å of coverage centred at 5187 Å, and including the lines of the Mg i b triplet. The signal-to-noise ratios range from 13 to 24 per resolution element of 8.5 km s-1. The wavelength calibration was established by means of exposures of a Th-Ar lamp before and after each science exposure, and all reductions were carried out with standard procedures as implemented in a dedicated pipeline (see Latham 1992).
Spectroscopic observations were also obtained in 2002 October using the 2.5-m Isaac Newton Telescope (INT) on La Palma. The 500 mm camera of the Intermediate Dispersion Spectrograph (IDS) was equipped with a holographic 2400 lines mm-1 grating. An EEV 4k × 2k CCD was used and exposure times were 300 s. From measurements of the full width at half maximum (FWHM) of arc lines taken for wavelength calibration, we estimated that the resolution is 0.2 Å. A total of 64 spectra were taken covering the interval 4230–4500 Å, with estimated signal-to-noise ratios of approximately 50 per pixel.
The reduction of all spectra was undertaken using optimal extraction (Horne 1986) as implemented in the software tools pamela and molly1 (Marsh 1989).
2.2. Photometry
The differential uvby light curves of V1094 Tau were observed at the Strömgren Automatic Telescope (SAT) at ESO, La Silla and its six-channel uvbyβ photometer on 72 nights between October 2000 and January 2008. They contain 670 points per band. HD 26736 and HD 26874 were used as comparison stars throughout. In addition HD 27989AB was used as comparison star until JD 2 451 889, but was found to be variable and was therefore replaced by HD 24702. HD 27989AB is now known to be a BY Dra star (Strassmeier et al. 2000). HD 24702 is constant within the observational accuracy, whereas HD 26736 and HD 26874 scatter slightly more than expected; see Table 1. For HD 26874 the effect seems to be random, whereas HD 26736 brightened by about 0.02 mag during one observing season. The light curves are calculated relative to HD 26874. Observations of HD 26736 (except for the bright period) and HD 24702 (when observed) were also used, shifting them first to the light level of HD 26874.
Photometric data for V1094 Tau and the comparison stars.
We also obtained light curves of V1094 Tau with the WebScope instrument at the NF/ Observatory (NFO) located near Silver City, New Mexico and the Undergraduate Research Studies in Astronomy (URSA) WebScope on the roof of the Kimpel Hall on the University of Arkansas campus at Fayetteville. The NFO instrument consists of a 24-inch Cassegrain reflector with a field-widening correcting lens near the focus housed in a roll-off roof structure (Grauer et al. 2008). At the focus is a camera based on the Kodak KAF-4301E charge coupled device (CCD) with a field of view of about 27 × 27 arcmin. V1094 Tau was observed at the NFO on 116 nights between 2 Jan. 2006 and 24 Mar. 2012, producing a total of 5714 observations from 30 s exposures with a Bessel V filter.
The URSA WebScope uses a 10-inch Meade LX200 Schmidt-Cassegrain telescope scope with a Santa Barbara Imaging Group (SBIG) ST8 CCD camera, housed in a Technical Innovations RoboDome enclosure. V1094 Tau was observed on 91 nights between 6 Mar 2001 and 25 Mar 2012, producing a total of 8085 observations from 30 s exposures, also with a Bessel V filter.
The images were automatically measured by using the applicationsMulti-MeasureandMeasurewritten by author Lacy. The software was used to locate the stars of interest in the calibrated images and to perform background subtraction and aperture photometry in a region 22 arcsec square around each star in the NFO images and 30 arcsec square for the URSA images. The comparison star used was HD 284196 and the check star was HD 284197. Differences in the atmospheric extinction were corrected for all three stars. To form the differential magnitudes for analysis we used the flux of both comparison and check star for the NFO images, whereas in the URSA images only the comparison star HD 284196 was used. The differences between the comparison and check star magnitudes averaged 0.008 mag for the URSA images on 88 nights and 0.006 mag for NFO images on 118 nights. These magnitude differences are similar to the residuals of the light curve model fits derived from the analysis below. The complete light curves obtain using the NFO, URSA and SAT telescopes are shown in Fig. 1.
 |
Fig. 1 Light curves of V1094 Tau obtained with the SAT (Strömgren u, v, b, and y) and at the NFO and URSA observatories (V-band). For clarity, differential magnitudes are plotted offset in multiples of 0.5 mag. |
3. Analysis
3.1. Eclipse ephemerides
We used the jktebop2 light curve model (Southworth 2013) to measure times of mid-eclipse from our SAT, NFO, and URSA photometry. We identified nights of data where our observations covered the majority of the either the primary or secondary eclipse. All the parameters of the light curve model except the time of mid-eclipse and the zero-point of the magnitude scale were fixed at values similar to those given in Sect. 3.3.3 for our adopted light curve solution. We then used a least-squares fit to the data from each night individually to determine the times of mid-eclipse given. The standard errors on these times were estimated using the cyclic residual permutation method (“prayer-bead” method).
We used a least-squares fit of a linear ephemeris to these new times of mid-eclipse and previously published values to obtain the optimum values for the reference times of primary and secondary eclipse and two independent estimates of the orbital period, one from the primary eclipses and one from the secondary eclipses. If we use the standard errors quoted on the published times of minimum and from the prayer-bead method for our new times of minimum we find that the reduced chi-squared value for the fit is much greater than 1. Our assumption is that this is due to systematic noise sources that are both instrumental and astrophysical in origin, and that all the times of minimum are equally affected by these noise sources. In order to achieve a reduced chi-squared value 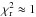 for the least-squares fit to the times of primary eclipse we have added 59 s in quadrature to the standard error estimates quoted on published values and also to the estimated standard errors for our new times of minimum. For the times of secondary eclipse we include an additional 52 s in the standard error estimates. The data used and the adopted standard errors are given in Table 2. The resulting linear ephemerides for the heliocentric Julian dates (HJD) of primary and secondary eclipse, respectively, are
for the least-squares fit to the times of primary eclipse we have added 59 s in quadrature to the standard error estimates quoted on published values and also to the estimated standard errors for our new times of minimum. For the times of secondary eclipse we include an additional 52 s in the standard error estimates. The data used and the adopted standard errors are given in Table 2. The resulting linear ephemerides for the heliocentric Julian dates (HJD) of primary and secondary eclipse, respectively, are 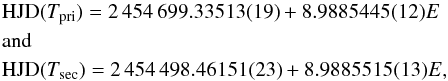 where E is the cycle number and the figures in parentheses are the standard errors in the two final digits for each free parameter.
where E is the cycle number and the figures in parentheses are the standard errors in the two final digits for each free parameter.
The difference in the orbital period obtained from the times of primary and secondary eclipse is significant (4σ) and is characteristic of binary stars in which the orientiation of the eccentric orbit is changing (apsidal motion).
Times of mid-eclipse for V1094 Tau.
We also analysed the photometry of V1094 Tau described by Wraight et al. (2011) but found that these data were too noisy to add any useful constraints on the ephemeris or the radii of the stars so we do not discuss them further here. We see no evidence for the periodic variation in eclipse times claimed by Wolf et al. (2010).
3.2. Radial velocity measurements
3.2.1. CfA spectroscopy
All our CfA spectra appear double-lined. Radial velocities were obtained using the two-dimensional cross-correlation technique todcor (Zucker & Mazeh 1994), with templates chosen from a large library of calculated spectra based on model atmospheres by Kurucz (see Nordström et al. 1994; Latham et al. 2002). The four main parameters of the templates are the effective temperature Teff, projected equatorial rotational velocity vsini, metallicity [m/H], and surface gravity log g. The parameters that have the largest effect on the measured radial velocities are Teff and vsini. Consequently, we held log g fixed at 4.0 for the hotter and more massive star (hereafter star 1, or primary star) and 4.5 for the cooler one (star 2, secondary star), which are near the final values reported below in Sect. 3.4, and we assumed solar metallicity. The optimum Teff and vsini values were determined by running grids of cross-correlations, seeking the maximum of the correlation coefficient averaged over all exposures and weighted by the strength of each spectrum (see Torres et al. 2002). The projected equatorial rotational velocities we obtained are vsini = 9.0 ± 2.0 km s-1 for star 1 and vsini = 4.4 ± 2.0 km s-1 for star 2. The vsini value for star 2 is much less than the instrumental broadening and so is very sensitive to the value of the macroturbulence assumed in the model grid. The effective temperatures derived are Teff,1 = 5860 ± 100 K for star 1 and Teff,2 = 5780 ± 100 K for star 2. The uncertainty in these values has little effect on the measured radial velocities.
As in previous studies using similar spectroscopic material, we made an assessment of potential systematic errors in our radial velocities that may result from residual line blending as well as lines shifting in and out of our narrow spectral window as a function of orbital phase (see Latham et al. 1996). We did this by performing numerical simulations analogous to those described by Torres et al. (1997), and we applied corrections to the raw velocities based on these simulations to mitigate the effect. The corrections were typically less than 0.5 km s-1 for both stars.
Radial velocities of V1094 Tau from CfA spectroscopy.
Finally, the stability of the zero-point of our velocity system was monitored by taking nightly exposures of the dusk and dawn sky, and small run-to-run corrections (typically under 1 km s-1) were applied to the velocities as described by Latham (1992). The adopted heliocentric velocities including all corrections are listed in Table 3.
3.2.2. INT spectroscopy
We also used todcor to measure the radial velocities of both stars from our INT spectra, but for these measurements we used spectra of HD 216435 (G0V) and HD 115617 (G5V) obtained from a library of high-resolution stellar spectra (Bagnulo et al. 2003) as templates for the primary and secondary stars, respectively. Both the INT spectra and the template spectra were interpolated onto a uniform logarithmic wavelength grid equivalent to 7.23 km s-1 per pixel using quadratic interpolation. The radial velocities were derived by fitting a minimum curvature surface to the peak of the two-dimensional cross correlation function and interpolating to the point of maximum correlation. The accuracy of the radial velocity measurements that can be obtained from our INT spectra is limited to about 1 km s-1 by instrumental effects (motion of the star in the slit, flexure, etc.) so we did not attempt to make any corrections for blending, etc. as we did for the CfA spectra. Radial velocities for spectra obtained near primary or secondary eclipse were found to be unreliable and are not reported here. The radial velocities derived from the 48 remaining spectra are given in Table 4.
Radial velocity measurements from INT spectroscopy for V1094 Tau.
3.3. Spectroscopic orbit and apsidal motion
We first performed least-squares fits of Keplerian orbits to the three sets of radial velocity data available to us, those from the CfA spectra, those from the INT/IDS spectra, and the radial velocities published by Griffin & Boffin (2003). The results from the three data sets were found to be consistent with each other except for the differences in the zero-point of the radial velocity scale between the different data sets. The offset between the INT radial velocities and the other radial velocity data is small compared to the instrumental resolution (14 km s-1) and is likely to be due to the uncertainty in the zero-point of the wavelength calibration for these spectra. The zero-point of the CfA radial velocity scale is within 0.14 km s-1 of the absolute reference frame set by minor planets, which we have observed regularly with the same instrument for 25 years.
There is clear evidence for apsidal motion in V1094 Tau from the measured times of mid-eclipse. There is also information about the rate of apsidal motion in the radial velocity data. In order to obtain the best possible estimate of the apsidal period, U, and to ensure that there is no systematic error in parameters of the spectroscopic orbit due to the variation in the longitude of periastron, ω, we used a program called omdot to perform a simultaneous least-squares fit to all three radial velocity data sets and all the measured times of mid-eclipse for the parameters of a Keplerian orbit in which the longitude of periastron changes at a constant rate 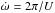 . The times of mid-eclipse are computed by calculating the times when the projected separation of the stars is at a minimum. The optimal solution is obtained using the Levenburg-Marquardt algorithm (Press et al. 1992). We were careful to assign accurate standard errors to all the data so that the relative weighting of the different data sets is correct and the standard error estimates for the free parameters are accurate. The free parameters in the fit were: a reference time of mid-eclipse, T0; the anomalistic period, Panom; the orbital eccentricty, e; the longitude of periastron at time T0, ω0;
. The times of mid-eclipse are computed by calculating the times when the projected separation of the stars is at a minimum. The optimal solution is obtained using the Levenburg-Marquardt algorithm (Press et al. 1992). We were careful to assign accurate standard errors to all the data so that the relative weighting of the different data sets is correct and the standard error estimates for the free parameters are accurate. The free parameters in the fit were: a reference time of mid-eclipse, T0; the anomalistic period, Panom; the orbital eccentricty, e; the longitude of periastron at time T0, ω0; 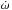 ; the semi-amplitudes of the spectroscopic orbits, K1 and K2; the radial velocity of the binary centre-of-mass for the CfA data, γCfA; two offsets between the different radial velocity scales, γGB − γCfA and γINT − γCfA. The orbital inclination has a negligible effect on the derived times of minimum and the spectroscopic orbit so we fix this quantity at the value i = 88.25°. The sidereal period (mean time between eclipses) is Psid = (1 /Panom + 1 /U)-1. The results from our least-squares fit are given in Table 5.
; the semi-amplitudes of the spectroscopic orbits, K1 and K2; the radial velocity of the binary centre-of-mass for the CfA data, γCfA; two offsets between the different radial velocity scales, γGB − γCfA and γINT − γCfA. The orbital inclination has a negligible effect on the derived times of minimum and the spectroscopic orbit so we fix this quantity at the value i = 88.25°. The sidereal period (mean time between eclipses) is Psid = (1 /Panom + 1 /U)-1. The results from our least-squares fit are given in Table 5.
The fit to the observed times of mid-eclipse is shown in Fig. 2. The variation in ω over the time covered by radial velocity measurements turns out to be small (<0.2°) so we show the fit to the radial velocities for a fixed value of ω and the best-fit values of K1 and K2 in Fig. 3.
 |
Fig. 2 Residuals from a linear ephemeris derived from the values of T0 and Psid given in Table 5 (points) together with the fit to these values from omdot for an eccentric orbit with apsidal motion (solid lines). Secondary eclipse is assumed to occur at phase 0.652 for this plot. Published times of mid-eclipse are plotted using diamond symbols, new times of mid-eclipse are plotted with dots (V-band) or open squares (SAT). |
 |
Fig. 3 Radial velocities for the primary (filled symbols) and secondary (open symbols) components of V1094 Tau relative to their barycentre. Triangles (black) are CfA data, circles (red) are INT data and squares (blue) are the data from Griffin & Boffin (2003). Spectroscopic orbits are shown (solid lines) for parameters given in Table 5 but with ω fixed at the value 333.61°. (Colour version on-line.) |
3.3.1. V-band and y-band luminosity ratios
There can be some degeneracy between the ratio of the radii and the luminosity ratio determined from the light curve for partially eclipsing binaries, so it is useful to include the luminosity ratio from the spectroscopy as an additional constraint in the least-squares fit. The analysis of the CfA spectra using todcor yields a luminosity ratio in the 45 Å region around 5190 Å of ℓ5190 = 0.534 ± 0.020. To convert this value into a luminosity ratio in the V-band we used the synthetic stellar spectra from the BaSel 3.1 library (Westera et al. 2002). We compared the flux integrated over the V-band response function (Bessell 1990) to the flux integrated over the 45 Å region around 5190 Å for a range of effective temperature and metallicity ([Fe/H]) similar to those derived below for the two stars in V1094 Tau. By taking the ratio of these integrated fluxes and then the ratio of that ratio for the two stars we can derive a factor to convert ℓ5190 to a luminosity ratio in the V-band, ℓV. Applying this correction we obtain ℓV = 0.557 ± 0.025, where the standard error estimate includes the additional uncertainty in this estimate due to the errors in the effective temperatures of the two stars and in [Fe/H]. A similar calculation for the Strömgren y-band gives the result ℓy = 0.533 ± 0.025. If we were to extrapolate the luminosity ratio at 5190 Å to other wavelengths the results will be sensitive to systematic errors in the synthetic stellar spectra, so we have only used the luminosity ratio in the V-band and y-band using this method.
3.3.2. Effective temperature and metallicity
The two stars in V1094 Tau are quite similar and so a useful estimate of the metallicity can be obtained by analysing the Strömgren photometry of this binary as though it were a single star. The reddening was estimated using the method of Olsen (1988) applied to the mean photometric colours out of eclipse from Table 1 and was found to be E(b − y) = 0.019 ± 0.007 mag. The calibration of Holmberg et al. (2007) applied to the de-reddened Strömgren photometry of V1094 Tau then yields the estimate [ Fe/H ] = −0.09 ± 0.11, where the error includes both the random error in the photometry and the systematic error in the calibration. Holmberg et al. (2007) also provide an effective temperature calibration which we can apply to our de-reddened Strömgren photometry to obtain the value 5680 ± 70 K. This value will be a weighted average of the individual effective temperatures for the two stars in V1094 Tau. The two stars have similar effective temperatures so the luminosity ratio is almost constant at optical wavelenghs, and so the relative weights between the two stars will be close to the luminosity ratio derived above for the y-band.
Parameters of the orbit for V1094 Tau derived using omdot.
The surface brightness ratio derived from the least-squares fits to the light curves, J, provides a useful constraint on the difference between the effective temperatures of the two stars, ΔTeff = Teff,1 − Teff,2. We used the synthetic stellar spectra from Kurucz (1993) to establish calibrations between surface brightness against Teff for the V-band, y-band and b-band assuming either log g = 4.0 (secondary) or log g = 4.5 (primary). As expected, the value of log g has little effect on the predicted surface brightness. We then interpolated between these calibrations to find the value of Teff,2 that gives the observed surface brightness ratio assuming Teff,1 = 5860 ± 100 K. We investigated how these calibrations are affected by the assumed metallicity using the synthetic stellar spectral library by Westera et al. (2002) and found that the estimate of ΔTeff changes by less than 10 K if the assumed value of [Fe/H] is changed by ± 0.1 dex. There is very good agreement between the ΔTeff values derived using the two different spectral libraries. The values of ΔTeff derived by this method are 125 ± 14 for the NFO V-band, 159 ± 15 for the URSA V-band, 170 ± 14 for the y-band, and 152 ± 14 for the SAT b-band. The weighted mean of these estimates for the temperature difference is ΔTeff = 150 ± 10 K, where we have quoted the standard error in the weighted mean based on the scatter between the four input values. This is only slightly larger (by about 30%) than the standard error in the weighted mean calculated from the standard errors of these values. This shows that the level of systematic error in our J values is low, i.e., the quoted errors on J are close to the true error in these values. The Strömgren u and v bands are strongly affected by details of the stellar models such as line blanketing and convection, so we have not attempted the same calculation at these wavelengths.
The three constraints on the effective temperatures of the stars are shown in Fig. 4 together with our adopted values Teff,1 = 5850 K and Teff,2 = 5700 K. We have assumed in this plot that the value of Teff derived from the Strömgren photometry is a weighted average of the two individual Teff values with a ratio of weights equal to the luminosity ratio in the y-band. Given the level of agreement between the three constraints and the estimated precision of the CfA effective temperature estimates, we have adopted estimated standard errors on both these values of ±100 K.
 |
Fig. 4 Adopted effective temperatures and standard errors (points with error bars) assuming [ Fe/H ] = −0.09. Constraints (1σ) on the effective temperatures are indicated as follows: solid lines – CfA spectroscopy, dotted lines – Strömgren photometry, dashed lines – V-band luminosity ratio. |
 |
Fig. 5 Upper panels: detail of the jktebop model fit to the URSA V-band light curve of V1094 Tau around primary eclipse and secondary eclipse. Lower panels: residuals from the jktebop model fit to our light curves of V1094 Tau, as labelled, in the region of the primary and secondary eclipse. For clarity, the residuals are offset in multiples of 0.1 mag. Note that night-to-night offsets calculated as part of the least-squares fits have been applied to the observed magnitudes. |
3.3.3. Light curve analysis
We used jktebop version 25 (Southworth 2013, and references therein) to analyse our six independent light curves of V1094 Tau (uvby, VNFO and VURSA) using the ebop light curve model (Etzel 1981; Popper & Etzel 1981). We only included data from nights covering the primary or secondary eclipse and we modified jktebop to include offsets in the zero-point of the magnitude scale between different nights as free parameters in the least-squares fit. This increases the number of free parameters in the least-squares fit, but it enables us to check that none of the parameters of interest is strongly affected by night-to-night offsets in the photometry. For light curves such as those presented here where data from different nights overlap in phase we find that the offsets are well constrained and uncorrelated with other parameters so including them in the least-squares fits does not cause any problems. The offsets typically have values of a few milli-magnitudes with standard errors of about 1 milli-magnitude, though a few nights have offsets of about 10 milli-magnitudes. Other free parameters in the least-squares fit were: a normalisation constant, the surface brightness ratio J = S2/S1, where S1 is the surface brightness of star 1 at the centre of the stellar disc and similarly for S2; the sum of the radii relative to semi-major axis, (R1 + R2) /a; the ratio of the radii, k = R2/R1; the orbital inclination, i; the phase of primary eclipse, Δ. We fixed the time of primary eclipse, the orbital period, e, and ω by using the results from omdot described above to calculate these value of the quantities at the mid-point of the observed data. Separate light curve solutions that included ecos(ω) and esin(ω) as free parameters showed that the values derived are consistent with those derived using omdot. The variation in these quantities during the span of the observations due to apsidal motion has a negligible effect on the results. For the V-band and y-band light curves the results presented here include the luminosity ratio calculated in Sect. 3.3.1 as an additional constraint in the least-squares fit. We also tried least-squares fits without including the luminosity ratio as a constraint and found that this has a negligible effect on the parameters derived.
Gravity darkening coefficients, β, were taken from the tabulation of Claret & Bloemen (2011), although gravity darkening has a negligible impact on the light curves for these nearly-spherical stars. We tried a quadratic limb darkening law for the fit to the b-band light curve and found that there was no improvement in the quality of the fit compared to a linear limb darkening law and that the parameters of interest are negligibly affected, so we adopt linear limb darkening laws for all our light curves. The linear limb darkening coefficients for the two stars used in our analysis (x1 and x2) are given in Table 6. These are representative of the values obtained from several tabulations of limb-darkening coefficients for the appropriate effective temperature, gravity and metallicity of the stars (van Hamme 1993; Diaz-Cordoves et al. 1995; Claret 2000; Claret & Hauschildt 2003). We estimate that the typical uncertainties on these values are about 0.04. The uncertainty on the limb-darkening coefficients has a small effect on the best-fit values of R1/a and R2/a derived from each light curve (≈0.5%). We assume that these errors are random so that the effect on the weighted mean values of R1/a and R2/a derived from the six light curves is negligible. The optimum values of the free parameters and their standard errors are given in Table 6, where we also provide the weighted mean values and their standard errors for the wavelength-independent parameters. The standard errors quoted are the standard error in the weighted mean based on the scatter between the six input values. This is only slightly larger (by about 30%) than the standard error in the weighted mean calculated from the standard errors on the six input values. This shows that the level of systematic error in these free parameters is low, i.e., the quoted errors on the model parameters are close to the true error on these values. In particular, we checked that there is no trend in the estimated inclination versus wavelength that might suggest contamination of the light curves by third light with a different spectrum to the stars in V1094 Tau. The best fit to the V-band photometry from URSA around the eclipses is shown in Fig. 5, together with the residuals from the least-squares fits for all six light curves.
Light curve parameters for V1094 Tau derived using jktebop.
3.4. Masses and radii
We have used jktabsdim3 to combine the parameters of the spectroscopic orbit from Table 5 and the weighted mean values of R1/a, R2/a and i from Table 6 to derive the masses and radii of the stars in V1094 Tau with their estimated standard errors given in Table 7. Table 7 also provides estimates of the luminosity and absolute V-band magnitude of the stars based on the estimates of the stars’ effective temperatures in Sect. 3.3.2. The comparison with stellar models discussed below suggests that V1094 Tau may be slightly more metal-rich than assumed in Sect. 3.3.2. The effective temperatures of the stars estimated from the CfA spectroscopy also increases by about 70 K if the assumed values of [Fe/H] is increased by 0.1 dex. For that reason, we also provide in Table 7 estimates of the effective temperature, luminosity and absolute V-band magnitude of the stars for an assumed metallicity [ Fe/H ] = +0.14. In both cases, we also provide an estimate of the distance to V1094 Tau based on the surface-brightness – effective temperature relation in the K-band from Kervella et al. (2004), and the apparent Ks-band magnitude of V1094 Tau from 2MASS transformed to the Johnson system (K = 7.468 ± 0.021, Skrutskie et al. 2006; Bessell 2005).
Absolute astrophysical parameters for both components of V1094 Tau determined with jktabsdim.
4. Discussion
Figure 6 shows the two stars in V1094 Tau in the mass-radius and mass-Teff planes compared to various models from Bressan et al. (2012). The primary star is close to the end of its main-sequence lifetime and so models for this star are sensitive to the assumed age of the binary. For each value of the metal abundance shown we have adjusted the age of the models in order to find a good match to the radius of the more massive star. For a fixed metallicity we find that we can determine the age of the system with a precision of about 0.1 Gyr. If we assume, as Bressan et al. do, that the metal abundance of the Sun is Z⊙ = 0.01774, and that the helium abundance of V1094 Tau is similar to the Sun, then our estimate [ Fe/H ] = −0.09 ± 0.11 corresponds to Z = 0.014 ± 0.005. It is clear that for Z = 0.014 the effective temperatures of both stars are too low compared to the models. Increasing the assumed metal abunance to Z = 0.020 provides a much better fit to the effective temperatures, particularly when we account for the increase in our estimates of Teff if the assumed metallicity is increased. A reasonable fit to all the observations can be obtained by assuming an intermediate value for the metal abundance, in which case the age of V1094 Tau is estimated to be about 6 Gyr. Very similar results are found using other stellar models grids such as VandenBerg et al. (2006) or Dotter et al. (2008).
There is good agreement between the projected equatorial velocity of the primary star quoted by Griffin & Boffin (2003) (9 ± 1 km s-1) and the value we have derived from our CfA spectroscopy (9.0 ± 2.0 km s-1). The agreement is less good for the secondary star (7 ± 1 km s-1 versus 4.4 ± 2.0 km s-1) but the lower value derived from the CfA spectroscopy is very sensitive to the assumed macroturbulence parameter used in the stellar model grid because the rotational broadening in less than the resolution of the instrument (8.5 km s-1). Nevertheless, both the primary and secondary stars appear to rotate slightly below the rate expected for pseudo-synchronous rotation (11.42 ± 0.05 km s-1 and 8.96 ± 0.05 km s-1, respectively). This suggests that V1094 Tau is close to the limit at which tidal interactions between the stars force them to rotate pseudo-synchronously with the orbital motion.
 |
Fig. 6 Mass, radius and effective temperature of the two components of V1094 Tau (errror bars) compared to models from Bressan et al. (2012) for various values of the initial metal abundance, Z. The assumed ages are 5.75 Gyr, 6.2 Gyr and 6.6 Gyr for Z = 0.014,0.017,0.020, respectively. The arrow in the lower-left panel indicates the effect of changing the assumed metallicity from [ Fe/H ] = −0.09 to [ Fe/H ] = +0.14. Small diamonds show the model grid points that have been interpolated to produce the isochrones in these plots. |
5. Conclusion
We have measured the masses of the stars in V1094 Tau to better than 0.4% and the radii of these stars to better than 0.6%. The error estimates on these values are robust as they are based on the analysis of multiple high-quality independent data sets. This level of precision and accuracy is among the best currently available for any solar-type star apart from the Sun itself. The sample of 95 well-studied eclipsing binary stars compiled by Torres et al. (2010) contains only one star with both its mass and radius measured to this accuracy (HD 124784 B).
We find that the current generation of stellar models are able to match the observed masses and radii of these stars within the constraints currently available on the effective temperatures of the stars and their metallicity. These models suggest that the age of V1094 Tau is about 6 Gyr. The rotation velocities of the stars suggest that V1094 Tau is close to the limit at which tidal interactions between the stars force them to rotate pseudo-synchronously with the orbit.
pamela and molly were written by Prof. Tom Marsh and are available at www.warwick.ac.uk/go/trmarsh
Acknowledgments
We thank the referee for their careful consideration of our manuscript and their constructive comments that have helped to improve the paper. Thanks to Dr. A. W. Neely for the maintenance and operation of the NFO and for preliminary processing and distribution of the images. G.T. acknowledges partial support from NSF grant AST-1007992. J.V.C. participated fully in the data collection and analysis up to the time of his death, but bears no responsibility for the final text of this paper.
References
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [NASA ADS] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S. 2005, ARA&A, 43, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Hauschildt, P. H. 2003, A&A, 412, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diaz-Cordoves, J., Claret, A., & Gimenez, A. 1995, A&AS, 110, 329 [NASA ADS] [Google Scholar]
- Diethelm, R. 2012a, IBVS, 6011, 1 [NASA ADS] [Google Scholar]
- Diethelm, R. 2012b, IBVS, 6029, 1 [NASA ADS] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, B., Collier Cameron, A., Parley, N. R., & Hebb, L. 2010, A&A, 516, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Etzel, P. B. 1981, in Photometric and Spectroscopic Binary Systems, eds. E. B. Carling, & Z. Kopal (Dordrecht: Reidel Publ. Co.), 111 [Google Scholar]
- Grauer, A. D., Neely, A. W., & Lacy, C. H. S. 2008, PASP, 120, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, R. F., & Boffin, H. M. J. 2003, The Observatory, 123, 203 [NASA ADS] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubscher, J. 2005, IBVS, 5643, 1 [NASA ADS] [Google Scholar]
- Hubscher, J., Paschke, A., & Walter, F. 2005, IBVS, 5657, 1 [Google Scholar]
- Kaiser, D. H. 1994, IBVS, 4119, 1 [NASA ADS] [Google Scholar]
- Kaiser, D. H., & Frey, G. 1998, IBVS, 4544, 1 [NASA ADS] [Google Scholar]
- Kaiser, D. H., Baldwin, M. E., Gunn, J., et al. 1995, IBVS, 4168, 1 [NASA ADS] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
- Latham, D. W. 1992, in Complementary Approaches to Double and Multiple Star Research, eds. H. A. McAlister, & W. I. Hartkopf, IAU Colloq. 135, ASP Conf. Ser., 32, 110 [Google Scholar]
- Latham, D. W., Nordström, B., Andersen, J., et al. 1996, A&A, 314, 864 [NASA ADS] [Google Scholar]
- Latham, D. W., Stefanik, R. P., Torres, G., et al. 2002, AJ, 124, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R. 1989, PASP, 101, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Nordström, B., Latham, D. W., Morse, J. A., et al. 1994, A&A, 287, 338 [NASA ADS] [Google Scholar]
- Olsen, E. H. 1988, A&A, 189, 173 [NASA ADS] [Google Scholar]
- Olsen, E. H. 1994, A&AS, 106, 257 [NASA ADS] [Google Scholar]
- Popper, D. M., & Etzel, P. B. 1981, AJ, 86, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing (Cambridge University Press) [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2013, A&A, 557, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K., Washuettl, A., Granzer, T., Scheck, M., & Weber, M. 2000, A&AS, 142, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, G., Stefanik, R. P., Andersen, J., et al. 1997, AJ, 114, 2764 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Neuhäuser, R., & Guenther, E. W. 2002, AJ, 123, 1701 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- VandenBerg, D. A., Bergbusch, P. A., & Dowler, P. D. 2006, ApJS, 162, 375 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- Westera, P., Lejeune, T., Buser, R., Cuisinier, F., & Bruzual, G. 2002, A&A, 381, 524 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, M., Claret, A., Kotková, L., et al. 2010, A&A, 509, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wraight, K. T., White, G. J., Bewsher, D., & Norton, A. J. 2011, MNRAS, 416, 2477 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, S., & Mazeh, T. 1994, ApJ, 420, 806 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
All Tables
Absolute astrophysical parameters for both components of V1094 Tau determined with jktabsdim.
All Figures
 |
Fig. 1 Light curves of V1094 Tau obtained with the SAT (Strömgren u, v, b, and y) and at the NFO and URSA observatories (V-band). For clarity, differential magnitudes are plotted offset in multiples of 0.5 mag. |
| In the text | |
 |
Fig. 2 Residuals from a linear ephemeris derived from the values of T0 and Psid given in Table 5 (points) together with the fit to these values from omdot for an eccentric orbit with apsidal motion (solid lines). Secondary eclipse is assumed to occur at phase 0.652 for this plot. Published times of mid-eclipse are plotted using diamond symbols, new times of mid-eclipse are plotted with dots (V-band) or open squares (SAT). |
| In the text | |
 |
Fig. 3 Radial velocities for the primary (filled symbols) and secondary (open symbols) components of V1094 Tau relative to their barycentre. Triangles (black) are CfA data, circles (red) are INT data and squares (blue) are the data from Griffin & Boffin (2003). Spectroscopic orbits are shown (solid lines) for parameters given in Table 5 but with ω fixed at the value 333.61°. (Colour version on-line.) |
| In the text | |
 |
Fig. 4 Adopted effective temperatures and standard errors (points with error bars) assuming [ Fe/H ] = −0.09. Constraints (1σ) on the effective temperatures are indicated as follows: solid lines – CfA spectroscopy, dotted lines – Strömgren photometry, dashed lines – V-band luminosity ratio. |
| In the text | |
 |
Fig. 5 Upper panels: detail of the jktebop model fit to the URSA V-band light curve of V1094 Tau around primary eclipse and secondary eclipse. Lower panels: residuals from the jktebop model fit to our light curves of V1094 Tau, as labelled, in the region of the primary and secondary eclipse. For clarity, the residuals are offset in multiples of 0.1 mag. Note that night-to-night offsets calculated as part of the least-squares fits have been applied to the observed magnitudes. |
| In the text | |
 |
Fig. 6 Mass, radius and effective temperature of the two components of V1094 Tau (errror bars) compared to models from Bressan et al. (2012) for various values of the initial metal abundance, Z. The assumed ages are 5.75 Gyr, 6.2 Gyr and 6.6 Gyr for Z = 0.014,0.017,0.020, respectively. The arrow in the lower-left panel indicates the effect of changing the assumed metallicity from [ Fe/H ] = −0.09 to [ Fe/H ] = +0.14. Small diamonds show the model grid points that have been interpolated to produce the isochrones in these plots. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


