| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201525755 | |
| Published online | 25 May 2015 | |
Testing the cooling flow model in the intermediate polar EX Hydrae
1 Instituto de Astronomía y Física del Espacio (IAFE, CONICET-UBA), CC 67, Suc. 28 (C1428ZAA), CABA, Argentina
e-mail: gjmluna@iafe.uba.ar
2 Harvard-Smithsonian Center for Astrophysics, 60 Garden st., Cambridge, MA 02138, USA
3 Lawrence Livermore National Laboratory, L-473, 7000 East Avenue, Livermore, CA 94550, USA
4 Institute for Astronomy and Astrophysics, Kepler Center for Astro and Particle Physics, Eberhard Karls University, Sand 1, 72076 Tübingen, Germany
5 Kazan (Volga Region) Federal University, Kremlevskaya 18, 420008 Kazan, Russia
Received: 27 January 2015
Accepted: 2 April 2015
We use the best available X-ray data from the intermediate polar EX Hydrae to study the cooling-flow model often applied to interpret the X-ray spectra of these accreting magnetic white dwarf binaries. First, we resolve a long-standing discrepancy between the X-ray and optical determinations of the mass of the white dwarf in EX Hya by applying new models of the inner disk truncation radius. Our fits to the X-ray spectrum now agree with the white dwarf mass of 0.79 M⊙ determined using dynamical methods through spectroscopic observations of the secondary. We use a simple isobaric cooling flow model to derive the emission line fluxes, emission measure distribution, and H-like to He-like line ratios for comparison with the 496 ks Chandra High Energy Transmission Grating observation of EX Hydrae. We find that the H/He ratios are not well reproduced by this simple isobaric cooling flow model and show that while H-like line fluxes can be accurately predicted, fluxes of lower-Z He-like lines are significantly underestimated. This discrepancy suggests that an extra heating mechanism plays an important role at the base of the accretion column, where cooler ions form. We thus explored more complex cooling models, including the change of gravitational potential with height in the accretion column and a magnetic dipole geometry. None of these modifications to the standard cooling flow model are able to reproduce the observed line ratios. While a cooling flow model with subsolar (0.1 ⊙) abundances is able to reproduce the line ratios by reducing the cooling rate at temperatures lower than ~107.3 K, the predicted line-to-continuum ratios are much lower than observed. We discuss and discard mechanisms, such as photoionization, departures from constant pressure, resonant scattering, different electron-ion temperatures, and Compton cooling. Thermal conduction transfers energy from the region above 107 K, where the H-like lines are mostly formed, to the cooler regions where the He-like ions of the lower-Z elements are formed, hence in principle it could help resolve the problem. However, simple models indicate that the energy is deposited below 106 K, which is too cool to increase the emission of the He-like lines we observe. We conclude that some other effect, such as thermally unstable cooling, modifies the temperature distribution.
Key words: novae, cataclysmic variables / radiation mechanisms: general / X-rays: individuals: EX Hydrae
© ESO, 2015
1. Introduction
Cooling flows have been postulated to occur in a diversity of settings, from clusters of galaxies, where the low-density, intracluster medium loses its gravitational energy by radiating X-rays (Fabian & Nulsen 1977; Binney & Cowie 1981), to accreting magnetic and nonmagnetic white dwarfs (WDs) in binary systems. In nonmagnetic WDs, such as dwarf novae (Patterson & Raymond 1985) and symbiotics (Luna & Sokoloski 2007), a cooling flow is present in the boundary layer of the accretion disk, where material has to dissipate its rotational energy before settling onto the WD surface. If the WD magnetic field is strong enough to disrupt the accretion disk, the material flowing through the magnetically-dominated accretion column reaches highly supersonic velocities and undergoes a strong shock near the WD surface, heating the plasma to keV temperatures; the material in the postshock region cools until it settles onto the WD surface.
In intermediate polars (IPs), the WD has a magnetic field strong enough to disrupt the accretion disk at the Alfvén radius Rin(Revnivtsev et al. 2011; Semena et al. 2014), where magnetic pressure balances the ram pressure of the accretion flow. The WD’s magnetic field then channels the material from the inner disk toward the magnetic poles. Most of the cooling radiation from the accretion column is emitted at X-ray wavelengths, predominantly as bremsstrahlung and line emission, i.e., a cooling flow.
For galaxy clusters, spatially resolved X-ray imaging observations are available, and surface brightness and temperature profiles have been compared with the predictions of the cooling flow model. The observations do not show the large amounts of cool X-ray emitting plasma at the center of the clusters predicted by the cooling flow model. This discrepancy is known as the cooling flow problem (Peterson & Fabian 2006). As the X-ray emitting region of the accreting WD cannot be spatially resolved, an analogous cooling flow problem has been more difficult to discern. Hints of problems with the simple cooling flow model came from residuals in the fits of low- and medium-resolution X-ray spectra. However, these residuals can be reduced by invoking complex absorption (e.g., Ramsay et al. 2008; Yuasa et al. 2010). Further progress has been stymied by the low resolution of CCD spectra and the limited number and quality of high-resolution grating spectra. Mukai et al. (2003) modeled the high-resolution Chandra X-ray spectra of EX Hydrae (EX Hya), two dwarf novae, and an old nova using a solar abundance cooling flow model, matching the line fluxes to within a factor of two. On the other hand, fits with the cooling flow model to the high-resolution X-ray spectra of the dwarf nova WX Hyi (Perna et al. 2003) and the likely magnetic system V426 Oph (Homer et al. 2004) showed good agreement with the high temperature part of the spectrum, but underpredicted emission from the cooler part of the flow. This discrepancy appears to be in opposite direction from that seen in galaxy clusters. It is possible that there is additional heat as the gas cools to 107 K in both cases, but that in EX Hya this heating simply increases the emission measure of the million degree gas, whereas in clusters the heating is strong enough to prevent the gas from cooling to lower temperatures.
Depending on the physical properties of the binary system, additional heating and cooling mechanisms can play important roles in the energy equation of the cooling flow; e.g., gravity is a source of extra thermal energy when the shock height is a significant fraction of the WD radius. The cooling mechanism has been the subject of many theoretical studies (e.g., Aizu 1973; Cropper et al. 1999; Canalle et al. 2005; Hayashi & Ishida 2014a), and the derived spectral models have shown reasonable success in tests on low- and medium-resolution X-ray spectra. Given that the shock temperature is proportional to the strength of the gravitational potential well, its measurement can be used to determine the mass of the accreting WD. Ishida et al. (1991) modeled the X-ray spectra of IPs observed with GINGA as bremsstrahlung emission and used the derived temperatures to determine the masses of the accreting WDs. Cropper et al. (1999) also derived WD masses from GINGA data, but considered additional terms in the energy equation of the cooling flow, such as gravity, as well as modifications of the observed spectra by reflection by the WD surface and absorption due to a warm absorber above the emission region. Suleimanov et al. (2005) and Brunschweiger et al. (2009) modeled RXTE and Swift/BAT spectra of a sample of IPs using the Cropper et al. (1999) model. Hayashi & Ishida (2014a) combined the magnetic field geometry, varying gravitational potential, nonequipartition between ions and electrons, and nonequilibrium ionization to derive a model for the postshock region of the accretion column, which was recently tested on Suzaku data of EX Hya (Hayashi & Ishida 2014b).
Given that the cooling plasma also produces line emission, Fujimoto & Ishida (1997) realized that the then-higher spectral resolution of ASCA CCD spectra could be used to determine the shock temperature, and hence the WD mass, through measurements of the line intensity ratios of the H-like to He-like ions. They assumed the temperature and density structures given by Aizu (1973), where cooling is due only to bremsstrahlung radiative losses. Although line fluxes and equivalent widths from Fe, Ar, S, Si, and Mg were measured, Mg lines were not used to determine the WD mass because they are blended with Fe L-shell lines at the ASCA/SIS spectral resolution.
Are the more recent, high-quality spectra obtained with the Chandra High-Energy Transmission Grating (HETG) compatible with the models proposed for the cooling of the accretion column in EX Hya? Luna et al. (2010) discovered high-velocity wings on several bright emission lines in the 496 ks HETG spectrum of EX Hya, which they attributed to photoionized gas in the accretion column above the shock. Since only a small fraction of the X-ray spectrum originates in the photoionized preshock material, with the rest attributed to collisionally ionized plasma, a cooling flow model of the postshock emission should give a good first-order match to the observed spectrum.
In Sect. 2 we describe the properties of EX Hya. We solve the long-standing controversy about the WD mass of EX Hya derived using X-ray spectral fits compared with optical/IR radial velocity measurements. We use the 496 ks Chandra HETG spectrum described in Sect. 3 to test models of the cooling in the postshock region (Sect. 4). We first determine the shock temperature, which matches the value implied by a WD mass of 0.79 M⊙, from the least-absorbed spin-phase in Sect. 4.1. We then utilize the H-like to He-like line ratios as a proxy for the temperature and density structure of the column. We start by computing a simple isobaric cooling flow spectrum due to bremsstrahlung and line emission. We compute the emission measure distribution (EMD), line fluxes, and line ratios (Sect. 4.2). We find that simple isobaric cooling flow models are not able to reproduce the observed spectrum and line ratios. Specifically, we find that the H-like line fluxes are well reproduced, whereas the same model underestimates the He-like line fluxes. This implies that either heat is not efficiently removed in the upper portion of the accretion column, or there is an extra source of heat in the lower portion of the accretion column. We then consider the effects on the EMD of a different geometrical configuration by calculating a magnetic dipole model (Sect. 4.3). We find that the line ratios predictions are mostly unaffected by the accretion column geometry. In Sect. 4.4 we compute subsolar abundance models. While models with very low abundances are able to reproduce the observed line ratios, they greatly underestimate the observed line-to-continuum ratios.
Motivated by recent studies of the importance of thermal conduction in the cooling of the intracluster medium of clusters of galaxies (e.g., Kim & Narayan 2003; Ruszkowski & Oh 2011) and WD boundary layers (Liu et al. 2008), we consider thermal conduction in the energy equation of the flow in the accretion column of EX Hya (Sect. 4.5). While this changes the EMD in the correct sense, the change is too small to alleviate the discrepancy. We conclude that another effect, such as thermally unstable cooling, must be responsible for the excess emission in the 106 to 107 K range. In Sect. 5 we discuss our findings and present concluding remarks. In the Appendix we discuss various approximations in the simple cooling model.
2. EX Hya
EX Hya is an IP, a magnetic cataclysmic variable (CV) whose magnetic field is strong enough to channel the accretion flow onto the magnetic poles, but not strong enough to entirely disrupt the accretion disk. The orbital and WD spin periods are 98.26 and 67.03 min, respectively. EX Hya has been extensively studied at optical, UV, EUV, and X-ray wavelengths (e.g., Rosen et al. 1988; Mauche 1999; Mukai et al. 2003; Brunschweiger et al. 2009). The luminosity and accretion rate are estimated to be (2.6 ± 0.6) × 1032 erg s-1 and (6.2 ± 1.5) × 10-11 (MWD/ 0.5M⊙)-1.61M⊙ yr-1 at a distance of 64.5 pc (Beuermann et al. 2003). There has been a long-standing discrepancy between the WD mass of 0.790 ± 0.026M⊙ derived from the radial velocities of optical and IR emission lines (Beuermann & Reinsch 2008) and masses of 0.42–0.66 M⊙ derived by equating the X-ray temperature to the shock temperature expected for free fall onto the WD (e.g., Yuasa et al. 2010).
Various models have been used to fit the X-ray spectrum of EX Hya, and different values for the WD masses have been obtained. Yuasa et al. (2010) modeled the Suzaku X-ray spectrum including gravity in the flow equations and obtained a mass of 0.42 ± 0.02M⊙; Suleimanov et al. (2005) modeled the RXTE X-ray spectrum also including gravity in the flow equations and obtained a mass of 0.50 ± 0.05M⊙; Brunschweiger et al. (2009) obtained a mass of 0.66 ± 0.17M⊙ fitting the Swift/BAT spectrum and using the same model as Suleimanov et al. (2005). Hayashi & Ishida (2014b) combined the magnetic field geometry, varying gravitational potential, nonequipartition between ions and electrons, and ionization nonequilibrium to develop a model that was applied to Suzaku data of EX Hya, and obtained a mass of 0.63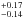 M⊙. Fujimoto & Ishida (1997) measured the ratio of the intensities of H-like to He-like emission lines in their study of the ASCA spectrum of EX Hya and obtained a mass of 0.48
M⊙. Fujimoto & Ishida (1997) measured the ratio of the intensities of H-like to He-like emission lines in their study of the ASCA spectrum of EX Hya and obtained a mass of 0.48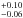 M⊙. Radial velocity measurements of the X-ray emission lines observed in a short (50 ks) Chandra observation, combined with velocity amplitude K2 of the secondary derived by Vande Putte et al. (2003) led Hoogerwerf et al. (2004) to derive a mass of 0.49 ± 0.13M⊙. Dynamical methods through optical and near-IR spectroscopic observations of the secondary by Beuermann & Reinsch (2008), significantly improved the measurements of K2 and concluded that the mass of the WD is 0.790 ± 0.026M⊙. The WD mass derived by Hoogerwerf et al. (2004) matches the value derived by Beuermann & Reinsch (2008) using their more accurate measurement of K2.
M⊙. Radial velocity measurements of the X-ray emission lines observed in a short (50 ks) Chandra observation, combined with velocity amplitude K2 of the secondary derived by Vande Putte et al. (2003) led Hoogerwerf et al. (2004) to derive a mass of 0.49 ± 0.13M⊙. Dynamical methods through optical and near-IR spectroscopic observations of the secondary by Beuermann & Reinsch (2008), significantly improved the measurements of K2 and concluded that the mass of the WD is 0.790 ± 0.026M⊙. The WD mass derived by Hoogerwerf et al. (2004) matches the value derived by Beuermann & Reinsch (2008) using their more accurate measurement of K2.
All the previous determinations of the WD mass based on the shock temperature of EX Hya, assumed that the material in the accretion column was at free-fall speed from infinity. However, in systems such as EX Hya, the inner radius of the accretion disk can be close to the WD surface (Revnivtsev et al. 2011) and therefore a factor that takes this into account has to be introduced in the free-fall speed equation as 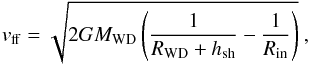 (1)where RWD is the radius of the WD and hsh is the height of the accretion column. If we use MWD = 0.79 M⊙, RWD = 7 × 108 cm, hsh = 0.1 × RWD, and Rin = 2.7 × RWD(Revnivtsev et al. 2011; Semena et al. 2014), we have vff = 4000 km s-1. Using the strong shock condition
(1)where RWD is the radius of the WD and hsh is the height of the accretion column. If we use MWD = 0.79 M⊙, RWD = 7 × 108 cm, hsh = 0.1 × RWD, and Rin = 2.7 × RWD(Revnivtsev et al. 2011; Semena et al. 2014), we have vff = 4000 km s-1. Using the strong shock condition 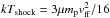 , we find that kTshock ~ 19 keV. Mukai et al. (2003) obtained a good fit to a short Chandra HETG observation with a shock temperature of 20 keV, Yuasa et al. (2010) obtained
, we find that kTshock ~ 19 keV. Mukai et al. (2003) obtained a good fit to a short Chandra HETG observation with a shock temperature of 20 keV, Yuasa et al. (2010) obtained 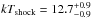 keV from their fit to Suzaku data, Brunschweiger et al. (2009) fit of Swift/BAT data yielded
keV from their fit to Suzaku data, Brunschweiger et al. (2009) fit of Swift/BAT data yielded 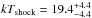 keV, whereas Fujimoto & Ishida (1997) obtained
keV, whereas Fujimoto & Ishida (1997) obtained 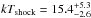 keV from the line ratios in the ASCA spectrum.
keV from the line ratios in the ASCA spectrum.
We therefore use a mass of 0.79 M⊙ and a radius of 7 × 108 cm for the WD. The preshock density is above 1015 cm-3(Luna et al. 2010), which, combined with the low magnetic field strength (~4 × 104 G), means that cyclotron cooling can be neglected.
3. Observations
 |
Fig. 1 Observed emission-line profiles with overlaid Gaussian models of a) O VII λ21.6 and O VII λ21.8 (MEG ± 1); b) O VIII λ18.97 (HEG ± 1); c) Ne IX λ13.45 and Ne IX λ13.55 (HEG ± 1); d) Ne X λ12.13 (HEG ± 1); e) Mg XI λ9.16 and Mg XI λ9.23 (HEG ± 1); f) Mg XII λ8.42 (HEG ± 1); g) Si XIII λ6.64, Si XIII λ6.68, and Si XIII λ6.74 (HEG ± 1); h) Si XIV λ6.18 (HEG± 1); i) S XV λ5.04, S XV λ5.06, and S XV λ5.10 (HEG ± 1); j) S XVI λ4.73 (HEG ± 1); k) Ar XVIII λ3.73, Ar XVII λ3.944 + Ar XVII λ3.961 + Ar XVII λ3.965, and Ar XVII λ3.994 + S XVI λ3.992 + S XVI λ3.991 (HEG ± 1); l) Ca XX λ3.02 and Ca XIX λ3.17 (HEG ± 1); and m) Fe XXVI λ1.78, Fe XXV λ1.85 and Fe XXV λ1.86 (HEG ± 1), where the HETG data and model profiles are shown with black and red histograms, respectively. Below each panel, we plot the fit residuals. Where overlapping, the HEG±1 and MEG±1 spectra were fit simultaneously; HEG±1 is shown for illustrative purposes. As discussed in Luna et al. (2010), the broad wings in the residuals to the fits of some of the emission lines – O VIII in particular – are due to emission by the photoionized preshock accretion flow. |
EX Hya was observed with Chandra using the ACIS-S/HETG combination for 496 ks. The observation was obtained in four segments (ObsIDs 7449: start time 2007 May 13 22:15:35 UT, exposure time 130.65 ks; 7452: start time 2007 May 17 03:12:38 UT, exposure time 49.17 ks, 7450: start time 2007 May 18 21:56:57 UT, exposure time 162.73 ks; and 7451: start time 2007 May 21 14:15:08 UT, exposure time 153.07 ks). We reduced the data using the Chandra Interactive Analysis of Observations (CIAO v.4.1) software package. Beyond the reduction of the Chandra data set already described in Luna et al. (2010), we combined the +1 and −1 orders of the HEG and MEG arms using the script add_grating_orders. The HEG ± 1 and MEG ± 1 spectra were thus fit simultaneously. Line fluxes were measured by using Gaussians to represent the emission lines and a first-order polynomial to represent the nearby continuum (see Fig. 1). We estimate that the measured fluxes differ by less than 2% using the more complex β-profile, which indeed was loaded with the RMF during the fit.
Table 1 lists the measured fluxes of individual H-like and He-like lines. For the analysis discussed below, H-like Lyα and the He-like resonance (r), intercombination (i), and forbidden (f) lines are required. For O, Ne, and Mg, the f lines are not observed. The r and i lines of Ar cannot be resolved by the HEG and these two lines are measured together using a single Gaussian component. Because the emissivity of the f line of Ar XVII λ3.994 peaks at log T = 7.3, while the emissivities of S XVI λ3.991 and λ3.992 peak at log T = 7.4 (AtomDB), the measured flux of the line at λ3.99 consists of the summed contribution of these three lines, and the models take this into account. Since the He-like r, i, and f lines of Ca XIX cannot be resolved, we used a single Gaussian to measure these lines. Finally, the i and f lines of Fe XXIV cannot be resolved and thus we measured these two lines together using a single Gaussian. As discussed by Luna et al. (2010), the broad wings in the residuals to the fits of some of the emission lines, in particular O VIII, are due to emission by the photoionized preshock accretion flow. Dielectronic recombination transitions, as well as other satellite lines located close enough to the He and H-like lines that cannot be resolved at the HEG spectral resolution were included in the measured fluxes and in the models described below. We found that they contribute to a small fraction (a few percent) of the line fluxes.
4. The postshock structure
4.1. Determining the shock temperature
To avoid the complications of modeling the complex absorber in an X-ray global fit, we exploited the high quality of the data set and filtered the data to obtain a spectrum at spin-phase maximum when the observer has a virtually unblocked view of the accretion flow. We divided the data into five spin-phase bins of width Δφ67 = 0.2 (φ67 refers to the phases at the spin period of 67.03 min) and fit the cooling flow model available in XSPEC (mkcflow) to the five spectra. We had already filtered in the binary phase range φ98 = 0.0–0.6 (φ98 refers to the phases at the orbital period of 98.26 min) to avoid the absorption by the accretion disk bulge (Hoogerwerf et al. 2006). As expected from observations at EUV wavelengths (Hurwitz et al. 1997; Mauche 1999) and from our spin-phase filter, the result of fitting the data in the spin-phase range φ67 = 0.9–1.1 yields a value for the absorption column NH smaller than 1020 cm-2 and 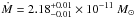 yr-1. This fit yields a value of
yr-1. This fit yields a value of 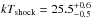 keV. If we allow the elemental abundances to vary (using the XSPEC model vmcflow), we get a temperature
keV. If we allow the elemental abundances to vary (using the XSPEC model vmcflow), we get a temperature 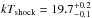 keV,
keV, 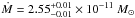 yr-1, and abundances (in units of the solar abundances of Anders & Grevesse 1989) of O = 0.92
yr-1, and abundances (in units of the solar abundances of Anders & Grevesse 1989) of O = 0.92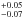 , Ne = 1.31
, Ne = 1.31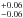 , Ar = 0.93
, Ar = 0.93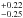 , Ca = 1.07
, Ca = 1.07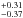 , Fe = 0.61
, Fe = 0.61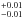 ; Mg, S, and Si are consistent with solar values (these abundances agree with the values derived by Fujimoto & Ishida 1997). Although these abundances look less anomalous in units of other modern solar abundance determinations (e.g., Lodders et al. 2009), we retain the Anders & Grevesse (1989) scale because AtomDB and XSPEC use them as defaults. The temperature derived is thus that predicted using Eq. (1) and the strong shock condition with a WD mass of 0.79 M⊙, in agreement with values determined dynamically. Therefore, throughout the following sections, we adopt a shock temperature kT = 19.7 keV and the abundances derived from the vmcflow model.
; Mg, S, and Si are consistent with solar values (these abundances agree with the values derived by Fujimoto & Ishida 1997). Although these abundances look less anomalous in units of other modern solar abundance determinations (e.g., Lodders et al. 2009), we retain the Anders & Grevesse (1989) scale because AtomDB and XSPEC use them as defaults. The temperature derived is thus that predicted using Eq. (1) and the strong shock condition with a WD mass of 0.79 M⊙, in agreement with values determined dynamically. Therefore, throughout the following sections, we adopt a shock temperature kT = 19.7 keV and the abundances derived from the vmcflow model.
 |
Fig. 2 Chandra MEG ± 1 order X-ray spectrum between spin-phases φ67 = 0.9 and 1.1 (i.e., the range of phases where the observer has the most unextinguished view of the accretion column) fit with an XSPEC variable-abundance isobaric cooling flow model (vmcflow). The absorption column, NH, is smaller than 1020 cm-2, as expected, while the shock temperature is |
4.2. The isobaric cooling flow. Derivation of a physically-based emission measure distribution
In the simplest scenario, the plasma in the accretion column radiates its excess energy in an isobaric flow where the cooling is determined by the radiative cooling function Λ(T) (Fig. 3). The cooling time can be expressed as 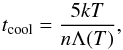 (2)where the density n = n0T0/T, with the 0 indicating values just beneath the shock. The rate of temperature change can be expressed as
(2)where the density n = n0T0/T, with the 0 indicating values just beneath the shock. The rate of temperature change can be expressed as 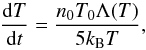 (3)where kB is the Boltzmann’s constant.
(3)where kB is the Boltzmann’s constant.
 |
Fig. 3 Upper panel: radiative cooling function derived using emissivities from AtomDB (in the low-density limit, see Sect. 4.2) and abundances (in units of the solar abundance of Anders & Grevesse 1989) of O = 0.92, Ne = 1.31, Ar = 0.93, Ca = 1.07, Fe = 0.61 (see Sect. 4.1). Lower panel: line emissivities as a function of temperature from AtomDB, normalized by their peak emissivity, for the H-like (full, black line) and He-like resonance+intercombination (dotted, red line) transitions of O, Ne, Mg, Si, S, Ar, Ca, and Fe. |
The speed in the cooling flow v = dx/ dt can be written as 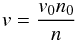 (4)from mass flux conservation, where v0 = vff/ 4. Then, at each place in the column, we can write
(4)from mass flux conservation, where v0 = vff/ 4. Then, at each place in the column, we can write 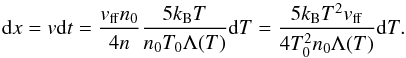 (5)The emission measure (EM) is defined as EM = ∫n2dV. A simple geometrical model for the accretion column is a cylinder, with a radius rspot and height hsh. In a cylinder, the area element dV/ dx = πr2 is constant, and using Eq. (5) and n = n0T0/T, we have the following expression for the EM:
(5)The emission measure (EM) is defined as EM = ∫n2dV. A simple geometrical model for the accretion column is a cylinder, with a radius rspot and height hsh. In a cylinder, the area element dV/ dx = πr2 is constant, and using Eq. (5) and n = n0T0/T, we have the following expression for the EM: 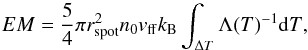 (6)where ΔT is the temperature range from the shock temperature to the minimum temperature (kTmin) of the gas when it reaches the WD surface. In practice, the value of kTmin is set by the lowest temperature for which the cooling function was calculated, which in our case is log T = 4. In fact, the assumption that the gas can be described in the coronal approximation, where the ions are in the ground state, breaks down below log T = 6, but that region makes no significant contribution to the X-ray emission lines discussed here (see Fig. 3).
(6)where ΔT is the temperature range from the shock temperature to the minimum temperature (kTmin) of the gas when it reaches the WD surface. In practice, the value of kTmin is set by the lowest temperature for which the cooling function was calculated, which in our case is log T = 4. In fact, the assumption that the gas can be described in the coronal approximation, where the ions are in the ground state, breaks down below log T = 6, but that region makes no significant contribution to the X-ray emission lines discussed here (see Fig. 3).
The flux of a given emission line is 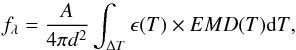 (7)where A is the elemental abundance, a constant that modifies the solar abundances (Anders & Grevesse 1989) already embedded in ϵ(T), the emissivity of the ion from AtomDB (Foster et al. 2012), EMD(T) is the distribution of the emission measure as function of temperature (i.e., the Emission Measure Distribution); note that Λ(T) was computed with the set of elemental abundances found in the global spectral fit in Sect. 4.1.
(7)where A is the elemental abundance, a constant that modifies the solar abundances (Anders & Grevesse 1989) already embedded in ϵ(T), the emissivity of the ion from AtomDB (Foster et al. 2012), EMD(T) is the distribution of the emission measure as function of temperature (i.e., the Emission Measure Distribution); note that Λ(T) was computed with the set of elemental abundances found in the global spectral fit in Sect. 4.1.
 |
Fig. 4 Measured ratios of the H-like Lyα line to the sum of the He-like resonance, intercombination, and forbidden lines from the Chandra spectrum of EX Hya (black diamonds with error bars). The histograms show the results from the models discussed in Sects. 4.2 to 4.5. For the empirically-derived EMD, the error bars indicate the 90% confidence level (Sect. 4.6). |
While most of the constants in Eq. (6) are unknown, they primarily affect the absolute intensities of the emission lines, so the ratios of H-like to He-like emission lines are more easily compared with observations (Fujimoto & Ishida 1997). The constants in Eq. (6) affect the EMD, and hence the line ratios indirectly, in that they determine the shock height and therefore contributions of the change in gravitational potential and compression due to dipole geometry of the postshock flow. In the present case, we neglect the dipole geometry and assume a shock height much less than the WD radius. From Eq. (7), we can express the H to He line ratio as 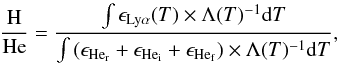 (8)where the subindices r, i, and f refer to the resonance, intercombination, and forbidden transitions, respectively, and Lyα includes contributions from both components of the doublet. Using Eqs. (6) and (8) with kTshock = 19.7 keV, we calculated the H/He line ratios for O, Ne, Mg, Si, S, Ar, Ca, and Fe and compared them with the ratios measured in the Chandra data (see Table 2). The observed ratios of the intensities of Fe XVII and Fe XXII lines (Mauche et al. 2001, 2003) indicate that the density in the accretion column is very high, with n ≳ 1014 cm-3. At these densities, the sum of the flux of the i and f lines is nearly constant, with the f line flux suppressed in favor of the i line flux as the density increases. Thus, the lack of observed f lines for O, Ne, and Mg should have a negligible effect on the sum of the observed He-like line fluxes. The r line is very weakly density dependent. Using the sum also reduces density-dependent effects. We use the public AtomDB emissivities, computed for ne = 1 cm-3, and thus although the flux of the forbidden lines at this low density is much higher than the flux of the intercombination lines, their sum is density independent.
(8)where the subindices r, i, and f refer to the resonance, intercombination, and forbidden transitions, respectively, and Lyα includes contributions from both components of the doublet. Using Eqs. (6) and (8) with kTshock = 19.7 keV, we calculated the H/He line ratios for O, Ne, Mg, Si, S, Ar, Ca, and Fe and compared them with the ratios measured in the Chandra data (see Table 2). The observed ratios of the intensities of Fe XVII and Fe XXII lines (Mauche et al. 2001, 2003) indicate that the density in the accretion column is very high, with n ≳ 1014 cm-3. At these densities, the sum of the flux of the i and f lines is nearly constant, with the f line flux suppressed in favor of the i line flux as the density increases. Thus, the lack of observed f lines for O, Ne, and Mg should have a negligible effect on the sum of the observed He-like line fluxes. The r line is very weakly density dependent. Using the sum also reduces density-dependent effects. We use the public AtomDB emissivities, computed for ne = 1 cm-3, and thus although the flux of the forbidden lines at this low density is much higher than the flux of the intercombination lines, their sum is density independent.
In Fig. 4 we plot the measured line ratios and model predictions. The isobaric cooling flow model overestimates the line ratios for ions with Z< 14. As the emissivities of H- and He-like ions peak at different temperatures (Fig. 3), they are emitted at different heights in the accretion column, and thus the observed disagreement in the line ratios suggests that the temperature and density structures of the accretion column are not adequately described by this simple model. Although the measured ratios were not corrected for absorption, the difference in the absorption cross section between the H- and He-like lines of the same ion is so small that low-Z lines, such as O VII λ21.60 and O VIII λ18.97, would have to be attenuated by orders of magnitude to change the line ratios by factors of 2.
To determine which physical mechanism could be missing in our simple model, we need to determine whether the model fails to reproduce the H-like line fluxes, the He-like line fluxes, or both. We can use Eq. (7) to calculate the line fluxes if we know the values of the constants in Eq. (6): the radius of the accretion spot rspot and the free-fall speed vff, which in turn is determined by the shock temperature. We assume vff as derived in Sect. 4.1 and 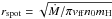 . The best match between data and model is obtained assuming an accretion rate Ṁ = 1.74 × 10-11M⊙ yr-1 (note that Beuermann et al. 2003 estimated Ṁ = 2.94 × 10-11M⊙ yr-1 for MWD = 0.79M⊙). The cooling flow model closely reproduces the H-like lines fluxes, whereas it underestimates the He-like lines fluxes (Table 1).
. The best match between data and model is obtained assuming an accretion rate Ṁ = 1.74 × 10-11M⊙ yr-1 (note that Beuermann et al. 2003 estimated Ṁ = 2.94 × 10-11M⊙ yr-1 for MWD = 0.79M⊙). The cooling flow model closely reproduces the H-like lines fluxes, whereas it underestimates the He-like lines fluxes (Table 1).
Using the specific accretion rate of a = 3 g cm-2 s-1 and f = 1.6 × 10-4, as recently obtained by Semena et al. (2014), resulted in both H- and He-like fluxes overestimated by more than an order of magnitude. Fujimoto & Ishida (1997) found that their cooling flow model fit the line ratios of high-Z ions (Z> 14), assuming that the bottom of the accretion column has a temperature kTB = 0.65 keV, preventing any cooling below this temperature. In this scenario, the H-like line intensities are well reproduced but the He-like lines of low-Z ions (Mg, Ne, O) are significantly underpredicted.
4.3. Magnetic dipole geometry
The simple cooling flow model (Model A in Table 2) makes a number of approximations, neglecting photoionization, departures from constant pressure, departures from planar geometry, variations of the gravitational potential with height, resonant scattering, thermal conduction, electron-ion temperature differences, and Compton cooling (see Appendix A). The formulation of Model A cannot be easily modified if we want to include other mechanisms. We therefore developed a modified version of the model presented by Suleimanov et al. (2005), using the radiative cooling function derived from AtomDB emissivities with the abundances derived in Sect. 4.1 and a magnetic dipole geometry as described by Canalle et al. (2005). We explored a range of specific accretion rates, a, between 0.2 and 2.0 g s-1 cm-2, resulting in a range of shock temperatures from 15.9 to 21.3 keV. The models use Rin = 2.7 RWD (Revnivtsev et al. 2011; Semena et al. 2014). Tables 1 and 2 list the resulting fluxes and line ratios from this model (Model B), respectively, with a shock temperature of 19.7 keV, which matches the shock temperature derived from the WD mass of 0.79 M⊙, a specific accretion rate of 0.6 g s-1 cm-2, and an accretion rate Ṁ = 1.74 × 10-11M⊙ yr-1. The line ratios are higher than the measurements, especially for low-Z elements. Line fluxes from H-like ions are greater than the measurements, while He-like lines are in closer agreement with the data. Although a model with a lower accretion rate would help to match the H-like line fluxes, there is a trade-off between matching these and the He-like lines fluxes and the continuum, which tends to be underestimated by models with very low Ṁ.
4.4. Varying the elemental abundances in the cooling function
In the analysis above, bremsstrahlung dominates the cooling between log Tshock and about log T = 7.3, since it gives the observed EMD and the relative H-like ion intensities (Table 1). Given that the low-Z He-like line fluxes are underpredicted, one possibility is that the cooling rate below log T = 7.3 is lower than the adopted cooling rate. One way of reducing the cooling rate below log T = 7.3 is to reduce the elemental abundances, thereby reducing the emission-line cooling from K-shell Mg, Si, and S and L-shell Fe, which dominate the cooling function for log T< 7.3(Foster et al. 2012). A model with reduced abundances can indeed reproduce the observed line ratios if the elemental abundances are about ~10% of the solar abundances (see Model C in Tables 1 and 2 and Fig. 4). However, since the bremsstrahlung continuum is not sensitive to these abundances, the line-to-continuum ratios of the H-like and He-like lines are drastically reduced and the observed spectrum is far from adequately fit.
4.5. Cooling model with thermal conduction
Another possibility is that extra heat is added in the regions of the column that are closer to the WD surface, thereby increasing the fluxes of the low-Z He-like lines. We discuss several possible mechanisms in Appendix A, along with several mechanisms that could potentially alter the line ratio diagnostics. We conclude that photoionization, steady-flow departures from pressure equilibrium, resonant scattering, Compton cooling, and electron-ion temperature differences are unlikely to explain the discrepancy. A dipole geometry and the gravitational potential difference between the top and bottom of the accretion column also fail to explain the discrepancy, as shown by the models discussed above. An additional possibility is thermally unstable cooling (Imamura & Chevalier 1984; Innes 1992). Thermal conduction seems promising in that it transfers heat from the region above 107 K, where the H-like lines are formed, to the cooler regions where the He-like lines of O, Ne, Mg, and Si are produced.
 |
Fig. 5 Emission measure distributions (EMDs) derived from models of the cooling of the postshock plasma discussed in Sects. 4.2 to 4.5. Error bars indicate the 90% confidence level of the empirically-derived EMD (Sect. 4.6). |
In clusters of galaxies, thermal energy from outer regions can be transported to the central cooling gas by conduction, but its importance in this context has been considered doubtful by several authors (Binney & Cowie 1981; Tucker & Rosner 1983; Bertschinger & Meiksin 1986). Early studies assumed that the magnetic fields strongly suppress conduction perpendicular to the field. Later, Narayan & Medvedev (2001) showed that a turbulent magnetohydrodynamic medium could support a conductive heat flux, which would play a significant role in the energy equation. In nonmagnetic accreting WDs, Liu et al. (2008) proposed that the X-ray spectra of dwarf nova can be fit with a model where the material in the innermost portion of the accretion disk is evaporated into a flow, forming a corona that surrounds the WD. They found that only small conductivities, of about 1% of the Spitzer value, are able to provide acceptable fits, presumably because the strong shear in the boundary layer produces magnetic fields nearly perpendicular to the temperature gradient.
In magnetic CVs, cooling flow models generally ignore thermal conduction because its effect is modest in the high-temperature part of the flow, reducing the emission measure by a few percent above a few times 107 K (Imamura & Chevalier 1984). However, that energy is comparable to the thermal energy of the gas below 107 K. The combination of lower temperature and higher radiative cooling coefficient creates steep temperature gradients in that region, and the divergence of thermal conduction is more important. If a large fraction of the conduction flux were deposited between about 2 × 106 and 107 K, it would alleviate the discrepancy in the H-like to He-like ratios of low-Z elements.
We computed simple models of a constant pressure flow cooling from a shock temperature of 19 keV with a constant mass flux. That is, n is inversely proportional to T, and v is inversely proportional to n (Eq. (4)). The choice of density is not important because the cooling rate is proportional to the density squared, while the cooling length scale is inversely proportional to density, and the divergence of the conductive flux is proportional to the inverse of the distance scale squared. We describe the previous discussion in the following equations:
![\begin{eqnarray} && P_{\rm rad} \propto n_{\rm e}^{2} , \\[1mm] && {\rm d}x \propto n_{\rm e}^{-1} , \\[1mm] && \nabla F_{\rm c} \propto {\rm d} x^{-2} \propto n_{\rm e}^{2} , \end{eqnarray}](/articles/aa/full_html/2015/06/aa25755-15/aa25755-15-eq145.png) where Fc is the standard Spitzer conductive flux and Prad is the radiative cooling rate. Thus, we have a one-parameter family of models provided that the shock jump conditions determine the relation between flow speed and maximum temperature.
where Fc is the standard Spitzer conductive flux and Prad is the radiative cooling rate. Thus, we have a one-parameter family of models provided that the shock jump conditions determine the relation between flow speed and maximum temperature.
We solved the equation for thermal energy by specifying a temperature grid and determining the distance needed to cool from one temperature to the next. If thermal conduction is ignored, we obtain a simple linear equation (see Sect. 4.2). With thermal conduction, the equation is cubic.
If Δti is the time needed to cool ΔTi = Ti−Ti + 1 and Vi is the flow speed, then the thickness of that cell is 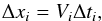 (12)and the contribution of that cell to the emission is
(12)and the contribution of that cell to the emission is 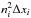 . We find
. We find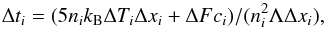 (13)where ΔFci is the difference in thermal conduction fluxes entering and leaving cell i. That yields the equation
(13)where ΔFci is the difference in thermal conduction fluxes entering and leaving cell i. That yields the equation 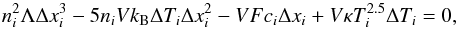 (14)where κ is the thermal conduction coefficient.
(14)where κ is the thermal conduction coefficient.
The effect of conduction is to transfer a few percent of the energy from the hot part of the flow to the cooler regions, increasing the emission measure at lower temperatures. Nearly all the conductive flux is deposited below 106 K, however, and the EMD at higher temperatures is almost indistinguishable from the model without conduction.
4.6. The empirical EMD
We can empirically derive an upper limit on the EMD using the observed emission line fluxes, their tabulated emissivities, and a fitting algorithm. To derive the empirical EMD, we use a Markov-Chain Monte Carlo process as implemented in PINTofALE (PoA; Kashyap & Drake 2000). A detailed explanation of the method, its potential, and its limitations can be found in Kashyap & Drake (1998). Given the nature of the method, the shape of the EMD depends on the emission lines chosen for fitting. Basically, the EMD is obtained by fitting the minimum of the loci curves. The loci curves are constructed by measuring the fluxes of emission lines using the relationship 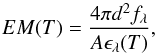 (15)where d is the distance to the source, fλ is the flux of the emission line in erg s-1 cm-2, A is the element abundance, and ϵλ(T) is the line emissivity as a function of temperature in units of erg cm3 s-1. Although the derived EMD depends on the assumed elemental abundances, PoA has the option of reconstructing an abundance-independent EMD using the measured line ratios of H- and He-like lines of O, Ne, Mg, Si, S, Ar, Ca, and Fe. The resulting best-fit solution for the EMD is shown in Fig. 5, while the range of fluxes and line ratios are listed in Tables 1 and 2 as Model D. The overall trend of the empirical EMD agrees with the physically-based EMDs derived above. The empirical EMD mostly differs from theoretical EMDs in temperatures where no emission lines were measured (e.g., log T ≳ 8.1 or log T ≲ 6.6) and there are only a few continuum, line-free regions (e.g., 2.2–3.2 Å).
(15)where d is the distance to the source, fλ is the flux of the emission line in erg s-1 cm-2, A is the element abundance, and ϵλ(T) is the line emissivity as a function of temperature in units of erg cm3 s-1. Although the derived EMD depends on the assumed elemental abundances, PoA has the option of reconstructing an abundance-independent EMD using the measured line ratios of H- and He-like lines of O, Ne, Mg, Si, S, Ar, Ca, and Fe. The resulting best-fit solution for the EMD is shown in Fig. 5, while the range of fluxes and line ratios are listed in Tables 1 and 2 as Model D. The overall trend of the empirical EMD agrees with the physically-based EMDs derived above. The empirical EMD mostly differs from theoretical EMDs in temperatures where no emission lines were measured (e.g., log T ≳ 8.1 or log T ≲ 6.6) and there are only a few continuum, line-free regions (e.g., 2.2–3.2 Å).
5. Discussion and conclusions
We used the high-quality spectra obtained with Chandra HETG from the IP EX Hya to test models for the cooling of the postshock flow, often applied to the X-ray emission from the accretion column of magnetic CVs. We have found that the fluxes of the H-like lines are well reproduced by models of an isobaric cooling flow, while fluxes of low Z He-like lines are underestimated, suggesting that either the cooling in the low-temperature region of the accretion column does not remove heat efficiently, or there is an additional source of heat. On the other hand, the X-ray data from clusters of galaxies show less low-temperature plasma than expected from the similar isobaric cooling flow scenario. Thus in galaxy clusters there must be an extra heat source that is strong enough to prevent the plasma from cooling below 107 K (e.g., Zhuravleva et al. 2014).
 |
Fig. 6 Comparison between the Chandra MEG±1 spectrum (black full line) and spectra obtained from the different models discussed in Sect. 4. Top: accretion column with a magnetic dipole geometry and change of gravitational potential with height (blue full line, Model B, see Sect. 4.3 for details). Bottom: EMD derived from the fit of the loci curves obtained from the flux measurements (orange full line, Model D, see Sect. 4.6 for details). The model-data panels show that the continuum emission from model B overestimates the data. Given that all the spectral models were derived assuming the same accretion rate, Ṁ = 1.74 × 1015 g s-1, model B requires lower accretion rates to match the data. |
We studied different variables that could affect the shape of the EMD and the emission line fluxes, such as a dipole geometry, gravity, and chemical abundances. Neither a dipole geometry nor the gravitational potential difference between the top and bottom of the column are able to modify the EMD in such a way as to match the observed line fluxes and continuum simultaneously, and because most of the continuum is due to the bremsstrahlung emission at the shock temperature, it is possible that the accretion column is not tall enough for these effects to be significant. A subsolar set of elemental abundances allows us to reproduce the observed line ratios, but the line fluxes are greatly underestimated as are the line-to-continuum ratios. Thermal conduction, which has been considered in clusters of galaxies, does not resolve the discrepancy.
A comparison of the predicted spectra from the different models discussed in Sect. 4 and the Chandra observation is shown in Fig. 6. The spectra from Models A and C are not shown in this figure because Model A reproduces the results already shown in Fig. 2, while Model C greatly overestimates the continuum and underestimates the line fluxes. Spectrum from Model B computed for an accretion rate of Ṁ = 1.74 × 10-11M⊙ yr-1 overestimates the continuum (Fig. 6, upper panel), indicating that the accretion rate from this model should be lower that the accretion rate found in the simple isobaric cooling flow model (model A). Model D (Fig. 6 lower panel) makes a reasonable prediction of the observed spectrum and line ratios, although it underpredicts the fluxes of emission lines in the ≈5–10 Å region.
The appendix discusses several other possible mechanisms that could modify the EMD and shows that they are unlikely to account for the discrepancies between the model and the observation for the flux of the He-like lines. Thermal conduction does not alleviate the problem. A possible explanation is the expected thermal instability of the cooling flow (Imamura & Chevalier 1984; Langer et al. 1982), so that the shock height and shock speed vary with time. Hydrodynamical simulations will be needed to determine whether such instabilities can change the H-like to He-like intensity ratios by the observed amount, but they should change the ratios in the correct sense. First, the nonlinear thermal instability causes the hot part of the flow to cool at constant density rather than constant pressure. That means that the energy each particle must lose is 3/2 kT rather than 5/2 kT. Second, the energy that is not converted to radiation in the constant density cooling produces secondary shock waves that reheat the gas. The secondary shocks should have speeds of a modest fraction of the intial shock speed, and they could plausibly produce temperatures of a few million K, leading to extra emission in He-like lines of the lower-Z elements. This simple picture is probably complicated by random variations in the density of the gas striking the shock.
Model D shows that the empirical EMD can be rather complex and better theoretical models will be needed to understand the high-resolution X-ray spectra of magnetic accreting WDs that will be obtained with ground-breaking future instruments such as the calorimeter onboard ASTRO-H.
Acknowledgments
We thanks Vinay Kashyap, Randall K. Smith, and Adam Foster. G.J.M.L. acknowledge support from: NASA to the Smithsonian Astrophysical Observatory (SAO) under Chandra GO7- 8026X; grants PICT 2011/269 (Agencia) and PIP D-4598/2012 (CONICET/Argentina). C.W.M.’s contribution to this work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344. V.S. was supported by German Research Foundation (DFG) grant WE 1312/48-1.
References
- Aizu, K. 1973, Prog. Theor. Phys., 49, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Bertschinger, E., & Meiksin, A. 1986, ApJ, 306, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., & Reinsch, K. 2008, A&A, 480, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Harrison, T. E., McArthur, B. E., Benedict, G. F., & Gänsicke, B. T. 2003, A&A, 412, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Cowie, L. L. 1981, ApJ, 247, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Brunschweiger, J., Greiner, J., Ajello, M., & Osborne, J. 2009, A&A, 496, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canalle, J. B. G., Saxton, C. J., Wu, K., Cropper, M., & Ramsay, G. 2005, A&A, 440, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cropper, M., Wu, K., Ramsay, G., & Kocabiyik, A. 1999, MNRAS, 306, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenbart, S., Beuermann, K., Reinsch, K., & Gänsicke, B. T. 2002, A&A, 382, 984 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., & Nulsen, P. E. J. 1977, MNRAS, 180, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, A. R., Ji, L., Smith, R. K., & Brickhouse, N. S. 2012, ApJ, 756, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, R., & Ishida, M. 1997, ApJ, 474, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Ghavamian, P., Schwartz, S. J., Mitchell, J., Masters, A., & Laming, J. M. 2013, Space Sci. Rev., 178, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, T., & Ishida, M. 2014a, MNRAS, 438, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, T., & Ishida, M. 2014b, MNRAS, 441, 3718 [NASA ADS] [CrossRef] [Google Scholar]
- Homer, L., Szkody, P., Raymond, J. C., et al. 2004, ApJ, 610, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Hoogerwerf, R., Brickhouse, N. S., & Mauche, C. W. 2004, ApJ, 610, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Hoogerwerf, R., Brickhouse, N. S., & Mauche, C. W. 2006, ApJ, 643, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Hurwitz, M., Sirk, M., Bowyer, S., & Ko, Y.-K. 1997, ApJ, 477, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Imamura, J. N., & Chevalier, R. A. 1984, ApJ, 280, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Imamura, J. N., & Durisen, R. H. 1983, ApJ, 268, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Innes, D. E. 1992, A&A, 256, 660 [NASA ADS] [Google Scholar]
- Ishida, M., Silber, A., Bradt, H. V., et al. 1991, ApJ, 367, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Kashyap, V., & Drake, J. 1998, in Cool Stars, Stellar Systems, and the Sun, eds. R. A. Donahue, & J. A. Bookbinder, ASP Conf. Ser., 154, 844 [Google Scholar]
- Kashyap, V., & Drake, J. J. 2000, BASI, 28, 475 [Google Scholar]
- Kim, W.-T., & Narayan, R. 2003, ApJ, 596, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, S. H., Chanmugam, C., & Shaviv, G. 1982, ApJ, 258, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, F. K., Meyer, F., Meyer-Hofmeister, E., & Burwitz, V. 2008, A&A, 483, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, Landolt Börnstein, 44 [Google Scholar]
- Luna, G. J. M., & Sokoloski, J. L. 2007, ApJ, 671, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, G. J. M., Raymond, J. C., Brickhouse, N. S., et al. 2010, ApJ, 711, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Mauche, C. W. 1999, ApJ, 520, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Mauche, C. W., Liedahl, D. A., & Fournier, K. B. 2001, ApJ, 560, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Mauche, C. W., Liedahl, D. A., & Fournier, K. B. 2003, ApJ, 588, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, K., Kinkhabwala, A., Peterson, J. R., Kahn, S. M., & Paerels, F. 2003, ApJ, 586, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Medvedev, M. V. 2001, ApJ, 562, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., & Raymond, J. C. 1985, ApJ, 292, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Perna, R., McDowell, J., Menou, K., Raymond, J., & Medvedev, M. V. 2003, ApJ, 598, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, J. R., & Fabian, A. C. 2006, Phys. Rep., 427, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ramsay, G., Wheatley, P. J., Norton, A. J., Hakala, P., & Baskill, D. 2008, MNRAS, 387, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, J. C. 1979, ApJS, 39, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M., Potter, S., Kniazev, A., et al. 2011, MNRAS, 411, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, S. R., Mason, K. O., & Cordova, F. A. 1988, MNRAS, 231, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Ruszkowski, M., & Oh, S. P. 2011, MNRAS, 414, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Semena, A. N., Revnivtsev, M. G., Buckley, D. A. H., et al. 2014, MNRAS, 442, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Suleimanov, V., Revnivtsev, M., & Ritter, H. 2005, A&A, 443, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suleimanov, V., Poutanen, J., Falanga, M., & Werner, K. 2008, A&A, 491, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tucker, W. H., & Rosner, R. 1983, ApJ, 267, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Van de Putte, D., Smith, R. C., Hawkins, N. A., & Martin, J. S. 2003, MNRAS, 342, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J., & Laming, J. M. 2003, ApJ, 584, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Yuasa, T., Nakazawa, K., Makishima, K., et al. 2010, A&A, 520, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhuravleva, I., Churazov, E., Schekochihin, A. A., et al. 2014, Nature, 515, 85 [Google Scholar]
Appendix A: Modifications to the cooling model
There are several physical processes that must operate at some level in the shock-heated plasma and that would in principle affect the relative intensities of the H-like emission lines.
Photoionization: X-rays from the hotter parts of the flow heat and ionize the cooler parts. X-ray emission from the photoionized accretion column above the shock was identified by Luna et al. (2010) in several lines in the form of very large velocity width components. In the shocked gas, the importance of photoionization is greatly reduced because of much higher density. We have estimated the effect of photoionization on the cooling flow by computing models of steady-flow shocks with the model of Raymond (1979). The atomic rates in this model have been updated over the years, but they are generally not as accurate as the AtomDB rates (see Smith et al. 2001, for a comparison). However, the percentage changes due to including processes such as photoionization should be reliable. Simple 3000 km s-1 shock wave models with and without photoionization showed no difference in the H-like to He-like line ratios.
Departure from constant pressure: the shocked plasma slows from 1/4 the shock speed to zero as it settles to the WD surface. That implies a pressure gradient that can influence the emission measure distribution. However, models with magnetic support cool at nearly constant density down to 106 K, and therefore nearly constant velocity. These models show changes in the line ratios at only a percent level compared to models without magnetic support. The perpendicular component of the magnetic field alone can support the cooling plasma and the field is entirely parallel to the flow in the standard shock model. However, observations of supernova remnants show strong amplification of the magnetic field, quite likely by an instability that produces perpendicular field (e.g., Vink & Laming 2003; Bell 2004), and this kind of mechanism may operate in accretion shocks as well.
Thermal instability: Larger changes in the EMD could result from the thermally unstable nature of the postshock cooling region (Imamura & Durisen 1983; Langer et al. 1982). The instability causes oscillations in the shock height and shock speed and the cooling gas can develop large low-pressure regions and subshocks (e.g., Innes 1992). It is not obvious whether thermal instability would increase or decrease the He-like to H-like ratio, or how big the effect would be. Hydrodynamic models are needed.
Resonant scattering: terada et al. (2001, 2004) investigated the effects of scattering in the resonance lines in magnetic CVs. They found that resonance scattering produced asymmetric emission and modulation on the spin period in polars, but not in IPs. Fujimoto & Ishida (1997) also showed that resonant scattering was not important in EX Hya.
Electron-ion temperature difference: if the shock wave heats ions, but not electrons, as is observed to occur in collisionless shocks in supernova remnants (Ghavamian et al. 2013), the electrons are gradually heated by Coulomb collisions. The result is that the peak electron temperature is a bit lower than the nominal shock temperature, and the electrons stay near that peak temperature longer than in a single temperature flow. Based on the shock models mentioned above, this increases the Fe XXVI line flux relative to the others, but not very strongly.
Compton Cooling: compton cooling can compete with bremsstrahlung if the density is low, reducing the bremsstrahlung emission at the highest temperatures. For a WD temperature of 25 000 K (Eisenbart et al. 2002) and the densities indicated by the Fe XVII and Fe XXII lines (Mauche et al. 2001, 2003), however, the Compton cooling rate is less than 1% of the bremsstrahlung cooling rate. Compton scattering is an additional cooling mechanism, which can potentially decrease the plasma temperature in the upper hot layers and, therefore, decrease the fluxes of H-like lines. However, this cooling mechanism is effective only for massive WDs (>1 M⊙) and high local mass accretion rates (a> 1 g s-1 cm-2) (Suleimanov et al. 2008).
All Tables
All Figures
 |
Fig. 1 Observed emission-line profiles with overlaid Gaussian models of a) O VII λ21.6 and O VII λ21.8 (MEG ± 1); b) O VIII λ18.97 (HEG ± 1); c) Ne IX λ13.45 and Ne IX λ13.55 (HEG ± 1); d) Ne X λ12.13 (HEG ± 1); e) Mg XI λ9.16 and Mg XI λ9.23 (HEG ± 1); f) Mg XII λ8.42 (HEG ± 1); g) Si XIII λ6.64, Si XIII λ6.68, and Si XIII λ6.74 (HEG ± 1); h) Si XIV λ6.18 (HEG± 1); i) S XV λ5.04, S XV λ5.06, and S XV λ5.10 (HEG ± 1); j) S XVI λ4.73 (HEG ± 1); k) Ar XVIII λ3.73, Ar XVII λ3.944 + Ar XVII λ3.961 + Ar XVII λ3.965, and Ar XVII λ3.994 + S XVI λ3.992 + S XVI λ3.991 (HEG ± 1); l) Ca XX λ3.02 and Ca XIX λ3.17 (HEG ± 1); and m) Fe XXVI λ1.78, Fe XXV λ1.85 and Fe XXV λ1.86 (HEG ± 1), where the HETG data and model profiles are shown with black and red histograms, respectively. Below each panel, we plot the fit residuals. Where overlapping, the HEG±1 and MEG±1 spectra were fit simultaneously; HEG±1 is shown for illustrative purposes. As discussed in Luna et al. (2010), the broad wings in the residuals to the fits of some of the emission lines – O VIII in particular – are due to emission by the photoionized preshock accretion flow. |
| In the text | |
 |
Fig. 2 Chandra MEG ± 1 order X-ray spectrum between spin-phases φ67 = 0.9 and 1.1 (i.e., the range of phases where the observer has the most unextinguished view of the accretion column) fit with an XSPEC variable-abundance isobaric cooling flow model (vmcflow). The absorption column, NH, is smaller than 1020 cm-2, as expected, while the shock temperature is |
| In the text | |
 |
Fig. 3 Upper panel: radiative cooling function derived using emissivities from AtomDB (in the low-density limit, see Sect. 4.2) and abundances (in units of the solar abundance of Anders & Grevesse 1989) of O = 0.92, Ne = 1.31, Ar = 0.93, Ca = 1.07, Fe = 0.61 (see Sect. 4.1). Lower panel: line emissivities as a function of temperature from AtomDB, normalized by their peak emissivity, for the H-like (full, black line) and He-like resonance+intercombination (dotted, red line) transitions of O, Ne, Mg, Si, S, Ar, Ca, and Fe. |
| In the text | |
 |
Fig. 4 Measured ratios of the H-like Lyα line to the sum of the He-like resonance, intercombination, and forbidden lines from the Chandra spectrum of EX Hya (black diamonds with error bars). The histograms show the results from the models discussed in Sects. 4.2 to 4.5. For the empirically-derived EMD, the error bars indicate the 90% confidence level (Sect. 4.6). |
| In the text | |
 |
Fig. 5 Emission measure distributions (EMDs) derived from models of the cooling of the postshock plasma discussed in Sects. 4.2 to 4.5. Error bars indicate the 90% confidence level of the empirically-derived EMD (Sect. 4.6). |
| In the text | |
 |
Fig. 6 Comparison between the Chandra MEG±1 spectrum (black full line) and spectra obtained from the different models discussed in Sect. 4. Top: accretion column with a magnetic dipole geometry and change of gravitational potential with height (blue full line, Model B, see Sect. 4.3 for details). Bottom: EMD derived from the fit of the loci curves obtained from the flux measurements (orange full line, Model D, see Sect. 4.6 for details). The model-data panels show that the continuum emission from model B overestimates the data. Given that all the spectral models were derived assuming the same accretion rate, Ṁ = 1.74 × 1015 g s-1, model B requires lower accretion rates to match the data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


