| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425453 | |
| Published online | 11 June 2015 | |
An X-ray variable absorber within the broad line region in Fairall 51
1
Astronomical Institute, Academy of Sciences, Boční II 1401, 14100
Prague, Czech
Republic
e-mail:
jiri.svoboda@asu.cas.cz
2
Dr. Karl Remeis Sternwarte, Sternwartstrasse 7, 96049
Bamberg,
Germany
3
European Space Astronomy Centre of ESA,
PO Box 78, Villanueva de la Cañada, 28691
Madrid,
Spain
4
Departamento de Astrofisica Extragalactica y Cosmologia, Instituto
de Astronomia, Universidad Nacional Autonoma de Mexico (UNAM),
Apartado Postal 70-264,
04510
México,
Mexico
5
Osservatorio Astronomico di Roma (INAF),
via Frascati 33, 00040
Monteporzio Catone Roma,
Italy
Received: 3 December 2014
Accepted: 13 April 2015
Context. Fairall 51 is a polar-scattered Seyfert 1 galaxy, a type of active galaxy believed to represent a bridge between unobscured type-1 and obscured type-2 objects. Fairall 51 has shown complex and variable X-ray absorption, but little is known about its origin.
Aims. In our research, we observed Fairall 51 with the X-ray satellite Suzaku in order to constrain a characteristic time scale of its variability.
Methods. We performed timing and spectral analysis of four observations separated by 1.5, 2, and 5.5 day intervals.
Results. We found that the 0.5–50 keV broadband X-ray spectra are dominated by a primary power-law emission (with the photon index ~2). This emission is affected by at least three absorbers with different ionisations (log ξ ≈ 1–4). The spectrum is shaped further by a reprocessed emission, possibly coming from two regions, the accretion disc and a more distant scattering region. The accretion disc emission is smeared by the relativistic effects, from which we measured the spin of the black hole as a ≈ 0.8 ± 0.2. We found that most of the spectral variability can be attributed to the least ionised absorber whose column density changed by a factor of two between the first (highest-flux) and the last (lowest-flux) observation.
Conclusions. A week-long scale of the variability indicates that the absorber is located at the distance ≈0.05 pc from the centre, i.e., in the broad line region.
Key words: galaxies: active / galaxies: Seyfert / galaxies: individual: Fairall 51
© ESO, 2015
1. Introduction
In the unification paradigm of active galactic nuclei (AGN) by Antonucci (1993), types-1 and 2 AGNs are distinguished by the inclination angle, more specifically whether the torus intercepts the line of sight. However, this standard picture that assumes a homogeneous dusty torus has been questioned by several studies (Nenkova et al. 2002; Elitzur 2012; Merloni et al. 2013). The clumpiness of the absorber is supposed to be another important parameter for any proper classification. The type of AGN is not determined entirely by the inclination angle but also by the probability that the absorption clouds intercept the line of sight. This is supported by a large and fast variability of the absorber observed in several sources (see, e.g., Risaliti et al. 2005; Bianchi et al. 2012). The statistical analysis based on the vast RXTE archive has recently been done by Markowitz et al. (2014), who constrain the probability of an absorption event due to clumpy material being 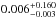 for type-1 and
for type-1 and 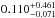 for type-2 AGNs.
for type-2 AGNs.
The absorption variability occurs on different time scales for different AGNs. Risaliti et al. (2002) investigated a sample of Seyfert 2 galaxies and revealed that most of them are variable on time scales of months to years. Similar variability has recently been reported based on Suzaku observations, e.g., by Braito et al. (2013) for NGC 4507 and Rivers et al. (2014) for NGC 2110. The variability time scale of months to years is typical of a clumpy torus at the distance ~1 pc. However, the absorption variability was later found on a time scale of days in several sources: NGC 4388 (Elvis et al. 2004), NGC 1365 (Risaliti et al. 2005), NGC 4151 (Puccetti et al. 2007), NGC 7582 (Bianchi et al. 2009b), PG 1535+547 (Ballo et al. 2008), Mrk 766 (Risaliti et al. 2011), NGC 5506 (Markowitz et al. 2014), NGC 3227 (Lamer et al. 2003; Beuchert et al., in prep.), or Swift J2127.4+5654 (Sanfrutos et al. 2013). The origin of such variability must be significantly closer to the central region. Recently, Torricelli-Ciamponi et al. (2014) have shown that X-ray eclipses are common when the expected occultation time is compatible with the exposure and that these events may be responsible for most of the spectral variability at energies higher than 2 keV. They associated the origin of the eclipsing clouds to the broad line region (BLR) of AGNs.
Suzaku observations from September 2013.
Knowing the location of the absorber in the so-called polar-scattered Seyfert 1 AGN is important for understanding the nature of this kind of object. Generally, Seyfert 1 galaxies do not exhibit polarised emission. It is believed that the total polarisation is washed out by the mutual interaction of polarised emission from two scattering regions, the equatorial plane and the ionisation cone (Smith et al. 2004; Batcheldor et al. 2011). The equatorial emission is obscured by a dusty torus in Seyfert 2 galaxies, so the polarised emission is only detected from the ionisation cone. Smith et al. (2004) argue that the detected polarisation depends on inclination and that polar-scattered Seyfert 1 galaxies represent a bridge between type-1 and type-2 galaxies. In this scenario, the enhanced variability of the absorber (with respect to the equatorial-scattered ones) is therefore expected because we may be seeing the AGN along a line of sight that grazes the torus rim.
The X-ray properties of polar-scattered Seyfert 1 galaxies were studied by Jiménez-Bailón et al. (2008) who realised that the luminosity and the index of a power-law emission are consistent with Seyfert 1 galaxies. A low inclination is also suggested from detection of a relativistically smeared iron line profile coming from the innermost accretion disc in most of the sources. The variability and complex absorption are common features of these sources.
More recently, investigation of the variability properties has been done for several sources. A clear example of the absorption variability was shown in the case of Mrk 704 (Matt et al. 2011; Laha et al. 2011), where the spectra from two different observations separated by three years were identical above 7 keV but very different at lower energies. The observed X-ray spectral variability of Mrk 231 below 10 keV can be interpreted as changes in a patchy absorber (Piconcelli et al. 2013; Teng et al. 2014). Beuchert et al. (in prep.) found the presence of a non-dusty absorber in NGC 3227 that varies on a time scale of about one week. They find that the absorber is partly ionised and partially covers the source. The spectral variability of another polar-scattered Seyfert 1 galaxy, ESO 323-G77, has been recently studied by Miniutti et al. (2014). They find two variable absorbers with a different time scale for their variability. The absorbers were associated to BLR clouds (month-long time scale) and a clumpy torus (year-long time scale) according to their variability.
Fairall 51 (also known as ESO 140-43) is a nearby galaxy with the cosmological redshift z = 0.0141, as measured in the 2MASS survey (Huchra et al. 2012). Fairall 51 is classified as Seyfert 1 since its optical spectrum contains broad lines with the full width at half maximum FWHM ≈ 3000 ± 1000 km s-1 (Schmid et al. 2001). The optical to UV flux is highly polarised (Martin et al. 1983). VLT-spectropolarimetry measurements by Schmid et al. (2001) revealed a polarisation degree ranging from 5% (red) to 13% (UV), which are one of the highest polarisation degrees observed for type-1 objects.
 |
Fig. 1 Left: XIS 0 (upper, with small circles) and HXD/PIN (lower) (all background subtracted) light curves in the 0.5−10 keV or 15−55 keV energy range, respectively. Right: XIS 0 light curves in two different energy bands, 0.5−3 keV and 3−10 keV (all background-subtracted), and the hardness ratio between the hard and the soft bands. The gaps between the observations are shrunk for clarity. The time bin size is 2880 s. |
Fairall 51 is very bright in X-rays (about 1 millicrab). It was observed twice with high-quality X-ray spectrometers on-board the XMM-Newton satellite. The first observation was performed in 2005 with the observed flux 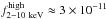 erg cm-2 s-1, and the second one about half a year later with the observed flux
erg cm-2 s-1, and the second one about half a year later with the observed flux 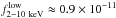 erg cm-2 s-1. The spectra differ significantly, and the complex soft X-ray spectrum may be described by three zones of a partially-covering warm absorber with high, moderate, and very low ionisation (Ricci et al. 2010).
erg cm-2 s-1. The spectra differ significantly, and the complex soft X-ray spectrum may be described by three zones of a partially-covering warm absorber with high, moderate, and very low ionisation (Ricci et al. 2010).
Short-time variability of this source was suggested from two Swift observations performed in 2008. The observations were separated by only five days. Although the exposures were very short (a few ks each), the spectra were qualitatively different below 7 keV (Ricci et al. 2010; Beuchert et al. 2013). Beuchert et al. (2013) determined that the variable absorber must be located no farther than the BLR based on the short variability time scale.
In this paper, we present the results of a recent monitoring of Fairall 51 by the Japanese X-ray satellite Suzaku (Mitsuda et al. 2007), during which four 30 ks exposures were performed separated by 1.5, 2, and 5.5 days. The paper is organised as follows: observations and data reduction are described in Sect. 2; results are presented in Sect. 3 and discussed in Sect. 4; main conclusions are summarised in Sect. 5.
2. Observations and data reduction
We observed Fairall 51 using the X-ray Suzaku satellite (Mitsuda et al. 2007) during four ~30 ks-long exposures in the first half of September 2013 (see Table 1). The observation identification numbers are 708046010, 708046020, 708046030, and 708046040. All the observations were performed at the XIS-nominal pointing position.
The Heasoft package version 6.141 was used for the data reduction and also for the subsequent spectral and timing analysis. The data were processed in a standard way following the Suzaku Data Reduction Guide2 (version 4). For all XIS detectors, we combined both 3 × 3 and 5 × 5 modes to extract the event files. The source spectra were obtained from a circle around the centre of the point spread function with the radius of 260′′. We defined the background extraction region as an annulus around the source circle with the outer radius of 360′′ to avoid any contamination from the calibration source at the edges. We created related response matrices and ancillary response files using the tools xisrmfgen and xissimarfgen. The HXD/PIN spectra were reduced with the tool hxdpinxbpi. The tuned background files3 were used to model the non X-ray background. The cosmic X-ray background was estimated using the model by Boldt (1987) in accordance with this guide.
We used the Xspec software (Arnaud 1996) version 12.8.2 for the spectral analysis. The cross-normalisation factors between the spectra of different Suzaku detectors were free for XIS 1 and XIS 3 and fixed to 1.16 for HXD/PIN according to the Suzaku Data Reduction Guide. Fits were performed in the 0.5−10 keV energy interval for the XIS spectrum and from 15 keV for the HXD/PIN spectrum. We fitted the HXD/PIN spectra up to the energy corresponding to a 5% source detection level above the background level, which is well above the reported systematic uncertainty in the guide. All but the second HXD/PIN spectra were considered in the 15–55 keV energy range. Only the HXD/PIN spectrum of the second observation was limited by 45 keV owing to a lower signal-to-noise ratio caused by a shorter exposure time (≈22 ks) compared to the other observations.
We used C-statistics (Cash 1979) for fitting the data. However, we also express the goodness of the fit with more familiar χ2 values that were used as test statistics. We binned the spectra to contain at least 30 counts per bin only for this purpose. All the quoted errors correspond to a 90% confidence level for one interesting parameter.
3. Results
3.1. Timing properties
We performed a series of four observations separated by 1.5, 2, and 5.5 day intervals to constrain the characteristic time scale of the short-term variability of Fairall 51. Figure 1 (left panel) shows the XIS0 and HXD/PIN light curves from all four observations. While the soft X-ray flux decreased by a factor of two between the first and the last observations, the hard X-ray flux stays more or less constant.
The soft X-ray variability is shown in more detail in the right-hand panel of Fig. 1 where the light curves in two energy bands, 0.5–3 and 3–10 keV, are shown together with the hardness ratio defined as the flux ratio between these two bands (hard to soft). The major change in the hardness is measured during the last observation, when the hardness ratio is significantly greater than in the previous three observations, suggesting a significant change in the spectrum during this observation.
The flux significantly varied also within the individual observations. It decreased almost to half during the second observation, but the source became brighter again during the third observation. This variability is accompanied by a small hump in the hardness ratio. However, a low signal-to-noise ratio limit prevented us from a detailed investigation of this feature in the light curve, and we then dealt with four time-averaged spectra of the individual observations.
 |
Fig. 2 Left: Up: X-ray spectra of four Suzaku observations (1st black, 2nd red, 3rd green, 4th blue). Bottom: data residuals from a simple absorbed power-law model with Γ ≈ 1.7. Right: a more detailed look at the iron line and Compton hump as residuals from the simple absorbed power-law model. Only XIS 0 and HXD/PIN spectra are plotted for clarity. Data are re-binned for plotting purposes alone. |
3.2. First look at X-ray spectra
To have a first look at the spectra, we employed a simple model consisting of a power law with its normalisation as the only variable parameter between the observations. The power law was affected by the photoelectric absorption by cold material, for which we used the tbabs model (Wilms et al. 2000) with solar abundances. The column density was a free parameter but linked between the four observations.
Figure 2 shows the X-ray spectra of all Suzaku observations, together with the data residuals from this simple model. The power-law photon index is Γ ≈ 1.7, and the absorber’s column density is NH ≈ 3.8 × 1022 cm-2. The quality of the fit is not acceptable with C/ν = 12033 / 6454 ≈ 1.9 and with clear data residuals from the model over the entire energy range (see the bottom left panel of Fig. 2). The spectral features around 2 keV might be affected by calibration uncertainties and therefore we omit the data at 1.6−2.4 keV.
The most evident spectral variability between the observations is at 2–6 keV, while the spectra do not seem to vary at very high and also very soft (≲1 keV) X-ray energies. The latter suggests that the spectrum is dominated by two different spectral components in the 0.5–1 and 2–6 keV energy bands. A dominating spectral component at the very low energies can be a scattered power-law emission that is not affected by a variable absorption of a circumnuclear matter that strongly affects the direct emission, similar to what has been found for other similar sources, e.g., ESO 323-G77 (Miniutti et al. 2014).
The simple power-law model fails to describe the hard X-ray emission (see the right-hand panel of Fig. 2). The spectral curvature might be explained by a reflection hump. Its presence close to the lower energy limit of the HXD/PIN spectrum suggests that the reflection emission is red-shifted. Other residuals from the simple power-law model occur at the iron line band. The emission-line profile itself seems to be asymmetrically broadened towards its red wing, especially in the lowest-flux observation. However, it would be premature to draw any conclusions about the iron line before finding an appropriate description for the continuum. Therefore, we started with a Gaussian model for the iron line.
Beyond the emission iron line, two absorption features are visible in the spectra. They are likely due to an ionised gas in the line of sight, probably associated to the warm absorber that was already revealed by Ricci et al. (2010) who identified in total three ionised absorbers with different ionisations based on the XMM-Newton spectral analysis.
3.3. Modelling the complex absorption
Next, we employed a model with two power-law components with the photon index linked between them – one affected by the local absorber and one not. The local absorber was first modelled by a cold absorber using the ztbabs model with the column density free to vary between the observations. We also used two Gaussian lines to model the absorption features in the iron-line energy band, with free energies and the redshift fixed to the cosmological redshift of the galaxy. Furthermore, we used a Gaussian line profile to account for the emission iron Kα line. The total model was then absorbed by the interstellar absorption in our Galaxy with the column density NH = 6.9 × 1020 cm-2 (Kalberla et al. 2005) using the tbabs model. Solar abundances were assumed in all absorption models.
We obtained a statistically better fit, but it was not yet acceptable with C/ν = 7730 / 5798 ≈ 1.3. The column density of the variable absorber was found to increase from 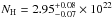 cm-2 during the first observation to NH = 6.8 ± 0.3 × 1022 cm-2 during the fourth observation. For the iron Kα emission line, we obtained E = 6.32 ± 0.03 keV, σ = 0.14 ± 0.03 keV, and an equivalent width ranging from
cm-2 during the first observation to NH = 6.8 ± 0.3 × 1022 cm-2 during the fourth observation. For the iron Kα emission line, we obtained E = 6.32 ± 0.03 keV, σ = 0.14 ± 0.03 keV, and an equivalent width ranging from 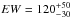 eV (1st observation) to EW = 320 ± 40 eV (4th observation). The line was found to be broadened and red-shifted from its intrinsic 6.4 keV energy. The FWHM widths of the absorption lines were found to be even larger. Their values were pegged at the upper limits, which we set to σ = 0.3 keV. The energy of the first absorption line was found to be E = 6.75 ± 0.1 keV for the first three observations and E = 6.6 ± 0.1 keV for the fourth observation. The energy of the second absorption line was found to be E = 8.2 ± 0.2 keV for all observations, which is consistent within the uncertainties.
eV (1st observation) to EW = 320 ± 40 eV (4th observation). The line was found to be broadened and red-shifted from its intrinsic 6.4 keV energy. The FWHM widths of the absorption lines were found to be even larger. Their values were pegged at the upper limits, which we set to σ = 0.3 keV. The energy of the first absorption line was found to be E = 6.75 ± 0.1 keV for the first three observations and E = 6.6 ± 0.1 keV for the fourth observation. The energy of the second absorption line was found to be E = 8.2 ± 0.2 keV for all observations, which is consistent within the uncertainties.
 |
Fig. 3 Data residuals from the different models for all observations (1st black, 2nd red, 3rd green, 4th blue). From top to bottom: residuals from the Models A–D. |
Spectral analysis of Fairall 51 – model parameters.
The power-law photon index in this simple model was Γ ≈ 1.5. Unusually flat spectral slopes have been often found to be due to a partially-covering ionised absorber (see, e.g., Piconcelli et al. 2004; Mathur et al. 2009; Svoboda et al. 2012). As the next step, we therefore employed a partially-covering ionised absorption to model the absorption features in the spectra. We replaced the absorption Gaussian lines by the zxipcf model (Reeves et al. 2008) using the xstar photo-ionisation code (Kallman & Bautista 2001). We first started with one component and refer to this model as “Model A”. The best-fit values are presented in Table 2, and the data residuals from the model are shown in the upper panel of Fig. 3. The photon index of the power law Γ ≈ 1.8 is consistent with the characteristic slope of Seyfert 1 galaxies (see, e.g., Bianchi et al. 2009a; Malizia et al. 2014). We found high ionisation of the absorber, log ξ ≳ 3, which is consistent with Ricci et al. (2010), but the column density, NH ≈ 1023−1024 cm-2, is roughly an order of magnitude higher. However, the global fit is not satisfactory with C/ν ≈ 1.1, and, in particular, residuals around ~7 keV indicate the need for another highly ionised absorption component.
The addition of another warm absorber component significantly improved the fit (from C/ν = 6399 / 5809 to 6297 / 5801). The statistical F-test using the χ2 test statistics gives the probability ≈3 × 10-19 that the improvement is just coincidental. We refer to this model as “Model B”, and the best-fit values are summarised in Table 2. The value of the ionisation of the second warm absorber is higher, log ξ ≈ 4, and it accounts for the residuals above 7 keV (see the second panel of Fig. 3). We also allowed the covering factors to vary, and we tried several tests with different initial values, but found no statistical improvement compared to fits when these parameters were fixed to 1. The ionisation parameter was also left free, but no significant change was detected across the observations. Only column densities of both cold and warm absorbers were required to vary significantly.
As a next step, we allowed the cold absorber to be ionised and partially covering. In XSPEC, we replaced the ztbabs model by another zxipcf component. We first allowed the redshift of this absorber to also vary. However, its value reached 0.1, which would correspond to an inflow of ≳25 000 km s-1. This is a quite extreme value that has not been reported in any similar source. Because the redshift in this case is not obtained from the frequency shift of a clearly defined absorption line, we considered this measurement as not indicative so we instead fix the redshift to the cosmological value of the galaxy. The obtained fit is significantly better than the previous one with C/ν = 6228 / 5804, i.e., ΔC/ν = 69. However, we realised that instead of having two highly-ionised and one low-ionised component, the fitting procedure converged to a low-ionised, mid-ionised, and one highly-ionised component. Unlike the previous model, the column densities of the highly ionised warm absorber were not required to vary between observations. Also, we found that the ionisation was not required to vary, and covering factors were consistent with being one for all observations. As a check of this result, we linked the column densities and checked whether variable covering factors and ionisations may describe the data as well. However, we obtained a statistically worse fit with C/ν = 6259 / 5795.
We checked the residuals and realised that the most significant improvement compared to Model B appeared at energies ≲1 keV, while the residuals at the iron line energy band got worse. We therefore added another absorber to again account for high ionisation. We found a new statistically better fit with four absorbers (C/ν = 6138 / 5797, ΔC/ν = 90 from the previous model). However, we did not obtain any significant improvement in modelling the residuals at energies above 10 keV.
3.4. Modelling the reflection
The models presented so far were not able to fully describe the data residuals in the iron line band and around 15 keV. The presence of iron emission line is required in all models, which indicates a significant contribution of X-ray reflection to the observed spectrum. To consistently treat the X-ray reflection, we replaced the Gaussian line by the reflection model pexmon (Nandra et al. 2007) that combines the iron line and the reflection continuum using the pexrav model (Magdziarz & Zdziarski 1995). We used the pexmon model only for reflection, i.e., with the reflection fraction parameter R fixed to − 14. The inclination was fixed to 45 degrees. We refer to this model as “Model C” and the best-fit values are presented in Table 2. The statistical improvement compared to the previous model is ΔC/ν = 43. However, the addition of the distant reflection component still did not improve satisfactorily the most prominent residuals at the HXD/PIN energy band (see the third panel of Fig. 3).
 |
Fig. 4 Final model (Model D) with its components. |
 |
Fig. 5 Final model (Model D) in the individual observations (1st black, 2nd red, 3rd green, 4th blue). |
Observed and intrinsic flux and luminosity measurements of Fairall 51.
As a next step, we employed reflection from the innermost region of the accretion disc where the radiation is significantly red-shifted from the effects of the general relativity. We therefore added a second reflection component to the model that is convolved with a relativistic disc kernel (Dovčiak et al. 2004). Free parameters of the relativistic model were the black hole spin, inclination angle, and radial-emissivity index. The inner radius was set to the marginally stable orbit depending on the spin value. The outer radius was set to 400 rg, where 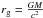 is the gravitational radius. The iron abundances were linked to the abundances of the distant reflection model. We still kept the inclination of the distant reflection fixed to 45 degrees, because the global fit is not very sensitive to this parameter.
is the gravitational radius. The iron abundances were linked to the abundances of the distant reflection model. We still kept the inclination of the distant reflection fixed to 45 degrees, because the global fit is not very sensitive to this parameter.
We further assumed that the relativistic reflection is affected by all absorbers, while the neutral reflection coming possibly from the distant polar scattering region is unaffected by the warm absorber. We obtained a significantly improved fit (C/ν = 5988 / 5806, ΔC/ν = 106 from the previous model). The best-fit values are presented in Table 2 as “Model D” parameters. We only considered three absorbers in this model, because we realised during the fitting procedure that the highest ionised absorber becomes less important with the new model. The difference between the model with three and four absorbers was only ΔC ≈ 10. Some of the absorption features at 7–10 keV were probably attributed to absorption edges of the reflection models.
The final model is statistically acceptable with no significant residuals across the entire Suzaku bandpass (see the bottom panel of Fig. 3). The model with its components is shown in Fig. 4. Figure 5 shows the comparison of the final model in all four observations. The low-ionised absorber is the one that is most responsible for the curvature of the spectrum at energies 1−10 keV. The scattered power-law emission dominates at 1 keV over the absorbed intrinsic flux and implies that the flux is not strongly variable there. The hard energy band is shaped by reflection. Relativistic smearing is responsible for shifting the Compton hump to lower energies.
We note a minor discrepancy between the data residuals and model predictions in the lower edge of the XIS spectrum, compare the data residuals at 0.5–0.7 keV shown in Fig. 2 with the model predictions shown in Fig. 5. This can, however, be an instrumental effect of the redistribution of the more energetic photons to lower energies that appears at the lower edge of the spectrum (Koyama et al. 2007).
4. Discussion
4.1. Variable spectral components
Our monitoring observational programme revealed that the short-term variability of Fairall 51 is partly caused by the variable column density of the absorbing gas and partly by the changes in the intrinsic luminosity that also significantly varies in the soft X-rays between the observations. Table 3 shows our measured values of the observed X-ray flux in the 2–10 keV range, the intrinsic 2–10 keV fluxes constrained from our final model, the observed luminosity determined using the cosmological distance5, and the estimation of the bolometric and ionising luminosity. The bolometric luminosity was constrained from the X-ray luminosity using a relation by Marconi et al. (2004).
Because the intrinsic X-ray luminosity decreased almost by a factor of two according to the final model, we got different values for the bolometric luminosity. We note, however, that these are only estimates based on measured X-ray luminosities, and the bolometric luminosity itself does not need to vary. The estimated values were Lbol ≈ 3.7 × 1044 erg s-1 for the first observation and Lbol ≈ 2 × 1044 erg s-1 for the last observation. This translates to Eddington ratios λEdd ≈ 0.03, and λEdd ≈ 0.02, respectively. We calculated the Eddington luminosity as LEdd = 1.26 × 1038(M/M⊙) erg s-1, where we used M ≈ 108M⊙ for the black hole mass (Bennert et al. 2006).
 |
Fig. 6 Relation between the intrinsic 2–10 keV flux and the column density of the cold (least ionised) absorber for Model D (black, circles) and Model B (red, triangles). |
To constrain the ionising luminosity, we used the relation by Vasudevan et al. (2010) to estimate the soft luminosity L13.6−100 eV = κ13.6−100 eVLbol, where κ13.6−100 eV goes from 0.21 to 0.59 for accretion rates from 0.01 to 0.61. By the linear interpolation, we constrained the factors for each observation depending on the estimated accretion rate. We determined the X-ray luminosity L0.1−13.6 keV by an extrapolation of the measured X-ray luminosity in 0.5−10 keV. To get the ionising luminosity, we summed the soft and the X-ray luminosity. The results are shown in the last column of Table 3. Figure 6 shows the relation between the column density of the least-ionised absorber and the intrinsic 2−10 keV flux. This relation depends on the model used, so we show this relation for Models B and D. Both results strongly indicate that the column density of the absorber increases with decreasing intrinsic flux.
Surprisingly, we have not detected any significant variability in the ionisation of the absorbers that would reflect the decrease in the illuminating flux. This would suggest that the absorber is not in the photo-ionisation equilibrium. Such behaviour has also been reported for some other sources, such as Mrk 335 (Longinotti et al. 2013) or NGC 3783 (Krongold et al. 2005). We note, however, that in our case, the models of the low- and mid-ionised absorbers are based on the continuum spectral shape and not on the individual absorption lines that would define the ionisation parameter more precisely. Therefore, no measured variability of the ionisation parameters may be simply due to the coarse resolution of the CCD detectors.
 |
Fig. 7 Contour plots between the column densities of the variable low- and mid-ionised absorbers. The colours correspond to different observations (1st black, 2nd red, 3rd green, 4th blue). The contours correspond to 1σ, 2σ, and 3σ levels. The best-fit values are indicated by a small cross in the graph. |
All the employed models suggest that the most variable spectral component is the least-ionised absorber. Figure 7 shows a contour plot between the column densities of the low- and mid-ionised absorbers in the final model D. All the free parameters of the final model were allowed to vary during the contour calculations. The column density of the low-ionised absorber changed by a factor of two between the first three and the last observation, while the column density of the mid-ionised absorber may stay unchanged within 3σ levels.
Since the values of column densities are similar and the ionisation parameters are not constrained from any discrete features, we tested a scenario where the low- and mid-ionised absorbers are replaced by one variable absorber. We considered two cases: (1) the column density and the ionisation are variable between the observations; and (2) the column density and the covering factor are variable. In both cases, the resulting fit is worse by ΔC ≈ 30 compared to the final model. The F-test using χ2 statistics gives the probability p ≈ 3 × 10-6 that the statistical improvement with two absorbers is just coincidental. Higher quality data would be needed to more precisely constrain the structure of the absorbing gas.
Furthermore, we investigated the possible variability of the highest ionised absorber. Figure 8 shows contour plots between the column density of the cold and highly ionised absorber. The left-hand panel shows results obtained by Model B. The right-hand panel shows the results obtained by a modified version of Model D, in which we allowed the warm absorber with high ionisation to vary instead of the mid-ionised absorber. While the warm-absorber column density is required to change in Model B, Model D shows that this parameter may stay unchanged during all observations.
 |
Fig. 8 Contour plots between the column densities of the variable cold and warm absorbers. The colours correspond to different observations (1st black solid, 2nd red dashed, 3rd green dotted, 4th blue dash-dotted). The contours correspond to 1σ, 2σ, and 3σ levels. Left: results obtained with tModel B. Right: results obtained with Model D with the highly-ionised warm absorber allowed to vary. |
4.2. Constraints on the variable absorber’s location
We found that the spectral change between the last observation from the previous three observations is mainly due to the increase in the column density of the cold or least ionised absorber. Based on the measured time scale of the spectral variability, we may estimate the location of this variable absorber. We assume that the main velocity of the absorbing cloud is the orbital velocity around the centre that can be approximated as the Keplerian velocity at the distance R: 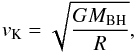 (1)where MBH is the black-hole mass, and G = 6.67 × 10-8 cm3 g-1 s-2 is the gravitational constant. For a cloud with characteristic size s, we can write
(1)where MBH is the black-hole mass, and G = 6.67 × 10-8 cm3 g-1 s-2 is the gravitational constant. For a cloud with characteristic size s, we can write 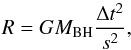 (2)where Δt is the time difference between the start and the end of occultation. Assuming a spherical symmetry and homogeneity, we can estimate the size of the cloud from the measured column density NH:
(2)where Δt is the time difference between the start and the end of occultation. Assuming a spherical symmetry and homogeneity, we can estimate the size of the cloud from the measured column density NH: 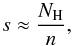 (3)where n is the particle density. We can now rewrite the Eq. (2) as
(3)where n is the particle density. We can now rewrite the Eq. (2) as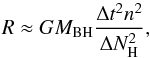 (4)where ΔNH is the change of the column density in the time interval Δt. We may rewrite Eq. (4) to have a form that is more appropriate to the typical values that are measured. We obtain an equation analogous to Eq. (3) in Risaliti et al. (2002):
(4)where ΔNH is the change of the column density in the time interval Δt. We may rewrite Eq. (4) to have a form that is more appropriate to the typical values that are measured. We obtain an equation analogous to Eq. (3) in Risaliti et al. (2002): 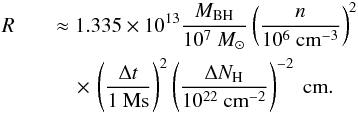 (5)With this equation, we can constrain the distance of the absorber from the change in the column density in a given time if we know the mass and the volume density. The mass of the black hole is usually constrained from different methods including reverberation mapping (Peterson 2014), stellar velocity dispersions (Ferrarese & Merritt 2000), bulge luminosities (Kormendy & Richstone 1995; Magorrian et al. 1998), or single optical emission lines due to a tight correlation between the luminosity and mass (see, e.g., Shen et al. 2008, and references therein). However, the volume density is unknown. The density should not exceed 106 particles per cm3 if it is part of a torus, and it should be about 109 particles per cm3 if the cloud belongs to the BLR (Weedman 1977).
(5)With this equation, we can constrain the distance of the absorber from the change in the column density in a given time if we know the mass and the volume density. The mass of the black hole is usually constrained from different methods including reverberation mapping (Peterson 2014), stellar velocity dispersions (Ferrarese & Merritt 2000), bulge luminosities (Kormendy & Richstone 1995; Magorrian et al. 1998), or single optical emission lines due to a tight correlation between the luminosity and mass (see, e.g., Shen et al. 2008, and references therein). However, the volume density is unknown. The density should not exceed 106 particles per cm3 if it is part of a torus, and it should be about 109 particles per cm3 if the cloud belongs to the BLR (Weedman 1977).
The volume density can be estimated if the ionisation ξ of the absorber is measured: 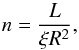 (6)where L is the illuminating luminosity the energy range 13.6 eV−13.6 keV. We can now replace the density in Eq. (4) and get
(6)where L is the illuminating luminosity the energy range 13.6 eV−13.6 keV. We can now replace the density in Eq. (4) and get ![\begin{equation} R \approx \left[GM_{\rm BH}\frac{\Delta t^2 L^2}{\Delta N_{\rm H}^2\xi^2}\right]^{\frac{1}{5}}\cdot \end{equation}](/articles/aa/full_html/2015/06/aa25453-14/aa25453-14-eq233.png) (7)Again, we can rewrite this equation with the quantities normalised to their typical values, and we obtain an equation analogous to Eq. (3) in Lamer et al. (2003):
(7)Again, we can rewrite this equation with the quantities normalised to their typical values, and we obtain an equation analogous to Eq. (3) in Lamer et al. (2003): ![\begin{eqnarray} \label{r_final} R && \approx 2.66 \times 10^{17} \, \left[\frac{M_{\rm BH}}{10^7~M_\odot}\left(\frac{\Delta t}{1~{\rm Ms}}\right)^2\left(\frac{\Delta N_{\rm H}}{10^{22}~{\rm cm}^{-2}}\right)^{-2}\right.\nonumber\\ &&\left. \quad\times\,\left(\frac{L}{10^{43}~{\rm erg\,s}^{-1}}\right)^2 \left(\frac{\xi}{\rm erg\,cm^{-2}\,s^{-1}}\right)^{-2}\right]^{\frac{1}{5}} ~{\rm cm}. \end{eqnarray}](/articles/aa/full_html/2015/06/aa25453-14/aa25453-14-eq234.png) (8)The black-hole mass of Fairall 51 was estimated as M ≈ 108M⊙ by Bennert et al. (2006) based on the relation between the luminosity at 5100 Å and the black hole mass (Peterson et al. 2004). We measured the change in the column density of the cold absorber ΔNH ≈ 4 × 1022 cm-2 to be ≈0.45 Ms (see Fig. 1). The ionising luminosity is taken as an average value between the third and fourth observations, L ≈ 1044 erg s-1 (see Table 3), and the ionisation is ξ ≈ 15 erg cm-2 s-1 (see Table 2). After inserting these values into Eq. (8) we get the estimation for the distance of the absorbing cloud from the centre:
(8)The black-hole mass of Fairall 51 was estimated as M ≈ 108M⊙ by Bennert et al. (2006) based on the relation between the luminosity at 5100 Å and the black hole mass (Peterson et al. 2004). We measured the change in the column density of the cold absorber ΔNH ≈ 4 × 1022 cm-2 to be ≈0.45 Ms (see Fig. 1). The ionising luminosity is taken as an average value between the third and fourth observations, L ≈ 1044 erg s-1 (see Table 3), and the ionisation is ξ ≈ 15 erg cm-2 s-1 (see Table 2). After inserting these values into Eq. (8) we get the estimation for the distance of the absorbing cloud from the centre: 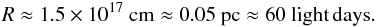 The distance of the BLR can be estimated from the optical luminosity. A tight relation between the BLR radius and the luminosity at 5100 Å was constrained by Kaspi et al. (2005) and recently updated by Bentz et al. (2013) who also subtracted contributions of the host galaxies. The luminosity of Fairall 51 is L5100 Å ≈ 1043 erg s-1 (Bennert et al. 2006). This corresponds to the BLR size of ~40 light days according to Bentz et al. (2013). This value is consistent with what we found for the variable X-ray absorber, when taking the general uncertainties of both estimations into account.
The distance of the BLR can be estimated from the optical luminosity. A tight relation between the BLR radius and the luminosity at 5100 Å was constrained by Kaspi et al. (2005) and recently updated by Bentz et al. (2013) who also subtracted contributions of the host galaxies. The luminosity of Fairall 51 is L5100 Å ≈ 1043 erg s-1 (Bennert et al. 2006). This corresponds to the BLR size of ~40 light days according to Bentz et al. (2013). This value is consistent with what we found for the variable X-ray absorber, when taking the general uncertainties of both estimations into account.
We can also derive the density of the absorbing cloud from our measurements. Using Eq. (6), we obtain 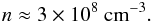 This value is slightly lower than the averaged expected density of BLR clouds (Peterson 2014). Our measurements of slightly lower density, larger radius, and low ionisation are consistent with the reverberation in optical spectral lines that revealed a stratification in the ionisation and the density of the BLR region (see, e.g., Gaskell & Sparke 1986), both decreasing with the radius.
This value is slightly lower than the averaged expected density of BLR clouds (Peterson 2014). Our measurements of slightly lower density, larger radius, and low ionisation are consistent with the reverberation in optical spectral lines that revealed a stratification in the ionisation and the density of the BLR region (see, e.g., Gaskell & Sparke 1986), both decreasing with the radius.
Although our measured location of the variable absorber is fully consistent with the BLR, we note that the innermost part of the torus cannot be ruled out either because its radius value is not well established. The most recent mid-infrared observations of nearby galaxies have revealed that there is a large scatter in the geometrical properties of their dusty tori (Burtscher et al. 2013), and even very complicated structures of the dust within the central parsec were reported (Tristram et al. 2014).
4.3. Scattering region
The presence of a scattering region that is not located on the line of sight is suggested from the optical polarisation measurements. Our X-ray spectra show significant spectral variability in the energy range 2−6 keV (see Fig. 2) that is best explained by a variable absorption. Less variability is evident around 1 keV, which can be explained by a scattered power-law emission that is not affected by a variable absorber. Although its intrinsic normalisation is lower than the normalisation of the direct power-law emission by two orders of magnitude, it dominates the spectrum at ~1 keV where the direct nuclear emission is heavily absorbed (see Fig. 4).
The scattering region could be associated with the extended narrow line region located at a rotational axis with the similar geometry as considered by Miniutti et al. (2014) for another polar-scattered Seyfert 1 galaxy ESO 323-G77 (see their Fig. 8) or in obscured Seyfert type-2 galaxies (see, e.g., Bianchi et al. 2006). This region is also supposed to be responsible for the measured polarisation degree that is unusually high for a type-1 object (Schmid et al. 2001).
An alternative explanation for the high polarisation degree in polar-scattered Seyfert 1 galaxies might be due to scattering on disc winds (on the external layers of the absorbing clouds) at the opposite side from the observer (Marin & Goosmann 2013). On an AGN sample including Fairall 51, Marin (2014) show that scattering on the disc wind corresponds better to the data than scattering in a polar region. Nevertheless, X-ray polarimetric measurements would be required to draw a clear conclusion about the geometry of the scattering region.
We note that two components were also detected for the reflection. A part of the reflected emission is coming from the innermost accretion disc and is also affected by the absorber. The other part originates in a farther region and is not smeared by the relativistic effects. The distant reflection may occur in the same scattering region as for the power law.
4.4. Geometrical constraints from the reflection models
The reflection features have been detected mainly owing to the broad-band coverage of the Suzaku satellite. Figure 2 shows the presence of both the iron line and the Compton hump. Although the very simple power-law model revealed a skewed profile of the iron line, especially for the fourth observation (see the right-hand panel of Fig. 2), these data residuals could be modelled reasonably well by complex absorption and a distant reflection (see Fig. 3).
However, the distant reflection was not able to reproduce the data residuals at energies around 15 keV. We found that the Compton hump is significantly red-shifted, which can be accounted for by relativistic reflection. Although hard excesses have also been successfully explained by other models, including an absorption scenario (e.g., Miller et al. 2008; Tatum et al. 2013) and complex reprocessing in the torus (Murphy & Yaqoob 2009), we have not succeeded at describing the data with simple tests that use these alternatives. We leave more complex analysis using these alternatives for future work.
 |
Fig. 9 Contour plots between the spin and the inclination in the relativistic model. The contours show 1σ, 2σ, and 3σ levels. |
With the relativistic reflection model, we were able to measure the spin and the inclination angle of the accretion disc, though with a large uncertainty given the complexity of the final model. We obtained a ≈ 0.8 and i ≲ 20°. The contour plot between these two parameters is shown in Fig. 9. The model parameters that are shown in Table 2 were all left free during this contour calculations. The spin is not constrained sharply. Its value can be anywhere between 0.6 and the maximum value within the 3σ level. The inclination is lower than would be expected from the polarisation measurements that suggest the inclination to be around 45 degrees. A possible explanation could be that the relativistic reflection also comprises a direct and scattered component. The scattered part can be relatively enhanced if the direct one is heavily obscured. However, in the final model, the scattered component of the primary power law is two orders of magnitudes lower than the direct part. Assuming that the primary and disc reflection emission do not originate far from each other, the explanation by reflection dominated by a scattered component seems highly unlikely.
Another explanation might be that the innermost accretion disc has a different orientation than the larger structures (see, e.g., Nayakshin 2005; Ulubay-Siddiki et al. 2009; Tremaine & Davis 2014). We can estimate a warped radius to which the accretion disc is forced to be in the equatorial plane using a relation by Tremaine & Davis (2014), which gives 6 × 1015 cm for the mass M ≈ 108M⊙. This is much closer than the distance measured for the X-ray absorbing gas (~× 1017 cm). This makes it possible that the innermost accretion disc has different orientation than the BLR. However, a detailed analysis of the optical broad spectral lines would be needed for a more relevant testing of this hypothesis since warping would have an impact on the asymmetry of the broad-line profiles (see, e.g., Wu et al. 2008).
4.5. Origin of the broad-line-region clouds
Our detection of an absorbing gas located in the same region as BLRs may shed light on their origin and geometrical configuration. In general, the broad optical lines are usually seen in AGNs viewed at a low inclination with a clear view of the nucleus. This implies that the BLR location is close to the equatorial plane. However, the origin and exact geometry of BLR is still relatively unknown and is highly debated in the literature (see, e.g., Sulentic et al. 2000; Gaskell 2009, and references therein).
Elitzur et al. (2014) suggest that the BLR and torus are most naturally a continuation of the accretion disc outflow. Miniutti et al. (2014) also argue that the BLR clouds might be the cold and dense clumps of the smoother warm and hot outflow. In Fairall 51, we have also detected highly ionised absorbers with an out-flowing velocity comparable to the velocity derived from the width of the optical spectral lines. However, the location of the highly ionised warm absorber cannot be directly constrained from our data since there is no strong evidence of its variability. If it is part of a BLR, it must constitute a large volume and have very low density. However, it can also originate closer to a black hole and be part of the innermost outflow. The higher ionisation can then be explained by stronger illumination from the centre.
Czerny & Hryniewicz (2011) propose another origin for the broad-line clouds. They find that the temperature in a BLR is close to the dust sublimation temperature, which gives rise to dusty winds from the accretion disc. Once they move up from the equatorial plane, the strong irradiation destroys the dust. The BLR clouds lose support from the radiation pressure, which is strong on dusty particles but much weaker on pure-gas clouds. As a result, the clouds falling back to the disc and again rise up. This process could explain why the BLR clouds get to the line of sight of the intermediate-type Seyferts like Fairall 51.
Moreover, the presence of the ionised outflow can provide better protection for the dusty winds from the destroying irradiation, and the clouds may move farther from the equatorial plane. Large anti-correlation of the column density of the absorber with the intrinsic flux of the nucleus (see Fig. 6) is consistent with this scenario. Lower flux would allow dusty winds to rise higher, thereby implying that more clouds may enter into the line of sight and thus increase the observed column density of the cold absorber. This relation can, however, also be caused by the changes in the gas opacity due to the decrease in illumination (see, e.g., Krongold et al. 2005). However, with no significant measurements of the change in the ionisation of the absorber, we have no quantitative indication of any temperature changes that would cause the changes in the gas opacity.
We note that our location estimation is based on assuming the Keplerian orbital velocity. Czerny et al. (2015) show that the vertical velocity of the clouds is of the order of z/R × ΩK. The z/R fraction should correspond to the fraction of sky that is covered by the BLR clouds, which is from the observations of the order of ≲0.3 (see, e.g., Goad & Koratkar 1998). This satisfies the use of the Keplerian velocity as the estimated velocity of the absorbing cloud.
Our results also indicate that the distance of the X-ray absorbing cloud(s) is beyond the warped radius. The warped radius may represent an outer radius of the accretion disc, because the disc becomes unstable beyond it (see, e.g., Collin & Zahn 2007). This makes it possible that the BLR clouds are created by fragmentation by still unstable accretion flow. Such clouds would not feel strong gravitational attraction towards the disc plane and may reach a more inclined orbit. This could be an alternative explanation of the origin of the BLR clouds and may indicate why they may move into the line of sight.
5. Conclusions
We performed a monitoring programme of Fairall 51 to constrain the characteristic time scale of its X-ray spectral variability using the Suzaku satellite. We obtained four new observations separated by 1.5, 2, and 5.5 day intervals. A significant spectral change was detected only for the last observation with the half flux compared to the first observation, although the flux also varied during the individual observations. By comparison of the light curves in the X-ray soft (0.5−10 keV) and hard (15−55 keV) energy bands, we found that the variability occurs almost entirely in the soft X-rays. The five-day-long variability implies that the location of the absorber is most likely in the BLR.
Our analysis revealed the spectral complexity in the X-ray band. The primary nuclear emission can be described well by a power law with the photon index Γ ≈ 2. It is strongly affected by at least three absorbers with different ionisations (log ξ ≈ 1−4, respectively), where the lower ionised one(s) are variable and cause the spectral variability. This variability is most prominent at 2–6 keV, while the part of the spectrum at ≲1 keV is probably dominated by a scattered power-law emission coming from either a polar region or an external part of the ionised wind itself.
The hard X-ray spectrum revealed an excess at ~15 keV, which can be explained by a reflection from an accretion disc that is affected by the relativistic smearing due to strong gravitational field around the super-massive black hole and very high orbital velocities in the accretion disc. Using the relativistic reflection model, we measured the black hole spin, a ≈ 0.8, but with large uncertainty due to the model complexity.
The spectral complexity and the rapid absorption variability makes Fairall 51 a very prominent source for further studies with X-ray instruments. In particular, detectors with high-quality spectral resolution would help to better constrain the ionisation structure of the absorber and its response to the continuum flux changes. Future high-resolution observations of Fairall 51 with, for example, the planned X-ray mission Astro-H will therefore be desirable.
We used a new version 2.2 updated on 2014 June 9 (http://heasarc.gsfc.nasa.gov/docs/suzaku/aehp_data_analysis.html)
Acknowledgments
The authors acknowledge suggestions by an anonymous referee who significantly helped to improve the paper. JS also acknowledges useful discussions with Leonard Burtscher, Giovanni Miniutti, Bozena Czerny, and Frederic Marin. This research was financially supported from the Grant Agency of the Czech Republic within the project No. 14-20970P. The research was also partially funded by the European Union Seventh Framework Programme (FP7/2007−2013) under grant 312789 and the Bundesministerium für Wirtschaft und Technologie through Deutsches Zentrum für Luft- und Raumfahrt Grant 50OR1311.
References
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Arnaud, K. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Ballo, L., Giustini, M., Schartel, N., et al. 2008, A&A, 483, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batcheldor, D., Robinson, A., Axon, D. J., et al. 2011, ApJ, 738, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006, A&A, 459, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Beuchert, T., Wilms, J., Kadler, M., et al. 2013, Conf. Proc. 10th Integr. Work. [arXiv:1309.6674] [Google Scholar]
- Bianchi, S., Guainazzi, M., & Chiaberge, M. 2006, A&A, 448, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., Guainazzi, M., Matt, G., Fonseca Bonilla, N., & Ponti, G. 2009a, A&A, 495, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., Piconcelli, E., Chiaberge, M., et al. 2009b, ApJ, 695, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Maiolino, R., & Risaliti, G. 2012, Adv. Astron., 2012, 17B [CrossRef] [Google Scholar]
- Boldt, E. 1987, Obs. Cosmol., 124, 611 [Google Scholar]
- Braito, V., Ballo, L., Reeves, J., et al. 2013, MNRAS, 428, 2516 [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L., Meisenheimer, K., Tristram, K. R. W., et al. 2013, A&A, 558, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Collin, S., & Zahn, J.-P. 2007, A&A, 477, 419 [Google Scholar]
- Czerny, B., & Hryniewicz, K. 2011, A&A, 525, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czerny, B., Modzelewska, J., Petrogalli, F., et al. 2015, Adv. Space Res., 55, 1806 [Google Scholar]
- Dovčiak, M., Karas, V., & Yaqoob, T. 2004, ApJS, 153, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M. 2012, ApJ, 747, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., Ho, L. C., & Trump, J. R. 2014, MNRAS, 438, 3340 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Risaliti, G., Nicastro, F., et al. 2004, ApJ, 615, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M. 2009, New Astron. Rev., 53, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M., & Sparke, L. S. 1986, ApJ, 305, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Goad, M., & Koratkar, A. 1998, 495, 718 [Google Scholar]
- Huchra, J. P., Macri, L. M., Masters, K. L., et al. 2012, ApJS, 199, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Bailón, E., Guainazzi, M., Matt, G., et al. 2008, Rev. Mex. Astron. Astrofis., 32, 131 [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 9 [Google Scholar]
- Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Maoz, D., Netzer, H., et al. 2005, ApJ, 629, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Richstone, D. 1995, ARA&A, 33, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, K., Tsunemi, H., Dotani, T., et al. 2007, PASJ, 59, S23 [NASA ADS] [CrossRef] [Google Scholar]
- Krongold, Y., Nicastro, F., Brickhouse, N. S., Elvis, M., & Mathur, S. 2005, ApJ, 622, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Laha, S., Dewangan, G. C., & Kembhavi, A. K. 2011, ApJ, 734, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Lamer, G., Uttley, P., & McHardy, I. 2003, MNRAS, 342, 5 [Google Scholar]
- Longinotti, A. L., Krongold, Y., Kriss, G. A., et al. 2013, ApJ, 766, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Malizia, A., Molina, M., Bassani, L., et al. 2014, ApJ, 782, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F. 2014, MNRAS, 441, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F., & Goosmann, R. W. 2013, MNRAS, 436, 2522 [NASA ADS] [CrossRef] [Google Scholar]
- Markowitz, A., Krumpe, M., & Nikutta, R. 2014, MNRAS, 439, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P., Thompson, I., Maza, J., & Angel, J. 1983, ApJ, 266, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., Golowacz, E. C., Williams, R., et al. 2009, AJ, 138, 1655 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Bianchi, S., Guainazzi, M., et al. 2011, A&A, 533, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merloni, A., Bongiorno, A., Brusa, M., et al. 2013, MNRAS, 437, 3550 [Google Scholar]
- Miller, L., Turner, T., & Reeves, J. 2008, A&A, 483, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miniutti, G., Sanfrutos, M., Beuchert, T., et al. 2014, MNRAS, 437, 1776 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mitsuda, K., Bautz, M., Inoue, H., et al. 2007, PASJ, 59, 1 [Google Scholar]
- Murphy, K. D., & Yaqoob, T. 2009, MNRAS, 397, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., O’Neill, P., George, I., & Reeves, J. 2007, MNRAS, 382, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S. 2005, MNRAS, 359, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Ivezić, Ž., & Elitzur, M. 2002, ApJ, 570, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M. 2014, Space Sci. Rev., 183, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2004, MNRAS, 351, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Piconcelli, E., Miniutti, G., Ranalli, P., et al. 2013, MNRAS, 428, 1185 [NASA ADS] [CrossRef] [Google Scholar]
- Puccetti, S., Fiore, F., Risaliti, G., et al. 2007, MNRAS, 377, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J., Done, C., Pounds, K., et al. 2008, MNRAS, 385, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Beckmann, V., Audard, M., & Courvoisier, T. J. 2010, A&A, 518, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Risaliti, G., Elvis, M., & Nicastro, F. 2002, ApJ, 571, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Elvis, M., Fabbiano, G., Baldi, A., & Zezas, A. 2005, ApJ, 623, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Nardini, E., Salvati, M., et al. 2011, MNRAS, 410, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Rivers, E., Markowitz, A., Rothschild, R., et al. 2014, ApJ, 786, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Sanfrutos, M., Miniutti, G., Agis-Gonzalez, B., et al. 2013, MNRAS, 436, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, H. M., Appenzeller, I., Camenzind, M., et al. 2001, A&A, 70, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, Y., Greene, J. E., Strauss, M. A., Richards, G. T., & Schneider, D. P. 2008, ApJ, 680, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. E., Robinson, A., Alexander, D. M., et al. 2004, MNRAS, 350, 140 [Google Scholar]
- Sulentic, J. W., Marziani, P., & Dultzin-Hacyan, D. 2000, ARA&A, 38, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Svoboda, J., Bianchi, S., Guainazzi, M., et al. 2012, A&A, 545, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tatum, M. M., Turner, T., Miller, L., & Reeves, J. N. 2013, ApJ, 762, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Teng, S. H., Brandt, W. N., Harrison, F. A., et al. 2014, ApJ, 785, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Torricelli-Ciamponi, G., Pietrini, P., Risaliti, G., & Salvati, M. 2014, MNRAS, 442, 2116 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S., & Davis, S. W. 2014, MNRAS, 441, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, K. R. W., Burtscher, L., Jaffe, W., et al. 2014, A&A, 563, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ulubay-Siddiki, A., Gerhard, O., & Arnaboldi, M. 2009, MNRAS, 398, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Fabian, A., Gandhi, P., Winter, L. M., & Mushotzky, R. F. 2010, MNRAS, 402, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Weedman, D. W. 1977, ARA&A, 15, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, S.-M., Wang, T.-G., & Dong, X.-B. 2008, MNRAS, 389, 213 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: XIS 0 (upper, with small circles) and HXD/PIN (lower) (all background subtracted) light curves in the 0.5−10 keV or 15−55 keV energy range, respectively. Right: XIS 0 light curves in two different energy bands, 0.5−3 keV and 3−10 keV (all background-subtracted), and the hardness ratio between the hard and the soft bands. The gaps between the observations are shrunk for clarity. The time bin size is 2880 s. |
| In the text | |
 |
Fig. 2 Left: Up: X-ray spectra of four Suzaku observations (1st black, 2nd red, 3rd green, 4th blue). Bottom: data residuals from a simple absorbed power-law model with Γ ≈ 1.7. Right: a more detailed look at the iron line and Compton hump as residuals from the simple absorbed power-law model. Only XIS 0 and HXD/PIN spectra are plotted for clarity. Data are re-binned for plotting purposes alone. |
| In the text | |
 |
Fig. 3 Data residuals from the different models for all observations (1st black, 2nd red, 3rd green, 4th blue). From top to bottom: residuals from the Models A–D. |
| In the text | |
 |
Fig. 4 Final model (Model D) with its components. |
| In the text | |
 |
Fig. 5 Final model (Model D) in the individual observations (1st black, 2nd red, 3rd green, 4th blue). |
| In the text | |
 |
Fig. 6 Relation between the intrinsic 2–10 keV flux and the column density of the cold (least ionised) absorber for Model D (black, circles) and Model B (red, triangles). |
| In the text | |
 |
Fig. 7 Contour plots between the column densities of the variable low- and mid-ionised absorbers. The colours correspond to different observations (1st black, 2nd red, 3rd green, 4th blue). The contours correspond to 1σ, 2σ, and 3σ levels. The best-fit values are indicated by a small cross in the graph. |
| In the text | |
 |
Fig. 8 Contour plots between the column densities of the variable cold and warm absorbers. The colours correspond to different observations (1st black solid, 2nd red dashed, 3rd green dotted, 4th blue dash-dotted). The contours correspond to 1σ, 2σ, and 3σ levels. Left: results obtained with tModel B. Right: results obtained with Model D with the highly-ionised warm absorber allowed to vary. |
| In the text | |
 |
Fig. 9 Contour plots between the spin and the inclination in the relativistic model. The contours show 1σ, 2σ, and 3σ levels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


