| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 37 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201425167 | |
| Published online | 16 June 2015 | |
Elemental abundances associated with gamma-ray bursts: nucleosynthesis in outflows⋆
1 Department of Automation, Shanghai University, 200072 Shanghai, PR China
e-mail: thu@shu.edu.cn
2 Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, Yunnan Observatories, 650011 Kunming, PR China
Received: 16 October 2014
Accepted: 6 April 2015
Aims. Outflows from accretion disks have been suggested to be suitable sites for producing heavy elements. The objective of this work is to investigate nucleosynthesis in the outflows launched from the inner accretion disks of collapsars that are associated with gamma-ray bursts (GRBs).
Methods. By using a collapsar model of advection-dominated accretion and an adiabatic expanding outflow model, we simulated chemical yields inside the outflows associated with GRBs. As a result of the extremely high temperature (above 1010 K), the dominated species existing in the inner region of the disk are proton, neutron, 2H, and 4He, which are photodisintegrated from heavy nuclei. Assuming that an explosive nucleosynthesis could operate in outflows from collapsar accretions associated with GRBs, heavier species including the iron-group will be synthesized significantly. Although various outflow models have been investigated carefully in the past, the uncertainties in predicting the outflow birthplace (ejected-radius rj) in the accretion disk are still quite large. Unlike recent researches on this topic that located the production of heavy elements in GRBs in the outer parts of the disk, in this study we focus our attention mainly on the outflows triggered from the inner region of collapsar accretion.
Results. We find 56Ni can be abundantly produced in all the outflow cases considered here from the inner collapsar disk. The highest 56Ni’s mass fraction in the outflows reaches 0.463, which can imply that the 56Ni-rich outflows will lead to an observable violent explosion of a GRB event. The mass fractions of 57Ni, 59Cu (decays to 59Ni), and 60Zn (decays to 60Ni) could be 10-2, and the abundance of 58Ni reaches 10-3. Our simulations support that the effective production of heavy elements can occur in the outflows from the inner regions of the collapsar accretion disks. Our results also show that the amount of heavy species produced in outflows depends on the eject-radius rj of the accretion disk where the outflows take place; outflows launched at larger radii can be helpful to increase the quantities of heavy nuclei by means of the lower disk temperature, which agrees with the conclusions of recent studies. Furthermore, a recently published article reported that some nuclei, such as 28Si, 32S, 36Ar, 40Ca, 44Ti, 48Cr, 54Fe, and 55−56Co, experience a dip and then rise in their mass fraction while evolving in the outflow, and this characteristic behavior has occurred in many more outflow cases, and this is reported for the first time in the literature. This characteristic phenomenon also occurs in our nucleosynthetic simulations.
Key words: nuclear reactions, nucleosynthesis, abundances / stars: abundances / galaxies: abundances
Tables 1−8 and full Figs. 3−5 are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The origin of chemical species has been an important subject of nuclear astrophysics. Normally, the standard channels for synthesizing heavy nuclei are the most widely discussed models of different nucleosynthesis sites for massive stellar nuclear evolutions (Diehl et al. 2006; Kn dlseder et al. 1999; Prantzos & Diehl 1996, etc.), but the uncertainties are still quite large and face some important difficulties (Limongi & Chieffi 2006; Prantzos 2004; Tur et al. 2010). Another possible site in which fresh chemical species might be synthesized is thought to be the hot regions of an accretion disk (Jin et al. 1989; Arai & Hashimoto 1992; Chakrabarti & Mukhopadhyay 1999; Mukhopadhyay & Chakrabarti 2000; Belyanin & Derishev 2001; Hu & Peng 2008; Hu 2011; Mukhopadhyay 2013); therefore, the accretion disks of collapsars associated with gamma-ray bursts (GRBs) could be quite efficient nuclear-pot to output fresh species. Nishimura et al. (2006) studied the r-elements and neutron-rich elements in a magnetohydrodynamic jet of core-collapse supernovae (SN). Fujimoto et al. (2007, 2008) investigated in detail the outcomes of r-elements in magnetically driven jets triggered by collapsars. Nagataki et al. (2003a) proposed that Ni can be produced in accretion disks that are accompanied by GRBs. Preut et al. (2004a, b) have investigated the nuclear products of the accretion disks of collapsars associated with GRBs, which have been suggested to be important sites for synthesizing Ni. Recent researches also showed that a fair amount of GRBs have been associated with the observations of fast-moving Ni (H
dlseder et al. 1999; Prantzos & Diehl 1996, etc.), but the uncertainties are still quite large and face some important difficulties (Limongi & Chieffi 2006; Prantzos 2004; Tur et al. 2010). Another possible site in which fresh chemical species might be synthesized is thought to be the hot regions of an accretion disk (Jin et al. 1989; Arai & Hashimoto 1992; Chakrabarti & Mukhopadhyay 1999; Mukhopadhyay & Chakrabarti 2000; Belyanin & Derishev 2001; Hu & Peng 2008; Hu 2011; Mukhopadhyay 2013); therefore, the accretion disks of collapsars associated with gamma-ray bursts (GRBs) could be quite efficient nuclear-pot to output fresh species. Nishimura et al. (2006) studied the r-elements and neutron-rich elements in a magnetohydrodynamic jet of core-collapse supernovae (SN). Fujimoto et al. (2007, 2008) investigated in detail the outcomes of r-elements in magnetically driven jets triggered by collapsars. Nagataki et al. (2003a) proposed that Ni can be produced in accretion disks that are accompanied by GRBs. Preut et al. (2004a, b) have investigated the nuclear products of the accretion disks of collapsars associated with GRBs, which have been suggested to be important sites for synthesizing Ni. Recent researches also showed that a fair amount of GRBs have been associated with the observations of fast-moving Ni (H flich & Khokhlov 1996; Iwamoto et al. 1998; Woosley et al. 1999; Nakamura et al. 2001; Patat et al. 2001; Hjorth et al. 2003; Maeda et al. 2003, etc.), which are the model-dependent estimates of the nickel abundance in GRBs.
flich & Khokhlov 1996; Iwamoto et al. 1998; Woosley et al. 1999; Nakamura et al. 2001; Patat et al. 2001; Hjorth et al. 2003; Maeda et al. 2003, etc.), which are the model-dependent estimates of the nickel abundance in GRBs.
Since the physical properties of collapsar accretion that is accompanied with GRBs are different from those of the normal accretion disk, the overall yields of chemical species ejected in the outflows would be recent. Although various outflow models have been investigated in the past, the uncertainties in predicting the outflow birthplace (rj) in accretion disk are still quite large. More recently, Janiuk (2014) and Banerjee & Mukhopadhyay (2013) have located the production of heavy elements in outflows in the outer parts of the disk (rj ≫ 107 cm). But Pruet et al. (2004a) estimated that the outflow ejection site lies in the inner region of rj ≤ 106.5−7 cm around the black hole. Surman et al. (2006, 2011) used starting points of rj ~ 107 cm to estimate where the outflow occurs. Hu & Peng (2008) and Hu (2011) also used rj ≤ 107 cm to simulate nucleosynthetic yields in the outflows. In this study, we calculate possible chemical abundance variances through explosive nucleosynthesis in the inner outflow-induced site of the disk, where in the region of [3rsch, 50rsch] is consistent with an outflow-induced region rj ~ 107 cm, as proposed by Pruet et al. (2004a) and Surman et al. (2006, 2011).
We study the contribution of collapsar accretion to the Galactic chemical evolution. We find that the dominated species existing in the inner disk are proton, neutron, 2H, and 4He. Assuming that explosive nucleosynthesis can take place in outflows from inner accretion accompanied with GRBs, heavier species including the Fe-group nuclei might be produced in abundance. It shows that 56Ni can increase quickly through explosive nucleosynthesis in outflows. The highest yield of 56Ni in our simulations can reach 0.463 M⊙ for 1 M⊙ matter ejected from outflows. The simulations indicate that the amount of nucleosynthetic outcome produced in outflows depends on the location rj in the outflow-induced region and on the mass of matter ejected (Mj) from outflows. Our results also show that the nucleosynthetic yields might be an indicator for estimating the collapsar mass accretion rate Ṁ.
The structure of this paper is as follows. The basic simulation method is described in Sect. 2. Results are shown in Sect. 3. The conclusions and discussions follow in Sect. 4.
2. Simulation method
2.1. Collapsar model
A variety of recent theories of GRBs show a common mechanism: an accretion disk accreting onto a stellar-mass black hole at a rate of 0.01−10 M⊙ s-1 (Popham et al. 1999, hereafter PWF99). The method used in our study is based on the advection-dominated accretion disk model of Gammie & Popham (1998, hereafter GP98) and Popham & Gammie (1998, hereafter PG98). We here give a simple review as follows.
If the units are set to be G = MB = c = 1 (MB, the black hole mass), we obtain the continuity equation, 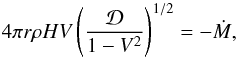 (1)where ρ is the rest-mass density and H and r are the accretion disk thickness and radius. V is the radial velocity measured in a corotating frame, and Ṁ is the rest mass accretion rate.
(1)where ρ is the rest-mass density and H and r are the accretion disk thickness and radius. V is the radial velocity measured in a corotating frame, and Ṁ is the rest mass accretion rate. 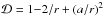 is a relativistic correction factor, here, the Kerr parameter a of the central black hole.
is a relativistic correction factor, here, the Kerr parameter a of the central black hole.
The gas energy expression is 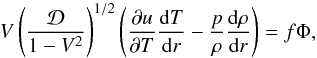 (2)where u the internal energy per unit volume, is given in detail in GP98 (Eq. (44)) and PG98 (Eq. (3)). T is the temperature, and p is the pressure. Here, f is the heating factor, if f = 1, all the dissipated energy is advected inward with the inflow. The dissipation function Φ is presented in detail in GP98 (Eq. (68)).
(2)where u the internal energy per unit volume, is given in detail in GP98 (Eq. (44)) and PG98 (Eq. (3)). T is the temperature, and p is the pressure. Here, f is the heating factor, if f = 1, all the dissipated energy is advected inward with the inflow. The dissipation function Φ is presented in detail in GP98 (Eq. (68)).
The expression of radial momentum is 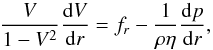 (3)where η = (ρ + p + u) /ρ is the enthalpy. The correction factor fr combines the effects of gravity and rotation and is given in detail in GP98 (Eq. (50)) and PG98 (Eq. (5)).
(3)where η = (ρ + p + u) /ρ is the enthalpy. The correction factor fr combines the effects of gravity and rotation and is given in detail in GP98 (Eq. (50)) and PG98 (Eq. (5)).
The angular momentum expression is given by 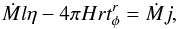 (4)where Ṁ is the mass accretion rate and j is the accretion rate of angular momentum. Ṁj is the total inward angular momentum. l is the specific angular momentum of the accreting matter.
(4)where Ṁ is the mass accretion rate and j is the accretion rate of angular momentum. Ṁj is the total inward angular momentum. l is the specific angular momentum of the accreting matter. 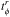 , the viscous stress, is very complex; a full mathematical discussion is given in GP98.
, the viscous stress, is very complex; a full mathematical discussion is given in GP98.
Based on GP98 and PG98, PWF99 presented an accretion disk model of a collapsar around a black hole associated with a GRB. MacFadyen & Woosley (1999, hereafter MW99) also reported on a set of numerical simulations of collapsar models. PWF99 and MW99 are fitted well. Based on these models, Nagataki et al. (2003b) presented an analytical model of the accretion disk that reproduces PWF99 and MW99 well; the key parameters of temperature, density, and disk thickness can be described as (Nagataki et al. 2003a, b) ![\begin{eqnarray} T &=& 2.67\times 10^{10} \left(\frac{M_{\rm B}}{3~{M}_\odot}\right)^{-0.2}\left(\frac{\dot{M}}{0.1~{M}_\odot}\right)^{0.108} \nonumber \\ &&\times \frac{1}{(r/r_s)^{0.425}[1+(r/r_s)]^{0.21}}\ \ \ \textrm{K}, \label{eq:5} \\ \rho &=& 8.23\times 10^{8} \left(\frac{M_{\rm B}}{3~{M}_\odot}\right)^{-1.7}\left(\frac{\dot{M}}{0.1~{M}_\odot}\right)^{1.03} \nonumber \\ &&\times \frac{1}{(r/r_s)^{1.07}[1+(r/r_s)]^{0.76}}\ \ \ \textrm{g\ cm}^{-3}, \label{eq:6} \\ H &=& 5.80\times 10^{6} \left(\frac{M_{\rm B}}{3~{M}_\odot}\right)^{0.9}\left(\frac{\dot{M}}{0.1~{M}_\odot}\right)^{-0.0183} \nonumber \\ &&\times \frac{1}{(r/r_s)^{-1.66}[1+(r/r_s)]^{0.39}}\ \ \ \textrm{cm}, \label{eq:7} \end{eqnarray}](/articles/aa/full_html/2015/06/aa25167-14/aa25167-14-eq55.png) where MB is the central black hole mass and rs is the core radius.
where MB is the central black hole mass and rs is the core radius.
Using this method, we obtained the local properties of collapsar accretion associated with GRBs.
2.2. Explosive model in outflow
We considered another possibility here: nucleosynthesis might continue to take place in outflows, where may be a candidate for producing GRBs (MW99; PWF99; Nagataki et al. 2003a, b, 2006; Pruet et al. 2004b). However, both the dynamic of outflows and the exact mechanism of the formation of GRBs still remain uncertain. From the observed data of SN 1998bw, Iwamoto et al. (1998) mentioned in their article that “The rapid rise of the light curve requires the presence of radioactive 56Ni near the surface, implying that large-scale mixing of material took place because of hydrodynamical instabilities”. The light-curve shape can be reproduced with different explosion models. Therefore, we considered the simple assumption that adiabatic expansion governs the nature in outflow regions (Surman & McLaughlin 2004; Laming & Titarchuk 2004). In the explosive nucleosynthesis model, we estimate that 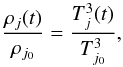 (8)and
(8)and 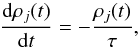 (9)where Tj(t) and ρj(t) are the temperature and density in the outflow, and Tj0 and ρj0 are the initial temperature and density at the ejection radius in the disk, from where the outflow is launched. The expansion timescale of outflows τ is written as (Woosley 1986; Nagataki et al. 2003a)
(9)where Tj(t) and ρj(t) are the temperature and density in the outflow, and Tj0 and ρj0 are the initial temperature and density at the ejection radius in the disk, from where the outflow is launched. The expansion timescale of outflows τ is written as (Woosley 1986; Nagataki et al. 2003a) 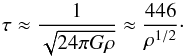 (10)We can also obtain the outflow density by using a formula for the entropy per baryon (S) of the outflow and ejecta (Qian & Woosley 1996), which has been adopted in our recent study for outflow (Hu 2011):
(10)We can also obtain the outflow density by using a formula for the entropy per baryon (S) of the outflow and ejecta (Qian & Woosley 1996), which has been adopted in our recent study for outflow (Hu 2011): 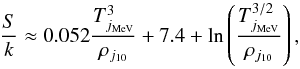 (11)where S is scaled in the Boltzmann constant k. TjMeV is the temperature in MeV and ρj10 is the density scaled in 1010 g cm3 in the outflow. By adopting an explosive outflow model that is thought to be adiabatic and freely expanding (Freiburghaus et al. 1999; Fujimoto et al. 2004; Banerjee & Mukhopadhyay 2013), TjMeV can be written as
(11)where S is scaled in the Boltzmann constant k. TjMeV is the temperature in MeV and ρj10 is the density scaled in 1010 g cm3 in the outflow. By adopting an explosive outflow model that is thought to be adiabatic and freely expanding (Freiburghaus et al. 1999; Fujimoto et al. 2004; Banerjee & Mukhopadhyay 2013), TjMeV can be written as 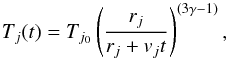 (12)where rj is the outflow-launched radius in the accretion disk and vj is the ejected velocity at rj, which is assumed to be constant during the outflow explosion and proportional to the Keplerian speed. Here γ is the adiabatic index chosen as γ = 5/3.
(12)where rj is the outflow-launched radius in the accretion disk and vj is the ejected velocity at rj, which is assumed to be constant during the outflow explosion and proportional to the Keplerian speed. Here γ is the adiabatic index chosen as γ = 5/3.
2.3. Nuclear network
In principle, all nuclei react with other nuclei in the hot nucleosynthetic pots; but except for some important exceptions, there are only 12 reactions to be considered for each species: linking the species to its neighbors by the release or capture of a proton, neutron, α or γ, etc. In fact, captures of free neutrons and isotopes of H and He on heavy nuclei are much faster than fusions of heavy species because of the repulsive Coulomb effect.
The network has a set of nonlinear partial differential equations, which are linearized to ordinary differential equations and evolve in time during the process of the model simulations. This standard method was given by Arnett & Truran (1969) and Woosley et al. (1973). We consulted the classical references presented by Wagoner et al. (1967), Fowler et al. (1975), Fuller et al. (1980, 1982), Wallace & Woosley (1981), Harris et al. (1983), and Angulo et al. (1999) regarding this network. Furthermore, the nuclear reaction rates we used are adapted from the theoretical or experimental estimates of Cyburt et al. (2010), Karakas (2010), Fisker et al. (2001), Rauscher & Thielemann (2000), and Bao et al. (2000), to name a few, and the relevant references therein. Here we would like to recommend useful websites for conveniently obtaining the nuclear reaction data, for instance, Astrophysical Cross Sections and Reaction Rates1, Rauscher & Thielemann (2000) and the JINA Reaclib Database2, Cyburt et al. (2010). Many helpful current studies on nuclear astrophysics are linked at these websites, for example, Rauscher (2012), Lederer et al. (2013, 2014), and Quinn et al. (2014).
In this network, when the temperature T ≤ 108 K, deuterium burning and p−p chain reactions can take place, and as T ≥ 108 K, the CNO cycle is triggered. Proton-, rapid-proton-, and neutron-capture begin to operate when the temperature T becomes higher; at the same time, α-capture, including the triple-α-capture reaction, can operate as well. Moreover, when the temperature becomes ultra-high, strong photodisintegration begins to break up heavier chemical elements and to release lighter species, etc. Possible decay reactions are also considered in this work.
The nuclear network we used has been implemented to simulate nucleosynthetic yields in accretion disks and outflows around black holes by Hu & Peng (2008) and Hu (2011). More recently, Hu & Wang (2014) also used this network code to study the chemical abundance evolution in the afterglow of a GRB. Following these works, our nuclear network here contains 521 chemical species and has been modified further by involving the properties of collapsar disks and outflows.
The mass fractions of some nuclei have shown a dip and then a rising trajectory in the outflows, as first reported by Banerjee & Mukhopadhyay (2013). This characteristic phenomenon is repeated in our network, see Sect. 3 for details.
 |
Fig. 1 Temperatures, densities, accretion velocities, and accretion timescales of collapsar models for cases A1-3 and B1-3. The accretion disk radius is scaled in Schwarzschild gravitational units. |
 |
Fig. 2 Production of chemical species produced in the collapsar accretion for case A1, which are selected from the top 25 mass fractions. The accretion disk radius is scaled in Schwarzschild gravitational units. |
3. Results
3.1. Nucleosynthetic yields in collapsar accretions
The key parameters of collapsar accretion include the central black hole mass MB, the mass accretion rate Ṁ, and the core radius rs. In general, MB would be MB = 3.0−3.5 M⊙ in such an accreting process (MW99), therefore, we chose the value MB = 3.0 M⊙ for case A and 3.5 M⊙ for case B. MW99 investigated collapsar models with a mass accretion rate of 0.07 ± 0.03 M⊙ s-1, and Nagataki et al. (2003a) chose Ṁ = 0.1 M⊙ s-1. Here we adopted three subcases for Ṁ = 0.1, 0.07, and 0.04 M⊙ s-1, as shown in Table 1 for cases A1-3 and B1-3. The rs was chosen as 107 cm, which conforms to Nagataki et al. (2003a). In the studies of Nagataki et al. (2003a), MacFadyen & Woosley (1999) and Popham et al. (1999), the viscosity parameter was adopted as the standard α = 0.1 and the spin parameter chosen to be a = 0, which matches the steady-state slim-disk model well.
To choose the initial composition of the inflows, it is difficult to establish a complete and detailed initial composition in outer collapsar disks. The solar composition is the only complete and detailed chemical composition in astrophysics. Many recent studies have used the solar abundance as the initial composition. Fields et al. (1996), for instance, investigated the nucleosynthesis production by supernova ejecta and assumed that the surrounding medium has solar abundance. Mukhopadhyay & Chakrabarti (2000) studied the nuclear outputs in accretion disks around black holes with 10−106 M⊙ and adopted a solar composition as the initial inflow composition. Schaefer et al. (2003) also tried to explain the spectra of GRB 021004 by adopting solar abundance for the composition in one of their simulations. However, it was found that the long GRBs originate mostly in metal-poor regions. The reason may be that the progenitor stars of long GRBs are thought to be massive stars; therefore, after they experienced a long period of star formation, heavy materials are much easier to accumulate and condense in the central core as a result of the powerful gravitational potential of these massive stars. This would led to the result that the progenitor stars’ surroundings or surfaces are metal-poor. This might explain why the long GRBs were mostly born in metal-poor regions, and it might be worth assuming that there would be no metal-poor regions inside such progenitor stars. The simulations of Tominaga et al. (2007) showed that the masses of ejected 56Ni from normal metal-poor stars (56Ni → 0.2M⊙) are higher than those from hyper-metal-poor stars (56Ni → 10-6 M⊙). It seems that a higher initial metallicity tends to increase the production of ejected 56Ni to match the observed data. Furthermore, until now, GRB events have tended to occur in the distant early universe, while in the later universe surrounding us, the GRBs probably have already been exploded, which means that some fraction of metal-poor regions might reflect the GRB events. It might also denote that the GRBs and SN would not explode twice in the same place. Moreover, we find that before the outflows launched from the inner accretion disk of collapsar, the temperature becomes high enough when the envelope materials from outside are accreting inward in the inner region of r ≤ 50rsch (rsch the Schwarzschild radius) to photodisintegrate the heavy species. This means that the dominated species that exist in the outflow-induced area are protons, neutrons, 2H, and 4He. The final nuclei in the inner disk (these final nuclei are also the initial composition in the outflows, where as a result of the accordingly lower temperature, these species can recombine to form heavier nuclei) would therefore not be sensitive to the initial composition from the outer parts of accretion. Banerjee & Mukhopadhyay (2013) also mentioned that for so high a temperature of the inner disk, the accreting matter in this region would mainly contain protons and neutrons that formed as a result of the destruction of all the heavy nuclides into free nucleons, that is, the initial composition in the outer disk is unimportant for the final products in the inner accretion disk. The initial chemical compositions were therefore considered to have solar system abundances here.
Table 1 lists the key parameters and the resulting data for cases A1-3 and B1-3, and Fig. 1 shows four panels with the temperatures, densities, mass accretion velocities, and accretion timescales of the collapsar models for cases A1-3 and B1-3. The temperature is given in K and the accretion disk radius is scaled in Schwarzschild gravitational units.
As shown in Fig. 2, the four panels show the nucleosynthesis outcome produced in the collapsar accretion of case A1, which were selected from the top 25 mass fractions. Panel a shows that the main final compositions existing in the inner disk are protons, neutrons, 2H, and 4He. Panel b shows that a very small amount of lithium-beryllium-boron (LiBeB) might exist in the inner accretion disk for a very short time (as shown in Fig. 1 panel d, the accretion timescale per Schwarzschild radius is very short). The high temperature would efficiently destroy these light elements, but they are also reproduced through photodisintegration of CNO+γ→LiBeB+(p, n, α) and α + α→(Li, Be)+H, which might for a time prevent complete destruction of the LiBeB isotopes; therefore panels c and d show that the isotopes of CNO and 4He decrease in the inner accretion through these processes, while in panel b the mass fractions of LiBeB increase, but their abundances are still quite small.
It has been suggested that the accreted matter close to the black hole is very neutron rich (e.g., Chakrabarti & Mukhopadhyay 1999; Pruet et al. 2003; Banerjee & Mukhopadhyay 2013). Our result in Table 1 shows the final products in the inner accretion before they are ejected from the disk, where the dominated nuclei are neutrons and protons. This agreese with the above results; as shown in Table 1, although they are both → 10-1, however, the final fraction of protons in the inner disk is twice that of neutrons. This probably results from the simplification used here to determine the disk structure, however, which neglects the contribution from degeneracy pressure to increase the proton abundance.
3.2. Nucleosynthetic yields in outflows associated with GRBs
We adopted fine-mesh zoning (per 10rsch) below 50rsch, that is, the calculated grids of the outflow-induced region of [3rsch, 50rsch] were divided into six subcases: the explosive nucleosynthesis inside outflows associated with GRBs were calculated at r = 3rsch, 10rsch, 20rsch, 30rsch, 40rsch, and 50rsch. The results are given in Tables 2−7, which list the produced species whose final abundances exceed 10-15. Tables 2−7 show the final results of explosive nucleosynthesis in the outflows associated with GRBs, where the neutron abundance is much lower than that of protons due to the capture-reactions involving neutrons. The r-process has been widely discussed in the wind of core-collapse SN (Woosley et al. 2002), and a successful r-process can be possible in the outflows associated with GRBs (e.g., Inoue et al. 2003; Fujimoto et al. 2007). Our results of Tables 2−7 for neutron agree with Umeda & Nomoto (2002), who were unable to find neutron in the top yields of ejected matter in the Tables 5−13 (Umeda & Nomoto 2002). Our simulations show that for an explosive nucleosynthesis that occurs in outflows from collapsar accretions accompanied with GRBs, heavier species including the Fe-group nuclei will be recombined quickly, meaning that GRBs can contribute significantly to heavy nuclei.
 |
Fig. 3 Explosive nucleosynthesis in the outflow region associated with GRB for case A1 at r = 3rsch (case A1r = 3). The radioactive decays have been taken into account within the dynamic process [ t0,tf), but did not include the final step (tf), which can prevent some decayed species, as shown in this picture, from precipitously dropping to zero in the final step tf. |
 |
Fig. 4 As Fig. 3, but for case A1 at r = 50rsch (case A1r = 50). It only shows the long (relative) half-life species (τ0.5> 1 day) by considering the timing of observations; the species with half-lives of τ0.5 ≤ 1 day are not plotted. The final abundances of nuclides as shown in this figure (selected from Table 7) exceed 10-11. |
 |
Fig. 5 Five up-species abundance increase when the value of collapsar accretion rate Ṁ increases in panels a–c in the left column and in panels d–f in the right column. The other five down-species abundances decrease as Ṁ increases. The abscissa is scaled in the value of Ṁ. In a same panel, the same colors denote the same chemical species. |
We only report below the chemical yields inside outflows at the innermost radius r = 3rsch for case A1r = 3 and the outer radius r = 50rsch for case A1r = 50. For other data we refer to Tables 2−7.
3.2.1. Chemical yields in outflow from 3rsch
Figures 3−5 display 18 (a−r) panels showing the possible chemical abundance variances due to the explosive nucleosynthesis at 3rsch in the outflow-induced site for case A1r = 3. Radioactive decays have been considered within the dynamic process [ t0,tf), but not including the final step (tf), which can prevent some decayed species as shown in Figs. 3−5 that precipitously drop to zero in the final step tf. As shown in panel a of Fig. 3, the isotopes of LiBeB are almost entirely eliminated, a very small amount of the residuals is due to the efficient photodisintegrations reaction on the CNO isotopes, which can for a short time prevent complete destruction of LiBeB. As shown in Figs. 4 and 5, the heavier Fe-group composition is produced in abundance. In this phase, proton- and rapid-proton-capture [(p, γ); (p, α)], neutron-capture [(n, γ); (n, p); (n, α)], α-capture [(α, γ); (α, p); (α, n)], and triple-α-capture reactions dominate, for instance, the processes 4He(2α, γ)12C(α, γ)16O(n, γ)17O(n, γ)18O(α, γ)22Ne(α, n)25Mg(p, γ)26Al, 50Cr(p, γ)51Mn(p, γ)52Fe, and 54Fe(p, γ)55Co(p, γ)56Ni. Other heavier elements generally come from p-capture (including rp), α-capture (including triple-α capture), and n-capture processes. Furthermore, the protons and neutrons can recombine to form heavier α-particles. The mass fraction of 56Ni produced in this case can reach 7.69 × 10-2 in the outflow.
3.2.2. Chemical yields in outflow from 50rsch
Figure 6 shows six panels for case A1 at r = 50rsch (case A1r = 50). It is as same as Fig. 3, but only shows the long (relative) half-life species by considering the timing of observations; the species with short half-lives have not plotted in this figure. The final abundances of species as shown in this figure (selected from Table 7) exceed 10-11. In Fig. 6, panels a−d display the ejected chemical species for stable isotopes. Panel e shows the radioactive isotopes with the half-lives (τ0.5) for one day <τ0.5< 10 yr, and panel f shows five long-life radioactive species of 26Al, 41Ca, 44Ti, 53Mn and 59Ni, whose lifetimes are longer than 104 yr. In this case, the mass fraction of resulting 56Ni reaches 0.463, which is the highest value in all outflow cases. For 1 M⊙ matter ejected from outflows, the highest yield of 56Ni would be 0.463 M⊙, but the mass of 57Ni, 59Cu (τ0.5 = 81.5 s, decays to 59Ni) and 60Zn (τ0.5 = 2.38 min, decays to 60Cu; 60Cu: τ0.5 = 23.7 min, decays to 60Ni) could be 10-2 M⊙, the yields of 58Ni could reach 10-3 M⊙, and the mass of 39K, 46Ti, 54Fe and 55Co would be 10-4 M⊙.
Banerjee & Mukhopadhyay (2013) pointed out that some species such as 28Si, 32S, 36Ar, 40Ca, 44Ti, 48Cr, 54Fe, and 55−56Co experience a dip and then rise in their mass fraction while evolving in the outflow, and this characteristic behavior can occur in many more outflow cases. They reported this for the first time in the literature. Our Figs. 3−6 also show this characteristic phenomenon. Moreover, as shown in Figs. 5, 6, 56Ni experiences monotone increasing curves, which are very similar to those of Banerjee & Mukhopadhyay (2013).
4. Discussions and conclusions
Our simulations include some assumptions and simplifications that are based on the stationary slim-disk analytical derivation, on an accretion-disk model accompanied by neutrino emission and annihilation to trigger GRB, which was first described by Popham et al. (1999). This model has been studied and considered in some subsequent researches, such as Kawanaka et al. (2013), Kawanaka & Mineshige (2007), Liu et al. (2007), Gu et al. (2006), Lee et al. (2005), Kohri et al. (2005), Pruet et al. (2004a), Kohri & Mineshige (2002), and Di Matteo et al. (2002). However, Di Matteo et al. (2002) argued that in the inner region of the accretion, due to the opaque and neutrino trapping effects, it might be difficult to trigger a GRB event. Gu et al. (2006) researched the vertical structure of the optically thick disk in more detail and found that such a neutrino-cooled accretion disk could be fit for GRBs. Lee et al. (2005), Kohri et al. (2005), and Kohri & Mineshige (2002) gave more advanced improvements in the study of electron degeneracy and the electron fraction, which have a great effect on the neutrino-emitted rates in this neutrino-cooled accretion disk. Pruet et al. (2004a) adopted a steady-state wind model to simulate the outflow and found that the electron fractions depend on the viscosity and accretion rate of the disk. Most recently, the detailed properties of the jet or outflow ejected by the system of accretion disk and black hole have been improved by many works (Hou et al. 2014; Liu et al. 2010; Reynoso et al. 2006, etc.), which can explain the shapes of observed profiles for a wide variety of GRBs.
From all the outflow cases A and B in this study, we deduce that the place at which the outflow is triggered from the accretion disk will have an effect on the nucleosynthetic yields. As shown in Tables 2−7, outputs of heavy species produced in outflow depend on the eject-radius rj of the accretion disk, where the outflow is expelled, that is, outflows launched at larger radius can help to increase the quantities of heavy nuclei because of the lower disk temperature, which agrees with the conclusions of Janiuk (2014) and Banerjee & Mukhopadhyay (2013); we not only support their views, but also propose that the effective production of heavy elements can take place in the outflow from the inner region of the collapsar accretion disk.
As shown in Figs. 3−6, the mass abundances of some newly produced nuclides might increase rapidly in the outflow regions; therefore, we here suggest that the chemical contributions of an accretion disk associated with GRBs may not be ignored. Assuming a matter ejected of 1 M⊙ from an outflow associated with a GRB, then the values of mass fractions listed in Tables 2−7 are also the values for these species’ ejected mass. In general, Tables 2−7 show that higher densities and lower temperatures in our simulations are beneficial for synthesizing heavier nuclides. The temperatures in collapsar accretions as shown in Tables 2−7 are very high, which is the reason that the case with relatively low temperature assumed here produced more heavier nuclides.
The total matter ejected from the outflow was chosen to be Mj = 1 M⊙. Figures 3−6 and Tables 2−7 show that GRBs may contribute significantly to the Fe-group elements; especially in case A1r = 50, the total ejected mass of 56Ni is 0.463 M⊙, which agrees with the nickel mass of 0.5−0.7 M⊙ ejected from bright bumps in some observed afterglows (H flich & Khokhlov 1996; Iwamoto et al. 1998; Woosley et al. 1999). Furthermore, the yield of nickel is sensitive to the location r in an outflow-induced site. As shown in Tables 2−7, the temperature at larger radius is lower than that at smaller radius, where the relatively low temperature can prevent spallation reactions from destroying heavier species. Therefore, the 56Ni output in case A1r = 3 (0.077 M⊙) is much lower than that in case A1r = 50 (0.463 M⊙). It would be helpful to assume that the 56Ni yield would be high at larger radius in an outflow-induced region. From the above, it seems that case A1r = 50 is more preferable for explaining the characteristics of outflows associated with GRBs. However, because this result is based on the assumption of 1M⊙ matter ejected from outflows, the uncertainty is still large for how much total matter would be ejected from the collapsar accretion. Iwamoto et al. (1999) made detailed simulations to study how nucleosynthetic outputs depend on deflagration speeds and ignition densities related to a white dwarf (WD) progenitor associated with a SN Ia. They found that the result of 56Ni is in the region 0.56−0.77 M⊙ in seven simulations. From their data, they suggested that nucleosynthetic yields might be helpful in providing constraints on the key parameters of their models. In our study, nucleosynthetic yields have changed as the chosen value of radius r varies in outflow-induced region. As mentioned above, case A1 shows that the output of 56Ni is smallest (0.077 M⊙) at r = 3rsch and largest (0.463 M⊙) at r = 50rsch for Mj = 1 M⊙, meaning that the outflow induced from a larger radius in an accretion disk can be helpful in producing the 56Ni. But for an outflow induced in the innermost point (small radius) in accretion, such as case A1r = 3, then to match the observed data of 0.5−0.7 M⊙ for 56Ni associated with GRBs, the total ejected matter should be Mj = 10 M⊙. This can indicate that the elemental abundances associated with GRBs depend on the location r in outflow-induced region and on the total ejected matter Mj.
flich & Khokhlov 1996; Iwamoto et al. 1998; Woosley et al. 1999). Furthermore, the yield of nickel is sensitive to the location r in an outflow-induced site. As shown in Tables 2−7, the temperature at larger radius is lower than that at smaller radius, where the relatively low temperature can prevent spallation reactions from destroying heavier species. Therefore, the 56Ni output in case A1r = 3 (0.077 M⊙) is much lower than that in case A1r = 50 (0.463 M⊙). It would be helpful to assume that the 56Ni yield would be high at larger radius in an outflow-induced region. From the above, it seems that case A1r = 50 is more preferable for explaining the characteristics of outflows associated with GRBs. However, because this result is based on the assumption of 1M⊙ matter ejected from outflows, the uncertainty is still large for how much total matter would be ejected from the collapsar accretion. Iwamoto et al. (1999) made detailed simulations to study how nucleosynthetic outputs depend on deflagration speeds and ignition densities related to a white dwarf (WD) progenitor associated with a SN Ia. They found that the result of 56Ni is in the region 0.56−0.77 M⊙ in seven simulations. From their data, they suggested that nucleosynthetic yields might be helpful in providing constraints on the key parameters of their models. In our study, nucleosynthetic yields have changed as the chosen value of radius r varies in outflow-induced region. As mentioned above, case A1 shows that the output of 56Ni is smallest (0.077 M⊙) at r = 3rsch and largest (0.463 M⊙) at r = 50rsch for Mj = 1 M⊙, meaning that the outflow induced from a larger radius in an accretion disk can be helpful in producing the 56Ni. But for an outflow induced in the innermost point (small radius) in accretion, such as case A1r = 3, then to match the observed data of 0.5−0.7 M⊙ for 56Ni associated with GRBs, the total ejected matter should be Mj = 10 M⊙. This can indicate that the elemental abundances associated with GRBs depend on the location r in outflow-induced region and on the total ejected matter Mj.
The ejected species can be estimated for the galactic chemical evolution. In one explosion, a particular nuclide driven out by the GRB jet and deposited in the host galaxy can be estimated by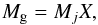 (13)where Mj is the total mass of expelled matter in one explosion and X is the mass abundance of the nuclide. Therefore, as an example, for Mj = 1 M⊙ and according to Table 2XNi56 = 7.69 × 10-2 (case A1r = 3), the 56Ni yields in one explosion in our simulations would be 0.077 M⊙, while in a recent investigation (Fujimoto et al. 2008) it was shown that the ejected mass of 56Ni is about 3.7 × 10-4 to 0.06 M⊙.
(13)where Mj is the total mass of expelled matter in one explosion and X is the mass abundance of the nuclide. Therefore, as an example, for Mj = 1 M⊙ and according to Table 2XNi56 = 7.69 × 10-2 (case A1r = 3), the 56Ni yields in one explosion in our simulations would be 0.077 M⊙, while in a recent investigation (Fujimoto et al. 2008) it was shown that the ejected mass of 56Ni is about 3.7 × 10-4 to 0.06 M⊙.
If we account for a long-life contamination-species’s total mass, its half-life τ0.5 can be expressed by 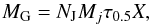 (14)where NJ is the number of collapsar accretions accompanied with GRBs per year in the host galaxy. We roughly estimate the 26Al-contamination associated with GRBs alone. The well-known quest for the origin of 26Al still remains open (Limongi & Chieffi 2006; Prantzos 2004; Tur et al. 2010) since the 1.809-MeV gamma-ray was first observed by the HEAO-3 satellite (Mahoney et al. 1982). Table 7 shows that the highest final mass fraction of 26Al is XAl26 = 1.49 × 10-7 (case B3r = 50). For Mj = 1 M⊙, and NJ = 10-5 yr-1, then in the 26Al lifetime of τ0.5 = 7.2 × 105 yr, from Eq. (14) the mass of 26Al produced from the collapsar accretion accompanied with GRBs is about 1.08 × 10-6 M⊙; this value is much lower than the 26Al observed data of (2−3) M⊙ (Diehl et al. 2006), therefore it would not be the key channel for synthesizing 26Al.
(14)where NJ is the number of collapsar accretions accompanied with GRBs per year in the host galaxy. We roughly estimate the 26Al-contamination associated with GRBs alone. The well-known quest for the origin of 26Al still remains open (Limongi & Chieffi 2006; Prantzos 2004; Tur et al. 2010) since the 1.809-MeV gamma-ray was first observed by the HEAO-3 satellite (Mahoney et al. 1982). Table 7 shows that the highest final mass fraction of 26Al is XAl26 = 1.49 × 10-7 (case B3r = 50). For Mj = 1 M⊙, and NJ = 10-5 yr-1, then in the 26Al lifetime of τ0.5 = 7.2 × 105 yr, from Eq. (14) the mass of 26Al produced from the collapsar accretion accompanied with GRBs is about 1.08 × 10-6 M⊙; this value is much lower than the 26Al observed data of (2−3) M⊙ (Diehl et al. 2006), therefore it would not be the key channel for synthesizing 26Al.
We here considered the decay reactions in the dynamic process [ t0,tf), but did not include the final step (tf), otherwise the decayed species as shown in Figs. 3−5 would precipitously drop to zero in the final step tf. Therefore, we also provide Table 8 to show the final results including radioactive decays in the final step tf, such as the β + or α decay process. As shown in Table 8, it includes the daughter nuclei (Col. 1) and their mother nuclei (Col. 5). Columns 4 and 6 show the yields of these nuclides before radioactive decays take place at tf, and Col. 8 give the total mass of daughter nuclei after their mother nuclei decays. For 1 M⊙ ejected matter, as shown in Table 8, decay reactions can further increase the mass (or mass fractions) of these species. The fastest increasing nuclide is 60Ni, it has increased by about 106 times the original value before 60Cu and 60Zn decay. Other increased species are as follows: increased by 105 times are 18O, 48V, 55Fe, 56Co and 57Co; 104 times: 43Ca, 45Sc, 47Ti, 51Cr and 52Mn; 103 times: 38Ar, 49V and 53Mn; and 102 times: 14N, 15N, 30Si and 59Ni. Among these species, the mass growth of 56Co comes from 56Ni decays. The output of 56Fe is low (XFe56< 10-15) in all of the cases A1-3 and B1-3, therefore it does not appear in Tables 2−7; but if we consider the continued radioactive decay on 56Co in the final step tf, then 56Fe will appear, up to 0.463 M⊙ in mass.
To compare our results with the observed spectroscopic data of GRBs, in Table 9, Col. 1 we show some detected chemical elements from recent studies, and these detected elements’ stable isotopes listed in Col. 3 are selected from Tables 2−8 in this work, which could contribute to the galactic chemical evolution. Among these nuclides, some stable isotopes of S, Ar, Ca, Ti and Fe might influence galactic metal contamination, for example, the total mass of 34S, 38Ar, 42Ca, 46Ti and 54Fe produced in one GRB explosion stored in its host galaxy can reach 10-4 M⊙, while the highest produced mass of 56Fe could be 0.463 M⊙ (56Ni→56Co→56Fe). However, considering the ejected mass of the elements, the contribution from the GRB event is small relative to the supernova. Table 10 shows the chemical yields from some recent supernova calculations. Some species produced by the GRBs in this study (Table 10, Col. 6) are less abundant than the supernova events. Furthermore, if we consider the frequency of the GRB event, the contribution from the GRBs would become even smaller compared to the supernovas.
The model we used adopted a constant mass accretion rate Ṁ, while in the collapsing star, the accretion rate Ṁ presumably decreases with time. We adopted three subcases of Ṁ = 0.1, 0.07, and 0.04 M⊙ s-1. This shows that the temperature in the accretion disk would increase as Ṁ increases, which can help improve or reduce the output mass of some nuclides. For example, as shown in Tables 2−7, the unstable 56Ni abundance decreases as the value of Ṁ decreases.
Our simulations also show that the nucleosynthetic yields might be an indicator for estimating the collapsar mass accretion rate Ṁ. As shown in Tables 2−7, some species’ abundances have monotonously increased or decreased as Ṁ increases. By considering the half-life of the nuclides and the timing of observations, among those monotone increasing or decreasing species whose half-lives exceed 40 min, we chose the top abundance isotope to represent its element for practical purposes as the indicator. From Tables 2−7, and considering the decay process (Table 8), we can find five increased-nuclides with long half-lives, for instance, the mass fractions of 21Ne (stable), 29Si (stable), 41Ca (τ0.5: 1.03E+5 yr), 53Mn (τ0.5: 3.74E+6 yr) and 58Ni (stable) increase as the accretion rate Ṁ increases. Nevertheless, this trend is reversed for the other five species of 26Al (τ0.5: 7.17E+5 yr), 27Al (stable), 40Ca (stable), 48V (τ0.5: 15.97 days) and 51Mn (τ0.5: 46.2 min). Except for these ten nuclides mentioned above, the rest of the nuclide abundances in this study show ups and downs, remains nearly constant as Ṁ increases, or is destroyed by the radioactive decay-process. These ten species are displayed in six panels in Fig. 7, where the abscissa are scaled in values of Ṁ. In a same panel, the same color represents the same chemical species. As shown in Fig. 7, 21Ne, 29Si, 41Ca, 53Mn, and 58Ni are displayed in panels a–c in the left column, while 26Al, 27Al, 40Ca, 48V, and 51Mn are shown in panels d–f in the right column, that is, the left column shows that the abundances of these up-species increase when Ṁ increases, and the down-species in the right column show the opposite trend.
Can all of these ten species become the indicator of mass accretion rate Ṁ? Among these monotonously increasing or decreasing nuclides, the mass fractions of 29Si and 40Ca are much closer to the solar value, which disqualifies them from becoming the indicator of Ṁ. 26Al is a well-known overabundant species in our Galaxy; its yields face some unsolved problems and uncertainties; the abundance of produced 27Al is lower than solar, perhaps they are both unsuitable to act as the indicator-species. The atomic number of 21Ne is relatively small, so it might easy to be produced by other nuclear processes, such as nucleosynthesis in various stellar nuclear-pots; therefore, just like 26Al and 40Ca, it may also be unsuitable to be an indicator of Ṁ. Usually, the species of 41Ca, 48V, 51,53Mn, and 58Ni were born in huge stellar nuclear-pot or in violent explosions in the end of massive stellars’ lifetime, which might qualify these species as the indicator. The initial abundances of 41Ca, 48V, and 51,53Mn adopted in this work are almost zero, but they are frequently produced nuclides (highest values of mass fractions as shown in Tables 2−8, 41Ca: 10-5; 48V: 10-5; 51Mn: 10-5 and 53Mn: 10-4) after the explosive nucleosynthesis compared to their initial values; therefore, 41Ca, 48V, and 51,53Mn might be the indicator of Ṁ. The produced 58Ni (10-3) is two orders of magnitude greater than its initial value (10-5); apparently, 58Ni can be an indicator as well. Therefore, we tentatively recommend adopting 41Ca, 48V, 51,53Mn, and 58Ni as a diagnostic of the collapsar mass accretion rate.
A hypernova (HN) is a massive core-collapse SN with tremendously large energy releases that can be more than one order of magnitude larger than that of normal SN. Hamuy (2003) reported that SN with a higher energy would produce more nickel nuclei, and Fujimoto et al. (2004) found that the yields of species heavier than calcium synthesized by a HN are almost greater than that by a normal SN. Our Tables 2−7 show that as the mass accretion rate Ṁ increases, the GRB tends to produce more 56Ni. Therefore, for the core-collapse SN, we here suggest that a high mass accretion rate would occur in highly energetic SN, namely in the HN sites, while a low accretion rate is associated with normal SN; therefore, the mass accretion rates would allow distinguishing normal SN from HN. Moreover, it might explain why not all the SN lead to GRBs. For the observed data, GRB 980425-SN 1998bw (Galama et al. 1998), GRB 030329-SN 2003dh (Stanek et al. 2003; Hjorth et al. 2003), and GRB 031203-SN 2003lw (Malesani et al. 2006) have been found to be GRB-SN connections, and they are all considered to be hypernovae. Non-GRB SN are supernova events without accompanying GRBs, such as SN 1997ef (Iwamoto et al. 2000), SN 2002ap (Mazzali et al. 2002) and SN 2003jd (Mazzali et al. 2005), which are less energetic than GRB-SN (Nomoto et al. 2007), that is, the mass accretion rates of non-GRB SN are lower than those of GRB-SN. We tentatively propose that the smaller mass accretion rates are too low in energy to trigger GRBs.
However, although we can learn some spectral techniques from recent studies (Vargas et al. 2013; Kirby et al. 2008, 2010; Konami et al. 2010; Shetrone et al. 2009; Aoki et al. 2007; Tolstoy et al. 2001, etc.), maybe the ejected nuclei mentioned above are still very difficult to observe; therefore we here only suggest the five above-mentioned nuclides (41Ca, 48V, 51,53Mn, and 58Ni) to be the indicator of mass accretion rate, without considering the available observational technique. 56Ni can also be such an indicator, as is shown in Tables 2−7, but it is an unstable nucleus and will decay to 56Co till 56Fe. There may be other sources that can produce these species, such as the hot nuclear-pots of normal stars; but Kobayashi et al.(2011) proposed that a large fraction of light species such as C, N, and F are produced by asymptotic giant branch stars (AGBs), while the products of heavier species (Na till Fe) are negligible (perhaps except for some specific nuclides heavier than Fe, e.g., Sr, Y, Zr, and Pb produced by s-process; Travaglio et al. 2001, 2004); it seems that the mass of these heavy species output per event by the normal channel are much lower than that from a GRB. In general, heavier nuclides such as the Fe-group are believed to born in violent explosions at the end of massive star lifetimes. This means that a SN blast itself can also produce these nuclides, which could contaminate the observed values; therefore, these species might be more suitable for dark-hypernovae (non-SN GRB) than for SN-GRB to be a diagnostic of the collapsar mass accretion rate.
Online material
Key parameters and mass fractions of nuclides (selected from the top 50 species) produced in collapsar accretions for cases A1-3 and B1-3.
Final mass fractions of explosive nucleosynthesis in the outflows associated with GRBs at r = 3rsch for cases A1-3 and B1-3.
As Table 2, but for cases A1-3 and B1-3 at r = 10rsch.
As Table 2, but for cases A1-3 and B1-3 at r = 20rsch.
As Table 2, but for cases A1-3 and B1-3 at r = 30rsch.
As Table 2, but for cases A1-3 and B1-3 at r = 40rsch.
As Table 2, but for cases A1-3 and B1-3 at r = 50rsch.
Total yields after radioactive decays in the final step tf for 1 M⊙ matter ejected from outflows associated with GRBs.
 |
Fig. 3 Explosive nucleosynthesis in the outflow region associated with GRB for case A1 at r = 3rsch (case A1r = 3). The radioactive decays have been taken into account within the dynamic process [ t0,tf), but did not include the final step (tf), which can prevent some decayed species, as shown in this picture, from precipitously dropping to zero in the final step tf. |
 |
Fig. 3 continued. |
 |
Fig. 3 continued. |
 |
Fig. 4 As Fig. 3, but for case A1 at r = 50rsch (case A1r = 50). It only shows the long (relative) half-life species (τ0.5> 1 day) by considering the timing of observations; the species with half-lives of τ0.5 ≤ 1 day are not plotted. The final abundances of nuclides as shown in this figure (selected from Table 7) exceed 10-11. |
 |
Fig. 5 Five up-species abundance increase when the value of collapsar accretion rate Ṁ increases in panels a)−c) in the left column and in panels d)−f) in the right column. The other five down-species abundances decrease as Ṁ increases. The abscissa is scaled in the value of Ṁ. In a same panel, the same colors denote the same chemical species. |
Acknowledgments
We are deeply grateful to the referee for the valuable and useful comments, which have greatly improved this paper. This work is supported by the National Natural Science Foundation of China (grant No. U1331103), and the foundation (No. OP201202) of Key Laboratory for the Structure and Evolution of Celestial Objects of Chinese Academy of Sciences.
References
- Angulo, C., Arnould, M., Rayet, M., & Descouvemont, P., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Honda, S, Beers, T. C., et al. 2007, ApJ, 660, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Arai, K., & Hashimoto, M. 1992, A&A, 254, 191 [NASA ADS] [Google Scholar]
- Arnett, W. D., & Truran, J. 1969, ApJ, 157, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, I., & Mukhopadhyay, B. 2013, ApJ, 778, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Bao, Y. Z., Beer, H., Käppeler, F., et al. 2000, At. Data Nucl. Data Tables, 76, 70 [Google Scholar]
- Barth, A. J., Sari, R., Cohen, M. H., et al. 2003, ApJ, 584, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Belyanin, A. A., & Derishev, E. V. 2001, A&A, 379, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chakrabarti, S. K., & Mukhopadhyay, B. 1999, A&A, 344, 105 [NASA ADS] [Google Scholar]
- Chen, H. W., Prochaska, J. X., Bloom, J. S., & Thompson, I. B. 2005, ApJ, 634, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- De, S., Timmes, F. X., Brown, E. F., et al. 2014, ApJ, 787, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Perna, R., & Narayan, R. 2002, ApJ, 579, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, R., Halloin, H., Kretschmer, K., et al. 2006, Nature, 439, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fields, B. D., Casse, M., Vangioni-Flam, E., & Nomoto, K., et al. 1996, ApJ, 462, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Fiore, F., D’Elia, V., Lazzati, D., et al. 2005, ApJ, 624, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Fisker, J. L., Barnard, V., Görres, J., et al. 2001, At. Data Nucl. Data Tables, 79, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Perley, D. A., Pooley, D., et al. 2006, ApJ, 645, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Fowler, W. A., Caughlan, G. R., & Zimmerman, B. A. 1975, ARA&A, 13, 69 [Google Scholar]
- Freiburghaus, C., Rembges, J.-F., Rauscher, T., et al. 1999, ApJ, 516, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Hashimoto, M., Arai, K., & Matsuba, R. 2004, ApJ, 614, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Hashimoto, M., Kotake, K., & Yamada, S. 2007, ApJ, 656, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Nishimura, N., & Hashimoto, M. 2008, ApJ, 680, 1350 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, G. M., Fowler, W. A., & Newmann, M. J. 1980, ApJS, 42, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, G. M., Fowler, W. A., & Newmann, M. J. 1982, ApJS, 48, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Galama, T., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C., & Popham, R. 1998, ApJ, 498, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, W. M., Liu, T., & Lu, J. F. 2006, ApJ, 643, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Hachinger, S., Mazzali, P. A., Sullivan, M., et al. 2013, MNRAS, 429, 2228 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M. 2003, ApJ, 582, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, M. J., Fowler, W. A., Gaughlan, G. R., & Zimmerman, B. A. 1983, ARA&A, 21, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., Sollerman, J., Møller, P., et al. 2003, Nature, 423, 847 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hou, S. J., Gao, H., Liu, T., et al. 2014, MNRAS, 441, 2375 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, T. 2011, MNRAS, 418, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, T., & Peng, Q. H. 2008, ApJ, 681, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, T., & Wang, M. 2014, MNRAS, 438, 3443 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., & Khokhlov, A. 1996, ApJ, 457, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, S., Iwamoto, N., Orito, M., & Terasawa, M. 2003, ApJ, 595, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Mazzali, P. A., Nomoto, K., et al. 1998, Nature, 395, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Iwamoto, K., Nakamura, T., Nomoto, K., et al. 2000, ApJ, 534, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Izutani, N., Umeda, H., & Tominaga, N. 2009, ApJ, 692, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, L. P., Arnett, W. D., & Chakrabarti, S. K. 1989, ApJ, 336, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Kawanaka, N., & Mineshige, S. 2007, ApJ, 662, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Kawanaka, N., Piran, T., & Krolik, J. H. 2013, ApJ, 766, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Guhathakurta, P., & Sneden, C. 2008, ApJ, 682, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Guhathakurta, P., Simon, J. D., et al. 2010, ApJS, 191, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Knödlseder, J., Bennett, K., Blooemen, H., et al. 1999, A&A, 344, 68 [NASA ADS] [Google Scholar]
- Kobayashi, C., Karakas, A. I., & Umeda, H. 2011, MNRAS, 414, 323 [Google Scholar]
- Kohri, K., & Mineshige, S. 2002, ApJ, 577, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Kohri, K., Narayan, R., & Piran, T. 2005, ApJ, 629, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Konami, S., Matsushita, K., Nagino, R., et al. 2010, PASJ, 62, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Laming, J. M., & Titarchuk, L. 2004, ApJ, 615, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Lederer, C., Massimi, C., Altstadt, S., et al. 2013, Phys. Rev. Lett., 110, 022501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lederer, C., Massimi, C., Berthoumieux, E., et al. 2014, Phys. Rev. C., 89, 025810 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, W. H., Ramirez-Ruiz, E., & Page, D. 2005, ApJ, 632, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2006, ApJ, 647, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, T., Gu, W. M., Xue, L., & Lu, J. F. 2007, ApJ, 661, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, T., Liang, E.-W., Gu, W.-M., et al. 2010, A&A, 516, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., Mazzali, P., Deng, J., et al. 2003, ApJ, 593, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Mahoney, W. A., Ling, J. C., Jacobson, A. S., & Lingenfelter, R. E. 1982, ApJ, 262, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Malesani, J., Tagliaferri, G., Chincarini, G., et al. 2006, ApJ, 609, L5 [Google Scholar]
- Mazzali, P. A., Deng, J., Maeda, K., et al. 2002, ApJ, 572, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., Kawabata, K. S., Maeda, K., et al. 2005, Science, 308, 1284 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mukhopadhyay, B. 2013, Phys. Lett. B, 721, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Mukhopadhyay, B., & Chakrabarti, S. K. 2000, A&A, 353, 1029 [NASA ADS] [Google Scholar]
- Nagataki, S., Mizuta, A., Takabe, H., & Sato, K. 2003a, ApJ, 596, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Nagataki, S., Kohri, K., Ando, S., & Sato, K. 2003b, Astropart. Phys., 18, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Nagataki, S., Mizuta, A., & Sato, K. 2006, ApJ, 647, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, T., Mazzali, P. A., Nomoto, K., & Iwamoto, K. 2001, ApJ, 550, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Nishimura, S., Kotake, K., Hashimoto, M.-A., et al. 2006, ApJ, 642, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Tominaga, N., Tanaka, M., et al. 2007, AIP Conf. Proc., 937, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Cappellaro, E., Danziger, J., et al. 2001, ApJ, 555, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Popham, R., & Gammie, C. 1998, ApJ, 504, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Popham, R., Woosley, S. E., & Fryer, C. 1999, ApJ, 518, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N. 2004, A&A, 420, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., & Diehl, R. 1996, Phys. Rep., 267, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Chen, H. W., & Bloom, J. S. 2006, ApJ, 648, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Pruet, J., Woosley, S. E., & Hoffman, R. D. 2003, ApJ, 586, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Pruet, J., Thompson, T. A., & Hoffman, R. D. 2004a, ApJ, 606, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Pruet, J., Surman, R., & McLaughlin, G. C. 2004b, ApJ, 602, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y. Z., & Woosley, S. E. 1996, ApJ, 471, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, S. J. 2014, Phys. Rev. C, 89, 054611 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, T. 2012, ApJ, 755, L10 [Google Scholar]
- Rauscher, T., & Thielemann, F.-K. 2000, At. Data Nucl. Data Tables, 75, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., Watson, D., Osborne, J. P., Pounds, K. A., & O’Brien, P. 2003, A&A, 403, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynoso, M. M., Romero, G. E., & Sampayo, O. A. 2006, A&A, 454, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaefer, B. E., Gerardy, C. L., Höflich, P., et al. 2003, ApJ, 588, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M. D., Siegel, M. H., Cook, D. O., & Bosler, T. 2009, AJ, 137, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., Matheson, T., Garnavich, P. M., et al. 2003, ApJ, 591, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Starling, R. L. C., Wijers, R. A. M. J., Hughes, M. A., et al. 2005, MNRAS, 360, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Surman, R., & McLaughlin, G. C. 2004, ApJ, 603, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstoy, E., Irwin, M. J., Cole, A. A., et al. 2001, MNRAS, 327, 918 [NASA ADS] [CrossRef] [Google Scholar]
- Tominaga, N., Maeda, K., Umeda, H., et al. 2007, ApJ, 657, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Gallino, R., Busso, M., & Gratton, R. 2001, ApJ, 549, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Gallino, R., Arnone, E., et al. 2004, ApJ, 601, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Tur, C., Heger, A., & Austin, S. M. 2010, ApJ, 718, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2002, ApJ, 565, 385 [NASA ADS] [CrossRef] [Google Scholar]
- van Marle, A. J., Langer, N., & García-Segura, G. 2005, A&A, 444, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vargas, L. C., Geha, M., Kirby, E. N., & Simon, J. D. 2013, ApJ, 767, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Vreeswijk, P. M., Ellison, S. L., Ledoux, C., et al. 2004, A&A, 419, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wallace, R. K., & Woosley, S. E. 1981, ApJS, 45, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Wagoner, R., Fowler, W. A., & Hoyle, F. 1967, ApJ, 148, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E. 1986, in Nucleosynthesis and Chemical Evolutions, eds. B. Hauck, A. Maeder, & G. Meynet (Geneva: Geneva Obs.), 1 [Google Scholar]
- Woosley, S. E., Arnett, W. D., & Clayton, D. D. 1973, ApJS, 26, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Eastman, R. G., & Schmidt, B. P. 1999, ApJ, 516, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Yamaguchi, H., Tanaka, M., Maeda, K., et al. 2012, ApJ, 749, 137 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Key parameters and mass fractions of nuclides (selected from the top 50 species) produced in collapsar accretions for cases A1-3 and B1-3.
Final mass fractions of explosive nucleosynthesis in the outflows associated with GRBs at r = 3rsch for cases A1-3 and B1-3.
Total yields after radioactive decays in the final step tf for 1 M⊙ matter ejected from outflows associated with GRBs.
All Figures
 |
Fig. 1 Temperatures, densities, accretion velocities, and accretion timescales of collapsar models for cases A1-3 and B1-3. The accretion disk radius is scaled in Schwarzschild gravitational units. |
| In the text | |
 |
Fig. 2 Production of chemical species produced in the collapsar accretion for case A1, which are selected from the top 25 mass fractions. The accretion disk radius is scaled in Schwarzschild gravitational units. |
| In the text | |
 |
Fig. 3 Explosive nucleosynthesis in the outflow region associated with GRB for case A1 at r = 3rsch (case A1r = 3). The radioactive decays have been taken into account within the dynamic process [ t0,tf), but did not include the final step (tf), which can prevent some decayed species, as shown in this picture, from precipitously dropping to zero in the final step tf. |
| In the text | |
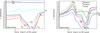 |
Fig. 4 As Fig. 3, but for case A1 at r = 50rsch (case A1r = 50). It only shows the long (relative) half-life species (τ0.5> 1 day) by considering the timing of observations; the species with half-lives of τ0.5 ≤ 1 day are not plotted. The final abundances of nuclides as shown in this figure (selected from Table 7) exceed 10-11. |
| In the text | |
 |
Fig. 5 Five up-species abundance increase when the value of collapsar accretion rate Ṁ increases in panels a–c in the left column and in panels d–f in the right column. The other five down-species abundances decrease as Ṁ increases. The abscissa is scaled in the value of Ṁ. In a same panel, the same colors denote the same chemical species. |
| In the text | |
 |
Fig. 3 Explosive nucleosynthesis in the outflow region associated with GRB for case A1 at r = 3rsch (case A1r = 3). The radioactive decays have been taken into account within the dynamic process [ t0,tf), but did not include the final step (tf), which can prevent some decayed species, as shown in this picture, from precipitously dropping to zero in the final step tf. |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 4 As Fig. 3, but for case A1 at r = 50rsch (case A1r = 50). It only shows the long (relative) half-life species (τ0.5> 1 day) by considering the timing of observations; the species with half-lives of τ0.5 ≤ 1 day are not plotted. The final abundances of nuclides as shown in this figure (selected from Table 7) exceed 10-11. |
| In the text | |
 |
Fig. 5 Five up-species abundance increase when the value of collapsar accretion rate Ṁ increases in panels a)−c) in the left column and in panels d)−f) in the right column. The other five down-species abundances decrease as Ṁ increases. The abscissa is scaled in the value of Ṁ. In a same panel, the same colors denote the same chemical species. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


