EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 577 (May 2015) A&A, 577 (2015) A90 Full HTML
Free Access
Issue
A&A
Volume 577, May 2015
Article Number A90
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201525774
Published online 08 May 2015

© ESO, 2015

1. Introduction

Stars are born rotating rapidly and can then lose angular momentum if they have a magnetised stellar wind. This observation leads to methods for estimating the age of single late-type stars from their rotation period, a technique known as gyrochronology (Barnes 2007). It is unclear whether exoplanet host stars can be considered as single stars in this context. If significant orbital angular momentum is transferred by tides from the orbit of a planet to the rotation of the host star (“tidal spin-up”) then the star may rotate faster than a genuine single star of the same age, i.e. its gyrochronological age (τgyro) will be an underestimate of its true age. There is currently no quantitative global theory to calculate the efficiency of tidal spin-up for stars with convective envelopes because the dissipation of tidal energy by the excitation and damping of waves in convective atmospheres is not fully understood (Zahn 1975, 1977; Goodman & Lackner 2009; Damiani & Lanza 2015; Ogilvie 2014). Alternatively, the planet may disrupt the magentic field geometry of the star and thereby reduce the efficiency of angular momentum loss in the magnetised stellar wind, although this is only likely to be a significant effect for F-type stars (Teff> 6000 K) with short-period planets (P< 10 d, Lanza 2010).

If a planet transits its host star then an analysis of the eclipse light curve can provide an accurate estimate for the radius of the star relative to the semi-major axis of the planet’s orbit, R⋆/a, provided that the eccentricity of the orbit is known. This estimate can be combined with Kepler’s laws to estimate the density of the host star (Seager & Mallén-Ornelas 2003). The density can be combined with estimates for the effective temperature and metallicity of the star to infer a mass and age for the star by comparison with stellar models. The age derived by comparing the properties of a star to a grid of stellar models is known as the isochronal age (τiso). It is not straightforward to calculate the statistical error on τiso because it is strongly correlated with the estimate of the stellar mass (M⋆) and the distribution can be strongly non-Gaussian. For example, for stars near the end of their main-sequence lifetime the probability distribution for τiso given the observed constraints (the posterior probability distribution) can be bi-modal (Maxted et al. 2015). There are also systematic errors in stellar models due to uncertainties in the input physics. For example, the efficiency of energy transport by convection is usually parameterised by the mixing length parameter αMLT (the path length of a convective cell in units of the pressure scale height) that is not known a priori but that can be estimated by finding the value of αMLT for which the models match the observed properties of the Sun. The initial helium abundance for the Sun is estimated in a similar way. The radii of some M- and K-type dwarf stars are not accurately predicted by these “solar-calibrated” stellar models (Hoxie 1973; Popper 1997). This “radius anomaly” for low-mass stars is an active research topic that is motivated by a need to better understand exoplanet host stars and is driven by advances in simulating convection in low-mass stars (Ludwig et al. 2008) and incorporating magnetic fields into stellar models (Feiden & Chaboyer 2013).

Pont (2009) found suggestive empirical evidence for excess rotation in stars with close-in giant planets (hot Jupiters) based on a sample of 28 stars. For three of these stars the rotation period was measured from the rotational modulation of the light curve by star spots. For the other 25 stars the rotation period was estimated from the projected equatorial rotation velocity measured from rotation line broadening (Vrotsini⋆). For 12 of the stars, Vrotsini⋆ was below the instrumental resolution. It is difficult to make accurate estimates of Vrotsini⋆ in these cases because it requires the deconvolution of the instrumental profile from the observed spectral line profiles and the results are sensitive to details of the stellar atmosphere models used to calculate the intrinsic stellar line profiles. Brown (2014) used a maximum likehood method to estimate the ages of 68 transiting exoplanet host stars using five different grids of stellar models and also applied four different methods to calculate the age using gyrochronology. The rotation periods for eight of the stars in that study were based on rotational modulation of the light curve, the remainder were estimated from Vrotsini⋆. Estimates of the rotation period based on Vrotsini⋆ are generally much less precise than those measured directly from the lightcurve and can be affected by systematic errors when the line broadening due to rotation is small compared to other poorly-understood line-broadening effects such as macro-turbulence. Additional uncertainty is introduced by the unknown inclination of the star’s rotation axis, i⋆. Brown found a “slight tendency for isochrones to produce older age estimates” but that the “evidence for any bias on a sample-wide level is inconclusive.”

Planet host stars are an interesting test case for our understanding of the tidal interactions because tidal spin-up will increase the star’s magnetic activity, which may increase the loss of rotational angular momentum through a magnetised stellar wind. The balance of these two effects may lead to a quasi-stationary state in which the planet’s orbit is stable in the long term (Damiani & Lanza 2015). However, if tidal interactions between stars and planets are strong enough to efficiently destroy massive, short-period planets then we might expect to only find hot Jupiters around young stars. To test this hypothesis it would be useful in these cases to be able to estimate an accurate isochronal age because it is likely that the star will be spun-up during the destruction of the planet and so its gyrochronological age will not be an accurate estimate of its true age. Comparing the isochronal and gyrochronological ages is not a straightforward problem because the uncertainties on these two age estimates are strongly non-Gaussian and τgyro depends on the assumed stellar mass, so τiso and τgyro are also correlated.

In Maxted et al. (2015) we developed a Markov chain Monte Carlo (MCMC) method that allows us to estimate the joint posterior probability distribution for τiso and M⋆ based on the observed density, effective temperature (Teff) and metallicity ([Fe/H]) of a star. In this paper we select a sample of 28 transiting exoplanet host stars with accurately measured rotation periods (Sect. 2). For two of the stars in this sample the rotation periods are new estimates based on the rotational modulation of the light curves. We then describe how we have extended the method of Maxted et al. (2015) to include a calculation of the posterior probability distribution for τgyro and present the results of applying this technique to our sample of 28 planet host stars (Sect. 3). The implication of these results for our understanding of tidal spin-up of exoplanet host stars and the reliability of solar-calibrated stellar models is discussed in Sect. 4 and our conclusions are given in Sect. 5.

Table 1

Observed properties of stars in our sample.

2. Sample definition and data selection

We have compiled a list of 28 transiting exoplanet host stars for which the rotation period has been measured directly from the rotational modulation of the light curve due to star spots or, in the case of 55 Cnc, spectroscopic variability in the Ca ii H and K emission line fluxes. For all these stars the existence of a transiting planet has been confirmed by multiple radial velocity measurements based on high-resolution spectroscopy or dynamical analysis of transit timing variations in multi-planet systems (e.g. Kepler-30). The observed properties of these stars are given in Table 1. For each star we list the rotation period, Prot, the orbital period, Porb, the effective temperature, Teff, the logarithmic surface iron abundance relative to the Sun, [Fe/H], the mean stellar density, ρ⋆, the flux from the star at the top of the Earth’s atmosphere, f⊕, and the logarithm of the stellar luminosity, log (L⋆).

We have used only one or two sources of input data for this analysis rather than attempting to reconcile or take the average of multiple studies for each system. We have excluded stars with masses that are too low to be covered by our grid of stellar models (< 0.6 M⊙) or too high for gyrochronology to be applicable (> 1.25 M⊙). We have also excluded stars where the density estimate is based on a Kepler long-cadance (LC) light curve alone because these density estimates appear to be biased compared to the density estimated using asteroseismology (Huber et al. 2013).

2.1. Luminosity measurements

We can include the observed luminosity of the star (L⋆) as an additional constraint in the analysis to derive the mass and age of the star. For stars that have a trigonometrical parallax in van Leeuwen (2007) with precision 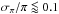\hbox{$\sigma_{\pi}/\pi \loa 0.1$} we calculate L⋆ using the flux at the top of the Earth’s atmosphere (f⊕) estimated by integrating a synthetic stellar spectrum fit by least-squares to the observed fluxes of the star. Optical photometry is obtained from the Naval Observatory Merged Astrometric Dataset (NOMAD) catalogue1 (Zacharias et al. 2004), the Tycho-2 catalogue (Høg et al. 2000), The Amateur Sky Survey (TASS, Droege et al. 1997) and the Carlsberg Meridian Catalog 14 (Muiños & Evans 2014). Near-infrared photometry was obtained from the Two Micron All Sky Survey (2MASS)2 and Deep Near Infrared Survey of the Southern Sky (DENIS)3 catalogues (The DENIS Consortium 2005; Skrutskie et al. 2006). The synthetic stellar spectra used for the numerical integration of the fluxes are from Kurucz (1993). Reddening can be neglected for these nearby stars given the accuracy of the measured fluxes and parallaxes. Standard errors are estimated using a simple Monte Carlo method in which we generate 65 536 pairs of π and f⊕ values from Gaussian distributions and then find the 68.3% confidence interval of the resulting log (L/L⊙) values. The 2MASS photometry for 55 Cnc is not reliable so for this star we have used the value of f⊕ from Boyajian et al. (2013).

2.2. Rotation periods

The rotation periods for the stars in Table 1 are taken from the published sources noted except for HAT-P-21 and WASP-5, for which we have measured the rotation periods using observations obtained by the WASP project (Pollacco et al. 2006) and the method described by Maxted et al. (2011). For HAT-P-21 we used 4185 observations obtained between 2007 Jan 2 and 2007 May 15. These data show a very clear sinusoidal signal with a period of 15.9 d with an amplitude of 0.012 magnitudes. This period agrees very well with the estimate Prot = 15.7 ± 2.2 d that is expected based on the projected equatorial rotation velocity (Vrotsini⋆ = 3.5 ± 0.5 km s-1, Bakos et al. 2011) and the radius of the star, assuming that the inclination of the star’s rotation axis is i ≈ 90°. The WASP data for HAT-P-21 are shown as a function of rotation phase in Fig. 1. The standard error on this value has been estimated from the full-width at half-maximum of the peak in the periodogram.

For WASP-5 we analysed six sets of data obtained with three different cameras in four different observing seasons, as detailed in Table 2. In all six data sets we detect a periodic signal consistent with a rotation period Prot ≈ 16 d if we allow for the possibility that the distribution of star spots can produce a signal at the first harmonic of the rotation period (i.e. at Prot/ 2). The value of Prot in Table 1 is the mean of the observed values calculated with this assumption and the error quoted in the standard error of the mean.

Mohler-Fischer et al. (2013) report a factor of 2 ambiguity in the rotational period of HATS-2. We have used Prot = 24.98 d for our analysis since this gives a value of τgyro that is more consistent with the value of τiso.

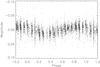thumbnail Fig. 1

WASP photometry for HAT-P-21 plotted as a function of rotation phase assuming Prot = 15.9 d.

Table 2

Periodogram analysis of the WASP light curves for WASP-5.

3. Analysis and results

We used version 1.1 of the program bagemass4 (Maxted et al. 2015) to calculate the joint posterior distribution for the mass and age of each star based on the observed values of Teff, [Fe/H], the mean stellar density ρ⋆ and, if available, L⋆. The stellar models used for our analysis were produced with the garstec stellar evolution code (Weiss & Schlattl 2008). The initial composition of the models is computed assuming a cosmic helium-to-metal enrichment ΔY/ ΔZ = (Y⊙ − YBBN) /Z⊙, where YBBN = 0.2485 is the primordial helium abundance due to big-bang nucleosynthesis (Steigman 2010), Z⊙ = 0.01826 is the solar metal abundance, and the initial solar helium abundance is Y⊙ = 0.26646 so ΔY/ ΔZ = 0.984. These models do not include rotation, but the rotation rates of the stars in our sample are low (<2% of breakup velocity in all but two cases) and so it is not expected that rotation plays a direct role in the structure of these stars. We do not rule out other, indirect effects, e.g. low convective efficiency associated with large magnetic fields, but these have to be modelled in an ad hoc manner. This is discussed later in this work, in relation to specific stars in the sample. The methods used to calculate and interpolate the stellar model grid are described in Serenelli et al. (2013) and Maxted et al. (2015). We set lower limits of 80 K on the standard error for Teff and 0.07 dex for the standard error on [Fe/H] (Bruntt et al. 2010) and assume flat prior distributions for the stellar mass and age. The results are given in Table 3, where the maximum-likelihood (best-fit) values of the stellar mass and age are denoted Mb and τiso,b, respectively. The mean and standard deviation of the posterior distributions for the mass and age are listed under ⟨ M⋆ ⟩ and ⟨ τiso ⟩. Also listed in this table are our estimates of the systematic errors in these values due to an assumed error of 0.2 for αMLT and an assumed error of 0.02 for the initial helium abundance, Y. The change in the estimated mass and age due to increasing Y by its assumed error are given by the quantities σM,Y and στ,Y, respectively. Similarly, σM,α and στ,α quantify the change in the estimated mass and age due to the error in αMLT. We show the best-fit values of M⋆ and τiso and the effects of changing Y and αMLT by their assumed uncertainties for all the stars in the sample in Fig. 2.

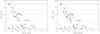thumbnail Fig. 2

Change in the best-fitting masses and ages of transiting exoplanet host stars due to a change in the assumed helium abundance or mixing length parameter. Dots show the best-fitting mass and age for the default values of Y and αMLT and lines show the change in mass and age due to an increase in helium abundance ΔY = +0.02 (left panel) or a change in mixing length parameter ΔαMLT = −0.2 (right panel). Horizontal lines indicate the age of the Galactic disc (dashed), the age of the Universe (dotted) and the highest age in our grid of stellar models (solid). The curved dotted line shows the terminal age main sequence (TAMS) for stars with solar composition.

thumbnail Fig. 3

Left panel: joint posterior distribution for the mass and age of CoRoT-13 estimated by our isochrone fitting technique. Right panel: joint posterior distribution for the age of CoRoT-13 estimated by our isochrone fitting technique and using gyrochronology. For clarity, only 10% of the points from the Markov chain are plotted.

3.1. Gyrochronological age estimates

Our Bayesian MCMC method produces a large set of points in the mass-age parameter space (Markov chain) that has the same distribution as the posterior probability distribution for these parameters. We used Eq. (32) from Barnes (2010) to calculate τgyro from the rotation period and the mass of the star for every point in the Markov chain for each star. The convective turn-over time scale that encapsulates the mass dependence of this mass-age-rotation relation was interpolated from Table 1 of Barnes & Kim (2010). This table suggests that stars with masses 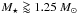\hbox{$M_{\star} \goa 1.25~M_{\sun}$} do not have convective envelopes so we have restricted our analysis to stars with P(M⋆< 1.25 M⊙) > 0.9 according to our MCMC results. We also checked that none of the stars are close to the end of the main sequence, where rapid changes in radius and internal structure are likely to make gyrochronological age estimates unreliable. The calculation of τgyro requires an estimate for the value of the parameter P0. We account for the uncertainty in this value by randomly generating a value of P0 uniformly distributed in the range 0.12 d to 3.4 d for each point in the Markov chain. In principle, there is some additional uncertainty in τgyro due to the stars’ surface differential rotation combined with the variation in the latitude of the active regions that produce the star spot modulation (Epstein & Pinsonneault 2014). We assume that this uncertainty affects the calibration sample used by Barnes (2010) to the same extent that it affects the stars in our sample so that this uncertainty is already accounted for by randomly perturbing the parameter P0. The uncertainties in the observed values of Prot are accounted for in a similar way, but using Gaussian random distributions for the standard errors shown in Table 1. Fig. 3 shows the joint posterior distributions for (M⋆, τiso) and (τiso, τgyro) calculated from the Markov chain using this method for CoRoT-13.

For each star we compare the values of τgyro calculated using the mass value at every point in the Markov chain to the corresponding τiso values for the same point in the Markov chain. To quantify the difference between τiso and τgyro we calculate the fraction of points pτ in the chain for which τgyro>τiso, i.e. pτ = P(τgyro>τiso) is the probability that the gyrochronogical age is greater than the isochronal age. The results of this comparison are given in Table 4 and are shown in Fig. 4. Also given in Table 4 is τtidal, which is a very approximate estimate of the time scale for tidal interactions between the star and the planet (Albrecht et al. 2012). It must be emphasised that the actual time scale for tidal spin-up in these systems is uncertain by a few orders of magnitude (Ogilvie 2014). For multi-planet systems, τtidal applies to the innermost planet. The values of τgyro as a function of τtidal are shown in Fig. 5.

Table 3

Bayesian mass and age estimates for the host stars of transiting extrasolar planets using garstec stellar models assuming αMLT = 1.78.

Table 4

Stellar ages estimated using our stellar models, τiso, and using gyrochronology, τgyro, and the probability pτ = P(τgyro>τiso).

thumbnail Fig. 4

Comparison of gyrochronological age estimates (τgyro) to isochronal age estimates (τiso) for planet host stars with measured rotation periods. Points with error bars indicate the mean and standard deviation of the posterior age distribution. The straight line is the relation τgyro = τiso.

thumbnail Fig. 5

Gyrochronological age estimates as a function of log (τtidal), a very approximate estimate of the time scale for tidal interaction between the star and the innermost planetary companion. We note that the time scale for tidal interactions is uncertain by a few orders of magnitude. Systems with significant differences between τiso and τgyro (p< 0.05) are plotted with filled symbols. 55 Cnc (τiso ≈ 9 Gyr, log (τtidal/ y) ≈ 13) is not shown here.

4. Discussion

It is clear that the gyrochronological age estimate is significantly lower than the isochronal age estimate for about half of the stars in this sample. This discrepancy is apparent from Fig. 4, but the errors on these values are correlated and non-Gaussian so to accurately quantify this discrepancy we need to use the values of pτ in Table 4. There is no obvious relation between the gyrochronological age estimates for these stars and the estimated time scale for tidal interactions between the star and the planet. This may not be surprising given that τtidal is uncertain by a few orders of magnitude (Ogilvie 2014). It is also apparent that there is an even spread of τgyro values from very young ages up to a maximum value of a few Gyr, i.e. there is no obvious pile-up of stars with very low or very high τgyro values as might be expected if some evolutionary or selection effect were biasing the age distribution of the stars in this sample.

The discrepancy between isochronal and gyrochronological age estimates for some planet host stars has been noted for more limited samples of planet host stars before, and has been cited as evidence for tidal spin-up of the stars by their planetary companions, or for the disruption of the normal spin-down process for these stars (Pont 2009; Lanza 2010; Poppenhaeger & Wolk 2014). However, there are other possibile explanations in some cases. It may be that the isochronal age estimates for some stars are not accurate because of missing physics in the stellar models. It is also possible for the distribution of active regions on a star to produce a modulation of the light curve with a period of half the rotation period. This is not a viable explanation for the low values of pτ in Table 4 in general, but may be an issue for a few stars with limited photometric data. We have been careful to select stars for our sample for which the observational data are robust, so the general appearance of distribution in Fig. 4 cannot be ascribed to observational errors, although there may be issues with the observed data for a few stars. The limitations of the observed data, the stellar models and the estimated value of τtidal affect different stars in this sample in different ways, so to understand the implication of these results we need to look at the results on a case-by-case basis.

4.1. HAT-P-11 and WASP-84 – helium rich stars?

There is no satisfactory fit to the observed properties of HAT-P-11 at any age or mass for our grid of standard stellar models, i.e. models using a mixing length calibrated on the solar model (αMLT = 1.78) and ΔY/ ΔZ = 0.984, consistent with the primordial helium abundance and the assumed initial solar composition. In Table 5 we summarise the published density estimates for HAT-P-11, including four studies based on the very high-quality Kepler short-cadence (SC) data for this star. The Kepler data clearly show distortions to the light curve due to the planet crossing dark spots on the face of the host star. Different investigators have accounted for these spot-crossing events in different ways, but the stellar densities derived are all consistent with the value we have used in our analysis. There are also three independent analyses of the spectrum of this star that have been used to derive the Teff and [Fe/H]. Again, all three values are consistent with each other, including the value we have used for our analysis.

Table 5

Independent measurements of the mean density (ρ⋆), effective temperature (Teff) and metallicity ([Fe/H]) for HAT-P-11 and their weighted mean values.

In principle, the Kepler short-cadence photometry for HAT-P-11 can be used to estimate the density of this star using asteroseismology. Christensen-Dalsgaard et al. (2010) analysed the Kepler data for HAT-P-11 from the commissioning period and the first month of regular observations and claimed definite evidence for solar-like oscillations, providing a preliminary estimate of its mean density. However, an analysis of the complete Kepler data set for this star shows no convincing evidence for solar-like oscillations because HAT-P-11 has a much higher level of photometric noise than a typical star of the same magnitude (Davies, priv. comm.).

In general, the analysis of the light curve for a transiting extrasolar planet makes the assumption that, apart from the effects of limb-darkening, the mean surface brightness of a star is the same as the surface brightness in the regions obscured by the planet. This would not be the case if, for example, the planet transits a chord near and approximately parallel to the stellar equator of a star with dark spots near its poles. If the star spots that are not occulted are equivalent to completely black spots that cover a fraction f of the stellar disc, then from Eq. (19) of Seager & Mallén-Ornelas (2003), we can estimate that the density will be systematically too high by a factor 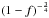(1−f)−34\hbox{$(1-f)^{-\frac{3}{4}}$}. The density of HAT-P-11 predicted by our stellar models based on the observed values of Teff, L⋆ and [Fe/H] assuming τiso< 10 Gyr is ρ⋆ = 1.9 ± 0.1ρ⊙. If this were to be explained by unocculted dark spots this would require f ≈ 0.3. Such a large value of f can be ruled out in the case of HAT-P-11 because of the unusual orbit of the planet relative to the rotation axis of the star. The rotation and orbital axes are almost perpendicular and the ratio of the orbital and rotation periods is close to 1:6. This means the planet effectively scans the stellar disc along six different lines of longitude. Distortions to the light curve are seen because the planet crosses star spots with a typical size of about 5° located in two bands of latitude, similar to the pattern of spots seen on the Sun (Sanchis-Ojeda & Winn 2011; Béky et al. 2014). These spots are too small to explain the large value of ρ⋆ inferred from the transit light curve of HAT-P-11.

In principle, we could find a set of stellar models that match the properties of HAT-P-11 by increasing the assumed mixing length parameter, but energy transport by convection is expected to be less efficient in magnetically active stars like HAT-P-11, not more efficient as a larger value of αMLT would imply (Feiden & Chaboyer 2013). A more plausible explanation for the high density of HAT-P-11 is that this star has an abnormally high helium abundance. We used garstec to calculate a grid of stellar models identical to the grid of standard stellar models described above, but with the helium abundance increased by ΔY = + 0.05. With this stellar model grid for very high helium enhancement we find a good fit to the observed properties of HAT-P-11 (χ2 = 0.34) for a mass ⟨ M⋆ ⟩ = 0.74 ± 0.02 M⊙ and an age ⟨ τ⋆ ⟩ = 1.7 ± 0.7 Gyr. Clearly, there is some additional systematic error in these values because the actual helium abundance of HAT-P-11 is unknown. It is very likely that other stars show variations in their helium abundance around the simple linear relation between Y and Z that we have used. Another star in our sample with τiso,b ≈ 0 and χ2 ≈ 0.5 for ν = 0 degrees of freedom is WASP-84. It is possible that this is a very young star for which the observational errors place the density slightly below the value predicted by our grid of standard stellar models, but the results for HAT-P-11 also opens up the possibility that this star has a more typical age and is helium-rich, particularly since it is not associated with any star forming region and does not show any other signs of extreme youth such as a high lithium abundance.

4.2. Qatar-2 and inflated K-dwarfs

It has long been known that some K-dwarfs appear to be larger by 5 per cent or more than the radius predicted by standard stellar models (Hoxie 1973; Popper 1997). This radius anomaly is correlated with the rotation rate of the star, but also shows some dependence on the mass and metallicity of the star (López-Morales 2007; Spada et al. 2013). The dependence on rotation is thought to be the result of the increase in magnetic activity for rapidly rotating stars. Magnetic activity can affect the structure of a star by producing a high coverage of starspots, which changes the boundary conditions at the surface of the star, or by reducing the efficiency of energy transport by convection. Whatever the cause of the radius anomaly in K-dwarfs, the existence of inflated K-dwarfs is one likely explanation for the appearance of stars in Table 3 that seem to be older than the Galactic disc (10 Gyr, Cojocaru et al. 2014) or older than the Universe (13.75 Gyr, Hinshaw et al. 2013).

One method that has been proposed to deal with the radius anomaly is to simulate the magnetic inhibition of convection by reducing the mixing length parameter (Chabrier et al. 2007). This phenomenological approach has some support from stellar models that incorporate magnetic fields in a self-consistent way (Feiden & Chaboyer 2013). Qatar-2 is one K-dwarf in our sample that has an isochronal age estimate that is clearly older than the age of the Galactic disc (P(τiso< 10 Gyr) = 0.001). We re-analysed the data for Qatar-2 using grids of stellar models similar to those described above but with various values of αMLT from 1.22 to 2.32. We find that models with 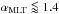\hbox{$\alpha_{\rm MLT} \loa 1.4$} can match the properties of this stars for ages lower than 10 Gyr.

The unknown value of αMLT is a source of systemic error that potentially affects the mass and age estimates for all the stars that we have studied. This includes the stars for which we have found a satisfatory fit to the observations for some age within the range expected (0 to 10 Gyr), i.e. it may be that we have assumed an inappropriate value of αMLT for some stars but that this is hidden by deriving incorrect (but plausible) values for the age and mass.

4.3. Stars with consistent isochronal and gyrochronological age estimates.

From Table 4 we see that there are nine stars for which there is good agreement between τiso and τgyro (pτ> 0.1). These include the stars HAT-P-11 and WASP-84 discussed above that may be helium-rich stars. As there is no good fit to the properties of these stars within our model grid we do not discuss them further in this section.

Of the seven remaining stars, HD 209458 and CoRoT-4 both have reasonably precise gyrochronological and isochronal age estimates. For the other stars the agreement between the two age estimates is partly due to the large uncertainty in one or both of these age estimates. The time scale for tidal spin-up of the star depends sensitively on the structure of the star and whether there is any resonance between the orbit of the planet and internal gravity wave modes in the star (Ogilvie 2014), so we should not expect that there is a precise value of log (τtidal/ yr) that divides systems with and without tidal spin-up. Nevertheless, the good agreeement between the isochronal and gyrochronological age estimates for HD 209458 and CoRoT-4 suggests that tidal spin-up for planet host stars may be inefficient for systems with log (τtidal/ yr) ≳ 12.5.

4.4. Rapidly rotating stars

Maxted et al. (2015) compared the observed masses of stars in detached eclipsing binaries to the masses predicted using bagemass based on their density, effective temperature and metallicity. They found that masses of some stars with orbital periods less than about 6 days were under-predicted by about 0.15 M⊙. The rotation periods of these stars are expected to be equal to their orbital periods because there are strong tidal interactions between the stars. There were no stars in the sample of eclipsing binaries used by Maxted et al. (2015) with orbital periods in the range 7−14 days, so it is not known whether stars with rotation periods in this range are affected by the same problem. The cause of this discrepancy is not known so the isochronal age estimates for some stars with rotation periods less than about 6 days will be unreliable, and there is also the possibility that this problem affects stars with rotation periods up to about 14 days.

There are four stars in our sample of planet host stars with rotation periods less than about 6 days (CoRoT-2, CoRoT-6, CoRoT-18 and Kepler-63). All four stars are clear examples of the gyrochronological age estimate being significantly lower than the isochronal age estimate (pτ < 0.02). Excluding these four stars from the sample does not have a strong affect on our conclusions as there are several other examples of stars with gyrochronological age estimates significantly lower than the isochronal age estimate.

If we take the more cautious approach and exclude all stars in our sample with rotation periods less than 14 days and HAT-P-11 (discussed above), we are left with a sample of 14 stars. Of these, about half have a gyrochronological age estimates significantly lower than their isochronal age estimates (pτ < 0.05).

CoRoT-6 and Kepler-63 are examples of stars where the tidal forces between the star and the planet are very weak, e.g. weaker than the approximate limit log (τtidal/ yr) ≳ 12.5 suggested in the previous section, above which limit it is reasonable to assume that there is no tidal spin-up for planet host stars. In these cases, we expect that the gyrochronological age estimate of the star should be reliable. If this is the case, then it may be that these G-dwarfs stars are affected by magnetic inhibition of convection in a similar way to K-dwarfs. WASP-41 is another G-dwarf for which the gyrochronological age estimate is significantly lower than its isochronal age estimate (pτ = 0.03) despite having a very long tidal time scale (log (τtidal/ yr) = 12.3). Although this is not a rapidly rotating star (Prot = 18.4 d) we mention it here because it is known to be a magnetically active G8-type star based on the appearance of chromospheric emission lines in its spectrum (Maxted et al. 2011). This is consistent with the idea that some G-type stars have isochronal age estimates that are not reliable (too high) as a result of magnetic activity that is related to the rotation of the star but that is not directly caused by rapid rotation.

4.5. Comparison to other studies

Brown (2014) found a “slight tendency for isochrones to produce older age estimates” but that the “evidence for any bias on a sample-wide level is inconclusive.” All eight stars in that sample with directly measured rotation periods have been re-analysed here. For seven of these stars, our results are consistent with those of Brown (2014). The exception is WASP-50, for which Brown uses a value of Teff based on photometric colour (Brown, priv. comm.), rather than the lower and more accurate value that we have used here based on an analysis of the spectrum from Gillon et al. (2011). From a comparison of the gyrochronological and isochronal age estimates, Brown notes that of these eight stars, two show “an age difference of a few Gyr”. We see very clear discrepancies between τiso and τgyro for seven of these eight stars, i.e. pτ< 0.1, often much lower. We have restricted our analysis to stars with directly measured Prot values and increased the number of such stars studied to 28 so we very clearly see that τiso and τgyro disagree for the majority of stars common to both studies. A key difference between our study and the study by Brown is the way that the uncertainties on the age estimates have been calculated. Brown calculated the range of isochronal ages corresponding to the 1σ error ellipse on Teff and ρ⋆ (the error on [Fe/H] was neglected) and then used this range as the standard deviation of a normal distribution to represent the posterior probability distribution for τiso. The correlation between τiso and τgyro via their mutual correlation with the assumed stellar mass was not considered. With our Markov chain method we can accurately account for the errors in τiso and τgyro from the errors in Teff, ρ⋆ and [Fe/H] and calculate the joint posterior distribution for these values (e.g. Fig. 3). This allows us to accurately calculate a statistic like pτ that has greater statistical power than the method used by Brown.

Pont (2009) used the full sample of 41 transiting exoplanet host stars known at that time to investigate whether there was empirical evidence for tidal evolution in these planetary systems. He identified two stars (HD 189733 and CoRoT-2) that show large excess rotation among the late-type stars in this sample (Teff< 6000 K). This is consistent with the values of pτ< 0.1 that we have derived for both these stars. Additional constraints on the age of both these stars are now available, so we discuss these stars in more detail below. Pont’s study also includes the stars WASP-4 and WASP-5, but the only information on the rotation of these stars available at them time was rotation velocities measured from spectral line broadening comparable to the instrumental resolution. With the rotation periods now available from photometry we find that both these stars show some evidence for excess rotation (pτ< 0.1). CoRoT-4 is also present in both samples and shows no evidence for excess rotation in either study (pτ = 0.4).

4.6. Other age constraints

Poppenhaeger & Wolk (2014) took a very different approach to testing whether hot Jupiters affect the rotation rate of their host stars. They compared the stellar coronal X-ray emission of five planet host stars with their companion stars in wide binary systems and used this activity indicator to estimate the age of both stars in each binary system. They found much higher magnetic activity levels in HD 189733 and CoRoT-2 than in their companion stars. The estimated age of HD 189733 based on the X-ray flux is τX = 1−2 Gyr and for CoRoT-2 is τX = 0.1−0.3 Gyr, whereas their companions both have τX> 5 Gyr. In contrast, there was no evidence for a difference in age between the companion and the planet host star for τ Boo (τX = 1−2 Gyr), ν And (τX> 5 Gyr) or 55 Cnc (τX> 5 Gyr). There is very good agreement between our estimate of τgyro and τX for CoRoT-2 and τgyro is consistent with τX in the case of 55 Cnc. The probability that τiso for CoRoT-2 calculated using our grid of standard stellar models is consistent with the value of τX for its companion is P(τiso> 5 Gyr) = 0.09, i.e. if we assume that the value of τX for the companion is an accurate estimate of actual age of CoRoT-2 then the isochronal age estimate is likely to be an underestimate of the true age. Increasing the helium abundance by about +0.04 or reducing αMLT by about 0.4, or changing both these factors by about half as much, would be sufficient to bring the τiso and τX into agreement. For 55 Cnc, both τiso and τgyro are consistent with each other and with the lower limit τX> 5 Gyr. Poppenhaeger & Wolk conclude from their observations that the presence of hot Jupiters may inhibit the spin-down of host stars with thick outer convective layers. With a sample of only five stars it is not yet possible to make precise estimates of what fraction of planet host stars may be affected by their planetary companions or what properties determine the strength of this interaction, but it is clear that τgyro is not a reliable estimate of the age for some planet host stars.

The lithium abundance at the surface of a star can provide useful constraints on the age of a star, particularly for stars younger than about 600 Myr where there are good data in various open clusters that can be used to calibrate the dependance of the lithium depletion rate on mass. We have compared the observed lithium abundances for the stars listed in the Table 4 to the calibration data from Sestito & Randich (2005) to see if the resulting constraints on the age are consistent with the values of τiso and τgyro. In general we can only set a lower limit to the 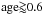\hbox{${\rm age} {\goa}0.6$} Gyr that is consistent with both of these age estimates. A notable exception is CoRoT-2, which has a surface lithium abundance that implies an age for this star of ≈ 0.2 Gyr (Schröter et al. 2011). This agrees very well with the gyrochronological age estimate for this star. There does not appear to be any simple way to reconcile the apparent young age of CoRoT-2 based on the available age indicators with the lack of X-ray emission from its K-dwarf companion.

Another case where there is evidence to support the gyrochronological age estimate is WASP-77. Maxted et al. (2013) used the projected rotational velocity of the K-dwarf companion to WASP-77 to infer an gyrochronological age of 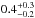0.4-0.2+0.3\hbox{$0.4^{+0.3}_{-0.2}$} Gyr, consistent with their estimate of 1.0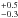+0.5-0.3\hbox{$^{+0.5}_{-0.3}$} Gyr for the gyrochronological age of WASP-77. Maxted et al. (2013) used a different calibration for the gyrochronological age to the one used here, but it is clear that the gyrochronological age estimate for the companion to WASP-77 is inconsistent with the age for WASP-77 estimated using a grid of standard stellar models. If we assume a lower helium abundance for WASP-77 (Fig. 2) we will obtain a slightly lower estimate for the isochronal age, but it is not possible to reconcile the gyrochronological and isochronal age estimates without using a helium abundance less than the lower limit set by the primordial content of the Universe. It is possible to reconcile the isochronal age estimate with the gyrochronological age estimate by using a reduced value of the mixing-length parameter αMLT much lower than the solar-calibrated value. WASP-77 shows chromospheric emission lines characteristic of magnetically active stars despite its moderate rotation period, Prot = 15.4 d. Reducing the value of αMLT is consistent with the idea of magnetic inhibition of convection that has been succesfully applied to explain the radius anomaly in K-dwarfs, but extends the idea in this case to a G-type star5.

4.7. Reliability of gyrochronological age estimates for single stars

Meibom et al. (2015) have recently used Kepler photometry of 30 stars in the open cluster NGC 6811 to measure their rotation periods. The calibration used here (Barnes 2010) predicts rotation periods for stars in good agreement with the observed values at the age of the cluster (2.5 Gyr) across the entire mass range studied (0.85−1.25 M⊙). Epstein & Pinsonneault (2014) criticised the method used by Barnes (2010) to derive their calibration. We used Figs. 7 and 8 of their paper to estimate by eye the gyrochronological age estimatess for all the stars in our sample and found that these generally agree well with the values derived here, particularly if the calibration using the Kawaler style wind mass loss rate is used. For rapidly rotating stars the calibration of Epstein & Pinsonneault (2014) only provides an upper limit of 0.5 Gyr. This is consistent with the young ages that we derive for these stars, but it may be that these very young gyrochronological age estimates are not reliable to the precision quoted here. This is unlikely to affect our conclusions substantially because an upper limit of 0.5 Gyr is generally sufficient to show that these rapidly rotating stars have gyrochronological age estimates inconsistent with the isochronal age estimates. The calibration of Epstein & Pinsonneault (2014) was also applied to the data for stars in NGC 6811 by Meibom et al. (2015) and found to give rotation periods that are too low by about 10% for stars with masses ≈ 0.85 M⊙ but that agree well with the observed rotation periods for stars with masses near 1 M⊙.

5. Conclusions

By using new data and improved analysis methods we have shown that there is now good evidence that some exoplanet host stars rotate more rapidly than expected. For our sample of 28 transiting exoplanet host stars, about half the sample have gyrochronological age estimates that are significantly lower than their isochronal age estimates. In a few such cases there are independent constraints on the age of the star that are consistent with the isochronal age, which suggests that tidal spin-up of the host star has occured in these systems. However, in several cases it is not clear that tidal interactions between the star and the planet are responsible for this discrepancy. For some K-type stars this is a result of the well-known radius anomaly that may be due to magnetic inhibition of convection. We find some evidence that this anomaly may also affect some of the rapidly rotating and/or magnetically active G-type stars in our sample, either from independent age constraints on the age of the star (WASP-77) or because it may be implausible that the strength of the tidal interaction with the planet is strong enough to spin-up the star (CoRoT-6, Kepler-63 and, perhaps, WASP-41).

Some planet-host stars (HAT-P-11 in particular) appear to be much denser than predicted by stellar models. These stars may be significantly enhanced in helium. This makes it difficult to assess the reliability of isochronal mass and age estimates for these stars. There is currently no simple explanation for the inconsistency between the young age of CoRoT-2 implied by stellar models, gyrochronology, its X-ray flux and its high lithium abundance with the very old age inferred for its K-type companion based on its lack of X-ray flux.

Our improved analysis methods have allowed us to show that there is now clear evidence that the gyrochronological age estimates for some transiting exoplanet host stars are significantly lower than the isochronal age estimates. However, a careful consideration of all the available data on a case-by-case basis shows that it is not always clear that this is good evidence for tidal spin-up of the host star by the planet.

5

We take the dividing line between K-type and G-type dwarfs to be 0.8 M⊙ in mass or Teff = 5300 K.

Acknowledgments

J.S. acknowledges financial support from the Science and Technology Facilities Council (STFC) in the form of an Advanced Fellowship. A.M.S. is supported by the MICINN ESP2013-41268-R grant and the Generalitat of Catalunya program SGR-1458. PM is grateful to Prof. Rob Jeffries for discussions about the lack of X-ray flux from the companion to CoRoT-2. We thank the referee for their careful reading of the manuscript and comments that have helped to improve this paper.

References

  1. Aigrain, S., Collier Cameron, A., Ollivier, M., et al. 2008, A&A, 488, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
  3. Anderson, D. R., Collier Cameron, A., Gillon, M., et al. 2012, MNRAS, 422, 1988 [NASA ADS] [CrossRef] [Google Scholar]
  4. Anderson, D. R., Collier Cameron, A., Delrez, L., et al. 2014, MNRAS, 445, 1114 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bakos, G. Á., Torres, G., Pál, A., et al. 2010, ApJ, 710, 1724 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bakos, G. Á., Hartman, J., Torres, G., et al. 2011, ApJ, 742, 116 [NASA ADS] [CrossRef] [Google Scholar]
  7. Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
  8. Barnes, S. A. 2010, ApJ, 722, 222 [NASA ADS] [CrossRef] [Google Scholar]
  9. Barnes, S. A., & Kim, Y.-C. 2010, ApJ, 721, 675 [NASA ADS] [CrossRef] [Google Scholar]
  10. Barros, S. C. C., Boué, G., Gibson, N. P., et al. 2013, MNRAS, 430, 3032 [NASA ADS] [CrossRef] [Google Scholar]
  11. Barros, S. C. C., Almenara, J. M., Deleuil, M., et al. 2014, A&A, 569, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Béky, B., Holman, M. J., Kipping, D. M., & Noyes, R. W. 2014, ApJ, 788, 1 [NASA ADS] [CrossRef] [Google Scholar]
  13. Boyajian, T. S., von Braun, K., van Belle, G., et al. 2013, ApJ, 771, 40 [NASA ADS] [CrossRef] [Google Scholar]
  14. Brown, D. J. A. 2014, MNRAS, 442, 1844 [NASA ADS] [CrossRef] [Google Scholar]
  15. Brown, D. J. A., Anderson, D. R., Armstrong, D. J., et al. 2014, ArXiv e-prints [arXiv:1412.7761] [Google Scholar]
  16. Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
  17. Cabrera, J., Bruntt, H., Ollivier, M., et al. 2010, A&A, 522, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Chabrier, G., Gallardo, J., & Baraffe, I. 2007, A&A, 472, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Christensen-Dalsgaard, J., Kjeldsen, H., Brown, T. M., et al. 2010, ApJ, 713, L164 [NASA ADS] [CrossRef] [Google Scholar]
  20. Christian, D. J., Gibson, N. P., Simpson, E. K., et al. 2009, MNRAS, 392, 1585 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cojocaru, R., Torres, S., Isern, J., & García-Berro, E. 2014, A&A, 566, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Damiani, C., & Lanza, A. F. 2015, A&A, 574, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Deming, D., Sada, P. V., Jackson, B., et al. 2011, ApJ, 740, 33 [NASA ADS] [CrossRef] [Google Scholar]
  24. Dragomir, D., Matthews, J. M., Winn, J. N., & Rowe, J. F. 2014, in IAU Symp. 293, ed. N. Haghighipour, 52 [Google Scholar]
  25. Droege, T. F., Albertson, C., Gombert, G., et al. 1997, BAAS, 29, 818 [NASA ADS] [Google Scholar]
  26. Epstein, C. R., & Pinsonneault, M. H. 2014, ApJ, 780, 159 [NASA ADS] [CrossRef] [Google Scholar]
  27. Fabrycky, D. C., Ford, E. B., Steffen, J. H., et al. 2012, ApJ, 750, 114 [NASA ADS] [CrossRef] [Google Scholar]
  28. Feiden, G. A., & Chaboyer, B. 2013, ApJ, 779, 183 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fridlund, M., Hébrard, G., Alonso, R., et al. 2010, A&A, 512, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Gillon, M., Doyle, A. P., Lendl, M., et al. 2011, A&A, 533, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Goodman, J., & Lackner, C. 2009, ApJ, 696, 2054 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hébrard, G., Evans, T. M., Alonso, R., et al. 2011, A&A, 533, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2014, AJ, submitted, ArXiv e-prints [arXiv:1410.6358] [Google Scholar]
  34. Henry, G. W., & Winn, J. N. 2008, AJ, 135, 68 [NASA ADS] [CrossRef] [Google Scholar]
  35. Henry, G. W., Baliunas, S. L., Donahue, R. A., Fekel, F. C., & Soon, W. 2000, ApJ, 531, 415 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [NASA ADS] [CrossRef] [Google Scholar]
  37. Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
  38. Hoxie, D. T. 1973, A&A, 26, 437 [NASA ADS] [Google Scholar]
  39. Huber, D., Chaplin, W. J., Christensen-Dalsgaard, J., et al. 2013, ApJ, 767, 127 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 Km s-1 grid. Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
  41. Lanza, A. F. 2010, A&A, 512, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Lanza, A. F., Pagano, I., Leto, G., et al. 2009, A&A, 493, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Lanza, A. F., Bonomo, A. S., Moutou, C., et al. 2010, A&A, 520, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. López-Morales, M. 2007, ApJ, 660, 732 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ludwig, H.-G., Caffau, E., & Kučinskas, A. 2008, in IAU Symp. 252, eds. L. Deng, & K. L. Chan, 75 [Google Scholar]
  46. Mancini, L., Ciceri, S., Chen, G., et al. 2013, MNRAS, 436, 2 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mancini, L., Southworth, J., Ciceri, S., et al. 2014, MNRAS, 443, 2391 [NASA ADS] [CrossRef] [Google Scholar]
  48. Maxted, P. F. L., Anderson, D. R., Collier Cameron, A., et al. 2011, PASP, 123, 547 [NASA ADS] [CrossRef] [Google Scholar]
  49. Maxted, P. F. L., Anderson, D. R., Collier Cameron, A., et al. 2013, PASP, 125, 48 [NASA ADS] [CrossRef] [Google Scholar]
  50. Maxted, P. F. L., Serenelli, A. M., & Southworth, J. 2015, A&A, 575, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Meibom, S., Barnes, S. A., Platais, I., et al. 2015, Nature, 517, 589 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  52. Mohler-Fischer, M., Mancini, L., Hartman, J. D., et al. 2013, A&A, 558, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Mortier, A., Santos, N. C., Sousa, S. G., et al. 2013, A&A, 558, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Muiños, J. L., & Evans, D. W. 2014, Astron. Nachr., 335, 367 [NASA ADS] [CrossRef] [Google Scholar]
  55. Müller, H. M., Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Ogilvie, G. I. 2014, ARA&A, 52, 171 [Google Scholar]
  57. Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
  58. Pont, F. 2009, MNRAS, 396, 1789 [NASA ADS] [CrossRef] [Google Scholar]
  59. Poppenhaeger, K., & Wolk, S. J. 2014, A&A, 565, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Popper, D. M. 1997, AJ, 114, 1195 [NASA ADS] [CrossRef] [Google Scholar]
  61. Sanchis-Ojeda, R., & Winn, J. N. 2011, ApJ, 743, 61 [NASA ADS] [CrossRef] [Google Scholar]
  62. Sanchis-Ojeda, R., Winn, J. N., Holman, M. J., et al. 2011, ApJ, 733, 127 [NASA ADS] [CrossRef] [Google Scholar]
  63. Sanchis-Ojeda, R., Winn, J. N., Marcy, G. W., et al. 2012, Nature, 487, 449 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  64. Sanchis-Ojeda, R., Winn, J. N., Marcy, G. W., et al. 2013, ApJ, 775, 54 [NASA ADS] [CrossRef] [Google Scholar]
  65. Schröter, S., Czesla, S., Wolter, U., et al. 2011, A&A, 532, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
  67. Serenelli, A. M., Bergemann, M., Ruchti, G., & Casagrande, L. 2013, MNRAS, 429, 3645 [NASA ADS] [CrossRef] [Google Scholar]
  68. Sestito, P., & Randich, S. 2005, A&A, 442, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Silva-Valio, A. 2008, ApJ, 683, L179 [NASA ADS] [CrossRef] [Google Scholar]
  70. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  71. Smith, A. M. S., Hebb, L., Collier Cameron, A., et al. 2009, MNRAS, 398, 1827 [NASA ADS] [CrossRef] [Google Scholar]
  72. Southworth, J. 2010, MNRAS, 408, 1689 [NASA ADS] [CrossRef] [Google Scholar]
  73. Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
  74. Southworth, J. 2012, MNRAS, 426, 1291 [NASA ADS] [CrossRef] [Google Scholar]
  75. Spada, F., Demarque, P., Kim, Y.-C., & Sills, A. 2013, ApJ, 776, 87 [NASA ADS] [CrossRef] [Google Scholar]
  76. Steigman, G. 2010, J. Cosmol. Astropart. Phys., 4, 29 [Google Scholar]
  77. The DENIS Consortium. 2005, VizieR Online Data Catalog: II/263 [Google Scholar]
  78. Torres, G., Fischer, D. A., Sozzetti, A., et al. 2012, ApJ, 757, 161 [NASA ADS] [CrossRef] [Google Scholar]
  79. Tregloan-Reed, J., & Southworth, J. 2013, MNRAS, 431, 966 [NASA ADS] [CrossRef] [Google Scholar]
  80. Tregloan-Reed, J., Southworth, J., & Tappert, C. 2013, MNRAS, 428, 3671 [NASA ADS] [CrossRef] [Google Scholar]
  81. Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  82. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [NASA ADS] [CrossRef] [Google Scholar]
  84. Zacharias, N., Monet, D. G., Levine, S. E., et al. 2004, BAAS, 36, 1418 [Google Scholar]
  85. Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
  86. Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]

All Tables

Table 1

Observed properties of stars in our sample.

In the text
Table 2

Periodogram analysis of the WASP light curves for WASP-5.

In the text
Table 3

Bayesian mass and age estimates for the host stars of transiting extrasolar planets using garstec stellar models assuming αMLT = 1.78.

In the text
Table 4

Stellar ages estimated using our stellar models, τiso, and using gyrochronology, τgyro, and the probability pτ = P(τgyro>τiso).

In the text
Table 5

Independent measurements of the mean density (ρ⋆), effective temperature (Teff) and metallicity ([Fe/H]) for HAT-P-11 and their weighted mean values.

In the text

All Figures

thumbnail Fig. 1

WASP photometry for HAT-P-21 plotted as a function of rotation phase assuming Prot = 15.9 d.

In the text
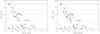thumbnail Fig. 2

Change in the best-fitting masses and ages of transiting exoplanet host stars due to a change in the assumed helium abundance or mixing length parameter. Dots show the best-fitting mass and age for the default values of Y and αMLT and lines show the change in mass and age due to an increase in helium abundance ΔY = +0.02 (left panel) or a change in mixing length parameter ΔαMLT = −0.2 (right panel). Horizontal lines indicate the age of the Galactic disc (dashed), the age of the Universe (dotted) and the highest age in our grid of stellar models (solid). The curved dotted line shows the terminal age main sequence (TAMS) for stars with solar composition.

In the text
thumbnail Fig. 3

Left panel: joint posterior distribution for the mass and age of CoRoT-13 estimated by our isochrone fitting technique. Right panel: joint posterior distribution for the age of CoRoT-13 estimated by our isochrone fitting technique and using gyrochronology. For clarity, only 10% of the points from the Markov chain are plotted.
In the text
thumbnail Fig. 4

Comparison of gyrochronological age estimates (τgyro) to isochronal age estimates (τiso) for planet host stars with measured rotation periods. Points with error bars indicate the mean and standard deviation of the posterior age distribution. The straight line is the relation τgyro = τiso.

In the text
thumbnail Fig. 5

Gyrochronological age estimates as a function of log (τtidal), a very approximate estimate of the time scale for tidal interaction between the star and the innermost planetary companion. We note that the time scale for tidal interactions is uncertain by a few orders of magnitude. Systems with significant differences between τiso and τgyro (p< 0.05) are plotted with filled symbols. 55 Cnc (τiso ≈ 9 Gyr, log (τtidal/ y) ≈ 13) is not shown here.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.