| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 18 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201425455 | |
| Published online | 07 May 2015 | |
Deep SDSS optical spectroscopy of distant halo stars
II. Iron, calcium, and magnesium abundances⋆,⋆⋆
1 Instituto de Astrofísica de Canarias, vía Láctea, 38205 La Laguna, Tenerife Spain
e-mail: emmafa_ext@iac.es
2 Universidad de La Laguna, Departamento de Astrofísica, 38206 La Laguna, Tenerife, Spain
3 Research School of Astronomy and Astrophysics, The Australian National University, ACT 2611 Weston, Australia
4 Department of Physics and JINA Center for the Evolution of the Elements, University of Notre Dame, Notre Dame, IN 46556, USA
5 Institut Utinam, CNRS UMR6213, Université de Franche-Comté, Observatoire de Besançon, 25000 Besançon, France
6 Department of Astronomy and Astrophysics, The Pennsylvania State University, University Park, PA 16802, USA
7 Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA
8 Department of Astronomy and Space Science, Chungnam National University, 305-764 Daejeon, Republic of Korea
9 Apache Point Observatory, PO Box 59, Sunspot, NM 88349-0059, USA
Received: 3 December 2014
Accepted: 20 February 2015
Aims. We analyze a sample of 3944 low-resolution (R ~ 2000) optical spectra from the Sloan Digital Sky Survey (SDSS), focusing on stars with effective temperatures 5800 ≤ Teff ≤ 6300 K, and distances from the Milky Way plane in excess of 5 kpc, and determine their abundances of Fe, Ca, and Mg.
Methods. We followed the same methodology as in the previous paper in this series, deriving atmospheric parameters by χ2 minimization, but this time we obtained the abundances of individual elements by fitting their associated spectral lines. Distances were calculated from absolute magnitudes obtained by a statistical comparison of our stellar parameters with stellar-evolution models.
Results. The observations reveal a decrease in the abundances of iron, calcium, and magnesium at large distances from the Galactic center. The median abundances for the halo stars analyzed are fairly constant up to a Galactocentric distance r ~ 20 kpc, rapidly decrease between r ~ 20 and r ~ 40 kpc, and flatten out to significantly lower values at larger distances, consistent with previous studies. In addition, we examine [Ca/Fe] and [Mg/Fe] as a function of [Fe/H] and Galactocentric distance. Our results show that the most distant parts of the halo show a steeper variation of [Ca/Fe] and [Mg/Fe] with iron. We found that at the range −1.6 < [Fe/H] < −0.4, [Ca/Fe] decreases with distance, in agreement with earlier results based on local stars. However, the opposite trend is apparent for [Mg/Fe]. Our conclusion that the outer regions of the halo are more metal-poor than the inner regions, based on in situ observations of distant stars, agrees with recent results based on inferences from the kinematics of more local stars, and with predictions of recent galaxy formation simulations for galaxies similar to the Milky Way.
Key words: Galaxy: halo / Galaxy: abundances / Galaxy: structure
Table 1 and beginning of Tables 2 and 3 are available in electronic form at http://www.aanda.org
Full Tables 2 and 3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/577/A81
© ESO, 2015
1. Introduction
In the half century since metal-poor stars were identified in the halo of the Galaxy (Chamberlain & Aller 1951), a great deal of effort has been devoted to clarifying their origin, detailed chemical abundance patterns, and observed kinematics (Beers & Christlieb 2005; Ivezić et al. 2012; Frebel & Norris 2013). One long standing debate was focused on whether the Galaxy was formed from the monolithic collapse of a protogalactic cloud (Eggen et al. 1962) or assembled from smaller substructures (Press & Schechter 1974; Searle & Zinn 1978). The current Λ-cold dark matter (Λ-CDM) scenario predicts that large galaxies, such as the Milky Way, formed hierarchically. If the Galactic halo formed from accreted subsystems, at least some spatial and kinematical substructures are expected to be observable (Helmi 2008; Klement 2010). This appears to be the case for the outer regions of the Galaxy, but the same scenario may not apply to the inner regions (Bell et al. 2008, 2010; Schlaufman et al. 2009, 2011, 2012, and references therein; Xue et al. 2011), which are expected to be more completely phase-mixed.
Chemical tagging of the Galaxy’s building blocks (Freeman & Bland-Hawthorn 2002) could provide important information about the evolution of the different components of the Milky Way. In particular, differences in the observed [α-element/Fe] for halo stars could be explained in terms of the different star-formation histories of the progenitor subgalactic systems that contributed the stars found in the halo today. Type-II SNe produce α-elements and iron, and explode on short timescales (~107 yr). Type-Ia SNe are thought to be the primary contributors to the iron abundance in the interstellar medium, but their evolutionary time scales are much longer (~109 yr).
During the past decade a number of authors have reported the possible existence of a dichotomy in the abundances of halo stars in the solar neighborhood, often related with their observed kinematics. Fulbright (2002), for example, found a correlation between the observed space velocities of a relatively small sample of stars (with metallicities in the range −2.0 ≤ [Fe/H] < −1.0) and their [α/Fe]; stars with lower [α/Fe] were argued to be associated with faster space motions. Gratton et al. (2003) reported that the stars in their sample with substantial prograde rotation about the Galactic center exhibited higher [α/Fe] than those with small or retrograde rotation, as confirmed later by Jonsell et al. (2005). Ishigaki et al. (2010) found that in the metallicity range −2 < [Fe/H] < − 1, stars on orbits reaching a maximum distance from the Galactic plane | Z | > 5 kpc possess [Mg/Fe] ~ 0.1 dex lower than those that only reach |Z| < 5 kpc.
The results of Nissen & Schuster (2010, 2011) reinforced the claims that there are (at least) two distinct stellar populations in the halo. Based on high-resolution spectroscopy of a very local sample of moderately low-metallicity stars, −1.6 < [Fe/H] < − 0.4, these authors observed two different trends in the [α/Fe] with metallicity, one higher and flatter, and the other comprising stars with lower mean [α/Fe] and a steeper slope, associated with stars having a higher velocity dispersion. Their suggested interpretation calls for an inner, old, flattened high α-element population with a prograde rotation, formed during a phase of dissipative collapse, and an outer, slightly younger spherical population, exhibiting counter-rotation, with lower values of [α/Fe], and presumably accreted from (relatively massive) dwarf-like galaxies.
These previous samples included relatively small numbers of stars, exploring a limited range of metallicity and kinematic phase-space. Recent spectroscopic surveys have been able to provide more comprehensive results based on their dramatically larger samples of stars. For example, the Sloan Digital Sky Survey (SDSS: York et al. 2000), in operation since 2000, and its extensions (SDSS-II: Abazajian et al. 2009; SDSS-III: Eisenstein et al. 2011), includes the stellar-specific program SEGUE-1 (Sloan Extension for Galactic Understanding and Exploration; Yanny et al. 2009), which was later extended with SEGUE-2. The total number of low-resolution stellar spectra gathered by SDSS and SEGUE is on the order of 750 000. The stars used for flux calibration are of particular interest because they were observed for every plug-plate and thereby benefit from the dense tiling of the SDSS footprint.
Carollo et al. (2007, 2010; see also Beers et al. 2012) made use of the calibration stars available at the time to separate the halo into (at least) two stellar populations, with clearly different spatial-density profiles, stellar orbits, and metallicity distribution functions, which they referred to as the inner-halo and outer-halo populations. According to their interpretation, the inner-halo population formed as the result of the dissipational mergers of (relatively more massive) subgalactic fragments, while the outer-halo population formed from dissipationless mergers of (relatively less massive) fragments. Their results have found observational support from analyses of photometric samples of SDSS stars (which are not subject to possible target-selection biases in the spectroscopic samples) in the work of de Jong et al. (2010) and An et al. (2013).
Of key importance in the analysis of Carollo et al. is the derivation of kinematical properties for the entire halo from a relatively local sample of calibration stars (d ≤ 4 kpc), for which reasonably accurate proper motions could be obtained. The distance estimates that they employed and used in concert with the observed radial velocities and proper motions to derive space motions have been criticized by Schönrich et al. (2011, 2014), who called into question their inferred division of the halo into inner and outer components. Beers et al. (2012) rejected this claim and presented additional evidence in support of the case for the dual halo.
To resolve this situation, and independent evaluation based on an in situ halo sample can shed light on the matter. In the present series of papers we conduct such an analysis, based on the original SDSS/SEGUE supplemented by new spectra obtained as in the course of the Baryon Oscillations Spectroscopic Survey (BOSS: Dawson et al. 2013), which is part of SDSS-III. In Paper I of this series (Allende Prieto et al. 2014), we analyzed a sample of the spectrophotometric calibration stars, including targets at large distances (in excess of 10 kpc) at high Galactic latitudes observed in BOSS. Stellar parameters and metallicity were derived, providing a first look at the in situ metallicity distribution function of halo stars from the deepest analysis yet obtained. Here we extend this sample and derive not only [Fe/H] from iron lines, but also abundances for two α-elements, [Ca/H] and [Mg/H]. In Sect. 2 we describe our sample. Section 3 explains our methodology and verifies the accuracy of the derived parameters. Our results are summarized in Sect. 4, followed by a discussion and conclusions in Sect. 5.
2. Observations
We employed stellar spectra from the tenth SDSS data release (DR10; Ahn et al. 2014), which contains SEGUE-1 and SEGUE-2 data, calibration stars from earlier SDSS observations, and those taken over the last four years as part of BOSS. The spectra were obtained with the 2.5 m telescope at Apache Point Observatory (Gunn et al. 2006), using a pair of double spectrographs connected to 640 (SDSS, SEGUE-1, SEGUE-2) or 1000 optical fibers (BOSS; see Smee et al. 2013), as explained in more detail in Paper I.
SEGUE-1 was conceived to explore the different stellar populations of the Galaxy, in particular to study the chemistry and kinematics of the spatial substructure found in the stellar halo from photometry in the original SDSS program. Stars at large distances (tens of kpc) were observed over a broad range of apparent magnitude (14.0 <g< 20.3) and Galactic latitude in order to extensively cover the large structures. A wide range of spectral types were included, from F/G, G, dK, dM, and type-L brown dwarfs, including a substantial number of thick-disk stars in the solar neighborhood. SEGUE-2 concentrated primarily on halo stars, increasing the number of red giant-branch (RGB) stars and blue horizontal-branch (BHB) stars, reaching distances of up to 100 kpc from the Sun. The spectra have low resolution, R ≡ λ/FWHM(λ) vary over 1500 <R< 2500, and cover the wavelength range 3900 Å <λ< 9000 Å.
The BOSS spectrophotometric calibration stars are mainly halo main-sequence turnoff (MSTO) stars at high Galactic latitudes and reach large distances into the halo, up to 100 kpc in some cases. They were obtained using an upgraded version of the spectrographs that resulted in increased sensitivity, an enlarged wavelength coverage (3600 <λ< 10 000 Å), and a resolution similar to the original spectrographs.
3. Analysis
The goal of this work is to investigate the observed distribution of the abundances of several elements in the Galaxy halo, in particular Fe, Ca, and Mg. Our strategy, following the work described in Paper I, is to determine these abundances from stars observed in situ and to examine how they vary as a function of distance. In addition, we study the [Ca/Fe] and [Mg/Fe] as a function of metallicity and distance from the center of the Galaxy, r, to examine whether different trends are detected throughout the halo.
3.1. Determining abundances
We determined the abundance of an element following the techniques explained in Paper I, which employ an updated version of the code FERRE1 (Allende Prieto et al. 2006). This code searches for the model spectrum in an n-dimensional grid of synthetic spectra that best fits the observed spectrum, using χ2 as the merit function and interpolating with a Bezier scheme. The search returns the values of the stellar atmospheric parameters of this synthetic spectrum. It is possible to fix some of these values before starting, so that the search is limited to the parameters of interest.
The analysis performed in Paper I used the entire spectrum in the fit to determine the atmospheric parameters (effective temperature Teff, surface gravity in logarithmic units log g, and metallicity [M/H]2). In the case of metallicity, the fit of the entire spectrum implies that several elements are involved in its determination. For example, at low metallicities, the Ca II resonance doublet and the Mg Ib triplet at 5180 Å are the main contributors to the metallicity determination, since they are the strongest features. However, if we only fit iron lines, we achieve a more direct, and provided they are measurable, more reliable determination of the iron abundance. Moreover, as the abundances of all the elements scale with the iron abundance in the generation of the synthetic spectra (for the α-elements an increase at low metallicities is taken into account – see Paper I), searching for metallicity by fitting lines that belong to other elements permits determining their abundances. In this manner, we determined estimates of the Fe, Ca and Mg abundances. Note that a different relation between the abundances of the elements in the composition of a star would affect the opacities and the equation of state, making this approximation fail. However, this does not seem the case for most of our program stars, and will not affect our statistical results.
We performed an analysis of our sample (BOSS spectra and all previous optical SDSS spectra that satisfied the condition of having a redshift | z | ≤ 10-2, 55 401 from BOSS and 645 354 from SDSS/SEGUE), using a grid of synthetic spectra covering the following stellar parameters and metallicity ranges: 4750 K <Teff< 6500 K, 0.5 < log g< 4.5 and −5.0 < [Fe/H] < + 0.5. This is the same grid as described in Paper I. We selected objects that were assigned an effective temperature between 5800 and 6300 K and χ2< 10 in this first analysis. Because of the systematic errors identified in Paper I for low gravity stars, we only considered stars with log g> 2.5. This includes 50 252 from BOSS and 95 536 from SDSS/SEGUE. To measure the chemical abundances of Fe and the two α-elements, Ca and Mg, we performed a second analysis in which we fit features dominated by transitions of a single element at a time, fixing Teff and log g to the values obtained in the first analysis.
We chose the most suitable Fe, Ca, and Mg lines to derive the corresponding abundances by identifying which features are most sensitive to abundance changes and were measurable at low spectral resolution. The sensitivity was determined by calculating the ratio between two synthetic spectra, generated for a given set of values for the effective temperature, gravity, and metallicity, but with a difference of 0.1 dex in the abundance of Fe, Ca, or Mg. For this test, we adopted Teff = 6000 K, log g = 4.0, and [Fe/H] = − 1.0. The ratio indicates the features with the highest sensitivity to a given abundance change. Figure 1 shows some of the most relevant lines used to derive the abundance of each element. Our analysis used the same model grid as in Paper I, but we selected only the specified regions that are most sensitive to the individual abundances.
 |
Fig. 1 Fit of the regions for two example spectra (with atmospheric parameters Teff = 6078 K, log g = 4.4, and [Fe/H] = − 1.4 and Teff = 6023 K, log g = 3.7, and [Fe/H] = − 1.6) that contains some of the Fe, Ca, and Mg lines that contribute most to the determination of their abundances. The red line corresponds to the fit spectrum, plotted over the observed spectrum (in black). The panels on the left show an spectrum with a S/N ~ 60; the panels on the right correspond to a spectrum with the median S/N of the data, ~30. |
In the case of Fe and Ca, several regions are sufficiently sensitive for use in deriving accurate abundance estimates. Although lines in the blue portion of the spectrum tend to show higher sensitivity, some lines in the red were chosen and analyzed as well. We performed several analyses, fitting one of the selected regions in isolation, and another fitting all the regions together. In the first case, the continuum was determined by dividing each region by its mean, and the fit was performed by calculating the χ2 using only a percentage of the region that includes the lines of interest and avoiding others that do not belong to the element. In the latter, these lines of interest were fit over the spectrum normalized as explained in Paper I, that is, by splitting the spectra into 200 Å bins and dividing the fluxes in each bin by the mean values. In Table 1 we list the selected spectral regions, the dominant lines in the regions, and the percentage of each region that was fit. We only considered estimates for which χ2<10, as in the analysis of the full spectrum, and a signal-to-noise ratio higher than 20, considering the median value of this ratio in the available spectral range. The comparison of the results obtained for each short region containing one or a few lines with the results obtained by fitting all of the lines simultaneously throughout the spectrum simultaneously (Figs. 2 and 3) provides the means to estimate the uncertainties in our determinations and a way to identify which regions in the spectrum contribute the most to the derivation of the abundance of a given element. For Mg, we performed only one analysis, fitting the blend of the MgH band at about 5140 Å and the Mg Ib triplet at ~5165–5190 Å.
 |
Fig. 2 Correlation between the values of [Fe/H] obtained by fitting different spectral regions containing Fe lines, compared with the estimation obtained by fitting all of the selected lines together. The bluest regions best contribute to the determination of [Fe/H], with rms values lower than 0.2 dex. The results of the fitting line for the four reddest regions exhibit little correlation with estimates using all of the regions simultaneously. |
 |
Fig. 3 Correlation of the [Ca/H] results calculated for a sample of 61 591 stars, using different spectral regions containing Ca lines (neutral and/or ionized), compared with the estimation obtained by fitting all of the selected lines together. The CaII lines are the most sensitive to changes in the abundance of calcium, in particular the Ca HK doublet, hence they are the primary features used. Of the neutral lines, the CaI line at 4226.73 Å is the most relevant. |
Figure 2 includes results for the SEGUE-1 and SEGUE-2 samples and earlier SDSS stellar spectra. This figure compares the iron abundance estimates from the fit of only one of the selected regions with the results obtained by fitting all the regions together for a sample of 46 065 objects. Inspection of this figure indicates that the Fe lines that contribute the most to determining [Fe/H] are those in the range of 5220–5350 Å, with a standard deviation σ ~ 0.13 dex. Two other windows exhibit a σ lower than 0.20 dex, but the results for the four reddest regions show little correlation with the [Fe/H] values obtained using all the windows together. However, we have verified by comparing with the [M/H] values obtained in Paper I that the estimates including all of the regions in the fitting are slightly more precise than those considering only one or a few of them, obtaining an offset of 0.11 dex and σ = 0.14 dex, whereas an analysis excluding the four reddest regions shows an offset of 0.13 dex and σ = 0.14 dex. For Ca (see Fig. 3) the CaII lines are the main contributors in determining [Ca/H], with rms deviations lower than 0.05 dex compared with measurements from all the calcium lines. Fitting only neutral lines results in an rms deviation of 0.20 dex, which increases at low metallicity. The most relevant feature of the neutral lines is the CaI line at 4226.73 Å.
 |
Fig. 4 Comparison of the [Fe/H], [Ca/H], and [Mg/H] estimates from SDSS/SEGUE and BOSS stars obtained by fitting individual lines with the metallicity results determined in Paper I, [M/H], which considered the entire spectrum in the analysis. The mean difference between x and y axes appears in the top left corner of each panel, evaluated in three ranges of [M/H]: [M/H] > −1.5, −2 < [M/H] < −1.5, and [M/H] < −2, and the corresponding standard deviations are written in the bottom right corner. The top panels show good agreement between [Fe/H] inferred from individual lines of this element, with an offset of ~0.1 dex. [Ca/H] estimates are offset by ~0.4 dex over [M/H], except at metallicities higher than [M/H] = −1.5, as expected. [Mg/H] estimates display a higher dispersion, increasing with decreasing metallicity, and lower deviations for BOSS stars with respect to SDSS/SEGUE stars. |
We now examine correlations of [Fe/H], [Ca/H] and [Mg/H] with the global metallicity, [M/H], derived in Paper I, which was calculated by fitting the entire spectrum. The top panels in Fig. 4 reveal an offset of about 0.1 dex between the overall metallicity [M/H] and the iron abundances inferred exclusively from iron lines, with a dispersion that increases at low metallicities. The values of [Ca/H] are offset by about 0.4 dex over [M/H], except at metallicities higher than [M/H] = − 1.5, as expected for metal-poor stars. Conversely, the [Mg/H] estimates exhibit a higher dispersion, increasing as the metallicity decreases. The BOSS and SDSS/SEGUE stars exhibit similar behaviors. However, the dispersion in [Fe/H] for the BOSS stars is lower for [M/H] < −2.0, and the [Mg/H] determinations in BOSS spectra exhibit deviations with respect to [M/H] that are significantly lower than for SDSS/SEGUE stars, approaching zero for stars with [M/H] < − 2.0.
3.2. Determining distances
To explore possible variations of the chemical trends with distance, we estimated the distances for each star from the Galactic plane and from the Galactic center. To obtain the distance from the Sun, d, we first derived the absolute magnitude, MV, following Allende Prieto et al. (2006). In this approach, the probability of a given star to have the adopted values of Teff, log g, and [Fe/H] is calculated by comparing it with a set of isochrones (e.g., Bertelli et al. 1994). Using this value of MV, we calculated the distance from the equation 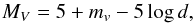 (1)where mv is the dereddened apparent magnitude V, determined from the relationship (Zhao & Newberg 2006)
(1)where mv is the dereddened apparent magnitude V, determined from the relationship (Zhao & Newberg 2006) 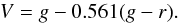 (2)The Galactocentric distance, r, was calculated using
(2)The Galactocentric distance, r, was calculated using 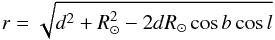 (3)and the distance from the plane, Z,
(3)and the distance from the plane, Z, 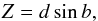 (4)adopting R⊙ = 8 kpc (Bovy et al. 2009).
(4)adopting R⊙ = 8 kpc (Bovy et al. 2009).
We evaluated the reliability of our results using distances estimated following other methods. A first validation was obtained by comparing with 10 Gyr empirically-calibrated YREC isochrones (An et al. 2009). Then, after identifying the closest isochrone in [Fe/H], they were matched in g − r color to obtain the ugriz absolute values, and comparing them with the corresponding isochrones from DR10. This method was designed by Schlesinger et al. (2012) for main-sequence stars, so we used it to verify distances corresponding to stars with log g > 4.1, ensuring they are dwarf stars. Another estimate of the distances for main-sequence stars was obtained using the photometric parallax relationship from Ivezic et al. (2008). We performed these tests for a subsample of SDSS/SEGUE stars with 4.1 < log g < 4.4, in our range of Teff (16 760 objects). The correlations of our estimates and these alternative approaches for dwarf stars are shown in the top panels of Fig. 5. They agree fairly well, although our results tend to be slightly lower, with a mean offset not greater than 0.6 kpc, and a dispersion ~1 kpc. The agreement is better with Schlesinger et al., probably because the YREC isochrones were designed to work with SEGUE data, while the photometric parallax relationship from Ivezic et al. (2008) requires a conversion from the Johnson-Cousins system to ugriz, increasing the uncertainties in the distance estimation (see Appendix B in Schlesinger et al. 2012).
 |
Fig. 5 Comparison of distances to the Sun (for pre-BOSS stars), d, calculated using the methodology followed in this work. The top left panel corresponds to the comparison of stars with 4.1 < log g< 4.4 and −2.0 < [Fe/H] < − 0.4, with distances calculated using the approach described by Schlesinger et al. (2012; see text). The top right panel shows distance estimates for the same sample following Ivezic et al. (2008). In the bottom left panel, distances based on parallaxes from the Hipparcos satellite are compared with our estimates for a sample of turn-off and giant stars with stellar parameters and metallicities from Ramirez et al. (2013) with 2.5 < log g< 4.1. The bottom right panel shows the comparison of distances calculated for a sample of SEGUE giants with 2.5 < log g< 3.5, compared with those obtained by Xue et al. (2014). Objects at | Z | > 5 kpc, calculated from our distance estimations, as well as their statistics, are shown in red. |
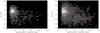 |
Fig. 6 Median [Fe/H] values, as a function of Galactocentric distance, r, shown as a Hess diagram that displays the relative density of stars for each bin of width 0.25 dex in [Fe/H] and 2.5 kpc in distance. The orange points with their error bars summarize the median values of the analyzed set of data with distance. The left panel corresponds to the BOSS F-type spectrophotometric calibration stars, and the right panel to the full SDSS/SEGUE sample (limited to the range described in Sect. 3.1, considering only stars with |Z| > 5 kpc). A clear gradient in [Fe/H], decreasing with distance, is seen for both samples. |
We also validated our methodology for giant stars by analyzing a sample of 120 stars from Ramirez et al. (2013), who determined stellar parameters for the stars in their sample for which Hipparcos parallaxes were available. The comparison is shown in the bottom left panel of Fig. 5 for stars with 2.5 < log g < 4.1 and effective temperature 5800 < Teff < 6300 K. The agreement is excellent. The formal comparison has essentially a zero offset and a σ ~ 0.004 kpc.
Finally, we derived distances using the parameters of the SEGUE Stellar Parameter Pipeline (SSPP; Lee et al. 2008a,b, 2011; Allende Prieto et al. 2008; Smolinski et al. 2011) from the sample of red giants analyzed by Xue et al. (2014), considering those with 2.5 < log g < 3.5 (493 objects), and comparing with their derived distance estimates (although their effective temperatures are somewhat lower than the range we are considering). The agreement is decent, but the dispersion (~7 kpc) increases with distance, and our estimates tend to be somewhat higher, as shown in the bottom right panel of Fig. 5.
The distances derived for our sample are listed in Tables 2 and 3. It is worthwhile to note that although in some cases the estimated errors are significant, a more restrictive selection limited to relative errors smaller than 50% does not change the results. For this reason we decided to include the entire sample. Our distance estimation code, get_amrv.pro, written in IDL, together with a file including a finely resampled version of the isochrones of Bertelli et al. is now publicly available on the web3.
 |
Fig. 7 Distribution of the median [Fe/H] vs. r, after splitting the SDSS/SEGUE sample into the target-selection categories with more than 50 stars, located at distances from near the center to up to beyond 20 kpc (www.sdss3.org/dr9/spectra/targets.php). Overall, the metallicity decreases with distance the profile depends on the category considered, however. |
4. Results
4.1. [Fe/H] vs. distance
Using the abundances and distances for our sample of stars, we now consider how [Fe/H] varies with distance from the center of the Galaxy, r. We determined the median value of [Fe/H] in 5 kpc distance bins, except when this range does not include at least 50 stars, in which case the bin was extended to cover the distance range needed to ensure this minimum number of data points. We first calculated the median value of the distance for stars in each bin. We selected only estimates with errors lower than the dispersion known for the halo, 0.5 dex (Allende Prieto et al. 2006; Paper I). Assuming that the errors in our estimates follow a Gaussian distribution, we calculated the error bars as the median absolute deviation (MAD4) divided by the square root of the number of points. Figure 6 shows the results of the BOSS spectrophotometric calibration stars and the SDSS/SEGUE stars, considering only those at a distance from the plane | Z | > 5 kpc to avoid disk contamination. These samples comprise 1109 objects from BOSS and 2835 from SDSS/SEGUE. The stellar parameters, [Fe/H], [Ca/H] and [Mg/H] abundances and distance estimates are included in Tables 2 and 3. It is clear, in both samples, that a gradient in the average value of [Fe/H] exists in the halo – at large distances the metallicity is clearly lower than closer to the center. However, the trend is not identical in the two cases. At the smallest distances, the iron abundances exhibit a constant value of [Fe/H] ~ − 1.7, begin to decrease at about 20 kpc, and flatten out at about 40 kpc. The SDSS/SEGUE stars appear to have slightly lower values of [Fe/H] at large distances.
 |
Fig. 8 Median values of [Fe/H], in bins of 1.5 kpc, for the XY,XZ, and YZ planes of the Galaxy. There are regions covered by the SDSS/SEGUE sample in the XZ and YZ planes (the BOSS sample is shown in the upper row; the SDSS/SEGUE sample is shown in the lower row) that are only poorly covered by the BOSS sample, in particular at higher [Fe/H]. These stars primarily correspond to r distances between 20 and 40 kpc. |
As noted above, the SDSS/SEGUE sample comprises a number of different target-selection categories, which may be responsible for the slightly different behaviors seen in Fig. 6. To examine this in more detail, we split our SDSS/SEGUE sample into its constituent target categories5, shown in Fig. 7 (those including stars at distances farther than 20 kpc, in order to be able to examine the trend beyond this point). The most abundant categories are the MSTO, metal-poor main-sequence (MPMS), and BHB stars. After applying the same algorithm as before for each subsample, the results exhibit the same decreasing trend of average [Fe/H] with increasing Galactocentric distance (the shapes of the decreasing curves depend on the stars considered). The median [Fe/H] value for BHB stars remains constant up to ~40 kpc, whereas for the MSTO and MPMS stars the metallicity begins to decrease at ~20 kpc, in agreement with the BOSS sample. The SDSS/SEGUE stars reach slightly lower values of [Fe/H] than the spectrophotometric standard stars of the BOSS sample.
Figure 8 displays the spatial distributions of the BOSS and SDSS/SEGUE samples (in this reference system the Sun is at X = + 8 kpc and Z points towards the North Galactic Pole). Inspection of this figure indicates that the SDSS/SEGUE stars cover a more extended range in the different Galactic directions than the BOSS stars. Stars in the transition region under discussion (20 kpc <r<40 kpc) were targeted with far greater density by the SDSS/SEGUE sample.
To test whether our selection criteria in the stellar parameters and colors could produce an artificial gradient, we have considered a simulation of the behavior of [Fe/H] with r, based on the Besançon model of the Galaxy (Czekaj et al. 2014), which assumes no gradient in the halo. We consider a simulation of the Galaxy that includes stars in several directions (those of BOSS plates), reaching distances up to 50 kpc. For each star we have the stellar parameters and metallicity values from the model, to which we added Gaussian noise (according to the errors estimated from the dispersions obtained in Paper I when comparing with the parameters from the SSPP: σTeff = 70 K, σlogg = 0.24 dex, and σ[Fe/H] = 0.11 dex), and calculate the distance following the same methodology as described above. Finally, we selected stars with 5800 K <Teff< 6300 K, 2.5 < log g< 4.4 and | Z | > 5 kpc and applied the color restrictions that apply to the BOSS spectrophotometric standard stars6, MSTO SEGUE stars7, MPMS SEGUE stars8 and the BHB SEGUE stars9. Figure 9 shows the results after applying our algorithm, including the color cuts used for BOSS and SDSS/SEGUE, as well our distance binning. The high-metallicity values at r< 20 kpc indicate that, unlike the observations, stars from the thick-disk component of the model survive to the cut in | Z | at 5 kpc. There were no stars that met the BHB color restrictions, but Fig. 9 demonstrates that for the other three cases these color cuts do not introduce an artificial gradient between 20–40 kpc. The uncertainties in our distance estimations cause oscillations in the median [Fe/H] values: a small decrease at r> 20 kpc and an increase at r> 50 kpc, but these variations are much smaller than what is observed in the analysis of the observed data. The last median value obtained at the largest distances deviates significantly with respect to the previous points and produces a positive gradient. However, this point is determined from few stars (26) and shows a wide dispersion in [Fe/H], unlike what is observed for real data.
 |
Fig. 9 Besançon simulation that reproduces stars in the directions on the sky covered by BOSS. The top panel shows the original simulation; the other three panels correspond to the same stars for the BOSS spectrophotometric sample and the SEGUE MSTO and MPMS target-selection cuts. In all cases we considered stars with atmospheric parameters in the ranges of Teff, log g, and [Fe/H] considered in this work. The plots show [Fe/H] with added noise vs. distance from the Galactic center. Red diamonds represent the resulting median [Fe/H] values (with error bars) after applying our algorithm, considering the distance values from the model. Black dots correspond to the median [Fe/H] results, but considering distances calculated from the stellar parameters and metallicity with added noise. Although uncertainties in distance estimates produce changes in the profile of [Fe/H] vs. r, it can be seen that neither the uncertainties in distance, nor the stellar parameters or the selection criteria considered in each case generate a significant gradient. |
4.2. [Ca/H] and [Mg/H] vs. distance
As described in Sect. 3.1, the calcium and magnesium abundances are estimated by searching for the value of metallicity among the theoretical spectra that best fit transitions of each element. From this value the [X/H] abundance is obtained, taking into account the relation between the iron and α-element abundances adopted in generating the synthetic spectra (see Paper I).
Figure 10 shows the observed [Ca/H] and [Mg/H] trends with Galactrocentric distance. These trends reinforce the conclusion that there exists a chemical gradient in the halo. Although there are some differences between the samples, stars at large distances exhibit lower [Ca/H] and [Mg/H] values. The trend observed for calcium is to decrease from [Ca/H] ~ − 1.2 to [Ca/H] ~ − 1.8 at the largest distances. The larger number of SDSS/SEGUE stars permits a greater number of [Ca/H] bins for the more distant stars, and from these data we conclude that there is a flat trend beyond 40 kpc.
For magnesium, the analysis of the BOSS sample shows a decreasing trend of [Mg/H] values that are ~0.2 dex lower than for SDSS/SEGUE stars at distances shorter than 40 kpc. It exhibits a constant value up to r ~ 20 kpc, and the same flat trend at the largest distances see for [Ca/H], at around the same median value.
 |
Fig. 10 Median [Ca/H] and [Mg/H] abundances as a function of Galactocentric distance, r. The upper panels correspond to the BOSS spectrophotometric sample, while the lower panels are for the SDSS/SEGUE sample. |
4.3. [Ca/Fe] and [Mg/Fe] ratios
Finally, we examine the [Ca/Fe] and [Mg/Fe] abundance ratios resulting from the [Ca/H], [Mg/H] and [Fe/H] estimates. Figure 11 presents the trends of these ratios with Galactocentric distance over four different ranges of metallicity. The observed trends are not identical for the BOSS and SDSS/SEGUE samples, but the results are fairly consistent. For this analysis, we note the small number statistics as a result of dividing the sample into several metallicity bins, especially for the BOSS sample. The figure clearly shows that metal-rich stars are missing at large distances.
For [Ca/Fe], both samples reveal that this ratio tends to become higher as the abundance of [Fe/H] decreases. Although the analysis with BOSS stars returns constant trends, SDSS/SEGUE stars exhibit a decreasing behavior with Galactocentric distance, except at the lowest metallicities, where the trend appears flatter. Similarly, the [Mg/Fe] estimates are lower for stars over the range −1.2 < [Fe/H] < − 0.4 than at lower values of [Fe/H]. At distances larger than 20 kpc it is not possible to distinguish a trend with metallicity. There is a subtle increasing trend with distance, mainly at r< 40 kpc and [Fe/H] > − 2. For this abundance ratio, it is difficult to analyze the outer region of the halo because of the large error bars and the high dispersion in [Mg/H] estimates for more metal-poor stars.
Figure 12 compares the [Ca/Fe] and [Mg/Fe] as a function of [Fe/H], split into three ranges of distance: 0 <r< 20 kpc, 20 <r< 40 kpc, and r> 40 kpc. The median [Fe/H] values were calculated in bins of 0.25 dex, or wider if the number of stars in this range does not reach at least 50. The BOSS sample exhibits a similar behavior for both abundance ratios: lower [α/Fe] ratios for the most distant stars with [Fe/H]< − 2, without significant differences between stars at r< 40 kpc. At the lowest [Fe/H], [Ca/Fe] increases significantly with distance. For the SDSS/SEGUE sample (which comprises more stars), the most metal-poor stars exhibit higher [α/Fe] than for the metal-rich stars, increasing with distance. The resulting [Ca/Fe] reveal a decreasing trend with metallicity from [Fe/H] ~ − 2.0 to the highest values considered. At [Fe/H] lower than ~−2, [Ca/Fe] remains almost constant for nearer stars, but increases steeply as the metallicity decreases for distant stars. The trend of [Mg/Fe] with [Fe/H] is very similar for stars at r< 20 kpc, but more distant stars exhibit a steeper trend with metallicity and higher values than nearer stars (although the metal-poor tail suggests the same trend with distance that is observed for Ca).
 |
Fig. 11 Median [Ca/Fe] and [Mg/Fe] abundance ratios as a function of the Galactocentric distance, r. The colored lines indicate different ranges of [Fe/H]. The trends of these ratios with distance depend on the range of metallicity and the element under consideration. |
 |
Fig. 12 Median [Ca/Fe] and [Mg/Fe] as a function of metallicity, [Fe/H]. The colored lines indicate different ranges of Galactocentric distance, r. The [α/Fe] ratio increases as the metallicity decreases to [Fe/H] ~ − 2, after with the trend flattens. Note the steeper trend observed for the SDSS/SEGUE stars at [Fe/H] < − 2.5 at the largest distances. |
4.4. Effects due to systematics
We now consider whether the presence of systematic offsets in our stellar parameter estimates might be introducing artificial effects in the determination of the abundances. In Paper I, we found that both [M/H] and surface gravity were systematically underestimated in low-metallicity giants. This effect was clearly seen in stars with log g< 2.5 in the globular cluster M 13. There is no obvious evidence of a systematic trend with log g for our [Mg/H] and [Fe/H] in M3. Conversely, [Ca/H] shows the same trend detected for [M/H] as in Paper I, as expected given that at very low metallicity the Ca II lines dominate the [M/H] determination from the entire spectrum. We trimmed our sample by keeping only stars with log g> 2.5 to prevent systematic errors.
The decision to cut at log g = 2.5 was made qualitatively. To ensure the adequacy of this choice, we verified in a sample of SDSS/SEGUE stars at 2.5 < log g< 3 that an increment of 0.3 (the offset detected in Paper I for stars at log g< 3 comparing with log g estimates from the SSPP) implies variations lower than 0.1 in the abundances of the three elements. The [Fe/H], [Ca/H] and [Mg/H] changes as a function of distance show higher variations. Consequently, they cannot be due to systematics. As described in Paper I, the comparison of our SDSS/SEGUE Teff estimates with those from the SSPP agrees very well and has no systematic offsets.We compared more than 90 stars that match our SDSS/SEGUE and BOSS samples. We found an offset in temperature of −80 ± 5 K that increases at lower temperatures. This is much too small an offset to compromise our conclusions.
5. Conclusions
We have performed an analysis of SDSS optical stellar spectra and derived elemental abundances for magnesium, calcium, and iron in individual stars in the halo of the Milky Way. We split these halo stars into two samples depending on whether they have been observed before (SDSS observations up to fall 2009) or after the update of the SDSS spectrographs (BOSS; Eisenstein et al. 2011).
For both samples, we observe a clear decreasing trend of metallicity with distance from the Galactic center. The decrease becomes obvious at r ~ 20 kpc, in fair agreement with earlier studies (Carollo et al. 2007, 2010; de Jong et al. 2010; Beers et al. 2012; Chen et al. 2014). The investigations of Carollo et al. and Beers et al. obtained their results from a spectroscopic analysis of nearby halo stars identified from their kinematics, while the work of de Jong et al. was based on photometry. Our analysis (and also that of Chen et al.), however, is based on halo stars observed spectroscopically in situ over a broad range of distances.
The individual abundances of the two α-elements Ca and Mg confirm the chemical gradient in the halo, which flattens out beyond r ~ 40 kpc. The trends inferred from this work for the [Ca/Fe] and [Mg/Fe] abundance ratios as a function of Galactocentric distance exhibit differences that depend on the metallicity range and the element considered: the ratios are roughly flat at metallicities [Fe/H] < −2 for Ca, but decrease with distance at higher metallicities. [Mg/Fe] shows the opposite trend: it increases with distance regardless of metallicity. However, the interpretation of [Mg/Fe] should be considered as preliminary, given the high dispersion detected in our [Mg/H] estimates and the apparent oscillations as a function of Galactocentric distance. Stars with [Fe/H] < −2 exhibit the highest values of the α/Fe abundance ratio in the halo. [Ca/Fe] and [Mg/Fe] decrease with the iron abundance, although there is a range in metallicity at which these ratios remain constant.
For the most metal-poor stars, a range where α/Fe ratios have not been studied in detail before, our analysis shows higher ratios than in more metal-rich stars. These trends are steeper at larger Galactocentric distances, suggesting different α-enrichment histories for the inner and outer parts of the halo.
The hierarchical assembly predicted by the Λ-CDM model for the formation of massive galaxies implies the total or partial disruption of the subgalactic systems from which the Milky Way halo would have been formed. The mixing of disrupted protogalaxies would form a smooth halo, and the surviving cores would appear as overdensities, with particular kinematical and chemical properties.
Nissen & Schuster (2010) reported evidence for two different [Mg/Fe] and [Ca/Fe] levels for halo stars in the solar neighborhood, with kinematics that indicate a low-α outer halo and a high-α inner halo. Their analysis is limited to stars at −1.6 < [Fe/H] < − 0.4. In this metallicity range, our Ca results agree with the assumption of distant stars with lower [α/Fe]; however, at the lowest metallicities we find no evidence of such a trend. On the contrary, we measure higher [Mg/Fe] abundance ratios for the most distant stars at all metallicities.
Tissera et al. (2013, 2014) performed an analysis of six simulated halos of Milky Way-like galaxies, taking into account supernova feedback, metal-dependent cooling, a prescription for star formation, and a multiphase model for the gas component. They found that outer-halo populations (defined using an energy criterion) are characterized by having low metallicity and high α-element enrichment. Their inner-halo populations comprise debris stars and disk-heated stars, the latter with lower α-element enhancements and more gravitationally bounded than the former. They have also considered that some (in particular more massive) subgalactic fragments (or satellites) can survive longer into the potential well of their parent galaxies, while retaining gas from which new stars can be formed (referred to as endo-debris stars), with low values of [Fe/H], but generally a lower α-element enrichment than debris stars. The disk-heated stars are mostly formed in the disk and later scattered to the halo, with low α-element enhancement due to contributions from Type Ia supernova yields. The simulations showed about 15% of accreted stars with higher α-element enhancement and larger dispersion, consistent with the properties of a thick-disk component. For five of the six cases, they determined their halo transition radii (the crossover point between regions that reflect dominant contributions from the inner-halo populations and outer-halo populations, respectively) were located at about 15–20 kpc from the Galactic center, similar to our results. One of their simulated halos exhibited a halo transition region located at ~40 kpc, similar to that reported for M 31 by Gilbert et al. (2014).
Our new sample is not the only one available to explore the properties of metal-poor stars in the distant halo. Chen et al. (2014) analyzed spectra of in situ halo red giants from the SDSS ninth data release (DR9; Ahn et al. 2012). Their study revealed a metallicity distribution function that transitioned from unimodal to bimodal at distances 20 < | Z | < 25 kpc and 35 <r<45 kpc, with peaks at [Fe/H] ~ −1.6 and [Fe/H] ~ −2.3, the first associated with an inner-halo population and the second with an outer-halo population. These values are similar to the median metallicity that we observe in the inner and outer regions of the Galactic halo. They also found the inner-halo population to dominate at 4 < |Z| < 10 kpc and located the transition point between the inner-halo and outer-halo populations at r ~ 35 kpc.
The predictions of Tissera et al. (2013, 2014) agree with our results that the most distant stars have higher α/Fe ratios than the inner region. In contrast, at higher metallicities our [Ca/Fe] are lower for more distant stars than nearer ones, in agreement with Nissen & Schuster, and in contradiction with the simulations of Tissera et al. The variation of [α/Fe] as a function of [Fe/H] that we find in the outer halo differs from the common image of a plateau caused by the α-enrichment due to SNII without the contribution from SNIa. The [α/Fe] curve as a function of the iron abundance in the outer regions shows a decline from the lowest [Fe/H], remains constant over a certain range, and decreases again.
This curve is the average of stars that are placed at the farthest distances in the halo. As we mentioned above, the accretion of subgalactic systems plays a role in the formation of the halo in the Λ-CDM model, and they are expected to be smaller structures than the resulting galaxy. There is observational evidence that low-mass systems show a decrease of [α/Fe] at lower [Fe/H]. As a result of the lack of mass, they are not expected to sustain the formation of massive stars for a long time. In addition, winds caused by the first SN are likely to remove the gas of the system, which reduces the star formation rate. This implies that SNIa start to enrich the interstellar medium at a lower Fe/H than in more massive systems (Venn et al. 2004).
If the subsystems accreted by our Galaxy would have covered a range of masses, their α/Fe vs. Fe/H curves would show a decrease at different Fe/H values. The average curve would be drawn by the superposition of all of them. From the results reported in this work, the lowest metallicities appear to be dominated by stars that belonged to very low-mass subsystems with the contribution of SNIa at very low [Fe/H]. On the other hand, an IMF biased to high masses would lead to higher α/Fe ratios (McWilliam 1997). The different slopes observed for [α/Fe] at the lowest metallicities, with higher levels at the outer most region, may be a signature of a different IMF, skewed to higher mass progenitors, in the most distant regions of the halo.
The inner parts of the halo are expected to be dominated by stars formed within the virial radius of the Galaxy, although a fraction of debris stars could also contribute, as suggested from the simulations of Tissera et al. For the nearest region the [α/Fe] trend with [Fe/H] that we observed is consistent with a higher star formation rate than outer regions.
Tissera et al. (2014) concluded that their simulated halos that exhibited a mild metallicity gradient had significant contributions from relatively more massive subgalactic fragments. On the other hand, the outer-halo populations that originated from low- or intermediate-mass systems would produce flatter metallicity profiles with distance. The abundance gradient observed in our study of the Milky Way halo, which flattens at large distances, appears to be the result of more massive subgalactic fragments contributing to the inner region, whereas the outer region would be formed from the accretion of systems with lower mass and lower metallicity, leading to a flat metallicity profile with distance.
SDSS optical observations will continue at least for another six years, and as result, a larger sample of F-type turn-off halo stars will soon be available, enabling further investigation and expansion of the results described in this study.
Online material
Lines used to determine chemical abundances.
Stellar parameters, chemical abundances, and distance estimates for our sample of SDSS/SEGUE stellar spectra.
The legends of the panels in Fig. 7 refer to the program of the survey and whether the target selection belongs to science targets (“primary” target bits) or technical targets (“secondary” target bits): “leg1”=“Legacy-primary target”, “leg2”=“Legacy-secondary target”, “SEG11”=“SEGUE1-primary target”, “SEG12”=“SEGUE1-secondary target”, “SEG21”=“SEGUE2-primary target”, “SEG22”=“SEGUE2-secondary target”. For more information about the target selection and the different categories and their classification we refer to the webpage www.sdss3.org/dr9/spectra/targets.php
Acknowledgments
T.C.B. acknowledges partial support for this work from grants PHY 08-22648; Physics Frontier Center/Joint Institute or Nuclear Astrophysics (JINA), and PHY 14-30152; Physics Frontier Center/JINA Center for the Evolution of the Elements (JINA-CEE), awarded by the US National Science Foundation. A.R. acknowledge the support of the French Agence Nationale de la Recherche under contract ANR-12-BS05-0015. BGM simulations were executed on computers from the Utinam Institute of the Université de Franche-Comté, supported by the Région de Franche-Comté and Institut des Sciences de l’Univers (INSU). Y.S.L. acknowledges partial support by the 2014 research fund of Chungnam National University. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, University of Cambridge, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Allen de Prieto, C., Beers, T. C., Wilhelm, R., et al. 2006, ApJ, 636, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Allen de Prieto, C., Sivarani, T., Beers, T. C., et al. 2008, AJ, 136, 2070 [NASA ADS] [CrossRef] [Google Scholar]
- Allen de Prieto, C., Fernández-Alvar, E., Schlesinger, K. J., et al. 2014, A&A, 568, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- An, D., Pinsonneault, M. H., Masseron, T., et al. 2009, ApJ, 700, 523 [NASA ADS] [CrossRef] [Google Scholar]
- An, D., Beers, T. C., Johnson, J. A., et al. 2013, ApJ, 763, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Carollo, D., Ivezić, Ž., et al. 2012, ApJ, 746, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Zucker, D. B., Belokurov, V., et al. 2008, ApJ, 680, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Xue, X. X., Rix, H.-W., Ruhland, C., & Hogg, D. W. 2010, AJ, 140, 1850 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS] [Google Scholar]
- Bovy, J., Hogg, D. W., & Rix, H.-W. 2009, ApJ, 704, 1704 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, D., Beers, T. C., Lee, Y. S., et al. 2007, Nature, 450, 1020 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Carollo, D., Beers, T. C., Chiba, M., et al. 2010, ApJ, 712, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Chamberlain, J. W., & Aller, L. H. 1951, ApJ, 114, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y. Q., Zhao, G., Carrell, K., et al. 2014, ApJ, 795, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Czekaj, M. A., Robin, A. C., Figueras, F., Luri, X., & Haywood, M. 2014, A&A, 564, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, K. S., Schlegel, D. J., Ahn, C. P., et al. 2013, AJ, 145, 10 [Google Scholar]
- de Jong, J. T. A., Yanny, B., Rix, H.-W., et al. 2010, ApJ, 714, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., & Norris, J. E. 2013, in Planets, Stars and Stellar Systems, eds. T. D. Oswalt, & G. Gilmore (Dordrecht: Springer), 55 [Google Scholar]
- Freeman, K., & Bland-Hawthorn, J. 2002, ARA&A, 40, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P. 2002, AJ, 123, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, K. M., Kalirai, J. S., Guhathakurta, P., et al. 2014, ApJ, 796, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Carretta, E., Desidera, S., et al. 2003, A&A, 406, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A. 2008, A&ARv, 15, 145 [CrossRef] [Google Scholar]
- Ishigaki, M., Chiba, M., & Aoki, W. 2010, PASJ, 62, 143 [NASA ADS] [Google Scholar]
- Ivezić, Ž., Sesar, B., Jurić, M., et al. 2008, ApJ, 684, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Beers, T.C., & Jurić, M., et al. 2012, ARA&A, 50, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Jonsell, K., Edvardsson, B., Gustafsson, B., et al. 2005, A&A, 440, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klement, R. J. 2010, A&ARv, 18, 567 [Google Scholar]
- Lee, Y. S., Beers, T. C., Sivarani, T., et al. 2008a, AJ, 136, 2022 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Beers, T. C., Sivarani, T., et al. 2008b, AJ, 136, 2050 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Beers, T. C., Allen de Prieto, C., et al. 2011, AJ, 141, 90 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A. 1997, ARA&A, 35, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2011, A&A, 530, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Allen de Prieto, C., & Lambert, D. L. 2013, ApJ, 764, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Schlaufman, K. C., Rockosi, C. M., Allen de Prieto, C., et al. 2009, ApJ, 703, 2177 [NASA ADS] [CrossRef] [Google Scholar]
- Schlaufman, K. C., Rockosi, C. M., Lee, Y. S., Beers, T. C., & Allen de Prieto, C. 2011, ApJ, 734, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Schlaufman, K. C., Rockosi, C. M., Lee, Y. S., et al. 2012, ApJ, 749, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Schlesinger, K. J., Johnson, J. A., Rockosi, C. M., et al. 2012, ApJ, 761, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., Asplund, M., & Casagrande, L. 2011, MNRAS, 415, 3807 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., Asplund, M., & Casagrande, L. 2014, ApJ, 786, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32 [Google Scholar]
- Smolinski, J. P., Lee, Y. S., Beers, T. C., et al. 2011, AJ, 141, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Tissera, P. B., Scannapieco, C., Beers, T. C., & Carollo, D. 2013, MNRAS, 432, 3391 [NASA ADS] [CrossRef] [Google Scholar]
- Tissera, P. B., Beers, T. C., Carollo, D., & Scannapieco, C. 2014, MNRAS, 439, 3128 [NASA ADS] [CrossRef] [Google Scholar]
- Venn, K. A., Irwin, M., Shetrone, M. D., et al. 2004, AJ, 128, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, X.-X., Rix, H.-W., Yanny, B., et al. 2011, ApJ, 738, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, X.-X., Ma, Z., Rix, H.-W., et al. 2014, ApJ, 784, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zhao, C., & Newberg, H. J. 2006, ArXiv e-prints [arXiv:astro-ph/0612034] [Google Scholar]
All Tables
Stellar parameters, chemical abundances, and distance estimates for our sample of SDSS/SEGUE stellar spectra.
All Figures
 |
Fig. 1 Fit of the regions for two example spectra (with atmospheric parameters Teff = 6078 K, log g = 4.4, and [Fe/H] = − 1.4 and Teff = 6023 K, log g = 3.7, and [Fe/H] = − 1.6) that contains some of the Fe, Ca, and Mg lines that contribute most to the determination of their abundances. The red line corresponds to the fit spectrum, plotted over the observed spectrum (in black). The panels on the left show an spectrum with a S/N ~ 60; the panels on the right correspond to a spectrum with the median S/N of the data, ~30. |
| In the text | |
 |
Fig. 2 Correlation between the values of [Fe/H] obtained by fitting different spectral regions containing Fe lines, compared with the estimation obtained by fitting all of the selected lines together. The bluest regions best contribute to the determination of [Fe/H], with rms values lower than 0.2 dex. The results of the fitting line for the four reddest regions exhibit little correlation with estimates using all of the regions simultaneously. |
| In the text | |
 |
Fig. 3 Correlation of the [Ca/H] results calculated for a sample of 61 591 stars, using different spectral regions containing Ca lines (neutral and/or ionized), compared with the estimation obtained by fitting all of the selected lines together. The CaII lines are the most sensitive to changes in the abundance of calcium, in particular the Ca HK doublet, hence they are the primary features used. Of the neutral lines, the CaI line at 4226.73 Å is the most relevant. |
| In the text | |
 |
Fig. 4 Comparison of the [Fe/H], [Ca/H], and [Mg/H] estimates from SDSS/SEGUE and BOSS stars obtained by fitting individual lines with the metallicity results determined in Paper I, [M/H], which considered the entire spectrum in the analysis. The mean difference between x and y axes appears in the top left corner of each panel, evaluated in three ranges of [M/H]: [M/H] > −1.5, −2 < [M/H] < −1.5, and [M/H] < −2, and the corresponding standard deviations are written in the bottom right corner. The top panels show good agreement between [Fe/H] inferred from individual lines of this element, with an offset of ~0.1 dex. [Ca/H] estimates are offset by ~0.4 dex over [M/H], except at metallicities higher than [M/H] = −1.5, as expected. [Mg/H] estimates display a higher dispersion, increasing with decreasing metallicity, and lower deviations for BOSS stars with respect to SDSS/SEGUE stars. |
| In the text | |
 |
Fig. 5 Comparison of distances to the Sun (for pre-BOSS stars), d, calculated using the methodology followed in this work. The top left panel corresponds to the comparison of stars with 4.1 < log g< 4.4 and −2.0 < [Fe/H] < − 0.4, with distances calculated using the approach described by Schlesinger et al. (2012; see text). The top right panel shows distance estimates for the same sample following Ivezic et al. (2008). In the bottom left panel, distances based on parallaxes from the Hipparcos satellite are compared with our estimates for a sample of turn-off and giant stars with stellar parameters and metallicities from Ramirez et al. (2013) with 2.5 < log g< 4.1. The bottom right panel shows the comparison of distances calculated for a sample of SEGUE giants with 2.5 < log g< 3.5, compared with those obtained by Xue et al. (2014). Objects at | Z | > 5 kpc, calculated from our distance estimations, as well as their statistics, are shown in red. |
| In the text | |
 |
Fig. 6 Median [Fe/H] values, as a function of Galactocentric distance, r, shown as a Hess diagram that displays the relative density of stars for each bin of width 0.25 dex in [Fe/H] and 2.5 kpc in distance. The orange points with their error bars summarize the median values of the analyzed set of data with distance. The left panel corresponds to the BOSS F-type spectrophotometric calibration stars, and the right panel to the full SDSS/SEGUE sample (limited to the range described in Sect. 3.1, considering only stars with |Z| > 5 kpc). A clear gradient in [Fe/H], decreasing with distance, is seen for both samples. |
| In the text | |
 |
Fig. 7 Distribution of the median [Fe/H] vs. r, after splitting the SDSS/SEGUE sample into the target-selection categories with more than 50 stars, located at distances from near the center to up to beyond 20 kpc (www.sdss3.org/dr9/spectra/targets.php). Overall, the metallicity decreases with distance the profile depends on the category considered, however. |
| In the text | |
 |
Fig. 8 Median values of [Fe/H], in bins of 1.5 kpc, for the XY,XZ, and YZ planes of the Galaxy. There are regions covered by the SDSS/SEGUE sample in the XZ and YZ planes (the BOSS sample is shown in the upper row; the SDSS/SEGUE sample is shown in the lower row) that are only poorly covered by the BOSS sample, in particular at higher [Fe/H]. These stars primarily correspond to r distances between 20 and 40 kpc. |
| In the text | |
 |
Fig. 9 Besançon simulation that reproduces stars in the directions on the sky covered by BOSS. The top panel shows the original simulation; the other three panels correspond to the same stars for the BOSS spectrophotometric sample and the SEGUE MSTO and MPMS target-selection cuts. In all cases we considered stars with atmospheric parameters in the ranges of Teff, log g, and [Fe/H] considered in this work. The plots show [Fe/H] with added noise vs. distance from the Galactic center. Red diamonds represent the resulting median [Fe/H] values (with error bars) after applying our algorithm, considering the distance values from the model. Black dots correspond to the median [Fe/H] results, but considering distances calculated from the stellar parameters and metallicity with added noise. Although uncertainties in distance estimates produce changes in the profile of [Fe/H] vs. r, it can be seen that neither the uncertainties in distance, nor the stellar parameters or the selection criteria considered in each case generate a significant gradient. |
| In the text | |
 |
Fig. 10 Median [Ca/H] and [Mg/H] abundances as a function of Galactocentric distance, r. The upper panels correspond to the BOSS spectrophotometric sample, while the lower panels are for the SDSS/SEGUE sample. |
| In the text | |
 |
Fig. 11 Median [Ca/Fe] and [Mg/Fe] abundance ratios as a function of the Galactocentric distance, r. The colored lines indicate different ranges of [Fe/H]. The trends of these ratios with distance depend on the range of metallicity and the element under consideration. |
| In the text | |
 |
Fig. 12 Median [Ca/Fe] and [Mg/Fe] as a function of metallicity, [Fe/H]. The colored lines indicate different ranges of Galactocentric distance, r. The [α/Fe] ratio increases as the metallicity decreases to [Fe/H] ~ − 2, after with the trend flattens. Note the steeper trend observed for the SDSS/SEGUE stars at [Fe/H] < − 2.5 at the largest distances. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


