| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 20 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201425326 | |
| Published online | 22 April 2015 | |
Stellar laboratories
IV. New Ga iv, Ga v, and Ga vi oscillator strengths and the gallium abundance in the hot white dwarfs G191−B2B and RE 0503−289⋆,⋆⋆,⋆⋆⋆,⋆⋆⋆⋆
1
Institute for Astronomy and Astrophysics, Kepler Center for Astro and
Particle Physics, Eberhard Karls University, Sand 1, 72076
Tübingen, Germany
e-mail: rauch@astro.uni-tuebingen.de
2
Astrophysique et Spectroscopie, Université de Mons –
UMONS, 7000
Mons,
Belgium
3
IPNAS, Université de Liège, Sart Tilman, 4000
Liège,
Belgium
4
NASA Goddard Space Flight Center, Greenbelt, MD
20771,
USA
Received: 13 November 2014
Accepted: 23 January 2015
Context. For the spectral analysis of high-resolution and high-signal-to-noise (S/N) spectra of hot stars, advanced non-local thermodynamic equilibrium (NLTE) model atmospheres are mandatory. These atmospheres are strongly dependent on the reliability of the atomic data that are used to calculate them.
Aims. Reliable Ga iv–vi oscillator strengths are used to identify Ga lines in the spectra of the DA-type white dwarf G191−B2B and the DO-type white dwarf RE 0503−289 and to determine their photospheric Ga abundances.
Methods. We newly calculated Ga iv–vi oscillator strengths to consider their radiative and collisional bound-bound transitions in detail in our NLTE stellar-atmosphere models for analyzing of Ga lines exhibited in high-resolution and high-S/N UV observations of G191−B2B and RE 0503−289.
Results. We unambiguously detected 20 isolated and 6 blended (with lines of other species) Ga v lines in the Far Ultraviolet Spectroscopic Explorer (FUSE) spectrum of RE 0503−289. The identification of Ga iv and Ga vi lines is uncertain because they are weak and partly blended by other lines. The determined Ga abundance is 3.5 ± 0.5 × 10-5 (mass fraction, about 625 times the solar value). The Ga iv/Ga v ionization equilibrium, which is a very sensitive indicator for the effective temperature, is well reproduced in RE 0503−289. We identified the strongest Ga iv lines (at 1258.801, 1338.129 Å) in the HST/STIS spectrum of G191−B2B and measured a Ga abundance of 2.0 ± 0.5 × 10-6 (about 22 times solar).
Conclusions. Reliable measurements and calculations of atomic data are a prerequisite for stellar-atmosphere modeling. The observed Ga iv–v line profiles in two white dwarf (G191−B2B and RE 0503−289) ultraviolet spectra were well reproduced with our newly calculated oscillator strengths. For the first time, this allowed us to determine the photospheric Ga abundance in white dwarfs.
Key words: atomic data / line: identification / stars: abundances / stars: individual: G191 / B2B / stars: individual: RE 0503−289 / virtual observatory tools
Based on observations with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26666.
Tables 1–6, 11, 12 and 15 are available in electronic form at http://www.aanda.org
Tables 7–9 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/577/A6
© ESO, 2015
1. Introduction
The spectral lines of ten trans-iron elements were detected by Werner et al. (2012) in the hydrogen-deficient DO-type white dwarf (WD) RE 0503−289. The authors used Far Ultraviolet Spectroscopic Explorer (FUSE) spectra with a high resolution and high signal-to-noise ratio (S/N). RE 0503−289 has an effective temperature of and a surface gravity of log (g/ cm/s2) = 7.5. (Dreizler & Werner 1996). Ga and Mo were identified for the first time in a WD. An abundance analysis was performed by Werner et al. (2012) for Kr and Xe (−4.3 ± 0.5 and −4.2 ± 0.6 in logarithmic mass fractions, respectively) alone because they lacked atomic data for the other newly identified, highly ionized species.
New calculations of reliable transition probabilities (not only for the identified lines themselves, but for the complete model atom that is considered in the model atmosphere and spectral energy distribution (SED) calculations) are mandatory for precise abundance analyses. These enabled us to measure the Zn (Rauch et al. 2014a), Ge (Rauch et al. 2012), and Ba (Rauch et al. 2014b) abundances in RE 0503−289 and the hydrogen-rich DA-type WD G191−B2B (, log g = 7.6, Rauch et al. 2013). The Sn abundance in G191−B2B was determined based on existing atomic data (Rauch et al. 2013). Our models strongly reduced the number of unidentified lines in the spectra of RE 0503−289 and G191−B2B.
Since Werner et al. (2012) identified more than a dozen Ga v lines in the FUSE spectrum of RE 0503−289, we computed Ga iv–vi transition probabilities (Sect. 2) and calculated non-local thermodynamic equilibrium (NLTE) model-atmosphere spectra (Sect. 4) for an accurate Ga-abundance determination (Sect. 5). We summarize our results and conclude in Sect. 6.
2. Atomic structure and radiative data calculation
Many spectral lines of Ga iv, Ga v, and Ga vi were observed in laboratories in the past. This allowed identifying very many energy levels of Ga iv, Ga v, and Ga vi that were listed by Shirai et al. (2007), who made a critical compilation of all the experimental data previously published by Mack et al. (1928), Moore (1971), Ryabtsev (1975), Ramonas & Ryabtsev (1990), and Ryabtsev & Churilov (1991) for Ga iv, Sawyer & Humphreys (1928), Kononov (1967), Joshi et al. (1972), Aksenov & Ryabtsev (1974), Dick (1974), van Deurzen (1977), and Ryabtsev & Ramonas (1985) for Ga v, and Podobedova et al. (1983, 1985) for Ga vi.
In the present work, new sets of oscillator strengths and transition probabilities were obtained for Ga iv, Ga v, and Ga vi. These were computed using the pseudo-relativistic Hartree-Fock (HFR) approach of Cowan (1981) combined with a semi-empirical least-squares fit of radial energy parameters. In each ion, many electron correlations were considered by means of extended multiconfiguration expansions that are included in the physical models. These expansions were chosen so as to include low-lying configurations for which energy levels are experimentally known together with some higher configurations with large configuration interaction Slater integrals Rk that connect these latter configurations to the former.
More precisely, in Ga iv, configuration interaction was explicitly considered among the configurations 3d10, 3d94s, 3d95s, 3d96s, 3d97s, 3d94d, 3d95d, 3d96d, 3d97d, 3d84s2, 3d84p2, 3d84d2, 3d84f2, 3d84s5s, 3d84s6s, 3d84s7s, 3d84s4d, 3d84s5d, 3d84s6d, 3d84s7d, and 3d84p4f for the even parity, and 3d94p, 3d95p, 3d96p, 3d97p, 3d94f, 3d95f, 3d96f, 3d97f, 3d84s4p, 3d84s5p, 3d84s6p, 3d84s7p, 3d84s4f, 3d84s5f, 3d84s6f, 3d84s7f, and 3d84p4d for the odd parity. Using experimental energy levels reported by Shirai et al. (2007), the radial integrals (average energy, Slater, spin-orbit parameters and effective interaction parameters) of 3d10, 3d94s, 3d95s, 3d96s, 3d97s, 3d94d, 3d95d, and 3d96d for even configurations and 3d94p, 3d95p, 3d96p, 3d94f, 3d84s4p for odd configurations were optimized by a well-established fitting procedure. The mean deviations between computed and experimental energy levels were 61 cm-1 (71 levels) and 52 cm-1 (116 levels) for even and odd parities, respectively.
For Ga v, the HFR method was used with, as interacting configurations, 3d9, 3d84s, 3d85s, 3d84d, 3d85d, 3d74s2, 3d74p2, 3d74d2, 3d74f2, 3d74s5s, 3d74s4d, and 3d74s5d for the even parity, and 3d84p, 3d85p, 3d84f, 3d85f, 3d74s4p, 3d74s5p, 3d74s4f, 3d74s5f, and 3d74p4d for the odd parity. The radial integrals corresponding to 3d9, 3d84s, 3d84p, and 3d84f were adjusted to minimize the differences between the calculated Hamiltonian eigenvalues and the experimental energy levels taken from Shirai et al. (2007). In this process, we found mean deviations equal to 34 cm-1 (17 levels) in the even parity and 108 cm-1 (74 levels) in the odd parity.
Finally, in the case of Ga vi, the configurations included in the HFR model were 3d8, 3d74s, 3d74d, 3d64s2, 3d64p2, 3d64d2, and 3d64s4d for the even parity, and 3d74p, 3d74f, 3d64s4p, 3d64s4f, and 3d64p4d for the odd parity. The experimental energy levels reported by Shirai et al. (2007) were used here as well to optimize the radial integrals characterizing the 3d8, 3d74s, and 3d74p configurations. This semi-empirical process led to average deviations with experimental data equal to 122 cm-1 (47 levels) and 161 cm-1 (110 levels) for even and odd parities, respectively.
The numerical values of the parameters adopted in the present calculations are reported in Tables 1–3, while the computed energies are compared with available experimental values in Tables 4–6, for Ga iv, Ga v, and Ga vi, respectively. Tables 7–9 give the HFR oscillator strengths (log gf) and transition probabilities (gA, in s-1) for Ga iv–vi, respectively, and the numerical values (in cm-1) of lower and upper energy levels and the corresponding wavelengths (in Å). In the last column of each table, we also give the absolute value of the cancellation factor CF as defined by Cowan (1981). We note that very low values of this factor (typically <0.05) indicate strong cancellation effects in the calculation of line strengths. In these cases, the corresponding gf and gA values could be very inaccurate and therefore need to be considered with some care. However, very few of the transitions appearing in Tables 7–9 are affected.
3. Observations
We analyzed the FUSE spectrum (910 Å <λ< 1188 Å, resolving power R = λ/ Δλ ≈ 20 000) of RE 0503−289 and for G191−B2B FUSE and Hubble Space Telescope/Space Telescope Imaging Spectrograph spectra (HST/STIS, 1145 Å <λ< 1750 Å). The latter is co-added from 105 observations with the highest resolution1. These spectra were previously described in detail by Werner et al. (2012) and Rauch et al. (2013), respectively.
In addition, we used our recently obtained (and later co-added) HST/STIS spectra of RE 0503−289 (2014-08-14, ObsIds OC7N01010, OC7N01020, grating E140M, R ≈ 45 800, total exposure time 5494 s).
All spectra are available via the Barbara A. Mikulski Archive for Space Telescopes (MAST2).
4. Model atmospheres and atomic data
The Tübingen NLTE model-atmosphere package (TMAP3, Werner et al. 2003; Rauch & Deetjen 2003) was used to calculate advanced plane-parallel and chemically homogeneous stellar model atmospheres in radiative and hydrostatic equilibrium.
In our recent abundance analyses of trans-iron elements (Rauch et al. 2014a,b), we encountered the problem that with a new species included in the models, our model-atmosphere code would not compile if the array sizes were increased to account for the higher number of atomic levels treated in NLTE and the respective higher number of radiative and collisional transitions. Therefore, we decided at that time to reduce the number of levels of various species in our model atoms that were treated in NLTE. This did not have a significant effect on the abundance analyses. However, since we plan to continue the abundance analyses of trans-iron elements, an incalculable, systematic error may arise.
To represent the elements with an atomic number <20 with sufficient detail, we took the prepared (“classical”) model atoms that are provided by the Tübingen Model-Atom Database (TMAD4, Rauch & Deetjen 2003). TMAD was constructed in the framework of the German Astrophysical Virtual Observatory (GAVO5).
We decided to construct the model atoms for the trans-iron elements similar to those of Ca to Ni (Rauch & Deetjen 2003). To reduce the number of atomic levels and spectral lines considered in our model-atmosphere calculations, we employed our program Iron Opacity and Interface (IrOnIc, Rauch & Deetjen 2003), which uses a statistical approach to calculate so-called super levels and super lines. Table 10 demonstrates the strongly extenuated level and line numbers for Ga.
IrOnIc was designed to read data in the Kurucz format6 (Kurucz 1991) as well as in the Opacity Project format7. We transferred our Zn, Ga, Ge, and Ba data into Kurucz-formatted files that were then ingested and processed by IrOnIc. The “statistical” model atoms that are created by this means were then used together with the “classical” model atoms for the lighter metals (see above) in our model atmosphere calculations.
To verify the reliability of this approach, we calculated models that consider only H+Ga and He+Ga with a 100 times solar Ga abundance (mass fraction 5.6 × 10-6, solar value from Asplund et al. 2009) for G191−B2B (, log g = 7.6) and RE 0503−289 (, log g = 7.5). Figure 1 displays the Ga ionization fractions in these models. Ga v–vi are the dominant ionization stages in the line-forming region (−4 ≲ log m ≲ 0.5). m is the column mass, measured from the outer boundary of our model atmospheres.
 |
Fig. 1 Ga ionization fractions in our models for G191−B2B (top panel, H+Ga model) and RE 0503−289 (bottom panel, He+Ga). |
 |
Fig. 2 Top: comparison of two SEDs from He+Ga composed model-atmospheres
(, log g = 7.5, 100 times
solar Ga abundance), on the one hand calculated with a classical (thick, blue in the
online version) and on the other hand with a statistical (thin, red) Ga model atom.
The SEDs are convolved with a Gaussian (FWHM = 0.06 Å) to simulate the FUSE resolution.
Inset: wider wavelength range (statistical Ga model atom only).
Bottom: |
Figure 2 shows a good agreement between two SEDs from models computed with a classical and a statistical Ga model atom. The continuum flux level is matched exactly, while deviations (of about 1%) are visible at the line locations. The reason is simply the difference in the frequency grids (Rauch & Deetjen 2003). For classical model atoms, all spectral lines have a very narrow frequency discretization around their centers, while IrOnIc uses a line-independent frequency grid for its opacity-sampling method (Rauch & Deetjen 2003) that is equidistant in λ, for example.
For G191−B2B and RE 0503−289, TMAP uses a frequency grid within 50 Å ≤ λ ≤ 300 000 Å with about 60 000 frequency points. Figure 2 (the inset) shows that the flux maximum in the model for RE 0503−289 is located around λ = 300 Å. In this region, we use a grid spacing of Δλ = 5 × 10-3 Å, while around λ = 1000 Å (about a factor of ten below the flux maximum), this is reduced to Δλ = 1 × 10-2 Å and, hence, the centers of the very narrow Ga lines do not match perfectly. To calculate synthetic spectra within a restricted wavelength range, for instance for FUSE (910 Å <λ< 1188 Å) and STIS (1150 Å <λ< 1780 Å), we use much finer frequency grids that, for example, consider the centers of Ga lines in detail (with 149 064 and 191 267 frequency points, respectively), and the SED agreement is even better.
For both stars, the final models of Rauch et al. (2014b) are adopted as start models for our calculations. For G191−B2B and RE 0503−289, the statistics of our model atoms are summarized in Tables 11 and 12, the model abundances in Tables 13 and 14.
The SEDs calculated for this analysis are available via the registered Theoretical Stellar Spectra Access (TheoSSA8) Virtual Observatory (VO) service.
5. Photospheric Ga abundances in G191−B2B and RE 0503−289
At a Ga abundance of 3.5 × 10-5 (mass fraction, 625 times the solar value), we were able to reproduce the identified Ga v lines (Table 15) in the FUSE spectrum of RE 0503−289 (Fig. 3).
Ga iv, Ga v, and Ga vi atomic levels and line transitions from Tables 7–9, respectively.
Same as Table 13, for RE 0503−289.
 |
Fig. 3 Strongest Ga v lines in the FUSE observation of RE 0503−289, labeled (green in the online version) with their wavelengths from Table 8. The vertical bar indicates 10 % of the continuum flux. Identified lines are marked. “unid.” denotes unidentified, “is” interstellar. |
The search for Ga lines in the FUSE observation of G191−B2B was entirely negative. Our models for G191−B2B showed that the strongest Ga iv lines given by Shirai et al. (2007, with intensities of 1000) are
located in the STIS wavelength range. These are Ga ivλ 1258.801 Å
(3d94s
3D3 – 3d94p 3F ), Ga ivλ 1303.540 Å
(3d94s
3D2 – 3d94p 3F
), Ga ivλ 1303.540 Å
(3d94s
3D2 – 3d94p 3F ), and Ga ivλ 1338.129 Å
(3d94s
3D3 – 3d94p 3P
), and Ga ivλ 1338.129 Å
(3d94s
3D3 – 3d94p 3P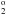 ). They have the largest equivalent widths of
all Ga lines in our models for G191−B2B and are
positively identified in the STIS observation (Fig. 4).
Ga ivλ 1303.540
Å is a blend with Fe v lines and, thus, uncertain, while the
other two lines are isolated. We can reproduce their observed strengths at an abundance of
2.0 × 10-6 (by
mass, 37 times solar, Fig. 4). At this abundance, four
of the next strongest Ga iv lines (Ga ivλλ 1170.585,1190.866,1295.881,1299.476
Å, with intensities of 220, 220, 650, and 600, respectively, Shirai et al. 2007) can also be identified and modeled,
but they appear just above the noise level (Fig. 5).
However, no detectable Ga line is predicted by our models in the FUSE wavelength range.
). They have the largest equivalent widths of
all Ga lines in our models for G191−B2B and are
positively identified in the STIS observation (Fig. 4).
Ga ivλ 1303.540
Å is a blend with Fe v lines and, thus, uncertain, while the
other two lines are isolated. We can reproduce their observed strengths at an abundance of
2.0 × 10-6 (by
mass, 37 times solar, Fig. 4). At this abundance, four
of the next strongest Ga iv lines (Ga ivλλ 1170.585,1190.866,1295.881,1299.476
Å, with intensities of 220, 220, 650, and 600, respectively, Shirai et al. 2007) can also be identified and modeled,
but they appear just above the noise level (Fig. 5).
However, no detectable Ga line is predicted by our models in the FUSE wavelength range.
Ga ivλλ 1258.801,1303.540,1338.129 Å are also visible in the STIS observation of RE 0503−289 (Fig. 4) and agree well with the Ga abundance (3.5 × 10-5 by mass) determined from the FUSE spectrum.
 |
Fig. 4 Strongest Ga iv lines in the STIS observations of G191−B2B (top) and RE 0503−289 (bottom), labeled (blue in the online version) with their wavelengths from Table 7. Identified lines of other species are marked. |
6. Results and conclusions
We have unambiguously identified Ga v lines in the observed high-resolution UV spectra of G191−B2B and RE 0503−289. These lines are well reproduced by our NLTE model-atmosphere calculations using our newly calculated Ga iv–vi oscillator strengths.
We determined photospheric abundances of log Ga = −5.69 ± 0.2 (mass fraction, 1.7−2.5 × 10-6, 30–44 times the solar abundance) and log Ga = −4.49 ± 0.1 (3.0−4.0 × 10-5, 536–715 times solar) for the DA-type white dwarf G191−B2B and the DO-type white dwarf RE 0503−289, respectively. These highly supersolar Ga abundances agree with the high abundances of other trans-iron elements in G191−B2B and RE 0503−289 (Fig. 6).
 |
Fig. 5 Weaker Ga iv lines in the STIS observation of G191−B2B, labeled (blue in the online version) with their wavelengths from Table 7. Identified lines of other species are marked. |
 |
Fig. 6 Solar abundances (Asplund et al. 2009, thick line; the dashed lines connect the elements with even and with odd atomic number) compared with the determined photospheric abundances of G191−B2B (blue circles, Rauch et al. 2013) and RE 0503−289 (red squares, Dreizler & Werner 1996; Werner et al. 2012; Rauch et al. 2013, 2014a,b, and this work). The uncertainties of the WD abundances are about 0.2 dex in general. Arrows indicate upper limits. |
The Ga iv/Ga v ionization balance is well reproduced in RE 0503−289 (Figs. 4, 5).
The identification of lines of Ga and its precise abundance determination became possible only because reliable transition probabilities for Ga iv, Ga v, and Ga vi were computed. Analogous calculations for other highly ionized trans-iron elements are very desirable. The precise measurement of their spectra, that is, their line wavelengths and relative strengths, as well as the determination of level energies and the calculation of transition probabilities remains a challenge for atomic and theoretical physicists.
Online material
Radial parameters (in cm-1) adopted for the calculations in Ga iv.
Comparison between experimental and calculated energy levels in Ga iv.
Same as Table 11, for RE 0503−289.
Strongest Ga lines in the stellar-atmosphere models of RE 0503−289.
Grating E140H, R ≈118 000, http://www.stsci.edu/hst/observatory/crds/calspec.html
GFxxyy.GAM, GFxxyy.LIN, and GFxxyy.POS files with xx = element number, yy = element charge, http://kurucz.harvard.edu/atoms.html
Acknowledgments
T.R. is supported by the German Aerospace Center (DLR, grant 05 OR 1402). Financial support from the Belgian FRS-FNRS is also acknowledged. P.Q. is research director of this organization. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX09AF08G and by other grants and contracts.
References
- Aksenov, V. P., & Ryabtsev, A. N. 1974, Opt. Spectr., 37, 492 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, R. D. 1981, The theory of atomic structure and spectra (Berkeley, CA: University of California Press) [Google Scholar]
- Dick, K. A. 1974, J. Opt. Soc. Am. (1917-1983), 64, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Dreizler, S., & Werner, K. 1996, A&A, 314, 217 [NASA ADS] [Google Scholar]
- Joshi, Y. N., Bhatia, K. S., & Jones, W. E. 1972, Sci. Light, 21, 113 [Google Scholar]
- Kononov, E. Y. 1967, Opt. Spectr., 23, 90 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1991, in Stellar Atmospheres – Beyond Classical Models, eds. L. Crivellari, I. Hubeny, & D. G. Hummer, NATO ASIC Proc., 341, 441 [Google Scholar]
- Mack, J. E., Laporte, O., & Lang, R. J. 1928, Phys. Rev., 31, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, C. E. 1971, Atomic Energy Levels, Natl. Stand. Ref. Data Ser., Natl. Bur. Stand. (US), 35/Vol. II [Google Scholar]
- Podobedova, L. I., Ryabtsev, A. N., & Ramonas, A. A. 1983, Sov. Phys. Collect., 23, 10 [Google Scholar]
- Podobedova, L. I., Ramonas, A. A., & Ryabtsev, A. N. 1985, Sov. Phys. Collect., 25, 66 [Google Scholar]
- Ramonas, A., & Ryabtsev, A. N. 1990, Lith. Phys. J., 37 [Google Scholar]
- Rauch, T., & Deetjen, J. L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 103 [Google Scholar]
- Rauch, T., Werner, K., Biémont, É., Quinet, P., & Kruk, J. W. 2012, A&A, 546, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Werner, K., Bohlin, R., & Kruk, J. W. 2013, A&A, 560, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Werner, K., Quinet, P., & Kruk, J. W. 2014a, A&A, 564, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Werner, K., Quinet, P., & Kruk, J. W. 2014b, A&A, 566, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryabtsev, A. N. 1975, Opt. Spectr., 39, 455 [NASA ADS] [Google Scholar]
- Ryabtsev, A. N., & Churilov, S. S. 1991, Spectroscopy of Multicharged Ions in Hot Plasmas, ed. U. I. Safronova (Akad. Nauk. SSSR. Inst. Spektrosk. Moscow) [Google Scholar]
- Ryabtsev, A. N., & Ramonas, A. 1985, Sov. Phys. Collect., 25, 77 [Google Scholar]
- Sawyer, R. A., & Humphreys, C. J. 1928, Phys. Rev., 32, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Shirai, T., Reader, J., Kramida, A. E., & Sugar, J. 2007, J. Phys. Chem. Ref. Data, 36, 509 [NASA ADS] [CrossRef] [Google Scholar]
- van Deurzen, C. H. H. 1977, J. Opt. Soc. Am., 67, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, K., Deetjen, J. L., Dreizler, S., et al. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 31 [Google Scholar]
- Werner, K., Rauch, T., Ringat, E., & Kruk, J. W. 2012, ApJ, 753, L7 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Ga iv, Ga v, and Ga vi atomic levels and line transitions from Tables 7–9, respectively.
All Figures
 |
Fig. 1 Ga ionization fractions in our models for G191−B2B (top panel, H+Ga model) and RE 0503−289 (bottom panel, He+Ga). |
| In the text | |
 |
Fig. 2 Top: comparison of two SEDs from He+Ga composed model-atmospheres
(, log g = 7.5, 100 times
solar Ga abundance), on the one hand calculated with a classical (thick, blue in the
online version) and on the other hand with a statistical (thin, red) Ga model atom.
The SEDs are convolved with a Gaussian (FWHM = 0.06 Å) to simulate the FUSE resolution.
Inset: wider wavelength range (statistical Ga model atom only).
Bottom: |
| In the text | |
 |
Fig. 3 Strongest Ga v lines in the FUSE observation of RE 0503−289, labeled (green in the online version) with their wavelengths from Table 8. The vertical bar indicates 10 % of the continuum flux. Identified lines are marked. “unid.” denotes unidentified, “is” interstellar. |
| In the text | |
 |
Fig. 4 Strongest Ga iv lines in the STIS observations of G191−B2B (top) and RE 0503−289 (bottom), labeled (blue in the online version) with their wavelengths from Table 7. Identified lines of other species are marked. |
| In the text | |
 |
Fig. 5 Weaker Ga iv lines in the STIS observation of G191−B2B, labeled (blue in the online version) with their wavelengths from Table 7. Identified lines of other species are marked. |
| In the text | |
 |
Fig. 6 Solar abundances (Asplund et al. 2009, thick line; the dashed lines connect the elements with even and with odd atomic number) compared with the determined photospheric abundances of G191−B2B (blue circles, Rauch et al. 2013) and RE 0503−289 (red squares, Dreizler & Werner 1996; Werner et al. 2012; Rauch et al. 2013, 2014a,b, and this work). The uncertainties of the WD abundances are about 0.2 dex in general. Arrows indicate upper limits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.