| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425280 | |
| Published online | 23 April 2015 | |
Revealing a hard X-ray spectral component that reverberates within one light hour of the central supermassive black hole in Ark 564
1
SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA
Utrecht, The
Netherlands
e-mail: m.giustini@sron.nl
2
XMM-Newton Science Operations Centre, ESA/ESAC,
Villafranca del Castillo, Apartado
78, 28692
Villanueva de la Cañada,
Spain
3
Center for Space Science and Technology, University of
Maryland, Baltimore County, 1000
Hilltop Circle, Baltimore, MD
21250,
USA
4
Department of Physics, University of Maryland Baltimore
County, Baltimore,
MD
21250,
USA
5
Astrophysics Group, School of Physical and Geographical Sciences,
Keele University, Keele, Staffordshire
ST5 5BG,
UK
6
Department of Physics, University of Oxford,
Denys Wilkinson Building, Keble
Road, Oxford,
OX1 3RH,
UK
7
Institute for Astrophysics and Computational Sciences, Department
of Physics, The Catholic University of America, Washington, DC
20064,
USA
Received:
5
November
2014
Accepted:
26
January
2015
Context. Arakelian 564 (Ark 564, z = 0.0247) is an X-ray-bright narrow-line Seyfert 1 galaxy. By using advanced X-ray timing techniques, an excess of “delayed” emission in the hard X-ray band (4−7.5 keV) following about 1000 s after “flaring” light in the soft X-ray band (0.4 − 1 keV) was recently detected.
Aims. We report on the X-ray spectral analysis of eight XMM-Newton and one Suzaku observation of Ark 564. Our aim is to characterise the X-ray spectral properties of the source in the light of these recently reported results.
Methods. High-resolution spectroscopy was performed with the RGS in the soft X-ray band, while broad-band spectroscopy was performed with the EPIC-pn and XIS/PIN instruments. We analysed time-averaged, flux-selected, and time-resolved spectra.
Results. Despite the strong variability in flux during our observational campaign, the broad-band spectral shape of Ark 564 does not vary dramatically and can be reproduced either by a superposition of a power law and a blackbody emission or by a Comptonized power-law emission model. High-resolution spectroscopy revealed ionised gas along the line of sight at the systemic redshift of the source, with a low column density (NH ~ 1021 cm-2) and a range of ionisation states (−0.8 < log (ξ/erg cm s-1) < 2.4). Broad-band spectroscopy revealed a very steep intrinsic continuum (photon index Γ ~ 2.6) and a rather weak emission feature in the iron K band (EW ~ 150 eV); modelling this feature with a reflection component requires highly ionised gas, log (ξ/erg cm s-1) > 3.5. A reflection-dominated or an absorption-dominated model are similarly able to well reproduce the time-averaged data from a statistical point of view, in both cases requiring contrived geometries and/or unlikely physical parameters. Finally, through time-resolved analysis we spectroscopically identified the “delayed” emission as a spectral hardening above ~4 keV; the most likely interpretation for this component is a reprocessing of the “flaring” light by gas located at 10−100 rg from the central supermassive black hole that is so hot that it can Compton-upscatter the flaring intrinsic continuum emission.
Key words: galaxies: active / galaxies: individual: Ark 564 / galaxies: Seyfert / X-rays: individuals: Ark 564 / black hole physics
© ESO, 2015
1. Introduction
Summary of XMM-Newton observations for Ark 564.
Arakelian 564 (Ark 564) is one of the X-ray-brightest AGN of the sky, with a 2−10 keV flux f2−10 ~ 10-11 erg s-1 cm-2. It is classified as narrow-line Seyfert 1 (NLS1), with a FWHM(Hβ) ~ 750 km s-1 (Stirpe 1990). Like many NLS1s, Ark 564 displays an extremely variable X-ray flux and a very steep spectral shape (Brandt et al. 1994; Turner et al. 2001; Edelson et al. 2002). Possible complexities in its X-ray spectrum related to the reprocessing of the primary continuum emission onto ionised matter have been reported by Vaughan et al. (1999), Turner et al. (1999), Comastri et al. (2001), Vignali et al. (2004), Matsumoto et al. (2004), Papadakis et al. (2007), Dewangan et al. (2007), Smith et al. (2008).
Legg et al. (2012) exploited a long XMM-Newton observational campaign to perform a detailed timing analysis of the X-ray properties of Ark 564. The main result was the discovery of an excess of emission in the hard (4−7.5 keV) band following soft (0.4−1 keV) flares that appeared ~1000 s after the flares and lasted ~1500 s. This is consistent with light reverberation on some scattering material located ~100rg from the continuum source (rg ≡ GMBH/c2).
The main goal of this work is characterising the X-ray spectral properties of Ark 564 in the light of the results reported by Legg et al. (2012). The paper is organised as follows: the observations are presented in Sect. 2, the spectral analysis is reported in Sect. 3, the results are summarised in Sect. 4, and conclusions are drawn in Sect. 5.
2. Observations and data reduction
In the following subsections we report on the data reduction of eight XMM-Newton and one Suzaku X-ray observations of Ark 564.
2.1. XMM-Newton observations
Ark 564 was observed by XMM-Newton eight times between May and July 2011. Data were processed using HEAsoft v.6.12 and SAS v.11.0.0.
The reflection grating spectrometer (RGS) data were processed using calibration files generated in June 2012. Background light curves were generated and inspected for the presence of flares: a uniform threshold of 0.1 ct s-1 for the background rate was then used to generate good time interval tables for each observation. Net exposure times after background flaring removal are reported in Table 1. First-order spectra and response matrices were extracted using the rgsproc task using source coordinates as given by NED (RA = 340.663939, Dec = +29.725364) as input to prevent possible offsets between different observations. While there is considerable flux variability between the different observations, the spectral shape is found not to vary, therefore we proceeded with stacking the eight observations using the task rgscombine. We obtained two high signal-to-noise spectra with ~412 ks of exposure each, and a total of ~106 counts for the combination of the two instruments, RGS1 and RGS2. Source spectra were rebinned by a factor of 3.
All the EPIC pn observations were performed in small window mode and used the thin optical blocking filter. The raw ODF pn event files were filtered, and we retained only best-quality (FLAG=0) single and double (PATTERN ≤4) events. Source events were extracted from circular regions with a 36′′ radius, while background events were extracted from two boxes of 61′′ × 100′′ and 51′′ × 51′′ in size. Background light curves were then extracted for single events alone in the 10−12 keV band for each observation. After inspecting these light curves, we removed strong flaring background time intervals using a conservative threshold of 0.1 ct s-1. The net exposure times after the flaring background removal is reported in Table 1. These values also account for the small window mode live time of ~71%.
The SAS task epatplot was then used to estimate the fraction of pile-up affecting the data. By using the standard energy interval 0.5−2 keV to estimate the pile-up fraction, excellent numerical results were obtained, with the single or double pattern observed distributions deviating by less than 1% from the predicted ones. However, a visual inspection of the pattern distribution revealed significant deviations both at energies below 1 keV (with an observed excess of single events) and at energies above 1 keV (with an observed excess of double events), the two effects compensating in the numerical estimate for the pile-up. We then re-estimated the pile-up fraction by focusing on the 1−9 keV band. Using this band as a reference, we found non-negligible deviations (of the order of 3−5%) of the observed pattern distribution from the predicted one in half of the observations. The cores of the PSF were then excised using a radius proportional to the amount of pile-up in the data, until we were able to recover the predicted pattern distribution within a 1−2% uncertainty over the whole energy range used in this work, that is, 0.4−10 keV. Excision radii are reported in the last column of Table 1. Redistribution matrices (RMF) and ancillary response files (ARF) were generated for each observation at the position of the source using tasks rmfgen and arfgen , taking into account the excision of the PSF core.
The EPIC-MOS data were heavily affected by pile-up and so were not useable.
2.2. Suzaku observation
Suzaku (Mitsuda et al. 2007) carries four co-aligned telescopes that focus X-rays onto a suite of CCD cameras comprising the X-ray Imaging Spectrometer (XIS; Koyama et al. 2007). XIS CCDs 0, 2, 3 are front-illuminated (FI) and XIS 1 is back-illuminated. XIS 1 has an enhanced soft-band response relative to the FI units, but has a lower effective area at 6 keV and a higher background level at high energies. XIS 2 failed on 2006 November 9 and hence was not used in our analysis. Suzaku also carries a non-imaging, collimated Hard X-ray Detector (HXD; Takahashi et al. 2007), whose PIN detector provides useful AGN data typically over the range 15−70 keV.
A Suzaku observation of Ark 564 was made in 2007 June 26−28 (OBSID 702117010), and the data were reduced using v6.16 of HEAsoft. We screened the XIS and PIN events to exclude data taken during passage through the South Atlantic Anomaly, starting and ending within 500 seconds of entry or exit. In addition, we excluded data with an Earth elevation angle smaller than 5°. Ark 564 was observed at the nominal centre position for the HXD. FI CCDs used 3 × 3 and 5 × 5 edit-modes, with normal clocking mode. Good events (with grades 0, 2, 3, 4, and 6) were selected and hot or flickering pixels removed using the SISCLEAN script. The spaced-row charge injection (SCI) was used. The net exposure times were 70 ks per XIS unit and 81 ks for the PIN. XIS products were extracted from circular regions of 2.9′ radius while background spectra were extracted from a region of the same size, offset from the source and avoiding the calibration sources in the chip corners.
For PIN analysis we used the model “D” background1. We checked the correctness of the model adopted by comparing it to the Earth-occulted data, finding an overestimation of the NXB of the level of 11.5%; this factor was taken into account into the subsequent analysis. Following standard practice, the time filter resulting from screening the observational data was applied to the background events model. The ftool hxdpinxbpi was used to create a PIN background spectrum from the screened background data, taking the shape and flux level of the cosmic X-ray background (Boldt 1987; Gruber et al. 1999) in the Suzaku PIN field of view into account. We used the response file ae_hxd_pinhxnome3_20080129.rsp for spectral fitting.
During the Suzaku observation Ark 564 was found to have source count rates 2.132 ± 0.006 (summed XIS 0, 3 over 0.75−10 keV) and 0.010 ± 0.002 (PIN over 15−50 keV) ct/s. The background was 1% of the total XIS count rate in the full band. The source comprised 3% of the total counts in the PIN band.
Spectral fits used data from XIS 0 and 3, in the energy range 0.75−10 keV and from the PIN over 15−50 keV. Data in the range 1.75−1.9 keV were excluded from the XIS spectral analysis owing to uncertainties in calibration around the instrumental Si K edge. XIS 1 was not used owing to the higher background level at high energies. The data were binned to have at least 20 counts per bin. In the spectral fitting, the PIN flux was scaled by a factor 1.18, which is appropriate for the cross calibration of the XIS and PIN for this observation epoch2. A systematic error of 3% was added to the data.
3. Spectral analysis
We used Xspec v.12.7.0 for the spectral analysis. We used the χ2 statistics as a goodness-of-fit measure, in a valid regime assured by the high number of counts in each energy channel for each analysed spectrum. All the models include a Galactic column density NH = 5.43 × 1020 cm-2 (Kalberla et al. 2005), modelled with tbabs for the low-resolution pn data (Wilms et al. 2000), with tbnew for the high-resolution RGS data (Wilms et al., in prep.). Errors are given at the 90% confidence level (Δχ2 = 2.706 for one parameter of interest). A cosmological redshift z = 0.02468 was adopted for the source. We first analysed the RGS data to constrain the physical properties of any possible soft-band absorbing or emitting component (Sect. 3.1); the results obtained for the soft band were then used as input in our modelling of the full-band EPIC pn and Suzaku XIS/PIN spectra (Sect. 3.2).
3.1. Grating analysis
Fit to the RGS continuum.
The RGS1 and RGS2 stacked spectra were simultaneously fitted over the 0.4−1.9 keV band. Bad channels were ignored, and a systematic error of 3% was added in quadrature with the photon shot noise to account for the calibration uncertainties between the two RGS (see e.g. Kaastra et al. 2011).
The spectral shape in this energy range is extremely steep, and a simple power-law emission model gives a very poor fit to the data (χ2/ν = 4700/1297). Adding a blackbody component significantly improves the fit statistic (Table 2). The black hole mass of Ark 564 is quite low (MBH ~ 2.6 × 106 M⊙, Botte et al. 2004), so we might expect the tail of the thermal emission from the accretion disk to emerge in the soft X-ray band − but a simple blackbody emission component is obviously only a phenomenological parametrization for the continuum shape.
We replaced the power law + blackbody model with optxagnf, which represents the expected emission spectrum from the inner accretion flow around a black hole (Done et al. 2012). This model assumes that the accretion luminosity (parametrized in terms of the mass accretion rate Ṁacc and the black hole spin a) is produced in a disk + corona system. A geometrically thin and optically thick accretion disk extends from an outer radius rout up to the innermost stable circular orbit around the black hole and emits as a colour-temperature corrected blackbody (i.e. it has an effective temperature higher than a standard SS disk at small radii within the region where electron scattering starts to dominate the disk opacity: this effect is strongest for the hottest accretion disks, such as for low black hole mass and high mass accretion rate AGN) up to a radius rcor. Inside this radius, the disk seed photons are Compton-upscattered in a two-phase hot medium: a fraction of them fpl is Comptonized on a very hot and optically thin medium (e.g. the “X-ray corona”), while the remaining (1−fpl) is Comptonized on a much colder and optically thick medium (e.g. the “inner disk” or a “disk atmosphere” or a “disk skin”). We fixed the black hole mass MBH = 2.6 × 106 M⊙ (Botte et al. 2004), the black hole spin a = 03, and the accretion disk outer radius rout = 105rg. The free parameters are then the mass accretion rate Ṁacc, the outer radius of the Compton-upscattering region rcor, the temperature kT and optical depth τ of its cold and optically thick portion, the fraction fpl of the energy that is upscattered in its hot and optically thin portion, and the observed photon index Γ. The optxagn model is also able to improve the fit statistics with respect to the power-law component alone and gives a statistically equivalent fit to the data as the power law + blackbody model (Table 2); however, given the two more free parameters required by optxagn and given the much faster performance of power law + blackbody, we proceeded to search for spectral residuals using the latter as the baseline model for the continuum. First, the residuals were modelled using Gaussian emission or absorption lines (Sect. 3.1.1), then a fit using Xstar tables was performed (Sect. 3.1.2).
3.1.1. Fit with Gaussians
 |
Fig. 1 RGS spectral residuals in the source rest frame. |
A threshold of 99.9% in statistical significance was adopted to consider the addition of a Gaussian line to the model as required by the data, that is, Δχ2> 16.3 for three degrees of freedom associated with each line: centroid energy, width, and intensity. The analysis was simultaneously performed on the RGS1 and RGS2 dataset, and only features significant in both detectors were included in the model (except for energy ranges with missing chips, i.e. E = 0.90−1.18 keV for the RGS1, and E = 0.52−0.62 keV for the RGS2).
We detected 16 absorption and 3 emission lines in the soft X-ray spectrum of Ark 564: they are shown as residuals against the continuum in Fig. 1, while their properties are listed in Table 3. For 14 out of 16 absorption lines we were able to associate a theoretical identification with H-like and He-like transitions of ions of C, N, O, Ne, and L-shell transitions of Fe: all of them are compatible with a zero-velocity shift. All the identified absorption lines are narrower than the instrumental RGS resolution except for the features observed between ~700−800 eV, which correspond to the Fe I-XVI M-shell UTA (Behar et al. 2001), and the two high-ionisation transitions identified with Fe XVII and Ne IX, which display a FWHM ~ 1000−1500 km s-1. The three emission lines are identified with H-like transitions of N VI, N VII, and O VII.
Two features remain unidentified at rest-frame energies of ~552 eV and ~619 eV; both of them are resolved by the RGS, but do fall in regions that are devoid of known strong spectral transitions of cosmically abundant elements. We note that within the measurements errors, they might be identified with N VII and O VII Kα absorption by allowing a net blueshift of ~0.1c.
Absorption and emission lines detected in the RGS stacked spectra of ARK 564.
 |
Fig. 2 Rest-frame plot of the three zones of warm absorbing gas detected in the RGS data. From top to bottom, the ionisation parameter and column density are log (ξ/erg cm s-1) ~ −0.8, 1.3,2.4 and log (NH/cm-2) ~ 20.1, 20.3, 20.9. |
3.1.2. Fit with Xstar tables
We generated a table using the latest version of Xstar v.2.2.1bn3 and a finely spaced energy grid, using 105 energy bins over the 0.1−20 keV energy range used for the computation. The incident ionising continuum was a power law with a steep photon index Γ = 2.5, appropriate for Ark 564. Solar abundances and a turbulent velocity of 100 km s-1 were adopted. The gas column density was sampled over 10 points from NH = 5 × 1018 cm-2 to NH = 1021 cm-2, while the gas ionisation state was sampled over 20 points from log (ξ/erg cm s-1) = −1.5 up to log (ξ/erg cm s-1) = 3.5.
The continuum emission was modelled with a power law plus a blackbody, and the model
included the three emission lines detected in the previous section. We obtained a fair
fit to the data (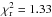 ) using three zones of photo-ionised gas.
We found no net velocity shift for any of the three zones. The relative contribution of
each zone in terms of absorption components is shown in Fig. 2. The least ionised zone is responsible for most of the opacity for
lowly ionised oxygen, that is, O IV, O V, and O VI; the intermediate zone reproduces the
H-like and He-like transitions of C VI, N VI-VII, and O VII-VIII, as well as the
least-ionised portion of the Fe M UTA; finally, the most-ionised zone contributes to
filling the O VIII H-like absorption as well as the higher ionisation states of the Fe M
UTA, the Fe L, and the H-like and He-like Ne lines. Fit parameters are reported in Table
4.
) using three zones of photo-ionised gas.
We found no net velocity shift for any of the three zones. The relative contribution of
each zone in terms of absorption components is shown in Fig. 2. The least ionised zone is responsible for most of the opacity for
lowly ionised oxygen, that is, O IV, O V, and O VI; the intermediate zone reproduces the
H-like and He-like transitions of C VI, N VI-VII, and O VII-VIII, as well as the
least-ionised portion of the Fe M UTA; finally, the most-ionised zone contributes to
filling the O VIII H-like absorption as well as the higher ionisation states of the Fe M
UTA, the Fe L, and the H-like and He-like Ne lines. Fit parameters are reported in Table
4.
We checked for partially covering gas along the line of sight by allowing any of the
three absorbing zones to be only partially covering the source. While there is no
statistical improvement when the zones are individually allowed to be partially
covering, a Δχ2 =
30 for one extra degree of freedom is found when all the three zones
share the same covering fraction 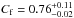 . While the gas ionisation state is not
affected by introducing an unabsorbed component along the line of sight, the column
densities measured in this scenario are of the order of 40% higher than those measured
in the scenario Cf ≡ 1.
. While the gas ionisation state is not
affected by introducing an unabsorbed component along the line of sight, the column
densities measured in this scenario are of the order of 40% higher than those measured
in the scenario Cf ≡ 1.
Fit to the RGS spectra with Xstar.
3.2. Broad-band analysis
We show in Fig. 3 full-band (0.4−10 keV) pn light curves for each observation, binned to 128 s. The count rates for the four excised observations have been rescaled to account for the loss of counts due to discarding the central region of the PSF. Given the very low residual background count rate (typically lower than 1% of the source one) after screening against the presence of strong flares, we show the source plus background light curves. The time variability of Ark 564 is striking on both short (kiloseconds) and long (hours and weeks) time scales. We first present the spectral analysis of the time-averaged spectra (Sect. 3.2.1) and of the flux-selected spectra (Sect. 3.2.2); we then present results of time-resolved spectral analysis (Sect. 3.2.3).
3.2.1. Time-averaged spectra
The eight pn spectra were stacked using mathpha. We generated an average background spectrum by appropriately weighting each individual background spectrum by the BACKSCAL ratio between each source and background extraction region, which varies among the different observations because of the different excision radii used to clean the spectra from pile-up effects. Average RMF and ARF were created using addrmf and addarf. Following Miller et al. (2008), each individual spectrum was binned at the HWHM instrumental energy resolution. A systematic error of 1% was added to the data below 2 keV to account for uncertainties in the instrument calibration4. Because of the different count losses due to excision of the PSF in different observations, we were unable to recover the intrinsic average flux of the source, hence we do not cite normalisation values for the spectral fit referred to the stacked pn spectrum. As a sanity check, we also fit simultaneously the eight spectra of each individual observation; in this case, we can recover the intrinsic flux of the source by correcting the count rate for the PSF count loss.
 |
Fig. 3 Light curves for the eight XMM-Newton observations extracted in the 0.4−10 keV band and binned to 128 s. |
The broad-band pn and XIS+PIN spectra are shown in Fig. 4 unfolded against a power law with Γ = 2. The spectra are extremely steep and show some structure in the Fe K band. We first fitted the 3−10 keV spectra to a simple power-law continuum emission. The fit statistics are χ2/ν = 484/512 for the XIS spectrum, χ2/ν = 190/113 for the stacked pn spectrum, and χ2/ν = 1084/905 for the simultaneous fit to the eight individual pn datasets. Spectral residuals to this model are plotted in Fig. 5, where the power law was fitted ignoring the Fe K region: even if a power law formally yields an excellent fit to the XIS data, significant residuals are evident. Adding a Gaussian emission line significantly improved the fit for all the datasets. Spectral parameters for this model are reported in Table 5. The emission line centroid energy and width (Eline ~ 6.6 keV, σline ~ 400 eV) were found to remain constant within the errors in the different observations. The line equivalent width EWline was found to vary during the 2011 XMM-Newton observational campaign; it was higher when the source flux was lower. We return to this point in Sect. 3.2.2 when we analyse the flux-selected pn spectra.
The single Gaussian line was replaced by the reflection model xillver (García et al. 2013), which simulates the reflected spectrum of a power-law incident on a plane-parallel optically thick slab. We used solar abundances and tied the slope of the incident continuum to that of the primary power law. Good fit statistics (respectively χ2/ν = 459/510, 112/111, and 957/903 for the XIS, the stacked pn, and the individual pn spectra) were obtained with a power law with Γ ~ 2.4 illuminating a highly ionised slab with log (ξ/erg cm s-1) = 3.2−3.8 (90% c.l.). Allowing the normalisation of the reflected component to be a free parameter in the simultaneous fit to the eight individual pn spectra did not improve the fit.
We then turned our attention to the full-band spectra, which were modelled including the three zones of photo-ionised gas and the three narrow emission lines detected in the RGS spectra (Sect. 3.1.2). There is a prominent excess of emission both at lower energies (down to E ~ 0.4 keV) and at higher energies (up to 30 keV with Suzaku). The broad-band spectral shape of the high S/N stacked pn spectrum can be roughly modelled by a combination of xillver and either a power law plus a phenomenological blackbody (χ2/ν = 607/181), or optxagn, where the black hole spin was fixed to zero and the disk outer radius to 105rg (χ2/ν = 432/179). However, a simple combination of optxagn plus an ionised reflector, as found for the fit to the 3−10 keV data, is unable to give a good fit to the broad-band data and leaves systematic residuals at E ≳ 5 keV. A further cold reflection component (modeled again with xillver) is able to well reproduce such high-energy residuals, but it strongly over-predicts the strength of soft emission lines at E ≲ 2 keV. The addition of a layer of ionised gas with a column log (NH/cm-2) ~ 23.5 in front of the cold reflector gave a good fit to the broad-band data by excluding such strong emission lines (see Table 6).
 |
Fig. 4 Observed frame EFEXMM-Newton EPIC pn (top) and Suzaku XIS+PIN (bottom) spectra unfolded against a power law with Γ = 2. |
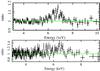 |
Fig. 5 Rest frame spectral residuals for a fit to a power law in the 3−6 and 7−10 keV band for the pn (top) and XIS (bottom) data. |
The same model (optxagn + ionised reflection + cold and absorbed reflection) was able to well reproduce the XIS+PIN spectra without significant variations of the model parameters with respect to the stacked pn ones. The observed variability for the eight individual pn spectra is driven by changes in the continuum amplitude. We found significant improvement of the fit statistics (Δχ2/ Δν = 151/7 and Δχ2/ Δν = 76/7, respectively) when allowing the photon index Γ and the fraction of energy dissipated in the hot corona fpl to vary between the observations; these variations were very weak, however, with a maximum ΔΓ ~ 0.1 and Δfpl ~ 0.05. The best-fit model spectral parameters are reported in Table 6, while the Suzaku and stacked pn spectra are plotted in Fig. 6 unfolded against the best-fit model, together with data-to-model ratios.
 |
Fig. 6 EPIC pn (top) and Suzaku XIS+PIN (bottom) spectra unfolded against the best-fit model described in Table 6, along with data-to-model ratios. The intrinsic continuum emission is modelled with optxagn (dotted-dashed black line); two reflectors are modelled with xillver, a highly ionised (dashed blue line) and a cold, absorbed one (solid magenta line). The total model is plotted in red. |
Fit to the 3−10 keV band with a power law plus a Gaussian emission line.
Fit to the full band with optxagn, an ionised reflector, and an absorbed cold reflector.
Flux-selected spectra.
A blurred reflection scenario.
We tested a blurred reflection scenario on the stacked pn spectrum. The intrinsic
continuum was modelled with a power law plus a blackbody; a reflection component
modelled with xillver was convolved with the relativistic smearing model kdblur (Laor 1991). The emissivity index q was fixed to 3 (a
value typical of isotropic illumination of the reflecting slab) and the iron abundance
was fixed to solar. A good fit (χ2/ν = 197/179) is
obtained with a power law with Γ = 2.45 ±
0.01 reflecting onto a ionised (log (ξ/erg
cm s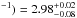 ) slab seen edge-on (inclination
i = 89 ±
1 deg), that extends close to a rapidly rotating black hole (with a
slab inner radius rin<
1.85rg at 90% c.l.); the unfolded
spectrum is plotted in the top panel of Fig. 7.
) slab seen edge-on (inclination
i = 89 ±
1 deg), that extends close to a rapidly rotating black hole (with a
slab inner radius rin<
1.85rg at 90% c.l.); the unfolded
spectrum is plotted in the top panel of Fig. 7.
 |
Fig. 7 Stacked pn spectrum unfolded against two different representations of a blurred reflection scenario. Top panel: continuum modelled with power law (black dotted-dashed line) + blackbody (blue dotted line), and blurred reflection modelled with kdblur*xillver (blue dashed line); bottom panel: same as above, but modelling the continuum with optxagn (black dotted-dashed line). |
 |
Fig. 8 Suzaku XIS+PIN spectra unfolded against a blurred reflection model, colour-coded as the bottom panel of Fig. 7. |
Replacing the power law + blackbody model with optxagn gave a good fit to the data as
well (χ2/ν = 167/177)
with the following parameters: an intrinsic X-ray continuum with a slope
Γ = 2.43 ± 0.01; a mass
accretion rate 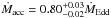 ; a coronal radius
; a coronal radius
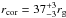 ; a fraction
; a fraction
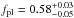 of accretion energy Comptonized in the
hot optically thin X-ray corona, the remaining (1 − fpl)
Comptonized in a colder (
of accretion energy Comptonized in the
hot optically thin X-ray corona, the remaining (1 − fpl)
Comptonized in a colder (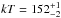 eV), optically thick (τ = 32 ± 5) medium. The
blurred reflection component has a high ionisation state (log (ξ/erg cm s
eV), optically thick (τ = 32 ± 5) medium. The
blurred reflection component has a high ionisation state (log (ξ/erg cm s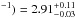 ) and extends down to rin<
1.59rg. The fraction of reflected or
direct flux is
) and extends down to rin<
1.59rg. The fraction of reflected or
direct flux is 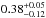 ,
,
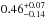 , and
, and
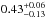 in the 0.4−1, 1−4, and 4−7.5 keV band, respectively. The
corresponding unfolded spectrum is plotted in the bottom panel of Fig. 7. A comparison between the top and bottom panels of
Fig. 7 shows the equivalent modelling of optxagn
and a power law + blackbody where the peak temperature of the latter is
kT ~
130 eV.
in the 0.4−1, 1−4, and 4−7.5 keV band, respectively. The
corresponding unfolded spectrum is plotted in the bottom panel of Fig. 7. A comparison between the top and bottom panels of
Fig. 7 shows the equivalent modelling of optxagn
and a power law + blackbody where the peak temperature of the latter is
kT ~
130 eV.
The application of the blurred reflection scenario to the broad-band Suzaku
data, with an emissivity index fixed to q = 3 and iron
abundances fixed to solar, gave a good fit (χ2/ν = 1084/1109)
with spectral parameters compatible within the errors with those derived for the
stacked pn spectrum, but for the inner radius of the reflecting slab, which is found
to be much higher: 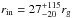 . The XIS+PIN spectrum unfolded against
this model is plotted in Fig. 8: despite the
formally excellent fit, significant residuals in the PIN band are present, with the
source flux being underestimated by the blurred reflection model.
. The XIS+PIN spectrum unfolded against
this model is plotted in Fig. 8: despite the
formally excellent fit, significant residuals in the PIN band are present, with the
source flux being underestimated by the blurred reflection model.
A partial covering scenario.
A partial covering scenario was tested by absorbing the intrinsic continuum
(modelled with optxagn) with zxipcf (Reeves et al.
2008). Both the stacked pn spectrum and the XIS+PIN spectra are well modelled
by these two components (χ2/ν = 198/178 and
1095/1110,
respectively). The absorber column density, ionisation parameter, and covering
fraction were log (NH/cm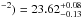 , log (ξ/erg cm
s
, log (ξ/erg cm
s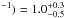 , and
, and
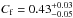 for the pn, and log (NH/cm
for the pn, and log (NH/cm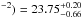 , log ξ/(erg cm
s
, log ξ/(erg cm
s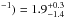 , and
, and
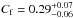 for the XIS+PIN data. The absorbed
component helps reproducing the spectral shape at high energies, basically replacing
the absorbed reflector plotted as the magenta line in Fig. 6. The intrinsic continuum model parameters were similar for the two
datasets and comparable with the parameters derived in the previous section and
reported in Table 6, except for the mass
accretion rate that in this scenario is estimated to be higher,
for the XIS+PIN data. The absorbed
component helps reproducing the spectral shape at high energies, basically replacing
the absorbed reflector plotted as the magenta line in Fig. 6. The intrinsic continuum model parameters were similar for the two
datasets and comparable with the parameters derived in the previous section and
reported in Table 6, except for the mass
accretion rate that in this scenario is estimated to be higher,
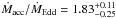 and
and
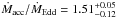 for the pn and XIS+PIN data.
for the pn and XIS+PIN data.
 |
Fig. 9 0.4−10 keV flux-selected spectra unfolded against a power law with Γ = 2: low (black), medium (red), and high (blue) flux states. |
3.2.2. Flux-selected spectra
The EPIC-pn source spectra were stacked according to three different flux levels selected after inspecting Fig. 3: a low flux state with a count rate <27 counts s-1, a medium flux state with 30 counts s-1< count rate < 40 counts s-1, and a high flux state with a count rate >45 counts s-1. Flux-selected spectra were then stacked according to the shape of the source extraction region and were fitted if they had >5000 net counts in the 4−10 keV band. The relative contribution of the different observations to each flux-selected spectrum is reported in Table 7, while the full-band unfolded spectra are plotted in Fig. 9: despite flux changes of over a factor of two, the spectral shape does not vary dramatically.
The 3−10 keV band of the three flux-selected spectra was fitted simultaneously to a power-law model: the fit statistics was quite poor (χ2/ν = 708/557), and there were residuals in the Fe K band. As with the singular spectra, the addition of a Gaussian emission line (where the width σ was fixed to 460 eV, i.e. the best-fit value found for the average stacked pn spectrum) significantly improved the fit (Δχ2/ Δν = 123/4). The line centroid energy is consistent with the one measured in the average spectra, but its equivalent width significantly decreases from lower to higher states (see Table 5 for values). This suggests the presence of a constant (or varying slower than the continuum) component that emerges when the intrinsic continuum is in a low state.
We applied the best-fit model found in Sect. 3.2.1 (optxagn + ionised xillver + absorbed cold xillver) to the flux-selected spectra, which yielded a good fit to the data (χ2/ν = 1008/907, Table 6) with the two reflection components remaining constant, and the observed variability being driven by variations in intrinsic continuum amplitude.
3.2.3. Time-resolved spectra
We aim at extracting the spectral signature of the “hard delayed excess” that follows flares of emission in Ark 564, as identified by Legg et al. (2012). To this end, we extracted the source spectra in time intervals centred on the position of the “soft flares”5, with a width of ±384 s. The associated delayed signal was extracted in a time interval 1088−2496 s after each peak centre, that is, the time interval when the hard delayed excess appears to be the strongest (see Fig. 6 of Legg et al. 2012). All the “soft flares” spectra were then stacked together, as were all the “delayed” spectra. For the spectral analysis we used the same scaled background as we used to analyse the average stacked pn spectrum. Figure 10 shows the unfolded broad-band spectra for the flaring (black) and their delayed (red) time intervals.
 |
Fig. 10 Top panel: soft flares (black) and their associated delayed signal (red) spectra unfolded against a power law with Γ = 2. Bottom panel: data-to-model ratio to a power law fitted on the 2−10 keV band. |
The variation in spectral shape is clear: while at energies E ≲ 2.5 keV the spectral shape is just shifted down in intensity (as found for the flux-selected spectra), at E ≳ 3 keV there is an evident hardening of the delayed spectrum. This can be seen in the bottom panel of the same figure where high-energy residuals to a fit to a power law with Γ ~ 2.4 are plotted.
We modelled the two spectra exploiting the constraints derived from the timing analysis by Legg et al. (2012) in terms of relative fractions of direct (flaring) and scattered (reprocessed) light. In particular, as the low-frequency lags are always positive with respect to the 0.4−1 keV band, the fraction of scattered light must increase from the softest to the hardest band: we used this constraint to construct a model able to reproduce the flaring and delayed spectra.
 |
Fig. 11 Top panel: soft flares (black) and their associated delayed signal (black) spectra unfolded against a reflection-dominated model: optxagn (dotted-dashed lines), a heavily absorbed cold reflector (dotted lines), and a slightly absorbed hot reflector (dashed lines). Bottom panel: same as above, but unfolded against a Compton-upscattering-dominated model: optxagn (dotted-dashed lines), a hot reflector (blue dashed line), and a hot Compton-upscattering model (dotted lines). |
First, we tested the best-fit model of Sect. 3.2.1 (i.e. optxagn plus an ionised reflector plus a cold, absorbed reflector,
both modelled with xillver). Within this model, optxagn represents the direct light,
while the two reflected components represent the scattered or reprocessed light. The
normalisation of the continuum was allowed to vary between the two data sets and is
~10% higher in the flares than in the
delayed spectrum. To match the constraints on the scattered or direct light fractions in
the different energy bands, another layer of ionised gas was introduced in front of the
ionised reflector. This model can reproduce the data very well (χ2/ν =
350/355) with continuum emission model parameters compatible with
those measured for the average spectra (Sect. 3.2.1, Table 6), but a higher flux in
the two reflected components for the delayed signal: the 0.4−10 keV observed flux is
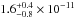 erg s-1 cm-2 and
erg s-1 cm-2 and
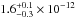 erg s-1 cm-2 for the ionised and cold
reflector in the delayed spectrum, respectively, as opposed to
erg s-1 cm-2 for the ionised and cold
reflector in the delayed spectrum, respectively, as opposed to
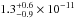 erg s-1 cm-2 and
erg s-1 cm-2 and
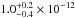 erg s-1 cm-2 in the flaring spectrum. The
ionised reflector is absorbed by a layer of gas with log (NH/cm
erg s-1 cm-2 in the flaring spectrum. The
ionised reflector is absorbed by a layer of gas with log (NH/cm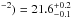 and log (ξ/erg cm
s
and log (ξ/erg cm
s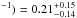 . The corresponding model and spectral
residuals are reported in the top panel of Fig. 11.
. The corresponding model and spectral
residuals are reported in the top panel of Fig. 11.
Alternatively, reprocessing may occur onto a hot medium such as to be able to
Compton-up-scatter the input (soft flares) photons. We tested this scenario by replacing
the cold absorbed reflector with the comptt model (Titarchuk 1994), where we assumed a disk-like geometry and a temperature for
the seed photons equal to the temperature of the warm, optically thick medium
responsible for the Compton-upscattering of disk photons inside rcor as
derived from optxagn, that is, kToptx ~ 150 eV.
Within this model, optxagn again represents the direct light, while the scattered or
reprocessed light is represented by comptt. This model can also well reproduce the data
(χ2/ν = 380/360) by
allowing again the optxagn normalisation to be higher in the flare spectrum than in the
spectrum with the delayed signal, and the Compton-upscattering component to emerge in
the delayed spectrum, with a 0.4−10 keV observed flux of 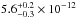 erg cm-2 s-1 and
erg cm-2 s-1 and
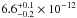 erg cm-2 s-1 for the flares and delayed
spectrum, respectively. The temperature of the Compton-upscattering material is found to
be
erg cm-2 s-1 for the flares and delayed
spectrum, respectively. The temperature of the Compton-upscattering material is found to
be 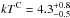 keV, its optical depth
keV, its optical depth
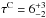 . The flares and delayed spectra unfolded
against this model, as well as spectral residuals, are plotted in the bottom panel of
Fig. 11.
. The flares and delayed spectra unfolded
against this model, as well as spectral residuals, are plotted in the bottom panel of
Fig. 11.
Detailed flare evolution.
 |
Fig. 12 Left panel: a segment of the 0.4−10 keV light curve of the pn observation 901 where a strong and sudden increase and decrease in flux is evident. Right panel: four 0.2−10 keV EPIC-pn spectral slices extracted at the beginning (during the first ks) of the high-flux level (black), during the remaining of the high-flux level (red), during the first ks of the decrease in flux (green), and during the remaining decreasing flux level (blue): the time intervals are marked in the top panel with the same colour-code. Error bars have been omitted for clarity. |
We have shown that the rapid source variability is dominated by intrinsic continuum amplitude variations (Sect. 3.2.1) and that a hard spectral component appears delayed with respect to the peaks of the emission (Sect. 3.2.3). A plausible interpretation is that the continuum light reverberates on some reprocessing material located ~1000 light-seconds away from the continuum source. If this is the case, we would expect to detect the reaction of this reprocessing gas following the longer-term source variability.
To test this expectation, we selected a time interval during the XMM-Newton observation 901 where there is a strong long-term flaring emission with large amplitude, namely the 7000−17 500 s segment. The total count rate undergoes amplitude oscillations of about a factor of two on a time scale of a few kiloseconds. In particular, there is a strong rise in flux just after the first 5 ks of the observation, when the flux increases by 50% in about 1500 s. The flux remains on a high level for about 6 ks, then decreases by a factor >2 in about 5000 s (Fig. 12, left panel). The corresponding spectra are plotted in the right panel of Fig. 12, omitting the error bars for clarity: spectral variability in response to the flux changes is evident. We can parametrise the spectral hardness by means of the ratio R of the observed count rate in a hard (4.5−7 keV) and in a soft (0.4−1 keV) energy band. During the first kilosecond of the flare (black spectrum) the source is soft, with R = 0.012; after one kilo second has elapsed, the hard band has had time to react to the increased soft flux (red spectrum) and is found to be in a medium hardness state, R = 0.017. Then the flux starts to drop: during the first kilosecond of decreasing flux (green spectrum) the hardness is highest (R = 0.019), given that the hard band still did not have time to adjust to the soft-band flux changes; then, after one kilosecond has elapsed, the source is found again in a medium hardness state (blue spectrum, R = 0.017).
4. Results
We present the results of both time-averaged and time-resolved X-ray spectroscopy of eight XMM-Newton and one Suzaku observations of the NLS1 Ark 564.
-
The Ark 564 X-ray continuum appears extremely steep in the whole energy band analysed in this work (0.4−30 keV, see Fig. 4). A fit to the RGS data in the range 0.4−1.9 keV gives an intrinsic slope Γ = 2.5−2.8 depending on the model adopted, optxagn or (powerlaw + blackbody) (Table 2). Modelling the broad-band data with a more physical model (optxagn + two reflectors) reveals a hard spectral component emerging above E ≳ 4 keV; the intrinsic continuum slope of Ark 564 thus ranges between Γ = 2.5−2.7 (Table 6).
-
High-resolution X-ray spectroscopy was performed in the soft band (E< 1.8 keV) with the RGS instrument (Sect. 3.1), and revealed the presence of ionised gas along the line of sight in the form of moderately ionised C, N, O, and Fe (Fig. 1 and Table 3).
-
Modelling the absorption features with the 2D photoionisation code Xstar requires three layers of absorbing gas, with ionisation parameter log (ξ/erg cm s-1) ~ −0.8, 1.3, and 2.4 and no velocity shift with respect to the systemic redshift of the source; the total measured absorbing column ranges from ~1021 cm-2 (fully covering absorber) to ~1.4 × 1021 cm-2 (allowing the absorber to be partially covering the continuum source), see Fig. 2 and Table 4.
-
A weak feature (EW ~ 150 eV, see Fig. 5) is detected in emission in the Fe K band, and it can be modelled either with a single broad Gaussian (σ ~ 300−600 eV) or with three narrow Gaussian emission lines with energies fixed to 6.4, 6.7, and 6.97 keV. The gas responsible for creating such features has a high ionisation state: replacing the Gaussians with a physically self-consistent reflection model such as xillver requires log (ξ/erg cm s-1) > 3.5.
-
Overall, the broad band spectrum of Ark 564 can be well reproduced by the superposition over the intrinsic continuum (modelled with optxagn) of two reflected components, both modelled with xillver: one hot (log (ξ/erg cm s-1) ~ 3−4), and one cold (log (ξ/erg cm s-1) < 1.2) and absorbed by a column density log (NH/cm-2) ~ 23−24 (see Fig. 6 and Table 6).
-
A blurred reflection scenario was also tested on the time-averaged spectra by convolving the reflected component with a relativistic convolution model (i.e. kdblur). Both the EPIC-pn and the Suzaku spectra can be reproduced statistically well in this scenario (Sect. 3.2.1, Fig. 7), albeit giving discrepant results in terms of the inner radius of the reflecting slab, which would be rin< 1.85rg in the case of the EPIC-pn, and
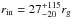 in the case of the Suzaku
data. This model underestimates the Suzaku PIN flux (see
Fig. 8).
in the case of the Suzaku
data. This model underestimates the Suzaku PIN flux (see
Fig. 8). -
A partial covering scenario is also able to well reproduce the EPIC-pn and Suzaku spectra, assuming that the intrinsic continuum is partially covered (Cf ~ 0.4−0.3) by a column of log (NH/cm-2) ~ 23.6−23.7 of moderately ionised gas (log (ξ/erg cm s-1) ~ 1−2), for the EPIC-pn and the Suzaku XIS+PIN data, respectively.
-
Given the highly variable X-ray flux of Ark 564 (see Fig. 3), spectral analysis was performed on three flux-selected spectra (Sect. 3.2.2). Despite variation in flux of a factor >2, the source spectral shape is does not vary dramatically (Fig. 9). Applying the best-fit model for the average spectra (optxagn + hot xillver + cold absorbed xillver) to the flux-selected spectra yields a good fit to the data, with the observed variability found to be driven by intrinsic continuum amplitude variations.
-
Time-resolved spectral analysis was performed on the eight XMM-Newton datasets by stacking all the time intervals identified by Legg et al. (2012) as “soft flares” as well as all the subsequent “delayed” emission (Sect. 3.2.3): the “delayed” excess of emission that follows the soft flares is spectroscopically identified as a spectral hardening at E ≳ 4 keV (Fig. 10).
-
The best-fit model for the time-averaged spectra was applied to the “soft flares” and the “delayed” spectra by using the additional constraints of the relative fractions of direct light (the “soft flaring” signal) and scattered or reprocessed light (the “delayed” signal) at different energies, as measured from the timing analysis by Legg et al. (2012) to “tune” the different spectral components.
-
In particular, from the notion that the fraction of scattered or direct light must be decreasing from high to low energies, we added to this model another layer of ionised gas with log (NH/cm-2) ~ 21.6 and log (ξ/erg cm s-1) ~ 0.2 in front of the ionised reflector. The model is thus optxagn + hot absorbed xillver + cold absorbed xillver. Within this model the observed spectral variability is driven by a decrease in continuum amplitude and an increase of the reflected flux in the “delayed” spectrum compared to the “flaring” spectrum. Given the time scales involved, a plausible physical scenario is to assume that the soft photons emitted during the continuum flare interact with the atoms of a gas located ~100rg from the continuum source and are scattered, which produces the hard “delayed” emission.
-
The gas responsible for scattering the soft flare emission could also be so hot as to be extremely ionised and thus be able to Compton up-scatter the flaring soft photons. We tested this scenario by replacing the cold absorbed reflector with the Comptonization model comptt and by removing the layer of absorbing gas in front of the ionised reflector (given the spectral shape of comptt, it is not necessary in this scenario). Again, we tuned the model following the constraints of the relative fractions of direct or scattered light in different energy bands. We found that this model is also able to reproduce the data with respect to the scattered or direct light fraction constraints in all energy bands,if the gas has a temperature kT ~ 4 keV and a moderate optical depth τ ~ 6 (Fig. 11).
-
A qualitative analysis of the detailed evolution of a single strong flare was presented. We showed that the source spectral shape hardens ~1 ks after a rise in flux, and that conversely, after a drop in flux it remains hard for ~1 ks before returning to its “usual” spectral shape (Fig. 12). This is hard to reconcile with relativistically blurred reflection-dominated scenarios because we would expect the soft and hard band to “communicate” on much shorter time scales (corresponding to a few light travel times instead of to ~a hundred), and strongly points, again, to reprocessing of the continuum photons by ionised gas located at 10 s−100 srg from the central supermassive black hole (SMBH).
5. Discussion and conclusions
Ark 564 has a very steep X-ray continuum: a simple power-law model fit to the Suzaku and EPIC-pn data above 3 keV yields a slope of Γ ~ 2.4 (Table 5). However, the intrinsic continuum is even steeper, being observationally diluted by a reflected or reprocessed component that emerges in the hard band above E ≳ 4 keV both in the time-averaged and in the time-resolved spectra. In a standard two-phase model for the X-ray emission of AGN (a cold optically thick accretion disk + a hot optically thin corona, Haardt & Maraschi 1991, 1993), such a steep intrinsic continuum would suggest a high optical depth (0.5 ≲ τ< 1) and/or a low temperature (Θ ≲ 50 keV) for the hot X-ray corona (Haardt et al. 1997).
To first order, the broad band spectra of Ark 564 are well modelled either by (power law + blackbody) or by optxagn and do not vary dramatically in shape despite flux variations of the order of a factor of ~2 (Fig. 9). There are clear signs of reprocessing gas in the inner regions of Ark 564, both in the soft and in the hard X-ray band.
In the soft band, a low column density of moderately ionised gas was found in the form of three different ionisation zones; the lowest ionisation state component of this absorbing gas might be the same as was observed in the UV band and studied by Crenshaw et al. (2002), who measured a modest velocity shift υUV ~ 200 km s-1 and a column density NH,UV ~ 1.5 × 1021 cm-2. Three zones of ionised gas, with a comparable total column density as measured in this work, as well as a modest (an upper limit of υout< 110 km s-1) outflowing velocity for the warm absorber was also found by Smith et al. (2008) in the analysis of five stacked XMM-Newton observations of Ark 564 performed between 2000 and 2001. A Chandra/HETG observation performed in 2000 also revealed multiple phases of ionised gas with a modest column density and zero net velocity shift (Matsumoto et al. 2004); new observations performed with the same instrument in 2008 resolved a velocity of about 100 km s-1 for the multiphase absorber (Gupta et al. 2013a). Using the same dataset, Gupta et al. (2013b) claimed the discovery of a mildly relativistic (υout ~ 0.1c) outflowing absorber by identifying three absorption features due to OVI and OVII. We note that the RGS data show two non-identified absorption features (Fig. 1), which, if identified with NVII and OVII Kα transitions, would suggest a similar outflow velocity υout ~ 0.1c. However, the identification of a wind phase based solely on two absorption troughs where most reasonable photo-ionisation models would predict a wealth of absorption lines due to many species is challenging, and we do not discuss these features further.
In the hard X-ray band, a weak feature (EW ~ 150 eV) is detected in emission in the Fe K band, and it can be modelled either with a single broad Gaussian (σ ~ 300−600 eV) or with three narrow Gaussian emission lines with energies fixed to 6.4, 6.7, and 6.97 keV. In any case, ionised iron in the inner regions of Ark 564 is required by the data. Given the width of the single Gaussian, simple Keplerian motion of a distribution of clouds around the SMBH would suggest a distance of the order of 100−1000 s rg. The same range of distance would be suggested by the lack of reaction of the iron emission complex to the large amplitude variations of the ionising flux (Sect. 3.2.2).
However, to reproduce the spectral shape at the highest energies probed in this study, a hard-dominated component is required. This can be modelled either with a second (colder) reflector, a partially covered component, or with a relativistically blurred reflector. In the cold reflection scenario, a column NH> 1023 cm-2 must absorb the reflected emission to not over-predict the strength of soft X-ray emission lines, which results in a quite contrived geometry. In the partial covering scenario, during the four years elapsed between the Suzaku and XMM-Newton observations the absorber covering factor would have significantly decreased while its ionisation state would have increased; in addition, the mass accretion rate in this scenario would be super-Eddington, which is unlikely. In the blurred reflection scenario, the XMM-Newton data require an accretion disk extending down to <2rg of the black hole, which is inconsistent with the Suzaku data, which require rin ~ 30rg. Noting also how the inclination angle of ~90 degrees would be hard to reconcile with the fact that Ark 564 is seen almost face-on (Smith et al. 2008), and the severe underestimation of the PIN flux in this scenario (Fig. 8), we do not consider this to be physically plausible. Kara et al. (2013) reported the discovery of high-frequency Fe K lags of about 100 s in the first half of the 2011 XMM-Newton observational campaign on Ark 564 and ascribed them to relativistic reflection close to the central SMBH. It is unclear, however, how to reconcile this scenario with the lack of any lag during the second half of the observational campaign. Relativistic effects might be at work in the inner regions of Ark 564, but probably not that extreme: given the black hole mass estimate for Ark 564, a time lag of 100 seconds corresponds to about ten gravitational radii. Emmanoulopoulos et al. (2014) inferred in the framework of a relativistic reflection lamp-post model a low spin of about 0.05 for the central SMBH of Ark 564, which again suggests that relativistic effects, if present, are not dominant in the very inner regions of Ark 564.
Alternatively, reprocessing of the soft photon flares could occur in a medium so hot as to be able to Compton-upscatter them, giving rise to the hard excess component. In this case, we would have three different regions where Compton-upscattering occurs: a fraction (about 75%) of the UV seed photons from the accretion disk within ~50rg from the central SMBH would be Comptonized in the very hot and optically thin X-ray corona (τ ≪ 1,kT ~ 100 keV), giving rise to the primary X-ray power-law emission; the remaining ~25% of the UV seed photons would be Comptonized in a warm and optically thick medium (τ ~ 40,kT ~ 150 eV) that contributes to the emission below ~2 keV; and all of this Comptonized emission would be then further Compton-upscattered in a hot and optically thick medium (τ ~ 6,kT ~ 4 keV) located 10 s to 100 s of gravitational radii from the central supermassive black hole, following flares of emission. It would then follow that Comptonization plays a fundamental role in explaining the physics of the inner regions of AGN: in recent years, evidence is growing for it to explain the broad-band spectrum of several AGN, see, for instance, Mrk 509 (Mehdipour et al. 2011; Petrucci et al. 2013), PG 1244+026 (Jin et al. 2013), 1H 0419-577 (Di Gesu et al. 2014), Ark 120 (Matt et al. 2014), and NGC 5548 (Mehdipour et al. 2015), and references therein. Future high-quality spectral and timing observations on extended energy ranges with satellites such as NuSTAR (Harrison et al. 2013) will be able to distinguish between the different physical scenarios and test the hypothesis that Comptonization is the main mechanism at work.
The spin parameter a is degenerate with the mass accretion rate unless one can constrain the latter with UV flux measurements from the disk (see e.g. Done et al. 2013), which we lack because of strong contamination of the host galaxy emission in this band; therefore we fixed for simplicity a = 0.
Soft flares are defined by Legg et al. (2012) as those only detected in the 0.4−1 keV band.
Acknowledgments
We acknowledge the referee for their useful comments that helped improving the manuscript. M.G. would like to thank Hiroki Akamatsu for useful discussions, and the NWO and the ESA Research Fellowship in Space Science program for financial support. Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration, and of the NASA Astrophysics Data System Bibliographic Services.
References
- Behar, E., Sako, M., & Kahn, S. M. 2001, ApJ, 563, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Boldt, E. 1987, Phys. Rep., 146, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Botte, V., Ciroi, S., Rafanelli, P., & Di Mille, F. 2004, AJ, 127, 3168 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, W. N., Fabian, A. C., Nandra, K., Reynolds, C. S., & Brinkmann, W. 1994, MNRAS, 271, 958 [NASA ADS] [Google Scholar]
- Comastri, A., Stirpe, G. M., Vignali, C., et al. 2001, A&A, 365, 400 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., Turner, T. J., et al. 2002, ApJ, 566, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Dewangan, G. C., Griffiths, R. E., Dasgupta, S., & Rao, A. R. 2007, ApJ, 671, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Di Gesu, L., Costantini, E., Piconcelli, E., et al. 2014, A&A, 563, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 420, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Jin, C., Middleton, M., & Ward, M. 2013, MNRAS, 434, 1955 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Turner, T. J., Pounds, K., et al. 2002, ApJ, 568, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Emmanoulopoulos, D., Papadakis, I. E., Dovčiak, M., & McHardy, I. M. 2014, MNRAS, 439, 3931 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Dauser, T., Reynolds, C. S., et al. 2013, ApJ, 768, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Gruber, D. E., Matteson, J. L., Peterson, L. E., & Jung, G. V. 1999, ApJ, 520, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Mathur, S., Krongold, Y., & Nicastro, F. 2013a, ApJ, 768, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Mathur, S., Krongold, Y., & Nicastro, F. 2013b, ApJ, 772, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Haardt, F., Maraschi, L., & Ghisellini, G. 1997, ApJ, 476, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, C., Done, C., Middleton, M., & Ward, M. 2013, MNRAS, 436, 3173 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S., de Vries, C. P., Steenbrugge, K. C., et al. 2011, A&A, 534, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kara, E., Fabian, A. C., Cackett, E. M., et al. 2013, MNRAS, 434, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, K., Tsunemi, H., Dotani, T., et al. 2007, PASJ, 59, 23 [Google Scholar]
- Laor, A. 1991, ApJ, 376, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Legg, E., Miller, L., Turner, T. J., et al. 2012, ApJ, 760, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, C., Leighly, K. M., & Marshall, H. L. 2004, ApJ, 603, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Marinucci, A., Guainazzi, M., et al. 2014, MNRAS, 439, 3016 [NASA ADS] [CrossRef] [Google Scholar]
- Mehdipour, M., Branduardi-Raymont, G., Kaastra, J. S., et al. 2011, A&A, 534, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mehdipour, M., Kaastra, J. S., Kriss, G. A., et al. 2015, A&A, 575, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, L., Turner, T. J., & Reeves, J. N. 2008, A&A, 483, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitsuda, K., Bautz, M., Inoue, H., et al. 2007, PASJ, 59, 1 [Google Scholar]
- Papadakis, I. E., Brinkmann, W., Page, M. J., McHardy, I., & Uttley, P. 2007, A&A, 461, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrucci, P.-O., Paltani, S., Malzac, J., et al. 2013, A&A, 549, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reeves, J., Done, C., Pounds, K., et al. 2008, MNRAS, 385, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. A. N., Page, M. J., & Branduardi-Raymont, G. 2008, A&A, 490, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stirpe, G. M. 1990, A&AS, 85, 1049 [NASA ADS] [Google Scholar]
- Takahashi, T., Abe, K., Endo, M., et al. 2007, PASJ, 59, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, T. J., George, I. M., & Netzer, H. 1999, ApJ, 526, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, T. J., Romano, P., George, I. M., et al. 2001, ApJ, 561, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Pounds, K. A., Reeves, J., Warwick, R., & Edelson, R. 1999, MNRAS, 308, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Brandt, W. N., Boller, T., Fabian, A. C., & Vaughan, S. 2004, MNRAS, 347, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Fit to the full band with optxagn, an ionised reflector, and an absorbed cold reflector.
All Figures
 |
Fig. 1 RGS spectral residuals in the source rest frame. |
| In the text | |
 |
Fig. 2 Rest-frame plot of the three zones of warm absorbing gas detected in the RGS data. From top to bottom, the ionisation parameter and column density are log (ξ/erg cm s-1) ~ −0.8, 1.3,2.4 and log (NH/cm-2) ~ 20.1, 20.3, 20.9. |
| In the text | |
 |
Fig. 3 Light curves for the eight XMM-Newton observations extracted in the 0.4−10 keV band and binned to 128 s. |
| In the text | |
 |
Fig. 4 Observed frame EFEXMM-Newton EPIC pn (top) and Suzaku XIS+PIN (bottom) spectra unfolded against a power law with Γ = 2. |
| In the text | |
 |
Fig. 5 Rest frame spectral residuals for a fit to a power law in the 3−6 and 7−10 keV band for the pn (top) and XIS (bottom) data. |
| In the text | |
 |
Fig. 6 EPIC pn (top) and Suzaku XIS+PIN (bottom) spectra unfolded against the best-fit model described in Table 6, along with data-to-model ratios. The intrinsic continuum emission is modelled with optxagn (dotted-dashed black line); two reflectors are modelled with xillver, a highly ionised (dashed blue line) and a cold, absorbed one (solid magenta line). The total model is plotted in red. |
| In the text | |
 |
Fig. 7 Stacked pn spectrum unfolded against two different representations of a blurred reflection scenario. Top panel: continuum modelled with power law (black dotted-dashed line) + blackbody (blue dotted line), and blurred reflection modelled with kdblur*xillver (blue dashed line); bottom panel: same as above, but modelling the continuum with optxagn (black dotted-dashed line). |
| In the text | |
 |
Fig. 8 Suzaku XIS+PIN spectra unfolded against a blurred reflection model, colour-coded as the bottom panel of Fig. 7. |
| In the text | |
 |
Fig. 9 0.4−10 keV flux-selected spectra unfolded against a power law with Γ = 2: low (black), medium (red), and high (blue) flux states. |
| In the text | |
 |
Fig. 10 Top panel: soft flares (black) and their associated delayed signal (red) spectra unfolded against a power law with Γ = 2. Bottom panel: data-to-model ratio to a power law fitted on the 2−10 keV band. |
| In the text | |
 |
Fig. 11 Top panel: soft flares (black) and their associated delayed signal (black) spectra unfolded against a reflection-dominated model: optxagn (dotted-dashed lines), a heavily absorbed cold reflector (dotted lines), and a slightly absorbed hot reflector (dashed lines). Bottom panel: same as above, but unfolded against a Compton-upscattering-dominated model: optxagn (dotted-dashed lines), a hot reflector (blue dashed line), and a hot Compton-upscattering model (dotted lines). |
| In the text | |
 |
Fig. 12 Left panel: a segment of the 0.4−10 keV light curve of the pn observation 901 where a strong and sudden increase and decrease in flux is evident. Right panel: four 0.2−10 keV EPIC-pn spectral slices extracted at the beginning (during the first ks) of the high-flux level (black), during the remaining of the high-flux level (red), during the first ks of the decrease in flux (green), and during the remaining decreasing flux level (blue): the time intervals are marked in the top panel with the same colour-code. Error bars have been omitted for clarity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


