| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 16 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201425191 | |
| Published online | 18 May 2015 | |
Ephemeris, orbital decay, and masses of ten eclipsing high-mass X-ray binaries⋆
1 International Space Science Institute Hallerstrasse 6 3012 Bern Switzerland
e-mail:
mfalanga@issibern.ch
2 International Space Science Institute Beijing, No.1 Nanertiao, Zhongguancun, Haidian District, 100190 Beijing, PR China
3 ISDC Data Centre for Astrophysics, Chemin d’Écogia 16, 1290 Versoix, Switzerland
4 Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32, 117997 Moscow, Russia
5 Service dAstrophysique (SAp), IRFU/DSM/CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
6 Universitätssternwarte der Ludwig-Maximilians-Universität München, Scheinerstrasse 1, 81679 München, Germany
Received: 20 October 2014
Accepted: 25 February 2015
We update the ephemeris of the eclipsing high-mass X-ray binary (HMXB) systems LMC X-4, Cen X-3, 4U 1700-377, 4U 1538-522, SMC X-1, IGR J18027-2016, Vela X-1,IGR J17252-3616, XTE J1855-026, and OAO 1657-415 with the help of more than ten years of monitoring these sources with the All Sky Monitor onboard RXTE and with the Integral Soft Gamma-Ray Imager onboard INTEGRAL. These results are used to refine previous measurements of the orbital period decay of all sources (where available) and provide the first accurate values of the apsidal advance in Vela X-1 and 4U 1538-522. Updated values for the masses of the neutron stars hosted in the ten HMXBs are also provided, as well as the long-term light curves folded on the best determined orbital parameters of the sources. These light curves reveal complex eclipse ingresses and egresses that are understood mostly as being caused by accretion wakes. Our results constitute a database to be used for population and evolutionary studies of HMXBs and for theoretical modeling of long-term accretion in wind-fed X-ray binaries.
Key words: stars: neutron / binaries: eclipsing / X-rays: binaries / pulsars: general
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
High-mass X-ray binaries (HMXB) are among the brightest X-ray sources in our Galaxy. They were discovered for the first time with the Uhuru satellite (Giacconi et al. 1971) and independently with balloon-born instruments (see e.g., Lewin et al. 1971). These sources typically host a compact object (often a neutron star, NS) that accretes material lost by a massive companion. Depending on the nature of the latter star, HMXBs are divided into Be or supergiant X-ray binaries (SgXBs). In the first case, a conspicuous X-ray emission is generated by accretion of matter from the dense decretion disk around the companion star, which leads to transient events (outbursts) of different types (see e.g., Reig 2011, for a review). In the SgXBs, the compact object can either accrete through the fast and dense wind produced by the companion, or in a few cases through the beginning of an atmospheric Roche-lobe overflow (Soberman et al. 1997). A number of systems showed evidence that both mechanisms contribute to the accretion onto the compact object and the overall X-ray emission (see, e.g., Chaty 2011, for a recent review).
Orbital parameters of the ten eclipsing HMXB systems in ascending order of the orbital period.
In Roche-lobe accreting systems, the inflowing material from the companion star is endowed with a high specific angular momentum, and thus accretion is generally mediated by a disk surrounding the compact object. As this is a very efficient way to accrete matter, disk-fed systems typically achieve a relatively high X-ray luminosity (~ 1038 erg s-1). In wind-accreting systems, the compact object is instead deeply embedded in the material lost by the companion star, which does not posses sufficient angular momentum to form an accretion disk, and which accretes quasi-spherically onto the NS (see, e.g., Bozzo et al. 2008; Shakura et al. 2012, for recent reviews). This process leads to a strongly variable X-ray emission, reaching values significantly lower than those attained by disk-accreting systems (ranging from 1034 to 1036 erg s-1; see, e.g., Joss & Rappaport 1984; Nagase 1996; Bildsten et al. 1997).
Since their discovery, HMXBs have been intensively monitored to test wind-accretion models onto magnetized NSs (see, e.g., Lamers et al. 1976; Bhattacharya & van den Heuvel 1991; Lutovinov et al. 2013, and references therein), measure the long-term spin-variation of NSs as a function of the mass accretion rate (probing the so-called accretion torques, see, e.g., Ghosh & Lamb 1979; Lovelace et al. 1995), and study the evolution of the orbital parameters of these systems, for instnace, by measuring the orbital period decay (see Bildsten et al. 1997, and references therein). In the majority of HMXBs, pulsations in the X-ray emission firmly established the NSs as accreting compact objects (see, e.g., Lutovinov et al. 2005; Lutovinov & Tsygankov 2009, for a recent review and HMXBs statistics), and the detection of cyclotron absorption spectral features permitted directly measuring their magnetic field strength (~ 1 − 5 × 1012 G; see, e.g., Coburn et al. 2002; Filippova et al. 2005; Caballero & Wilms 2012). In the HMXBs that did not show clear evidence of pulsations, black hole companions still cannot be firmly ruled out (see, e.g., the case of 4U 1700-377, Rubin et al. 1996; Clark et al. 2002).
Only in a few sources among more than one hundred HMXBs is the inclination of the system high enough for the compact star to be periodically occulted along our line of sight by the companion, giving rise to X-ray eclipses. For these sources, it is possible to infer a number of orbital parameters (e.g., orbital period) from the measured duration of the eclipse. The energy-dependent profile of the X-ray light curve during the eclipse ingress and egress also reveals details of the OB stellar wind structure (e.g., White et al. 1995). In systems in which orbital ephemerides can be accurately measured over several decades, it is expected that changes in the orbital period can also be revealed, which will provide further insight into tidal interaction and mass transfer mechanisms that regulated the accretion onto the compact object. In eccentric systems, accurate ephemerides can also be used to infer the angle of periastron and the apsidal advance (see, e.g., van der Klis & Bonnet-Bidaud 1984, and references therein).
We take advantage of the available long-term monitoring observations of ten eclipsing HMXBs1, carried out with the hard X-ray imager IBIS/ISGRI (17 keV−200 keV) onboard INTEGRAL and the All Sky Monitor (ASM) onboard RXTE (2−12 keV) to obtain the most accurate ephemeris available so far for these sources (Liu et al. 2006). We note that Coley (2015) also performed long term studies of five eclipsing sources by using Swift Burst Alert Telescope (BAT) data. These authors included in their source list also the eclipsing HMXBs SAX J18027.7-2017 and XTE J1855-026. We significantly improve their previously measured orbital periods, eclipse durations, and the masses of the accreting NSs they host. Measurements of the orbital period decay and apsidal motion are presented for the first time for several of these systems, and measurements are provided for all the others that are refined from those currently available in the literature. We discuss the energy-dependent profile of the long-term light curve during the eclipse ingress and egress for all these systems in terms of X-ray absorption expected in wind- and/or disk-accreting systems.
1.1. Ten eclipsing HMXBs
In Table 1 we list the ten sources selected for the present work and provide a summary of their main characteristics, as measured in the most recently available literature: the orbital epoch, the orbital period Porb, the spin period Ps, the orbital period change Ṗorb/Porb, the projected semi-major axis axsin i, the eccentricity e, and the periastron angle ω. All these systems show evidence for alternate spin-up and spin-down phases. In some cases the average spin evolution led to an effective long-term increase or decrease of the NS spin rate (see e.g., Bildsten et al. 1997; Inam et al. 2010, for more details), and thus the spin periods reported in Table 1 should only be considered as indicative. The spin period of the NS (possibly) hosted in 4U1700-377 is currently unknown.
For the two HMXBs EXO 1722-363 and SAX J1802.7-2017, we also indicate in Table 1 the associated INTEGRAL source names IGR J17252-3616 and IGR J18027-2016 (Zurita Heras et al. 2006; Revnivtsev et al. 2004). These two sources are classified as highly absorbed HMXBs (see, e.g., Walter et al. 2006), and indeed, these are the only sources in which no eclipse is evident from their soft X-ray light curves (<12 keV, see Sect. 4).
The ten selected sources comprise both disk- and wind-accreting systems. A different shape of the eclipse ingress and egress is expected in these two cases as a function of the energy (see Sect. 4). The relatively high X-ray luminosity of LMC X−4, Cen X−3, and SMC X−1 makes these sources the prime candidates for being disk-fed systems, whereas 4U 1700−377, 4U 1538−522, SAX J1802.7−2017, XTE J1855−026, Vela X−1, and EXO 1722−363 are all thought to be wind-fed systems. OAO 1657−415 is unique among the known HMXBs as it is believed to be a wind-fed system for most of the time, and to only sporadically undergo episodes of accretion from a temporary disk. Since the binary is too wide for Roche-lobe overflow to occur, this may provide the first clear evidence that winds in HMXBs possess sufficient angular momentum to form accretion disks (see, e.g., Bildsten et al. 1997; Chakrabarty et al. 1993). Additional information on the ten sources can be found in Liu et al. (2006).
2. Observations and data
All the eclipsing HMXBs reported in Table 1 have been continuously monitored in the X-ray domain by the ASM since the beginning of 1996 and by the IBIS/ISGRI since the early 2003. We used publicly available IBIS/ISGRI light curves retrieved from the on-line tool High-Energy Astrophysics Virtually ENlightened Sky (HEAVENS)2. HEAVENS data reduction was performed using the standard Offline Science Analysis (OSA) version 9.0 distributed by the INTEGRAL Science Data Center (Courvoisier et al. 2003). For each source we downloaded the ISGRI high-energy light curve binned over each pointing (science window) of roughly 2 ks, in the 17−40 keV and 40−150 keV band. The RXTE/ASM light curves were retrieved from the NASA HEARSAC FTP server3 binned dwell by dwell (90 s bins) in the 1.5−3 keV, 3−5 keV, and 5−12 keV energy bands. In Table 2, we report the observation time interval and the total effective exposure time of the ASM and ISGRI data for each of the selected sources. All the photons arrival times of the INTEGRAL/ISGRI and RXTE/ASM light curves were corrected to the barycenter reference time of the solar system. We used the OSA task barycent for the ISGRI data and the procedure described in the RXTE cookbook4 for the ASM data. The barycentric correction is usually considered mainly to perform a high-precision timing analysis on a short observational time interval. However, in the present case, it was required to ensure uniformity over a long-term set of data spanning more than a decade.
For each of the eclipses found in the ISGRI and ASM light curves we measured the ingress, egress, and the mid-eclipse time as described in Sect. 3.1.
Log of INTEGRAL/ISGRI and RXTE/ASM observations of the ten selected eclipsing HMXBs.
Updated epochs, orbital periods, and period decay of the ten sources obtained by using all the available mid-eclipse times.
 |
Fig. 1 All measured mid-eclipses, Tecl, mean longitudes, Tπ/ 2, and orbital epochs are shown with the best-fit models as a function of the orbit numbers. In all cases, the best-fit model is a quadratic or linear fit to the epochs. The lower panel in each figure shows the residual from the best fit. |
3. Best-fit ephemerides
3.1. Orbital period and orbital period decay
For each of the selected sources we first determined the mid-eclipse (superior conjunction) times, Tecl, of all the eclipses found in the ISGRI and ASM data by using the e-fold method. We then improved these values by fitting the newly determined epochs together with those derived from earlier observations (Tn; see Appendix A.1 and references therein) using the quadratic orbital change function: 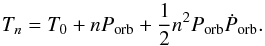 (1)Here Porb is the orbital period in days, Ṗorb is the period derivative at the epoch T0, and n is the integer number of elapsed binary orbits. All the new measured orbital ephemeris are reported in Table 3. We show in Fig. 1 the best-fit models to the data obtained by assuming either a simple linear orbital evolution or including a quadratic orbital decay term (the residuals from these fits are also shown). For all systems that are characterized by a non-negligible eccentricity (≳0.1), we fitted the mid-eclipse epochs, Tecl, and the mean longitude, Tπ/ 2, epochs separately. For OAO 1657-415 we fit the epochs of Tecl and Tπ/ 2 together because the periastron angle of the source is known to be about 90° and therefore Tecl ≈ Tπ/ 2 (see Sect. 3.2). All the least-squares fits in this work were performed by using the IDL tool MPFIT (Markwardt 2009). We obtained in all cases
(1)Here Porb is the orbital period in days, Ṗorb is the period derivative at the epoch T0, and n is the integer number of elapsed binary orbits. All the new measured orbital ephemeris are reported in Table 3. We show in Fig. 1 the best-fit models to the data obtained by assuming either a simple linear orbital evolution or including a quadratic orbital decay term (the residuals from these fits are also shown). For all systems that are characterized by a non-negligible eccentricity (≳0.1), we fitted the mid-eclipse epochs, Tecl, and the mean longitude, Tπ/ 2, epochs separately. For OAO 1657-415 we fit the epochs of Tecl and Tπ/ 2 together because the periastron angle of the source is known to be about 90° and therefore Tecl ≈ Tπ/ 2 (see Sect. 3.2). All the least-squares fits in this work were performed by using the IDL tool MPFIT (Markwardt 2009). We obtained in all cases 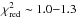 .
.
For the five sources LMC X-4, Cen X-3, 4U 1700-377, SMC X-1, and OAO1657-415 we measured a significant orbital period derivative (see Table 3). For 4U 1538-522, the 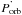 value was obtained excluding the mid-eclipse times derived from the Uhuru and Ariel light curves (Cominsky & Moraes 1991; Davison et al. 1977); for OAO 1657-415 we excluded the orbital epoch time reported by Barnstedt et al. (2008). All these values were affected by larger uncertainties than the others and did not provide significant improvements to the fits. For the five sources characterized by a value of
value was obtained excluding the mid-eclipse times derived from the Uhuru and Ariel light curves (Cominsky & Moraes 1991; Davison et al. 1977); for OAO 1657-415 we excluded the orbital epoch time reported by Barnstedt et al. (2008). All these values were affected by larger uncertainties than the others and did not provide significant improvements to the fits. For the five sources characterized by a value of 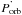 consistent with zero (see Table 3), the reported orbital epochs and periods were determined by using the linear orbital change function (see Eq. (1)).
consistent with zero (see Table 3), the reported orbital epochs and periods were determined by using the linear orbital change function (see Eq. (1)).
3.2. Apsidal advance
In eccentric orbits the time of mid-eclipse, Tecl, determined from the eclipses in the X-ray light curves, and the time of mean longitude, Tπ/ 2, determined through the pulse arrival time technique, do not coincide. In this case we distinguished the orbital period, Porb,π/ 2, defined as the time elapsed between two successive passages at the same mean-longitude 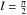 , and the eclipse period, Porb,ecl, defined as the difference between two successive mid-eclipse epochs. The mean orbital longitude l can be expressed as l = M + ω, where, M is the mean anomaly and ω is the argument of periapsis. With the orbital relations, expressed in the first order of the eccentricity, the time delay between Tecl and Tπ/ 2 can be written as (see, e.g., van der Klis & Bonnet-Bidaud 1984, and references therein)
, and the eclipse period, Porb,ecl, defined as the difference between two successive mid-eclipse epochs. The mean orbital longitude l can be expressed as l = M + ω, where, M is the mean anomaly and ω is the argument of periapsis. With the orbital relations, expressed in the first order of the eccentricity, the time delay between Tecl and Tπ/ 2 can be written as (see, e.g., van der Klis & Bonnet-Bidaud 1984, and references therein) 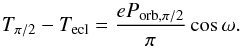 (2)For an eccentricity of e ~ 0.1 and a periastron angle of ω ~ 150° as in Vela X-1, this can result in a lag of 0.3 day. This periodic lag is zero for eccentric orbits if ω = ± 90° and highest when ω = 0 or 180°. If the periastron angle ω is constant, then Porb,ecl = Porb,π/ 2. However, if the periastron is moving at a rate
(2)For an eccentricity of e ~ 0.1 and a periastron angle of ω ~ 150° as in Vela X-1, this can result in a lag of 0.3 day. This periodic lag is zero for eccentric orbits if ω = ± 90° and highest when ω = 0 or 180°. If the periastron angle ω is constant, then Porb,ecl = Porb,π/ 2. However, if the periastron is moving at a rate 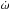 , the difference between Porb,ecl and Porb,π/ 2 at the first order of its eccentricity, e, can be obtained by differentiating Eq. (2)(see Deeter et al. 1987)
, the difference between Porb,ecl and Porb,π/ 2 at the first order of its eccentricity, e, can be obtained by differentiating Eq. (2)(see Deeter et al. 1987) 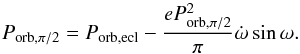 (3)Equations (2)and (3)allow estimating ω and
(3)Equations (2)and (3)allow estimating ω and 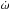 if sinω ≠ 0. For circular orbits we have Tecl = Tπ/ 2 and thus Porb,ecl = Porb,π/ 2. From Eq. (3) and the value of ΔPobs = Porb,ecl − Porb,π/ 2 determined from the observations, we also calculated the apsidal motion
if sinω ≠ 0. For circular orbits we have Tecl = Tπ/ 2 and thus Porb,ecl = Porb,π/ 2. From Eq. (3) and the value of ΔPobs = Porb,ecl − Porb,π/ 2 determined from the observations, we also calculated the apsidal motion 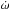 . The same epoch time was used to calculate (Tecl,Porb,ecl) and (Tπ/ 2,Porb,π/ 2), as this time corresponds to the epoch of ω (see Table 1).
. The same epoch time was used to calculate (Tecl,Porb,ecl) and (Tπ/ 2,Porb,π/ 2), as this time corresponds to the epoch of ω (see Table 1).
Of the four sources with e ≳ 0.04 considered in the present work (see Table 1), we were unable carry out a detailed comparison of the measured epoch time lag ΔTobs = Tπ/ 2 − Tecl, obtained from our best-fit ephemerides with the predicted lag, with ΔTcalc = ePorb,π/ 2cosω/π, for OAO 1657-415 (its periastron angle is ω ≈ 90° and thus Tecl ≃ Tπ/ 2), XTE J1855-026 (only one Tπ/ 2 and Porb,π/ 2 are available to date; see Appendix A.1), and EXO 1722-363 (no reliable eccentricity measurement is available in the literature; Thompson et al. 2007). For 4U 1538-522 we used the eccentricity, e, and the periastron angle, ω, from Clark (2000) and Mukherjee et al. (2006); for Vela X-1 we used the ephemeris and orbital parameters from Rappaport et al. (1976, see also Table 1. For these two sources the best fits were obtained using the linear orbital change function (Eq. (1)). All results are reported in Table 4. For 4U 1538-522 two different fits are reported. In the first, we fit all the mean longitude epochs (Tπ/ 2) until 1997 with the last one reported by Clark (2000); in the second, we included all the longitude epochs until 2003, with the last one reported by Mukherjee et al. (2006). The two cases only yield compatible results (to within the uncertainties) if the epochs reported from Clark (2000) are excluded from the second fit. Note that the same mid-eclipse time, Tecl, was used for both fits (see Table 4).
4. Folded light curves
The updated ephemerides we obtained for the ten HMXBs allowed folding their light curves with an unprecedented accuracy. We folded for each source the dwells RXTE/ASM light curves in the 1.3−3 keV, 3−5 keV, and 5−12 keV bands, and the INTEGRAL/ISGRI light curves in the 17−40 keV and 40−150 keV energy bands by using 128 phase bins (see Figs. 2 and 3). For LMC X-4, Cen X-3, 4U 1700-377, SMC X-1, and OAO 1657-415 the orbital period derivative was also taken into account during the folding. Given the values of Ṗorb/Porb in Table 3, we obtained for these sources a maximum variation of the orbital period (between the first and last mid-eclipse time of the RXTE/ASM dataset) of ~0.088, 0.158, 0.139, 0.310, and 0.299 days. These delays were calculated by using the quadratic term in Eq. (1)rewritten as (Δt)2Ṗorb/Porb (we replaced nPorb by the observational elapsed time, Δt). The orbital derivatives for these sources are significant because the derived correction factors in time are larger than a phase bin (1 / 128), and the including these corrections significantly improves the shape of the folded light curves.
The fluxes (cts/s) of the ten sources measured during the occultation of the compact object by the companion star are reported in Table 5. In all cases, the fluxes in the lower energy bands (1.3−3 keV, 3−5 keV, and 5−12 keV energy bands) are consistent with zero. This suggests that in the soft X-ray domain the source emission is strongly absorbed by the extended corona of the companion star and from the companion star itself (in the literature, residual fluxes have been reported at a level that is too low to be detectable by the ASM onboard RXTE; see, e.g., Ebisawa et al. 1996; Lutovinov et al. 2000; Vrtilek et al. 2001). At higher energies (17−40 keV and 40−150 keV), the observed residual X-ray fluxes are most likely caused by an extended X-ray scattering region (e.g., the accretion disk around the compact object, the X-ray irradiated surface of the companion star, or a cloud of material diffused around the system and produced by the intense wind of the supergiant star). These findings, together with the different shapes of the eclipse ingress and egress in Figs. 2 and 3, are discussed in Sect. 5.4.
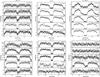 |
Fig. 2 Folded light curves of the first six eclipsing HMXBs in Table 1. Data in the energy range 1.3−12 keV were obtained from the RXTE/ASM, while harder X-ray data are taken from INTEGRAL/ISGRI (17−150 keV). In all cases, the light curves have been folded by using the updated ephemerides obtained in the present work. |
4.1. Semi-eclipse angles
We used the folded light curves in the energy band 17−40 keV to estimate the semi-eclipse angle, θe, of each eclipse observed from the ten selected sources in Table 1. In this energy band, all eclipses look sharp and symmetric, thus permitting to achieve an unprecedented accuracy in the determination of the occultation time (see Figs. 2 and 3). We followed the fitting method described in Rubin et al. (1996). The duration of each eclipse was calculated from the measured phase of the eclipse ingress and egress.
Measured cts/s during the occultation phases of the ten selected sources in this work.
The average phase φ(i,e) (defined as the phase at which 99% of the source flux is occulted at eclipse ingress or egress) and the transition phase width τ(i,e) were estimated by independently fitting the ISGRI light curve in the 17−40 keV and (whenever possible) in the 40−150 keV band with the function ![\begin{equation} F_{j} = F_{\rm cons}\, {\rm exp}\,\left\{ {\rm ln}(0.01)\,{\rm exp}\,\left[-(\phi_{j}-\phi_{\rm (i,e)})/\tau_{\rm (i,e)}\right]\right\}. \label{eq:4} \end{equation}](/articles/aa/full_html/2015/05/aa25191-14/aa25191-14-eq90.png) (4)Here j is the phase bin number and Fcons is the averaged count rate of the source outside the eclipse determined before the fit. The 0.5−1.0 orbital phase was considered to fit the eclipse ingress, the 1.0−1.5 orbital phase was used for the egress. The duration of each X-ray eclipse for the ten sources was calculated as Δϕ = (1.0 − φi) + φe in the (17−40 keV) band, thus providing the semi-eclipse angles, θe, reported in Table 6 (all uncertainties are given at 1σ c.l.). We verified that the eclipse semi-angles measured in the 17−40 keV and 40−150 keV energy band are compatible to within the uncertainties.
(4)Here j is the phase bin number and Fcons is the averaged count rate of the source outside the eclipse determined before the fit. The 0.5−1.0 orbital phase was considered to fit the eclipse ingress, the 1.0−1.5 orbital phase was used for the egress. The duration of each X-ray eclipse for the ten sources was calculated as Δϕ = (1.0 − φi) + φe in the (17−40 keV) band, thus providing the semi-eclipse angles, θe, reported in Table 6 (all uncertainties are given at 1σ c.l.). We verified that the eclipse semi-angles measured in the 17−40 keV and 40−150 keV energy band are compatible to within the uncertainties.
All the semi-eclipse angles we measured and reported in Table 6 are a few degrees shorter than the values reported in the literature, the only two exceptions being 4U 1700-377 and LMC X-4. For 4U 1700-377, our measured ingress phase is shorter than that measured by Rubin et al. (1996) and consequently translates into a slightly longer eclipsing phase. For LMC X-4 our determined semi-eclipse angle of θe ≈ 16° is about half the value ~27° reported in the literature (Li et al. 1978). This is most likely due to the very few number of eclipses available in the past and the different energy band used to estimate θe (White 1978; Pietsch et al. 1985). The usage of the long-term observations available at present allow reducing the temporal variable distortions of the eclipse profile and provide a more reliable measurement of the semi-eclipse angle and eclipse duration.
5. Discussion
5.1. Masses of the ten neutron stars
Determining the equation of state (EoS) of matter at densities comparable to those inside NSs is one of the most challenging problems of modern physics and can only be addressed based on observations of astrophysical sources. Models proposed in the past years can be tested against observational results, especially by evaluating the highest NS mass that each EoS model is able to sustain (see, e.g., Lattimer & Prakash 2001). Very soft EoSs predict highest NS masses in the 1.4−1.5 M⊙ range (this occurs when the NS core is made of exotic matter such as kaons, hyperons, and pions), whereas stiff EoSs can reach up to 2.4−2.5 M⊙. More massive NSs can thus provide stronger constraints on the EoS models. As discussed by Rappaport & Joss (1983), eclipsing HMXBs hosting X-ray pulsars provide a means to measure the NS mass and thus place constraints on their EoS.
Best-fit orbital profile parameters in units of the orbital phase.
Input and output parameters for the MC simulations used to finally estimate the mass of the NSs hosted in the ten HMXBs.
In eclipsing HMXB the parameters needed to solve the equations that lead to the determination of the NS mass are the system orbital period Porb, the projected semi-major axis axsini, the eccentricity e, the periastron angle ω, and the duration of the eclipse expressed as the semi-eclipse angle θe (see Sect. 4.1). The semi-amplitude of the NS radial velocity can be inferred from the results of the timing analysis, which provide Kx = 2πaxsin i/ (Porb(1 − e2)1 / 2). The semi-amplitude of the radial velocity of the optical component, Kopt, can be determined by optical and/or UV spectra of this star (see Table 7; we note that the values of Kopt determined through these techniques might be affected by uncertainties related to the companion star modeling5; see, e.g., Hammerschlag-Hensberge et al. 2003; Abubekerov 2004; Koenigsberger et al. 2012). The NS radial velocities, Kx, reported in Table 7 are inferred using the values of axsini, e, and Porb reported in Tables 1 and 3. Two additional key parameters are required and can be estimated from theoretical arguments: (i) the Roche -lobe filling factor β (i.e., the ratio of the supergiant radius to that of its Roche lobe β = Ropt/RL) and (ii) the ratio of the spin period of the supergiant to its orbital period Ω.
For the sake of completeness, we review below the main equations to determine the NS masses (see also Rappaport & Joss 1983). The masses of the optical supergiant companion, Mopt, and the neutron star, Mx, can be written in terms of the mass functions 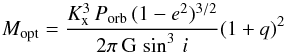 (5)and
(5)and 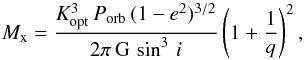 (6)where the mass ratio q is defined as q ≡ Mx/Mopt = Kopt/Kx. Assuming a spherical companion star, the inclination angle of the system, i, is found to be related to the semi-eclipse angle through the geometric relation
(6)where the mass ratio q is defined as q ≡ Mx/Mopt = Kopt/Kx. Assuming a spherical companion star, the inclination angle of the system, i, is found to be related to the semi-eclipse angle through the geometric relation 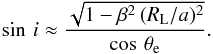 (7)We also made use here of the equation β = Ropt/RL. The ratio between the Roche-lobe radius and the separation of the two stars, RL/a, can be approximated as (Joss & Rappaport 1984)
(7)We also made use here of the equation β = Ropt/RL. The ratio between the Roche-lobe radius and the separation of the two stars, RL/a, can be approximated as (Joss & Rappaport 1984) 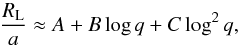 (8)where
(8)where 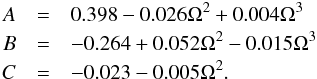 (9)For HMXBs with circular orbits the ratio RL/a is constant. When the orbit is eccentric, the Roche-lobe filling factor, β, is defined at periastron, RL, and the separation between the centers of masses of the two stars varies with the orbital phase. In these cases, the separation between the centers of the two stars at mid-eclipse time is given by a′ = a(1 − e2) / (1 + ecos ω), where ω is the argument of periastron reported in Table 1. In our calculation the Roche-lobe radius is estimated at the eclipse phase. The approximated Roche lobe radius, RL, is determined with an accuracy of about 2% over the ranges of
(9)For HMXBs with circular orbits the ratio RL/a is constant. When the orbit is eccentric, the Roche-lobe filling factor, β, is defined at periastron, RL, and the separation between the centers of masses of the two stars varies with the orbital phase. In these cases, the separation between the centers of the two stars at mid-eclipse time is given by a′ = a(1 − e2) / (1 + ecos ω), where ω is the argument of periastron reported in Table 1. In our calculation the Roche-lobe radius is estimated at the eclipse phase. The approximated Roche lobe radius, RL, is determined with an accuracy of about 2% over the ranges of 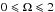 and
and 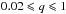 (Joss & Rappaport 1984). Once the full set of input parameters above are given, the values of i, Mx, Mopt, a, RL, and Ropt can be determined at 1σ c.l. by means of Monte Carlo (MC) simulations. Uncertainties on all parameters are evaluated in the simulations by assuming that their values follow a Gaussian distribution. We used a linear distribution for the Roche-lobe filling factor, β, spanning the range 0.9−1.0. Note that for all the HMXBs considered here it is known from their optical light curves that the supergiant stars hosted in these systems are nearly filling their Roche lobes (see, e.g., Tjemkes et al. 1986, and references therein).
(Joss & Rappaport 1984). Once the full set of input parameters above are given, the values of i, Mx, Mopt, a, RL, and Ropt can be determined at 1σ c.l. by means of Monte Carlo (MC) simulations. Uncertainties on all parameters are evaluated in the simulations by assuming that their values follow a Gaussian distribution. We used a linear distribution for the Roche-lobe filling factor, β, spanning the range 0.9−1.0. Note that for all the HMXBs considered here it is known from their optical light curves that the supergiant stars hosted in these systems are nearly filling their Roche lobes (see, e.g., Tjemkes et al. 1986, and references therein).
Following this technique, we first computed for the four sources with known Ω (LMC X-4, Cen X-3, SMC X-1, and Vela X-1) the remaining output parameters reported in Table 7. To verify the reliability of this method, we compared the observational reported projected stellar rotation velocity, vrotsin i, measurements with our calculated value using results in Table 7 and the following equation: 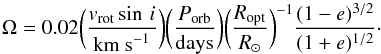 (10)In Table 8 we compare the calculated and measured vrotsin i values. These values agree well within the uncertainties. Based on these results, we assumed for the sources 4U 1538-522, SAX J1802.7-2017, XTE J1855-026, EXO 1722-363, and OAO 1657-415 a mean value of Ω = 0.91(20). As these systems are not circularized, Ω is unlikely to be too close to unity. If tides are efficient, then we might expect that the rotation of the donor is synchronized at periastron, where the tides are most effective (Hut 1981). In this case, the stellar angular velocity is higher than the orbital velocity at mid-eclipse, which leads to Ω ≳ 1. For this reason, we increased the uncertainty on Ω to include values slightly higher than unity.
(10)In Table 8 we compare the calculated and measured vrotsin i values. These values agree well within the uncertainties. Based on these results, we assumed for the sources 4U 1538-522, SAX J1802.7-2017, XTE J1855-026, EXO 1722-363, and OAO 1657-415 a mean value of Ω = 0.91(20). As these systems are not circularized, Ω is unlikely to be too close to unity. If tides are efficient, then we might expect that the rotation of the donor is synchronized at periastron, where the tides are most effective (Hut 1981). In this case, the stellar angular velocity is higher than the orbital velocity at mid-eclipse, which leads to Ω ≳ 1. For this reason, we increased the uncertainty on Ω to include values slightly higher than unity.
Comparison between the calculated and measured values of vrotsin i.
Source 4U 1700-377 was considered separately beause its projected semi-major axis axsini is unknown and thus the corresponding Kx cannot be determined as for all other sources. For this source, we first estimated Ω from Eq. (10)by using the observationally measured value of vrotsin i, Porb, and the companion star radius Ropt = 21.9(1.9) R⊙ (see Table 7 and Clark et al. 2002). We thus performed several MC simulations with a variable Kx, until the Ropt obtained from one of the simulations was compatible (to within the uncertainties) with the observational value. The outputs of this simulation were then used to fill all other relevant parameters for source 4U 1700-377 in Table 7.
Our findings on all neutron star masses for the considered HMXBs are summarized in Fig. 4 together with previously published values. The neutron star masses for LMC X-4, Cen X-3, 4U 1538-52, SMC X-1, and Vela X-1 are taken from Rawls et al. (2011), while the mass of the neutron star hosted in 4U 1700-377 is derived from Clark et al. (2002). The corresponding values for SAX J1802.7-2017, EXO 1722-363, and OAO 1657-415 are obtained from Mason et al. (2011, 2010, 2012). We note that our estimated uncertainties on the neutron star masses are somewhat more conservative than those reported by Rawls et al. (2011) and slightly smaller than those obtained by Clark et al. (2002) and Mason et al. (2011, 2010, 2012). The reason behind these differences is that these authors derived their uncertainties either from analytical calculations or through numerical simulations including a particularly refined treatment for the Roche-lobe size of the supergiant star. In the present work, all uncertainties were instead derived directly from the MC simulations and account for the most recently updated system parameters obtained from multiwavelength observations. In particular, we reporte for all sources in Table 6 the most accurately measured values of the semi-eclipse angles, which play a crucial role in the MC simulations. We note that in all cases our measured semi-eclipse angle is smaller than the values reported in the literature (see Table 6), and thus the NS masses we estimated are generally higher. This seems reasonable especially for 4U 1538-522 and SMC X-1, as the NS masses estimated before where ≲1 M⊙. The only exception to this trend is 4U 1700-377, for which our estimated semi-eclipse angle is similar to that obtained by Rubin et al. (1996).
 |
Fig. 4 Masses of the ten eclipsing HMXBs. The neutron star masses determined in this work are shown with solid lines. Values from the literature are represented with dashed lines. The error bars correspond to uncertainties at 1σ c.l. The dashed vertical line indicates the canonical neutron star mass of 1.4 M⊙. |
5.2. Orbital period change
Five of the ten HMXBs showed evidence for a significant orbital period decay, that is, LMC X-4, Cen X-3, 4U 1700-377, SMC X-1, and OAO 1657-415 (our values can be compared with previous measurements published in the literature by using the references reported in the tables in Appendix A.1). For all these sources, a number of different mechanisms have been invoked to explain the orbital period decay (see, e.g., Kelley et al. 1983; van der Klis 1983; van der Klis & Bonnet-Bidaud 1984; Levine et al. 1993, 2000; Rubin et al. 1996; Safi Harb et al. 1996; Jenke et al. 2012). The hypothesis that the period change is entirely due to angular momentum loss in the stellar wind, that is, to mass transfer without interaction, can be ruled out. More realistic models proposed that the orbital decay is mostly driven by the tidal interaction and the rapid mass transfer between the two objects. The latter takes occurs because of the fast winds that characterize most of the donor stars in HMXBs. In these models, the asynchronism between the orbit and the rotation of the donor star is maintained by the evolutionary expansion of the donor star (see, e.g., Lecar et al. 1976; Safi Harb et al. 1996; Levine et al. 2000; van der Klis & Bonnet-Bidaud 1984, and references therein). If the donor star is rotating with an angular velocity close to synchronization, the matter ejected leaves the system and carries additional momentum due to this rotation. This loss of rotational momentum only affects the orbital period if the rotation of the donor star and the orbit of the neutron star are coupled. Tidal interactions could synchronize the orbit with the rotation of the donor star and allow the transfer of rotational momentum of the primary star to the orbital momentum. Tidal effects on the radial velocity curve of the donor star in Vela X-1 have been investigated deeply, but no final conclusions could be drawn because the quality of the data is limited (Koenigsberger et al. 2012). Tidal interactions in close binary systems have also been investigated in detail theoretically by using different approaches, for example, by assuming that the rotation of the donor star is synchronized or pseudosynchronized6 with the orbital motion of the compact star (see, e.g., Moreno et al. 2011; Hut 1981; Zahn 1977; Lecar et al. 1976). A number of other works argued that the combined effects of the evolutionary growth of the moment of inertia (expansion of the donor star) and mass loss by stellar wind from a donor star can explain the orbital decay in HMXBs (Bagot 1996; Levine et al. 1993). In these models, it is considered that as the companion star evolves, it expands and increases its moment of inertia, leading to a slow-down of the stellar rotation. Tidal torques would then transfer orbital momentum to synchronize the binary system, finally causing orbital decay (see, e.g., Levine et al. 1993, and references therein). As the lifetime of a supergiant star does not exceed a few 106 yr, we expect that most of the systems considered in this work are nearly synchronized, but not fully circularized yet. This agrees with the non-negligible values of the eccentricity measured in some of the eclipsing HMXBs (see Table 1).
The updated and newly reported estimates of the orbital period decay of the ten HMXBs can be used as input in future works on these topics. We expect that this might help distinguishin among the different mechanisms proposed to explain the orbital period decay in HMXBs and to estimate their orbital circularization and synchronization timescales, as well as to discuss the Darwin instability (see, e.g., Lai et al. 1994) for these systems. Additional calculations on all these effects are beyond the scope of this paper.
To help future works that aim to numerically evaluate different theoretical models, we finally also report for reference the stellar wind velocities and mass-loss rates of all sources considered in this paper in Table 9. These were calculated by assuming the spectral types reported in Table 1. In Table 9 we indicate the terminal wind velocities inferred from observations in the literature and those calculated theoretically. For the latter we followed Martins et al. (2005) and Kudritzki & Puls (2000) for O-stars and Markova & Puls (2008), Crowther et al. (2006), Lefever et al. (2007) for B-stars. In all cases, the nominal mass-loss rates were reduced by a factor of ~3 to account for clumping, and uncertainties on the terminal wind velocities were assumed to be about 30% (Markova & Puls 2008; Repolust et al. 2004). As all data in Table 9 were calculated assuming that the wind is emitted by an isolated massive star, it is possible that in a number of systems the disturbance of the neutron star leads to substantially different wind properties. Detailed numerical simulations have shown that this could be the case especially for short orbital period systems with high X-ray luminosities (Watanabe et al. 2006; Manousakis et al. 2014). Unfortunately, direct measurements of the wind properties for the systems considered here are challenged by the relatively high absorption local to the sources and their large distance (Chaty 2013).
Properties of the stellar winds in the ten HMXBs as inferred from observations and theoretical calculations.
5.3. Apsidal motion
In addition to asteroseismology (see, e.g., Dupret et al. 2011, and references therein), measuring the apsidal advance in eccentric binary systems offers an alternative possibility to investigate the internal structure of stars compared to theoretical calculations and numerical modeling. The rate at which the longitude of periastron of an eccentric orbit advances can be related to the absidal motion constant, which depends on the model of the mass distribution inside the star (Kopal 1978; Batten 1973). X-ray pulsars in HMXBs have frequently been considered the most promising laboratories for accurately measuring the apsidal advance (see also Raichur & Paul 2010a, for the case of 4U0115+63). The neutron star in these systems can be well approximated as a point source with a negligible absidal motion constant with respect to that of the massive companion. The latter thus dominates the apsidal advance (Rappaport et al. 1980).
Our long-term analysis allowed us to provide the most accurate apsidal advance measurement for Vela X-1 and 4U 1538-522 (note, however, that for the former source the measurement is only marginally significant at 1.5σ).
For Vela X-1, the theoretical estimated apsidal motion is 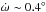 yr-1, assuming a companion star surface temperature of 25 000 K (as predicted accordingly to its spectral type; see, e.g., Avni & Bahcall 1975; Conti 1978). The measurement reported in Table 4 is thus fully consistent with the theoretically expected value (see Deeter et al. 1987, and references therein). To the best of our knowledge, this is the first time that such a match is reported, given the reduced uncertainty on the measured value of
yr-1, assuming a companion star surface temperature of 25 000 K (as predicted accordingly to its spectral type; see, e.g., Avni & Bahcall 1975; Conti 1978). The measurement reported in Table 4 is thus fully consistent with the theoretically expected value (see Deeter et al. 1987, and references therein). To the best of our knowledge, this is the first time that such a match is reported, given the reduced uncertainty on the measured value of 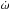 (even though this is still only marginally significant).
(even though this is still only marginally significant).
For 4U 1538-522, no firm measurement of the apsidal motion was reported in the literature. We note that the tentative value provided by Mukherjee et al. (2006) was estimated by comparing only two measurements of ω collected in 1997 and 2003 and thus is not comparable to the refined estimate reported in the present work. Our measurement thus provides the first consolidated estimate of 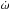 for 4U 1538-522.
for 4U 1538-522.
5.4. Eclipse asymmetry
The updated ephemeris for all the ten HMXBs in Table 3 that we obtained in this work allowed us to fold with an unprecedented accuracy the long-term ASM and ISGRI light curves of these objects in different energy bands. The results are shown in Figs. 2 and 3. The available broad-band energy coverage permitted studying the averaged profile of the eclipse ingress at egress for each object in detail. We note that for SAX J1802.7-2017, XTE J1855-026, and EXO 1722-363, this study could not be easily carried out at low energies because of the strong absorption affecting the X-ray emission from these sources (this is expected because they are classified as highly obscured HMXBs; see, e.g. Chaty 2013, for a recent review). In most of the other sources we found peculiar asymmetries that are more pronounced at lower energies and slightly more enhanced in objects characterized by a non-negligible eccentricity. Remarkable asymmetries are recorded for the eclipse ingresses and egresses of 4U 1700-377 and Vela X-1. Evident eclipse asymmetries are also displayed by 4U 1538-522 and OAO 1657-415.
In most of the sources we considered, single-eclipse profiles have been studied in the past by using focusing X-ray instruments capable of high-resolution spectroscopy (e.g., XMM-Newton and Chandra; see Watanabe et al. 2006, and references therein). These observations proved to be particularly powerful to analyze how the X-ray emission from HMXBs is affected by inhomogeneities in the stellar winds (Sako et al. 2003). Such inhomogeneities (clumps, see, e.g. Puls et al. 2008, for a recent review) are transported away from the star with typical velocities of a smooth wind and thus can induce changes in the mass accretion rate (and X-ray luminosity) on timescales as short as 100−1000 s. The feedback of X-ray radiation is also known to affect the structure of the wind on similar timescales because high-energy photons ionize the metal ions in the wind and dramatically reduce the wind acceleration mechanism (which in turn affects the velocity and density profile of outflows from the massive stars).
The eclipse profiles we discussed above provide, instead, important information on the interaction between the compact object and the stellar wind on much longer timescales (~yr). The influence of wind inhomogeneities is in all cases compensated by the long-term integration, and only the effect of X-ray irradiation on the wind averaged on hundreds of orbital revolutions can be observed from these curves. Under these assumption, we argue that the eclipse asymmetries are most likely caused by accretion wakes. These structures are commonly observed in HMXBs and form as a consequence of the intense gravity and conspicuous X-ray emission of the compact object (see, e.g., Fig. 5 in Blondin et al. 1990 and Figs. 1−5 in Manousakis et al. 2012).
As the accretion wake usually trails the neutron star during its orbital revolution around the companion and can lead to an increase of the wind density around the compact object by a factor of ~10−100 (Manousakis et al. 2014), it is expected that the absorption column density in the direction of the X-ray source progressively increases before the occurrence of the X-ray eclipse. During the egress from the eclipse, the accretion wake is located beyond the compact object along the line of sight to the observer and thus does not lead to any apparent increase of the local absorption column density.
An interesting possibility is also that this effect is enhanced in systems endowed with a non-negligible orbital eccentricity due to the different degree of ionization of the stellar wind material when the neutron star approaches or recedes from the companion. It is well known that in case of eccentric orbits, the absolute value of the vectorial sum of the neutron star orbital velocity and the stellar wind velocity reaches a minimum while the compact object approaches the companion, and then increases toward the upper conjunction (see, e.g., Ducci et al. 2010, and references therein). In a wind-accreting system, the amount of material that a neutron star can capture from the companion at any time is roughly comparable to 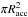 , where
, where 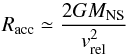 (11)and vrel is the relative velocity mentioned above. It is thus expected that a higher X-ray luminosity is released at lower values of vrel because the enhanced accretion rate (see, e.g., Bozzo et al. 2008, and references therein). As the ionization of the wind is proportional to the X-ray flux and acts to substantially inhibit the wind acceleration mechanism, a higher density would also be expected around a bright X-ray emitting neutron star approaching the companion. Furthermore, the X-ray flux could be evaporating additional material from the massive star around this orbital phase, possibly enhancing the absorption column density in the direction of the source during the eclipse ingress (Blondin & Woo 1995). We note that in short orbital period systems, the formation of (at least) temporary accretion disks when the neutron star is at the closest distance from the companion could also provide enhanced accretion rates and thus positively contribute to increase the mass density around the neutron star (e.g., Ducci et al. 2010). A quantitative estimate of all these effects would require more detailed calculations that also combine the effect of the neutron star spin and magnetic field.
(11)and vrel is the relative velocity mentioned above. It is thus expected that a higher X-ray luminosity is released at lower values of vrel because the enhanced accretion rate (see, e.g., Bozzo et al. 2008, and references therein). As the ionization of the wind is proportional to the X-ray flux and acts to substantially inhibit the wind acceleration mechanism, a higher density would also be expected around a bright X-ray emitting neutron star approaching the companion. Furthermore, the X-ray flux could be evaporating additional material from the massive star around this orbital phase, possibly enhancing the absorption column density in the direction of the source during the eclipse ingress (Blondin & Woo 1995). We note that in short orbital period systems, the formation of (at least) temporary accretion disks when the neutron star is at the closest distance from the companion could also provide enhanced accretion rates and thus positively contribute to increase the mass density around the neutron star (e.g., Ducci et al. 2010). A quantitative estimate of all these effects would require more detailed calculations that also combine the effect of the neutron star spin and magnetic field.
6. Conclusions
We performed orbital mid-eclipse time measurements on the ten known eclipsing HMXBs using publicly available pre-processed RXTE/ASM and INTEGRAL/ISGRI data. For each source, we determined several new orbital mid-eclipse times and used them together with all previously published values (to the best of our knowledge) to obtain the most updated and homogeneous set of ephemerides to date. The latter allowed us in particular to update the orbital periods of all the ten binaries, as well as the decay of these periods. In five sources (LMC X-4, Cen X-3, 4U 1700-377, SMC X-1, and OAO 1657-415) we measured a significant orbital period decay, with values in the range of 1.0 − 3.5 × 10-6 yr-1; in all other case no significant decay was revealed, even though more than 30 yr of X-ray observations were used. For the eccentric systems Vela X-1 and 4U 1538-522 we accurately determined for the first time a significant apsidal advance by comparing it with previously expected values.
Using our best estimated mid-eclipse epoch, orbital period, and period derivative for each source, we folded the light curves of the ten binaries obtained from the long-term monitoring carried out with the ASM onboard RXTE (1.3−12 keV) and ISGRI onboard INTEGRAL (17−150 keV). We discussed the asymmetric profiles of the eclipse ingresses and egresses by comparing them with theoretical expectations from simulations of accreting wind-fed systems.
Finally, we used all above mentioned results within the MC simulations to consistently and systematically evaluate the masses of the NS hosted in the ten eclipsing HMXBs. The results reported in this paper constitute an important database for population and evolutionary studies of HMXBs, as well as for theoretical modeling of long-term accretion in wind-fed X-ray binaries.
Online material
Appendix A: Ephemeris tables
LMC X-4.
Cen X-3.
4U 1700-377.
4U 1538-522.
SMC X-1.
SAX J1802.7-2017.
XTE J1855-026.
Vela X-1.
EXO 1722-363.
OAO 1657-415.
Be X-ray binaries are not expected to show long detectable X-ray eclipses because the radial extent of the companion is smaller than that of supergiant stars in HMXBs and the orbital periods are typically much longer and are characterized by high eccentricities (Reig 2011).
The strong stellar wind that is responsible for the mass transfer makes the task of generating a radial velocity curve of the donor star difficult. Another matter that can result in difficulties is when the compact companion heats up one side of the donor star, thereby distorting spectral line profiles, i.e., X-ray heating takes place.
Pseudosynchronized systems are binaries in which the donor star is synchronized only at periastron, where the tides are more effective (Hut 1981).
Acknowledgments
M.F. acknowledge ISSI (Switzerland) for financial support during the visit of R. Vuillez in Bern, and thanks F. Mattana, R. Vuillez, J.A. Zurita-Heras, and A. Goldwurm for their contributions on an earlier version of the manuscript. A.L. acknowledges support by the grant RFBR 12-02-01265. We acknowledge support from ISSI through funding for the International Team meeting on Unified View of Stellar Winds in Massive X-ray Binaries (ID 253).
References
- Abubekerov, M. K. 2004, Astron. Rep., 48, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Augello, G., Iaria, R., Robba, N. R., et al. 2003, ApJ, 596, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Avni, Y., & Bahcall, J. N. 1975, ApJ, 202, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Bagot, P. 1996, A&A, 314, 576 [NASA ADS] [Google Scholar]
- Barnstedt, J., Staubert, R., Santangelo, A., et al. 2008, A&A, 486, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batten, A. H. 1973, Binary and multiple systems of stars (Oxford, New York: Pergamon Press) [Google Scholar]
- Baykal, A., Inam, S. Ç., & Beklen, E. 2006, A&A, 453, 1037 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baykal, A., Inam, S. C., Icdem, B., & Beklen, E. 2011, PoS(HTRS 2011)051 [Google Scholar]
- Becker, R. H., Swank, J. H., Boldt, E. A., et al. 1977, ApJ, 216, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., & Woo, J. W. 1995, ApJ, 445, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Kallman, T. R., Fryxell, B. A., & Taam, R. E. 1990, ApJ, 356, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnet-Bidaud, J. M., & van der Klis, M. 1981, A&A, 97, 134 [NASA ADS] [Google Scholar]
- Boroson, B., Kallman, T., McCray, R., Vrtilek, S. D., & Raymond, J. 1999, ApJ, 519, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Bozzo, E., Falanga, M., & Stella, L. 2008, ApJ, 683, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Branduardi, G., Mason, K. O., & Sanford, P. W. 1978, MNRAS, 185, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, I., & Wilms, J. 2012, Mem. Soc. Astron. It, 83, 230 [Google Scholar]
- Chakrabarty, D., Grunsfeld, J. M., Prince, T. A., et al. 1993, ApJ, 403, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Charles, P. A., Mason, K. O., White, N. E., et al. 1978, MNRAS, 183, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Chaty, S. 2011, in Evolution of Compact Binaries, eds. L. Schmidtobreick, M. R. Schreiber, & C. Tappert, ASP Conf. Ser., 447, 29 [Google Scholar]
- Chaty, S. 2013, Adv. Space Res., 52, 2132 [Google Scholar]
- Clark, G. W. 2000, ApJ, 542, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, G. W., Minato, J. R., & Mi, G. 1988, ApJ, 324, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, J. S., Goodwin, S. P., Crowther, P. A., et al. 2002, A&A, 392, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coburn, W., Heindl, W. A., Rothschild, R. E., et al. 2002, ApJ, 580, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Coley, A. 2015, ArXiv e-prints [arXiv:1503.04775] [Google Scholar]
- Cominsky, L. R., & Moraes, F. 1991, ApJ, 370, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Conti, P. S. 1978, A&A, 63, 225 [NASA ADS] [Google Scholar]
- Corbet, R. H. D., & Mukai, K. 2002, ApJ, 577, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Corbet, R. H. D., Woo, J. W., & Nagase, F. 1993, A&A, 276, 52 [NASA ADS] [Google Scholar]
- Corbet, R. H. D., Markwardt, C. B., & Swank, J. H. 2005, ApJ, 633, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Courvoisier, T. J.-L., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davison, P. J. N., Watson, M. G., & Pye, J. P. 1977, MNRAS, 181, 73P [NASA ADS] [CrossRef] [Google Scholar]
- Deeter, J. E., Boynton, P. E., Lamb, F. K., & Zylstra, G. 1987, ApJ, 314, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Denis, M., Bulik, T., & Marcinkowski, R. 2005, unpublished, ArXiv e-prints [arXiv:astro-ph/0503291] [Google Scholar]
- Dennerl, K. 1991, Ph.D. Thesis, Universität München, MPE Rep., 232 [Google Scholar]
- Ducci, L., Sidoli, L., & Paizis, A. 2010, MNRAS, 408, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M.-A., Godart, M., Belkacem, K., & Noels, A. 2011, in IAU Symp. 272, eds. C. Neiner, G. Wade, G. Meynet, & G. Peters, 457 [Google Scholar]
- Ebisawa, K., Day, C. S. R., Kallman, T. R., et al. 1996, PASJ, 48, 425 [NASA ADS] [Google Scholar]
- Fabbiano, G., & Schreier, E. J. 1977, ApJ, 214, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Filippova, E. V., Tsygankov, S. S., Lutovinov, A. A., & Sunyaev, R. A. 2005, Astron. Lett., 31, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Forman, W., Jones, C., Tananbaum, H., et al. 1973, ApJ, 182, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Giacconi, R., Gursky, H., Kellogg, E., Schreier, E., & Tananbaum, H. 1971, ApJ, 167, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Haberl, F., White, N. E., & Kallman, T. R. 1989, ApJ, 343, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Hammerschlag-Hensberge, G., van Kerkwijk, M. H., & Kaper, L. 2003, A&A, 407, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, A. B., Walter, R., Knigge, C., et al. 2005, A&A, 439, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howarth, I. D., Siebert, K. W., Hussain, G. A. J., & Prinja, R. K. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, S. K., Primini, F. A., Bautz, M. W., et al. 1983, ApJ, 272, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Inam, S. Ç., Baykal, A., & Beklen, E. 2010, MNRAS, 403, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Jain, C., Paul, B., & Dutta, A. 2009, Res. Astron. Astrophys., 9, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Jenke, P. A., Finger, M. H., Wilson-Hodge, C. A., & Camero-Arranz, A. 2012, ApJ, 759, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C., Forman, W., Tananbaum, H., et al. 1973, ApJ, 181, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Joss, P. C., & Rappaport, S. A. 1984, ARA&A, 22, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Kelley, R. L., Jernigan, J. G., Levine, A., Petro, L. D., & Rappaport, S. 1983, ApJ, 264, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Koenigsberger, G., Moreno, E., & Harrington, D. M. 2012, A&A, 539, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kopal, Z., 1978, Dynamics of close binary systems, Astrophys. Space. Sci. Lib., 68 [Google Scholar]
- Kreykenbohm, I., Wilms, J., Kretschmar, P., et al. 2008, A&A, 492, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R.-P., & Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., Rasio, F. A., & Shapiro, S. L. 1994, ApJ, 423, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., van den Heuvel, E. P. J., & Petterson, J. A. 1976, A&A, 49, 327 [NASA ADS] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2001, ApJ, 550, 426 [Google Scholar]
- Lecar, M., Wheeler, J. C., & McKee, C. F. 1976, ApJ, 205, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Lefever, K., Puls, J., & Aerts, C. 2007, A&A, 463, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levine, A., Rappaport, S., Putney, A., Corbet, R., & Nagase, F. 1991, ApJ, 381, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, A., Rappaport, S., Deeter, J. E., Boynton, P. E., & Nagase, F. 1993, ApJ, 410, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, A. M., Rappaport, S. A., & Zojcheski, G. 2000, ApJ, 541, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G., Ricker, G. R., & McClintock, J. E. 1971, ApJ, 169, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Li, F., Rappaport, S., & Epstein, A. 1978, Nature, 271, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2006, A&A, 455, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovelace, R. V. E., Romanova, M. M., & Bisnovatyi-Kogan, G. S. 1995, MNRAS, 275, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Lutovinov, A., & Tsygankov, S. 2009, PoS(extremesky 2009)010 [Google Scholar]
- Lutovinov, A. A., Grebenev, S. A., Pavlinsky, M. N., & Sunyaev, R. A. 2000, Astron. Lett., 26, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Lutovinov, A., Revnivtsev, M., Gilfanov, M., et al. 2005, A&A, 444, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutovinov, A. A., Revnivtsev, M. G., Tsygankov, S. S., & Krivonos, R. A. 2013, MNRAS, 431, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Makishima, K., Koyama, K., Hayakawa, S., & Nagase, F. 1987, ApJ, 314, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Manousakis, A., & Walter, R. 2011, A&A, 526, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manousakis, A., Walter, R., & Blondin, J. M. 2012, A&A, 547, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manousakis, A., Walter, R., & Blondin, J. 2014, in EPJ Web Conf., 64, 2006 [Google Scholar]
- Markova, N., & Puls, J. 2008, A&A, 478, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Markwardt, C. B., & Swank, J. H. 2003, ATel, 179, 1 [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, A. B., Norton, A. J., Clark, J. S., Negueruela, I., & Roche, P. 2010, A&A, 509, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, A. B., Norton, A. J., Clark, J. S., Negueruela, I., & Roche, P. 2011, A&A, 532, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, A. B., Clark, J. S., Norton, A. J., et al. 2012, MNRAS, 422, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, E., Koenigsberger, G., & Harrington, D. M. 2011, A&A, 528, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mukherjee, U., Raichur, H., Paul, B., Naik, S., & Bhatt, N. 2006, JA&A, 27, 411 [NASA ADS] [Google Scholar]
- Murakami, T., Inoue, H., Kawai, N., et al. 1983, ApJ, 264, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Nagase, F. 1996, in Compact Stars in Binaries, ed. J. van Paradijs, E. P. J. van den Heuvel, & E. Kuulkers, IAU Symp., 165, 289 [Google Scholar]
- Nagase, F., Hayakawa, S., Kunieda, H., et al. 1981, Nature, 290, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Nagase, F., Hayakawa, S., Makino, F., Sato, N., & Makishima, K. 1983, PASJ, 35, 47 [NASA ADS] [Google Scholar]
- Nagase, F., Hayakawa, S., Tsuneo, K., et al. 1984, PASJ, 36, 667 [NASA ADS] [Google Scholar]
- Nagase, F., Corbet, R. H. D., Day, C. S. R., et al. 1992, ApJ, 396, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Naik, S., & Paul, B. 2004, A&A, 418, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ogelman, H., Beuermann, K. P., Kanbach, G., et al. 1977, A&A, 58, 385 [NASA ADS] [Google Scholar]
- Pietsch, W., Voges, W., Pakull, M., & Staubert, R. 1985, Space Sci. Rev., 40, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Primini, F., Rappaport, S., & Joss, P. C. 1977, ApJ, 217, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quaintrell, H., Norton, A. J., Ash, T. D. C., et al. 2003, A&A, 401, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raichur, H., & Paul, B. 2010a, MNRAS, 406, 2663 [NASA ADS] [CrossRef] [Google Scholar]
- Raichur, H., & Paul, B. 2010b, MNRAS, 401, 1532 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S. A., & Joss, P. C. 1983, in Accretion-Driven Stellar X-ray Sources, eds. W. H. G. Lewin & E. P. J. van den Heuvel, 13 [Google Scholar]
- Rappaport, S., Joss, P. C., & McClintock, J. E. 1976, ApJ, 206, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Stothers, R., & Joss, P. C. 1980, ApJ, 235, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Rawls, M. L., Orosz, J. A., McClintock, J. E., et al. 2011, ApJ, 730, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P. 2011, Ap&SS, 332, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Repolust, T., Puls, J., & Herrero, A. 2004, A&A, 415, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Revnivtsev, M. G., Sunyaev, R. A., Varshalovich, D. A., et al. 2004, Astron. Lett., 30, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, A. P., Hilditch, R. W., Bell, S. A., & Hill, G. 1993, MNRAS, 261, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, B. C., Finger, M. H., Harmon, B. A., et al. 1996, ApJ, 459, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, B. C., Finger, M. H., Scott, D. M., & Wilson, R. B. 1997, ApJ, 488, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Safi Harb, S., Ogelman, H., & Dennerl, K. 1996, ApJ, 456, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Sako, M., Kahn, S. M., Paerels, F., et al. 2003, invited review at the High-resolution X-ray Spectroscopy Workshop with XMM-Newton and Chandra, MSSL, Oct. 24, 25, 2002, ArXiv e-prints [arXiv:astro-ph/0309503] [Google Scholar]
- Schreier, E., Giacconi, R., Gursky, H., Kellogg, E., & Tananbaum, H. 1972, ApJ, 178, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N., Postnov, K., Kochetkova, A., & Hjalmarsdotter, L. 2012, MNRAS, 420, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620 [NASA ADS] [Google Scholar]
- Thompson, T. W. J., Tomsick, J. A., in ’t Zand, J. J. M., Rothschild, R. E., & Walter, R. 2007, ApJ, 661, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Tjemkes, S. A., van Paradijs, J., & Zuiderwijk, E. J. 1986, A&A, 154, 77 [NASA ADS] [Google Scholar]
- Tuohy, I. R. 1976, MNRAS, 174, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Tuohy, I. R., & Rapley, C. G. 1975, ApJ, 198, L69 [NASA ADS] [CrossRef] [Google Scholar]
- van der Klis, M. B. M. 1983, Ph.D. Thesis, University of Amsterdam [Google Scholar]
- van der Klis, M., & Bonnet-Bidaud, J. M. 1984, A&A, 135, 155 [NASA ADS] [Google Scholar]
- van der Klis, M., Bonnet-Bidaud, J. M., & Robba, N. R. 1980, A&A, 88, 8 [NASA ADS] [Google Scholar]
- van der Meer, A., Kaper, L., van Kerkwijk, M. H., Heemskerk, M. H. M., & van den Heuvel, E. P. J. 2007, A&A, 473, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Kerkwijk, M. H., van Paradijs, J., & Zuiderwijk, E. J. 1995a, A&A, 303, 497 [NASA ADS] [Google Scholar]
- van Kerkwijk, M. H., van Paradijs, J., Zuiderwijk, E. J., et al. 1995b, A&A, 303, 483 [NASA ADS] [Google Scholar]
- van Loon, J. T., Kaper, L., & Hammerschlag-Hensberge, G. 2001, A&A, 375, 498 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vrtilek, S. D., Raymond, J. C., Boroson, B., et al. 2001, ApJ, 563, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, R., Zurita Heras, J., Bassani, L., et al. 2006, A&A, 453, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watanabe, S., Sako, M., Ishida, M., et al. 2006, ApJ, 651, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, M. G., & Griffiths, R. E. 1977, MNRAS, 178, 513 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E. 1978, Nature, 271, 38 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., Nagase, F., & Parmar, A. N. 1995, X-ray Binaries, 1 [Google Scholar]
- Wojdowski, P., Clark, G. W., Levine, A. M., Woo, J. W., & Zhang, S. N. 1998, ApJ, 502, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Wojdowski, P. S., Liedahl, D. A., Sako, M., Kahn, S. M., & Paerels, F. 2003, ApJ, 582, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J. W., Clark, G. W., Levine, A. M., Corbet, R. H. D., & Nagase, F. 1996, ApJ, 467, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zuiderwijk, E. J. 1995, A&A, 299, 79 [NASA ADS] [Google Scholar]
- Zurita Heras, J. A., de Cesare, G., Walter, R., et al. 2006, A&A, 448, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Orbital parameters of the ten eclipsing HMXB systems in ascending order of the orbital period.
Log of INTEGRAL/ISGRI and RXTE/ASM observations of the ten selected eclipsing HMXBs.
Updated epochs, orbital periods, and period decay of the ten sources obtained by using all the available mid-eclipse times.
Measured cts/s during the occultation phases of the ten selected sources in this work.
Input and output parameters for the MC simulations used to finally estimate the mass of the NSs hosted in the ten HMXBs.
Properties of the stellar winds in the ten HMXBs as inferred from observations and theoretical calculations.
All Figures
 |
Fig. 1 All measured mid-eclipses, Tecl, mean longitudes, Tπ/ 2, and orbital epochs are shown with the best-fit models as a function of the orbit numbers. In all cases, the best-fit model is a quadratic or linear fit to the epochs. The lower panel in each figure shows the residual from the best fit. |
| In the text | |
 |
Fig. 2 Folded light curves of the first six eclipsing HMXBs in Table 1. Data in the energy range 1.3−12 keV were obtained from the RXTE/ASM, while harder X-ray data are taken from INTEGRAL/ISGRI (17−150 keV). In all cases, the light curves have been folded by using the updated ephemerides obtained in the present work. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but for the remaining four sources in Table 1. |
| In the text | |
 |
Fig. 4 Masses of the ten eclipsing HMXBs. The neutron star masses determined in this work are shown with solid lines. Values from the literature are represented with dashed lines. The error bars correspond to uncertainties at 1σ c.l. The dashed vertical line indicates the canonical neutron star mass of 1.4 M⊙. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


