| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201425141 | |
| Published online | 30 April 2015 | |
Spectral and spatial imaging of the Be+sdO binary ϕ Persei⋆,⋆⋆
1
Laboratoire Lagrange, UMR 7293 UNS-CNRS-OCA, Boulevard de
l’Observatoire,
BP 4229,
06304
Nice Cedex 4,
France
e-mail: denis.mourard@oca.eu
2
Department of Astronomy, University of Michigan,
Ann Arbor, MI
48109,
USA
3
CHARA, Georgia State University, PO Box 3969, Atlanta, GA
30302-3969,
USA
4
Univ. Grenoble Alpes, IPAG, 38000
Grenoble,
France
5
CNRS, IPAG, 38000
Grenoble,
France
6
Physics and Astronomy Department, Vanderbilt
University, 6301 Stevenson
Center, Nashville,
TN
37235,
USA
7
CHARA Array, Mount Wilson Observatory,
Mount Wilson, CA
91023,
USA
8
University of Exeter, School of Physics,
Stocker Road, Exeter
EX4 4QL,
UK
9
Department of Astronomy and Astrophysics, Pennsylvania State
University, University
Park, PA
16802,
USA
10
Heriot-Watt University, Edinburgh, Scotland
EH4 4AS,
UK
11
Université de Lyon, 69003
Lyon,
France
12
Université Lyon 1, Observatoire de Lyon,
9 avenue Charles André,
69230
Saint Genis Laval Cedex,
France
13
CNRS, UMR 5574, Centre de Recherche Astrophysique de Lyon,
Université Lyon, 19 Avenue Charles André, 69561
Saint Genis Laval Cedex,
France
14
École Normale Supérieure, 69007
Lyon,
France
15
National Optical Astronomy Observatory,
PO Box 26732, Tucson, AZ
85726,
USA
Received:
10
October
2014
Accepted:
24
February
2015
Aims. The rapidly rotating Be star ϕ Persei was spun up by mass and angular momentum transfer from a now stripped-down, hot subdwarf companion. Here we present the first high angular resolution images of ϕ Persei made possible by new capabilities in long-baseline interferometry at near-IR and visible wavelengths. We analyzed these images to search for the companion, to determine the binary orbit, stellar masses, and fluxes, and to examine the geometrical and kinematical properties of the outflowing disk surrounding the Be star.
Methods. We observed ϕ Persei with the MIRC and VEGA instruments of the CHARA Array. MIRC was operated in six-telescope mode, whereas VEGA was configured in four-telescope mode with a change of quadruplets of telescopes during two nights to improve the (u,v) plane coverage. Additional MIRC-only observations were performed to track the orbital motion of the companion, and these were fit together with new and existing radial velocity measurements of both stars to derive the complete orbital elements and distance. We also used the MIRC data to reconstruct an image of the Be disk in the near-IR H-band. VEGA visible broadband and spectro-interferometric Hα observations were fit with analytical models for the Be star and disk, and image reconstruction was performed on the spectrally resolved Hα emission line data.
Results. The hot subdwarf companion is clearly detected in the near-IR data at each epoch of observation with a flux contribution of 1.5% in the H band, and restricted fits indicate that its flux contribution rises to 3.3% in the visible. A new binary orbital solution is determined by combining the astrometric and radial velocity measurements. The derived stellar masses are 9.6 ± 0.3 M⊙ and 1.2 ± 0.2 M⊙ for the Be primary and subdwarf secondary, respectively. The inferred distance (186 ± 3 pc), kinematical properties, and evolutionary state are consistent with membership of ϕ Persei in the α Per cluster. From the cluster age we deduce significant constraints on the initial masses and evolutionary mass transfer processes that transformed the ϕ Persei binary system. The interferometric data place strong constraints on the Be disk elongation, orientation, and kinematics, and the disk angular momentum vector is coaligned with and has the same sense of rotation as the orbital angular momentum vector. The VEGA visible continuum data indicate an elongated shape for the Be star itself, due to the combined effects of rapid rotation, partial obscuration of the photosphere by the circumstellar disk, and flux from the bright inner disk.
Key words: stars: individual: ϕPersei / binaries: general
Table 2 and Appendix A are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
For about 30 years, Be stars have been favorite targets of optical interferometers (Thom et al. 1986; Mourard et al. 1989), and they are important objects to study the role of rotation in the link between a star and its close environment. Be stars are rapidly rotating, main-sequence B-stars that eject gas into circumstellar disks (Rivinius et al. 2013). The “e” suffix in their spectral classification refers to the presence of Balmer emission lines that form in their outflowing disks. Such emission appears in B-stars with equatorial velocities above approximately 75% of the critical rate, and processes related to nonradial pulsation and/or small-scale magnetic fields probably aid mass loss into the disk (Rivinius et al. 2013). In some circumstances, these processes may produce high-energy X-rays. The Be star γ Cassiopeiae, for example, exhibits thermal X-ray emission. In a recent series of two papers on γ Cas, Smith et al. (2012) and Stee et al. (2012) have reviewed the most remarkable features of this star: X-ray activity, magnetic field, critical rotation, Keplerian rotation, disk elongation, and binarity. These papers have also shown once more that a multiwavelength and multitechnique approach is key to making progress in understanding the physics of these complex systems.
The origin of the rapid spin of Be stars is unknown. Most Be stars appear to be somewhat evolved objects (McSwain & Gies 2005; Zorec et al. 2005), so that their fast spin represents processes that occur well into their main-sequence lives. One possibility is that B-stars spin up as they conclude core H-burning due to the redistribution of internal angular momentum (Ekström et al. 2008; Granada et al. 2013; Granada & Haemmerlé 2014). A second possibility is that Be stars were spun up by mass and angular momentum transfer in a binary (Pols et al. 1991; de Mink et al. 2013). In this case, the companion would lose most of its envelope and would appear as a hot, stripped-down He-star remnant. The Be binary star ϕ Persei represents the first detection of a Be star with a hot, faint companion (Poeckert 1981; Thaller et al. 1995; Gies et al. 1998), and it is one of three such systems known at present (Peters et al. 2013). Clearly it is important to study such Be binaries to determine the physical properties of the stars at the conclusion of their transformative interaction.
This paper is an analysis of the results obtained on ϕ Persei thanks to a combined visible and infrared interferometric campaign with the instruments VEGA (Mourard et al. 2009) and MIRC (Monnier et al. 2008) on the CHARA Array (ten Brummelaar et al. 2005) and is complemented with a new analysis of a collection of radial velocity measurements. In Sect. 2 we summarize the known facts on ϕ Persei relevant to this study, and we compile radial velocity measurements in Sect. 3. The journal of interferometric observations is presented in Sect. 4, and MIRC data are presented in Sect. 5 along with a global astrometric and radial velocity analysis. The VEGA data and analysis are presented in Sect. 6. The scientific implications of our results are presented and discussed in Sect. 7, and we conclude in Sect. 8.
2. Main characteristics of ϕ Persei
The source ϕ Persei (HD 10516, HIP 8068) is a bright star (mV = 4.09) in the northern sky that is classified as B1.5 V:e-shell (Slettebak 1982). The Hipparcos parallax (van Leeuwen 2007) is π = 4.54 ± 0.2 millisecond of arc (mas), which gives a distance d = 220 ± 10 pc. Using the interstellar Ca II distance scale, Megier et al. (2009) estimate a distance of d = 195 ± 32 pc.
Campbell (1895) published a list of 32 stars presenting both bright and dark hydrogen lines and addressed the question of explaining these interesting and varying features. ϕ Persei appears in this list, and about 120 years later, we are still considering it as a puzzle. Until 1960, most of the papers published on ϕ Persei after this discovery were dedicated to samples of stars and statistical studies. More detailed work followed this period, and Slettebak (1966) (confirmed later on by Abt et al. 2002) published a measurement of the projected rotational velocity of Vsini = 410–450 km s-1, which is estimated to be around 85% of the equatorial breakup velocity.
Poeckert (1981) presented the first evidence of a companion in ϕ Persei and identified it as a helium star. Based on the velocity curves, he estimated masses of Mp = 21M⊙ and Ms = 3.4M⊙. The primary is the Be star, whereas the secondary is the hot companion with an effective temperature estimated to be around 50 000 K in order to ionize helium. The photospheric spectrum of the hot companion was first detected in spectra from the International Ultraviolet Explorer satellite by Thaller et al. (1995), who showed that the spectrum appears similar to that of the sdO6 subdwarf star HD 49798. Božić et al. (1995) presented a comprehensive review of the available photometric and radial velocity data, and they proposed an orbital solution with a period P = 126.6731 days, an epoch of Be star superior conjunction Tsc = HJD 2 435 046.73 (HJD = heliocentric Julian Date), and revised masses: Mp between 16 and 22 M⊙ and Ms between 1.7 and 2.2 M⊙. They classified the primary star as B0.5e. The companion was finally confirmed by Gies et al. (1998) thanks to high-resolution UV spectroscopy with the Hubble Space Telescope (HST). The subdwarf-to-Be flux ratio is 0.165 ± 0.006 (resp. 0.154 ± 0.009) for the 1374 Å region (resp. 1647 Å). Moreover, they derived a double-lined solution for the radial velocity curve that yields masses of Mp = 9.3 ± 0.3M⊙ and Ms = 1.14 ± 0.04M⊙. The lower mass estimates with respect to the results from Božić et al. (1995) are explained by a much smaller secondary semiamplitude in the RV measurements, which leads to a smaller projected semimajor axis and thus lower masses. The subdwarf effective temperature is Teff = 53 000 ± 3000 K and the surface gravity is log g = 4.2 ± 0.1.
Through the study of the helium lines, Štefl et al. (2000) argued for an origin of the emission in the outer parts of the disk surrounding the primary star. Their observations agree with a scenario where the outer parts of an axisymmetric disk are illuminated by the radiation of the secondary. They also favor inhomogeneities in the global density pattern of the inner regions as evidenced by the emission line asymmetry. The model of the Fe II 5317 Å and He I 6678 Å and 5876 Å emission lines of ϕ Persei proposed by Hummel & Štefl (2001) yields the size and shape of the excitation region in the circumprimary disk. The Fe II emission originates within 12 stellar radii in an axisymmetric disk around the primary, whereas the He I emission is best fit by a disk sector with a radius of 15 stellar radii and opening angle of ≃ 120° facing the secondary (Hummel & Štefl 2003). They also confirmed that the complex structure of the emission line profiles is due to an external illumination.
Polarimetric studies of ϕ Persei were made in the late 1990s through the work of Clarke & Bjorkman (1998) and Ghosh et al. (1999). A wavelength dependence of the polarimetric fluctuations was detected and associated with events deep inside the binary system, the amount of scattered radiation being primarily controlled by the opacity of the primary star’s disk. Ghosh et al. (1999) measured an intrinsic polarization of ϕ Persei equal to 1.57 ± 0.11% (resp. 1.36 ± 0.10%, 1.19 ± 0.09% and 0.98 ± 0.08%) in the B (resp., V,R and I) band. The position angle (measured east from the north celestial pole) of the scattering disk normal axis is PA = 27 ± 2°.
Optical interferometric observations of ϕ Persei (see Table 1) were first reported in 1997 with the MarkIII interferometer (Quirrenbach et al. 1997). Using a wide spectral band of 54 Å centered on Hα, they fitted their data with a model of a Gaussian disk plus a stellar uniform disk of 0.39 mas contributing 23% of the flux in the spectral band. Using the NPOI interferometer with an Hα filter of width 39 ± 3 Å, Tycner et al. (2006) used the same model as Quirrenbach et al. (1997) and obtained similar results. The authors also derived an inclination angle i ≥ 74°. Finally, Gies et al. (2007), using the CHARA Array in the K′-band, fitted a model with a Gaussian elliptical disk plus a central source and a secondary object accounting for 6% of the flux (ΔK′ = 2.9 mag). The flux contribution from the central source is estimated as 53.8 ± 1.5%.
Interferometric estimates of disk parameters.
The main features of the system may be summarized as follows: the system is a known spectroscopic binary with a period of almost 127 days. The primary object is a Be star with a very high rotational velocity (450 km s-1) that presumably presents a very elongated photosphere seen almost equator-on. As evidenced by the first interferometric measurement and in accordance to its shell classification, it is expected that the inclination angle is at almost 90°. The companion is a hot subdwarf star. We can estimate from the UV flux a contribution of 8% or less in the V- and H-band continuum. The main goals of our study are to attempt a direct detection of the companion in the optical to determine its physical and orbital properties and to continue the study of the disk geometry and kinematics.
3. Spectroscopic orbital determination from radial velocity measurements
A combined analysis of the astrometric and radial velocity orbits provides the key step to determining the stellar masses and distance. However, a comprehensive spectroscopic orbit was last determined by Božić et al. (1995), so it is worthwhile to reassess the spectroscopic orbital elements based on observations that are more contemporaneous with the interferometric observations. Here we present new radial velocity measurements for the Be primary and for the elusive sdO secondary.
Božić et al. (1995) showed that the wings of the Hα emission line that are formed in the inner disk close to the Be star display radial velocity variations of the Be star. Thus, we collected the available Hα spectroscopy from the Be Star Spectra Database1 (Neiner et al. 2011) and from the work of Grundstrom (2007). These were supplemented by several spectra we obtained with the KPNO Coude Feed telescope and one spectrum published by Tomasella et al. (2010). All of these are high S/N spectra with a resolving power generally better than R = λ/ △ λ = 5000. The reduced heliocentric Julian dates (RJD) of observation and origins of these 79 spectra are listed in Table 2. The Hα emission strength changed by a factor of two during these observations (with local maximum strength in 2005 and local minimum strength in 2011), and there were changes visible in the shape of the line core. However, the shapes of the emission wings remained more or less constant throughout this period, and this suggests that fast-moving gas close to the base of the disk at the photosphere was present throughout. Consequently, measurements of the Doppler shifts from the wing bisector should provide a reasonable estimate of the motion of the gas closest to the Be star itself. Božić et al. (1995) came to a similar conclusion and found no evidence of systematic deviations in the resulting velocities (which might be present, for example, if high-speed gas streams contributed to the emission flux).
We measured the Hα wing velocity by determining the emission line bisector position using the method described by Shafter et al. (1986). The radial velocity is found by cross-correlating the observed profile with a pair of oppositely signed Gaussian functions offset to positions of ±250 km s-1 from line center and then measuring the zero-crossing position of the resulting cross-correlation function. The uncertainties in the resulting measurements were estimated using the semi-empirical expression from Grundstrom (2007), but we caution that these estimates do not account for long-term changes in the emission profile that also influence the wing measurements. In most cases we were able to also measure accurate positions of the nearby atmospheric telluric lines, and we used these to make small corrections to the wavelength calibration in the topocentric frame. The resulting radial velocity measurements appear in Col. 3 of Table 2. For convenience, we also include a set of six radial velocities measured by Gies et al. (1998) for the Be star photospheric lines in far-ultraviolet spectra obtained with the HST.
We made a single-lined spectroscopic orbital determination from these radial velocities alone using the program SBCM described by Morbey & Brosterhus (1974). We began making circular fits with the period derived by Božić et al. (1995), P = 126.6731 ± 0.0071 d, and we derived an orbital semiamplitude of Ka = 11.4 ± 1.0 km s-1. This agrees within the uncertainties with the value reported by Gies et al. (1998), Ka = 10.0 ± 0.8 km s-1.
The measurement of radial velocities for the sdO companion is much more difficult. There are several features in the optical spectrum that display the antiphase Doppler shifts expected for the companion, but these are usually associated with gas near the companion star. These include weak He II 4686 Å emission that may form in a disk close to the companion (Poeckert 1981), He I 4026 Å, 4471 Å “shell” lines formed farther away (Poeckert 1981), and the He I 6678 Å emission line that probably originates in the outer disk of the Be star facing the hot subdwarf (Štefl et al. 2000; Hummel & Štefl 2001). There are only six HST measurements of the photospheric lines of the companion itself that were made in the far-ultraviolet spectrum by Gies et al. (1998), and we include these in Table 2. There are also 16 high-resolution FUV spectra of ϕ Persei available in the archive of the International Ultraviolet Explorer Satellite (Thaller et al. 1995), and we successfully detected the spectral signature of the companion in each of these using the cross-correlation methods described by Peters et al. (2013). We measured radial velocities for the companion using the same model template spectrum adopted in the work of Gies et al. (1998), and our derived radial velocities appear at the bottom of Table 2. The uncertainties associated with these velocities are probably larger than reported in the table. Indeed, since they are too faint, the interstellar lines in the spectrum of ϕ Persei cannot be used to correct for zero-point shifts of the star position with respect to the slit in the large-aperture observations (Peters et al. 2013).
We made a single-lined spectroscopic orbital solution for the secondary again using the orbital period from Božić et al. (1995), and we obtained a semiamplitude of Kb = 83.6 ± 2.1 km s-1 that agrees within errors with the determination from the HST spectra of Kb = 81.2 ± 0.6 km s-1 (Gies et al. 1998). Elliptical fits provided no improvement in the residuals. Thus, the IUE measurements tend to confirm the results from the HST spectra. On the other hand, because the measurement errors are larger for the IUE velocities, it is not clear whether or not including them improves our estimate of the semiamplitude Kb. In the following section, we restrict our considerations to the HST velocities of the companion. Note that the FUV derived estimate of the secondary semiamplitude is somewhat lower than that found from optical studies (Kb = 105 ± 7 km s-1 from He II 4686 Å, Poeckert 1981; Kb ≈ 90 km s-1 from He I 4026 Å, 4471 Å, Poeckert 1981; Kb = 101 ± 6 km s-1 from He I 6678 Å, Božić et al. 1995) presumably because the latter are influenced by gas motions and a location of origin that differ from that of the hot companion. The He I 6678 Å emission, for example, probably originates in the outer disk facing the companion at a position closer to the Be star and thus with a higher Keplerian orbital speed than that of the companion.
4. Interferometric observations and data analysis principles
Interferometric observations were carried out on the CHARA Array (ten Brummelaar et al. 2005), located at Mount Wilson Observatory. It consists of six 1 m telescopes sending their beams, after compression, through vacuum pipes to the recombining lab, through the fixed and movable delay lines with the correction of longitudinal dispersion, and the beams are re-arranged before feeding the instruments. For the purpose of this work we have used the MIRC instrument (Monnier et al. 2004, 2008) operated in the H band using all six CHARA telescopes (Che et al. 2012a) and the VEGA spectrograph used in the 4-T mode (Mourard et al. 2011). The spectral configurations used with the different instruments are summarized in Table 3. The different configurations we used during these observations are presented in Table 4. The corresponding (u,v) coverage, generated with the Aspro2 service2, is presented in Fig. 1.
 |
Fig. 1 Top: (u,v) plane coverage for MIRC. Bottom: (u,v) plane coverage for VEGA. The two figures use the same spatial frequency scale. |
For the VEGA observations, VEGA and MIRC were used simultaneously, MIRC with six telescopes in H band and VEGA with two different four-telescope configurations. MIRC was used as a 6-T group delay sensor, and corrections were sent directly to the main delay lines. An initial cophasing of the two instruments was made using a reference target thanks to the fine adjustments of the MIRC feeding optics and corresponding corrections on the main delay lines. The observing sequence was then 1) MIRC finds and stabilizes the fringes; 2) MIRC and VEGA start recording data; 3) at the end of the VEGA sequence, MIRC does its shutter and photometry sequence.
Two different calibrators were used for the VEGA observations: HD 3360 and HD 25642. They were identified using the SearchCal service3 (Bonneau et al. 2006, 2011) and the CDS Astronomical Databases SIMBAD and VIZIER4. We used the SearchCal spectrophotometric uniform disk angular diameter determinations in the R and H bands, which led to θUD − R = 0.284 ± 0.020 mas and θUD − H = 0.287 ± 0.020 mas for HD 3360 and to θUD − R = 0.439 ± 0.031 mas and θUD − H = 0.447 ± 0.031 mas for HD 25642. In addition to these calibrators, MIRC calibration employed the additional calibrators 7 And (0.65 ± 0.03 mas), θ Cas (0.57 ± 0.04 mas), and HD 33167 (0.50 ± 0.04 mas).
The data processing followed the standard MIRC (Monnier et al. 2007, 2012) and VEGA (Mourard et al. 2009, 2011) procedures. Based upon our understanding of the current VEGA limitations (Mourard et al. 2012), we decided to reject all closure phase measurements with VEGA and to set a conservative lower limit to the absolute uncertainty of the squared visibility measurements at the level of 0.05.
5. Near-IR image reconstruction and companion detection
5.1. MIRC results
For the purposes of this paper, we wished to extract two major findings from the MIRC data. First, we sought to directly detect the companion for the first time to determine the visual orbit of the ϕ Persei binary system. Secondly, we aimed to take advantage of the dense and complete (u,v)-coverage from MIRC to create an image using aperture synthesis and to constrain the inclination angle of the disk.
Basic parameters of the H-band disk model from MIRC observations.
Position of the companion as a function of the RJD as detected in the various MIRC data sets.
First, to extract the companion location, we fitted a binary model to each of the ten best observing epochs with six-telescope MIRC data. The model for each epoch has 11 parameters: fraction of H-band light from the primary, uniform disk diameter for the primary, fraction of light from the companion, uniform disk diameter for the companion, separation and position angle of the companion compared to the primary, Gaussian model for disk emission with three parameters describing the symmetric component (FWHM of the major axis, FWHM of the minor axis, position angle on the sky of the major axis), and two parameters to describe any asymmetric disk emission (skew angle and skew fraction; see description in Monnier et al. 2006; Che et al. 2012b). In our case, the uniform disk diameter (UDD) of the primary was fixed at 0.3 mas and the UDD of the companion was fixed as 0.056 mas, on the basis of spectrophotometric estimations. We might expect the skewness to change from epoch to epoch (as was found for δ Sco by Che et al. 2012b). This is indeed confirmed by our results at each epoch, but unfortunately, no conclusion could be drawn. Based on our fitting, we report the median and one-sigma range of the H-band disk parameters in Table 5, while the locations of the companion for all epochs are collected in Table 6. The typical reduced χ2 achieved during fitting was ~1.9. A synthetic view of the MIRC data is presented in Fig. 2.
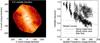 |
Fig. 2 Left panel: two-dimension visibility function for ϕ Persei from MIRC. We combined all our epochs together and averaged with a 30 m smoothing window, maintaining each wavelength channel. Right panel: same averaged data as a function of radial spatial frequency unit. In addition, we have included model visibilities for position angles along the major and minor axes of the average disk model (see Table 5). |
We used the MACIM imaging algorithm (Ireland et al. 2006) along with the dark energy regularizer to carry out image reconstruction by combining all the MIRC data together. Since the primary star contains ~70% of the total flux, it is important to remove this component explicitly as part of the image reconstruction, as explained in detail in Che et al. (2012b). We accounted for the moving secondary based on an orbital model, although this has only a small effect since the companion only contributes ~1.5% of the total light in the system. Figure 3 shows our image reconstruction of the disk alone, along with the locations of the secondary star for each epoch. The dynamic range appears to be noticeably smaller than most MIRC imaging (background noise is about ten times below peak emission), but this is because the central star has been removed from this image through modeling. If we were to add back the central star, we would find a dynamic range of ~100 in this image. The reduced χ2 for this image is ~2.0, only slightly worse than found using disk modeling for each individual epoch. We expect some time variation between epochs, and so it is not too surprising that the χ2 is not as low as typically found when imaging with MIRC.
We briefly mention some known limitations of our method and point out future work. First, the disk model is quite simplistic. As discussed elsewhere (e.g., Kraus et al. 2012; Che et al. 2012b), the gas disk is expected to have a hole in the center where the star is, and we also expect significant obscuration of the central star at this high-inclination angle. Furthermore, the imaging suggests a Gaussian disk profile, which is probably not a realistic model. The asymmetric component of the disk emission changes the photo center of the primary object, thus adding errors to our estimate of the secondary separation vector. Indeed, it seems the companion location of 2012 Nov. 06 is physically impossible, and our estimate might have been affected by changing asymmetries in the inner disk that were not accurately modeled by our method.
5.2. Orbital solution for the companion
Based on the radial velocity measurements presented in Sect. 3 and on the companion positions determined in Sect. 5.1, we performed a joint astrometric and radial velocity solution of the orbit. We adopted the period from Božić et al. (1995), P = 126.6731 ± 0.0071 d, in the first combined fit. By combining the epochs of the ascending node of the companion (equal to the velocity maximum for the secondary and the velocity minimum for the Be star primary) from Božić et al. (1995), Gies et al. (1998) (119 orbital cycles later), and our new solution (166 orbital cycles later), we then derived improved estimates for the period and epoch. The revised period P = 126.6982 ± 0.0035 d is 3σ larger than that found by Božić et al. (1995), but we use this revised period and epoch (TRV min = RJD 56 110.00 ± 0.12) to reference the orbital phase in the rest of this paper.
We fixed the period to P = 126.6982 and assumed a circular orbit for our final solution. To assess the errors in the orbital parameters, we carried out a bootstrap analysis, for which we resampled the astrometric and RV data to create 100 synthetic data sets. Initially, we found the reduced χ2 for the RV data to be 69, clearly revealing systematic errors not accounted for in the original RV error analysis. In response to this, we treated all data with uniform error bars scaled to achieve a reduced χ2 of unity. The corresponding errors become thus ± 8.6 km s-1 (resp. ±1.35 km s-1 and ±3 km s-1) for the Hα set (resp. the primary and secondary HST data set from Gies et al. 1998). As mentioned earlier, we also chose to remove the epoch of 2012 Nov. 06 from our astrometric fit because it has a much larger discrepancy with the orbital prediction than any other observation, and it must be an outlier due to unmodeled disk substructure or a calibration problem (we have included it in Fig. 3 for reference).
The result of our best-fit model along with 100 bootstraps is shown in Fig. 3, the RV curve is shown in Fig. 4. The results on the orbital parameters, masses, and distance appear in Table 7 and are discussed in Sect. 7.
 |
Fig. 3 Image reconstruction made with MIRC data in the H band. Here we have separately modeled the contributions from the Be star and the companion, and this image represents the emission from the disk alone, contributing about ~29% of the total H-band flux. We have marked the location of the companion at the ten epochs reported here with error ellipses and show the best-fit circular orbit (see text). The colored band shows the results from 100 bootstrap fits to illustrate the errors on our orbital solution. East is left and north is up. |
 |
Fig. 4 Radial velocity measurements of the primary star along with predicted orbit from the joint MIRC+RV fit (see Table 7). Open symbols represent Hα wing bisector measurements, while filled symbols represent HST measurements from Gies et al. (1998). 1σ error bars have been fixed to ±8.6 km s-1 as explained in the text. The width of the solid line illustrates the errors on our orbital solution estimated from 100 bootstrap fits. The RV is negative at zero phase because we have chosen an astrometric orbital ephemeris of the secondary relative to the primary, which is opposite in sign to the radial velocity convention, where the velocity of the primary star is measured relative to the center-of-mass. |
6. Visible data and disk properties
6.1. Visible broadband data and model fitting
Using the VEGA wide spectral band measurements, we first performed a model fitting using the software LITpro5 (Tallon-Bosc et al. 2008). We first used the three bands containing continuum and then, separately, the band containing the Hα line as defined in Table 3.
In a first approach, we just used a simple uniform disk model. We found a diameter in the continuum of 0.343 ± 0.006 mas and in the line of 0.423 ± 0.012 with a reduced χ2 of 9.3 and 14.4, respectively (Table 8, first section). The larger equivalent diameter in the line indicates the presence of an extended structure, corresponding to the line emission associated with the disk. The residuals clearly indicate that the size of the object varies with position angle, and thus we used a second model with the addition of an elongated Gaussian disk. The results are presented in Table 8 (second section). We tried to detect the companion in the VEGA data but, despite the very good (u,v) coverage, the data quality at low visibility level does not permit this direct detection. We therefore decided to adopt the position of the companion found by MIRC, but consider its flux as a free parameter. To avoid the complication introduced by the change in the companion’s position, we only used the data of 2011 October 18 and 19 (RJD = 55 852 and 55 853) for this analysis.
The results clearly show the significant departure from a spherical object, both in the continuum and in the band containing Hα. As evidenced by the evolution of the reduced χ2, an improvement is found with a model consisting of a uniform disk + an elongated Gaussian disk (Table 8, third section), and the results are even better if we consider the companion (Table 8, fourth section). The difference in size and orientation of the elongated object between the continuum and Hα is the signature of the difference between the disk emitting in the Hα line and the continuum, and the elongated object potentially consists of a rotationally distorted photosphere plus the contribution from the disk. In fact, a large portion of the stellar photosphere is obscured by the disk, but this fraction is not the same in the continuum and in the Hα band. We also note that the position angle value found in the emission line region, where the disk is dominating the flux, is closer to the position angle found in the H band (PA = −64° ± 3°) and is compatible within 2σ despite the difference of wavelength.
6.2. Spectrally resolved Hα data and model fitting
Differential visibilities are estimated through the standard VEGA procedure (Mourard et al. 2009). For the purpose of the ϕ Persei work, we have established the absolute orientation of the differential phases in any of the CHARA+VEGA configurations (Mourard et al. 2012). Some examples of differential measurements are presented in Fig. 5, bottom part. The photon-counting detectors of VEGA suffer from a local saturation effect in presence of bright spectral lines that attenuates the line intensity. This nonlinearity in the photometric response of the detector does not generate bias in the derived complex visibilities as explained by Delaa et al. (2011).
To model the spectrally resolved visibility and differential phase in the Hα emission line, we used the simple kinematic model developed for fast model-fitting of a geometrically and optically thin equatorial disk in rotation described in detail by Delaa et al. (2011) and Meilland et al. (2012).
The model parameters can be classified into four categories:
-
1.
The stellar disk parameters: stellar polar radius (R⋆), stellar flattening (f), distance (d), inclination angle (i), and major-axis position angle (PA).
-
2.
The kinematic parameters: rotational velocity (Vrot) at the disk inner radius (i.e., photosphere) and the rotation power-law index (β).
-
3.
The disk continuum parameters: disk FWHM in the continuum (ac) and disk continuum flux normalized by the total continuum flux (Fc).
-
4.
The disk emission line parameters: disk FWHM in the line (al) and line equivalent width (EW).
The model produces a data cube consisting of narrow spectral band images through the Hα line at the instrumental spectral resolution. Visibilities and differential phases for our baseline configurations are then extracted from the data cube and are compared to the observation using the standard χ2 method.
 |
Fig. 5 Top: 0.65 μm continuum visibility for the best-fit model is plotted as a function of the spatial frequency, whereas the blue zone represents the extent of the model visibility for the various orientations of the baseline. Bottom: examples of differential visibilities and phases (in red + error bar in yellow) for the best-fit model (in blue) for various baselines between 32 and 278 m. |
Values of the VEGA best-fit kinematic model parameters.
Except for the distance, the ten parameters are free and can vary within a range of realistic values. The parameter values for the best-fit model are presented in Table 9. The reduced χ2 for this model is 4.0. Interestingly, with this more representative model of the system geometry, the position angle and inclination of the disk is fully compatible with the one found with the MIRC imaging.
The 0.65 μm continuum-squared visibilities for the best-fit model are plotted as a function of the spatial frequency in Fig. 5, top part. Some examples of differential visibilities and phases for the best-fit model for various baselines between 32 and 278 m are plotted in Fig 5, bottom part. As already explained in Delaa et al. (2011), phase variations for baselines overresolving the object (i.e., 60 m in the major-axis orientation and 200 m in the minor-axis one in the case of ϕ Persei) are only poorly fitted. The jumps seen for some baselines might be either due to inhomogeneity in the disk or to VEGA data reduction biases at very low visibility. We also note that some of the very short baselines show an increase of visibility instead of a drop in the Hα line, which corresponds to a smaller object in the line. This effect might be due to the high opacity of the disk seen edge-on and can only be modeled using a radiative transfer code.
6.3. Spectrally resolved image reconstruction around Hα
 |
Fig. 6 Top row: sequence of intensity maps (6.4 × 6.4 mas) as a function of wavelength with north up and east left as imaged by VEGA (upper sequence), as computed from the kinematic model in Sect. 6.2 (middle sequence), and as imaged through a simulated observation of the above model (lower sequence). Middle row: at the left, we present the continuum image convolved to the diffraction limit of VEGA (0.2 mas) together with contours at 50, 5, 0.5 and 0.05% of the peak intensity to show the disk contour. The middle and right panels show the selected zones to extract the spectra presented below together with an unconvolved continuum image of the system. Bottom row: extracted spectra for the different spatial components: 1) Bottom middle: extracted fluxes (top: total flux, pink absorption feature: “star” zone, blue emission feature: “disk” zone, and dashed spectrum: all other contributions); 2) bottom right: decomposition of the “disk” zone: the top spectrum is the total flux. The blue and red lines correspond to the blue- and redshifted emission features, while the central zeroshifted emission feature comes from all other parts of the “disk” zone. |
We used the MiRA software (Thiebaut & Giovannelli 2010) combined with an improved self-calibration method (Millour et al. 2011) to reconstruct wavelength-dependent images of ϕ Persei in the visible wavelength range. The data set contains the broadband V2 defined in Table 3 and the wavelength-dependent differential visibilities and phases, but no closure phases, as previously said. Therefore, the self-calibration method had to be modified. The different steps of our method, and the additions made in this work, are presented in Appendix A. The so-called SELF-CAL software and its documentation are available online6.
The image reconstruction leads to an (x,y,λ) image cube that covers a field of view of 6.4 mas with 64 × 64 pixels, a wavelength range between 646 nm and 666 nm with a spectral resolution of ≈1640. This translates into ≈10 spectral channels in the Hα emission line.
The images in Fig. 6 exhibit little variation of morphology throughout the continuum. They display three prominent features:
-
an elongated central source (the “star”) that can be contained in an ellipse with ≈0.6 × 0.4 mas major and minor axes, and ≈20° position angle for the minor axis,
-
an extended flattened source (the “disk”) whose extension is weakly constrained. We can set an upper limit to its size to an ellipse ≈3.9 × 1.8 mas, and ≈20° position angle of the minor axis,
-
a significant amount of unconstrained flux (≈15% of the continuum flux, throughout all wavelengths), which could be linked to the companion star or to image-reconstruction artifacts.
The images in the emission line are very different from those in the continuum, showing emission that sweeps across the “disk” feature. In the upper part of Fig. 6, we compare the spectral images and the maps deduced from the model presented in the previous section. We also provide a set of reconstructed images from simulated data based on the kinematic model.
To extract information from these images from milli-arcsecond integral-field spectroscopy, we multiplied the images by the system spectrum (as MiRA provides total-flux-normalized images) and selected different zones with binary masks to extract their spectra. The result of this process is shown in the bottom part of Fig. 6.
The “star” zone exhibits an absorption spectrum, characteristic of a stellar spectrum. The “disk” zone bears most of the emission of the system, while the unconstrained flux has a flat spectrum.
The results of the VEGA imaging and model fitting are discussed in general in Sect. 7.
7. Discussion
7.1. Fundamental stellar parameters
We first consider the dimensions of the binary system. The astrometric measurements from MIRC (Table 6) were combined with the radial velocity measurements for the two components (Table 2) in a joint solution for the binary orbital elements and distance that is summarized in Table 7. Our derived values of the stellar masses, Ma = 9.6 ± 0.3 M⊙ and Mb = 1.2 ± 0.2 M⊙, agree well with those determined previously by Gies et al. (1998). Our distance estimate d = 186 ± 3 pc is about 4.2σ closer than the estimate from the revised Hipparcos distance or 1.1σ closer than the original Hipparcos distance. We note, however, that ϕ Persei is flagged as ”unsolved variable” in the Hipparcos catalog; we could then expect an underestimated error for the parallax in the revised Hipparcos catalog.
A knowledge of the distance to ϕ Persei has consequences for the size of the Be star. We can estimate the stellar radius from the predicted angular size and distance. We first consider the angular size from a comparison from a of the observed and predicted photospheric fluxes, a task that is best accomplished in the ultraviolet part of the spectrum where the circumstellar disk flux is negligible. Touhami et al. (2013) fit the observed UV spectrum of ϕ Persei using a Kurucz flux model for the adopted temperature (from Frémat et al. 2005) of the Be star and a standard extinction law (ignoring the small flux contribution of the hot companion), and they derived a limb-darkened, angular diameter for the Be star of 0.235 ± 0.008 mas. This is similar to the minor-axis diameter derived from the VEGA broadband observations (0.18 ± 0.01 mas, Table 8). Then, for an adopted distance of 186 pc, the stellar radius is estimated to be Ra/R⊙ = 4.7 ± 0.4. This is somewhat lower but consistent within error bars to that given in Table 9 and prorated for the adopted lower distance (Ra/R⊙ = 5.9 ± 1.7). The difference may be partially due to the neglect of UV flux scattered away from the line of sight by electron scattering in the inner disk so that the stellar UV flux (and hence angular size) is somewhat higher than estimated from the observed UV spectrum. Furthermore, the estimate of stellar diameter from the VEGA measurements may be influenced by the assumed flux distribution in the disk.
The mass and radius of the Be star match the mass – radius relationship for main-sequence stars derived from eclipsing binaries (Torres et al. 2010). Furthermore, the effective temperature Teff = 29.3 kK (Gies et al. 1998) and luminosity log La/L⊙ = 4.16 ± 0.10 (for Ra/R⊙ = 4.7) are consistent with those of eclipsing binary stars of similar mass (Torres et al. 2010). The Be star’s rotation rate, however, is exceptional. Adopting the estimate of projected rotational velocity from Frémat et al. (2005), Vsini = 462 ± 33 km s-1, we derive a ratio of equatorial velocity to orbital velocity at the equator (Rivinius et al. 2013) of (Vsini/ sini) /Vcrit = 0.93 ± 0.08 for the mass and radius given above and an inclination from Table 5 (assuming coalignment of the spin and orbital vectors; see below). Note that we have tacitly assumed that the radius derived from the UV flux and the distance corresponds to the star’s polar radius, whereas it may represent some value between the polar and (larger) equatorial radius. For example, if our radius estimate corresponds to the equatorial radius in a near critical rotation star, then R± polar = Ra/ 1.5 and (Vsini/ sini) /Vcrit = 0.76 ± 0.08. On the other hand, the measured projected velocity may underestimate the actual value of Vsini because of gravity darkening (Townsend et al. 2004). Despite these uncertainties, the clear conclusion is that the Be star is rotating very rapidly. The companion’s rotational velocity is low, vrotsini< 10 km s-1 (Gies et al. 1998).
Gies et al. (1998) derived a radius ratio of Rb/Ra = 0.20 from the observed flux ratio in the ultraviolet spectrum. Adopting the Be star radius given above, the radius and luminosity of the hot companion are Rb/R⊙ = 0.94 ± 0.09 and log Lb/L⊙ = 3.80 ± 0.13 (for Teff = 53 ± 3 kK; Gies et al. 1998). Thus, although the Be star is five times larger than the sdO companion, it is only twice as luminous. In the Rayleigh-Jeans tail of the spectrum in the near-IR, we would expect that the surface flux varies with effective temperature, so the flux ratio would be Fb/Fa ≈ (Tb/Ta)(Rb/Ra)2. Based upon the temperature and radius ratios estimated by Gies et al. (1998), the predicted optical/IR flux ratio is 8%. This value is similar to the observed flux ratio in the optical (F3 /F1 = 7.5 ± 1.7%; Table 8), but higher than found in the H band (f2/f1 = 2.1 ± 0.5%; Table 5). We speculate that the discrepancy is due to obscuration of the sdO companion by circumstellar gas that becomes more significant at longer wavelength (see below).
7.2. Birthplace and age
We next consider the possible birthplace and age of ϕ Persei. Our derived distance is consistent with that of the nearby α Per cluster (Melotte 20; Per OB3) at 177 pc (de Zeeuw et al. 1999), and ϕ Persei is located at a similar angular separation (15.9°) from the cluster center as some of the α Per “halo stars” identified by de Zeeuw et al. (1999). Furthermore, the proper motion of ϕ Persei (μαcosδ = 24.6 mas yr-1, μδ = −14.0 mas yr-1; van Leeuwen 2007) is similar to that of the α Per cluster (μαcosδ = 22.7 mas yr-1, μδ = −26.5 mas yr-1; Lodieu et al. 2012). Likewise, the systemic radial velocity of ϕ Persei (−2.2 km s-1; Table 7) is similar to the mean value for the α Per cluster (−1.0 km s-1; de Zeeuw et al. 1999). Thus, the distance, position, and kinematical properties of ϕ Persei suggest that it may be an outlying member of the α Per cluster. If so, then the age of ϕ Persei is the cluster age, ≈52 Myr (Kharchenko et al. 2005; Makarov 2006; Lyubimkov et al. 2010). This is much older than the main-sequence lifetime of ≈25 Myr for a 10 M⊙ mass star like the Be primary (Brott et al. 2011), which suggests that the Be star attained its high mass relatively recently.
The age of the α Per cluster is consistent with the binary evolutionary scenario for ϕ Persei. The ϕ Persei binary probably began its life as a pair of 6 M⊙ + 5 M⊙ stars with a shorter orbital period in the range of 7 d (Vanbeveren et al. 1998a) to 14 d (Vanbeveren et al. 1998b). As the initially more massive star completed core-hydrogen burning, it expanded and began mass and angular momentum transfer to the companion. The binary separation increased following mass ratio reversal, reaching its current state of wide separation between the stripped-down remnant of the mass donor (the hot subdwarf star) and the rapidly rotating mass gainer (the Be star). If we assume that the mass transfer was approximately conservative (i.e., negligible mass lost from the system), then the progenitor of the hot subdwarf had a mass at least as high as half the current total mass of the system (5.4 M⊙; Table 7). Indeed, given the current advanced evolutionary state of the donor as a hot subdwarf star, it must have had an original mass in excess of that for any H-burning star still in the α Per cluster. The most massive star in the α Per cluster (aside from ϕ Persei) is α Per itself, with a mass estimated in the range of 6.7 M⊙ (Makarov 2006) to 7.3 M⊙ (Lyubimkov et al. 2010). Thus, the original mass of the donor star was probably Mb orig ≈ 7 M⊙, so that the mass gainer (Be star) accreted most of the difference Mb orig − Mb ≈ 6 M⊙ during mass transfer. This wholesale transformation of the mass gainer led to its current high mass and fast spin, and the Be disk found today represents the Be star’s means to shed its excess angular momentum. We now know of two other Be plus sdO binaries, FY CMa and 59 Cygni, that share many of the properties of ϕ Persei (Peters et al. 2013), and it is probable that other hot companions of Be stars await discovery (Koubský et al. 2012, 2014).
7.3. Properties of the Be-star disk
We next consider the properties of the Be star disk. Interferometric observations have now resolved the disk in the continuum at several wavelengths. The angular size derived depends in part on the adopted model for the flux distribution in the sky, but we list in Table 1 the results for an assumed uniform disk star and Gaussian elliptical disk. The Gaussian FWHM along the disk major axis θmaj appears to increase with wavelength from R through H and K′ bands as expected because of the increase in hydrogen free-free opacity with wavelength that causes the optical depth unity radius to appear larger when moving into the near-infrared (Touhami et al. 2011). The Hα diameter measured from the VEGA observations is somewhat smaller than that derived from earlier Hα measurements and is comparable to or lower than the contemporaneous near-IR continuum estimates. This is surprising given that the Hα sizes are generally larger than the near-IR continuum sizes in most Be stars (Touhami et al. 2013). We note, however, that the Hα emission equivalent width at the time of the VEGA observations (Wλ = −25 Å) was much weaker than at some times in the past (Wλ = −46 Å in 2001), and if the disk size scales with the emission strength (Grundstrom & Gies 2006), then the disk dimensions may have been larger at earlier epochs. It is possible that gravitational interactions with the companion limit the physical boundary of the gaseous disk, as occurs in many Be X-ray binaries (Negueruela & Okazaki 2001).
The interferometric observations indicate that the spin angular momentum axis of the disk is coaligned with the orbital angular momentum axis. The position angle of the long axis of the projected disk (PA in Tables 1, 5, 8, and 9) agrees with the longitude of the ascending node in the astrometric orbital solution (Ω in Table 7). The position angle of the disk normal (PA + 90°) agrees with the intrinsic polarization angle, as expected by Quirrenbach et al. (1997). Furthermore, the disk inclination derived from the ratio of projected minor to major axis (i = 75° ± 9° from r = cosi in Tables 1 and 9) is consistent within errors with the astrometric orbital inclination (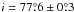 in Table 7). Finally, the sense of the disk rotation (moving away in the northwestern part; Fig. 6) is the same as the sense of orbital motion (Fig. 3). Thus, we find that the disk and orbital angular momentum vectors are coaligned, verifying the prediction from the binary interaction model that the spin-up of the Be star was caused by mass and angular momentum transfer from the donor companion. Note that in general we expect that the inclination derived from the projected shape of the disk will be smaller than actual because of disk flaring that increases the apparent size of the minor axis (Grundstrom & Gies 2006), so the small difference we find between inclination estimates from the disk and orbit is probably consistent with some disk flaring. The increase in disk thickness with radius (flaring) means that there will be a range in inclination below 90° where the disk may occult our view of the Be star photosphere, and this may explain the presence of narrow “shell” lines that are observed in the spectra of some Be stars (Rivinius et al. 2013). ϕ Persei has a well-observed shell line spectrum, so our inclination estimate would appear to indicate that the disk half-opening angle may amount to as much as 90°−i = 12° in this case. Curiously, Hanuschik (1996) used a statistical study of the numbers of Be-shell and normal Be stars to arrive at a similar half-opening angle of 13°. The agreement may be coincidental, and detailed models of disk line formation show that shell line spectra may form over a wider range below i = 90° (Silaj et al. 2014).
in Table 7). Finally, the sense of the disk rotation (moving away in the northwestern part; Fig. 6) is the same as the sense of orbital motion (Fig. 3). Thus, we find that the disk and orbital angular momentum vectors are coaligned, verifying the prediction from the binary interaction model that the spin-up of the Be star was caused by mass and angular momentum transfer from the donor companion. Note that in general we expect that the inclination derived from the projected shape of the disk will be smaller than actual because of disk flaring that increases the apparent size of the minor axis (Grundstrom & Gies 2006), so the small difference we find between inclination estimates from the disk and orbit is probably consistent with some disk flaring. The increase in disk thickness with radius (flaring) means that there will be a range in inclination below 90° where the disk may occult our view of the Be star photosphere, and this may explain the presence of narrow “shell” lines that are observed in the spectra of some Be stars (Rivinius et al. 2013). ϕ Persei has a well-observed shell line spectrum, so our inclination estimate would appear to indicate that the disk half-opening angle may amount to as much as 90°−i = 12° in this case. Curiously, Hanuschik (1996) used a statistical study of the numbers of Be-shell and normal Be stars to arrive at a similar half-opening angle of 13°. The agreement may be coincidental, and detailed models of disk line formation show that shell line spectra may form over a wider range below i = 90° (Silaj et al. 2014).
Next, we offer a few comments about the surface brightness distribution of the Be disk. Similar to other investigators, we have used Gaussian elliptical models for surface brightness because they generally provide good fits of the interferometric visibility. However, models of the spatial appearance of disk flux often predict more complicated distributions (Fig. 6), and in particular, in models where the circumstellar gas becomes optically thick, the surface brightness distribution appears more or less constant in the parts of the disk close to the photosphere (Gies et al. 2007). Thus, for example, the relatively small minor axis fit to the MIRC observations (Table 5) may be partially due to the non-Gaussian appearance of the foreshortened disk brightness distribution (Fig. 3). It is probably unrealistic to assume that the disk is azimuthally symmetric, because many Be stars including ϕ Persei display long-lived asymmetries in their emission line profiles that probably form in one-armed spiral structures (Rivinius et al. 2013). The Hα profile observed over the time span of the CHARA observations displayed a stronger red than blue peak (see Fig. 8 of Silaj et al. 2010), which indicates that some asymmetry in the Hα disk surface brightness did exist at this time. We note that there is a hint in the Hα image reconstructions shown in Fig. 6 that the northwestern (redshifted) extension of the disk is slightly brighter than the southeastern extension (blueshifted). The VEGA observations were obtained near orbital phase 0.0 when the companion appears near its northwestern, maximum elongation, and the part of the disk facing the companion may be brighter (Hummel & Štefl 2001). Thus, the Hα interferometry offers tentative evidence for the presence of the surface brightness asymmetries expected from disk density structures and heated zones.
Finally we note that reverse mass transfer from the Be disk to the hot subdwarf may occur. The fact that the observed circumstellar disk radius appears smaller than the semimajor axis (Fig. 3) does not necessarily imply that disk gas never reaches the vicinity of the companion. The interferometric observations record the spatial distribution of the brightest parts of the disk emission, and it is possible that lower density and fainter disk gas does extend to the orbit of the companion as it slowly moves outward from the Be star. Indeed, Hummel & Štefl (2003) argued that the He I 6678 Å emission extends to the outer edge of the disk at RRoche/a = 0.56. We would expect that some of this gas will be captured by the gravitational pull of the companion to form an accretion disk around the subdwarf star. The double-peaked appearance of the He II 4686 Å emission that forms near the companion may be evidence of such an accretion disk (Poeckert 1981). It is possible that gas around the companion may obscure our view of the hot subdwarf star itself, and the attenuation would increase with wavelength if free-free processes dominate the continuum opacity. This may explain why the companion appears fainter than expected in the near-IR.
8. Conclusion
Thanks to advanced visible and infrared interferometric instrumentation at the CHARA Array, we have been able to obtain the first high angular resolution images of the Be binary ϕ Persei, including the first spectrally resolved images in the visible (made with VEGA in four-telescope mode). These images show the highly inclined circumstellar disk surrounding the Be star, and the helium star remnant of the mass donor star is detected for the first time through MIRC observations of its orbital motion.
The relative angular orbital motion of the hot companion was combined with new orbital radial velocity measurements of both components to derive a full, three-dimensional orbit of the binary system. We obtain masses of 9.6 ± 0.3 M⊙ and 1.2 ± 0.2 M⊙ for the Be star primary and subdwarf secondary, respectively. The distance derived from the joint astrometric and spectroscopic solution is 186 ± 3 pc. We note that ϕ Persei shares the same distance, kinematical, and evolutionary properties as members of the α Per star cluster, and if this association is confirmed, then the cluster age will place significant constraints on the initial masses and evolutionary mass transfer processes that transformed the ϕ Persei binary system. The Be star (mass gainer) has a mass, radius, and effective temperature that are typical of an early B-type main-sequence star, but it is rotating very rapidly (93 ± 8% of the critical rate) as a consequence of angular momentum gained during past mass transfer. The sdO secondary star (remnant of the mass donor) is fainter in the near-IR than predicted from the FUV flux ratio (Gies et al. 1998), due perhaps to obscuration by circumstellar gas in its vicinity.
The circumstellar gas disk of the Be star primary was resolved in the optical and near-IR H-band, and we estimated the disk flux contributions in each of the Hα emission lines and the optical and near-IR continua. The apparent ellipticity and position angle of the disk in the sky is similar in each band. The size of the disk in the continuum flux is larger at longer wavelength, presumably due to the increasing free-free optical depth of the disk at longer wavelength. The disk appears largest in the spectrally resolved Hα observations (Fig. 6), but the visible flux appears to be confined well within the Roche lobe of the Be star. We find that the angular momentum vector of the disk is aligned with and shows the same sense of rotation as the binary orbital angular momentum vector. This agreement confirms the evolutionary prediction that the Be star was spun up by mass transfer in the binary and that this excess angular momentum is now being shed into the Be star disk.
The appearance of the Be disk is presented in the first nonparametric images reconstructed from the MIRC H-band observations (Fig. 3) and from the spectrally dispersed VEGA observations of Hα (Fig. 6). These images reveal the brighter, inner parts of the disk, and there is some evidence in the spectrally dispersed Hα maps from VEGA of an asymmetry in the azimuthal light distribution of the circumstellar disk. The northwestern part of the disk that is moving away from us appears slightly brighter than the southeastern part that is approaching (Fig. 6), consistent with the relatively stronger red peak of the Hα profile observed at this time. Such asymmetries probably originate in long-lived disk structures (perhaps a one-armed spiral instability), and long-baseline interferometric observations now appear to offer the means of exploring the time evolution of these disk processes.
Online material
Radial velocity measurements.
Appendix A: Visible-image reconstruction process
Appendix A.1: Self-calibration
We used the software MiRA (Thiebaut & Giovannelli 2010) combined with an improved self-calibration method (Millour et al. 2011) to reconstruct wavelength-dependent images of ϕ Persei in the visible wavelength range. The data set contains only broadband V2 defined in Table 3 and the wavelength-dependent differential visibilities and phases, but no closure phases. Therefore, the self-calibration method had to be updated: the first step of image-reconstruction is made using the broadband V2 only. The first tentative map is therefore the same for all wavelengths. Then we had to self-calibrate the visibility gains in addition to the differential phases offsets. We outline below the different steps of our method and the additions made in this work. We also refer to the review of Pearson & Readhead (1984) for an overview of the self-calibration methods in radio-astronomy. The so-called SELF-CAL software and its documentation are available online7.
-
1.
Initial image reconstruction: we call I0(x,y,λ0) the first tentative imagereconstruction using the V2(u,v,λ0) only,
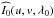 its Fourier transform, and dV(u,v,λ), dφ(u,v,λ) thedifferential visibilities and phases provided by VEGA.
its Fourier transform, and dV(u,v,λ), dφ(u,v,λ) thedifferential visibilities and phases provided by VEGA. -
2.
Self-calibration: in the self-calibration process we search for complex gain values g(u,v) that are a function of the (u,v) coordinates and have the following equalities:
![\appendix \setcounter{section}{1} \begin{eqnarray} ||\widehat{I_0}(u,v,\lambda)|| & =& ||g(u,v)|| \times {\rm d}V(u,v,\lambda) \\ \arg[\widehat{I_0}(u,v,\lambda)] & = & \arg[g(u,v)] \times {\rm d}\phi(u,v,\lambda). \end{eqnarray}](/articles/aa/full_html/2015/05/aa25141-14/aa25141-14-eq228.png)
-
3.
(x,y,λ)Image reconstruction: these gain values are then applied to the differential phases and visibilities, which become amplitude and phase of a complex visibility that is stored to a new OIFITS file (Pauls et al. 2005). This OIFITS file is fed again to the MiRA software to produce a (x,y,λ) image.
This new image serves as a basis to a new step of self-calibration. The self-calibration process can be repeated until a reasonable convergence is achieved. Here, we decided to arbitrarily stop at the second step, as in Millour et al. (2011).
Appendix A.2: Selecting proper image reconstruction parameters
For the image reconstruction process, we had to select the field of view, the pixel size and the reconstruction hyperparameter μ values.
Field of view.
The field of view of our images was selected thanks to the following relation: 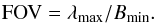 (A.3)Here, the smallest available baseline was Bmin = 32 m and λmax = 665 nm, hence a field of view of 4.2 mas.
(A.3)Here, the smallest available baseline was Bmin = 32 m and λmax = 665 nm, hence a field of view of 4.2 mas.
Pixel size.
The pixel size was selected thanks to 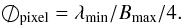 (A.4)The factor 4 comes from a double factor 2: the diffraction limit of the interferometer as defined as in Monnier et al. (2007), and an additional “super-resolution” factor 2. We have a maximum baseline of 312 m, which translates into a 0.1 mas pixel size.
(A.4)The factor 4 comes from a double factor 2: the diffraction limit of the interferometer as defined as in Monnier et al. (2007), and an additional “super-resolution” factor 2. We have a maximum baseline of 312 m, which translates into a 0.1 mas pixel size.
In addition, for computing time considerations, we had to select a power of 2 for the pixel number. Therefore, we selected images with 64 × 64 pixels of 0.1 mas.
Hyperparameter selection.
For the images presented here, we used the total variation regularization as suggested in Renard et al. (2011), a number of iterations per wavelength of 50, and we selected the hyperparameter value μ = 105 thanks to the same method as described in Domiciano de Souza et al. (2014).
Available at http://www.jmmc.fr/aspro
Available at http://www.jmmc.fr/searchcal
Available at http://cdsweb.u-strasbg.fr/
LITpro software available at http://www.jmmc.fr/litpro
Available at http://self-cal.oca.eu
Available at http://self-cal.oca.eu
Acknowledgments
The CHARA Array is operated with support from the National Science Foundation through grant AST-0908253, the W. M. Keck Foundation, the NASA Exoplanet Science Institute, and from Georgia State University. VEGA is a collaboration between CHARA and OCA-Lagrange/UJF-IPAG/UCBL-CRAL that has been supported by the French programs PNPS and ASHRA, by INSU and by the Région PACA. We acknowledge the use of the electronic database from the CDS, Strasbourg and electronic bibliography maintained by the NASA/ADS system. Part of this material is based upon work supported by the National Science Foundation under Grant No. AST-1009080 (DRG) and grants NSF-AST0707927 and NSF-AST1108963 (JDM). We finally warmly thank Dietrich Baade, our referee, for his accurate review.
References
- Abt, H. A., Levato, H., & Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Bonneau, D., Clausse, J.-M., Delfosse, X., et al. 2006, A&A, 456, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonneau, D., Delfosse, X., Mourard, D., et al. 2011, A&A, 535, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Božić, H., Harmanec, P., Horn, J., et al. 1995, A&A, 304, 235 [NASA ADS] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell, W. W. 1895, ApJ, 2, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Che, X., Monnier, J. D., Kraus, S., et al. 2012a, SPIE Conf. Ser., 8445 [Google Scholar]
- Che, X., Monnier, J. D., Tycner, C., et al. 2012b, ApJ, 757, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, D., & Bjorkman, K. S. 1998, A&A, 331, 1059 [NASA ADS] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Delaa, O., Stee, P., Meilland, A., et al. 2011, A&A, 529, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Moser Faes, D., et al. 2014, A&A, 569, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frémat, Y., Zorec, J., Hubert, A.-M., & Floquet, M. 2005, A&A, 440, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghosh, K., Iyengar, K. V. K., Ramsey, B. D., & Austin, R. A. 1999, AJ, 118, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., Bagnuolo, Jr., W. G., Ferrara, E. C., et al. 1998, ApJ, 493, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., Bagnuolo, Jr., W. G., Baines, E. K., et al. 2007, ApJ, 654, 527 [Google Scholar]
- Granada, A., & Haemmerlé, L. 2014, A&A, 570, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Granada, A., Ekström, S., Georgy, C., et al. 2013, A&A, 553, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grundstrom, E. D. 2007, Ph.D. Thesis, Georgia State University [Google Scholar]
- Grundstrom, E. D., & Gies, D. R. 2006, ApJ, 651, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuschik, R. W. 1996, A&A, 308, 170 [NASA ADS] [Google Scholar]
- Hummel, W., & Štefl, S. 2001, A&A, 368, 471 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hummel, W., & Štefl, S. 2003, A&A, 405, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ireland, M. J., Monnier, J. D., & Thureau, N. 2006, in SPIE Conf. Ser., 6268 [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005, A&A, 440, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koubský, P., Kotková, L., Votruba, V., Šlechta, M., & Dvořáková, Š. 2012, A&A, 545, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koubský, P., Kotková, L., Kraus, M., et al. 2014, A&A, 567, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, S., Monnier, J. D., Che, X., et al. 2012, ApJ, 744, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Lodieu, N., Deacon, N. R., Hambly, N. C., & Boudreault, S. 2012, MNRAS, 426, 3403 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubimkov, L. S., Lambert, D. L., Rostopchin, S. I., Rachkovskaya, T. M., & Poklad, D. B. 2010, MNRAS, 402, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V. 2006, AJ, 131, 2967 [NASA ADS] [CrossRef] [Google Scholar]
- McSwain, M. V., & Gies, D. R. 2005, ApJS, 161, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Megier, A., Strobel, A., Galazutdinov, G. A., & Krełowski, J. 2009, A&A, 507, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meilland, A., Millour, F., Kanaan, S., et al. 2012, A&A, 538, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millour, F., Meilland, A., Chesneau, O., et al. 2011, A&A, 526, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monnier, J. D., Berger, J.-P., Millan-Gabet, R., & ten Brummelaar, T. A. 2004, in New Frontiers in Stellar Interferometry, ed. W. A. Traub, Proc. SPIE, 5491, 1370 [Google Scholar]
- Monnier, J. D., Berger, J.-P., Millan-Gabet, R., et al. 2006, ApJ, 647, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2008, SPIE Conf. Ser., 7013 [Google Scholar]
- Monnier, J. D., Che, X., Zhao, M., et al. 2012, ApJ, 761, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Morbey, C. L., & Brosterhus, E. B. 1974, PASP, 86, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Mourard, D., Bosc, I., Labeyrie, A., Koechlin, L., & Saha, S. 1989, Nature, 342, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Mourard, D., Clausse, J. M., Marcotto, A., et al. 2009, A&A, 508, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mourard, D., Bério, P., Perraut, K., et al. 2011, A&A, 531, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mourard, D., Challouf, M., Ligi, R., et al. 2012, SPIE Conf. Ser., 8445 [Google Scholar]
- Negueruela, I., & Okazaki, A. T. 2001, A&A, 369, 108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neiner, C., de Batz, B., Cochard, F., et al. 2011, AJ, 142, 149 [Google Scholar]
- Pauls, T. A., Young, J. S., Cotton, W. D., & Monnier, J. D. 2005, PASP, 117, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, T. J., & Readhead, A. C. S. 1984, ARA&A, 22, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, G. J., Pewett, T. D., Gies, D. R., Touhami, Y. N., & Grundstrom, E. D. 2013, ApJ, 765, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Poeckert, R. 1981, PASP, 93, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Cote, J., Waters, L. B. F. M., & Heise, J. 1991, A&A, 241, 419 [NASA ADS] [Google Scholar]
- Quirrenbach, A., Bjorkman, K. S., Bjorkman, J. E., et al. 1997, ApJ, 479, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Renard, S., Thiébaut, E., & Malbet, F. 2011, A&A, 533, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
- Shafter, A. W., Szkody, P., & Thorstensen, J. R. 1986, ApJ, 308, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Silaj, J., Jones, C. E., Tycner, C., Sigut, T. A. A., & Smith, A. D. 2010, ApJS, 187, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Silaj, J., Jones, C. E., Sigut, T. A. A., & Tycner, C. 2014, ApJ, 795, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Slettebak, A. 1966, ApJ, 145, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Slettebak, A. 1982, ApJS, 50, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. A., Lopes de Oliveira, R., Motch, C., et al. 2012, A&A, 540, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stee, P., Delaa, O., Monnier, J. D., et al. 2012, A&A, 545, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tallon-Bosc, I., Tallon, M., Thiébaut, E., et al. 2008, Proc. SPIE, 7013 [Google Scholar]
- tenBrummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Thaller, M. L., Bagnuolo, Jr., W. G., Gies, D. R., & Penny, L. R. 1995, ApJ, 448, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Thiebaut, E., & Giovannelli, J.-F. 2010, IEEE Signal Processing Magazine, 27, 97 [CrossRef] [Google Scholar]
- Thom, C., Granes, P., & Vakili, F. 1986, A&A, 165, L13 [NASA ADS] [Google Scholar]
- Tomasella, L., Munari, U., & Zwitter, T. 2010, AJ, 140, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Touhami, Y., Gies, D. R., & Schaefer, G. H. 2011, ApJ, 729, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Touhami, Y., Gies, D. R., Schaefer, G. H., et al. 2013, ApJ, 768, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Townsend, R. H. D., Owocki, S. P., & Howarth, I. D. 2004, MNRAS, 350, 189 [Google Scholar]
- Tycner, C., Gilbreath, G. C., Zavala, R. T., et al. 2006, AJ, 131, 2710 [NASA ADS] [CrossRef] [Google Scholar]
- Štefl, S., Hummel, W., & Rivinius, T. 2000, A&A, 358, 208 [NASA ADS] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanbeveren, D., De Loore, C., & Van Rensbergen, W. 1998a, A&ARv, 9, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Vanbeveren, D., van Rensbergen, W., & De Loore, C., 1998b, Astrophys. Space Sci., 232 [Google Scholar]
- Zorec, J., Frémat, Y., & Cidale, L. 2005, A&A, 441, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Position of the companion as a function of the RJD as detected in the various MIRC data sets.
All Figures
 |
Fig. 1 Top: (u,v) plane coverage for MIRC. Bottom: (u,v) plane coverage for VEGA. The two figures use the same spatial frequency scale. |
| In the text | |
 |
Fig. 2 Left panel: two-dimension visibility function for ϕ Persei from MIRC. We combined all our epochs together and averaged with a 30 m smoothing window, maintaining each wavelength channel. Right panel: same averaged data as a function of radial spatial frequency unit. In addition, we have included model visibilities for position angles along the major and minor axes of the average disk model (see Table 5). |
| In the text | |
 |
Fig. 3 Image reconstruction made with MIRC data in the H band. Here we have separately modeled the contributions from the Be star and the companion, and this image represents the emission from the disk alone, contributing about ~29% of the total H-band flux. We have marked the location of the companion at the ten epochs reported here with error ellipses and show the best-fit circular orbit (see text). The colored band shows the results from 100 bootstrap fits to illustrate the errors on our orbital solution. East is left and north is up. |
| In the text | |
 |
Fig. 4 Radial velocity measurements of the primary star along with predicted orbit from the joint MIRC+RV fit (see Table 7). Open symbols represent Hα wing bisector measurements, while filled symbols represent HST measurements from Gies et al. (1998). 1σ error bars have been fixed to ±8.6 km s-1 as explained in the text. The width of the solid line illustrates the errors on our orbital solution estimated from 100 bootstrap fits. The RV is negative at zero phase because we have chosen an astrometric orbital ephemeris of the secondary relative to the primary, which is opposite in sign to the radial velocity convention, where the velocity of the primary star is measured relative to the center-of-mass. |
| In the text | |
 |
Fig. 5 Top: 0.65 μm continuum visibility for the best-fit model is plotted as a function of the spatial frequency, whereas the blue zone represents the extent of the model visibility for the various orientations of the baseline. Bottom: examples of differential visibilities and phases (in red + error bar in yellow) for the best-fit model (in blue) for various baselines between 32 and 278 m. |
| In the text | |
 |
Fig. 6 Top row: sequence of intensity maps (6.4 × 6.4 mas) as a function of wavelength with north up and east left as imaged by VEGA (upper sequence), as computed from the kinematic model in Sect. 6.2 (middle sequence), and as imaged through a simulated observation of the above model (lower sequence). Middle row: at the left, we present the continuum image convolved to the diffraction limit of VEGA (0.2 mas) together with contours at 50, 5, 0.5 and 0.05% of the peak intensity to show the disk contour. The middle and right panels show the selected zones to extract the spectra presented below together with an unconvolved continuum image of the system. Bottom row: extracted spectra for the different spatial components: 1) Bottom middle: extracted fluxes (top: total flux, pink absorption feature: “star” zone, blue emission feature: “disk” zone, and dashed spectrum: all other contributions); 2) bottom right: decomposition of the “disk” zone: the top spectrum is the total flux. The blue and red lines correspond to the blue- and redshifted emission features, while the central zeroshifted emission feature comes from all other parts of the “disk” zone. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


