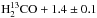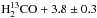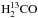| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424342 | |
| Published online | 22 April 2015 | |
Solid-state formation of CO2 via the H2CO + O reaction⋆
1
Université de Cergy Pontoise, UMR 8112, LERMA,
95000
Cergy Pontoise Cedex,
France
2
LERMA, Observatoire de Paris, PSL Research University, CNRS, UMR
8112, 75014
Paris,
France
e-mail:
marco.minissale@obspm.fr
3
Sorbonne Universités, UPMC Univ. Paris 6, UMR 8112, LERMA, 75005
Paris,
France
4
ISM – Université de Bordeaux – CNRS, UMR 5255,
351 cours de la Libération,
33405
Talence Cedex,
France
Received: 5 June 2014
Accepted: 15 December 2014
Context. The formation of carbon dioxide ice in quiescent regions of molecular clouds has not yet been fully understood, even though CO2 is one the most abundant species in interstellar ices.
Aims. CO2 formation was studied via oxidation of formaldehyde molecules on cold surfaces under conditions close to those encountered in quiescent molecular clouds to evaluate the efficiency and the activation barrier of the H2CO + O reaction.
Methods. Formaldehyde ices were exposed to O atoms using a differentially pumped beam line. The H2CO + O reaction experiments were carried out on two different surfaces of astrophysical interest (amorphous water ice and oxidised graphite) held at 10 or 55 K. The products were probed via infrared and mass spectroscopy by using RAIRS and temperature-programmed desorption techniques.
Results. In this paper we show that the H2CO + O reaction can efficiently form carbon dioxide in the solid phase. The activation barrier for the reaction, based on a model fit to the experimental data, was estimated to be 335 ± 55 K.
Conclusions. The H2CO+O reaction on cold surfaces can be added to the set of pathways that lead to carbon dioxide in the interstellar ices. Astrophysically, the abundance of CO2 in quiescent molecular clouds may potentially be explained by three reactions occurring on cosmic grains: CO + OH,CO + O, and H2CO + O.
Key words: astrochemistry / atomic processes / ISM: atoms / ISM: clouds / ISM: molecules / molecular processes
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Formaldehyde (H2CO) was the first polyatomic organic molecule detected in the interstellar medium (ISM; Zuckerman et al. 1970). It was detected through the 111−110 ground-state rotational transition at 4830 MHz (Snyder et al. 1969), and its distribution was found to be similar to HII and CO in different environments, such as our Galaxy (Davies & Few 1979; Tang et al. 2013, and references therein), and in Galactic radio sources (Downes et al. 1980).
H2CO has been observed in some comets (Crovisier & Bockeleé-Morvan 1999; Mumma et al. 2005) and in interstellar ices (Keane et al. 2001). Its abundance with respect to water ice varies from 1% to 6% in high (Keane et al. 2001; Dartois 2005) or low (Boogert et al. 2008) mass protostars, or hot corinos (Maret et al. 2004). Gas-phase reactions (Shalabiea & Greenberg 1994) and UV photolysis of H2O-CO ice (Allamandola et al. 1988; Schutte et al. 1996; Watanabe et al. 2007) can efficiently produce formaldehyde, but surface reactions, such as hydrogenation of CO ice (studied experimentally by Hiraoka et al. 1994, Watanabe & Kouchi 2002, and Madzunkov et al. 2009, and theoretically by Rimola et al. 2014) are needed to explain the observed abundance of H2CO in the solid phase.
Formaldehyde is a key species for the grain-surface chemistry of interstellar clouds (Schutte et al. 1993a,b). Hidaka et al. (2004) and Fuchs et al. (2009) show that formaldehyde can form methanol (CH3OH) through H-atom additions or produce CO via H-atom abstractions. Moreover, H2CO is involved in the formation of large molecules containing C-H, C-O, O-H, and C-N bonds (Schutte et al. 1993b). During the warm-up of the ice on grains, formaldheyde can react with NH3, H2O, and itself (H2CO) to form amines, diols, or [-CH2-O-]n groups (Noble et al. 2012b; Theulé et al. 2013; Mispelaer et al. 2013); for this reason, it could be considered a primary precursor of some complex organic materials (Schutte et al. 1993b). In this paper, we present an experimental study showing that formaldehyde reacts with ground-state O(3P) atoms to form CO2, one of the most abundant species of interstellar ices. Formaldehyde seems to play a crucial role in the chemistry of interstellar ices and, in particular, in the balance between CO2, CH3OH, and CO.
This paper is organised as follows. The experimental set-up and methods are described in the next section. In Sect. 3, we present our experimental results showing how H2CO is consumed by O to form CO2. In Sect. 4, we present a rate equation model that simulates our results and gives relevant energetic parameters, and we discuss the solid-state network by presenting DFT calculations. In the last section, we discuss the main conclusions and astrophysical implications of this study.
 |
Fig. 1 Detail of the experimental set-up and scheme of the depolymerization process of paraformaldehyde and preparation of the formaldehyde beam. |
Ion count per second of masses 30, 29, 28, and 18 a.m.u. as a function of pumping time of the paraformaldehyede powder held at 62 °C.
2. Experimental
The experiments were conducted with the FORMOLISM (FORmation of MOLecules in the InterStellar Medium) set-up described extensively elsewhere (Amiaud et al. 2006; Congiu et al. 2012). It consists of a UHV main chamber with a base pressure of 10-10–10-11 mbar and two triply differentially pumped atom lines. The ultra-high vacuum chamber contains an oxidised slab of high-oriented pyrolytic graphite (HOPG, 0.9 cm in diameter), operating at temperatures between 8 K and 400 K. The temperature is controlled by a calibrated silicon-diode sensor and a thermocouple (AuFe/Chromel K-type) clamped on the sample holder. Adsorbates and products were probed in situ through Fourier Transform Reflection Absorption InfraRed Spectroscopy (FT-RAIRS) and a quadrupole mass spectrometer (QMS) used for measuring the beam flux and beam composition and for performing the temperature-programmed desorption (TPD) experiments. Amorphous solid water (ASW) ice was grown on the graphite sample, maintained at 120 K, through a leak valve positioned at 2 cm far from the surface.
All the experiments were performed by sending O atoms on formaldehyde ice films previously grown on the cold sample. The two species were deposited by using the same beam line at different times. Figure 1 shows how gaseous formaldehyde is obtained: paraformaldehyde (a white crystalline powder) contained in a pyrex phial is depolymerizated by immersion in a bath at 62 °C. The products of the depolymerization process are H2CO, CO, and H2O. Table 1 shows the resulting beam composition measured with QMS (direct beam) at a source pressure of 0.42 mbar as a function of the pumping time. In particular, we report the difference between the signal recorded with the flag1 open and the signal recorded with the flag closed to account for noise signals.
As shown in Table 1, the ratio between these species varies during the depolymerization process: at the beginning the H2O/H2CO ratio is 920/(Mass30+Mass29) ≈ 0.92 and becomes 0 after 90 min of pumping. This means that the sublimation process of paraformaldehyde is able to purify the sample by eliminating the residual H2O. Similar behaviour concerns the CO/H2CO ratio, which goes from 1.3 to 0.1; in this case, the resulting gas contains some residual CO even after 90 min of pumping. For this reason, formaldehyde ice films were grown at temperatures higher than those of CO desorption (>55 K). As we discuss in Sect. 3 and Appendix A, we used different isotopologues of formaldehyde to constrain our findings better, i.e., H CO, D
CO, D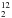 CO, and H
CO, and H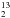 CO. In the case of D
CO. In the case of D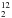 CO, the purity is of about 98%, while for H
CO, the purity is of about 98%, while for H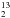 CO is of 99%. Hereafter we refer to 12C simply as C.
CO is of 99%. Hereafter we refer to 12C simply as C.
Oxygen atoms are generated by (in the 3P ground state) dissociating O2 molecules in a quartz tube placed within a Surfatron cavity, which can deliver a maximum microwave power of 200 W at 2.45 GHz (Minissale et al. 2014). We studied the electronic state composition of oxygen beam by tuning the energy of the ionizing electrons of the QMS. This technique allows ground state or electronic excited atoms and molecules to be selectively detected, as described in Congiu et al. (2009). We find that our source is free of O(1D) and O2(a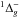 ) and is composed only of O(3P) and O2(X
) and is composed only of O(3P) and O2(X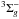 ) (see details in Minissale 2014 and Minissale et al. 2014).
) (see details in Minissale 2014 and Minissale et al. 2014).
With the microwave source turned on, the dissociation efficiency of O2 was τ = 70 ± 5%, where τ represents the percentage of dissociated O2 molecules and τ is proportional to the microwave power used, so it also defines the O/O2 ratio in the beamline. If τ is 0.7, every ten O2 molecules, we will have 14 O atoms and 3 O2 undissociated molecules. Atoms and undissociated molecules are cooled and instantaneously thermalised upon surface impact with the walls of the quartz tube.
We calibrated the molecular beam as described in Amiaud et al. (2007) and Noble et al. (2012). The first monolayer (1 ML = 1015 molecules cm-2) of formaldehyde was reached after an exposure time of about 12 min, and 1 ML of O2 was reached after six minutes, which give a flux of φH2CO = (1.3 ± 0.4) × 1012 and φO2off = (3.0 ± 0.3) × 1012 molecules cm-2 s-1, respectively. Once the O2 discharge is turned on, the O-atom flux is φO = 2τφO2off = 5.4 × 1012 atoms cm-2 s-1 and the O2 flux φO2on = (1−τ) φO2off = 1012 molecules cm-2 s-1.
List of experiments.
CO2 formation was investigated on two different surfaces, ASW and an oxidised slab of HOPG. In Table 2 we display a complete list of experiments providing details on the species and dose of the reactive molecule deposited. Different doses of O (+O2) were sent onto formaldehyde ice. (The coverage of H2CO ices was always <2.5 ML.) During each phase (ices growth or O-atom deposition), the surface was held at a given constant temperature. After each O-atom deposition, the products were probed using RAIR spectroscopy. After about 5 ML of oxygen, atoms were deposited, and the surface was heated with a linear temperature ramp of 10 K/min, until the adsorbates had fully desorbed from the surface (around 200 K). For each substrate (ASW ice or graphite), we adopted two deposition temperatures (10 and 60 K). We also performed experiments to determine whether CO2 was formed via H2CO + O2 and H2CO + O3. For this purpose, we performed two sets of TPD experiments. First, the H2CO+O2 reaction was checked by depositing 2 ML of O2 on top of H2CO films. The H2CO+O3 reaction was studied through a similar experiment except that H2CO was deposited on top of O3. In fact, for technical reasons, we had previously produced ozone via the O+O2 reaction on the surface at 10 K, eliminated the residual O2 by heating the surface to 50 K, and only then deposited H2CO at 60 K.
3. Experimental results
3.1. Oxygenation of H2CO ices
In this section we present the experimental results showing the products of the reactions H2CO + Ox (O, O2, and O3). The oxygen beam that we used to irradiate formaldehyde also contains O2 molecules, therefore O3 can be formed on the surface at temperatures lower than <55 K (Minissale et al. 2014). For this reason, we first studied the reactions H2CO + O2/ O3, then the reaction H2CO + O. Figure 2 shows three TPD spectra of mass 30 a.m.u. (H2CO) after depositing 1 ML of H2CO, 1 ML of H2CO + O2, and 1 ML of H2CO + O3 on oxidised HOPG held at 10 K . The three TPD curves and their integrated areas are very similar, suggesting that H2CO has not been consumed by O2 or O3.
 |
Fig. 2 H2CO TPD traces obtained after deposition of 1 ML of H2CO (black line), H2CO+O2 (red line), and H2CO+O3 (green line) on oxidised HOPG held at 10 K. |
Actually, this is not a surprising result since the reactions 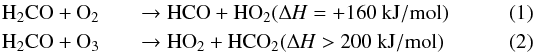 are endothermic2 and present high (>1600 K/kb) activation barriers (Michael et al. 1999; Braslavsky & Heicklen 1976). Moreover, the inefficiency of reactions (1) and (2) is confirmed by the absence of newly formed species.
are endothermic2 and present high (>1600 K/kb) activation barriers (Michael et al. 1999; Braslavsky & Heicklen 1976). Moreover, the inefficiency of reactions (1) and (2) is confirmed by the absence of newly formed species.
Figure 3 shows the TPD curves of CO2 (mass 44, left panel) and H2CO (mass 30, right panel) for three different sequential deposition experiments on oxidised HOPG held at 10 K: 2 ± 0.5 ML of H2CO, 2 ± 0.5 ML of H2CO + 5 ± 0.3 ML of O atoms alone, and 5 ± 0.3 ML of O atoms.
 |
Fig. 3 CO2 (left panel) and H2CO (right panel) TPD traces obtained after deposition of 2 ML of H2CO (black line), 5 ML of O (green line), and 2 ML of H2CO + 5 ML of O atoms (red line) on oxidised HOPG held at 10 K. |
The green line represents a control experiment carried out to be certain that CO2 is not present in the O beam and that carbon dioxide was actually formed on the surface because of H2CO oxygenation. In fact, a signal at mass 44 (CO2) is visible in Fig. 3 (left panel) and could come either from the O beam or from oxygenation of residual CO. In either case, it is ten times weaker than the mass-44 signal coming from H2CO oxygenation experiment (left panel of Fig. 3). For this reason, it is fair to believe that H2CO ice is consumed upon oxygen irradiation (right panel) and that CO2 is formed.
Further evidence of H2CO consumption and CO2 formation is provided by the RAIR spectra shown in Fig. 4. Curve a in Fig. 4 shows the RAIR spectrum after deposition of 2 ML of H2CO on an oxidised HOPG held at 60 K to avoid CO adsorption. We assign the band at 1732 cm-1 to the CO stretch of H2CO. H2CO was then exposed to increasing doses of O atoms. Curves b and c in Fig. 4 show the cases of 2 ML H2CO + 0.8 ± 0.1 and 5 ± 0.4 ML of O atoms. Here two new bands are visible: the first one, peaking between 2349−2345 cm-1, is assigned to the anti symmetric stretch of CO2. The second band, peaking at 1047 cm-1, is due to the ν3 asymmetric stretching mode of O3 and is also present in spectrum d, where O atoms were deposited on the bare surface. All the IR bands of interest for this paper are listed in Table 3.
 |
Fig. 4 Four RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of H2CO; (b) 2 ± 0.5 ML of H2CO + 0.8 ± 0.1 ML of O atoms; (c) 2 ± 0.5 ML of H2CO + 5 ± 0.4 ML of O atoms; (d) 5 ± 0.4 ML of O atoms on oxidised HOPG held at 10 K. (H2CO was always deposited at 60 K.) |
 |
Fig. 5 Six RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of H2CO; (b) 2 ± 0.5 ML of H2CO + 0.5 ± 0.1 ML of O atoms; (c) 2 ± 0.5 ML of H2CO + 0.8 ± 0.1 ML of O atoms; (d) 2 ± 0.5 ML of H2CO + 1.2 ± 0.2 ML of O atoms; (e) 2 ± 0.5 ML of H2CO + 2.0 ± 0.3 ML of O atoms; (f) 2 ± 0.5 ML of H2CO + 3.8 ± 0.3 ML of O atoms, on a ASW ice held at 10 K. (H2CO was always deposited at 60 K.) |
 |
Fig. 6 Left panel: seven RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of H2CO; (b) 2 ± 0.5 ML of H2CO + 0.5 ± 0.1 ML of O atoms; (c) 2 ± 0.5 ML of H2CO + 0.8 ± 0.1 ML of O atoms; (d) 2 ± 0.5 ML of H2CO + 1.2 ± 0.2 ML of O atoms; (e) 2 ± 0.5 ML of H2CO + 2.0 ± 0.3 ML of O atoms; (f) 2 ± 0.5 ML of H2CO + 2.8 ± 0.3 ML of O atoms; (g) 2 ± 0.5 ML of H2CO + 3.8 ± 0.3 ML of O atoms, on a ASW ice held at 55 K (H2CO was always deposited at 60 K). Right Panel: integrated areas of the H2CO and CO2 bands as a function of O-atom dose. |
We obtained similar results when the experiments were performed on ASW ices. Figure 5 shows RAIR spectra recorded after irradiation at 10 K, of 2 ± 0.5 ML of H2CO with increasing doses of oxygen atoms (0, 0.5, 0.8, 1.2, 2, 3.8 ML from curves a to f, respectively). As in the previous case, three main spectral features are visible: at 1048 cm-1 due to O3, at 1734 cm-1 due to the CO stretch of H2CO, and finally at 2347 cm-1 where the antisymmetric stretch of CO2 appeared. Also, we assign the weak and broad band at 1502 cm-1 to the CH2 scissoring of H2CO.
The different substrates (HOPG or compact ASW ice) are responsible for small shifts in the IR features, as well as for a change in the band intensities. Actually, under the same conditions (equal amount of O sent onto H2CO), HOPG facilitates CO2 formation slowing down that of O3, while the ASW substrate favours O3 formation. This is a consequence of two effects:
-
different diffusion constants of O atoms on oxidised HOPG and on ASW ice, i.e., kdiff−HOPG<kdiff−ASW (Congiu et al. 2014);
-
different probabilities of chemical desorption for O2, i.e., ϵdiff−HOPG>ϵdiff−ASW (Dulieu et al. 2013; Minissale & Dulieu 2014).
Fast diffusion of O atoms and the low probability of chemical desorption of O2 on ASW allow O atoms to allotropize into O2 and into O3 ([O3] ≫ [CO2]). Conversely, on HOPG, the surface density of O2 decreases due to chemical desorption. The O atoms stay on the surface longer, have a higher probability of reacting with H2CO and form CO2( [ O3 ] ≈ [ CO2 ]), owing to the lack of O2 and the lower mobility of O atoms.
3.2. Temperature effects: O-atom irradiation at 55 K
Minissale et al. (2013b; 2014) show that solid-state formation of O3 is efficient at temperatures lower than 55 K. In fact, temperatures higher than 55 K prevent O2 adsorption on the surface so O3 can no longer be formed. Figures 4 and 5 show that O3 is the main product after H2CO is exposed to O atoms. To avoid O3 formation, we thus sent O atoms onto H2CO ice held at 55 K. Figure 6 shows seven RAIR spectra after O irradiation of 2 ± 0.5 ML of H2CO, previously adsorbed on ASW, at 55 K (from curve a to g, 0, 0.5, 0.8, 1.2, 2, 3.8 ML of O, respectively, were sent onto H2CO). The right-hand panel of Fig. 6 shows the integrated areas of the bands at 1732 and 1502 cm-1 of H2CO (triangles and circles, respectively) and the one at 2345 cm-1 of CO2 (black circles). The spectra of Fig. 6 differ from those in Fig. 5 for two main features: the O3 band is not present and the band at 2347 cm-1 (CO2) increases steadily with O-exposure time. These two main differences, as discussed in detail in the model section, facilitate the evaluation of the H2CO + O activation barrier.
3.3. Experiments with isotopologues
To confirm the results presented above and for a better understanding of the solid state reaction network, we also performed experiments using another isotopologue of formadehyde, D2CO. Further experiments in which H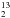 CO was used are described in Appendix A.
CO was used are described in Appendix A.
 |
Fig. 7 Top panel: three RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of D2CO; (b) 2 ± 0.5 ML of D2CO + 1.4 ± 0.1 ML of O atoms; (c) 2 ± 0.5 ML of D2CO + 3.8 ± 0.3 ML of O atoms, on oxidised HOPG held at 60 K. Bottom panel: CO2 (via mass 44) and D2CO (via masses 32 and 30) TPD mass spectra obtained after deposition of 2 ± 0.5 ML of D2CO + 3.8 ± 0.3 ML of O atoms on oxidised HOPG held at 60 K. |
The top panel of Fig. 7 shows three RAIR spectra recorded after deposition of oxygen atoms (0, 1.4, and 3.8 ML from curves a to c, respectively) on 2 ± 0.5 ML of D2CO held at 55 K. Three spectral features are apparent. D2CO is detected through the CO stretch mode at 1680 cm-1 (decreasing in intensity from a to c) and the asymmetric stretch of CD2 at 2154 cm-1; the latter is visible only in spectrum a; the third feature at 2359 cm-1 is due to the antisymmetric stretch of CO2 and increases in intensity from spectrum a to spectrum c. Also, a very weak band due to O3 is visible at 1043 cm-1 (not shown). The TPD traces in the bottom panel were obtained after deposition of 2 ± 0.5 ML of D2CO + 3.8 ± 0.3 ML of O atoms on ASW ice. Newly formed CO2 desorbs between 70 and 90 K and is detected via mass 44. The fraction of D2CO molecules that did not react desorb between 85 K and 140 K and are detected via the fragments D2CO+ (mass 32) and DCO+ (mass 30). TPD results corroborate the previous spectral assignments of the infrared bands and give additional information. Figure 8 shows TPD traces of mass 18, 19, and 20 between 130 and 200 K. The black lines represent TPDs after deposition of 2 ± 0.5 ML of D2CO on oxidised HOPG held at 55 K, while red lines were obtained by irradiating the same amount of D2CO with 3.8 ± 0.3 ML of O. The signal at mass 20 comes from the ionisation of heavy water (D2O+): it is almost zero in the black curve, while it has a peak in the red curve. Mass 19 (HDO+ and 18 (H2O+ and OD+) signals are present in both cases, even if the peak areas of the red curve are twice bigger than the peaks of the black curve. These mass spectra support the formation of D2O after D2CO oxygenation. We discuss this point extensively in the next section.
 |
Fig. 8 TPD traces of mass 18, 19, and 20 obtained after deposition of 2 ± 0.5 ML of D2CO (black curves) and 2 ± 0.5 ML of D2CO + 3.8 ± 0.3 ML of O atoms (red curves) on oxidised HOPG held at 60 K. |
4. Model and discussion
4.1. Quantum chemical calculations on the O + H2CO reaction
The focus of this paper is on the investigation of solid-state reactions involving formaldehyde ices and oxygen atoms at low temperatures. All the experiments presented in Sect. 3 show that when formaldehyde is exposed to O atoms, H2CO is consumed and CO2 is formed. In this section, we describe quantum chemical calculations on O + H2CO reaction in detail. However, we have used prevalently gas-phase energetic data to carry out our calculations. We would like to stress that solid-state reactivity is somewhat different than the gas-phase one, because of interactions between adsorbate and adsorbent. For this reason, the goal of our quantum chemical calculations is essentially to provide a first estimation of the trend of the different channels studied. The energetic data, present in this section, have to be taken just as qualitative values, since they would be substantially influenced by the solid-state phase chemistry.
Our experimental results are very similar to those obtained by different experimental groups at high (>300 K) temperature in gas phase, i.e. Chang & Barker (1979) and Wellman et al. (1991). Chang & Barker (1979) proposed that CO2 formation occurs in the following steps:
-
1.
O-atom addition to the doubly-bonded carbon atom in H2CO and the following formation of a vibrationally excited triplet of methylenebis(oxy) (H2CO2);
-
2.
H2CO2 is formed in the 3B2 state, and owing to a hydrogen shift, it forms vibrationally excited formic acid (H-atom migration process);
-
3.
Once formed, the triplet formic acid is decomposed by several pathways (HCO+OH, HCO2+H, HOCO+H);
-
4.
Further fragmentation of HOCO and HCO2 or oxygenation of HCO would lead to CO2 formation.
On the other hand, Wellman et al. (1991) proposed that H2CO+O proceeds via a direct hydrogen abstraction (H2CO+O→OH+HCO), and a secondary reaction of oxygen atoms with HCO may lead to CO2 formation. In the gas phase, despite some ambiguities, the reaction mainly leads to abstraction products, HCO + OH, through a barrier measured as equal to 1540 K (Klemm 1979; Klemm et al. 1980), with a CO2 product-branching ratio inferior to 5% (Wellman et al. 1991). We stress that neither Chang & Barker (1979) nor Wellman et al. (1991) have shown direct measurements of HCOOH and HCO. This is consistent with our experimental results. Theoretical calculations (Dupuis & Lester 1984) show that CO2 production via the addition channel (3OCH2O, second reaction) should be unlikely, since it involves a transition state above the O + H2CO entrance channel. Moreover, H2CO+O could lead to the formation of the Criegee species (CH2OO) in its triplet state. Nevertheless, we can neglect this channel in our system, thanks to its wide endothermicity (+115 kJ/mol, see Table C.2).
To understand how CO2 is formed in our system, we carried out a series of DFT calculations (see Appendix C for details). We suppose that H2CO+O can lead to various products:  where enthalpies of reactions have been taken from the literature (Baulch et al. 2005, for the first reaction; Dupuis & Lester 1984, for the second value of second reaction) or evaluated in the present work.
where enthalpies of reactions have been taken from the literature (Baulch et al. 2005, for the first reaction; Dupuis & Lester 1984, for the second value of second reaction) or evaluated in the present work.
In the case of surface reaction (i.e., ice or graphite), the surface interactions have a complex effect on barrier heights (Bromley et al. 2014). For the H + H2CO reaction on water ice, a small reduction (≈130 K) in the activation barrier was calculated for the addition reaction, while the barrier for abstraction reaction was increased significantly (increased by 725 K) (Goumans 2011). It is reasonable to imagine that the O reaction with H2CO ice presents a similar effect. To get a better picture of the various mechanisms, we performed theoretical calculations using the Gaussian 093 package. Calculations details are presented in Appendix C. The energy diagram calculated for the first step of the O + H2CO reaction (energy values are close to the CCSD(T)/cc-pVTZ and MP2/cc-pVTZ values including zero-point energies, ZPE) is presented in Fig. 9.
 |
Fig. 9 Relative energy diagram for the O + H2CO reaction. |
The reaction pathway is initiated by the formation of a pre-reactive complex (PRC) O...H2CO corresponding to a long-range interaction between O atom and H2CO.
From the PRC, two reactive pathways have been found, one leading to OH + HCO formation through a transition state for H atom abstraction, TS1, and the other leading to oxygen atom addition through TS2 transition state. The energy barrier for the H-atom abstraction depends on the calculation level, ranging from 1 kJ/mol at M06-2X level to 39 kJ/mol at MP2 level and equal to 21 kJ/mol at CCSD(T) level, and the energy barrier for the oxygen atom addition ranging from 30 kJ/mol at M06-2X level to 93 kJ/mol at MP2 level and equal to 53 kJ/mol at CCSD(T) level. Calculations show that in the gas phase, the reaction happens mainly through H atom abstraction with a barrier around 10−20 kJ/mol. They are qualitatively in good agreement with observations, considering that DFT with M06-2X method underestimates the barrier height and MP2 overestimates the barrier (Loison et al. 2014; 2014b). In the case of oxygen-atom addition, it is very unlikely that surface interactions have such an effect on the addition barrier to make this channel important. Moreover, tunneling should be efficient for H-atom abstraction and less efficient for O-atom addition.
The main exit channel for O atom reaction with H2CO on a cold surface is very likely HCO + OH. The newly formed HCO and OH should have low kinetic energy owing to
-
low exothermicity of reaction;
-
large amount of available energy localized into vibrational and rotational degrees of freedom.
Probably, HCO and OH will then stay relatively close on the surface and should mainly recombine on the singlet surface (2HCO + 2OH correlate with singlet and triplet surface) without barrier, leading to excited HCOOH**. If some OH and HCO can move on the surface, OH will quickly react with H2CO leading to H2O + HCO (Xu et al. 2006; Yetter et al. 1989). The low amount of water formed in the experiments is a strong indication that OH does not move on the surface but rather form HCOOH**. We performed theoretical calculations at the M06-2X level to characterise stationary points in the HCOOH* evolution. Our results (in good agreement with previous calculations for the HCOOH dissociation, Chang et al. 2007) are presented in Fig. 10.
 |
Fig. 10 Relative energy diagram for the HCOOH decomposition calculated at M06-2X/cc-pVTZ level. |
Theoretical calculations on energy transfer from HCOOH* toward phonon modes of the ice is far beyond the scope of this article (and is also far from being well understood). HCOOH* has an internal energy equal to 460 kJ/mol corresponding to the strength of the OC(H)-OH bond, so well above the dissociation barrier towards H2 + CO2 and H2O + CO.
To estimate the evolution of excited HCOOH** and its unimolecular decomposition, we use our experimental results showing that neither HCOOH nor H2O were formed and then we mainly consider CO2 + H2 formation. That CO2 + H2 is favoured is in good agreement with theoretical calculations for the H + HOCO reaction (Yu & Francisco 2008) leading to similar HCOOH** energized adducts. The most surprising experimental result is the low amount of HCOOH stabilized, which should be a function of energy relaxation efficiency through surface interaction. The low efficiency of HCOOH stabilization in our experiments clearly shows the complexity of surface reactions, and it is definitively an important experimental result because the competition between adduct stabilization and bimolecular exit channel happens for a majority of surface reactions (i.e., C + NO → CN + O/CO + N/CNO/NCO, CH + CH4 → C2H5/ C2H5 + H,H + HO2 → H2O2/ OH + OH/H2 + O2, H2O + O, and so on). We propose the following simplified chemical pathways:
-
a.1)
H2CO + O → (OH + HCO)cage
-
a.2)
(OH + HCO)cage → HCOOH∗∗
-
a.3)
HCOOH∗∗ → (CO2 + H2) or (H2O + CO)
-
b)
O + O → O2
-
c)
O2 + O → O3
-
d)
O + CO → CO2
where reaction a1 has a barrier of 335 K (fitted using EOdiff = 700 K, see previous section). Reactions a2 (radical-radical reaction), b, and c have no barrier; reaction a3 presents a 95%−5% (±5%) branching ratio; and reaction d presents a barrier of 600 K (Minissale et al. 2013a).
In the next section, we describe the model used to evaluate the activation barrier of the H2CO + O reaction.
 |
Fig. 11 Comparison between model (lines) and experimental data (symbols); IR yields of H2CO (red) and CO2 (black) are shown as a function of O-atom coverage. Four values of EOdiff are used: 900 K/kb (solid line), 800 K/kb (dashed line), 700 K/kb (dotted line), 600 K/kb (dashed-dotted line). From panels α to δ, Ea is 550 K/kb, 390 K/kb, 280 K/kb, and 200 K/kb, respectively. |
4.2. Evaluation of the H2CO+O barrier
In this section we present the model used to fit our experimental data and, in particular, to evaluate the activation barrier of the H2CO + O reaction. The model is composed of a set of five differential equations that account for the surface population of H2CO, O atoms, O2, O2, and CO2 (see Appendix B for further details). In fact, we considered only the most abundant species present on the surface, and the three main reaction pathways:
-
a)
H2CO + O → CO2 + H2
-
b)
O + O → O2
-
c)
O2 + O → O3.
H2 was not included in our model, since our experiments were performed at high surface temperature and H2 has a very short residence time under these conditions. In any case, H2 is inert at low temperature and cannot affect the surface density of other species. The surface reactions listed above can occur through two mechanisms: the Eley-Rideal (ER) and the Langmuir-Hinshelwood (LH) mechanisms. In the ER mechanism one molecule is already adsorbed on the surface, and the other comes from the gas phase (i.e., the beam line). The ER becomes more efficient as the surface coverage increases. In the LH mechanism, both molecules are physisorbed to the surface, and they can meet each other by diffusing on the surface and eventually react. LH is highly dependent on the surface temperature. With these considerations in mind, we chose to fit the data of Fig. 6 (right panel) to give a more precise evaluation of the H2CO+O activation barrier. Actually, the physicochemical conditions in these experiments allow us to simplify our model and reduce the errors:
-
O-atom diffusion is very fast, and the majority of adsorbed O atoms are consumed through reaction (b);
-
reaction (c) can be neglected, since it is impeded by O2 desorption4;
-
reaction (a) is more likely to occur via ER, since O atoms are deposited on the H2CO ice.
Clearly the last point does not exclude that reaction (a) could occur via the LH mechanism, and this actually represents the main source of error in the barrier determination. The LH mechanism depends strongly on the O-atom diffusion barrier (EOdiff), one of the free parameters of the model. The barrier EOdiff is a pure thermal diffusion barrier since quantum effects are negligible at high temperatures (Minissale et al. 2013a), and it has an upper limit of 900 K/kb (Cazaux et al. 2010) and a lower limit given by ozone formation in our experiments (<0.05 ML). A value lower than 600 K/kb for EOdiff increases the efficiency of reaction (b) and produces more than 0.05 ML of ozone. Within these two boundaries, the total amount of CO2 formed via LH changes by 20%, if EOdiff = 900 K/kb, or 5%, if EOdiff = 600 K/kb. This indetermination, as we see below, complicates the evaluation of the activation barrier Ea of reaction (a), the second free parameter of the model. A priori, Ea is a positive real number and becomes zero in the case of a barrierless reaction. Figure 11 shows the results of the model (lines) compared with experimental data. We used four values for Ea: 550 K/kb (panel α), 390 K/kb (panel β), 280 K/kb (panel γ), and 200 K/kb (panel δ). We varied EOdiff in the 600−900 K/kb range, and Fig. 11 shows the four cases: 600, 700, 800, and 900 K/kb. Panel α shows that a value of Ea that is too high (>550 K/kb) is not able to fit our data for any value of EOdiff: small amounts of CO2 are formed, small amounts H2CO are consumed, and a large amount of ozone is formed. On the other hand, a value that is too small (<200 K/kb) for Ea has an opposite effect, CO2 is formed too rapidly and H2CO is consumed too quickly by O atoms (panel δ). Couples of values of Ea and EOdiff ranging in 390−280 K/kb and 600−900 K/kb, respectively (panels β and γ), give an excellent fit to the experimental data. Because the fit depends on two parameters, we are not able to give a precise value of the activation barrier of reaction (a). However, we have to stress that a given choice of EOdiff, automatically determines the value of Ea: by using EOdiff = 700 ± 150 K/kb, we found Ea = 335 ± 55 K/kb.
The activation barrier that we have found for solid state reaction H2CO+O (>300 K) is lower than gas phase barrier (>1560 K, Wellman et al. 1991). The reason for such a low activation barrier is probably the catalytic effect of the surface.
5. Astrophysical conclusions
In this paper we have shown that O(3P) atoms are able to react with H2CO on cold surfaces, such as amorphous water or oxidised graphite, under conditions encountered in interstellar dense clouds. Using a model, we estimated a value of 335 ± 55 K/kb for its activation barrier, and CO2 was found to be the main product of the reaction. This reaction is relevant to astrochemistry because it may account for CO2 abundances, as well as for CH3OH ones, in interstellar ices. Actually, carbon dioxide is one of the most common and abundant types of ice, and it has been detected in many interstellar environments, from comets (Ootsubo et al. 2010) to other galaxies (Shimonishi et al. 2010; Oliveira et al. 2011). Its high abundances observed in interstellar ices are explained through some solid-phase reactions. Energetic formation processes leading to efficient formation of CO2 include irradiation of CO ices (pure or mixed with H2O) with photons, charged particles or electrons (Ioppolo et al. 2009; Laffon et al. 2010). On the other hand, Whittet et al. (1998) invoke chemical pathways occurring without the addition of energy to explain the CO2 detection in those interstellar environments where a lack of UV photons forbids ice processing (i.e., molecular cloud Taurus). To date, only two (non energetic) pathways were considered:
-
d)
CO + O → CO2
-
e)
CO + OH → CO2 + H.
Roser et al. (2001) and Raut & Baragiola (2011) successfully showed that the formation of CO2 is possible through reaction (d). Recently, Minissale et al. (2013b) have confirmed these results and estimated an activation barrier of about 600 K/kb. Recently, Noble et al. (2011) and Oba et al. (2011) have shown experimentally the CO2 formation through reaction (e), but no consistent values were obtained for the activation barrier. In this paper, we showed that also reaction (a) (H2CO+O → CO2+H2) can efficiently form CO2 in the ISM. Moreover, this reaction can help to explain the CH3OH abundances variability (from <3% to 25−30% with respect to water) in interstellar ices (Dartois et al. 1999; Whittet et al. 2011). Formation of CO2 and CH3OH in “hot” environments (high UV fluxes or/and Tgrain> 50 K) can be explained through energetic processing of icy mantles (Moore & Hudson 1999; Ioppolo et al. 2009, and references therein), but as opposed to CO2, CH3OH formation is strongly dependent on the ice composition.
In cold environments, where energetic routes are not efficient, methanol and carbon dioxide are believed to form via the solid state reactions shown in Fig. 12 and listed in Table 4. In summary, we can say that:
-
CH3OH is formed via four CO hydrogenations (with a total energy barrier >800 K/kb, Fuchs et al. 2009), leading to the formation of two unstable products, HCO and CH3O, and one stable molecule, namely H2CO;
-
CO2 is formed following three different chemical pathways: reaction (a), (d), and (e);
-
H2CO is a precursor not only of CH3OH, but also of CO2.
These considerations can have two consequences for the CH3OH/CO2 ratio in interstellar ice: (1) where large abundances of atomic oxygen (O/H ratio >0.1) are observed (i.e., Sgr B2 and L1689N2), the CH3OH/CO2 ratio tends to zero; (2) where low O/H ratios (<0.1) are observed, the increase in CH3OH/CO2 ratio is difficult to predict a priori because it may depend on other factors. For example, the large CO hydrogenation energy barrier and H2CO+O reaction could hinder CH3OH formation and favour CO2 formation.
 |
Fig. 12 Energetics of the CO+H/O reaction pathways. The enthalpies of CO2 and CH3OH and the activation barrier of each reaction are listed in Table 3. The enthalpies of H2CO and CO are −115.9 and −110.5 kJ/mol, respecively (http://webbook.nist.gov/chemistry/). |
List of solid state reactions and their activation barriers to form CO2 and CH3OH.
Online material
Appendix A: Additional experiments
To validate the formation of carbon dioxide, we performed further experiments using the H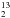 CO isotopologue of formaldehyde: the results are presented below. The top panel in Fig. A.1 shows three RAIR spectra recorded after irradiation of 2 ± 0.5 ML of H
CO isotopologue of formaldehyde: the results are presented below. The top panel in Fig. A.1 shows three RAIR spectra recorded after irradiation of 2 ± 0.5 ML of H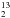 CO with increasing doses of oxygen atoms (0, 1.4, and 3.8 ML, respectively from a to c spectra) on oxidised HOPG at 55 K. Three main features are visible: at 1502 and 1697 cm-1 due to H
CO with increasing doses of oxygen atoms (0, 1.4, and 3.8 ML, respectively from a to c spectra) on oxidised HOPG at 55 K. Three main features are visible: at 1502 and 1697 cm-1 due to H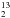 CO, 13CH2 scissoring and 13CO stretch mode, respectively; at 2285 cm-1 due to the antisymmetric stretch of 13CO2. Moreover, a very weak band due to O3 is present at 1042 cm-1 (not shown). Each IR band varies in intensity from curve to curve. In particular, the H
CO, 13CH2 scissoring and 13CO stretch mode, respectively; at 2285 cm-1 due to the antisymmetric stretch of 13CO2. Moreover, a very weak band due to O3 is present at 1042 cm-1 (not shown). Each IR band varies in intensity from curve to curve. In particular, the H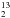 CO bands decrease from spectrum a to spectrum c, and the reverse occurs to the bands of 13CO2. This indicates that H
CO bands decrease from spectrum a to spectrum c, and the reverse occurs to the bands of 13CO2. This indicates that H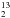 CO is consumed and 13CO2 is formed subsequently to O irradiation. The infrared assignments are confirmed by TPD results shown in the bottom panel of Fig. A.1. These TPD traces were obtained after deposition of 2 ± 0.5 ML of
CO is consumed and 13CO2 is formed subsequently to O irradiation. The infrared assignments are confirmed by TPD results shown in the bottom panel of Fig. A.1. These TPD traces were obtained after deposition of 2 ± 0.5 ML of  ML of O atoms on oxidised HOPG held at 60 K. Newly formed 13CO2 desorbs between 70 and 90 K and is detected via mass 45. Unreacted H
ML of O atoms on oxidised HOPG held at 60 K. Newly formed 13CO2 desorbs between 70 and 90 K and is detected via mass 45. Unreacted H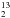 CO molecules desorb between 85 and 140 K and are detected via two fragments: +H
CO molecules desorb between 85 and 140 K and are detected via two fragments: +H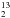 CO (mass 31) and +H13CO (mass 30).
CO (mass 31) and +H13CO (mass 30).
 |
Fig. A.1 Top panel: three RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of H |
 |
Fig. C.1 Optimized geometries: pre-reactive complex (PRC), Transition State 1 (TS1), and Transition State 2 (TS2), from the left to the right panels, respectively. |
Calculated activation energies of the O + H2CO reaction.
Appendix B: Rate equations
The model used to fit our experimental data is very similar to the one described in Minissale (2014) and Minissale et al. (2013b; 2014). It is composed of five differential equations, one for each of the species considered: H2CO molecules, deposited on the surface; O atoms, coming exclusively from the beam; O3 and CO2, formed only on the surface; and finally O2, coming both from the beam and formed on the surface. Each differential equation is composed of different terms:
-
positive terms indicate a contribution to the increase in the surface density of the species, i.e., a molecule (or atom) arrives from the gas phase or is formed on the surface;
-
negative terms indicate a decrease in the surface density of the species, i.e., a molecule (or atom) is consumed on the surface or desorbs and returns to the gas phase.
Likewise, the terms involving the ER and LH mechanisms are independent of one another, thus we are able to determine the amount of a species formed (or consumed) via the ER or the LH mechanism. For the sake of simplicity, the differential equations were divided into two sets, accounting for the two formation mechanism separately. Below is the list of equations governing the CO2 formation by the ER mechanism: 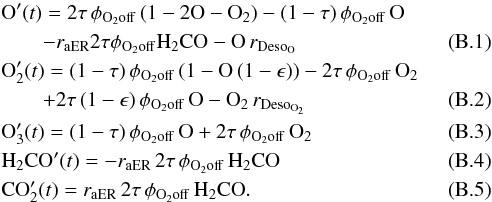 O, O2, O3, H2CO, and CO2 are the surface densities (expressed in fractions of ML) of the species, τ is the dissociated fraction of O2 defined in Sect. 2, φO2off is the flux (0.003 cm-2 s-1) of O2, ϵ is the evaporation probability – due to chemical desorption − of O2 formed on the surface (Dulieu et al. 2013), and
O, O2, O3, H2CO, and CO2 are the surface densities (expressed in fractions of ML) of the species, τ is the dissociated fraction of O2 defined in Sect. 2, φO2off is the flux (0.003 cm-2 s-1) of O2, ϵ is the evaporation probability – due to chemical desorption − of O2 formed on the surface (Dulieu et al. 2013), and  are the reaction probability of H2CO+O via ER and the desorption probabilities of O and O2, respectively; ν = 1012 is the trial frequency for attempting a new event. Finally, simple calculations show that 2τφO2off and (1 − τ)φO2off are the O and O2 flux, respectively, when the discharge is on. Similarly, as for CO2 formation by the LH mechanism, we have
are the reaction probability of H2CO+O via ER and the desorption probabilities of O and O2, respectively; ν = 1012 is the trial frequency for attempting a new event. Finally, simple calculations show that 2τφO2off and (1 − τ)φO2off are the O and O2 flux, respectively, when the discharge is on. Similarly, as for CO2 formation by the LH mechanism, we have  where
where  are the thermal diffusion probability of O atoms and the reaction probability of H2CO+O via LH, respectively. The activation barrier Ea is derived inverting the normalized Arrhenius equation:
are the thermal diffusion probability of O atoms and the reaction probability of H2CO+O via LH, respectively. The activation barrier Ea is derived inverting the normalized Arrhenius equation: 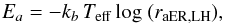 (B.16)with either raER or raLH according to the mechanism at play. Here
(B.16)with either raER or raLH according to the mechanism at play. Here 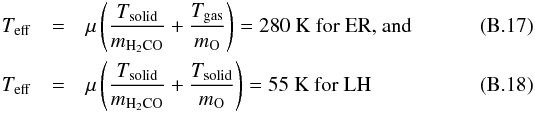 (see Minissale et al. 2013b for more details).
(see Minissale et al. 2013b for more details).
Appendix C: Theoretical calculations
The geometries (Fig. C.1) and energies (Tables C.1 and C.2) were optimized either using DFT with the hybrid meta exchange-correlation functional M06-2X or using classical MP2 method, both methods coupled to the Dunning’s correlation (Dunning 1989) consistent polarized valence triple zeta basis set cc-pVTZ. The highly nonlocal M06-2X functional developed by Truhlar et al. (Zhao & Truhlar 2008) is relatively well suited to structures and energetics calculations of the transition states even though this method slightly underestimates barrier energy. We then also calculate the barrier height using full optimized MP2
method, as well as single point CCSD(T) with MP2 geometries in some cases. The unrestricted Hartree-Fock (UHF) formulation has been used since it is a convenient way to describe open-shell and bond-breaking processes. Its use is justified in our study by the fact that we did not observe any significant spin contamination for all the stationary points explored, the quantum average value ⟨S2⟩ of the square of the total spin operator remaining close to 2.00, i.e. the characteristic value for a triplet state. Full geometry optimization was performed throughout. We checked carefully that all the saddle points found are correctly connected to two minima and are characterized by the existence of only one negative eigenvalue of the Hessian matrix corresponding to an imaginary frequency in the normal mode analysis.
Enthalpies of reaction and activation energies calculated at M06-2X/cc-pVTZ level.
Acknowledgments
The LERMA-LAMAp team in Cergy acknowledges the support of the national PCMI programme founded by CNRS. M.M. acknowledges financial support by LASSIE, a European FP7 ITN Community’s Seventh Framework Programme under Grant Agreement No. 238258. M.M. also thanks Dr. M. E. Palumbo and Dr. E. Dartois for fruitful discussions.
References
- Allamandola, L. J., Sandford, S. A., & Valero, G. J. 1988, Icarus, 76, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Amiaud, L., Fillion, J.-H., Baouche, S., et al. 2006, J. Chem. Phys., 124, 094702 [NASA ADS] [CrossRef] [Google Scholar]
- Amiaud, L., Dulieu, F., Fillion, J.-H., Momeni, A., & Lemaire, J. L. 2007, J. Chem. Phys., 127, 144709 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Baulch, D. L., Bowman, C. T., Cobos, C. J., et al. 2005, J. Phys. Chem. Ref. Data, 34, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Boogert, A. C. A., Pontoppidan, K. M., Knez, C., et al. 2008, ApJ, 678, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Braslavsky, S., & Heicklen, J., 1976, Int. J. Chem. Kinet., 8, 801 [CrossRef] [Google Scholar]
- Bromley, S. T., Goumans, F., Herbst, E., Jones, A., & Slater, B. 2014, Phys. Chem. Chem. Phys., 16, 18623 [CrossRef] [Google Scholar]
- Cazaux, S., Cobut, V., Marseille, M., Spaans, M., & Caselli, P. 2010, A&A, 74, A522 [Google Scholar]
- Chang, J. S., & Barker, J. R., 1979, JPC, 83, 3059 [CrossRef] [Google Scholar]
- Chang, J.-G., Chen, H.-T., Xu, S., & Lin, M. C. 2007, J. Phys. Chem. A, 111, 6789 [CrossRef] [Google Scholar]
- Congiu, E., Matar, E., Kristensen, L. E., Dulieu, F., Lemaire, J. L. 2009, MNRAS, 397, L96 [NASA ADS] [CrossRef] [Google Scholar]
- Congiu, E., Chaabouni, H., Laon, C., et al. 2012, J. Chem. Phys., 137, 054713 [NASA ADS] [CrossRef] [Google Scholar]
- Congiu, E., Minissale, M., Baouche, S., et al. 2014, Faraday Discussion, 168, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Crovisier, J., & Bockeleé-Morvan, D. 1999, Space Sci. Rev., 90, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E. 2005, Space Sci. Rev., 119, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E., Schutte, W., Geballe, T. R., et al. 1999, A&A, 342, L32 [NASA ADS] [Google Scholar]
- Davies, R. D., & Few, R. W., 1979, IAU Symp., 84, 81 [NASA ADS] [Google Scholar]
- Downes, D., Wilson, T. L., Bieging, J., & Wink, J. 1980, A&AS, 40, 379 [NASA ADS] [Google Scholar]
- Dulieu, F., Congiu, E., Noble, J. 2013, Scientific Rep., 3, 1338 [Google Scholar]
- Dunning, Jr., T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Dupuis, M., & Lester, W. A. 1984, J. Chem. Phys., 80, 4193 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goumans, T. P. M. 2011, MNRAS, 413, 2615 [NASA ADS] [CrossRef] [Google Scholar]
- Hiraoka, K., Ohashi, N., Kihara, Y., et al. 1994, Chem. Phys. Lett., 229, 408 [Google Scholar]
- Hidaka, H., Watanabe, N., Shiraki, T., Nagaoka, A., & Kouchi, A. 2004, ApJ, 614, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, R. L., & Moore, H. M. 1999, Icarus, 140, 451 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ioppolo, S., Palumbo, M. E., Baratta, G. A., & Mennella, V. 2009, A&A, 493, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keane, J. V., Tielens, A. G. G. M., Boogert, A. C. A., Schutte, W. A., & Whittet, D. C. B. 2001, A&A, 376, 254 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klemm, R. B. 1979, J. Chem. Phys., 71, 1987 [NASA ADS] [CrossRef] [Google Scholar]
- Klemm, R. B., Skolnik, E. G., & Michael, J. V. 1980, J. Chem. Phys., 72, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Laffon, C., Lasne, J., Bournel, F., et al. 2010, Phys. Chem. Chem. Phys., 12, 10865 [CrossRef] [Google Scholar]
- Loison, J.-C., Wakelam, V., Hickson, K. M., Bergeat, A., & Mereau, R. 2014a, MNRAS, 437, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J. C., Hickson, K. M., & Wakelam, V. 2014b, MNRAS, 443, 398 [Google Scholar]
- Maret, S., Ceccarelli, C., Caux, E., et al. 2004, A&A, 416, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madzunkov, S. M., MacAskill, J. A., Chutjian, A., et al. 2009, ApJ, 697, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Michael, J. V., Kumaran, S. S., & Su, M.-C. J. 1999, Phys. Chem. A, 103, 5942 [CrossRef] [Google Scholar]
- Minissale, M. 2014, Ph.D. Thesis, University of Cergy-Pontoise, France, available at http://www.u-cergy.fr/_attachments/theses-soutenues-au-lamap-article/Marco_MINISSALE_2014.pdf?download=true [Google Scholar]
- Minissale, M., & Dulieu, F. 2014, J. Chem. Phys., 141, 014304 [NASA ADS] [CrossRef] [Google Scholar]
- Minissale, M., Congiu, E., Baouche, S., et al. 2013a, Phys. Rev. Lett., 111, 053201 [NASA ADS] [CrossRef] [Google Scholar]
- Minissale, M., Congiu, E., Manicò, G., Pirronello, V., & Dulieu, F. 2013b, A&A, 559, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minissale, M., Congiu, E., & Dulieu, F. 2014, J. Chem. Phys., 140, 074705 [NASA ADS] [CrossRef] [Google Scholar]
- Mispelaer, F., Theulé, P., Aouididi, H., et al. 2013, A&A, 555, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mumma, M. J., DiSanti, M. A., Magee-Sauer, K., et al. 2005, Science, 310, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, J. A., Dulieu, F., Congiu, E., & Fraser, H. J., 2011, ApJ, 735, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, J. A., Congiu, E., Dulieu, F., & Fraser, H. J. 2012a, MNRAS, 421, 768 [NASA ADS] [Google Scholar]
- Noble, J., Theule, P., Mispelaer, F., et al. 2012b, A&A, 543, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oba, Y., Watanabe, N., Kouchi, A., Hama, T., & Pirronello, V. 2011, Phys. Chem. Chem. Phys., 13, 15792 [NASA ADS] [CrossRef] [Google Scholar]
- Oliveira, J. M., van Loon, J. Th., Sloan, G. C., et al. 2011, MNRAS, 411, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Ootsubo, T., Usui, F., Kawakita, H., et al. 2010, ApJ, 717, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Raut, U., & Baragiola, R., ApJ, 737, L14 [Google Scholar]
- Rimola, A., Taquet, V., Ugliengo, P., Balucani, N., & Ceccarelli, C. 2014, A&A, 572, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roser, J. E., Vidali, G., Manicó, G., & Pirronello, V. 2001, ApJ, 555, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Shalabiea, O. M., & Greenberg, J. M. 1994, A&A, 290, 266 [NASA ADS] [Google Scholar]
- Shimonishi, T., Onaka, T., Kato, D., et al. 2010, A&A, 514, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schutte, W. A., Allamandola, L. J., & Sandford, S. A. 1993a, Science, 259, 1143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schutte, W. A., Allamandola, L. J., & Sandford, S. A. 1993b, Icarus, 104, 118 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schutte, W. A., Gerakines, P. A., Geballe, T. R., et al. 1996, A&A, 309, 633 [NASA ADS] [Google Scholar]
- Snyder, L. E., Buhl, D., Zuckerman, B., & Palmer, P. 1969, Phys. Rev. Lett., 22, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, X. D., Esimbek, J., Zhou, J. J., et al. 2013, A&A, 551, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Theulé, P., Duvernay, F., Danger, G., et al. 2013, Adv. Space Res., 52, 1567 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N, Mouri, O., Nagaoka, A., et al. 2007, ApJ, 668, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Wellman, J., Park, J., & Hershberger, J. F. 1991, Chem. Phys. Lett., 178, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Geralines, P. A., Tielens, A. G. G. A., et al. 1998, ApJ, 498, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Cook, A. M., Herbst, E, Chiar, J. E., & Shenoy, S. S. 2011, ApJ, 742, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, S., Zhu, R. S., & Lin, M. C. 2006, Int. J. Chem. Kinet., 38, 322 [CrossRef] [Google Scholar]
- Yetter, R. A., Rabitz, H., Dryer, F. L., Maki, R. G., & Klemm, R. B. 1989, J. Chem. Phys., 91, 4088 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H.-G., & Francisco, J. S. 2008, J. Chem. Phys., 128, 4315 [Google Scholar]
- Zhao, Y., & Truhlar, D. 2008, Theor. Chem. Accounts, 120, 215 [Google Scholar]
- Zuckerman, B., Buhl, D., Palmer, P., & Snyder, L. E. 1970, ApJ, 160, 485 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Ion count per second of masses 30, 29, 28, and 18 a.m.u. as a function of pumping time of the paraformaldehyede powder held at 62 °C.
List of solid state reactions and their activation barriers to form CO2 and CH3OH.
Enthalpies of reaction and activation energies calculated at M06-2X/cc-pVTZ level.
All Figures
 |
Fig. 1 Detail of the experimental set-up and scheme of the depolymerization process of paraformaldehyde and preparation of the formaldehyde beam. |
| In the text | |
 |
Fig. 2 H2CO TPD traces obtained after deposition of 1 ML of H2CO (black line), H2CO+O2 (red line), and H2CO+O3 (green line) on oxidised HOPG held at 10 K. |
| In the text | |
 |
Fig. 3 CO2 (left panel) and H2CO (right panel) TPD traces obtained after deposition of 2 ML of H2CO (black line), 5 ML of O (green line), and 2 ML of H2CO + 5 ML of O atoms (red line) on oxidised HOPG held at 10 K. |
| In the text | |
 |
Fig. 4 Four RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of H2CO; (b) 2 ± 0.5 ML of H2CO + 0.8 ± 0.1 ML of O atoms; (c) 2 ± 0.5 ML of H2CO + 5 ± 0.4 ML of O atoms; (d) 5 ± 0.4 ML of O atoms on oxidised HOPG held at 10 K. (H2CO was always deposited at 60 K.) |
| In the text | |
 |
Fig. 5 Six RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of H2CO; (b) 2 ± 0.5 ML of H2CO + 0.5 ± 0.1 ML of O atoms; (c) 2 ± 0.5 ML of H2CO + 0.8 ± 0.1 ML of O atoms; (d) 2 ± 0.5 ML of H2CO + 1.2 ± 0.2 ML of O atoms; (e) 2 ± 0.5 ML of H2CO + 2.0 ± 0.3 ML of O atoms; (f) 2 ± 0.5 ML of H2CO + 3.8 ± 0.3 ML of O atoms, on a ASW ice held at 10 K. (H2CO was always deposited at 60 K.) |
| In the text | |
 |
Fig. 6 Left panel: seven RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of H2CO; (b) 2 ± 0.5 ML of H2CO + 0.5 ± 0.1 ML of O atoms; (c) 2 ± 0.5 ML of H2CO + 0.8 ± 0.1 ML of O atoms; (d) 2 ± 0.5 ML of H2CO + 1.2 ± 0.2 ML of O atoms; (e) 2 ± 0.5 ML of H2CO + 2.0 ± 0.3 ML of O atoms; (f) 2 ± 0.5 ML of H2CO + 2.8 ± 0.3 ML of O atoms; (g) 2 ± 0.5 ML of H2CO + 3.8 ± 0.3 ML of O atoms, on a ASW ice held at 55 K (H2CO was always deposited at 60 K). Right Panel: integrated areas of the H2CO and CO2 bands as a function of O-atom dose. |
| In the text | |
 |
Fig. 7 Top panel: three RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of D2CO; (b) 2 ± 0.5 ML of D2CO + 1.4 ± 0.1 ML of O atoms; (c) 2 ± 0.5 ML of D2CO + 3.8 ± 0.3 ML of O atoms, on oxidised HOPG held at 60 K. Bottom panel: CO2 (via mass 44) and D2CO (via masses 32 and 30) TPD mass spectra obtained after deposition of 2 ± 0.5 ML of D2CO + 3.8 ± 0.3 ML of O atoms on oxidised HOPG held at 60 K. |
| In the text | |
 |
Fig. 8 TPD traces of mass 18, 19, and 20 obtained after deposition of 2 ± 0.5 ML of D2CO (black curves) and 2 ± 0.5 ML of D2CO + 3.8 ± 0.3 ML of O atoms (red curves) on oxidised HOPG held at 60 K. |
| In the text | |
 |
Fig. 9 Relative energy diagram for the O + H2CO reaction. |
| In the text | |
 |
Fig. 10 Relative energy diagram for the HCOOH decomposition calculated at M06-2X/cc-pVTZ level. |
| In the text | |
 |
Fig. 11 Comparison between model (lines) and experimental data (symbols); IR yields of H2CO (red) and CO2 (black) are shown as a function of O-atom coverage. Four values of EOdiff are used: 900 K/kb (solid line), 800 K/kb (dashed line), 700 K/kb (dotted line), 600 K/kb (dashed-dotted line). From panels α to δ, Ea is 550 K/kb, 390 K/kb, 280 K/kb, and 200 K/kb, respectively. |
| In the text | |
 |
Fig. 12 Energetics of the CO+H/O reaction pathways. The enthalpies of CO2 and CH3OH and the activation barrier of each reaction are listed in Table 3. The enthalpies of H2CO and CO are −115.9 and −110.5 kJ/mol, respecively (http://webbook.nist.gov/chemistry/). |
| In the text | |
 |
Fig. A.1 Top panel: three RAIR spectra obtained after deposition of (a) 2 ± 0.5 ML of H |
| In the text | |
 |
Fig. C.1 Optimized geometries: pre-reactive complex (PRC), Transition State 1 (TS1), and Transition State 2 (TS2), from the left to the right panels, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.