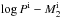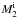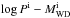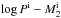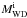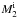EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 576 (April 2015) A&A, 576 (2015) A86 Full HTML
Free Access
Issue
A&A
Volume 576, April 2015
Article Number A86
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201425294
Published online 02 April 2015

© ESO, 2015

1. Introduction

Type Ia supernovae (SNe Ia) have been successfully used as standard candles for measuring cosmological distances, resulting in the determination of the accelerating expansion of the Universe that is driven by dark energy (e.g., Riess et al. 1998; Perlmutter et al. 1999). There is theoretical consensus that SNe Ia are thermonuclear explosions of carbon-oxygen white dwarfs (CO WDs; see Hoyle & Fowler 1960; Nomoto et al. 1997). However, SN Ia progenitor systems and the physics of their explosion mechanism are still uncertain (for recent reviews see Wang & Han 2012; Hillebrandt et al. 2013; Maoz et al. 2014; Ruiz-Lapuente 2014), which may affect the precision of results of the current cosmological model (e.g., Howell 2011).

Depending on the nature of the mass donor stars, two ways have been proposed by which CO WDs in binary systems can accrete mass towards the Chandrasekhar limit and then cause SNe Ia. These are the single-degenerate (SD) and the double-degenerate (DD) model. In the SD model, a CO WD accretes material from a non-degenerate star to increase its mass to the Chandrasekhar mass limit, which then leads to an SN Ia explosion (e.g., Whelan & Iben 1973; Nomoto et al. 1984). In the DD model, two CO WDs in a close binary are brought together by gravitational wave radiation and merge, which results in an SN Ia explosion (e.g., Webbink 1984; Iben & Tutukov 1984; Nelemans et al. 2001; Geier et al. 2007; Ruiter et al. 2009; Chen et al. 2012). For recent observational constraints to theoretical models see, e.g., Maoz et al. (2014), Wang & Han (2012), Liu et al. (2012a), Wang et al. (2013b) and Graur et al. (2014a,b).

The most commonly considered variation in the SD model is the WD+MS channel (known as the supersoft channel), in which the WD accretes material from a main-sequence (MS) star or a slightly evolved subgiant star (e.g., Hachisu et al. 1996, 1999; Li & van den Heuvel 1997; Langer et al. 2000; Han & Podsiadlowski 2004; Wang et al. 2010; Claeys et al. 2014; Ablimit et al. 2014). This channel has been suggested to be accompanied by recurrent novae and supersoft X-ray sources in the past two decades (see Parthasarathy et al. 2007; van den Heuvel et al. 1992; Rappaport et al. 1994). We did not study the SD WD+RG channel here because the SN Ia birthrate from that channel is much lower than the birthrate from the WD+MS channel (e.g., Yungelson & Livio 1998; Lü et al. 2006; Mennekens et al. 2010; Claeys et al. 2014).

The accretion of H-rich material onto WDs is crucial for understanding SNe Ia from the WD+MS channel. If the mass-accretion rate is too high, the WD will evolve into a red-giant-like star as a result of the pileup of the accreted material on its surface. If the mass-accretion rate is too low, the nuclear burning is unstable and H-shell flashes occur, which expels the accreted shell. Thus, there is only a narrow range in which the accreted H-rich material could steadily burn on the surface of WDs. This in turn means that theoretical SN Ia birthrates from the WD+MS channel are much lower than those of observations (e.g., Yungelson et al. 1996). An optically thick wind assumption was proposed to solve this problem, in which the H-rich material is transformed into He at a critical rate, while the unprocessed material is blown off in the form of the optically thick wind (see Hachisu et al. 1996, 1999; Nomoto et al. 2007). However, the optically thick wind assumption is still quite controversial (see Langer et al. 2000). In addition, this assumption does not work when the metallicity is lower than 0.002 (see Kobayashi et al. 1998), while SNe Ia with a metallicity lower than this threshold have been observed (e.g., Prieto et al. 2008; Badenes et al. 2009).

Ma et al. (2013) recently proposed an alternative way to replace the optically thick wind regimes, which is called the super-Eddington wind scenario. In this scenario, the super-Eddington wind is triggered when the luminosity of the accreting WD exceeds the Eddington luminosity. The super-Eddington wind can naturally prevent the CO WDs with high mass-accretion rates from forming red-giant-like stars. In contrast to the optically thick wind, the super-Eddington wind does not significantly depend on the metallicity, which could be triggered even for Z = 10-6 (see Fig. 4 of Ma et al. 2013). This indicates that this scenario may contribute to SNe Ia at high redshifts. In this work, we aim to investigate theoretical SN Ia birthrates and delay-time distributions of the WD+MS channel by adopting the super-Eddington wind scenario.

As mentioned above, at low mass-accretion rates, the accreting WD would experience H-shell flashes similar to nova outbursts. However, H-shell flashes are poorly understood because of the numerical difficulties in modeling nova outbursts. For example, only one cycle of a H-shell flash has been followed in most simulations of nova outbursts; a multicycle evolution of the H-shell flash is difficult to compute (e.g., Kovetz & Prialnik 1985; Iben et al. 1992; Schwartzman et al. 1994). The H-shell flashes are important for understanding the SN Ia progenitor scenario studied in this paper; a low mass-accumulation efficiency of H-shell flashes will lead to a low birthrate of SNe Ia. Denissenkov et al. (2013a) recently constructed multicycle nova evolutionary sequences with WDs using the stellar evolution code called modules for experiments in stellar astrophysics (MESA). Adopting a similar method to Denissenkov et al. (2013a), Ma et al. (2013) obtained the mass-accumulation efficiency of H-shell flashes for a wide range of WD masses. A more detailed binary population synthesis (BPS) approach is needed to study the influence of the H-shell flashes on the final results and to give SN Ia birthrates, which is also addressed in this work.

This paper is organized as follows: the numerical code for the binary evolution calculations is described in Sect. 2, and the corresponding results are provided in Sect. 3. The BPS method and results are presented in Sect. 4. Our discussion and summary are then presented in Sect. 5.

2. Numerical code for binary evolution

In the WD+MS channel, the mass donor star is an MS star or a slightly evolved subgiant star that transfers H-rich material onto the surface of the WD. The accreted H-rich material is burned into He, and then the He is converted into carbon and oxygen, resulting in a mass increase of the WD. We assume that the WD explodes as an SN Ia once its mass grows to 1.378 M⊙, which is the critical mass limit of nonrotating WDs for carbon ignition (e.g., Nomoto et al. 1984)1. We calculated the evolution of the WD+MS systems using the Eggleton stellar evolution code (Eggleton 1973; Han et al. 1994; Pols et al. 1995, 1998; Eggleton & Kiseleva-Eggleton 2002). The initial setup and basic input physics for this code are similar to those in Wang et al. (2010). The MS star models in our calculations are composed of metallicity Z = 0.02, H abundance X = 0.70, and He abundance Y = 0.28.

thumbnail Fig. 1

Properties of H-shell burning on the surface of accreting WDs in the plane of WD mass and mass-accretion rate. We compared the critical mass-accretion rate between the super-Eddington wind scenario and the optically thick wind model. The solid lines are taken from Ma et al. (2013), while the dashed lines are adopted from Nomoto et al. (2007).

The mass transfer begins once the MS star fills its Roche-lobe. We define the values of mass-accumulation efficiency for H-shell burning on the surface of the WD, ηH, as 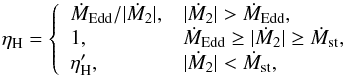ηH={ṀEdd/|Ṁ2|,|Ṁ2|>ṀEdd,1,ṀEdd≥|Ṁ2|≥Ṁst,ηH′,|Ṁ2|<Ṁst,\begin{equation} \eta_{\rm H}=\left\{ \begin{array}{ll} \dot{M}_{\rm Edd}/|\dot{M}_{\rm 2}|, & |\dot{M}_{\rm 2}|> \dot{M}_{\rm Edd},\\ 1, & \dot{M}_{\rm Edd}\geq |\dot{M}_{\rm 2}|\geq\dot{M}_{\rm st},\\ \eta'_{\rm H}, & |\dot{M}_{\rm 2}|< \dot{M}_{\rm st}, \end{array}\right. \end{equation}(1)where Ṁ2, ṀEdd and Ṁst are the mass-transfer rate, the Eddington critical accretion rate, and the minimum accretion rate for stable H-shell burning, respectively. In the following, we describe in detail: (1) if the mass-transfer rate, Ṁ2, is above the Eddington critical accretion rate, ṀEdd, we assume that the accreted H steadily burns on the surface of the WD, and that the H-rich material is converted into He at a rate of ṀEdd, 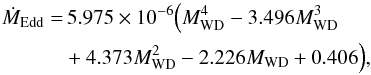ṀEdd= 5.975×10-6(MWD4−3.496MWD3+4.373MWD2−2.226MWD+0.406),\begin{eqnarray} \dot{M}_{\rm Edd}&=&\,5.975\times10^{-6}\Big({M}_{\rm WD}^4-3.496{M}_{\rm WD}^3\notag\\ &+4.373{M}_{\rm WD}^2-2.226{M}_{\rm WD}+0.406\Big), \end{eqnarray}(2)where MWD is the mass of the WD in units of M⊙, and ṀEdd is in units of M⊙ yr-1. The unprocessed material can be lost from the system in the form of the super-Eddington wind with a mass-loss rate of (| Ṁ2 | − ṀEdd). In Fig. 1, we compare the critical mass-accretion rate of the super-Eddington wind scenario and the optically thick wind model (for a more detailed discussion of this figure see Sect. 5). (2) When | Ṁ2 | is lower than ṀEdd but higher than the minimum accretion rate for stable H-shell burning, Ṁst, the burning of the H layer is steady and no mass is lost from the system. The values of Ṁst are 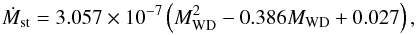Ṁst=3.057×10-7(MWD2−0.386MWD+0.027),\begin{equation} \dot{M}_{\rm st}=3.057\times 10^{-7}\left({M}_{\rm WD}^2-0.386{M}_{\rm WD}+0.027\right), \end{equation}(3)where Ṁst is in units of M⊙ yr-1 (see Fig. 1). (3) H-shell flashes are triggered once | Ṁ2 | is lower than Ṁst. The mass-accumulation efficiency for H-shell flashes, 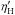ηH′\hbox{$\eta'_{\rm H}$}, is linearly interpolated from a detailed grid (see Fig. 2), in which a wide range of WD masses and mass-accretion rate were calculated by Ma et al. (2013).

thumbnail Fig. 2

Mass-accumulation efficiency of H-shell flashes, ηH, plotted against mass-accretion rate for various initial WD masses. The data points are taken from Ma et al. (2013).

Helium is assumed to be ignited once the mass of the He layer under the H-shell burning reaches a certain value. The mass-growth rate of the He layer is defined as 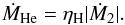ṀHe=ηH|Ṁ2|.\begin{equation} \dot{M}_{\rm He}=\eta _{\rm H}|\dot{M}_{\rm 2}|. \end{equation}(4)If He-shell flashes occur, we assume that a part of the layer mass is blown off. In this case, we adopt the prescription of Kato & Hachisu (2004) for mass-accumulation efficiency of He-shell flashes2. We define the mass-growth rate of the WD, ṀCO, as 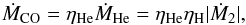ṀCO=ηHeṀHe=ηHeηH|Ṁ2|,\begin{equation} \dot{M}_{\rm CO}=\eta_{\rm He}\dot{M}_{\rm He}=\eta_{\rm He}\eta_{\rm H}|\dot{M}_{\rm 2}|, \end{equation}(5)where ηHe is the mass-accumulation efficiency of He-shell flashes.

thumbnail Fig. 3

Representative example of binary evolution calculations, where the binary system is in the weak H-shell flash phase at the moment of the SN explosion. In panel a), the solid, dashed, and dashed-dotted curves present Ṁ2, ṀCO, and MWD, varying with time. In panel b), the evolutionary track of the donor in the Hertzsprung-Russell diagram is shown as a solid curve, and the evolution of orbital period is shown as a dashed-dotted curve. Dotted vertical lines in both panels indicate the position where the WD produces an SN Ia.

The evolution of the orbital periods of these WD+MS systems is mainly decided by the wind mass-loss of the WD, which carries away the orbital angular momentum of the binaries. We assume that the mass lost from these systems takes away the specific orbital angular momentum of the WD, but the mass lost from the wind of the mass donors is negligible (e.g., Wang et al. 2010). Finally, dense model grids of binary evolution calculations are obtained.

3. Binary evolution results

In Fig. 3, we present a representative example of binary evolution calculations. The binary system is in the weak H-shell flash phase at the moment of SN explosion. The initial condition for this binary is (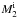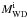M2i\hbox{$M_2^{\rm i}$}, MWDi\hbox{$M_{\rm WD}^{\rm i}$}, log (Pi/ day)) = (2.1, 0.9, 0.4), where 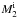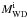M2i\hbox{$M_2^{\rm i}$}, MWDi\hbox{$M_{\rm WD}^{\rm i}$} and Pi are the initial masses of the MS star and the CO WD in solar masses, and the initial orbital period in days, respectively. The MS star first fills its Roche-lobe after exhausting the central H (it now contains a He core), which leads to early Case B mass transfer; the orbital period of the binary system is not changed until the MS star fills its Roche-lobe, see panel b of Fig. 3. The mass-transfer rate | Ṁ2 | exceeds ṀEdd soon after the onset of Roche-lobe overflow, resulting in a wind phase in which a part of the transferred mass is blown off in the form of the super-Eddington wind, and the remainder is accumulated on the WD; the wind carries away the specific orbital angular momentum of the WD, which results in the decrease of the orbital period. After about 1.6 × 106 yr, | Ṁ2 | drops below ṀEdd, but is still higher than Ṁst. At this stage, the H-shell burning is stable, but the super-Eddington wind ceases. With the decrease of | Ṁ2 |, the WD quickly enters a weak H-shell flash phase. The orbital period of the binary starts to increase when the accreting WD is more massive than the donor star. The WD always grows in mass until it explodes as an SN Ia in the weak H-shell flash phase. When the WD increases its mass to 1.378 M⊙, the mass of the donor star is 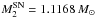M2SN=1.1168 M⊙\hbox{$M^{\rm SN}_2=1.1168\,M_{\odot}$} and the orbital period is log (PSN/ day) = 0.2092.

Figure 4 presents the initial contours for producing SNe Ia in the orbital period and secondary mass plane for various initial WD masses (i.e., 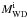MWDi\hbox{$M_{\rm WD}^{\rm i}$} = 0.90, 1.0, 1.1 and 1.2 M⊙). The enclosed region almost vanishes for WDs with 0.9 M⊙, which is then assumed to be the minimum initial WD mass for producing SNe Ia from the WD+MS channel. We note that the critical mass-accretion rate for WDs is still uncertain (e.g., Cassisi et al. 1998; Langer et al. 2000; Nomoto et al. 2007; Shen & Bildsten 2007; Bours et al. 2013). In the observations, some binaries that contain a neutron star or a black hole can lose their masses at rates that exceed the Eddington accretion rate of the compact object by several times (e.g., Cyg X-2 and SS 433; Podsiadlowski & Rappaport 2000; Blundell et al. 2001). In Fig. 5, we show the initial contours for producing SNe Ia after adopting 2ṀEdd as the critical mass-accretion rate; we did not change the values of the minimum accretion rate for stable H-shell burning (i.e., Ṁst) in our calculations. This is an unphysical extreme assumption, but we can use this to examine the influence of the critical mass-accretion rate on the final results. From this figure, we can see that the initial contours for producing SNe Ia are significantly enlarged. This is because a larger regime for stable H-shell burning is adopted.

The left boundaries of the initial contours in Figs. 4, 5 are constrained by the condition that Roche-lobe overflow begins when the mass donor star is in the zero-age MS stage, while systems beyond the right boundary experience mass transfer at a relatively high rate as a result of the rapid expansion of the donor stars in the Hertzsprung gap, and they lose too much mass via the super-Eddington wind, preventing the WDs from increasing their masses to the Chandrasekhar mass. The upper boundaries are set by a high mass-transfer rate owing to a high mass ratio between the mass donor star and the WD, while the lower boundaries are constrained by the condition that the mass-transfer rate should be high enough to ensure the mass growth of the WD during H-shell flashes.

thumbnail Fig. 4

Regions in the logPi−M2i\hbox{$\log P^{\rm i}-M^{\rm i}_2$} plane for WD+MS binaries that ultimately produce SNe Ia for various initial WD masses, where Pi and M2i\hbox{$M^{\rm i}_2$} are the initial orbital period and the initial mass of the MS star.

thumbnail Fig. 5

Similar to Fig. 4, but for results obtained after adopting 2ṀEdd as the critical mass-accretion rate.

4. BPS assumptions and results

4.1. Method of BPS

To obtain SN Ia birthrates and delay times for the WD+MS channel, we performed a series of Monte Carlo BPS simulations. The random number generator algorithm in our Monte Carlo simulations is adopted from Press et al. (1992). It provides a uniform probability density in the range of (0, 1). The repetition period of the random number generator in our simulations is ≳1018, which is infinite for practical calculations.

For each BPS simulation, we employed the rapid binary evolution code of Hurley (Hurley et al. 2002) to simulate the evolution of 107 primordial binaries, and adopted a metallicity of Z = 0.02. These binaries are followed from the star formation to the formation of the WD+MS systems based on three binary evolutionary ways (see Fig. 1 of Wang & Han 2012). If the initial parameters of a CO WD+MS system at the onset of the Roche-lobe overflow are located in the SN Ia production regions in the plane of (log Pi, 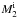M2i\hbox{$M_2^{\rm i}$}) for its specific 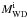MWDi\hbox{$M_{\rm WD}^{\rm i}$}, then an SN Ia is assumed to occur. We adopted a linear interpolation if 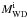MWDi\hbox{$M_{\rm WD}^{\rm i}$} is not among the masses listed in Figs. 4, 5.

Seven sets of Monte Carlo BPS simulations were conducted to investigate the birthrates of SNe Ia (see Table 1), in which sets 1 and 2 are the two best models from Camacho et al. (2014). These two best models result in a good overall fit to the properties of the WD+MS binary population in the Sloan Digital Sky Survey (SDSS) Data Release 7. The following basic assumptions for these Monte Carlo simulations were adopted:

  • (1)

    A constant star formation rate (SFR) of 5 M⊙ yr-1 is simply assumed over the past 14 Gyr or, alternatively, it is modeled as a delta function, that is, a single instantaneous starburst (1010M⊙ in stars is assumed). We intend the constant SFR to approximate spiral galaxies, and the delta function to provide a rough description of elliptical galaxies or globular clusters (e.g., Wang et al. 2013a).

  • (2)

    All stars are assumed to be members of binaries. The primordial binary samples are generated via a Monte Carlo method and an initially circular orbit was supposed for all binaries. The distribution of initial orbital separations is assumed to be constant in log a for wide binaries, where a is the orbital separation (e.g., Han et al. 1995).

  • (3)

    The initial mass function (IMF) of the primordial primary star is taken from Miller & Scalo (1979, MS79). Alternatively, we also considered the IMF of Scalo (1986, S86).

  • (4)

    A constant mass-ratio distribution is assumed, that is, n(q) = 1, or a distribution proportional to the mass ratio, n(q) ∝ q (e.g., Camacho et al. 2014).

  • (5)

    The common-envelope (CE) evolution is still uncertain (e.g., Zuo & Li 2014). The standard energy equations are used to describe the output during the CE stage (e.g., Webbink 1984). There are two uncertain parameters for this prescription of the CE ejection: αCE (the CE ejection efficiency) and λ (a structure parameter that depends on the evolutionary stage of the mass donor). λ is usually set to be 0.5 for the purpose of constraining αCE (see de Kool 1990). Here, we set αCE to be 0.3, 1.0 and 3.0 to examine its influence on the final results.

4.2. Results of BPS

Table 1

Galactic SN Ia birthrates for seven simulation sets, in which sets 1 and 2 are the two best models from Camacho et al. (2014).

thumbnail Fig. 6

Evolution of SN Ia birthrates for a constant star-formation rate (SFR = 5.0 M⊙ yr-1) with different BPS simulation sets.

According to the seven sets of simulations for the WD+MS channel, the estimated birthrates of SNe Ia are strongly sensitive to the choice of some initial conditions, for instance, the critical mass-accretion rate, the CE ejection efficiency, initial mass-ratio distribution and initial mass function, etc. It is obvious that, if we adopt 2ṀEdd as the critical mass-accretion rate, the SN Ia birthrate will increase significantly. This is because a larger initial contours for producing SNe Ia are adopted.

thumbnail Fig. 7

Delay-time distributions of SNe Ia with different BPS simulation sets. The open circles are taken from Maoz et al. (2011), while the filled squares are adopted from Totani et al. (2008).

thumbnail Fig. 8

Similar to Fig. 7, but for the case of set 1, where ten random initial seeds are adopted in our simulations.

In Fig. 6, we show the evolution of SN Ia birthrates with time by adopting metallicity Z = 0.02 and star formation rate SFR = 5 M⊙ yr-1. This study presents an SN Ia birthrate of ~0.009−0.315 × 10-3 yr-1 by adopting ṀEdd as the critical accretion rate, which is far lower than the observed value (i.e., 3−4 × 10-3 yr-1; Cappellaro & Turatto 1997)3. Thus, we speculate that the WD+MS channel only contributes to a small part of all SNe Ia (<10%); some other formation channels or mechanisms may also contribute to SNe Ia (for a recent review see Wang & Han 2012). If we adopt 2ṀEdd as the critical accretion rate, the birthrate of SNe Ia will increase to ~0.712−0.955 × 10-3 yr-1 (see sets 5 and 7). This value is still lower than that of observations, but it provides an upper limit on the birthrate of SNe Ia for the WD+MS channel. This means that the variation of the critical accretion rate has a significant influence on the SN Ia birthrates.

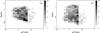thumbnail Fig. 9

Distribution of properties of initial WD+MS systems that can ultimately produce SNe Ia. Panel a) shows the results in the logPi−MWDi\hbox{$\log P^{\rm i}-M^{\rm i}_{\rm WD}$} plane, while panel b) gives the results in the logPi−M2i\hbox{$\log P^{\rm i}-M^{\rm i}_{\rm 2}$} plane, where Pi, MWDi\hbox{$M^{\rm i}_{\rm WD}$} and M2i\hbox{$M^{\rm i}_{\rm 2}$} are the initial orbital period, the initial WD masses, and the initial mass of the MS star. Here, we present the case of set 1.

SN Ia delay times are defined as the time interval from star formation to the SN explosion. In Fig. 7, we display the SN Ia delay-time distributions for the WD+MS channel with different BPS simulation sets, which are obtained from a single starburst. From this figure, we can see that the estimated delay times for this channel are ~110 Myr−1200 Myr after the starburst, which may have a contribution to the SNe Ia with intermediate delay times. Note that a low value of αCE results in a higher birthrate of SNe Ia. This is because for a low value of αCE the primordial binary systems need to release more orbital energy to eject the CE and then produce WD+MS binaries. In this case, WD+MS binaries tend to have slightly closer orbital separations and are more likely to be located in the SN Ia production region (e.g., Figs. 4, 5). We note that, in any Monte Carlo simulations the initial seed of the random number generator results in a given and specific simulated population. In Fig. 8, we show the delay-time distributions of SNe Ia for the case of set 1, in which ten random initial seeds are adopted in our simulations. From this figure, we found that there is no significant difference among these simulations, meaning that our Monte Carlo BPS results are not sensitive to the initial seed of the random number generator.

In the observations, some WD+MS systems are suggested to be candidates of SN Ia progenitors (for recent reviews see Wang & Han 2012; Parthasarathy et al. 2007, and references therein). In Fig. 9, we give some properties of initial WD+MS systems that can produce SNe Ia based on our BPS calculations, which would be useful for identifying potential progenitor candidates of SNe Ia. For these WD+MS systems, SN Ia explosions in our simulations occur for the ranges 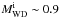MWDi~0.9\hbox{$M_{\rm WD}^{\rm i}\sim0.9$}−1.2 M⊙, 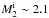M2i~2.1\hbox{$M_{\rm 2}^{\rm i}\sim2.1$}−3.1 M⊙ and Pi ~ 0.5−5 days. However, recent observations in the SDSS have not found massive MS stars in WD+MS systems, where the MS stars have masses <0.6 M⊙ (e.g., Zorotovic et al. 2011; Nebot Gómez-Morán et al. 2011; Rebassa-Mansergas et al. 2012, 2013; Toonen & Nelemans 2013; Camacho et al. 2014; Li et al. 2014), which cannot afford enough material for the WDs to increase their masses to the Chandrasekhar limit.

5. Discussion and conclusions

Previous studies frequently assumed that when the mass-transfer rate is lower than 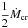12Ṁcr\hbox{$\dfrac{1}{2}\dot{M}_{\rm cr}$} but higher than 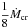18Ṁcr\hbox{$\dfrac{1}{8}\dot{M}_{\rm cr}$} (see dashed lines in Fig. 1), a weak H-shell flash is triggered, but no mass is lost from the binary system, which would mean that H is totally converted into He during the mass-accretion phase (e.g., Hachisu et al. 1999; Han & Podsiadlowski 2004; Meng et al. 2009; Chen & Li 2009; Wang et al. 2010; Tauris et al. 2013). However, we here adopted a detailed mass-accumulation efficiency for H-shell flashes once the mass-transfer rate is below Ṁst (see Fig. 2), the value of which is lower than in previous studies, leading to a low birthrate of SNe Ia. Note that there is a heated debate about the mass-accumulation efficiency on WDs; it is still uncertain whether nova outbursts remove more mass from the WD than the accreted material (e.g., Prialnik & Kovetz 1995; Cassisi et al. 1998; Yaron et al. 2005; Idan et al. 2012; Newsham et al. 2014).

Denissenkov et al. (2013b) recently proposed a new type of WDs, the hybrid CONe WDs, which have an unburned CO core surrounded by a thick ONe shell. In a subsequent investigation, Chen et al. (2014) found that this type of hybrid WDs could be as large as 1.3 M⊙. Following the works of Chen et al. (2014), Meng & Podsiadlowski (2014) studied the hybrid WD+MS channel of SN Ia progenitors based on a detailed BPS approach and calculated the birthrates ~0.026−0.24 × 10-3 yr-1. If this kind of hybrid WDs can really undergo a thermonuclear runaway when increasing their masses to a critical limit, then the SN Ia birthrates from the WD+MS channel can be increased significantly. Note that hybrid WDs could reach a state of explosive carbon ignition, but this depends on some mixing assumptions and the convective Urca process (see Denissenkov et al. 2015).

When the WD in the WD+MS channel explodes as an SN Ia, the mass donor star in this channel would survive and potentially be identifiable (e.g., Liu et al. 2012b; Pan et al. 2014). Tycho G was referred as the surviving companion of Tycho’s SN from the WD+MS channel (e.g., Ruiz-Lapuente et al. 2004; Wang & Han 2010), although it is still debatable (e.g., Ihara et al. 2007; Kerzendorf et al. 2009; Liu et al. 2013). The surviving companions from this channel may also provide a way to explain the formation of single low-mass He WDs in the observations (e.g., Justham et al. 2009; Wang & Han 2010).

The process of mass accretion onto CO WDs is important for understanding the SD model of SNe Ia, which has a direct effect on the theoretical birthrates of SNe Ia (see also Bours et al. 2013). In this article, by employing the Eggleton stellar evolution code and adopting detailed mass-accumulation efficiencies of H-shell flashes on the WDs, we performed binary evolution calculations for the WD+MS channel in detail based on the super-Eddington wind scenario and computed the initial parameter spaces for producing SNe Ia with various initial WD masses. We found that a CO WD with a mass as low as 0.9 M⊙ can potentially accrete enough mass and then reach the Chandrasekhar mass limit if we adopt ṀEdd as the critical accretion rate. By incorporating the results of the detailed binary evolution calculations into a detailed BPS approach, we obtained the evolution of SN Ia birthrates with time. The SN Ia birthrate from the WD+MS channel is much lower than the value obtained from observations. This means that the contributions of the WD+MS channel to the total SN Ia birthrates are quite inefficient. However, this result is strongly sensitive to uncertainties in some initial conditions, especially the efficiency of mass accretion. If we adopt 2ṀEdd as the critical accretion rate, the SN Ia birthrate is increased significantly. Additionally, the values of αCE also have an influence on the birthrates of SNe Ia. To set further constraints on the WD+MS channel, large samples of observed massive WD+MS systems and surviving companions are needed, and the process of mass accretion on WDs should be examined carefully.

1

We did not consider the influence of rotation on the evolution of the accreting WD in this work; the maximum stable mass for a rotating WD may be above the standard Chandrasekhar mass limit (see Uenishi et al. 2003; Yoon et al. 2004; Wang et al. 2014).

2

Yoon et al. (2004) argued that the burning of He layer is less violent when rotation is considered, which may increase the mass-accumulation efficiency of He-rich material.

3

The upper mass limit for CO WDs has been suggested to be ~1.07 M⊙ (see Umeda et al. 1999). If this mass limit is adopted in Fig. 4, the SN Ia birthrate from the WD+MS channel will decrease to ~0.009−0.215 × 10-3 yr-1.

Acknowledgments

We acknowledge the anonymous referee for valuable comments that helped us to improve the paper. We thank Xiangdong Li, Fenghui Zhang and Xiangcun Meng for their useful discussions. We also thank Yan Gao for his kind help to improve the language of this paper. This study is supported by the National Basic Research Program of China (973 program, 2014CB845700), the National Natural Science Foundation of China (Nos. 11322327, 11390374 and U1331117), the Chinese Academy of Sciences (No. XDB09010202), and the Natural Science Foundation of Yunnan Province (Nos. 2013FB083 and 2013HB097).

References

  1. Ablimit, I., Xu, X.-J., & Li, X.-D. 2014, ApJ, 780, 80 [NASA ADS] [CrossRef] [Google Scholar]
  2. Badenes, C., Harris, J., Zaritsky, D., & Prieto, J. L. 2009, ApJ, 700, 727 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blundell, K. M., Mioduszewski, A. J., Muxlow, T. W., Podsiadlowski, P., & Rupen, M. P. 2001, ApJ, 562, L79 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bours, M. C. P., Toonen, S., & Nelemans, G. 2013, A&A, 552, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Camacho, J., Torres, S., García-Berro, E., et al. 2014, A&A, 566, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Cappellaro, E., & Turatto, M. 1997, in Thermonuclear Supernovae, eds. P. Ruiz-Lapuente, R. Cannal, & J. Isern (Dordrecht: Kluwer), 77 [Google Scholar]
  7. Cassisi, S., Iben, I., & Tornambè, A. 1998, ApJ, 496, 376 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chen, W.-C., & Li, X.-D. 2009, ApJ, 702, 686 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chen, X., Jeffery, C. S., Zhang, X., & Han, Z. 2012, ApJ, 755, L9 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chen, M. C., Herwig, F., Denissenkov, P. A., & Paxton, B. 2014, MNRAS, 440, 1274 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Claeys, J. S. W., Pols, O. R., Izzard, R. G., Vink, J., & Verbunt, F. W. M. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. de Kool, M. 1990, ApJ, 358, 189 [NASA ADS] [CrossRef] [Google Scholar]
  13. Denissenkov, P. A., Herwig, F., Bildsten, L., & Paxton, B. 2013a, ApJ, 762, 8 [NASA ADS] [CrossRef] [Google Scholar]
  14. Denissenkov, P. A., Herwig, F., Truran, J. W., & Paxton, B. 2013b, ApJ, 772, 37 [NASA ADS] [CrossRef] [Google Scholar]
  15. Denissenkov, P. A., Truran, J. W., Herwig, F., et al. 2015, MNRAS, 447, 2696 [NASA ADS] [CrossRef] [Google Scholar]
  16. Eggleton, P. P. 1973, MNRAS, 163, 279 [NASA ADS] [CrossRef] [Google Scholar]
  17. Eggleton, P. P., & Kiseleva-Eggleton, L. 2002, ApJ, 575, 461 [NASA ADS] [CrossRef] [Google Scholar]
  18. Geier, S., Nesslinger, S., Heber, U., et al. 2007, A&A, 464, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Graur, O., Maoz, D., & Shara, M. M. 2014a, MNRAS, 442, L28 [NASA ADS] [CrossRef] [Google Scholar]
  20. Graur, O., Rodney, S. A., Maoz, D., et al. 2014b, ApJ, 783, 28 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hachisu, I., Kato, M., Nomoto, K., & Umeda, H. 1999, ApJ, 519, 314 [NASA ADS] [CrossRef] [Google Scholar]
  23. Han, Z., & Podsiadlowski, P. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
  24. Han, Z., Podsiadlowski, Ph., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
  25. Han, Z., Podsiadlowski, Ph., & Eggleton, P. P. 1995, MNRAS, 272, 800 [NASA ADS] [Google Scholar]
  26. Hillebrandt, W., Kromer, M., Röpke, F. K., & Ruiter, A. J. 2013, Frontiers of Physics, 8, 116 [Google Scholar]
  27. Howell, D. A. 2011, Nature Comm., 2, 350 [Google Scholar]
  28. Hoyle, F., & Fowler, W. A. 1960, ApJ, 132, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
  30. Iben, I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
  31. Iben, I., Fujimoto, M. Y., & MacDonald, J. 1992, ApJ, 388, 521 [NASA ADS] [CrossRef] [Google Scholar]
  32. Idan, I., Shaviv, N. J., & Shaviv, G. 2012, J. Phys. Conf. Ser., 337, 012051 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ihara, Y., Ozaki, J., Doi, M., et al. 2007, PASJ, 59, 811 [NASA ADS] [Google Scholar]
  34. Justham, S., Wolf, C., Podsiadlowski, P., & Han, Z. 2009, A&A, 493, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Kato, M., & Hachisu, I. 2004, ApJ, 613, L129 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kerzendorf, W. E., Schmidt, B. P., Asplund, M., et al. 2009, ApJ, 701, 1665 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kobayashi, C., Tsujimoto, T., Nomoto, K., Hachisu, I., & Kato, M. 1998, ApJ, 503, L155 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kovetz, A., & Prialnik, D. 1985, ApJ, 291, 812 [NASA ADS] [CrossRef] [Google Scholar]
  39. Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, A&A, 362, 1046 [NASA ADS] [Google Scholar]
  40. Li, X.-D., & van den Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS] [Google Scholar]
  41. Li, L.-F., Zhang, F., Han, Q., Kong, X., & Gong, X. 2014, MNRAS, 445, 1331 [NASA ADS] [CrossRef] [Google Scholar]
  42. Liu, J.-F., Di Stefano, R., Wang, T., & Moe, M. 2012a, ApJ, 749, 141 [NASA ADS] [CrossRef] [Google Scholar]
  43. Liu, Z.-W., Pakmor, R., Röpke, F. K., et al. 2012b, A&A, 548, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Liu, Z.-W., Pakmor, R., Röpke, F. K., et al. 2013, A&A, 554, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Lü, G., Yungelson, L., & Han, Z. 2006, MNRAS, 372, 1389 [NASA ADS] [CrossRef] [Google Scholar]
  46. Ma, X., Chen, X., Chen, H., Denissenkov, P. A., & Han, Z. 2013, ApJ, 778, L32 [NASA ADS] [CrossRef] [Google Scholar]
  47. Maoz, D., Mannucci, F., Li, W., et al. 2011, MNRAS, 412, 1508 [NASA ADS] [CrossRef] [Google Scholar]
  48. Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [NASA ADS] [CrossRef] [Google Scholar]
  49. Meng, X., & Podsiadlowski, Ph. 2014, ApJ, 789, L45 [NASA ADS] [CrossRef] [Google Scholar]
  50. Meng, X., Chen, X., & Han, Z. 2009, MNRAS, 395, 2103 [NASA ADS] [CrossRef] [Google Scholar]
  51. Mennekens, N., Vanbeveren, D., De Greve, J. P., & De Donder, E. 2010, A&A, 515, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Miller, G. E., & Scalo, J. M. 1979, ApJS, 41, 513 (MS79) [NASA ADS] [CrossRef] [Google Scholar]
  53. Nebot Gómez-Morán, A., Gänsicke, B. T., Schreiber, M. R., et al. 2011, A&A, 536, A43 [CrossRef] [Google Scholar]
  54. Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Newsham, G., Starrfield, S., & Timmes, F. 2014, ASP Conf. Ser., 490, 287 [NASA ADS] [Google Scholar]
  56. Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
  57. Nomoto, K., Iwamoto, K., & Kishimoto, N. 1997, Science, 276, 1378 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  58. Nomoto, K., Saio, H., Kato, M., & Hachisu, I. 2007, ApJ, 663, 1269 [NASA ADS] [CrossRef] [Google Scholar]
  59. Pan, K.-C., Ricker, P. M., & Taam, R. E. 2014, ApJ, 792, 71 [NASA ADS] [CrossRef] [Google Scholar]
  60. Parthasarathy, M., Branch, D., Jeffery, D. J., & Baron, E. 2007, New Astron. Rev., 51, 524 [NASA ADS] [CrossRef] [Google Scholar]
  61. Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
  62. Podsiadlowski, P., & Rappaport, S. 2000, ApJ, 529, 946 [NASA ADS] [CrossRef] [Google Scholar]
  63. Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
  64. Pols, O. R., Schröder, K. P., Hurly, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
  65. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, in Numerical recipes in FORTRAN. The art of scientific computing (Cambridge University Press), 271 [Google Scholar]
  66. Prialnik, D., & Kovetz, A. 1995, ApJ, 445, 789 [NASA ADS] [CrossRef] [Google Scholar]
  67. Prieto, J. L., Stanek, K. Z., & Beacom, J. F. 2008, ApJ, 673, 999 [NASA ADS] [CrossRef] [Google Scholar]
  68. Rappaport, S., Di Stefano, R., & Smith, J. D. 1994, ApJ, 426, 692 [NASA ADS] [CrossRef] [Google Scholar]
  69. Rebassa-Mansergas, A., Nebot Gómez-Morán, A., Schreiber, M. R., et al. 2012, MNRAS, 419, 806 [NASA ADS] [CrossRef] [Google Scholar]
  70. Rebassa-Mansergas, A., Agurto-Gangas, C., Schreiber, M. R., Gänsicke, B. T., & Koester, D. 2013, MNRAS, 433, 3398 [NASA ADS] [CrossRef] [Google Scholar]
  71. Riess, A., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  72. Ruiter, A. J., Belczynski, K., & Fryer, C. L. 2009, ApJ, 699, 2026 [NASA ADS] [CrossRef] [Google Scholar]
  73. Ruiz-Lapuente, P. 2014, New Astron. Rev., 62, 15 [NASA ADS] [CrossRef] [Google Scholar]
  74. Ruiz-Lapuente, P., Comeron, F., Méndez, J., et al. 2004, Nature, 431, 1069 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  75. Scalo, J. M. 1986, Fund. Cosm. Phys., 11, 1 (S86) [Google Scholar]
  76. Schwartzman, E., Kovetz, A., & Prialnik, D. 1994, MNRAS, 269, 323 [NASA ADS] [CrossRef] [Google Scholar]
  77. Shen, K. J., & Bildsten, L. 2007, ApJ, 660, 1444 [NASA ADS] [CrossRef] [Google Scholar]
  78. Tauris, T. M., Sanyal, D., Yoon, S.-C., & Langer, N. 2013, A&A, 558, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Toonen, S., & Nelemans, G. 2013, A&A, 557, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Totani, T., Morokuma, T., Oda, T., Doi, M., & Yasuda, N. 2008, PASJ, 60, 1327 [NASA ADS] [CrossRef] [Google Scholar]
  81. Uenishi, T., Nomoto, K., & Hachisu, I. 2003, ApJ, 595, 1094 [NASA ADS] [CrossRef] [Google Scholar]
  82. Umeda, H., Nomoto, K., Yamaoka, H., & Wanajo, S. 1999, ApJ, 513, 861 [NASA ADS] [CrossRef] [Google Scholar]
  83. van den Heuvel, E. P. J., Bhattacharya, D., Nomoto, K., & Rappaport, S. A. 1992, A&A, 262, 97 [NASA ADS] [Google Scholar]
  84. Wang, B., & Han, Z. 2010, MNRAS, 404, L84 [NASA ADS] [Google Scholar]
  85. Wang, B., & Han, Z. 2012, New Astron. Rev., 56, 122 [NASA ADS] [CrossRef] [Google Scholar]
  86. Wang, B., Li, X.-D., & Han, Z. 2010, MNRAS, 401, 2729 [NASA ADS] [CrossRef] [Google Scholar]
  87. Wang, B., Justham, S., & Han, Z. 2013a, A&A, 559, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Wang, X.-F., Wang, L., Filippenko, A. V., Zhang, T., & Zhao, X. 2013b, Science, 340, 170 [NASA ADS] [CrossRef] [Google Scholar]
  89. Wang, B., Justham, S., Liu, Z., et al. 2014, MNRAS, 445, 2340 [NASA ADS] [CrossRef] [Google Scholar]
  90. Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
  91. Whelan, J., & Iben, I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  92. Yaron, O., Prialnik, D., Shara, M. M., & Kovetz, A. 2005, ApJ, 623, 398 [NASA ADS] [CrossRef] [Google Scholar]
  93. Yoon, S.-C., Langer, N., & Scheithauer, S. 2004, A&A, 425, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Yungelson, L., & Livio, M. 1998, ApJ, 497, 168 [NASA ADS] [CrossRef] [Google Scholar]
  95. Yungelson, L., Livio, M., Truran, J. W., Tutukov, A., & Fedorova, A. 1996, ApJ, 466, 890 [NASA ADS] [CrossRef] [Google Scholar]
  96. Zorotovic, M., Schreiber, M. R., & Gänsicke, B. T. 2011, A&A, 536, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Zuo, Z.-Y., & Li, X.-D. 2014, MNRAS, 442, 1980 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Galactic SN Ia birthrates for seven simulation sets, in which sets 1 and 2 are the two best models from Camacho et al. (2014).

In the text

All Figures

thumbnail Fig. 1

Properties of H-shell burning on the surface of accreting WDs in the plane of WD mass and mass-accretion rate. We compared the critical mass-accretion rate between the super-Eddington wind scenario and the optically thick wind model. The solid lines are taken from Ma et al. (2013), while the dashed lines are adopted from Nomoto et al. (2007).

In the text
thumbnail Fig. 2

Mass-accumulation efficiency of H-shell flashes, ηH, plotted against mass-accretion rate for various initial WD masses. The data points are taken from Ma et al. (2013).

In the text
thumbnail Fig. 3

Representative example of binary evolution calculations, where the binary system is in the weak H-shell flash phase at the moment of the SN explosion. In panel a), the solid, dashed, and dashed-dotted curves present Ṁ2, ṀCO, and MWD, varying with time. In panel b), the evolutionary track of the donor in the Hertzsprung-Russell diagram is shown as a solid curve, and the evolution of orbital period is shown as a dashed-dotted curve. Dotted vertical lines in both panels indicate the position where the WD produces an SN Ia.
In the text
thumbnail Fig. 4

Regions in the logPi−M2i\hbox{$\log P^{\rm i}-M^{\rm i}_2$} plane for WD+MS binaries that ultimately produce SNe Ia for various initial WD masses, where Pi and M2i\hbox{$M^{\rm i}_2$} are the initial orbital period and the initial mass of the MS star.

In the text
thumbnail Fig. 5

Similar to Fig. 4, but for results obtained after adopting 2ṀEdd as the critical mass-accretion rate.
In the text
thumbnail Fig. 6

Evolution of SN Ia birthrates for a constant star-formation rate (SFR = 5.0 M⊙ yr-1) with different BPS simulation sets.
In the text
thumbnail Fig. 7

Delay-time distributions of SNe Ia with different BPS simulation sets. The open circles are taken from Maoz et al. (2011), while the filled squares are adopted from Totani et al. (2008).
In the text
thumbnail Fig. 8

Similar to Fig. 7, but for the case of set 1, where ten random initial seeds are adopted in our simulations.

In the text
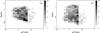thumbnail Fig. 9

Distribution of properties of initial WD+MS systems that can ultimately produce SNe Ia. Panel a) shows the results in the logPi−MWDi\hbox{$\log P^{\rm i}-M^{\rm i}_{\rm WD}$} plane, while panel b) gives the results in the logPi−M2i\hbox{$\log P^{\rm i}-M^{\rm i}_{\rm 2}$} plane, where Pi, MWDi\hbox{$M^{\rm i}_{\rm WD}$} and M2i\hbox{$M^{\rm i}_{\rm 2}$} are the initial orbital period, the initial WD masses, and the initial mass of the MS star. Here, we present the case of set 1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.