| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424922 | |
| Published online | 13 March 2015 | |
White dwarf evolutionary sequences for low-metallicity progenitors: The impact of third dredge-up
1 Grupo de Evolución Estelar y Pulsaciones, Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
e-mail: althaus@fcaglp.unlp.edu.ar
2 IALP – CONICET Centro Científico Tecnológico La Plata, Consejo Nacional de Investigaciones Científicas y Técnicas, Calle 8 No. 1467, B1904CMC La Plata, Buenos Aires, Argentina
3 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild Strasse 1, 85748 Garching, Germany
4 Departament de Física Aplicada, Universitat Politècnica de Catalunya, c/Esteve Terrades 5, 08860 Castelldefels, Spain
5 Institute for Space Studies of Catalonia, c/Gran Capita 2–4, Edif. Nexus 201, 08034 Barcelona, Spain
Received: 5 September 2014
Accepted: 10 February 2015
Context. White dwarfs are nowadays routinely used as reliable cosmochronometers, allowing several stellar populations to be dated.
Aims. We present new white dwarf evolutionary sequences for low-metallicity progenitors. This is motivated by the recent finding that residual H burning in low-mass white dwarfs resulting from Z = 0.0001 progenitors is the main energy source over a significant part of their evolution.
Methods. White dwarf sequences have been derived from full evolutionary calculations that take the entire history of progenitor stars into account, including the thermally pulsing and the post-asymptotic giant branch (AGB) phases.
Results. We show that for progenitor metallicities in the range 0.00003 ≲ Z ≲ 0.001, and in the absence of carbon enrichment from the occurrence of a third dredge-up episode, the resulting H envelope of the low-mass white dwarfs is thick enough to make stable H burning the most important energy source even at low luminosities. This has a significant impact on white dwarf cooling times. This result is independent of the adopted mass-loss rate during the thermally-pulsing and post-AGB phases and in the planetary nebulae stage.
Conclusions. We conclude that in the absence of third dredge-up episodes, a significant part of the evolution of low-mass white dwarfs resulting from low-metallicity progenitors is dominated by stable H burning. Our study opens the possibility of using the observed white dwarf luminosity function of low-metallicity globular clusters to constrain the efficiency of third dredge up episodes during the thermally-pulsing AGB phase of low-metallicity progenitors.
Key words: stars: evolution / stars: interiors / white dwarfs
© ESO, 2015
1. Introduction
White dwarf stars are the most common end point of stellar evolution. These old stellar remnants encode valuable information about the evolutionary history of their progenitors, providing a wealth of information about the physical evolutionary processes of stars and the star formation history and about the characteristics of various stellar populations. Moreover, their structure and evolutionary properties are now well understood (see Fontaine & Brassard 2008; Winget & Kepler 2008; and Althaus et al. 2010b, for specific reviews). As a result, white dwarf cooling ages are currently considered one of the best age indicators for a wide variety of Galactic populations, including open and globular clusters (see Winget et al., 2009; García-Berro et al., 2010; Jeffery et al., 2011; Bono et al., 2013; Hansen et al., 2013, for some recent applications). Consequently, the use of white dwarfs as reliable clocks for dating stellar populations has led to renewed efforts to compute both the full evolutionary models for these stars, taking all the relevant sources and sinks of energy into account, and the evolutionary history of progenitor stars (Renedo et al., 2010; Salaris et al., 2010).
It has been generally accepted that white dwarf evolution is almost insensitive to the initial metal content of progenitor star. This is a consequence of the strong gravity that characterizes white dwarf atmospheres. The effect of strong surface gravity is that metals in the very outer layers of these stars are depleted on relatively short timescales, and thus the cooling rates do not depend on the initial metal content – see, for instance, Salaris et al. (2010). Accordingly, age determinations based on white dwarf cooling times are not very affected by uncertainties in the determination of the metallicity of the parent population. However, the metallicity of the progenitor stars may play some role in determining the core chemical composition of a given white dwarf, and thus could affect the cooling rates. In particular, because of difference in the initial progenitor mass – that could result from the dependence of the initial-to-final-mass relation on the progenitor metallicity – different oxygen profiles for a given white dwarf mass could be expected depending on the progenitor metallicity.
Nevertheless, the impact of progenitor metallicity on white dwarf evolution could be much more relevant than hitherto assumed. Recently, Miller Bertolami et al. (2013) have computed the first white dwarf sequences resulting from the full evolution of progenitor stars with very low metallicity (Z = 0.0001). They find that owing to the low metallicity of the progenitor stars, white dwarfs are born with thicker H envelopes, leading to more intense H-burning shells than with their solar metallicity counterparts. Specifically, they find that for this metallicity and for white dwarf masses lower than ~ 0.6 M⊙, nuclear reactions are the main contributor to the stellar luminosity for luminosities as low as log (L/L⊙) ≃ − 3.2, delaying the white dwarf cooling for significant time intervals. This contrasts with the standard assumption of neglecting residual H burning made in all the existing calculations of white dwarf cooling. This assumption is usually justified because stable H shell burning is expected to be a minor source of energy for stellar luminosities below ~ 100 L⊙. However, H burning never ceases completely, and depending on the mass of the white dwarf and on the precise mass of H left during the previous evolutionary phases – which depends critically on metallicity, see Iben & MacDonald (1986) – it may become a non-negligible energy source for white dwarfs with H atmospheres. As shown by Miller Bertolami et al. (2013), a correct assessment of the role played by residual H burning during the cooling phase requires a detailed calculation of the white dwarf progenitor history, particularly during the thermally pulsing asymptotic giant branch (TP-AGB) phase.
In view of this important finding, we present new white dwarf evolutionary sequences here for a wide range of metallicities that cover the metal content expected in some metal-poor stellar populations, such as the galactic halo or the Galactic population of globular clusters. These sequences are of interest for the cosmochronology of old stellar systems. We compute the full evolution of white dwarf stars by consistently evolving the progenitor stars through all the stellar phases, including the zero age main sequence (ZAMS), the red giant branch (RGB), the core helium flash (whenever it occurs), the stable core helium burning, the AGB phase, and the entire thermally-pulsing and post-AGB phases.
With the aim of determining at which metallicity residual H burning becomes relevant for white dwarf evolution, we considered four progenitor metallicities: Z = 0.001, 0.0005, 0.0001, and 0.00003. To the best of our knowledge, this is the first set of fully evolutionary calculations of white dwarfs resulting from low-metallicity progenitors covering the relevant range of initial main sequence and, correspondingly, white dwarf masses. We emphasize that our complete evolutionary calculations of the history of the progenitors of white dwarfs allowed us to have self-consistent initial white dwarf models. That means that in our sequences the residual masses of the H-rich envelopes and of the helium shells were obtained from evolutionary calculations, instead of using typical values and artificial initial white dwarf models.
The paper is organized as follows. In Sect. 2 we briefly describe our numerical tools and the main ingredients of the evolutionary sequences, while in Sect. 3 we present our evolutionary results in detail. There, we also explore the dependence of the final H content on the mass loss and the treatment of overshooting during the TP-AGB phase. Finally, in Sect. 4 we summarize the main findings of the paper, and we elaborate our conclusions.
2. Numerical setup and input physics
The evolutionary calculations presented in this work were done using the LPCODE stellar evolutionary code (Althaus et al., 2003, 2005, 2012). This is a well-tested and calibrated code that has been amply used in studying different aspects of low-mass star evolution. In particular, it has been employed to compute very accurate and realistic white dwarf models, including the formation and evolution of extremely low-mass white dwarfs (see Miller Bertolami et al. 2008, 2011; Althaus et al. 2013, 2010a; García-Berro et al. 2010; Renedo et al. 2010; Wachlin et al. 2011; and Córsico et al. 2012 and references therein for recent applications).
LPCODE has been tested against another white dwarf evolutionary code, and uncertainties in the white dwarf cooling ages arising from the different numerical implementations of the stellar evolution equations were found to be below 2% (Salaris et al., 2013). A detailed description of the input physics and numerical procedures can be found in these works. Briefly, extra mixing due to diffusive convective overshooting has been considered during the core H and He burning, but not during the TP-AGB. The breathing pulse instability occurring toward the end of core helium burning has been suppressed. The nuclear network accounts explicitly for the following elements: 1H, 2H, 3He, 4He, 7Li, 7Be, 12C, 13C, 14N, 15N, 16O, 17O, 18O, 19F, 20Ne, and 22Ne, together with 34 thermonuclear reaction rates for the pp chains, CNO bi-cycle, and helium burning that are identical to those described in Althaus et al. (2005), with the exception of the reactions 12C+p→ 13N + γ → 13C + e+ + νe and 13C(p, γ)14N, which are taken from Angulo et al. (1999). In addition, the reaction rate 14N(p, γ)15O was taken from Imbriani et al. (2005). Radiative and conductive opacities are taken from OPAL (Iglesias & Rogers, 1996) and from Cassisi et al. (2007), respectively. The equation of state during the main sequence evolution is that of OPAL for H- and helium-rich composition, and of a given metallicity. Updated low-temperature molecular opacities with varying C/O ratios are used, which is relevant for a realistic treatment of progenitor evolution during the TP-AGB phase (Weiss & Ferguson, 2009). For this purpose, we adopted the low-temperature opacities of Ferguson et al. (2005) and presented in Weiss & Ferguson (2009). In LPCODE, molecular opacities are computed by adopting the opacity tables with the correct abundances of the unenhanced metals (e.g., Fe) and C/O ratio. Interpolation is carried out by means of separate cuadratic interpolations in R = ρ/T63, T, and XH, but linearly in NC/NO.
Basic model properties for sequences with Z = 0.00003, 0.0001, 0.0005, and 0.001.
For the white dwarf regime, we use the equation of state of Magni & Mazzitelli (1979) for the low-density regime, while for the high-density regime we consider the equation of state of Segretain et al. (1994), which accounts for all the important contributions for both the liquid and solid phases. We also take the effects of element diffusion due to gravitational settling into account (Isern et al., 1991; García-Berro et al., 2008), chemical and thermal diffusion of 1H, 3He, 4He, 12C, 13C, 14N, and 16O (see Althaus et al. 2003, for details). For the white dwarf regime and for effective temperatures lower than 10 000 K, outer boundary conditions for the evolving models are derived from non-gray model atmospheres (Rohrmann et al., 2012). All relevant energy sources are taken into account in the simulations, including nuclear burning, the release of latent heat of crystallization, as well as the release of the gravitational energy associated with the carbon-oxygen phase separation induced by crystallization. In particular, H burning is considered down to log (L/L⊙) ≈ −4. The inclusion of all these energy sources is done self-consistently and locally coupled to the full set of equations of stellar evolution (see Althaus et al. 2012, for a detailed description).
The full calculation of the evolutionary stages leading to the formation of the white dwarf is mandatory for correctly evaluating the possible role of residual nuclear burning in cool white dwarfs. The present version of LPCODE improves considerably over the one used in Renedo et al. (2010), both in the microphysics and in the numerical treatment of stellar equations and mesh distribution. This has allowed us to follow the progenitor evolution through the entire TP-AGB phase. In fact, in contrast to this previous study, where it was necessary to artificially modify the opacity profile close to the base of the convective envelope to circumvent the numerical difficulties arising at the end of the TP-AGB, in the present work all of the progenitors have been evolved naturally throughout the entire TP-AGB; that is, we have not forced our models to abandon the TP-AGB phase early in order to get realistic white dwarf structures.
In computing our new set of white dwarf sequences, overshooting was disregarded during the TP-AGB phase. Our reason for this choice is that we want to constrain how important residual H burning can be for the evolution of low-mass low-metallicity white dwarfs. As a result, it is expected that the mass of the H-free core of our sequences gradually grows as evolution goes through the TP-AGB. In fact, including overshooting at all convective boundaries during the TP-AGB leads to a strong enhancement of third dredge-up events, which prevent the growth of the hydrogen-free core (Salaris et al., 2009). In the absence of overshooting, third dredge up in low-mass stars is very feeble. As a result, mass loss plays a major role in determining the final mass of the H-free core at the end of the TP-AGB evolution, hence the initial-final mass relation. In this work, mass loss during the RGB was taken from Schröder & Cuntz (2005). For the AGB phase, we again use Schröder & Cuntz (2005) for pulsation periods shorter than 50 days. For longer periods, mass loss is taken as the maximum of the rates of Schröder & Cuntz (2005) and Groenewegen et al. (2009) for oxygen-rich stars, or the maximum of the rates of Schröder & Cuntz (2005) and Groenewegen et al. (1998) for carbon-rich stars. In all of our calculations, mass loss was suppressed after the post-AGB remnants reached log Teff = 4. This choice does not have any consequences for the final mass of the H content that will characterize the white dwarf (see next section).
The initial models for our white dwarf sequences correspond to stellar configurations derived from the full evolutionary calculations of their progenitor stars. Four metallicities for the progenitor stars have been considered: Z = 0.001,0.0005,0,0001, and 0.00003. The initial H abundances, by mass, are 0.752, 0.7535, 0.7547, and 0.7549, respectively. A total of 30 evolutionary sequences were computed self-consistently from the ZAMS, through the giant phase and helium core flash, the thermally-pulsing phase, and the planetary nebulae stage. They encompass a range of initial stellar masses from 0.80 to 2.5 M⊙. The initial mass of the progenitor stars at the ZAMS and the resulting white dwarf mass, together with other quantities that will be discussed below, are listed in Table 1. In all cases, the white dwarf evolution was computed down to log (L/L⊙) = −5.0. Moreover, additional sequences were computed to assess the impact on the final H content owing to mass loss and overshooting (and the occurrence of third dredge-up in low-mass progenitors) during the TP-AGB phase, see Sect. 3.1.
3. Evolutionary results
We see that in the absence of third dredge-up episodes during the AGB phase, most of the evolution of white dwarfs resulting from low-mass (M ≲ 1.25 M⊙) low-metallicity progenitors is dominated by stable H burning. In particular, the occurrence of third dredge-up reduces the final mass H content with which the white dwarfs enter their cooling track, thus weakening the role played by residual H burning (see Sect. 3.1). Unlike the situation of metal-rich progenitors, for which there are direct observational inferences about the occurrence of third dredge-up in AGB stars with stellar masses higher than M ~ 1.5 M⊙ (Lebzelter et al., 2008), the situation for their metal-poor counterparts does not seem to be clear, particularly for the low-mass AGB stars.
Evidence pointing toward the occurrence of third dredge-up in progenitor stars with very low metallicity is provided by observations of carbon-enhanced metal-poor stars (CEMP) stars. However, the origin of the carbon-enhancement for CEMP stars is not fully understood. A possible scenario involves binary pairings of a low-mass star (the one observed today) and a more massive binary companion that can donate carbon in a mass-transfer event. This requires that the more massive star to be in the right mass range to pass through an AGB phase with significant production of carbon (and s-process elements), roughly between 1.3 and 6.0 M⊙ (Carollo et al., 2014). Thus, the CEMP phenomenon is associated with massive and intermediate-mass progenitor stars, and not with the low-mass stars that are relevant for our study. It is worth noting that the third dredge-up evidence suggested by the CEMP stars is in line with our calculations for the Z = 0.0001 progenitors, which predict a strong carbon enrichment even in the absence of overshooting for stellar masses higher than ~ 1.5 M⊙ (Table 1).
This evidence is not conclusive about the occurrence of third dredge-up episodes in low-mass, low-metallicity AGB stars. On the theoretical side, turning on convective overshooting at the base of the convective envelope artificially triggers the occurrence of third dredge-up (Mowlavi, 1999). But the initial-final mass relation of solar metallicity stars suggests that third dredge-up episodes should be less relevant than predicted by evolutionary models that include overshooting at all convective boundaries during the TP-AGB phase (Salaris et al., 2009). This expectation is in line with simple hydrodynamical arguments, suggesting that the penetration of the convective envelope though the H/He transition is expected to be minor. A simple estimate can be done on the basis of the bulk Richardson number (RiB). In particular, Meakin & Arnett (2007) propose that the bulk Richardson number could be used as a dimensionless estimation of the “stiffness” of a stable layer against convection. This dimensionless number could thus be used to constrain the strength of extra-mixing episodes. These authors suggest that high values of RiB should inhibit the occurrence of appreciable extra-mixing. This is in line with terrestrial simulations that show that the entrainment process in the ocean is estimated to operate up to RiB ~ 105 − 106 (Meakin & Arnett, 2007).
To assess the possibility that the outer convection zone penetrates the carbon-rich layers, we have calculated RiB along de H/He transition for our 0.90 M⊙ sequence with Z = 0.0001, following Eq. (2) in Meakin & Arnett (2007). This calculation was performed at the moment when the outer convective zone reaches its maximum depth, during the second thermal pulse (TP) when third dredge-up episodes are expected to occur. We find that the RiB values range from ~ 1 in the H rich zone up to ~ 5 × 105 in the outermost layers, which have been enriched in carbon by the pulse-driven convection zone. Although this does not mean that some extra-mixing should not occur, this last value is high enough to prompt us to suspect it is not entirely correct to assume that extra-mixing occurs through the entire H-He transition layers. On the basis of this hydrodynamical argument, it can therefore not be conclusive about the occurrence of appreciable third dredge-up episodes in these low-mass stars. In view of these results, we believe it to be worthwhile to compute sequences considering and disregarding extra-mixing during the TP-AGB phase and to explore the consequences for white dwarf evolution.
In all of our sequences, evolution starts from the ZAMS and is followed through the stages of stable H and helium core burning – the stage of mass loss during the entire TP-AGB, the domain of the planetary nebulae at high effective temperature, and finally the terminal white dwarf cooling track – until very low surface luminosities are reached. For most of them, evolution has proceeded the helium core flash on the tip of the RGB, and the subsequent recurrent subflashes, before the progenitors reach the stable core helium-burning stage on the horizontal branch. The final white dwarf mass (in solar masses) of these sequences can be found in Table 1, together with the corresponding evolutionary times (in Gyr) for the main relevant stages of progenitor stars. Also listed in this table are the total mass of residual H at the point of maximum effective temperature at the onset of the cooling track, the number of TPs on the AGB, and the final C/O ratio after the end of the TP-AGB phase.
An expected result shown in Table 1 is that the residual H content left by prior evolution decreases with increasing white dwarf masses, a fact that helps to understand the dependence of residual nuclear burning on the stellar mass discussed below. Another trend that can be seen in Table 1 is that the residual H content displays a marked dependence on the metallicity of the progenitor. This is related to the well-known result that low-metallicity progenitors depart from the AGB with more massive envelopes (Iben & MacDonald, 1986), leading to white dwarfs with thicker H envelopes. Indeed, we find that, in general, for a given white dwarf mass, more H content is expected to be left as the metallicity progenitor decreases, the only exception being the sequences with the lowest metallicity (Z = 0.00003). This can be best appreciated in Fig. 1, where the total mass of H (in solar units) obtained in our calculations at the beginning of the cooling branch is shown for Z = 0.0001,0.0005, and 0.001 as a function of the white dwarf stellar mass. In addition, the predictions of Renedo et al. (2010) for Z = 0.001 and Z = 0.01 progenitors are shown. As a result of the more massive H envelopes, residual H burning is expected to become more relevant in low-mass white dwarfs with low-metallicity progenitors ( see later in this section).
We show in Sect. 3.1 that for a given progenitor metallicity, the amount of H with which the remnant will enter the cooling branch is intimately connected with the occurrence of the third dredge-up during the TP-AGB phase. During the third dredge-up, the envelope becomes carbon-enriched as a result of surface convection penetrating carbon-rich deeper layers. In this regard, in Fig. 2 we display the final ratio of carbon to oxygen abundances at the end of the TP-AGB phase, as a function of the white dwarf mass for Z = 0.0001, 0.0005, and 0.001. This figure shows that for lower metallicities, the effect of the third dredge-up on the C/O ratio is pronounced. We note that in our calculations, we did not find any third dredge-up episode except for the two more massive sequences – those with initial ZAMS masses 2.0 and 2.5 M⊙ – with Z = 0.0001 and Z = 0.0005. The occurrence of third dredge-up in these sequences is clear from Fig. 2, where a sudden increase in the final C/O ratio can be seen – at a white dwarf mass of ~ 0.65 M⊙. The third dredge-up reduces the amount of mass of residual H, as inferred from the change in the corresponding curves shown in Fig. 1. Since the role played by nuclear burning during white dwarf evolution is strongly tied to the residual H mass, which is essentially a function of the occurrence of third dredge-up and the metallicity of the progenitor, our derived values for the H envelopes should be considered as upper limits. In fact, as already mentioned, we disregarded overshooting during the TP-AGB phase. In particular, third dredge-up in our simulations is much less efficient in the absence of overshooting. Thus our choice of neglecting overshooting favors the formation of white dwarfs with larger amounts of H (see Sect. 3.1).
 |
Fig. 1 Logarithm of the total mass of H (in solar masses) at the point of maximum effective temperature of the cooling sequence versus the white dwarf mass for Z = 0.0001,0.0005, and 0.001. In addition, we show the predictions of Renedo et al. (2010) for Z = 0.001 and Z = 0.01 progenitors. |
 |
Fig. 2 Ratio of the carbon-to-oxygen abundances at the end of the TP-AGB phase as a function of the white dwarf mass for Z = 0.0001,0.0005, and Z = 0.001 progenitors – solid, dotted, and dashed lines, respectively. In addition, we show with filled and hollow squares the predictions from our low-mass Z = 0.0001 progenitors in the case that overshooting is considered during the TP-AGB phase and the corresponding results of Weiss & Ferguson (2009) for Z = 0.0005 progenitors. |
In connection with this, we mention that the mass of the H that is left on the white dwarf (listed in Table 1) is independent of the occurrence of mass loss during the planetary nebulae stage. As mentioned before, mass loss was suppressed for all our sequences after the post-AGB remnants reach log Teff = 4. To test the impact of additional mass loss on the residual mass of H, we computed the post-AGB evolution of our 0.80 M⊙ sequence again with Z = 0.0005 from this effective temperature, but now consider mass loss during the full planetary nebulae stage, including the hot stages of white dwarf evolution, following the prescription of the mass loss rates for hot central stars of planetary nebulae provided by Bloecker (1995) from the results of Pauldrach et al. (1988). We find that the mass of H with which the white dwarf enters its cooling track is not altered by the occurrence of mass loss during these stages. Mass loss during this phase increases the rate of evolution of the post-AGB remnant (since the H envelope is reduced now by both nuclear burning and mass loss) with the result that the remnant reaches a given effective temperature with the same mass of the H content irrespective of whether mass loss is considered or not.
We would like to point out that the residual masses of H in our Z = 0.001 sequences are somewhat higher than those found in our previous study (Renedo et al., 2010) for the same metallicity (see Fig. 1). This might be due to the several numerical and physical updates in LPCODE. In particular, unlike in our previous study, we have not artificially altered the opacity at the base of the convective envelope in order to get initial white dwarf structures (see Sect. 2). Instead, our sequences were computed self-consistently throughout this stage and during the departure from the AGB.
 |
Fig. 3 Fraction of the total white dwarf luminosity due to H nuclear reactions for the four different metallicities studied in this work. For Z = 0.0001 and Z = 0.0005, residual H burning becomes the main energy source in low-mass white dwarfs, even at low luminosities. |
 |
Fig. 4 Impact of residual nuclear burning on the cooling times of three selected white dwarf sequences resulting from progenitors with Z = 0.0001. The solid line illustrates the evolution in the case in which H burning is taken into account, whereas the dotted line shows the case in which nuclear burning is disregarded. For the 0.53512 M⊙ white dwarf cooling sequence we also show the evolution when diffusion is neglected (dashed line). |
As a result of the more massive H envelopes, residual H burning is expected to become more relevant in white dwarfs with low-metallicity progenitors. This is borne out by Miller Bertolami et al. (2013), who find that for white dwarfs with progenitors of metallicity Z = 0.0001, stable H burning becomes one of the main energy sources of low-mass white dwarfs for substantial periods of time. The calculations performed here show that this is also true even for white dwarfs that result from progenitors with metallicities as high as Z ≈ 0.001. This is inferred from Fig. 3, where we plot the fraction of the total luminosity that results from H burning at different stages of the white – dwarf cooling phase for the four metallicities explored in our work. It is clear that the luminosity of low-mass white dwarfs resulting from progenitors with metallicity in the range 0.0001 ≲ Z ≲ 0.001 is completely dominated by nuclear burning, even at rather low luminosities. Specifically, we note that for white dwarfs with M ≲ 0.6 M⊙, the energy release of H burning is the main energy source at intermediate luminosities (−3.2 ≲ log (L/L⊙) ≲ − 1, or 7800 ≲ Teff(K) ≲ 26 000). In sharp contrast, the role played by residual H burning is much less relevant in the case of white dwarfs resulting from progenitors with Z = 0.00003. At such very low metallicities, all the progenitor sequences we computed experience an H ingestion flash during the first TPs, resulting in a strong carbon enrichment of the outer layers (see Table 1), and in white dwarfs with thin H envelopes that are unable to sustain appreciable nuclear burning. According to our calculations, therefore, progenitors with metallicities lower than Z ~ 0.00003 are not expected to form white dwarfs in which residual H burning is appreciable.
The impact of residual H burning on the cooling times is depicted in Figs. 4−6 for progenitor metallicities of Z = 0.0001, 0.0005, and 0.001, respectively, and for three selected white dwarf sequences. The right-hand panels of each figure display the corresponding delays (in Myr) introduced by nuclear burning. Clearly, nuclear burning leads to substantial delays in the cooling times, as compared with the situation encountered in white dwarfs that result from Solar metallicity progenitors, for which nuclear burning does not play a leading role, and most of the energy release comes from the thermal energy stored in the interior. This is most noticeable for those white dwarfs that result from progenitor stars with metallicity of Z = 0.0001 – (see Miller Bertolami et al., 2013) – but also for white dwarfs resulting from progenitors with larger metallicities (Z = 0.0005). Neglecting the energy released by nuclear burning leads to a marked underestimation of the cooling times, by more than a factor of 2 at intermediate luminosities. Even at log (L/L⊙) ~ − 4, residual H burning leads to an increase in the cooling times of the low-mass white dwarfs by 20 − 40% (see Table 2). Also for more massive white dwarfs, the impact of H burning on cooling times is much less relevant. In the case of progenitors with higher metallicity (Z = 0.001), the delay introduced by H burning is also apparent in the least massive white dwarfs and, as expected from the earlier discussion, more relevant than found in our previous calculations (Renedo et al., 2010) for the same metallicity. Here, H burning increases the cooling times by 10 − 20% at log (L/L⊙) ~ − 4 in the case of low-mass white dwarfs. It is clear that stable nuclear burning in low-mass, low-metallicity white dwarfs can constitute a main energy source, thereby substantially delaying their cooling times at low luminosities.
White dwarf cooling ages for H-burning sequences and their corresponding time delays compared to the sequences in which nuclear burning is neglected.
To assess the influence of element diffusion on H burning, we computed the evolution of the 0.53512 M⊙ white dwarf sequences with Z = 0.0001 again for the extreme situation of neglecting all of the diffusion processes. The resulting cooling time is shown in Fig. 4. Even in this extreme case, substantial delays in the cooling times are expected as a result of H burning.
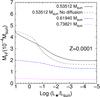 |
Fig. 7 Run of the total H content as a function of luminosity for the 0.53512, 0.61940, and 0.73821 M⊙ cooling sequences (solid, dot-dashed, and dotted lines, respectively). Also shown is the H content for the 0.53512 M⊙ white dwarf sequence when element difussion processes are neglected (dashed line). The metallicity of the progenitor is Z = 0.0001. |
Figure 7 shows the evolution of the mass of H for three selected white dwarf sequences with Z = 0.0001. The mass of the initial H layer decreases – by almost a factor of two – for a period during which H burning supplies most of the surface luminosity of the white dwarf. However, as soon as the mass of the H layer decreases below a certain threshold that depends on the white dwarf mass, the pressure at the bottom of the envelope can no longer support nuclear reactions, and the total H mass of the model reaches a constant value. For comparison purposes, the run of the mass of H for the 0.53512 M⊙ white dwarf sequence when element difussion processes are neglected is also shown in the figure. In the absence of element diffusion, more of the H content of the star is burnt at higher luminosities than in the case where diffusion is allowed to operate.
In Fig. 8 we show the time dependence of the various energy sources and sinks during the white dwarf cooling phase for the 0.53512 M⊙ and the 0.82623 M⊙ sequences. These sequences result, respectively, from progenitor stars with masses 0.85 and 2.5 M⊙ and a metallicity Z = 0.0001. For the more massive sequence, except for the short-lived stages at very high luminosities (not shown in the figure), H burning never represents an appreciable source of energy. This is quite different from the situation for the 0.53512 M⊙ sequence. Here, the H-burning energy release resulting from the proton-proton chain becomes the main source of energy over long periods of time at advanced ages, providing a contribution to the surface luminosity until log t ~ 9.4 that is much greater than is given by the release of gravothermal energy. The impact of proton-proton burning on the resulting cooling curve is apparent. Indeed, toward the end of proton-proton burning phase, there is a change in slope in the cooling curve, until crystallization sets in at the center of the white dwarf and the cooling process slows down (for surface luminosities less than log (L/L⊙) ~ − 4). This is a result of the release of latent heat and gravitational energy caused by carbon-oxygen phase separation. In passing, we note that the contribution of the CNO bi-cycle to the surface luminosity is restricted to the first 106 yr of the white dwarf evolution. However, except at very high luminosities, its contribution is always much smaller than the release of gravothermal energy, which drives evolution during these first stages.
 |
Fig. 8 Time dependence of the various energy sources and sinks for our 0.53512 M⊙ and 0.82623 M⊙ white dwarf sequences resulting from progenitors with Z = 0.0001. It depicts the surface luminosity L⋆ (solid line), the luminosities arising from the proton-proton chain Lpp (dashed line), and from the CNO bi-cycle LCNO (dotted line), the energy loss by neutrino emission Lν (dot dashed line), and the gravothermal (compression plus thermal) energy release Lg (long dotted line). The domain of the main energy source is also indicated. Time is measured in years since the moment when the star reaches the maximum effective temperature. The progenitors masses are 0.85 and 2.5 M⊙. |
As mentioned before, all the white dwarf sequences computed in this work were obtained following the progenitor evolution throughout the entire TP-AGB phase. That is, we did not force our models to abandon this phase early in order to get white dwarf structures. Given that the mass loss adopted is just a rough extrapolation of what is known at higher metallicities, the initial-to-final mass relation offers a good testbed for our sequences. Then, we believe it is worthwhile showing the initial-to-final mass relation resulting from our full evolutionary sequences. This is done in Fig. 9, where our resulting white dwarf masses as a function of the initial mass at ZAMS are compared with the results of Renedo et al. (2010) for progenitors with Z = 0.01 and Z = 0.001, and with the final mass obtained by Weiss & Ferguson (2009) for Z = 0.0005. In addition, we include the mass of the H-free core at the first TP as a function of the initial mass of the progenitor for the case Z = 0.0005. It should be mentioned that Weiss & Ferguson (2009) consider overshooting during the TP-AGB phase, which considerably reduces the growth of the H-free core. Thus, in this case, the final mass is not expected to be very different from the mass of the H-free core at the first TP. With this consideration in mind, it is worth noting the good agreement between our mass of the H-free core at the first TP with the final mass found by Weiss & Ferguson (2009). By comparing our two sequences with Z = 0.0005, it is clear that, in the absence of overshooting in the TP-AGB phase, as assumed in our study, the mass of the H-free core grows considerably during the TP-AGB. In this case, therefore, the final mass will be strongly dependent on the assumed mass-loss rates. This explains the steep slope of the initial-final mass relationship we find for the sequences presented in this study, since lower mass-loss rates are expected at lower metallicities. Nevertheless, it should be emphasized that theoretical initial-to-final mass relationships cannot be accurately predicted, because they depend on two little known processes in the TP-AGB phase, i.e., winds and the occurrence of a third dredge-up episode.
 |
Fig. 9 Theoretical initial-to-final mass relations resulting from our sequences. In addition, we display the results of Renedo et al. (2010) for progenitors with Z = 0.01 and Z = 0.001, the mass of the H free core at the first thermal pulse for our Z = 0.0005 sequences, and the initial-to-final mass relationship of Weiss & Ferguson (2009) for the same metallicity. |
3.1. The importance of mass loss and overshooting
 |
Fig. 10 Logarithm of the total mass of H (in solar units) at the point of maximum effective temperature of the cooling sequence versus the white dwarf mass. The dotted (solid) line shows the predictions from our Z = 0.0001 progenitors when overshooting during the TP-AGB is considered (neglected). In addition, we show the results for the case of an enhanced mass loss rate during the TP-AGB and the following early post-AGB phases (dashed line). |
We have shown that the mass of H that is left on the white dwarf at the beginning of its cooling branch is independent of mass loss occurring during the planetary nebulae stage. Here, we explore the role played by mass loss during the TP-AGB phase in fixing the final H content of the white dwarf, hence the importance of residual H burning. We concentrate on those white dwarf masses for which we find residual H burning to be the main source of white dwarf energy. To this end, we recomputed the full evolution of our 0.80, 0.90, 1.0, and 1.25 M⊙ progenitors with Z = 0.0001 from the first TP on the AGB all the way to the beginning of the white dwarf cooling track, by artificially increasing the mass loss rates by a factor of two. This is done during the entire TP-AGB stage, as well as during the subsequent post-AGB stage. The resulting mass of H at the beginning of the cooling branch predicted by these numerical experiments is displayed in Fig. 10.
These predictions are compared to the results obtained with our standard Z = 0.0001 progenitors with no enhanced mass loss. As expected, increasing the mass-loss rate yields lower white dwarf masses. But for a given white dwarf mass, the final mass of H is the same, irrespective of the adopted mass-loss rate. In fact, the agreement in the relation H mass versus white dwarf mass is surprisingly good. This important experiment shows that the H content with which a white dwarf of a given stellar mass enters its cooling track is independent of the adopted mass loss rates during progenitor evolution. As a result, our prediction that stable nuclear burning is the main source of energy over most of the evolution of low-mass white dwarfs coming from low-metallicity progenitors are valid independently of the rate at which mass is lost during prior evolution.
On the contrary and in view of our previous discussion, the occurrence of third dredge-up during the TP-AGB phase is expected to reduce the final H content and thus the impact of residual nuclear burning. To be more quantitative, we computed some of our sequences again but then allowing overshooting from the beginning of the TP-PAGB phase. It is well known that at low metallicities, overshooting favors the occurrence of a third dredge-up episode also for very low stellar masses (Weiss & Ferguson, 2009). To this end, we follow the evolution of our 0.85, 0.90, 1.0, and 1.25 M⊙ progenitor stars with Z = 0.0001 from the first TP and include diffusive overshooting with the overshooting parameter set to f = 0.015 at each convective boundary: see Renedo et al. (2010); Weiss & Ferguson (2009) for details.
At this point, all these sequences experience appreciable third dredge-up, with the result that the C/O ratio is strongly increased (see Fig. 2). The C/O ratio reaches values of about 3−6, in good agreement with the predictions of Weiss & Ferguson (2009) for Z = 0.0005 progenitors. The carbon enrichment of the envelope by more than three orders of magnitude as a result of a third dredge-up episode eventually leads to a more intense CNO burning, which strongly reduces the final H content of the resulting white dwarf, as can be appreciated in Fig. 10. A reduction by more than a factor of two in the mass of the final H layer is expected if third dredge-up takes place. This strongly reduces the impact of residual H burning during the white dwarf regime.
We conclude that the occurrence of third dredge-up during the TP-AGB evolution of low-mass stars (due, for instance, to the occurrence of overshooting) prevents H burning from being a relevant energy source in cool white dwarfs that result from low-metallicity progenitors. In this sense, since the third dredge-up is strongly reduced in the sequences we presented in this paper (due to our neglect of overshooting), the final H content of our white dwarf sequences and the consequent impact of residual H burning on white dwarf cooling times should be considered as upper limits.
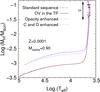 |
Fig. 11 Evolution of the residual H content (in solar units) in terms of the effective temperature for our 0.9 M⊙ progenitor with Z = 0.0001 during the thermally pulsing and post-AGB phases. Our standard sequence is depicted with a dot-dashed line. The sequence including overshooting during the TP-AGB phase is shown with a solid line. Two additional artificial sequences with no overshooting are included: one in which the carbon and oxygen enrichment expected from the third dredge-up is only considered in the envelope opacity computation (dotted line), and another one in which the abundances of carbon and oxygen have been altered according to the predictions of the third dredge-up (see text for details). |
To obtain a better understanding of the impact of overshooting on the final H content, we recomputed the evolution of the 0.9 M⊙ progenitor star with Z = 0.0001 from the first TP, this time neglecting overshooting (hence with no dredge-up), but artificially considering the carbon and oxygen enrichment expected from the third dredge-up only in the envelope opacity. The result is shown in Fig. 11, where the resulting evolution of the residual H content (in solar units) is depicted in terms of the effective temperature during the thermally pulsing and post-AGB phases. Our standard sequence with no overshooting is depicted with the prediction of a similar sequence that includes overshooting during the TP-AGB phase. It is clear from this figure that most of the reduction of the H content that characterizes the sequences with overshooting is not an opacity effect. Another artificial sequence neglecting overshooting was computed for which the abundances of carbon and oxygen in the entire model envelope have been altered according to the predictions expected from the third dredge-up. In doing this, we neglect any other consequence of overshooting on the evolution. Clearly, it is the chemical enrichment of the envelope that is responsible for the thinner H envelopes, not as an induced opacity effect, but rather as an increase in the H burning via CNO.
4. Summary and conclusions
In view of the recent finding that residual H burning in low-mass white dwarfs resulting from Z = 0.0001 progenitors could be the main energy source during most of their evolution (Miller Bertolami et al., 2013), we presented new white dwarf evolutionary sequences resulting from progenitor stars characterized by a wide range of low-metallicity values. These new sequences are thus appropriate for studying low-metallicity stellar populations. We computed the full evolution of white dwarf stars by consistently evolving the progenitor stars through all the stellar phases, including the ZAMS, the RGB, the core helium flash (when it occurs), the stable core helium burning, the AGB phase, and the entire thermally pulsing and post-AGB phases. Four progenitor metallicities have been considered: Z = 0.001, 0.0005, 0.0001, and 0.00003. To the best of our knowledge, this is the first set of fully evolutionary calculations of white dwarfs resulting from low-metallicity progenitors covering the relevant range of initial main sequence and, correspondingly, white dwarf masses. A relevant aspect of our sequences is that the masses of the H-rich envelopes and of the helium shells were obtained from evolutionary calculations, instead of using typical values and artificial, initial white dwarf models. In computing this new set of white dwarf sequences, overshooting was disregarded during the TP-AGB phase. Consequently, third dredge-up is much less efficient than in sequences that include overshooting at all convective boundaries. Independent of the fact that evidence is not completely clear about the possible occurrence of appreciable overshooting during the TP-AGB phase (even more in the low-metallicity regime), our reason for this choice is that we are interested in providing white dwarf sequences for which the residual H burning has its maximum impact on white dwarf cooling times (see below).
We found that in the absence of third dredge-up episodes, most of the evolution of low-mass white dwarfs resulting from low-metallicity progenitors in the range 0.00003 ≲ Z ≲ 0.001 is dominated by stable H burning. Specifically, we find that for white dwarfs with M ≲ 0.6 M⊙ energy released by H burning constitutes the main energy source at intermediate luminosities (−3.2 ≲ log (L/L⊙) ≲ − 1), thus resulting in substantial delays in the cooling times. At intermediate luminosities, residual H burning increases the cooling times by more than a factor of 2, and even at log (L/L⊙) ~ − 4, such delays amount to 20 − 40% in low-mass white dwarfs.
Our finding that stable H burning is a main energy source that could be sustained over a long period of evolution in the low-mass white dwarfs that result from low-metallicity progenitors opens the possibility that this stable burning could have an impact on the pulsational stability properties of these white dwarfs. The existence of low-order g mode destabilized by the ε mechanism in hot H-rich pre-white-dwarf models has recently been reported (Córsico & Althaus, 2014). The assessment of fully nonadiabatic pulsation properties and a stability analysis of our models constitute an important issue, since this could provide the first evidence that ε-destabilized modes could be expected in evolutionary models of cool, standard carbon-oxygen white dwarfs; see Córsico & Althaus (2014) for a recent report of the evidence of ε-destabilized modes in helium-core white dwarfs. However, this question is beyond the scope of the present paper, but will be explored in a near future.
We also showed that our prediction that stable nuclear burning might be the main source of energy over most of evolution of low-mass white dwarfs resulting from low-metallicity progenitors remains valid independently of the rate at which stellar mass is lost during the thermally pulsing and post-AGB phases and during the planetary nebula stage. However, we find that the mass of H of the resulting white dwarfs becomes substantially lower (by a factor of two) as a result of third dredge-up during the TP-AGB phase. In this sense, we find that the carbon enrichment of the progenitor envelope resulting from the third dredge-up prevents H burning from being a relevant energy source in cool white dwarfs that result from low-metallicity progenitors.
According to our simulations, white dwarfs populating low-metallicity globular clusters could be characterized by significant residual H burning, so as to leave some signature on the observed white dwarf luminosity function of such clusters. NGC 6397, a metal-poor ([Fe/H] = −2.1), old globular cluster, whose well-determined white-dwarf luminosity function has been proposed as a tool for constraining white dwarf physics (Winget et al., 2009), is particularly relevant in this context. In particular, this cluster could be used as a testbed for determining the occurrence of stable nuclear burning in their white dwarfs, which in view of the results of our study, could be used in turn to constrain the efficiency of third dredge-up episodes and the ensuing carbon enrichment during the TP-AGB phase of low-metallicity progenitors.
Acknowledgments
We thank Aldo Serenelli for helping us to improve some numerical aspects of the LPCODE evolutionary code. We acknowledge the comments and suggestions of our referee that improved the original version of this paper. M3B is supported by a fellowship for postdoctoral researchers from the Alexander von Humboldt Foundation. Part of this work was supported by AGENCIA through the Programa de Modernización Tecnolǵica BID 1728/OC-AR, by the PIP 112-200801-00940 grant from CONICET, by MCINN grant AYA2011-23102, and by the European Union FEDER funds. This research has made use of NASA Astrophysics Data System.
References
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., et al. 2010a, ApJ, 717, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010b, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Miller Bertolami, M. M. 2012, A&A, 537, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Miller Bertolami, M. M., & Córsico, A. H. 2013, A&A, 557, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Bloecker, T. 1995, A&A, 299, 755 [NASA ADS] [Google Scholar]
- Bono, G., Salaris, M., & Gilmozzi, R. 2013, A&A, 549, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carollo, D., Freeman, K., Beers, T. C., et al. 2014, ApJ, 788, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2014, ApJ, 793, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., et al. 2012, MNRAS, 424, 2792 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Althaus, L. G., Córsico, A. H., & Isern, J. 2008, ApJ, 677, 473 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Groenewegen, M. A. T., Whitelock, P. A., Smith, C. H., & Kerschbaum, F. 1998, MNRAS, 293, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T., Sloan, G. C., Soszyński, I., & Petersen, E. A. 2009, A&A, 506, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, B. M. S., Kalirai, J. S., Anderson, J., et al. 2013, Nature, 500, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & MacDonald, J. 1986, ApJ, 301, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isern, J., Hernanz, M., Mochkovitch, R., & Garcia-Berro, E. 1991, A&A, 241, L29 [NASA ADS] [Google Scholar]
- Jeffery, E. J., von Hippel, T., DeGennaro, S., et al. 2011, ApJ, 730, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Lebzelter, T., Lederer, M. T., Cristallo, S., et al. 2008, A&A, 486, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Unglaub, K., & Weiss, A. 2008, A&A, 491, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Rohrmann, R. D., Granada, A., & Althaus, L. G. 2011, ApJ, 743, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., & García-Berro, E. 2013, ApJ, 775, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Mowlavi, N. 1999, A&A, 344, 617 [NASA ADS] [Google Scholar]
- Pauldrach, A., Puls, J., Kudritzki, R. P., Mendez, R. H., & Heap, S. R. 1988, A&A, 207, 123 [NASA ADS] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rohrmann, R. D., Althaus, L. G., García-Berro, E., Córsico, A. H., & Miller Bertolami, M. M. 2012, A&A, 546, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., Serenelli, A., Weiss, A., & Miller Bertolami, M. 2009, ApJ, 692, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Cassisi, S., Pietrinferni, A., Kowalski, P. M., & Isern, J. 2010, ApJ, 716, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schröder, K.-P., & Cuntz, M. 2005, ApJ, 630, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Segretain, L., Chabrier, G., Hernanz, M., et al. 1994, ApJ, 434, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Wachlin, F. C., Miller Bertolami, M. M., & Althaus, L. G. 2011, A&A, 533, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., & Ferguson, J. W. 2009, A&A, 508, 1343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., Kepler, S. O., Campos, F., et al. 2009, ApJ, 693, L6 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Basic model properties for sequences with Z = 0.00003, 0.0001, 0.0005, and 0.001.
White dwarf cooling ages for H-burning sequences and their corresponding time delays compared to the sequences in which nuclear burning is neglected.
All Figures
 |
Fig. 1 Logarithm of the total mass of H (in solar masses) at the point of maximum effective temperature of the cooling sequence versus the white dwarf mass for Z = 0.0001,0.0005, and 0.001. In addition, we show the predictions of Renedo et al. (2010) for Z = 0.001 and Z = 0.01 progenitors. |
| In the text | |
 |
Fig. 2 Ratio of the carbon-to-oxygen abundances at the end of the TP-AGB phase as a function of the white dwarf mass for Z = 0.0001,0.0005, and Z = 0.001 progenitors – solid, dotted, and dashed lines, respectively. In addition, we show with filled and hollow squares the predictions from our low-mass Z = 0.0001 progenitors in the case that overshooting is considered during the TP-AGB phase and the corresponding results of Weiss & Ferguson (2009) for Z = 0.0005 progenitors. |
| In the text | |
 |
Fig. 3 Fraction of the total white dwarf luminosity due to H nuclear reactions for the four different metallicities studied in this work. For Z = 0.0001 and Z = 0.0005, residual H burning becomes the main energy source in low-mass white dwarfs, even at low luminosities. |
| In the text | |
 |
Fig. 4 Impact of residual nuclear burning on the cooling times of three selected white dwarf sequences resulting from progenitors with Z = 0.0001. The solid line illustrates the evolution in the case in which H burning is taken into account, whereas the dotted line shows the case in which nuclear burning is disregarded. For the 0.53512 M⊙ white dwarf cooling sequence we also show the evolution when diffusion is neglected (dashed line). |
| In the text | |
 |
Fig. 5 Same as Fig. 4 but for the white dwarf sequences of progenitors with Z = 0.0005. |
| In the text | |
 |
Fig. 6 Same as Fig. 4 but for the case of white dwarf progenitors with Z = 0.001. |
| In the text | |
 |
Fig. 7 Run of the total H content as a function of luminosity for the 0.53512, 0.61940, and 0.73821 M⊙ cooling sequences (solid, dot-dashed, and dotted lines, respectively). Also shown is the H content for the 0.53512 M⊙ white dwarf sequence when element difussion processes are neglected (dashed line). The metallicity of the progenitor is Z = 0.0001. |
| In the text | |
 |
Fig. 8 Time dependence of the various energy sources and sinks for our 0.53512 M⊙ and 0.82623 M⊙ white dwarf sequences resulting from progenitors with Z = 0.0001. It depicts the surface luminosity L⋆ (solid line), the luminosities arising from the proton-proton chain Lpp (dashed line), and from the CNO bi-cycle LCNO (dotted line), the energy loss by neutrino emission Lν (dot dashed line), and the gravothermal (compression plus thermal) energy release Lg (long dotted line). The domain of the main energy source is also indicated. Time is measured in years since the moment when the star reaches the maximum effective temperature. The progenitors masses are 0.85 and 2.5 M⊙. |
| In the text | |
 |
Fig. 9 Theoretical initial-to-final mass relations resulting from our sequences. In addition, we display the results of Renedo et al. (2010) for progenitors with Z = 0.01 and Z = 0.001, the mass of the H free core at the first thermal pulse for our Z = 0.0005 sequences, and the initial-to-final mass relationship of Weiss & Ferguson (2009) for the same metallicity. |
| In the text | |
 |
Fig. 10 Logarithm of the total mass of H (in solar units) at the point of maximum effective temperature of the cooling sequence versus the white dwarf mass. The dotted (solid) line shows the predictions from our Z = 0.0001 progenitors when overshooting during the TP-AGB is considered (neglected). In addition, we show the results for the case of an enhanced mass loss rate during the TP-AGB and the following early post-AGB phases (dashed line). |
| In the text | |
 |
Fig. 11 Evolution of the residual H content (in solar units) in terms of the effective temperature for our 0.9 M⊙ progenitor with Z = 0.0001 during the thermally pulsing and post-AGB phases. Our standard sequence is depicted with a dot-dashed line. The sequence including overshooting during the TP-AGB phase is shown with a solid line. Two additional artificial sequences with no overshooting are included: one in which the carbon and oxygen enrichment expected from the third dredge-up is only considered in the envelope opacity computation (dotted line), and another one in which the abundances of carbon and oxygen have been altered according to the predictions of the third dredge-up (see text for details). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


