| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 15 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201424885 | |
| Published online | 17 April 2015 | |
Three-dimensional hydrodynamical CO5BOLD model atmospheres of red giant stars
IV. Oxygen diagnostics in extremely metal-poor red giants with infrared OH lines ⋆,⋆⋆
1
Institute of Theoretical Physics and Astronomy, Vilnius
University,
Goštauto 12,
01108
Vilnius,
Lithuania
e-mail:
vidas.dobrovolskas@tfai.vu.lt
2
Vilnius University Astronomical Observatory,
M. K. Čiurlionio 29,
03100
Vilnius,
Lithuania
3
GEPI, Observatoire de Paris, CNRS, Université Paris
Diderot, Place Jules
Janssen, 92190
Meudon,
France
4
Landessternwarte – Zentrum für Astronomie der Universität
Heidelberg, Königstuhl
12, 69117
Heidelberg,
Germany
5
Leibniz-Institut für Astrophysik Potsdam,
An der Sternwarte 16,
14482
Potsdam,
Germany
Received: 30 August 2014
Accepted: 26 January 2015
Context. Although oxygen is an important tracer of Galactic chemical evolution, measurements of its abundance in the atmospheres of the oldest Galactic stars are still scarce and rather imprecise. This is mainly because only a few spectral lines are available for the abundance diagnostics. At the lowest end of the metallicity scale, oxygen can only be measured in giant stars and in most of cases such measurements rely on a single forbidden [O i] 630 nm line that is very weak and frequently blended with telluric lines. Although molecular OH lines located in the ultraviolet and infrared could also be used for the diagnostics, oxygen abundances obtained from the OH lines and the [O i] 630 nm line are usually discrepant to a level of ~ 0.3−0.4 dex.
Aims. We study the influence of convection on the formation of the infrared (IR) OH lines and the forbidden [O i] 630 nm line in the atmospheres of extremely metal-poor (EMP) red giant stars. Our ultimate goal is to clarify whether a realistic treatment of convection with state-of-the-art 3D hydrodynamical model atmospheres may help to bring the oxygen abundances obtained using the two indicators into closer agreement.
Methods. We used high-resolution (R = 50 000) and high signal-to-noise ratio (S/N ≈ 200−600) spectra of four EMP red giant stars obtained with the VLT CRIRES spectrograph. For each EMP star, 4–14 IR OH vibrational-rotational lines located in the spectral range of 1514−1548 and 1595−1632 nm were used to determine oxygen abundances by employing standard 1D local thermodynamic equilibrium (LTE) abundance analysis methodology. We then corrected the 1D LTE abundances obtained from each individual OH line for the 3D hydrodynamical effects, which was done by applying 3D–1D LTE abundance corrections that were determined using 3D hydrodynamical CO5BOLD and 1D hydrostatic LHD model atmospheres.
Results. We find that the influence of convection on the formation of [O i] 630 nm line in the atmospheres of EMP giants studied here is minor, which leads to very small 3D–1D abundance corrections (Δ3D−1D ≤ −0.01 dex). On the contrary, IR OH lines are strongly affected by convection and thus the abundance corrections for these lines are significant, Δ3D−1D ≈ −0.2···−0.3 dex. These abundance corrections do indeed bring the 1D LTE oxygen abundances of EMP red giants obtained using IR OH lines into better agreement with those determined from the [O i] 630 nm line. Since in the EMP red giants IR OH lines are typically at least a factor of two stronger than the [O i] line, OH lines may be useful indicators of oxygen abundances in the EMP stars, provided that the analysis is based on 3D hydrodynamical model atmospheres.
Key words: stars: Population II / stars: late-type / stars: atmospheres / stars: abundances / techniques: spectroscopic / convection
Based on observations obtained at the European Southern Observatory (ESO) Very Large Telescope (VLT) at Paranal Observatory, Chile (observing programme 089.D-0079).
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Oxygen is the most abundant element in the Universe, after hydrogen and helium, and is the main product of the Type II SNe (see e.g. Arnett 1996, and references therein). Massive stars have lifetimes of the order of 106 to 107 years and end their lives as supernovae, releasing oxygen into the interstellar medium (see e.g. Matteucci 2012, and references therein). As a first approximation it may be expected that the oxygen abundance in extremely metal-poor (EMP) stars correlates with their age, the most oxygen-poor stars being the oldest. On closer consideration it becomes clear that the oxygen abundance at any given time also depends on the star formation rate. In a complex system, like our Galaxy, that may host populations of different origins (perhaps some accreted by dwarf satellite galaxies) the evolution of the O/Fe ratio with time depends on the details of the chemical evolution of the different populations. The abundance ratio of oxygen to other elements, and in particular to iron, places strong constraints on proposed scenarios of Galactic chemical evolution. The precise knowledge of oxygen abundances in the oldest Galactic populations is important since it allows us to discriminate among different models (see Matteucci 2012, Chap. 5.3, for a discussion).
In spite of these virtues, the oxygen abundance is actually very difficult to measure in the metal-poor stellar atmospheres: the only indicators available in the EMP stars are (i) the forbidden [O i] line at 630 nm for giants; (ii) the permitted O i IR triplet for dwarfs (777.2−777.5 nm); and (iii) OH lines in the UV and IR, for both giants and dwarfs. Unfortunately, these different indicators often provide discrepant oxygen abundances, which may be due to non-local thermodynamic equilibrium (NLTE) effects (especially for the IR triplet), 3D hydrodynamical effects (especially for the OH lines but also for the triplet), incorrectly determined atmospheric parameters (e.g. [O i] is very sensitive to the surface gravity; see e.g. Cayrel et al. 2001; García Pérez et al. 2006), and so on. Consequently, reliable oxygen abundances of the EMP stars are scarce: the number of objects in which they have been measured so far is small while the measurements themselves are frequently not sufficiently reliable. This has led different groups to claim the existence of different trends of [O / Fe] with decreasing metallicity (see e.g. Boesgaard et al. 1999; Israelian et al. 2001; Akerman et al. 2004), which makes discriminating between the various proposed scenarios of Galactic oxygen evolution very difficult. Clearly, such a situation is unsatisfactory and calls for the re-assessment of oxygen abundances in EMP stars.
It should be noted that oxygen abundances in the EMP giants are nearly always obtained from the measurements of a single forbidden [O i] 630 nm line. One reason why OH lines have rarely been used for the abundance determinations so far (Meléndez et al. 2001; Meléndez & Barbuy 2002; Barbuy et al. 2003) is that the oxygen abundances obtained from these lines are significantly different from those determined using the [O i] line (e.g. Barbuy et al. 2003). Part of the problem may be related to the [O i] line measurements, because this line is very weak and often blended with telluric lines. On the other hand, molecular lines may be prone to 3D hydrodynamical effects, such as horizontal temperature fluctuations, which may lead to substantial differences in the oxygen abundances derived with the 3D hydrodynamical and classical 1D hydrostatic models (see e.g. Collet et al. 2007; Dobrovolskas et al. 2013). It may thus be reasonable to anticipate that oxygen abundances obtained from OH lines and those determined using the [O i] line could be brought closer if these effects are properly taken into account in the model atmospheres used in the abundance determination. If this were proved to be true, OH lines could be used as independent valuable indicator of the oxygen abundance, with the advantage that (i) OH lines are numerous in the infrared and thus one would not need to rely on a single line for measuring the oxygen abundance, as in the case with the forbidden [O i] 630 nm line; and (ii) infrared (IR) OH lines are at least a factor of 2 stronger than the [O i] 630 nm line is, which makes them easier to measure and may lead to a better accuracy in the determined oxygen abundances.
In this pilot study we therefore investigate whether such considerations are indeed valid in the case of EMP red giant stars. For this purpose, we used high-resolution and high signal-to-noise spectra of four EMP giants obtained with the CRIRES spectrograph at the VLT UT1 telescope to determine 1D LTE oxygen abundances using IR OH lines. Then, 3D hydrodynamical CO5BOLD (Freytag et al. 2012) and 1D hydrostatic LHD (Caffau & Ludwig 2007) model atmospheres were used in order to assess the role and influence of convection on the formation of IR OH lines and the forbidden [O i] line, as well as to determine the 3D-corrected abundances of oxygen from IR OH lines. Finally, we discuss the possible role of various other effects that may influence the formation of IR OH lines and that may need to be taken into account in the abundance determinations using IR OH lines.
2. Methodology
2.1. Observations and data reduction
Since IR OH lines are very weak in EMP giants, one needs to have access to spectra with very high S/N in order to obtain reliable oxygen abundances. For this reason, we limited our target list to objects with V< 12.0; these are the brightest EMP giants in the list of Cayrel et al. (2004). This has allowed us to keep the observing time request within reasonable limits even in the case of the faintest star, CS 31082-001; we note that except for HD 122563, no EMP giants have been observed with CRIRES so far. The list of our EMP targets is provided in Table 1.
High-resolution H-band near-infrared spectra of the four EMP giants were obtained in service mode with the CRIRES spectrograph (Käufl et al. 2004) located at the VLT UT1 telescope (programme ID 089.D-0079(A), PI: A. Kučinskas). We used the entrance slit width of 0.4 arcsec for our observations and did not use the adaptive optics system. The spectra were acquired in ABBA nodding pattern for dark current and sky emission removal, using two CRIRES settings: order 37 with the central wavelength of 1536.4 nm and a spectral range of 1513.4−1548.6 nm; and order 35 with the central wavelength of 1619.4 nm and a spectral range of 1594.9−1632.5 nm. The targets were observed with a spectral resolution of R = 50 000 and signal-to-noise ratio per pixel S/N ≈ 200−600. Standard steps involved in the reduction of the raw spectra (bad pixel correction, detector non-linearity correction, flat-fielding, and wavelength calibration) were performed using the CRIRES pipeline (v.2.3.1) in the command-line (EsoRex) mode.
Unfortunately, the wavelength calibration solution provided by the CRIRES pipeline had systematic shifts which made spectral line identification difficult. Therefore, we performed a custom wavelength calibration using telluric lines present in the observed spectral range. For this purpose, we computed the synthetic telluric spectrum using the TAPAS online service1 (Bertaux et al. 2014) for the conditions matching those of our observations (location, date, time, and air-mass). We did not attempt to clean stellar spectra from the telluric lines, thus for further spectroscopic analysis we used only those OH lines which were free from telluric contamination. In fact, we observed a telluric star HD 24388, but because of a significantly lower S/N this spectrum was not used to correct the target star spectra for the telluric features. Instead, we chose the synthetic telluric spectrum computed using TAPAS to identify telluric lines in our CRIRES spectra and to avoid them in further abundance analysis. Continuum normalization of the observed CRIRES spectra was made using the DECH20T package (Galazutdinov 1992).
EMP giants observed with CRIRES.
2.2. Model atmospheres
Three types of model atmospheres were employed in this study. First, 1D LTE oxygen abundances were determined by using model atmospheres computed with the ATLAS9 code (Kurucz 1993). We used the ATLAS9 version that was ported to Linux by Sbordone et al. (2004) and Sbordone (2005). The models were calculated using opacity distribution functions (ODFNEW) from Castelli et al. (2003); the latter were computed with the microturbulence velocity of ξ = 2 km s-1. All ATLAS9 model atmospheres were calculated using the mixing length parameter αMLT = 1.25, with overshooting switched off.
In addition, 3D hydrodynamical and 1D hydrostatic model atmospheres were used for computing 3D–1D abundance corrections (see Sect. 3.2). For this purpose we employed a single 3D hydrodynamical model atmosphere computed using the CO5BOLD model atmosphere package (Freytag et al. 2012) with the following atmospheric parameters: Teff = 4595 K,log g = 1.6,[M / H] = −2.5 (Klevas et al., in prep.). Our choice was determined by the fact that 3D hydrodynamical models are rather expensive to compute and thus they are not yet available for all combinations of atmospheric parameters. Nevertheless, atmospheric parameters of this particular model atmosphere are sufficiently similar to those of EMP giants studied here: even in the most extreme cases the differences do not exceed ΔTeff = 230 K, Δlog g = 0.3, and Δ[M / H] = 0.5, while generally they are even smaller (see Table 1).
The 3D hydrodynamical model atmosphere was computed in Cartesian geometry with a spatial resolution of 220 × 220 × 280 cells in the x,y,z directions, respectively, which corresponds to spatial dimensions of 3.85 × 3.85 × 2.21 Gm. The horizontal size of the model was large enough to accommodate ≈10 granules which allowed convective dynamics to be reliably captured in the stellar atmosphere (see Collet et al. 2007; Ludwig & Kučinskas 2012; Kučinskas et al. 2013). We used opacities from the MARCS model atmosphere package, which – in order to make the model computations faster – were grouped into six opacity bins using opacity binning (Nordlund 1982; Ludwig 1992; Ludwig et al. 1994; Vögler et al. 2004). Solar chemical composition from Grevesse & Sauval (1998) with α-element enhancement of +0.4 dex was used in the model calculations. For CNO elements, we used solar values of A(C) = 8.41, A(N) = 7.8, and A(O) = 8.66 taken from Asplund et al. (2005), which were then scaled down to the metallicity of our 3D hydrodynamical model atmosphere with α-element enhancement of +0.4 dex.
In order to speed up the 3D spectral line synthesis calculations, we selected 20 3D model structures computed at different instants in time (snapshots). When making the snapshot selection we tried to ensure that the average properties of the selected snapshot subsample would remain similar to the average properties of the full 3D model simulation run (see e.g. Kučinskas et al. 2013, for the details on the snapshot selection procedure). This snapshot subsample was used in subsequent 3D spectral synthesis computations.
The 20-snapshot ensemble was also used to compute average ⟨3D⟩ model, which was obtained by averaging the 3D structures in the 20-snapshot subsample on surfaces of equal optical depth. As has been already discussed in our previous studies, such average ⟨3D⟩ models are useful in evaluating the role of horizontal temperature fluctuations in the spectral line formation. Since the average ⟨3D⟩ models do not contain information about the horizontal fluctuations of thermodynamic properties, the 3D–⟨3D⟩ differences provide important information about the role of these fluctuations in the spectral line formation (see e.g. Dobrovolskas et al. 2013; Kučinskas et al. 2013).
The 1D hydrostatic model atmospheres that we used in the evaluation of 3D–1D abundance corrections were computed using LHD model atmosphere package (Caffau et al. 2008). It is important to note that 3D hydrodynamical and 1D hydrostatic LHD model atmospheres employed in the computation of abundance corrections shared identical atmospheric parameters, chemical composition, opacities, and equation of state. This allowed us to make a strictly differential comparison and to estimate the impact of convection on the formation of spectral lines. Therefore, we used the (differential) 3D–1D abundance corrections obtained in this way to correct the abundances determined using the ATLAS9 hydrostatic model atmosphere computed with different opacities. The 1D LHD models were calculated with the mixing-length parameter αMLT = 1.0.
Oxygen abundances in EMP giants.
We note that effects of sphericity may in fact affect the structure of the model atmosphere, both in 1D (see e.g. Heiter & Eriksson 2006) and, possibly, in 3D as well. To assess the size of these effects in 1D, we performed a comparison of a spherically symmetric and a plane-parallel model atmospheres with Teff = 4500 K,log g = 1.5,[M / H] = −2.5. The choice was dictated by the available models, and in fact the spherical model was a MARCS model, the plane-parallel an ATLAS9 model. The spherical model had a radius of 29 R⊙ and an atmospheric extension of 0.5 R⊙. We synthesized a few typical OH lines and the [O i] line with Linfor3D, under the assumption of Cartesian geometry. Despite this approximation, according to Heiter & Eriksson (2006), the main effect should be captured by this procedure. We found a slight strengthening of the [O i] line (≈0.01 dex), and a modest strengthening of the OH lines (≈0.06 dex) in the spherical versus the plane-parallel model. From this we conclude that sphericity effects are indeed present but on a level significantly smaller than the 3D effects.
Unfortunately, we are currently not able to assess the size of sphericity effects on the 3D hydrodynamical model structures because the computation of spherical 3D hydrodynamical CO5BOLD models is not yet feasible. Nevertheless, we do not expect that sphericity effects play a major role for the 3D–1D abundance corrections discussed here since the modest extension of the atmosphere is unlikely to change the granular dynamics noticeably. The overall effect of the geometry should largely cancel out because of the differential nature of the 3D–1D corrections.
3. Results
3.1. 1D LTE oxygen abundances
To determine oxygen abundances in the target EMP giants, we used infrared OH vibrational-rotational lines (X2Π) from the first-overtone sequence (Δv = 2) located between 1514−1548 and 1595−1632 nm (see Table A.1 and Figs. B.1−B.4). We note that the spin-orbit interaction gives rise to two spin-split substates: 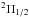 and
and 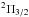 . All the lines that we consider are from the P-branch (ΔJ = −1), the rotational levels are subject to Λ-doubling, i.e. splitting that is due to perturbation by the rotational levels of other electronic states (see Coxon & Foster 1982). The equivalent widths of the observed lines were measured using the splot task in IRAF2 and are provided in Table A.1. Although some of the OH lines used in the abundance determination are contaminated by telluric lines, these telluric lines are in fact very weak. Therefore, we did not correct for their influence when measuring the equivalent widths of OH lines. We note that all observed targets have known [O i] line strengths, as well as oxygen abundances determined using this line (provided in Table 2). As expected, in most cases the IR OH lines are significantly stronger than the forbidden [O i] line at 630 nm.
. All the lines that we consider are from the P-branch (ΔJ = −1), the rotational levels are subject to Λ-doubling, i.e. splitting that is due to perturbation by the rotational levels of other electronic states (see Coxon & Foster 1982). The equivalent widths of the observed lines were measured using the splot task in IRAF2 and are provided in Table A.1. Although some of the OH lines used in the abundance determination are contaminated by telluric lines, these telluric lines are in fact very weak. Therefore, we did not correct for their influence when measuring the equivalent widths of OH lines. We note that all observed targets have known [O i] line strengths, as well as oxygen abundances determined using this line (provided in Table 2). As expected, in most cases the IR OH lines are significantly stronger than the forbidden [O i] line at 630 nm.
We also note that although there are CN lines in the spectral range investigated in this study, they are very weak (≤0.05% depth from continuum) and their influence on the oxygen abundance determination is negligible, even in cases where they blend with OH lines. All the stars investigated in this study have a normal or low carbon abundance of [C/Fe] < 0.2 (Takeda & Takada-Hidai 2013), which leads to very weak CN lines in their IR spectra.
Oxygen 1D LTE abundances were determined using the curve-of-growth method, employing ATLAS9 model atmospheres computed as described in Sect. 2.2 above. The ATLAS9 models were calculated using the atmospheric parameters of the individual EMP giants that were taken from the literature and are provided in Table 1. Synthetic spectra used in the abundance determination were computed using the Linux version of the SYNTHE spectral synthesis package (Sbordone et al. 2004; Sbordone 2005). We then measured the equivalent widths of the OH lines in the synthetic spectra using the splot task in IRAF, i.e. using the same methodology as for the observed lines. Finally, 1D LTE oxygen abundances were determined by interpolating between the curves of growth at the equivalent widths of IR OH lines that we measured in each EMP giant (Table 2).
We estimate that the uncertainty in the determined oxygen abundance arising due to the uncertainty in the continuum level determination (which we estimate to be ± 0.2 %) is ± 0.06 dex. The uncertainty in the measured oxygen abundance provided in Table 2 is a square root of the sum of (i) the dispersion due to line-to-line variations of the determined oxygen abundance for each EMP star and (ii) the squared uncertainty due to continuum placement.
Many OH lines studied here form from transitions that involve rotational levels which, because of perturbations by other electronic states, are split into two sub-levels (Λ-doubling). Therefore, the two lines arising because of such transitions should give identical oxygen abundances. Since in reality this, apparently, is not the case, the difference between abundances obtained from the two individual components may provide additional constraints on the size of the uncertainties in the determined oxygen abundances. In our case, we find that the largest difference in the oxygen abundance obtained from two lambda-doubling components is ~0.12 dex, which is comparable with the uncertainties provided in Table 2.
3.2. 3D–1D abundance corrections and 3D LTE oxygen abundances
The 3D LTE abundances of oxygen were obtained by using 3D–1D abundance corrections. The 3D–1D abundance correction, Δ3D−1D = A(Xi)3D − A(Xi)1D, is the difference in the abundance of element Xi that would be obtained at a fixed equivalent width of a given spectral line with 3D hydrodynamical and 1D hydrostatic model atmospheres, respectively. In this work, abundance corrections were obtained using the curves of growth computed with 3D hydrodynamical CO5BOLD and 1D hydrostatic LHD model atmospheres. Synthetic spectral line profiles were calculated under the assumption of LTE in 3D and 1D, in both cases using the Linfor3D3 spectral synthesis package. Abundance corrections were then computed by measuring the difference between the curves of growth obtained with the 3D hydrodynamical and 1D hydrostatic model atmospheres, respectively.
The 3D–1D abundance corrections were determined for all IR OH lines used in this work, as well as for the forbidden [O i] 630 nm line, using the line parameters provided in Table A.1 and Tables B.1−B.4. Apart from Δ3D−1D correction, we also computed two additional corrections, Δ3D − ⟨ 3D ⟩ = A(Xi)3D − A(Xi)⟨ 3D ⟩, and Δ⟨ 3D ⟩ − 1D = A(Xi)⟨ 3D ⟩ − A(Xi)1D. The former is useful in assessing the importance of horizontal fluctuations of thermodynamic and hydrodynamical quantities in 3D hydrodynamical model atmospheres, while the latter allows the role of differences to be estimated between the temperature profiles in the average ⟨3D⟩ and 1D model atmospheres (see Sect. 4). Abundance corrections for IR OH lines used in this work with all EMP giants are provided in Tables B.1–B.4. In these tables we also provide abundance corrections for the forbidden [O i] 630 nm line.
 |
Fig. 1 3D LTE oxygen abundance in HD 122563, HD 186478, BD − 18:5550, and CS 31082-001 (top to bottom), as determined from IR OH lines, shown as the function of reduced equivalent width. |
 |
Fig. 2 3D LTE oxygen abundance in HD 122563, HD 186478, BD − 18:5550, and CS 31082-001 (top to bottom), as determined from IR OH lines, shown as the function of excitation potential. |
 |
Fig. 3 Top: temperature stratifications in the 3D hydrodynamical (grey scales indicating the temperature probability density), average ⟨3D⟩ (solid red line), and 1D LHD (dashed red line) model atmospheres computed with Teff = 4600 K,log g = 1.6,[M / H] = −2.5. Horizontal bars show the optical depth intervals where 90% of the OH line (λ = 1605.5 nm,χ = 0.48 eV) and [O i] line (λ = 630.0 nm,χ = 0.00 eV) equivalent width is formed (i.e. 5% to 95%): black and dashed blue bars correspond to the line forming regions in the full 3D and 1D model atmospheres (the equivalent widths of OH and [O i] lines are 1.6 pm and 0.4 pm). Bottom: root mean square (rms) value of horizontal temperature fluctuations, ΔTrms, in the 3D model (black line) and temperature difference between the average ⟨3D⟩ and 1D models (dashed blue line). |
 |
Fig. 4 Oxygen-to-iron ratios in Galactic EMP stars plotted versus [Fe / H] ratio. Abundances of EMP giants studied here are marked by triangles: open red triangles – oxygen abundances in the programme stars determined determined in this work with classical 1D model atmospheres; filled red triangles – oxygen abundances corrected for 3D hydrodynamical effects. Solid grey circles show oxygen abundances in red giants, subgiants, and main sequence stars determined using the forbidden [O i] 630 nm line (Gratton & Ortolani 1986; Barbuy & Erdelyi-Mendes 1989; Kraft et al. 1992; Barbuy 1988; Sneden et al. 1991; Fulbright & Kraft 1999; Cayrel et al. 2001; Cowan et al. 2002; Cayrel et al. 2004). Black triangles highlight oxygen abundances determined from [O i] 630 nm line in Cayrel et al. (2004) for the same stars as studied here. The solid line is the evolutionary model of the oxygen abundance from François et al. (2004). We note that [O i] abundances from Cayrel et al. (2004) and the theoretical model from François et al. (2004) were shifted to the reference scale used in our study where solar oxygen abundance is A(O) = 8.66. |
The 3D LTE oxygen abundances were obtained by adding Δ3D−1D correction to 1D LTE oxygen abundances obtained in Sect. 3.1 above. Although we are clearly aware of the many limitations of such approach (see Sect. 4 for discussion), we nevertheless think that the 3D-corrected oxygen abundances, when compared to those derived in 1D LTE, may provide important qualitative information for the assessment of the role of convection in the spectral line formation taking place in the atmospheres of EMP giants. The obtained 3D LTE abundances are listed in Table 2 for all EMP giants studied here. The obtained abundances are plotted in Fig. 1 versus the line reduced equivalent width, log (EW/λ), and in Fig. 2 versus the line excitation potential, χ, for all four EMP stars studied here.
We point out that our 3D–1D oxygen abundance corrections for different programme stars were computed using a single 3D hydrodynamical model atmosphere, whereas the atmospheric parameters of the programme stars differ by up to + 230 K and − 0.3 dex in Teff and log g with respect to those of the 3D model atmosphere. With the 1D ATLAS9 models, this would amount to differences in the determined oxygen abundance of up to + 0.65 dex and + 0.12 dex, respectively. These numbers are very similar to those obtained by Barbuy et al. (2003). Unfortunately, our 3D hydrodynamical model grid is too sparse to estimate the size of temperature and gravity sensitivity of the 3D–1D abundance corrections. Nevertheless, our crude estimate is that an increase in the effective temperature by + 230 K (from Teff = 4600 K) would change the full Δ3D−1D abundance correction by − 0.06···−0.08 dex (depending on the particular OH line).
The OH lines investigated in this work are weak and situated on the linear part of the curve of growth. It makes the spectral lines under consideration insensitive to the choice of the microturbulence velocity value. Changing the microturbulence velocity by 1 km s-1 from the values listed in Table 1 would change 3D–1D abundance correction and the average oxygen abundance by less than 0.01 dex.
4. Discussion
Abundance corrections provided in Tables B.1–B.4 clearly show that horizontal temperature fluctuations caused by convective motions in the stellar atmosphere have significantly larger impact on the strengths of IR OH lines than the influence of the different temperature stratifications in the average ⟨3D⟩ and 1D model atmospheres. This is indicated by the different size of Δ3D− ⟨ 3D ⟩ and Δ⟨ 3D ⟩ −1D abundance corrections; the former is always larger than the latter (i.e. in absolute value). The physical reasons behind such behaviour are in fact rather obvious. As can be seen in Fig. 3, horizontal temperature fluctuations (as measured by 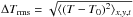 , where ⟨ . ⟩ x,y,t denotes temporal and horizontal averaging on surfaces of equal optical depth, while T0 = ⟨ T ⟩ x,y,t, is the depth-dependent average temperature) become increasingly larger in the outer atmosphere, reaching ΔTrms ≈ 800 K at log τRoss ≈ −5. Since IR OH lines form rather high in the atmosphere, this leads to large non-linear horizontal variations of OH number densities and, thus, line opacities in the line forming regions. The result is that IR OH lines become stronger in 3D, which in turn leads to negative (and relatively large) Δ3D− ⟨ 3D ⟩ abundance corrections. On the other hand, the temperature difference between ⟨ 3D ⟩ and 1D is small (and mostly positive) at all optical depths, which results in weaker lines in ⟨3D⟩ and, thus, small (and positive) Δ⟨ 3D ⟩ −1D corrections.
, where ⟨ . ⟩ x,y,t denotes temporal and horizontal averaging on surfaces of equal optical depth, while T0 = ⟨ T ⟩ x,y,t, is the depth-dependent average temperature) become increasingly larger in the outer atmosphere, reaching ΔTrms ≈ 800 K at log τRoss ≈ −5. Since IR OH lines form rather high in the atmosphere, this leads to large non-linear horizontal variations of OH number densities and, thus, line opacities in the line forming regions. The result is that IR OH lines become stronger in 3D, which in turn leads to negative (and relatively large) Δ3D− ⟨ 3D ⟩ abundance corrections. On the other hand, the temperature difference between ⟨ 3D ⟩ and 1D is small (and mostly positive) at all optical depths, which results in weaker lines in ⟨3D⟩ and, thus, small (and positive) Δ⟨ 3D ⟩ −1D corrections.
In contrast, the influence of convection on the formation of the [O i] oxygen line at 630 nm is very small. This is in line with our earlier findings (see e.g. Dobrovolskas et al. 2013) and is quite easily understood. Neutral oxygen is a majority species in the regions where the [O i] 630 nm line forms, and because of its high ionization potential its abundance is insensitive to temperature fluctuations. At the same time, differences between the T profiles in the average ⟨3D⟩ and 1D models in the line formation regions are small (Fig. 3). This results in small Δ3D− ⟨ 3D ⟩ and Δ⟨ 3D ⟩ −1D abundance corrections, and thus, in small total correction, Δ3D−1D. It is important to mention in this respect that the [O i] line at 630 nm is equally insensitive to NLTE effects (e.g. Asplund 2005, and references therein). One may therefore make a relatively safe assumption that 1D LTE abundances obtained using the [O i] 630 nm line are essentially unaffected by the 3D and NLTE effects, and may thus serve as an important reference point for validating oxygen abundances obtained from other lines. In this respect, we find it reassuring that in our EMP giants the 3D LTE oxygen abundances obtained from IR OH lines agree well with the abundances determined from the forbidden line (Table 2, Fig. 4).
We also find that measuring the IR OH lines in metal-poor giants is feasible at a resolution of 50 000, provided a high S/N of a few hundred can be obtained. The lines are sufficiently numerous so that a few of them are always likely to be free from contamination of telluric lines. In this respect the synthetic spectra of the terrestrial atmosphere computed by TAPAS (Bertaux et al. 2014) are precious for identifying the contaminated lines. In the present study we had enough clean lines and thus we felt it was not necessary to attempt to subtract the telluric components. Nevertheless, the fidelity of the TAPAS spectra is high enough so that subtraction of the telluric lines may be envisaged in cases in which a use of a larger number of lines is desirable.
Although our modelling of the formation of these lines is not entirely satisfactory, as can be deduced from the existence of slight trends of abundance with equivalent width and excitation potential shown in Figs. 1 and 2, respectively, we believe that the use of 3D model-atmospheres improves the modelling. We arrive at this conclusion by noting that on average 1D LTE oxygen abundances from the IR OH lines are obviously too high with respect to what would be expected for the EMP stars in this [Fe / H] range4. On the other hand, 3D LTE abundances obtained from OH lines agree significantly better with the measurements obtained from [O i] line than the 1D LTE estimates do (Fig. 4).
We note that similar trends of oxygen abundance with equivalent width were also noticed in the investigations of Meléndez & Barbuy (2002) and Barbuy et al. (2003) and they remain unexplained. We also investigated if the determined oxygen abundances depend on quantum number J, but could find no clear correlation. It is encouraging that, ignoring the trends, the line-to-line scatter of the abundances derived from the different lines is small enough so that the mean can be considered a reasonable estimate of the oxygen abundance in a given star.
One can conclude that there are hints of a slight dependence of abundance on excitation potential in the case of BD–18:5550 (and perhaps also CS 31081-001; see Fig. 2). Nevertheless, in the case of BD–18:5550 the two lines with the highest excitation potential and the highest oxygen abundance also significantly deviate in the abundance-equivalent width plane (Fig. 1). Why abundances obtained from these two lines differ is not clear; we note, however, that these lines are the weakest ones measured in the spectrum of this star.
We identify two ways to improve our modelling of these lines. The first is to increase the number of 3D model atmospheres used in the analysis. One clear limitation of the present investigation is the use of just one model atmosphere to describe the four programme stars, that, although they have been selected with very similar atmospheric parameters, span a range in surface gravities, effective temperatures, and metallicities. In particular, the sensitivity of the 3D corrections to the variations of atmospheric parameters needs to be investigated. Such an investigation is hampered by the long time needed to fully relax a 3D model atmosphere of a giant star.
The second way is the investigation of possible departures from the assumption of LTE, that has been made in the present investigation. Departures could occur both in the chemical equilibrium (formation and dissociation of OH molecules here are assumed to be an equilibrium process); and in the occupation number of different energy levels of the OH molecule (the Boltzmann law was assumed here).
In Fig. 4 we show the [O/Fe] ratios in the four programme stars together with data taken from the literature based on the 630 nm [O i] line. The oxygen abundances are the ones we determined from the IR OH lines and the iron abundances have been taken from Cayrel et al. (2004). The points labelled 3D mean that only the oxygen abundance has been corrected for the 3D effect, but not the iron. In the case of iron, the 3D correction for such a model atmosphere should be around − 0.2 dex (Bonifacio et al. 2009; Dobrovolskas et al. 2013), although strongly dependent on excitation potential (Collet et al. 2007; Collet et al. 2009; Dobrovolskas et al. 2013). On the other hand, we also know that Fe i lines imply NLTE corrections of the same order of magnitude but in the opposite direction. In their comprehensive study of NLTE effects on iron in HD 122563 Mashonkina et al. (2011) determined a NLTE correction of +0.16 dex (for collisions with neutral hydrogen treated with the Drawin formalism and an efficiency SH = 0.1; neglecting the collisions raises the NLTE correction to +0.35). On the other hand, Mashonkina et al. (2013) demonstrated that the 3D and NLTE corrections for iron cannot simply be added; this approach for HD 122563 leads to a discrepancy of − 0.75 dex between the abundance derived from the Fe i and Fe ii lines. The abundance of iron probably requires a full 3D-NLTE analysis, and we are currently unable to perform it. In this state of affairs we prefer to adopt the 1D LTE result for iron.
With this choice, the 3D [O / Fe] values obtained from OH lines appear to be in better agreement with the general trend defined by the abundances based on [O i]. The average 3D LTE oxygen abundance for the four stars obtained from OH lines is ⟨ A(O) ⟩ = 6.61 ± 0.21, while that obtained from the 630 nm line is ⟨ A(O) ⟩ = 6.52 ± 0.33. We note that in 1D LTE we obtained ⟨ A(O) ⟩ = 6.86 ± 0.22 from OH lines; errors in all cases here indicate the scatter due to star-to-star abundance variations.
The results shown in Fig. 4 are, by and large, consistent with those derived from the OH UV lines by González Hernández et al. (2010) in metal poor dwarfs, although these authors have adopted the strategy of adding 3D corrections and 1D NLTE correction for Fe i. This means that a direct comparison of the two results is not possible. Nevertheless, the results of González Hernández et al. (2010, see their Fig. 14) show an average [O / Fe] = 0.6−0.8, corrected for 3D and NLTE effects at [Fe / H] = −3.0. In our case, we obtain an average [O / Fe] = 0.7, corrected only for 3D effects, at [Fe / H] = −3.0. On the other hand, the results of the two studies agree well with theoretical model of François et al. (2004) which predicts [O / Fe] = 0.8 for the same metallicity (in this comparison, [O/Fe] values from González Hernández et al. 2010 and François et al. 2004 were recomputed to the Asplund et al. 2005 solar oxygen abundance scale). In the future we plan to investigate the consistency of abundances obtained from IR OH and UV lines in the same EMP stars.
5. Conclusions
The results obtained in our pilot project have demonstrated that infrared OH vibrational-rotational lines could be used successfully to determine oxygen abundance in EMP giants. This, however, requires high-resolution spectra obtained with S/N of at least a few hundred. Fortunately, IR OH lines are significantly stronger than the [O i] 630 nm line and thus can be more easily measured. In addition, quite a large number of IR OH lines unaffected by telluric lines are typically available for the measurements, which makes the statistical significance of the determined oxygen abundance higher.
To determine oxygen abundances from IR OH lines in EMP stars, however, the use of 3D hydrodynamical model atmospheres is imperative because these lines form in the outer atmosphere where horizontal temperature fluctuations (caused by convective motions) are large, which leads to large variations in line opacities. This results in significantly different line strengths predicted with the 3D hydrodynamical and 1D hydrostatic model atmospheres, with the resulting 3D–1D differences in oxygen abundances of − 0.2···−0.3 dex. When corrected for these effects with the aid of 3D hydrodynamical model atmospheres, oxygen abundances obtained from IR OH lines generally agree well with those determined using the [O i] 630 nm line, which is insensitive to either 3D or NLTE effects. Obviously, the role of NLTE effects in the IR OH line formation still needs to be clarified, as well as the combined 3D NLTE effects for iron, something that is anticipated from the forthcoming studies.
Online material
Appendix A: List of infrared OH lines for oxygen abundance determination
In this work we used a number of vibrational-rotational lines (X-2Π) from the first-overtone sequence (Δv = 2) located in
the spectral range between 1514−1548 and 1595−1632 nm. The atomic parameters of the IR OH lines and their equivalent widths measured in the target EMP giants and also the derived oxygen abundances are provided in Table A.1.
OH spectral lines used in the abundance analysis.
Appendix B: 3D–1D abundance corrections for IR OH lines and the forbidden oxygen line
In Tables B.1–B.4 we provide 3D–1D abundance corrections that were computed for all OH lines and forbidden oxygen line, in each EMP giant studied here.
Abundance corrections for HD 122563.
 |
Fig. B.1 Excerpts from CRIRES spectra centred on IR OH lines in HD 122563 (black dots). Gaussian best-fits to the observed IR OH line profiles are shown as red lines. Blue solid lines show the synthetic telluric spectrum computed with the TAPAS online service (Bertaux et al. 2014) which is shifted downwards by 0.01 for better readability. Rest frame wavelengths (λ0) and measured equivalent width values (EW) of the IR OH lines are provided at the bottom of each panel. |
 |
Fig. B.2 continued. |
The [O/Fe] abundance ratios from Cayrel et al. (2004) were obtained using solar oxygen abundance of A(O) = 8.74, whereas in our case we used A(O) = 8.66 from Asplund et al. (2005). To make the direct comparison possible, the [O/Fe] ratios from Cayrel et al. (2004) and the theoretical model of François et al. (2004) were shifted to the reference scale where the solar abundance is A(O) = 8.66.
Acknowledgments
We thank Jonas Klevas and Dainius Prakapavičius for their contribution during various stages of the paper preparation. This work was supported by grants from the Research Council of Lithuania (MIP-065/2013) and the bilateral French-Lithuanian programme “Gilibert” (TAP LZ 06/2013, Research Council of Lithuania; 28471NE, Campus France). E.C. is grateful to the FONDATION MERAC for funding her fellowship. H.G.L. acknowledges financial support by the Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject A4 and A5) of the German Research Foundation (DFG). We also thank the staff of ESO VLT for performing observations in service mode.
References
- Akerman, C. J., Carigi, L., Nissen, P. E., Pettini, M., & Asplund, M. 2004, A&A, 414, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnett, D. 1996, Supernovae and Nucleosynthesis by David Arnett (Princeton University Press) [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, ASP Conf. Rev., 336, 25 [Google Scholar]
- Barbuy, B. 1988, A&A, 191, 121 [NASA ADS] [Google Scholar]
- Barbuy, B., & Erdelyi-Mendes, M. 1989, A&A, 214, 239 [NASA ADS] [Google Scholar]
- Barbuy, B., Meléndez, J., Spite, M., et al. 2003, ApJ, 588, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Bertaux, J. L., Lallement, R., Ferron, S., Boonne, C., & Bodichon, R. 2014, A&A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boesgaard, A. M., King, J. R., Deliyannis, C. P., & Vogt, S. S. 1999, AJ, 117, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., Spite, M., Cayrel, R., et al. 2009, A&A, 501, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., & Ludwig, H.-G. 2007, A&A, 467, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2008, A&A, 488, 1031 [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modeling of Stellar Atmospheres, eds. N. Piskunov, et al., Proc. IAU Symp., 210, poster A20 [Google Scholar]
- Cayrel, R., Andersen, J., Barbuy, B., et al. 2001, New Astron. Rev., 45, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collet, R., Asplund, M., & Trampedach, R. 2007, A&A, 469, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collet, R., Nordlund, Å., Asplund, M., Hayek, W., & Trampedach, R. 2009, Mem. Soc. Astron. It., 80, 719 [NASA ADS] [Google Scholar]
- Cowan, J. J., Sneden, C., Burles, S., et al. 2002, ApJ, 572, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Coxon, J. A., & Foster, S. C. 1982, J. Mol. Spectr., 91, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Creevey, O. L., Thévenin, F., Boyajian, T. S., et al. 2012, A&A, 545, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobrovolskas, V., Kučinskas, A., Steffen, M., et al. 2013, A&A, 559, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- François, P., Matteucci, F., Cayrel, R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comp. Phys., 231, 919 [Google Scholar]
- Fulbright, J. P., & Kraft, R. P. 1999, AJ, 118, 527 [Google Scholar]
- Galazutdinov, G. A. 1992, Special Astrophysical Observatory Preprint, 92, 2 [Google Scholar]
- García Pérez, A. E., Asplund, M., Primas, F., Nissen, P. E., & Gustafsson, B. 2006, A&A, 451, 621 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- González Hernández, J. I., Bonifacio, P., Ludwig, H.-G., et al. 2010, A&A, 519, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., & Ortolani, S. 1986, A&A, 169, 201 [NASA ADS] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Heiter, U., & Eriksson, K. 2006, A&A, 452, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Israelian, G., Rebolo, R., García, L., et al. 2001, ApJ, 551, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Käufl, H. U., Ballester, P., Biereichel, P. 2004, Proc. SPIE, 5492, 1218 [CrossRef] [Google Scholar]
- Kraft, R. P., Sneden, C., Langer, G. E., & Prosser, C. F. 1992, AJ, 104, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Kučinskas, A., Steffen, M., & Ludwig, H.-G. 2013, A&A, 549, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid, Kurucz CD-ROM, 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) [Google Scholar]
- Ludwig, H.-G. 1992, Ph.D. Thesis, Univ. Kiel [Google Scholar]
- Ludwig, H.-G., & Kučinskas, A. 2012, A&A, 547, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., Jordan, S., & Steffen, M. 1994, A&A, 284, 105 [NASA ADS] [Google Scholar]
- Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Ludwig, H.-G., Korn, A., Sitnova, T., & Caffau, E. 2013, Mem. Soc. Astron. It. Suppl., 24, 120 [Google Scholar]
- Matteucci, F. 2012, Chemical Evolution of Galaxies, Astron. Astrophys. Library (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Meléndez, J., & Barbuy, B. 2002, ApJ, 575, 474 [Google Scholar]
- Meléndez, J., Barbuy, B., & Spite, F. 2001, ApJ, 556, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, Å. 1982, A&A, 107, 1 [Google Scholar]
- Sbordone, L. 2005, Mem. Soc. Astron. It., 8, 61 [Google Scholar]
- Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. It., 5, 93 [Google Scholar]
- Sneden, C., Kraft, R. P., Prosser, C. F., & Langer, G. E. 1991, AJ, 102, 2001 [NASA ADS] [CrossRef] [Google Scholar]
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y., & Takada-Hidai, M. 2013, PASJ, 65, 65 [NASA ADS] [Google Scholar]
- Vögler, A., Bruls, J. H. M. J., & Schüssler, M. 2004, A&A, 421, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 3D LTE oxygen abundance in HD 122563, HD 186478, BD − 18:5550, and CS 31082-001 (top to bottom), as determined from IR OH lines, shown as the function of reduced equivalent width. |
| In the text | |
 |
Fig. 2 3D LTE oxygen abundance in HD 122563, HD 186478, BD − 18:5550, and CS 31082-001 (top to bottom), as determined from IR OH lines, shown as the function of excitation potential. |
| In the text | |
 |
Fig. 3 Top: temperature stratifications in the 3D hydrodynamical (grey scales indicating the temperature probability density), average ⟨3D⟩ (solid red line), and 1D LHD (dashed red line) model atmospheres computed with Teff = 4600 K,log g = 1.6,[M / H] = −2.5. Horizontal bars show the optical depth intervals where 90% of the OH line (λ = 1605.5 nm,χ = 0.48 eV) and [O i] line (λ = 630.0 nm,χ = 0.00 eV) equivalent width is formed (i.e. 5% to 95%): black and dashed blue bars correspond to the line forming regions in the full 3D and 1D model atmospheres (the equivalent widths of OH and [O i] lines are 1.6 pm and 0.4 pm). Bottom: root mean square (rms) value of horizontal temperature fluctuations, ΔTrms, in the 3D model (black line) and temperature difference between the average ⟨3D⟩ and 1D models (dashed blue line). |
| In the text | |
 |
Fig. 4 Oxygen-to-iron ratios in Galactic EMP stars plotted versus [Fe / H] ratio. Abundances of EMP giants studied here are marked by triangles: open red triangles – oxygen abundances in the programme stars determined determined in this work with classical 1D model atmospheres; filled red triangles – oxygen abundances corrected for 3D hydrodynamical effects. Solid grey circles show oxygen abundances in red giants, subgiants, and main sequence stars determined using the forbidden [O i] 630 nm line (Gratton & Ortolani 1986; Barbuy & Erdelyi-Mendes 1989; Kraft et al. 1992; Barbuy 1988; Sneden et al. 1991; Fulbright & Kraft 1999; Cayrel et al. 2001; Cowan et al. 2002; Cayrel et al. 2004). Black triangles highlight oxygen abundances determined from [O i] 630 nm line in Cayrel et al. (2004) for the same stars as studied here. The solid line is the evolutionary model of the oxygen abundance from François et al. (2004). We note that [O i] abundances from Cayrel et al. (2004) and the theoretical model from François et al. (2004) were shifted to the reference scale used in our study where solar oxygen abundance is A(O) = 8.66. |
| In the text | |
 |
Fig. B.1 Excerpts from CRIRES spectra centred on IR OH lines in HD 122563 (black dots). Gaussian best-fits to the observed IR OH line profiles are shown as red lines. Blue solid lines show the synthetic telluric spectrum computed with the TAPAS online service (Bertaux et al. 2014) which is shifted downwards by 0.01 for better readability. Rest frame wavelengths (λ0) and measured equivalent width values (EW) of the IR OH lines are provided at the bottom of each panel. |
| In the text | |
 |
Fig. B.2 The same as in Fig. B.1 but for HD 186478. |
| In the text | |
 |
Fig. B.2 continued. |
| In the text | |
 |
Fig. B.3 The same as in Fig. B.1 but for BD –18:5550. |
| In the text | |
 |
Fig. B.4 The same as in Fig. B.1 but for CS 31082-001. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


