| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424153 | |
| Published online | 27 March 2015 | |
The first stars: CEMP-no stars and signatures of spinstars
1
Geneva Observatory, Geneva University,
1290
Sauverny,
Switzerland
e-mail: andre.maeder@unige.ch; georges.meynet@unige.ch
2
Leibniz-Institut für Astrophysik Potsdam,
An der Sternwarte 16,
14482
Potsdam,
Germany
e-mail:
cristina.chiappini@aip.de
Received: 7 May 2014
Accepted: 1 December 2014
Aims. The CEMP-no stars are “carbon-enhanced-metal-poor” stars that in principle show no evidence of s- and r-elements from neutron captures. We try to understand the origin and nucleosynthetic site of their peculiar CNO, Ne–Na, and Mg–Al abundances.
Methods. We compare the observed abundances to the nucleosynthetic predictions of AGB models and of models of rotating massive stars with internal mixing and mass loss. We also analyze the different behaviors of α- and CNO-elements, as well the abundances of elements involved in the Ne–Na and Mg–Al cycles.
Results. We show that CEMP-no stars exhibit products of He-burning that have gone through partial mixing and processing by the CNO cycle, producing low 12C/13C and a broad variety of [C/N] and [O/N] ratios. From a 12C/13C vs. [C/N] diagram, we conclude that neither the yields of AGB stars (in binaries or not) nor the yields of classic supernovae can fully account for the observed CNO abundances in CEMP-no stars. Better agreement is obtained once the chemical contribution by stellar winds of fast-rotating massive stars is taken into account, where partial mixing takes place, leading to various amounts of CNO being ejected. The [(C+N+O)/H] ratios of CEMP-no stars vary linearly with [Fe/H] above [Fe/H] = −4.0 indicating primary behavior by (C+N+O). Below [Fe/H] = −4.0, [(C+N+O)/H] is almost constant as a function of [Fe/H], implying very high [(C+N+O)/Fe] ratios up to 4 dex. In view of the timescales, such abundance ratios reflect more individual nucleosynthetic properties, rather than an average chemical evolution. The high [(C+N+O)/Fe] ratios (as well as the high [(C+N+O)/α-elements]) imply that stellar winds from partially mixed stars were the main source of these excesses of heavy elements now observed in CEMP-no stars. The ranges covered by the variations of [Na/Fe], [Mg/Fe], and [Al/Fe] are much broader than for the α-elements (with an atomic mass number above 24) and are comparable to the wide ranges covered by the CNO elements. Nevertheless, the ratios [Na/N] and [Mg/Al] are about constant for CEMP-no stars of different [Fe/H]. This is consistent with the view that the Ne–Na and Mg–Al cycles were significantly operating in the source stars. The very different properties of CNO, Ne–Na, and Mg–Al elements from those of α-elements further support the idea that these elements (which all give to CEMP-no stars their peculiarities) originate in slow stellar winds of massive stars experiencing partial mixing.
Conclusions. CEMP-no stars present a wide variety in the [C/Fe], [N/Fe], [O/Fe], [Na/Fe], [Mg/Fe], [Al/Fe], and [Sr/Fe] ratios. We show that back-and-forth, partial mixing between the He- and H-regions may account for this variety. Some s-elements, mainly of the first peak, may even be produced by these processes in a small fraction of the CEMP-no stars. We propose a classification scheme for the CEMP-no and low-s stars, based on the changes in composition produced by these successive back-and-forth mixing motions.
Key words: stars: abundances / stars: Population III / stars: massive / stars: carbon
© ESO, 2015
1. Introduction
The stars belonging to the first stellar generations in the Universe, as shown by their very low metallicity content, had very different physical properties from the stars presently forming in the Milky Way. They were much more compact objects, which are denser and hotter than stars with solar composition, and they have a different evolution as well. In particular, even moderately rotating stars reach the break-up limit during the main-sequence (MS) phase. They evolve rapidly to the red after the core H-burning phase (an effect that depends on the treatment of shear mixing), and important surface enrichment in CNO elements occurs at the supergiant stage (Meynet et al. 2005; Ekström et al. 2008; Georgy et al. 2013). Some traces of the properties of these first stars may be revealed by the initial chemical enrichment of the Galaxy, owing to their peculiar chemical yields.
Among the stars with low Fe-content, typically [Fe/H] < −2.5 (i.e., a number ratio of iron to hydrogen atoms at least 300 times less than the solar ratio), the “CEMP-no” stars form an interesting group that dominates at the lowest [Fe/H] ratios (Aoki et al. 2002; Masseron et al. 2010; Allen et al. 2012; Yong et al. 2013; Norris et al. 2013). They may show impressive enhancements, up to more than a factor 104, of [C/Fe], as well as of the [N/Fe] and [O/Fe] ratios. Their distinctive property, which differentiates them from the other classes of carbon-enhanced metal-poor (CEMP) stars, is the relative absence of “s” and “r elements”, in particular Ba and Eu synthesized via neutron captures. This is why these stars are called “CEMP-no” stars. For the definition and properties of CEMP stars, see the review by Beers & Christlieb (2005).
CEMP-no stars are a kind of still-living stellar fossil. They are very old low-mass stars (about 0.8 M⊙ or less), which are surviving from the early times, and they preserve the characteristics of the nucleosynthetic enrichments of the early days. Some of these stars are still on the MS or are subgiants close to it, while others are in the red giant phase. Thus, the particular abundances of CEMP-no stars are not due to self-enrichment, but are more likely due to these stars having been formed in an environment polluted by the particular nucleosynthetic enrichments from objects called the source stars.
CEMP-no stars are generally thought to belong to the outer halo population (Carollo et al. 2012) and have also been found in dwarf spheroidal galaxies (Gilmore et al. 2013). The frequency of CEMP-no stars relative to low-metallicity stars without C-excesses rapidly increases for the lowest [Fe/H] values (Norris et al. 2013). The reason for the dominant presence of CEMP stars (of various types) at the low [Fe/H] was interpreted (Gilmore et al. 2013) as due to a rapid gas cooling for a C-rich medium, thus these C-rich stars formed more rapidly than other stars.
Several star models and scenarios have been developed to explain the peculiarities of the CEMP stars. They have been recently reviewed by Nomoto et al. (2013), and are the following:
-
The models of faint supernovae from Pop. III stars with mixing and fallback (Tominaga et al. 2014; Takahashi et al. 2014),
-
A two-step scenario with the combination of a normal supernova from a 15 M⊙ star and a dark supernova from a more massive star (35 M⊙) with strong fallback ejecting only its outer layers (Limongi et al. 2003),
-
The mass transfer from an AGB binary companion that may produce a star with strong CNO enhancements since the AGB yields show these characteristics (Herwig 2004; Karakas & Lattanzio 2007),
-
The models of low-metallicity stars with an average rotation experiencing efficient rotational mixing and mass loss (Meynet et al. 2005, 2006, 2010),
-
The self enrichment within the observed stars as has been proposed to account for the CN excesses (Campbell et al. 2010).
The scenario of binary mass transfer from an AGB companion appears to fit many properties of the CEMP-s stars remarkably. For them, the enrichments may be due to the 13C neutron source in low-mass AGB stars, as suggested, for example, by Masseron et al. (2010), who provide several pieces of evidence for that. These authors interpret the r- and s-enrichments in CEMP-rs stars as resulting from a unique process: the 22Ne source during the very hot conditions of the thermal pulses in an AGB star, which then contaminates its low-mass companion. The binary scenario is also considerably reinforced, at least for the CEMP-s stars, because a study of their radial velocities suggests that all CEMP-s stars are binaries (Lucatello et al. 2005).
The situation is not the same for the CEMP-no stars, for which the binary scenario seems difficult to accept. From a study of the binary properties of the different classes of CEMP stars, Starkenburg et al. (2014) conclude that the CEMP-no dataset is inconsistent with the binary properties of the CEMP-s class. Although the CEMP-no binary fraction is still poorly constrained, their population resembles the binary properties in the solar neighborhood more, so that their chemical peculiarities are most probably not related to their being in binary systems. Lee et al. (2014) point out that the relative number frequency of CEMP stars with [Fe/H] < −3.0 (essentially CEMP-no stars) is much too high to be accounted for by the AGB model, and they support the view that “one or more additional mechanisms, not associated with AGB stars, are required to produce carbon-rich material below [Fe/H] = −3.0”. Also, Norris et al. (2013) carefully examined the possible variations in radial velocities for these stars and found no evidence of variations at the level of 3 km s-1 in the large majority of them.
The aim of the present work is to examine various abundance ratios of CEMP-no stars and compare them to nucleosynthetic properties of massive stars at low metallicities, as predicted by models of rotating stars. In Sect. 2, we briefly review the known properties in the chemical evolution of galaxies that speak for the significant role of mixing and mass loss in the early galactic evolution. In Sect. 3, we discuss some properties of the models of rotating massive stars and of the “fallback and mixing” models (Nomoto et al. 2013). In Sect. 4, we show more new evidence or signatures of partial mixing and of mass loss of CNO elements by massive stars provided by the CEMP-no stars. Section 5 examines the relation or, more exactly, the absence of relation between CNO- and α-elements and the constraints that it provides. In Sect. 6, the abundances related to the Ne–Na and Mg–Al cycles are studied and the differences with the anticorrelations found in globular clusters are elucidated. In Sect. 7, a classification scheme of CEMP-no stars is proposed, and the case of stars with a significant Sr content is examined. Section 8 provides the conclusions.
2. The six known signatures of spinstars
2.1. Evolution of the chemical abundances in spinstars
The first indication of the possible faster rotation of stars with lower metallicity Z was finding that the relative frequency of Be stars was strongly increasing from samples in the solar neighborhood, to the Large Magellanic Cloud (LMC) and Small Magellanic Cloud (SMC; Maeder et al. 1999). This has been confirmed by subsequent works (Martayan et al. 2007). It does not mean that this trend is necessarily going on at lower Z. However, theoretical models of the formation of the first stars indicate that stars of very low Z should have very high rotational velocities, and thus experience mixing (Stacy et al. 2011). The model of spinstars has been developed to represent this kind of object (Meynet et al. 2010; Maeder & Meynet 2012): massive stars generally of low Z with fast rotation, strong mixing, and high mass loss.
The mixing in spinstars, due mainly to shear instabilities (Maeder 2009), currently brings products of the CNO-burning (14N and 13C) to the stellar surface. It may happen that products of the He-burning (C and O) are mixed in H-burning regions, thus producing primary 14N and 13C (Meynet & Maeder 2002b), which may reach the stellar surface (primary means produced from the initial H and He). During H-burning, especially in low Z models, which are hotter and denser than models at solar composition, the Ne–Na and Mg–Al reactions (or cycles) also significantly occur that involve the various isotopes of these elements.
In the He-burning regions, 22Ne is produced from α-captures on 14N. Further reactions may also occur in models of very low Z, such as the 22Ne(α,γ)26Mg and 22Ne(α,n)25Mg reactions, which produce other daughters of nitrogen. The 16O(α,γ)20Ne and the 20Ne(α,γ)24Mg reactions may also operate during He-burning in the hot conditions of low Z stars. These various reactions produce elements able to reach the stellar surface and modify the compositions of the winds and the chemical yields of the first stellar generations (Meynet et al. 2006).
The mixing processes enrich the stellar surface in elements, which like carbon, increase the opacity of the outer layers and enhance the mass loss rates of the models having initially very low Z. Without mixing, the models would have kept inefficient stellar winds, while with metallicity enrichment the stellar winds can reach the strength of those in the Magellanic Clouds (Meynet et al. 2006; Hirschi 2007). The consequence is that the contribution of the stellar winds to the chemical yields can be very significant in advanced evolutionary phases. We could even think that the winds may be the main source of chemical enrichment for massive stars (say above 25 M⊙), which end their life as a black hole with a large fallback.
Stellar winds, particularly from red supergiants, have much lower velocities than the ejecta from supernovae. Thus, the nucleosynthetic production of supernovae is more likely to escape from the region of star formation, while the slower ejecta by stellar winds could remain kept inside this region. This possibility is all the more likely in the outer galactic halo to which CEMP-no stars are thought to mostly belong. At the same time, this could also account for the very small enrichments in α-elements with atomic mass higher than that of Mg and other heavy elements observed in CEMP-no stars. This makes it plausible that CEMP-no stars were formed mostly from material coming from the winds of spinstars.
2.2. First two signatures: galactic chemical evolution of N/O and C/O at low Z
In a recent review paper, Chiappini (2013) recalled five existing results in the chemical evolution of the Milky Way, which may support the model of spinstars acting in the early evolution of galaxies. We briefly recall these five signatures.
The production of primary nitrogen by rotational mixing in low-metallicity asymptotic giant branch (AGB) and massive stars is a significant effect (Meynet & Maeder 2002a,b; Hirschi 2007). These model predictions are in good agreement with the constant N/O ratios observed in very metal-poor normal stars of the galactic halo (Chiappini et al. 2006). Considerations of the lifetimes of galactic chemical evolution support the view that the chemical enrichments are more likely due to massive stars than to AGB stars. The same kind of result is also present for the C/O ratios. The above models indicate increasing stellar yields of C at lower metallicities, because more C is ejected by mass loss (since the surface enrichments are stronger at lower Z) and escapes further nuclear destruction in the star. These yields lead to good agreement with the observed increase in the C/O ratios in very low-metallicity stars (Chiappini et al. 2006; Fabbian et al. 2009).
2.3. The third signature: chemical evolution of 12C/13C
Chiappini et al. (2008) have also considered the effects of spinstars on the evolution of the ratio 12C/13C. The predictions of chemical models of galactic evolution (without the yields of fast rotators) indicate values of 12C/13C between 4500 and 31 000 for [Fe/H] ratios between −3.5 and −5.0, while spinstars lead to ratios between 30 and 300. The isotopic ratios observed for very metal-poor “unmixed” giants (Spite et al. 2006) in the galactic halo with [Fe/ H] between −2.6 and −4.0 lie between 10 and 100. If the stars observed by Spite et al. are really unmixed and have a surface composition representative of their initial composition, then these observations favor spinstars (Chiappini et al. 2008). However, it is not guaranteed that these stars have not suffered the first dredge-up.
2.4. The fourth signature: primary behavior of Be and B
A fourth signature of the action of spinstars has been provided by the study of the formation of the light elements Be and B (Prantzos 2012). For some time, it had been shown that B and Be are produced by spallation of CNO nuclei by galactic cosmic rays (GCR) in the interstellar medium (ISM). The discovery that Be and B behave as primary elements (i.e., growing linearly with [O/H] or [Fe/H]) by Gilmore et al. (1992) contradicted theoretical expectations at that time. Indeed, if GCR protons hit O nuclei in the ISM, [Be/H] and [B/H] would grow like 2 [O/H] (secondary elements). The reason for this dependence like 2 [O/H] is that the rate of supernova explosions intervenes twice (Duncan et al. 1992), because both GCR protons and oxygen nuclei are produced by different supernovae in the course of the evolution of galaxies.
However, if GCR are accelerated from the CNO rich stellar winds of rotating massive stars by the forward shock of the subsequent SN, the CNO content in the GCR remains constant with respect to the metallicity (Prantzos 2012). Be or B produced by fast CNO nuclei hitting protons and α-particles of the ISM will no longer depend on the metallicity, and thus one expects that the Be/O ratio remains constant as a function of [O/H].
Remarks on the various possible dependences (such as [O/H] or 2[O/H]) had already been made by Gilmore et al. (1992) and Duncan et al. (1992). With models of galactic evolution, Prantzos studied the observations of the Be and B abundances as a function of [Fe/H] and emphasized the need for a CNO contribution by the winds of massive rotating stars to the early chemical evolution of galaxies.
2.5. The fifth signature: production of s-elements
Another interesting test has been shown by Chiappini et al. (2011). Below [Fe/H] = −2, the ratio [Sr/Ba] shows an enormous scatter over about 4 dex, extending from [Sr/Ba] = −2 to about + 2. We recall here that Sr is the typical element of the first peak of the s elements, while Ba is the typical representative of the second peak. Thus, [Sr/Ba] expresses the ratio of abundances in the first peak with respect to the abundances in the second one. The standard models for producing r-elements shows a very low scatter of the [Sr/Ba] ratio (about 0.2 dex) according to Cescutti et al. (2013). The models of binary mass transfer from an AGB star to a lower mass companion (Herwig 2004; Karakas & Lattanzio 2007) account for the stars very well with [Sr/Ba] between −2 and 0, as confirmed by several authors (Masseron et al. 2010; Allen et al. 2012). This is the domain of CEMP-s stars, which in addition are all likely to be binary stars (Lucatello et al. 2005).
The problem was really to explain the stars with [Sr/Ba] > 0. Cescutti et al. (2013) have shown that chemical evolution models, which also include the yields in s-elements produced by fast rotating massive stars, help to reproduce the distribution of the ratios [Sr/Ba] toward high values. This is based on the models of rotating massive stars by Frischknecht et al. (2012), who have shown that massive stars may in some cases moderately contribute to the first peak of s-elements and contribute little to the second peak and nothing to the third one. Thus, when both the contribution of AGB binaries and that of rotating massive stars are accounted for, the full extension of the observed range of [Sr/Ba] values from −2 to + 2 may be reproduced (Cescutti et al. 2013).
2.6. A possible sixth signature: the high initial He of a fraction of the stars in globular clusters
A double MS band has been found first in the globular cluster ω Cen (Bedin et al. 2004) and then in several other globular clusters with even a double sequence of blue stragglers (Dalessandro et al. 2013). The double MS band was interpreted (Piotto et al. 2005) as resulting from two populations of stars with different He contents within the globular cluster. The bluer sequence has a helium content Y = 0.38 compared to the standard value of Y = 0.24. This implies a He difference ΔY = 0.14 for a metallicity difference ΔZ = 0.002. Such He contents have been confirmed by study of red giant spectra, which show two different He abundances, one Y = 0.22, and one in the range 0.39−0.44, implying a value of at least ΔY = 0.17 (Dupree & Avrett 2013).
The above observations support relative helium to metal enrichments ΔY/ ΔZ of about 70 or more, while the ratio from standard supernova nucleosynthesis is around 4. Maeder & Meynet (2006) suggested that this extreme ΔY/ ΔZ ratio results from the winds of massive and intermediate stars. However, we noted that this is not the only possibility. It could also result from the escape of the high velocity and high Z ejecta of supernova explosions from the globular clusters. Models of chemical evolution support the idea that there is an escape of heavy elements in the supernova winds, while the slower He-rich winds of massive stars and AGB stars are kept in the shallow potential well of globular clusters (Romano et al. 2010). The question as to whether spinstars are involved in the high He contents observed is not definitely settled. However the very high observed amplitude ΔY in some clusters pleads for huge amounts of He ejected at some stages, and this is not inconsistent with the role of spinstars in the early galactic evolution. A major issue in this context is also to know whether CEMP-no stars have a high He content as suggested by Meynet et al. (2010).
In globular clusters, there are some anticorrelations of chemical abundances (Sect. 6) that point toward H-burning products, while CEMP-no stars are characterized by both H- and He-burning products. It is possible that the main mass loss phase does not occur at the same stage of stellar evolution. To account for the anticorrelations in globular clusters, stellar mass loss needs to occur during the core H-burning phase, while for CEMP-no stars, it is while He-burning sources are active. For globular clusters, reaching the critical limit or close binary evolution with tidal mixing during the MS phase offers interesting candidate effects. For CEMP-no stars, in contrast, the source stars need to lose mass in the advanced phases, when both H- and He-burning products appear at the stellar surface.
One can wonder what makes this difference in the time of mass loss. We note that the metallicity is different, since CEMP-no stars do occur at much lower metallicities than globular clusters. This appears to be the main difference. At a very low metallicity, little mass is lost by a star reaching the critical velocity limit. A lot of mass could be lost by stellar winds in the advanced phases, when due to self surface enrichment in CNO elements, the opacity of the outer layers become greater and line-driven stellar winds stronger. At a slightly higher metallicity in globular clusters, stars reaching the critical rotational velocity could experience strong mass loss (Decressin et al. 2007). We emphasize that this remains very speculative. The explanation we have tried to propose may, however, make sense for these intriguing differences.
At this stage, the six above facts already form an interesting basis for supporting the view that spinstars, with mixing and mass loss, significantly contribute to the early chemical enrichment of the galaxies, in particular by their large He and CNO yields. Below, we examine how the properties of the CEMP-no stars further support this view.
3. Comparison between “mixing and fallback” and “spinstar” models
The models of binary mass transfer from an AGB companion applies well to CEMP-s stars, as seen above. For the CEMP-no stars, the models of mixing and fallback and those of massive rotating stars (with mixing and mass loss) are the most promising according to Norris et al. (2013). Although very different in their physics, they lead to rather similar consequences, as far as the chemical yields are concerned. Here, we briefly summarize the main properties of both models.
3.1. Models of “mixing and fallback”
The models of “mixing and fallback” have been proposed by Nomoto and colleagues (Nomoto et al. 2013) to account for the possible internal mixing in stars and for the fact that only a fraction of the “onion skin layers” of the presupernova is ejected. The rest collapses into the remnant object, whether a black hole or a neutron star. In mixing and fallback models, the region between two limiting shells, chosen differently in each star model to explain the observations, is considered to be fully mixed. The models assume that a fraction of the star is ejected and another fraction is locked into the remnant. The separation essentially occurs at the time of the supernova (SN) explosion. Below some chosen cutoff-mass, matter is kept in the remnant, and above it matter is ejected and participates in the further chemical evolution of galaxies. Such events produce faint supernovae with low kinetic energy resulting in a very small amount of 56Ni ejected (typically a few 10-3M⊙) (Nomoto et al. 2013). They occur in the range of 10 to 13 M⊙, and up to about 30M⊙ for stars that experience a significant fallback, thus letting only small amounts of heavy elements escape into the ISM.
Tominaga et al. (2014) have performed extensive and impressive comparisons between predicted values and observed abundances in metal poor stars. They use models from Iwamoto et al. (2005) for 25 and 40 M⊙ without enhanced mixing and a model of 25 M⊙ with enhanced mixing. The mixing is made at the time of the SN explosion and occurs between two arbitrary limits. The authors note that the mixing could, for example, be due to rapid rotation, but no calculations of rotational effects are performed. Mixing and fallback in models of faint supernovae lead to generally good agreement with observed abundances of CEMP stars as shown by Tominaga et al. The authors then exploit the parameter space (assuming different values for the region, which is mixed, and for the cutoff mass) for each CEMP star in order to find the best model that matches the observations of that particular object. This gives much freedom in the adjustments to the observations.
3.2. Models of “spinstars”
In the “spinstar” models, a fraction of the stellar interior is chemically mixed. The mixing has a rotational origin, then is progressive during evolution and not necessarily complete. Finally, it results from calculations of shear mixing and meridional circulation; at the same time, the transport of angular momentum is accounted for. This mixing is computed with diffusion coefficients, which are also used for comparisons between models and observations for rotating stars in the solar neighborhood (surface compositions and surface velocities, populations of massive stars as red and blue supergiants, Wolf-Rayet stars). Thus, the physics used in very metal-poor stars is the same as in normal metallicity stars. What is different are the consequences of the physics implied by the very low metallicity considered.
3.3. Similarities and differences
In spinstar models, the physics triggering the mixing is discussed in detail and an explanation is provided for why strong mixing occurs at very low metallicity. The main difference is that in mixing and fallback models, the mixing does not occur progressively during the evolutionary stages, but occurs at the time of the explosion and with an efficiency that is a free parameter. In both sets of models, a fraction of the star is ejected, and another fraction is locked into the remnant. In spinstar models, the mass loss rates by the winds in all stages before the SN are calculated, and this provides the yields of various elements from the winds. The winds are enhanced by the rotational enrichment of the surface by CNO elements. Interestingly, other processes can trigger strong mass losses in metal-free stars and likely in very metal poor stars, too. Recently, Moriya & Langer (2015) have suggested that the very massive metal-free stars, which evolve into red supergiants, become pulsationally unstable shortly before they explode, thus experiencing extreme mass-loss rates despite the tiny metal content of the envelopes. The ejected matter escapes further nuclear destruction in the star. This particularly concerns some relatively fragile isotopes, like 14N and 13C, produced by the CNO cycle. In spinstar models, the yields of these isotopes are relatively high.
Further enrichment by the subsequent SN explosion may also be modeled or not in spinstar models. (In some models the “wind” and the “wind+ SN” contributions are both provided.) In that case, as for mixing and fallback models, the mass cut is considered as a free parameter, but chosen to be identical for all models. Some fallback processes (and perhaps mixing) could also occur at the time of the SN explosion in spinstars models. It is still unknown by how much the cutoff mass, which is a critical parameter, is different in models with rotation. A combination of the rotational effects and fallback, and maybe mixing, at the time of SN explosions may provide the best solution. A recent work by Takahashi et al. (2014) shows the interest in this kind of approach.
Below in Sect. 4.5, we examine whether some observations allow us to distinguish between these two kinds of models. The inspection of the figures given by Tominaga et al. (2014) shows that the fallback and mixing models often have difficulty accounting for the high observed N-abundances. Concerning the ratio 13C/12C ratio, which as shown below has a strong discriminating power, we have found no predictions in the quoted models. In conclusion, we point out that the stellar wind and fallback+ mixing models appear more complementary than contradictory.
Abundance data for the sample stars considered.
4. Signatures of spinstars from CNO data for CEMP-no stars
As already mentioned, the abundances of CEMP-no stars reflect the chemical yields of some star(s), the source star(s), in a previous generation, which may be the first one. We examine here the properties of CEMP-no stars, typically in the range of [Fe/H] = −2.5 to −7.1, where they occur, and compare them to model data of AGB and spinstars, when available. We use the data on spectroscopic determinations of chemical abundances collected by Masseron et al. (2010), Allen et al. (2012), and completed by recent observations by Norris et al. (2013). When different values of the abundance parameters are given by these three groups, we use the most recent ones, although the small differences between authors have no consequences on the results. Moreover, the data tables often provide only upper bounds for the chemical abundances. Norris et al. (2013) point out that their sample contains 30% of near turnoff or subgiants stars, the other ones being red giants. Two stars (HE 0107-5240 and HE 1327-2326) in their sample only have upper limits for Ba, thus they cannot formally be cataloged as CEMP-no objects, but they do point out that all their other properties correspond to CEMP-no objects. We include them in our sample (Table 1). We further discuss HE 1327-2326 in Sect. 7.2
We also include four other stars: CS 22945-017, CS 22956-028, CS 31080-095, and HE 1410+0213, cataloged as CEMP-no stars by Masseron et al. (2010) and as Ba-low (with 0 < [Ba/Fe] < 1) by Allen et al. (2012). These stars are indicated by “b-” in the last column of Table 1 and labeled with an additional horizontal bar over the representative points in all figures. Table 1 also contains two stars cataloged as low-s stars by Masseron et al. (2010) and considered as “b-” by Allen et al. (2012): HE 1419-1324 and CS 30322-023. They are also indicated as above in the table and figures. There is a third low-s star given by Masseron et al. (2010), HE 1001-0243, while it has been cataloged as Ba-rich by Allen et al. (2012). We do not include this star in the sample.
We also include some data for the extremely metal-poor star SMSS 0313-6708 (also noted SMSS J 031300.36-670839.3) with [Fe/H] < −7.1 analyzed recently by Keller et al. (2014). These authors give upper limits for the abundance ratios with respect to hydrogen, except in the cases of Li, C, Mg, and Ca, where the values of the ratios to H are provided. An upper limit is also given for [Fe/H]. Thus, we can give lower limits for the ratios [C/Fe], [Mg/Fe], and [Ca/Fe]. The other abundance ratios remain undefined. The ensemble of the considered data are given in Table 1, where 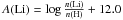 with n(Li) the abundance in number and as usual [Fe/H] =
with n(Li) the abundance in number and as usual [Fe/H] = 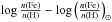 .
.
4.1. The case of the Li-poor stars
A special case concerns the stars that are Li-poor, i.e., with a Li abundance much lower than the cosmological value of A(Li) = log n(Li) /n(H) + 12 = 2.72. Li is generally destroyed in stars. Thus, if the matter ejected by a star, either by stellar winds or SN explosion, is diluted with original interstellar gas having more or less the cosmological Li abundance, the Li abundance is raised up to some fraction of the cosmological value. Thus, the level of the Li abundance in CEMP stars gives information (Meynet et al. 2010) on the importance of the dilution factor (defined as the ratio MISM/Mejected of the matter from the original interstellar gas to the matter ejected by the star). Of course, this is correct as long as Li is not strongly destroyed by internal mixing processes having occurred in the CEMP-no star itself, a hypothesis that is confirmed in the case of HE 1327-2326 by the computations by Korn et al. (2009) and that may apply to the dwarf and subgiant CEMP-no stars.
Thus, we may expect that the Li-poor near MS stars that have not destroyed the Li in their outer layers reflect the original composition of the ejecta with little dilution remarkably well. This may strongly constrain the properties of the source star, which has produced the heavy elements observed. If we take log g ≥ 3.25 as a limit for MS stars and subgiants, we are only left with three stars having a low Li content: G 77-61, HE 1300+0157 and the very low [Fe/H] star HE 1327-2326. These stars generally occupy no peculiar position in the various plots. Moreover, their number is too small to allow us to draw conclusions.
 |
Fig. 1 Observations of 12C/13C ratios vs. [C/N], represented by black dots (Norris et al. 2013) and blue dots (Masseron et al. 2010). (The observations by Allen et al. (2012), represented by black squares in other figures, do not appear in this plot, because these authors do not provide data for the C-isotopes.) A vertical bar indicates MS or subgiant stars with low Li content, and a horizontal bar indicates CEMP-no or low-s stars by Masseron et al. which are also cataloged as “b-” by Allen et al. The big points apply to MS stars or to subgiants close to the turnoff with Teff> 5500 K and log g ≥ 3.25, as by Norris et al. (2013), while the small points represent the bright giants with lower Teff and log g. The Li-poor star G 77-61, which has Teff = 4000 K and log g = 5.05, is considered as a dwarf (Plez & Cohen 2005), so it is represented by a big point. Some of the 12C/13C values are lower bounds indicated by a vertical arrow. If at the same time, the N value is an upper bound, the arrow is oblique. Rectangles indicate the solar value and the CNO equilibrium value. AGB models with Z = 10-4 are indicated by broken red lines, the upper line comes from Karakas & Lattanzio (2007) in the range of 1 to 6 M⊙, and the lower one is by Herwig (2004) in the range of 2 to 6 M⊙ (Masseron et al. 2010), the low masses being on the top and the high ones at the bottom of the lines. A red star shows a fast-rotating AGB model of 7 M⊙ with Z = 10-5 (model F) by Meynet et al. (2010). Green stars show models of rapidly rotating massive stars A, B, C, D with masses from 40 to 85 M⊙ and Z = 10-8 from Hirschi (2007). Model E and E′ have a mass of 60 M⊙ with Z = 10-5 and are given in Table 4 by Meynet et al. (2006), respectively the left and right columns; they differ by the value of the mass loss rates (higher in E′). A parenthesis (wind+SN) indicates the values when both the wind and the supernova contributions are counted. The approximate directions of CN burning is indicated by blue arrows. |
4.2. The 12C/13C vs. [C/N] relation for CEMP-no stars
The test here concerns CEMP-no stars in the range of [Fe/H] = −2.5 to −7.1. Figure 1 presents the 12C/13C vs. [C/N] ratios for the stars of Table 1 and compares these data to those of the AGB and spinstar models. The MS stars and subgiants (large symbols) are distinguished from the bright giants (small symbols), where mixing may have occurred. The many other details concerning this and other figures are given in the caption of Fig. 1.
From the physics of nuclear reactions, we may say the following. At the very beginning of CN burning, 12C burning produces some 13C and 14N, which makes some significant slope in Fig. 1. Then the ratio 12C/13C stays constant, while 12C continues to be turned to 14N, which produces a flat slope in the figure. High ratios 12C/13C and [C/N] indicate very partial H-burning by the CNO cycle, as well as a possible 12C addition (for example by a supernova or a WC star). Moderate and low ratios 12C/13C (and low [C/N]) cannot be anything but a signature of H-burning by the CNO cycle, since further reactions would destroy 13C by α-captures, if 13C is brought into a region of He-burning. Thus, the isotopic 12C/13C and the [C/N] ratios provide a constraining test on the degree of CNO processing. From Fig. 1, which is rich in information, we draw the following results.
4.2.1. Sign of partial mixing
The solar values, as well as those of CNO equilibrium in massive stars, are indicated. CEMP-no stars have low 12C/13C ratios providing evidence of CNO burning. However, the relatively huge amounts of C (as well as O) necessarily imply some synthesis of C and O by the 3α reaction during He-burning. Thus, CEMP-no stars generally exhibit products of He-burning that have gone through partial mixing and some processing by the CNO cycle, producing low 12C/13C and a broad variety of [C/N] ratios.
We emphasize the partial character of the mixing. Partial mixing means that there are not a large number of turnovers between the H- and He-burning regions. Some C and O coming by mixing from the He-burning region has been turned into nitrogen, but some variable fractions of this C and O have not been further processed by the CNO cycle. (This is like a further addition of C and O.) If we had full mixing as in a convective zone, the 13C would be rapidly destroyed by the 13C(α,n)16O reaction by going into the He-burning region, leading to high 12C/13C ratios. The stars would show s-elements, resulting from neutron captures of the neutrons emitted by the reactions 13C(α,n)16O and 22Ne(α,n)25Mg. To put it precisely, CEMP-no stars are generally characterized by an absence of s-elements (but see Sect. 7), thus this is consistent with partial mixing.
Then, if the matter of the outer stellar layers of the source star is ejected by stellar winds, it escapes further nuclear processing. It is thus possible by the combination of partial mixing, CNO processing, and mass loss to produce chemical yields corresponding to the kind of abundances observed in CEMP-no stars.
One low s-star (CS 30322-023) shows abundances corresponding to the CNO equilibrium values. This is an indication of very strong CNO processing either in the source star or in the star itself, but of incomplete mixing between the H- and He-burning regions, since the amount of s-elements is low. Partial mixing is also consistent with the presence of 13C in this star. However, it is the extreme giant in the sample, and there is probably some large CNO processing in this object (as well as some Li destruction). Nevertheless, because many MS and subgiant stars (noted by large points) have very low 12C/13C, we may consider that the CNO processing is generally coming from the source stars and not from self-enrichment.
4.2.2. Discrepancy with the AGB nucleosynthesis
The model data for AGB envelopes with masses from 2 to 6 M⊙ and metallicity Z = 0.0001 (Herwig 2004) and those of 1 to 6 M⊙ and Z = 0.0001 (Karakas & Lattanzio 2007) are also shown in Fig. 1, see also Masseron et al. (2010). The comparison with observations reveals a large difference between CEMP-no stars and the location of AGB stars in this diagram, as already shown by Masseron et al. (2010). For all the [C/N] values, the predicted 12C/13C ratios are generally higher than observed, even in the region between the solar and the CNO equilibrium values. The composition of a 7 M⊙ fast-rotating E-AGB envelope (Meynet et al. 2010) agrees with the other AGB data and thus also with observations. Thus, the yields from AGB models have difficulties to account for the abundances of CEMP-no stars.
In models of galactic chemical evolution, stars may only contribute to the chemical enrichments after a certain time given by stellar evolution properties. In the case of AGB stars, their yields influence the chemical abundances only for [Fe/H] ratios higher than about −3.0, as shown for example in Fig. 10 by Nomoto et al. (2013), and also Chiappini et al. (2008) and Matteucci (2012). In such galactic models for the halo, a Fe/H equal to −3 occurs at an age of 45 Myr, which corresponds to the lifetime of a 7 M⊙ star. Therefore AGB stars of moderate masses should not play a significant role for the present plot of CEMP-no stars.
4.2.3. Stellar winds and SN contributions
Some models (Meynet et al. 2006, 2010) provide the total yields, summing the wind and the supernova contributions. These models are represented in the figure with a parenthesis “(wind+SN)”. These results cannot account for the CEMP-no observed abundances (see also Cescutti & Chiappini 2010). We notice that the lines that would connect models C, E, and E′ to models C(wind+SN), E(wind+SN), and E′(wind+SN) have a slope of about 1.0 corresponding to the addition of 12C. The physical reason is clear: supernovae produce much 12C, while they produce little 13C and 14N, thus making a slope of 1.0. This plot indicates that CEMP-no stars do not receive the complete addition of the 12C layer from the source stars from the “onion skin model” during supernovae explosions.
4.2.4. Spinstar stellar winds
Models taking the chemical enrichment due to winds of rotating massive stars in the range of 40 to 120 M⊙ and a variety of mass loss rates into account (Meynet et al. 2006, 2010) are represented in Fig. 1. In these models, significant amounts of C and O produced by He-burning in the core are transported by mixing processes (mainly shear diffusion) in the H-burning shell. There, the new C and O may participate in the CNO cycles and be more or less transformed to 13C and 14N. Depending on whether the burning is complete or incomplete, the fractions of 13C and 14N produced may be different, and the same is true for the fractions of 12C and 16O. This produces the variety of abundance ratios observed in this diagram (as well as in Fig. 2 below).
The massive star models reproduce the flat part of the curve of the observations well on the lefthand side of Fig. 1 before the observed data rise for [C/N] > 0. The relatively flat part on the left results from the fact that 12C/13C nearly keeps its equilibrium value even when the whole CNO cycle is not at complete equilibrium. On the right of the plot, the CNO burning is very partial, making higher 12C/13C and [C/N] ratios.
 |
Fig. 2 Comparison of the abundance ratios [O/N] and [C/N] of CEMP-no stars with model data. The same codes as in Fig. 1 are adopted to represent the observations and models. The small red rectangles show the AGB models by Herwig (2004) connected by a red broken line. The general trend of the CNO burning is represented by a big reddish arrow. The small vertical arrows indicate upper limits for [O/Fe] and the small oblique arrows upper limits for [N/Fe]. The star HE 1201-1512 was not indicated because of many lower limits. |
We notice that the models of spinstars do not completely cover the range of the observed values of CEMP-no stars. They cover the range of abundance ratios from CNO equilibrium values up to [ C / N ] ≈ 0.2, but not the higher [C/N] ratios. In this respect, we emphasize that the initial values of [C/N] and [O/N] play a major role in the location of the model points in Figs. 1 and 2 and may be responsible for some differences. We consider two cases to illustrate this problem:
-
A)
The case of mild mixing with a moderate entry of C and O from the He-burning core into an active H-burning zone. The representative model points in the figures will be at some distance from the initial values in the direction of the CNO equilibrium point. The size of the deviation from the initial values depends on the amount of mixed C and O. Small entries of C and O make small deviations, large entries make large ones.
-
B)
The case of mixing with an entry of C and O into a relatively inactive H-burning zone. The formation of nitrogen will be very small. Thus, the representative model points are shifted upward and rightward (with high [O/N] and [C/N]) in the mentioned figures with respect to the chosen initial values. The size of the shifts depends on the amounts of new C and O entered into the inactive H-burning zone. (In the two cases, the history of the mass loss rates of the source star may also play a role.)
For such initial ratios, mixing like in case A would distribute the model points from these high initial ratios all the way down to the left of the figures. That solar ratios have been adopted in spinstar models explains why the righthand part of the figures was not covered by the models.
The representative points of some AGB models are located to the right upwards of the solar values in Figs. 1 and 2. These are AGB stars with low initial masses (≤2.5 M⊙). This location is consistent with the above type B scenario. The H-burning layers in these low-mass AGB stars have relatively low temperatures (see Fig. 26.18 in Maeder 2009). Hot bottom burning is also absent in these stars (below 4 M⊙). As a consequence of these effects, the CNO burning remains weak, little nitrogen is produced, and mixing, even if convective, may only lead to largely positive [C/N] and[O/N] values. This explains why some AGB models have [C/N] and [O/N] higher than solar.
As a result, solar ratios should not be taken as initial values in future spinstars and AGB models aimed at being the sources of CEMP-no stars.
4.2.5. Differences between spinstar and mixing and fallback
In light of Sect. 3, it is likely that the predictions of the two sets of models should be different, although this cannot be quantified yet. The main characteristics of CEMP-no stars result mainly from the mixing of the products of He-burning into the H-burning shell. Thus, mixing at the time of the SN explosion or a progressive and partial mixing during the evolution should lead to significant differences. The physical conditions and timescales of the two cases are not the same, and this should influence the abundance of temperature-sensitive isotopes like 13C and 14N.
In conclusion, model grids of spinstars with appropriate initial abundance ratios, a broader range of rotation velocities and mass loss rates, as well as predictions for the 12C/ 13C ratios from mixing and fallback models, are all very needed in the future to extend the comparisons with observations.
4.3. The [O/N] vs. [C/N] relation for CEMP-no stars
Figure 2 shows the [O/N] vs. [C/N] diagram (labels as in Fig. 1). The stars in this figure are not exactly the same as the ones shown in Fig. 1 because not all stars have 12C, 13C, and oxygen abundances reported. Most stars in this figure are located in the upper righthand quadrant, hence far from the CNO equilibrium value. This again suggests partial mixing and CNO-processing to have occurred in these objects.
A recent study (Maeder et al. 2014) of the N/C vs. N/O plot, or similar plots like Fig. 2, shows that the slope for moderate CNO burning is model independent. For example, over a range of log(N/O) ratios of about 0.5 dex, the scatter in log(N/C) should be less than 0.15 dex, regardless of the models. The curve in this kind of diagram is determined by:
-
The physics of nuclear processes.
-
The initial number ratios of CNO elements.
 The slope of the relation in Fig. 2 is therefore given by
The slope of the relation in Fig. 2 is therefore given by  (3)where the initial C/N ratios can be used.
(3)where the initial C/N ratios can be used.
We have typical relations between the bracket terms and number ratios, as in the example below, ![\begin{eqnarray} \log\rm (C/N) = [C/N] + \log (C/N)_{\odot} . \end{eqnarray}](/articles/aa/full_html/2015/04/aa24153-14/aa24153-14-eq78.png) (4)We adopt (C/N)⊙ = 4.03 and (O/N)⊙ = 7.59 (Asplund et al. 2005, 2009). The initial values of (C/N) and (O/N) are determined by the C and O matter diffused into the H-burning shell. Formally, in the case considered here, these ratios are both infinite at the beginning of CNO processing, thus Eq. (3) leads to a slope of 1.0 in Fig. 2. If we adopt the highest values in the sample stars for the initial values of (C/N) and (O/N), i.e., where relatively less N has been processed, we have
(4)We adopt (C/N)⊙ = 4.03 and (O/N)⊙ = 7.59 (Asplund et al. 2005, 2009). The initial values of (C/N) and (O/N) are determined by the C and O matter diffused into the H-burning shell. Formally, in the case considered here, these ratios are both infinite at the beginning of CNO processing, thus Eq. (3) leads to a slope of 1.0 in Fig. 2. If we adopt the highest values in the sample stars for the initial values of (C/N) and (O/N), i.e., where relatively less N has been processed, we have ![\begin{eqnarray} \rm [C/N]= 2.0 \quad \mathrm{and} \quad [O/N]=1.6 , \end{eqnarray}](/articles/aa/full_html/2015/04/aa24153-14/aa24153-14-eq81.png) (5)which lead to C/N = 403 and O/N = 302. The slope of the relation O / N vs. C / N is thus
(5)which lead to C/N = 403 and O/N = 302. The slope of the relation O / N vs. C / N is thus 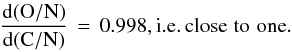 (6)In the second approximation, we use the fact that in massive stars the CN cycle rapidly brings the C-content to an almost constant value, so that the increase in the N-content mainly results in the O-destruction. Thus, we have
(6)In the second approximation, we use the fact that in massive stars the CN cycle rapidly brings the C-content to an almost constant value, so that the increase in the N-content mainly results in the O-destruction. Thus, we have 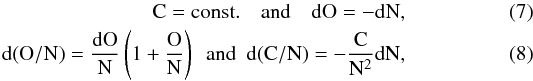 and the slope becomes
and the slope becomes 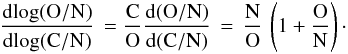 (9)With the number ratios we had above, we get a slope of 1.003. This means that, regardless of the assumptions, a slope of 1.0 represents the CNO processing in Fig. 2 well. This slope is represented by a broad arrow in this figure.
(9)With the number ratios we had above, we get a slope of 1.003. This means that, regardless of the assumptions, a slope of 1.0 represents the CNO processing in Fig. 2 well. This slope is represented by a broad arrow in this figure.
From Fig. 2, we note the following points:
-
1.
It is noticeable that CEMP-no stars span a range of more than 103 in the C/N and O/N ratios! About 77% of the CEMP-no stars have either C/N or O/N ratios higher than solar, while currently MS and red giants have values that only cover a fraction of the range between solar and equilibrium values. These high ratios are consistent with products of He-burning having experienced very partial CNO processing. In a He-burning region, both the C/N and O/N ratios tend to infinity, thus the evolution due to the CNO processing moves from the upper righthand corner down to the lower lefthand corner in Fig. 2, as shown by the broad arrow. These high ratios may also be consistent with the addition of fresh carbon and oxygen from the He-burning region of the source star.
-
2.
With [O/N] on the vertical axis, there is now some continuity in models of AGB envelopes and models of massive rotating stars, which was not the case with 12C/13C on the vertical axis. The reason is that the [O/N] ratio does not reach an equilibrium value early during H-burning and keeps some intermediate values, while 12C/13C rapidly comes close to its equilibrium ratio and is a more discriminating parameter, as shown above.
-
3.
The models of AGB and winds of massive stars both have difficulty reproducing the observed points. Again, as discussed in the previous section, this may be, at least in part, related to the choice of the initial solar [C/N] and [O/N] ratios in both kinds of models. Indeed, if we adopted the initial values given in relations (5), we see that the observations would lie more or less on a straight line connecting these initial values to the those of the CNO equilibrium. This also supports the view of partial mixing of He-products into the H-burning region.
Finally, we would like to point out that the AGB and rotating massive star models are often considered to be different (and sometimes opposite) scenarios. This is not very meaningful. For interpreting CEMP-no stars, which typically occur for [Fe/H] < −2.5, models of both massive stars and intermediate-mass stars should be considered down to a mass limit based on the timescales compatible with galactic evolution models (Matteucci 2012). As mentioned above, for the present sample a lower mass limit of 7 M⊙ seems reasonable.
4.4. The sum of CNO elements at extremely low [Fe/H]
Masseron et al. (2010) have shown that the sum of CNO elements in CEMP-no stars correlates linearly with metallicity. In Fig. 3 we plot the Masseron et al. data along with three other stars showing low abundances of s-elements. This linear relation is not expected according to standard scenarios (see Masseron et al. for a discussion).
In terms of galactic chemical evolution, a slope of 1.0 as a function of metallicity is an indication of primary behavior. This would imply that the sum of CNO elements over Fe remains constant. In the framework of the spinstar scenario, this happens naturally because C and O are primary elements made in the He-burning core, and their production depends on the massive star formation rate as for supernovae. Thus, the ratio (C+O)/Fe should be constant. However, because the C and O elements then undergo partial H-burning creating some N, this is the sum (C+N+O)/Fe that stays constant, instead of (C+O)/Fe.
 |
Fig. 3 Sum of CNO elements [(C+N+O)/H] vs. [Fe/H] for CEMP-no stars with indications of upper limits as in Fig. 21 from Masseron et al. (2010). The large points represent MS or subgiant stars near the MS turnoff, while smaller points represent giant stars. The small horizontal lines on the circles denote low s-elements. Two lines of constant [(C+N+O)/Fe] ratios are indicated. |
 |
Fig. 4 Sum of CNO elements [(C+N+O)/H] vs. [Fe/H] from various sources down to the lowest [Fe/H] known. The codes for representing stars are the same as in Fig. 1. Upper bounds on [(C+N+O)/H] are indicated by arrows. The brown points at [Fe/H] = −7.1 represent the star SMSS 0313-6708, which has the limits as indicated in the text. |
As shown by Fig. 4, the more recent data by Norris et al. (2013) and Keller et al. (2014) allow us to extend the plot toward lower [Fe/H] values than in Fig. 3. We notice several facts:
-
First, the linear relation found by Masseron et al. (2010) for CEMP-no stars with [Fe/H] > -4.0 is further supported.
-
Surprisingly, the decreasing linear relation does not go on for lower [Fe/H]. Below a limit around [Fe/H] = − 3.5 to − 4.0, the extremely iron poor stars keep a more or less constant [(C+N+O)/H] ratio, or it decreases only very slowly. This means that [(C+N+O)/Fe] becomes very high for very low values of [Fe/H].
-
There are MS stars and subgiants both with high and low [(C+N+O)/H] ratios, and the same for the giant stars. Thus, the difference between the steep and the flat relations is probably not due to self-enrichment in CEMP-no stars.
-
The two objects that are Li-poor and near MS stars have relatively low [(C+N+O)/H] ratios. However, the number of such stars is very small.
-
The case of SMSS 0313-6708 with [Fe/H] < −7.1 deserves some explanations. Mostly upper limits of the abundance ratios [X/H] are given by Keller et al. (2014). We can estimate an upper limit [(C+N+O)/H] < −2.49, which is indicated in Fig. 4. Then, if we assume that the sum of C+N+O in the star just consists of C, with no N and O (which is certainly not the case), we get a lower limit [(C+N+O)/H] > −3.09. (Here, one has to be careful about the fact that N and O are not zero in the Sun, thus [(C+N+O)/H] ≠ [C/H] in this case!) This lower limit is also indicated in the figure. We see that the [(C+N+O)/H] ratio is relatively well confined.
-
How do we interpret the very high [(C+N+O)/Fe] ratios up to + 4 for the lowest [Fe/H]? We first notice that in view of the models of chemical evolution of the Galaxy, [Fe/H] values below −4 are relevant to very short stellar lifetimes and thus imply source stars with high masses, above 30 M⊙. In such short times, it is not possible to build an average chemical galactic evolution, all the more so for objects belonging to the outer galactic halo. In this most early period, the abundance ratios reflect the individual nucleosynthetic contributions more, rather than an average composition of the galactic environment, hence the need for inhomogeneous chemical evolution models (Cescutti & Chiappini 2014). Such high [(C+N+O)/Fe] ratios indicate that the typical yields from classical supernovae (Arnett 1996; Maeder 1992) do not significantly contribute to the early galactic enrichment of CEMP-no stars, which may preferably result from spinstars, mixing and fallback models, or some combination of both. Whether the high-velocity SN ejecta escape from the region of further star formation could also be a part of the explanation.
4.5. The case of nitrogen
Models of supernovae with mixing and fallback, constructed to interpret CEMP-no stars, generally have some difficulty producing sufficient nitrogen, and the [C/N] ratios are often higher by 1 or 2 dex than observed. For example, the comparison of the example CEMP-no star CS 29498-043 with the appropriate model by Nomoto et al. (2013) (see also Tominaga et al. 2014) shows that the observations give [C/N] = −0.40 (Norris et al. 2013), while the SN model with mixing and fallback gives [C/N] = + 1.6. The models of normal supernovae and hypernovae with mixing and fallback constructed to interpret stars with [Fe/H] in the range of −3.5 to −4.2 also produce insufficient N by about one to two orders of magnitude. Thus, nitrogen may be a problem for the mixing and fallback models, which generally show remarkable agreement for heavier elements. The very constraining ratio 13C/12C would further help to distinguish between the two sets of models.
The contribution of the winds of the “source stars” is likely to be responsible for the particularities of CEMP-no stars. These particularities necessarily originate in massive stars in view of the timescale of galactic chemical evolution. Massive stars become red supergiants with high CNO abundances, a composition known to lead to dust formation and high mass loss rates (van Loon et al. 1999, 2005; Srinivasan et al. 2011). Thus, as stated in Sect. 3, a combination of the rotational effects (mild mixing and high mass-loss rates due to composition changes), together with the possible effects of fallback (and may be further mixing) at the time of SN explosions, may provide satisfactory results. A recent work by Takahashi et al. (2014) confirms the increase in the abundance of nitrogen (and daughter elements Na and Al) resulting from including the effects of rotational mixing in the models.
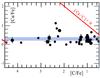 |
Fig. 5 Abundance ratios [Ca/Fe] vs. [C/Fe] of CEMP-no stars. The same codes for the observations and models as in Fig. 1 are adopted; no data on Ca are provided by Masseron et al. (2010). A thick horizontal blue line indicates the approximate average of the [Ca/Fe] ratios. The location corresponding to a solar ratio [Ca/C] = 0 is shown with a red line. The star SMSS 0313-6708 (Keller et al. 2014) is represented by a brown point and is a lower limit on both coordinates. |
5. Relation of CNO to α-elements
CEMP-no stars bear the traces of α-elements, such as Si, S, and Ca, which are formed in the onion-skin layers of the pre-supernovae. The strongly enhanced CNO elements, which make CEMP-no stars so particular, necessarily imply some other major effect(s), as mentioned above. In this section, we perform additional tests showing the huge difference between the properties of the α-elements, such as calcium and silicon, and those of the C, N, and O elements. The interest of the abundances of elements like Si and Ca, produced deeper in stars than are the lighter elements, has already been emphasized by Norris et al. (2013) in relation to the possibility of distinguishing between spinstar and mixing and fallback models to account for the properties of CEMP-no stars. These authors also emphasize the need “to have more accurate abundances in a larger sample of C-rich stars for comparison with more detailed model predictions for the two classes of models”.
Figure 5 shows the [Ca/Fe] ratios vs. the [C/Fe] ratios for CEMP-no stars. In this plot the stars with low [Fe/H] are on the left, since [C/Fe] is higher for lower [Fe/H] ratios. We see no correlation between calcium and carbon abundances. The scatter around an average of [Ca/Fe] = 0.2 to 0.3 is small (≈0.2 dex, i.e., about the same size as the observational errors). This flat curve means that the enrichments in Ca were the same as those in Fe from the core of the source stars, while carbon was, incredibly, produced much more than Fe and Ca at very low [Fe/H] values. The average [Ca/Fe] ratio around 0.2 is the same as the one observed in normal halo stars. While the [Ca/Fe] ratios of CEMP-no stars are within a range of about 1 dex (most stars lying within a range of 0.5 dex), the [C/Fe] values cover a range of 4 dex! Inspection of the figures representing the standard classical chemical yields of supernovae (Maeder 1992; Hirschi et al. 2005; Hirschi 2007) clearly shows that classic supernova models cannot produce such large changes of [C/Fe] while producing such limited changes of [Ca/Fe].
 |
Fig. 6 Abundance ratios [Ca/Fe] vs. [O/Fe] of CEMP-no stars. The stars are not all the same ones as in Fig. 5, because not all stars that have C-data necessarily have O-data. A thick horizontal blue line indicates the approximate average of the [Ca/Fe] ratios. The location corresponding to a solar ratio [Ca/O] = 0 is shown with a red line. |
Figure 6 shows the [Ca/Fe] vs. the [O/Fe] ratios. The same absence of correlation emerges as before. This was not evident since in pre-supernova models the O-rich layer lies deeper inside than the C rich layer and is the thickest one, making oxygen the most abundant of the α-elements. Thus, in the framework of classical supernova models, it is surprising that the behavior of oxygen has absolutely nothing to do with calcium’s behavior. In this connection, we may point out that supernovae models for Population III stars, as well as those for very low Z stars, show a positive relation between the Ca and O productions (see Fig. 5 by Nomoto et al. 2013). In addition, as in the case of C, the ratio [O/Fe] varies by 4 dex, while the range of [Ca/Fe] values is very limited.
Figure 7 shows the same kind of relation between [Si/Fe] and [C/Fe]. In pre-supernovae models, the silicon layer lies above the calcium layer and is close to the oxygen one. Again, there is no correlation between [Si/Fe] and [C/Fe], and the ranges covered by [Si/Fe] and [C/Fe] are very different, as in the two previous figures. This further confirms the completely different origin of the CNO and α-elements. As a matter of fact, the [Ca/Fe] and [Si/Fe] ratios of CEMP-no stars are fairly similar to the ones found in normal halo stars (see Fig. 4 in Chiappini 2013).
Norris et al. (2013) noticed that some relative enhancements of Si and Ca exist in some CEMP-no stars. Indeed, from Table 1 we see that some stars that have a high [Si/Fe] abundance ratio also have a high [Ca/Fe] content, for example HE 1012-150 and Segue 1-7.
The results of Figs. 5–7 clearly confirm the huge differences in the enrichments of CEMP-no stars in CNO-elements and α-elements (other than oxygen) and the relative lack of the α-elements at the very low [Fe/H]. These elements have necessarily been produced in the pre-supernova stages. Thus, where are they? We think there are essentially two hypotheses to explain this situation: either the stellar remnants retain the α-rich onion skin layers, as assumed in the mixing and fallback models, or these α layers, ejected at high velocities, partially escape from the outer galactic halo where CEMP-no stars went on to form. Whether the presence of small amounts of heavy elements and the differences between these heavy elements favor one of the two possible proposed explanations remains to be investigated.
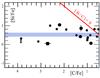 |
Fig. 7 Abundance ratios [Si/Fe] vs. [C/Fe] of CEMP-no stars. The stars are not all the same ones as in Fig. 5, because not all stars that have Ca data necessarily have Si data. A thick horizontal blue line indicates the approximate average of the [Si/Fe] ratios. The location corresponding to a solar ratio [Si/C] = 0 is shown with a red line. |
6. The elements of the Ne–Na and Mg–Al cycles
These two cycles, which accompany the CNO cycles, are not significant for energy production, but they do influence some abundances and isotopic ratios (Maeder 2009). If the anomalous abundances in CEMP-no stars are products of He-burning (mainly C, O, 22Ne, etc.) partially gone through CNO H-burning, there should also be some effects visible in the elements participating in the Ne–Na and Mg–Al cycles, which proceed by successive (p,γ) reactions and e+ emissions. Thus, we may expect some specific relations between the elements involved in these cycles, especially more since the light elements Na, Mg, and Al are enhanced relative to Fe in about the half of the CEMP-no stars, as shown by Norris et al. (2013). Also there should be some broad distributions of the concerned chemical abundances, rather than narrow ones as seen above for Ca and Si. Several nuclear rates involved in the two cycles are still highly uncertain, so that detailed quantitative predictions are difficult. As shown by Decressin et al. (2007), some rates have to be “pushed” to their possible limits and even increased by a factor of 1000 in order to account for some anticorrelations of abundances observed in globular clusters.
6.1. The Ne–Na cycle
The main effect of the Ne–Na cycle is to transform the various Ne isotopes (20Ne, 21Ne, 22Ne) into 23Na at relatively high temperatures above 4 × 107 K. Excesses of sodium have been found in massive supergiants by Boyarchuk et al. (1988) and further confirmed by many works. The Ne–Na cycle is also responsible of the “Na–O anticorrelation” observed for the stars in some globular clusters (Gratton et al. 2001). Many stellar sites have been proposed for this effect, most noticeably massive stars (Decressin et al. 2007). The anticorrelation is likely the result of H-burning, during which Ne is turned by (p,γ) reactions to Na by the Ne–Na cycle. At the same time, O is also transformed into N by the ON loops of the CNO cycle, thus creating the observed anticorrelation. In a cluster, the importance of mixing is different for each star so that different amounts of Na and CNO elements become visible at the surface, and this variety in the transport process allows one to see some relations between different elements. This may be the effect at the origin of the Na-O anticorrelation, observed for stars within a given globular cluster, although a variety of interpretations have been proposed (see Decressin et al. 2007, for further references).
The problem of the CEMP-no stars is different. The CEMP-no stars cover a very wide range of [Fe/H] values, from [Fe/H] = −7.1 to −2.5. The abundances of the CNO-elements may vary by a factor of 104 or more. These variations largely dominate the limited amplitudes of the observed Na–O and Mg–Al anticorrelations, which amount to less than 1 dex (and even 0.4 dex for Mg and Al), according to Gratton et al. (2001). Thus, the possible anticorrelations are largely overwhelmed by the global variations in the CNO as a function of [Fe/H], which may be up to 1000 times larger for CEMP-no stars. The Ne–Na chain reactions, active in the H-burning shell, only contribute to increasing the scatter around the general trends, scatter that is not negligible as we will see.
 |
Fig. 8 Abundance ratios [Na/Fe] vs. [N/Fe] of CEMP-no stars. The dots represent the star by Norris et al. (2013), the squares by Allen et al. (2012). The small vertical bars on the points indicate the main sequence or subgiant Li-poor stars. The small horizontal bars indicate the low-s stars (also noted b-). The light thick blue band represents the main trend of the observed points. The big blue arrow describes the effect of nuclear burning of 14N → 22Ne → 23Na, which contributes to the scatter of the figure. Small arrows indicate upper limits. |
For examining the Ne–Na cycle in the absence of Ne-data, we try to use the N data, because of the strong relations between nitrogen and neon. First, at the beginning of He-burning in the core, 14N is transformed into 22Ne. Then, the neon that diffuses to the H-burning shell is transformed by the Ne–Na cycle to 23Na. As the He-burning further proceeds, some amounts of 20Ne are created, which by diffusion in the H-burning region may also participate in the Ne–Na cycle (see for example Fig. 27.17 by Maeder 2009).
Figure 8 shows the relation between the [Na/Fe] and [N/Fe] ratios. We notice the following properties:
-
There is some correlation between the abundances of Na and N. The scatter is the same for MS stars and giants, which suggests that self-enrichment does not significantly influence this plot. The scatter is relatively large, which is not surprising since the nuclear-burning chain 14N → 22Ne → 23Na acts almost perpendicularly to the main trend of the data, as shown in Fig. 8.
-
Despite the scatter, we see that the global slope of the main trend is not far from 1. This means that the ratio Na/N stays almost constant through the range of CEMP-no stars, a fact consistent with the operation of the Ne–Na cycle.
-
The main trend results from the very large variation in the [N/Fe] among the CEMP-no stars: stars that have lots of N also produce lots of Na. This effect, which spans several dex, overwhelms the fact that at a given metallicity, the partial production of 23Na implies some 14N-destruction. This last effect only contributes to increasing the scatter of the general relation, as illustrated in Fig. 8.
-
The abundances of Na vary by orders of magnitude, as is the case for C, N, and O elements. This is much more than the variations in Ca and Si, typically produced in the onion-skin layers of supernovae. Thus, the amplitude of the variations suggests that at least a large portion of the Na in CEMP-no stars has an origin related to the H-burning cycles.
6.2. The Mg–Al cycle
The main effect of the Mg–Al cycle is to transform, also by (p,γ) reactions and e+ emissions, the various 24,25,26Mg isotopes into 27Al. (This cycle also produces the long-lived radioactive 26Al, responsible for the galactic γ-emission.) The cycle operates in H-burning regions typically at temperatures above 5 × 107 K (Decressin et al. 2007). An anticorrelation Mg–Al has been observed in globular clusters (Gratton et al. 2001). It has generally been interpreted in terms of the Mg–Al cycle: as Mg is destroyed by (p,γ) reactions, new Al is formed. Various kinds of stars have been considered as a potential site of these reactions, the case of massive stars with internal mixing has been studied by Decressin et al. (2007).
Here, we have data for the relevant elements of the Mg–Al cycle. Figure 9 illustrates the [Al/Fe] vs. [Mg/Fe] relation for CEMP-no stars. The blue arrow indicates the direction of the burning of Mg to Al, and this effect also contributes to the scatter around the general trend. We note the following facts:
 |
Fig. 9 Abundance ratios [Al/Fe] vs. [Mg/Fe] of CEMP-no stars. The wide light blue band describes the main trend. The thick blue arrow illustrates the direction of the burning by the Mg-Al cycle. Same remarks as for Fig. 8. |
-
Both Mg and Al increase simultaneously (for lower [Fe/H]) with a slope of about 1.0. This means that the ratio of Mg to Al stays about constant throughout the range of CEMP-no stars, a fact that is consistent with the operation of the Mg–Al cycle for these stars. There are two other arguments that support the view that Al is mainly due to the destruction of Mg produced in the helium-burning core.
-
First, models show that the high Mg abundance needed before the Mg-Al cycle comes into play may be created in low Z stars during the final part of the He-burning phase (Meynet et al. 2006). A fraction of this element may be conveyed to the stellar surface, where it may escape in the winds. This is illustrated well by models of rotating massive stars with Z = 10-5 by Meynet et al. (2006), which show that the winds present enrichments in Mg (summing over the 3 isotopes) by a factor 24 with respect to the initial Mg content, as shown in Table 4 of the mentioned reference.
-
Second, the synthesis of Mg near the end of the He-burning phase of low Z stars does not exclude some production of this element by supernovae. However, the amplitudes of the variations in Mg and Al do not plead so much for this hypothesis as a dominant process for these elements. In Fig. 9, both elements Mg and Al vary by two orders of magnitude. This is more than the cases of Si and Ca, which are ejected at the time of the supernova explosion.
-
Thus, the relation shown in Fig. 9, together with amplitudes of the variations in the abundances of Mg and Al, supports a scenario in which the largest part of these two elements comes from the migration of core He-burning products into the H-burning shell.
The “mother-daughter” relations with slopes of about 1.0 for N-Na (more a relation between grand mother and grand daughter) and Mg–Al are in agreement with partial H-burning of some products (Ne, Mg) of He-burning by the CNO and related cycles. That we do not observe the anticorrelations present in globular clusters is not at all contradictory, because the CEMP-no star composition is not the result of H-processing alone, but also the result of material produced by He-burning (in very variable amounts) and partially further transformed by H-burning. The extremely broad range of the CNO elements (and Na, Mg, and Al) present in CEMP-no stars largely overwhelms the effect of the H-burning cycles producing the anticorrelations.
In summary, the present analysis strongly suggests that elements such as Na, Mg, and Al, which are present in CEMP-no stars, behave like the CNO elements. These elements are thus produced by the Ne–Na and Mg–Al cycles operating in H-burning regions of the source stars.
Possible steps in the physical processes of partial mixing and nuclear H- and He-burning in massive very low Z stars.
7. An attempt to organize the CEMP-no stars
In natural sciences, a first step toward a better understanding often goes through classification of the objects under investigation. Since the extraordinary peculiarities of CEMP-no stars result from the partial mixing of products of He-burning into the H-burning shell, before escaping from the source stars, we may use this property to build a classification scheme by considering successive steps in the process of mixing. We note that the timescale of mixing is relatively short for rotating stars (Maeder 2009) so that a fraction of the newly synthesized elements can make a few back-and-forth motions between the He- and H-burning regions. This may result in further nuclear chains operating in the layers where some of the new elements enter. Mixing is always partial, affecting only a part of the new elements synthesized. Some H-burning reactions, such as the Ne–Na and Mg–Al cycles, cannot operate as long as some isotopes have not been created by the succession of back-and-forth matter exchanges between the H- and He-burning layers.
7.1. A possible classification scheme
Table 2 is an attempt to establish a classification on the basis of simple considerations based on the reactions involved in H- and He-burning regions and mixing between them. From the initial, very low Z composition (Z ≥ 10-9), if mixing brings some products of H-burning to the surface, the star keeps its very low CNO content, but with N enrichments (step 0+). These are just EMP-stars. Steps 1 and 1+ consist of stars where pure products of He-burning become visible at the stellar surface. In case 1+, the (α,γ) reactions lead to the production of some 20Ne, in addition to small amounts of 22Ne resulting from 14N. These 1 and 1+ objects are stars like WC and WO stars. It is still uncertain whether such objects exist at extremely low metallicities.
Steps 2 and 2+ consist of stars where some quantities of C and O from the He-burning core (case 1) have been partially mixed into the H-burning shell, where partial burning is forming some 14N. Then large amounts of CNO become visible at the stellar surface as a result of mixing and/or mass loss. We distinguish Case 2 where mixing is very mild (or H-burning proceeds weakly), which leads to [C/N] > 0 and [O/N] > 0 and Case 2+ where the H-burning of the mixed matter is more complete, leading to ratios [C/N] < 0 and [O/N] < 0, as well as to low 13C/12C ratios. Steps 2Na and 2+Na are just the same as the previous ones, but starting from Case 1+, where some Ne has also been produced. If the temperature is high enough, this allows the Ne–Na cycle to operate and to produce some 23Na, which may be observable.
In Steps 3 and after, we consider that some products of Steps 2 and 2+ are again mixed from the H-burning into the He-burning region, leading to new element synthesis, in particular from the reactions, ![\begin{eqnarray} ^{14}\mathrm{N}(\alpha,\gamma)^{18}\mathrm{F}(\,,{\rm e}^+ \nu_{\mathrm{e}})^{18}\mathrm{O}(\alpha,\gamma)^{22}\mathrm{Ne} \longrightarrow \; \; (\alpha, n)^{25}\mathrm{Mg} \quad \quad \\[1mm] \searrow \; \;(\alpha, \gamma)^{26}\mathrm{Mg} . \quad \; \; \label{ne22} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24153-14/aa24153-14-eq127.png) In the first case (Step 3), we consider that reaction (10) leads to a small amount of the relatively rare isotope 18O and then goes up to 22Ne, without reaching a significant formation of 25,26Mg isotopes, the formation of which requires higher temperatures. These more advanced stages of (α,γ) and (α,n) captures occur in Step 3+ with the complete reactions (10) and (11) operating. At the same time, there is some formation of 20Ne from the reaction
In the first case (Step 3), we consider that reaction (10) leads to a small amount of the relatively rare isotope 18O and then goes up to 22Ne, without reaching a significant formation of 25,26Mg isotopes, the formation of which requires higher temperatures. These more advanced stages of (α,γ) and (α,n) captures occur in Step 3+ with the complete reactions (10) and (11) operating. At the same time, there is some formation of 20Ne from the reaction 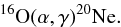 (12)The capture of neutrons coming from reaction (11) leads to the formation of some s-elements from the first peak, like strontium Sr and yttrium Y, as shown by Frischknecht et al. (2012). In Step 3++, the captures of neutrons from reaction (10) goes further in the production of s-elements with, in addition to the s-elements of the first peak, a significant production of s-elements from the second peak, such as barium Ba and lanthanum La. The star is likely no longer considered as a CEMP-no star, according to the current classification criteria, but rather as a low s-star or a “b-” (Masseron et al. 2010; Allen et al. 2012; Norris et al. 2013).
(12)The capture of neutrons coming from reaction (11) leads to the formation of some s-elements from the first peak, like strontium Sr and yttrium Y, as shown by Frischknecht et al. (2012). In Step 3++, the captures of neutrons from reaction (10) goes further in the production of s-elements with, in addition to the s-elements of the first peak, a significant production of s-elements from the second peak, such as barium Ba and lanthanum La. The star is likely no longer considered as a CEMP-no star, according to the current classification criteria, but rather as a low s-star or a “b-” (Masseron et al. 2010; Allen et al. 2012; Norris et al. 2013).
When the products of partial mixing into the He-burning zone are those coming from Steps 2Na and 2+Na, the same reactions as the previous ones may occur, leading to the same nucleosynthetic products, simply with Na present in addition to those already mentioned. This leads to Steps 3Na, 3+Na and 3++Na as indicated in Table 2.
In Step 4, some elements of Step 3 are again mixed into the H-burning zone, and this may allow the Ne–Na cycle to operate and produce some Na. Simultaneously some N is also synthesized from the C and O present in Step 3, and its abundance may be high again. In Steps 4+ and 4++, some elements of the corresponding Stages 3+ and 3++ (with or without Na) are brought into the H-burning region, where now the cycles Ne–Na and Mg–Al are both operating. This then leads to the presence of all the isotopes of elements Ne, Na, Mg, and Al occurring in these cycles, in addition to those created in the previous phases including the s-elements.
The main conclusion of what precedes is the extraordinary variety of compositions that may result from partial mixing between the H- and He-burning phases. In Table 2, there are 17 different cases that are theoretically possible. We could even have considered more of them, for example, by introducing further distinctions based on [C/N] and [O/N] ratios that are greater or less than 0, as we did in Steps 2 where this seems appropriate. It is possible that we do not find stars corresponding to some of the cases we have considered. Future works may hopefully try to analyze the observed CEMP-no and low s-stars in terms of the proposed scheme. Even some stars with a significant [Ba/Fe] ratio might belong to the genetic group of the descendants of spinstars. More objects with accurate data are certainly necessary for this undertaking, which may also lead to improvements in the proposed classification scheme.
7.2. The stars with [Sr/Fe] > 0
In principle, CEMP-no stars contain no or few s-elements. The ratios [Sr/Fe] and [Ba/Fe] are generally negative (Norris et al. 2013). Sr, like Rb, Y, Zr, Nb, etc., are s-elements of the first peak (corresponding to “a magic number” of neutrons N = 50). Ba, like Cs, La, Ce, etc., are s-elements of the second peak (corresponding to a magic number N = 82). There are four stars in Table 1 with positive [Sr/Fe] ratios, which we now discuss briefly.
The star HE 1327-2326 has [Sr/Fe] = 1.04, the highest ratio in the sample, and for barium an upper limit [Ba/Fe] < 1.46 (Norris et al. 2013), which is formally too high for a CEMP-no star, as already mentioned. We note that this star has a high [Mg/Fe] ratio of 1.55, consistent with the operation of the α-capture by 22Ne and neutron emission producing the synthesis of the s-elements. In this context, we recall that the models of massive rotating stars by Frischknecht et al. (2012) show that, although the s-elements produced mainly belong to the first peak, there are cases, especially for high rotation velocities, where a substantial number of elements of the second peak are formed. Thus, HE 1327-2326 is probably a member of the same genetic family as the formal CEMP-no stars, simply with much more complete mixing and nuclear burning than the average. This view is well supported by the fact that the other significant ratios are very high, with [Na/Fe] = 2.48, [Mg/Fe] = 1.55 and [Al/Fe] = 1.23, which indicates that relatively large quantities of the elements of the Ne–Na and Mg–Al cycles are reaching the stellar surface. In terms of our classification of Table 2, we would consider it as a 4++ star, which is the extreme case.
The three stars other with positive [Sr/Fe] values are CS 22949-037, BS 16929-005, and 53327-2044-515, with [Sr/Fe] = 0.55, 0.54, 0.81, and [Ba/Fe] = −0.52, −0.41, <0.15, respectively (Norris et al. 2013). Thus, these stars essentially have s-elements of the first peak and little from the second peak (in agreement with the formal definition of a CEMP-no star). Also, the lower Mg content of these stars (especially the last two) is consistent with fewer s-elements. The small abundances of aluminum indicate a relative absence of the Mg–Al cycle for the three stars, while the products of the Ne-Na cycle are visible in CS 22949-037.
The beautiful variety of the compositions of CEMP-no stars is likely to result from the intensity of the various nuclear reaction chains and cycles, as well as from the importance of mixing and mass loss in the source stars. These different effects probably depend on the different values of the stellar parameters, such as the initial masses (above about 7 M⊙), the different [Fe/H] ratios, and rotational velocities.
8. Conclusions
The extraordinary properties of the CEMP-no stars are a gift of Nature to help us to try to understand the first generations of stars in the Universe. We suggest the following tentative conclusions and lines of further exploration.
-
Chemical abundances support the view that CEMP-no stars exhibit products of He-burning that has partially gone through CNO processing. A portion of the elements may have experienced successive back-and-forth motions between the He- and H-burning zones in the source stars.
-
The comparison of the 12C/13C vs. [C/N] ratios of models and observations showed that the mass transfer in binaries with an AGB star is an unlikely source for the CEMP-no stars. This further confirms partial mixing, because full mixing would have destroyed the 13C isotopes.
-
Models of massive rotating stars with partial mixing and nuclear processing, and with strong mass loss in the He-burning and later phases, agree relatively well with the observed compositions. In this context, we note that the solar ratios should not be used to define the initial abundances ratios of the CNO and related elements, because this creates some artificial differences between models and observations of CEMP-no stars. Future models that take this remark into account may have more discriminating power.
-
As a marginal remark, we point out that four stars in the sample have log g> 4.60, which is surprising for such old objects. This may support the hypothesis of a relatively high density for these objects, owing to high He-content.
-
We confirm the finding by Masseron et al. (2010) of a linear relation between the [(C+N+O)/H] and [Fe/H] ratios for CEMP-no stars down to [Fe/H] ≈ − 3.5 or − 4.0. This means that the [(C+N+O)/Fe] ratios are constant, indicating a primary behavior of the CNO elements in the considered range of [Fe/H].
-
Below [Fe/H] = −4.0, the ratios [(C+N+O)/H] appear to no longer vary the same way, since they are either constant or show only a slight decrease with [Fe/H], so that the [(C+N+O)/Fe] ratios become very high, reaching about 4 dex. These values may just correspond to individual nucleosynthetic properties of the source stars, because in view of the timescales, there is no effective average galactic chemical evolution for such low [Fe/H].
-
The α-elements with atomic mass number >24, such as Si and Ca, present properties that are completely different from those of the CNO, Ne–Na, and Mg–Al elements: the ratios [α-elements/Fe] stay constant with a small scatter, while CNO and related elements show strong increases of the [CNO,.../Fe] ratios for lower [Fe/H]. These behaviors suggest that the heavy elements of the onion-skin layers of the presupernovae contributed less than the stellar winds from partially mixed stars in the earliest phases of the chemical enrichment of the Galaxy. Some possible reasons for this effect were proposed.
-
The elements Na, Mg, and Al show a range of variations, which is much greater than for the α-elements and is more similar to that of the CNO elements. Nevertheless, [Na/N] and [Al/Mg] stay about constant for the low [Fe/H] ratios. This supports the view that the Ne–Na and Mg–Al cycles were efficiently operating in the source stars.
-
The CNO, Ne–Na, and Mg–Al elements of CEMP-no stars present a wide variety of abundances. Continuous partial mixing leading some matter to experience several consecutive phases of He- and H-burning may explain this variety. We propose a classification of CEMP-no stars based on the properties of these successive phases.
-
The succession of the phases of He- and H-burning may lead to the formation of s-elements, mainly of the first peak with Sr and Y. In case of sustained neutron emissions from the reaction 22Ne (α,n)25Ne, some elements of the second s-peak may also be produced. In the sample of Table 1, there are four such stars with [Sr/Fe] > 0, and one of them (HE 1327-2326) may also show significant Ba-enrichment. Even, if it is not formally cataloged as a CEMP-no star according to the current criteria, it belongs to the same family, showing all its characteristics (Norris et al. 2013).
Acknowledgments
We thank an anonymous referee for very useful remarks that have significantly improved the manuscript.
References
- Allen, D. M., Ryan, S. G., Rossi, S., Beers, T. C., & Tsangarides, S. A. 2012, A&A, 548, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aoki, W., Norris, J. E., Ryan, S. G., Beers, T. C., & Ando, H. 2002, ApJ, 567, 1166 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, D. 1996, Supernovae and Nucleosynthesis (Princeton University Press) [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, III, & F. N. Bash (San Francisco: ASP), 25 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarchuk, A. A., Denisenkov, P. A., Hubeny, I., et al. 1988, in IAU Colloq. 108: Atmospheric Diagnostics of Stellar Evolution, ed. K. Nomoto (Berlin: Springer Verlag), Lect. Not. Phys., 305, 94 [Google Scholar]
- Campbell, S. W., Lugaro, M., & Karakas, A. I. 2010, A&A, 522, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carollo, D., Beers, T. C., Bovy, J., et al. 2012, ApJ, 744, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Cescutti, G., & Chiappini, C. 2010, A&A, 515, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., & Chiappini, C. 2014, A&A, 565, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Chiappini, C., Hirschi, R., Meynet, G., & Frischknecht, U. 2013, A&A, 553, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C. 2013, Astron. Nachr., 334, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Hirschi, R., Meynet, G., et al. 2006, A&A, 449, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Ekström, S., Meynet, G., et al. 2008, A&A, 479, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Frischknecht, U., Meynet, G., et al. 2011, Nature, 474, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Dalessandro, E., Ferraro, F. R., Massari, D., et al. 2013, ApJ, 778, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, D. K., Lambert, D. L., & Lemke, M. 1992, ApJ, 401, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K., & Avrett, E. H. 2013, ApJ, 773, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Meynet, G., Chiappini, C., Hirschi, R., & Maeder, A. 2008, A&A, 489, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabbian, D., Nissen, P. E., Asplund, M., Pettini, M., & Akerman, C. 2009, A&A, 500, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frischknecht, U., Hirschi, R., & Thielemann, F.-K. 2012, A&A, 538, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgy, C., Ekström, S., Eggenberger, P., et al. 2013, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Gustafsson, B., Edvardsson, B., & Nissen, P. E. 1992, Nature, 357, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Koposov, S., Norris, J. E., et al. 2013, The Messenger, 151, 25 [NASA ADS] [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herwig, F. 2004, ApJS, 155, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R. 2007, A&A, 461, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2005, A&A, 433, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iwamoto, N., Umeda, H., Tominaga, N., Nomoto, K., & Maeda, K. 2005, Science, 309, 451 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Karakas, A., & Lattanzio, J. C. 2007, PASA, 24, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, S. C., Bessell, M. S., Frebel, A., et al. 2014, Nature, 506, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Korn, A. J., Richard, O., Mashonkina, L., et al. 2009, ApJ, 698, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Suda, T., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 788, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., Chieffi, A., & Bonifacio, P. 2003, ApJ, 594, L123 [CrossRef] [Google Scholar]
- Lucatello, S., Tsangarides, S., Beers, T. C., et al. 2005, ApJ, 625, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1992, A&A, 264, 105 [NASA ADS] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin, Heidelberg: Springer) [Google Scholar]
- Maeder, A., & Meynet, G. 2006, A&A, 448, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Meynet, G. 2012, Rev. Mod. Phys., 84, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., Grebel, E. K., & Mermilliod, J.-C. 1999, A&A, 346, 459 [NASA ADS] [Google Scholar]
- Maeder, A., Przybilla, N., Nieva, M.-F., et al. 2014, A&A, 565, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martayan, C., Frémat, Y., Hubert, A.-M., et al. 2007, A&A, 462, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., Johnson, J. A., Plez, B., et al. 2010, A&A, 509, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matteucci, F. 2012, Chemical Evolution of Galaxies (Berlin, Heidelberg: Springer) [Google Scholar]
- Meynet, G., & Maeder, A. 2002a, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2002b, A&A, 381, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Maeder, A., & Ekström, S. 2005, in The Fate of the Most Massive Stars, eds. R. Humphreys, & K. Stanek, ASP Conf. Ser., 332, 228 [Google Scholar]
- Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010, A&A, 521, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moriya, T. J., & Langer, N. 2015, A&A, 573, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Yong, D., Bessell, M. S., et al. 2013, ApJ, 762, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B., & Cohen, J. G. 2005, A&A, 434, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N. 2012, A&A, 542, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, D., Tosi, M., Cignoni, M., et al. 2010, MNRAS, 401, 2490 [NASA ADS] [CrossRef] [Google Scholar]
- Spite, M., Cayrel, R., Hill, V., et al. 2006, A&A, 455, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Srinivasan, S., Sargent, B. A., & Meixner, M. 2011, A&A, 532, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stacy, A., Bromm, V., & Loeb, A. 2011, MNRAS, 413, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Starkenburg, E., Shetrone, M. D., McConnachie, A. W., & Venn, K. A. 2014, MNRAS, 441, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, K., Umeda, H., & Yoshida, T. 2014, ApJ, 794, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Tominaga, N., Iwamoto, N., & Nomoto, K. 2014, ApJ, 785, 98 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. T., Groenewegen, M. A. T., de Koter, A., et al. 1999, A&A, 351, 559 [NASA ADS] [Google Scholar]
- van Loon, J. T., Marshall, J. R., & Zijlstra, A. A. 2005, A&A, 442, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venn, K. A., & Lambert, D. L. 2008, ApJ, 677, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Norris, J. E., Bessell, M. S., et al. 2013, ApJ, 762, 27 [CrossRef] [Google Scholar]
All Tables
Possible steps in the physical processes of partial mixing and nuclear H- and He-burning in massive very low Z stars.
All Figures
 |
Fig. 1 Observations of 12C/13C ratios vs. [C/N], represented by black dots (Norris et al. 2013) and blue dots (Masseron et al. 2010). (The observations by Allen et al. (2012), represented by black squares in other figures, do not appear in this plot, because these authors do not provide data for the C-isotopes.) A vertical bar indicates MS or subgiant stars with low Li content, and a horizontal bar indicates CEMP-no or low-s stars by Masseron et al. which are also cataloged as “b-” by Allen et al. The big points apply to MS stars or to subgiants close to the turnoff with Teff> 5500 K and log g ≥ 3.25, as by Norris et al. (2013), while the small points represent the bright giants with lower Teff and log g. The Li-poor star G 77-61, which has Teff = 4000 K and log g = 5.05, is considered as a dwarf (Plez & Cohen 2005), so it is represented by a big point. Some of the 12C/13C values are lower bounds indicated by a vertical arrow. If at the same time, the N value is an upper bound, the arrow is oblique. Rectangles indicate the solar value and the CNO equilibrium value. AGB models with Z = 10-4 are indicated by broken red lines, the upper line comes from Karakas & Lattanzio (2007) in the range of 1 to 6 M⊙, and the lower one is by Herwig (2004) in the range of 2 to 6 M⊙ (Masseron et al. 2010), the low masses being on the top and the high ones at the bottom of the lines. A red star shows a fast-rotating AGB model of 7 M⊙ with Z = 10-5 (model F) by Meynet et al. (2010). Green stars show models of rapidly rotating massive stars A, B, C, D with masses from 40 to 85 M⊙ and Z = 10-8 from Hirschi (2007). Model E and E′ have a mass of 60 M⊙ with Z = 10-5 and are given in Table 4 by Meynet et al. (2006), respectively the left and right columns; they differ by the value of the mass loss rates (higher in E′). A parenthesis (wind+SN) indicates the values when both the wind and the supernova contributions are counted. The approximate directions of CN burning is indicated by blue arrows. |
| In the text | |
 |
Fig. 2 Comparison of the abundance ratios [O/N] and [C/N] of CEMP-no stars with model data. The same codes as in Fig. 1 are adopted to represent the observations and models. The small red rectangles show the AGB models by Herwig (2004) connected by a red broken line. The general trend of the CNO burning is represented by a big reddish arrow. The small vertical arrows indicate upper limits for [O/Fe] and the small oblique arrows upper limits for [N/Fe]. The star HE 1201-1512 was not indicated because of many lower limits. |
| In the text | |
 |
Fig. 3 Sum of CNO elements [(C+N+O)/H] vs. [Fe/H] for CEMP-no stars with indications of upper limits as in Fig. 21 from Masseron et al. (2010). The large points represent MS or subgiant stars near the MS turnoff, while smaller points represent giant stars. The small horizontal lines on the circles denote low s-elements. Two lines of constant [(C+N+O)/Fe] ratios are indicated. |
| In the text | |
 |
Fig. 4 Sum of CNO elements [(C+N+O)/H] vs. [Fe/H] from various sources down to the lowest [Fe/H] known. The codes for representing stars are the same as in Fig. 1. Upper bounds on [(C+N+O)/H] are indicated by arrows. The brown points at [Fe/H] = −7.1 represent the star SMSS 0313-6708, which has the limits as indicated in the text. |
| In the text | |
 |
Fig. 5 Abundance ratios [Ca/Fe] vs. [C/Fe] of CEMP-no stars. The same codes for the observations and models as in Fig. 1 are adopted; no data on Ca are provided by Masseron et al. (2010). A thick horizontal blue line indicates the approximate average of the [Ca/Fe] ratios. The location corresponding to a solar ratio [Ca/C] = 0 is shown with a red line. The star SMSS 0313-6708 (Keller et al. 2014) is represented by a brown point and is a lower limit on both coordinates. |
| In the text | |
 |
Fig. 6 Abundance ratios [Ca/Fe] vs. [O/Fe] of CEMP-no stars. The stars are not all the same ones as in Fig. 5, because not all stars that have C-data necessarily have O-data. A thick horizontal blue line indicates the approximate average of the [Ca/Fe] ratios. The location corresponding to a solar ratio [Ca/O] = 0 is shown with a red line. |
| In the text | |
 |
Fig. 7 Abundance ratios [Si/Fe] vs. [C/Fe] of CEMP-no stars. The stars are not all the same ones as in Fig. 5, because not all stars that have Ca data necessarily have Si data. A thick horizontal blue line indicates the approximate average of the [Si/Fe] ratios. The location corresponding to a solar ratio [Si/C] = 0 is shown with a red line. |
| In the text | |
 |
Fig. 8 Abundance ratios [Na/Fe] vs. [N/Fe] of CEMP-no stars. The dots represent the star by Norris et al. (2013), the squares by Allen et al. (2012). The small vertical bars on the points indicate the main sequence or subgiant Li-poor stars. The small horizontal bars indicate the low-s stars (also noted b-). The light thick blue band represents the main trend of the observed points. The big blue arrow describes the effect of nuclear burning of 14N → 22Ne → 23Na, which contributes to the scatter of the figure. Small arrows indicate upper limits. |
| In the text | |
 |
Fig. 9 Abundance ratios [Al/Fe] vs. [Mg/Fe] of CEMP-no stars. The wide light blue band describes the main trend. The thick blue arrow illustrates the direction of the burning by the Mg-Al cycle. Same remarks as for Fig. 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


