| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201425386 | |
| Published online | 10 March 2015 | |
A connection between the instability strips of ZZ Ceti and V777 Herculis white dwarfs
Pulsating accreting GW Lib white dwarfs
1 Institut d’Astrophysique et de Géophysique, Université de Liège, 17 allée du 6 Août, 4000 Liège, Belgium
e-mail: valerie.vangrootel@ulg.ac.be
2 Département de Physique, Université de Montréal, CP 6128, Succursale Centre-Ville, Montréal, QC H3C 3J7, Canada
Received: 21 November 2014
Accepted: 23 January 2015
Aims. We aim to determine the theoretical instability strips of white dwarfs with diverse H and He content in their atmospheres, from a solar composition to a H-depleted atmosphere. Pulsators with mixed H-He atmospheres are indeed known to exist, and these are the white dwarfs in cataclysmic accreting systems of the GW Lib type. We thus also aim to determine the range of periods of excited pulsation modes, and to qualitatively compare these to the observed periods in GW Lib white dwarf pulsators.
Methods. In the first full nonadiabatic stability analysis of pulsators of this kind, we applied a time-dependent convection treatment and an energy leakage argument to compute, for cooling models of white dwarfs with various masses and envelope compositions, the location of the blue and the red edges, as well as the properties of pulsation modes.
Results. We find that our derived instability strips form a true continuum in the log g-Teff plane and that their individual location depends uniquely on the assumed atmospheric composition, from the solar composition models at low effective temperatures to the H-depleted models at much higher temperatures. Taking into account our previous results from the ZZ Ceti (pure H atmosphere) and V777 Her (pure He atmosphere) white dwarf pulsators, this implies that all of these instability domains are connected via the same fundamental driving mechanism. Applying our results to the case of white dwarf pulsators of the GW Lib type, we find that our theoretical instability strips can qualitatively account for all of the known cases. The computed range of periods of excited modes also compares qualitatively very well to the observed ones.
Conclusions. The GW Lib pulsators are very similar in nature to ZZ Ceti and V777 Her white dwarfs. It is the diverse chemical compositions in their atmosphere and envelope that defines their specific pulsation properties. Beyond GW Lib pulsators, white dwarfs can sometimes exhibit mixed H-He atmospheres, such as in the recently found proto-He white dwarf pulsators. Our results open the way towards quantitative asteroseismology of these various kinds of white dwarfs.
Key words: stars: oscillations / white dwarfs
© ESO, 2015
1. Introduction
The cooling sequence of the Hertzsprung-Russell (HR) diagram harbors various and distinct families of pulsating white dwarfs, showing multiperiodic luminosity variations generally caused by g-mode oscillations (see, e.g., Fontaine & Brassard 2008, for a detailed review). Among these, the V777 Her or DBV (He-atmosphere) pulsating white dwarfs tightly group around Teff ~ 25 000 K, while the ZZ Ceti or DAV (H-atmosphere) stars are significantly cooler pulsating white dwarfs in the HR diagram, clustering around Teff ~ 12 000 K. The driving mechanism for oscillations in ZZ Ceti and V777 Her white dwarfs is conceptually the same: the stars are in a phase of their cooling sequence where hydrogen (ZZ Ceti) or helium (V777 Her) in the outer envelope recombines, leading to a huge increase in the envelope opacity. This in turn strangles the flow of radiation, and finally causes pulsational instabilities in the form of g-mode oscillations (see, e.g., Winget et al. 1982; Winget 1982).
Huge progress has been made recently in determining the boundaries of both the empirical and the theoretical instability strips of ZZ Ceti white dwarfs. On the observational side, the detailed mapping of the instability strip has been a long-term objective pursued by the Montréal group, starting with Bergeron et al. (1995), with the latest results reported by Gianninas et al. (2011, 2014). These efforts have led to the most reliable determination of the empirical strip currently available. In addition, pulsations in low and extremely low-mass DA white dwarfs have been found recently (Hermes et al. 2013, and references therein). These new pulsators are significantly less compact and cooler than the more usual ZZ Ceti stars, but they have H-dominated atmospheres (Gianninas et al. 2014) and form a natural extension of this family (Van Grootel et al. 2013).
On the theoretical front, the introduction of a time-dependent convection (TDC) treatment allowed us to precisely reproduce the blue edge of the ZZ Ceti instability strip, as well as to arrive at a correct understanding of the onset and development of pulsational instabilities at that blue edge as functions of cooling (Van Grootel et al. 2012). For the red edge, whose theoretical determination has remained elusive over the years (Van Grootel et al. 2012, and references therein), we recently resurrected the idea of energy leakage of the oscillation modes through the atmosphere (Hansen et al. 1985). According to this theory, the red edge occurs when the thermal timescale in the driving region (located at the base of the H convection zone) becomes equal to the critical period beyond which gravity modes cease to exist. Using these approaches (TDC and the energy leakage argument), we found that our theoretical ZZ Ceti instability strip accounts remarkably well for the boundaries of the empirical strip, including the low-gravity, low-temperature regime where the new low- and extremely low-mass pulsators are found (Van Grootel et al. 2013).
The V777 Her white dwarfs have received, in comparison, less attention over the years and are much less numerous than their ZZ Ceti counterparts. There are two reasons for this scarcity: first, they are significantly hotter and cool more quickly than ZZ Ceti stars; second, the fraction of DB stars drops to less than 20% of all the white dwarfs in the range of effective temperature where the DB pulsators are found (Bergeron et al. 2011). The spectroscopic determination of the empirical boundaries of the V777 Her instability strip still strongly relies on the work of Beauchamp et al. (1999), who carried out a systematic and consistent investigation of the time-averaged class properties of the pulsating DB white dwarfs. One difficulty that arises is the sensitivity of effective temperature and surface gravity determinations to spectroscopically undetectable (in the optical domain) small traces of H that may be present in the He-dominated atmospheres. This has been most recently discussed by Bergeron et al. (2011) who have also provided the most up-to-date view of the DBV instability strip.
On the theoretical front, Dupret et al. (2008) introduced a TDC treatment to pulsate, in a more realistic way than before, cooling models of DB white dwarfs with a pure He envelope (see also Quirion et al. 2008)1. They were able to find a credible blue edge compared to the empirical one (given the uncertainties mentioned above on Teff/log g determinations for DB stars), as well as a credible red edge. Contrary to ZZ Ceti white dwarfs, the theoretical DB red edge obtained with TDC satisfactorily reproduces the empirical one, provided the turbulent pressure variations δPturb is enhanced by a factor of 4. It is not yet clear why this is so (Dupret et al. 2008; Quirion et al. 2008). The period interval of the unstable g-modes predicted by these computations is also broader than what is observed, leaving room for improvement. The energy leakage argument also remains to be tested in pulsating DB models.
Pulsations in white dwarfs belonging to cataclysmic systems are also known to exist. Indeed, the discovery of nonradial pulsations in the white dwarf component of the cataclysmic binary GW Librae was reported by Warner & van Zyl (1998). Since then, a dozen more systems of this type, called pulsators of GW Lib type after the prototype, have been uncovered and intensively studied (see, e.g., Szkody et al. 2010, and references therein). Given the close binary nature of these systems, it has remained difficult to characterize the individual pulsating white dwarfs through standard spectroscopy. In particular, no direct information is available from spectroscopy on the surface gravity and on the atmospheric chemical composition. Although, in the latter case, it should reflect that of the donor component, i.e., anywhere from a solar mixture to a highly enriched He composition if the donor is well evolved. On the other hand, reliable estimates of the effective temperature have been derived, indicating that GW Lib pulsators occupy a significantly wider domain in effective temperature than the V777 Her or ZZ Ceti stars do, while overlapping the latter.
To our knowledge, no detailed nonadiabatic studies have ever been carried out for the GW Lib pulsators. Only the paper of Arras et al. (2006) actually addressed the question of pulsational instabilities in GW Lib white dwarfs, but using a semi-analytic argument that boils down to a necessary condition for mode driving in white dwarfs. However, it is important to realize that this so-called thermal timescale argument, which states that pulsation modes may be driven if their periods are comparable to the local thermal timescale at the base of the convection zone, is not a sufficient condition. It allows for rough estimates of the location of the blue edge of a potential instability strip, but can say nothing about the reality of such a strip and about the range of periods and actual modes being excited in a stellar model. In short, the approach needs to be validated through detailed nonadiabatic studies, which cannot be avoided if one wants to fully exploit the potential of stellar pulsation theory. We note that Arras et al. (2006) made excellent use of the thermal timescale approach, emphasizing, in particular, how the blue edge could depend on the chemical composition and the surface gravity for GW Lib instability strips. At the same time, and quite correctly, they warned in their conclusion section that their approach needs to be validated through full nonadiabatic pulsation calculations. We followed that path in the present work.
We aim to determine by full nonadiabatic computations the theoretical instability strips of white dwarfs with diverse H and He content in their atmospheres, from a solar composition to a H-depleted atmosphere. We present our cooling white dwarf models and stability analysis tools (e.g., TDC treatment and energy leakage argument) in Sect. 2. Section 3 is devoted to the resulting theoretical instability strips, while Sect. 4 presents the computed ranges of the excited modes we obtained. These two sections have a special emphasis on the relation to the observed properties of pulsating white dwarfs in GW Lib systems. We discuss our results and finally conclude in Sect. 5.
 |
Fig. 1 Structure of the envelope of a representative 0.6 M⊙ model, for eight different envelope chemical compositions ranging from solar (upper left quadrant of upper panel) to a H-less mixture (lower right figure of lower panel). The boundaries of the outer convection zone(s) are indicated by heavy dots. The three dotted curves in each plot correspond to a Rosseland optical depth of 0.1, 1.0, and 10.0, from top to bottom. The boundaries of the instability strip for each case considered are indicated by blue and red vertical dotted lines. |
 |
Fig. 2 Left panel: details of the structure of the outer layers of a representative evolving 0.6 M⊙ white dwarf with a solar composition in the envelope. The ordinate gives the fractional mass depth in logarithmic units. On this scale, the center of the star is at log q = 0; only the envelope layers are depicted here. The small dots define “isocontours” of opacity, and some are labelled by their value of log κ. The small filled circles indicate the boundaries of the superficial convection zones that develop due to He and H recombination. It should be pointed out that the top of the convection zones always resides in the photospheric layers, while the base sinks deeper into the star as it cools, until degenerate conduction takes over in the cooler, more evolved phases. The vertical dashed lines indicate the blue and red edges obtained with our TDC treatment with ML2/α = 1.0. Right panel: similar to left panel, but the small dots now define isocontours of the local convective turnover timescale log τc expressed in seconds. The boundaries of the convection zones are well defined in this plot, so the small filled circles used in the left panel are not necessary. |
2. Theoretical tools
2.1. Cooling white dwarf models
In this study, we used evolutionary models computed with the white dwarf stellar code briefly presented in Fontaine et al. (2001) and continuously updated since then. For the present needs, i.e., for a nonadiabatic survey, it is more than sufficient to consider simplified evolutionary models since the nonadiabatic physics is concentrated in the envelope. Hence, to save considerable computing time, we constructed simplified models made of a pure C core surrounded by an envelope with a fractional mass log q = log (1 − M(r) /M∗) = −4.5 of diverse compositions. Eight envelope compositions were considered, from solar (X = 0.70,Y = 0.28; X and Y being the fractional mass of H and He respectively) to a H-less mixture (X = 0.00,Y = 0.98). Each of the chosen compositions contains metals in the solar proportions, with Z = 0.02. For each of the eight envelope compositions considered, we computed four distinct evolutionary sequences characterized by a total mass of 0.3, 0.6, 0.9, and 1.2 M⊙. Each of the 32 evolutionary tracks covers a very wide range of effective temperature, from above 60 000 K down to about 1000 K, more than enough to cover the empirical V777 Her and ZZ Ceti instability strips, and for the effective temperatures of the known pulsating white dwarfs in GW Lib systems.
We note that the particular choices of model parameters such as the core composition, the actual location of the base of the thick envelope, or the detailed composition profile between the core and the envelope do not affect in any significant way the nonadiabatic physics associated with the driving mechanism. These choices do influence the period spectrum, but not the range of excited periods or the efficiency of driving. An explicit demonstration of this property has been presented in Sect. 3.2 of Van Grootel et al. (2013) in the context of the recently-discovered DA pulsators with extremely low masses. On the other hand, the stability analysis depends critically on how convection is handled in the equilibrium white dwarf models. In the present work, we adopted the ML2/α = 1.0 flavor for mixing-length theory, which was found to best match the empirical data for ZZ Ceti stars (Van Grootel et al. 2013). Furthermore, we included a detailed treatment of the feedback of convection on the structure of the envelope (see Van Grootel et al. 2012 for a recent discussion of this important point, their Fig. 5 in particular).
Figure 1 presents some details of the outer envelopes of eight cooling models of the same total mass of 0.6 M⊙, but with eight different envelope chemical compositions, ranging from solar to a H-less mixture. The atmospheric layers are mapped through the use of the three dotted curves in each plot, corresponding to a Rosseland optical depth of 0.1, 1.0, and 10.0. The boundaries of the outer convection zone(s) are indicated by heavy dots. We note the complex double structure associated with HeII and HI−HeI ionization zones. With cooling, these distinct convection zones merge together through pressure effects in white dwarfs. This point is of some importance because envelope models based on an ideal gas equation of state (such as those used by Arras et al. 2006, for example) would retain, to much lower effective temperatures than shown here, these two separate convection zones and influence the details of the driving process.
2.2. Stability analysis tools
We used the same approach as in Van Grootel et al. (2013) for the stability analysis of the 32 evolutionary sequences with diverse envelope compositions. We thus employed a version of the MAD nonadiabatic pulsation code (Dupret 2002) that includes a TDC treatment for pulsations in presence of convection. We refer to Van Grootel et al. (2012) for the technical details of the adaptation of the TDC treatment to the white dwarf models; the basic theory, along with the latest improvements, can be found in Grigahcène et al. (2005). In a nutshell, the TDC recipe included in MAD is developed within the framework of mixing-length theory, and the stability of the solution is studied by a linear perturbative method. The treatment of convection is local, for consistency with the white dwarf models. The adopted expression for the perturbation of the mixing length l = αHp (Hp is the pressure scale height) is 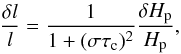 (1)where \begin{lxirformule}$\sigma$\end{lxirformule} is the pulsational frequency and τc the convective turnover timescale. We retrieve the two limiting cases δl/l → δHp/Hp when στc ≪ 1 (instantaneous adaptation of convection) and δl/l → 0 when στc ≫ 1 (frozen convection). Both for the ZZ Ceti and V777 Her models, the convective turnover timescale is much smaller than the pulsation periods of interest at the blue edge (reducing TDC to instantaneous adaptation of convection), while as the star cools the convective turnover timescale become on the order of the pulsation periods, requiring a full TDC treatment like ours (Van Grootel et al. 2012; Dupret et al. 2008; Quirion et al. 2008).
(1)where \begin{lxirformule}$\sigma$\end{lxirformule} is the pulsational frequency and τc the convective turnover timescale. We retrieve the two limiting cases δl/l → δHp/Hp when στc ≪ 1 (instantaneous adaptation of convection) and δl/l → 0 when στc ≫ 1 (frozen convection). Both for the ZZ Ceti and V777 Her models, the convective turnover timescale is much smaller than the pulsation periods of interest at the blue edge (reducing TDC to instantaneous adaptation of convection), while as the star cools the convective turnover timescale become on the order of the pulsation periods, requiring a full TDC treatment like ours (Van Grootel et al. 2012; Dupret et al. 2008; Quirion et al. 2008).
 |
Fig. 3 Predicted GW Lib instability strips for models with envelope compositions ranging from solar (upper left figure of upper panel) to a H-less mixture (lower right figure of lower panel). The dotted vertical lines correspond to the effective temperature for each of the 11 pulsating white dwarfs of the GW Lib type listed in Table 6 of Szkody et al. (2010). |
The right panel of Fig. 2 shows that this particular behavior of the convective turnover timescale is also at work in models with an intermediate H–He envelope composition, at least in the cooler evolutionary phases associated with g-mode instabilities. Given that the lowest radial order (k = 1) g-mode corresponds to a period on the order of 100 s in a representative 10 000−15 000 K, 0.6 M⊙ white dwarf, the described behavior is well illustrated in that plot. We also note that the convection zone associated with HeII partial ionization at high effective temperatures is characterized by convective turnover timescales comparable to or longer than the reference period. No pulsational instabilities are found at these high temperatures, however. To complement this, the left panel of Fig. 2 shows a similar plot, but emphasizing the opacity profiles in the same evolutionary models. Because of the simultaneous presence of H and He, the opacity shows an intricate pattern due to the different partial ionization zones. This plot should be compared to Figs. 2 and 3 of Van Grootel et al. (2012) for the case of pure H envelopes.
Despite the inclusion of a TDC approach in our white dwarf investigations, the determination of the red edge has remained elusive. For the ZZ Ceti stars, the predicted red edge from our nonadiabatic calculations is much cooler than the empirical value, typically by thousands of degrees (Van Grootel et al. 2012). As briefly mentioned in the Introduction, and in contrast, a credible red edge for the V777 Her stars has been found in such computations. However, this was achieved at the price of postulating a turbulent pressure variations δPturb enhanced by a factor of 4 (Dupret et al. 2008; Quirion et al. 2008). It is still unclear how this can be physically justified. Furthermore, the DB models that have been used in these studies do not include convective feedback on the atmospheric structure, which shifts inwards the whole of the superficial convection zone. The impact of such a feedback is to move the full instability strip towards higher effective temperatures, possibly degrading the agreement with the empirical strip. The importance of the shift remains to be quantified for these DB pulsators.
In the present work, which includes convective feedback, we adopt the approach proposed by Van Grootel et al. (2013) to estimate the location of the red edge for each of the instability strips that we uncovered. This is based on the energy leakage argument referred to above according to which the red edge occurs when the thermal timescale in the driving region becomes larger than the critical period beyond which g-mode oscillations cease to exist. As mentioned in the Introduction, such a hypothesis accounts remarkably well for the red edge of the empirical strip of ZZ Ceti white dwarfs (Van Grootel et al. 2013), and this is our main justification for using the method again in the present context.
 |
Fig. 4 Predicted ranges of excited dipole (ℓ = 1) g-modes for representative models near the red edge of the instability strips from 1.2 M⊙ (lower left and shorter periods) to 0.3 M⊙ (upper right and larger periods). The bigger the dot, the more unstable the mode. |
3. Theoretical instability strips
We computed with the MAD code (in the ML2/α = 1.0 version) the properties of the g-mode oscillations for all models belonging to our 32 evolutionary sequences. We also applied the criterion τth ≃ Pcrit to these models to evaluate the red edge. Figure 3 presents the main results of our stability analysis, here for g-mode oscillations with ℓ = 1. The fact that we used only four distinct evolutionary sequences of different mass (0.3, 0.6, 0.9, and 1.2 M⊙) for a given envelope composition leads to a somewhat coarse covering in the log g direction as can be seen in the plots. Each blue or red edge is defined in terms of only four points corresponding to these four different masses, but this was deemed sufficient in the present context. For a solar envelope composition, the instability strip is relatively narrow and the red edge slope is slightly more pronounced than the blue one, making the strip narrower towards lower masses. Qualitatively, this behavior is quite similar to that of the ZZ Ceti (pure H atmosphere) instability strip (Van Grootel et al. 2013). With increasing He abundance, both the blue and the red edge move towards higher effective temperatures, although at a different pace. Furthermore, the blue edge gets initially warmer at a faster pace for the low-mass models. In the limit of H-less (X = 0.00,Y = 0.98) envelopes, the instability strip has become significantly hotter and wider than for a solar or pure-H envelope. Furthermore, the blue and red edges have approximately the same slope. This behavior is now very similar to the theoretical instability strip of DB (pure He atmosphere) white dwarfs (Dupret et al. 2008; Quirion et al. 2008).
We note that the exploratory results of Arras et al. (2006), which are based on the thermal timescale argument discussed in the Introduction, are approximately in line with our detailed nonadiabatic results. In particular, the migration of the blue edge at higher effective temperatures with increasing He abundance and the dependency of the surface gravity have been well described in the approach of Arras et al. (2006), at least at the qualitative level. There are differences though, such as the fact that our detailed calculations do not reveal the existence of a regime in which two distinct instability strips could exist for a given envelope composition. This is an example of the limitations of the predicting power of the thermal timescale argument, which remains, as noted above, a necessary but not sufficient condition for driving.
For comparison purposes, we also plot in Fig. 3 the values of the effective temperature for each of the 11 pulsating white dwarfs of the GW Lib type listed in Table 6 of Szkody et al. (2010) in the form of vertical dotted lines. Taking into account the uncertainties on these estimates (provided in that table), and allowing for variations in the envelope composition from one star to another (which is difficult to determine spectroscopically given the binary nature of these objects), we can qualitatively account for all of the known cases. Diverse envelope compositions seem possible, although our results exclude the most extreme H-poor (X< 0.10) envelopes, at least for the white dwarf pulsators discussed in Szkody et al. (2010). Figure 3 also suggests that the coolest GW Lib pulsators are likely low-mass objects. Finally, as already suggested by Arras et al. (2006), the different atmospheric He content from one object to another provides a natural explanation as to why white dwarfs in cataclysmic binaries of the GW Lib type do not show pulsations in the same range of effective temperature. In addition, the narrowness of the instability strip, especially for the H-rich models, is in line with the suggestion that heating (cooling) due to variable accretion can move a star in and out of a given strip, thus leading to phases of pulsational activity (quiescence) in a given GW Lib star (Szkody et al. 2010).
We show in Fig. 1 the instability strips of our 0.6 M⊙ models for the eight different envelope chemical compositions. In a way similar to that found for the ZZ Ceti and V777 Her stars, pulsational instabilities start to develop when the base of the main convection zone sinks significantly with decreasing effective temperature (Dupret et al. 2008; Van Grootel et al. 2012).
4. Range of excited modes
Figure 4 shows our predicted ranges of excited dipole (ℓ = 1) g-modes for representative models inside each of the instability strips, but near the red edge. For each envelope composition illustrated, we present the range of excited periods for a massive 1.2 M⊙ model near the red edge (lower left and shorter periods on average) as well as for the other masses considered in our evolutionary calculations, including a less massive 0.3 M⊙ model near the red edge (upper right and larger periods than average). Each dot represents an excited dipole mode, and the size of the dot is a logarithmic measure of the imaginary part of the complex frequency. The bigger the dot, the more unstable the mode. Figure 4 illustrates explicit predictions as to the range of excited periods in GW Lib pulsators.
As an example, if we adopt a value of 15 200 K for the effective temperature of the pulsating white dwarf component in GW Lib itself (Szkody et al. 2010), a mass of about 0.84 M⊙ according to van Spaandonk et al. (2010), the dominant modes with periods of 230, 370, and 650 s (van Zyl et al. 2004) can easily be accounted for at the qualitative level if the donor is rather He-rich.
5. Discussion and conclusion
We have presented in this paper the theoretical instability strips of white dwarf models having diverse H and He content in their atmospheres, from a solar composition to a H-depleted atmosphere. We applied the same stability analysis tools as in our previous investigations, namely the TDC treatment and the energy leakage argument, in order to derive the location of the blue and the red edges of the instability strip in the log g–Teff diagram. We find that the shape and location of the instability strip depends strongly on the assumed envelope composition. With increasing He content the strip moves towards higher effective temperatures and broadens as well, with the blue edge moving faster than the red edge. Furthermore, the widening of the strip is initially (low values of Y) faster in low-mass models. The instability strip of white dwarfs with atmospheres of solar composition is qualitatively very similar to the ZZ Ceti strip (Van Grootel et al. 2013), while the instability strip of H-depleted atmosphere white dwarfs qualitatively behaves as the V777 Her strip computed for pure He atmospheres (Dupret et al. 2008; Quirion et al. 2008). This strongly suggests that DAV and DBV instability strips are indeed connected, with a continuum of pulsation modes that are excited by a convective driving mechanism related to the H–He recombination in the stellar envelope.
Pulsating white dwarfs with mixed H-He atmospheres are known to exist, and these are the GW Lib stars (pulsating white dwarfs that accrete material from a solar composition or He-enriched donor in a cataclysmic system). The exact envelope composition and surface gravity of these white dwarfs in cataclysmic binaries are difficult to derive, but good estimates of the effective temperature have been obtained for 11 pulsators of the GW Lib type so far (Szkody et al. 2010). Taking into account the uncertainties on these estimates, and allowing for variations in the envelope composition from one star to another, our theoretical instability strips can qualitatively account for all of the known cases. We also computed the range of excited pulsation modes for representative models of diverse masses, qualitatively accounting for the periods observed in these objects. In the case of GW Lib itself, for which the white dwarf mass was measured through gravitational redshift of a resolved absorption feature (van Spaandonk et al. 2010), the dominant modes can easily be accounted for at the qualitative level if the donor is rather He-rich. This exercise may be repeated with other pulsators when mass determinations become available.
It is also well known that DB white dwarfs often show small, but nonnegligible traces of H in their atmospheres (Voss et al. 2007; Bergeron et al. 2011). As shown here, the exact H-He content has a strong impact on the determination of the instability strip and on the range of excited periods. This deserves more attention in a future reevaluation of the V777 Her instability domain. White dwarfs with mixed H–He atmospheres also exist in the very low-mass regime (Gianninas et al. 2014), and these are the He-core white dwarf components of binary systems emerging from common envelope evolution. So far, pulsations have been discovered in a handful of cooling low-mass white dwarfs (Hermes et al. 2013), but the known pulsators are all H-dominated (DA) stars and fall in the extended ZZ Ceti strip (Van Grootel et al. 2013; Gianninas et al. 2014). However, the jury is still out on the possibility that low-mass cooling white dwarfs having a He-enriched atmosphere and envelope may also pulsate at higher effective temperatures, as theoretically predicted here. In addition, the recent discovery of pulsations in pre-low-mass white dwarfs (i.e., belonging to the contraction phase as opposed to the cooling phase) with apparently mixed H-He atmospheres (Maxted et al. 2013, 2014) strongly suggests that calculations similar to the ones considered in this paper are of interest. Our results pave the way towards quantitative asteroseismology of these mixed-atmosphere white dwarf pulsators. Asteroseismology can indeed shed light on the internal structure, composition, origin, and evolution of various kinds of white dwarfs, as best exemplified by the recent asteroseismic determination of the bulk core composition and envelope layering for the ZZ Ceti star Ross 548 (Giammichele et al. 2014).
It is this especially adapted treatment that was also used later by Van Grootel et al. (2012, 2013) to study pulsations in the presence of convection for the ZZ Ceti stars.
Acknowledgments
V.V.G. is an F.R.S.-FNRS Research Associate. This work was supported in part by the Natural Sciences and Engineering Research Council of Canada. G.F. also acknowledges the contribution of the Canada Research Chair Program.
References
- Arras, P., Townsley, D. M., & Bildsten, L. 2006, ApJ, 643, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Beauchamp, A., Wesemael, F., Bergeron, P., et al. 1999, ApJ, 516, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeron, P., Wesemael, F., Lamontagne, R., et al. 1995, ApJ, 449, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeron, P., Wesemael, F., Dufour, P., et al. 2011, ApJ, 737, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupret, M.-A. 2002, Bull. Soc. Roy. Sci. Liège, 71, 249 [Google Scholar]
- Dupret, M.-A., Quirion, P.-O., Fontaine, G., Brassard, P., & Grigahcène, A. 2008, J. Phys. Conf. Ser., 118, 012051 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., & Bergeron, P. 2001, PASP, 113, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Giammichele, N., Fontaine, G., & Brassard, P. 2014, in 6th Meeting on Hot Subdwarf Stars and Related Objects, eds. V. Van Grootel, E. Green, G. Fontaine, & S. Charpinet, ASP Conf. Ser., 481, 187 [Google Scholar]
- Gianninas, A., Bergeron, P., & Ruiz, M. T. 2011, ApJ, 743, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Gianninas, A., Dufour, P., Kilic, M., et al. 2014, ApJ, 794, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Grigahcène, A., Dupret, M.-A., Gabriel, M., Garrido, R., & Scuflaire, R. 2005, A&A, 434, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, C. J., Winget, D. E., & Kawaler, S. D. 1985, ApJ, 297, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Hermes, J. J., Montgomery, M. H., Gianninas, A., et al. 2013, MNRAS, 436, 3573 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Serenelli, A. M., Miglio, A., et al. 2013, Nature, 498, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maxted, P. F. L., Serenelli, A. M., Marsh, T. R., et al. 2014, MNRAS, 444, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Quirion, P.-O., Dupret, M.-A., Fontaine, G., Brassard, P., & Grigahcène, A. 2008, in Hydrogen-Deficient Stars, eds. A. Werner, & T. Rauch (San Francisco: ASP), ASP Conf. Ser., 391, 183 [Google Scholar]
- Szkody, P., Mukadam, A., Gänsicke, B. T., et al. 2010, ApJ, 710, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Van Grootel, V., Dupret, M.-A., Fontaine, G., et al. 2012, A&A, 539, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Grootel, V., Fontaine, G., Brassard, P., & Dupret, M.-A. 2013, ApJ, 762, 57 [NASA ADS] [CrossRef] [Google Scholar]
- van Spaandonk, L., Steeghs, D., Marsh, T. R., & Parsons, S. G. 2010, ApJ, 715, L109 [NASA ADS] [CrossRef] [Google Scholar]
- van Zyl, L., Warner, B., O’Donoghue, D., et al. 2004, MNRAS, 350, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Voss, B., Koester, D., Napiwotzki, R., Christlieb, N., & Reimers, D. 2007, A&A, 470, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warner, B., & van Zyl, L. 1998, in New Eyes to See Inside the Sun and Stars, eds. F.-L. Deubner, J. Christensen-Dalsgaard, & D. Kurtz, IAU Symp., 185, 321 [Google Scholar]
- Winget, D. E. 1982, Ph.D. Thesis, The University of Rochester [Google Scholar]
- Winget, D. E., van Horn, H. M., Tassoul, M., et al. 1982, ApJ, 252, L65 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Structure of the envelope of a representative 0.6 M⊙ model, for eight different envelope chemical compositions ranging from solar (upper left quadrant of upper panel) to a H-less mixture (lower right figure of lower panel). The boundaries of the outer convection zone(s) are indicated by heavy dots. The three dotted curves in each plot correspond to a Rosseland optical depth of 0.1, 1.0, and 10.0, from top to bottom. The boundaries of the instability strip for each case considered are indicated by blue and red vertical dotted lines. |
| In the text | |
 |
Fig. 2 Left panel: details of the structure of the outer layers of a representative evolving 0.6 M⊙ white dwarf with a solar composition in the envelope. The ordinate gives the fractional mass depth in logarithmic units. On this scale, the center of the star is at log q = 0; only the envelope layers are depicted here. The small dots define “isocontours” of opacity, and some are labelled by their value of log κ. The small filled circles indicate the boundaries of the superficial convection zones that develop due to He and H recombination. It should be pointed out that the top of the convection zones always resides in the photospheric layers, while the base sinks deeper into the star as it cools, until degenerate conduction takes over in the cooler, more evolved phases. The vertical dashed lines indicate the blue and red edges obtained with our TDC treatment with ML2/α = 1.0. Right panel: similar to left panel, but the small dots now define isocontours of the local convective turnover timescale log τc expressed in seconds. The boundaries of the convection zones are well defined in this plot, so the small filled circles used in the left panel are not necessary. |
| In the text | |
 |
Fig. 3 Predicted GW Lib instability strips for models with envelope compositions ranging from solar (upper left figure of upper panel) to a H-less mixture (lower right figure of lower panel). The dotted vertical lines correspond to the effective temperature for each of the 11 pulsating white dwarfs of the GW Lib type listed in Table 6 of Szkody et al. (2010). |
| In the text | |
 |
Fig. 4 Predicted ranges of excited dipole (ℓ = 1) g-modes for representative models near the red edge of the instability strips from 1.2 M⊙ (lower left and shorter periods) to 0.3 M⊙ (upper right and larger periods). The bigger the dot, the more unstable the mode. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


