| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425278 | |
| Published online | 19 February 2015 | |
Chemical Enrichment RGS cluster Sample (CHEERS): Constraints on turbulence⋆
1 Institute of Astronomy, Madingley Road, CB3 0HA Cambridge, UK .
e-mail: cpinto@ast.cam.ac.uk
2 Max-Planck-Institut fur extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
3 Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, 452 Lomita Mall, Stanford, CA 94305-4085, USA
4 Department of Physics, Stanford University, 382 via Pueblo Mall, Stanford, CA 94305-4060, USA
5 SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
6 Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
7 Department of Physics, University of Helsinki, 00014 Helsinki, Finland
Received: 5 November 2014
Accepted: 24 December 2014
Context. Feedback from active galactic nuclei, galactic mergers, and sloshing are thought to give rise to turbulence, which may prevent cooling in clusters.
Aims. We aim to measure the turbulence in clusters of galaxies and compare the measurements to some of their structural and evolutionary properties.
Methods. It is possible to measure the turbulence of the hot gas in clusters by estimating the velocity widths of their X-ray emission lines. The Reflection Grating Spectrometers aboard XMM-Newton are currently the only instruments provided with sufficient effective area and spectral resolution in this energy domain. We benefited from excellent 1.6 Ms new data provided by the Chemical Enrichment RGS cluster Sample (CHEERS) project.
Results. The new observations improve the quality of the archival data and allow us to place constraints for some clusters, which were not accessible in previous work. One-half of the sample shows upper limits on turbulence less than 500 km s-1. For several sources, our data are consistent with relatively strong turbulence with upper limits on the velocity widths that are larger than 1000 km s-1. The NGC 507 group of galaxies shows transonic velocities, which are most likely associated with the merging phenomena and bulk motions occurring in this object. Where both low- and high-ionization emission lines have good enough statistics, we find larger upper limits for the hot gas, which is partly due to the different spatial extents of the hot and cool gas phases. Our upper limits are larger than the Mach numbers required to balance cooling, suggesting that dissipation of turbulence may prevent cooling, although other heating processes could be dominant. The systematics associated with the spatial profile of the source continuum make this technique very challenging, though still powerful, for current instruments. In a forthcoming paper we will use the resonant-scattering technique to place lower-limits on the velocity broadening and provide further insights on turbulence. The ASTRO-H and Athena missions will revolutionize the velocity estimates and discriminate between different spatial regions and temperature phases.
Key words: X-rays: galaxies: clusters / X-rays: galaxies / galaxies: clusters: intracluster medium / techniques: spectroscopic / turbulence / galaxies: kinematics and dynamics
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Clusters of galaxies are the most massive, individual, bound objects in the Universe. In their gravitational potential well, the gas, called the intra-cluster medium (ICM), is heated to temperatures of 107−8 K and, therefore, strongly emits at X-ray energies. The ICM is commonly thought to be in hydrostatic equilibrium, but there are several factors that may affect the dynamical state of the gas. The feedback from active galactic nuclei (AGN) creates bubbles that may drive turbulence up to about 500 km s-1 (see, e.g., Brüggen et al. 2005; Fabian et al. 2005). Sloshing of gas within the gravitational potential may produce similar velocities, while galactic mergers can give rise to even higher velocities of about 1000 km s-1 (see, e.g., Lau et al. 2009; Ascasibar & Markevitch 2006).
The AGN feedback is thought to offset radiative losses and to suppress cooling in isolated giant elliptical galaxies and in larger systems up to the richest galaxy clusters (see, e.g., McNamara & Nulsen 2007; Fabian 2012). Simulations and observations have confirmed that AGN feedback may prevent cooling through the production of turbulence (see, e.g., Ruszkowski et al. 2004; Zhuravleva et al. 2014; Gaspari et al. 2014). Other work suggests that turbulent mixing may also be an important mechanism through which AGN heat cluster cores (see, e.g., Banerjee & Sharma 2014).
It is possible to measure velocity broadening on the order of few hundreds km s-1 directly in the X-ray emission lines produced by the hot ICM. The Reflection Grating Spectrometers (RGS, den Herder et al. 2001) aboard XMM-Newton are currently the only X-ray instruments, which have enough collecting area and spectral resolution to enable this measurement. However, the spatial extent of clusters complicates the process due to the slitless nature of the RGS. Sanders et al. (2010) made the first measurement of cluster velocity broadening using the luminous cluster A 1835 at redshift 0.25. Due to the limited spatial extent of its bright core, an upper limit of 274 km s-1 was obtained. Sanders et al. (2011) then constrained turbulent velocities for a large sample of 62 sources observed with XMM-Newton/RGS, which included clusters, groups, and elliptical galaxies. Half of them show velocity broadening below 700 km s-1. Recently, Sanders & Fabian (2013) used continuum-subtracted emission line surface brightness profiles to account for the spatial broadening. This technique is affected by systematic errors of up to 150 km s-1.
Werner et al. (2009) and de Plaa et al. (2012) measured turbulent velocities through the ratio of the Fe xvii emission lines at 15 and 17 Å. When the velocity broadening is low, the gas is optically thick in the 15 Å line due to resonant scattering, while the 17 Å lines remain optically thin. The comparison of observed with simulated line ratios for different Mach numbers constrains the level of turbulence. This method is very efficient for cool core clusters rich in Fe xvii emission lines, but it is partly limited by the systematic uncertainty (~20%) in the line ratio for an optically thin plasma.
In this work, we measure the velocity broadening for the 44 sources of the Chemical Enrichment RGS cluster Sample (CHEERS), which is connected to a Very Large Program accepted for XMM-Newton AO-12. We model the line spatial broadening using CCD images. This method has systematics due to the spatial profile of the continuum, which may overestimate the line spatial broadening, but it is still a useful technique to measure the level of velocity broadening when deep, high-spatial resolution maps are lacking. We also test an alternative method, which uses a variable spatial-broadening. The paper is organized as follows. In Sect. 2, we give a brief description of the CHEERS project. In Sect. 3, we present the data reduction. Our method is described in Sect. 4. We discuss the results in Sect. 5 and give our conclusions in Sect. 6. Further useful material is reported in Appendix A to speed up the paper reading.
2. The CHEERS project
The current catalog includes 44 nearby, bright clusters, groups of galaxies, and elliptical galaxies with a value of a ≳ 5σ detection for the O viii 1s−2p line at 19 Å and with a well-represented variety of strong, weak, and non cool-core objects. This catalog also contains 19 new observations of 1.6 Ms in total, which are taken during AO-12, PI: J. de Plaa (see Table 1). More detail on the sample choice is provided by another paper (de Plaa et al., in prep.). Among the several goals of this large project, we mention the following ones:
-
to understand the ICM metal enrichment by differentSN types (see, e.g., Mernieret al. 2015);
-
to study substructures, asymmetries and multiphaseness;
-
to study heating and cooling in cluster cores;
-
to measure turbulence (this paper);
-
to improve the cross-calibration between X-ray satellites.
3. Data
The data used in this paper are listed in Table 1. In boldface, we show the new observations taken during AO-12. A few archival exposures have not been used, since they were too short.
The XMM-Newton satellite is equipped with two types of X-ray detectors: The CCD-type European Photon Imaging Cameras (EPIC) and the Reflection Grating Spectrometers (RGS). The European photon imaging cameras are MOS 1, MOS 2, and pn (Strüder et al. 2001; Turner et al. 2001). The RGS camera consists of two similar detectors, which have both high effective area and spectral resolution between 6 and 38 Å (den Herder et al. 2001). The MOS cameras are aligned with the RGS detectors and have higher spatial resolution than the pn camera. We have used MOS 1 for imaging and RGS for spectral analysis.
 |
Fig. 1 RGS extraction regions and MOS 1 stacked image of M 87. |
3.1. RGS and MOS 1 data reduction
The data were reduced with the XMM-Newton Science Analysis System (SAS) v13.5.0. We processed the RGS data with the SAS task rgsproc and the MOS 1 data with emproc to produce event files, spectra, and response matrices for RGS and MOS data.
To correct for contamination from soft-proton flares, we used the SAS task evselect to extract light curves for MOS 1 in the 10−12 keV energy band, while we used the data from CCD number 9 for RGS where hardly any emission from each source is expected. We binned the light curves in 100 s intervals. A Poissonian distribution was fitted to the count-rate histogram, and all time bins outside the 2σ level were rejected. We built the good time intervals (GTI) files with the accepted time events for the MOS and RGS files through the SAS task tabgtigen and reprocessed the data again with rgsproc and emproc. The RGS 1 total clean exposure times are quoted in Table 1.
XMM-Newton/RGS observations used in this paper.
3.2. RGS spectra extraction
We extracted the RGS source spectra in two alternative regions centered on the emission peak: a broader 3.4′ region, which includes most of the RGS field of view and a narrower 0.8′ region that provides the cluster cores but with high statistics. This was done by launching rgsproc twice by setting the xpsfincl mask to include 99% and 90% of point-source events inside the spatial source extraction mask, respectively. We have used the model background spectrum created by the standard RGS rgsproc pipeline, which is a template background file, based on the count rate in CCD 9. The RGS spectral extraction regions and the MOS 1 image of M 87 are shown in Fig. 1. The spectra were converted to SPEX1 format through the SPEX task trafo. During the spectral conversion, we chose the option of sectors in the task trafo to create as many sectors as the different exposures of each source. This permits us to simultaneously fit the multiple RGS spectra of each source by choosing which parameters to either couple or unbind in the spectral models of different observations.
3.3. MOS 1 spatial broadening profiles
The RGS spectrometers are slitless, and, therefore, the spectra are broadened because of the spatial extent of the source in the dispersion direction. The effect of this spatial broadening is described by the following wavelength shift 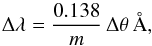 (1)where m is the spectral order and θ is the offset angle of the source in arcmin (see the XMM-Newton Users Handbook).
(1)where m is the spectral order and θ is the offset angle of the source in arcmin (see the XMM-Newton Users Handbook).
The MOS 1 DET Y direction is parallel to the RGS 1 dispersion direction and can be used to correct for the spatial broadening. With evselect, we extracted MOS 1 images for each exposure in the 0.5−1.8 keV (7−25 Å) energy band and their surface brightness profiles in the dispersion direction. We account for spatial broadening using the lpro multiplicative model in SPEX, which convolves the RGS response with our model of the spatial extent of the source. We show some cumulative profiles of spatial broadening in Fig. 2. We have also produced stacked Fe-L band (10–14 Å) images for each source. The central 10′ region contains most of the cluster emission (see Fig. A.1).
 |
Fig. 2 MOS 1 average 7–25 Å cumulative spatial profiles. |
4. Spectral modeling
Our analysis focuses on the 7−28 Å (0.44−1.77 keV) first and second order RGS spectra. We model the spectra with SPEX version 2.03.03. We scale elemental abundances to the proto-Solar values of Lodders & Palme (2009), which are the default in SPEX. We adopt C-statistics and 1σ errors throughout the paper, unless otherwise stated, and the updated ionization balance calculations of Bryans et al. (2009).
Clusters of galaxies are not isothermal, and most of them have both hot and cool gas phases (see e.g. Frank et al. 2013). Therefore, we have used a two-temperature thermal plasma model of collisional ionization emission (CIE). This model is able to fit all the spectra in our database. The cie model in SPEX calculates the spectrum of a plasma in collisional ionization equilibrium. The basis for this model is given by the mekal model, but several updates have been included (see the SPEX manual). Free parameters in the fits are the emission measure Y = nenH dV, the temperature T, the abundances (N, O, Ne, Mg, and Fe), and the turbulent broadening v of the two cie models.
We bind the parameter v and the abundances of two cie components with each other and assume that the gas phases have the same turbulence and abundances. This decreases the degree of degeneracy. This assumption is certainly not true, but some clusters just need one CIE component and the spectra of several clusters do not have good enough statistics in both high- and low-ionization emission lines, which prohibits constraining the velocities and the abundances for both hot and cool phases. We attempt to constrain the turbulence in the different phases in Sect. 5.1.
The cie models are multiplied by a redshift model and a model for Galactic absorption, which is provided by the hot model in SPEX with T = 0.5 eV and 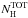 , as estimated through the tool of Willingale et al. (2013). This tool includes the contribution to absorption from both atomic and molecular hydrogen. The redshifts and column densities that have been adopted are shown in Table 1. To correct for spatial broadening, we have multiplied the spectral model by the lpro component that receives as input the surface brightness profile extracted in the MOS 1 images (see Sect. 3.3 and Fig. 2).
, as estimated through the tool of Willingale et al. (2013). This tool includes the contribution to absorption from both atomic and molecular hydrogen. The redshifts and column densities that have been adopted are shown in Table 1. To correct for spatial broadening, we have multiplied the spectral model by the lpro component that receives as input the surface brightness profile extracted in the MOS 1 images (see Sect. 3.3 and Fig. 2).
We do not explicitly model the cosmic X-ray background in the RGS spectra because any diffuse emission feature would be smeared out into a broad continuum-like component.
For a few sources, including the Perseus and Virgo (M 87) clusters, we have added a further power-law emission component of slope ~ 2 to take the emission from the central AGN into account. This component is not convolved with the spatial profile because it is produced by a central point-like source.
 |
Fig. 3 Left panel: velocity 68% (red) and 90% (green) limits for the 0.8′ region with the spatial broadening determined with MOS 1 images (see Sect. 4.1). Right panel: velocity limits obtained using the best-fit spatial broadening (see Sect. 4.2). |
To avoid the systematic effects due to the stacking of multiple observations with different pointing, we have simultaneously fitted the individual spectra of each source extracted in the two regions defined in Sect. 3.2 and shown in Fig. 1. The plasma model is coupled between the observations. The only uncoupled parameters are the emission measures of the two collisional-ionized gas components. For each observation we adopt the spatial profile extracted in the MOS 1 image taken during that exposure. For those exposures, during which the MOS 1 detector had a closed filter, we have adopted an exposure-weighted average profile as given by the other available observations, but the δλ parameter in the lpro component is left free. This factor allows us to shift the model lines by the same amount (in Å) for each specific spectrum and strongly decreases the systematic effects. The δλ parameter is always free in our fits to account for any redshift variation, which would otherwise affect the line modeling (see e.g. Sanders et al. 2011).
The simultaneous modeling of multiple observations has been done through the use of the sectors option in SPEX (see also Sect. 3.2). The RGS 1 and 2 spectra of the same observation have exactly the same model and provide a single sector, while RGS spectra of other observations contribute additional sectors and have the cie normalizations uncoupled.
4.1. Results using a fixed spatial broadening
We have successfully applied this multi-temperature model to both the 3.4′ and 0.8′ RGS spectra. We show the spectral modeling for the 3.4′ region of the 44 sources in Figs. A.5−A.7 in Appendix A. We display the first-order stacked spectra to underline the high quality of these observations and to show the goodness of the modeling.
For some sources like Fornax, M 49, M 86, NGC 4636, and NGC 5813, the 15 and 17 Å Fe xvii emission lines are not well fitted. Precisely, the model underestimates the line peaks and overestimates the broadening. This may be due to the different spatial distribution of the gas responsible for the cool Fe xvii emission lines and for the one producing most of the high-ionization Fe-L and O viii lines. The cool gas is indeed to be found predominantly in the center of the clusters showing a profile more peaked than that one of the hotter gas. The estimated spatial profiles depend on the emission of the hotter gas due to its higher emission measure, and, therefore, they overestimate the spatial broadening of the 15–17 Å lines. It is hard to extract a spatial profile for these lines because MOS 1 has a limited spectral resolution, and the images extracted in such a short band lack the necessary statistics (see e.g. Sanders & Fabian 2013). In Sect. 5.1, we attempt to constrain the turbulence for lines of different ionization states. The 15 Å/17 Å line ratio is also affected by resonant scattering, which would require a different approach. We refer to a forthcoming paper on the analysis of the resonant scattering in the CHEERS sources.
We skip the discussion of the abundances and the supernova yields because these will be treated by other papers of this series (de Plaa et al., in prep.; Mernier et al. 2015).
In Fig. 3 (left panel), we show the upper limits on the velocity broadening obtained with the simultaneous fits of the 0.8′ 7–28 Å RGS spectra. We obtain upper limits for most clusters, while NGC 507 shows high kinematics. More detail on our results for the 3.4′ and 0.8′ regions and their comparison are reported in Table A.1 and Fig. A.2 (left panel). The 3.4′ limits are more affected by the source continuum, as clearly seen for M 87, AWM 7, and A 4038, which makes them less reliable.
4.2. Results using the best-fit spatial broadening
It is known that the spatial profile of the source continuum may be broader than the spatial distribution of the lines. The MOS 1 images are strongly affected by the profile of the source continuum and, therefore, may overestimate the spatial line broadening and underestimate the residual velocity broadening. For instance, NGC 1316 and NGC 5846 show 1σ limits of 20 km s-1, which are not realistic (see Table A.1).
To obtain more conservative limits, we have simultaneously modeled the spatial and the velocity broadening. This was done by fitting the RGS 0.8′ spectra with a free s parameter in the lpro component. This factor simply scales the width of the spatial broadening by a factor free to vary (see the SPEX manual). The free s parameter increases the degeneracy in the model but provides conservative upper limits on the residual velocity broadening, which is measured with the v parameter of the cie component. The new limits on the velocities are plotted in Fig. 3 (right panel) and quoted in the last two columns of Table A.1. In Fig. A.2 (right panel), we compare the velocity upper limits estimated with the standard method (MOS 1 spatial profile with s ≡ 1 in the lpro component) with this new approach using a free s parameter. They generally agree, but the new upper limits on the hotter Abell clusters are systematically larger by an average factor ~ 2. This confirms that some of the previous velocity limits were underestimated due to the broader spatial profiles. Therefore, we believe the new upper limits to be the most conservative. Interestingly, the conservative velocity limits of the hot clusters are generally higher than the cool galaxy groups with the exception of NGC 507, which is expected since the sound speed scales as a power of the temperature (see Sect. 5.2).
4.3. Further tests
To estimate the contribution of the spatial broadening to the line widths, we have temporarily removed the convolution of the spectral model for the spatial profile and re-fitted the data. In these fits the v parameter of the cie component accounts for any contribution to the line broadening. The total (spatial + velocity) widths are also quoted in Table A.1.
We have also tested the continuum-subtracted line surface brightness profiles introduced by Sanders & Fabian (2013). This new method consists of subtracting the surface brightness profiles of two regions that are clearly line-dominated (core) and continuum-dominated (outskirts). It can be applied only to those objects with a narrow core where it is possible to distinguish between line-rich and line-poor regions. We have locally fitted the O viii 19.0 Å emission line of A 2597, A 3112, Hydra-A, Fornax (NGC 1399), and NGC 4636 and we have found a general agreement with the results of Sanders & Fabian (2013). However, our MOS 1 images have much lower spatial resolution than the Chandra maps used by them, which increases the uncertainties that are present in this method. A thorough, extensive, analysis would require deep Chandra maps that are not yet available.
5. Discussion
In this work we have analyzed the data of 44 clusters, groups of galaxies, and elliptical galaxies included in the CHEERS project, a Very Large Program that was accepted for XMM-Newton AO-12 (see Sect. 2) together with complementary archival data.
We have measured upper limits of velocity broadening for these objects with a method similar to the previous one used by Bulbul et al. (2012) and Sanders & Fabian (2013). This consists of fitting high-quality grating spectra by removing the spatial broadening through surface brightness profiles of the sources as provided by CCD imaging detectors. These profiles are unfortunately affected by the source continuum and tend to overestimate the line spatial broadening with a consequent shrinking of the residual velocity broadening. Sanders & Fabian (2013) addressed this point in their Sect. 2.2 on A 3112 where they decreased these systematic effects by using Chandra continuum-subtracted line spatial profiles. We have tested this method by using the MOS 1 observations that were taken simultaneously with the RGS spectra (see Fig. A.1). XMM-Newton CCDs have a spatial resolution lower than Chandra CCDs, which increase the systematic effects in the creation of continuum-subtracted maps. Deep Chandra observations, enabling an accurate subtraction of different energy bands, are missing for most sources. We have therefore tried to use the MOS 1 integral maps and to fit the contribution of the spatial broadening as an alternative method.
5.1. Temperature dependence of the upper limits
So far we adopted the same velocity broadening for all the emission lines. For most sources it is possible to measure the velocity broadening of the O viii and Fe xx-to-xxiv emission lines, which are mainly produced by hot gas. Only a few sources have high-statistics Fe xvii lines produced by cool (T< 1 keV) gas. Six objects exhibit both strong low- and high-ionization lines and allow to fit the velocity broadening of the two cie components, separately, in the full-band spectral fits. 17 sources allow to measure 90% upper limits on turbulence for the O viii, Fe xvii, and Fe xx lines, by fitting the 18.0 − 23.0 Å, 14.0 − 18.0 Å, and 10.0 − 14.3 Å rest-frame wavelength ranges, respectively. For each local fit we adopt an isothermal model and correct for spatial broadening by using additional surface-brightness profiles calculated through MOS 1 images extracted in the same rest-frame wavelength ranges using the same method shown in Sect. 3.3. These profiles are still affected by the continuum but provide a better description of the spatial broadening in each line. In Fig. 4 we compare the O viii velocity limits with those measured for the Fe xvii and Fe xx line systems. The high-ionization Fe lines clearly show higher upper limits, which is confirmed by the results of the full-band fits: the hotter (T1) CIE component allows for higher values of velocity broadening. The hotter gas is distributed over a larger extent than that of the cold (T2) gas and has larger spatial broadening, which affects the T1-T2 results shown in this plot. The O viii, Fe xvii, and Fe xx lines were fitted by subtracting the spatial broadening extracted exactly in their energy band, which should partly correct this systematic effect, but it is difficult to estimate the systematic uncertainties due to the low spatial (and spectral) resolution of the CCD data. On some extent, the hotter phase may still have larger turbulence. For clarity, we also tabulate these line-band fits in Table A.2. We also note that the velocity limits of low- and high-ionization iron lines fall at opposite sides of the Fe–O viii 1:1 line, which means that the metallicity distribution in the sources should not affect our broad-band, multi-ion, limits shown in Fig. 3.
 |
Fig. 4 90% upper limits on velocity broadening obtained in the 0.8′ region for the O viii lines compared with those measured for high-ionization Fe xx (open red triangles) and for the low-ionization Fe xvii (filled black triangles) line systems. For six sources we could also measure the limits for the hot (open green circles) and the cool (open magenta boxes) CIE components (see Sect. 5.1). |
5.2. Turbulence
In Fig. 3 we show the velocity broadening of the RGS spectra extracted in the 0.8′ core region. We find upper limits to the velocity broadening with the possible exception of NGC 507. They generally range between 200 and 600 km s-1. For several objects like A 85, A 133, M 49, and most NGC elliptical we found velocity levels below 500 km s-1, which would suggest low turbulence. The broader 3.4′ region is more affected by spatial broadening as shown by the higher upper limits, but non-detection, of A 4038, AWM 7, and M 87 (see Table A.1 and Fig. A.2). For these sources it is difficult to constrain the velocity broadening because their large extent smears out the emission lines.
To understand how much energy can be stored in turbulence, we compare our upper limits with the sound speeds and the temperatures of dominant cie component in these objects. The sound speed is given by 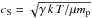 , where γ is the adiabatic index, which is 5/3 for ideal monoatomic gas, T is the RGS temperature, μ = 0.6 is the mean particle mass, and mp is proton mass. The ratio between turbulent and thermal energy is εturb/εtherm = γ/ 2 M2, where M = vturb/cS is the Mach number (see also Werner et al. 2009). In Fig. A.2 we compare our 2σ upper limits on the velocities in the central 0.8′ region with the sound speed and some fractions of turbulent energy. We also show the more conservative velocity upper limits that were measured with a variable spatial broadening. At least for half of the sample, our 90% upper limits are below the sound speed in the system. In about ten objects the turbulence contains less than the 40% of the thermal energy. This is similar to the previous results of Sanders & Fabian (2013). Apparently, the hotter objects allow for higher velocities.
, where γ is the adiabatic index, which is 5/3 for ideal monoatomic gas, T is the RGS temperature, μ = 0.6 is the mean particle mass, and mp is proton mass. The ratio between turbulent and thermal energy is εturb/εtherm = γ/ 2 M2, where M = vturb/cS is the Mach number (see also Werner et al. 2009). In Fig. A.2 we compare our 2σ upper limits on the velocities in the central 0.8′ region with the sound speed and some fractions of turbulent energy. We also show the more conservative velocity upper limits that were measured with a variable spatial broadening. At least for half of the sample, our 90% upper limits are below the sound speed in the system. In about ten objects the turbulence contains less than the 40% of the thermal energy. This is similar to the previous results of Sanders & Fabian (2013). Apparently, the hotter objects allow for higher velocities.
We note that the spectral extraction region had a fixed angle, and, therefore, the actual physical scale – where we estimated the velocity broadening – depends on the source distance. In Fig. A.4 (left panel), we show the Mach numbers for the 90% conservative upper limits as a function of the temperature, and we compare the average upper limits on Mach number calculated within different ranges of physical scales. There is no significant trend with the temperature, but the average upper limit on the Mach number is lower for narrower physical scales. Assuming a Kolmogorov spectrum for the turbulence in these objects, the root-mean-square velocity scale depends on the 1/3rd power of the physical length. Therefore, we scaled the upper limits by (sc/scmin)1/3, where scmin is the minimum physical scale per arcsec ~ 0.07 kpc/1′′ of NGC 4636, the nearest object in our sample. In other words, we divided our upper limits by the relative physical scale per arcsec relative to NGC 4636, which is equivalent to normalizing by the ratio between the size of the spectral extraction region of each cluster and that one of NGC 4636. The scaled upper limits on the Mach numbers are tabulated in Table A.2 and plotted in Fig. A.4 (right panel). They are randomly distributed around Ma ~ 0.8 and do not depend any more on the physical scale. We coded the point-size and the colors with the values of r500 and K0 taken from the literature. The r500 is the radius within which the mean over-density of the cluster is 500 times the critical density at the cluster redshift, and K0 is the value of the central entropy in the same cluster. All the adopted values and their references are reported in Table A.2. We do not find any significant relation between the upper limits on the Mach number and these physical properties, possibly due to the limited sample.
To understand whether dissipation of turbulence may prevent cooling in our sample, we computed the Mach number that is required to balance the heating and cooling, according to the following equation: 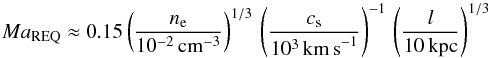 (2)where ne is the density at the cavity location, cs the sound speed that we have estimated through the RGS temperature, and l the characteristic eddy size, which we take as the average cavity size (see Zhuravleva et al. 2014). The Mach numbers required to balance cooling are tabulated in Table A.2. Most cavity sizes were taken from Panagoulia et al. (2014b). For clusters with multiple cavities, we used an average size. For the 19 sources outside of their sample, we used their r − T relation to determine the cavity size. Most densities were taken from the ACCEPT catalog.
(2)where ne is the density at the cavity location, cs the sound speed that we have estimated through the RGS temperature, and l the characteristic eddy size, which we take as the average cavity size (see Zhuravleva et al. 2014). The Mach numbers required to balance cooling are tabulated in Table A.2. Most cavity sizes were taken from Panagoulia et al. (2014b). For clusters with multiple cavities, we used an average size. For the 19 sources outside of their sample, we used their r − T relation to determine the cavity size. Most densities were taken from the ACCEPT catalog.
In Fig. 5, we compare the ratios between the conservative upper limits of the scaled Mach numbers assuming Kolmogorov turbulence, and those that are required to balance cooling with the RGS temperatures. For most sources, our upper limits are larger than the balanced Mach numbers, which means that dissipation of turbulence can provide enough heat to prevent the cooling of the gas in the cores.
It is difficult to know which is the main mechanism that produces turbulence in these objects. Our scaled upper limits are mostly below 500 km s-1, which can be produced by bubbles inflated by past AGN activity (see, e.g., Brüggen et al. 2005). For some objects, our upper limits are consistent with velocities up to 1000 km s-1, which would correspond to Mach numbers larger than one. For NGC 507, we detect transonic motions presumably due to merging (see, e.g., Ascasibar & Markevitch 2006). In a forthcoming paper, we will analyze the resonant scattering of the Fe xvii lines exhibited by half of our sample to place lower limits on turbulent broadening and provide more insights on its origin and its role in preventing cooling.
 |
Fig. 5 Ratios between the 90% conservative upper limits on the Mach number (velocity/sound speed) that are scaled by the 1/3rd power of the spatial scale assuming Kolmogorov turbulence (see Sect. 5.2), and the Mach number, which is required to make a heating-cooling balance (see Eq. (2)). The point size provides the r500, and the color is coded according to the central entropy, K0, in units of keV cm2. |
5.3. Comparison with previous results
Our velocity limits broadly agree with the previous results obtained by Sanders & Fabian (2013) using a similar method and by other authors, who use the measurements of resonant scattering (Werner et al. 2009; de Plaa et al. 2012). In particular, our limits for M 49 (also known as NGC 4472), NGC 4636, and NGC 5813 agree with the 100 km s-1 upper limit obtained by Werner et al. (2009). We also found upper limits of a few 100 s km s-1 for A 3112, which is similar to the results of Bulbul et al. (2012). However, we measured higher limits with a variable spatial broadening that agree with continuum-subtracted profiles method of Sanders & Fabian (2013).
Recently, Zhuravleva et al. (2014) used the surface brightness fluctuations in the Chandra images of the Perseus and Virgo clusters to derive turbulent velocities in the range 70–210 km s-1 for Perseus and 43−140 km s-1 for Virgo, where the smaller values refer to the central 1.5′ region. Our upper limits in the cores of the clusters are consistent with their values, especially when normalized by the physical scale factor 1.5′/ 0.4′. They show that these turbulent motions should dissipate enough energy to offset the cooling of the central ICM in these clusters. For ten objects, the scaled Mach number can be transonic, and a major fraction of energy can be stored in turbulence, which could significantly heat the gas through dissipation (see, e.g., Ruszkowski et al. 2004). Recently, Gaspari et al. (2014) noted that even if the turbulence in the hot gas is subsonic, it may be transonic in the cooler gas phases. Zhuravleva et al. (2014) reported that dissipation of turbulence may balance cooling even under subsonic regime. Our upper limits on Mach number are larger than the values necessary to balance cooling and are consistent with this scenario. However, it is possible that other processes are dominant, such as turbulent mixing (see, e.g., Banerjee & Sharma 2014).
The NGC 507 group exhibits velocities larger than 1000 km s-1 in both the 0.8′ and 3.4′ regions, corresponding to a scaled Mach number Ma = 4.2 ± 1.7 (1σ). The 15 Å Fe xvii line is stronger than the one at 17 Å, which would suggest low resonant scattering (see Fig. A.7) and, therefore, high kinematics in the galaxy group. This object is known to have a disturbed shape and to host radio lobes presumably in a transonic expansion/inflation (Kraft et al. 2004). However, our high values suggest the presence of bulk motions. In Fig. 6, we show the velocities of the galaxies in the NGC 507 group as taken from Zhang et al. (2011). They are not necessary linked to that of the ICM, but there are high kinematics and hints of infalling clumps, which indicate a substructure extended toward the observer. In this group, the galaxy velocities generally double those observed in NGC 4636, where we measure lower velocity broadening (see also the different line widths in Fig. A.7).
 |
Fig. 6 Line-of-sight velocity versus projected distance from the central cD galaxy for the member galaxies of NGC 507 group. Optical spectroscopic redshifts are taken from Zhang et al. (2011). |
5.4. Toward ASTRO-H
The RGS gratings aboard XMM-Newton are currently the only instruments that can measure 100 s km s-1 velocities in X-ray spectra of extended sources like clusters of galaxies. However, they are slitless spectrometers and, therefore, affected by spatial broadening. We have partly solved this issue by using line surface brightness profiles, but there are still systematic uncertainties larger than 100 km s-1. Our models provide an important workbench once the new ASTRO-H X-ray satellite (Takahashi et al. 2010) is launched. The spectra, as provided by its microcalorimeter (SXS), do not suffer from spatial broadening as for the RGS and will revolutionize the method. Moreover, its constant spectral resolution in terms of energy increases the sensitivity at high energies, which allows us to use higher-ionization lines up to 6−7 keV (Fe-K line complex) necessary to constrain the turbulence in hotter gas phases. The position of the lines unveil evidence of bulk motions.
In Fig. 7 (left panel), we compare the effective area of the ASTRO-H SXS with that of the first order RGS 1 and 2. ASTRO-H provides clearly better results than the sum of RGS 1 and 2 below 14 Å (above 1 keV). The RGS has still a better spectral resolution than the SXS in the wavelength range that includes the Fe xvii lines of the cool gas, but the absence of spurious line-broadening in the SXS makes it a great alternative tool. We have simulated a 100 ks exposure with the ASTRO-H SXS for four interesting objects in our catalog: Perseus (500 km s-1), NGC 5846 (10 km s-1), NGC 4636 (100 km s-1), and NGC 507 (1000 km s-1, see Fig. 7 right panel). We have used the model fitted for the full (−1.7′, +1.7′) RGS spectra as a template, which are shown in Fig. A.7, because this extraction region is comparable to the 3.05′ × 3.05′ field-of-view of the microcalorimeter. The spatial broadening was excluded from the model. The simulated SXS spectra are characterized by a richness of resolved emission lines, which provides velocity measurements with an accuracy of 50 km s-1 or better. The line widths clearly increase throughout NGC 5846, NGC 4636, and NGC 507. The hotter gas present in the Perseus cluster produces strong higher-ionization lines above 1 keV, which constrain the turbulence in different (Fe-L and Fe-K) gas phases.
We also note that the 1′ spatial resolution of ASTRO-H provides, for the first time the means for a spatially-resolved high-resolution spectral analysis and the measurements of turbulence in different regions of the clusters. The ATHENA X-ray observatory that is to be launched by the late 2020s will further revolutionize our measurements due to its combined high spectral (2.5 eV) and spatial (< 5′′) resolution.
6. Conclusion
We have presented a set of upper limits and measurements of the velocity widths for the soft X-ray emitting gas of a sample of clusters, groups of galaxies, and elliptical galaxies included in the CHEERS project. We have subtracted the instrumental spatial broadening through the use of surface brightness profiles extracted in the MOS 1 images.
 |
Fig. 7 Left panel: RGS 1 and 2 first order and ASTRO-H SXS effective area. Right panel: ASTRO-H SXS 100 ks simulations for the bright Perseus cluster and three groups of galaxies zoomed in the RGS energy band (see Sect. 5.4). We adopted the 3.4′ RGS models as a template (see Fig. A.7). |
For most sources, we obtain upper limits ranging within 200−600 km s-1, where the turbulence may originate in AGN feedback or sloshing of the ICM. However, for some sources, such as NGC 507, we find upper limits of 1000 km s-1 or larger, suggesting other origins, such as mergers and bulk motions. The measurements depend on the angular scale and the temperature. For a small sample producing strong high- and low-ionization lines, we measured significantly broader upper limits for the hot gas phase, which may be partly due to its larger spatial extent as compared to the cool phase. When we normalize the Mach numbers for the physical scale, assuming Kolmogorov turbulence, we constrain upper limits ranging within 0.3 <Ma< 1.5. These values are above the Mach numbers necessary to balance cooling, which means that the dissipation of turbulence may be the dominant mechanism to heat the gas and quench cooling flows. However, it is possible that additional processes are heating the ICM. In a forthcoming paper, we will use the resonant-scattering technique to place some lower limits on the velocities in half of our sample, which are characterized by strong Fe xvii emission lines, and make an extensive use of higher-resolution Chandra maps. This will provide alternative measurements and further insights on the origin and the role of turbulence in clusters, groups of galaxies, and elliptical galaxies.
The current techniques are partly limited by systematics associated with the spatial line broadening, but the future ASTRO-H and ATHENA missions will dramatically improve the method due to their high broadband spectral resolution and to the absence of issues concerning the spurious spatial broadening. They will also enable spatially-resolved turbulence measurements.
Online material
Appendix A: Maps, spectra, and velocity limits
We have placed the MOS 1 images, the RGS spectra, and the velocity limits in this section to unburden the paper reading.
The MOS 1 images (Fig. A.1) are obtained by stacking the Fe-L (10–14 Å) band images extracted in each exposure (see Sect. 3.3). We zoomed on the central 10′ region.
In Table A.1, we quote all our velocity results. In Fig. A.2 (left panel), we compare the 2σ upper limits on the velocity broadening as measured for the 3.4′ and 0.8′ regions by subtracting the MOS 1 spatial profiles. In Fig. A.2 (right panel), we compare the 0.8′2σ upper limits estimated by subtracting the adopted and the best-fit, spatial-line-broadening (see Sect. 4.2). In Table A.1, we also show the total line widths as result of spatial plus Doppler broadening with their 68% uncertainties. These total widths are clearly dominated by the spatial broadening.
In Table A.2, we report the values of r500 and K0 adopted with with the physical scales, the RGS temperatures estimated with an isothermal model, the conservative upper limits on the velocities and the Mach numbers, the limits separately measured for the O viii, Fe xvii, and Fe xx-to-xxiv emission lines, and finally the velocity limits for the two CIE components where it was possible to fit them separately. The separate
 |
Fig. A.1 MOS 1 stacked Fe-L band images: Central 10′ × 10′ region. The starred clusters are part of our new campaign (see also Sect. 3.3). |
Fe xvii and 2-T fits were accessible only for a very limited sample of sources with both strong high- and low-ionization Fe lines (see Sect. 5.1). In Fig. A.3, we compare the velocity upper limits estimated with both the standard and the conservative methods with the average RGS temperature measured with an isothermal model, the sound speed, and the fractions of thermal energy stored in turbulence. In Fig. A.4 (left panel), we show the Mach number as a function of the temperature with the pointsize and, it is color coded according to the physical scale and the central entropy, respectively. The lines show the average Mach number calculated within particular ranges of physical scales. In Fig. A.4 (left panel), we show the Mach number scaled by the 1/3rd power of the physical scale, assuming Kolmogorov turbulence (see also Sect. 5.2).
In Figs. A.5−A.7, we show the RGS spectra extracted in the 3.4′ cross-dispersion region (see also Sect. 3.2). The spectra were combined with the rgscombine task for plotting purposes. We have adapted the spectral model from the bestfit obtained for the parallel modeling of the individual exposures. Most spectra were fitted with a multi-temperature, two-cie model (see Sect. 4). A few of them require just a single cie component. The spectral modeling involved the 7 − 28 Å band, but we focus on the shorter 10 − 21 Å band containing the Fe, Ne, and O lines.
 |
Fig. A.2 Left panel: velocity broadening at 2σ upper limits for the (−1.7′, +1.7′) and the (−0.4′, +0.4′) regions at comparison. The spatial broadening was removed through the MOS 1 surface brightness profiles. Right panel: (−0.4′, +0.4′) velocity 2σ upper limits compared with those estimated in the same region but with the variable best-fit, spatial broadening (scale parameter, s, is free in the lpro component, see Sect. 4.2 and Table A.1). |
 |
Fig. A.3 90% upper limits on velocity broadening obtained in the 0.8′ region versus RGS temperature (the red arrows provide the conservative limits measured with the best-fit spatial broadening, see Sect. 4.2). The sound speed and the fractions of thermal energy in turbulence are shown. |
 |
Fig. A.4 Left panel: 90% conservative upper limits on Mach number versus temperature. Point size refers to the physical scale and the color is coded according to the central entropy, K0, in units of keV cm-2. The lines show the upper limits on Mach number averaged in the four ranges of physical scales to underline its dependence on the source distance. Right panel: same as before, but here the limits on Mach number are scaled by the 1/3rd power of the physical scale for a comparison between sources at different redshift (assuming Kolmogorov turbulence, see Sect. 5.2). |
 |
Fig. A.5 RGS spectral fits for the (−1.7′,+1.7′) region with the 7−25 Å spatial broadening profile (Part I). For displaying purposes, the spectra were combined using the XMM-SAS task rgscombine. |
 |
Fig. A.6 RGS spectral fits for the (−1.7′,+1.7′) region with the 7−25 Å spatial broadening profile (Part II). For displaying purposes, the spectra were combined using the XMM-SAS task rgscombine. |
 |
Fig. A.7 RGS spectral fits for the (−1.7′,+1.7′) region with the 7−25 Å spatial broadening profile (Part III). For displaying purposes, the spectra were combined using the XMM-SAS task rgscombine. |
Velocity broadening upper limits and total line widths.
Additional results and physical properties.
Acknowledgments
This work is based on observations obtained with XMM-Newton, an ESA science mission funded by ESA Member States and the USA (NASA). Y.Y.Z. acknowledges the BMWi DLR grant 50 OR 1304. We thank Electra Panagoulia for kindly providing the values of central entropy and the anonymous referee for very useful comments on the paper.
References
- Ascasibar, Y., & Markevitch, M. 2006, ApJ, 650, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, N., & Sharma, P. 2014, MNRAS, 443, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Brüggen, M., Hoeft, M., & Ruszkowski, M. 2005, ApJ, 628, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Bryans, P., Landi, E., & Savin, D. W. 2009, ApJ, 691, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Bulbul, G. E., Smith, R. K., Foster, A., et al. 2012, ApJ, 747, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Reiprich, T. H., Böhringer, H., Ikebe, Y., & Zhang, Y.-Y. 2007, A&A, 466, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J., Zhuravleva, I., Werner, N., et al. 2012, A&A, 539, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Sanders, J. S., Taylor, G. B., & Allen, S. W. 2005, MNRAS, 360, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Pietsch, W., Aschenbach, B., & Miniati, F. 2004, A&A, 415, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, K. A., Peterson, J. R., Andersson, K., Fabian, A. C., & Sanders, J. S. 2013, ApJ, 764, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Oh, S. P., & Ruszkowski, M. 2014, MNRAS, submitted [arXiv:1410.7769] [Google Scholar]
- Kraft, R. P., Forman, W. R., Churazov, E., et al. 2004, ApJ, 601, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, E. T., Kravtsov, A. V., & Nagai, D. 2009, ApJ, 705, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., & Palme, H. 2009, Meteor. Planet. Sci. Suppl., 72, 5154 [Google Scholar]
- Mernier, F., de Plaa, J., Lovisari, L., et al. 2015, A&A, 575, A37 [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Panagoulia, E. K., Fabian, A. C., & Sanders, J. S. 2014a, MNRAS, 438, 2341 [NASA ADS] [CrossRef] [Google Scholar]
- Panagoulia, E. K., Fabian, A. C., Sanders, J. S., & Hlavacek-Larrondo, J. 2014b, MNRAS, 444, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ruszkowski, M., Brüggen, M., & Begelman, M. C. 2004, ApJ, 615, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. S., & Fabian, A. C. 2013, MNRAS, 429, 2727 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. S., Fabian, A. C., Smith, R. K., & Peterson, J. R. 2010, MNRAS, 402, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. S., Fabian, A. C., & Smith, R. K. 2011, MNRAS, 410, 1797 [NASA ADS] [Google Scholar]
- Snowden, S. L., Mushotzky, R. F., Kuntz, K. D., & Davis, D. S. 2008, A&A, 478, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, T., Mitsuda, K., Kelley, R., et al. 2010, in SPIE Conf. Ser., 7732 [Google Scholar]
- Tashiro, M., Ito, K., Abe, K., & Isobe, N. 2006, in ESA SP, 604, The X-ray Universe 2005, ed. A. Wilson, 569 [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, N., Zhuravleva, I., Churazov, E., et al. 2009, MNRAS, 398, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, N., Allen, S. W., & Simionescu, A. 2012, MNRAS, 425, 2731 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y.-Y., Andernach, H., Caretta, C. A., et al. 2011, A&A, 526, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhuravleva, I., Churazov, E., Schekochihin, A. A., et al. 2014, Nature, 515, 85 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 RGS extraction regions and MOS 1 stacked image of M 87. |
| In the text | |
 |
Fig. 2 MOS 1 average 7–25 Å cumulative spatial profiles. |
| In the text | |
 |
Fig. 3 Left panel: velocity 68% (red) and 90% (green) limits for the 0.8′ region with the spatial broadening determined with MOS 1 images (see Sect. 4.1). Right panel: velocity limits obtained using the best-fit spatial broadening (see Sect. 4.2). |
| In the text | |
 |
Fig. 4 90% upper limits on velocity broadening obtained in the 0.8′ region for the O viii lines compared with those measured for high-ionization Fe xx (open red triangles) and for the low-ionization Fe xvii (filled black triangles) line systems. For six sources we could also measure the limits for the hot (open green circles) and the cool (open magenta boxes) CIE components (see Sect. 5.1). |
| In the text | |
 |
Fig. 5 Ratios between the 90% conservative upper limits on the Mach number (velocity/sound speed) that are scaled by the 1/3rd power of the spatial scale assuming Kolmogorov turbulence (see Sect. 5.2), and the Mach number, which is required to make a heating-cooling balance (see Eq. (2)). The point size provides the r500, and the color is coded according to the central entropy, K0, in units of keV cm2. |
| In the text | |
 |
Fig. 6 Line-of-sight velocity versus projected distance from the central cD galaxy for the member galaxies of NGC 507 group. Optical spectroscopic redshifts are taken from Zhang et al. (2011). |
| In the text | |
 |
Fig. 7 Left panel: RGS 1 and 2 first order and ASTRO-H SXS effective area. Right panel: ASTRO-H SXS 100 ks simulations for the bright Perseus cluster and three groups of galaxies zoomed in the RGS energy band (see Sect. 5.4). We adopted the 3.4′ RGS models as a template (see Fig. A.7). |
| In the text | |
 |
Fig. A.1 MOS 1 stacked Fe-L band images: Central 10′ × 10′ region. The starred clusters are part of our new campaign (see also Sect. 3.3). |
| In the text | |
 |
Fig. A.2 Left panel: velocity broadening at 2σ upper limits for the (−1.7′, +1.7′) and the (−0.4′, +0.4′) regions at comparison. The spatial broadening was removed through the MOS 1 surface brightness profiles. Right panel: (−0.4′, +0.4′) velocity 2σ upper limits compared with those estimated in the same region but with the variable best-fit, spatial broadening (scale parameter, s, is free in the lpro component, see Sect. 4.2 and Table A.1). |
| In the text | |
 |
Fig. A.3 90% upper limits on velocity broadening obtained in the 0.8′ region versus RGS temperature (the red arrows provide the conservative limits measured with the best-fit spatial broadening, see Sect. 4.2). The sound speed and the fractions of thermal energy in turbulence are shown. |
| In the text | |
 |
Fig. A.4 Left panel: 90% conservative upper limits on Mach number versus temperature. Point size refers to the physical scale and the color is coded according to the central entropy, K0, in units of keV cm-2. The lines show the upper limits on Mach number averaged in the four ranges of physical scales to underline its dependence on the source distance. Right panel: same as before, but here the limits on Mach number are scaled by the 1/3rd power of the physical scale for a comparison between sources at different redshift (assuming Kolmogorov turbulence, see Sect. 5.2). |
| In the text | |
 |
Fig. A.5 RGS spectral fits for the (−1.7′,+1.7′) region with the 7−25 Å spatial broadening profile (Part I). For displaying purposes, the spectra were combined using the XMM-SAS task rgscombine. |
| In the text | |
 |
Fig. A.6 RGS spectral fits for the (−1.7′,+1.7′) region with the 7−25 Å spatial broadening profile (Part II). For displaying purposes, the spectra were combined using the XMM-SAS task rgscombine. |
| In the text | |
 |
Fig. A.7 RGS spectral fits for the (−1.7′,+1.7′) region with the 7−25 Å spatial broadening profile (Part III). For displaying purposes, the spectra were combined using the XMM-SAS task rgscombine. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


