EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 575 (March 2015) A&A, 575 (2015) A128 Full HTML
Free Access
Issue
A&A
Volume 575, March 2015
Article Number A128
Number of page(s) 15
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201425261
Published online 11 March 2015

© ESO, 2015

1. Introduction

Tight correlations between the mass of the central supermassive black hole (SMBH) and properties of the hosting galaxy, particularly its central bulge component, have been found (Magorrian et al. 1998; Ferrarese & Merritt 2000; Marconi & Hunt 2003; Häring & Rix 2004; Graham & Driver 2007; Savorgnan et al. 2013) and are seen as evidence of a co-evolution of black holes and their host galaxies. More recent studies have revealed galaxies that do not follow these relations: Kormendy et al. (2011) discuss that only “classical bulges” that formed from galaxy mergers show correlations with the SMBH, while disk-like “pseudobulges” that are forming by secular evolution do not. Other authors suggest that different formation processes (gaseous formation processes vs. dry merging) might become visible in differing SMBH-bulge scaling relations (Graham & Scott 2013; Scott et al. 2013). Furthermore, Läsker et al. (2014) claim that, provided there has been a thorough decomposition, the correlation between black hole mass and total host galaxy luminosity could be just as tight as the correlation between black hole mass and bulge luminosity.

Table 1

Comparison of the nearest Seyfert-1 galaxy NGC 3227, our source HE 1029-1831, and the nearest quasar 3C 273.

In our recent study (Busch et al. 2014), we have probed the MBH − Lbulge relation of low-luminosity type-1 quasi-stellar objects (LLQSOs). We performed a careful decomposition of K-band images with the Budda-code (de Souza et al. 2004; Gadotti 2008) and find that the bulges do not follow the published MBH − Lbulge relations for inactive galaxies of Marconi & Hunt (2003), Vika et al. (2012), Graham & Scott (2013), and Kormendy & Ho (2013). A deviation of type-1 active galactic nuclei (AGN) from the SMBH-bulge relations is in agreement with previous studies in the optical (Nelson et al. 2004; Kim et al. 2008; Bennert et al. 2011). Assuming that a SMBH-bulge relation traces a co-evolution, this could hint at a different evolution of inactive and active galaxies. On the other hand, a deviation from the relations of inactive galaxies could hint at different properties of active galaxies compared to inactive ones, caused by direct interaction through AGN feedback. Particularly, we discussed an undermassive black hole that is growing “toward” the relation or an overluminosity of the bulge produced by young and/or intermediate-age stellar populations. With the emergence of AO-assisted integral-field spectroscopy, many studies have been focused on the circumnuclear star formation properties in AGN (e.g., Zuther et al. 2007; Davies et al. 2007; Böker et al. 2008; Riffel et al. 2010). However, the impact on the bulge and overall host galaxy, and the interaction between central star formation and AGN feedback is still under discussion.

The LLQSO sample is a subsample of the Hamburg/ESO survey for bright UV-excess QSOs (Wisotzki et al. 2000) that contains only the 99 brightest and nearest QSOs with a redshift z ≤ 0.06. In many properties, such as redshift, gas masses, and luminosities, the LLQSO-sample lies between the NUGA sample (NUclei of GAlaxies; e.g., García-Burillo et al. 2003, 2005; Combes et al. 2004; Krips et al. 2007a) and the Palomar Green (PG) QSO sample. This connects the advantages of cosmological proximity and of higher spatial coverage. The first enables us to observe the processes in the centers of the galaxies in detail with high spatial resolution. The latter raises the probability of observing QSOs with high luminosity and accretion rate (Krips et al. 2007b; Bertram et al. 2007; Moser et al. 2012).

In Table 1, we compare the source HE 1029-1831 with NGC 3227, the nearest Seyfert-1 galaxy, and 3C 273, the nearest quasar. We see that the LLQSO has a much higher bolometric luminosity and accretion rate (traced by the Eddington ratio) than the nearby Seyfert galaxy. However, it is much closer than the next quasar, the resolution being better by a factor of four. Thus, LLQSOs form an ideal sample to study active galaxies with significant accretion activity at a resolution that is still good enough for detailed analysis.

Bertram et al. (2007) and Krips et al. (2007b) have observed 39 galaxies from the LLQSO sample in CO from which 27 have been detected. They report that most galaxies are rich in molecular gas, with a range of gas masses from 0.4 × 109 M⊙ to 9.7 × 109 M⊙. Furthermore, they find that the gas mass is correlated with the star formation and AGN activity as indicated by the far-infrared (FIR) luminosity. König et al. (2009) searched for 21 cm H i emission in these 27 CO-detected galaxies with the Effelsberg 100 m-telescope. They find neutral atomic gas masses ranging from 1.1 × 109 M⊙ to 3.8 × 1010 M⊙ but no strong correlation between gas mass and infrared emission that traces star formation and AGN activity. Fischer et al. (2006) have observed nine galaxies from the sample with the near-infrared (NIR) spectrograph ISAAC (VLT) and find that the spectra show signs for both AGN activity and star formation. In our NIR study (Busch et al. 2012, 2014), we find that the LLQSOs do not follow published MBH − Lbulge relations for inactive galaxies. A reason could be massive star formation in the circumnuclear regions. Integral-field spectroscopy with SINFONI is the preferred tool for examining the excitation mechanisms of emission lines, as well as the kinematics of gas and stars, in a spatially resolved way and learn about the properties of star formation and AGN in the centers of LLQSOs.

Since HE 1029-1831 shows strong CO(1–0) emission (Krips et al. 2007b, corresponding to a cold gas mass of ~ 1.2 × 1010 M⊙), it is an ideal object for a pilot study to demonstrate that with SINFONI we can successfully trace star formation regions, as well as hot molecular and ionized gas reservoirs also in LLQSOs, which are more distant than most of the previously analyzed objects (e.g., by the NUGA team).

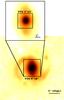thumbnail Fig. 1

ISAAC K-band image of HE1029-1831. The 8″ × 8″ and 3″ × 3″ FOVs of our SINFONI observations are marked. The image has been smoothed with a 3-pixel Gaussian and cleared from bad pixels.

Fischer et al. (2006) analyzed NIR JHK-images, as well as H + K-longslit spectra, of nine LLQSOs, including HE 1029-1831, obtained with ISAAC at the VLT. In Fig. 1, we see that HE 1029-1831 is a barred spiral galaxy with two prominent spiral arms. The bar has a length of about 8″ ≈ 6.4 kpc. In their spectra, they can separate the Paα line into broad and narrow components; the broad component has a full width at half maximum (FWHM) of 2081 km s-1. Furthermore, they find extended molecular hydrogen emission. Owing to the FWHM(Paα) of about 2000 km s-1, they classify HE 1029-1831 as a narrow-line Seyfert-1 galaxy (NLSy1). This is supported by Rodríguez-Ardila et al. (2000) using the name “CTS J04.08”, who find a FWHM(Hα) of 1870 km s-1 (but see discussion about NLSy1s in Valencia-S. et al. 2012b).

Krips et al. (2007b) observed HE 1029-1831 in the CO(1–0) and CO(2–1) line emission with the IRAM Plateau de Bure Interferometer and obtained a total gas mass of M(H2 + He) ≈ 8 × 109 M⊙. For the spatial extent of the emission, they find a FWHM of ≈(7 ± 2)″, which means that the observed CO emission comes from a region including the complete stellar bar. The H i mass has been measured from observations with the Effelsberg 100m-telescope and is (6.6 ± 0.6) × 109 M⊙ (König et al. 2009).

From optical line ratios, HE 1029-1831 is classified as a Seyfert 1.5 galaxy in the 12th catalog of quasars and AGN by Véron-Cetty & Véron (2006). Kewley et al. (2001) took optical spectra and determine the position of the galaxy in optical diagnostic diagrams (using the name IRAS 10295-1831). Depending on the diagram, the galaxy is classified as AGN, starburst, or composite. From this, we expect that in HE 1029-1831 contributions from both AGN and starburst are important.

In this paper, we present NIR integral-field spectroscopy of HE 1029-1831 with SINFONI. HE 1029-1831 is the first of a set of galaxies from the LLQSO sample that has been observed with SINFONI. From the 3D-spectroscopy, we aim to learn about the stellar and gas masses, as well as kinematics in LLQSOs. We determine reliable mass-to-light ratios and trace the star formation history in the centers of type-1 AGN.

The paper is organized as follows: in Sect. 2, we present the observations with SINFONI, as well as preceding observations with ISAAC (NIR image), and describe our reduction procedures. In Sect. 3, we describe our methods, that is the bulge-disk decomposition with Budda, emission line fitting, and stellar continuum subtraction with pPXF, and present the results. In Sect. 4, we discuss the results, particularly we estimate black hole masses, determine gas masses and gas excitation mechanisms, and discuss the impact of star formation. In Sect. 5, we give a short summary and conclusions.

Throughout this paper, we use a standard cosmology with H0 = 70 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7. At a redshift of z = 0.0404, this results in a luminosity distance of DL = 177 Mpc and a scale of 0.8 kpc /″.

2. Observation and data reduction

2.1. SINFONI integral-field spectroscopy

We present results of high-resolution NIR observations of HE 1029-1831 that have been carried out April 20–22, 2014 with SINFONI at the Unit Telescope 4 of the ESO Very Large Telescope in Chile (VLT, Eisenhauer et al. 2003; Bonnet et al. 2004).

We started the observations with the 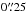\hbox{$0\farcs25$} plate scale, corresponding to a field-of-view (FOV) of 8″ × 8″ without adaptive optics. Then, we used the 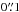\hbox{$0\farcs1$} plate scale with adaptive optics assistance, resulting in higher spatial resolution but with a smaller FOV of 3″ × 3″. We used the H + K grating providing a spectral resolution of RH + K = 1500. A TST... (T: target, S: sky) pattern with 150 s integration time each was used to produce sky-subtracted frames. Furthermore, a jitter pattern with offsets of ± 1″ for the 8″ × 8″-FOV and 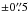\hbox{$\pm 0\farcs5$} for the 3″ × 3″-FOV was used to minimize the impact of dead pixels. The total integration time on source was 4500 s for the large and 3000 s for the small FOV, with additional 2250 s and 1500 s for sky observations. In between, telluric standards have been observed.

In the raw files, detector specific problems occured that we corrected following the procedure described in the appendix of Smajić et al. (2014). Then, we used the SINFONI pipeline for data reduction up to single-exposure-cube reconstruction. The alignment and final coaddition of the single-exposure-cubes has been performed with our own dpuser1 routines.

For the telluric correction, we used G2V stars that we have observed in between. A high-quality solar spectrum (Maiolino et al. 1996) that has been convolved down to the resolution of the telluric spectrum was used to correct the features of the G2V star. At the spectral edges and in the spectral region between H- and K-band, the solar spectrum had to be interpolated by a black body function with T = 5800 K.

The FWHM of the point spread function (PSP) was measured by fitting Gaussians to the telluric standard stars that are supposed to be point sources. We measure a FWHM of 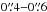\hbox{$0\farcs4{-}0\farcs6$} for the FOV of 8″ × 8″, which corresponds to linear scales of 320 − 500 pc. For the FOV of 3″ × 3″, we measure a FWHM of 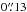\hbox{$0\farcs13$}, corresponding to 110 pc.

Calibration was done during the telluric correction. We summed up the counts of the telluric standard star within a radius of three times the FWHM of the PSF, centered on the peak position. The standard star counts at λ2.159 μm were taken as a reference for the science target. The magnitude of the standard star was taken from the 2MASS point source catalog (Skrutskie et al. 2006). In order to convert the 2MASS magnitude into a flux density, we use the Spitzer Science Center Magnitude to Flux Density converter2.

2.2. ISAAC K-band imaging

A K-band image of HE1029-1831, observed with ISAAC (Moorwood et al. 1998) at the VLT on April 20, 2003, is available in the ESO-archive. ISAAC provides a FOV of 152″ × 152″ with a pixelscale of 0.1484″/pixel. Four frames have been observed in a TSST jitter pattern with an exposure time of 2 s each. After subtracting the sky frames, the two frames have been shifted to a common reference frame and a mean image was created. Calibration was done using 2MASS magnitudes of foreground stars. For details on the data, see Fischer et al. (2006).

thumbnail Fig. 2

Decomposition of HE 1029-1831 with Budda. We show (from left to right) the original K-band ISAAC-image, the Budda-model, and the residuum obtained by division galaxy/model. Here, blue indicates that the original image has more flux than the model while red indicates that the model has more flux than the original image. In the lower row, we show an elliptically averaged radial profile of the galaxy, the single components, and the model. Next to it, we show the difference galaxy-model, ellipticity, and position angle.

3. Results

3.1. Bulge-disk decomposition

Parametric modeling of galaxy images is an important tool to disentangle the light of different galaxy components, such as bulge, disk, bar, AGN, to measure their structural parameters, and to determine light fractions of the galactic components. These values are essential for estimates of stellar masses and are used to establish relations e.g. between black hole mass and bulge luminosity.

In this work, we use Budda3 (Bulge/Disk Decomposition Analysis; de Souza et al. 2004; Gadotti 2008) for the two-dimensional decomposition of the K-band image.

To model the disk component, we use an exponential function 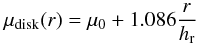μdisk(r)=μ0+1.086rhr\begin{equation} \mu_\mathrm{disk}(r) = \mu_0 + 1.086 \frac{r}{h_{\rm r}} \end{equation}(1)with central surface density μ0 and the characteristic scale-length hr (Freeman 1970).

Bulge and bar component are modeled by a Sérsic function μ(r)=μe+cn[(rre)1/n−1]\begin{equation} \mu(r) = \mu_{\rm e} + c_n \left[\left( \frac{r}{r_{\rm e}} \right)^{1/n} -1 \right] \end{equation}(2)with an effective radius re that is the radius that includes half of the light emitted by the respective component (“half-light radius”) and the effective surface brightness μe ≡ μ(re). n is the Sérsic index and cn = 2.5(0.868n − 0.142) is a parameter that depends on n (Sersic 1968; Caon et al. 1993).

The AGN component is modeled by a Moffat function with width fixed to that of the seeing PSF (measured by fitting Gaussian functions to point sources). The width is therefore kept fixed and only the peak intensity value is varied. Budda calculates the minimum valid count as the square root of the noise level. Here, the limiting surface brightness is μK = 21.5 mag arcsec-2. All pixels with count level below will be masked. Busch et al. (2014) give more details on the fitting process and limits of 2D-decomposition.

Figure 2 shows the results of the 2D-decomposition of HE 1029-1831: in the upper row, from left to right the original K-band image, the Budda model image, and a residual image. In the lower row, we show radial profiles that have been extracted using the Ellipse task of Iraf. In the fits of the model components, ellipticity and position angle have been fixed to the values of the original image.

The fit results in a bulge component with an effective radius of re = 0.59″ (= 0.47 kpc) and an apparent magnitude of mbulge = 12.69 (absolute magnitude: Mbulge = −23.57). The disk has a scale length of hr = 2.70″ (= 2.16 kpc) and a magnitude of mdisk = 13.04 (Mdisk = −23.22). The luminosity fractions are: 29% (bulge), 21% (disk), 22% (bar), and 28% (AGN).

The Sérsic index of the bulge is n = 1.2. A Sérsic index below 2 is indicative for a disk-like pseudobulge (Kormendy & Kennicutt 2004). However, on the one hand the Sérsic index should not be used as a sole indicator (Gadotti 2009) and on the other hand, since the central light distribution is heavily affected by the nuclear point source, it is almost impossible to determine the Sérsic index reliably.

thumbnail Fig. 3

Continuum emission map and typical spectra. In the upper panels we show the continuum emission around 2.2 μm in the 8″ × 8″ and the 3″ × 3″ FOV, in units of 10-18 W m-2μm-1. In the bottom panels, spectra extracted from three apertures with radius \hbox{$0\farcs15$} in the 3″ × 3″-FOV and from one aperture with radius \hbox{$0\farcs5$} in the 8″ × 8″-FOV that are marked in the continuum images are shown. The emission lines and the CO absorption band heads are marked in the spectra.

3.2. Emission-line fits

The spectra obtained with SINFONI show a big variety of emission lines. In the top right panel of Fig. 3, we mark three spots, the nuclear region, and two off-nuclear regions with a radius of 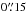\hbox{$0\farcs15$} each. Furthermore, we extract one spectrum from an aperture 2″ south of the nucleus (Fig. 3, top left). Here we chose a larger aperture with a radius of 0.5″ matching the lower spatial resolution in the 8″ × 8″ data set. The maps show the continuum emission around 2.2 μm from the SINFONI-cube, left for the 8″ × 8″ and right for the 3″ × 3″ FOV. In the lower panels, we show four spectra that are extracted from these regions. In the nuclear spectrum, broad line components and the coronal line [Si vi] are apparent, which indicate the presence of strong radiation from the central AGN. In the off-nuclear spectra, stellar features like the CO band heads become more prominent. Moreover, 3D-spectroscopy enables us to extract spectra and fit the emission lines in every spectral pixel (spaxel), which results in maps of the emission line fluxes.

thumbnail Fig. 4

Three examples for the fits applied to the cubes. The plots show the fits of the corresponding complex in the nuclear aperture.

Table 2

Emission-line fluxes for three positions, the center and two off-center spots. Apertures have a radius of 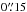\hbox{$0\farcs 15$}.

All emission lines have been fitted with a single Gaussian component plus zero-order polynomial. In case of the hydrogen recombination lines Paα and Brγ, a second component, accounting for the light emitted from the broad line region (BLR) was added. Emission lines that are close to each other (e.g., [Si vi] and H2λ1.96 μm) have been fitted simultaneously. Examples for these fits are displayed in Fig. 4. We use the python-implementation of mpfitexpr (Markwardt 2009). Errors of the fit parameters are calculated from the covariance matrix. For testing purposes, we also determined uncertainties by generating 100 Monte Carlo realizations of the input spectrum, adding Gaussian noise with a width corresponding to the standard deviation in a line-free region. Both methods deliver comparable results. If not noted otherwise, we clipped values in the maps with a relative error larger than 30%.

In Table 2, we present the flux measurements for the emission lines in three apertures of radius 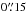\hbox{$0\farcs15$} each that are marked in the continuum image in Fig. 3.

Two strong hydrogen recombination lines were detected: Brγ and Paα. In the central region, both show two spectral components, a broad and a narrow one. The broad components show a FWHM of ≈2000 km s-1, indicative for a type-1 AGN. According to the unified model (e.g., Antonucci 1993; Urry & Padovani 1995), this emission stems from clouds very close (r ~ lightdays, see review of Peterson 1993) to the central SMBH, which are moving at high velocities.

HE 1029-1831 shows extended narrow emission in Brγ and Paα. In the Paα emission two spiral arms in the ionized gas emission are clearly visible (Fig. 5). Since Brγ is less strong, the arms are not as prominent (Fig. A.1). The AO-assisted 3″ × 3″-observations reveal a patchy ring in ionized gas emission of about 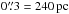\hbox{$0\farcs3=240\,\mathrm{pc}$} in radius and an ellipticity of ϵ = 0.29. This is in good agreement with the range of values that Böker et al. (2008) find in a SINFONI study of the circumnuclear starforming rings of five nearby spiral galaxies. At the points where the gas spirals meet the ring, the gas emission is particularly high. The [Fe ii]-emission does not peak in the center but in two off-nuclear regions that are identical with the two off-nuclear Paα/Brγ peaks (Fig. 6). Thus, we conclude that the strong circumnuclear gas emission does not mainly stem from the narrow-line region (NLR) but traces a circumnuclear star-formation region.

Furthermore, we see emission from the coronal line [Si vi]. We fit a Gaussian function to the spatial distribution and get a FWHM of 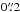\hbox{$0\farcs2$} for the 3″ × 3″-FOV and 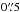\hbox{$0\farcs5$} for the 8″ × 8″ FOV. Coronal lines are forbidden transitions in the ground levels of highly ionized atoms that have ionization potentials above 100 eV. Thus, they are free of contribution from star formation and directly associated with the AGN. Müller Sánchez et al. (2006) argue that coronal line emission stems from the inner NLR and that they are probably associated with outflows. Recently, Müller-Sánchez et al. (2011) and Mazzalay et al. (2013a) observed extended emission in the coronal lines of NGC 1068, as well as a great complexity in the morphology and kinematics. This indicates that the nature of coronal line emission is far from being understood.

For the broad components of Paα and Brγ, we find a FWHM of 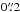\hbox{$0\farcs2$} for the 3″ × 3″-FOV and 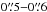\hbox{$0\farcs5{-}0\farcs6$} for the 8″ × 8″-FOV. For the 8″ × 8″ FOV, these values agree with the values derived from the telluric star observations in Sect. 2.1. For the 3″ × 3″-FOV, the values derived here are slightly higher. We claim that they are a more robust method to derive the spatial resolution since they are extracted from the analyzed data itself.

Several H2 molecular hydrogen emission lines are detected: H2(1–0)S(3) λ1.96 μm, H2(1–0)S(2) λ2.03 μm, H2(1–0)S(1) λ2.12 μm, H2(1–0)S(0) λ2.22 μm, and H2(2–1)S(1) λ2.25 μm. Other lines that are visible are He i, as well as several CO stellar absorption bands.

thumbnail Fig. 5

From left to right: flux and equivalent width of the narrow component of the hydrogen recombination line Paα. Upper row: FOV 8″ × 8″, lower row: FOV 3″ × 3″. The center of the continuum emission is marked by a ×.

thumbnail Fig. 6

From left to right: flux of H2(1–0)S(3) λ1.96 μm, H2(1–0)S(1) λ2.12 μm, and [Fe ii] λ1.64 μm. The center of the continuum emission is marked by a ×. The three apertures nucleus, spot1, and spot2 are marked as well.

thumbnail Fig. 7

Fit of the stellar kinematics of the K-band spectrum of HE 1029-1831. The radius of the aperture is r = 0.6″ = 470 pc, corresponding to the effective radius. The spectrum is shown in black, the best fitting combination of NIFS templates in red. Spectral regions that are contaminated by emission lines or telluric features are masked and are marked by the shaded areas. The residuum, shifted vertically for clarity, is shown in gray.

3.3. Stellar continuum

Under the assumption that the central bulge component is supported by random motion rather than ordered rotation, the stellar velocity dispersion can be used for virial mass estimates and black hole estimates via the MBH − σ∗ relation. To measure the stellar velocity dispersion σ∗, we fit stellar templates to the K-band spectrum that we integrated over an aperture corresponding to the effective radius measured in Sect. 3.1. We use the penalized pixel-fitting algorithm (pPXF, Cappellari & Emsellem 2004) and take stellar templates from the Gemini Spectral Library of Near-IR Late-Type Stellar Templates (Winge et al. 2009) which consists of 11 giant and supergiant stars with spectral classes from G8 to M5 that have been observed with the GEMINI integral-field spectrograph NIFS. The H + K grating of SINFONI has a spectral resolution of R = 1500 at a wavelength of around λ = 1.9 μm which we confirmed by measuring the width of OH-lines. The stellar templates have a different spectral resolution. Therefore, the templates had to be degraded down to the resolution of SINFONI first. Regions that contain emission lines or telluric features are masked. Figure 7 shows the best fit with a stellar velocity dispersion of σ∗ = (96 ± 12) km s-1. To test our results, we also use a set of theoretical spectra of red giant and supergiant stars from Lançon et al. (2007) and get a consistent result σ∗ = (111 ± 14) km s-1. In the following sections, we use a mean value of σ∗ = 104 km s-1. To estimate the uncertainties, we perform a Monte Carlo simulation. We generate 1000 spectra by adding Gaussian noise to the original spectrum. The width of the normal distribution of the noise is given by the standard deviation of the flux in a line-free region. The uncertainty is then given by the standard deviation of the 1000 fit results.

3.4. Extinction

Extinction can have a significant effect on the line fluxes. Therefore, we use hydrogen recombination line ratios to estimate the extinction. We follow the extinction law derived by Cardelli et al. (1989) to estimate the extinction in the NIR: 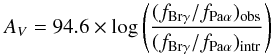AV=94.6×log((fBrγ/fPaα)obs(fBrγ/fPaα)intr)\begin{equation} A_V = 94.6 \times \log \left( \frac{ ( f_{\mathrm{Br}\gamma}/f_{\mathrm{Pa}\alpha} )_\mathrm{obs}}{( f_{\mathrm{Br}\gamma}/f_{\mathrm{Pa}\alpha} )_\mathrm{intr}} \right) \end{equation}(3)where (fBrγ/fPaα)obs is the observed line ratio between Brγ and Paα that is divided by the intrinsic line ratio (fBrγ/fPaα)intr = 0.083 taken from Osterbrock & Ferland (2006) assuming case B recombination with a typical electron density of ne = 104 cm-3 and a temperature T = 104 K. In the nuclear aperture, we measure an extinction of AV = 1.6 from the narrow lines. For the two other apertures, we get values of AV = 1.2 (spot 1) and AV = −1.6 (spot 2). The uncertainties of AV are up to 100%. Thus, we decide not to correct the NIR fluxes for extinction. However, we have to keep in mind that this introduces an error. In particular, ignoring an extinction of AV = 2 will cause a loss in flux of around 30%.

4. Discussion

4.1. The central black hole

The observed correlations between black hole mass and host galaxy properties imply that the evolution of the central SMBHs and their hosts might be connected to each other. Black hole masses are thus of great interest. From single epoch spectroscopy, we expect a black hole mass of around log (MBH/M⊙) = 7.3 − 7.4. We compare this mass to other mass estimates (Table 3) and find an Eddington ratio of λ ≈ 0.3, implying that the black hole is efficiently growing.

Table 3

Black hole mass estimates from different relations.

For 74 galaxies from the LLQSO sample, BH masses are available from Schulze et al. (2009), Schulze & Wisotzki (2010), and Schulze (priv. comm.). From single epoch spectroscopy, they compute BH masses using the scaling relation between BLR size and continuum luminosity (Bentz et al. 2009) 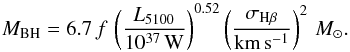MBH=6.7 f (L51001037 W)0.52(σHβkm s-1)2 M⊙.\begin{equation} M_\mathrm{BH} = 6.7\, f\, \left( \frac{L_{5100}}{10^{37}\,\mathrm{W}} \right)^{0.52} \left(\frac{\sigma_{\mathrm{H}\beta}}{\mathrm{km}\,\mathrm{s}^{-1}} \right)^2\, M_\odot . \end{equation}(4)We use their measurements for L5100 and σHβ and apply the recent scale factor f = 5.9 for active galaxies (Woo et al. 2013). The resulting black hole mass for HE 1029-1831 is log (MBH/M⊙) = 7.4.

Scharwächter et al. (in prep.) use QDeblend3D (Husemann et al. 2013, 2014) in order to deblend QSO and host galaxy emission in optical IFS-datacubes obtained with WIFES (Dopita et al. 2007, 2010) and estimate a black hole mass of log (MBH/M⊙) = 7.3 from L5100 and the FHWM of the broad Hβ component.

We derive the black hole mass from the broad Paα component following Kim et al. (2010)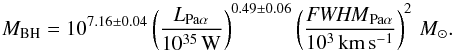MBH=107.16±0.04(LPaα1035 W)0.49±0.06(FWHMPaα103 km s-1)2 M⊙.\begin{equation} M_\mathrm{BH} = 10^{7.16\pm 0.04} \left( \frac{L_{\mathrm{Pa}\alpha}}{10^{35}\,\mathrm{W}} \right)^{0.49\pm 0.06} \left(\frac{\mathit{FWHM}_{\mathrm{Pa}\alpha}}{10^3\,\mathrm{km}\,\mathrm{s}^{-1}} \right)^2 \,M_\odot. \end{equation}(5)We measure a luminosity in the broad Paα component of LPaα,broad = 1.04 × 1034 W. With a broad line width of FWHM = 2150 km s-1, we get a black hole mass of log MBH = 7.3. However, because of the uncertainties discussed in Sect. 3.4, we did not correct for extinction. Extinction correction would result in a higher estimate.

The stellar velocity dispersion, derived from the stellar continuum fit in Sect. 3.3, can be used to estimate the black hole mass from the MBH − σ∗ relation. From the velocity dispersion σ∗ = 104 km s-1, we find the following estimates for log (MBH/M⊙): 7.0, 6.7, and 7.4 (using the relations of Gültekin et al. 2009; Graham et al. 2011; Kormendy & Ho 2013). Recently, Riffel et al. (2015) reported that the stellar velocity dispersion in spiral galaxies derived from CO  band heads in the NIR (σCO) and from the Calcium triplet in the optical (σopt) differ from each other significantly. In the above mentioned MBH − σ∗ relations, the optical velocity dispersion is assumed. For HE 1029–1831, we correct our NIR velocity dispersion using their best fit and derive a corresponding velocity dispersion of σopt = 134 km s-1 in the optical. This results in BH masses that are higher by a factor of ≈0.5 dex what is in good consistency with the black hole masses derived with other methods.

One has to note that the BH masses derived from the BH-mass scaling relations like the MBH − σ∗ relation are only estimations. The uncertainty will be high, at least 0.5 dex, since it includes measurement uncertainties but also the intrinsic scatter of the relations.

With the bulge magnitude Mbulge = −23.57 (Sect. 3.1), we can estimate the black hole mass that would be expected from MBH − Lbulge relations for inactive galaxies. The mass estimates log (MBH/M⊙) range from 8.0 to 8.4 (following Marconi & Hunt 2003; Vika et al. 2012; Graham & Scott 2013; Kormendy & Ho 2013). As observed previously for other LLQSOs, the measured black hole masses are lower by a factor of ≈1 dex than the black hole masses from the MBH − Lbulge relations of inactive galaxies. As discussed in Busch et al. (2014), this could be caused by overluminous host galaxies that contain young stellar populations or by black holes that are in a growing phase and still undermassive in comparison to their inactive counterparts.

The Eddington ratio is a measure of the accretion efficiency and is defined as λ ≡ Lbol/LEdd. The bolometric luminosity can be derived from the X-ray luminosity. The soft X-ray flux from ROSAT has been measured to be fsoft X − ray = (2.93 ± 0.49) × 10-15 W m-2 (Mahony et al. 2010), corresponding to a luminosity of Lsoft X − ray = (1.1 ± 0.2) × 1036 W. With a conversion factor of ≈50 (Hopkins et al. 2007), we get a bolometric luminosity of Lbol,X − ray = (6 ± 1) × 1037 W.

Another possibility is to derive the bolometric luminosity from the AGN continuum luminosity at 5100 Å. Scharwächter et al. (in prep.) subtract the host galaxy contribution using QDeblend3D and derive a flux of F5100 Å = 1.0 × 10-15 erg s-1 cm-2 Å-1. Using Lbol = fL × L5100 Å with fL = 9 following Kaspi et al. (2000), this results in a bolometric luminosity of Lbol = 1.9 × 1037 W.

The Eddington luminosity is given by LEdd ≅ 1.26 × 1031(MBH/M⊙) W. Thus, the range of black hole mass estimates of log (MBH) = (6.7 − 7.4) corresponds to Eddington luminosities LEdd = (6 − 32) × 1037 W. With the bolometric luminosities Lbol = (2 − 6) × 1037 W, we can estimate the Eddington ratio to be around λ = (0.06 − 1.0), with a mean of λ = 0.3. Although the range is very broad, we can point out that even the lowest possible Eddington ratio is high, indicating an actively accreting black hole, i.e. a central black hole in a phase of substantial growth.

4.2. Emission line excitation mechanisms

In our spectra, we observe a variety of emission lines, most of them originate from ionized or molecular hydrogen but also [Fe ii]. In recent 3D spectroscopy studies, it has been shown that the H2 and the [Fe ii] emitting gas often have different flux distributions and kinematics. We find that [Fe ii] and hydrogen recombination lines (Paα and Brγ) show similar distribution while H2 is more centrally distributed (see Figs. 5 and 6). The AGNIFS group interprets the distinct flux distributions and kinematics of molecular gas and [Fe ii] as an indication that molecular gas is rather a tracer of the feeding of the AGN while [Fe ii] is more likely a tracer of the feedback (e.g., Riffel et al. 2006, 2008; Riffel & Storchi-Bergmann 2011a,b).

Rotational and vibrational H2 emission lines are in particular the dominant way to cool warm molecular gas. Line ratios of these transitions and ionized hydrogen emission lines give important information on their excitation mechanisms (Davies et al. 2003, 2005). In the case of HE 1029-1831, they indicate a significant contribution of currently occuring star formation and/or young stellar populations in the central region.

In general, the H2 emission lines can be excited by two kinds of processes: (1) thermal processes, e.g. produced by X-ray (Maloney et al. 1996) or by shock heating (Hollenbach & McKee 1989) and (2) non-thermal processes like UV fluorescence (Black & van Dishoeck 1987): UV-photons with 912Å <λ< 1500Å are absorbed by the H2 molecule in the Lyman- and Werner bands, exciting the next two electronic levels (B1Σ − X1Σ and C1Π − X1Σ). With a probability of 90%, a decay into a bound but excited rovibrational level within the electronic ground level X1Σ will take place. By this mechanism, H2 rovibrational levels will be populated, which could not be populated by collisions. Possible sources are OB stars or strong AGN continuum emission.

thumbnail Fig. 8

Left: molecular hydrogen diagnostic diagram with 2–1S(1)/1–0S(1) vs. 1–0S(2)/1–0S(0) (Mouri 1994). Spot 1 and 2 are indicated by blue and red points. The location of thermal UV excitation (Sternberg & Dalgarno 1989) and non-thermal models (Black & van Dishoeck 1987), as well as the thermal emission curve from 1000 K to 3000 K, are plotted in gray. The X-ray heating models (Draine & Woods 1990) are marked by yellow triangles, the shock-heating model (Brand et al. 1989) by a green circle. Right: diagnostic diagram with line ratios 1–0S(1)λ2.121 μm/Brγ vs. [Fe ii]λ1.257 μm/Paβ (for details see text). The positions of three apertures are indicated by circles. Open symbols correspond to literature values from Larkin et al. (1998), Dale et al. (2004), and Rodríguez-Ardila et al. (2004, 2005). The lines indicate regions that are typically populated by starburst galaxies, AGNs, and LINERs resp. Dashed lines: Rodríguez-Ardila et al. (2005) and Riffel et al. (2010), dotted lines: Riffel et al. (2013).

Different excitation mechanisms can be discriminated by observing H2 line ratios. In particular, the H2 line ratio 2–1S(1)/ 1–0S(1) is useful to distinguish between thermal and non-thermal processes while H2 1–0S(2)/1–0S(0) can be used to distinguish between excitation by X-rays and by shocks. Figure 8 (left) shows the diagnostic diagram with the H2 line ratios 2–1S(1)/1–0S(1) vs. 1–0S(2)/1–0S(0) with the two chosen apertures in blue and red (see e.g., Mouri 1994; Zuther et al. 2007; Mazzalay et al. 2013b; Smajić et al. 2014; Falcón-Barroso et al. 2014). Furthermore, we indicate the positions of models for thermal UV excitation (Sternberg & Dalgarno 1989), UV fluorescence (Black & van Dishoeck 1987), X-ray heating (Draine & Woods 1990), shock-heating (Brand et al. 1989), and a thermal emission curve. The position in the diagram shows that the H2 excitation in the two apertures cannot be explained by thermal excitation alone. A significant contribution from UV fluorescence is necessary. This is in good consistency with star formation activity in the two spots. Previous studies show that in the case of AGN, collisional excitation, e.g. by interaction of the radio-jet with the circumnuclear interstellar medium, might be more important than the fluorescent process (Riffel et al. 2006, 2010). However, other studies see strong evidence that fluorescent excitation plays indeed a major role in the H2 excitation in ULIRGs (Davies et al. 2003) and AGNs (Davies et al. 2005), in concordance with our findings.

The rotational temperature can be determined from two ortho/para lines that belong to the same vibrational level, whereas the vibrational temperature can be determined by connecting two transitions with same J but from consecutive v levels: 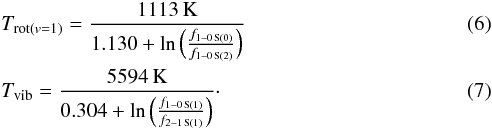Trot(v=1)=1113 K1.130+ln(f1−0 S(0)f1−0 S(2))Tvib=5594 K0.304+ln(f1−0 S(1)f2−1 S(1))·\begin{eqnarray} \label{eq:temprot}&&T_{\mathrm{rot}(v=1)} = \frac{1113\,\mathrm{K}}{1.130+\ln \left( \frac{f_\mathrm{1-0\, S(0)}}{f_\mathrm{1-0\, S(2)}} \right)} \\ \label{eq:tempvib} &&T_\mathrm{vib} = \frac{5594\,\mathrm{K}}{0.304+\ln \left( \frac{f_\mathrm{1-0\, S(1)}}{f_\mathrm{2-1\, S(1)}} \right)} \cdot \end{eqnarray}Using the flux measurements listed in Table 2, we estimate a rotational temperature of Trot = (1100 ± 300) K in spot 1 and Trot = (900 ± 200) K in spot 2. The vibrational temperature is Tvib(spot1) = (3700 ± 600) K and Tvib(spot2) = (3200 ± 500) K. In Fig. 8 (left), the rotational and vibrational temperatures are shown as right and upper axis.

In case of purely thermal emission, we expect the H2 molecules to be in local thermal equilibrium. In this case, Tvib ≈ Trot. In particular, Rodríguez-Ardila et al. (2005) and Riffel et al. (2013) show that star forming galaxies show Tvib ≳ Trot while AGNs and LINERs tend to have similar values for Tvib and Trot. In HE 1029-1831, the temperatures differ significantly from each other. This points at a significant contribution from the non-thermal process of UV-fluorescence, consistent with star formation in the circumnuclear region.

Further support for this hypothesis is given by the line ratios of log ([Fe ii] /Brγ) that are expected to be <0.3 for star formation regions (Alonso-Herrero et al. 1997). In our three apertures we find log ([Fe ii] /Brγ)nucl = 0.04, log ([Fe ii] /Brγ)spot1 = −0.01, and log ([Fe ii] /Brγ)spot2 = 0.05.

Rodríguez-Ardila et al. (2004, 2005) suggest a NIR diagnostic diagram with the line ratios log (H2(1 − 0)S(1)/Brγ) and log ([Fe ii] λ1.257 μm/Paβ). The diagnostic is supposed to distinguish between excitation from pure photoionization and from pure shocks and shows a transition from starburst galaxies to LINERS, passing AGNs where both excitation mechanisms are of importance (see also models by Dors et al. 2012). Since we are lacking J-band information, we use the conversion factors [Fe ii] λ1.644 μm/ [Fe ii] λ1.257 μm = 0.744 (Nussbaumer & Storey 1988) and Paα/ Paβ = 2.05 (Osterbrock & Ferland 2006). The line ratios [log (H2/ Brγ),log ( [Fe ii] /Paβ)] = [−0.32, −0.60] for the nuclear region, [−0.42, −0.66] for spot1, and [−0.30, −0.59] for spot2 are consistent with a mixture of starburst activity and AGN excitation (see Fig. 8 right). Previous studies (e.g., Riffel et al. 2010; Schönell et al. 2014) show that the centers of active galaxies often show line ratios characteristic of a mixture of starburst and AGN excitation.

4.3. Mass of ionized and molecular gas

A sufficient reservoir of gas is necessary to fuel star formation and black hole accretion. We show that the LLQSO HE 1029-1831 is rich in ionized and molecular gas.

We estimate the mass of ionized hydrogen as MH ii = mpneVH ii with the electron density ne and the volume VH ii of the emitting region. Using the line coefficients from Osterbrock & Ferland (2006), assuming an electron temperature of T = 104 K and a density in the range 102<ne< 104 cm-3, we can calculate the Paα flux as 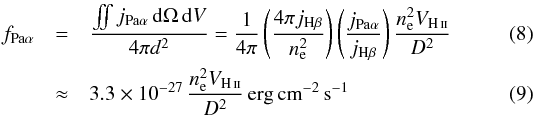fPaα=!jPaα dΩ dV4πd2=14π(4πjHβne2)(jPaαjHβ)ne2VH iiD2≈3.3×10-27 ne2VH iiD2 erg cm-2 s-1\begin{eqnarray} f_{\mathrm{Pa}\alpha} &=& \frac{\iint j_{\mathrm{Pa}\alpha}\,\mathrm{d}\Omega\,\mathrm{d}V}{4\pi d^2} = \frac{1}{4\pi} \left( \frac{4\pi j_{\mathrm{H}\beta}}{n_\mathrm{e}^2} \right) \left(\frac{j_{\mathrm{Pa}\alpha}}{j_{\mathrm{H}\beta}} \right) \frac{n_\mathrm{e}^2 V_\ion{H}{ii}}{D^2} \\ &\approx& 3.3\times 10^{-27}\, \frac{n_\mathrm{e}^2 V_\ion{H}{ii}}{D^2}\,\mathrm{erg}\,\mathrm{cm}^{-2}\,\mathrm{s}^{-1} \end{eqnarray}where D is the distance to the galaxy in cm. The ionized gas mass is then given by 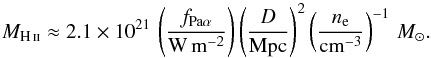MH ii≈2.1×1021 (fPaαW m-2)(DMpc)2(necm-3)-1 M⊙.\begin{equation} M_\ion{H}{ii} \approx 2.1\times 10^{21}\, \left(\frac{f_{\mathrm{Pa}\alpha}}{\mathrm{W}\,\mathrm{m}^{-2}} \right) \left(\frac{D}{\mathrm{Mpc}}\right)^2 \left(\frac{n_\mathrm{e}}{\mathrm{cm}^{-3}} \right)^{-1} \,M_\odot. \end{equation}(10)In an aperture with radius 4″, the flux in Paα is fPaα(r ≤ 4″) = 43 × 10-18 W m-2. Assuming an electron density of ne = 100 cm-3, this corresponds to a mass in ionized hydrogen of MH ii(r ≤ 4″) = 2.9 × 107 M⊙.

The mass of warm H2 can be estimated by 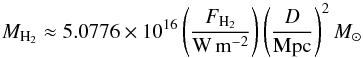MH2≈5.0776×1016(FH2W m-2)(DMpc)2M⊙\begin{equation} M_{\mathrm{H}_2} \approx 5.0776 \times 10^{16} \left( \frac{F_{\mathrm{H}_2}}{\mathrm{W}\,\mathrm{m}^{-2}} \right) \left( \frac{D}{\mathrm{Mpc}} \right)^2 M_\odot \end{equation}(11)following Scoville et al. (1982), Wolniewicz et al. (1998), and Riffel et al. (2010). In an aperture of radius 4″, we measure a H2(1–0)S(1) flux fH2 = 290 × 10-20 W m-2. This corresponds to a warm H2 gas mass of 4700 M⊙. We see that the mass of ionized gas is a factor of ≈6000 higher than the mass of warm molecular hydrogen. This is in good agreement with typical ratios that are of the order 103 − 104 (Riffel et al. 2014, and references therein). With the conversion factor of Mazzalay et al. (2013b), MH2(cold)/MH2(warm) = (0.3 − 1.6) × 106, we derive a cold gas mass of (1.4 − 7.5) × 109 M⊙. Other cold-to-warm H2 gas mass ratios have been found by Dale et al. (2005) (105 − 107) or Müller Sánchez et al. (2006) (2.5 × 106 with a 1σ uncertainty of a factor of 2) which result in cold gas masses that are consistent with our results.

Krips et al. (2007b) and Moser et al. (in prep.) derive the molecular gas mass from CO(1–0) measurements. They estimate masses of a few to several 109 M⊙, which is in good consistency with our results.

For NUGA sources, cold molecular gas masses have been calculated from CO-emission, ranging from 2 × 108 − 2 × 1010 M⊙ with typical masses of the order of several 109 M⊙ (Moser et al. 2012, and references therein). The AGNIFS group obtained masses in a range of 66 M⊙ ≤ MH2 ≤ 3300 M⊙ and 0.1 × 106 M⊙ ≤ MH ii ≤ 17 × 106 M⊙ in the nuclear regions of nearby galaxies (Riffel et al. 2008, 2009, 2010; Storchi-Bergmann et al. 2009; Schönell et al. 2014). We conclude that the LLQSO HE 1029-1831 has a large reservoir of cold molecular gas that is needed and apparently used for both star formation and black hole fueling.

4.4. The impact of star formation in the bulge

In our previous study (Busch et al. 2014), we found that the observed LLQSOs do not follow published MBH − Lbulge relations for inactive galaxies and speculated about the influence of young or intermediate-age stellar populations in the bulge lowering the mass-to-light ratio. Here, we estimate star formation rates (SFRs) and the dynamical mass of the bulge. Furthermore, we use the equivalent width of Brγ, the supernova rate (SNR), and the mass-to-light ratio as diagnostics to contrain possible star formation histories and estimate the impact of star formation in the bulge.

4.4.1. Star formation rates

Since dust grains absorb the radiation of young stars and re-radiate it in the FIR, the FIR luminosity LFIR is a tracer of star formation activity on 100–300 Myr timescales.

From the IRAS faint source catalog (Moshir et al. 1992), we calculate the FIR luminosity LFIR = 4π(DL/ Mpc)2 × 1.2 × 1031(2.58 f60 + f100) W = 4.9 × 1037 W, where fλ is the flux density at 60 μm and 100 μm resp. (Helou et al. 1988; Sanders & Mirabel 1996). With the calibration of Panuzzo et al. (2003), we estimate a global star formation rate of 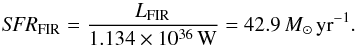SFRFIR=LFIR1.134×1036 W=42.9 M⊙ yr-1.\begin{equation} \mathit{SFR}_\mathrm{FIR} = \frac{L_\mathrm{FIR}}{1.134 \times 10^{36}\,\mathrm{W}} = 42.9\,M_\odot\,\mathrm{yr}^{-1}. \end{equation}(12)The FIR luminosity could be heavily affected by the AGN emission. Therefore, the star formation rate should only be taken as an upper limit.

Furthermore, we calculate the FIR colors log (f25/f12) = 0.47 ± 0.13, log (f60/f25) = 0.79 ± 0.05, log (f100/f25) = 0.95 ± 0.12, and log (f60/f12) = 1.26 ± 0.12. According to Dopita et al. (1998) and Kewley et al. (2000), these ratios are in the range of AGN with more than 90% contribution to the FIR luminosity from star formation. Together with SFRFIR calculated above, this implies that HE 1029-1831 is actively star forming.

With our high-resolution data, we can calculate current star formation rates in the spatially resolved nuclear regions. We use Brγ as a star formation indicator according to Panuzzo et al. (2003)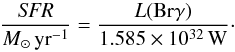SFRM⊙ yr-1=L(Brγ)1.585×1032 W·\begin{equation} \frac{\mathit{SFR}}{M_\odot\,\mathrm{yr}^{-1}} = \frac{L(\mathrm{Br}\gamma)}{1.585\times 10^{32}\,\mathrm{W}}\cdot \end{equation}(13)In the two off-nuclear spots, we measure SFRspot1 = 0.89 M⊙ yr-1 and SFRspot2 = 0.52 M⊙ yr-1. This corresponds to star formation rate densities of ΣSFR,spot1 = 19 M⊙ yr-1 kpc-2 and ΣSFR,spot2 = 12 M⊙ yr-1 kpc-2. Our aperture has a radius of 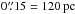\hbox{$0\farcs15 = 120\,\mathrm{pc}$}. Thus, our values are in agreement with the expected star formation rate densities in Seyfert galaxies of (1 − 50) M⊙ yr-1 kpc-2 on hundreds of parsecs scales and (50 − 500) M⊙ yr-1 kpc-2 on tens of parsecs scales (Valencia-S. et al. 2012a, and references therein).

Furthermore, we can compare the star formation rate densities to the gas mass densities (estimated from the hot molecular gas mass) and find log (Σgas,spot1/M⊙ pc-2) = 3.7 and log (Σgas,spot2/M⊙ pc-2) = 3.6. This means that the star formation regions follow the Schmidt law (Kennicutt 1998) and the high gas mass is efficiently transformed into stars.

4.4.2. Dynamical bulge mass

The combination of the image analysis that provides us with the effective radius and the kinematical analysis that provides us with the stellar velocity dispersion, allows us to calculate the dynamical mass of the central bulge component. Sani et al. (2011), following Cappellari et al. (2006), adopt 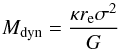Mdyn=κreσ2G\begin{equation} M_\mathrm{dyn} = \frac{\kappa r_{\rm e} \sigma^2}{G} \end{equation}(14)with κ = 5 to derive the dynamical mass in a bulge with effective radius re. With the values for re and σ derived in Sects. 3.1 and 3.3, this results in Mdyn = 6 × 109 M⊙.

thumbnail Fig. 9

Results from the Starburst99 simulations. Brγ equivalent width (left) and supernova rate (right) as a function of age for five star formation histories: instantaneous starburst (“fixed mass” in Starburst99), continuous star formation, and three exponentially decaying starbursts. The values derived from our data are shown in gray, blue and green.

From the H2 flux in an aperture with radius re, we can estimate the cold H2 gas mass in the bulge region (see Sect. 4.3). We multiply with 1.36 in order to allow for the contribution of Helium gas and obtain (1.0 − 4.9) × 109 M⊙. This corresponds to a gas fraction of 20% − 80%, depending on the warm-to-cold gas conversion factor applied. We subtract the gas mass from the derived dynamical mass to get an estimate for the stellar mass only: M∗ = (1.1 − 5.0) × 109 M⊙.

Several correlations between the black hole mass and the (stellar) bulge mass have been found in the last years. We use the dynamical bulge mass estimate to find the corresponding black hole mass: log (MBH/M⊙) = 6.0 − 7.5 (using the relations of Häring & Rix 2004; Sani et al. 2011; Scott et al. 2013; Kormendy & Ho 2013). Interestingly, these estimates agree well with the black hole masses derived in Sect. 4.1, in contrast to estimates from MBH − Lbulge relations. This can be interpreted as hint that the deviation of LLQSOs from the MBH − Lbulge relation observed in Busch et al. (2014) is – at least in the case of HE 1029-1831 – primarily caused by the higher luminosity of young stellar populations rather than a significantly undermassive black hole.

4.4.3. Star formation history

To follow this trace, we use Starburst99 (Leitherer et al. 1999; Vázquez & Leitherer 2005; Leitherer et al. 2010, 2014) to model the mass-to-light ratio (M∗/LK ratio), Brγ equivalent width, and supernova rate which can then be compared to observations (Davies et al. 2006, 2007; Levesque & Leitherer 2013). We show that the bulge is dominated by young/intermediate-age populations (~100 Myr) and find traces for a declining starburst ~200 Myr ago.

For the simulations, we use the Padova tracks with AGB stars at solar metallicity and a Kroupa initial mass function. We consider five different star formation histories: an instantaneous starburst, single starbursts with decay times of τSF = 10 Myr, 50 Myr, and 100 Myr, as well as continuous star formation. The decaying starbursts were simulated by adding up instantaneous starbursts scaled to exponentially decaying intensity with the respective time scales.

Brγ equivalent width

The equivalent width of the stellar Brγ emission is supposed to be a good estimator for the stellar age since it decreases monotonically with time (see Fig. 9, left). However, the measurement could be affected by the nonstellar AGN continuum. Davies et al. (2007) conclude that every stellar population that contains late-type stars should show an equivalent width of the stellar absorption feature CO(2–0) at λ2.29 μm of WCO(2 − 0) ≈ 12 Å independent of the star formation history and age with an uncertainty of about 20%. Thus, they suggest that the fraction of the stellar light, contaminated by nonstellar-AGN continuum, can be estimated by fstellar = Wobs/Wintr with the observed equivalent width of CO(2–0), Wobs, and the intrinsic Wintr = 12 Å.

We use the definitions of Origlia et al. (1993) and measure the absorption in the interval 2.2924 μm − 2.2977 μm and the continuum between 2.2880 μm − 2.2920 μm. This results in equivalent widths of CO(2–0) of WCO,nucl = 2.0 Å, WCO,spot1 = 7.1 Å, and WCO,spot2 = 9.6 Å, corresponding to stellar-light fractions of fstellar,nucl = 17%, fstellar,spot1 = 59%, and fstellar,spot2 = 80%. We measure the Brγ equivalent width in the three apertures. After correcting for the non-stellar contribution, we gain WBrγ,nucl,corr = (8.8 ± 1.2) Å, WBrγ,spot1,corr = (15.8 ± 0.5) Å, and WBrγ,spot2,corr = (9.6 ± 0.4) Å.

Supernova rate

The forbidden iron transition [Fe ii] λ1.644 μm is a good shock tracer. Since we see no indication for jets and outflows, we assume that the line is mainly excited by shocks from supernovae. The supernova rate can then be calculated SNRCal97=5.38 L[Fe ii]1035 W yr-1\begin{equation} \mathit{SNR}_\mathrm{Cal97} = 5.38 \, \frac{L_{[\ion{Fe}{ii}]}}{10^{35}\,\mathrm{W}}\,\mathrm{yr}^{-1} \end{equation}(15)following Calzetti (1997) or, following Alonso-Herrero et al. (2003), SNRAH03=8.08 L[Fe ii]1035 W yr-1.\begin{equation} \mathit{SNR}_\mathrm{AH03} = 8.08 \, \frac{L_{[\ion{Fe}{ii}]}}{10^{35}\,\mathrm{W}}\,\mathrm{yr}^{-1}. 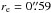\end{equation}(16)We measure the [Fe ii] emission in an aperture corresponding to the half-light radius \hbox{$r_{\rm e}=0\farcs59$} and get L[Fe ii] = 1.03 × 1033 W. This corresponds to supernova rates of SNRCal97 = 0.055 yr-1 and SNRAH03 = 0.083 yr-1. In Fig. 9 (right), we show the supernova rate divided by the stellar mass (normalized by 109 M⊙) as simulated by Starburst99. As bulge mass estimate, we use the dynamical mass derived above.

To estimate the stellar mass in the two spots, we assume that the bulge mass is smoothly distributed following a Sérsic law with the parameters derived in the bulge-disk decomposition. The mass fraction of the spots can then easily be estimated whereas we determine the supernova rate from the [Fe ii] flux in the apertures. The supernova rates in the two spots are SNR(spot1) = 0.007 − 0.010 yr-1 and SNR(spot2) = 0.005 − 0.008 yr-1. The supernova rates should be taken as upper limits only, since contamination from the AGN cannot be excluded.

thumbnail Fig. 10

K-band mass-to-light ratio as a function of the age of the stellar population, result from the Starburst99 simulations. The M∗/LK ratio range derived from the dynamical mass and the bulge-disk decomposition (see Sect. 4.4) is indicated in gray.

Mass-to-light ratio

Figure 10 shows that the ratio of the stellar mass to the K-band luminosity can be used as a diagnostic for the age of the stellar population for ages ≥107 yr-1 since it increases monotonically with time. However, two caveats have to be kept in mind: first, we cannot measure the stellar mass directly. Instead, we will take the dynamical mass corrected for the cold gas mass as an estimate. Second, the model assumes that only one stellar component is discussed. However, we expect to have a mixture of an old population (≈1010 yr) that could be mixed with one or more young populations that have been formed in later starbursts. The age estimate from the mass-to-light ratio can thus only be an upper limit for the young population. With the bulge mass Mbulge ≈ (1 − 5) × 109 M⊙ and the bulge magnitude Mbulge = −23.57 derived from the bulge-disk decomposition in Sect. 3.1, we derive a mass-to-light ratio of M∗/LK = 0.03 − 0.13.

The calculated ratios are presented in Figs. 9 and 10 together with the Starburst99 models. From these diagrams, immediate conclusions can be drawn: From the equivalent width of Brγ and the supernova rate, we can rule out an instantaneous starburst scenario for spots 1 and 2 since from WBrγ, we would estimate a starburst age of about 5–6 Myr but in this case the supernova rate should be much higher than observed. Continuous star formation is also rather inconsistent with our models: from WBrγ, we expect an age of around 800 Myr, while from the supernova rate the age would be around 200–500 Myr. The favored model is an exponentially decaying starburst with time scale τSF = 50 − 100 Myr that began 100–200 Myr ago.

For the overall bulge, we can again exclude an instantaneous starburst model from the supernova rates. The favored model for the two spots is consistent with supernova rates and the mass-to-light ratio for the overall bulge, indicating that the bulge is dominated by the star formation regions. However, continuous star formation that began around 500 Myr ago is also consistent with the data.

We conclude that we observe an intermediate-age stellar population with an age of around 100 Myr in the two spots that dominate the overall bulge emission. The star formation time scale is of the order of 50–100 Myr. This implies that the star formation is declining, in accordance with the derived current star formation rates that were high compared to quiescent galaxies but not as extraordinary as expected for a starburst galaxy, and with the high value derived from the FIR luminosity that is sensitive to star formation on timescales of 100–300 Myr. Furthermore, this is in good consistency with the finding of Davies et al. (2007) that AGNs accreting at lower efficiency (λ ≤ 0.1) have younger starbursts (≤50−100 Myr) while AGNs accreting at higher efficiency (λ ≥ 0.1) have older starbursts (≥50−100 Myr).

To conclude, the three diagnostics hint at star formation as an important factor in the central region of the LLQSO HE 1029-1831. Although the star formation activity has already reached its maximum more than 100 Myr ago, the effect is still visible: The presence of intermediate-age stellar population lowers the mass-to-light ratio by a factor of 10 compared to a bulge purely consisting of an old stellar population (see Fig. 10).

Interestingly, the dynamical mass estimate that was derived here is consistent with predictions from the MBH − Mbulge relations. Thus, at least in the particular case of HE 1029-1831, we conclude that the observed offset of LLQSOs from the MBH − Lbulge relations for inactive galaxies is caused by recent star formation activity in the central region.

An alternative explanation is the presence of a pseudo-bulge which is supported by the low Sérsic index. Pseudo-bulges are thought not to evolve from galaxy mergers but from secular evolution, therefore not obeying the relations of classical bulges and ellipticals (Kormendy & Kennicutt 2004, and references therein). Other authors suggest that there exist two relations for two different formation mechanisms (gaseous formation mechanism and dry mergers, Graham & Scott 2013), meaning that the replacement from the linear scaling relation is not necessarily caused by undermassive black holes or overluminous bulges but by different formation processes. In particular, the MBH − Lbulge relation for galaxies which originate from gaseous formation mechanisms has a large scatter. Within this scatter, our galaxy might follow the relation. However, in our previous study (Busch et al. 2014) with 11 objects, we show that LLQSOs (like HE 1029-1831) are systematically shifted from the Graham & Scott-relation to the right.

We emphasize that both explanations are not inconsistent with our findings since in both scenarios the central component (“pseudo-bulge” or “Sérsic spheroid”) is expected to be rich in gas and to contain younger stellar populations than classical (dry) bulges.

5. Summary and conclusions

We have observed the inner 6.4 kpc of the low-luminosity QSO HE 1029-1831 without AO and the inner 2.4 kpc at a resolution of 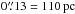\hbox{$0\farcs13=110\,\mathrm{pc}$} with AO, using the integral-field spectrograph SINFONI mounted at the VLT UT4 in Paranal. The main results of our analysis are the following:

  • The H ii emission shows a different fluxdistribution than the stellar continuum. Two gas spiral arms arelocated within the stellar bar. At smaller scales, a patchycircumnuclear ring is seen.

  • The flux distribution of the shock tracer [Fe ii] follows the H ii insofar as the emission is strongest in the points where the gas spiral arms meet the ring. Diagnostic line ratios as e.g. log (H2/ Brγ), log ([Fe ii] /Brγ), or molecular hydrogen line ratios are indicative for star formation regions.

  • The mass of ionized hydrogen in the inner 3.2 kpc is MH ii = 2.9 × 107 M⊙. The mass of cold molecular hydrogen within 3.2 kpc is MH2,cold = (1.4 − 7.5) × 109 M⊙. This is in good agreement with H2-mass estimates from CO measurements and comparable to gas masses derived for NUGA galaxies. We conclude that HE 1029-1831 has a massive reservoir of gas that is available for star formation and AGN fueling.

  • A bulge-disk decomposition with Budda reveals that the bulge luminosity does not follow published MBH − Lbulge relations for inactive galaxies. This is expected for LLQSOs (Busch et al. 2014). The dynamical mass of the bulge, however, is in good agreement with common MBH − Mbulge relations.

  • From the M∗/LK ratio and diagnostics like the Brγ equivalent width and the supernova rate, we find evidence of the presence of young/intermediate-age stellar populations in the circumnuclear region. The favored model is an exponentially decaying starburst with time scale 50–100 Myr that began around 100–200 Myr ago. The light of the bulge component is dominated by this intermediate-age stellar population.

We conclude that circumnuclear star formation is a crucial factor in HE 1029-1831 that has to be taken into account for any thorough analysis (see also, e.g., Jahnke et al. 2004; Cid Fernandes et al. 2004). We find evidence that, at least in the case of HE 1029-1831, the offset from the MBH − Lbulge relations can be explained by an overluminosity of the bulge component due to stellar populations that are younger than commonly observed in bulges.

As pointed out in Sect. 4.1, the Eddington ratio (λ ≳ 0.06) is high, meaning that the black hole is in a growing phase. Though, since the black hole mass and – at least the dynamical – mass obey published MBH − Mbulge relations, from our data it seems rather unlikely that the offset from the MBH − Lbulge relation is caused by a significantly undermassive black hole that would grow “toward” the MBH − Lbulge relation.

With a larger sample of LLQSOs that have high-resolution data, in spatial and spectral dimension, we will be able to further investigate the star-formation properties in the circumnuclear regions.

Acknowledgments

The authors thank the anonymous referee for the helpful report. G. Busch thanks Marcus Bremer for many fruitful discussions. This work was supported in part by the Deutsche Forschungsgemeinschaft (DFG) via SFB 956. G. Busch is member of the Bonn-Cologne Graduate School of Physics and Astronomy (BCGS). S. Smajić is member of the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics Bonn/Cologne. J. Scharwächter acknowledges the European Research Council for the Advanced Grant Program Number 267399-Momentum. M. Valencia-S. received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 312789.

References

  1. Alonso-Herrero, A., Rieke, M. J., Rieke, G. H., & Ruiz, M. 1997, ApJ, 482, 747 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., & Kelly, D. M. 2003, AJ, 125, 1210 [NASA ADS] [CrossRef] [Google Scholar]
  3. Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
  4. Bennert, V. N., Auger, M. W., Treu, T., Woo, J.-H., & Malkan, M. A. 2011, ApJ, 726, 59 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bentz, M. C., Peterson, B. M., Netzer, H., Pogge, R. W., & Vestergaard, M. 2009, ApJ, 697, 160 [Google Scholar]
  6. Bertram, T., Eckart, A., Fischer, S., et al. 2007, A&A, 470, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Black, J. H., & van Dishoeck, E. F. 1987, ApJ, 322, 412 [NASA ADS] [CrossRef] [Google Scholar]
  8. Böker, T., Falcón-Barroso, J., Schinnerer, E., Knapen, J. H., & Ryder, S. 2008, AJ, 135, 479 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bonnet, H., Abuter, R., Baker, A., et al. 2004, The Messenger, 117, 17 [NASA ADS] [Google Scholar]
  10. Brand, P. W. J. L., Toner, M. P., Geballe, T. R., et al. 1989, MNRAS, 236, 929 [NASA ADS] [CrossRef] [Google Scholar]
  11. Busch, G., Zuther, J., Valencia-S., M., Moser, L., & Eckart, A. 2012, in Proc. Nuclei of Seyfert galaxies and QSOs – Central engine & conditions of star formation, PoS(Seyfert 2012)060 [Google Scholar]
  12. Busch, G., Zuther, J., Valencia-S. M., et al. 2014, A&A, 561, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Calzetti, D. 1997, AJ, 113, 162 [NASA ADS] [CrossRef] [Google Scholar]
  14. Caon, N., Capaccioli, M., & D’Onofrio, M. 1993, MNRAS, 265, 1013 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cappellari, M., Bacon, R., Bureau, M., et al. 2006, MNRAS, 366, 1126 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cid Fernandes, R., Gu, Q., Melnick, J., et al. 2004, MNRAS, 355, 273 [NASA ADS] [CrossRef] [Google Scholar]
  19. Combes, F., García-Burillo, S., Boone, F., et al. 2004, A&A, 414, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Dale, D. A., Roussel, H., Contursi, A., et al. 2004, ApJ, 601, 813 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dale, D. A., Sheth, K., Helou, G., Regan, M. W., & Hüttemeister, S. 2005, AJ, 129, 2197 [NASA ADS] [CrossRef] [Google Scholar]
  22. Davies, R. I., Sternberg, A., Lehnert, M., & Tacconi-Garman, L. E. 2003, ApJ, 597, 907 [NASA ADS] [CrossRef] [Google Scholar]
  23. Davies, R. I., Sternberg, A., Lehnert, M. D., & Tacconi-Garman, L. E. 2005, ApJ, 633, 105 [NASA ADS] [CrossRef] [Google Scholar]
  24. Davies, R. I., Thomas, J., Genzel, R., et al. 2006, ApJ, 646, 754 [NASA ADS] [CrossRef] [Google Scholar]
  25. Davies, R. I., Müller Sánchez, F., Genzel, R., et al. 2007, ApJ, 671, 1388 [NASA ADS] [CrossRef] [Google Scholar]
  26. de Souza, R. E., Gadotti, D. A., & dos Anjos, S. 2004, ApJS, 153, 411 [NASA ADS] [CrossRef] [Google Scholar]
  27. Dopita, M. A., Heisler, C., Lumsden, S., & Bailey, J. 1998, ApJ, 498, 570 [NASA ADS] [CrossRef] [Google Scholar]
  28. Dopita, M., Hart, J., McGregor, P., et al. 2007, Ap&SS, 310, 255 [NASA ADS] [CrossRef] [Google Scholar]
  29. Dopita, M., Rhee, J., Farage, C., et al. 2010, Ap&SS, 327, 245 [NASA ADS] [CrossRef] [Google Scholar]
  30. Dors, Jr. O. L.,, Riffel, R. A., Cardaci, M. V., et al. 2012, MNRAS, 422, 252 [NASA ADS] [CrossRef] [Google Scholar]
  31. Draine, B. T., & Woods, D. T. 1990, ApJ, 363, 464 [NASA ADS] [CrossRef] [Google Scholar]
  32. Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1548 [Google Scholar]
  33. Falcón-Barroso, J., Ramos Almeida, C., Böker, T., et al. 2014, MNRAS, 438, 329 [NASA ADS] [CrossRef] [Google Scholar]
  34. Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
  35. Fischer, S., Iserlohe, C., Zuther, J., et al. 2006, A&A, 452, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] [Google Scholar]
  37. Gadotti, D. A. 2008, MNRAS, 384, 420 [NASA ADS] [CrossRef] [Google Scholar]
  38. Gadotti, D. A. 2009, MNRAS, 393, 1531 [NASA ADS] [CrossRef] [Google Scholar]
  39. García-Burillo, S., Combes, F., Hunt, L. K., et al. 2003, A&A, 407, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. García-Burillo, S., Combes, F., Schinnerer, E., Boone, F., & Hunt, L. K. 2005, A&A, 441, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Graham, A. W., & Driver, S. P. 2007, ApJ, 655, 77 [NASA ADS] [CrossRef] [Google Scholar]
  42. Graham, A. W., & Scott, N. 2013, ApJ, 764, 151 [NASA ADS] [CrossRef] [Google Scholar]
  43. Graham, A. W., Onken, C. A., Athanassoula, E., & Combes, F. 2011, MNRAS, 412, 2211 [NASA ADS] [CrossRef] [Google Scholar]
  44. Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
  45. Häring, N., & Rix, H.-W. 2004, ApJ, 604, L89 [NASA ADS] [CrossRef] [Google Scholar]
  46. Helou, G., Khan, I. R., Malek, L., & Boehmer, L. 1988, ApJS, 68, 151 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hollenbach, D., & McKee, C. F. 1989, ApJ, 342, 306 [NASA ADS] [CrossRef] [Google Scholar]
  48. Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef] [Google Scholar]
  49. Husemann, B., Wisotzki, L., Sánchez, S. F., & Jahnke, K. 2013, A&A, 549, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Husemann, B., Jahnke, K., Sánchez, S. F., et al. 2014, MNRAS, 443, 755 [NASA ADS] [CrossRef] [Google Scholar]
  51. Jahnke, K., Kuhlbrodt, B., & Wisotzki, L. 2004, MNRAS, 352, 399 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
  53. Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
  54. Kewley, L. J., Heisler, C. A., Dopita, M. A., et al. 2000, ApJ, 530, 704 [NASA ADS] [CrossRef] [Google Scholar]
  55. Kewley, L. J., Heisler, C. A., Dopita, M. A., & Lumsden, S. 2001, ApJS, 132, 37 [NASA ADS] [CrossRef] [Google Scholar]
  56. Kim, M., Ho, L. C., Peng, C. Y., et al. 2008, ApJ, 687, 767 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kim, D., Im, M., & Kim, M. 2010, ApJ, 724, 386 [NASA ADS] [CrossRef] [Google Scholar]
  58. König, S., Eckart, A., García-Marín, M., & Huchtmeier, W. K. 2009, A&A, 507, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
  60. Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
  61. Kormendy, J., Bender, R., & Cornell, M. E. 2011, Nature, 469, 374 [NASA ADS] [CrossRef] [Google Scholar]
  62. Krips, M., Eckart, A., Krichbaum, T. P., et al. 2007a, A&A, 464, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Krips, M., Eckart, A., Neri, R., et al. 2007b, A&A, 464, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Lançon, A., Hauschildt, P. H., Ladjal, D., & Mouhcine, M. 2007, A&A, 468, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Larkin, J. E., Armus, L., Knop, R. A., Soifer, B. T., & Matthews, K. 1998, ApJS, 114, 59 [NASA ADS] [CrossRef] [Google Scholar]
  66. Läsker, R., Ferrarese, L., van de Ven, G., & Shankar, F. 2014, ApJ, 780, 70 [NASA ADS] [CrossRef] [Google Scholar]
  67. Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
  68. Leitherer, C., Ortiz Otálvaro, P. A., Bresolin, F., et al. 2010, ApJS, 189, 309 [NASA ADS] [CrossRef] [Google Scholar]
  69. Leitherer, C., Ekström, S., Meynet, G., et al. 2014, ApJS, 212, 14 [NASA ADS] [CrossRef] [Google Scholar]
  70. Levesque, E. M., & Leitherer, C. 2013, ApJ, 779, 170 [NASA ADS] [CrossRef] [Google Scholar]
  71. Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
  72. Mahony, E. K., Croom, S. M., Boyle, B. J., et al. 2010, MNRAS, 401, 1151 [NASA ADS] [CrossRef] [Google Scholar]
  73. Maiolino, R., Rieke, G. H., & Rieke, M. J. 1996, AJ, 111, 537 [NASA ADS] [CrossRef] [Google Scholar]
  74. Maloney, P. R., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 466, 561 [NASA ADS] [CrossRef] [Google Scholar]
  75. Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
  76. Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
  77. Mazzalay, X., Rodríguez-Ardila, A., Komossa, S., & McGregor, P. J. 2013a, MNRAS, 430, 2411 [NASA ADS] [CrossRef] [Google Scholar]
  78. Mazzalay, X., Saglia, R. P., Erwin, P., et al. 2013b, MNRAS, 428, 2389 [NASA ADS] [CrossRef] [Google Scholar]
  79. Moorwood, A., Cuby, J.-G., Biereichel, P., et al. 1998, The Messenger, 94, 7 [NASA ADS] [Google Scholar]
  80. Moser, L., Zuther, J., Busch, G., Valencia-S., M., & Eckart, A. 2012, in Proc. Nuclei of Seyfert galaxies and QSOs – Central engine & conditions of star formation, PoS(Seyfert 2012)069 [Google Scholar]
  81. Moshir, M., Kopman, G., & Conrow, T. A. O. 1992, IRAS Faint Source Survey, Explanatory supplement version 2 (California Institute of Technology) [Google Scholar]
  82. Mouri, H. 1994, ApJ, 427, 777 [NASA ADS] [CrossRef] [Google Scholar]
  83. Müller Sánchez, F., Davies, R. I., Eisenhauer, F., et al. 2006, A&A, 454, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Müller-Sánchez, F., Prieto, M. A., Hicks, E. K. S., et al. 2011, ApJ, 739, 69 [NASA ADS] [CrossRef] [Google Scholar]
  85. Nelson, C. H., Green, R. F., Bower, G., Gebhardt, K., & Weistrop, D. 2004, ApJ, 615, 652 [NASA ADS] [CrossRef] [Google Scholar]
  86. Nussbaumer, H., & Storey, P. J. 1988, A&A, 193, 327 [NASA ADS] [Google Scholar]
  87. Origlia, L., Moorwood, A. F. M., & Oliva, E. 1993, A&A, 280, 536 [NASA ADS] [Google Scholar]
  88. Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei (University Science Books) [Google Scholar]
  89. Panuzzo, P., Bressan, A., Granato, G. L., Silva, L., & Danese, L. 2003, A&A, 409, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Peterson, B. M. 1993, PASP, 105, 247 [NASA ADS] [CrossRef] [Google Scholar]
  91. Riffel, R. A., & Storchi-Bergmann, T. 2011a, MNRAS, 411, 469 [NASA ADS] [CrossRef] [Google Scholar]
  92. Riffel, R. A., & Storchi-Bergmann, T. 2011b, MNRAS, 417, 2752 [NASA ADS] [CrossRef] [Google Scholar]
  93. Riffel, R. A., Storchi-Bergmann, T., Winge, C., & Barbosa, F. K. B. 2006, MNRAS, 373, 2 [NASA ADS] [CrossRef] [Google Scholar]
  94. Riffel, R. A., Storchi-Bergmann, T., Winge, C., et al. 2008, MNRAS, 385, 1129 [NASA ADS] [CrossRef] [Google Scholar]
  95. Riffel, R. A., Storchi-Bergmann, T., Dors, O. L., & Winge, C. 2009, MNRAS, 393, 783 [NASA ADS] [CrossRef] [Google Scholar]
  96. Riffel, R. A., Storchi-Bergmann, T., & Nagar, N. M. 2010, MNRAS, 404, 166 [NASA ADS] [Google Scholar]
  97. Riffel, R., Rodríguez-Ardila, A., Aleman, I., et al. 2013, MNRAS, 430, 2002 [NASA ADS] [CrossRef] [Google Scholar]
  98. Riffel, R. A., Vale, T. B., Storchi-Bergmann, T., & McGregor, P. J. 2014, MNRAS, 442, 656 [NASA ADS] [CrossRef] [Google Scholar]
  99. Riffel, R. A., Ho, L. C., Mason, R., et al. 2015, MNRAS, 446, 2823 [NASA ADS] [CrossRef] [Google Scholar]
  100. Rodríguez-Ardila, A., Pastoriza, M. G., & Donzelli, C. J. 2000, ApJS, 126, 63 [NASA ADS] [CrossRef] [Google Scholar]
  101. Rodríguez-Ardila, A., Pastoriza, M. G., Viegas, S., Sigut, T. A. A., & Pradhan, A. K. 2004, A&A, 425, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Rodríguez-Ardila, A., Riffel, R., & Pastoriza, M. G. 2005, MNRAS, 364, 1041 [NASA ADS] [CrossRef] [Google Scholar]
  103. Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
  104. Sani, E., Marconi, A., Hunt, L. K., & Risaliti, G. 2011, MNRAS, 413, 1479 [NASA ADS] [CrossRef] [Google Scholar]
  105. Savorgnan, G., Graham, A. W., Marconi, A., et al. 2013, MNRAS, 434, 387 [NASA ADS] [CrossRef] [Google Scholar]
  106. Schönell, A. J., Riffel, R. A., Storchi-Bergmann, T., & Winge, C. 2014, MNRAS, 445, 414 [NASA ADS] [CrossRef] [Google Scholar]
  107. Schulze, A., & Wisotzki, L. 2010, A&A, 516, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Schulze, A., Wisotzki, L., & Husemann, B. 2009, A&A, 507, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Scott, N., Graham, A. W., & Schombert, J. 2013, ApJ, 768, 76 [NASA ADS] [CrossRef] [Google Scholar]
  110. Scoville, N. Z., Hall, D. N. B., Ridgway, S. T., & Kleinmann, S. G. 1982, ApJ, 253, 136 [NASA ADS] [CrossRef] [Google Scholar]
  111. Sersic, J. L. 1968, Atlas de galaxias australes (Cordoba: Observatorio de Universidad de Cordoba) [Google Scholar]
  112. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  113. Smajić, S., Moser, L., Eckart, A., et al. 2014, A&A, 567, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Sternberg, A., & Dalgarno, A. 1989, ApJ, 338, 197 [NASA ADS] [CrossRef] [Google Scholar]
  115. Storchi-Bergmann, T., McGregor, P. J., Riffel, R. A., et al. 2009, MNRAS, 394, 1148 [NASA ADS] [CrossRef] [Google Scholar]
  116. Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
  117. Valencia-S., M., Zuther, J., Eckart, A., et al. 2012a, A&A, 544, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Valencia-S., M., Zuther, J., Eckart, A., et al. 2012b, in Proc. Nuclei of Seyfert galaxies and QSOs – Central engine & conditions of star formation, PoS(Seyfert 2012)017 [Google Scholar]
  119. Vázquez, G. A., & Leitherer, C. 2005, ApJ, 621, 695 [NASA ADS] [CrossRef] [Google Scholar]
  120. Véron-Cetty, M.-P., & Véron, P. 2006, A&A, 455, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  121. Vika, M., Driver, S. P., Cameron, E., Kelvin, L., & Robotham, A. 2012, MNRAS, 419, 2264 [NASA ADS] [CrossRef] [Google Scholar]
  122. Winge, C., Riffel, R. A., & Storchi-Bergmann, T. 2009, ApJS, 185, 186 [NASA ADS] [CrossRef] [Google Scholar]
  123. Wisotzki, L., Christlieb, N., Bade, N., et al. 2000, A&A, 358, 77 [NASA ADS] [Google Scholar]
  124. Wolniewicz, L., Simbotin, I., & Dalgarno, A. 1998, ApJS, 115, 293 [NASA ADS] [CrossRef] [Google Scholar]
  125. Woo, J.-H., & Urry, C. M. 2002, ApJ, 579, 530 [NASA ADS] [CrossRef] [Google Scholar]
  126. Woo, J.-H., Schulze, A., Park, D., et al. 2013, ApJ, 772, 49 [NASA ADS] [CrossRef] [Google Scholar]
  127. Zuther, J., Iserlohe, C., Pott, J.-U., et al. 2007, A&A, 466, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A

thumbnail Fig. A.1

Same as Fig. 5 but for Brγ.

All Tables

Table 1

Comparison of the nearest Seyfert-1 galaxy NGC 3227, our source HE 1029-1831, and the nearest quasar 3C 273.

In the text
Table 2

Emission-line fluxes for three positions, the center and two off-center spots. Apertures have a radius of \hbox{$0\farcs 15$}.

In the text
Table 3

Black hole mass estimates from different relations.

In the text

All Figures

thumbnail Fig. 1

ISAAC K-band image of HE1029-1831. The 8″ × 8″ and 3″ × 3″ FOVs of our SINFONI observations are marked. The image has been smoothed with a 3-pixel Gaussian and cleared from bad pixels.
In the text
thumbnail Fig. 2

Decomposition of HE 1029-1831 with Budda. We show (from left to right) the original K-band ISAAC-image, the Budda-model, and the residuum obtained by division galaxy/model. Here, blue indicates that the original image has more flux than the model while red indicates that the model has more flux than the original image. In the lower row, we show an elliptically averaged radial profile of the galaxy, the single components, and the model. Next to it, we show the difference galaxy-model, ellipticity, and position angle.
In the text
thumbnail Fig. 3

Continuum emission map and typical spectra. In the upper panels we show the continuum emission around 2.2 μm in the 8″ × 8″ and the 3″ × 3″ FOV, in units of 10-18 W m-2μm-1. In the bottom panels, spectra extracted from three apertures with radius \hbox{$0\farcs15$} in the 3″ × 3″-FOV and from one aperture with radius \hbox{$0\farcs5$} in the 8″ × 8″-FOV that are marked in the continuum images are shown. The emission lines and the CO absorption band heads are marked in the spectra.
In the text
thumbnail Fig. 4

Three examples for the fits applied to the cubes. The plots show the fits of the corresponding complex in the nuclear aperture.
In the text
thumbnail Fig. 5

From left to right: flux and equivalent width of the narrow component of the hydrogen recombination line Paα. Upper row: FOV 8″ × 8″, lower row: FOV 3″ × 3″. The center of the continuum emission is marked by a ×.
In the text
thumbnail Fig. 6

From left to right: flux of H2(1–0)S(3) λ1.96 μm, H2(1–0)S(1) λ2.12 μm, and [Fe ii] λ1.64 μm. The center of the continuum emission is marked by a ×. The three apertures nucleus, spot1, and spot2 are marked as well.
In the text
thumbnail Fig. 7

Fit of the stellar kinematics of the K-band spectrum of HE 1029-1831. The radius of the aperture is r = 0.6″ = 470 pc, corresponding to the effective radius. The spectrum is shown in black, the best fitting combination of NIFS templates in red. Spectral regions that are contaminated by emission lines or telluric features are masked and are marked by the shaded areas. The residuum, shifted vertically for clarity, is shown in gray.
In the text
thumbnail Fig. 8

Left: molecular hydrogen diagnostic diagram with 2–1S(1)/1–0S(1) vs. 1–0S(2)/1–0S(0) (Mouri 1994). Spot 1 and 2 are indicated by blue and red points. The location of thermal UV excitation (Sternberg & Dalgarno 1989) and non-thermal models (Black & van Dishoeck 1987), as well as the thermal emission curve from 1000 K to 3000 K, are plotted in gray. The X-ray heating models (Draine & Woods 1990) are marked by yellow triangles, the shock-heating model (Brand et al. 1989) by a green circle. Right: diagnostic diagram with line ratios 1–0S(1)λ2.121 μm/Brγ vs. [Fe ii]λ1.257 μm/Paβ (for details see text). The positions of three apertures are indicated by circles. Open symbols correspond to literature values from Larkin et al. (1998), Dale et al. (2004), and Rodríguez-Ardila et al. (2004, 2005). The lines indicate regions that are typically populated by starburst galaxies, AGNs, and LINERs resp. Dashed lines: Rodríguez-Ardila et al. (2005) and Riffel et al. (2010), dotted lines: Riffel et al. (2013).
In the text
thumbnail Fig. 9

Results from the Starburst99 simulations. Brγ equivalent width (left) and supernova rate (right) as a function of age for five star formation histories: instantaneous starburst (“fixed mass” in Starburst99), continuous star formation, and three exponentially decaying starbursts. The values derived from our data are shown in gray, blue and green.
In the text
thumbnail Fig. 10

K-band mass-to-light ratio as a function of the age of the stellar population, result from the Starburst99 simulations. The M∗/LK ratio range derived from the dynamical mass and the bulge-disk decomposition (see Sect. 4.4) is indicated in gray.
In the text
thumbnail Fig. A.1

Same as Fig. 5 but for Brγ.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.